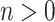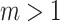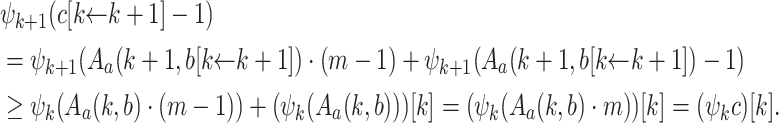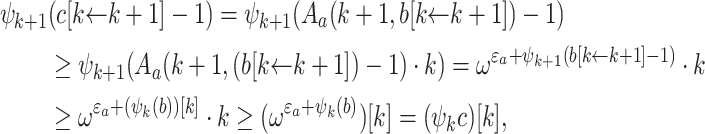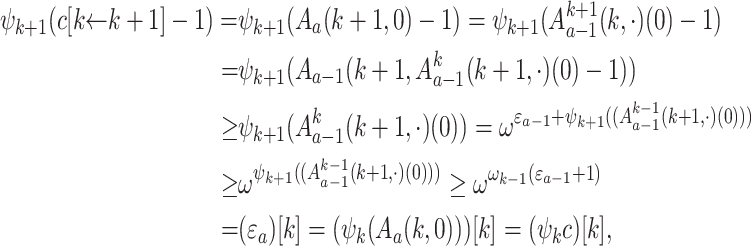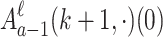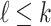Abstract
The original Goodstein process proceeds by writing natural numbers in nested exponential k-normal form, then successively raising the base to  and subtracting one from the end result. Such sequences always reach zero, but this fact is unprovable in Peano arithmetic. In this paper we instead consider notations for natural numbers based on the Ackermann function. We define two new Goodstein processes, obtaining new independence results for
and subtracting one from the end result. Such sequences always reach zero, but this fact is unprovable in Peano arithmetic. In this paper we instead consider notations for natural numbers based on the Ackermann function. We define two new Goodstein processes, obtaining new independence results for  and
and 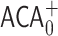 , theories of second order arithmetic related to the existence of Turing jumps.
, theories of second order arithmetic related to the existence of Turing jumps.
Keywords: Goodstein sequences, Independence proofs, Ordinal notation systems
Introduction
Goodstein’s principle [6] is arguably the oldest example of a purely number-theoretic statement known to be independent of  , as it does not require the coding of metamathematical notions such as Gödel’s provability predicate [4]. The proof proceeds by transfinite induction up to the ordinal
, as it does not require the coding of metamathematical notions such as Gödel’s provability predicate [4]. The proof proceeds by transfinite induction up to the ordinal 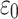 [5].
[5].  does not prove such transfinite induction, and indeed Kirby and Paris later showed that Goodstein’s principle is unprovable in
does not prove such transfinite induction, and indeed Kirby and Paris later showed that Goodstein’s principle is unprovable in 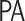 [8].
[8].
Goodstein’s original principle involves the termination of certain sequences of numbers. Say that m is in nested (exponential) base-k normal form if it is written in standard exponential base k, with each exponent written in turn in base k. Thus for example, 20 would become 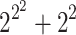 in nested base-2 normal form. Then, define a sequence
in nested base-2 normal form. Then, define a sequence 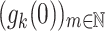 by setting
by setting 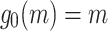 and defining
and defining 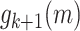 recursively by writing
recursively by writing 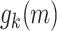 in nested base-
in nested base-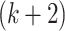 normal form, replacing every occurrence of
normal form, replacing every occurrence of 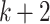 by
by  , then subtracting one (unless
, then subtracting one (unless  , in which case
, in which case 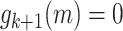 ).
).
In the case that  , we obtain
, we obtain
 |
and so forth. At first glance, these numbers seem to grow superexponentially. It should thus be a surprise that, as Goodstein showed, for every m there is  for which
for which  .
.
By coding finite Goodstein sequences as natural numbers in a standard way, Goodstein’s principle can be formalized in the language of arithmetic, but this formalized statement is unprovable in  . Independence can be shown by proving that the Goodstein process takes at least as long as stepping down the fundamental sequences below
. Independence can be shown by proving that the Goodstein process takes at least as long as stepping down the fundamental sequences below 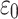 ; these are canonical sequences
; these are canonical sequences  such that
such that 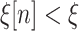 for all
for all  and for limit
and for limit  ,
, 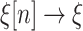 as
as 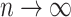 . For standard fundamental sequences below
. For standard fundamental sequences below 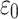 ,
, 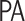 does not prove that the sequence
does not prove that the sequence  is finite.
is finite.
Exponential notation is not suitable for writing very big numbers (e.g. Graham’s number [7]), in which case it may be convenient to use systems of notation which employ faster-growing functions. In [2], T. Arai, S. Wainer and the authors have shown that the Ackermann function may be used to write natural numbers, giving rise to a new Goodstein process which is independent of the theory 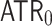 of arithmetical transfinite recursion; this is a theory in the language of second order arithmetic which is much more powerful than
of arithmetical transfinite recursion; this is a theory in the language of second order arithmetic which is much more powerful than 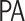 . The main axiom of
. The main axiom of 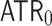 states that for any set X and ordinal
states that for any set X and ordinal  , the
, the 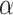 -Turing jump of X exists; we refer the reader to [13] for details.
-Turing jump of X exists; we refer the reader to [13] for details.
The idea is, for each 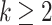 , to define a notion of Ackermannian normal form for each
, to define a notion of Ackermannian normal form for each 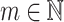 . Having done this, we can define Ackermannian Goodstein sequences analogously to Goodstein’s original version. The normal forms used in [2] are defined using an elaborate ‘sandwiching’ procedure first introduced in [14], approximating a number m by successive branches of the Ackermann function. In this paper, we consider simpler, and arguably more intuitive, normal forms, also based on the Ackermann function. We show that these give rise to two different Goodstein-like processes, independent of
. Having done this, we can define Ackermannian Goodstein sequences analogously to Goodstein’s original version. The normal forms used in [2] are defined using an elaborate ‘sandwiching’ procedure first introduced in [14], approximating a number m by successive branches of the Ackermann function. In this paper, we consider simpler, and arguably more intuitive, normal forms, also based on the Ackermann function. We show that these give rise to two different Goodstein-like processes, independent of  and
and 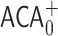 , respectively. As was the case for
, respectively. As was the case for 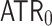 , these are theories of second order arithmetic which state that certain Turing jumps exist.
, these are theories of second order arithmetic which state that certain Turing jumps exist. 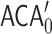 asserts that, for all
asserts that, for all 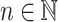 and
and 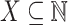 , the n-Turing jump of X exists, while
, the n-Turing jump of X exists, while 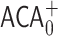 asserts that its
asserts that its  -jump exists; see [13] for details. The proof-theoretic ordinal of
-jump exists; see [13] for details. The proof-theoretic ordinal of  is
is  [1], and that of
[1], and that of 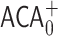 is
is  [9]; we will briefly review these ordinals later in the text, but refer the reader to standard texts such as [10, 12] for a more detailed treatment of proof-theoretic ordinals.
[9]; we will briefly review these ordinals later in the text, but refer the reader to standard texts such as [10, 12] for a more detailed treatment of proof-theoretic ordinals.
Basic Definitions
Let us fix 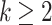 and agree on the following version of the Ackermann function.
and agree on the following version of the Ackermann function.
Definition 1
For 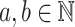 we define
we define  by the following recursion.
by the following recursion.
 ,
, ,
,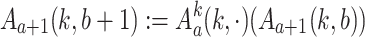 .
.
Here, the notation  refers to the k-fold composition of the function
refers to the k-fold composition of the function 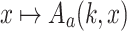 . It is well known that for every fixed a, the function
. It is well known that for every fixed a, the function 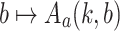 is primitive recursive and the function
is primitive recursive and the function 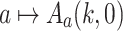 is not primitive recursive. We use the Ackermann function to define k normal forms for natural numbers. These normal forms emerged from discussions with Toshiyasu Arai and Stan Wainer, which finally led to the definition of a more powerful normal form defined in [14] and used to prove termination in [2].
is not primitive recursive. We use the Ackermann function to define k normal forms for natural numbers. These normal forms emerged from discussions with Toshiyasu Arai and Stan Wainer, which finally led to the definition of a more powerful normal form defined in [14] and used to prove termination in [2].
Lemma 1
Let  . For all
. For all 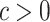 , there exist unique
, there exist unique  such that
such that ![]()
We write  in this case. This means that we have in mind an underlying context fixed by k and that for the number c we have uniquely associated the numbers a, b, m, n. Note that it could be possible that
in this case. This means that we have in mind an underlying context fixed by k and that for the number c we have uniquely associated the numbers a, b, m, n. Note that it could be possible that  , so that we have to choose the right representation for the context; in this case, item 2 guarantees that a is chosen to take the maximal possible value.
, so that we have to choose the right representation for the context; in this case, item 2 guarantees that a is chosen to take the maximal possible value.
By rewriting iteratively b and n in such a normal form, we arrive at the Ackermann k-normal form of c. If we also rewrite a iteratively, we arrive at the nested Ackermann k-normal form of c. The following properties of normal forms are not hard to prove from the definitions.
Lemma 2
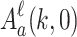 is in k-normal form for every
is in k-normal form for every  such that
such that 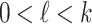 .
.if
 is in k-normal form, then for every
is in k-normal form, then for every  , the number
, the number  is also in k-normal form.
is also in k-normal form.
In the sequel we work with standard notations for ordinals. We use the function 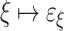 to enumerate the fixed points of
to enumerate the fixed points of  . With
. With  we denote the binary Veblen function, where
we denote the binary Veblen function, where  enumerates the common fixed points of all
enumerates the common fixed points of all 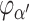 with
with  . We often omit parentheses and simply write
. We often omit parentheses and simply write 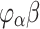 . Then
. Then 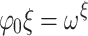 ,
, 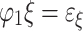 ,
, 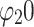 is the first fixed point of the function
is the first fixed point of the function  ,
,  is the first common fixed point of the function
is the first common fixed point of the function  , and
, and 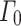 is the first ordinal closed under
is the first ordinal closed under 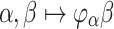 . In fact, not much ordinal theory is presumed in this article; we almost exclusively work with ordinals less than
. In fact, not much ordinal theory is presumed in this article; we almost exclusively work with ordinals less than 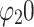 , which can be written in terms of addition and the functions
, which can be written in terms of addition and the functions 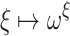 ,
, 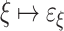 . For more details, we refer the reader to standard texts such as [10, 12].
. For more details, we refer the reader to standard texts such as [10, 12].
Goodstein Sequences for 
In this section we define a Goodstein process that is independent of  . We do so by working with unnested Ackermannian normal forms. Such normal forms give rise to the following notion of base change.
. We do so by working with unnested Ackermannian normal forms. Such normal forms give rise to the following notion of base change.
Definition 2
Given 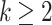 and
and 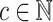 , define
, define 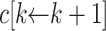 by:
by:
 .
.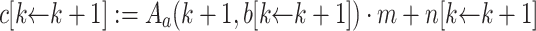 if
if 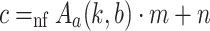 .
.
With this, we may define a new Goodstein process, based on unnested Ackermannian normal forms.
Definition 3
Let 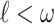 . Put
. Put  Assume recursively that
Assume recursively that  is defined and
is defined and 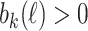 . Then
. Then 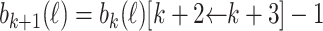 . If
. If 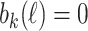 , then
, then 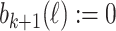 .
.
We will show that for every  there is i with
there is i with  . In order to prove this, we first establish some natural properties of the base-change operation.
. In order to prove this, we first establish some natural properties of the base-change operation.
Lemma 3
Fix 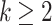 and let
and let 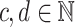 . Then:
. Then:
 .
.If
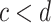 , then
, then  .
.
Proof
The first assertion is proved by induction on c. It clearly holds for 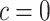 . If
. If 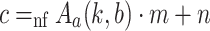 then the induction hypothesis yields
then the induction hypothesis yields 
The second assertion is harder to prove. The proof is by induction on d with a subsidiary induction on c. The assertion is clear if  . Let
. Let  and
and  . We distinguish cases according to the position of a relative to
. We distinguish cases according to the position of a relative to  , the position of b relative to
, the position of b relative to 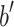 , etc.
, etc.
-
Case 1 (
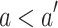 ). We sub-divide into two cases.
). We sub-divide into two cases.- Case 1.1 (
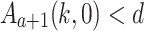 ). Then, the induction hypothesis applied to
). Then, the induction hypothesis applied to 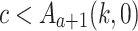 yields
yields 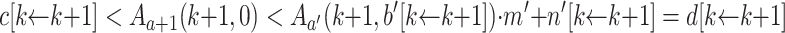 .
. - Case 1.2 (
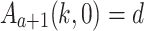 ). In this case,
). In this case,  ,
,  ,
,  , and
, and 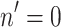 . We have
. We have  . For
. For 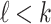 we have that
we have that  is in k-normal form by Lemma 2. Thus the induction hypothesis yields
is in k-normal form by Lemma 2. Thus the induction hypothesis yields 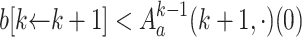 . The number
. The number  is in k-normal form and so the induction hypothesis applied to
is in k-normal form and so the induction hypothesis applied to  yields
yields  . Moreover we have that
. Moreover we have that  . This yields
. This yields
where the second inequality follows from
and the last from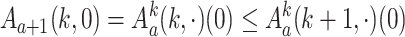
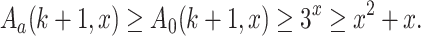
1
Case 2 (
 ). This case does not occur since then
). This case does not occur since then 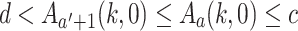 .
.-
Case 3 (
 and
and 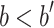 ). The induction hypothesis yields
). The induction hypothesis yields 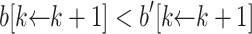 and
and 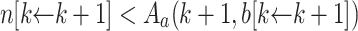 . Now, consider two sub-cases.
. Now, consider two sub-cases.- Case 3.1 (
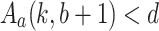 ). Since d is in k-normal form and
). Since d is in k-normal form and 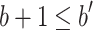 we see that
we see that  is in k-normal form by Lemma 2. Then, the induction hypothesis yields
is in k-normal form by Lemma 2. Then, the induction hypothesis yields  .
. -
Case 3.2 (
 ). We know that
). We know that  . Consider two further sub-cases.
. Consider two further sub-cases.- Case 3.2.1 (
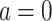 ). This means that
). This means that  ,
, 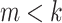 , and
, and  , where d has k-normal form
, where d has k-normal form  . The induction hypothesis yields
. The induction hypothesis yields 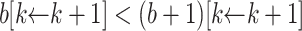 and
and  . We then have that
. We then have that 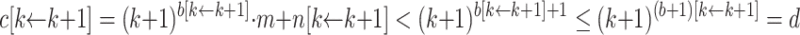 .
. - Case 3.2.2 (
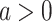 ). Then,
). Then,
where the second inequality uses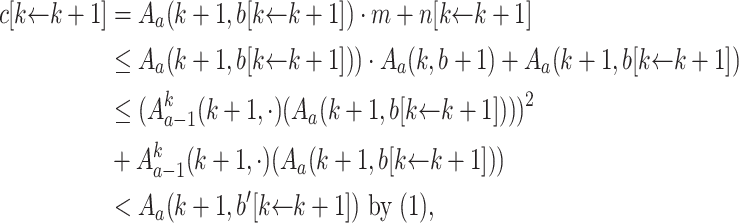
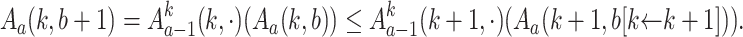
Case 4 (
 and
and  ). This case does not appear since otherwise
). This case does not appear since otherwise  .
.- Case 5 (
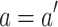 and
and 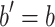 and
and  ). Then the induction hypothesis yields
). Then the induction hypothesis yields 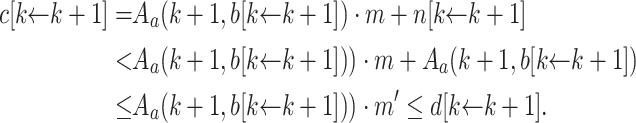
Case 6 (
 and
and 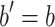 and
and 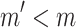 ). This case is not possible given the assumptions.
). This case is not possible given the assumptions.- Case 7 (
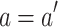 and
and  and
and 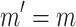 ). Then
). Then  and the induction hypothesis yields
and the induction hypothesis yields 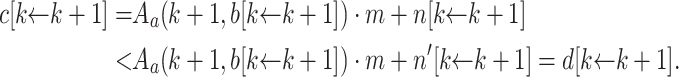
Thus, the base-change operation is monotone. Next we see that it also preserves normal forms.
Lemma 4
If  is in k-normal form, then
is in k-normal form, then 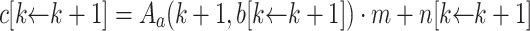 is in
is in 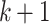 normal form.
normal form.
Proof
Assume that 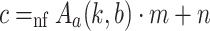 . Then,
. Then,  ,
, 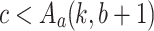 , and
, and 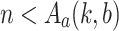 . Clearly,
. Clearly,  . By Lemma 2,
. By Lemma 2,  is in k-normal form, so that by Lemma 3,
is in k-normal form, so that by Lemma 3,  yields
yields 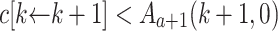 . Since
. Since 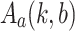 is in k-normal form, Lemma 3 yields
is in k-normal form, Lemma 3 yields  . It remains to check that we also have
. It remains to check that we also have 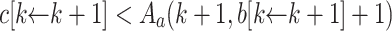 .
.
If 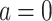 , then
, then  means that
means that 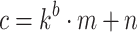 with
with 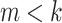 and
and 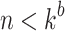 . Then,
. Then,  and
and 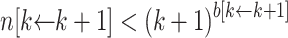 . Thus
. Thus  and thus
and thus 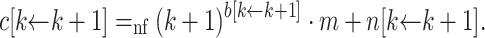 In the remaining case, we have for
In the remaining case, we have for 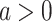 that
that
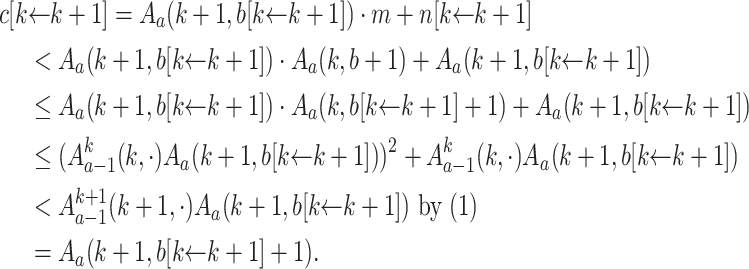 |
So 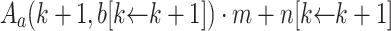 is in
is in 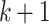 -normal form.
-normal form.
These Ackermannian normal forms give rise to a new Goodstein process. In order to prove that this process is terminating, we must assign ordinals to natural numbers, in such a way that the process gives rise to a decreasing (hence finite) sequence. For each k, we define a function 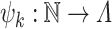 , where
, where  is a suitable ordinal, in such a way that
is a suitable ordinal, in such a way that  is computed from the k-normal form of m. Unnested Ackermannian normal forms correspond to ordinals below
is computed from the k-normal form of m. Unnested Ackermannian normal forms correspond to ordinals below  , as the following map shows.
, as the following map shows.
Definition 4
For 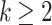 , define
, define  as follows:
as follows:
 .
.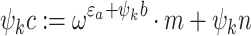 if
if 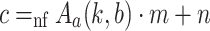 .
.
Lemma 5
If 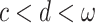 then
then 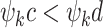 .
.
Proof
Proof by induction on d with subsidiary induction on c. The assertion is clear if  . Let
. Let  and
and 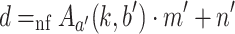 . We distinguish cases according to the position of a relative to
. We distinguish cases according to the position of a relative to  , the position of b relative to
, the position of b relative to  , etc.
, etc.
Case 1 (
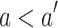 ). We have
). We have 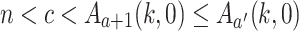 and, since
and, since 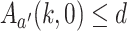 , the induction hypothesis yields
, the induction hypothesis yields 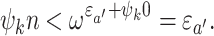 We have
We have  and the induction hypothesis yields
and the induction hypothesis yields 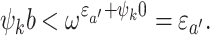 It follows that
It follows that  , hence
, hence 
Case 2 (
 ). This case is not possible since this would imply that
). This case is not possible since this would imply that 
-
Case 3 (
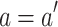 ). We consider several sub-cases.
). We consider several sub-cases.- Case 3.1 (
 ). The induction hypothesis yields
). The induction hypothesis yields  . Hence
. Hence 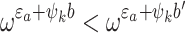 . We have
. We have 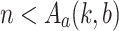 , and the subsidiary induction hypothesis yields
, and the subsidiary induction hypothesis yields 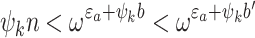 . Putting things together we see
. Putting things together we see 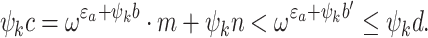
- Case 3.2 (
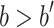 ). This case is not possible since this would imply
). This case is not possible since this would imply  .
. -
Case 3.3 (
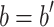 ). This case is divided into further sub-cases.
). This case is divided into further sub-cases.- Case 3.3.1 (
 ). We have
). We have 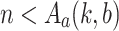 and the subsidiary induction hypothesis yields
and the subsidiary induction hypothesis yields 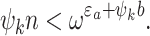 Hence
Hence 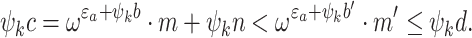
- Case 3.3.2 (
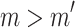 ). This case is not possible since this would imply
). This case is not possible since this would imply 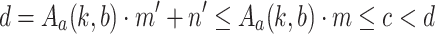 .
. - Case 3.3.3 (
 ). The inequality
). The inequality  yields
yields  and the induction hypothesis yields
and the induction hypothesis yields  . Hence
. Hence  .
.
Our ordinal assignment is invariant under base change, in the following sense.
Lemma 6
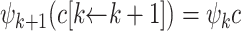 .
.
Proof
Proof by induction on c. The assertion is clear for 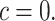 Let
Let 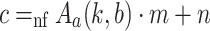 . Then,
. Then, 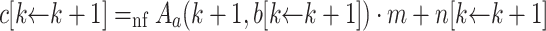 , and the induction hypothesis yields
, and the induction hypothesis yields
 |
It is well-known that the so-called slow-growing hierarchy at level  matches up with the Ackermann function, so one might expect that the corresponding Goodstein process can be proved terminating in
matches up with the Ackermann function, so one might expect that the corresponding Goodstein process can be proved terminating in  . This is true but, somewhat surprisingly, much less is needed here. We can lower
. This is true but, somewhat surprisingly, much less is needed here. We can lower  to
to 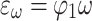 .
.
Theorem 1
For all  , there exists a
, there exists a  such that
such that 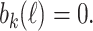 This is provable in
This is provable in  .
.
Proof
Define  If
If  , then, by the previous lemmata,
, then, by the previous lemmata,
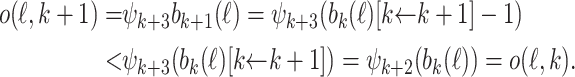 |
Since 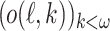 cannot be an infinite decreasing sequence of ordinals, there must be some k with
cannot be an infinite decreasing sequence of ordinals, there must be some k with 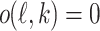 , yielding
, yielding  .
.
Now we are going to show that for every 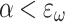 ,
,  This will require some work with fundamental sequences.
This will require some work with fundamental sequences.
Definition 1
Let 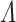 be an ordinal. A system of fundamental sequences on
be an ordinal. A system of fundamental sequences on
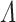 is a function
is a function  such that
such that 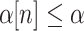 with equality holding if and only if
with equality holding if and only if  , and
, and  whenever
whenever 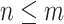 . The system of fundamental sequences is convergent if
. The system of fundamental sequences is convergent if  whenever
whenever 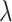 is a limit, and has the Bachmann property if whenever
is a limit, and has the Bachmann property if whenever 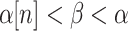 , it follows that
, it follows that  .
.
It is clear that if  is an ordinal then for every
is an ordinal then for every  there is n such that
there is n such that  , but this fact is not always provable in weak theories. The Bachmann property that will be useful due to the following.
, but this fact is not always provable in weak theories. The Bachmann property that will be useful due to the following.
Proposition 1
Let  be an ordinal with a system of fundamental sequences satisfying the Bachmann property, and let
be an ordinal with a system of fundamental sequences satisfying the Bachmann property, and let 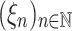 be a sequence of elements of
be a sequence of elements of 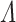 such that, for all n,
such that, for all n,  . Then, for all n,
. Then, for all n,  .
.
Proof
Let 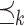 be the reflexive transitive closure of
be the reflexive transitive closure of  . We need a few properties of these orderings. Clearly, if
. We need a few properties of these orderings. Clearly, if 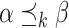 , then
, then 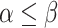 . It can be checked by a simple induction and the Bachmann property that, if
. It can be checked by a simple induction and the Bachmann property that, if  , then
, then  . Moreover,
. Moreover,  is monotone in the sense that if
is monotone in the sense that if  , then
, then 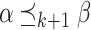 , and if
, and if  , then
, then  (see, e.g., [11] for details).
(see, e.g., [11] for details).
We claim that for all n, 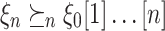 , from which the desired inequality immediately follows. For the base case, we use the fact that
, from which the desired inequality immediately follows. For the base case, we use the fact that 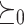 is transitive by definition. For the successor, note that the induction hypothesis yields
is transitive by definition. For the successor, note that the induction hypothesis yields  , hence
, hence  . Then, consider three cases.
. Then, consider three cases.
Case 1 (
 ). By transitivity and monotonicity,
). By transitivity and monotonicity,  yields
yields  .
.Case 2 (
 ). Then,
). Then, 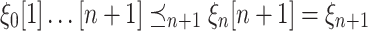 .
.Case 3 (
 ). The Bachmann property yields
). The Bachmann property yields 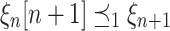 , and since
, and since 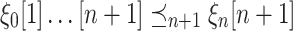 , monotinicity and transitivity yield
, monotinicity and transitivity yield  .
.
Let 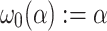 and
and 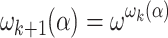 . Let us define the standard fundamental sequences for ordinals less than
. Let us define the standard fundamental sequences for ordinals less than  as follows.
as follows.
If
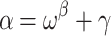 with
with 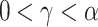 , then
, then 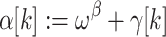 .
.If
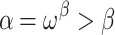 , then we set
, then we set  if
if 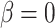 ,
, 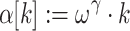 if
if  , and
, and 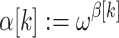 if
if  .
.If
 , then
, then 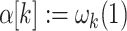 if
if  ,
, 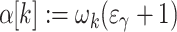 if
if  , and
, and  if
if  .
.
This system of fundamental sequences enjoys the Bachmann property [11].
In view of Proposition 1, the following technical lemma will be crucial for proving our main independence result for  .
.
Lemma 7
Given 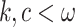 with
with 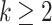 ,
,  .
.
Proof
We prove the claim by induction on c. Let 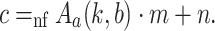
-
Case 3 (
 and
and  ). We consider several sub-cases.
). We consider several sub-cases.- Case 3.3 (
 and
and  ). Then the induction hypothesis yields similarly as in Case 3.1:
). Then the induction hypothesis yields similarly as in Case 3.1:
since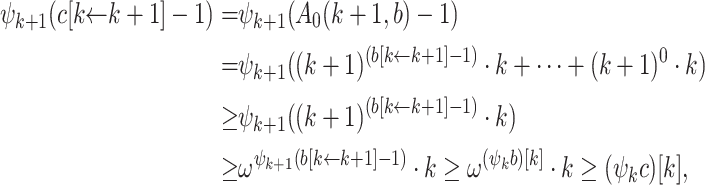
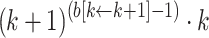 is in
is in 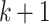 normal form.
normal form. - Case 3.4 (
 and
and  ). The assertion follows trivially since then
). The assertion follows trivially since then 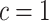 .
.
Theorem 2
Let 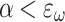 . Then
. Then  Hence
Hence 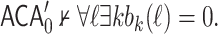
Proof
Assume for a contradiction that  Then
Then 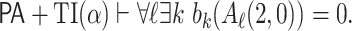 Recall that
Recall that  . We have
. We have 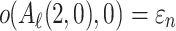 . Lemma 7 and Lemma 5 yield
. Lemma 7 and Lemma 5 yield  , hence Proposition 1 yields
, hence Proposition 1 yields 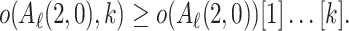 So the least k such that
So the least k such that 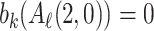 is at least as big as the least k such that
is at least as big as the least k such that  . But by standard results in proof theory [3],
. But by standard results in proof theory [3], 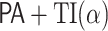 does not prove that this k is always defined as a function of
does not prove that this k is always defined as a function of 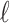 . This contradicts
. This contradicts 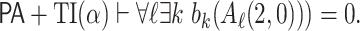
Goodstein Sequences for 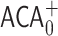
In this section, we indicate how to extend our approach to a situation where the base change operation can also be applied to the first argument of the Ackermann function. The resulting Goodstein principle will then be independent of 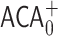 . The key difference is that the base-change operation is now performed recursively on the first argument, as well as the second.
. The key difference is that the base-change operation is now performed recursively on the first argument, as well as the second.
Definition 5
For 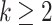 and
and 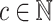 , define
, define  by:
by:

 if
if  .
.
Note that in this section, 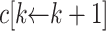 will always indicate the operation of Definition 5. We can then define a Goodstein process based on this new base change operator.
will always indicate the operation of Definition 5. We can then define a Goodstein process based on this new base change operator.
Definition 6
Let 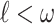 . Put
. Put  Assume recursively that
Assume recursively that 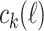 is defined and
is defined and  . Then,
. Then, 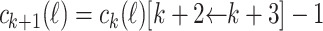 . If
. If 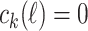 , then
, then 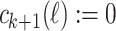 .
.
Termination and independence results can then be obtained following the same general strategy as before. We begin with the following lemmas, whose proofs are similar to those for their analogues in Sect. 3.
Lemma 8
If 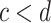 and
and 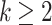 , then
, then  .
.
Lemma 9
If 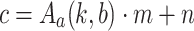 is in k-normal form, then
is in k-normal form, then 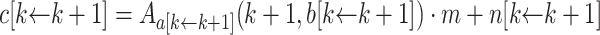 is in
is in  normal form.
normal form.
It is well-known that the so-called slow-growing hierarchy at level  matches up with the functions which are elementary in the Ackermann function, so one might expect that the corresponding Goodstein process can be proved terminating in
matches up with the functions which are elementary in the Ackermann function, so one might expect that the corresponding Goodstein process can be proved terminating in  . This is true but, somewhat surprisingly, much less is needed here. Indeed, nested Ackermannian normal forms are related to the much smaller ordinal
. This is true but, somewhat surprisingly, much less is needed here. Indeed, nested Ackermannian normal forms are related to the much smaller ordinal  by the following mapping.
by the following mapping.
Definition 7
Given 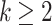 , define a function
, define a function 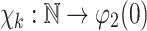 given by:
given by:
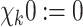 .
.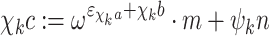 if
if 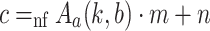 .
.
As was the case for the mappings 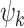 , the maps
, the maps 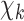 are strictly increasing and invariant under base change, as can be checked using analogous proofs to those in Sect. 3.
are strictly increasing and invariant under base change, as can be checked using analogous proofs to those in Sect. 3.
Lemma 10
Let 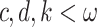 with
with 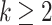 .
.
If
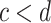 , then
, then 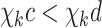 .
.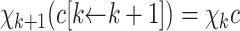 .
.
Theorem 3
For all 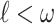 , there exists a
, there exists a 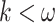 such that
such that 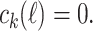 This is provable in
This is provable in 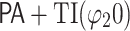 .
.
Next, we show that for every 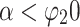 ,
,  For this, we need the following analogue of Lemma 7.
For this, we need the following analogue of Lemma 7.
Lemma 11
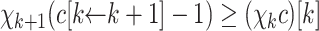 .
.
Proof
We proceed by induction on c. Let 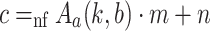 . Let us concentrate on the critical case
. Let us concentrate on the critical case  and
and 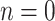 , where
, where 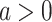 and
and  .
.
The induction hypothesis yields
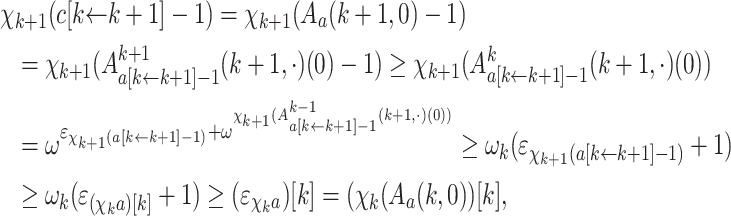 |
since 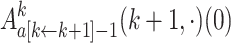 is in
is in  normal form.
normal form.
The remaining details of the proof of the theorem can be carried out similarly as before.
Theorem 4
For every 
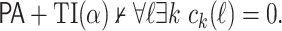 Hence
Hence 
Contributor Information
Marcella Anselmo, Email: manselmo@unisa.it.
Gianluca Della Vedova, Email: gianluca.dellavedova@unimib.it.
Florin Manea, Email: flmanea@gmail.com.
Arno Pauly, Email: arno.m.pauly@gmail.com.
David Fernández-Duque, Email: David.FernandezDuque@UGent.be.
Andreas Weiermann, Email: Andreas.Weiermann@UGent.be.
References
- 1.Afshari B, Rathjen M. Ordinal analysis and the infinite Ramsey theorem. In: Cooper SB, Dawar A, Löwe B, editors. How the World Computes; Heidelberg: Springer; 2012. pp. 1–10. [Google Scholar]
- 2.Arai, T., Fernández-Duque, D., Wainer, S., Weiermann, A.: Predicatively unprovable termination of the Ackermannian Goodstein process. In: Proceedings of the AMS (2019). 10.1090/proc/14813
- 3.Cichon E, Buchholz W, Weiermann A. A uniform approach to fundamental sequences and hierarchies. Math. Logic Q. 1994;40:273–286. doi: 10.1002/malq.19940400212. [DOI] [Google Scholar]
- 4.Gödel K. Über Formal Unentscheidbare Sätze der Principia Mathematica und Verwandter Systeme. I. Monatshefte für Mathematik und Physik. 1931;38:173–198. doi: 10.1007/BF01700692. [DOI] [Google Scholar]
- 5.Goodstein R. On the restricted ordinal theorem. J. Symb. Logic. 1944;9(2):33–41. doi: 10.2307/2268019. [DOI] [Google Scholar]
- 6.Goodstein R. Transfinite ordinals in recursive number theory. J. Symb. Logic. 1947;12(4):123–129. doi: 10.2307/2266486. [DOI] [Google Scholar]
-
7.Graham RL, Rothschild BL. Ramsey’s theorem for
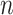 -dimensional arrays. Bull. Am. Math. Soc. 1969;75(2):418–422. doi: 10.1090/S0002-9904-1969-12202-0. [DOI] [Google Scholar]
-dimensional arrays. Bull. Am. Math. Soc. 1969;75(2):418–422. doi: 10.1090/S0002-9904-1969-12202-0. [DOI] [Google Scholar] - 8.Kirby L, Paris J. Accessible independence results for Peano arithmetic. Bull. Lond. Math. Soc. 1982;14(4):285–293. doi: 10.1112/blms/14.4.285. [DOI] [Google Scholar]
- 9.Leigh G, Rathjen M. An ordinal analysis for theories of self-referential truth. Arch. Math. Log. 2010;49(2):213–247. doi: 10.1007/s00153-009-0170-2. [DOI] [Google Scholar]
- 10.Pohlers W. Proof Theory, The First Step into Impredicativity. Heidelberg: Springer; 2009. [Google Scholar]
- 11.Schmidt D. Built-up systems of fundamental sequences and hierarchies of number-theoretic functions. Arch. Math. Log. 1977;18(1):47–53. doi: 10.1007/BF02007256. [DOI] [Google Scholar]
- 12.Schütte K. Proof Theory. Heidelberg: Springer; 1977. [Google Scholar]
- 13.Simpson S. Subsystems of Second Order Arithmetic. New York: Cambridge University Press; 2009. [Google Scholar]
- 14.Weiermann, A.: Ackermannian Goodstein principles for first order Peano arithmetic. In: Sets and computations. Lecture Notes Series, Institute for Mathematical Sciences, National University of Singapore, vol. 33, pp. 157–181. World Scientific, Hackensack (2018). English summary