Abstract
Amalgamation SNP (ASNP) is a fragment of existential second-order logic that strictly contains binary connected MMSNP of Feder and Vardi and binary connected guarded monotone SNP of Bienvenu, ten Cate, Lutz, and Wolter; it is a promising candidate for an expressive subclass of NP that exhibits a complexity dichotomy. We show that ASNP has a complexity dichotomy if and only if the infinite-domain dichotomy conjecture holds for constraint satisfaction problems for first-order reducts of binary finitely bounded homogeneous structures. For such CSPs, powerful universal-algebraic hardness conditions are known that are conjectured to describe the border between NP-hard and polynomial-time tractable CSPs. The connection to CSPs also implies that every ASNP sentence can be evaluated in polynomial time on classes of finite structures of bounded treewidth. We show that the syntax of ASNP is decidable. The proof relies on the fact that for classes of finite binary structures given by finitely many forbidden substructures, the amalgamation property is decidable.
Introduction
Feder and Vardi in their groundbreaking work [15] formulated the famous dichotomy conjecture for finite-domain constraint satisfaction problems, which has recently been resolved [11, 26]. Their motivation to study finite-domain CSPs was the question which fragments of existential second-order logic might exhibit a complexity dichotomy in the sense that every problem that can be expressed in the fragment is either in P or NP-complete. Existential second-order logic without any restriction is known to capture NP [14] and hence does not have a complexity dichotomy by an old result of Ladner [24]. Feder and Vardi proved that even the fragments of monadic SNP and monotone SNP do not have a complexity dichotomy since every problem in NP is polynomial-time equivalent to a problem that can be expressed in these fragments. However, the dichotomy for finite-domain CSPs implies that monotone monadic SNP (MMSNP) has a dichotomy, too [15, 23].
MMSNP is also known to have a tight connection to a certain class of infinite-domain CSPs [7]: an MMSNP sentence is equivalent to a connected MMSNP sentence if and only if it describes an infinite-domain CSP. Moreover, every problem in MMSNP is equivalent to a finite disjunction of connected MMSNP sentences. The infinite structures that appear in this connection are tame from a model-theoretic perspective: they are reducts of finitely bounded homogeneous structures (see Sect. 4.1). CSPs for such structures are believed to have a complexity dichotomy, too; there is even a known hardness condition such that all other CSPs in the class are conjectured to be in P [8]. The hardness condition can be expressed in several equivalent forms [1, 2].
In this paper we investigate another candidate for an expressive logic that has a complexity dichotomy. Our minimum requirement for what constitutes a logic is relatively liberal: we require that the syntax of the logic should be decidable. The same requirement has been made for the question whether there exists a logic that captures the class of polynomial-time solvable decision problems (see, e.g., [19, 20]). The idea of our logic is to modify monotone SNP so that only CSPs for model-theoretically tame structures can be expressed in the logic; the challenge is to come up with a definition of such a logic which has a decidable syntax. We would like to require that the (universal) first-order part of a monotone SNP sentence describes an amalgamation class. We mention that the Joint Embedding Property (JEP), which follows from the Amalgamation Property (AP), has recently been shown to be undecidable [10]. In contrast, we use the fact that the AP for binary signatures is decidable (Sect. 5). We call our new logic Amalgamation SNP (ASNP). This logic contains binary connected MMSNP; it also contains the more expressive logic of binary connected guarded monotone SNP. Guarded monotone SNP (GMSNP) has been introduced in the context of knowledge representation [3] (see Sect. 6). We show that ASNP has a complexity dichotomy if and only if the infinite-domain dichotomy conjecture holds for constraint satisfaction problems for first-order reducts of binary finitely bounded homogeneous structures. In particular, every problem that can be expressed in ASNP is a CSP for some countably infinite  -categorical structure
-categorical structure  . In Sect. 7 we present an example application of this fact: every problem that can be expressed in one of these logics can be solved in polynomial time on instances of bounded treewidth.
. In Sect. 7 we present an example application of this fact: every problem that can be expressed in one of these logics can be solved in polynomial time on instances of bounded treewidth.
Constraint Satisfaction Problems
Let  be structures with a finite relational signature
be structures with a finite relational signature  ; each symbol
; each symbol  is equipped with an arity
is equipped with an arity
 . A function
. A function  is called a homomorphism from
is called a homomorphism from
 to
to
 if for every
if for every  and
and  we have
we have  ; in this case we write
; in this case we write  . We write
. We write  for the class of all finite
for the class of all finite  -structures
-structures  such that
such that  .
.
Example 1
If 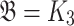 is the 3-clique, i.e., the complete undirected graph with three vertices, then
is the 3-clique, i.e., the complete undirected graph with three vertices, then  is the graph 3-colouring problem, which is NP-complete [18].
is the graph 3-colouring problem, which is NP-complete [18].
Example 2
If  then
then  is the digraph acyclicity problem, which is in P.
is the digraph acyclicity problem, which is in P.
Example 3
If  for
for  then
then  is the Betweenness problem, which is NP-complete [18].
is the Betweenness problem, which is NP-complete [18].
A homomorphism h from  to
to  is called an embedding of
is called an embedding of
 into
into
 if h is injective and for every
if h is injective and for every  and
and  we have
we have  if and only if
if and only if  ; in this case we write
; in this case we write  . The union of two
. The union of two  -structures
-structures  is the
is the  -structure
-structure  with domain
with domain  and the relation
and the relation  for every
for every  . The intersection
. The intersection
 is defined analogously. A disjoint union of
is defined analogously. A disjoint union of  and
and  is the union of isomorphic copies of
is the union of isomorphic copies of  and
and 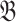 with disjoint domains. As disjoint unions are unique up to isomorphism, we usually speak of the disjoint union of
with disjoint domains. As disjoint unions are unique up to isomorphism, we usually speak of the disjoint union of  and
and 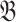 , and denote it by
, and denote it by 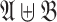 . A structure is connected if it cannot be written as a disjoint union of at least two structures with non-empty domain. A class of structures
. A structure is connected if it cannot be written as a disjoint union of at least two structures with non-empty domain. A class of structures  is closed under inverse homomorphisms if whenever
is closed under inverse homomorphisms if whenever  and
and  homomorphically maps to
homomorphically maps to  we have
we have  . If
. If  is a finite relational signature, then it is well-known and easy to see [5] that
is a finite relational signature, then it is well-known and easy to see [5] that  for a countably infinite
for a countably infinite  -structure
-structure  if and only if
if and only if  is closed under inverse homomorphisms and disjoint unions.
is closed under inverse homomorphisms and disjoint unions.
Monotone SNP
Let  be a finite relational signature, i.e.,
be a finite relational signature, i.e.,  is a set of relation symbols R, each equipped with an arity
is a set of relation symbols R, each equipped with an arity
 . An SNP (
. An SNP ( -) sentence is an existential second-order (
-) sentence is an existential second-order ( -) sentence with a universal first-order part, i.e., a sentence of the form
-) sentence with a universal first-order part, i.e., a sentence of the form
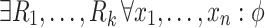 |
where  is a quantifier-free formula over the signature
is a quantifier-free formula over the signature  . We make the additional convention that the equality symbol, which is usually allowed in first-order logic, is not allowed in
. We make the additional convention that the equality symbol, which is usually allowed in first-order logic, is not allowed in  (see [15]). We write
(see [15]). We write  for the class of all finite models of
for the class of all finite models of  .
.
Example 4
 for the SNP
for the SNP  -sentence
-sentence  given below.
given below.
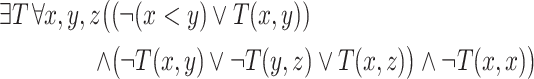 |
A class  of finite
of finite  -structures is said to be in SNP if there exists an SNP
-structures is said to be in SNP if there exists an SNP  -sentence
-sentence  such that
such that  ; we use analogous definitions for all logics considered in this paper. We may assume that the quantifier-free part of SNP sentences is written in conjunctive normal form, and then use the usual terminology (clauses, literals, etc).
; we use analogous definitions for all logics considered in this paper. We may assume that the quantifier-free part of SNP sentences is written in conjunctive normal form, and then use the usual terminology (clauses, literals, etc).
Definition 1
An SNP  -sentence
-sentence  with quantifier-free part
with quantifier-free part  and existentially quantified relation symbols
and existentially quantified relation symbols  is called
is called
monotone if each literal of
 with a symbol from
with a symbol from  is negative, i.e., of the form
is negative, i.e., of the form  for
for  .
.monadic if all the existentially quantified relations are unary.
connected if each clause of
 is connected, i.e., the following
is connected, i.e., the following  -structure
-structure  is connected: the domain of
is connected: the domain of  is the set of variables of the clause, and
is the set of variables of the clause, and  if and only if
if and only if  is a disjunct of the clause.
is a disjunct of the clause.
The SNP sentence from Example 4 is monotone, but not monadic, and it can be shown that there does not exist an equivalent MMSNP sentence [4].
Theorem 1
([5]). Every sentence in connected monotone SNP describes a problem of the form  for some relational structure
for some relational structure  . Conversely, for every structure
. Conversely, for every structure 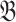 , if
, if  is in SNP then it is also in connected monotone SNP.
is in SNP then it is also in connected monotone SNP.
Amalgamation SNP
In this section we define the new logic Amalgamation SNP (ASNP). We first revisit some basic concepts from model theory.
The Amalgamation Property
Let  be a finite relational signature and let
be a finite relational signature and let  be a class of
be a class of  -structures. We say that
-structures. We say that  is finitely bounded if there exists a finite set of finite
is finitely bounded if there exists a finite set of finite  -structures
-structures  such that
such that  if and only if no structure in
if and only if no structure in  embeds into
embeds into  ; in this case we also write
; in this case we also write  . Note that
. Note that  is finitely bounded if and only if there exists a universal
is finitely bounded if and only if there exists a universal  -sentence
-sentence  (which might involve the equality symbol) such that for every finite
(which might involve the equality symbol) such that for every finite  -structure
-structure  we have
we have  if and only if
if and only if  . We say that
. We say that  has
has
the Joint Embedding Property (JEP) if for all structures
 there exists a structure
there exists a structure  that embeds both
that embeds both  and
and  .
.the Amalgamation Property (AP) if for any two structures
 such that
such that  induce the same substructure in
induce the same substructure in  and in
and in  (a so-called amalgamation diagram) there exists a structure
(a so-called amalgamation diagram) there exists a structure  and embeddings
and embeddings  and
and  such that
such that  for all
for all  .
.
Note that since  is relational, the AP implies the JEP. A class of finite
is relational, the AP implies the JEP. A class of finite  -structures which has the AP and is closed under induced substructures and isomorphisms is called an amalgamation class.
-structures which has the AP and is closed under induced substructures and isomorphisms is called an amalgamation class.
The age of  is the class of all finite
is the class of all finite  -structures that embed into
-structures that embed into  . We say that
. We say that  is finitely bounded if
is finitely bounded if  is finitely bounded. A relational
is finitely bounded. A relational  -structure
-structure  is called homogeneous if every isomorphism between finite substructures of
is called homogeneous if every isomorphism between finite substructures of  can be extended to an automorphism of
can be extended to an automorphism of  . Fraïssé’s theorem implies that for every amalgamation class
. Fraïssé’s theorem implies that for every amalgamation class  there exists a countable homogeneous
there exists a countable homogeneous  -structure
-structure  with
with  ; the structure
; the structure  is unique up to isomorphism, also called the Fraïssé-limit of
is unique up to isomorphism, also called the Fraïssé-limit of  . Conversely, it is easy to see that the age of a homogeneous
. Conversely, it is easy to see that the age of a homogeneous  -structure is an amalgamation class. A structure
-structure is an amalgamation class. A structure  is called a reduct of a structure
is called a reduct of a structure  if
if  is obtained from
is obtained from  by restricting the signature. It is called a first-order reduct of
by restricting the signature. It is called a first-order reduct of  if
if  is obtained from
is obtained from 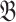 by first expanding by all first-order definable relations, and then restricting the signature. An example of a first-order reduct of
by first expanding by all first-order definable relations, and then restricting the signature. An example of a first-order reduct of  is the structure
is the structure  from Example 3.
from Example 3.
Defining Amalgamation SNP
As we have mentioned in the introduction, the idea of our logic is to require that a certain class of finite structures associated to the first-order part of an SNP sentence is an amalgamation class. We then use the fact that for binary signatures, the amalgamation property is decidable (Sect. 5).
Definition 2
Let  be a finite relational signature. An Amalgamation SNP
be a finite relational signature. An Amalgamation SNP
 -sentence is an SNP sentence
-sentence is an SNP sentence  of the form
of the form  where
where
 are binary;
are binary; is a conjunction of
is a conjunction of  -formulas and of conjuncts of the form
-formulas and of conjuncts of the form  where
where  and
and  is a
is a  -formula;
-formula;the class of
 -reducts of the finite models of
-reducts of the finite models of  is an amalgamation class.
is an amalgamation class.
Note that ASNP inherits from SNP the restriction that equality symbols are not allowed. Also note that Amalgamation SNP sentences are necessarily monotone. This implies in particular that the class of  -reducts of the finite models of
-reducts of the finite models of  is precisely the class of finite
is precisely the class of finite  -structures that satisfy the conjuncts of
-structures that satisfy the conjuncts of  that are
that are  -formulas (i.e., that do not contain any symbol from
-formulas (i.e., that do not contain any symbol from  ).
).
Example 5
The monotone SNP sentence from Example 4 describing  is in ASNP. The problem
is in ASNP. The problem  from Example 3 can be expressed by the ASNP sentence
from Example 3 can be expressed by the ASNP sentence
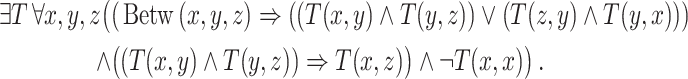 |
Note that every finite-domain CSP can be expressed in ASNP; this can be seen similarly as in the argument of Feder and Vardi that finite-domain CSPs can be expressed in MMSNP [15].
Then the class of finite models of the first-order part of  has the JEP, and since equality is not allowed in SNP the class is even closed under disjoint unions; it follows that also
has the JEP, and since equality is not allowed in SNP the class is even closed under disjoint unions; it follows that also  is closed under disjoint unions. It can be shown as in the proof of Theorem 1 that every Amalgamation SNP sentence can be rewritten into an equivalent connected Amalgamation SNP sentence.
is closed under disjoint unions. It can be shown as in the proof of Theorem 1 that every Amalgamation SNP sentence can be rewritten into an equivalent connected Amalgamation SNP sentence.
ASNP and CSPs
We present the link between ASNP and infinite-domain CSPs.
Theorem 2
For every ASNP  -sentence
-sentence  there exists a first-order reduct
there exists a first-order reduct  of a binary finitely bounded homogeneous structure such that
of a binary finitely bounded homogeneous structure such that  .
.
Proof
Let  be the set of existentially quantified relation symbols of
be the set of existentially quantified relation symbols of  . Let
. Let  , for a quantifier-free formula
, for a quantifier-free formula  in conjunctive normal form, be the first-order part of
in conjunctive normal form, be the first-order part of  . Let
. Let  be the class of
be the class of  -reducts of the finite models of
-reducts of the finite models of  ; by assumption,
; by assumption,  is an amalgamation class. Moreover,
is an amalgamation class. Moreover,  is finitely bounded because it is the class of models of a universal
is finitely bounded because it is the class of models of a universal  -sentence. Let
-sentence. Let  be the Fraïssé-limit of
be the Fraïssé-limit of  ; then
; then 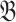 is a finitely bounded homogeneous structure. Let
is a finitely bounded homogeneous structure. Let  be the
be the  -structure which is the first-order reduct of the structure
-structure which is the first-order reduct of the structure  where the relation
where the relation  for
for  is defined as follows: if
is defined as follows: if  are all the
are all the  -formulas such that
-formulas such that  contains the conjunct
contains the conjunct  for all
for all  , then the first-order definition of S is given by
, then the first-order definition of S is given by  .
.
Claim 1
If  is a finite
is a finite  -structure such that
-structure such that  , then
, then  .
.
Let  be a homomorphism. Let
be a homomorphism. Let  be the
be the  -expansion of
-expansion of  where
where  of arity l denotes
of arity l denotes  . Then
. Then  satisfies
satisfies  : to see this, let
: to see this, let  and let
and let  be a conjunct of
be a conjunct of  . Since
. Since  we have in particular that
we have in particular that 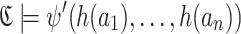 and so there must be a disjunct
and so there must be a disjunct  of
of  such that
such that  . Then one of the following cases applies.
. Then one of the following cases applies.
 is a
is a  -literal and hence must be negative since
-literal and hence must be negative since  is a monotone SNP sentence. In this case
is a monotone SNP sentence. In this case  implies
implies  since h is a homomorphism.
since h is a homomorphism. is a
is a  -literal. Then by the definition of
-literal. Then by the definition of  we have that
we have that  if and only if
if and only if  .
.
Hence,  . Since the conjunct
. Since the conjunct  of
of  and
and  were arbitrarily chosen, we have that
were arbitrarily chosen, we have that  . Hence,
. Hence,  satisfies
satisfies  .
.
Claim 2
If  is a finite
is a finite  -structure such that
-structure such that  , then
, then 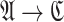 .
.
If  has a
has a  -expansion
-expansion  that satisfies
that satisfies  , then there exists an embedding from the
, then there exists an embedding from the  -reduct
-reduct  of
of  into
into  by the definition of
by the definition of  . This embedding is in particular a homomorphism from
. This embedding is in particular a homomorphism from  to
to  .
. 
Theorem 3
Let  be a first-order reduct of a binary finitely bounded homogeneous structure
be a first-order reduct of a binary finitely bounded homogeneous structure  . Then
. Then  can be expressed in ASNP.
can be expressed in ASNP.
Proof
Let  be the signature of
be the signature of  and
and  the signature of
the signature of  . We may assume without loss of generality that
. We may assume without loss of generality that  contains a binary relation E that denotes the equality relation; it is easy to see that an expansion by the equality relation preserves finite boundedness. Consider the structure
contains a binary relation E that denotes the equality relation; it is easy to see that an expansion by the equality relation preserves finite boundedness. Consider the structure  with the domain
with the domain  where
where
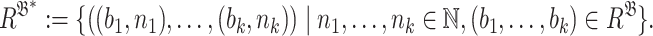 |
To show that  is homogeneous, let h be an isomorphism between finite substructures of
is homogeneous, let h be an isomorphism between finite substructures of  . Let
. Let  be the set of all first entries of elements of the first structure. Define
be the set of all first entries of elements of the first structure. Define  by picking for
by picking for  an element of the form
an element of the form  and defining by
and defining by  . This is well-defined: if h is defined on
. This is well-defined: if h is defined on  and on
and on  , then
, then  , and hence
, and hence  . The same consideration for
. The same consideration for  shows that g is a bijection, and in fact an isomorphism between finite substructures of
shows that g is a bijection, and in fact an isomorphism between finite substructures of  . By the homogeneity of
. By the homogeneity of  there exists an extension
there exists an extension  of g. For each
of g. For each  pick a permutation
pick a permutation  of
of  that extends the bijection given by
that extends the bijection given by  . Then the map
. Then the map  given by
given by  is an automorphism of
is an automorphism of  that extends h. Since
that extends h. Since  is finitely bounded, there exists a universal
is finitely bounded, there exists a universal  -formula
-formula  such that
such that  . Note that
. Note that  might contain the equality symbol (which we do not allow in SNP sentences). Let
might contain the equality symbol (which we do not allow in SNP sentences). Let  be the formula obtained from
be the formula obtained from  by
by
replacing each occurrence of the equality symbol by the symbol
 ;
;joining conjuncts that imply that E denotes an equivalence relation;
- joining for every
 of arity n the conjunct
of arity n the conjunct
(implementing indiscernibility of identicals for the relation E).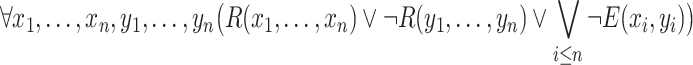
We claim that  . To see this, let
. To see this, let  be a finite
be a finite  -structure. If
-structure. If  satisfies
satisfies  , then every induced substructure
, then every induced substructure  of
of  with the property that
with the property that  implies that at most one of x and y is an element of A, satisfies
implies that at most one of x and y is an element of A, satisfies  , and hence is a substructure of
, and hence is a substructure of  . This in turn means that
. This in turn means that  is in
is in  . The implications in this statement can be reversed which shows the claim.
. The implications in this statement can be reversed which shows the claim.
Let  be the formula obtained from
be the formula obtained from  as follows. For each
as follows. For each  let
let  be the first-order definition of
be the first-order definition of  in
in  ; since
; since  is homogeneous we may assume that
is homogeneous we may assume that  is quantifier-free [21]. Furthermore, we may assume that
is quantifier-free [21]. Furthermore, we may assume that  is given in conjunctive normal form. Let k be the arity of S. We then add for each conjunct
is given in conjunctive normal form. Let k be the arity of S. We then add for each conjunct  of
of  the conjunct
the conjunct
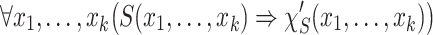 |
By construction, the sentence  obtained from
obtained from  by quantifying all relation symbols of
by quantifying all relation symbols of  is an ASNP
is an ASNP  -sentence.
-sentence. 
Corollary 1
ASNP has a complexity dichotomy if and only if the infinite-domain dichotomy conjecture is true for first-order reducts of binary finitely bounded homogeneous structures.
Deciding Amalgamation
In this section we show how to algorithmically decide whether a given existential second-order sentence is in ASNP. The following is a known fact in the model theory of homogeneous structures (the first author has learned the fact from Gregory Cherlin), but we are not aware of any published proof in the literature.
Theorem 4
Let  be a finite set of finite binary relational
be a finite set of finite binary relational  -structures. There is an algorithm that decides whether
-structures. There is an algorithm that decides whether  has the amalgamation property.
has the amalgamation property.
Proof
Let m be the maximal size of a structure in  , and let
, and let  be the number of isomorphism types of two-element structures in
be the number of isomorphism types of two-element structures in  . It is well-known and easy to prove that
. It is well-known and easy to prove that  has the amalgamation property if and only if it has the so-called 1-point amalgamation property, i.e., the amalgamation property restricted to diagrams
has the amalgamation property if and only if it has the so-called 1-point amalgamation property, i.e., the amalgamation property restricted to diagrams  where
where  . Suppose that
. Suppose that  is such an amalgamation diagram without amalgam. Let
is such an amalgamation diagram without amalgam. Let  . Let
. Let  and
and  . Let
. Let  be a
be a  -structure
-structure  with domain
with domain  such that
such that  and
and  are substructures of
are substructures of  . Since
. Since  by assumption is not an amalgam for
by assumption is not an amalgam for  , there must exist
, there must exist  such that the substructure of
such that the substructure of  induced by
induced by  embeds a structure from
embeds a structure from  .
.
Note that the number of such  -structures
-structures  is bounded by
is bounded by  since they only differ by the substructure induced by p and q. So let
since they only differ by the substructure induced by p and q. So let  be a list of sets witnessing that all of these structures
be a list of sets witnessing that all of these structures  embed a structure from
embed a structure from  . Let
. Let  be the substructure of
be the substructure of  induced by
induced by  and
and  be the substructure of
be the substructure of  induced by
induced by  . Suppose for contradiction that
. Suppose for contradiction that  has an amalgam
has an amalgam  ; we may assume that this amalgam is of size at most
; we may assume that this amalgam is of size at most  . Depending on the two-element structure induced by
. Depending on the two-element structure induced by  in
in  , there exists an
, there exists an  such that the structure induced by
such that the structure induced by 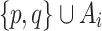 in
in  embeds a structure from
embeds a structure from  , a contradiction.
, a contradiction. 
Corollary 2
There is an algorithm that decides for a given existential second-order sentence  whether it is in ASNP.
whether it is in ASNP.
Proof
Let k be the maximal number of variables per clause in the first-order part  of
of  , and let
, and let  be the set of all structures at most the elements
be the set of all structures at most the elements  that do not satisfy
that do not satisfy  . Then
. Then  and the result follows from Theorem 2.
and the result follows from Theorem 2. 
Guarded Monotone SNP
In this section we revisit an expressive generalisation of MMSNP introduced by Bienvenu, ten Cate, Lutz, and Wolter [3] in the context of ontology-based data access, called guarded monotone SNP (GMSNP). It is equally expressive as the logic MMSNP introduced by Madelaine [25]1. We will see that every GMSNP sentence is equivalent to a finite disjunction of connected GMSNP sentences (Proposition 1), each of which lies in ASNP if the signature is binary (Theorem 5).
introduced by Madelaine [25]1. We will see that every GMSNP sentence is equivalent to a finite disjunction of connected GMSNP sentences (Proposition 1), each of which lies in ASNP if the signature is binary (Theorem 5).
Definition 3
A monotone SNP  -sentence
-sentence  with existentially quantified relations
with existentially quantified relations  is called guarded if each conjunct of
is called guarded if each conjunct of  can be written in the form
can be written in the form
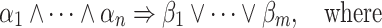 |
 are atomic
are atomic  -formulas, called body atoms,
-formulas, called body atoms, are atomic
are atomic  -formulas, called head atoms,
-formulas, called head atoms,for every head atom
 there is a body atom
there is a body atom  such that
such that  contains all variables from
contains all variables from  (such clauses are called guarded).
(such clauses are called guarded).
We do allow the case that  , i.e., the case where the head consists of the empty disjunction, which is equivalent to
, i.e., the case where the head consists of the empty disjunction, which is equivalent to  (false).
(false).
The next proposition extends a well-known fact for MMSNP to guarded SNP.
Proposition 1
Every GMSNP sentence  is equivalent to a finite disjunction
is equivalent to a finite disjunction  of connected GMSNP sentences.
of connected GMSNP sentences.
Proof
We prove Proposition 1. Let  be a guarded SNP sentence. Suppose that the quantifier-free part of
be a guarded SNP sentence. Suppose that the quantifier-free part of  has a disconnected clause
has a disconnected clause  (Definition 1). By definition the variable set can be partitioned into non-empty variable sets
(Definition 1). By definition the variable set can be partitioned into non-empty variable sets  and
and  such that for every negative literal
such that for every negative literal  of the clause either
of the clause either  or
or  . The same is true for every positive literal, since otherwise the definition of guarded clauses would imply a negative literal on a set that contains
. The same is true for every positive literal, since otherwise the definition of guarded clauses would imply a negative literal on a set that contains  , contradicting the property above. Hence,
, contradicting the property above. Hence,  can be written as
can be written as  for non-empty disjoint tuples of variables
for non-empty disjoint tuples of variables  and
and  . Let
. Let  be the formula obtained from
be the formula obtained from  by replacing
by replacing  by
by  , and let
, and let  be the formula obtained from
be the formula obtained from  by replacing
by replacing  by
by  .
.
Let  be the existential predicates in
be the existential predicates in  , and let
, and let  be the input signature of
be the input signature of  . It suffices to show that for every
. It suffices to show that for every  -expansion
-expansion  of
of  we have that
we have that  satisfies
satisfies  if and only if
if and only if  satisfies
satisfies  or
or  . If
. If  falsifies a clause of
falsifies a clause of  , there is nothing to show since then
, there is nothing to show since then  satisfies neither
satisfies neither  nor
nor  . If
. If  satisfies all clauses of
satisfies all clauses of  , it in particular satisfies a literal from
, it in particular satisfies a literal from  ; depending on whether this literal lies in
; depending on whether this literal lies in  or in
or in  , we obtain that
, we obtain that  satisfies
satisfies  or
or  , and hence
, and hence  or
or 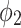 . Iterating this process for each disconnected clause of
. Iterating this process for each disconnected clause of  , we eventually arrive at a finite disjunction of connected guarded SNP sentences.
, we eventually arrive at a finite disjunction of connected guarded SNP sentences. 
It is well-known and easy to see [17] that each of  can be reduced to
can be reduced to  in polynomial time. Conversely, if each of
in polynomial time. Conversely, if each of  is in P, then
is in P, then  is in P, too. It follows in particular that if connected GMSNP has a complexity dichotomy into P and NP-complete, then so has GMSNP.
is in P, too. It follows in particular that if connected GMSNP has a complexity dichotomy into P and NP-complete, then so has GMSNP.
Theorem 5
For every sentence  in connected GMSNP there exists a reduct
in connected GMSNP there exists a reduct  of a finitely bounded homogeneous structures such that
of a finitely bounded homogeneous structures such that  . If all existentially quantified relation symbols in
. If all existentially quantified relation symbols in  are binary then it is equivalent to an ASNP sentence.
are binary then it is equivalent to an ASNP sentence.
In the proof of Theorem 5 we use a result of Cherlin, Shelah, and Shi [12] in a strengthened form due to Hubička and Nešetřil [22], namely that for every finite set  of finite
of finite  -structures, for some finite relational signature
-structures, for some finite relational signature  , there exists a finitely bounded homogeneous
, there exists a finitely bounded homogeneous  -structure
-structure 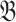 such that a finite
such that a finite  -structure
-structure  homomorphically maps to
homomorphically maps to  if none of the structures in
if none of the structures in  homomorphically maps to
homomorphically maps to  . We now prove Theorem 5.
. We now prove Theorem 5.
Proof
Let  be a
be a  -sentence in connected guarded monotone SNP with existentially quantified relation symbols
-sentence in connected guarded monotone SNP with existentially quantified relation symbols  . Let
. Let  be the signature which contains for every relation symbol
be the signature which contains for every relation symbol  two new relation symbols
two new relation symbols  and
and  of the same arity and for every relation symbol
of the same arity and for every relation symbol  a new relation symbol
a new relation symbol  . Let
. Let  be the first-order part of
be the first-order part of  , written in conjunctive normal form, and let n be the number of variables in the largest clause of
, written in conjunctive normal form, and let n be the number of variables in the largest clause of  . Let
. Let  be the sentence obtained from
be the sentence obtained from  by replacing each occurrence of
by replacing each occurrence of  by
by  and each occurrence of
and each occurrence of  by
by  , and finally each occurrence of
, and finally each occurrence of  by
by 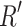 . Let
. Let  be the (finite) class of all finite
be the (finite) class of all finite  -structures with at most n elements that do not satisfy
-structures with at most n elements that do not satisfy  . We apply the mentioned theorem of Hubička and Nešetřil to
. We apply the mentioned theorem of Hubička and Nešetřil to  , and obtain a finitely bounded homogeneous
, and obtain a finitely bounded homogeneous  -structure
-structure  such that the age of the
such that the age of the  -reduct
-reduct  of
of  equals
equals  . We say that
. We say that  is correctly labelled if for every
is correctly labelled if for every  of arity m and
of arity m and  we have
we have  if and only if
if and only if  . Let
. Let  the
the  -expansion of
-expansion of  where
where  of arity m denotes
of arity m denotes
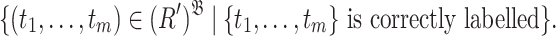 |
Since  is finitely bounded homogeneous,
is finitely bounded homogeneous,  is finitely bounded homogeneous, too. Let
is finitely bounded homogeneous, too. Let  be the
be the  -reduct of
-reduct of  . We claim that
. We claim that  . First suppose that
. First suppose that  is a finite
is a finite  -structure that satisfies
-structure that satisfies  . Then it has an
. Then it has an  -expansion
-expansion  that satisfies
that satisfies  . Let
. Let  be the
be the  -structure with the same domain as
-structure with the same domain as  where
where
 denotes
denotes  for each
for each  ;
; denotes
denotes  for each
for each  ;
; denotes
denotes  for each
for each  .
.
Then  satisfies
satisfies  , and hence embeds into
, and hence embeds into  . This embedding is a homomorphism from
. This embedding is a homomorphism from  to
to  since the image of the embedding is correctly labelled by the construction of
since the image of the embedding is correctly labelled by the construction of  .
.
Conversely, suppose that  has a homomorphism h to
has a homomorphism h to  . Let
. Let  be the
be the  -expansion of
-expansion of  by defining
by defining  if and only if
if and only if  , for every n-ary
, for every n-ary  . Then each clause of
. Then each clause of  is satisfied, because each clause of
is satisfied, because each clause of  is guarded: let
is guarded: let  be the variables of some clause of
be the variables of some clause of  . If
. If  satisfy the body of this clause, and
satisfy the body of this clause, and  is a head atom of such a clause, then the set
is a head atom of such a clause, then the set  is correctly labelled. This implies that some of the head atoms of the clause must be true in
is correctly labelled. This implies that some of the head atoms of the clause must be true in  because
because  satisfies
satisfies  . The second statement follows from Theorem 3.
. The second statement follows from Theorem 3. 
The following example shows that GMSNP does not contain ASNP.
Example 6
 is in ASNP (see Example 5) but not in GMSNP. Indeed, suppose that
is in ASNP (see Example 5) but not in GMSNP. Indeed, suppose that  is a GMSNP sentence which is true on all finite directed paths. We assume that the quantifier-free part
is a GMSNP sentence which is true on all finite directed paths. We assume that the quantifier-free part  of
of  is in conjunctive normal form. Let
is in conjunctive normal form. Let  be the existentially quantified relation symbols of
be the existentially quantified relation symbols of  , let
, let  , and let l be the number of variables in
, and let l be the number of variables in  . Every directed path, viewed as a
. Every directed path, viewed as a  -structure, satisfies
-structure, satisfies  , and therefore has an
, and therefore has an  -expansion
-expansion  that satisfies
that satisfies  . Note that there are finitely many different
. Note that there are finitely many different  -expansions of a path of length
-expansions of a path of length  ; let
; let  be this number. Hence, for a path of length
be this number. Hence, for a path of length  , there must be
, there must be  with
with  such that the substructures of
such that the substructures of  induced by
induced by  and by
and by  are isomorphic. We then claim that the directed cycle
are isomorphic. We then claim that the directed cycle  satisfies
satisfies  : this is witnessed by the
: this is witnessed by the  -expansion inherited from
-expansion inherited from  which satisfies
which satisfies  since each clause in
since each clause in  is guarded. Hence,
is guarded. Hence,  does not express digraph acyclicity.
does not express digraph acyclicity.
Application: Instances of Bounded Treewidth
If a computational problem can be formulated in ASNP or in GMSNP, then this has remarkable consequences besides a potential complexity dichotomy. In this section we show that every problem that can be formulated in ASNP or in GMSNP is in P when restricted to instances of bounded treewidth. The corresponding result for Monadic Second-Order Logic (MSO) instead of ASNP is a famous theorem of Courcelle [13]. We strongly believe that ASNP is not contained in MSO (consider for instance the Betweenness Problem from Example 3), so our result appears to be incomparable to Courcelle’s.
In the proof of our result, we need the following concepts from model theory. A first-order theory T is called  -categorical if all countable models of T are isomorphic [21]. A structure
-categorical if all countable models of T are isomorphic [21]. A structure  is called
is called  -categorical if its first-order theory (i.e., the set of first-order sentences that hold in
-categorical if its first-order theory (i.e., the set of first-order sentences that hold in  ) is
) is  -categorical. Note that with this definition, finite structures are
-categorical. Note that with this definition, finite structures are  -categorical. Another classic example is the structure
-categorical. Another classic example is the structure  . The definition of treewidth can be treated as a black box in our proof, and we refer the reader to [6].
. The definition of treewidth can be treated as a black box in our proof, and we refer the reader to [6].
Theorem 6
Let  be an ASNP or a connected GMSNP
be an ASNP or a connected GMSNP  -sentence and let
-sentence and let  . Then the problem to decide whether a given finite
. Then the problem to decide whether a given finite  -structure
-structure  of treewidth at most k satisfies
of treewidth at most k satisfies  can be decided in polynomial time with a Datalog program (of width k).
can be decided in polynomial time with a Datalog program (of width k).
Proof
Since structures that are homogeneous in a finite relational language are  -categorical [21] and first-order reducts of
-categorical [21] and first-order reducts of  -categorical structures are
-categorical structures are  -categorical [21], Theorem 2 and Theorem 5 imply that the problem to decide whether a finite
-categorical [21], Theorem 2 and Theorem 5 imply that the problem to decide whether a finite  -structure satisfies
-structure satisfies  can be formulated as CSP
can be formulated as CSP for an
for an  -categorical structure
-categorical structure  . Then the statement follows from Corollary 1 in [6].
. Then the statement follows from Corollary 1 in [6]. 
Remark 1
In Theorem 6 it actually suffices to assume that the core of  has treewidth at most k.
has treewidth at most k.
Corollary 3
Let  be a GMSNP
be a GMSNP  -sentence and let
-sentence and let  . Then there is a polynomial-time algorithm that decides whether a given
. Then there is a polynomial-time algorithm that decides whether a given  -structure of treewidth at most k satisfies
-structure of treewidth at most k satisfies  .
.
Proof
Conclusion and Open Problems
ASNP is a candidate for an expressive logic with a complexity dichotomy: every problem in ASNP is NP-complete or in P if and only if the infinite-domain dichotomy conjecture for first-order reducts of binary finitely bounded homogeneous structures holds. See Fig. 1 for the relation to other candidate logics that are known to have a dichotomy, might have a complexity, or provably do not have a dichotomy.
Fig. 1.
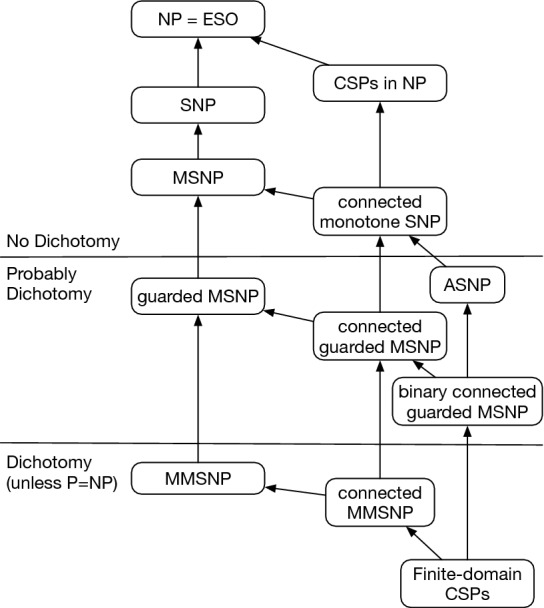
Fragments of existential second-order logic and complexity dichotomies.
We presented an application of ASNP concerning the evaluation of computational problems on classes of structures of bounded treewidth. We also proved that the syntax of ASNP is algorithmically decidable. The following problems concerning ASNP are open.
Is the Amalgamation Property decidable for (not necessarily binary) classes given by finitely many forbidden substructures?
Is every binary CSP in Monadic Second-Order Logic (MSO) also in ASNP?
Is every problem in NP polynomial-time equivalent to a problem in Amalgamation SNP if we drop the monotonicity assumption?
Is there a natural logic (which in particular has an effective syntax) that contains both ASNP and connected GMSNP and which describes CSPs for reducts of finitely bounded homogeneous structures?
Footnotes
MMSNP relates to MMSNP as Courcelle’s MSO
relates to MMSNP as Courcelle’s MSO relates to MSO [13].
relates to MSO [13].
This work has been supported by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (Grant Agreement No 681988, CSP-Infinity) and by DFG Graduiertenkolleg 1763 (QuantLA).
Contributor Information
Marcella Anselmo, Email: manselmo@unisa.it.
Gianluca Della Vedova, Email: gianluca.dellavedova@unimib.it.
Florin Manea, Email: flmanea@gmail.com.
Arno Pauly, Email: arno.m.pauly@gmail.com.
Manuel Bodirsky, Email: manuel.bodirsky@tu-dresden.de.
References
-
1.Barto, L., Kompatscher, M., Olšák, M., Pham, T.V., Pinsker, M.: Equations in oligomorphic clones and the constraint satisfaction problem for
 -categorical structures. J. Math. Logic, 19(2), #1950010 (2019). An extended abstract appeared at the Proceedings of the 32nd Annual ACM/IEEE Symposium on Logic in Computer Science - LICS’17
-categorical structures. J. Math. Logic, 19(2), #1950010 (2019). An extended abstract appeared at the Proceedings of the 32nd Annual ACM/IEEE Symposium on Logic in Computer Science - LICS’17
- 2.Barto, L., Pinsker, M.: The algebraic dichotomy conjecture for infinite domain constraint satisfaction problems. In: Proceedings of the 31th Annual IEEE Symposium on Logic in Computer Science, LICS 2016, pp. 615–622 (2016). Preprint arXiv:1602.04353
- 3.Bienvenu M, ten Cate B, Lutz C, Wolter F. Ontology-based data access: a study through disjunctive datalog, CSP, and MMSNP. ACM Trans. Database Syst. 2014;39(4):33. doi: 10.1145/2661643. [DOI] [Google Scholar]
- 4.Bodirsky, M.: Constraint satisfaction with infinite domains. Dissertation, Humboldt-Universität zu Berlin (2004)
- 5.Bodirsky, M.: Complexity classification in infinite-domain constraint satisfaction. Mémoire d’habilitation à diriger des recherches, Université Diderot - Paris 7. arXiv:1201.0856 (2012)
- 6.Bodirsky M, Dalmau V. Datalog and constraint satisfaction with infinite templates. J. Comput. Syst. Sci. 2013;79:79–100. doi: 10.1016/j.jcss.2012.05.012. [DOI] [Google Scholar]
- 7.Bodirsky, M., Madelaine, F., Mottet, A.: A universal-algebraic proof of the complexity dichotomy for Monotone Monadic SNP. In: Proceedings of the Symposium on Logic in Computer Science (LICS), pp. 105–114 (2018). Preprint available under arXiv:1802.03255
- 8.Bodirsky, M., Pinsker, M., Pongrácz, A.: Projective clone homomorphisms. J. Symb. Logic (2014). Preprint arXiv:1409.4601
- 9.Bodirsky, M., Rydval, J.: Temporal constraint satisfaction problems in fixed point logic (2019). Preprint
- 10.Braunfeld, S.: Towards the undecidability of atomicity for permutation classes via the undecidability of joint embedding for hereditary graph classes (2019). Preprint available at arXiv:1903.11932
- 11.Bulatov, A.A.: A dichotomy theorem for nonuniform CSPs. In: 58th IEEE Annual Symposium on Foundations of Computer Science, FOCS 2017, Berkeley, CA, USA, 15–17 October 2017, pp. 319–330 (2017)
- 12.Cherlin G, Shelah S, Shi N. Universal graphs with forbidden subgraphs and algebraic closure. Adv. Appl. Math. 1999;22:454–491. doi: 10.1006/aama.1998.0641. [DOI] [Google Scholar]
- 13.Courcelle B, Engelfriet J. Graph Structure and Monadic Second-Order Logic: A Language-Theoretic Approach. New York: Cambridge University Press; 2012. [Google Scholar]
- 14.Fagin R. Generalized first-order spectra and polynomial-time recognizable sets. Complex. Comput. 1974;7:43–73. [Google Scholar]
- 15.Feder T, Vardi MY. The computational structure of monotone monadic SNP and constraint satisfaction: a study through Datalog and group theory. SIAM J. Comput. 1999;28:57–104. doi: 10.1137/S0097539794266766. [DOI] [Google Scholar]
- 16.Feder, T., Vardi, M.Y.: Homomorphism closed vs. existential positive. In: Proceedings of the Symposium on Logic in Computer Science (LICS), pp. 311–320 (2003)
- 17.Foniok J, Nešetřil J. Generalised dualities and maximal finite antichains in the homomorphism order of relational structures. Eur. J. Combin. 2008;29(4):881–899. doi: 10.1016/j.ejc.2007.11.017. [DOI] [Google Scholar]
- 18.Garey M, Johnson D. A Guide to NP-Completeness. Stanford: CSLI Press; 1978. [Google Scholar]
- 19.Grohe, M.: The quest for a logic capturing PTIME. In: Proceedings of ACM/IEEE Symposium on Logic in Computer Science (LICS), pp. 267–271 (2008)
- 20.Gurevich Y. Toward logic tailored for computational complexity. In: Börger E, Oberschelp W, Richter MM, Schinzel B, Thomas W, editors. Computation and Proof Theory; Heidelberg: Springer; 1984. pp. 175–216. [Google Scholar]
- 21.Hodges W. Model Theory. Cambridge: Cambridge University Press; 1993. [Google Scholar]
- 22.Hubička J, Nešetřil J. Homomorphism and embedding universal structures for restricted classes. Multiple-Valued Logic Soft Comput. 2016;27(2–3):229–253. [Google Scholar]
- 23.Kun G. Constraints, MMSNP, and expander relational structures. Combinatorica. 2013;33(3):335–347. doi: 10.1007/s00493-013-2405-4. [DOI] [Google Scholar]
- 24.Ladner RE. On the structure of polynomial time reducibility. J. ACM. 1975;22(1):155–171. doi: 10.1145/321864.321877. [DOI] [Google Scholar]
- 25.Madelaine F. Universal structures and the logic of forbidden patterns. In: Ésik Z, editor. Computer Science Logic; Heidelberg: Springer; 2006. pp. 471–485. [Google Scholar]
- 26.Zhuk, D.: A proof of CSP dichotomy conjecture. In: 58th IEEE Annual Symposium on Foundations of Computer Science, FOCS 2017, Berkeley, CA, USA, 15–17 October 2017, pp. 331–342 (2017). https://arxiv.org/abs/1704.01914



