Electroencephalogram Microstate Abnormalities in Early-Course Psychosis

Abstract

BACKGROUND:

Microstates are periods of characteristic electroencephalographic signal topography that are related to activity in brain networks. Previous work has identified abnormal microstate parameters in individuals with psychotic disorders. We combined microstate analysis with sample entropy analysis to study the dynamics of resting-state networks in patients with early-course psychosis.

METHODS:

We used microstate analysis to transform resting-state high-density electroencephalography data from 22 patients with early-course psychosis and 22 healthy control subjects into sequences of characteristic scalp topographies. Sample entropy was used to calculate the complexity of microstate sequences across a range of template lengths.

RESULTS:

Patients and control subjects produced similar sets of 4 microstates that agree with a widely reported canonical set (A, B, C, and D). Relative to control subjects, patients had decreased frequency of microstate A. In control subjects, sample entropy decreased as template length increased, suggesting that sequence of microstate transitions is self-similar across multiple transitions. In patients, sample entropy did not decrease, suggesting a lack of self-similarity in transition sequences. This finding was unrelated to data length or microstate topography. Entropy was elevated in unmedicated patients, and it decreased in patients who were administered medication. We identified patterns of transitions between microstates that were overrepresented in control data compared with representation in patient data.

CONCLUSIONS:

Our findings suggest that patients with early-course psychosis have abnormally chaotic transitions between brain networks. This chaos may reflect an underlying abnormality in allocating neural resources and effecting appropriate transitions between distinct activity states in psychosis.

The brain relies on the coordinated activity of large-scale neural assemblies. This activity is evident in large-scale oscillations in the electroencephalogram (EEG) and networks in functional magnetic resonance imaging (fMRI). Proper functioning relies on the tuning of these networks and on well-timed transitions between neural assemblies. This coordination allows the brain to efficiently process information and adapt appropriately to incoming stimuli. The activity of these networks changes with behavior—for example, patterns of neural activity during sleep are different from those exhibited during wake time (1,2) and are disrupted during seizure activity (3).

Psychotic disorders are common and severe mental illnesses with poorly understood pathophysiology. Psychosis has been conceptualized as disruption in both the content and the flow of thought (4). Clinical descriptions of patients with psychosis detail bizarre, tangential, or circumstantial thought processes, unusual sensory experiences, and aberrant processing of sensory input. The dysconnection hypothesis proposes that these symptoms arise from dysconnectivity within and across brain networks (5).

EEG research provides a window into these purported abnormalities. Most of the energy in the EEG signal can be captured by a small number of characteristic EEG topographies called microstates (6). Microstates typically persist for tens of milliseconds before the brain enters another microstate (7). Multiple studies have identified 4 canonical microstates that are found in quiet rest, during sleep, and during performance of many tasks (7–9). The neural activity underlying these microstates partially overlaps with resting-state networks that were independently identified with fMRI (10). Microstate analysis enables investigators to study brain networks at a time scale more functionally relevant than the longer time scales available with fMRI (7). The functional role of microstates remains unclear. Although microstates were initially hypothesized to represent quantal units of thought, later studies have linked specific microstates to distinct cognitive tasks or to differential inhibition of components of the default mode network (11–14).

Microstate analysis provides a powerful tool to probe the functioning of brain networks in patients with psychotic disorders. Over the past 2 decades, investigators have identified potential abnormalities in the microstates of these patients (15). Studies have explored the microstate topography, duration, frequency, and transition probabilities. Interpretation of these studies is complicated by small sample sizes and variation in analysis techniques. Overall, the data suggest that one canonical microstate, microstate C, may occur more frequently in patients with schizophrenia, possibly at the expense of microstate D (15). However, these findings have not been replicated in all studies (16,17). In addition, 2 studies have reported that in patients with psychotic disorders there are more transitions from microstate D to C and fewer from C to D (17,18).

Entropy analyses have also been used to characterize neural activity in patients with psychotic disorders (19,20). Most studies have reported that patients with psychotic disorders, especially those early in the course of the disease and those who are medication naive, have increased entropy when compared with healthy control subjects. Regional increases and decreases in entropy have also been reported (21,22). The clinical heterogeneity of patient populations and the difficulty of relating EEG activity to its neural generators limit the ability of researchers to make connections between entropy and psychopathology (19,23).

We combined microstate analysis and entropy measures to probe how the dominant activity pattern of the brain transitions between large-scale networks. Microstate analysis enabled us to reduce the multichannel EEG data into categories that correlate with distinct distributions of neural activity. We hypothesized that we would identify a similar number of microstates in control subjects and patients and that the microstates would have similar topographies. We also hypothesized that there would be a relative increase of microstate C in patients, consistent with the prior literature. Calculation of entropy allowed us to quantify the predictability of microstate transitions. We hypothesized that patients would have higher entropy, reflecting less predictable transitions.

METHODS AND MATERIALS

Participants and Procedures

Study procedures were approved by the institutional review board of the Partners HealthCare System. We recruited 25 patients with early-course psychosis (within 3 years of initial diagnosis of a psychotic disorder) from inpatient units and outpatient clinics at McLean Hospital (Table 1) (24). We excluded individuals with a history of neurological disorders. Patients underwent an independent evaluation of their capacity to provide informed consent for participation. All participants provided informed consent. Patients completed a video-recorded Structured Clinical Interview for the Positive and Negative Syndrome Scale (25), and 5 symptom factors were computed (26). For patients taking antipsychotic medication, we calculated chlorpromazine dose equivalents using linear equations extrapolated from consensus dosage guidelines (27). We recruited 25 age-matched healthy control subjects using advertisements posted in the community.

Table 1.

Demographic Information

	Control Subjects	Patients
Sample Size	22	22
Age, Years, Mean ± SEM	23.1 ± 2.7	22.0 ± 2.7
Sex, nMale/nFemale	11/11	15/7
Chlorpromazine Equivalents, mg, Mean ± SEM	–	232.7 ± 181.0
Diagnosis, n
SZ/SZA	–	7
BP	–	12
Other	–	3
PANSS Positive Factor, Mean ± SEM	–	7.5 ± 2.8
PANSS Negative Factor, Mean ± SEM	–	11.4 ± 3.6
PANSS Disorganized Factor, Mean ± SEM	–	4.7 ± 2.1
PANSS Excited Factor, Mean ± SEM	–	5.8 ± 2.3
PANSS Depressed Factor, Mean ± SEM	–	4.4 ± 1.6

Note that this information was previously reported in Murphy and Öngür (24).

BP, bipolar with psychotic features; PANSS, Positive and Negative Syndrome Scale; SZ, schizophrenia; SZA, schizoaffective.

Electroencephalography

We collected EEG data in an electrically and acoustically shielded room using a 129 Ag-AgCl electrode Geodesic Sensor Net (Electrical Geodesics; Koninklijke Philips, Amsterdam, The Netherlands). Data were collected at a 1-kHz sampling rate with a vertex reference. Impedances were maintained below 65 kΩ. Three minutes of eyes-closed resting-state data were recorded with participants in a seated position. Participants were monitored via closed-circuit camera during this time to ensure that they remained seated with eyes closed. Data were preprocessed using 0.5- to 40-Hz bandpass filtering. Corrupted channels, identified by visual inspection and automated thresholding, were interpolated with spherical splines (28). A semiautomated procedure was used to identify and exclude artifactual segments of data such as eye movements. Data were then re-referenced to average reference. Data from 3 patients and 3 control subjects were excluded because of broadband signal artifact across all channels, reducing the final sample to 22 patients and 22 control subjects. A previous article based on this data set reported no differences in power between the groups in any frequency from 0.5 to 40 Hz and reported that both groups had voltage topographies dominated by posterior alpha activity (24).

Microstate Analysis

We used Cartool software by Denis Brunet (cartoolcommunity.unige.ch) to extract EEG microstates from resting-state data. We calculated global mean field power across all electrodes for each participant. We limited analyses to time points at which global mean field power had a local maximum because microstates tend to switch at or near global mean field power local minima (29,30). We ran a polarity-insensitive k-means clustering analysis on this downsampled data, with k ranging from 1 to 10 (7,30). The Krzanowski-Lai criterion was used to select the number of microstates for further analyses (29,31). The chosen set of microstates was then fitted back into the original data set. To calculate microstate fitting, for each time point in the data we chose the microstate map that most closely resembled it. This fitting process is polarity invariant and is driven only by the spatial topography of the EEG data (13,29).

Entropy Calculations

We used sample entropy to represent the complexity of the microstate sequences for each participant (32). Sample entropy depends on the data; a template length, m; and a tolerance, r. The sample entropy for a sequence is the negative natural logarithm of the conditional probability that two patterns that are identical for m points remain identical at point m + 1 within a tolerance r. Sample entropy is always positive, and lower values of sample entropy indicate that a sequence is more predictable.

For our analysis, we labeled the microstates with the numbers 1 to 4 and set r to 0.1. Because these labels are discrete and nonordered, this method ensured that only subsequences that were completely identical were counted. Because we were interested in studying the order of the microstates across multiple state transitions, we ranged our values of m from 1 to 10.

Statistical Analyses

Each recording had a unique distribution of microstate labels. To control for any effect of these differences on the sample entropy, for each recording we created 1000 random permutations of the microstate sequence labels such that the same microstate labels could not be adjacent. We calculated the sample entropy on each permuted sequence. We concatenated the resulting entropy values with the entropy value from the true sequence and used the resulting distribution to transform the true entropy value into a z score. These z scores were used to compare control subjects with patients and to correlate entropy with clinical features. MATLAB scripts (The MathWorks, Inc., Natick, MA) to calculate sample entropy on real and permuted microstate sequences have been provided in the Supplement.

RESULTS

Control Subjects and Patients With Early-Course Psychotic Disorders Have Similar Microstate Topographies but Different Microstate Distributions

Microstate segmentation of the resting-state EEG recordings from the control and patient groups produced 4 EEG microstate topographies for each group (Figure 1A). These topographies align with one another and with the 4 canonical microstates, A to D (7,8,9,31). Average correlation coefficients and standard errors between microstate maps and EEG data were .57 ± .01 for control subjects and .57 ± .02 for patients, indicating that the fits were similar for each group. Average microstate duration was reduced in patients relative to that of control subjects (44.0 ± 0.96 ms and 48.2 ± 1.02 ms, p = .005, unpaired t test, Cohen’s d = 0.9). For microstate duration, an analysis of variance showed evidence of an interaction between group and microstate (F_3,175 = 4.26, p = .006). Post hoc unpaired t tests showed that microstate A (37.70 ± 1.01 ms in patients and 44.14 ± 1.36 ms in control subjects, Bonferroni p_adjusted = .002, Cohen’s d = 1.1) and microstate C (48.95 ± 1.83 ms in patients and 56.28 ± 1.80 ms in control subjects, Bonferroni p_adjusted = .026, Cohen’s d = 0.9) had shorter duration in patients relative to control subjects.

Figure 1.

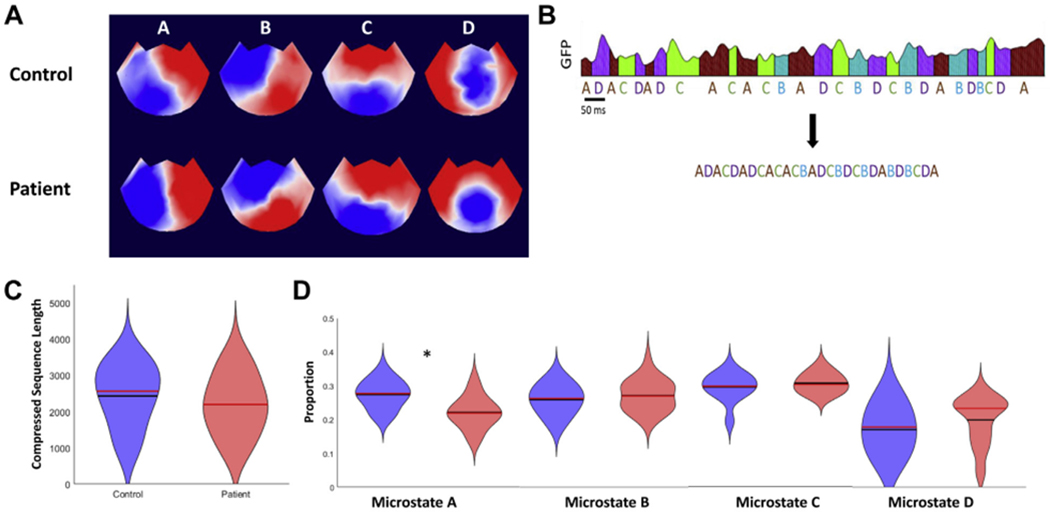
Microstate analysis and fitting. (A) Electroencephalogram (EEG) topoplots showing microstate topographies derived from quiet rest EEG recordings in control subjects and patients. Note that although red is positive and blue is negative, microstate analysis ignores polarity. The extracted microstates closely resemble the canonical 4 microstates A to D, which have been widely reported in the literature (62). (B) An EEG data set that has been fitted with microstates is then compressed by removing information about microstate duration. (C) Violin plot showing the distributions of compressed microstate sequence length for the control group (blue) and patient group (red) (63). The black lines are the means and the red lines are the medians. (D) Violin plots for the proportions of microstates A to D in the patient and control groups. *p_adjusted = .001. GFP, global field power.

Previous studies have explored the fractal structure of microstate sequences (10,18). To compare our data with these results, we embedded our microstate sequences into a random walk and calculated the Hurst exponent for each walk. In agreement with the findings of past work (33), we found average Hurst exponents >0.5 for both control subjects (0.74 ± 0.01) and patients (0.70 ± 0.01), suggesting long-range temporal dependence in microstate sequences.

To test this idea that microstate transitions are meaningful independent of duration, we compressed the sequences of fitted microstates by removing information about microstate duration (Figure 1B). We found no statistically significant differences in compressed sequence length between control subjects and patients (2432 ± 182 and 2196 ± 175, respectively, p = .363, unpaired t test) (Figure 1C). We compared the counts for each microstate label in the two groups. Analysis of variance showed an interaction between group and microstate (F_3,175 = 5.05, p = .002). Post hoc t tests showed that microstate A frequency was reduced in patients relative to control subjects (p_adjusted = .001, unpaired t test, Bonferroni corrected; Cohen’s d = 1.2). There were no statistically significant differences in the frequency of microstates B to D.

Entropy Decreases for Longer Microstate Patterns in Control Subjects but Not in Patients

We quantified the complexity of the microstate patterns for control subjects and patients using sample entropy calculated on the compressed microstate sequences (which do not contain information about microstate duration) (32). To evaluate complexity across several scales of microstate transitions, we ranged the value of the template pattern lengths, m, from 1 to 10. For each recording, we created 1000 random permutations of the compressed microstate labels such that adjacent microstate labels could not be identical. We calculated sample entropy on each permuted sequence with m = 1:10. At short scales (m = 1 and 2), the sample entropy in control subjects was indistinguishable from the permuted sequences. However, as m increased, the average sample entropy in control subjects was less than that of the permuted sequences (Figure 2A). For patients, we found that the sample entropy in true sequences was never statistically significantly different from the permuted sequences. To test whether this finding was related to the specific topographies of the control subject and patient microstates, we fitted each group with the microstates from the other group. As expected, given the similarity between the microstate topographies, we again found that entropy decreased after m = 3 in control subjects and did not separate from permutations in patients (Figure 2B). Although there was no statistically significant difference in sequence length between control subjects and patients, we wanted to determine whether the observed differences in entropy were related to sequence length. We found no correlation between sequence length and entropy at any pattern length in either patients or control subjects. Furthermore, we calculated mean entropy curves for the subgroup of control subjects with sequence length shorter than the mean patient sequence length (n = 5) and the subgroup of patients with sequence length greater than the mean control sequence length (n = 7) (Figure 2C). Within these subgroups, we again found that entropy in control subjects decreased after m = 3 by amounts similar to that seen for all control subjects, and we found no decrease in entropy in patients. We also found no statistically significant correlations between entropy at any scale m and microstate duration (all Bonferroni-adjusted p values were > .21).

Figure 2.

Entropy curves. (A) Pattern length (m = 1:10) vs. average entropy across participants. The left panel shows control data (blue curve, shaded region is standard error of the mean) and random permutations of control data (black line and black shaded region). The right panel shows patient data (red curve and red shaded region) and random permutations of patient data (black line and black shaded region) (B) The same analysis as in A but with control data fitted by patient-derived microstates and patient data fitted by control-derived microstates. (C) The same analysis as in panel (A) but only using control subjects with total sequence length less than the mean patient sequence length and only using patients with total sequence length greater than the mean control sequence length. (D) Violin plots of entropy z scores for control subjects (red) and patients (blue) at pattern length m = 3:10. The black lines are the means and the red lines are the medians. The dashed gray line indicates a z score of zero. *P_adjusted < .001 in panel (A) and P_adjusted = .03 elsewhere; P_adjusted < .001; **p_adjusted < .0001;.

To compare control subjects and patients, we used the sample entropy values for each of the permutations to transform the true sample entropy values into z scores. We compared the z scores at the pattern lengths m = 3:10 (Figure 2D). Even after correction for multiple comparisons, z scores for the control group were statistically significantly lower than for the patient group at all 7 template lengths. Cohen’s d for these comparisons ranged from 0.94 at m = 3 to 1.62 for m = 6.

Microstates Frequently Oscillate Between Microstate A and B and C and D in Healthy Control Subjects

Entropy for pattern lengths m > 2 in the control resting-state data was lower than expected from a random permutation of that distribution of microstate labels. This finding indicates that some patterns of microstate sequences preferentially recurred. We wanted to determine whether these patterns were similar across subjects. We analyzed pattern length m = 7 because the greatest entropy decrease in control subjects was for template length m = 6. We generated a list of all 2916 possible microstate patterns. For each subject, we counted the number of times each such pattern appeared in both the true data and the 1000 permutations. We used the values from the permuted data to generate z scores for the true data. We transformed the z scores to p values using a 2-sided hypothesis. To find Bonferroni corrections for multiple comparisons, we thresholded these p values at .05/(22 × 2916). For each pattern, we counted all the subjects in which the calculated p value was lower than this threshold value (Figure 3A). To exceed the threshold, a pattern had to be roughly 5 SDs more frequent than would be expected from a random permutation of microstate labels. Five patterns were statistically significantly increased in more than half of all control subjects: ABABABA, BABABAB, BCBCBCB, CDCDCDC, and DCDCDCD (Figure 3B). In the patient group, these patterns were statistically significantly more frequent in 2, 4, 3, 2, and 0 patients, respectively. The biggest difference between control subjects and patients was found for sequence CDCDCDC, which was increased in frequency in 18 of 22 control subjects and only 2 of 22 patients. Each of these patterns is a repeated oscillation between 2 microstates, and there are 2 frameshifted pairs. However, other repeated oscillations, such as DADADA or DBDBDB, were not overrepresented in the control data. In patients, no patterns were statistically significantly overrepresented in more than half of participants. In both control subjects and patients, no pattern appeared significantly less frequently than would be expected by chance given the distributions of microstate labels for that participant.

Figure 3.

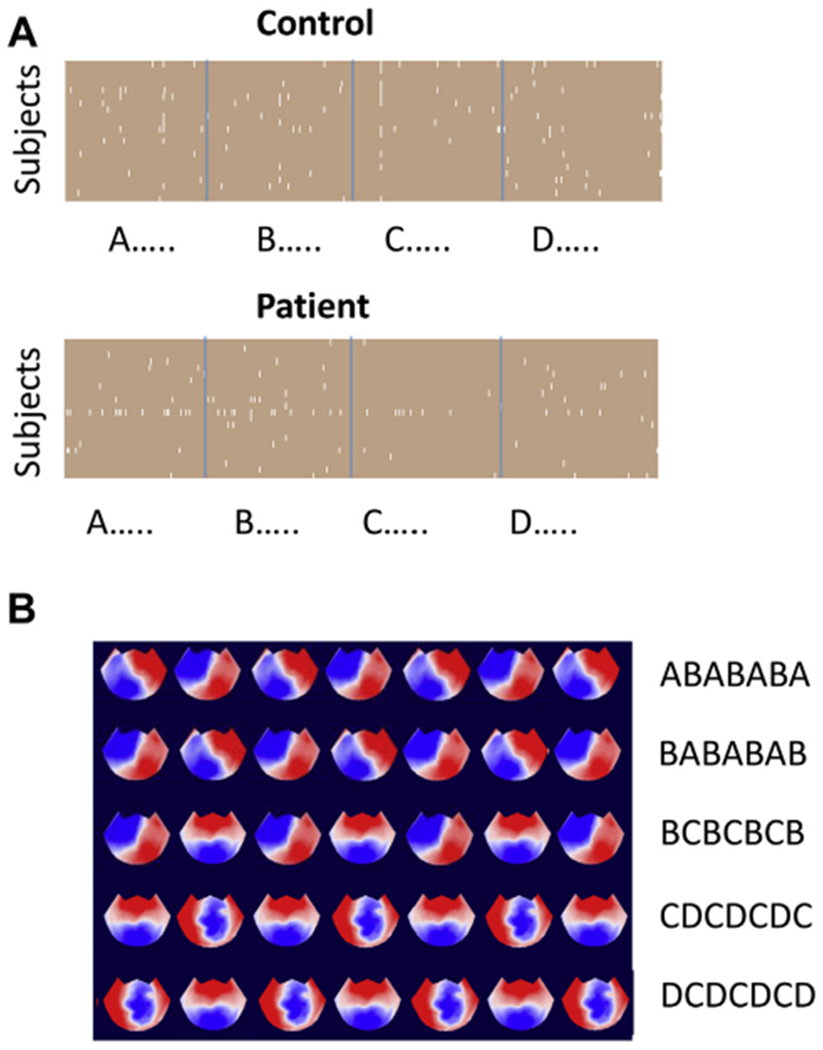
Analysis of microstate patterns of length 7. (A) Plots for control subjects and patients showing which patterns were statistically more likely than chance (white) in control subjects and patients. (B) The microstate patterns that occurred above chance in more than half of all control subjects.

Entropy Is Negatively Correlated With Medication Load

We evaluated whether entropy was related to medication or symptom burden. For each pattern length, we calculated the correlation between patient entropy z scores and chlorpromazine equivalents (27,34) (Figure 4A). At pattern lengths 7 and 8, there was a statistically significant negative correlation between z scores and medication load (Pearson’s r = −.62, Bonferroni-corrected p_adjusted = .023 for m = 7 and Pearson’s r = −.64, p_adjusted = .014 for m = 8) (Figure 4B). In other words, higher medication load was associated with z scores closer to the healthy control range. These results should be interpreted with caution given the limitations of using chlorpromazine equivalents to compare medication doses (27). The unmedicated patients in our sample all had z scores at or above zero, i.e., farther away from the healthy control range (Figure 4B).

Figure 4.

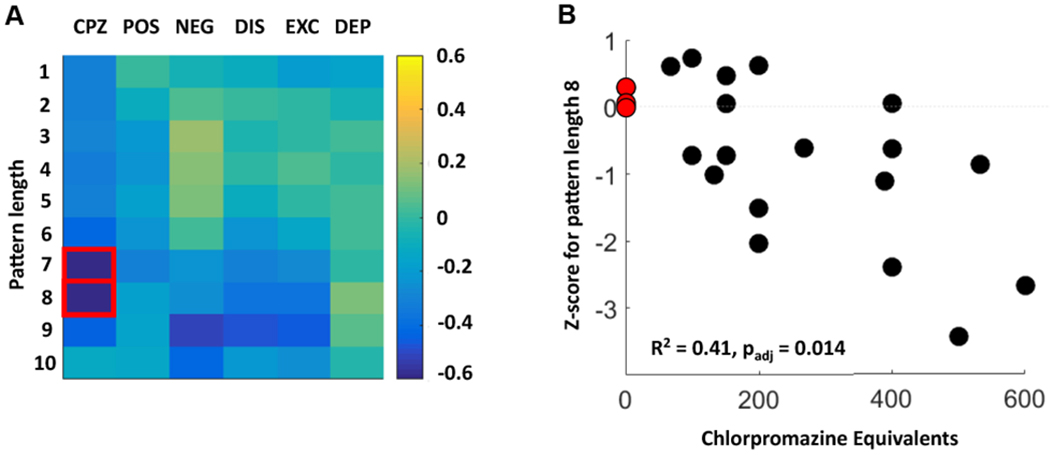
Correlations between entropy and clinical features in patients. (A) This grid shows the correlation coefficients for patients between entropy z scores for pattern length m = 1:10 and chlorpromazine (CPZ) equivalents in addition to 5 symptom factors calculated from the Positive and Negative Syndrome Scale. These symptom factors are positive symptoms (POS), negative symptoms (NEG), disorganized symptoms (DIS), excited symptoms (EXC), and depressed symptoms (DEP). The red boxes indicate statistically significant correlations after correction for multiple comparisons. (B) Scatter plot showing the relationship between CPZ equivalents (in milligrams) and entropy z scores for pattern length m = 8. Note that the 3 unmedicated patients (red circles) all had z scores close to zero. The dashed gray line indicates a z score of zero. p_adj, Bonferroni-adjusted p value.

We also calculated the correlations between z scores and 5 symptom factors derived from the Positive and Negative Syndrome Scale (26). No statistically significant correlation emerged between any symptom factors and z scores at any pattern length (Figure 4A).

DISCUSSION

We used microstate fitting and sample entropy to analyze—in a fully data-driven way—high-density resting-state EEGs from patients with early-course psychotic disorders and from healthy control subjects. In keeping with the findings from previous work, we found that data were captured by 4 microstates whose topographies aligned with those of the canonical 4 microstates (7,9). This finding is significant because most previous microstate studies have used EEG caps with far fewer channels than the ones used in this study, which indicates that canonical EEG microstate topographies are not driven by low spatial sampling (7). We hypothesized that sequences of microstates obtained from quiet rest would contain information independent of microstate. We found that at pattern lengths greater than m = 3, control subjects showed a high degree of self-similarity when compared with random permutations of the microstate labels, i.e., knowledge of the order of m consecutive microstates is useful in predicting the m + 1 microstate in the sequence. In contrast, patients showed no such self-similarity. This effect was observed whether each group was fitted to its own microstates or to microstates derived from the other group. The decreased entropy in control subjects was partially due to repeated oscillations between microstates A and B and microstates C and D. Finally, we report a negative association between medication and entropy, suggesting that the increased entropy in patients is not a medication effect.

Neurophysiological Correlates of Microstates

Distinct microstate maps are generated by distinct patterns of neural activity. During periods of eyes-closed quiet waking, microstate topography and transitions are largely driven by underlying patterns of cortical alpha activity (14). One EEG source-imaging study found that all 4 canonical microstates are related to activity in the posterior cingulate cortex and that the neural correlates of microstates B to D incorporate other components of the default mode network (35). This finding was partially supported by a subsequent source-imaging study that found common involvement of the posteromedial and anterior cingulate cortices (36). Furthermore, microstate A was related to neural activity in the auditory and insular cortices, while microstate B was related to activity in the visual and insular cortices (36). Combined fMRI-EEG imaging studies indicate that the neural assemblies generating microstates overlap with resting-state networks independently identified with fMRI (10,37,38). One study found that none of the canonical microstates was associated with the default mode network; rather, each microstate was related to a resting-state network: microstate A to the auditory network, B to the visual network, C to the salience network, and D to the attention network (10). However, a study using a different methodology and different set of microstates found that each microstate was related to activity in multiple resting-state networks, including the default mode network (38). Direct comparison between studies is hampered by differences in data acquisition methods and microstate segmentation algorithms. Furthermore, even within studies that used the canonical 4 microstates, there is significant disagreement about microstate topography, particularly for labels C and D (7). Nevertheless, the literature supports a connection between EEG microstates and fMRI brain networks based in part on the observation that microstate time series exhibit scale-free dynamics over time scales of 256 to 16,000 ms, which overlap with the time scale of fMRI (33). This finding suggests that fMRI resting-state networks, which are generally thought of as being stably activated for multiple seconds, may be transiently activating at the subsecond time scale of microstate analysis. Furthermore, source-imaging results suggest that the default mode network is composed of several hubs, whose differential inhibition via alpha activity produces distinct EEG microstates (14). In this model, transitions between microstates arise from changes in alpha activity within components of the default mode network as the brain cycles between a set of characteristic cortical alpha topographies. Therefore, microstates do not precisely align with fMRI brain networks; rather, they provide novel information about the brain’s connectional architecture that cannot be obtained with fMRI (14).

Microstates and Psychosis

A modest body of literature describes resting-state microstate abnormalities in topography, duration, frequency of occurrence, and transition probabilities in patients with schizophrenia (15,18,31,39,40). Microstate B may be shifted leftward and posterior in patients with schizophrenia (41). A recent meta-analysis suggests that duration of time spent in microstate C is elevated and that the duration in microstate D is reduced in patients with schizophrenia (15). Elevations and reductions have been reported for the duration of microstate B, and some groups reported increases in time spent in microstate A (17,18,41). Microstates B and D have decreased average duration in patients compared with control subjects (15,31). Reduced microstate duration has been reported in unmedicated patients, and it partially improves following treatment with antipsychotic medication (42,43). Control subjects are more likely than patients to transition from microstate A to C and from microstate D to A (16). Our finding of decreased microstate A in patients does not align with the literature discussed above. However, past results are from patients with schizophrenia only, as there have been no previous studies of microstates in bipolar disorder with psychotic features (31,44); such patients were included in our sample.

Complexity and Psychosis

Investigators have used entropy measures to characterize the complexity of EEG and magnetoencephalogram signals in patients with psychotic disorders (19,20). With these measures, investigators leverage the millisecond-scale temporal resolution of EEG and magnetoencephalogram to elucidate dysconnectivity within large-scale brain networks and abnormal temporal relationships between networks. The results have been mixed, and they depend in part on the measure chosen, spatial distribution of sensors, data preprocessing, behavioral state (i.e., resting vs. task), and clinical features of the patient population (20). Several studies, some of which included medication-naive and early-course populations, reported increased entropy in patients with schizophrenia (22,42,43,45–47). Elevated complexity was reduced but not eliminated by treatment with antipsychotic medication (22). However, other studies reported unchanged or decreased complexity in patients with schizophrenia (20,48–50). Task-related modulation of complexity is also abnormal in schizophrenia (45).

Low values of entropy suggest that data are highly predictable and regular, while high values indicate that data are chaotic and unpredictable. Data that are meaningfully complex have an intermediate value for entropy. Our findings indicate that sample entropy for microstate sequences decreases as the number of transitions being analyzed increases in control subjects but not in patients, indicating that EEG data from control subjects are more predictable than data from patients. On the other hand, our findings also indicate that control data have a structure that patient data do not.

Calculation of entropy requires the EEG data to be divided into discrete categories (50–52). However, these methods do not necessarily segment the data in a functionally meaningful way. We used EEG microstates to make a coarse-grained separation of the data into functionally relevant categories, recognizing that microstates are hypothesized to be the quantal units of brain information processing and that transition probabilities and low-order Markov models are not sufficient to capture the structure of microstate sequences (13,53).

Microstates, Complexity, and Psychosis

We identified novel patterns in how the brain switches between multiple resting-state networks, and we provide direct evidence for temporal structure in these switches created by the predominance of favored patterns of transitions between networks. We note that during quiet rest in control subjects, there is a pattern of repeated oscillations between visual and auditory resting-state networks and between salience and attention networks. Patients lack this structure and instead transition between networks in a more random fashion. The absence of structure across transitions in patients is in keeping with the dysconnection hypothesis of schizophrenia (5). Our findings align with the long-standing clinical conception of psychosis as a disorder of both the content and the sequencing of thought (4). The transition pattern that was most underrepresented in patients included repeated transitions between components of the salience network and the attention network. This may reflect the abnormal processing of salience information as hypothesized in the aberrant salience model of psychosis (54). Thalamic dysfunction has been repeatedly implicated in schizophrenia (55–57). Although thalamic neurons do not generally contribute measurable signals to the scalp EEG, the cortical alpha activity that drives microstates is shaped by interactions between cortical alpha generators and thalamic alpha pacemakers, including the lateral geniculate and pulvinar nuclei (58,59). Previous work suggests that cortical alpha generators are largely intact in psychotic disorders, suggesting that the microstate disorganization we report in this study may indicate failure of thalamic pacemakers to appropriately orchestrate transitions between global patterns of alpha activity (24). Tuning of the thalamic pacemakers depends in part on the action of metabotropic glutamate receptors and muscarinic acetylcholine receptors (58). Our findings are consistent with the hypothesis that psychotic disorders may be related to abnormalities in thalamic cholinergic and glutaminergic tone (58,60). The microstate sequence abnormalities that we report here were detected in a sample of patients with early psychosis, suggesting that they are not related to chronic exposure to antipsychotic medication or to long-term progression of disease. Future work should include studying the effect of anticholinergic medications on microstate sequences. The canonical 4 microstates also occur during sleep, when alpha activity is relatively low (8). The dominant EEG rhythms of sleep—spindles and slow waves—rely on different thalamic pacemakers, including the thalamic reticular nucleus (61). Future work should include studying microstate sequences during sleep in patients and healthy control subjects. If patients have increased entropy in sleep relative to control subjects, that would suggest broad-ranging deficits in thalamocortical loops as opposed to specific deficits in the pulvinar or lateral geniculate nucleus.

Limitations

One limitation of this study is that our cross-sectional design limits our ability to assess the effect of illness severity, progression, or medication exposure. These topics are worthy of future investigation. In addition, there is considerable variety in EEG microstate analysis techniques and results across laboratories, which makes identification of the physiological correlates of the microstates somewhat tentative (7). However, there is agreement that microstates arise from the coordinated activity of large-scale brain networks, and we present evidence using a high-density EEG system for aberrant transition patterns between these networks, independent of the identities of the networks. Finally, a transdiagnostic sample of patients makes it difficult to directly compare our results with those of previous work on patients with schizophrenia alone.

Conclusions

We analyzed microstates and microstate sequences during quiet eyes-closed rest in healthy control subjects and patients with early-course psychotic disorders. We found that 4 canonical microstates most parsimoniously explained the variance in the EEG signal. We used sample entropy ranging across multiple transition scales to calculate the complexity of the microstate sequences, independent of microstate duration. Patients had increased entropy across microstate transitions compared with control subjects. Our results provide evidence for abnormal transitions between large patterns of cortical inhibition, possibly because of subtle dysfunction of thalamic alpha pacemakers in patients with psychotic disorders.