Abstract
We review the literature on uncertainty shocks and business cycle research. First, we motivate the study of uncertainty shocks by documenting the presence of time-variation in the volatility of macroeconomic time series. Second, we enumerate the mechanisms that researchers have postulated to link uncertainty shocks and business cycles. Third, we outline how we can specify uncertainty shocks. Fourth, we postulate a real business cycle model augmented with financial frictions and uncertainty shocks. Fifth, we use the model to illustrate our previous discussions and to show how uncertainty shocks can be expansionary, a useful finding in several contexts.
Keywords: Uncertainty shocks, Business cycles, Financial frictions
1. Introduction
During the last decade, a vibrant literature has explored the role of uncertainty and its time-variation in driving business cycles.2 From the empirical side, Baker et al. (2016) have demonstrated that simple indices of uncertainty measured from newspaper articles, the number of federal tax code provisions set to expire in future years, and forecasters' disagreements clearly correlate with economic activity. In particular, macro uncertainty seems to be countercyclical: times of high uncertainty are times of low economic activity (at this moment, this statement does not imply any causal direction). Dozens of papers, too numerous to cite here, have asserted the robustness of this basic finding along with a multitude of modifications of the research design, econometric approaches, and data sets.
From a theoretical perspective, the work by Bloom (2009), Fernández-Villaverde et al. (2011), Fernández-Villaverde et al. (2015a), and Justiniano and Primiceri (2008) has presented equilibrium models where “uncertainty shocks,” i.e., increases in the standard deviation of the shocks that hit the economy, can account for a significant share of aggregate fluctuations. These papers move beyond Baker et al. (2016) and assert causality: uncertainty shocks drive part of the business cycle. An extensive literature has followed these pioneering studies and extended the theoretical models in many directions.
This paper reviews this literature on uncertainty shocks and business cycle research. In the interest of space, we will focus on equilibrium models of the business cycle with a representative agent in the tradition of most of the papers in Cooley (1995). To display many of the ideas, we will postulate, solve, and calibrate a real business cycle model with financial frictions.
This model will be rich enough to incorporate most of the mechanisms outlined in the literature linking uncertainty shocks with business cycles and, yet, simple enough to be understood quickly. For example, we will not add nominal rigidities or extra layers of real rigidities. And, instead of a multitude of shocks, we will have only six shocks –three level and three uncertainty shocks– joined in pairs of one level and one uncertainty shock. The first pair will work as demand shocks. The second pair will work as supply shocks. The third and final pair will work as financial friction shocks. The trinity of demand, supply, and financial shocks will capture the intuition often used by researchers to organize their thinking about business cycles and be easy enough to separate from each other.
We will organize the rest of our exposition as follows. Section 2 will document some basic time-series evidence that justifies the study of uncertainty shocks. Section 3 will review the different mechanisms that relate uncertainty shocks and aggregate variables in equilibrium models of the business cycle. Section 4 will discuss how to model uncertainty shocks. Section 5 will present a real business cycle model with financial frictions and time-varying uncertainty. Sections 6 and 7 will explain the computation and calibration of the model, including several methodological points of interest about how to handle the inherent non-linearities of models with uncertainty shocks. Section 8 will report our quantitative results in terms of moments of the model, the role of uncertainty shocks, its impulse-response functions, and persistence. Section 9 will offer some concluding remarks and propose lines of future research.
2. Why uncertainty shocks
Nearly every time series in macroeconomics displays time-varying volatility, that is, a standard deviation that changes over time instead of being stationary (Engle, 1982). To illustrate this point, we will work with three time series: i) a time series that is representative of aggregate real variables (output growth); ii) a time series that is representative of prices (the GDP deflator); and iii) a time series that is representative of policy instruments (the federal funds rate). However, these three series are just examples. Plenty of other series of interest, from risk premia or exchange rates to unemployment or tax rates, display similar features. Fernández-Villaverde et al. (2011) and Fernández-Villaverde et al. (2015a) show many more examples.3
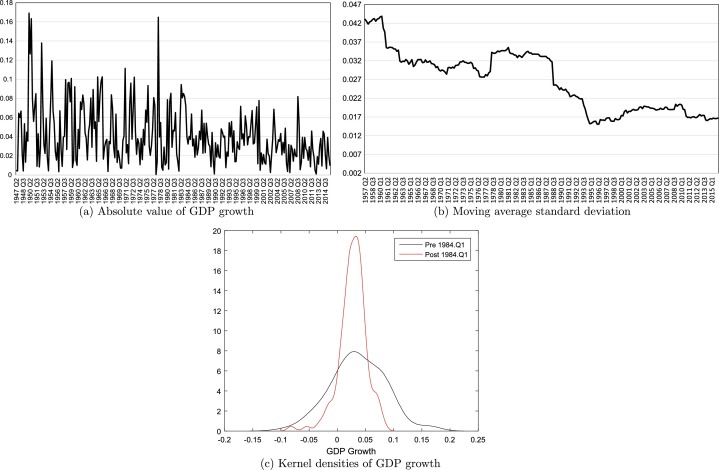
Panel 1 a of Fig. 1 plots the absolute value of GDP growth in the U.S. after World War II (we take absolute values to focus on volatility, not signs). Even the most casual observer can see that output growth fluctuates less at the end of the series than at the start.
Fig. 1.
GDP growth.
This observation is clearer in Panel 1b, where we plot a 10-year moving average standard deviation of the same series. This moving average standard deviation is a measure of the realized volatility of output growth.4 Especially during the 1980s, the realized volatility of output dropped at a fast pace and it has stayed low since then, even after the convulsions of the financial crisis of 2007-2008. This is, of course, the “great moderation” of business cycle fluctuations (Stock and Watson, 2003, and Bernanke, 2004), which –as Panels 1a and 1b show– survived until the health crisis of 2020 (whether it will return after the pandemic abates is too soon to tell).
An alternative way to report the same finding is to compute the kernel densities of output growth before and after 1984.Q1 (a conventional start of the “great moderation”). Panel 1c of Fig. 1 shows a much more concentrated density after 1984, with thinner tails. See Kim and Nelson (1999) and McConnell and Pérez-Quirós (2000), for similar findings about the change in volatility in the mid-1980s.
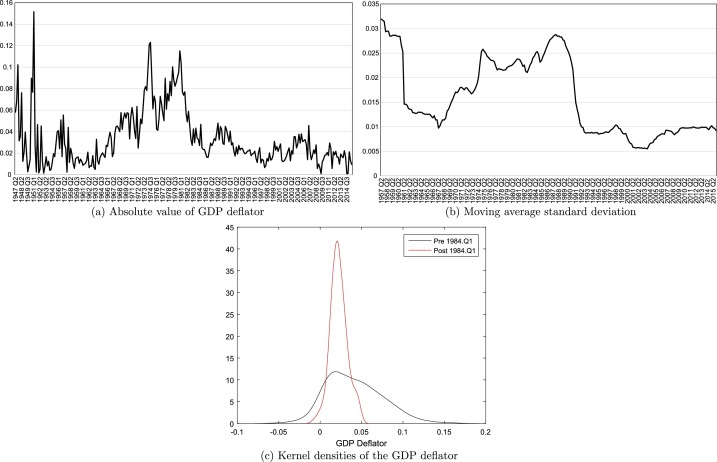
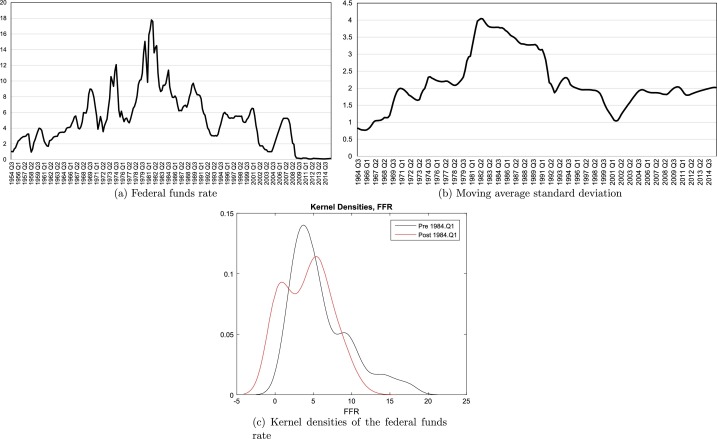
Fig. 2, Fig. 3 show the same results, but now with respect to the GDP deflator and the federal funds rate, respectively. Fig. 2 documents the big spike in inflation in the 1960s, the only substantial peace-time inflation in U.S. history, and its “conquest” in the 1980s (Sargent, 1999). Fig. 3 tells us a similar story, but even more sharply, with the period of zero (or close-to-zero) nominal interest rates at the end.
Fig. 2.
GDP deflator.
Fig. 3.
Federal funds rate.
As we mentioned before, the same properties of time-variation in volatility appear in many other time series. The literature on uncertainty shocks has paid close attention to financial variables (see Bloom, 2009, Jurado et al., 2015, and Arellano et al., 2019, among several others) and to eliciting how financial-market uncertainty interacts with the real sector of the economy. This point is essential to remember as our model, later on, will place financial frictions at the center of its dynamics.
How can we think about these changes in the volatility of the time series over time? One possibility is to consider that the economy has undergone some form of structural transformation. For example, the move from manufacturing into services and improved supply-chain management might account for a lower volatility of output (Davis and Kahn, 2008). Similarly, financial innovations in the early 1990s might have stabilized the economy (Guerrón-Quintana, 2009). And monetary policy might be conducted now with more deftness than in the past by responding more aggressively to inflation (Lubik and Schorfheide, 2004, and Cogley and Sargent, 2005).
However, there are so many examples of time-variation (with reversals in the direction of change!) that relying too much on structural transformation or better policies seems unwise. More importantly, when we try to capture the dynamics of macroeconomic time series with a vector autoregression (VAR) where we allow both for changes in the autoregressive coefficients and for variations in the matrix of variance-covariances of shocks, the likelihood function sharply prefers the latter as the primary driver of time-variation in volatility. This point was demonstrated in a classic paper by Sims and Zha (2006) and drove many researchers (including us!) into centering their study on changing standard deviations.
Thus, a more parsimonious approach is to consider that the shocks that induce aggregate fluctuations have time-varying volatility. Since a change in variance moves the dispersion of the future distributions of the shock, we can call these changes “uncertainty shocks,” (or second-moment shocks) in comparison with more traditional shocks to levels (of productivity, preferences, tax rates, etc.; all of them first-moment shocks). In Section 4, we will return to the question of how to model these uncertainty shocks, and we will define them more precisely.
Unfortunately, uncertainty cannot be measured directly in the same way as output or inflation. We cannot open a financial newspaper or visit the webpage of a statistical agency and read about the uncertainty in the economy from a well-laid table. To discipline the uncertainty shocks that we can introduce in a model and gauge their quantitative significance, researchers need to come up with measures of uncertainty.
The three most popular approaches in the literature have been to estimate a formal econometric model and use it to back up a measure of realized volatility and future uncertainty, to use some proxy of uncertainty, or to build surveys of subjective expectations of uncertainty (see Cascaldi-Garcia et al., 2020, for a recent survey of many measures of risk, uncertainty, and volatility).
The first route, estimating a formal econometric model, is followed by Fernández-Villaverde et al. (2011) and Fernández-Villaverde et al. (2015a). These papers propose a stochastic volatility process for the variables of interest (such as interest rates, risk premia, or tax rates) and estimate such a process using the likelihood approach (see Fernández-Villaverde et al., 2016, for methodological details). Section 4 will explain why a stochastic volatility process is a natural process to be taken to the data.
The second route is to search for a proxy of uncertainty. Bloom (2009) popularized the idea of using the VIX index of 30-day implied volatility on the S&P 500 stock market index. This proposal, however, has been criticized because it is hard to determine the direction of causality. Instead of uncertainty shocks triggering aggregate fluctuations, we can have aggregate fluctuations generating time-varying volatility in the stock market (in fact, given a standard stochastic discount factor model of asset pricing, part of the variance in the stock market should be the product of level shocks). More in general, an alternative reading of Fig. 1, Fig. 2, Fig. 3 is that economic fluctuations cause uncertainty to increase, not the other way around.5
A more direct proxy can be to count occurrences of events related to uncertainty. In an influential paper, Baker et al. (2016) proposed building policy uncertainty indexes through the aggregation of three components. The first component counts words related to uncertainty in newspaper articles. More words such as “uncertainty,” “unknowns,” and similar in any given period mean higher uncertainty. The second component counts the number of federal tax code provisions set to expire in future years: more tax code provisions set to expire means more uncertainty about future policies.6 The third component uses disagreement among economic forecasters as a proxy for uncertainty.
The idea of counting words related to uncertainty in newspaper articles has proven to be particularly popular. It is easy to do with modern statistical packages and search engines, and it can be combined with natural language processing, a booming sub-field of machine learning (see Blei et al., 2003, and, applied to uncertainty, Larsen, 2017).
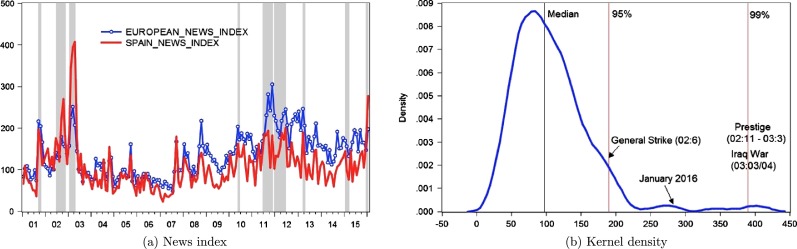
Fig. 4 shows an example of such a news index. Panel 4a plots, in continuous line, the European monthly index built by Scott R. Baker, Nicholas Bloom, and Steven Davis using articles from Le Monde and Le Figaro for France, Handelsblatt and Frankfurter Allgemeine Zeitung for Germany, Corriere Della Sera and La Stampa for Italy, El Mundo and El Pais for Spain, and The Times of London and Financial Times for the United Kingdom.7 The same panel also plots, in the lines with circles, the index for Spain between 2001:1 and 2016:1. Shaded areas show local peaks of uncertainty.
Fig. 4.
News and the density of uncertainty.
Panel 4b plots the kernel density of the Spanish index and points out well-known political events in Spain during the period. For instance, we see that the times of highest uncertainty were related to the Iraq War and the Prestige oil spill (which severely damaged the reputation of the government due to its perceived mismanagement of the accident). The uncertainty at the time was at the 99th percentile of the distribution. We also see that the uncertainty distribution is asymmetric, and it has a long right tail. In Section 8, we will see how this evidence of long tails motivates the study of two-standard-deviation uncertainty shocks.
One can easily relate peaks and drops in the news index with changes in economic activity (for instance, with a simple VAR or local projections) and obtain an estimate of the effects of this news on output, inflation, and other variables of interest. See Bloom (2009), Baker et al. (2016), and Baker et al. (2020a) for examples of well-known measurement estimation along those lines.
Finally, researchers can build surveys of subjective uncertainty by asking relevant agents, such as professional forecasters or CEOs. Among the studies focused on the evolution of uncertainty, we can highlight the monthly panel Survey of Business Uncertainty, which started in 2014 and now covers about 1,750 firms across all 50 states of the U.S. (Altig et al., 2019). This survey has documented that subjective uncertainty is highly predictive of forecast errors and, therefore, a useful instrument for empirical work. See Bachmann et al. (2013), Scotti (2016), Manski (2017), Awano et al. (2018), and Bloom et al. (2019) for further examples of this approach.
The question is, thus, how to build mechanisms that link these empirical patterns with standard economic theory.
3. Different mechanisms
Many mechanisms link uncertainty and its variation over time with aggregate fluctuations in economic models. Instead of reviewing each of them in detail, we will focus on three mechanisms that we consider the most important given the model with financial frictions that we present in Section 5. The first mechanism will be precautionary behavior. The second mechanism will be the Oi-Hartman-Abel effect. The third mechanism will be the real rigidities caused by financial frictions.
For those readers interested in complementing our exposition, Fernández-Villaverde and Rubio-Ramírez (2013) and Bloom (2014) are two concise reviews of the literature on uncertainty and business cycles up to its development a few years ago. These reviews dig deeper than we do into the microfoundations of why uncertainty may vary over time. Note also that, to keep the paper at a reasonable length, we will focus on the effect of uncertainty shocks in models with a representative agent and only discuss the implications of uncertainty shocks in models with heterogeneous agents in passing. Similarly, we will ignore the literature that relates uncertainty and long-run growth (for example, through the incentives to innovate in models of endogenous growth or the long-run effects of uncertainty on financial constraints). See Aghion and Banerjee (2005) for more details on such a subfield.
3.1. Precautionary behavior
The most transparent mechanism to link uncertainty shocks and business cycles is to have agents in the model whose preferences display precautionary behavior. When the utility function of an economic agent (usually an individual but, if we ignore for a moment the issues of aggregation, also a household, a firm, or another group) is concave, the agent dislikes uncertainty. Expected utility from consumption is lower than the utility from expected consumption:
| (1) |
where is the expectation operator, is the utility function, and c is consumption (which might be a vector of goods including services from durables, home production, and leisure, not just a scalar). Therefore, mean-preserving increases in the distribution of c will lower expected utility.
However, risk aversion does not necessarily imply that economic agents will behave differently (i.e., they will display precautionary behavior) than in the absence of uncertainty. A trivial example is to consider an endowment economy, where the stochastic process for c is exogenously given. Prices in equilibrium will move in such a way that the level of consumption will always be equal to the endowment, regardless of the level of uncertainty in the endowment.8
A more sophisticated example is the celebrated result of certainty equivalence first documented by Simon (1956) and Theil (1957). These researchers showed how, under some conditions on the objective function and the constraint set of a dynamic programming problem, the optimal action of a decision-maker under uncertainty who maximizes her expected utility is identical to the action that neglects uncertainty by maximizing utility under perfect foresight. Certainty equivalence will hold, for instance, when the objective function is quadratic and the constraints are linear. This may occur in the original formulation of the problem or it may appear as a consequence of a solution algorithm, such as the linear-quadratic approximation in Kydland and Prescott (1982), which yields a certainty equivalence solution (even when the original problem does not).
Leland (1968) and Sandmo (1970) broke this certainty equivalence property by showing that a sufficient condition for risk aversion to translate into precautionary behavior is the convexity of marginal utility. In this case, agents want to avoid large fluctuations in marginal utility across states of the world by saving a buffer stock of assets. Mathematically, risk aversion depends on the sign of the second derivative of the utility function (a negative sign means the agent is risk-averse). Precautionary behavior, instead, depends on the third derivative. In particular, agents will save more, everything else equal, if the third derivative of the utility function is positive (this is also known as “prudence”).9
To see this point, we can compare, in Table 1 , two commonly used utility functions in macroeconomics: a quadratic utility function and a CRRA utility function. We will assume that consumption is positive and, in the case of the quadratic utility, below the satiation point .
Table 1.
Utility functions and derivatives.
| Quadratic | CRRA | |
|---|---|---|
| Level | , α1,α2 > 0 | , σ > 0 |
| u′ | α1 − α2c | c−σ |
| u″ | −α2 | −σc−σ−1 |
| u‴ | 0 |
Both utility functions have positive first derivatives (i.e., more consumption is better than less) and negative second derivatives (i.e., agents are risk-averse). However, the third derivative of the linear-quadratic utility function is zero (i.e., we do not have precautionary behavior), but the third derivative of the CRRA utility function is positive (i.e., we have precautionary behavior).10 Note also how, for a CRRA utility function, the same parameter, σ, controls risk aversion and prudence (and, obviously, the elasticity of intertemporal substitution).
The extension of this explanation to the case with time-varying uncertainty is straightforward. Imagine that we have an uncertainty shock that increases the variance of productivity innovations, demand shifts, or fiscal and monetary policy changes. After an uncertainty shock, consumers with prudence will react by increasing their precautionary behavior, everything else equal.
What are the aggregate consequences of these changes in precautionary behavior? In a benchmark equilibrium business cycle model with flexible prices and a standard calibration, the effects are limited. With a CRRA utility function, precautionary behavior typically appears as precautionary saving. Thus, an increase in uncertainty leads to a higher demand for savings. But a higher demand for savings lowers the real interest rate that clears the investment-savings market. Often, and depending on the concrete details of the model, there is also a fall in demand for investment, which further lowers the interest rate. By inducing more consumption today, the lower interest rate undoes most of the contractionary effects of higher precautionary savings. See Basu and Bundick (2017) for a quantitative assessment of this mechanism.
This result also appears in models with heterogeneous agents and incomplete markets (Heathcote et al., 2009). In this class of environments, an increase in uncertainty, either at an individual or an aggregate level, leads to increases in aggregate savings and a lower interest rate. The effect on the cross-sectional distribution of wealth is, however, contingent on the calibration of the model. For instance, the persistence of the shocks to income is key to determining how agents will react to changes in uncertainty. When shocks are very persistent, higher uncertainty might translate into significant increases in precautionary behavior and aggregate allocations.
How can we get around this quantitative irrelevance result of time-variations in uncertainty? Our previous description of this result lays out a map of the different possibilities in front of researchers: selecting different parameter values, having several assets, and introducing nominal rigidities.
3.1.1. Different parameter values
The first possibility is to move away from standard parameter values, by either increasing risk aversion or the size of the change in uncertainty. The latter can be accomplished by selecting different target moments in a calibration or by modifying the specification of the model and the associated likelihood function.
Higher risk aversion can be achieved, for example, by using recursive preferences à la Epstein and Zin (1989). With these preferences, we can select parameters that deliver high risk aversion –and with it, high and varying risk premia– while keeping the relatively high intertemporal elasticities of substitution needed to ensure sound business cycle properties for the model (see Tallarini, 2000, for a documentation of this “quasi-separation” of prices and quantities).11
An even more radical departure from standard models than using Epstein-Zin preferences is to move to a specification of preferences that displays explicit ambiguity aversion as in Gilboa and Schmeidler (1989), Epstein (1999), and Epstein and Schneider (2007). Here, we can think about changes in uncertainty as being reflected in changes in the range of the multiple priors that an agent considers. Since usually in these models agents adopt a max-min policy rule that leads them to behave as if under a worst-case scenario, an increase in the range of priors is, loosely speaking, equivalent to the agents believing that some parameter or some shock will take its worst possible realization. Two notable examples of such a line of research are Ilut and Schneider (2014) and Bianchi et al. (2017). Since there is a link between Epstein-Zin preferences, concerns for robustness, and ambiguity aversion, most of the ideas in these last two paragraphs apply to each of three situations (Barillas et al., 2009, Maccheroni et al., 2006, and Strzalecki, 2013).
We can obtain higher uncertainty by increasing the probability of rare disasters (a small risk of a large macroeconomic shock), as argued in Gabaix (2012). We can think about rare disasters as the possibility of a war, a natural catastrophe, a pandemic, or massive political upheavals that disrupt economic activity.12 For instance, a rare disaster uncertainty shock can be a sudden change in geopolitical factors that increases the probability of a war in the near future, changes in climate that make a devastating flood in a coastal country more likely, or the appearance of a previously unknown virus that raises the chances of a major global pandemic.
In asset pricing, Bansal and Yaron (2004) illustrate how the combination of recursive preferences, a small long-run predictable component, and stochastic volatility on the consumption endowment can account for the equity premium, the risk-free rate, and the volatility of the market return, risk-free rate, and the price-dividend ratio. This message is reinforced by Drechsler and Yaron (2011), who document a quantitatively significant role for transient non-Gaussian shocks to fundamentals that affect agents' views of economic uncertainty and asset prices.
Fernández-Villaverde and Levintal (2018) make a similar point in the context of both standard real business cycle and fully fledged New Keynesian models. Even in the presence of production, Epstein-Zin preferences and rare disasters can match basic asset pricing observations while delivering excellent business cycle properties.
3.1.2. One-sided shocks
Motivated by our previous discussion, one can think about a change in the probability of a rare disaster as a change in the skewness of the distribution of shocks. Thus, a possible area of research, much unexplored, is to consider skewness shocks. Most increases in uncertainty in the real world are one-sided. A financial crisis increases the probabilities of a major recession, but not the probabilities of an unseen boom. And a pandemic, such as the 2020 COVID-19 crisis, usually means there is much more downside health risk, but it rarely means there is a simultaneous higher probability of much better health outcomes.
A quick-and-dirty way to get a first approximation of this problem in an equilibrium business cycle model is to consider a simultaneous negative level shock and a positive uncertainty shock (i.e., an increase in variance). This exercise, however, does not fully capture the shifting in distributions that we are envisioning.
In the context of models with heterogeneous firms, Salgado et al. (2019) have recently shown that a negative shock to the skewness of firms' productivity growth generates a persistent drop in output, investment, hiring, and consumption. In a related idea, Baker et al. (2020b) use natural disasters, terrorist attacks, and political shocks to show that uncertainty shocks lower growth. Hopefully, more research will soon come from this direction.
3.1.3. Several assets
Much of the attenuation of the effects of uncertainty shocks comes from the fact that, in a standard neoclassical growth model (and its real business cycle and New Keynesian model variations), agents only have access to one asset in positive net supply: physical capital.
Why is the presence of only one asset key? Because when uncertainty increases and agents want to engage in more precautionary behavior, the only asset in which that precautionary behavior can be reflected –physical capital– also becomes typically riskier. Capital is riskier either because we have more productivity uncertainty or its valuation becomes riskier (for example, because of higher discount factor uncertainty).13 There are, therefore, two counterbalancing forces: a higher demand for capital, because of precautionary behavior, and a lower demand for capital, because of higher risk.
Fernández-Villaverde et al. (2011) show a straightforward path out of this effect: the presence of several assets. Specifically, Fernández-Villaverde et al. (2011) model open market economies where agents can also save in foreign assets. If we assume, for instance, that higher uncertainty in Spain does not translate into higher uncertainty in Japan (or that the correlation among these assets is less than 1), then Spanish agents can shift from Spanish assets into Japanese assets and self-insure against higher uncertainty. Through the changes that such a shift induces on investment and labor supply both in Spain and in Japan, uncertainty shocks can have large real effects.
3.1.4. Nominal frictions
By preventing the counterbalancing effect of prices that attenuated the effects of uncertainty shocks above, nominal rigidities can increase the consequences of volatility and induce its own type of precautionary behavior.
A clear case is Fernández-Villaverde et al. (2015a). In this paper, firms encounter nominal rigidities while setting up prices: they need to set up a price before seeing the realization of shocks and must pay a cost to change it. Firms are more worried about setting a relative price that is too low ex-post than too high. A relative price that is too low ex-post forces the firm to sell too much at an unfavorable price (New Keynesian models assume a full-service obligation at posted prices). A relative price that is too high ex-post, instead, compensates for the low sales with a high margin. In other words, the profit function is asymmetric with respect to the relative price: it falls more quickly to the right of the optimal relative price than to the left. The strength of this effect depends positively on the elasticity of substitution among goods.
A higher level of uncertainty, by increasing the dispersion of where the relative price will fall ex-post, induces an upward pricing bias. Firms will increase their expected mark-up and, thus, reduce the percentage of times their relative prices are too low ex-post. However, a higher mark-up increases the distortions in the economy, lowering output, hours worked, investment, and consumption. This last point is remarkable. In many other models of uncertainty shocks, firms are induced to lower investment after uncertainty spikes. However, since the economy is as productive in the current period as before, consumption must increase to clear markets. Higher consumption is, however, counterfactual. By highlighting the role of the upward pricing bias and the distortions it creates in allocation, Fernández-Villaverde et al. (2015a) can fix this problem.
3.2. The Oi-Hartman-Abel effect
In the previous subsection, we focused on precautionary behavior, typically in the form of saving and pricing decisions. We now analyze how uncertainty can affect the production decisions of the economy. We will discuss first the Oi-Hartman-Abel effect and, in the next subsection, the consequences of real rigidities.
Our starting point for doing so is to go back to Oi (1961), Hartman (1972), and Abel (1983). Imagine that we have a firm that uses capital, , rented at rate , and labor, , paid at wage to produce a final good with a Cobb-Douglas production function
where is the productivity level at period t. Assume as well that the production function shows decreasing-returns-to-scale . The optimality conditions for the firm are:
| (2) |
| (3) |
where and . These optimality conditions lead to a period profit , where .
These results show how the input demands and profits are convex on . Thus, a mean-preserving increase in the uncertainty regarding will increase, everything else equal, the ex-post dispersion of input demands, profits, and output.
The key in this example is that the firm, by endogenously choosing its size, can take advantage of a higher volatility. When good shocks arrive, the firm can expand, and when bad shocks arrive, the firm can contract. The concavity of the production function ensures that such decision rules deliver higher profits when fluctuates due to uncertainty shocks than when is constant.14
Interestingly, the closer the firm is to constant-returns-to-scale, the larger is the effect, until it completely collapses when we reach and the size of the firm becomes indeterminate. However, if there are adjustment costs to capital or some other friction that prevents a constant-returns-to-scale firm from fully adjusting to shocks, we will recover a “quasi-Oi-Hartman-Abel effect.” This mechanism will appear, later on, with the quantitative results of our model. On the other hand, if the inputs are entirely fixed, for instance, because we have a putty-clay technology as in Gilchrist and Williams (2000), the effect will disappear.
A related situation appears in search models in the labor market. Leduc and Liu (2016) show how, in a model with search frictions and nominal rigidities, an increase in uncertainty resembles an aggregate demand shock because it increases unemployment and lowers inflation. Cacciatore and Ravenna (2020) present a related mechanism where occasional deviations from efficient wage setting trigger a strong state-dependent amplification of uncertainty shocks.
3.3. Real frictions
The most common real friction in models with uncertainty shocks is the presence of non-convex adjustment costs in investment as in Bertola and Caballero (1990), Dixit and Pindyck (1994), Abel and Eberly (1994), and Bloom (2009). When we have these adjustment costs, firms typically follow Ss rules. Firms have a band of inactivity where they do not adjust their capital. If the shocks move the target capital too far away from the existing capital (that is, the firm moves outside the Ss band), the firm will incur the non-convex adjustment cost and invest.15
Bloom (2009) points out that if uncertainty about the future increases, the Ss band will become wider, as firms want to be more cautious before readjusting capital. Then, in the short run, fewer firms will move outside the Ss band, and investment will fall. The effect will be particularly salient if the distribution of firms has a lot of mass close to the bands, perhaps due to some past aggregate shocks. In the absence of an uncertainty shock, many of these firms would have jumped out of the band in the current period.
However, since the economy is still as productive as before, consumption must increase to clear markets (recall our discussion above when we analyzed nominal frictions). Thus, one needs to enrich the model with mechanisms that prevent this counterfactual increase in consumption.
In our model in Section 5, we will tackle a different real friction that has received comparatively less attention: financial frictions.16 By changing the distribution of future realizations, uncertainty shocks modify the probability of a financial friction binding in the future (or the severity of the constraint). Thus, economic agents will undertake actions today to protect themselves against such realizations. For example, if capital provides liquidity services that are particularly valuable when the financial constraints are more severe, the agents will increase their investment in the current period in the shape of “precautionary investment,” a close relative of the option value effect of Bernanke (1983) and Dixit and Pindyck (1994). Or, if getting external financing is harder when uncertainty is higher, firms might keep more cash on hand. We will return to these ideas in Section 8.
4. How to model uncertainty shocks
The next question we face is how to model, in a simple yet effective way, the changes in uncertainty over time. To make things more concrete, imagine that we have the volatility, , of some random variable of interest , such as productivity or a preference shifter, that evolves as:
| (4) |
To simplify the exposition, we are assuming that follows an AR(1), but the extension to more general structures is straightforward.
The literature has identified three main alternatives to specify : stochastic volatility, GARCH processes, and Markov regime switching. Stochastic volatility (SV) models the evolution of as an ARMA process, often an AR(1) of the form:
| (5) |
The AR(1) is written in logs to ensure .17 We will call the “uncertainty shocks” in contrast with the “level shock” . This neat separation between uncertainty and level shocks allows an easier isolation of the effects of the former in the data and in the equilibrium economic model. Also, we rescale the variance of the uncertainty shocks to make them invariant to changes in their persistence .
We usually assume that the uncertainty and level shocks are uncorrelated. Nevertheless, it is quite direct to correlate and if needed (Fernández-Villaverde et al., 2011). This correlation is sometimes called the “leverage effect” of level shocks on uncertainty shocks because, in asset pricing, one can get this correlation through the presence of leverage in a firm's balance sheet. Also, nothing prevents us from having innovations that are not Gaussian, such as in Cúrdia et al. (2014). Since models with uncertainty shocks need to be solved with non-linear solution methods in any case, we can deal with a large class of distributions for the innovations.
Many researchers are attracted to SV because of its simplicity. For example, with an AR(1) specification, we only have to deal with two new parameters: , the persistence of , and υ, the standard deviation of the innovations to volatility (σ, the mean of volatility, still needs to be estimated when we take volatility as constant). Also, SV models are easily estimated using sequential Monte Carlo methods, either by themselves or jointly with the rest of the equilibrium business cycle model (Fernández-Villaverde et al., 2016). As we will discuss later, sequential Monte Carlo methods are particularly well-adapted to massive parallelization.
Despite its parsimony, SV can capture much of the dynamics of the data. Also, the combination of exponents of in equation (4) and levels in its evolution (5) shifts the distribution of the volatility into flexible shapes that can accommodate many time series. See Shephard and Andersen (2009) for a more complete discussion.
The second approach is to model as a GARCH process (Bollerslev, 1986):
that is, the variance is a function of its own past and the squared scaled innovation (). As we argued with SV, instead of our simple GARCH specification, we could think about much richer structures as in the many incarnations of GARCHs proposed in econometrics (Bollerslev, 2008).
The main difference between SV and GARCH is that, in the latter, there is only one shock, , driving the dynamics of the level and volatility of . Therefore, it is impossible to separate a volatility shock from a level shock: higher volatilities are triggered only by large past level innovations.
In reduced-form time series econometrics, since we are mainly concerned with forecasting, this constraint is not much of an issue. However, when we deal with equilibrium business cycle models, the assumption is too restrictive. Furthermore, while estimating time-series GARCHs is much easier than estimating an SV model, solving an equilibrium business cycle model with either GARCH or SV shocks is roughly equivalent in terms of complexity. Finally, SV models tend to do better in terms of fitting the data (Nakajima, 2012). Therefore, we see GARCH specifications as clearly dominated by SV for studying uncertainty shocks in dynamic macroeconomics and we will not discuss them further.
The third approach to modeling the evolution of is to specify a Markov regime-switching structure. For instance, we can assume that follows a Markov chain that takes two values, and , where L stands for low uncertainty and H stands for high uncertainty (). The transition matrix is, then:
Even with only two points, different choices of and capture a large range of interesting behaviors. A typical example is calibrating , which can be read as low uncertainty being the regular times and high uncertainty as the rare times (this is similar to our idea of rare disasters in Section 3, but now in terms of uncertainty). Extending the Markov chain process to an arbitrary n number of points (or even to induce variation in the entries of the transition matrix) to encompass a richer set of events is straightforward (Hamilton, 2016).
How do we compare SV and Markov regime-switching models? There is no obviously superior approach. SV assumes that uncertainty varies as a continuously changing process. Markov regime-switching models evolve more abruptly, with discrete jumps interrupted by periods of constant uncertainty.
Some researchers can argue that a continuously changing process better reflects their reading of the evidence. For example, the uncertainty about future fiscal policy might evolve daily as news about the state of the economy arrives or the political game in Congress unravels day-by-day. Other researchers can reply that some events are better characterized as discrete jumps, such as the election of a new president or the appointment of a new governor of a central bank.
Many time series of interest probably share both continuous and discrete components, and we could consider an encompassing model where the change in the standard deviation is given by:
where is is a discrete jump with a Bernoulli scheme distribution (this class of models is popular in finance; see Bates, 1996).
The challenge for this encompassing specification is that with fewer than 300 observations, as we have in the U.S. national income and product accounts (and much fewer for other countries), estimating such a model is a tall order.18
A small technical advantage of the SV specification is that we can take derivatives with respect to the volatility level, which we cannot in a Markov regime-switching specification. Taking derivatives will be convenient when, in Section 6, we defend the use of perturbation methods to solve equilibrium models with uncertainty shocks. This advantage will make us opt for SV in the model in the next section.
On the other hand, SV has its own problems. For instance, if the real process has a discrete jump, the SV specification will “anticipate” the change by showing changes in volatility before they happen (Diebold, 1986). The likelihood function (or most other estimating functions) dislikes huge changes in one period and prefers a sequence of smaller before and after the actual change to an exceptionally large that would account for the jump.
We are now finally ready to introduce our real business cycle model with financial frictions and uncertainty shocks.
5. Our model
To illustrate the impact of uncertainty shocks on aggregate fluctuations, we propose a standard real business cycle model augmented with a financial friction in the tradition of Kiyotaki and Moore (1997). In this economy, time is discrete, and there is a continuum of households with measure one. Each household has a unit mass of members who are ex-ante identical. However, in the middle of every period, family members are separated into entrepreneurs and workers. Each member receives a shock that determines her role within the period (Shi, 2015). An individual can be an entrepreneur with probability π or a worker with probability . Since a law of large numbers applies in this economy, π is also the fraction of individuals that become entrepreneurs. An entrepreneur can invest in capital, but she does not work. In comparison, a worker cannot invest, but she can work. Both entrepreneurs and workers can trade equity claims in the financial market subject to constraints to be specified below. In particular, entrepreneurs cannot raise enough funds to invest at an efficient scale because they need to keep some minimum “skin in the game” equity position. Occupations are assigned for one period only. In the next period, all the members' identities are reshuffled.
For parsimony, we will introduce only three level shocks in the model: i) a “supply-side” productivity shock; ii) a “demand-side” preference shock; and iii) a “real-rigidity” financial friction shock. Associated with each of these level shocks will be three corresponding uncertainty shocks, for a total of six shocks. While six shocks might not be enough to capture all the dynamics in the data, it will be sufficient to illustrate the main mechanisms that link uncertainty shocks with aggregate fluctuations and that we explained in Section 3. Other supply, demand, or rigidity shocks (such as price and wage stickiness) will, to no small extent, behave in similar ways and we can skip them in the interest of transparency (see Fernández-Villaverde et al., 2015a, and Justiniano and Primiceri, 2008, for much richer models with uncertainty shocks).
5.1. Three stages
A period is divided into three stages: i) decision making by the household; ii) production; and iii) consumption and investment. In the decision stage, all members of the household start the period united and share their assets, which are equal to equity claims. One equity claim, with price , gives its holder the ownership of one unit of capital. Thus, is also the total amount of capital of the household and its valuation.
Next, the aggregate shocks to exogenous state variables are realized. Because, at this stage, all the members of the household are identical, the head of the household divides the equity claims among the members evenly. These members also receive contingency plans to follow after they are assigned roles. If the agent becomes an entrepreneur, she would invest units of the consumption good, consume units of the consumption good, and make necessary trades in the stock market to ensure that she would hold units of equity claims at the end of the period. In contrast, if the member becomes a worker, she would supply units of labor, consume units of the consumption good, and make necessary trades in the stock market to ensure that she would hold units of equity claims at the end of the period. We will discuss below how the head of the household decides these instructions. After receiving their directives, the members depart to the market. The members remain separated for the rest of the period.
At the beginning of the production stage, each member receives the shock whose realization determines whether the individual is an entrepreneur or a worker. Next, these members move to the input markets, and they rent their labor and capital services to a representative competitive firm. The capital services are the product of the total units of capital, , and its utilization rate, . This utilization rate controls depreciation, . A higher utilization rate causes faster depreciation according to:
Here, for and is depreciation in the deterministic steady state (DSS). In this formulation, we can have , which we interpret as capital being used above the average rate for which it was designed.
The representative competitive firm produces a final good using the inputs rented from the members of the household with a constant-returns-to-scale Cobb-Douglas production technology:
| (6) |
The final good can be used for consumption or investment. Here, is a technology shock, which both households and firms take as given and evolves as an AR(1) process:
| (7) |
We normalize to 1 (this is just a choice of units) and impose the reflective barrier . Given our calibration and the fact that we will focus on studying impulse-response functions around the DSS, such a barrier is irrelevant in our computations.19
Equation (7) incorporates time-varying volatility into productivity . In particular, the volatility also obeys an AR(1) process:
| (8) |
with mean and persistence . This is an example of the SV specification we discussed in Section 4 and that we argued is particularly convenient for equilibrium business cycle models. The innovation to volatility, , is the first of the uncertainty shocks that we consider in this model and, by shifting productivity, it can be interpreted as a “supply-side” uncertainty shock.
Let and denote the rental price of capital and the wage rate, respectively. Therefore, the optimality conditions for the firm are the common equalities of marginal productivities of inputs to their prices:
and
After production, workers receive wage income, equity holders collect dividends, and a fraction of capital depreciates.
In the third stage of the period, consumption takes place, and entrepreneurs seek finance to undertake investment projects. To do so, an entrepreneur has access to a linear technology that transforms units of the final good into units of new capital.
The period ends after the events in the three states. The members of the household get together, their identities are reset, and the next period begins.
5.2. Constraints of the head of the household
The contingency plans that the head of the household provides to each of its members must meet several constraints. The first constraint is that the plans must satisfy the budget constraint of the entrepreneurs:
| (9) |
and the workers:
| (10) |
The right-hand side of equation (9) indicates the resources available to entrepreneurs. First, entrepreneurs have the return from renting their equity holdings at utilization rate in the inputs market, . Second, they have , their depreciated equity claims valued at price . Third, entrepreneurs have the net value of their investment, , determined by the difference between the price of the new capital, , and its cost, . In Subsection 5.4, we will return to this last term to explain its importance. The left-hand side of equation (9) shows that those resources can be used either for the consumption of the entrepreneur, , or the purchase of equity claims, . The interpretation of equation (10) is analogous to our description of equation (9), except that the worker does not invest but she has labor income .
The second constraint is that the total equity position of the household must be equal to the sum of the equity positions of its entrepreneurs and workers:
| (11) |
where, recall, π is the fraction of individuals that become entrepreneurs.
The third constraint is that the contingency plans cannot avoid the financial frictions in the economy. In particular, an entrepreneur cannot raise enough funds to finance all her capital holdings. In the case of new capital, , an entrepreneur can issue at most of equity and must retain . In the case of existing capital, , an entrepreneur can sell at most a fraction of it and must retain .
These limits ensure that entrepreneurs keep a minimum “skin in the game” in their investment and, thus, a sufficient incentive to fulfill their contractual obligations to outside investors. See, for example, the evidence about the limitations of external financing gathered by Hennessy and Whited (2007), and the follow-up literature. Summing the two financial frictions, we derive a lower bound to the entrepreneur's equity holdings:
| (12) |
The financial constraints induced by the minimum “skin in the game” condition (12) are different from those in models that emphasize the existence of idiosyncratic productivity risk in the tradition of Bernanke et al. (1999), Cooley and Quadrini (2001), and Buera et al. (2011). These alternative constraints imply that highly productive firms cannot borrow as much as they would desire. Condition (12) highlights, instead, that incentives need to be scaled by the stakes of the game and that, consequently, both high- and low-productivity firms face financial constraints. In that sense, we are closer to the spirit of Jermann and Quadrini, 2012, who assume a stochastic level of productivity common to all firms. Condition (12) also allows for a straightforward aggregation and related constraints have been shown to trigger the non-linear and multimodal dynamics of aggregate variables that are otherwise difficult to replicate (see Adrian et al., 2019, and Fernández-Villaverde et al., 2019a).
In our specification of the financial constraint, we have two different parameters, one for new capital, , and one for existing capital, ϕ, to capture the idea that the difficulty in evaluating the quality of an investment and inducing the right behavior on the part of the entrepreneur is different in new projects than in ongoing ones. At this moment, we are not assuming that one parameter value is larger than the other, just that they can be different.
Furthermore, while is time-varying, ϕ is constant. This distinction captures the idea that there are more fluctuations in the conditions surrounding new investment than in reselling existing capital. Sometimes the new investment is much harder to evaluate and monitor than existing capital. For example, this can occur when most investment in the economy is related to the arrival of a new general-purpose technology, and outside investors know little about it (or they know less than insiders). On other occasions, new investment is not harder to evaluate than existing capital. In our previous example, this can occur when most investment in the economy is adding to a mature general-purpose technology. In the former case, is low (the entrepreneur can issue little outside equity against hard-to-evaluate new projects). In the latter case, is high (the entrepreneur can issue more outside equity).20 See Stock and Watson (2012) for the correlation between uncertainty and financial shocks, Jurado et al. (2015), Caldara et al. (2016), and Alessandri and Mumtaz (2019) for measurements of how uncertainty regarding financial markets fluctuates in the data and for its possible interpretations, and Alfaro et al. (2018) for a related and complementary model of financial frictions and uncertainty shocks.
To capture the idea that some new technologies are harder to monitor than others, we assume that the salable part of investment, , follows an AR(1) process:
with reflecting barriers at , mean θ. Again, given our calibration and quantitative exercises, the numerical consequences of the reflecting barriers for are minor for the ideas in this paper.
The volatility of this process is another AR(1) process:
| (13) |
This financial friction volatility will be the second source of uncertainty shocks in our model and we will call it the “financial friction” uncertainty shock.
Financial frictions also create an equivalent lower bound to equation (12) for the case of workers' capital holding:
| (14) |
However, this friction does not bind in equilibrium. Since workers are net buyers of equities in the equilibrium we are interested in, we have that always holds and, thus, equation (14) is automatically satisfied and we can forget about it.
Finally, there are non-negativity constraints for , , , , and , but we ignore these as well because they do not bind either along the equilibrium path.
5.3. The problem of the head of the household
The head of the household chooses directives for its members to maximize the household's total utility:
| (15) |
subject to the budget constraints (9) and (10) and the financial constraints (11) and (12). Here, is the discount factor, ρ is the parameter controlling the elasticity of intertemporal substitution, η is the parameter controlling the labor supply of workers, and is a preference shock shifter.
This preference shock shifter is a stand-in for fluctuations in tastes, demographics, and fiscal policy, among others, that we do not model explicitly. We will impose the conventional normalization and assume that it changes as an AR(1) process:
| (16) |
Through the variable , equation (16) introduces the third and final source of time-varying volatility in our model: a “demand-side” shock. As we did before, we will assume that the evolution of also obeys an AR(1) process:
| (17) |
The structure of this equation and the parameters follow the same interpretation as in equations (8) and (13). We can interpret as a “real-rigidity” financial friction uncertainty shock.
5.4. Inspecting the problem of the household
To understand the problem of the household better, we multiply equation (9) by π and equation (10) by , add them, and use equation (11) to aggregate equity holdings and obtain:
| (18) |
Equation (18) is a standard budget constraint at the household level except that the depreciation rate is a function of utilization, , and, more importantly, because we have the last term of the right-hand side, . Let us spend some time analyzing its importance.
If , i.e., if the price of equity is the cost of producing one extra unit of capital, we have and we revert to a standard household budget constraint. If , i.e., if the price of equity is above the cost of producing one extra unit of capital, relaxes the budget constraint. If , the contingency plan of the household calls for , so we can ignore this possibility. In other words, the household can make a profit out of investment: the household takes one unit of the final good and obtains one unit of capital with a valuation above one.
But, because funding is limited by the financial frictions, there is a limit to how much the household can benefit from this scheme. Specifically, substituting equation (9) into equation (12), we find the upper bound on :
| (19) |
The left-hand side of equation (19) is the minimum amount entrepreneurs have to self-finance to conduct investment . This amount is smaller than , the quantity of the final good invested, because entrepreneurs can issue of outside equity against the new capital. The right-hand side of equation (19) is the maximum liquidity available to entrepreneurs, equal to their equity income, , plus the value of the equity that can be sold to outside investors after depreciation, , minus their consumption, . We can think of equation (19) as the feasibility constraint for investment.
We can draw three implications from equations (18) and (19). The first implication is that, when , the term with disappears from the household budget constraint (18) and any level of satisfying equation (19) can be optimal. In equilibrium, will be determined through the choice of . Intuitively, investment and equity purchases are perfect substitutes because, when , the price of existing capital is identical to the marginal costs of creating new capital and the inequality constraint (19) does not bind.
The second implication is that, if , the inequality constraint (19) must bind at the optimum. If not, the household could increase by without violating equation (19) and make an extra profit. This increase would loosen the household budget constraint, allowing the household to raise utility by purchasing an additional quantity of the final good for consumption. In other words, if the household can make money from investment, it should utilize this opportunity up to the limit.
The third implication is that the capital price must be strictly less than the inverse of in equilibrium. If not, we would have that and the inequality constraint (19) would hold for an arbitrarily large positive . Because also holds in this case, the household could relax the budget constraint (18), which would violate market clearing. Intuitively, if is not strictly less than the inverse of , entrepreneurs could fully finance the costs of investment by issuing outside equity, and they would be able to engage in an unlimited amount of arbitrage.
As in Shi (2015), we will restrict our attention to the most interesting case in which the equilibrium price of capital always exceeds one. Then, the second implication above gives us that the inequality constraint (19) always binds and the third implication that . Then, we can combine equations (18) and (19) to obtain:
| (20) |
Now we see why the last term of the right-hand side in the previous equation is key. It is a product of three components: i) the fraction of entrepreneurs π; ii) the liquidity held by entrepreneurs after consumption, ; and iii) the liquidity services implied by the financial frictions . Since , these liquidity services, , are positive. An entrepreneur can convert one unit of liquidity into units of capital by leveraged investment, each of which is worth in the market. Hence, is the price of this liquidity for the household head.
5.5. Optimality conditions
Once we have derived our modified household budget constraint (20), we can find the optimality conditions of the household head for , , , , and by maximizing the utility function (15) subject to equation (20).
The optimality condition for labor supply is:
This condition is standard: the household head equates the marginal rate of substitution of leisure for consumption to wages. Importantly, since the members of the household who become workers are free from the liquidity concern, there is no wedge between the marginal rate of substitution of leisure for consumption and wage. This result does not imply, however, that financial frictions do not have consequences for labor supply. Both and are different from what they would otherwise be because of investment changes along the equilibrium path due to those frictions.
The optimality condition for the intra-household consumption allocation ( vs. ) is:
This equation shows a wedge between the entrepreneur's marginal utility from consumption and the worker's, . Specifically, the entrepreneur's marginal utility is larger than the worker's because liquidity services, , are positive. The reason comes from the budget constraint (20). The entrepreneur's consumption increases the uses in the left-hand side of the equation and reduces the resources on the right-hand side. In comparison, the worker's consumption increases the uses on the left-hand side while leaving resources untouched. In other words: the household head understands that the entrepreneur's consumption has a higher opportunity cost than the worker's. Every extra amount of resources that the household head allocates to the consumption of entrepreneurs reduces the liquidity of the latter and, with it, the additional profits that investment delivers under financial frictions.
The Euler equation for investment (or equivalently, for equity claims and, hence, intertemporal allocations) is:
This condition determines the price of capital . Notice that the worker's marginal utilities are in the stochastic discount factor because workers are the marginal investors purchasing the outside equity. We also have the ratio of of preference shifters that tell the household head how much to discount the present relative to the future with respect to the average discount factor β. As we discussed before, the term in the right-hand side summarizes the benefits of holding equity, among which the last term is for providing liquidity to entrepreneurs.
The last optimality condition is with respect to the utilization rate of capital. The condition equates the marginal return of using the capital at a higher rate with the marginal depreciation it triggers.
The competitive equilibrium for this economy is standard, and, in the interest of space, we skip its explicit definition. It is worthwhile, however, to recall that the market-clearing conditions for final goods, factor services, and equity are, for all t:
Finally, the capital accumulation rule relies on the investment by entrepreneurs and the decisions on the utilization rate of capital .
6. Computation
Because our model has no closed-form solution, we solve it numerically. The solution method is standard, and it is described in detail in Fernández-Villaverde et al. (2016). We first find the DSS of the model.21 Next, we take a third-order approximation in levels of the system of equations characterizing the equilibrium around such a steady state.22 Third, we compute the generalized impulse response functions, GIRFs, of variables of interest to different shocks (Koop et al., 1996, and Andreasen et al., 2018). In particular, we will report the GIRFs in percentage points from the DSS, when all the other shocks are at their mean levels.
Three points deserve further discussion. First, our choice of a perturbation solution. Models with uncertainty shocks are high-dimensional. In addition to the standard state variables (i.e., capital, preference shocks, productivity levels, etc.), we need to keep track of the volatility levels, which become additional state variables when they are time-varying. In our case, we have seven state variables: the three level shocks, the three uncertainty shocks, and capital. Thus, dynamic programming and projection methods, both of which suffer from an acute curse of dimensionality, can be hard to implement. Perturbation, in comparison, can handle large state spaces without a problem and often delivers outstanding accuracy even far away from the perturbation point (Aruoba et al., 2006, and Caldara et al., 2012).
A promising alternative to perturbation is Taylor projection. As described in Fernández-Villaverde and Levintal (2018), Taylor projection is a hybrid of perturbation and projection methods that yields excellent accuracy even when the shocks are large, the solution of the model presents high curvature, and the state variables are far away from the DSS. Indeed, an advantage of Taylor projection is that the series expansion can be undertaken in points different, for instance depending on values of the state variables. Fernández-Villaverde and Levintal (2018) show how a Taylor projection can handle models with time-varying rare disasters, like those described in Section 3, quickly and efficiently.
An even more radical departure with respect to existing solution methods is the use of machine learning algorithms, such as neural networks and deep learning. Thanks to a smart choice of basis functions and a simulation approach to the selection of coefficients weighting these basis functions, these algorithms can break the curse of dimensionality and deal even with the strongest non-linearities. Therefore, they are particularly promising for this class of problems. See Fernández-Villaverde et al. (2019a) for details.
Second, we perform a third-order perturbation because we are interested in tracing the effects of an uncertainty shock. As we discussed in Section 3, a first-order perturbation is certainty equivalent and, therefore, not useful to study uncertainty shocks. A second-order perturbation incorporates the effects of uncertainty shocks, but only in terms involving cross-products of level and volatility shocks. It is in the third-order perturbation that we find terms in the solution that only involve uncertainty shocks and, hence, we can compute their GIRFs (which is, intuitively, a partial derivative over time). Fernández-Villaverde et al. (2015b) present a formal proof of this claim.23
Sometimes, and for accuracy purposes, one may need to go to higher perturbation orders, but for our model, in this paper terms of order higher than three are of minor quantitative importance. See, nevertheless, Levintal (2017) for examples and advice on how to implement such higher-order perturbations.
Third, we compute GIRFs because, once one is dealing with a non-linear solution, the responses of variables of interest to shocks are state-dependent: they are a function of the size and sign of the shock, and the point in the state space where the economy is at the arrival of the shock. In comparison, in a linear model, the regular impulse response functions are independent of the point in the state space where the economy is, and their shape is just a scale up or down of the size and sign of the shock.24
7. Calibration
Our next step is to take the model to the data. To do so, the literature has opted for one of two approaches. The first route is to estimate the model formally using econometric tools. When the model is solved using a third-order perturbation, this can be easily done by building the moments of the ergodic distributions of variables of interest and minimizing a quadratic distance to the analogous moments in the data. This point is often crucial because, when the model is solved non-linearly, the first moments of the ergodic distribution and the DSS can be far away from each other due to precautionary behavior (although, in our current model, this concern is not of great importance; see Table 3 below). Andreasen et al. (2018) show how this moment matching can be done in a few seconds by providing analytic formulae for all the relevant expressions.
Table 3.
Selected variables and their moments.
| Variables | Benchmark |
No Un. Shocks |
Financial Un. |
Fin. and Demand Un. |
||
|---|---|---|---|---|---|---|
| DSS | Mean | Std. | Std. | Std. | Std. | |
| ce | 0.51 | 0.51 | 0.07 | 0.47 | 0.53 | 0.90 |
| cw | 1.16 | 1.15 | 0.08 | 0.50 | 0.56 | 0.81 |
| l | 0.35 | 0.35 | 0.01 | 0.55 | 0.76 | 0.99 |
| k | 18.78 | 17.45 | 3.44 | 0.49 | 0.60 | 0.93 |
| u | 1.00 | 1.01 | 0.10 | 0.48 | 0.62 | 0.96 |
| y | 1.42 | 1.42 | 0.12 | 0.48 | 0.63 | 0.76 |
| q | 2.26 | 2.32 | 0.28 | 0.50 | 0.61 | 0.90 |
Alternatively, we can use a particle filter to evaluate the likelihood function implied by the model and, then, rely on a Markov chain Monte Carlo to either sample from the posterior (if we specify a prior and adopt the Bayesian approach) or search for a maximum (if we stay within a frequentist paradigm). Fernández-Villaverde (2010) and Fernández-Villaverde et al. (2016) explain these ideas in detail. See also Guerrón-Quintana (2010) for advice in the selection of observables to feed into the likelihood function. One advantage of sequential Monte Carlos (such as the particle filters) is that they are particularly amenable to massive parallelization, an enormous advantage in an era of graphic processing units (GPUs), field-programmable gate arrays (FPGAs), and cloud services. See Fernández-Villaverde and Valencia (2018) and Peri (2020) for tutorials on how to do so.
The second route is to implement a standard calibration. Since the goal of this paper is to illustrate how uncertainty shocks affect aggregate fluctuations, we follow this latter route: it is simpler than a formal structural estimation, and it saves us plenty of space that we can put to good use in providing further intuition.
To match data from national income and product accounts, we pick a quarter of a year as our period. Many of the parameter value choices are standard in the literature. For instance, we set the discount factor to and the parameter controlling risk aversion to . Similarly, we set the utilization rate to 1 in the steady state and the elasticity of to 0.33 as in Comín and Gertler (2006).
We follow Shi (2015) in setting the fraction of investors to and the capital share to , and in assuming that the fraction of new equity θ is equal to the steady-state resealability ϕ.
We move now to our explicit targets. We calibrate three parameters –the steady-state resealability, ϕ, the curvature in leisure in the utility function, η, and the capital depreciation rate δ– using three observations from the U.S. economy commonly employed in business cycle research: the aggregate hours of work in the DSS (1/3), the ratio of capital to annual output in the DSS (3.30), and the ratio of annual investment to capital in the steady state (0.075).
Our last task is to determine the parameters of the six shocks. We start with the persistence of the level shocks. A conventional value for the persistence of technology, , is 0.95 (Cooley and Prescott, 1995). For symmetry, we pick the same persistence for preferences, , and the financial friction, . We deem these parameter values as reasonable given the empirical evidence from Bloom et al. (2018) and Fernández-Villaverde et al. (2015a). All the persistences of the uncertainty shocks are set to 0.75, roughly around the mean of the persistences estimated by Fernández-Villaverde et al. (2015a).
Next, we need the means of uncertainty shocks. As a target for the mean of the demand uncertainty, , we use the estimate of in Fernández-Villaverde et al. (2015a). For the mean of the technology uncertainty, , we use from Cooley and Prescott (1995). For the mean of the financial friction uncertainty, , we use from Guerrón-Quintana and Jinnai (2019a).
Finally, we select the scale of the uncertainty shocks (i.e., the parameters , , and ) to yield that a one-standard-deviation positive innovation to the uncertainty shocks doubles its level. The literature on uncertainty shocks typically studies relatively large shocks, such as two- or three-standard-deviation innovations. The reason is that these are the range of changes in uncertainty associated with events such as geopolitical crises, financial turbulence, political upheavals, and similar developments. This area of research does not seek to replace regular level shocks, such as productivity or demand innovations that drive fluctuations in average quarters, but to complement them by studying the consequences of large events. Thus, all the GIRFs to uncertainty shocks reported in Section 8 plot the evolution of the aggregate variables after a two-standard-deviation positive innovation to the corresponding uncertainty shock.
Table 2 summarizes our calibration (and where u.s. stands for uncertainty shock).
Table 2.
Parameters and calibration targets.
| Parameter | Value | Calibration target |
|---|---|---|
| β: discount factor | 0.994 | Exogenously chosen |
| ρ: relative risk aversion | 2 | Exogenously chosen |
| π: fraction of entrepreneurs | 0.06 | Annual fraction of investing firms = 0.24 |
| η: curvature in leisure utility | 1.525 | Hours of work = 1/3 |
| α: capital share | 0.36 | Labor income share |
| δ0: capital depreciation rate | 0.016 | Annual investment/capital = 0.065 |
| δ1: slope depreciation function | 0.013 | Pinned down by steady state |
| δ2: curvature depreciation function | Comín and Gertler (2006) | |
| ϕ: resealability | 0.095 | Capital stock/annual output = 3.30 |
| θ: mean fraction of new equity | 0.095 | Set equal to ϕ |
| ρd: persistence of preferences | 0.95 | Exogenously chosen |
| ρA: persistence of technology | 0.95 | Cooley and Prescott (1995) |
| ρθ: persistence of financial friction | 0.95 | Exogenously chosen |
| : persistence of u.s. | 0.75 | Fernández-Villaverde et al. (2015a) |
| σd: volatility of preference u.s. | Fernández-Villaverde et al. (2015a) | |
| σA: volatility of technology u.s. | Cooley and Prescott (1995) | |
| σθ: volatility of financial friction u.s. | Guerrón-Quintana and Jinnai (2019b) |
8. Results
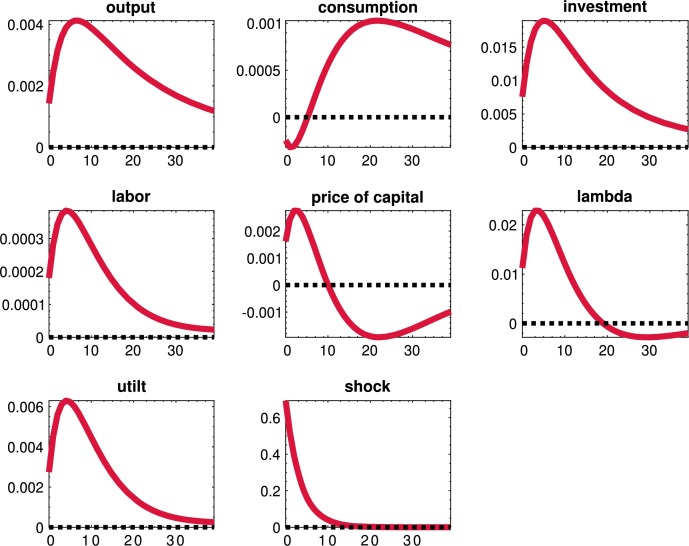
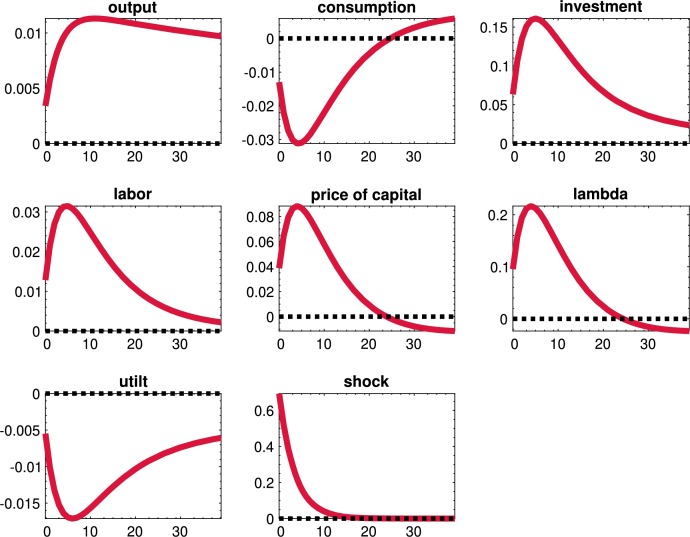
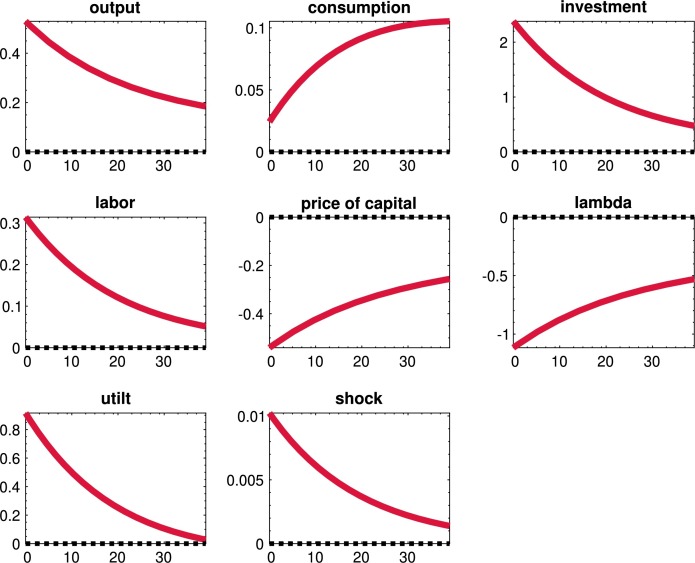
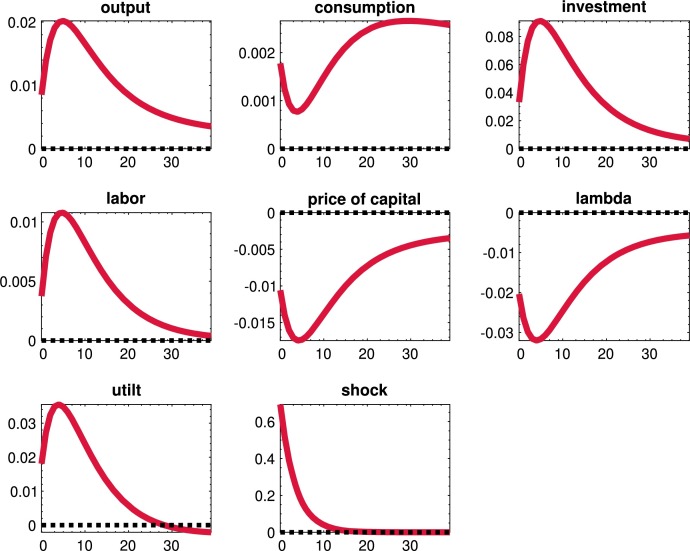
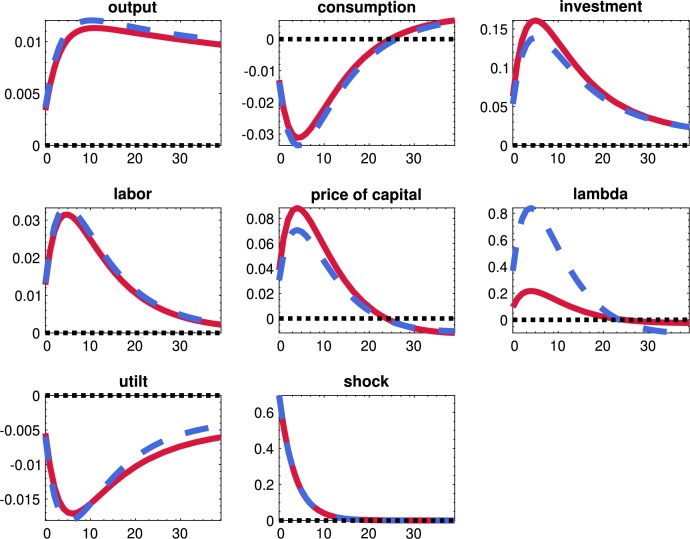
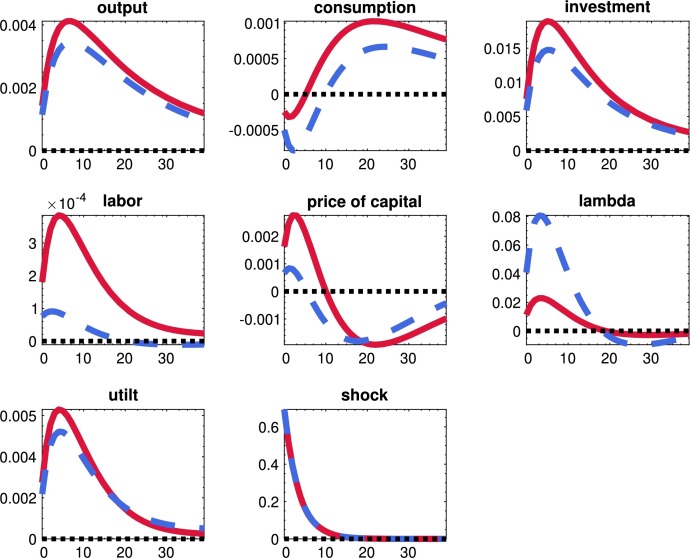
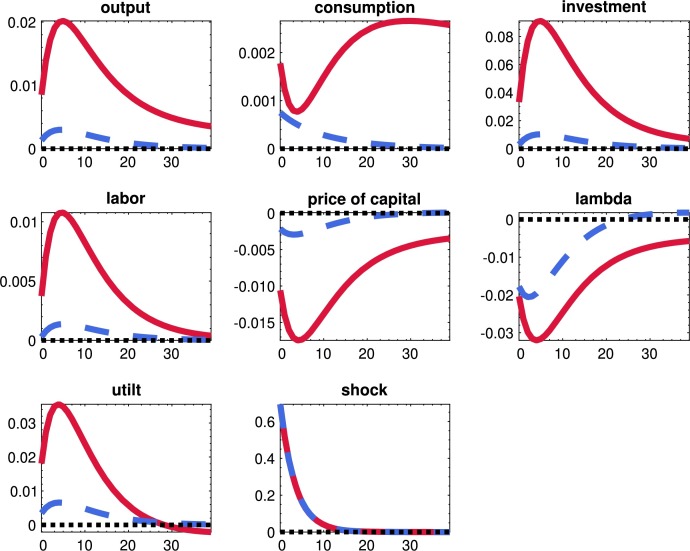
We now study the quantitative effects of the uncertainty shocks in the model. We will do so in three steps. In the first subsection, we will report some moments of our economy, and we will document the importance of uncertainty shocks to account for business cycle research by switching them on and off in different combinations. In the second subsection, we will analyze the dynamics of aggregate variables after uncertainty shocks to preferences, productivity, and the financial friction. In the third subsection, we will study how the propagation of the three uncertainty shocks changes as we modify the tightness of the financial friction. A central part of the discussion regarding uncertainty shocks has been how much persistence they can generate, and this subsection helps in framing such a discussion.
8.1. Moments of the economy and the role of uncertainty shocks
Table 3 presents the first and second moments for selected variables in our model. The three columns under the “Benchmark” umbrella report the DSS, the mean of the ergodic distribution (“mean”), and the standard deviations (“std.') of each variable.
By comparing the DSS and mean columns, we can gauge the correction for risk that the shocks introduce in the economy. Due to the presence of level and uncertainty shocks, households lower their exposure to risk by reducing their holdings of physical capital (17.45 in the mean of the ergodic distribution vs. 18.78 in the DSS). While capital provides precautionary savings against shocks, it also exposes households to financial shocks. In particular, if liquidity increases in the economy, the value of capital drops. Overall, this latter channel weighs more on the household's decisions than the precautionary savings mechanism. The reduction in the amount of capital increases its mean price by around 3% (2.32 in the mean of the ergodic distribution vs. 2.26 in the DSS) and its utilization rate (1.01 in the mean of the ergodic distribution vs. 1.00 in the DSS).
In terms of volatility, the ratio of the standard deviation of output to its ergodic mean, 0.085, is 0.085. This figure corresponds to around 70% of the observed volatility of filtered output after 1984 (Gali and Gambetti, 2009). Given that we do not incorporate nominal frictions, which account for 18-30% of volatility in models close to this one (Christiano et al., 1999 and Christiano et al., 2005), this result shows that our model can account for a crucial component of aggregate fluctuations. Other volatility ratios, such as consumption over output, are in line with the data. However, our model fails to generate any meaningful variations in hours worked since we did not incorporate labor market frictions or fiscal shocks that we would require to effectively move the labor supply (this point has been understood since at least Christiano and Eichenbaum, 1992).
We can now assess the importance of uncertainty shocks in driving aggregate fluctuations. Since a critical issue regarding uncertainty shocks is to assess how much they contribute to aggregate fluctuations, we will document the moments implied by four variations of the model: with all the uncertainty shocks, with no uncertainty shocks, with just the financial uncertainty shock, and with the financial and demand uncertainty shock. For clarity of exposition, we will skip the other combinations of uncertainty shocks since those are less relevant for our investigation. Also, since we are working with a non-linear model, we cannot perform a conventional variance decomposition: we have cross-product terms between the shocks that reinforce their contribution to fluctuations. Instead, we switch the different uncertainty shocks on and off in each variation of the model.
The column “No Un. Shocks” in Table 3 shows the standard deviation of different variables when the level shocks are in place, but the uncertainty shocks are not. The standard deviations are expressed as a fraction of their counterpart in the benchmark scenario. For our calibration, the level shocks account for a bit more than 50% of the fluctuations of all variables of interest.
This result documents two key lessons. First, uncertainty shocks are an important component of business cycles, contributing perhaps to slightly less than half of aggregate fluctuations. Second, they are somewhat less important than level shocks. A researcher should not think about the latter as a replacement of the former but as a complementary mechanism. Think, for example, about the health crisis of the spring of 2020: the U.S. economy experienced both a considerable negative productivity shock (as many workers could not operate their factories and shops) and a large uncertainty shock (as it was extremely difficult to forecast how long this situation would last). See Dingel and Neiman (2020) and Brinca et al. (2020) for evidence on the former and Baker et al. (2020a) for the latter. Both the level and the uncertainty shocks likely reinforced each other.
The column “Financial Un.” in Table 3 reports the standard deviations when the level shocks and the uncertainty shock in the financial sector are activated. The shocks combined accounts for around 60% of the variables' volatilities. This finding supports the view that financial uncertainty shocks help us accounting for around 10% of aggregate volatility, with peaks of importance when the uncertainty shock is as high as three or four standard deviations (such as during the financial crisis of 2007-2008).
The column “Fin. and Demand Un.” documents the standard deviations when all the shocks except the uncertainty in productivity are turned on. This last column shows that the financial and demand uncertainty shocks are the critical drivers among the uncertainty disturbances and that the shocks to uncertainty in productivity have a minor impact except for output. This finding is hardly surprising since the main friction in our model is placed in the demand part of the economy and that the estimated uncertainty shocks to productivity in the U.S. economy are small. See, for further documentation, the GIRFs in Fig. 6 for the small impact of uncertainty shocks to productivity. This last result would change in economies that have more significant shocks to productivity or, as argued by Aguiar and Gopinath (2007), where there are shocks to the trend growth of the economy.
Fig. 6.
Impact of an increase in uncertainty on productivity shock. NOTE: Variables correspond to percentage deviations from their DSSs.
8.2. The dynamics of uncertainty shocks
Our next step is to analyze the dynamics of the economy after an uncertainty shock. In the interest of concision, we will not report the GIRFs of level shocks to preferences and productivity (these GIRFs are, though, rather conventional). To ease interpretation, we will include the GIRFs of the level shock to the financial friction.
8.2.1. Uncertainty shock to preferences
Fig. 5 displays the GIRFs to an increase in the uncertainty of the preference shifter, our “demand-side” shock, that doubles its standard deviation (center panel, bottom row). That is, upon impact, the volatility of goes up to (recall the scaling in our calibration).
Fig. 5.
Impact of an increase in uncertainty on preference shock. NOTE: Variables correspond to percentage deviations from their DSSs.
We see in Fig. 5 that, after the preference uncertainty shock, output (left panel, top row), investment (right panel, top row), and labor (left panel, middle row) go up, while consumption falls (center panel, top row). Higher uncertainty about future preferences means that the household faces a larger probability of an event where marginal utility is very high (remember that the utility function is multiplied by the demand shifter ). The household also faces a larger probability of an event where marginal utility is very low, but such an event is of lower concern for the maximization problem because of the concavity of the utility function.
To limit the effect of these high marginal utility events, the head of the household orders an increase in precautionary savings. More concretely, the head of the household instructs its members to consume less, save (i.e., invest) more, and work harder than before. The strong desire to save is more than enough to offset the decline in consumption, resulting in a boom in output. In the absence of nominal rigidities, labor increases to meet the additional production. Additionally, higher savings from workers raise the demand for equity, and hence its price, (center panel, middle row). Consequently, the liquidity services (right panel, middle row) increase.
The shock leads to relatively persistent deviations, with output reaching its peak at around 12 quarters after impact. The model generates hump-shaped GIRFs in output, hours worked, consumption, and investment despite the absence of habit formation and adjustment costs in investment. These GIRFs are a remarkable finding since simulations in Basu and Bundick (2017) show that real business cycle models fail to generate hump-shaped dynamics after a preference uncertainty shock.
Our model triggers those responses because of two forces. Upon impact, demand for new capital rises, which pushes the price of capital up and increases the liquidity services provided by capital. The jump in relaxes the financial constraint (19), allowing the household to invest more. This force resembles the valuation mechanism at the center of the model by Kiyotaki and Moore (1997), except that we are dealing with an uncertainty shock, not with a productivity level shock. At the same time, the newly created capital competes with already existing capital in the provision of liquidity, which makes adding more capital unappealing for the household. Eventually, this second force dominates, driving down investment, prices, and liquidity.
Three additional points are salient to understanding Fig. 5. First, despite the output boom, the utilization rate goes down (left panel, bottom row): since capital is now more valuable, the household head wants to maintain it for the future (when a bad preference shock might arrive) by reducing depreciation.
Second, the movements in the variables occur even if no fundamental has changed. What has changed is the probability of future changes in fundamentals (e.g., the demand shifter). Thus, a researcher who does not appreciate the importance of uncertainty shocks might find herself puzzled by the co-movement of aggregate variables displayed in Fig. 5: variables move in different directions and, yet, no obvious (traditional) shock has arrived.
Third, even if output goes up, the period utility at impact is lower: the household is working more and consuming less. With uncertainty shocks, we must be careful in reading positive welfare implications from output booms.
8.2.2. On the expansionary nature of uncertainty shocks in our model
It is intriguing that, in our model, a demand uncertainty shock is “expansionary” (at least in terms of output, the household is consuming less and working more; we will get similar results for the other uncertainty shocks). Technically, this is because our model lacks the nominal and real rigidities of Bloom (2009) and Fernández-Villaverde et al. (2015a) that transform the reductions in investment or consumption into declines in output. We opted for this absence of rigidities for three reasons.
First, because it shows that economic theory, in general, does not impose constraints regarding the sign of the effects of uncertainty shocks: they can be either expansionary or contractionary. This point has not been sufficiently appreciated in the literature and needs to be made more emphatically. We believe that there are situations where uncertainty shocks, such as the increase in the dispersion of future productivity brought about by the widespread adoption of the internet in the late 1990s, are clearly expansionary.
Second, because the presence of an expansionary uncertainty shock is a word of caution for naive econometric methods that find mild effects of uncertainty variations. These methods might be just mixing the effects of simultaneous expansionary and contractionary uncertainty shocks and delivering a misleading reading of the empirical evidence.
Third, because the papers cited above have already shown, in much detail, how to get a contractionary effect of an uncertainty shock. In particular, by showing how expansionary uncertainty shocks can be in the absence of rigidities, we can learn about how strong such rigidities need to be to match the empirical results from VARs such as in Bloom (2009) and Fernández-Villaverde et al. (2015a). Given that we have outside evidence on the size of nominal and real rigidities, such an exercise provides us with valuable information to judge the role of uncertainty shocks in business cycles. In other words: are the documented rigidities large enough to induce the model to deliver the impulse-response functions documented by VARs?
8.2.3. Uncertainty shock to productivity
Fig. 6 shows the dynamics of macroeconomic variables following an increase in the volatility of the productivity shock, , our “supply-side shock.” As we did with the preference shock, we look at the case when the volatility of productivity doubles after the increase in uncertainty. The ordering of the panels is the same as in Fig. 5, except that the uncertainty shock (center panel, bottom row) is now the productivity one, instead of the uncertainty shock to preferences.
After the arrival of the uncertainty shock, output, investment, and labor go up, while consumption drops for a few quarters and, then, soon recovers. Similarly, the price of capital and the liquidity services go up. The utilization rate of capital, in contrast to Fig. 5, increases. Note also the differences in the scale of the x-axis: as we discuss in Subsection 8.1, the estimated uncertainty shocks in the U.S. economy are small and, thus, we cannot get much action out of them.
At first sight, Fig. 5, Fig. 6 look very similar in shape. However, the divergent evolution of the utilization rate of capital (lower after a preference volatility shock, bigger after a productivity volatility shock) reveals that very different mechanisms are at work.
Precautionary behavior is behind Fig. 5. In comparison, the Oi-Hartman-Abel effect is behind Fig. 6 (recall Subsection 3.2). While the production function of the representative firm in our economy is constant-returns-to-scale, the presence of financial frictions reduces the elasticity of capital supply, with q departing from 1 (which would always be the case without those financial frictions). This departure amounts, in practice, to a behavior of the firm that closely resembles the case where the production function has decreasing-returns-to-scale and triggers the Oi-Hartman-Abel effect.
The head of the household responds to this Oi-Hartman-Abel effect by asking the household members to work harder, invest more, and utilize the capital more. The utilization rate goes up because the Oi-Hartman-Abel effect tells the household to increase the capital services that the representative firm employs, which in the short run can be achieved through higher utilization of capital, even if at the cost of higher depreciation. Investment goes up so much that consumption goes down at impact. In other words, the household wants to be ready for the situation where a particularly good productivity shock arrives (the uncertainty shock makes it more likely than before).
Also, accumulating extra capital has the additional advantage for the household of providing extra insurance if the production shock is very negative (capital can be transformed back into consumption or used to produce more of the final good for consumption). Note, however, that these effects are quantitatively smaller than the ones in our previous uncertainty preference shock.
8.2.4. Level shock to the financial friction
Before we can study the consequences of an uncertainty shock to the financial friction, we need to spend some time studying the level effect of a change in , since some of the impulse responses are not obvious (compare, for instance, our model with the regular financial accelerator model of Bernanke et al., 1999).
Fig. 7 reports the consequences of a positive one-standard-deviation shock to (note how, for level shocks, we report a traditional one-standard-deviation GIRF). The ordering of the panels is the same as in Fig. 5, except that the center panel, bottom row, reports the level shock to .
Fig. 7.
Impact of θ. NOTE: Variables correspond to percentage deviations from their DSSs.
The increase in means that entrepreneurs can issue more equity against new capital. There are different possible interpretations for such exogenous changes in the financial markets and their willingness to buy outside equity. For instance, we can have a tightening in the regulation protecting outside investors, or as we mentioned before, the concentration of investment in a general-purpose technology that is easier to monitor.
After rises, the investment constraint in equation (19) relaxes. This relaxation leads to more investment and, with it, to a lower price of capital. The newly created capital provides additional liquidity, and liquidity services fall. The drop in makes investment even cheaper, leaving additional resources for the households to consume. Hence, consumption goes up. Firms meet the additional demand by increasing utilization and hiring more labor.
The reduction in goes against the standard intuition that an improvement in financial conditions (in this case, easier issuance of outside equity) should lead to a stock market boom. Shi (2015) shows that this counterintuitive result is a general problem of models with financial frictions.25 Guerrón-Quintana and Jinnai (2019b) use an endogenous-growth mechanism to restore the dynamics in asset prices after a financial shock.
8.2.5. Uncertainty shock to the financial friction
With this background in place, we can discuss the impact of a financial uncertainty shock . We report our findings in Fig. 8 . A financial uncertainty shock makes it more likely that will increase in the next period by a large amount. Since pledging capital will be easier in the future than today, the household head orders entrepreneurs to postpone investment and increase consumption today.
Fig. 8.
Impact of an increase in uncertainty on financial shock. NOTE: Variables correspond to percentage deviations from their DSSs.
However, the probability that goes down significantly in the next period has increased too. Under this scenario, the pledgeability of capital will decline sharply, making investment more expensive. The entrepreneurs do not want to be caught in a situation of not having enough resources to invest because of a tighter financial friction ( down) and low installed capital (resulting in low ). This channel pushes investment up in the current period, because, in such a way, there will be more installed capital to be used as collateral in the next period. We can call this mechanism “precautionary investment.” The economic intuition is related, but not equal, to the option value effect of investment under irreversibility (Bernanke, 1983, and Dixit and Pindyck, 1994).
Because of the concavity of the utility function, the second scenario –the large drop in – is more adverse for the household than the first one. Thus, the head of the household instructs entrepreneurs to increase investment and the utilization of capital, and workers to work longer hours. As in other cases, a higher investment lowers the price of capital and the value of liquidity services. The household, as a response to the lower price of capital, consumes more to smooth marginal utilities over time.
Finally, note that the expansion induced by an uncertainty shock to the financial friction is larger than the effects of the other two uncertainty shocks. This quantitative result backs up the conjecture that the relations between financial markets and uncertainty are at the very core of how uncertainty operates in terms of allocations. This point has been highlighted in Fernández-Villaverde et al. (2011) and Arellano et al. (2019), it is implicit in the empirical results in Bloom (2009), and it motivates our next experiment.
8.3. Financial frictions and the propagation of uncertainty shocks
Given our previous findings, a natural question is: how important are financial frictions for the propagation of uncertainty shocks, even those that do not come from the financial market? To answer this question, we vary the degree of liquidity in the economy and report our results in Fig. 9, Fig. 10, Fig. 11 . In each of these figures (again, with the same ordering of variables that we followed in previous figures), we consider two scenarios: our benchmark calibration (red solid line) and looser financial constraints (blue discontinuous line) where , i.e., the mean pledgeability is roughly twice as high as in the benchmark calibration and more outside equity can be issued (we keep θ at the same level as in the benchmark calibration). Because of our calibration strategy, the looser financial constraint implies a higher investment-to-capital ratio.
Fig. 9.
Role of financial friction in propagation of uncertainty in preferences. NOTE: Variables correspond to percentage deviations from their DSSs.
Fig. 10.
Role of financial friction in propagation of productivity uncertainty. NOTE: Variables correspond to percentage deviations from their DSSs.
Fig. 11.
Role of financial friction in propagation of uncertainty in financial shock. NOTE: Variables correspond to percentage deviations from their DSSs.
In the case of uncertainty shocks to preferences (Fig. 9), the effect of modifying the financial friction is quite small: output increases slightly more, but consumption, investment, and labor remain roughly unchanged. The liquidity services increase substantially more, but this has a minor impact on allocations.
In contrast, a looser financial constraint has a significant impact on the propagation of the productivity uncertainty shock (Fig. 10) and, in particular, on the propagation of the uncertainty shock to the financial friction (Fig. 11).
The intuition for the case of the productivity uncertainty shock is straightforward. When the financial friction is looser, the Oi-Hartman-Abel effect is weaker. The head of the household can instruct entrepreneurs to invest more when the good productivity shock arrives, and it does not need to accumulate as much capital in the expectation that such a shock will arrive in the near future and it cannot invest as much as it desires.
The mechanism in the case of the financial friction uncertainty shock is related. If the financial restriction is relaxed, the economy enjoys more liquidity, and entrepreneurs can issue more equity against their new investment when the good shocks arrive. Entrepreneurs are less concerned about a future decline in θ (because of higher uncertainty today). Hence, they choose to increase investment by a smaller fraction than in the benchmark scenario, and output rises much less.
In summary, our exercise illustrates that financial frictions make uncertainty shocks much more significant. Based on this observation, we close this section with two conjectures for future research. First, in the presence of household heterogeneity, such effects could be even more significant. Second, the reason why many emerging economies have wilder business cycle fluctuations than advanced economies can be related, in part, to this interaction between uncertainty shocks and financial frictions. Our prior is that emerging economies are subject both to larger uncertainty shocks and to tighter financial frictions.
9. Conclusion
In this paper, we have shown how uncertainty shocks can help us understand important aspects of business cycle fluctuations. More concretely, we have investigated how uncertainty shocks interact in a non-trivial way with financial frictions. By complicating future investment in physical capital, tighter financial frictions induce large contemporary reactions to uncertainty shocks.
However, there is much that we can do in this literature. We now outline four avenues of research. First, we can take this class of models to the next level, evaluating the interactions of financial frictions and heterogeneity in a context with changing volatility. Fernández-Villaverde et al. (2019a) show the rich non-linear dynamics generated by the interaction of financial frictions and heterogeneity and show how they are related to the underlying level of uncertainty in the economy. However, the paper does not explore the role of transitory uncertainty shocks.
Second, uncertainty shocks can also interact with models with a multiplicity of equilibria. An example of this interaction is in Fernández-Villaverde et al. (2019b). In most models analyzed by the literature (including the one in this paper), the effect of uncertainty shocks is transitory. In comparison, Fernández-Villaverde et al. (2019b) show that changes in uncertainty can have considerable effects on the ergodic distributions of aggregate variables that resemble the multimodalities documented by Adrian et al. (2019). When the economy can fluctuate between two different equilibria, one with high economic activity and low unemployment and one with low economic activity and high unemployment, the level of uncertainty will determine how often we switch between these two equilibria. Fajgelbaum et al. (2017) and Fernández-Villaverde et al. (2019b) deliver such results through strategic complementarities, but there are many other ways to achieve the same outcome. Uncertainty shocks can, therefore, have long-lasting effects.
Third, we need further explorations of the role of endogeneity in uncertainty shocks. Are business cycles driven by uncertainty shocks, or are uncertainty shocks driven by business cycles, as argued, for example, by Bachmann and Moscarini (2011) and Bachmann et al. (2013)? For example, Van Nieuwerburgh and Veldkamp (2006) have defended the idea that when firms produce less, the flow of new information to other agents in the economy slows down, and uncertainty increases (imagine a situation where production decisions by firms inform other agents about the productivity of a new technology; see Saijo, 2017). Atkinson et al. (2020) show that a model that departs from a Cobb-Douglas production function and assumes that capital and labor are gross complements, first-moment shocks can generate fluctuations in uncertainty. Or might we have a situation where we face a mix of the two causality directions, as defended by Ludvigson et al. (2015)? For instance, an uncertainty shock can lower economic activity and, with it, the flow of information.
Fourth, we should study in more depth the interaction between models of endogenous growth and uncertainty shocks. At the core of endogenous growth models, we have technology adoption decisions that depend on valuations of future profits from such adoption. By shifting such a valuation, uncertainty shocks can have permanent effects on the level of output.
We hope to see many more papers coming in this literature during the next decade from young and adventurous researchers.
Footnotes
Knight (1921) famously distinguished between “risk,” which he argued is the situation where the distribution over a set of events is known, and “uncertainty,” where the distribution over a set of events is not known. In Knight's language, rolling dice is risky; betting on a future war is uncertain. Nowadays, much of the literature has moved toward calling the later phenomenon “ambiguity,” and uses “uncertainty” to denote situations where distributions are known. See Epstein (1999) and Epstein and Schneider (2007) as examples of such a practice. We will follow the more recent convention in our paper.
Bloom (2014) summarizes related and quite similar evidence regarding micro time series (e.g., the dispersion of firms' productivity, wages, income, etc.), but given the thrust of our paper, we will omit their discussion. Suffice it to say that the macro and micro evidence is highly complementary.
Although both concepts are often mixed, it is useful to remember the difference between uncertainty about future volatilities (a forward-looking variable) and the realized volatility of past observations (a backward-looking variable). See Bollerslev et al. (2009) for an application based on this distinction.
Bekaert et al. (2013) show evidence that, indeed, uncertainty shocks drive much of VIX volatility. Nevertheless, we will return to the issue of the endogeneity of uncertainty in Section 9.
Measuring legal uncertainty, its change over time, and its impact on aggregate fluctuations is a promising avenue of research. Gomes et al. (2019) have shown, for example, that the legal uncertainty surrounding the elimination of the gold clauses in the U.S. between 1933 and 1935 was a key factor behind the reduction in corporate investment.
See, for details and updates, http://www.policyuncertainty.com/europe_monthly.html.
Certainty equivalence does not mean that studying uncertainty is pointless in this class of models. As mentioned in the main text, since markets must clear, changes in uncertainty in an endowment economy will impact the valuation of assets that define claims to the stream of consumption. Similarly, there will be relevant welfare implications. After all, each exercise in asset pricing is, through the back door, an exercise in welfare analysis (Álvarez and Jermann, 2005).
We keep repeating the caveat “everything else equal.” This point matters. For instance, if the agents' demand for saving moves to the right due to precautionary behavior, their labor supply will also typically increase in general equilibrium. A higher labor income will increase consumption.
This point also illustrates why the first-order perturbation of an equilibrium business cycle around the deterministic steady state is certainty equivalent (Fernández-Villaverde et al., 2016). A first-order perturbation only uses information about the first and second derivative of the utility function (we take derivatives of an Euler equation, which has a first derivative itself). Given a CRRA utility function with parameter σ and a steady-state consumption , we can calibrate and . With this calibration, the quadratic utility function and the CRRA would have the same first and second derivatives at and, thus, a first-order perturbation must deliver the same answer for both utilities.
See also Swanson (2012) for an important insight about how to compute risk aversion in models with endogenous labor supply.
Barro (2006), Barro and Ursúa (2008), Gabaix (2011), and Gourio (2012) have emphasized the importance of tail-end risk -in particular, disaster risk- as a driver of aggregate fluctuations and asset pricing. Note, however, that here we are not discussing the effects of these tail-end shocks, but the impact of changes in the probability of one of those shocks arriving in any given period.
This statement, however, must be qualified: in some particular models, an increase in uncertainty might not affect the riskiness of capital, although it typically does.
In fact, a similar phenomenon can appear on the household side in a standard real business cycle model. Since the household can adjust its labor supply after a productivity shock, even with a concave utility function, expected utility can be higher with more uncertainty than with less. The intuition is that, while the direct utility function is concave in its inputs, the indirect utility function can be convex in prices. See Cho et al. (2015) for a quantitative exploration of this point and an example of a simple economy where business cycles increase welfare. In addition, this result should make us cautious about interpolating the welfare costs of business cycles, including uncertainty shocks, derived from experiments with endowment economies à la Lucas (1985) into production economies. This comment, of course, has sharp consequences for asset prices as well.
The intuition behind these Ss rules and their response to variations in uncertainty also holds for other firm activities that look like an investment, such as hiring workers when there are labor adjustment costs (Schaal, 2017), for joint venture formation (Fernández-Villaverde et al., 2019b), and for consumer durables (Bertola et al., 2005).
See, nevertheless, Alfaro et al. (2018) for a complementary approach to ours that focuses on interactions of the external financing costs of firms and uncertainty shocks and Christiano et al. (2014) for the consequences of letting the volatility of cross-sectional idiosyncratic uncertainty fluctuate over time in a model with a financial accelerator mechanism. There is also a growing empirical literature relating uncertainty shocks and financial conditions that we will introduce later.
In an alternative formulation, we can write the AR process as and model the evolution of in logs.
A possibility to do so could be to mix aggregate variables and micro data to enrich the information set, as we described in Section 2.
Note the absence of long-run growth in productivity. In a model such as this one, such an absence is of secondary importance. In the presence of a deterministic or stochastic trend in , we can rescale all variables by such a trend and obtain a stationary representation with properties nearly identical to the version of the model we study here.
An alternative interpretation is that some technologies are harder for outsiders to monitor (i.e., IT) than others (i.e., manufacturing). When new investment is skewed toward the IT sector, is low. When new investment is skewed toward the manufacturing sector, is high.
The DSS is the fixed point of the equilibrium conditions of the model when the volatility of all shocks has been driven to zero. In contrast, the stochastic steady state is the fixed point of the equilibrium conditions of the model when the realization of all shocks in the period is zero. These two steady states will be different in general because of precautionary behavior. Also, even when the DSS is unique, we can encounter multiple stochastic steady states. See Fernández-Villaverde et al. (2019a) for an example of such a situation.
A technical note is relevant here. It is most advisable to perform the perturbation around the DSS, even in the presence of uncertainty shocks that may move the stochastic steady state substantially. First, all the theoretical results involving the consistency of a perturbation with respect to the exact but unknown solution depend on such a perturbation being taken around the DSS. Second, we know how to evaluate all the relevant derivatives only at the DSS. Otherwise, we need to engage in an iterative procedure that quickly goes astray.
There is a caveat. Except in a few particular cases, we do not have a proof that the decision rules that we solve for are differentiable with respect to the uncertainty shocks. This is a problem, however, for higher-order perturbation methods in general, regardless of whether they deal with uncertainty shocks. However, note that perturbation methods only require the existence of partial derivatives, not total differentiability.
The linear approximation to the log-deviation of output, , in a standard real business cycle model, is a linear function of the log-deviation of capital, , productivity at the start of the period, , and the productivity shock, : . Thus, the effect of on is through , regardless of the values of and . In addition, the effect is a linear function of . In a higher-order perturbation, we encounter terms of the form that induce state-dependence and terms of the form that make the shape of the response depend on the size and sign of the shock.
Similarly, this idea is also behind why models with bubbles can increase investment (Farhi and Tirole, 2012). Anything that increases the value of capital above “fundamentals” leads, in general, to more investment. By giving capital a liquidity service, financial frictions tend to have this implication as well.
Contributor Information
Jesús Fernández-Villaverde, Email: jesusfv@econ.upenn.edu.
Pablo A. Guerrón-Quintana, Email: pguerron@gmail.com.
References
- Abel A. Optimal investment under uncertainty. The American Economic Review. 1983;73:228–233. [Google Scholar]
- Abel A., Eberly J. A unified model of investment under uncertainty. The American Economic Review. 1994;84:1369–1384. [Google Scholar]
- Adrian T., Boyarchenko N., Giannone D. Federal Reserve Bank of New York; 2019. Multimodality in Macro-Financial Dynamics. Staff Report 903. [Google Scholar]
- Aghion P., Banerjee A. Oxford University Press; 2005. Volatility and Growth. [Google Scholar]
- Aguiar M., Gopinath G. Emerging market business cycles: the cycle is the trend. Journal of Political Economy. 2007;115:69–102. [Google Scholar]
- Alessandri P., Mumtaz H. Financial regimes and uncertainty shocks. Journal of Monetary Economics. 2019;101:31–46. [Google Scholar]
- Alfaro I., Bloom N., Lin X. National Bureau of Economic Research; 2018. The Finance Uncertainty Multiplier. Working Paper 24571. [Google Scholar]
- Altig D., Barrero J.M., Bloom N., Davis S.J., Meyer B.H., Parker N. National Bureau of Economic Research; 2019. Surveying Business Uncertainty. Working Paper 25956. [Google Scholar]
- Álvarez F., Jermann U.J. Using asset prices to measure the persistence of the marginal utility of wealth. Econometrica. 2005;73:1977–2016. [Google Scholar]
- Andreasen M., Fernández-Villaverde J., Rubio-Ramírez J. The pruned state-space system for non-linear DSGE models: theory and empirical applications. The Review of Economic Studies. 2018;85:1–49. [Google Scholar]
- Arellano C., Bai Y., Kehoe P.J. Financial frictions and fluctuations in volatility. Journal of Political Economy. 2019;127:2049–2103. [Google Scholar]
- Aruoba S.B., Fernández-Villaverde J., Rubio-Ramírez J.F. Comparing solution methods for dynamic equilibrium economies. Journal of Economic Dynamics and Control. 2006;30:2477–2508. [Google Scholar]
- Atkinson T., Plante M.D., Richter A.W., Throckmorton N. Federal Reserve Bank of Dallas; 2020. Complementarity and Macroeconomic Uncertainty. Working Papers 2009. [Google Scholar]
- Awano G., Bloom N., Dolby T., Mizen P., Riley R., Senga T., Reenen J.V., Vyas J., Wales P. Economic Statistics Centre of Excellence; 2018. A Firm-level Perspective on Micro- and Macro-level Uncertainty: an Analysis of Business Expectations and Uncertainty from the UK Management and Expectations Survey. Discussion Papers ESCoE DP-2018-10. [Google Scholar]
- Bachmann R., Elstner S., Sims E. Uncertainty and economic activity: evidence from business survey data. American Economic Journal: Macroeconomics. 2013;5:217–249. [Google Scholar]
- Bachmann R., Moscarini G. Society for Economic Dynamics; 2011. Business Cycles and Endogenous Uncertainty. 2011 Meeting Papers 36. [Google Scholar]
- Baker S.R., Bloom N., Davis S.J. Measuring economic policy uncertainty. The Quarterly Journal of Economics. 2016;131:1593–1636. [Google Scholar]
- Baker S.R., Bloom N., Davis S.J., Terry S.J. National Bureau of Economic Research; 2020. COVID-Induced Economic Uncertainty. Working Paper 26983. [Google Scholar]
- Baker S.R., Bloom N., Terry S.J. National Bureau of Economic Research; 2020. Using Disasters to Estimate the Impact of Uncertainty. Working Paper 27167. [Google Scholar]
- Bansal R., Yaron A. Risks for the long run: a potential resolution of asset pricing puzzles. Journal of Finance. 2004;59:1481–1509. [Google Scholar]
- Barillas F., Hansen L.P., Sargent T.J. Doubts or variability? Journal of Economic Theory. 2009;144:2388–2418. [Google Scholar]
- Barro R.J. Rare disasters and asset markets in the twentieth century. The Quarterly Journal of Economics. 2006;121:823–866. [Google Scholar]
- Barro R.J., Ursúa J.F. National Bureau of Economic Research; 2008. Macroeconomic Crises since 1870. Working Paper 13940. [Google Scholar]
- Basu S., Bundick B. Uncertainty shocks in a model of effective demand. Econometrica. 2017;85:937–958. [Google Scholar]
- Bates D.S. Jumps and stochastic volatility: exchange rate processes implicit in Deutsche mark options. The Review of Financial Studies. 1996;9:69–107. [Google Scholar]
- Bekaert G., Hoerova M., Lo Duca M. Risk, uncertainty and monetary policy. Journal of Monetary Economics. 2013;60:771–788. [Google Scholar]
- Bernanke B., Gertler M., Gilchrist S. The financial accelerator in a quantitative business cycle framework. In: Taylor J.B., Woodford M., editors. Handbook of Macroeconomics, 1st ed., vol. 1. Elsevier; 1999. Part C, chap. 21, 1341–1393. [Google Scholar]
- Bernanke B.S. Irreversibility, uncertainty, and cyclical investment. The Quarterly Journal of Economics. 1983;98:85–106. [Google Scholar]
- Bernanke, B.S., 2004. The Great Moderation, Remarks by Governor Ben S. Bernanke, at the meetings of the Eastern Economic Association, February 20. Washington, DC. 2004.
- Bertola G., Caballero R. vol. 5. University of Chicago Press; 1990. Kinked adjustment costs and aggregate dynamics; pp. 237–296. (NBER Macroeconomics Annual). [Google Scholar]
- Bertola G., Guiso L., Pistaferri L. Uncertainty and consumer durables adjustment. The Review of Economic Studies. 2005;72:973–1007. [Google Scholar]
- Bianchi F., Ilut C.L., Schneider M. Uncertainty shocks, asset supply and pricing over the business cycle. The Review of Economic Studies. 2017;85:810–854. [Google Scholar]
- Blei D.M., Ng A.Y., Jordan M.I. Latent Dirichlet allocation. Journal of Machine Learning Research. 2003;3:993–1022. [Google Scholar]
- Bloom N. The impact of uncertainty shocks. Econometrica. 2009;77:623–685. [Google Scholar]
- Bloom N. Fluctuations in uncertainty. The Journal of Economic Perspectives. 2014;28:153–176. [Google Scholar]
- Bloom N., Bunn P., Chen S., Mizen P., Smietanka P., Thwaites G. Bank of England; 2019. The Impact of Brexit on UK Firms. Bank of England working papers 818. [Google Scholar]
- Bloom N., Floetotto M., Jaimovich N., Saporta-Eksten I., Terry S.J. Really uncertain business cycles. Econometrica. 2018;86:1031–1065. [Google Scholar]
- Bollerslev T. Generalized autoregressive conditional heteroskedasticity. Journal of Econometrics. 1986;31:307–327. [Google Scholar]
- Bollerslev T. Department of Economics and Business Economics, Aarhus University; 2008. Glossary to ARCH (GARCH) CREATES Research Papers 2008-49. [Google Scholar]
- Bollerslev T., Tauchen G., Zhou H. Expected stock returns and variance risk premia. The Review of Financial Studies. 2009;22:4463–4492. [Google Scholar]
- Brinca, P., Duarte, J.B., Faria-e-Castro, M., 2020. Measuring Sectoral Supply and Demand Shocks during COVID-19. Unpublished. [DOI] [PMC free article] [PubMed]
- Buera F.J., Kaboski J.P., Shin Y. Finance and development: a tale of two sectors. The American Economic Review. 2011;101:1964–2002. [Google Scholar]
- Cacciatore M., Ravenna F. CEPR; 2020. Uncertainty, Wages, and the Business Cycle. Tech. Rep. DP14715. [Google Scholar]
- Caldara D., Fernández-Villaverde J., Rubio-Ramírez J.F., Yao W. Computing DSGE models with recursive preferences and stochastic volatility. Review of Economic Dynamics. 2012;15:188–206. [Google Scholar]
- Caldara D., Fuentes-Albero C., Gilchrist S., Zakrajšek E. The macroeconomic impact of financial and uncertainty shocks. European Economic Review. 2016;88:185–207. [Google Scholar]
- Cascaldi-Garcia, D. Sarisoy, C. Londono, J.M. Rogers, J. Datta, D. Grishchenko, T.F.O. Jahan-Parvar, M.R. Loria, F. Ma, S. Rodriguez, M. Zer, I., What is certain about uncertainty? Board of Governors of the Federal Reserve System (2020).
- Cho J.-O., Cooley T., Kim H.S. Business cycle uncertainty and economic welfare. Review of Economic Dynamics. 2015;18:185–200. [Google Scholar]
- Christiano L., Motto R., Rostagno M. Risk shocks. The American Economic Review. 2014;104:27–65. [Google Scholar]
- Christiano L.J., Eichenbaum M. Current real-business-cycle theories and aggregate labor-market fluctuations. The American Economic Review. 1992;82:430–450. [Google Scholar]
- Christiano L.J., Eichenbaum M., Evans C.L. Monetary policy shocks: what have we learned and to what end? In: Taylor J.B., Woodford M., editors. vol. 1. Elsevier; 1999. pp. 65–148. (Handbook of Macroeconomics). [Google Scholar]
- Christiano L.J., Eichenbaum M., Evans C.L. Nominal rigidities and the dynamic effects of a shock to monetary policy. Journal of Political Economy. 2005;113:1–45. [Google Scholar]
- Cogley T., Sargent T. Drift and volatilities: monetary policies and outcomes in the post WWII U.S. Review of Economic Dynamics. 2005;8:262–302. [Google Scholar]
- Comín D., Gertler M. Medium-term business cycles. The American Economic Review. 2006;96:523–551. [Google Scholar]
- Cooley T.F. Princeton University Press; 1995. Frontiers of Business Cycle Research. [Google Scholar]
- Cooley T.F., Prescott E.C. Economic growth and business cycles. In: Cooley T.F., editor. Frontiers of Business Cycle Research. Princeton University Press; Princeton: 1995. pp. 1–38. [Google Scholar]
- Cooley T.F., Quadrini V. Financial markets and firm dynamics. The American Economic Review. 2001;91:1286–1310. [Google Scholar]
- Cúrdia V., Del Negro M., Greenwald D.L. Rare shocks, great recessions. Journal of Applied Econometrics. 2014;29:1031–1052. [Google Scholar]
- Davis S.J., Kahn J.A. Interpreting the great moderation: changes in the volatility of economic activity at the macro and micro levels. The Journal of Economic Perspectives. 2008;22:155–180. [Google Scholar]
- Diebold F.X. Modeling the persistence of conditional variances: a comment. Econometric Reviews. 1986;5:51–56. [Google Scholar]
- Dingel J.I., Neiman B. National Bureau of Economic Research; 2020. How Many Jobs Can Be Done at Home? Working Paper 26948. [Google Scholar]
- Dixit A., Pindyck R. Princeton University Press; 1994. Investment Under Uncertainty. [Google Scholar]
- Drechsler I., Yaron A. What's vol got to do with it. The Review of Financial Studies. 2011;24:1–45. [Google Scholar]
- Engle R.F. Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation. Econometrica. 1982;50:987–1007. [Google Scholar]
- Epstein L.G. A definition of uncertainty aversion. The Review of Economic Studies. 1999;66:579–608. [Google Scholar]
- Epstein L.G., Schneider M. Learning under ambiguity. The Review of Economic Studies. 2007;74:1275–1303. [Google Scholar]
- Epstein L.G., Zin S.E. Substitution, risk aversion, and the temporal behavior of consumption and asset returns: a theoretical framework. Econometrica. 1989;57:937–969. [Google Scholar]
- Fajgelbaum P.D., Schaal E., Taschereau-Dumouchel M. Uncertainty traps. The Quarterly Journal of Economics. 2017;132:1641–1692. [Google Scholar]
- Farhi E., Tirole J. Bubbly liquidity. The Review of Economic Studies. 2012;79:678–706. [Google Scholar]
- Fernández-Villaverde J. The econometrics of DSGE models. SERIEs, Journal of the Spanish Economic Association. 2010;1:3–49. [Google Scholar]
- Fernández-Villaverde J., Guerrón-Quintana P., Kuester K., Rubio-Ramírez J. Fiscal volatility shocks and economic activity. The American Economic Review. 2015;105:3352–3384. [Google Scholar]
- Fernández-Villaverde J., Guerrón-Quintana P., Rubio-Ramírez J.F. Estimating dynamic equilibrium models with stochastic volatility. Journal of Econometrics. 2015;185:216–229. [Google Scholar]
- Fernández-Villaverde J., Guerrón-Quintana P., Rubio-Ramírez J.F., Uribe M. Risk matters: the real effects of volatility shocks. The American Economic Review. 2011;101:2530–2561. [Google Scholar]
- Fernández-Villaverde J., Hurtado S., Nuño G. National Bureau of Economic Research; 2019. Financial Frictions and the Wealth Distribution. Working Paper 26302. [Google Scholar]
- Fernández-Villaverde J., Levintal O. Solution methods for models with rare disasters. Quantitative Economics. 2018;9:903–944. [Google Scholar]
- Fernández-Villaverde J., Mandelman F., Yu Y., Zanetti F. National Bureau of Economic Research; 2019. Search Complementarities, Aggregate Fluctuations, and Fiscal Policy. Working Paper 26210. [Google Scholar]
- Fernández-Villaverde J., Rubio-Ramírez J., Schorfheide F. Chapter 9 - solution and estimation methods for DSGE models. In: Taylor J.B., Uhlig H., editors. Handbook of Macroeconomics, vol. 2. Elsevier; 2016. pp. 527–724. [Google Scholar]
- Fernández-Villaverde J., Rubio-Ramírez J.F. Macroeconomics and volatility: data, models, and estimation. In: Acemoglu D., Arellano M., Dekel E., editors. Advances in Economics and Econometrics: Tenth World Congress. vol. 3. Cambridge University Press; 2013. pp. 137–183. (Econometric Society Monographs). [Google Scholar]
- Fernández-Villaverde J., Valencia D.Z. National Bureau of Economic Research; 2018. A Practical Guide to Parallelization in Economics. Working Paper 24561. [Google Scholar]
- Gabaix X. Disasterization: a simple way to fix the asset pricing properties of macroeconomic models. The American Economic Review. 2011;101:406–409. [Google Scholar]
- Gabaix X. Variable rare disasters: an exactly solved framework for ten puzzles in macro-finance. The Quarterly Journal of Economics. 2012;127:645–700. [Google Scholar]
- Gali J., Gambetti L. On the sources of the great moderation. American Economic Journal: Macroeconomics. 2009;1:26–57. [Google Scholar]
- Gilboa I., Schmeidler D. Maxmin expected utility with non-unique prior. Journal of Mathematical Economics. 1989;18:141–153. [Google Scholar]
- Gilchrist S., Williams J.C. Putty-clay and investment: a business cycle analysis. Journal of Political Economy. 2000;108:928–960. [Google Scholar]
- Gomes J.F., Kilic M., Plante S. University of Pennsylvania; 2019. Leverage Risk and Investment: the Case of Gold Clauses in the 1930s. Working papers. [Google Scholar]
- Gourio F. Disaster risk and business cycles. The American Economic Review. 2012;102:2734–2766. [Google Scholar]
- Guerrón-Quintana P. Money demand heterogeneity and the great moderation. Journal of Monetary Economics. 2009;56:255–266. [Google Scholar]
- Guerrón-Quintana P.A. What you match does matter: the effects of data on DSGE estimation. Journal of Applied Econometrics. 2010;25:774–804. [Google Scholar]
- Guerrón-Quintana P.A., Jinnai R. Financial frictions, trends, and the great recession. Quantitative Economics. 2019;10:735–773. [Google Scholar]
- Guerrón-Quintana P.A., Jinnai R. Boston College; 2019. On Asset Prices and Liquidity Shocks. Working paper. [Google Scholar]
- Hamilton J.D. Macroeconomic regimes and regime shifts. In: Taylor J.B., Uhlig H., editors. vol. 2. Elsevier; 2016. pp. 163–201. (Handbook of Macroeconomics). [Google Scholar]
- Hartman R. The effects of price and cost uncertainty on investment. Journal of Economic Theory. 1972;5:258–266. [Google Scholar]
- Heathcote J., Storesletten K., Violante G.L. Quantitative macroeconomics with heterogeneous households. Annual Review of Economics. 2009;1:319–354. [Google Scholar]
- Hennessy C.A., Whited T.M. How costly is external financing? Evidence from a structural estimation. The Journal of Finance. 2007;62:1705–1745. [Google Scholar]
- Ilut C.L., Schneider M. Ambiguous business cycles. The American Economic Review. 2014;104:2368–2399. [Google Scholar]
- Jermann U., Quadrini V. Macroeconomic effects of financial shocks. The American Economic Review. 2012;102:238–271. [Google Scholar]
- Jurado K., Ludvigson S.C., Ng S. Measuring uncertainty. The American Economic Review. 2015;105:1177–1216. [Google Scholar]
- Justiniano A., Primiceri G.E. The time-varying volatility of macroeconomic fluctuations. The American Economic Review. 2008;98:604–641. [Google Scholar]
- Kim C.-J., Nelson C.R. Has the U.S. economy become more stable? A Bayesian approach based on a Markov-switching model of the business cycle. Review of Economics and Statistics. 1999;81:608–616. [Google Scholar]
- Kiyotaki N., Moore J. Credit cycles. Journal of Political Economy. 1997;105:211–248. [Google Scholar]
- Knight F.H. Hart, Schaffner & Marx; Boston: 1921. The Measurement of Durable Goods Prices. [Google Scholar]
- Koop G., Pesaran M.H., Potter S. Impulse response analysis in nonlinear multivariate models. Journal of Econometrics. 1996;74:119–147. [Google Scholar]
- Kydland F.E., Prescott E.C. Time to build and aggregate fluctuations. Econometrica. 1982;50:1345–1370. [Google Scholar]
- Larsen V. Norges Bank; 2017. Components of Uncertainty. Tech. Rep. 5/2017. [Google Scholar]
- Leduc S., Liu Z. Uncertainty shocks are aggregate demand shocks. Journal of Monetary Economics. 2016;82:20–35. [Google Scholar]
- Leland H.E. Saving and uncertainty: the precautionary demand for saving. The Quarterly Journal of Economics. 1968;82:465–473. [Google Scholar]
- Levintal O. Fifth-order perturbation solution to DSGE models. Journal of Economic Dynamics and Control. 2017;80:1–16. [Google Scholar]
- Lubik T.A., Schorfheide F. Testing for indeterminacy: an application to U.S. monetary policy. The American Economic Review. 2004;94:190–217. [Google Scholar]
- Lucas R., Jr. Blackwell; 1985. Models of Business Cycles. [Google Scholar]
- Ludvigson S.C., Ma S., Ng S. National Bureau of Economic Research; 2015. Uncertainty and Business Cycles: Exogenous Impulse or Endogenous Response? Working Paper 21803. [Google Scholar]
- Maccheroni F., Marinacci M., Rustichini A. Ambiguity aversion, robustness, and the variational representation of preferences. Econometrica. 2006;74:1447–1498. [Google Scholar]
- Manski C.F. Survey measurement of probabilistic macroeconomic expectations: progress and promise. In: Eichenbaum M., Parker J.A., editors. NBER Macroeconomics Annual 2017, vol. 32. University of Chicago Press; 2017. pp. 411–471. [Google Scholar]
- McConnell M.M., Pérez-Quirós G. Output fluctuations in the United States: what has changed since the early 1980's? The American Economic Review. 2000;90:1464–1476. [Google Scholar]
- Nakajima J. Bayesian analysis of generalized autoregressive conditional heteroskedasticity and stochastic volatility: modeling leverage, jumps and heavy-tails for financial time series. Japanese Economic Review. 2012;63:81–103. [Google Scholar]
- Oi W.Y. The desirability of price instability under perfect competition. Econometrica. 1961;29:58–64. [Google Scholar]
- Peri A. A hardware approach to value function iteration. Journal of Economic Dynamics and Control. 2020;114 doi: 10.1016/j.jedc.2020.103894. [DOI] [Google Scholar]
- Saijo H. The uncertainty multiplier and business cycles. Journal of Economic Dynamics and Control. 2017;78:1–25. [Google Scholar]
- Salgado S., Guvenen F., Bloom N. National Bureau of Economic Research; 2019. Skewed Business Cycles. Working Paper 26565. [Google Scholar]
- Sandmo A. The effect of uncertainty on saving decisions. The Review of Economic Studies. 1970;37:353–360. [Google Scholar]
- Sargent T. Princeton University Press; 1999. The Conquest of American Inflation. [Google Scholar]
- Schaal E. Uncertainty and unemployment. Econometrica. 2017;85:1675–1721. [Google Scholar]
- Scotti C. Surprise and uncertainty indexes: real-time aggregation of real-activity macro-surprises. Journal of Monetary Economics. 2016;82:1–19. [Google Scholar]
- Shephard N., Andersen T.G. Stochastic volatility: origins and overview. In: Mikosch T., Kreiß J.-P., Davis R.A., Andersen T.G., editors. Handbook of Financial Time Series. Springer; 2009. pp. 233–254. [Google Scholar]
- Shi S. Liquidity, assets and business cycles. Journal of Monetary Economics. 2015;70:116–132. [Google Scholar]
- Simon H.A. Dynamic programming under uncertainty with a quadratic criterion function. Econometrica. 1956;24:74–81. [Google Scholar]
- Sims C.A., Zha T. Were there regime switches in U.S. monetary policy? The American Economic Review. 2006;96:54–81. [Google Scholar]
- Stock J.H., Watson M.W. Has the business cycle changed and why? In: Gertler M., Rogoff K., editors. NBER Macroeconomics Annual 2002, vol. 17. MIT Press; 2003. pp. 159–230. [Google Scholar]
- Stock J.H., Watson M.W. Disentangling the channels of the 2007-09 recession. Brookings Papers on Economic Activity. 2012:81–141. [Google Scholar]
- Strzalecki T. Temporal resolution of uncertainty and recursive models of ambiguity aversion. Econometrica. 2013;81:1039–1074. [Google Scholar]
- Swanson E.T. Risk aversion and the labor margin in dynamic equilibrium models. The American Economic Review. 2012;102:1663–1691. [Google Scholar]
- Tallarini T.D., Jr. Risk-sensitive real business cycles. Journal of Monetary Economics. 2000;45:507–532. [Google Scholar]
- Theil H. A note on certainty equivalence in dynamic planning. Econometrica. 1957;25:346–349. [Google Scholar]
- Van Nieuwerburgh S., Veldkamp L. Learning asymmetries in real business cycles. Journal of Monetary Economics. 2006;53:753–772. [Google Scholar]