Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Mar 25;11(8):2891–2895. doi: 10.1021/acs.jpclett.0c00819

Crystal Structure Influences Migration along Li and Mg Surfaces

Ingeborg Treu Røe 1, Sverre M Selbach 1, Sondre Kvalvåg Schnell 1,*
PMCID: PMC7311081  PMID: 32208701

Abstract

graphic file with name jz0c00819_0005.jpg

Dendrite formation on Li metal anodes hinders commercialization of more energy-dense rechargeable batteries. Here, we use the migration energy barrier (MEB) for surface transport as a descriptor for dendrite nucleation and compare Li to Mg. Density functional theory calculations show that the MEB for the hexagonal close-packed structure is 40 and 270 meV lower than that of the body-centered cubic structure for Li and Mg, respectively. This is suggested as a reason why Mg surfaces are less prone to form dendrites than Li. We show that the close-packed facets exhibit lower MEBs because of smaller changes in atomic coordination during migration and thereby less surface distortion.

Dendrite formation on Li metal surfaces occurs during repeated charge and discharge cycles with Li anodes. The phenomenon leads to a substantial reduction in Coulombic efficiency, poor cycling stability, and short-circuiting and prevents commercialization of rechargeable Li metal batteries.1 However, compared to the common graphite intercalation anode, the Li metal anode promises a 10-fold increase in the capacity2 and around 50% increase in the specific energy density on the cell level.3 Thus, extensive effort has been put into preventing the dendrite growth over the past decade,1,3,4 resulting in prevention strategies that include surface engineering (and nanostructuring),5−8 electrolyte additives,9−11 and solid electrolyte interface (SEI) manipulation.12 In a complex electrochemical cell, it is difficult to separate different reaction and growth mechanisms from one another. All the same, the aforementioned work has increased the understanding of how the composition and morphology of the electrolyte and the SEI affect the nucleation and growth of dendrites. In addition, limiting the current density and overpotential is important to avoid dendrite formation.13−16 Neither the current density nor the chemical environment can fully explain why Li is more susceptible to dendrite growth than other metal anodes. In particular, Mg metal anodes are less prone to form dendrites compared to Li,17 indicating that there are differences inherent to the elements that are important for nucleation.18,19 At room temperature, Li crystallizes in the body-centered cubic (bcc) and Mg in the hexagonal close-packed (hcp) structure.20,21 The (001) bcc and (0001) hcp facets are the most prominent and were used by Jäckle and co-workers to examine the difference in migration energy barrier (MEB) between Li and Mg. They found a barrier of 140 and 20 meV, respectively, explaining the differences in the dendrite formation.22 The MEB was found to be higher for the (111) surface of Li in the bcc structure, coinciding with experimental results showing a more pronounced dendritic growth along the ⟨111⟩ direction,23 as well as a reduced tendency for dendrite formation as the mobility of Li is increased.18,24 Together with large-scale simulations indicating the impact of MEBs on the growth of dendrites,25 this suggests that the MEB can be used as a descriptor for dendrite nucleation. While Jäckle and co-workers investigated perfect surfaces, Huang et al.26 investigated the effect of defects on the binding energy and energy landscape of Li metal surfaces using density functional theory (DFT). They found that defects increase the binding energies as well as the MEBs and argue that this further enhances dendrite growth. However, a detailed understanding of the influence of the crystal structure on dendrite formation is still lacking.

In this study, we explore the effect of the crystal structure of the surface on the MEB of both Li and Mg metal using DFT. We find that the structure of the surface has significant impact on the MEB. Typically, the close-packed surfaces of the face-centered cubic (fcc) and hcp crystal structures exhibit low MEBs, in contrast to the less densely packed facets of the bcc structure. The MEB depends on a balance between the coordination number of the migrating atom and displacements of bulk and surface atoms during migration events. Lesser changes in the coordination of the migrating atom results in lower MEBs. While the displacements of the rest of the surface facilitate smaller coordination changes, they also increase the MEB. In Mg, the changes in the electronic structure of the surface atoms upon displacement are larger than in Li, and the energy penalty of displacement is higher. Our calculations show that Li in the close-packed fcc and hcp structures exhibits as low MEB as Mg, implying that dendrite nucleation can be inhibited if Li is stabilized in the hcp or fcc structure.

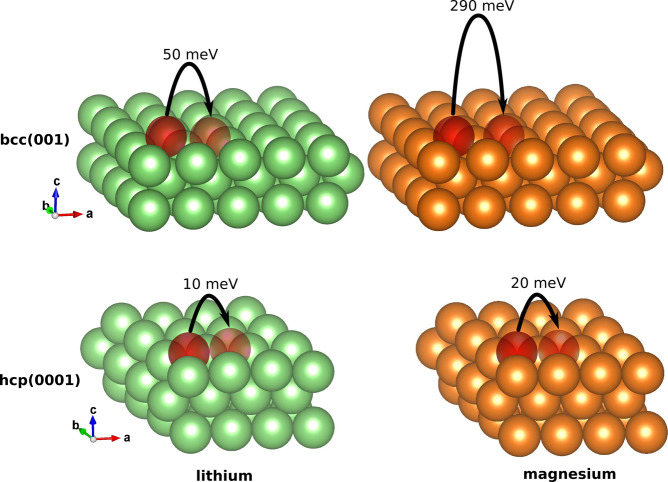
We start by comparing the DFT-calculated MEBs of Li and Mg in different crystal structures. The MEBs of the minimum-energy path of Li and Mg in both the bcc (001) and hcp (0001) structures are illustrated in Figure 1. Notably, the MEB of both Li and Mg decreases as the crystal structure changes from bcc (001) to hcp (0001), as shown in Figure 1, indicating that the crystal structure influences the MEB. This sheds light on the differences in surface migration barriers between Li bcc and Mg hcp surfaces, emphasizing the importance of the crystal structure, and may help illuminate why Li is more prone to dendrite nucleation than Mg.

Figure 1.

Figure 1

Open in a new tab

Minimum energy path and the corresponding migration energy barrier for Li (left) and Mg (right) in the bcc (001) (upper) and hcp (0001) (lower) structures. The figure shows only the three top layers of the supercell.

Our calculated MEB for Li on the bcc (001) surface is 80 meV lower than that reported by Jäckle et al. While this is in agreement with the work of Gaissmaier et al. across step edges27 (see the Supporting Information Figure S4), the resulting difference between the MEB of Li bcc (001) and Mg hcp (0001) is 30 meV. Thus, the migration on Li bcc (001) facets will be around two times faster than on Mg hcp (0001) at room temperature (calculated by 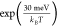Inline graphic, where kBT = 25.7 meV), which may not be a sufficient difference to explain the different dendritic behavior of Li and Mg metal surfaces. The causality between the MEB and the dendrite nucleation and growth is not investigated in the presented work, and whether the MEB can be used as a sole descriptor for dendrite nucleation and growth therefore requires further investigation.

We find an exchange mechanism for the migration on the Li bcc (111) surface, which lowers the MEB by 270 meV compared to the MEB found by Jäckle et al. and results in a difference across the Li bcc surfaces of 100 meV, as depicted in Figure 2. As the Li fcc and hcp facets exhibit low MEBs, the total span across all Li structures is 140 meV while the corresponding span for Mg is 720 meV. This indicates that the MEB is influenced by factors apart from the crystal structure, which we will discuss further below. Interestingly, the span of the MEB across the facets is reflected in the span of the surface energies, shown in Figure 2. The Li facets vary with 0.11 J m–2, compared to 0.28 J m–2 for the Mg facets. This trend where lower surface energy yields lower MEB is found for individual crystal structures such as the Mg bcc facets, but we do not find a one-to-one relation between the MEB and the surface energy. That is, a low surface energy does not necessarily correspond to a low MEB as seen in all of the Li surfaces and Mg fcc facets.

Figure 2.

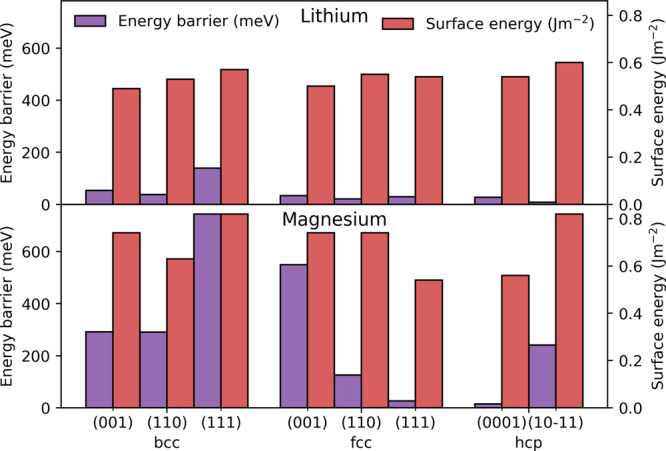
Figure 2

Open in a new tab

Migration energy barrier of the minimum energy path (purple bars) and the surface energy (red bars) of different surfaces of Li (upper) and Mg (lower).

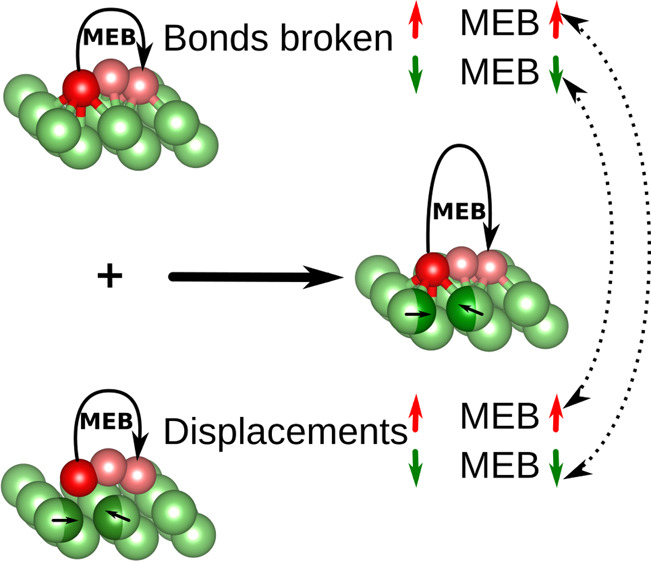
We find a relation between the atomic coordination of the surface atoms and the MEB. In a simplified model, the MEB arises from the difference in the bond energy as the migrating atom moves from its (stable) starting position to the saddle point, and the bond energy is proportional to the number of nearest neighbors. Hence, the MEB increases with a larger change in the coordination. Unfortunately, the nearest-neighbor coordination number is not a uniquely defined value. Here, we have defined a weighted coordination, c, using a Fermi function:28

graphic file with name jz0c00819_m002.jpg 1

where rij is the distance between atom i and j, γ = 1.45rc, σ = 0.2rc, and rc is the typical bond length in the bulk (for example, Li bcc has rc = 2.95 Å).

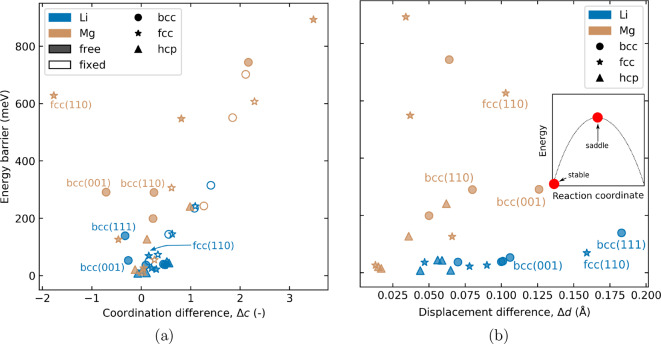
In this model, where change in coordination is the only parameter, we expect it to scale linearly with the MEB. That is, increasing change in coordination causes a corresponding increase in the MEB. This is seen in Figure 3a (open symbols), which depicts the MEB as a function of Δc for migration on surfaces where the atoms are fixed in place. Note that the close-packed fcc and hcp structures exhibit low Δc, consistent with the low MEB on the hcp (0001) surface in Figure 1. However, the fixed surface is highly artificial, and we observe a large degree of displacement of the surface atoms when these are free to move. This is seen in Figure 3b, showing the difference in total displacement of the surface atoms between the stable and saddle position, which is calculated using eq 2:

graphic file with name jz0c00819_m003.jpg 2

where di is the displacement of atom i from its relaxed position when no atom is adsorbed on the surface and N is the number of atoms in the simulation cell that are free to move. In the fixed surfaces experiencing large Δc, the surface displacements caused by releasing the surface atoms help the migrating atom to maintain its coordination at the saddle position, and the Δc is decreased. Thus, the linear correlation between the MEB and Δc disappears as shown with filled markers in Figure 3a, but the MEB remains high because of the energy penalty of the surface displacements. This is less pronounced in the close-packed fcc and hcp structures compared to the less densely packed facets. The balance between the Δc and Δd is illustrated for Mg bcc(001) and bcc(110). The two points exhibit almost equal MEB, but opposing trends for Δc, that is, Δc < 0 for bcc(001) and Δc > 0 for bcc(110). Considering the Δd, however, the trend is turned: Δdbcc(001) > Δdbcc(110). Consequently, the MEBs become equal. In other words, the MEB results from a complex interplay between Δc and Δd. Interestingly, the magnitude of the MEB on the fixed Mg surfaces remains relatively constant as the surface atoms are unconstrained. In contrast, the free Li facets experience a decrease in the MEB compared to the fixed surfaces, indicating that the penalty of surface displacements is higher for Mg than Li.

Figure 3.

Figure 3

Open in a new tab

(a) MEB as a function of the Δc, the difference between the coordination parameter, c, at the stable state and the saddle point. The fixed surfaces (open) follow a linear trend. The free surfaces (closed) have high MEB at high Δc. The points labeled Mg fcc(110) and Li bcc(001) and bcc(111) do not follow this trend. (b) MEB as a function of the difference in displacement between the stable and the saddle position, Δd, (as defined in eq 2). The stable and saddle positions on the energy landscape are depicted in the inset.

An adaptive common neighbor analysis (CNA)29 of the local structure of the top layers of the surfaces shows that displacements of the atoms in a Li surface tend to result in a different local crystal structure than that of the bulk (see Table S3). In contrast, the crystal structure of the Mg surfaces are less sensitive to displacements and retain to a greater extent the crystal structure of the bulk. While this is a qualitative difference between Li and Mg, it is hard to quantify the effect the local crystal structure change has on the MEB. It is possible that the change of the local crystal structure is beneficial for lowering the MEB, but if that is so, it is unclear why the same behavior is not seen for Mg.

One cause of the amplified penalty of surface displacements may be found in the electronic structure of the different surfaces.

In all the Li structures, the valence band density of states (vDOS) of the stable and saddle point structures are very similar, while Mg exhibits much larger differences, as shown in Figure 4. This phenomenon may arise from the different contribution of the p-orbital to the metallic properties of Li compared to Mg. In Li, the p-orbital does not contribute to the electronic conduction as Li’s s-orbital is half-filled, whereas in Mg, the metallic behavior arises from an overlap between the s- and p-orbitals. Because the p-orbitals are more directional than the s-orbitals, displacements of the surface atoms may change the s–p-orbital overlap and increase the energy of the electrons. Consequently, the energy penalty of surface displacements becomes higher for Mg compared to Li.

Figure 4.

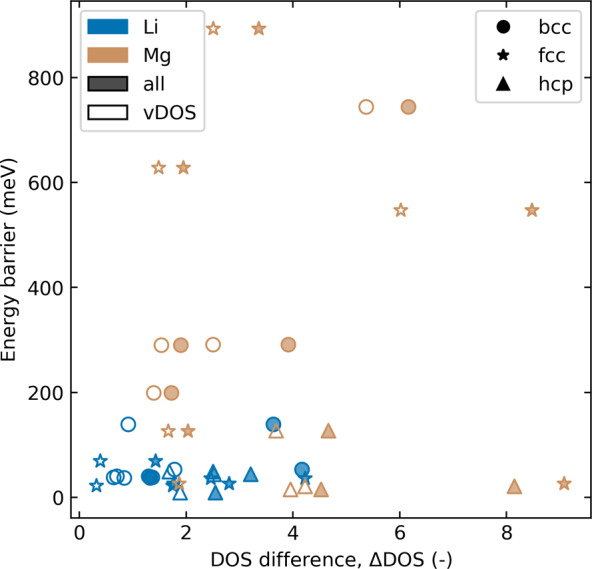
Figure 4

Open in a new tab

MEB as a function of the difference in the integrated density of states (DOS) between the stable and the saddle position. The difference between summation over the s- and p-bands (filled markers, “all”) and only the (s-band) valence states (open markers, “vDOS”) is depicted.

In summary, the MEBs of different facets of the Li and Mg bcc, fcc, and hcp structures were investigated using DFT. We show that the MEB depends on the crystal structure through a complex interplay between the coordination of the migrating atom, the displacement of the surface atoms, and the reorganization of the electronic structure. Notably, the MEB of Li in the close-packed structures (fcc (111) and hcp (0001)) becomes similar to that of Mg in the hcp (0001) structure, indicating that the close-packed hcp and fcc structures are less prone to dendrite formation than bcc structures. Moreover, the present study provides fundamental insights into migration on a metal surface and indicates that low MEBs are obtained for elements and surfaces in close-packed structures that facilitate migration without large changes in coordination of the migrating atom and simultaneously attain the original structure of the surface. Thus, both atomic and electronic reorganization is avoided, resulting in a low MEB. However, the Li facets exhibit MEBs comparable to the thermal energy, kBT, at room temperature, and may be insufficient as the sole descriptor for dendrite nucleation. Additional insight into the impact of the electric field gradient and electrolyte and solid electrolyte interface chemistry may be necessary to describe the dendrite nucleation satisfactorily.

Simulation Details

The MEBs were calculated using the DFT-code Vienna Ab initio Simulation Package (VASP)30,31 together with the climbing image Nudged Elastic Band (c-NEB) method.32−35 The Li_sv and Mg projector augmented wave (PAW)36 pseudopotentials were expanded to cutoff energies of 500 eV for Li and 350 eV for Mg, and the PBEsol functional was used. The c-NEB calculations were carried out on simulation cells exposing different bcc, fcc and hcp facets, with dimensions exceeding 15 Å in all directions and an additional vacuum of more than 15 Å in the z-direction. The four upper layers of the c-NEB simulation cells were free, while the rest were fixed in space to mimic the bulk (see Figure S1). All bulk and surface structures were relaxed to within 0.001 eV/Å. The max force on each of the c-NEB images was relaxed to within 0.01 eV/Å. Further details on the simulations and the convergence of the calculations is found in the Supporting Information.

Acknowledgments

The authors thank Sigma2 for CPU time through the project NN9566k. The Faculty of Natural Sciences at NTNU is acknowledged for financial support.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpclett.0c00819.

  • Further details regarding the simulation methods and convergence data, details on the surface energy and adaptive common neighbor analysis, and a discussion on differences between the present work and literature (PDF)

The authors declare no competing financial interest.

Supplementary Material

jz0c00819_si_001.pdf (3.3MB, pdf)

References

  1. Lin D.; Liu Y.; Cui Y. Reviving the lithium metal anode for high-energy batteries. Nat. Nanotechnol. 2017, 12, 194–206. 10.1038/nnano.2017.16. [DOI] [PubMed] [Google Scholar]
  2. McCloskey B. D. Attainable Gravimetric and Volumetric Energy Density of Li-S and Li Ion Battery Cells with Solid Separator-Protected Li Metal Anodes. J. Phys. Chem. Lett. 2015, 6, 4581–4588. 10.1021/acs.jpclett.5b01814. [DOI] [PubMed] [Google Scholar]
  3. Albertus P.; Babinec S.; Litzelman S.; Newman A. Status and challenges in enabling the lithium metal electrode for high-energy and low-cost rechargeable batteries. Nature Energy 2018, 3, 16–21. 10.1038/s41560-017-0047-2. [DOI] [Google Scholar]
  4. Liu H.; Cheng X.-B.; Huang J.-Q.; Kaskel S.; Chou S.; Park H. S.; Zhang Q. Alloy Anodes for Rechargeable Alkali-Metal Batteries: Progress and Challenge. ACS Materials Letters 2019, 1, 217–229. 10.1021/acsmaterialslett.9b00118. [DOI] [Google Scholar]
  5. Wang X.; Zeng W.; Hong L.; Xu W.; Yang H.; Wang F.; Duan H.; Tang M.; Jiang H. Stress-driven lithium dendrite growth mechanism and dendrite mitigation by electroplating on soft substrates. Nature Energy 2018, 3, 227–235. 10.1038/s41560-018-0104-5. [DOI] [Google Scholar]
  6. Kozen A. C.; Lin C.-F.; Pearse A. J.; Schroeder M. A.; Han X.; Hu L.; Lee S.-B.; Rubloff G. W.; Noked M. Next-Generation Lithium Metal Anode Engineering via Atomic Layer Deposition. ACS Nano 2015, 9, 5884–5892. 10.1021/acsnano.5b02166. [DOI] [PubMed] [Google Scholar]
  7. Ryou M.-H.; Lee Y. M.; Lee Y.; Winter M.; Bieker P. Mechanical Surface Modification of Lithium Metal: Towards Improved Li Metal Anode Performance by Directed Li Plating. Adv. Funct. Mater. 2015, 25, 834–841. 10.1002/adfm.201402953. [DOI] [Google Scholar]
  8. Becking J.; Gröbmeyer A.; Kolek M.; Rodehorst U.; Schulze S.; Winter M.; Bieker P.; Stan M. C. Lithium-Metal Foil Surface Modification: An Effective Method to Improve the Cycling Performance of Lithium-Metal Batteries. Adv. Mater. Interfaces 2017, 4, 1700166. 10.1002/admi.201700166. [DOI] [Google Scholar]
  9. Ding F.; Xu W.; Chen X.; Zhang J.; Shao Y.; Engelhard M. H.; Zhang Y.; Blake T. A.; Graff G. L.; Liu X.; et al. Effects of cesium cations in lithium deposition via self-healing electrostatic shield mechanism. J. Phys. Chem. C 2014, 118, 4043–4049. 10.1021/jp4127754. [DOI] [Google Scholar]
  10. Lu Y.; Tu Z.; Archer L. A. Stable lithium electrodeposition in liquid and nanoporous solid electrolytes. Nat. Mater. 2014, 13, 961–969. 10.1038/nmat4041. [DOI] [PubMed] [Google Scholar]
  11. Zheng J.; Engelhard M. H.; Mei D.; Jiao S.; Polzin B. J.; Zhang J. G.; Xu W. Electrolyte additive enabled fast charging and stable cycling lithium metal batteries. Nature Energy 2017, 2, 17012. 10.1038/nenergy.2017.12. [DOI] [Google Scholar]
  12. Nishikawa K.; Mori T.; Nishida T.; Fukunaka Y.; Rosso M. Li dendrite growth and Li+ ionic mass transfer phenomenon. J. Electroanal. Chem. 2011, 661, 84–89. 10.1016/j.jelechem.2011.06.035. [DOI] [Google Scholar]
  13. Chazalviel J.-N. Electrochemical aspects of the generation of ramified metallic electrodeposits. Phys. Rev. A: At., Mol., Opt. Phys. 1990, 42, 7355. 10.1103/PhysRevA.42.7355. [DOI] [PubMed] [Google Scholar]
  14. Monroe C.; Newman J. Dendrite Growth in Lithium/Polymer Systems. J. Electrochem. Soc. 2003, 150, A1377. 10.1149/1.1606686. [DOI] [Google Scholar]
  15. Ely D. R.; Garcia R. E. Heterogeneous Nucleation and Growth of Lithium Electrodeposits on Negative Electrodes. J. Electrochem. Soc. 2013, 160, A662–A668. 10.1149/1.057304jes. [DOI] [Google Scholar]
  16. Seong I. W.; Hong C. H.; Kim B. K.; Yoon W. Y. The effects of current density and amount of discharge on dendrite formation in the lithium powder anode electrode. J. Power Sources 2008, 178, 769–773. 10.1016/j.jpowsour.2007.12.062. [DOI] [Google Scholar]
  17. Matsui M.; Takahashi K.; Sakamoto K.; Hirano A.; Takeda Y.; Yamamoto O.; Imanishi N. Phase stability of a garnet-type lithium ion conductor Li7La3Zr2O12. Dalton transactions (Cambridge, England: 2003) 2014, 43, 1019–1024. 10.1039/C3DT52024B. [DOI] [PubMed] [Google Scholar]
  18. Steiger J.; Richter G.; Wenk M.; Kramer D.; Mönig R. Comparison of the growth of lithium filaments and dendrites under different conditions. Electrochem. Commun. 2015, 50, 11–14. 10.1016/j.elecom.2014.11.002. [DOI] [Google Scholar]
  19. Harry K. J.; Hallinan D. T.; Parkinson D. Y.; MacDowell A. A.; Balsara N. P. Detection of subsurface structures underneath dendrites formed on cycled lithium metal electrodes. Nat. Mater. 2014, 13, 69–73. 10.1038/nmat3793. [DOI] [PubMed] [Google Scholar]
  20. Faglioni F.; Merinov B. V.; Goddard W. A. Room-Temperature Lithium Phases from Density Functional Theory. J. Phys. Chem. C 2016, 120, 27104–27108. 10.1021/acs.jpcc.6b08168. [DOI] [Google Scholar]
  21. Clendenen G. L.; Drickamer H. G. Effect of Pressure on the Volume and Lattice Parameters of Magnesium. Phys. Rev. 1964, 135, A1643. 10.1103/PhysRev.135.A1643. [DOI] [Google Scholar]
  22. Jäckle M.; Groß A. Microscopic properties of lithium, sodium, and magnesium battery anode materials related to possible dendrite growth. J. Chem. Phys. 2014, 141, 174710. 10.1063/1.4901055. [DOI] [PubMed] [Google Scholar]
  23. Li Y.; Li Y.; Pei A.; Yan K.; Sun Y.; Wu C. L.; Joubert L. M.; Chin R.; Koh A. L.; Yu Y.; et al. Atomic structure of sensitive battery materials and interfaces revealed by cryo-electron microscopy. Science 2017, 358, 506–510. 10.1126/science.aam6014. [DOI] [PubMed] [Google Scholar]
  24. Chen Y.; Dou X.; Wang K.; Han Y. Lithium Dendrites Inhibition via Diffusion Enhancement. Adv. Energy Mater. 2019, 9, 1900019. 10.1002/aenm.201900019. [DOI] [Google Scholar]
  25. Hao F.; Verma A.; Mukherjee P. P. Electrodeposition stability of metal electrodes. Energy Storage Materials 2019, 20, 1–6. 10.1016/j.ensm.2019.05.004. [DOI] [Google Scholar]
  26. Huang K.; Liu Y.; Liu H. Understanding and Prediction of Lithium Crystal Growth on Perfect and Defective Interfaces: A Kohn-Sham Density Functional Study. ACS Appl. Mater. Interfaces 2019, 11, 37239–37246. 10.1021/acsami.9b10893. [DOI] [PubMed] [Google Scholar]
  27. Gaissmaier D.; Borg M.; Fantauzzi D.; Jacob T. Microscopic Properties of Na and Li-A First Principle Study of Metal Battery Anode Materials. ChemSusChem 2020, 13, 771. 10.1002/cssc.201902860. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Gasparotto P.; Meißner R. H.; Ceriotti M. Recognizing Local and Global Structural Motifs at the Atomic Scale. J. Chem. Theory Comput. 2018, 14, 486–498. 10.1021/acs.jctc.7b00993. [DOI] [PubMed] [Google Scholar]
  29. Stukowski A. Visualization and analysis of atomistic simulation data with OVITO-the Open Visualization Tool. Modell. Simul. Mater. Sci. Eng. 2010, 18, 015012. 10.1088/0965-0393/18/1/015012. [DOI] [Google Scholar]
  30. Kresse G.; Furthmüller J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. 10.1016/0927-0256(96)00008-0. [DOI] [PubMed] [Google Scholar]
  31. Kresse G.; Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B: Condens. Matter Mater. Phys. 1999, 59, 1758–1775. 10.1103/PhysRevB.59.1758. [DOI] [Google Scholar]
  32. Jonsson H.; Mills G.; Jacobsen K. W. Nudged elastic band method for finding minimum energy paths of transitions. Classical and Quantum Dynamics in Condensed Phase Simulations - Proceedings of the International School of Physics 1997, 385–404. 10.1142/9789812839664_0016. [DOI] [Google Scholar]
  33. Henkelman G.; Uberuaga B. P.; Jónsson H. A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phys. 2000, 113, 9901. 10.1063/1.1329672. [DOI] [Google Scholar]
  34. Henkelman G.; Jónsson H. Improved tangent estimate in the nudged elastic band method for finding minimum energy paths and saddle points. J. Chem. Phys. 2000, 113, 9978. 10.1063/1.1323224. [DOI] [Google Scholar]
  35. Sheppard D.; Xiao P.; Chemelewski W.; Johnson D. D.; Henkelman G. A generalized solid-state nudged elastic band method. J. Chem. Phys. 2012, 136, 074103. 10.1063/1.3684549. [DOI] [PubMed] [Google Scholar]
  36. Blöchl P. E. Projector augmented-wave method. Phys. Rev. B: Condens. Matter Mater. Phys. 1994, 50, 17953. 10.1103/PhysRevB.50.17953. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jz0c00819_si_001.pdf (3.3MB, pdf)

Articles from The Journal of Physical Chemistry Letters are provided here courtesy of American Chemical Society

RESOURCES