Drug Antagonism and Single Agent Dominance Result from Differences in Death Kinetics

Abstract

Cancer treatment generally involves drugs used in combinations. Most prior work has focused on identifying and understanding synergistic drug-drug interactions; however, understanding antagonistic interactions remains an important and understudied issue. To enrich for antagonism and reveal common features of these combinations, we screened all pairwise combinations of drugs characterized as activators regulated cell death. This network is strongly enriched for antagonism, particularly a form of antagonism that we call “single agent dominance”. Single agent dominance refers to antagonisms in which a two-drug combination phenocopies one of the two agents. Dominance results from differences in death onset time, with dominant drugs acting earlier than their suppressed counterparts. We explored mechanisms by which parthanatotic agents dominate apoptotic agents, finding dominance in this scenario caused by mutually exclusive and conflicting use of PARP1. Taken together, our study reveals death kinetics as a predictive feature of antagonism, due to inhibitory crosstalk between death pathways.

Cancer therapies are often limited by acquired drug resistance and partial killing of a tumor cell population^1,2. To combat these limitations, many efforts focus on the development of combination drug therapies^3-5. Generally, prior studies focused on identifying combinations that produce synergistic drug-drug interactions. In contrast to expectations, recent reports demonstrate that synergy is not observed in clinically efficacious drug combinations, which instead are typically additive/independent⁶. Synergistic combinations tend to reinforce killing that would be induced by one of the drugs within the combination, rather than facilitating killing of new cells that would not be killed by either drug alone^7,8. Furthermore, synergistic combinations favor the evolution of resistant clones⁹. While these data may limit the value of identifying drug synergies, understanding the sources of antagonism still remains an important issue. It stands to reason that antagonism – particularly very strong response antagonism – may limit the efficacy of a drug combination. Predicting which drug combinations will result in antagonism is challenging due to the lack of transparent “rules” underlying this phenomenon, and the unpredictable often genotype-specific nature of drug-drug interactions¹⁰. Thus, an unmet need is the identification of robust guiding principles to more efficiently identify, predict, or even improve upon antagonistic drug-drug interactions.

In the absence of principles that enable prediction of non-additive drug interactions, a common approach is to screen drug combinations, prioritizing testing drugs that target proteins with complementary functions. Several recent studies have used known or predicted network topologies to enrich for non-additive drug combinations^11-14. Furthermore, network simulations have revealed topological features, such as negative feedback and mutual inhibition that may underlie the antagonism of drug combinations¹⁵. We envisioned that principles of drug-drug antagonism may emerge from studying drugs targeting a network enriched for antagonistic interactions.

In recent years it has become clear that at least twelve mechanistically distinct forms of cell death exist¹⁶. Because these death pathways function in a mutually exclusive manner, we reasoned that drug combinations designed to co-activate multiple types of death may be enriched for antagonistic interactions. Several lines of evidence exist to suggest negative interaction and/or interdependent and mutually exclusive function among the various forms of cell death^17,18. For instance, necroptosis requires inhibition of extrinsic apoptosis, due to cleavage of the pro-necroptotic protein RIPK1 by caspase-8¹⁹. Similarly, PARP1, the initiator of parthanatos, is cleaved by caspase-3, suggesting that apoptosis inhibits the ability to activate parthanatos²⁰. From these data, a model is beginning to emerge that mutually exclusive activation of cell death pathways may be enforced through inhibitory crosstalk between death regulatory pathways¹⁶.

To identify a robust set of antagonistic interactions, we tested all pairwise combinations of the canonical activators for different death subtypes. We find that drug combinations comprised of cell death targeting drugs are enriched for drug antagonism, and in particular, strongly enriched for an extreme form of antagonism that we call “single agent dominance” (SAD). In SAD, the two-drug combination phenocopies one of the two single drugs. Importantly, this occurs even when the dominant drug is the less efficacious of the two compounds. Using statistical modeling we find that a key feature driving SAD is a discrepancy in the relative timing of death onset, with faster acting drugs suppressing slower acting drugs, leading to strong antagonism. These antagonistic phenotypes could be relieved by temporally phasing drug addition to promote synchronized co-activation of multiple death pathways. Finally, we explore the molecular mechanisms of SAD involving apoptotic and parthanatotic agents, finding that mutually exclusive but conflicting use of PARP1 drives dominance in these scenarios. Taken together, these findings highlight that the interconnected nature of cell death causes unexpected behaviors when these pathways are co-activated. Furthermore, death onset time is a feature of antagonistic drug responses, with a previously unappreciated role in dictating interactions between cell death processes.

RESULTS

A high-throughput assay for monitoring death kinetics

Drugs that induce different forms of death vary substantially in terms of their efficacy and activation rate²¹. To evaluate drug combinations comprised of apoptotic and non-apoptotic agents, we first developed an assay that could be performed in high-throughput while also retaining accurate analysis of death kinetics. Methods have been developed for high-throughput measurement of cell death using SYTOX green in a fluorescence plate reader¹⁷. Furthermore, SYTOX fluorescence is specific to death, but largely agnostic to the mechanism by which cells die²². We made experimental and computational modifications to prior methods to enable an accurate inference of the numbers of live, dead, and total cells (Fig. 1a and Supplementary Fig. 1). Understanding drug-induced death kinetics requires quantification of both live and dead cells over time, as inferences built from either measurement alone can be misleading (Supplementary Fig. 1b)²¹. To gain these insights, we measured the lethal fraction (LF%) prior to drug addition (e.g. percentage of dead cells relative to total cells), and at the assay end (Fig. 1a). To determine LF at intermediate times, experimentally measured dead cell numbers were compared to computationally inferred total cell numbers at matching time points (Fig. 1a-b). We estimated total cell numbers using an exponential model, constrained by the observed population size at the beginning and end of the assay. Although the growth of drug treated cells is not likely to always be exponential, and may not even be uniform over time, simulations of LF kinetics under varied population growth models reveal similar values regardless of which growth model was chosen (Fig. 1c-f and Supplementary Fig. 1). This procedure enables quantification of drug-induced changes in growth rate, death rate, and LF% over time, including an analytical estimation of death onset time (Fig. 1b). Furthermore, all of these measurements are computed from a single assay, and without the need for any specialized equipment.

Figure 1 – A high-throughput assay to monitor cell death kinetics.

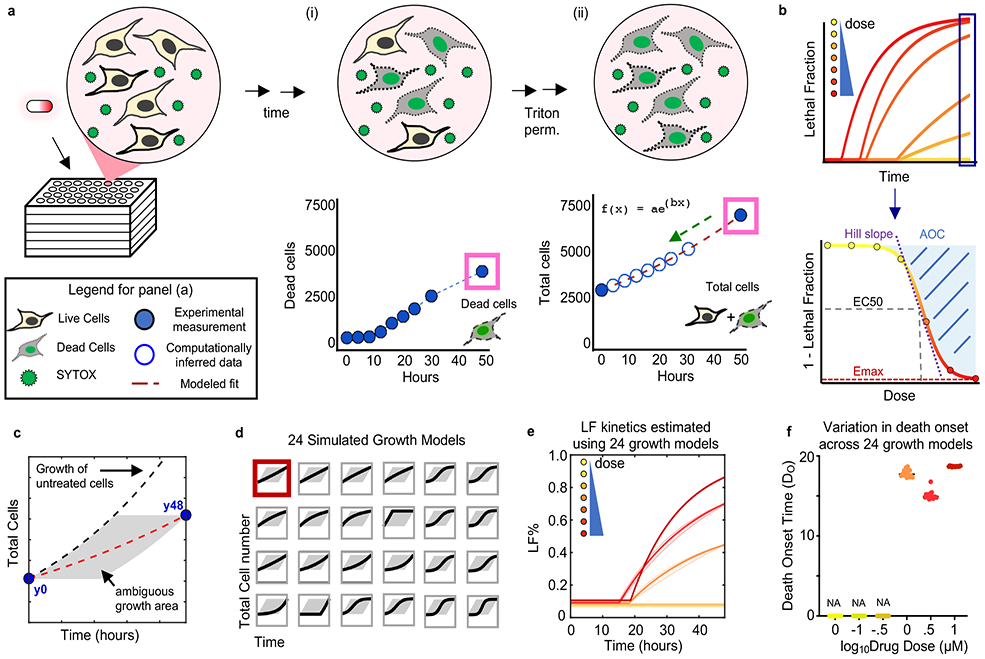
(a) Schematic of SYTOX assay. (i) Dead cells counted over time using SYTOX fluorescence. (ii) After permeabilization total cell counts can be determined at 0 and 48-hour time points (filled blue circles). Total cell counts at intermediate times are inferred by modeling to an exponential fit (red dashed line). (b) Modeled total cell counts used to infer LF at all time points. LF fit to a kinetic model to quantify death onset (D_O) and rate (D_R) following cell permeabilization. Percent viability at 48-hours used to quantify pharmacological parameters. See also Supplementary Fig. 1 and 2. (c-f) Death kinetic estimates under varied population growth models. (c) Ambiguity of growth over time of a drug treated population. Experimental measurements for total cells made only at the beginning (y0) and end (y48) of assay. Any trajectory through the grey area is feasible. Red dashed line is exponential model used in this study. Black dashed line is growth rate of untreated cells. Example data shown are from cells treated with 0.1 μM Camptothecin. (d) 24 varied growth models evaluated. Red box highlights the exponential growth model used in this study. Other growth models tested include linear, various sigmoidal models, and models with non-uniform rates over time. (e) LF kinetics for camptothecin at various doses, computed using different estimated growth models shown in (d). Thick line is exponential model. Shaded area around line represents SD among 24 simulated growth models in (d). See also Supplementary Dataset 1. (f) Range of death onset times computed for different doses of camptothecin. Each dot is the D_O estimated using a different population growth model from (d).

Kinetic analysis for apoptotic and non-apoptotic agents

To evaluate assay sensitivity, we tested cell dilutions over a wide range of cell concentrations. SYTOX green fluorescence of U2OS cells was linearly correlated with cell number from approximately 50 – 20,000 cells per well, allowing accurate quantification of death rates even as low as 1% above background (Fig. 2a). To determine the accuracy of our assay – and in particular the accuracy of our death rate estimates – we compared our approach to STACK, an automated-microscopy-based approach that enables direct measurement live and dead cells²¹. Overall, we found a strong correlation between our computationally inferred death rates and those computed from direct measurement of live and dead cells (Fig. 2b-e and Supplementary Fig. 2).

Figure 2 – Accurate analysis of death kinetics for apoptotic and non-apoptotic agents.

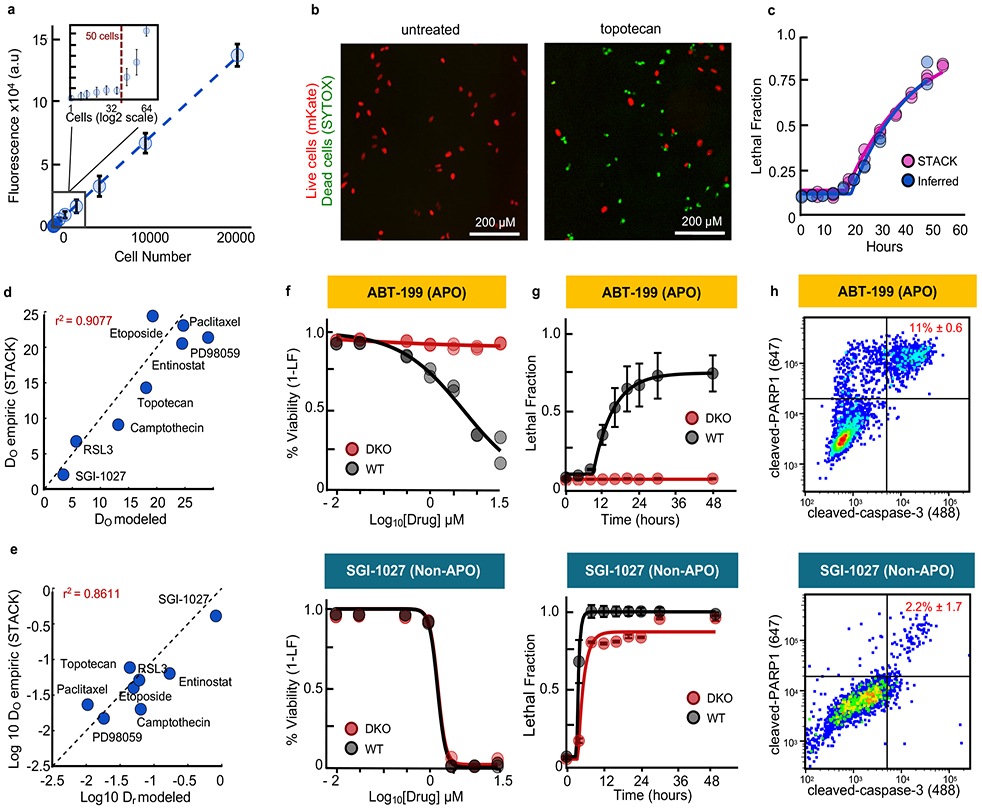
(a) SYTOX plate reader sensitivity. (b-e) Computational estimates of death kinetics compared to experimental measurements using STACK²¹. Data are mean +/− SD from biological replicates (n = 6). (b) Example image from cells treated with topotecan (31.6 μM) or untreated. Images are representative of 4 independent experiments, each with similar results. Scale bars, 200 μm. (c-e) Comparisons between plate reader-based estimates or STACK for (c) LF data and kinetic fits for topotecan as in (b), or (d) death onset time (D_O), and (e) death rate (D_R) for drugs with varied mechanisms of action. For (d) and (e) each drug was tested at a saturating LFmax dose (3.16 - 31.6 μM). (f-h) Examples of apoptotic (top) or non-apoptotic (bottom) drugs. Drugs tested in U2OS (WT) or U2OS-BAX/BAK^−/− (DKO) cells at 7 doses over 48-hours. See also Supplementary Fig. 3-5. (f) Percent viability across doses at 48 hours. (g) LF kinetics at the highest drug concentration. Data are mean +/− SD from biological replicates (n = 4). (h) Apoptosis quantified by flow cytometry. Cleaved-PARP1/cleaved-Casp3 double positivity was quantified 24hr post-treatment. Percentages are the mean +/− SD from biological replicates (n = 3).

To determine if our assay could reliably measure death induced by both apoptotic and non-apoptotic mechanisms, we quantified responses to a panel of 54 drugs reported to kill cells using different forms of regulated cell death^16,23-30. Drug responses were screened in U2OS, a cancer cell line with wild-type p53, which respond well to a diverse array of death-inducing agents. Due to limited availability of markers for some forms of death, we focused on a simplified classification scheme, categorizing drugs as non-lethal, apoptotic, or non-apoptotic. Non-lethal compounds were those whose effects were exclusively due to modulation of growth rate, without any drug-induced killing (Supplementary Fig. 3a-b). To distinguish between apoptotic and non-apoptotic drugs, we scored the degree to which the observed response was modulated in a BAX/BAK double knockout (DKO) genetic background, relative to wild-type (WT) U2OS cells (Fig. 2f-h and Supplementary Fig. 3). BAX and BAK are pro-apoptotic members of the BCL2 family and are pore forming proteins required for mitochondrial outer membrane permeabilization³¹. We defined drugs that primarily induce apoptosis as those in which the maximum LF was decreased by greater than 50% in DKO, compared to WT (Supplementary Fig. 3-5). Of the 54 drugs profiled, 34 were apoptotic using this threshold. 11 drugs primarily induced non-apoptotic death, as drug sensitivity was largely unchanged in DKO cells (Fig. 2f-h, Supplementary Fig. 3). To validate the use of a 50% threshold, we also used multivariate analyses, such as PCA and t-SNE, which integrated the kinetic and pharmacological data for each drug and did not require thresholds for the degree of difference between WT and DKO (Supplementary Fig. 3f-g). Both PCA and t-SNE recovered the same classifications as our simplified LF_max-based convention. Drug classifications based on relative DKO vs. WT sensitivity also agreed with categorization based on caspase-3 cleavage, a marker of apoptosis (Fig. 2h). Thus, our computational inference-based method accurately quantifies drug-induced death and death kinetics for a wide variety of drugs, including those with apoptotic and non-apoptotic mechanisms.

Co-activation of death pathways causes antagonism

Different subtypes of death are activated in a mutually exclusive manner due to inhibitory interactions between death pathways¹⁶. These features are common among antagonistic interactions¹⁵. We next tested if co-activation of multiple death pathways would enrich for drug antagonism. Our strategy was to test all pairwise combinations of the 54 cell death-activating drugs that we evaluated as single agents. All combinations were tested across 7 doses at a fixed dose ratio (i.e. constant ratio dosing), and responses were measured at 9 time points over 48 hours (Fig. 3a-b). Drugs were tested on multiple days and across wells on a given day, and both technical and biological replicates were highly correlated, suggesting a high degree of reproducibility within our assay (Fig. 3c and Supplementary Fig. 6).

Figure 3 – Combination drug screen to evaluate co-activation of apoptotic and non-apoptotic death pathways.

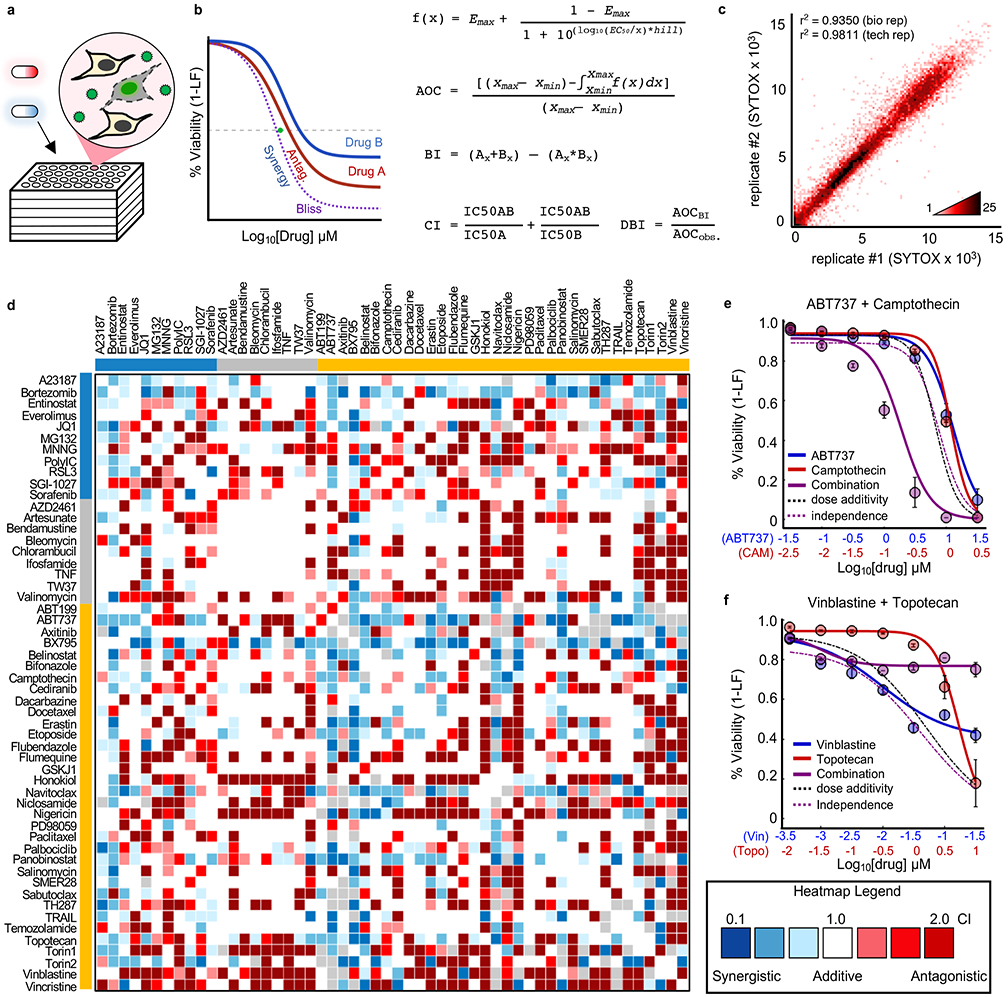
(a) SYTOX assay for drug combinations. (b) Calculation of drug-drug interactions. Equations shown for calculating dose curves, expectation under Bliss Independence (BI), Combination Index (CI, green dot) and Deviation from Bliss Independence (DBI). (c) Density plot of replicates from drug combination screen. Pearson correlation coefficient shown for biological replicates (tested across different days, n = 2) and technical replicates (tested across multiple wells of a plate, n = 2). (d) Drug combination screen. Heatmap of all CIs determined from screening 54x54 drug combinations. Colored bars depict drug class: Blue – Non-apoptotic; Grey – non-lethal; Gold – apoptotic. See also Supplementary Fig. 6-7. (e-f) Examples of synergistic/antagonistic drug combinations. (e) ABT737 (blue) and camptothecin (red). (f) Vinblastine (blue) and topotecan (red). For (e) and (f) purple – observed combination; dashed black – predicted assuming dose additivity; dashed purple – predicted assuming drug independence. Data are mean +/− SD from biological replicates (n = 4).

To score drug-drug interactions, we focused on 2 common reference models for estimating the expected response in the absence of interactions: Chou-Talalay combination index (CI) and Deviation from Bliss Independence (DBI). CI calculates interactions by comparing the observed IC50 dose for a drug combination to that expected assuming dose additivity, whereas DBI scores interactions by comparing the observed response to the response expected given independent drug action for the two single drugs (Fig. 3d and Supplementary Fig. 7a-b)^32-34. Both reference models are supported by well-validated quantitative principles; however, as CI is focused on dose additivity and DBI scores relative to response independence, these models tend to capture different types of interactions^35-37. For both models, thresholds for synergy/antagonism were determined by identifying CI or DBI values that produce less than 5% false positive rates when comparing experimental replicates (Supplementary Fig. 7). Drug-drug interaction scores were highly reproducible upon retesting with other assays (Fig. 3e-f, and Supplementary Fig. 6).

In our combinatorial drug screen approximately half of all combinations resulted in a drug-drug interaction (53.4% by CI; 46.6% by DBI). Furthermore, regardless of the scoring convention used, greater than 30% of all combinations resulted in antagonism (Supplementary Table 1). By comparison, other large-scale screens comprised of “random” combinations have identified antagonism at a frequencies of 2-10% (Supplementary Fig. 8)^11,38-40. Thus, as expected, combinations of cell death activating drugs are strongly enriched for antagonistic drug-drug interactions.

Death-inducing drug pairs yield single agent dominance

To more deeply analyze our data, we focused on a large set of strong antagonisms that we uncovered (Supplementary Fig. 8a). We noticed that many antagonistic responses were of an unexpected form, in which the two-drug combination phenocopied one of the two single agents (Fig. 4a). We call this response “single agent dominance” (SAD). The characteristic feature of SAD is that an otherwise efficacious drug becomes fully suppressed by a second agent. For example, both SGI-1027, a DNMT1 inhibitor that induces non-apoptotic death, and topotecan, a topoisomerase I inhibitor that induces apoptosis, produced strong killing in U2OS when applied as single agents (Fig. 4a). The combination of these two agents, however, resulted in precisely the same response as SGI-1027 alone. One trivial explanation of this phenotype could be that very potent drugs tend to dominate simply because no additional cells remain to be killed. To test this idea directly we tested all dose-dose combinations, to determine if low concentrations of a dominant drug would suppress high concentrations of a suppressed drug. We found that even non-efficacious concentrations of SGI-1027 were sufficient to block death induced by high concentrations of topotecan (Fig. 4b-d).

Figure 4 – Combinations of apoptotic and non-apoptotic cell death drugs are enriched for antagonism and single agent dominance.

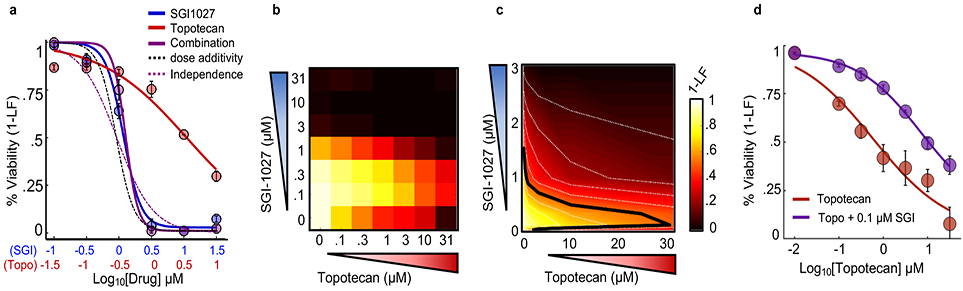
(a) Example SAD combination. Drugs given at constant dose ratio and measured using SYTOX at 48 hours. Blue – SGI-1027; Red – Topotecan; Purple – Combination; Dashed black – expected given dose additivity; Dashed purple – expected given response independence. (b) Percent viability response matrix for all-by-all dose combinations. (c) Isobologram analysis of (b). Doses plotted on a linear scale with 10% isobols shown and 50% isobol highlighted with a black line. (d) 1-LF for topotecan alone at varied doses (red) or topotecan in the presence of 0.1 μM SGI-1027. Data are mean +/− SD from independent biological replicates (n = 4).

To identify other drug combinations that feature SAD, we quantified the Euclidian distance in dose-response profiles between every drug combination and its two component drugs. We focused only on combinations that were antagonistic and required that a suppressed drug induce significant levels of death when used alone. Overall, we identified 130 SAD combinations, which were 30% of all antagonistic interactions (Supplementary Fig. 9).

Death onset time is a key determinant of drug dominance

Considering the prominence of the SAD phenotype in our data, we sought to gain a deeper understanding of dominant antagonism by identifying features that were enriched within SAD combinations. We performed a multivariate analysis on the kinetic and pharmacological data generated in our screen. To reduce dimensionality, we used principal component analysis (PCA). Six principal components were identified that captured over 85% of the variation in drug-induced death kinetic and pharmacological measurements (Fig. 5a-c). To determine which dimensions were capturing information related to drug dominance, we scored the statistical enrichment for SAD combinations on each PC. SAD combinations were enriched only on PC2, which captured 19% of the overall drug response variation (Fig. 5d and Supplementary Fig. 10).

Figure 5 – Statistical modeling reveals death onset kinetics as a key determinant of SAD combinations.

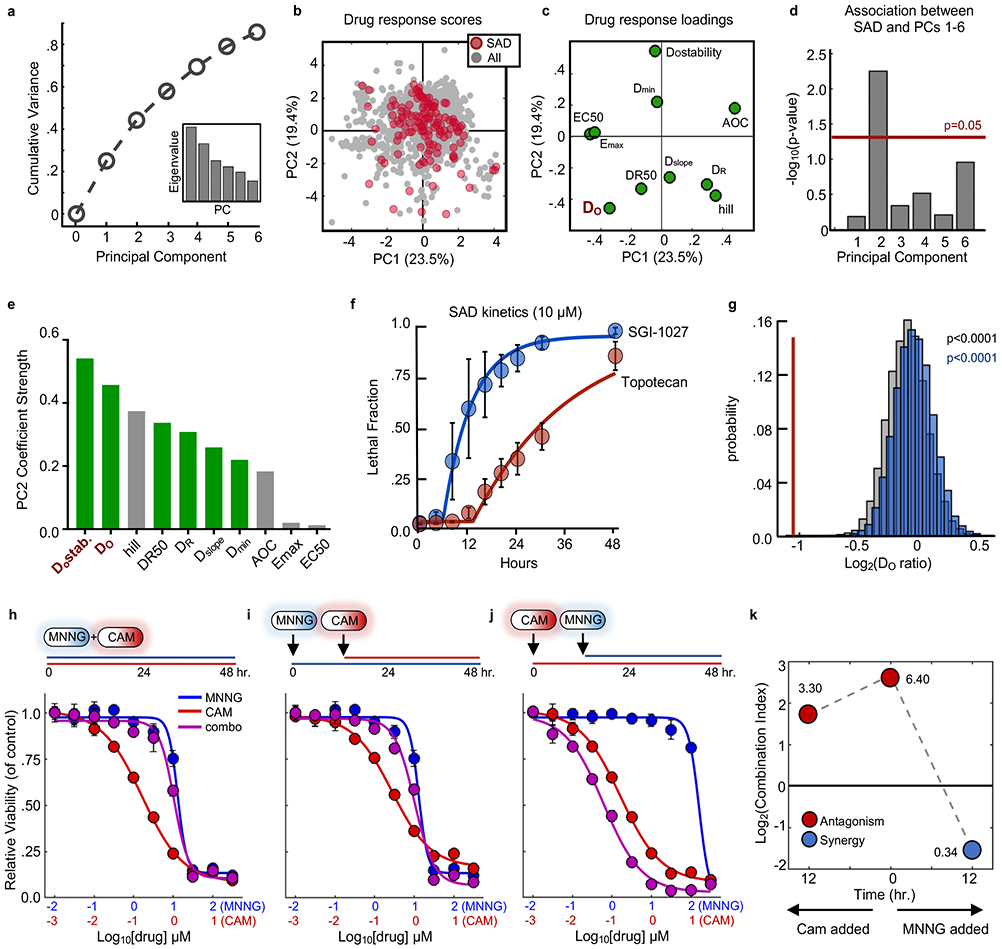
(a) Cumulative variation captured by PC1-6. Inset – Eigenvalues for PC1-6. (b) PCA scores plot for all single drugs and combinations from the cell death screen. SAD combinations are colored red while all other combinations/drugs are colored grey. (c) Loadings plot for PCs 1 and 2. (d) Enrichment of SAD for PCs 1-6. Enrichment for each PC was calculated using a one-tailed Fisher’s exact test. For panels (b-d) data are from the drug combination screen shown in Figure 3 (54 single drugs; 1431 combinations; n = 4 biological replicates). (e) Absolute value of parameter loading coefficients on PC2. Green – rate metrics; Grey – pharmacological metrics. (f) LF kinetics for an example SAD combination. Blue – dominant drug; red – suppressed drug. (g) Distribution of average onset ratios for all combinations (grey), non-SAD combinations (blue), or SAD combinations (red). Empiric p-value calculated by bootstrapping 10,000 iterations of 130 random drug combinations. (h-j) Dose response functions for MNNG and camptothecin (CAM) combinations added simultaneously (h) or sequentially (i and j). Blue – MNNG; Red – CAM; Purple – combination. (k) Combination indices over time for MNNG + CAM. Red – antagonistic; blue – synergistic. For panels (f), and (h-j), data are mean ± S.D. from biological replicates (n = 4).

Considering the enrichment for SAD combinations on PC2, we next identified the drug response features captured uniquely on this component. The response loading coefficients revealed that features related to death onset time (D_O and D_Ostability) were the variables most strongly associated with SAD combinations (Fig. 5c and e). D_O refers to the estimated death onset time from our kinetic measurements, while D_Ostability refers to the similarity of onset times for a given drug across doses. Features that are related to potency, such as AOC, E_max and EC50, were not captured on this component. To determine what aspect of death onset time was related to dominance, we examined death kinetics for the individual drugs that make up SAD combinations. We noticed a discrepancy in the rates of activation for dominant and suppressed drugs. For instance, in combinations of SGI-1027 and topotecan – a combination in which SGI-1027 is dominant – SGI-1027 kills cells earlier and at a faster rate than topotecan (Fig. 5f). To determine if differences in rates of activation were a common feature of SAD combinations, we explored the kinetic ratios for all 130 SAD combinations compared to 10,000 iterations of 130 random drug combinations in our data. This analysis confirmed that dominant drugs activate significantly earlier than their suppressed counterparts (Fig. 5g).

To test if the statistical correlation between onset time asymmetry and drug dominance was indicative of a causative relationship, our strategy was to temporally stagger the addition of dominant drugs, such that their activity occurred concomitantly with their suppressed counterparts. We tested this concept with the combination of MNNG and camptothecin, which results in robust domination by MNNG (Fig. 5h). The addition of the suppressed drug later in time relative to the dominant drug did not affect overall drug response or the degree of MNNG dominance (Fig. 5i); however, antagonism and dominance were relieved when MNNG addition was staggered such that the suppressed agent is active at the same time as the dominant drug (Fig. 5j-k).

To further test the robustness of the association between dominance and onset time asymmetry, we tested the extent to which drug dominance for a given combination would be conserved in other cell contexts. In our preliminary drug titrations for this study, we found several drugs for which rates differed significantly across cell lines. For instance, ABT199 induced death faster in MDA-MB-231, whereas panobinostat induced death much later in A549 compared to other cells. Alternatively, SGI-1027 tended to activate death very quickly across all cell lines tested. To determine if these rate differences alter drug dominance or if SAD combinations would persist even in the absence of onset time asymmetry, we re-tested SAD combinations in other cell lines. Combinations of SGI-1027 and camptothecin consistently produced dominance in other cell lines (Supplementary Fig. 11a-c). Thus, when onset time asymmetry was observed in other cell lines, drug dominance was conserved. Alternatively, when death onset times differed in other cell contexts, drug dominance was also changed. Combinations of ABT737 and ABT199 ceased to produce dominance in MDA-MB-231 cells, where the onset times for these two drugs were similar (Supplementary Fig. 11d-f). Also, BX795 and panobinostat, which induced death with similar onset times in U2OS, produced a SAD phenotype in A549 cells, a context in which panobinostat kills with similar efficacy but is activated later than in U2OS (Supplementary Fig. 11g-i). Thus, these data suggest that faster acting drugs suppress slower acting drugs, leading to antagonism and single agent dominance.

Predictive modeling to identify new SAD combinations

To further determine the generalizability of our findings, we aimed to predict new SAD combinations from drugs that have not yet been tested in combination. Although onset time asymmetry was a characteristic of SAD combinations, our data suggest that this feature alone would be poorly predictive of dominance. To identify other features that are important for generating drug dominance, we explored our PCA map to identify additional characteristics of SAD combinations, dominant drugs, or the relationships between dominant and suppressed drugs. Our PCA analysis showed that SAD combinations were enriched only on PC2; however, when comparing dominant and suppressed drugs rather than their combinations, we found that dominant drugs were significantly farther away from their suppressed counterparts in our PCA projections, suggesting that the vector projections of single drugs could themselves be used to predict new SAD combinations (Supplementary Fig. 12a-c).

We mined publicly available data for pharmacological and kinetic response profiles for single drugs, which could be projected into our PCA map. From these single drug projections, we identified drug pairs whose projection was similar to that observed for experimentally identified SAD combinations (Supplementary Fig. 12d). Full kinetic data for drugs at varied doses were not available for any drugs; however, kinetic data were available for limited doses for a large panel of drugs from a recent study that explored the kinetics of cell death²¹. We incorporated these kinetic data with publicly available pharmacological data for drug responses in U2OS cells⁴¹, and together these data were used to determine probable vector projections for new drugs in PC1 and PC2 (Supplementary Fig. 12d).

Using this publicly available data, we tested 77 combinations among 15 drugs, which included 48 combinations whose relative single agent profiles suggested possible drug dominance. We validated these predictions using our SYTOX based death assay (Supplementary Fig. 12e-g). Our validation screen was strongly enriched for antagonism (>60%), and greater than 77% of the predicted SAD combinations resulted in a dominant antagonistic interaction (p = 2.3 x 10⁻⁵; Supplementary Fig. 12h-i). Thus, even in the absence of any information about the drugs and their mechanisms of action, an analysis of single drug death kinetic properties was sufficient to identify new SAD combinations.

Interactions between death pathways mediate dominance

Our drug combination screen and subsequent computational analyses revealed the overall prevalence and a critical mechanism driving drug dominance. Next we sought to gain a molecular understanding of these drug-drug interactions. Non-additivity is a feature often related to the underlying network structure of a drug’s target proteins¹². Given the diversity of drugs tested and the limited understanding of pathways that regulate most forms of death, we focused on studying a SAD combination featuring drugs with known regulatory pathway interactions. For example, hyper-activation of PARP1 causes parthanatos, a form of non-apoptotic death^16,42. Conversely, inhibition of PARP1 causes apoptosis due to “PARP trapping” and stabilization of DNA lesions⁴³. Furthermore, PARP1 is cleaved and inactivated by caspase-3²⁰. These data suggest a negative interaction between apoptotic and parthanatotic pathways, possibly due to the conflicting use of PARP1. To test this, we first evaluated pathway activation dynamics of parthanatotic and apoptotic drugs at the level of PARP1 activation/inhibition. MNNG exposure leads to a transient hyper-activation of PARP1, causing increased protein PARylation (Fig. 6a). PARP1 hyper-activation began minutes after drug exposure, and returned to baseline by roughly one hour. When treated with apoptotic drugs like camptothecin, PARP1 was not activated, but rather cleaved and inactivated by caspase-3 (Fig. 6b). PARP1 cleavage did not occur until roughly 8-12 hours after camptothecin exposure (Fig. 6c). Thus, following exposure to MNNG or camptothecin, perturbations to PARP1 activity occur in distinct temporal windows, and in a mutually exclusive manner. When cells are exposed to both MNNG and camptothecin, PARP1 activation follows an MNNG-like dynamic pattern, consistent with the observed phenotypic dominance by MNNG over camptothecin (Fig. 6a-c).

Figure 6 – PARP1-dependent interactions mediate single agent dominance and choice between parthanatotic or apoptotic death.

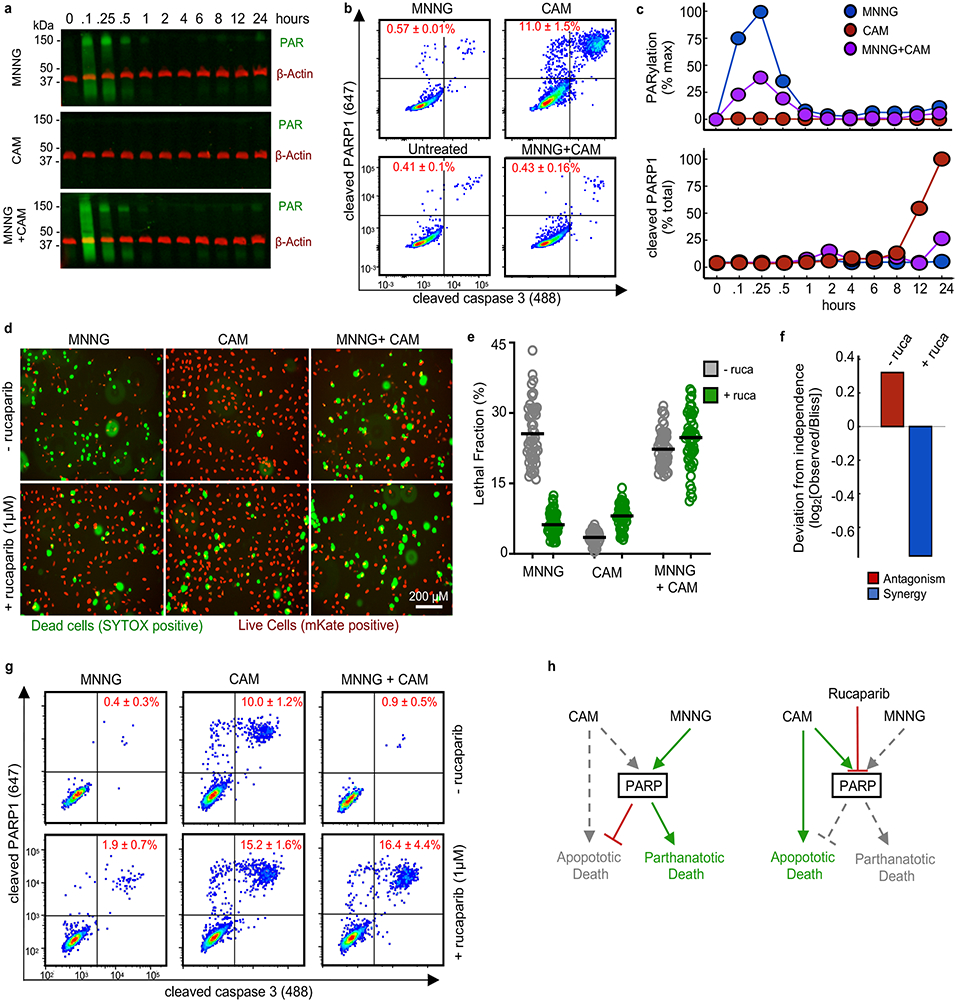
(a-c) Dynamics of drug-induced changes in PARP1 activity. Samples were treated with MNNG (31.6 μM), camptothecin (CAM, 3.16 μM), or MNNG+CAM for indicated times. (a) Representative Western blot of total protein PARylation. Green – total PAR; red – β-actin. Data are representative of 2 biological replicates. See also Supplementary Fig. 13a. (b) Cleaved-PARP1 quantified by FACS (12 hr. treatment shown). Data are % cleaved PARP1 as mean +/− SD from independent biological replicates (n = 2). (c) Quantification of PAR (top) and cleaved-PARP1 (bottom) activation dynamics. PAR quantified as % max signal. Cleaved PARP1 is shown as a percent of total cells. Data are the mean from independent biological replicates (n = 2). (d) Live cell imaging using STACK. U2OS cells expressing nuclear localized mKate2 (red) were treated with MNNG, CAM, or MNNG+CAM, +/− 1 μM rucaparib (ruca). Representative images from 48 hours post treatment from 2 independent replicates. Scale bars, 200 μm (e) Quantification of imaging in panel (d). Data are LF per image (50 images per condition). Line represents mean per treatment condition. (f) Deviation from expected response. Expected combination response calculated relative to Bliss independence using the quantified LF values from (e). (g) Apoptotic activity of MNNG+CAM. Cleaved-PARP1/cleaved-caspase3 quantified 12 hours after treatment. Data are the mean +/− SD from independent biological replicates (n = 4). (h) A model for a PARP mediated interaction between parthanatotic and apoptotic death leading to SAD.

Having determined that parthanatotic and apoptotic perturbations of PARP1 occur in a mutually exclusive manner, we next determined if PARP1 is mechanistically involved in the MNNG-camptothecin SAD phenotype. To do so, we explored the fate of cells treated with MNNG and/or camptothecin in the presence or absence of a PARP1 inhibitor, rucaparib. Although PARP1 inhibition by rucaparib can induce apoptosis, we used rucaparib at a sub-lethal dose, which was sufficient for blocking PARP1 activity (Supplementary Fig. 13). Consistent with expectations, PARP1 inhibition blocked MNNG-mediated death, but enhanced camptothecin sensitivity (Fig. 6d-e). The MNNG dominance over camptothecin was lost when PARP1 was inhibited by rucaparib. Instead, in the presence of rucaparib, combinations of MNNG and camptothecin led to synergistic levels of cell death (Fig. 6f). Parthanatotic death, by definition, should not occur when PARP1 is inhibited¹⁶. Thus, we suspected that PARP1 inhibition changed not only the nature of the drug-drug interaction, but also changed the mechanism of death induced by this combination. To test this, we began by evaluating markers of activation of apoptotic cell death. Using flow cytometry to measure caspase-3 activation, we found that PARP1 inhibition by rucaparib switched the mechanism of killing induced by MNNG-camptothecin combinations from parthanatotic to apoptotic (Fig. 6g-h). Thus, these data confirm that PARP1 mediates an interaction between parthanatotic and apoptotic death pathways, leading to antagonism and single agent dominance.

DISCUSSION

When defining drug-drug interactions a common goal is to identify drug combinations that may be beneficial therapies. For many years an implicit assumption was that drug synergy was conceptually interchangeable with clinically beneficial; however, recent studies have shed light onto the flaws in that prior thinking^6-8. Drug synergy – at least when defined relative to a dose additivity reference – generally suggests that similar results could be obtained at a lower dose. Synergy does not guarantee that a combination will kill cells that would not have been killed by either of the single agents alone. Similarly, antagonism may not be clinically harmful, and this is true even for some SAD combinations. For instance, a simple explanation for some SAD combinations would be that both drugs have the capacity to kill the exact same population of cells. These combinations would score as antagonistic relative to a response independence reference (but additive relative to dose additivity). In this study, however, we found that drug combinations comprised of death activating drugs tend to induce antagonism both when compared to dose additivity and response independence references (Supplementary Fig. 7). Furthermore, for many SAD combinations the maximum response of the combination killed fewer cells than at least one of the two component drugs. In these cases, it is likely that using these drugs in combination rather than individually would negatively affect treatment efficacy.

Importantly, our study also reveals some promising avenues for ways to generate potent combinations of death inducing drugs. In the case of MNNG+camptothecin, these drugs alone and in combination kill to the same fractional limit, leaving ~10% of the cells viable at saturating high doses. Interestingly, when these drugs were temporally phased to relieve MNNG dominance, the overall killing was improved to greater than 98%, suggesting that correctly timed drug combinations could kill cells that would not have been killed by drug A or B alone.

The phenotypes uncovered in this study underscore the complexities of death regulation and the need for a greater mechanistic understanding of how different forms of cell death are controlled, both regarding the molecular mechanisms and kinetics of activation. Regulated cell death provides an attractive target for therapeutic intervention, as cell killing is required for curative therapies⁴⁴. Many different mechanisms are likely contributing to the SAD combinations that we have identified, including modulation of cell cycle progression (in particular when cell cycle inhibitors are combined with drugs that are more toxic to cells in S-phase). As we demonstrated in the case of parthanatos and apoptosis, however, pathway “crosstalk” likely accounts for many non-additive responses observed in these drug combinations. The case explored in detail is also particularly important, as PARP1 inhibitors are being tested in clinical settings, generally in combination with other cytotoxic therapies, and generally without regard to whether these companion therapies induce apoptotic or parthanatotic death^45,46. Thus, for PARP inhibitors, our data suggest that the effectiveness of these agents should depend on the mechanisms by which companion compounds kill cells and, more importantly, the relative rates of activation of these drugs. More generally, considering the overall degree of antagonism and SAD within combinations of cell death targeting drugs, our data highlight the potential existence of widespread inhibitory crosstalk between death pathways. In most cases, however, we simply lack requisite knowledge on the death pathways activated by each drug and the molecular mechanisms by which most forms of cell death are regulated.

A major benefit from our study is the identification of a generalizable principle that can be used to streamline the evaluation of drug combinations, namely that rates of drug-induced cell death can be used to predict drug antagonisms. ⁶Since drug-drug interactions are difficult to predict, current strategies rely on screening drug combinations. This process is laborious due to the combinatorial expansion of possible combinations to test, which is further complicated by the fact that drug-drug interactions often depend on the doses used, the order in which the drugs are applied, the environment in which the drugs are applied, and the genotype(s) under evaluation^5,10,47-49. Our study suggests that drugs may not need to be tested in combination in order to avoid SAD combinations, if the rates of drug induced death onset are known or can be measured (Supplementary Fig. 14). Furthermore, our data suggest that rate asymmetry may be a more reliable predictor of SAD than the identity of the drugs themselves. Using rates, we correctly predicted new SAD combinations among drugs that had not been previously tested. Also, we found that drug pairs that produced SAD phenotypes often differed across cell lines; however, these cell type-specific differences could also be predicted based on death onset asymmetry. These data suggest an opportunity for a new paradigm in cancer therapy, one that prioritizes conserved rules rather than conserved drug identities.

Currently, standard approaches do not typically evaluate drug activation kinetics, instead focusing on the relationship between efficacy/potency and dose. These “dose-response” relationships have been the central focus of drug pharmacology data for over a century, and these relationships clearly reveal important insights about a given drug. The kinetic features of a drug are generally not predictable from single time point dose-response data. Our study reveals that these “rate-response” relationships are observable in kinetic data, and that these relationships also produce unique insights into the nature of a given drug or drug combination. Given the complementarity of pharmacological and kinetic data, evaluation of both of these types of data should become a new standard.

ONLINE METHODS

Cell lines and reagents

U2OS, A549, MCF10A, and MDA-MB-231 cells were obtained from ATCC and maintained at low passage numbers (generally less than 20 passages from the original vial). U2OS, A549, and MDA-MB-231 cells were grown in Dulbecco’s modified eagles medium (DMEM) supplemented with 10% FBS, 2 mM glutamine, and penicillin/streptomycin. MCF10A cells were grown in DMEM/F12 media, supplemented with 5% horse serum, 20 ng/ml EGF, 0.5 mg/ml hydrocortisone, 100 ng/ml cholera toxin, 10 μg/ml insulin, and penicillin/streptomycin. Drugs were purchased from either Selleck Chemicals, APEXBio Technology, or Sigma-Aldrich. SYTOX green was purchased from Thermo-Fisher. Poly/Mono ADP Ribose Rabbit mAb (83732) was purchased from Cell Signaling Technologies. Purified rabbit anti-active caspase 3 (559565) and Alexa Fluor® 647 conjugated mouse anti-cleaved PARP (558710) were purchased from BD Pharmingen. Secondary antibodies were purchased from LICOR Biosciences and BD Biosciences. See also Supplementary Table 2.

SYTOX based measurement of cell death

The total number of dead cells at given time points can be determined by measuring SYTOX fluorescence. SYTOX green was tested for linearity by plating cells at a 2-fold cell dilution from 20,000 cells to 1 cell in 5 μM SYTOX. After adhering, cells were lysed with 0.1% triton in PBS for 1.5 hours. Fluorescence was measured on a Tecan M1000 plate reader at 503/524 excitation/emission. Gain was set to capture linearity and for fluorescence to be at ~85% saturation of the detector. For drug-induced cell death measurements, cells were seeded at 1500 cells per well of 384-well optical bottom black-walled plates, or 2500 cells per well of 96-well optical bottom black-walled plates, and adhered overnight on the day prior to drug addition (“day −1”). On day 0, drugs were prepared at 5X final concentration (10X for 96-well experiments) in DMEM containing 25 μM SYTOX green (50 μM in 96 well experiments). 7-point half-log dilutions were prepared in 96 well plates. Drug dilutions were added using an Integra ViaFlo96 electronic pipettor (Integra). Fluorescence readings (504ex/523em) were taken at 0, 4, 8, 12, 16, 20, 24, 30, and 48 hours on a Tecan M1000 plate reader. Additionally, an untreated plate was lysed at t = 0 for initial cell counts by adding 0.1% triton in PBS and incubating 1.5 hours at 37°C at 5% CO₂. After the 48-hour reading, all experimental wells were lysed and a final fluorescence reading was taken. Lethal fraction and relative viability was calculated using the pre- and post-triton permeabilized fluorescence readings.

Modeling lethal fraction kinetics

Using the procedure above, a lethal fraction (LF%) measurement can be experimentally determined only at 0 and 48 hours (see Supplementary Figure 1a). To determine LF% at intermediate time points, it was necessary to estimate the growth of the drug treated cells from 0 to 48 hours, as the number of dead cells can in some cases produce false insights (e.g. for drugs that induce potent cell death very quickly at high doses and more slowly at low doses, lower doses can yield more dead cells; see for example Supplementary Figure 1b). Although the population size at the beginning (y0) and end (y48) of the assay are experimentally determined, some ambiguity does exist regarding the shape/kinetics of population growth in the drug treated conditions (i.e. the dynamics of population growth as cells respond to drug; see Supplementary Figure 1c). In this study, we considered the “area of ambiguity” for population growth to be constrained by two assumptions: 1) the population size (e.g. live cells + dead cells) is never less than observed in the initial measurement (y0), and 2) the population size is never greater than observed in the final measurement (y48). Assumptions 1 and 2 are met if dead cells can be measured using SYTOX (i.e. dead cells do not decay to the point that they are no longer SYTOX positive), and live cells can be observed by STYOX following triton permeabilization. These assumptions are well met in our data, due to the relatively short time course of our study (48 hours) and the durability of SYTOX fluorescence, which we and others find to be stable for at least 72 hours²¹. In this study, for simplicity we used an exponential population growth model, which assumes a uniform rate of growth over time (see Supplementary Figure 1d). In the context of drug treatment, the growth rate is generally decreased, and this is observable in the pre- and post-triton cell data, which is used to constrained by the experimentally observed minimum and maximum total cell numbers at the beginning and end of the assay. From the growth curve, the total number of cells could be determined for each condition at any time between 0 and 48 hours. Together with dead cell counts, a LF was determined for each drug at all time points and doses measured. Kinetic LFs were modeled using a Lag Exponential Death (LED) equation described previously²¹:

$$LF(t)=L{F}_0+(L{F}_p-L{F}_0)\ast (1-e^{-D_R(t-D_O)})$$

where LF₀ is the lethal fraction at time 0, LF_p is the death plateau, D_O is the onset time of death, and D_R is maximum rate of death. The model was constrained by 0< D_O < 48, LF_p < 1, and D_R < 2. LF₀ was left unconstrained to allow for variation in basal levels of cell death. Drugs that did not produce max LF values 2x greater than the LFmax value for DMSO treated samples were fit to a linear model.

Notably, this approach makes an assumption about uniform exponential growth for drug treated cells; however, assay accuracy does not depend on the uniform growth rate assumption. We also tested in total 24 population growth models including many that were not exponential and many with non-uniform growth rates over time to determine a possible range for LF% kinetics (see Supplementary Figure 1d). In general, death kinetic terms (D_O and D_R) are invariant regardless of the population growth model chosen for non-lethal drugs, for death inducing drugs at low concentrations, and for death inducing drugs at very high concentrations. Some variation is observed at intermediate doses for death inducing drugs and variation is largest for drugs with particularly early death onset times as fluctuations in the growth model alter death rates and death plateau values. These data are reported as confidence intervals for death kinetic parameters in Supplementary Dataset 1.

U2OS mKate²⁺ and BAX/BAK^−/− cell-line generation

NucLight red mKate2+ U2OS cells were generated by spin-fecting 6.33x10⁶ TU/mL of NucLight Red virus (Essen Biosciences) with 8 μg/mL Polybrene and 1.5x10⁶ cells at 2,000 rpm for 2 hours at 37°C. After spinning, fresh DMEM was added and the cells were incubated overnight. On the next day, cells were replated onto a 10 cm dish and grown to 80% confluence. mKate+ cells were selected by FACS. BAX/BAK−/− U2OS cell line was generated using the pX330-puro plasmid with a hSpCas9 and BAX (GACAGGGGCCCTTTTGCTTC) or BAK (AGACCTGAAAAATGGCTTCG) sgRNA insert. U2OS cells were transiently transfected using FuGENE HD transfection reagent (Promega). BAX/BAK−/− cells were selected for using the BH3 mimetic Navitoclax (10 μM) for 5 days. Following Navitoclax treatment, cells were seeded as single cell clones and BAX/BAK double knockouts cells were confirmed by sequencing.

Quantitative microscopy and STACK image analysis

mKate2 expressing U2OS cells were seeded either at 200,000 cells per well of 6-well plates, or at 2,500 cells on 96-well plates and adhered O/N. On day 0, drugs were added to wells in addition to 50 nM SYTOX. Images were captured using an EVOS FL Auto microscope with a 10X objective using GFP (470/510) and Texas Red (585/624) light cubes (Life Technologies). 25 images were collected per well for experiments on 6-well plates, and 4 images per well for experiments on 96-well plates, with 2 wells per treatment condition. Live cell and dead cell counting was performed using the incucyte software. The average number of total cells counted per image was 284 (range 108 – 812 cells per image). Lethal fraction was computed as in Forcina et al.²¹

Classification of drug mechanisms of cell death

Drugs were classified as non-lethal, apoptotic, and non-apoptotic. Non-lethal compounds were those that did not induce significant cell killing over background even at the highest doses tested. Significant killing was defined in this study based on the LFmax observed at the assay end point. More specifically, the LF values for DMSO treatment reached ~ 8% at the end of the assay, so drugs were categorized as non-lethal if they induced less than 16% death at their max concentration at 48 hours. In our kinetic evaluation, these drugs fit to a linear model rather than a lag exponential death model, consistent with the lack of any observable drug-induced increase in the rate of cell killing. For the remaining 45 drugs, apoptotic and non-apoptotic classes were distinguished using a two-pronged approach, either using quantitative thresholds or a multivariate analysis of our pharmacological and kinetic data. Both approaches focused on differences in the measured death between WT and BAX/BAK double knockout (DKO) cells. For the threshold-based strategy, we characterized apoptotic drugs as those in which the maximum lethal fraction observed in our data in DKO was decreased by greater than 50% relative to WT (i.e. the death was “mostly apoptotic).

To validate these classifications, and to validate the use of a 50% threshold (and essentially to avoid the use of any thresholds), we also analyzed the full complement of pharmacological and kinetic data for each drug using principal component analysis (PCA). PC1 captured response features related to potency (Emax, LFmax, etc.), whereas PC2 captured the degree to which responses were changed in DKO vs. WT cells (i.e. DKO/WT ratio, see Supplementary Fig. 3f). Drug classifications based on a 50% difference in DKO vs. WT LFmax were consistent with PCA projections and also with other data dimensionality reduction methods, such as t-SNE. Of note, both PCA and t-SNE based analyses identified two different groups within the apoptotic class. For 17 drugs, responses were completely lost in DKO cells (i.e. both kinetic and dose-response curves fit to a linear model). For the remaining 17 apoptotic drugs, measures of drug response were diminished in DKO cells, but not as dramatically (see for example, Supplementary Fig. 3e, 2 groups of apoptotic drugs with respect to death onset times in DKO cells). In our analyses, these two classes were combined into one apoptotic class for simplicity. See also Supplementary Dataset 1.

Drug combination screen

For combinations of cell death inducing drugs, we used a “fixed dose ratio” scheme rather than an “all-by-all” dose matrix (i.e. isobologram analysis). For most drugs the highest drug concentration tested was 31.6 μM; however, to maintain similar levels of potency in the combination drug screen several drugs were tested starting at higher or lower ranges. See Supplementary Dataset 2 and Supplementary Table 3. For graphing purposes, these drugs are plotted on a shared “normalized” dose axis, reporting two dose scales when needed (see for example, Fig. 2e-f). Drug dilutions were pinned onto 96 well plates manually by the following procedure: A source plate contained stock concentrations of 54 drugs arrayed in wells 1-54. From the source plate, a single row of 10 drugs was diluted to 5x the highest concentration in DMEM using a 12-channel pipette. This array of 54 drugs was considered the “B drug”. To the array of B drugs, the “A drug” was added manually at 5x the highest concentration using a repeat pipettor. In wells in which the A and B drugs were identical (i.e. “A+A combinations”), an equivalent volume of DMSO was added in place of the A drug. Thus, no self-self drug pairs were tested in this screen, both to conserve on drug, and to create day-to-day replicates of each drug to evaluate data robustness. These A+B drug combinations in the pin plate were subsequently diluted at half log dilutions for a total of 7 doses. 10 μL of 5x drug dilutions were added to 384-well plates using an Integra via-flo 96-well head automatic pipettor.

Calculating drug-drug interactions

Drug-drug interactions were calculated using both the Chou-Talalay Combination Index (CI) and a Deviation from Bliss Independence (DBI). For both the response data used was “1-LF” (i.e. lethal fraction measurement represented in terms of viable fraction). CI was calculated according to the convention:

$$CI=\frac{DA}{da}+\frac{DB}{db}$$

Where da and db are the IC50 doses of “drug a” (alone) and “drug b” (alone), and DA and DB refer to the doses of drugs A and B in the AB combination that resulted an IC50 response. A similar calculation was also performed using the EC50 of a, b, and the AB combination, as well as the GR50 (dose of 50% growth reduction). For GR index, relative viability (live cells in drug treated compared to live cells in vehicle treated) was used rather than 1-LF, based on the established convention for GR Index⁵⁰. In figures where a dose curve is shown for a predicted additive drug response estimated a curve using a three parameter logistic regression, with the EC50 set to the predicted IC50 at a CI = 1, Emax set to the minimum observed between drug a and b, and the hill slope set to the mean of hill slopes for drugs a and b.

For computing DBI the expected response at each dose was computed according the Bliss Independence convention:

$$BlissExpectedResponse=Ra+Rb-(Ra\ast Rb)$$

Where Ra and Rb refer to the lethal fraction observed at each dose for drug a and drug b. The Bliss expected response at each dose was then fit to a logistic regression model. DBI was computed as:

$$DBI=\frac{[AOCBlissExpectedResponse]}{[AOCObservedResponse]}$$

Where the area over the curve (AOC) was computed for the observed data and the Bliss Expected dose response curve. For each of the methods described above thresholds for non-additive interactions were determined by comparing the error among biological replicates. Specifically, CI or DBI scores were computed from each replicate separately. Replicate 1 was selected as “true” and the threshold for drug-drug interaction was iteratively increased from 1 to 10 (for antagonism) or decreased from 1 to 0 (for synergy). This process was repeated using each other replicate as “true” and evaluating “hit” specificity using replicate 1. Threshold values for interaction were selected at values where false positive rates were below 5%. Thresholds and numbers of positive/negative interactions are shown in Supplementary Table 1, and Supplementary Figure 7.

Quantitative identification of drug combinations featuring single agent dominance

To identify drug combinations that feature single agent dominance in a quantitative and unbiased manner, we quantified the Euclidean distance between the pharmacological dose curves for every drug combination and its component single drugs. A drug was considered dominant if the distance between a drug combination and is closest single drug was less than 2x the error rate observed in our assay (i.e. closer than ~ 12% variation). This process also selects relatively trivial versions of dominance where the “suppressed” drug was inefficacious. Thus, we also did not allow suppressed drugs to result in less than 16% killing (the same threshold used to define non-lethal compounds). Using this approach dominant antagonism was observed for 130 combinations when the CI metric was used to define antagonism, and 159 combinations when the DBI metric was used to define antagonism. See also Supplementary Dataset 3-4.

CellTiter-Glo based measurement of relative viability

Cells were seeded at 2500 cells per well in 96-well plates and adhered overnight. On the day of drug addition 10X drug solutions were prepared as above in DMEM and added to the wells. 48 hours post-treatment, cells were lysed using according to the CellTiter-Glo (Promega) manufacturer instructions and luminescence was read on a Tecan Spark I plate reader. Relative viability was calculated as percent of DMSO control wells on the same plate.

Flow cytometry-based analysis of apoptosis

Cells were seeded at 200,000 cells per well of 6 well dishes on the day prior to treatment and adhered overnight. For time course experiments, drugs were added in a manner such that all samples were collected at the same time. Post treatment, cells were collected and fixed with 4% formaldehyde for 15 minutes. After two washes with PBS, cells were exposed to 100% methanol at −20°C for >2 hours. Cells were washed with PBS and incubated with the active caspase-3 antibody (1:500 dilution, BD Biosciences) in a 50/50 (v/v) PBS-T:Odyssey blocking buffer solution (LICOR). Cells were washed with PBS-T and incubated with the Alexa-fluor 647 cleaved PARP primary and Alexa-fluor 488 goat anti-rabbit secondary antibodies (1:500 dilution, BD Bioscience) overnight at room temperature. FACS samples were run on an LSR II machine with excitation lasers of 488 and 640 nm.

Western blot analysis of PARylation

Cells were seeded at 200,000 cells per well in 6-well dishes and adhered overnight. All drugs were added at t = 0 and cell lysates were prepared at indicated time points. Briefly, media was removed from the well and washed 2x with 2 mL of PBS. Cells were lysed by adding 400 μL of SDS-Lysis buffer (50 mM Tris-HCl, 2% SDS, 5% glycerol, 5mM EDTA, 1 mM NaF, 10 mM β-GP, 1 mM PMSF, 1mM Na₃VO₄, protease inhibitor and phosphatase inhibitor tablet). Lysates were spin-filtered through 0.2 μm multi-well filters to remove DNA (Pall). After filtration, lysate concentration was determined by the Pierce BCA Protein assay kit according to the manufacturer’s instructions (Thermo). Lysate concentrations were normalized to 0.5 mg/mL for SDS-PAGE loading. Samples were run on pre-cast 48-well gels and transferred using a semi-dry fast transfer (i-BLOT, Invitrogen). Membranes were blocked in a 50/50 (v/v) PBS-T/Odyssey blocking buffer solution for 1 hour at room temperature, incubated overnight at 4°C in primary antibody, and then stained with secondary antibodies conjugated to infrared dyes (LICOR). Blots were visualized using a LICOR Odyssey CLx scanner.

Data analysis and statistics

All statistical analyses and curve fitting was performed using MATLAB software. PCA was performed in MATLAB after z-scoring data using the built-in function ‘pca’. Analysis of flow cytometry data was performed using FlowJo, and Western blot analysis was done using LICOR Image Studio. Pearson correlation coefficients were calculated in MATLAB using the built-in function ‘corrcoef’. Fisher’s exact tests were performed in MATLAB using the built-in function ‘fishertest’, with right tailed (e.g. enrichment) specified. t-SNE was performed on z-scored data in MATLAB using the built-in function ‘tsne’ under default conditions.

Data availability

Source data for the evaluation of drug mechanism of cell death are included in Supplementary Dataset 1. Source data for the drug combination screen in Fig. 2d are included in Supplementary Dataset 2. PCA scores data related to Fig. 4a-c are included in Supplementary Dataset 3. The list of 130 SAD combinations identified in this study are included in Supplementary Dataset 4. All other data will be made available upon request.

Code availability

Custom analysis code for computing lethal fraction kinetics from end point data are included in the MATLAB script ‘backfitting and LED.m’. Other analysis code will be made available upon request.