Motor cortical thickness is related to effort-based decision-making in humans

Abstract

Although motor cortex is integral in driving physical exertion, how its inherent properties influence decisions to exert is unknown. In this study, we examined how anatomical properties of motor cortex are related to participants’ subjective valuations of effort and their decisions to exert effort. We used computational modeling to characterize participants’ subjective valuation of physical effort during an effort-based decision-making task in which they made choices about exerting different levels of hand-grip exertion. We also acquired structural MRI data from these participants and extracted anatomical measures of each individual’s hand knob, the region of motor cortex recruited during hand-grip exertion. We found that individual participants’ cortical thickness of hand knob was associated with their effort-based decisions regarding hand exertion. These data provide evidence that the anatomy of an individual’s motor cortex is an important factor in decisions to engage in physical activity.

NEW & NOTEWORTHY How effortful a task feels is an integral aspect of human decision-making that influences choices to engage in physical activity. We show that properties of motor cortex (the brain region responsible for physical exertion) are related to assessments of effort and decisions to exert. These findings provide a link between the anatomical properties of motor cortex and the cognitive function of effort-based choice.

INTRODUCTION

We must constantly decide if it is worth exerting effort to obtain reward. These decisions require an assignment of value to the costs and benefits at stake. A number of studies have shown that appetitive value judgments are a function of the constituent characteristics of the rewards in question (Howard et al. 2015; Howard and Gottfried 2014; Suzuki et al. 2017). However, less is known about what characteristics are integrated to generate valuations of effort.

Studies in humans (Bonnelle et al. 2016; Chong et al. 2017; Croxson et al. 2009; Hogan et al. 2019; Klein-Flügge et al. 2016; Kurniawan et al. 2010, 2013; Prévost et al. 2010; Skvortsova et al. 2014) and animals (Floresco et al. 2008; Hillman and Bilkey 2012; Rudebeck et al. 2008; Walton et al. 2002, 2009) have examined how the brain represents the value of effort and makes decisions to trade effort for reward. These works have implicated a network of brain regions including the anterior cingulate cortex, insula, and ventromedial prefrontal cortex in the encoding of effort costs and effort cost trade-offs. However, these studies did not examine the constituent characteristics that give rise to effort valuation. In particular, cortical anatomy and physiology may be important characteristics that contribute to representations of effort value since they are related to motor performance and capacity (Anderson et al. 2002; Díaz et al. 1994; List et al. 2013).

Increased cortical thickness has been associated with higher resting motor thresholds (List et al. 2013), and alterations in motor cortical physiology have been associated with increased perceptions of effort in clinical populations (Kuppuswamy et al. 2015). Moreover, a number of neurological conditions have been associated with changes in cortical thickness and associated deficits in behavior (Brodtmann et al. 2012; Calabrese et al. 2007; Duering et al. 2012; Hartikainen et al. 2012; Richards et al. 2009). Despite these links between neuroanatomy, motor capacity, and behavior, to our knowledge the relationship between motor cortical anatomy and decisions to engage in physical activity has never been investigated.

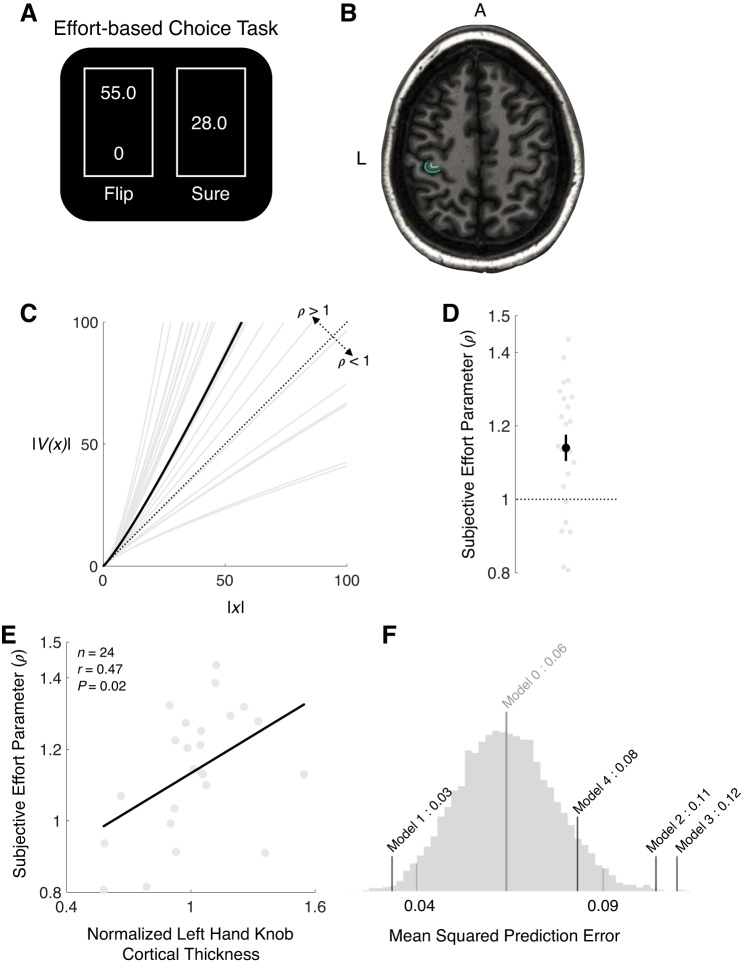
In this study, we examined whether the thickness of the hand knob, the region of the motor cortex responsible for grip exertion (Yousry et al. 1997), varies with individual variations in subjective valuation of effort and prospective decisions to exert. We first acquired structural brain scans of healthy right-handed individuals with magnetic resonance imaging (MRI). After scanning, participants underwent an effort-based decision-making task (Fig. 1A) in which they made risky forced choices involving two options, a small, sure amount of grip effort, required with certainty, or a risky option that could result in even more grip exertion or none at all (with equal probability). The data from this choice paradigm allowed us to generate parametric measures of participants’ subjective valuation of prospective effort, which is representative of their effort-based decision-making (Hogan et al. 2019), and we related these choice parameters to anatomical metrics of the hand knob acquired from the structural brain scans.

Fig. 1.

Experimental task, behavioral data, and correlation between structural imaging data and behavior. A: during effort-based choice trials participants were presented a series of risky decisions that involved choosing between 2 options: exerting a low amount of effort with certainty (“sure”) or taking a gamble that could result in either a higher level of exertion or no exertion, with equal probability (“flip”). The effort amounts were presented on a 0–100 scale, on which participants were trained during an Association phase before choice. An effort level of 0 corresponded to no exertion and 100 to 80% of a participant’s maximum exertion. Gambles were not realized after a choice. At the end of the Choice phase, to ensure that participants revealed their true preferences for effort, 10 choices were randomly selected and played out such that any effort required would need to be exerted before they completed the experiment. B: a structural image (transverse slice) from an exemplar participant, illustrating a tracing of the left hand knob (in green). L, left. A, anterior. C: the estimated subjective effort cost function [V(x) = x^ρ] for each participant (gray) and the group median (black). The dashed line indicates an objective valuation of effort (ρ = 1), with curves above this line representing that an incremental change in the effort level results in a greater subjective cost of effort for higher effort levels. D: parameter estimates ρ for individual participants (gray) and the group median (black). The error bar represents the SE. E: between-participant regression considering the relationship between effort subjectivity parameters acquired from the behavioral choice data and normalized left hand knob cortical thickness. Left hand knob thickness was normalized by contralateral hand knob thickness. This relationship illustrates that individuals with a larger hand knob thickness find prospective effort to be more costly (indicated by a larger ρ). F: prediction errors from cross-validation analyses assessing the predictive power of anatomical measures and monetary subjective preferences on subjective effort parameters. Model 0: ρ = unif(ρ_min, ρ_max); model 1: ρ = β₀ + β₁ × LHK_Thickness; model 2: ρ = β₀ + β₁ · LHK_Thickness + β₂ · LHK_SurfaceArea + β₃ · LHK_Volume + β₄ · LM1_Thickness + β₅ · LM1_SurfaceArea + β₆ · LM1_Volume; model 3: ρ = β₀ + β₁ ·LHG_Thickness + β₂ · LHG_SurfaceArea + β₃ · LHG_Volume; model 4: ρ = β₀ + β₁ · λ + β₂ · α, where LHK is left hand knob and LM1 is left primary motor cortex, The histogram represents 10,000 samples from the null model (model 0). The mean (center of the distribution) and 95% confidence intervals (tails of the distribution) of the null model are indicated with gray lines. The black lines represent the mean squared prediction errors of the leave-one-out analyses of the other models.

METHODS

Participants

All participants were right-handed and prescreened to ensure the absence of prior history of neurological or psychiatric illness. The Johns Hopkins School of Medicine Institutional Review Board approved this study, and all participants gave written informed consent.

Data from 25 healthy individuals were analyzed for this study. All of these participants performed the effort-based choice task, and 20 performed the monetary choice task. One participant was excluded from the monetary choice regressions because of inconsistent choices that did not allow for reliable fits of model parameters. One participant was excluded because their normalized hand knob thickness was outside three standard deviations of the population mean. The final analyses included 24 participants in total (mean age 23.13 yr, age range 18–34 yr; 12 men and 12 women). The control analyses involving monetary risk and loss aversion included 19 participants.

Note that a portion of these data, pertaining to behavioral modeling of subjective effort valuation, was previously reported in Hogan et al. (2019). This previous study reported findings from functional (f)MRI data acquired at the time of effort decision and did not explore how subjective effort preferences were related to parameters acquired from structural images. The results presented here are from an exploratory set of analyses to determine the relationship between hand knob thickness and the subjective valuation of prospective hand grip effort.

Experimental Procedures

MRI protocol.

A 3-T Philips Achieva Quasar X-series MRI scanner and radio frequency coil was used for all the MR scanning sessions. A high-resolution structural image was collected with a standard MPRAGE pulse sequence, providing full brain coverage at a resolution of 1 mm × 1 mm × 1 mm, repetition time (TR) 2,800 ms, echo time (TE) 30 ms, and flip angle 70°.

Behavioral experiments.

Presentation of visual stimulus and acquisition of behavioral data were accomplished with custom MATLAB (https://www.mathworks.com) scripts implementing the Psychtoolbox libraries (http://psychtoolbox.org). Visual feedback was presented via a projector. An MRI-compatible hand clench dynamometer (TSD121B-MRI; BIOPAC Systems, Inc., Goleta, CA) was used to record grip force effort. During experiments, signals from this sensor were sent to our custom-designed software for visual real-time feedback of participants’ effort exertion. Effort exertion was performed while participants held the force transducer in their right hand. To record participants’ choices, we used an MRI-compatible multiple button-press response box (Cedrus RB-830; Cedrus Corp., San Pedro, CA).

effort paradigm.

Before the experiment, participants were informed that they would receive a fixed show-up fee of $30. It was made clear that this fee did not depend on performance or behavior over the course of the experiment. The Association, Recall, and Choice experimental phases, described below, are identical to those we have previously described in detail (Hogan et al. 2019).

The experiment began with acquiring participants’ maximum voluntary contraction (MVC) by selecting the maximum force achieved over the course of three consecutive repetitions on the hand clench dynamometer. During these repetitions, participants did not have knowledge of the subsequent experimental phases and were instructed and verbally encouraged to squeeze with their maximum force.

Next, participants performed an Association phase in which they were trained to associate effort levels (defined relative to MVC) with the force they exerted against the hand dynamometer. Effort levels were presented on a scale that ranged from 0 (corresponding to no exertion) to 100 (corresponding to a force equal to 80% of a participant’s MVC). A single training block consisted of five trials of training for each target level, where the target levels varied from 10 to 80 in increments of 10, and training blocks were presented in a randomized order. We did not perform association trials at the highest levels of effort to minimize the possibility that participants would become fatigued during this phase. A single trial of a training block began with the numeric display of the target effort level (2 s), followed by an effort task with visual feedback in the form of a black vertical bar, similar in design to a thermometer, which increased in height the harder participants gripped the dynamometer (4 s). The bottom and top of this effort gauge represented effort levels 0 and 100, respectively. Participants were instructed to reach the target zone (defined as ±5 effort levels of the target) as fast as possible and to maintain their force within the target zone for as long as possible over the course of 4 s. The visual indication of the target zone was colored green if the effort produced was within the target zone and red otherwise. At the end of the effort exertion, if individuals were within the target zone for more than two-thirds of the total time (2.67 s) during squeezing the trial was counted a success. These success criteria were meant to ensure that participants were exerting effort for a similar duration across all effort conditions. To minimize participants’ fatigue, a fixation cross (2–5 s) separated the trials within a training block and 60 s of rest was provided between training blocks.

After the Association phase, we performed a Recall phase to test whether participants successfully developed an association between the effort levels and the actual effort exerted. Participants were tested on each of the previously trained effort levels (10–80, increments of 10), six times per level, presented in a random order. Each recall trial consisted of the display of a black horizontal bar that participants were instructed to completely fill by gripping the transducer, turning the force feedback from red to green once the target effort level was reached. For the Recall phase, the full bar did not correspond to effort level 100 as in the previous phase but instead was representative of the target effort level being tested on a particular trial. Participants were instructed to reach the target zone as fast as possible, to maintain their produced force as long as possible, and to get a sense of what effort level they were gripping during exertion (4 s). After this exertion, participants were presented a number line (from 0 to 100) and told to select the effort level they believed they had just gripped. Selection was accomplished by using two push-buttons to move a cursor left and right along the number line and a third button to enter their final value. Participants had a limited amount of time to make this effort assessment (4 s), and if no effort level was selected within the allotted time the trial was considered missed. No feedback was given to participants as to the accuracy of their selection. As previously reported, participants generated extremely accurate associations between the effort levels and the actual effort exerted (Hogan et al. 2019).

After the Recall phase, participants performed the Choice phase of the experiment, in which they were presented with a series of effort gambles and the choices from these gambles were used to characterize how individuals subjectively valued effort. Before being presented with the effort gambles, participants were told that 10 of their decisions would be selected at random at the end of the experiment and that they would have to remain in the testing area until they achieved the exertions required. This was done to ensure that participants were properly incentivized on each trial. A single effort gamble consisted of choosing between two options shown on the screen under a time constraint (4 s): one option entailed exerting a low amount of force (f_s) with certainty (known as the “sure” option), whereas the other entailed taking a risk that could result in either high exertion (f_g) or no exertion, with equal probability (known as the “flip” option). The effort levels were presented with the 0–100 scale that participants were trained on during the Association phase. Participants made their choices by pressing one of the two buttons on a handheld button-box with their right hand with either their first or second digits. Gambles were not resolved after choice, and participants did not perform the squeeze task during this phase of the experiment. Effort gambles (170 in total) were presented consecutively in a randomized order. Participants were encouraged to make a choice on every trial; however, there was no penalty for failing to decide within the 4-s time window. Failure to make a choice on time was logged as a missed trial and was not repeated.

At the end of the Choice phase, the computer selected 10 of the trials at random to be implemented. The outcomes of the selected trials, and only those trials, were implemented. In this way, participants did not have to worry about spreading their effort exertion over all of their trials. Critically, participants were instructed that the experiment would not be completed, and they were to remain in the testing area, until they achieved the exertions randomly implemented from the Choice phase.

The effort amounts for the choice set were chosen to accommodate a range of effort preferences. We reasoned that participants would primarily exhibit increasing marginal utility for effort, and we defined a ratio η = f_g/f_s and a range of η ϵ [1.75, 2.75]. In our gamble set, the effort levels associated with the sure option ranged from 5 to 35 in increments of 3.25 and were multiplied by the ratio η to generate 100 unique effort gambles, all with effort levels below 100. To span a broader range of η, additional gambles were designed in a similar method described above, except that the ratio of flip to sure (η) was halved and then multiplied by the sure values (η_1/2 ϵ [0.88, 1.38]). Thirty of these 100 additional effort gambles resulted in trivial (f_g, f_s) pairings with the flip values less than sure values (η < 1) and were thus excluded. This procedure resulted in 170 effort gambles with η ϵ [1.00, 2.75].

This effort choice paradigm exploits the theoretical equivalence between risk preferences and subjective valuation in order to measure subjective valuation via the presentation of risky choices, a widely accepted practice in economics and decision neuroscience (Camerer et al. 2005; Rangel et al. 2008). Moreover, choice prospects only involved varying amounts of physical effort (i.e., no prospective rewards were involved), which allowed us to isolate how processes related to effort valuation, separate from the effects of reward valuation or effort/reward trade-offs. We have previously used this choice set to extract computational parameters that capture an individual’s subjective valuation of physical effort (Hogan et al. 2019).

monetary choice task.

To investigate whether there was a relationship between subjective preferences for effort, cortical thickness, and monetary gains and losses (i.e., risk aversion, loss aversion), a subset of participants (n = 20) performed a binary forced-choice task for money outside of the scanner. In this task, independent of the effort choice experiment, participants made a series of choices between a certain option involving a payout with 100% probability and a risky option involving gain and loss with equal probability. This paradigm has been used in a number of studies to elicit subjective preferences for monetary gains and losses (Chib et al. 2014; Frydman et al. 2011; Sokol-Hessner et al. 2009).

Participants first received an endowment of $25 in cash (separate from their show-up fee) and were told that, at the end of the experiment, one trial would be selected randomly and a payment would be made according to their actual decision during the experiment. They were also told that their $25 endowment was given to them so that they could pay any eventual losses at the end of the experiment. Any amount from the endowment that remained after subtracting a loss was theirs to keep, and similarly any eventual gain earned in the experiment was added to the initial endowment. During the experiment, participants made choices among 140 different pairs of monetary gambles. Each pair contained a certain option involving a payout with 100% probability and a risky option involving gain and loss with equal probability. Participants had 4 s to make a choice. The values for the gain G, loss L, and sure S options were the exact same as those used in previous studies that estimated individuals' loss aversion (Chib et al. 2014; Frydman et al. 2011; Sokol-Hessner et al. 2009). Specifically, gambles involving a potential gain or loss and an alternative sure amount of $0 were generated from the combination of G ∈ {2,4,5,6,8,9,10,12} and L ∈ [0.25 × G, 2 × G] in multiplier increments of 0.125. For the options involving a potential gain for an alternative sure amount, the set was (G,S) ∈ {(2,1), (3,1), (4,2), (5,2), (7,3), (8,3), (12,6), (12,5), (12,4), (13,5), (19,8), (22,10), (23,10), (25,9), (25,10), (26,10), (26,12), (28,13), (30,12)}. The gambles involving gain and loss were used to assess participants’ loss aversion, and those involving a gain and a sure amount were used to assess participants’ risk aversion.

Data Analysis

Image analysis.

preprocessing.

The Brain GPS application on MRI Cloud (https://mricloud.org/) was used to perform a T1 Multi Atlas Segmentation of the MPRAGE scans. Specifically, the LDDMM (Large Deformation Diffeomorphic Metric Mapping) used the T1 multi-atlas (Adult_286labels_10atlases_mV5L), generated from 10 adult atlases, to parcellate each MRI scan into 286 cortical and subcortical regions (Mori et al. 2016). From these segmentations, the left and right precentral gyrus and the left and right Heschl’s gyrus were then extracted.

identification of hand knob and heschl’s gyrus.

Seg3D (http://www.sci.utah.edu/cibc-software/seg3d.html) was used to edit the ROI of the right and left precentral gyrus (labels 26 and 25, respectively) to identify and cut the hand knob region. The hand knob region was identified as a hook or a knoblike region on the precentral gyrus in both hemispheres, by standard identification procedures (Yousry et al. 1997). For participants with two lobes of hand knob, both were included in the cutting. The Heschl’s gyrus segmentations were edited with the rules developed by Honeycutt et al. (2000) and Ratnanather et al. (2003).

Triangulated surfaces were created from the binary segmentations with restricted Delaunay triangulation (Amenta et al. 2000; Cazals and Giesen 2006; Cohen-Steiner and Morvan 2003). Since the results critically depended on the quality of segmentations as well as the surface reconstruction, quality control (i.e., visual inspection) was performed at every stage.

The surfaces were manually cut into two surfaces: the pial surface and the gray matter-white matter boundary surface. Specifically, the boundaries were defined by using dynamic programming to find the shortest geodesic path between user-defined landmarks (Ratnanather et al. 2003). These landmarks included points on the caudal, rostral, lateral, and medial ends of the superior and inferior sides of the two surfaces. Then the inner surface was mapped to the outer surface via a constrained diffeomorphic mapping (Ratnanather et al. 2019) to generate a field of normal vectors whose lengths were averaged to yield the cortical thickness. Final cortical surface area was calculated as the area of the gray matter-white matter boundary surface. Cortical volume was calculated by applying the divergence theorem to the unedited triangulated structure.

To assess hand knob [and, as a control region, Heschl’s gyrus (HG) (Mai et al. 2016; Ratnanather et al. 2003)] cortical thickness we identified anatomical landmarks in participants’ structural images and manually carved this region from an automatically generated segmentation of motor cortex (Fig. 1B). The analysis of structural imaging data was performed by an experimenter who did not collect the behavioral and imaging data and was blinded to participants’ choice data. To adjust for individual differences in participant’s cortical anatomy, measures of the left hand knob (LHK) and HG thickness were divided by their contralateral region thickness. It is well established that the structural morphology of motor cortex is related to hand use, with regions of the cortex associated with the dominant hand being larger than those associated with the nondominant hand (Díaz et al. 1994; Luders et al. 2006; Toga and Thompson 2003; Zilles et al. 1996). We chose to normalize by the ipsilateral properties, reasoning that the ipsilateral region would have properties similar to those of the contralateral region, the main differences being related to the increased use associated with the dominant hand. Furthermore, we reasoned that after normalizing for individual differences in motor cortical anatomy, these use-based differences could be related to subjective effort preferences for exertion of the dominant hand.

Effort choice analysis.

We used a two-parameter model to estimate participants’ subjective effort cost functions. We assumed a participant’s cost function V(x) for effort x as a power function of the form

$$V\left(x\right)=x^{\rho },x\le 0$$ (1)

In this formulation of effort cost force production is assumed to be perceived as a loss. We previously showed that this effort cost function best described choices for prospective effort (Hogan et al. 2019). The parameter ρ represents sensitivity to changes in subjective effort value as the effort level changes. ρ < 1 indicates decreasing sensitivity to changes in subjective effort cost as effort level increases. ρ > 1 indicates increasing sensitivity to changes in subjective effort cost as effort level increases. ρ = 1 indicates that subjective effort costs coincide with objective effort costs. Essentially, ρ captures an individual’s bias to choose the gamble or sure option, given options of equal expected value.

Representing the effort levels as prospective costs, and assuming that participants combine probabilities and utilities linearly, the relative value between the two effort options (with the sure prospect as the reference) can be written as follows:

$${\text{RV}}_{\text{sure}}\left(f_{\text{g}},f_{\text{s}}\right)=\text{value}\left(\text{sure}\right)-\text{value}\left(\text{gamble}\right)$$ (2)

$${\text{RV}}_{\text{sure}}\left(f_{\text{g}},f_{\text{s}}\right)=-{\left(-f_{\text{s}}\right)}^{\rho }-\left(-0.5{\left(-f_{\text{g}}\right)}^{\rho }\right)$$ (3)

$${\text{RV}}_{\text{sure}}\left(f_{\text{g}},f_{\text{s}}\right)=0.5{\left(-f_{\text{g}}\right)}^{\rho }-{\left(-f_{\text{s}}\right)}^{\rho }$$ (4)

where RV_sure denotes the difference in value between the two options and both f_g < 0 and f_s < 0 for all trials.

We then assume that the probability that a participant chooses the sure option for the kth trial is given by the softmax function

$$P_k\left({\text{RV}}_{\text{sure}}\left(f_{\text{g}},f_{\text{s}}\right)\right)=1/\left[1+\exp \left(-\tau {\text{RV}}_{\text{sure}}\left(f_{\text{g}},f_{\text{s}}\right)\right)\right]$$ (5)

where τ is a temperature parameter representing the stochasticity of a participant’s choice (τ = 0 corresponds to random choice).

We used maximum likelihood to estimate parameters ρ and τ for each participant, using 170 trials of effort choices (f_g,f_s) with a participant’s choice denoted by y ∈ {0,1}. Here, y = 1 indicates that the participant chose the sure option. This estimation was performed by maximizing the likelihood function separately for each participant:

$${\displaystyle \sum _{k=1}^{170}{y}_i\log \left(P_k\left({\text{RV}}_{\text{sure}}\left(f_{\text{g}},f_{\text{s}}\right)\right)\right)}+\left(1-y_i\right)\log \left(1-P_k\left({\text{RV}}_{\text{sure}}\left(f_{\text{g}},f_{\text{s}}\right)\right)\right)$$ (6)

Monetary choice analysis.

A separate maximum likelihood procedure was used to estimate parameters for monetary reward, in a similar manner that has been used in a number of previous studies (Chib et al. 2014; Frydman et al. 2011; Sokol-Hessner et al. 2009), estimating both risk and loss aversion parameters for each participant. We expressed participants’ utility function u for monetary values x as

$$u\left(x\right)=\left\{\begin{array}{c}{x}^{\alpha },x\ge 0\\ \lambda x^{\alpha },x<0\end{array}\right.$$ (7)

In this formulation, λ represents the relative weighting of losses to gains and α represents the degree of a participant’s risk aversion. Assuming that participants combine probabilities and utilities linearly, the expected utility of a mixed gamble can be written as U(G,L,S) = (0.5G^α + 0.5λL) − S^α, where G, L, and S are the respective gain, loss, and sure options of the presented risky option.

The probability that a participant chooses the risky option for the kth trial is given by the softmax function

$$P_k\left(U\left(G,L,S\right)\right)=1/\left[1+\exp \left(-\tau U\left(G,L,S\right)\right)\right]$$ (8)

where τ is a temperature parameter representing the stochasticity of a participant’s choice (τ = 0 corresponds to random choice).

The maximum likelihood procedure was accomplished by using 140 gambles with participant response y ϵ {0,1}. Here, y = 1 indicates that the participant chose to make a gamble. The estimation was performed by maximizing the likelihood function:

$${\displaystyle \sum _{k=1}^{140}{y}_i\log \left(P_k\left(U\left(G,L,S\right)\right)\right)}+\left(1-y_i\right)\log \left(1-P_k\left(U\left(G,L,S\right)\right)\right)$$ (9)

Of the 20 participants who performed both the effort and monetary gamble tasks, 1 was excluded from this monetary analysis on the basis of inconsistent choices during the monetary task (random or near random choices, characterized by a temperature parameter < 0.001).

Cross-validation of relationships between explanatory variables and effort parameters.

We performed a leave-one-out cross validation (LOOCV) analysis to test whether different models were better predictors of participants’ subjective effort parameters than randomly sampling a uniform distribution of subjective effort parameters (null model). In this analysis we computed prediction errors for the following models:

model 0:

$$\rho =\text{unif}\left({\rho }_{\min },{\rho }_{\max }\right)$$ (10)

model 1:

$$\rho ={\beta }_0+{\beta }_1\times {\text{LHK}}_{\text{Thickness}}$$ (11)

model 2:

$$\rho ={\beta }_0+{\beta }_1\cdot {\text{LHK}}_{\text{Thickness}}+{\beta }_2\cdot {\text{LHK}}_{\text{SurfaceArea}}+{\beta }_3\cdot {\text{LHK}}_{\text{Volume}}+{\beta }_4\cdot {\text{LM1}}_{\text{Thickness}}+{\beta }_5\cdot {\text{LM1}}_{\text{SurfaceArea}}+{\beta }_6\cdot {\text{LM1}}_{\text{Volume}}$$ (12)

model 3:

$$\rho ={\beta }_0+{\beta }_1\cdot {\text{LHG}}_{\text{Thickness}}+{\beta }_2\cdot {\text{LHG}}_{\text{SurfaceArea}}+{\beta }_3\cdot {\text{LHG}}_{\text{Volume}}$$ (13)

model 4:

$$\rho ={\beta }_0+{\beta }_1\cdot \lambda +{\beta }_2\cdot \alpha$$ (14)

These models tested the predictive power of different explanatory variables’ (related to cortical anatomy and subjective valuation) ability to predict subjective effort parameters. The null model (model 0) assumed that subjective effort parameters were randomly sampled from a uniform distribution bounded by the minimum and maximum subjective effort parameters. Model 1 evaluated how well an individual’s LHK cortical thickness predicted subjective effort parameters. Model 2 evaluated the predictive power of an extended model that included LHK cortical thickness, surface area, and volume in addition to overall left motor cortex (LM1) cortical thickness, surface area, and volume. Model 3 examined the predictive power of left Heschl’s gyrus (LHG) cortical thickness, surface area, and volume. Notably, the properties of LHG are generally unrelated to motor performance. Finally, model 4 evaluated the predictive power of subjective reward preferences (i.e., loss aversion λ, risk aversion α).

To assess the prediction error of these models we calculated the mean squared error between the left-out observation/participant’s subjective effort parameter and the predicted effort parameter obtained from the model fit of the remaining data. Since the null model involved randomly sampling from a uniform distribution, we repeated this procedure 10,000 times, over the collected sample population (n = 24), to generate a distribution of model prediction errors.

RESULTS

Performance in this task can be characterized with a standard prospect theory model (Hogan et al. 2019). The statistically optimal behavior is to multiply the magnitude and probability of each option and choose the one with the lowest value (since larger efforts are more aversive). Our model [V(x) = x^ρ] includes a parameter ρ that captures how an individual participant’s choices deviate from the optimal behavior, consistent with their subjective preferences resulting in a warping of the effort-value space (see Hogan et al. 2019 for details). This model parameter ρ represents a participant’s subjective valuation of effort V(x), describing how increasing effort levels x result in marginal changes in subjective effort value.

On average, we found that participants exhibited ρ > 1, indicating increasing sensitivity to changes in subjective effort cost as objective effort level increased [$\overline{\rho }$ = 1.14 (SD = 0.18); 2-tailed 1-sample t test against the null hypothesis that the mean of ρ is equal to 1: t(23) = 3.87, P < 0.001; Fig. 1, C and D]. ρ > 1 corresponds to participants being risk averse for effort and that a 1-unit increase in the amount of effort feels like more of an increase in effort value for larger efforts than for smaller efforts. In more relatable terms, the difference between exerting 10 N and 15 N feels like less of a change in effort value than the difference between exerting 100 N and 105 N. There was considerable individual variability in participants’ ρ, reflecting individual differences in subjective preferences for effort. Notably, individuals’ subjective effort parameters were not significantly correlated with maximum grip strength (n = 24, r = −0.30, P = 0.15) or measures of monetary subjective preferences obtained from a separate decision-making task involving risky decisions for money (risk aversion: n = 19, r = −0.40, P = 0.10; loss aversion: n = 19, r = 0.10, P = 0.69). These results suggest that subjective preferences for effort were not simply the by-product of maximum strength or similar risk attitudes across decisions for different types of goods.

Our main regression analysis revealed that individuals who found effort to be more subjectively costly (i.e., larger ρ) had a larger hand knob thickness (linear regression: n = 24, r = 0.47, P = 0.02; Fig. 1E). This relationship held even when controlling for other properties of hand knob (i.e., surface area, volume; Table 1). Furthermore, including all measures of motor cortical anatomy showed that hand knob thickness described the largest percentage of variance in ρ (75.78%; Table 1). We also assessed the relationship between individuals’ subjective effort preferences and cortical thickness and anatomical properties of the entire precentral gyrus/motor cortex. We failed to find a significant relationship between them (Table 1), suggesting that subjective effort preferences for grip exertion are better described by the specific properties of the hand knob and not the entire motor cortex.

Table 1.

Results from control linear regressions

Explanatory Variable	ρ (n = 24)	λ (n = 17)	α (n = 24)
LHKThickness	0.47, 2.31, 0.46, (0.03), 75.78%	0.39, 1.14, 0.23, (0.28), 16.59%	−0.09, −0.39, 0.003, (0.71), 2.91%
LHKSurfaceArea	−0.05, −0.23, −0.15, (0.82), 0.76%	−0.07, −0.23, −0.36, (0.82), 0.69%	−0.03, −0.13, −0.01, (0.90), 0.32%
LHKVolume	0.13, 0.51, 0.33, (0.61), 3.75%	−0.56, −1.94, −0.31, (0.08), 48.44%	0.57, 1.94, 0.39, (0.07), 76.71%
LM1Thickness	−0.24, −0.91, −0.32, (0.37), 11.82%	−0.10, −0.38, −0.24, (0.71), 1.83%	0.26, 0.87, −0.13, (0.49), 15.31%
LM1SurfaceArea	−0.13, −0.63, 0.02, (0.54), 5.55%	−0.45, −1.57, −0.25, (0.15), 31.67%	−0.11, −0.47, −0.04, (0.64), 4.57%
LM1Volume	0.08, 0.41, 0.02, (0.69), 2.33%	−0.07, −0.25, −0.24, (0.81), 0.78%	0.02, 0.09, −0.04, (0.93), 0.17%

Standardized regression coefficients (β), t values, bivariate correlation values, and P values (2-tailed, in parentheses) and % variance in subjective valuation of prospective effort (ρ), loss aversion (λ), or risk aversion (α) accounted for by the regressor. Results with P < 0.05 are shown in bold. Brain anatomy measures (thickness, surface area, and volume) were divided by their contralateral region thickness to correct for individual differences in cortical anatomy. LHK, left hand knob; LM1, left primary motor cortex.

To assess discriminant validity, we examined the relationship between subjective effort parameters and properties of Heschl’s gyrus (Mai et al. 2016; Ratnanather et al. 2003), a brain region responsible for audition (a sensation unrelated to physical exertion) that has a cortical thickness similar to the hand knob. These analyses revealed no significant relationships between Heschl’s gyrus thickness, surface area, or volume and subjective effort parameters (Table 2).

Table 2.

Results from control linear regression including Heschl’s gyrus

Explanatory Variable	ρ (n = 24)
LHGThickness	0.19, 0.90, 0.19 (0.38), 27.51%
LHGSurfaceArea	0.23, 1.00, 0.23 (0.33), 0.55%
LHGVolume	0.35, 1.77, 0.35 (0.09), 71.94%

Standardized regression coefficients (β), t values, bivariate correlation values, and P values (2-tailed, in parentheses) and % variance in subjective valuation of prospective effort (ρ) accounted for by the regressor. Brain anatomy measures (thickness, surface area, and volume) were divided by their contralateral region thickness to correct for individual differences in cortical anatomy. LHG, left Heschl’s gyrus.

Also supporting the discriminant validity of our relationship between hand knob thickness and subjective effort parameters, we found that the hand knob did not relate to participant’s maximum grip strength or measures of subjective reward preferences (linear regression: n = 24, r = −0.30, P = 0.15). A formal model comparison of the relationship between hand knob thickness and these choice measures revealed that subjective effort preference had the lowest Akaike information criterion (AIC) (LHK = β₀ + β₁ × ρ, AIC_ρ = −0.48; LHK = β₀ + β₁ × λ, AIC_λ = 2.15; LHK = β₀ + β₁ × α, AIC_α = 2.16), suggesting that individual differences in hand knob thickness were best described by subjective effort preferences.

We also performed a leave-one-out cross validation (LOOCV) analysis to test whether hand knob thickness (model 1) is a better predictor of a participant’s subjective effort parameters than a variety of other anatomical measures (model 2, model 3), parameters related to subjective preferences (model 4), or randomly sampling a uniform distribution of subjective effort parameters (null model, model 0). In this analysis, we iteratively left out each participant and determined how well a model fit to the remaining data was able to predict the left-out participant. We found that the LOOCV mean squared error was lowest for a linear model including only LHK cortical thickness (Fig. 1F), indicating that LHK cortical thickness provided the smallest error between predicted and actual subjective effort parameters. This shows that LHK thickness is a better predictor of subjective effort parameters than any other model. Notably, the model 1 LOOCV prediction error falls outside the lower bound of the 95% confidence interval of the null model, which shows that the linear model exhibits significantly lower prediction error than the null model. Moreover, none of the other models had LOOCV that fell outside the lower bound of the 95% confidence interval of the null model, which illustrates that these models did not provide predictive power that was significantly better than the random sampling of effort preferences. An extended regression model that included LHK thickness, other measures related to LHK, and LM1 anatomy fell outside the upper bound of the random model. This shows that the extended regression was a significantly worse predictor of subjective effort preferences than the null model, even though it included more explanatory variables related to properties of motor cortex. This suggests that LHK thickness alone is the best predictor of subjective effort parameters. Together these results further support our finding of a linear relationship between hand knob thickness and subjective effort parameters.

DISCUSSION

To the best of our knowledge, these findings demonstrate the first link between low-level features of motor cortical anatomy and the higher-level function of decisions to exert physical effort. Although our findings do not directly test a functional hypothesis that links motor physiology to anatomy and effort preferences, they align with the idea that greater cortical thickness is associated with increased resting motor thresholds (List et al. 2013) and with recent results showing that motor cortical physiology is related to subjective valuations of reward and effortful performance (Galaro et al. 2019). In the framework of our effort-choice paradigm, larger effort subjectivity parameters, which are indicative of high subjective effort costs (i.e., more costly effort) (Hogan et al. 2019) and associated with larger motor cortical thickness, could be a reflection of a higher resting motor threshold, making it more difficult to initiate motor output. Our finding of an association between effort preferences and motor cortical anatomy could guide future work aimed at examining the mechanistic link between an individual’s motor cortical physiology and decision-making about exertion.

Studies in humans and animals have shown that motor cortical thickness increases with physical training (Anderson et al. 2002; Díaz et al. 1994; Draganski et al. 2004, 2006; Draganski and May 2008; May 2011), and it has been suggested that these increases in thickness are associated with the development of more synapses per neuron (Anderson et al. 2002). Although such an increase in synapses could be associated with more descending drive, it could also serve to increase sensory modulation of motor cortical activity through connectivity with thalamus or indirect connections through somatosensory cortex. This increased sensory connectivity could result in individuals with a thicker motor cortex having more perceptual acuity for effort (i.e., how well one is able to assess different levels of effort) and other motor behaviors.

Perceptual acuity for effort could be an important factor that influences subjective valuation of effort. However, it is important to realize that perceptual acuity and subjective valuation of effort are separate concepts. Whereas perceptual acuity relates to an individual’s ability to perceive different levels of effort, subjective valuation of effort reflects decisions about prospective effort. One reason the participants might express marginal utility for effort could be related to perceptual acuity for effort—as efforts increase it becomes more difficult to perceive changes in effort, and this increasing perceptual uncertainty for effort could be expressed through an increasing subjective effort value (i.e., larger ρ). Although the relationship between perceptual acuity for effort and effort valuation is important, the present study was not designed to test these ideas, and future work will be needed to understand how they interact.

A recent TMS study that examined the causal roles of supplementary motor area (SMA) and primary motor cortex (M1) on effort perception found that SMA was causally related to perceptions of recalled levels of effort, whereas M1 was not (Zénon et al. 2016). From these results, the authors concluded that feelings of effort may arise from SMA and regions upstream of M1. It is important to note that that study examined retrospective perceptions of effort and not prospective valuations of effort as in the present study. Although our finding of a link between motor cortical properties and subjective preferences of effort might seem contrary to previous work that failed to find a link between motor physiology and effort perception, it is important to realize that these studies were polling different time periods over the course of effort valuation/exertion. Our study was concerned with decisions about the prospective valuation of effort, whereas Zénon et al. (Zénon et al. 2016) were interested in retrospective perceptions of effort. It is possible that motor cortical properties are more of a factor when deciding about prospective exertion, since information about the state of motor cortex could critically influence an individual’s willingness to exert. Sensory information, incorporated in SMA, might be more important when retrospectively evaluating effort and making judgments about how effortful previous exertions felt. Taken together, these findings suggest a possible dissociation between motor cortical areas influencing prospective valuation of effort and sensory areas influencing retrospective perceptions. Further work will be needed to map the neural contributions to effort valuation and perception through the full-time course of effort-based decision-making.

It is important to mention that the development and progression of a number of neurological and psychiatric disorders have been associated with changes in cortical thickness (Gao et al. 2018; Suh et al. 2019; Tillema et al. 2016; van Haren et al. 2011). Notably, changes in cortical thickness have been associated with Parkinson’s disease, Huntington’s disease, multiple sclerosis, and lateral sclerosis (Nourbakhsh et al. 2016; Reetz et al. 2009; Tereshchenko et al. 2019; Turner et al. 2011), in which feelings of fatigue are a prominent symptom. In the future, it will be interesting to examine whether specific changes to motor cortical thickness in these patient populations are related to subjective preferences in effort and associated feelings of fatigue.

How effortful an action feels plays a critical role in our decisions to engage in physical activity. The subjective nature of effort impacts diverse decisions from when we exercise to whether we choose to walk a bit farther to get an espresso from our favorite coffee shop. It is possible that a thinner motor cortex might enable us to more efficiently recruit motor cortical resources, resulting in efforts feeling less costly, and therefore making us more willing to choose to engage in physical activity.

GRANTS

This work was supported by the Eunice Kennedy Shriver National Institute of Child Health and Human Development of the National Institutes of Health under Award Numbers K12 HD-073945 and R01 HD-097619 and by National Institute of Mental Health Award Numbers R56 MH-113627 and R01 MH-119086 to V.S.C. J.T.R. was supported in part by National Institutes of Health Grant P41 EB-051909.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

A.U., P.S.H., J.T.R., and V.S.C. conceived and designed research; P.S.H. performed experiments; A.U., K.S.K., P.S.H., and V.S.C. analyzed data; A.U., J.T.R., and V.S.C. interpreted results of experiments; A.U., K.S.K., and V.S.C. prepared figures; A.U. and V.S.C. drafted manuscript; A.U., K.S.K., P.S.H., J.T.R., and V.S.C. edited and revised manuscript; A.U., K.S.K., P.S.H., J.T.R., and V.S.C. approved final version of manuscript.