Abstract
Plantarflexors such as the soleus (SOL) and medial gastrocnemius (MG) play key roles in controlling bipedal stance; however, how the central nervous system controls the activation levels of these plantarflexors is not well understood. Here we investigated how the central nervous system controls the plantarflexors’ activation level during quiet standing in a cosine tuning manner where the maximal activation is achieved in a preferred direction (PD). Furthermore, we investigated how spinal cord injury affects these plantarflexors’ activations. Thirteen healthy adults (AB) and thirteen individuals with chronic, incomplete spinal cord injury (iSCI) performed quiet standing trials. Their body kinematics and kinetics as well as electromyography signals from the MG and SOL were recorded. In the AB group, we found that the plantarflexors followed the cosine tuning manner during quiet standing. That is, MG was most active when the ratio of plantarflexion torque to knee extension torque was ~2:-3, whereas SOL was most active when the ratio was ~2:1. This suggests that the SOL muscle, despite being a monoarticular muscle, is sensitive to both ankle plantarflexion and knee extension during quiet standing. The difference in the PDs accounts for the phasic activity of MG and for the tonic activity of SOL. Unlike the AB group, the MG’s activity was similar to the SOL’s activity in the iSCI group, and the SOL PDs were similar to those in the AB group. This result suggests that chronic iSCI affects the control strategy, i.e., cosine tuning, for MG, which may affect standing balance in individuals with iSCI.
NEW & NOTEWORTHY Soleus muscle shows a tonic activity whereas medial gastrocnemius muscle shows a phasic activity during quiet standing. Cosine tuning and their preferred direction account for the different muscle activation patterns between these two muscles. In individuals with chronic incomplete spinal cord injury, the preferred direction of gastrocnemius medial head is affected, which may result in their deteriorated standing balance.
Keywords: cosine tuning, plantarflexors, posture, preferred direction, spinal cord injury
INTRODUCTION
Upright standing is a fundamental motor task in our daily lives. Understanding how the brain controls quiet standing is one of the key research topics in the field. The ankle joint is the first major joint connecting the body to the external environment and thus is the critical joint for the control of quiet standing. Indeed, ankle joint torque, which is approximately proportional to the location of the center of pressure, is highly correlated with the center of mass location in space (Gatev et al. 1999; Masani et al. 2003; Winter et al. 1998). Therefore, how the ankle joint torque is controlled is an important question to be solved to understand the control mechanism of balance in quiet standing.
As the body is in front of the ankle joint during quiet standing (Smith 1957), the ankle joint needs to continuously exert an extension torque, i.e., plantarflexion torque. The soleus (SOL) and medial gastrocnemius (MG) are two major plantarflexors that synergistically play a key role in controlling the plantarflexion torque. Although the levels of both muscles’ activation are highly correlated (Masani et al. 2003), their fluctuations of activation appear quite different (Héroux et al. 2014). That is, the MG tends to be more phasic (i.e., marked by periods of inactivity and activity with a large dynamic range), whereas the SOL tends to be tonic (i.e., constantly active with a small dynamic range). This difference has been speculated to be due to the physiological differences of the muscle fiber properties: the SOL predominantly consists of slow muscle fibers (95% confidence interval for type I fibers: 74.5–98.5%), whereas the MG is a more even mix between slow and fast muscle fibers (95% confidence interval for type I fibers: 45.6–56.0%) (Johnson et al. 1973). Additionally, the SOL and MG have functional differences during quiet standing. The SOL is a monoarticular muscle that is responsible for plantarflexion torque, whereas the MG is a biarticular muscle that contributes to plantarflexion torque and knee flexion torque. It is easy to assume that muscle activity is proportional to the torque of the joints it spans, similar to the “muscle equivalent model” proposed by Bouisset (Bouisset 1973). However, this concept is too simplistic to explain quiet standing. To date, no experimental investigation has been performed to determine the cause of the differences in the muscle activation of the SOL and the MG during quiet standing.
Single neurons in the primary motor cortex (M1) follow a cosine tuning pattern, peaking at the preferred direction (PD) of the action of interest. More specifically, the highest firing frequency of a neuron in the M1 occurs when the end-point force direction of the limb movement aligns with the PD. As the direction of action ventures further from this PD, the firing frequency decreases in an orderly manner, i.e., a cosine tuning manner (Caminiti et al. 1990; Georgopoulos et al. 1982; Schwartz et al. 1988). Further work has demonstrated that these cosine tuning properties of the M1 neurons are well represented in the degree of whole muscle activity measured as the amplitude of the electromyogram (EMG), as it represents the population activity of the M1 neurons well. That is, the EMG amplitude appears to be cosine tuned as well along with the end-point force direction (Hoffman and Strick 1999; Kalaska et al. 1989).
Additionally, the end-point force direction of a desired action is determined by the linear summation of exerted torques at multiple joints. Therefore, the muscle activity correlates with a unique combination of related joint torques, which can be represented as a specific direction on the torque plane, i.e., PD. For example, Kurtzer et al. (2006b) demonstrated in primates that the muscle activity of each upper limb muscle is represented as a linear summation of elbow and shoulder joint torques, indicating that each muscle has a PD in the elbow-shoulder torque plane. For lower limb muscles in humans, Nozaki et al. (2005a, 2005b) showed that the activity of each muscle in the lower limb has a PD in the knee-hip torque plane during an isometric force exertion task. Specifically, they recorded the exerted knee and hip joint torques as well as the EMGs from seven thigh muscles where the participant was asked to exert the end-point force in various directions in the sagittal plane. In the three-dimensional space of EMG-knee-hip joint torques, they demonstrated that the EMG was represented by a linear summation of both joint torques: EMG = c1T1 + c2T2 = |C||T|cosθ, where c1 and c2 represent the regression coefficients, θ is the angle between C = [c1,c2] and T = [T1,T2], and the PD then is (Fig. 1A). The knee and hip joint torques were denoted as T1 and T2 respectively, while |x| represents the magnitude of the vector. This indicates that thigh muscle activation is proportional to the orthogonal projection from the knee-hip torque linear summation to the muscle’s PD, which represents the direction on the torque plane in which the muscle activation is most sensitive (Fig. 1B). They demonstrated that each thigh muscle has a unique PD (Fig. 1C), indicating that the brain controls each muscle activation uniquely based on the torque requirements of adjacent joints. Furthermore, both Kurtzer et al. (2006a, 2006b) and Nozaki et al. (2005a, 2005b) found that monoarticular muscle activity was dependent on not just the joint it spanned but also the adjacent joint it did not span, thus demonstrating the ability of the cosine tuning analysis to explain differences in muscle activity between mono- and biarticular muscles based on adjacent joint torque. The same strategy may be applied in controlling standing by considering the adjacent joint torque (i.e., plantarflexion and knee torque) requirements in relation to the SOL and MG, which may account for their different activation patterns during quiet standing. Therefore, the first purpose of this study was to investigate the PDs of the SOL and MG during quiet standing, to reveal how the brain controls these key plantarflexors in maintaining the body balance in the upright posture.
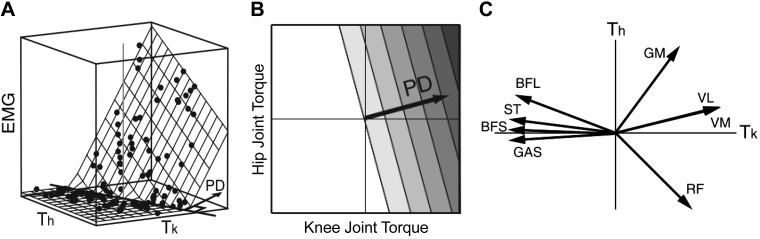
Fig. 1.
A: the electromyography (EMG) level with respect to both joints is approximated by a plane. A multiple regression analysis was used (), where M is the EMG level, Tk and Th are the knee and hip joint torques, respectively, and a and b are fitting parameters. Additionally, where EMG was restricted to be 0 or greater, and only EMG above 0 was used for analysis. B: contour plot indicating the activity level of a muscle obeying cosine tuning on the torque plane. Darker shades are larger muscle activity. The preferred direction (PD) is the direction in which the muscle activity level increases the greatest. C: mean value of PDs of each (thigh) muscle from experimental data (n = 11). BFL, biceps femoris long head; BFS, biceps femoris short head; GAS, medial gastrocnemius; GM, gluteus maximus; RF, rectus femoris; ST, semitendinosus; VL, vastus lateralis; VM, vastus medialis. A and C are reproduced with modification from Nozaki et al. (2005b), their Figures 4A and 1C, respectively. B is reproduced with modification from Nozaki et al. (2005a), their Figure 3A.
Spinal cord injury affects the neural control of plantarflexors and hence affects their standing balance. Therefore, individuals with incomplete spinal cord injury (iSCI) tend to have reduced standing balance (Lemay et al. 2013). The deteriorations of standing balance can be a result of physiological changes in their muscles such as muscle atrophy and/or muscle fiber type recomposition (Biering-Sørensen et al. 2009; Burnham et al. 1997). The latter means that the SOL is predominantly made of type I slow twitch fibers that are largely fatigue resistant (Johnson et al. 1973), whereas after spinal cord injury there is a transition of these fiber types to fast twitch type II fibers (Burnham et al. 1997; Shields 1995). These changes may affect the brain’s control strategy of muscles resulting in differences of PDs in the SOL and MG compared with able-bodied individuals. Thus, the second purpose of this study was to investigate the PDs of the SOL and MG in individuals with chronic iSCI during quiet standing, to determine how iSCI affects the control of these key plantarflexors while attempting to maintain body balance in upright posture.
MATERIALS AND METHODS
Participants.
Quiet standing data from individuals with iSCI used in this study were previously collected in another work by Chan et al. (2019). Thirteen healthy adults (AB) (10 women, 3 men; age: 57.1 ± 10.5 yr) and thirteen individuals with iSCI (iSCI) (9 women, 4 men; age: 52.6 ± 13.9 yr, time since injury: 7.4 ± 13.9 yr) participated in this study. The able-bodied participants had no medical history of neurological disorders. The recruited participants with iSCI had moderate trunk control, could stand for at least 30 s without mobility aids, and were American Spinal Injury Association Impairment Scale (AIS) C or D (Marino et al. 2003). The recruited participants were age- and sex-matched between the AB and iSCI groups, but because of technical issues with the motion capture system during the experiments the data presented are only for those with complete motion capture data. The participants’ demographic data are summarized in Table 1. There was no significant difference in age between the two groups (t test, P = 0.366). Body weight was significantly larger in participants with iSCI (t test, P = 0.008). All participants gave their written informed consent to participate in the study, whose experimental procedures were approved by the local ethics committee.
Table 1.
Summary of participant information
| iSCI1 | iSCI2 | iSCI3 | iSCI4 | iSCI5 | iSCI6 | iSCI7 | iSCI8 | iSCI9 | iSCI10 | iSCI11 | iSCI12 | iSCI13 | Mean (SD) | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sex | F | M | F | F | F | F | F | F | F | M | F | M | F | |
| Age, yr | 32 | 60 | 43 | 57 | 59 | 55 | 38 | 54 | 56 | 88 | 38 | 51 | 53 | 52.6 (12.9) |
| Weight, kg | 49.9 | 109.2 | 47.3 | 102 | 62.3 | 47.5 | 55.6 | 83.3 | 73.7 | 77.2 | 79.9 | 81.9 | 68.9 | 72.2 (19.7) |
| Level of injury | C4 | C5 | T6 | C2 | C1 | C5 | T4 | C4 | L5 | C6 | T11 | C3 | C4 | |
| Time since injury, yr | 1 | 3.2 | 3.9 | 2.9 | 1.1 | 9.1 | 1.3 | 13.4 | 1.2 | 5.3 | 6.8 | 7.9 | 38.6 | 7.4 (10.1) |
| CB&M (/96) | 89 | 70 | 78 | 29 | 3 | 26 | N/A | 27 | 33 | 20 | 63 | 52 | 33 | 40.2 (27.9) |
| LE strength (/120)* | 92 | 115 | 102.5 | 88 | 81.5 | 94 | 74.5 | 78.5 | 72.5 | 81.5 | 91 | 97 | 76 | 88.0 (12.3) |
| Gait speed without aid, m/s | 1.29 | 1.28 | 1.05 | 0.79 | 0.43 | 0.88 | 0.75 | 0.91 | 0.94 | 0.83 | 1.03 | 1.29 | 0.95 | 0.954 (0.244) |
| Usual walking aid | None | None | None | Cane | 4WW | Cane | 4WW | Cane | None | None | None | Poles/4WW | Poles | |
| Mini-BESTest score (/28) | 25 | 25 | 24 | 17 | 4 | 20 | 5 | 14 | 17 | 12 | 26 | 15 | 18 | 17.1 (7.2) |
| Fall history† | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | |
| AB1 | AB2 | AB3 | AB4 | AB5 | AB6 | AB7 | AB8 | AB9 | AB10 | AB11 | AB12 | AB13 | Mean (SD) | |
| Sex | F | F | F | M | F | F | M | F | F | F | F | M | F | |
| Age, yr | 54 | 57 | 47 | 67 | 59 | 53 | 57 | 84 | 62 | 56 | 55 | 51 | 40 | 57.1 (10.5) |
| Weight, kg | 61.9 | 42.3 | 55.5 | 57.4 | 49.6 | 45 | 75.4 | 43.9 | 55.7 | 44.7 | 45.3 | 69.9 | 53.6 | 53.9 (10.4) |
AB, healthy group; C, cervical; CB&M, Community Balance and Mobility Scale; iSCI, incomplete spinal cord injury group; L, lumbar; LE, lower extremity; mini-BESTest, mini-Balance Evaluation Systems Test; T, thoracic; 4WW, 4-wheeled walker.
LE strength measured with manual muscle testing of 12 muscles per LE. Maximum score per muscle is 5, resulting in a total score of 120 for 2 LE.
Retrospective falls in the previous 3 mo.
A registered physical therapist performed the lower extremity (LE) manual muscle test to evaluate motor function of the MG, SOL, tibialis anterior, rectus femoris, vastus lateralis, vastus medialis, biceps femoris, semitendinosus, semimembranosus, iliopsoas, gluteus medius, and gluteus maximus (Kendall et al. 2005). Additionally, the mini Balance Evaluation Systems Test (mini-BESTest) (Franchignoni et al. 2010) and Community Balance and Mobility (CB&M) (Inness et al. 2011) assessment were performed to assess balance ability. The CB&M Scale is a test designed to evaluate balance and mobility in ambulatory individuals who have balance impairments that reduce their full engagement in community living. It has been found to have less of a ceiling effect compared with the typical Berg Balance Scale and a better ability to capture change in these higher-functioning individuals and is a valid measure for individuals with iSCI (Chan et al. 2017; Inness et al. 2011). Participants are not allowed to use a walking aid during the CB&M assessment; as a result, one participant was unable to perform the CB&M because of this restriction. Higher values indicate the higher functions.
Procedure.
Participants performed two quiet standing trials, with eyes open (EO) and eyes closed (EC). For each condition, participants stood quietly in shoes with their arms across their chest for a duration of 150 s. In the EO condition, participants were instructed to focus on a visual target placed at eye level and 2 m in front of them for the duration of the trial. All participants wore a safety harness that was connected to the ceiling to prevent participant falls for all trials. The harness was set up such that it did not support the weight of participants during standing tasks. A dual force plate (AccuSway ACS-DUAL; Advanced Mechanical Technology, Watertown, MA) was used to measure the ground reaction force during quiet standing. Surface EMGs were recorded from the left SOL and MG and other muscles, although we only focus on the left SOL and MG in this report. The EMGs were amplified and band-pass filtered between 20 and 500 Hz (Bagnoli 8 EMG System; Delsys, Boston, MA). The force plate data and EMG data were sampled at 2 kHz and stored on a personal computer for subsequent analysis. Body kinematics were recorded at 200 Hz with a motion capture system with six cameras (Rapter-E; Motion Analysis Corp., United States). Thirty-five reflective markers were placed on anatomical landmarks to define the body segments identified by Winter et al. (Winter 2014) and modified around the trunk according to de Leva (de Leva 1996) to accommodate the safety harness worn by participants. Before the standing trials, resting EMG levels were recorded in a seated posture for 30 s.
Data processing.
All data processing was performed in a computational software (MATLAB 2018a; MathWorks, United States). We focused on the anterior-posterior (AP) direction given that the body movement during quiet standing is primarily in this direction and that the plantarflexors primarily contribute to body motion in this direction. For each 150-s trial, the first and last 15 s of the time series data were trimmed to ensure analysis of steady-state standing, which yielded the analyzed period of 120 s. After trimming, the remaining 120 s was separated into two 60-s windows to minimize the effect of subtle body shifts over time. The subsequent analyses were applied for each 60-s window, and the average of the two parameters was used for each participant’s parameter.
The ground reaction force components obtained from the force plate were low-pass, zero-phase-lag filtered with a cutoff frequency of 4 Hz with a fourth-order Butterworth filter (Masani et al. 2003, 2011) since the study focuses on muscle activity due to low-frequency body movements (Fitzpatrick et al. 1992). To quantify the postural sway during quiet standing, the center of pressure (COP) displacement was first calculated with the ground reaction force. Then the center of pressure velocity (COPVEL) was calculated as a measure of postural sway. Additionally, the center of mass acceleration (COMACC) was calculated with the horizontal ground reaction force (filtered with a 4th-order Butterworth high-pass filter with a cutoff frequency of 0.15 Hz) according to COMACC = fAP/m, where fAP is the horizontal force in the anterior-posterior direction and m is the participant’s body mass (M) without their feet (m = 0.971 M) (Winter 2014). The calculation of the COMACC required an additional high-pass filter at 0.15 Hz (essentially becoming band-pass filtered) to exclude the trend of the horizontal force component (Gage et al. 2004; Lafond et al. 2004). The root mean squares of COPVEL and COMACC were used to quantify the postural sway for each participant.
Ankle and knee joint torque were computed with inverse dynamics, as shown in Eqs. 3 and 6, respectively, where a positive torque represents joint extension.
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
where ANKX/Y and KNX/Y denote the ankle and knee joint displacements, respectively, GRFX,Y,Z is the ground reaction force as measured by the force plate, FX,KN/ANK and FZ,KN/ANK represent the joint reaction forces, COMX/Y/Z,foot/shank is the center of mass of each body segment as calculated from Winter (Winter 2014), I is the moment of inertia of each body segment also calculated from Winter (Winter 2014), and is the angular acceleration of each joint.
The body kinematic data were also smoothed with a fourth-order Butterworth low-pass, zero-phase-lag filter with a cutoff frequency of 4 Hz. Representative ankle and knee joint locations (average of both ankle and knee joints) were calculated. Ankle and knee joint torque were computed with inverse dynamics using the body kinematics data and the ground reaction force, where a positive torque represents joint extension.
The EMGs of the SOL and MG were rectified and smoothed with a fourth-order Butterworth low-pass, zero-phase-lag filter with a cutoff frequency of 1 Hz (Vette et al. 2017) as the estimates of muscle activity levels. To confirm the different fluctuations between the SOL and MG, the coefficient of variation (CV) for each of the SOL and MG was calculated. The PDs of the SOL and MG muscles were estimated as described in the following paragraph. Additionally, the PDs were used to predict the MG and SOL EMG activity with the ankle and knee torque. Subsequently, the Pearson’s correlation was calculated between the actual EMG and predicted EMG time series. The Pearson’s correlation between the actual EMG and predicted EMG is the same as the square root of the coefficient of determination (R2) from the regression analysis, but for simplicity it will be simply described as the correlation coefficient in the remainder of the text.
As described by Nozaki et al. (Nozaki et al. 2005a, 2005b), the data distributions of EMG activity and joint torques were constructed into a three-dimensional plot, where the z-axis represents the muscle activity as a function of ankle (x-axis) and knee (y-axis) joint torques. Then, a linear single plane that described the muscle activation distribution modeled by Eq. 7 below was identified using a multiple regression analysis utilizing only the periods of active EMG activity (Nozaki et al. 2005b):
| (7) |
where c1 and c2 are the regression coefficients for the plantarflexion (TANK) and knee (TKN) torque, respectively. Each muscle’s active periods were selected based on a threshold of the mean EMG amplitude + 3 standard deviations (SDs) during a resting period before the standing trials. Finally, the PD for this muscle was identified with the following equation:
| (8) |
Statistical analyses.
Two-factor mixed analysis of variance (ANOVA) tests [vision (EO/EC) × group (AB/iSCI)] were used to examine the effect of eye condition and group on the COPVEL and COMACC. Another two-factor ANOVA test [vision (EO/EC) × muscle (MG/SOL)] was used to examine the effect of eye condition and muscle on the CV and the PD for each group. For each ANOVA, Bonferroni post hoc tests were performed when significant effects were found. Values are reported as means ± standard deviation (SD). Statistical software (SPSS Statistics version 25, IBM Corp., United States) was used for all statistical tests. P < 0.05 served as the significance level.
RESULTS
Plantarflexor activity in AB individuals during quiet standing.
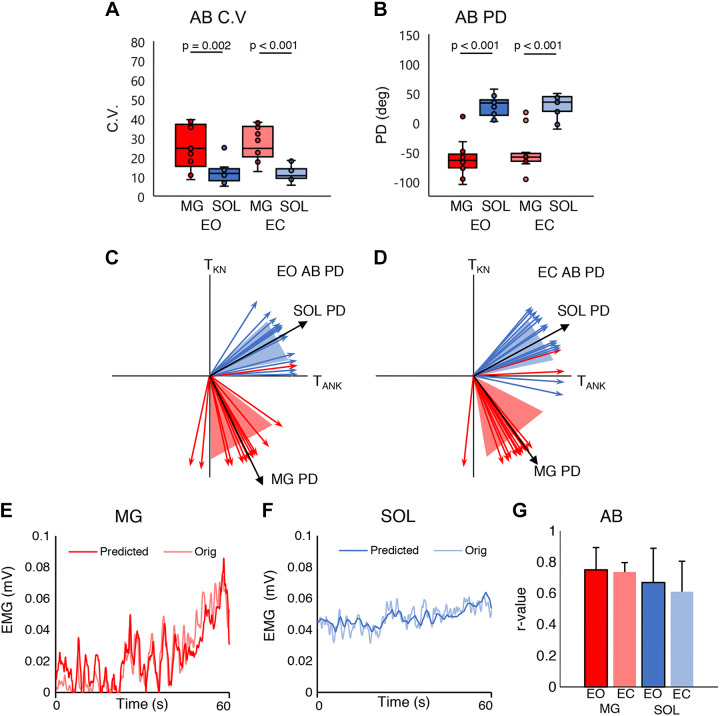
The CVs of the MG and SOL muscles of the AB group are shown in both EO and EC conditions in Fig. 2A. A two-way mixed ANOVA revealed a significant main effect of muscle [F(1,24) = 26.118, P < 0.001, η2 = 0.521] where the CV was larger in MG than in SOL. No significant main effect of eye condition was found [F(1,24) = 1.176, P = 0.289, η2 = 0.047]. Also, no significant interaction effect was found [F(1,24) = 1.167, P = 0.291, η2 = 0.046]. The post hoc test revealed that the MG CV was significantly larger than the SOL CV for both conditions (EO: P = 0.002, EC: P < 0.001) (Fig. 2A).
Fig. 2.
A: distribution of medial gastrocnemius (MG) and soleus (SOL) coefficients of variation (CVs) for eyes open (EO) and eyes closed (EC) conditions in the healthy (AB) group. B: distribution of MG and SOL preferred directions (PDs) for EO and EC conditions in the AB group. Each horizontal bar indicates a P value < 0.05 between the 2 groups under each condition (n = 13 participants). Horizontal lines represent the group median, and the vertical bars represent the furthest outlier or 1.5 times the interquartile range. C: mean ± SD of SOL and MG PDs for the EO condition in the AB group. D: mean ± SD of SOL and MG PDs for the EC condition in the AB group. The black vector is the mean and the shaded area is the SD for each muscle. TANK, plantarflexion torque; TKN, knee torque. E: example time series of the original and predicted AB group’s MG EMG signal; the thick opaque line is the predicted signal, and the thinner translucent line is the original signal. F: example time series of the original and predicted AB group’s SOL EMG signal; the thick opaque line is the predicted signal, and the thinner translucent line is the original signal. G: AB group averages of the correlation coefficient (r) of the predicted and actual MG and SOL EMG activity. Red represents the MG and blue the SOL. Dark colors are EO condition; pale colors are EC condition.
Figure 2B shows PDs of the MG and SOL of the AB group for both EO and EC conditions. A two-way mixed ANOVA revealed a significant main effect of muscle [F(1,24) = 117.612, P < 0.001, η2 = 0.831] where PD was smaller in MG than in SOL. No significant main effect of eye condition was found [F(1,24) = 0.804, P = 0.379, η2 = 0.032]. No significant interaction was found, either [F(1,24) = 0.874, P = 0.359, η2 = 0.035]. The post hoc test revealed that the SOL PD was significantly larger than the MG PD for both conditions (EO: P < 0.001, EC: P < 0.001) (Fig. 2B).
Figure 2, C and D, show PDs for the MG and SOL on the TANK–TKN plane in the EO and EC conditions. Figure 2, E and F, show the original and predicted EMG time series of the MG and SOL for 60 s. The correlation coefficients between the original and the predicted EMG were found to be moderate to strong (Chan 2003; Schober et al. 2018), are shown in Fig. 2G, and were r = 0.751 ± 0.143 and r = 0.736 ± 0.060 and r = 0.670 ± 0.219 and r = 0.610 ± 0.196, respectively, for the MG and SOL for both conditions.
Postural control.
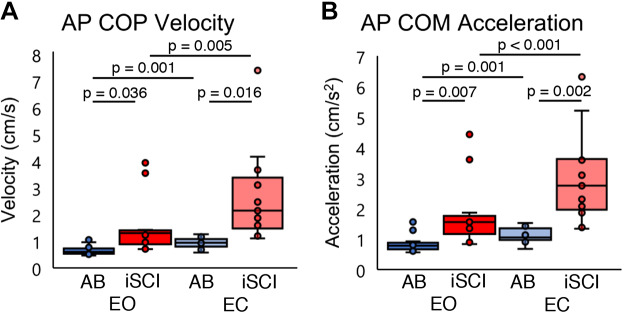
Figure 3 shows the group results for the postural control measures. For COPVEL, a two-way mixed ANOVA revealed significant main effects of group [F(1,24) = 11.878, P = 0.002, η2 = 0.331] and condition [F(1,24) = 27.387, P < 0.001, η2 = 0.533]. A significant interaction [F(1,24) = 9.665, P = 0.005, η2 = 0.287] was also found. The post hoc test revealed that the COPVEL was significantly larger in the iSCI group than in the AB group for both conditions (EO: P = 0.036, EC: P = 0.016). The iSCI group’s EC condition had a significantly larger COPVEL than the iSCI group’s EO condition (P = 0.005), and in the AB group COPVEL was significantly larger in the EC condition than the EO condition (P = 0.001) (Fig. 3A).
Fig. 3.
A: distribution of the center of pressure velocity (COPVEL) fluctuations in the anterior-posterior (AP) direction for eyes open (EO) and eyes closed (EC) conditions. B: distribution of the center of mass acceleration (COMACC) in the AP direction for EO and EC conditions. Each horizontal bar indicates a P value < 0.05 between the 2 groups under each condition (n = 13 participants). Dark colors are EO condition; pale colors are EC condition. n = 13 participants for all conditions. Horizontal lines represent the group median, and the vertical bars represent the furthest outlier or 1.5 times the interquartile range. AB, healthy; iSCI, incomplete spinal cord injury.
For COMACC, a two-way mixed ANOVA revealed significant main effects of group [F(1,24) = 16.801, P < 0.001, η2 = 0.412] and condition [F(1,24) = 48.244, P < 0.001, η2 = 0.668]. A significant interaction [F(1,24) = 18.141, P < 0.001, η2 = 0.430] was also found. COMACC was significantly larger in the iSCI group than the AB group for both conditions (EO: P = 0.007, EC: P = 0.002). In the iSCI group, COMACC was significantly larger in the EC condition than in the EO condition (P < 0.001), and in the AB group COMACC was significantly larger in the EC condition than the EO condition (P = 0.001) (Fig. 3B).
Plantarflexor activity in individuals with iSCI during quiet standing.
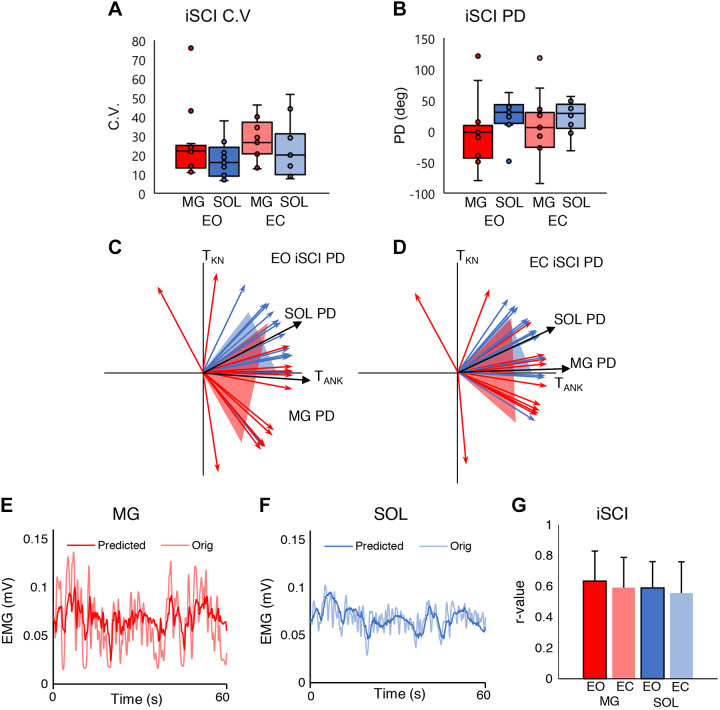
The CVs of the MG and SOL muscles of the iSCI group are shown in both EO and EC conditions in Fig. 4A. A two-way mixed ANOVA revealed no significant main effect of muscle [F(1,24) = 1.664, P = 0.209, η2 = 0.065], where the CV was similar between the MG and SOL. No significant main effect of eye condition was found [F(1,24) = 2.661, P = 0.116, η2 = 0.100]. Also, no significant interaction effect was found [F(1,24) = 0.266, P = 0.611, η2 = 0.011]. Figure 4B shows PDs of the MG and SOL of the iSCI group for both EO and EC conditions. A two-way mixed ANOVA revealed no significant main effect of muscle [F(1,24) = 2.273, P = 0.145, η2 = 0.087], where the PDs of the MG and SOL were similar. No significant main effect of eye condition was found [F(1,24) = 0.854, P = 0.365, η2 = 0.034], where the EO PD was similar to the EC PD. No significant interaction was found, either [F(1,24) = 0.708, P = 0.408, η2 = 0.029]. Figure 4, C and D, show the PDs for the MG and SOL on the TANK–TKN plane in the EO and EC conditions. Figure 4, E and F, show the original and predicted EMG time series of the MG and SOL for 60 s. The correlation coefficients between the original and the predicted EMG were found to be moderate (Chan 2003; Schober et al. 2018), are shown in Fig. 4G, and were r = 0.634 ± 0.194 and r = 0.591 ± 0.197 and r = 0.589 ± 0.171 and r = 0.557 ± 0.202, respectively, for the MG and SOL for both conditions.
Fig. 4.
A: distribution of medial gastrocnemius (MG) and soleus (SOL) coefficients of variation (CVs) for eyes open (EO) and eyes closed (EC) conditions in the incomplete spinal cord injury (iSCI) group. B: distribution of MG and SOL preferred directions (PDs) for EO and EC conditions in the iSCI group. Horizontal lines represent the group median, and the vertical bars represent the furthest outlier or 1.5 times the interquartile range. C: mean ± SD of SOL and MG PDs for the EO condition in the iSCI group (n = 13 participants). D: mean ± SD of SOL and MG PDs for the EC condition in the iSCI group (n = 13 participants). The black vector is the mean and the shaded area is the SD for each muscle. TANK, plantarflexion torque; TKN, knee torque. E: example time series of the original and predicted iSCI group’s MG EMG signal; the thick opaque line is the predicted signal, and the thinner translucent line is the original signal. F: example time series of the original and predicted iSCI group’s SOL EMG signal; the thick opaque line is the predicted signal, and the thinner translucent line is the original signal. G: iSCI group averages of the correlation coefficient (r) of the predicted and actual MG and SOL EMG activity. Red represents the MG and blue the SOL. Dark colors are EO condition; pale colors are EC condition.
Differences in plantarflexor activity during quiet standing in AB and iSCI individuals.
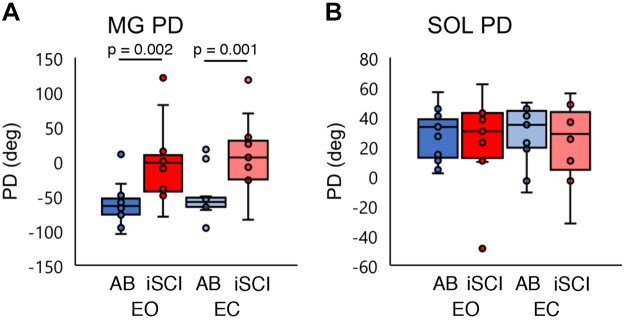
Figure 5 shows the group comparisons for the plantarflexor activity measures; these values are repeated from the AB group (Fig. 2, A and B) and the iSCI group (Fig. 4, A and B) for statistical purposes (Fig. 5). For the MG PD, a two-way mixed ANOVA revealed a significant main effect of group [F(1,24) = 14.165, P = 0.001, η2 = 0.371]. No significant main effect of condition [F(1,24) = 2.579, P = 0.121, η2 = 0.097] or significant interaction effect was found [F(1,24) < 0.001, P = 0.984, η2 < 0.001]. The post hoc test revealed that the MG PD was significantly larger in the iSCI group than in the AB group for both conditions (EO: P = 0.002, EC: P = 0.001) (Fig. 5A).
Fig. 5.
A: distribution of the medial gastrocnemius (MG) preferred direction (PD) in both healthy (AB) and incomplete spinal cord injury (iSCI) groups for the eyes open (EO) and eyes closed (EC) conditions. B: distribution of the soleus (SOL) PD in both AB and iSCI groups for the EO and EC conditions. Blue represents the AB group and red the iSCI group. Each horizontal bar indicates a P value < 0.05 between the 2 groups under each condition (n = 13 participants). Dark colors are EO condition, pale colors are EC condition. n = 13 for all conditions. Horizontal lines represent the group median, and the vertical bars represent the furthest outlier or 1.5 times the interquartile range.
For the SOL PD, a two-way mixed ANOVA revealed no significant main effect of group [F(1,24) = 0.270, P = 0.608, η2 = 0.011] or condition [F(1,24) = 0.001, P = 0.979, η2 < 0.001]. There was no significant interaction effect [F(1,24) = 0.005, P = 0.945, η2 = 0.000] (Fig. 5B).
Individual analyses of iSCI.
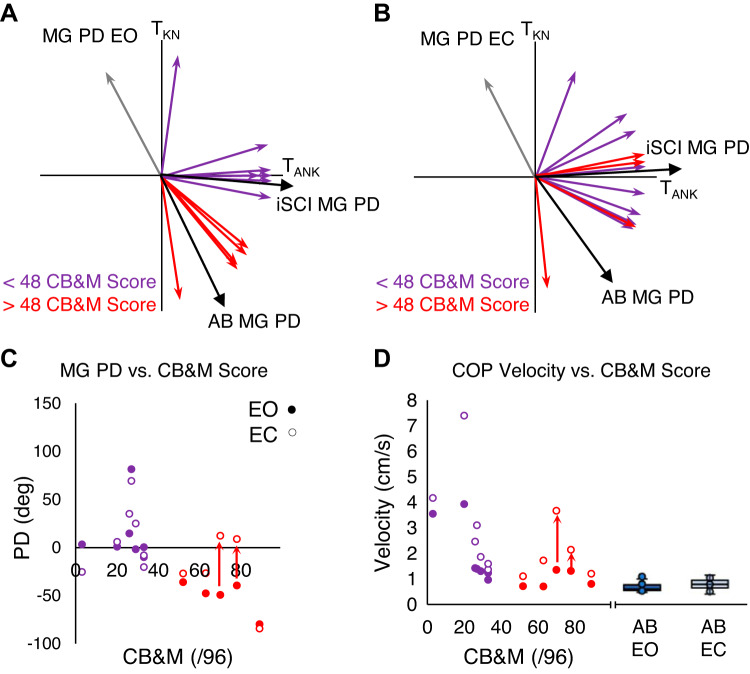
In general, participants with iSCI tend to have high heterogeneity in motor functions, and individual analyses may help to understand the study results better. Figure 6, A and B, show the individual MG PDs for participants with iSCI, with a color code for their motor function using Community Balance and Mobility (CB&M) scores. The purple arrows indicate a CB&M < 48, and the red arrows indicate CB&M > 48. The participant unable to perform the CB&M test had an MG PD over 100° (gray arrows in Fig. 6, A and B).
Fig. 6.
A: distribution of medial gastrocnemius (MG) preferred directions (PDs) in participants with incomplete spinal cord injury (iSCI) in the eyes open (EO) condition. B: distribution of MG PDs in participants with iSCI in the eyes closed (EC) condition. Participants with a Community Balance and Mobility (CB&M) score > 48 are in red, and those with a score < 48 are in purple. The gray arrows are the individual who did not perform the CB&M assessment. C: scatterplot of MG PDs in participants with iSCI in both EO and EC condition against the CB&M score. D: scatterplot of center of pressure velocity (COPVEL) in EO and EC conditions. Red arrows indicate direction of change for the MG PD from the EO to EC condition in the 2 individuals with iSCI who demonstrated a high CB&M score but had postural sways greater than those typically observed in the healthy (AB) group. Box plots indicating the median (middle line), 75th and 25th percentile values (top and bottom of box), and 1.5 times the interquartile range (top and bottom whiskers) are shown for the AB group’s COPVEL in EO (solid blue) and EC (light blue) conditions on right of scatterplots for comparison.
In the EO condition, there were five participants with iSCI with MG PDs similar to the AB group (red arrows in Fig. 6A). These participants corresponded with higher CB&M scores (>48/96). Two of these five participants (CB&M = 78, 70) demonstrated MG PDs (−39.6°, −49.3°) in the EO condition comparable to the AB group’s MG PDs but positive MG PDs (8.72°, 12.3°) in the EC condition. The remaining two participants (CB&M = 63, 52) showed MG PDs similar to the AB group in both conditions (EO: −47.7°, −36.2°, EC: −26.7°, −27.1°) (Fig. 6C). The iSCI participants (CB&M = 89, 63, 52) with similar MG PDs in both conditions demonstrated COPVEL similar to the AB groups in both conditions (EO: 0.803, 0.705, 0.708 cm/s, EC: 1.20, 1.72, 1.11 cm/s), but the iSCI participants (CB&M = 78, 70) whose MG PD changed between EO and EC conditions did not have COPVEL similar to the AB group for either condition (EO: 1.31, 1.35 cm/s, EC: 2.14, 3.66 cm/s) (Fig. 6D). Red arrows indicate direction of change for the MG PD from the EO to EC condition in the two individuals with iSCI who demonstrated a high CB&M score but had postural sways greater than those typically observed in AB (Fig. 6, C and D).
Similar trends were observed among all other clinical measures including the mini-BESTest, LE strength, and gait speed (supplemental results; all Supplemental Material is available at http://doi.org/10.17632/jr4drtrtn4.2), but here we chose to focus on the CB&M, as it does not allow for the use of any aids. The mini-BESTest also measures balance ability but enables participants with iSCI to use aids, with a subsequent score reduction. The use of any aids during balance ability testing allows participants to utilize compensatory mechanisms developed around their aid and consequently may not be representative of their unsupported quiet standing as performed in these experiments.
DISCUSSION
Cosine tuning of the plantarflexors in the intact physiological control system.
For healthy individuals, we confirmed that the SOL shows tonic muscle activation whereas the MG shows more phasic activation (Fig. 2A), agreeing with previous observations (Nozaki et al. 2004). As fluctuations of activities in both muscles highly correlate with the COP (Gatev et al. 1999; Masani et al. 2003; Winter et al. 1998), both muscle activations must be highly correlated. Thus, the difference between these two muscles are dynamic ranges, i.e., SOL has a smaller dynamic range of muscle activation whereas MG has a larger range. This difference can be accounted for by the difference of PDs between MG and SOL, as follows.
We found that Eq. 7 fits well in our experimental data, by moderate correlation coefficients shown in Fig. 2G. This validates that each of the two muscles has a unique activity plane on the ankle-knee torque plane, each muscle is activated in a cosine tuning manner, and each muscle has a unique PD. The MG PD is approximately −57° whereas the SOL PD is 28° (Fig. 2, B–D) on the ankle-knee torque plane. The MG PD of about −57° indicates a strong sensitivity of the MG’s muscle activity to both plantarflexion torque and knee flexion torque. This is unsurprising given the anatomical insertion points and function of the biarticular MG muscle [a mechanical direction of about −27° utilizing methods and information provided by Delp (Delp 1990)]. Interestingly, the SOL’s PD is ~28°, indicating a sensitivity to plantarflexion torque (its physiological function) but also knee extension torque (a joint in which the SOL is not attached). This deviation of the PD from the mechanical direction of monoarticular muscles has been reported previously (Cabel et al. 2001; Kurtzer et al. 2006b; Nozaki et al. 2005a). These studies reported a rotation of the mechanical directions of the monoarticular muscles to the largest gap in the torque plane. The suggested reason for such a rotation is that the central nervous system is attempting to minimize the sum of the squared muscular activity (Fagg et al. 2002; Kurtzer et al. 2006b; Nozaki et al. 2005a). Since the plantarflexor muscles reside in the fourth quadrant (ankle extension and knee flexion) or on the x-axis (ankle extension only), it stands to reason that the SOL PD rotated into the first quadrant (further away from the MG PD). Through these rotations of the PDs, there is an overall reduction in the total muscular activity.
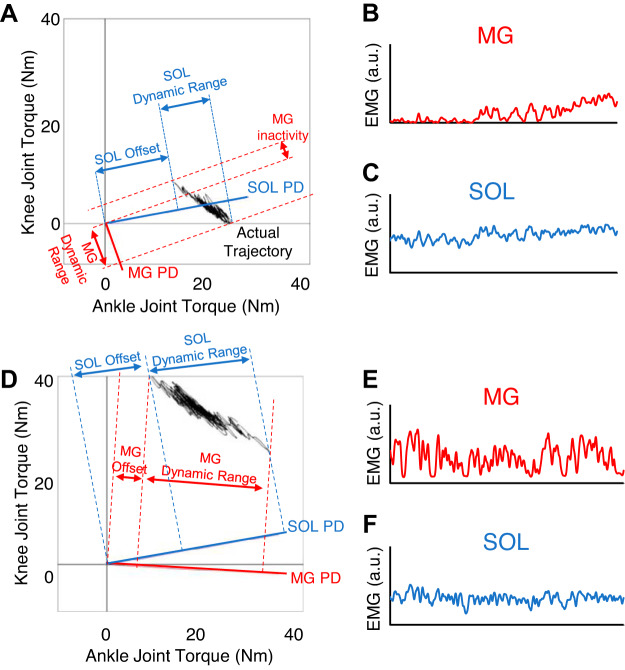
Figure 7 shows a set of examples of the exerted joint torque relation between the ankle and knee joints (Fig. 7A) as well as the corresponding muscle activities in the AB group (Fig. 7, B and C). The TANK and TKN relationship shown in Fig. 7A is characteristic of quiet standing control due to the center of mass being in front of the ankle joint and usually located behind the knee joint. More specifically, plantarflexion torque is always required and is mostly accompanied by knee extension torque (Fig. 7A). Since cosine tuning muscle activity is proportional to the orthogonal projection of the torque vector (TANK, TKN) to the PD of the muscle, it is possible to explain the differences in activation patterns of the SOL and MG during quiet standing (Nozaki et al. 2004). More specifically, if the ankle and knee joint torque requirements follow the direction of the PD, then it is expected that the EMG activity of that muscle will have a large gain (i.e., if the torque trajectory on the joint torque plane is parallel to the muscle’s PD the EMG activity will have a large gain) (Fig. 7B). Conversely, if the PD of a muscle is orthogonal to the torque trajectory, the EMG activity will have a very small gain (Fig. 7C). The MG PD is almost parallel to the joint trajectory (Fig. 7A), making it highly sensitive to postural sway (large gains and inactivity regions); alternatively, the SOL PD is almost orthogonal to the joint torque trajectory (Fig. 7A), so it is insensitive to postural sways (low gain and tonic activity) (Nozaki et al. 2004). Thus, the different PDs for the MG and SOL (Fig. 2B), which indicate how the central nervous system recruits muscles, consequently explain the differences of the muscle activity patterns between the MG and SOL during quiet standing (Fig. 2A).
Fig. 7.
A: representative image of joint torque trajectory during quiet standing in a healthy (AB) individual along with the orthogonal projection to both the medial gastrocnemius (MG) and soleus (SOL) preferred directions (PDs). B: representative 60-s time series of the MG muscle activity to highlight its phasic activity. C: representative 60-s time series of the SOL muscle activity to highlight its tonic activity. B and C are representative time series from an individual in the AB group. D: representative image of joint torque trajectory during quiet standing in an incomplete spinal cord injury (iSCI) individual along with the orthogonal projection to both the MG and SOL PDs. E: representative 60-s time series of the MG muscle activity to highlight its phasic activity. F: representative 60-s time series of the SOL muscle activity to highlight its tonic activity. E and F are representative time series from an individual in the iSCI group. a.u., Arbitrary units.
Control of plantarflexor muscles in iSCI.
We confirmed that individuals with iSCI sway more compared with AB individuals (Fig. 3), agreeing with previous studies (Lemay et al. 2013). Also, our finding agrees with Lemay et al. (2013) that eliminating visual information further impacts the balance ability of individuals with iSCI, as iSCI often results in decreased proprioceptive ability. That is, the postural sway in EC was much larger than in EO, especially in individuals with iSCI (AB 150%, iSCI 170% larger EC than EO, for both COPVEL and COMACC postural sway measures).
In individuals with iSCI, Eq. 7 also fits well for each muscle, indicated by the moderate correlation (Fig. 4G). This suggests that the muscle activation in participants with iSCI also follows the cosine tuning. However, we demonstrated that the MG PD is different from that of the AB group. The MG PD is approximately −3° whereas that for SOL was 24° for participants with iSCI (Fig. 4, B–D). This MG PD was larger in participants with iSCI (Fig. 5A), whereas there was no difference in the SOL PD (Fig. 5B). The larger MG PD is closer to the SOL PD and is closer to being orthogonal to the torque trajectory on the ankle-knee torque plane during quiet standing (Fig. 7D). As mentioned above, since muscle activity is proportional to the orthogonal projection of the torque vector to the PD, a larger (more positive) MG PD results in a decreased sensitivity to the postural sway and an overall more tonic muscle activity profile in the MG in participants with iSCI like their SOL muscle activity (Fig. 7, E and F).
Heterogeneity in balance ability among individuals with iSCI.
The MG PDs of participants with iSCI were larger than the MG PDs of AB participants and closer to their SOL PDs (Fig. 5A); however, the SOL PDs of both groups were comparable for both EO and EC conditions (Fig. 5B). In general, participants with iSCI tend to have high heterogeneity in balance abilities, and individual analyses may help to understand the study results better. The individuals unable to perform the CB&M test had the most dramatic shift away from the MG PDs of the AB group, suggesting significant changes to the control of their MG. Interestingly, of the five high CB&M scoring participants, the participants who showed small postural sway with values very close to AB participants had MG PDs similar to the AB group. Conversely, participants who demonstrated drastic changes of MG PDs in the EO condition comparable to the AB group’s MG PDs, to positive MG PDs, also demonstrated a large increase of postural sway from the EO to EC condition (Fig. 6, B–D). Taken together, higher balance ability and smaller postural sway related to MG PD values closer to those in AB participants. This implies that the control strategy of plantarflexors is affected by iSCI, which results in deteriorated balance in individuals with iSCI.
These changes to their MG PD during the EC condition may be due to a compensatory mechanism. Since the visual system is such a critical source of minimizing postural sway in both AB and iSCI groups (Fig. 3), removing it in individuals with iSCI may force typically high-functioning individuals during the EO condition into a different balance strategy during the EC condition. Thus, during the EC condition for these higher-scoring individuals with iSCI, they utilize a strategy similar to the individuals with iSCI with lower CB&M scores. In their previous study, Nozaki et al. (2005a) noted that although PDs are independent of physiological factors such as moment arm or cross-section area, the PDs of muscles are highly interdependent. That is, changes in movement/balance strategy between the lower limb joints in lower-function individuals with iSCI could affect the MG PD during quiet standing. Alternatively, this change in MG PD may be a consequence of the damaged motor pathway in their spinal cord. The central nervous system may be attempting to or sending the same signals as it would in healthy individuals, but because of the damage to the pathway the signal is not being delivered appropriately to the muscles (specifically the MG) and consequently the activity pattern is altered. Finally, a combination of the compensatory and motor deficits experienced by individuals with iSCI may result in a decreased use or control of the knee joint during quiet standing. Consequently, this may mitigate the differences between mono- and biarticular muscles around the knee joint (i.e., the SOL and MG), and the PDs of the respective muscles become more similar.
Limitations.
A limitation with this study may be the ambiguity of the hip torque in our analysis. For instance, Nozaki et al. (2005a) previously tested the MG as a pseudomonoarticular muscle during their isometric thigh muscle experiments but could not properly identify a cosine tuning pattern. However, they cited the ambiguity of ankle joint torque as a source of variability in their experiment. Although we consider both physiologically connected joints to the MG in our study, the hip should also be considered, as there are joint interactions.
Another limitation for this study may be the limited dynamic range of the quiet standing tasks for the regression used to identify the muscle PDs. Despite the limited dynamic range, the correlations between actual and predicted EMGs were overall similarly high to moderate; thus we believe that our PD estimates were verified. Additionally, the use of the safety harness on participants with iSCI may have impacted their quiet standing through perceived additional support, similar to the effects of light touch (Kouzaki and Masani 2008). This was unavoidable because of safety considerations.
The participants all wore shoes while performing the standing trials. Although this is not ideal, it was necessary for the safety of our participants with iSCI, and consequently our AB group wore shoes as well to create similar scenarios. Although some studies utilizing high heels suggest that type of shoe affects the torque and COP (Farrag and Elsayed 2016; Hyun et al. 2016), our participants were instructed to wear comfortable walking shoes whose sole height/stiffness did not vary much. Thus, although the participants had to wear shoes, they all wore similar styled/type shoes, which may affect our between-participant differences, but we believe that this should not impact our conclusion.
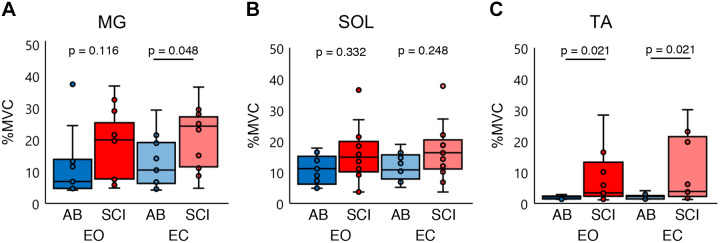
Finally, a limitation of our analyses and interpretation may be from our focus on the plantarflexor muscles (MG and SOL) while ignoring the lateral gastrocnemius and tibialis anterior (TA), which can also contribute to the ankle joint torque. We did not collect EMG activity from the lateral gastrocnemius; however, we did for the TA. Figure 8 shows the muscle activity of the MG, SOL, and TA for both groups in EO and EC conditions. There was a tendency that the iSCI group utilized similar muscle activity in the MG and SO compared with the AB group, whereas TA activity was clearly larger in the iSCI group than the AB group. Previous studies in the literature investigated PD based solely on the muscle of interest’s activity and adjacent exerted joint torque regardless of antagonists’ and/or agonists’ activities (Nozaki et al. 2005b, 2005a); we believe that we can keep our present conclusion. However, we should note that the group difference may be affected by this clear difference of muscle activation patterns. We applied the same calculation to identify the TA PD for both the AB and iSCI groups. However, the regressions showed only low R2 values, suggesting poor reliability; as a result we were not able to identify the TA PD. Future experiments should incorporate a greater range of motion toward the posterior to truly activate the TA as well as lateral gastrocnemius muscle.
Fig. 8.
Percent maximum voluntary contraction (%MVC). A: distribution of the medial gastrocnemius (MG) %MVC in both healthy (AB) and incomplete spinal cord injury (iSCI) groups for the eyes open (EO) and eyes closed (EC) conditions. B: distribution of the soleus (SOL) %MVC in both AB and iSCI groups for the EO and EC conditions. C: distribution of the tibialis anterior (TA) %MVC in both AB and iSCI groups for the EO and EC conditions. Blue represents the AB group and red the iSCI group. Group differences were tested with a Mann–Whitney U nonparametric test. Each horizontal bar indicates a P value < 0.05 between the 2 groups, Bonferroni corrected. Dark colors are EO condition, and pale colors are EC conditions. n = 13 participants for all conditions. Horizontal lines represent the group median, and the vertical bars represent the furthest outlier or 1.5 times the interquartile range.
Conclusions.
The present study quantified the preferred directions of the plantarflexor muscles. First, in able-bodied participants, we demonstrated that the central nervous system uses cosine tuning to control the plantarflexors during quiet standing, and this can explain the unique muscle activity patterns of MG and SOL. In participants with iSCI, we demonstrated that the MG PD significantly differs from that of able-bodied participants, and this may closely relate to impaired standing balance in participants with iSCI.
GRANTS
This work was supported by grants from the Natural Sciences and Engineering Research Council of Canada (grant no. DG RGPIN-2017-06790) and the Ontario Neurotrauma Foundation (grant no. 2016-RHI-PREV-1019).
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the authors.
AUTHOR CONTRIBUTIONS
J.U., K.C., K.E.M., and K.M. conceived and designed research; J.W.L., J.U., and K.C. performed experiments; K.L.F. analyzed data; K.L.F. and K.M. interpreted results of experiments; K.L.F. prepared figures; K.L.F. drafted manuscript; K.L.F., J.W.L., J.U., K.C., D.N., K.E.M., and K.M. edited and revised manuscript; K.L.F., J.W.L., J.U., K.C., D.N., K.E.M., and K.M. approved final version of manuscript.
ACKNOWLEDGMENTS
The authors thank Dr. Hikaru Yokoyama for support and input during the preparation of this manuscript.
REFERENCES
- Biering-Sørensen B, Kristensen IB, Kjaer M, Biering-Sørensen F. Muscle after spinal cord injury. Muscle Nerve 40: 499–519, 2009. doi: 10.1002/mus.21391. [DOI] [PubMed] [Google Scholar]
- Bouisset S. EMG and muscle force in normal motor activities. In: New Concepts of the Motor Unit, Neuromuscular Disorders, Electromyographic Kinesiology, edited by Desmedt J. Basel: Karger, 1973, p. 547–583. [Google Scholar]
- Burnham R, Martin T, Stein R, Bell G, MacLean I, Steadward R. Skeletal muscle fibre type transformation following spinal cord injury. Spinal Cord 35: 86–91, 1997. doi: 10.1038/sj.sc.3100364. [DOI] [PubMed] [Google Scholar]
- Cabel DW, Cisek P, Scott SH. Neural activity in primary motor cortex related to mechanical loads applied to the shoulder and elbow during a postural task. J Neurophysiol 86: 2102–2108, 2001. doi: 10.1152/jn.2001.86.4.2102. [DOI] [PubMed] [Google Scholar]
- Caminiti R, Johnson PB, Urbano A. Making arm movements within different parts of space: dynamic aspects in the primate motor cortex. J Neurosci 10: 2039–2058, 1990. doi: 10.1523/JNEUROSCI.10-07-02039.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chan K, Guy K, Shah G, Golla J, Flett HM, Williams J, Musselman KE. Retrospective assessment of the validity and use of the community balance and mobility scale among individuals with subacute spinal cord injury. Spinal Cord 55: 294–299, 2017. doi: 10.1038/sc.2016.140. [DOI] [PubMed] [Google Scholar]
- Chan K, Unger J, Lee JW, Johnston G, Constand M, Masani K, Musselman KE. Quantifying balance control after spinal cord injury: reliability and validity of the mini-BESTest. J Spinal Cord Med 42, Suppl 1: 141–148, 2019. doi: 10.1080/10790268.2019.1647930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chan YH. Biostatistics 104: correlational analysis. Singapore Med J 44: 614–619, 2003. [PubMed] [Google Scholar]
- de Leva P. Adjustments to Zatsiorsky-Seluyanov’s segment inertia parameters. J Biomech 29: 1223–1230, 1996. doi: 10.1016/0021-9290(95)00178-6. [DOI] [PubMed] [Google Scholar]
- Delp S. Surgery Simulation: A Computer Graphics System to Analyze and Design Musculoskeletal Reconstructions of the Lower Limb (PhD thesis). Stanford, CA: Stanford University, 1990. [Google Scholar]
- Fagg AH, Shah A, Barto AG. A computational model of muscle recruitment for wrist movements. J Neurophysiol 88: 3348–3358, 2002. doi: 10.1152/jn.00621.2002. [DOI] [PubMed] [Google Scholar]
- Farrag A, Elsayed W. Habitual use of high-heeled shoes affects isokinetic soleus strength more than gastrocnemius in healthy young females. Foot Ankle Int 37: 1008–1016, 2016. doi: 10.1177/1071100716649172. [DOI] [PubMed] [Google Scholar]
- Fitzpatrick RC, Gorman RB, Burke D, Gandevia SC. Postural proprioceptive reflexes in standing human subjects: bandwidth of response and transmission characteristics. J Physiol 458: 69–83, 1992. doi: 10.1113/jphysiol.1992.sp019406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Franchignoni F, Horak F, Godi M, Nardone A, Giordano A. Using psychometric techniques to improve the Balance Evaluation Systems Test: the mini-BESTest. J Rehabil Med 42: 323–331, 2010. doi: 10.2340/16501977-0537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gage WH, Winter DA, Frank JS, Adkin AL. Kinematic and kinetic validity of the inverted pendulum model in quiet standing. Gait Posture 19: 124–132, 2004. doi: 10.1016/S0966-6362(03)00037-7. [DOI] [PubMed] [Google Scholar]
- Gatev P, Thomas S, Kepple T, Hallett M. Feedforward ankle strategy of balance during quiet stance in adults. J Physiol 514: 915–928, 1999. doi: 10.1111/j.1469-7793.1999.915ad.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Georgopoulos AP, Kalaska JF, Caminiti R, Massey JT. On the relations between the direction of two-dimensional arm movements and cell discharge in primate motor cortex. J Neurosci 2: 1527–1537, 1982. doi: 10.1523/JNEUROSCI.02-11-01527.1982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Héroux ME, Dakin CJ, Luu BL, Inglis JT, Blouin JS. Absence of lateral gastrocnemius activity and differential motor unit behavior in soleus and medial gastrocnemius during standing balance. J Appl Physiol (1985) 116: 140–148, 2014. doi: 10.1152/japplphysiol.00906.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoffman DS, Strick PL. Step-tracking movements of the wrist. IV. Muscle activity associated with movements in different directions. J Neurophysiol 81: 319–333, 1999. doi: 10.1152/jn.1999.81.1.319. [DOI] [PubMed] [Google Scholar]
- Hyun SH, Kim YP, Ryew CC. Effect on the parameters of the high-heel shoe and transfer time of ground reaction force during level walking. J Exerc Rehabil 12: 451–455, 2016. doi: 10.12965/jer.1632592.296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Inness EL, Howe JA, Niechwiej-Szwedo E, Jaglal SB, McIlroy WE, Verrier MC. Measuring balance and mobility after traumatic brain injury: validation of the community balance and mobility scale (CB&M). Physiother Can 63: 199–208, 2011. doi: 10.3138/ptc.2009-45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson MA, Polgar J, Weightman D, Appleton D. Data on the distribution of fibre types in thirty-six human muscles. An autopsy study. J Neurol Sci 18: 111–129, 1973. doi: 10.1016/0022-510X(73)90023-3. [DOI] [PubMed] [Google Scholar]
- Kalaska JF, Cohen DA, Hyde ML, Prud’homme M. A comparison of movement direction-related versus load direction-related activity in primate motor cortex, using a two-dimensional reaching task. J Neurosci 9: 2080–2102, 1989. doi: 10.1523/JNEUROSCI.09-06-02080.1989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kendall FP, McCreary EK, Provance PG, Crosby RW, Andrews PJ, Krause C. Muscles: Testing and Function with Posture and Pain. Baltimore, MD: Lippincott Williams & Wilkins, 2005. [Google Scholar]
- Kouzaki M, Masani K. Reduced postural sway during quiet standing by light touch is due to finger tactile feedback but not mechanical support. Exp Brain Res 188: 153–158, 2008. doi: 10.1007/s00221-008-1426-5. [DOI] [PubMed] [Google Scholar]
- Kurtzer I, Herter TM, Scott SH. Nonuniform distribution of reach-related and torque-related activity in upper arm muscles and neurons of primary motor cortex. J Neurophysiol 96: 3220–3230, 2006a. doi: 10.1152/jn.00110.2006. [DOI] [PubMed] [Google Scholar]
- Kurtzer I, Pruszynski JA, Herter TM, Scott SH. Primate upper limb muscles exhibit activity patterns that differ from their anatomical action during a postural task. J Neurophysiol 95: 493–504, 2006b. doi: 10.1152/jn.00706.2005. [DOI] [PubMed] [Google Scholar]
- Lafond D, Duarte M, Prince F. Comparison of three methods to estimate the center of mass during balance assessment. J Biomech 37: 1421–1426, 2004. doi: 10.1016/S0021-9290(03)00251-3. [DOI] [PubMed] [Google Scholar]
- Lemay JF, Gagnon D, Duclos C, Grangeon M, Gauthier C, Nadeau S. Influence of visual inputs on quasi-static standing postural steadiness in individuals with spinal cord injury. Gait Posture 38: 357–360, 2013. doi: 10.1016/j.gaitpost.2012.11.029. [DOI] [PubMed] [Google Scholar]
- Marino RJ, Barros T, Biering-Sorensen F, Burns SP, Donovan WH, Graves DE, Haak M, Hudson LM, Priebe MM; ASIA Neurological Standards Committee 2002 . International standards for neurological classification of spinal cord injury. J Spinal Cord Med 26, Suppl 1: S50–S56, 2003. doi: 10.1080/10790268.2003.11754575. [DOI] [PubMed] [Google Scholar]
- Masani K, Popovic MR, Nakazawa K, Kouzaki M, Nozaki D. Importance of body sway velocity information in controlling ankle extensor activities during quiet stance. J Neurophysiol 90: 3774–3782, 2003. doi: 10.1152/jn.00730.2002. [DOI] [PubMed] [Google Scholar]
- Masani K, Vette AH, Abe MO, Nakazawa K, Popovic MR. Smaller sway size during quiet standing is associated with longer preceding time of motor command to body sway. Gait Posture 33: 14–17, 2011. doi: 10.1016/j.gaitpost.2010.08.012. [DOI] [PubMed] [Google Scholar]
- Nozaki D, Hirano T, Nakazawa K, Akai M. Cosine tuning can predict different activity patterns among triceps surae muscles during human quiet standing (Abstract). Neuroscience 2004 San Diego, CA, October 23–27, 2004, p. 306.5. [Google Scholar]
- Nozaki D, Nakazawa K, Akai M. Uncertainty of knee joint muscle activity during knee joint torque exertion: the significance of controlling adjacent joint torque. J Appl Physiol (1985) 99: 1093–1103, 2005a. doi: 10.1152/japplphysiol.00365.2005. [DOI] [PubMed] [Google Scholar]
- Nozaki D, Nakazawa K, Akai M. Muscle activity determined by cosine tuning with a nontrivial preferred direction during isometric force exertion by lower limb. J Neurophysiol 93: 2614–2624, 2005b. doi: 10.1152/jn.00960.2004. [DOI] [PubMed] [Google Scholar]
- Schober P, Boer C, Schwarte LA. Correlation coefficients: appropriate use and interpretation. Anesth Analg 126: 1763–1768, 2018. doi: 10.1213/ANE.0000000000002864. [DOI] [PubMed] [Google Scholar]
- Schwartz AB, Kettner RE, Georgopoulos AP. Primate motor cortex and free arm movements to visual targets in three-dimensional space. I. Relations between single cell discharge and direction of movement. J Neurosci 8: 2913–2927, 1988. doi: 10.1523/JNEUROSCI.08-08-02913.1988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shields RK. Fatigability, relaxation properties, and electromyographic responses of the human paralyzed soleus muscle. J Neurophysiol 73: 2195–2206, 1995. doi: 10.1152/jn.1995.73.6.2195. [DOI] [PubMed] [Google Scholar]
- Smith JW. The forces operating at the human ankle joint during standing. J Anat 91: 545–564, 1957. [PMC free article] [PubMed] [Google Scholar]
- Vette AH, Sayenko DG, Jones M, Abe MO, Nakazawa K, Masani K. Ankle muscle co-contractions during quiet standing are associated with decreased postural steadiness in the elderly. Gait Posture 55: 31–36, 2017. doi: 10.1016/j.gaitpost.2017.03.032. [DOI] [PubMed] [Google Scholar]
- Winter DA. Biomechanics and Motor Control of Human Movement (4th ed.). Hoboken, NJ: John Wiley & Sons, 2014. [Google Scholar]
- Winter DA, Patla AE, Prince F, Ishac M, Gielo-Perczak K. Stiffness control of balance in quiet standing. J Neurophysiol 80: 1211–1221, 1998. doi: 10.1152/jn.1998.80.3.1211. [DOI] [PubMed] [Google Scholar]