Stationary distribution and extinction of stochastic coronavirus (COVID-19) epidemic model

Abstract

Similar to other epidemics, the novel coronavirus (COVID-19) spread very fast and infected almost two hundreds countries around the globe since December 2019. The unique characteristics of the COVID-19 include its ability of faster expansion through freely existed viruses or air molecules in the atmosphere. Assuming that the spread of virus follows a random process instead of deterministic. The continuous time Markov Chain (CTMC) through stochastic model approach has been utilized for predicting the impending states with the use of random variables. The proposed study is devoted to investigate a model consist of three exclusive compartments. The first class includes white nose based transmission rate (termed as susceptible individuals), the second one pertains to the infected population having the same perturbation occurrence and the last one isolated (quarantined) individuals. We discuss the model’s extinction as well as the stationary distribution in order to derive the the sufficient criterion for the persistence and disease’ extinction. Lastly, the numerical simulation is executed for supporting the theoretical findings.

1. Introduction

The 2019- novel coronavirus has been known to the virologist’s community as Severe Acute Respiratory Syndrome Coronavirus-2 (SARS-CoV-2) [1]. The COVID-19 refers to the virus associated syndrome. SARS-CoV-2 being previously unrecognized novel-strain of the coronavirus in humans [2], [3]. Coronaviruses in general circulate among various animals with some being highly susceptible for infecting humans. Among these animals, naturally bats are thought to be proven hosts of such novel coronaviruses, nevertheless, various species of other animals are also considered an active cause for such spreads [4]. At present, the Middle East Respiratory Syndrome Coronavirus (MERS-CoV) which is much similar to COVID-19 was spread from camels to humans, while the civet cats have been considered as source of Severe Acute Respiratory Syndrome Coronavirus-1 (SARS-CoV-1) for transmission into human. Bunch of information are presented in the ECDC factsheet on coronaviruses [4], [5].

Though the animals are understood to be a proven source, however, currently, human-to-human transmission is also considered as one of the spread source. At present, the epidemiological information are sparse for the determination of an effortless spread of this virus among the people, nonetheless, currently, on average, it is estimated that, infection in one person can cause the spread among 2-3 more people [1], [5]. The virus appears to be transferred mostly through narrow respiratory droplets by coughing, sneezing, or people’s interaction in close proximity (usually less than one meter) with each other for a certain time frame. These droplets can further be inhaled, or can stay on the surfaces being came in contact by the infected person, that can cause infection in others by touching their nose, mouth or eyes. The virus possesses ability to survive on various surfaces commencing several hours (e.g. copper, cardboard) up to a few days (e.g. plastic and stainless steel). Nonetheless, the quantity of the viable virus certainly decays over a time span and might not be present in sufficient quantity for causing the infection. It is currently estimated that the appearance of symptoms and initial infections in case of COVID-19 almost lies between 1-14 days [1], [5], [6]. Moreover till today there is no proper treatment in term of vaccine etc. However, the scientists are working faster to develop vaccine for the novel COVID-19, which will take enough time. Therefore the only way to stop the spread of this disease is to quarantine or isolate the initially infected population as showed by the Chinese Govt and also the guide line of WHO.

It could be also noted that most of the real world phenomenon are not simply deterministic, because in deterministic models, the output of the model is fully determined by the parameter values and the initial conditions. Stochastic models possess some inherent randomness. The same set of parameter values and initial conditions will lead to an ensemble of different outputs or we can say in simple world a deterministic model is one that uses numbers as inputs, and produces numbers as outputs. A stochastic model includes a random component that uses a distribution as one of the inputs, and results in a distribution for the output. These distributions may reflect the uncertainty in what the input should be (e.g. a deterministic input plus noise), or may reflect a random process (i.e. a stochastic input) [7], [8], [9].

For describing the changing behavior of several epidemic diseases in a realistic sense, the mathematical modeling is considered as an influential tool. Several epidemic models have been developed by various mathematicians and ecologists for comprehending and controlling various epidemic diseases in a region. In last twenty years, mathematical modeling is widely used for characterizing the communication of various infectious diseases (see e.g. [10], [11]. Recently various comprehensions have been made to deepen the understanding about the novel coronavirus (COVID-19) particularly grasping the valuable inferences through mathematical modeling [12], [13], [14]. The modelsdescribe the dynamics of infectious diseases, however, for modeling biological phenomenon, it is appropriate to use the stochastic differential equations due to its realistic approach. Compared to deterministic models, the stochastic models can generally result in more valuable output, by several times execution, a distribution of the expected results can be built, such as the average infections at any time t, whereas the deterministic models result in a single predicted value [15], [16], [17], [18]. Numerous approaches and methods exist for studying stochastic models (such as Binomial moment equation etc.) [19], [20].

The most basic stochastic epidemic models are those involving global transmission, meaning that infection rates depend only on the type and state of the individuals involved, and not on their location in the population. How can a model be defined explaining the sometimes-observed scenario of frequent mid-sized epidemic outbreaks? How can evolution of the infectious agent transmission rates be modeled and fitted to data in a robust way? In this paper we understand the transmission mechanism of the COVID-19 mathematically, we have formulated a model using the available literature on modeling epidemics, we propose a stochastic epidemic model for the transmission dynamics of COVID-19 virus with a varying population environment for a long-term behavior. We categorize the total population into three different classes. The first class is the susceptible individuals in which the transmission rate is distributed by white noise. The second class includes the infected individuals in which the same transmission occurs. The third class consists of the quarantine individuals with white noise.

In the recent study, we proposed a stochastic epidemic model for the transmission dynamics of the COVID-19 with a changing environment considering long term behavior. The overall population has been divided into three exclusive classes: the susceptible individuals with white noise transmission rate distribution, the infected individuals in which the same perturbation occur and quarantined individuals. Then, we will discuss the disease’ extinction and stationary distribution and develop the sufficient condition for the COVID-19. Furthermore, sample simulations are find out with the help of stochastic Runge-Kutta method for supporting the theoretical results.

2. Mathematical Model for COVID-19 model

The present section is devoted to formulation of a model based on stochastic theory for studying the transmissions dynamic of the novel virus i.e., COVID-19 pandemic. We propose a susceptible-infected-quarantined epidemic model as according to the characteristic of the disease. We also take the varying population environment to study the dynamics of the COVID-19 particularly its long-term behavior. Before to present the model, we put some assumption as given by the following assertions.

(A ₁). The total population at any time t is symbolized by N(t) and it is stratified into three exclusive groups of individual: the susceptible class S(t), the COVID-19 infected people I(t) and the quarantined Q(t), i.e., $S\left(t\right)+I\left(t\right)+Q\left(t\right)=N\left(t\right)$ which is changing with t.

(A ₂). The state variables and parameters included in the model are assumed to be nonnegative.

(A ₃) The initially infected individuals move to the quarantined class as performed by the Chinese in Wuhan city.

(A ₄). Once the infection confirmed then the quarantined will go back to the infected compartment.

In the light of the above assumption $\left(A_1\right)-\left(A_4\right),$ the proposed model leads to the following stochastic epidemic problem which consist of three stochastic differential equations

$$\begin{array}{c}\mathit{dS}\left(t\right)=[\Lambda -\frac{\beta S\left(t\right)I\left(t\right)}{N}-{\mu }_{0}S\left(t\right)]\mathit{dt}+{\eta }_{1}S\left(t\right)d{B}_1\left(t\right),\hfill \\ \mathit{dI}\left(t\right)=(\frac{\beta S\left(t\right)I\left(t\right)}{N}-({\gamma }_1+{\mu }_1+{\mu }_0)I\left(t\right)+\sigma Q\left(t\right))\mathit{dt}+{\eta }_{2}I\left(t\right)d{B}_2\left(t\right),\hfill \\ \mathit{dQ}\left(t\right)=({\gamma }_{1}I\left(t\right)-({\mu }_0+\mu +\sigma )Q\left(t\right))\mathit{dt}+{\eta }_{3}Q\left(t\right)d{B}_3\left(t\right).\hfill \end{array}$$ (1)

Here in the model, Λ represents the per capita constant fecundity rate. μ ₀, μ ₁ and μ represents the natural mortality rate and disease-related mortality rate, respectively. γ ₁ represents the constant rate at which people getting quarantined from COVID-19 infected class. B(t) is considered to be the usual Brownian motion with intensity η ₁, η ₂ and η ₁ taken to be positive.

3. Preliminaries

Let (Ω, {F_t}_t ≥ 0, P) be the complete probability space with filtration {F_t}_t ≥ 0 which satisfy the normal conditions, $X\left(t\right)=(S\left(t\right),I\left(t\right),Q\left(t\right)),\left|X\left(t\right)\right|=(S^2\left(t\right)+I^2\left(t\right)+Q^2\left(t\right)){}^{\frac{1}{2}},$ and ${\mathbb{R}}_{+}^d=\{x\in {\mathbb{R}}^d:{\chi }_j>0,j=1,\cdots ,d\}$.

Considering a d-dimensional SDE

$$dz\left(t\right)=f(z\left(t\right),t)dt+g(z\left(t\right),t)dB\left(t\right)t\ge t_o,$$ (2)

along with condition $z\left(t_0\right)=z_0\in {\mathbb{R}}^d,$ where B(t) denotes an m-dimensional usual Brownian motion. Define the operator $\mathcal{L}$ related to (4) by

$$\mathcal{L}=\frac{\partial }{\partial t}+\sum _{i=1}^d{f}_i(z,t)\frac{\partial }{\partial z_i}+\frac{1}{2}\sum _{i,j=1}^d{\left[g^T(z,t)g(z,t)\right]}_{\mathit{ij}}\frac{{\partial }^2}{\partial z_i\partial z_j}.$$

By operating $\mathcal{L}$ on V (a function from the space $C^{2,1}({\mathbb{R}}^d\times [t_0,\infty );{\mathbb{R}}_{+})$), then we have

$$\mathcal{L}V(z,t)=V_t(z,t)+V_z(z,t)f(z,t)+\frac{1}{2}\mathit{trace}\left[g^T(z,t)V_{\mathit{zz}}(z,t)g(z,t)\right],$$

where

$$\begin{array}{ccc}& & V_t=\frac{\partial V}{\partial t},\hfill \\ & & V_z={(\frac{\partial V}{\partial z_1},...,\frac{\partial V}{\partial z_d})}^T,\hfill \\ & & V_{\mathit{zz}}={\left(\frac{{\partial }^{2}V}{\partial z_i\partial z_j}\right)}_{d\times d}.\hfill \end{array}$$

By generalized It$\widehat{o}$’s formula, we have

$$\mathit{dV}(z\left(t\right),t)=\mathcal{L}V(z\left(t\right),t)\mathit{dt}+V_z(z\left(t\right),t)g(z\left(t\right),t)\mathit{dB}\left(t\right),$$

whenever $z\left(t\right)\in {\mathbb{R}}^d$.

4. The existence and uniqueness of solution to COVID-19 model

This section is about studying the existence and uniqueness of solution of the proposed stochastic COVID-19 model (1).

Theorem 1

The triplet (S(t), I(t), Q(t)) being solution of the developed stochastic COVID-19 epidemic model (1) is unique for t ≥ 0 with initial condition $(S\left(0\right),I\left(0\right),Q\left(0\right))\in R_{+}^3$ . Further, the solution will always remains in $R_{+}^3$ with unit probability, that is, $(S\left(t\right),I\left(t\right),Q\left(t\right))\in R_{+}^3\forall t\ge 0$ almost surely (a.s).

Proof: As for initial value of the state variables $(S\left(0\right),I\left(0\right),Q\left(0\right))\in R_{+}^3,$ the coefficients used in equations are continuous and locally lipschitz. Thus, there must exists a local unique solution (S(t), I(t), Q(t)) of the model over t ∈ [0, τ_e). For detail analysis of the explosion time τ_e one must see the references [21], [22]. To prove the global nature of the solution, we must show that ${\tau }_e=\infty$ a.s. Assume that we have a sufficiently large nonnegative number k ₀ such that all of the initial conditions on the state lie within $[\frac{1}{k_0},k_0]$. Let for each positive integer k ≥ k ₀, the finishing time be defined as

$$\begin{array}{c}\hfill {\tau }_k=\left\{\begin{array}{c}t\in [0,{\tau }_e):min\{S\left(t\right),I\left(t\right),Q\left(t\right)\}\le \frac{1}{k}\hfill \\ or\hfill \\ max\left\{S\right(t),I(t),Q(t\left)\right\}\ge k\hfill \end{array}\right\}.\end{array}$$ (3)

Throughout this manuscript, we must choose $\inf \varphi =\infty$ where ϕ stand for the null set. Definition of τ_k force us to say that it is increasing as k tends to ∞. Setting ${\tau }_{\infty }={\lim }_{k\to \infty }$ with τ_e ≥ τ _∞ a.s. Upon showing ${\tau }_{\infty }=\infty$ a.s., we will declare that ${\tau }_e=\infty$ and hence (S(t), I(t), Q(t)) will lies in $R_{+}^3$ a.s. ∀t ≥ 0. Thus, it is suffice to prove that ${\tau }_e=\infty$ a.s. In otherwise case, there must exists two positive constants ϵ from (0,1) and T such that

$$P\{T\ge {\tau }_{\infty }\}>ϵ.$$ (4)

Hence there is an integer k ₁ ≥ k ₀, such that

$$P\{T\ge {\tau }_k\}\ge ϵ,\forall k_1\le k.$$

Next, we will define a C ²-function $H:R_{+}^3\to R_{+}$ in such a way that

$$H(S,I,Q)=S+I+Q-3-\log S-\log I-\log Q.$$ (5)

It is to be noted that the H is a nonnegative function, and it can be verified from the fact that $0\le y-\text{logy}-1,\forall 0<y$. Assume that k ₀ ≤ K and 0 < T are arbitrary. Upon applying $It\widehat{o}$ formula to Eq. (5) gives us

$$\begin{array}{ccc}\hfill dH(S,I,Q)& =& LH(S,I,Q)+{\eta }_1(S-1)B_1\left(t\right)+{\eta }_2(I-1)B_2\left(t\right)\hfill \\ & & +{\eta }_3(Q-1)B_3\left(t\right)\hfill \end{array}$$ (6)

In Eq. (6), $LH:R_{+}^3\to R_{+}$ is defined by the following equation

$$\begin{array}{c}{\displaystyle \mathit{LH}(S,I,Q)=(1-\frac{1}{S})(\Lambda -\frac{\beta S\left(t\right)I\left(t\right)}{N}-{\mu }_{0}S\left(t\right))+\frac{{{\eta }_1}^2}{2}}\hfill \\ {\displaystyle +(1-\frac{1}{I})(\frac{\beta S\left(t\right)I\left(t\right)}{N}-({\mu }_0+{\gamma }_1+{\mu }_1)I\left(t\right)+\sigma Q\left(t\right))+\frac{{{\eta }_2}^2}{2}}\hfill \\ {\displaystyle +(1-\frac{1}{Q})({\gamma }_{1}I\left(t\right)-({\mu }_0+\mu +\sigma )Q\left(t\right))+\frac{{{\eta }_3}^2}{2},}\hfill \\ {\displaystyle =\Lambda -{\mu }_{0}S-\frac{\Lambda }{S}+\frac{\beta I}{N}+{\mu }_0}\hfill \\ {\displaystyle -({\mu }_0+{\mu }_1)I-\beta S+({\mu }_0+{\gamma }_1+{\mu }_1)-\sigma \frac{Q\left(t\right)}{I\left(t\right)}}\hfill \\ {\displaystyle -({\mu }_0+\mu )Q\left(t\right)-{\gamma }_1\frac{I\left(t\right)}{Q\left(t\right)}+({\mu }_0+\mu +\sigma )+\frac{{{\eta }_1}^2+{{\eta }_2}^2+{{\eta }_3}^2}{2},}\hfill \\ {\displaystyle \le \Lambda +\beta +3{\mu }_0+{\mu }_1+{\gamma }_1+\mu +\sigma +\frac{{{\eta }_1}^2+{{\eta }_2}^2+{{\eta }_3}^2}{2}:=K.}\hfill \end{array}$$ (7)

Thus,

$$\begin{array}{c}{\displaystyle E\left[H(S({\tau }_k\wedge T),I({\tau }_k\wedge T),Q({\tau }_k\wedge T))\right]}\hfill \\ {\displaystyle \le H(S\left(0\right),I\left(0\right),Q\left(0\right))+E\left[{\int }_0^{{\tau }_k\wedge T}\mathit{Kdt}\right],}\hfill \\ {\displaystyle \le H(S\left(0\right),I\left(0\right),Q\left(0\right))+\mathit{KT}.}\hfill \end{array}$$ (8)

Setting ${\Omega }_k=\{{\tau }_k\le T\}$ for k ≥ k ₁ and by Eq. (4), P(Ω_k) ≥ ϵ. Note that for each ω from Ω_k there must exist one or more than one S(τ_k, ω), I(τ_k, ω), Q(τ_k, ω) which equals $\frac{1}{k}$ or k. As a result H(S(τ_k), I(τ_k), Q(τ_k)) is no less then $\frac{1}{k}-1+\text{log}k$ or $k-1-\text{log}k$. Therefore,

$$H(S\left({\tau }_k\right),I\left({\tau }_k\right),Q\left({\tau }_k\right))\ge (\frac{1}{k}-1+\text{log}k)\wedge E(k-1-\text{log}k).$$ (9)

By using Eqs. (4) and (8), we can write

$$\begin{array}{cc}H\left(S\right(0),I(0),Q(0\left)\right)+KT\hfill & \ge E\left[1_{\Omega \left(\omega \right)}H\right(S\left({\tau }_k\right),I({\tau }_k,Q\left({\tau }_k\right))\left)\right]\hfill \\ & \ge ϵ\left[\right(\frac{1}{k}-1+\text{log}k)\wedge (k-1-\text{log}k)].\hfill \end{array}$$ (10)

Here 1_Ω(ω) represent the indicator function of Ω. Approaching k to ∞ will lead us to the contradiction $\infty >H\left(S\right(0),I(0),Q(0\left)\right)+MT=\infty$ showing that ${\tau }_{\infty }=\infty$ a.s.

Theorem 2

For any initial data (S(0), I(0), Q(0)) in $R_{+}^3,$ the solution of the developed model (1) will remains in $R_{+}^3$ with unit probability, that is, $(S\left(t\right),I\left(t\right),Q\left(t\right))\in R_{+}^3$ for all t ≥ 0 almost surely.

Proof: Letting $I\subset [0,+\infty )$ and assuming that a solution of the proposed stochastic COVID-19 pandemic model (1) exists in I, then for each time t ∈ I, solution of the first equation of the model (1) becomes

$$\begin{array}{c}{\displaystyle S\left(t\right)=e^{-{\mu }_{0}t-{\int }_0^t(\frac{\beta I\left(u\right)}{N}+\frac{1}{2}{\eta }_1^2{I}^2\left(u\right))\mathit{du}-{\eta }_1{\int }_0^{t}I\left(u\right)d{B}_1\left(u\right)}}\hfill \\ {\displaystyle \times [S\left(0\right)+\Lambda {\int }_0^t{e}^{{\mu }_{0}u+{\int }_0^u(\frac{\beta I\left(u\right)}{N}+\frac{1}{2}{\eta }_1^2{I}^2\left(u\right))\mathit{du}+{\eta }_1{\int }_0^{u}I\left(u\right)d{B}_1\left(u\right)}]\mathit{du},}\hfill \end{array}$$ (11)

which implies that S(t) > 0. Solving the second equation of the model (1) gives us

$$\begin{array}{ccc}\hfill I\left(t\right)& =& I\left(0\right)e^{-({\mu }_0+{\mu }_1+{\gamma }_1-{\gamma }_{1}S\left(u\right))t+{\int }_0^t(\frac{\beta S\left(u\right)}{N}+\sigma Q\left(u\right)+\frac{1}{2}{\eta }_2^2{S}^2\left(u\right))\mathit{du}+{\eta }_2{\int }_0^{t}S\left(u\right)d{B}_2\left(u\right)}\hfill \\ & & +e^{-({\mu }_0+{\mu }_1+{\gamma }_1-{\gamma }_{1}S\left(u\right))t+{\int }_0^t(\frac{\beta S\left(u\right)}{N}+\sigma Q\left(u\right)+\frac{1}{2}{\eta }_2^2{S}^2\left(u\right))\mathit{du}+{\eta }_2{\int }_0^{t}S\left(u\right)d{B}_2\left(u\right)}\hfill \\ & & \times {\int }_0^t\frac{\beta S\left(u\right)}{N}{e}^{({\mu }_0+{\mu }_1+{\gamma }_1-{\gamma }_{1}S\left(u\right))\mathit{du}-{\int }_0^t(\frac{\beta S\left(u\right)}{N}+\sigma Q\left(u\right)+\frac{1}{2}{\eta }_2^2{S}^2\left(u\right))\mathit{du}-{\eta }_2{\int }_0^{t}S\left(u\right)d{B}_2\left(u\right)}\hfill \\ & & \times \mathit{du},\hfill \end{array}$$

which simply means that 0 ≤ I(t). It is handy to shown that 0 < Q(t). Hence $(S\left(t\right),I\left(t\right),Q\left(t\right))\in R_{+}^3,$ for all t ≥ 0, which proves the conclusion.

Remark 1

Clearly, Theorems 1 and 2 guarantees that for the initial data $(S\left(0\right),I\left(0\right),Q\left(0\right))\in R_{+}^3,$ there is a unique global solution (S(t), I(t), Q(t)) of the model (1) in $R_{+}^3$ almost surely. Thus

$$dN\left(t\right)\le \Lambda -{\mu }_{0}N\left(t\right).$$ (12)

By solving the differential inequality Eq. (12) yields

$$N\left(t\right)\le \frac{\Lambda }{{\mu }_0}+e^{-{\mu }_{0}t}(\Lambda -{\mu }_{0}N\left(t\right))(N\left(0\right)-\frac{\Lambda }{{\mu }_0}).$$ (13)

If $\frac{\Lambda }{{\mu }_0}\ge N\left(0\right),$ then $\frac{\Lambda }{{\mu }_0}\ge N\left(t\right),$ a.s. Thus the desired region for the problem becomes

$${\Omega }^{*}=\{(S,I,Q):S>0,I\ge 0,Q>0,N\le \frac{\Lambda }{{\mu }_0}\}.$$ (14)

In upcoming study, we shall always assume that (S(0), I(0), Q(0)) ∈ Ω* unless otherwise stated.

5. The Extinction and Stationary Distribution of COVID-19 model

As for as the stochastic systems are concerned, they have no endemic equlibria. Thus, the stability analysis cannot be used as a tool for studying the disease’ persistence. As a result, one must turn his/her attention to the existence/uniqueness theory of the stationary distribution which in some sense, will work for persistence of the disease. For this purpose, we will cite a famous result from Hasminskii [23].

Let

$$<X\left(t\right)>=\frac{1}{t}{\int }_0^{t}x\left(r\right)dr.$$ (15)

Lemma 1

[16,17](Strong Law of Large Number) Let$M={\left\{M\right\}}_{t\ge 0}$be a continuous real valued local martingale and vanishing at$t=0,$then

$$\begin{array}{ccc}& & \underset{t\to \infty }{\lim }<M,M{>}_t=\infty ,\text{a.s.,}\text{implies}\text{that}\underset{t\to \infty }{\lim }\frac{M_t}{<M,M{>}_t}\hfill \\ & & =0,\text{a.s.},\text{and}\text{also},\hfill \\ & & \underset{t\to \infty }{\lim }sup\frac{<M,M{>}_t}{t}<0,\text{a.s.,}\text{implies}\text{that}\underset{t\to \infty }{\lim }\frac{M_t}{t}=0,\text{a.s.}\hfill \end{array}$$ (16)

Lemma 2

[16,17]Assume that f ∈ C[[0, ∞) × Ω(0, ∞)] and F(t) is in C([0, ∞) × Ω, R). If there exist three positive constant λ, λ ₀ and T, such that

$$\begin{array}{cc}& logf\left(t\right)\le \lambda t-{\lambda }_0{\int }_0^{t}f\left(s\right)ds+F\left(t\right)\text{a.s.,}\forall t\ge T\text{and}\hfill \\ & \underset{t\to \infty }{\lim }\frac{F\left(t\right)}{t}=0\text{a.s.,}then\underset{t\to \infty }{\lim }sup\frac{1}{t}{\int }_0^{t}f\left(s\right)ds\le \frac{\lambda }{{\lambda }_0}\text{a.s.}\hfill \end{array}$$ (17)

5.1. Stationary distribution

Suppose that X(t) is a regular Markov process (time-homogeneous) in $R_{+}^n$ whose dynamics is given by

$$dX\left(t\right)=b\left(X\right)dt+\sum _r^k{\sigma }_{r}d{B}_r\left(t\right).$$

The diffusion matrix is of the form

$$A\left(X\right)=\left[a_{ij}\left(x\right)\right],a_{ij}\left(x\right)=\sum _{r=1}^k{\sigma }_r^i\left(x\right){\sigma }_j^r\left(x\right).$$

Lemma 3

([16,17]).The process X(t) has the unique stationary distribution m(.) if there exist a bounded domain with regular boundary such that$U,\overline{U}\in R^d$$\overline{U}$closure$\overline{U}\in R^d,$having the following properties

• 1.In the open domain U and in its neighborhood, the least eigenvalue of A(t) is bounded away from zero.
• 2.If x ∈ R^dU, the mean time τ (at which a path starting from x reach the set U) is finite, and Sup _x ∈ k E^xτ < ∞ for each compact subset K ⊂ Rⁿ. Further, if f(.) is an integrable function having measure π, then

$$P(\underset{T\to \infty }{\lim }\frac{1}{T}{\int }_0^{T}f\left(X_x\left(t\right)\right)dt={\int }_{R^d}f\left(x\right)\pi \left(dx\right))=1$$

for all x ∈ R^d.

Define a parameter

$$R_0^s=\frac{d\rho \gamma }{(d+\frac{{\sigma }_1^2}{2})(\gamma +\delta +d+\alpha +\frac{{\sigma }_2^2}{2})}.$$ (18)

Theorem 3

The solution (S(t), I(t), Q(t)) of the model (1) is ergodic as well as there is a unique stationary distribution π(.) whenever $R_0^S>1$ .

Proof

In order to verify condition (2) of Lemma 3, we need to develop a non-negative $C^2-$function $V:R_{+}^3\to R_{+}.$ For this, we will first define

$$V_1=S+I+Q-c_{1}lnS-c_{2}lnI,$$

where c ₁, c ₂ are the positive constant and need to be determined later on. By using the Ito’s formula and the proposed model (1), we obtain

$$\begin{array}{c}\mathcal{L}(S+I+Q)=\Lambda -{\mu }_0(S+I+Q)-{\mu }_{1}I-\mu Q,\hfill \\ \mathcal{L}(-lnS)=-\frac{\Lambda }{S}+\frac{\beta I\left(t\right)}{N}+{\mu }_0+\frac{{\eta }_1^2}{2},\hfill \\ \mathcal{L}(-lnI)=-\frac{\beta S\left(t\right)}{N}+({\mu }_0+{\mu }_1+{\gamma }_1)-\sigma \frac{Q}{I}+\frac{{\eta }_2^2}{2},\hfill \\ \mathcal{L}(-lnQ)=-\frac{{\gamma }_{1}I}{Q}+({\mu }_0+\mu +\sigma )+\frac{{\eta }_3^2}{2}.\hfill \end{array}$$ (19)

Therefore, we have

$$\begin{array}{c}{\displaystyle \mathcal{L}{V}_1=(1-\frac{c_1}{S})(\Lambda -\frac{\beta \mathit{SI}}{N}-{\mu }_{0}S)+\frac{1c_1}{2S^2}{\eta }_1^2{S}^2}\hfill \\ {\displaystyle +(1-\frac{c_2}{S})(\frac{\beta S\left(t\right)I\left(t\right)}{N}-({\mu }_0+{\mu }_1+{\gamma }_1)I\left(t\right)+\sigma Q\left(t\right))}\hfill \\ {\displaystyle +\frac{1c_2}{2S^2}{\eta }_2^2{I}^2+({\gamma }_{1}I\left(t\right)-({\mu }_0+\mu +\sigma )Q\left(t\right)).}\hfill \\ {\displaystyle \le -3{\left({\mu }_0(S+I+Q)\frac{c_1\Lambda }{S}\frac{c_2\beta S}{N}\right)}^{\frac{1}{3}}-{\mu }_{1}I-\mu Q\left(t\right)+\Lambda +\frac{c_1\beta I}{N}}\hfill \\ {\displaystyle +{\mu }_0{c}_1+\frac{c_1}{2}{\eta }_1^2+c_2({\mu }_0+{\mu }_1+{\gamma }_1)+\frac{c_2}{I}\sigma Q+\frac{c_2}{2}{\eta }_2^2.}\hfill \end{array}$$

The above implies that

$$\begin{array}{c}\mathcal{L}{V}_1\le -3\left(c_1{c}_2{\mu }_0\beta \Lambda \right){}^{\frac{1}{3}}+c_1({\mu }_0+\frac{{\eta }_1^2}{2})\hfill \\ +c_2({\mu }_0+{\mu }_1+{\gamma }_1+\frac{{\eta }_2^2}{2})+c_1\frac{\beta I\left(t\right)}{N}+c_2\left(\frac{\sigma Q\left(t\right)}{I}\right)\hfill \\ +\Lambda -{\mu }_{1}I-\mu Q.\hfill \end{array}$$

Let

$$c_1({\mu }_0+\frac{{\eta }_1^2}{2})=c_2({\mu }_0+{\mu }_1+{\gamma }_1+\frac{{\eta }_2^2}{2})=\Lambda .$$

Namely

$${\displaystyle c_1=\frac{\Lambda }{({\mu }_0+\frac{{\eta }_1^2}{2})},c_2=\frac{\Lambda }{({\mu }_0+{\mu }_1+{\gamma }_1+\frac{{\eta }_2^2}{2})}.}$$ (20)

Consequently

$$\begin{array}{c}\mathcal{L}{V}_1\le -3(\frac{{\Lambda }^3{\mu }_0\beta }{({\mu }_0+\frac{{\eta }_1^2}{2})({\mu }_0+{\mu }_1+{\gamma }_1+\frac{{\eta }_2^2}{2})}-\Lambda )\hfill \\ +c_1\frac{\beta I\left(t\right)}{N}+c_2\frac{\sigma Q\left(t\right)}{I}-{\mu }_{1}I-\mu Q.\hfill \end{array}$$ (21)

$$\mathcal{L}{V}_1\le -3\Lambda [\left(R_0^S\right){}^{1/3}-1]+\frac{c_1\beta I}{N}+c_2\frac{\sigma Q}{I}.$$

In addition, we can obtain

$$\begin{array}{ccc}\hfill V_2& =& c_3(S+I+Q-c_1\ln S-c_2\ln I)-(\ln S+\ln Q)+S\left(t\right)\hfill \\ & & +I\left(t\right)+Q\left(t\right)\hfill \\ & =& (c_3+1)(S\left(t\right)+I\left(t\right)+Q\left(t\right))-(c_3{c}_1+1)\ln S-c_3{c}_2\ln I-\ln Q,\hfill \end{array}$$

where the constant c ₃ > 0 to be determined at later stages. It is handy to show that

$$\underset{(S,I,Q)\in {\mathbb{R}}_{+}^3\setminus U_k}{lim\; inf}{V}_2(S,I,Q)=+\infty ,ask\to \infty ,$$ (22)

where $U_k=(\frac{1}{k},k)\times (\frac{1}{k},k)\times (\frac{1}{k},k)$. The next step is to prove that V ₂(S, I, Q) has one and only one minimum value V ₂(S ₀, I ₀, Q ₀).

The partial derivative of V ₂(S, I, Q) with respect to S, I, Q is as follow

$$\begin{array}{cc}\frac{\partial V_2(S,I,Q)}{\partial S}\hfill & =1+c_3-\frac{1+c_1{c}_3}{S},\hfill \\ \frac{\partial V_2(S,I,Q)}{\partial I}\hfill & =1+c_3-\frac{c_3{c}_2}{I},\hfill \\ \frac{\partial V_2(S,I,Q)}{\partial Q}\hfill & =1+c_3-\frac{c_3}{Q}.\hfill \end{array}$$

It could be easily obtain that V ₂ have unique stagnation point $(S_0,I_0,Q_0)=(\frac{1+c_1{c}_3}{1+c_3},\frac{c_3{c}_2}{1+c_3},\frac{1}{1+c_3})$. Moreover, the Hesse matrix of V ₂(S, I, R) at (S ₀, I ₀, Q ₀) is

$$B=\left[\begin{array}{ccc}\frac{1+c_3{c}_1}{S_0^2}& 0& 0\\ 0& \frac{c_3{c}_2}{I_0^2}& 0\\ 0& 0& \frac{1}{Q_0^2}\end{array}\right].$$

Obviously, the Hesse matrix is positive definite. Thus, V ₂(S, I, Q) has a minimum value V ₂(S ₀, I ₀, Q ₀). According to Eq. (22) and from the continuity of V ₂(S, I, Q), we can say that V ₂(S, I, Q) has one and only one minimum value V ₂(S ₀, I ₀, Q ₀) inside $R_{+}^3$.

Next, we will define a non-negative $C^2-$function $V:{\mathbb{R}}_{+}^3\to {\mathbb{R}}_{+}$ as follows

$$V(S,I,Q)=V_2(S,I,Q)-V_2(S_0,I_0,Q_0).$$

Applying the Itô’s formula and using the proposed model, we get

$$\begin{array}{c}\mathcal{L}\left(V\right)\le c_3\{-3\Lambda [\left(R_0^S\right){}^{1/3}-1]+\frac{c_1\beta I}{N}+c_2\frac{\sigma Q}{I}\}\hfill \\ -\frac{\Lambda }{S}+\frac{\beta I}{N}+{\mu }_0+\frac{{\eta }_1^2}{2}-\frac{{\gamma }_{1}I}{Q}+{\mu }_0+\mu +\sigma +\frac{{\eta }_3^2}{2}\hfill \\ +\Lambda -{\mu }_0(S+Q+I)-{\mu }_{1}I-\mu Q,\hfill \end{array}$$ (23)

which leads to the following assertion

$$\begin{array}{c}\mathcal{L}V\le -c_3{c}_4+c_1{c}_3\frac{\beta I}{N}+c_2{c}_3\frac{\sigma Q}{I}-\frac{\Lambda }{S}+\beta +2{\mu }_0+\frac{{\eta }_2^2+{\eta }_3^2}{2}+\hfill \\ \mu +\sigma +\Lambda -{\mu }_o(S+I+Q)-\frac{{\gamma }_{1}I}{Q},\hfill \end{array}$$ (24)

where

$$C_4=3\Lambda [\left(R_0^S\right){}^{1/3}-1]>0.$$

The next step is to define the set

$$D=\{{\delta }_1<S<\frac{1}{{\delta }_4},{\delta }_2<I<\frac{1}{{\delta }_5},{\delta }_3<Q<\frac{1}{{\delta }_6}\},$$

where δ_i > 0 for $(i=1,\cdots ,6)$ are infinitesimally small constants to be determined later. For the sake of simplicity, we will divide the whole ${\mathbb{R}}_{+}^3\setminus D$ into the following regions

$$\begin{array}{c}{D}_1=\{(S,I,Q)\in {\mathbb{R}}_{+}^3,0<S\le {\delta }_1\},D_2=\{(S,I,Q)\in {\mathbb{R}}_{+}^3,0<I\le {\delta }_2,S>{\delta }_1\},\hfill \\ D_3=\{(S,I,Q)\in {\mathbb{R}}_{+}^3,0<Q\le {\delta }_3,I>{\delta }_2\},D_4=\{(S,I,Q)\in {\mathbb{R}}_{+}^3,S\ge \frac{1}{{\delta }_4}\},\hfill \\ D_5=\{(S,I,Q)\in {\mathbb{R}}_{+}^3,I\ge \frac{1}{{\delta }_5}\},D6=\{(S,I,Q)\in {\mathbb{R}}_{+}^3,Q\ge \frac{1}{{\delta }_6}\}.\hfill \end{array}$$

Next, we shall prove that LV(S, I, Q) < 0 on ${\mathbb{R}}_{+}^3\setminus D$ which is the same as displaying it on the above-mentioned six regions.

Case 1. If (S, I, Q) ∈ D ₁, then by Eq. (24), we get

$$\begin{array}{c}{\displaystyle \mathcal{L}V\le -c_3{c}_4+c_1{c}_3\frac{\beta I}{N}+c_2{c}_3\frac{\sigma Q}{I}-\frac{\Lambda }{S}+\beta +2{\mu }_0+\frac{{\eta }_2^2+{\eta }_3^2}{2}+\mu }\hfill \\ {\displaystyle +\sigma +\Lambda -{\mu }_0(S+I+Q)-\frac{{\gamma }_{1}I}{Q}}\hfill \\ {\displaystyle \le c_1{c}_3\beta +c_2{c}_3\sigma +\beta +2{\mu }_0+\frac{{\eta }_2^2+{\eta }_3^2}{2}+\mu +\sigma +\Lambda -\frac{\Lambda }{S}}\hfill \\ {\displaystyle \le c_1{c}_3\beta +c_2{c}_3\sigma +\beta +2{\mu }_0+\frac{{\eta }_2^2+{\eta }_3^2}{2}+\mu +\sigma +\Lambda -\frac{\Lambda }{{\delta }_1}}\hfill \end{array}$$

We can choose a small constant δ ₁ > 0 in such a way that $c_1{c}_3\beta +c_2{c}_3\sigma +\beta +2{\mu }_0+\frac{{\eta }_2^2+{\eta }_3^2}{2}+\mu +\sigma +\Lambda -\frac{\Lambda }{{\delta }_1}\le 0$ so we can get $\mathcal{L}V<0$ for each (S, I, Q) ∈ D ₁.

Case 2. If (S, I, Q) ∈ D ₂, then from Eq. (24), we can obtain

$$\begin{array}{c}{\displaystyle \mathcal{L}V\le -c_3{c}_4+c_1{c}_3\frac{\beta I}{N}+c_2{c}_3\frac{\sigma Q}{I}-\frac{\Lambda }{S}+\beta +2{\mu }_0+\frac{{\eta }_2^2+{\eta }_3^2}{2}+\mu }\hfill \\ +\sigma +\Lambda -{\mu }_0(S+I+Q)-\frac{{\gamma }_{1}I}{Q}\hfill \\ {\displaystyle \le c_1{c}_3\beta \frac{I}{S}+c_2{c}_3\sigma +\beta +2{\mu }_0+\frac{{\eta }_2^2+{\eta }_3^2}{2}+\mu +\sigma +\Lambda -c_3{c}_4}\hfill \\ {\displaystyle \le c_1{c}_3\beta \frac{{\delta }_2}{{\delta }_1}+c_2{c}_3\sigma +\beta +2{\mu }_0+\frac{{\eta }_2^2+{\eta }_3^2}{2}+\mu +\sigma +\Lambda -c_3{c}_4.}\hfill \end{array}$$

Let ${\delta }_1^2={\delta }_2,$ we can select enough large c ₃ > 0 and as small as possible δ ₁ > 0 such that $c_1{c}_3\beta {\delta }_1+c_2{c}_3\sigma +\beta +2{\mu }_0+\frac{{\eta }_2^2+{\eta }_3^2}{2}+\mu +\sigma +\Lambda -c_3{c}_4\le 0,$ so we can get $\mathcal{L}V<0$ for any (S, I, Q) ∈ D ₂.

Case 3. If (S, I, Q) ∈ D ₃, then from Eq. (24), we can obtain

$$\begin{array}{c}{\displaystyle \mathcal{L}V\le -c_3{c}_4+c_1{c}_3\frac{\beta I}{N}+c_2{c}_3\frac{\sigma Q}{I}-\frac{\Lambda }{S}+\beta +2{\mu }_0+\frac{{\eta }_2^2+{\eta }_3^2}{2}}\hfill \\ {\displaystyle +\mu +\sigma +\Lambda -{\mu }_0(S+I+Q)-\frac{{\gamma }_{1}I}{Q}}\hfill \\ {\displaystyle \le c_1{c}_3\beta +c_2{c}_3\sigma +\beta +2{\mu }_0+\frac{{\eta }_2^2+{\eta }_3^2}{2}+\mu +\sigma +\Lambda -\frac{{\gamma }_{1}I}{Q}}\hfill \\ {\displaystyle \le c_1{c}_3\beta +c_2{c}_3\sigma +\beta +2{\mu }_0+\frac{{\eta }_2^2+{\eta }_3^2}{2}+\mu +\sigma +\Lambda -\frac{{\gamma }_1{\delta }_2}{{\delta }_3}.}\hfill \end{array}$$

By choosing small δ ₃ > 0 such that $c_1{c}_3\beta +c_2{c}_3\sigma +\beta +2{\mu }_0+\frac{{\eta }_2^2+{\eta }_3^2}{2}+\mu +\sigma +\Lambda -\frac{{\gamma }_1{\delta }_2}{{\delta }_3}\le 0,$ so we can get $\mathcal{L}V<0$ for each (S, I, Q) ∈ D ₃.

Case 4. If(S, I, Q) ∈ D ₄, from Eq. (24), we can obtain

$$\begin{array}{c}{\displaystyle \mathcal{L}V\le -c_3{c}_4+c_1{c}_3\frac{\beta I}{N}+c_2{c}_3\frac{\sigma Q}{I}-\frac{\Lambda }{S}+\beta +2{\mu }_0+\frac{{\eta }_2^2+{\eta }_3^2}{2}}\hfill \\ {\displaystyle +\mu +\sigma +\Lambda -{\mu }_0(S+I+Q)-\frac{{\gamma }_{1}I}{Q}}\hfill \\ {\displaystyle \le c_1{c}_3\beta +c_2{c}_3\sigma +\beta +2{\mu }_0+\frac{{\eta }_2^2+{\eta }_3^2}{2}+\mu +\sigma +\Lambda -{\mu }_{0}S}\hfill \\ {\displaystyle \le c_1{c}_3\beta +c_2{c}_3\sigma +\beta +2{\mu }_0+\frac{{\eta }_2^2+{\eta }_3^2}{2}+\mu +\sigma +\Lambda -\frac{{\mu }_0}{{\delta }_4}.}\hfill \end{array}$$

We can select enough small δ ₄ > 0 such that $c_1{c}_3\beta {\delta }_1+c_2{c}_3\sigma +\beta +2{\mu }_0+\frac{{\eta }_2^2+{\eta }_3^2}{2}+\mu +\sigma +\Lambda -\frac{{\mu }_0}{{\delta }_4}\le 0,$ so we can get $\mathcal{L}V<0$ for each (S, I, Q) ∈ D ₄.

Case 5. If (S, I, Q) ∈ D ₅, from Eq. (24), we can obtain

$$\begin{array}{c}{\displaystyle \mathcal{L}V\le -c_3{c}_4+c_1{c}_3\frac{\beta I}{N}+c_2{c}_3\frac{\sigma Q}{I}-\frac{\Lambda }{S}+\beta +2{\mu }_0+\frac{{\eta }_2^2+{\eta }_3^2}{2}}\hfill \\ {\displaystyle +\mu +\sigma +\Lambda -{\mu }_0(S+I+Q)-\frac{{\gamma }_{1}I}{Q}}\hfill \\ {\displaystyle \le c_1{c}_3\beta +c_2{c}_3\sigma +\beta +2{\mu }_0+\frac{{\eta }_2^2+{\eta }_3^2}{2}+\mu +\sigma +\Lambda -{\mu }_{0}I}\hfill \\ {\displaystyle \le c_1{c}_3\beta +c_2{c}_3\sigma +\beta +2{\mu }_0+\frac{{\eta }_2^2+{\eta }_3^2}{2}+\mu +\sigma +\Lambda -\frac{{\mu }_0}{{\delta }_5}.}\hfill \end{array}$$

We can choose sufficiently small δ ₅ > 0 such that $c_1{c}_3\beta {\delta }_1+c_2{c}_3\sigma +\beta +2{\mu }_0+\frac{{\eta }_2^2+{\eta }_3^2}{2}+\mu +\sigma +\Lambda -\frac{{\mu }_0}{{\delta }_5}\le 0,$ so we can get $\mathcal{L}V<0$ for any (S, I, Q) ∈ D ₅.

Case 6. If (S, I, Q) ∈ D ₆, from Eq. (24), we can obtain

$$\begin{array}{c}{\displaystyle \mathcal{L}V\le -c_3{c}_4+c_1{c}_3\frac{\beta I}{N}+c_2{c}_3\frac{\sigma Q}{I}-\frac{\Lambda }{S}+\beta +2{\mu }_0+\frac{{\eta }_2^2+{\eta }_3^2}{2}}\hfill \\ {\displaystyle +\mu +\sigma +\Lambda -{\mu }_0(S+I+Q)-\frac{{\gamma }_{1}I}{Q}}\hfill \\ {\displaystyle \le c_1{c}_3\beta +c_2{c}_3\sigma +\beta +2{\mu }_0+\frac{{\eta }_2^2+{\eta }_3^2}{2}+\mu +\sigma +\Lambda -{\mu }_{0}Q}\hfill \\ {\displaystyle \le c_1{c}_3\beta +c_2{c}_3\sigma +\beta +2{\mu }_0+\frac{{\eta }_2^2+{\eta }_3^2}{2}+\mu +\sigma +\Lambda -\frac{{\mu }_0}{{\delta }_6}.}\hfill \end{array}$$

We can choose sufficiently small δ ₆ > 0 such that $c_1{c}_3\beta {\delta }_1+c_2{c}_3\sigma +\beta +2{\mu }_0+\frac{{\eta }_2^2+{\eta }_3^2}{2}+\mu +\sigma +\Lambda -\frac{{\mu }_0}{{\delta }_6}\le 0,$ so we can get $\mathcal{L}V<0$ for any (S, I, Q) ∈ D ₆.

Thus, we reach to the conclusion that there exist a constant W > 0 such that

$$LV(S,I,Q)<-W<0\text{for}\text{all}(S,I,Q)\in {\mathbb{R}}_{+}^3\setminus D.$$

Hence

$$\begin{array}{c}{\displaystyle \mathit{dV}(S,I,Q)<-\mathit{Wdt}+[(c_3+1)S-(c_3{c}_1+1){\sigma }_1]d{B}_1\left(t\right)}\hfill \\ {\displaystyle +[(c_3+1)I-c_3{c}_2\sigma 2]d{B}_2\left(t\right)+[(c_3+1)R-{\sigma }_3]d{B}_3\left(t\right).}\hfill \end{array}$$ (25)

Assume that $(S\left(0\right),I\left(0\right),Q\left(0\right))=(x_1,x_2,x_3)=x\in {\mathbb{R}}_{+}^3\setminus D,$ and τ^x is that time at which a path starting from x reach to the set D,

$${\tau }_n=inf\{t:|X\left(t\right)|=n\}\text{and}{\tau }^{\left(n\right)}\left(t\right)=\min \{{\tau }^x,t,{\tau }_n\}.$$

Upon integration of both sides of the inequality (25) from zero to τ ⁽ⁿ⁾(t), taking expectation, and then by applying Dynkin’s formula, we obtain

$$\begin{array}{c}{\displaystyle \mathit{EV}(S\left({\tau }^{\left(n\right)}\left(t\right)\right),I\left({\tau }^{\left(n\right)}\left(t\right)\right),Q\left({\tau }^{\left(n\right)}\left(t\right)\right))V\left(x\right)}\hfill \\ {\displaystyle =E{\int }_0^{\tau \left(n\right)\left(t\right)}\mathit{LV}(S\left(u\right),I\left(u\right),Q\left(u\right))\mathit{du}}\hfill \\ {\displaystyle \le E{\int }_0^{\tau \left(n\right)\left(t\right)}-\mathit{Wdu}=-\mathit{WE}{\tau }^{\left(n\right)}\left(t\right).}\hfill \end{array}$$

Since V(x) is non-negative, therefore

$$E{\tau }^{\left(n\right)}\left(t\right)\le \frac{V\left(x\right)}{W}.$$

Following the proof of Theorem 3 we have $P\{{\tau }_e=\infty \}=1$. Alternatively, one can say that the system (1) is regular. Thus, if we let t → ∞ and n → ∞ then we have τ(n)(t) → τ^xalmost surely.

Accordingly, with the help of Fatou’s lemma we get

$$E{\tau }^{\left(n\right)}\left(t\right)\le \frac{V\left(x\right)}{W}<\infty$$

Obviously, sup _x ∈ K Eτ^x < ∞, where K being a compact subset of ${\mathbb{R}}_{+}^3$. It directly proves the condition (ii) of Lemma 3.

Moreover, the diffusion matrix for system (1) is given by

$$B=\left[\begin{array}{ccc}{\eta }_1^2{S}^2& 0& 0\\ 0& {\eta }_2^2{I}^2& 0\\ 0& 0& {\eta }_3^2{Q}^2\end{array}\right]$$

Choosing $M={\min }_{(S,I,Q)\in \overline{D}\in R_{+}^3}\{{\eta }_1^2{S}^2,{\eta }_2^2{I}^2,{\eta }_3^2{Q}^2\},$ we can obtain that

$$\sum _{i,j=1}^3{a}_{ij}(S,I,Q){\xi }_i{\xi }_j={\eta }_1^2{S}^2{\xi }_1^2+{\eta }_2^2{I}^2{\xi }_2^2+{\eta }_3^2{Q}^2{\xi }_3^2\ge M{\left|\xi \right|}^2,(S,I,Q)\in \overline{D},$$

$\xi =({\xi }_1,{\xi }_2,{\xi }_3)\in {\mathbb{R}}_{+}^3.$

It means, condition (1) of Lemma 3 also holds.

Concluding the above discussion, we can say that Lemma 3 guarantees that system (1) is ergodic as well as it has one and only one stationary distribution. Hence the proof, (Figs. 1 , 2 , 3 ). □

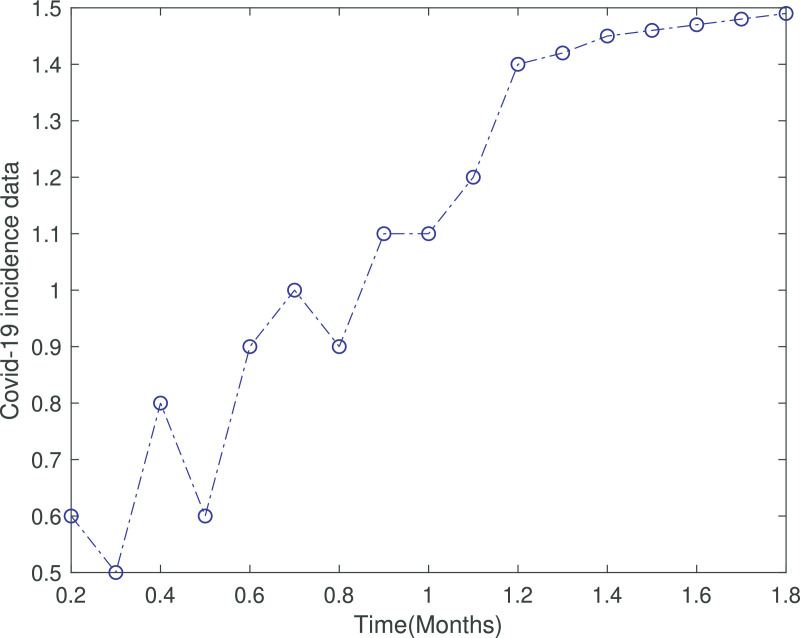
Fig. 1.

The incidence data of covid-19 from Khyber Pakhtunkhwa, Pakistan.

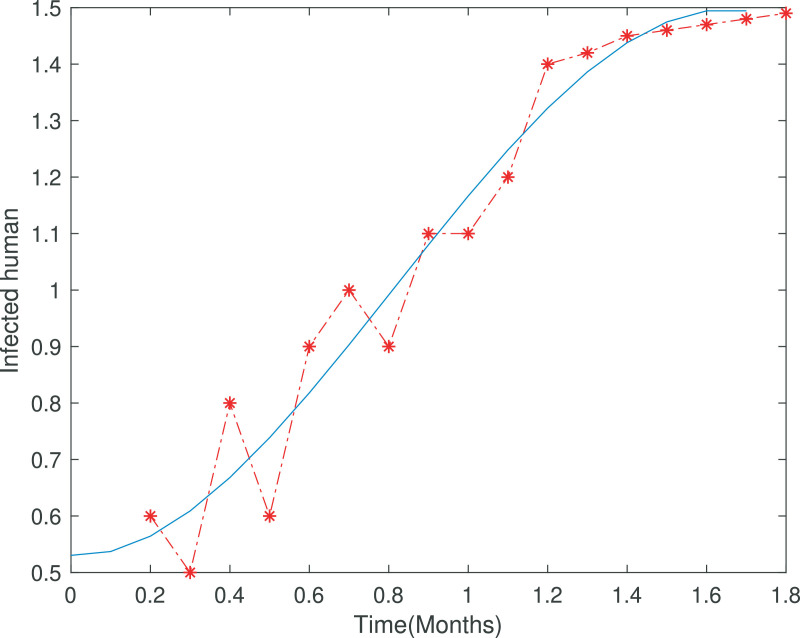
Fig. 2.

Covid-19 model comparison with real data of Khyber Pakhtunkhawa, Pakistan.

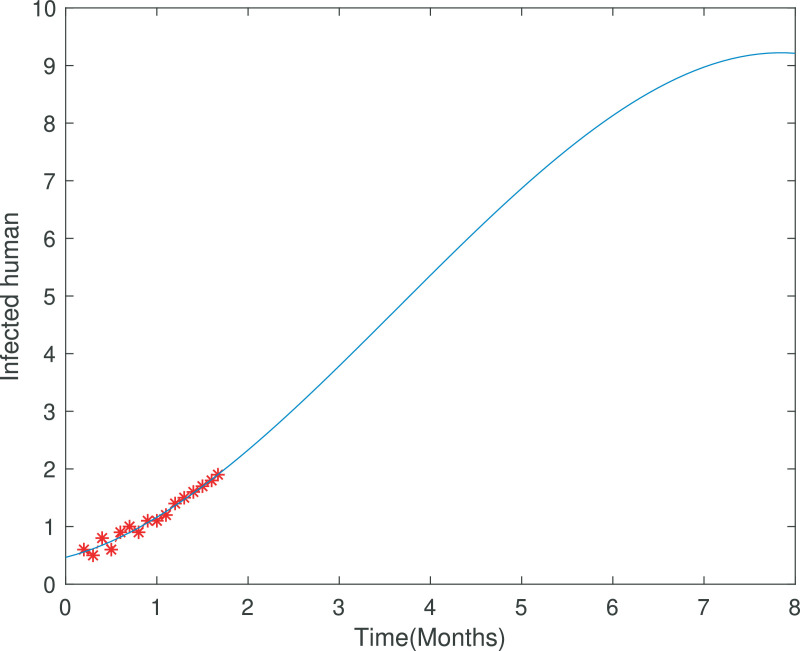
Fig. 3.

The incidence data of covid-19 from Khyber Pakhtunkhwa, Pakistan.

5.2. Extinction

Theorem 4

Assume that (S(t), I(t), Q(t)) be a solution of the developed COVID-19 model (1) along with initial data $(S\left(0\right),I\left(0\right),Q\left(0\right))\in {\mathbb{R}}_{+}^3,$ then $\lim su{p}_{t\to \infty }(S\left(t\right)+I\left(t\right)+Q\left(t\right))<\infty$ a.s. Further

$$\underset{t\to \infty }{\lim }\frac{S\left(t\right)}{t}=0,\underset{t\to \infty }{\lim }\frac{I\left(t\right)}{t}=0,\underset{t\to \infty }{\lim }\frac{Q\left(t\right)}{t}=0\text{a.s},$$

$$\begin{array}{c}\hfill \underset{t\to \infty }{\lim }\frac{\text{ln}S\left(t\right)}{t}=0,\underset{t\to \infty }{\lim }\frac{\text{ln}I\left(t\right)}{t}=0,\\ \hfill \underset{t\to \infty }{\lim }\frac{\text{ln}Q\left(t\right)}{t}=0\text{a.s}.\end{array}$$

and

$$\begin{array}{c}\hfill \underset{t\to \infty }{\lim }\frac{1}{t}{\int }_0^{t}S\left(u\right)d{B}_1\left(u\right)=0,\underset{t\to \infty }{\lim }\frac{{\int }_0^{t}I\left(u\right)d{B}_2\left(u\right)}{t}=0,\\ \hfill \underset{t\to \infty }{\lim }\frac{{\int }_0^{t}Q\left(u\right)d{B}_3\left(u\right)}{t}=0\text{a.s}.\end{array}$$ (26)

Proof

From the proposed model (1) we can write

$$\begin{array}{c}{\displaystyle d(S+I+Q)=\Lambda -{\mu }_0(S\left(t\right)+I\left(t\right)+Q\left(t\right))}\hfill \\ {\displaystyle -{\mu }_{1}I-\mu Q+{\eta }_1\mathit{Sd}{B}_1\left(t\right)+{\eta }_2\mathit{Id}{B}_2\left(t\right)+{\eta }_3\mathit{Qd}{B}_3\left(t\right).}\hfill \end{array}$$ (27)

The integration of both sides yields

$$\begin{array}{c}{\displaystyle S\left(t\right)+I\left(t\right)+Q\left(t\right)=\frac{\Lambda }{{\mu }_0}+(S\left(0\right)+Q\left(0\right)+I\left(0\right)-\frac{\Lambda }{{\mu }_0})e^{-{\mu }_{0}t}}\hfill \\ {\displaystyle -{\mu }_1{\int }_0^{t}I\left(u\right)e^{-{\mu }_0(t-u)}\mathit{dt}+{\eta }_1{\int }_0^{t}S\left(u\right)e^{-{\mu }_0(t-u)}d{B}_1\left(u\right)}\hfill \\ {\displaystyle +{\eta }_2{\int }_0^{t}I\left(u\right)e^{-{\mu }_0(t-u)}d{B}_2\left(u\right)+{\eta }_3{\int }_0^{t}Q\left(u\right)e^{-{\mu }_0(t-u)}d{B}_3\left(u\right)}\hfill \\ {\displaystyle -{\mu }_0{\int }_0^{t}Q\left(u\right)e^{-{\mu }_0(t-u)}\mathit{dt}\le \frac{\Lambda }{{\mu }_0}+(S\left(0\right)+Q\left(0\right)+I\left(0\right)-\frac{\Lambda }{{\mu }_0})e^{-{\mu }_{0}t}}\hfill \\ {\displaystyle +{\eta }_1{\int }_0^{t}S\left(u\right)e^{-{\mu }_0(t-u)}d{B}_1\left(u\right)+{\eta }_2{\int }_0^{t}I\left(u\right)e^{-{\mu }_0(t-u)}d{B}_2\left(u\right)}\hfill \\ {\displaystyle +{\eta }_3{\int }_0^{t}Q\left(u\right)e^{-{\mu }_0(t-u)}d{B}_3\left(u\right).}\hfill \end{array}$$ (28)

We define

$$X\left(t\right)=A\left(t\right)+M\left(t\right)-Q\left(t\right)+X\left(0\right),$$ (29)

where

$$\begin{array}{c}{\displaystyle X\left(0\right)=S\left(0\right)+Q\left(0\right)+I\left(0\right),}\hfill \\ {\displaystyle A\left(t\right)=\frac{\Lambda }{\mu }(1-e^{-{\mu }_{0}t}),}\hfill \\ {\displaystyle Q\left(t\right)=(S\left(0\right)+Q\left(0\right)+I\left(0\right))(1-e^{-{\mu }_{0}t}),}\hfill \\ {\displaystyle M\left(t\right)={\eta }_1\int S\left(u\right)e^{-{\mu }_0(t-u)}d{B}_1\left(u\right)+{\eta }_2{\int }_0^{t}S\left(u\right)e^{-{\mu }_0(t-u)}d{B}_2\left(u\right)}\hfill \\ {\displaystyle +{\eta }_3{\int }_0^{t}Q\left(u\right)e^{-{\mu }_0(t-u)}d{B}_3\left(u\right).}\hfill \end{array}$$ (30)

Clearly, M(t) is a continuous local martingale with $M\left(0\right)=0$. From relation (28), we have $S\left(t\right)+I\left(t\right)+Q\left(t\right)\le X\left(t\right)$ a.s. for all positive t. One can observe that Q(t) and A(t) are continuous adapted increasing processes on t ≥ 0 with $A\left(0\right)=Q\left(0\right),$ we get lim_t → ∞ X(t) ≤ ∞ a.s. Thus

$$\underset{t\to \infty }{\lim }\sup (S\left(t\right)+I\left(t\right)+Q\left(t\right))<\infty ,\text{a.s}.$$ (31)

Thus, Eq. (4) holds. Keeping in view relation (31), it is handy to show that

$$\underset{t\to \infty }{\lim }\frac{S\left(t\right)}{t}=0,\underset{t\to \infty }{\lim }\frac{I\left(t\right)}{t}=0,\underset{t\to \infty }{\lim }\frac{Q\left(t\right)}{t}=0\text{a.s},$$

$$\begin{array}{c}\hfill \underset{t\to \infty }{\lim }\frac{\text{ln}S\left(t\right)}{t}=0,\underset{t\to \infty }{\lim }\frac{\text{ln}I\left(t\right)}{t}=0,\\ \hfill \underset{t\to \infty }{\lim }\frac{\text{ln}Q\left(t\right)}{t}=0\text{a.s}.\end{array}$$

Setting

$$\begin{array}{ccc}& & M_1\left(t\right)={\int }_0^{t}S\left(u\right)d{B}_1\left(u\right),M_2\left(t\right)={\int }_0^{t}I\left(u\right)d{B}_3\left(u\right),\hfill \\ & & M_3\left(t\right)={\int }_0^{t}Q\left(u\right)d{B}_3\left(u\right).\hfill \end{array}$$

Because of the quadratic variation, we can write

$$<M_1\left(t\right),M_2\left(t\right)>={\int }_0^t{S}^2\left(u\right)du\le \left(su{p}_{t\ge 0}{S}^2\left(t\right)\right)t.$$ (32)

By using Lemma 1 (see for detail [16], [17], [18]) and (31), we get

$$\underset{t\to \infty }{\lim }\frac{{\int }_0^{t}S\left(u\right)d{B}_1\left(u\right)}{t}=0,\text{a.s}.$$

Similarly, we also get

$$\underset{t\to \infty }{\lim }\frac{{\int }_0^{t}I\left(u\right)d{B}_2\left(u\right)}{t}=0,\underset{t\to \infty }{\lim }\frac{{\int }_0^{t}Q\left(u\right)d{B}_3\left(u\right)}{t}=0,\text{a.s},$$

which proves Eq. (26) and hence the Lemma 4.1.

For the purpose of disease’ extinction, we have to state and prove the following theorem. □

Theorem 5

Suppose that (S(t), I(t), Q(t)) be a solution of the COVID-19 model (1) along with subsidiary conditions $(S\left(0\right),I\left(0\right),Q\left(0\right))\in {\mathcal{R}}_{+}^3$ . If a. ${\tilde{R}}_0^S=\frac{(\beta +\sigma )}{({\mu }_0+{\mu }_1+{\gamma }_1+\frac{{\eta }_2^2}{2})}<1,$ then

$$\underset{t\to \infty }{\lim }sup\left(\frac{\log I\left(t\right)}{t}\right)\le ({\mu }_0+{\mu }_1+{\gamma }_1)({\tilde{R}}_0^S-1)<0,$$

a.s., (I(t) approaches zero exponentially a.s., i.e., the COVID-19 infection will dies out from the community with unit probability). Moreover

$$\underset{t\to \infty }{\lim }〈S\left(t\right)〉=\frac{\Lambda }{{\mu }_0},\underset{t\to \infty }{\lim }〈Q\left(t\right)〉=0,a.s.$$ (33)

Proof

To prove the theorem, we shall apply direct integration to the proposed stochastic COVID-19 model (1). First of all, we will apply the $It\widehat{o}$ formula to the second equation of system (1)

$$d\text{ln}I\left(t\right)=[\frac{\beta SI}{N}-(\mu +{\mu }_1+{\gamma }_1)I+\sigma Q\left(t\right)]\frac{1}{I}dt-\frac{1}{2}{\eta }_2^{2}dt+{\eta }_{2}d{B}_2\left(t\right).$$ (34)

$$d\text{ln}I\left(t\right)=[\frac{\beta S}{N}-(\mu +{\mu }_1+{\gamma }_1)+\frac{\sigma Q\left(t\right)}{I}-\frac{1}{2}{\eta }_2^2]dt+{\eta }_{2}d{B}_2\left(t\right).$$ (35)

By integrating relation (35) from zero to t and dividing it by t leads to

$$\text{ln}I\left(t\right)-\text{ln}I\left(0\right)\le {\int }_0^t[\beta -({\mu }_0+{\gamma }_1+{\mu }_1+\frac{{\eta }_2^2}{2})+\sigma ]ds+{\eta }_2{B}_2\left(t\right),$$ (36)

$$\text{ln}I\left(t\right)-\text{ln}I\left(0\right)\le [(\beta +\sigma )-({\mu }_0+{\gamma }_1+{\mu }_1+\frac{{\eta }_2^2}{2})]t+{\eta }_2{B}_2\left(t\right),$$ (37)

$$\begin{array}{ccc}& & \text{ln}I\left(t\right)-\text{ln}I\left(0\right)\le ({\mu }_0+{\gamma }_1+{\mu }_1+\frac{{\eta }_2^2}{2})\hfill \\ & & \times [\frac{(\beta +\sigma )}{({\mu }_0+{\mu }_1+{\gamma }_1+\frac{{\eta }_2^2}{2})}-1]t+{\eta }_2{B}_2\left(t\right),\hfill \end{array}$$ (38)

$$\text{ln}I\left(t\right)-\text{ln}I\left(0\right)\le ({\mu }_0+{\gamma }_1+{\mu }_1+\frac{{\eta }_2^2}{2})[R_0^s-1]t+{\eta }_2{B}_2\left(t\right),$$ (39)

By using the theorem related to large number for local martingales, we obtain

$$\underset{t\to \infty }{\lim }\frac{B_2\left(t\right)}{t}=0\text{a.s.}$$

By taking the limit superior of both sides

$$\begin{array}{c}\hfill \underset{t\to \infty }{\lim }sup\frac{\text{ln}I\left(t\right)}{t}\le ({\mu }_0+{\gamma }_1+{\mu }_1+\frac{{\eta }_2^2}{2})({\tilde{R}}_0^S-1)\\ \hfill <0,\text{a.s.}\end{array}$$

It means that whenever ${\tilde{R}}_0^S<1,$ then

$$\underset{t\to \infty }{\lim }I\left(t\right)=0,\text{a.s.}$$

and

$$\underset{t\to \infty }{\lim }〈I\left(t\right)〉=0,\text{a.s.}$$

Now from the model (1)

$$\begin{array}{c}{\displaystyle \frac{1}{t}(S\left(t\right)-S\left(0\right))=\Lambda -\beta <\frac{S\left(t\right)I\left(t\right)}{N}>-{\mu }_0<S\left(t\right)>+\frac{{\eta }_1}{t}{\int }_0^t\mathit{Sd}{B}_1\left(s\right),}\hfill \\ {\displaystyle \frac{1}{t}(I\left(t\right)-I\left(0\right))=\beta <\frac{S\left(t\right)I\left(t\right)}{N}>-({\mu }_0+{\gamma }_1+{\mu }_1)<I\left(t\right)>}\hfill \\ {\displaystyle +\sigma <Q\left(t\right)>+\frac{{\eta }_2}{t}{\int }_0^t\mathit{Id}{B}_2\left(s\right),}\hfill \\ {\displaystyle \frac{1}{t}(Q\left(t\right)-Q\left(0\right))={\gamma }_1<I\left(t\right)>-({\mu }_0+\mu +\sigma )<Q\left(t\right)>+\frac{{\eta }_3}{t}{\int }_0^t\mathit{Qd}{B}_3\left(s\right).}\hfill \end{array}$$ (40)

Adding respective sides of equations (40), we get

$$\begin{array}{cc}& \frac{S\left(t\right)-S\left(0\right)}{t}+\frac{I\left(t\right)-I\left(0\right)}{t}+\frac{Q\left(t\right)-Q\left(0\right)}{t}\hfill \\ & =\Lambda -{\mu }_0<S\left(t\right)>-({\mu }_0+{\mu }_1)<I\left(t\right)>-({\mu }_0+\mu )<Q\left(t\right)>\hfill \\ & +\frac{{\eta }_1}{t}{\int }_0^{t}Sd{B}_1\left(s\right)+\frac{{\eta }_2}{t}{\int }_0^{t}Id{B}_2\left(s\right)+\frac{{\eta }_3}{t}{\int }_0^{t}Qd{B}_3\left(s\right).\hfill \end{array}$$ (41)

Calculation leads to

$$<S\left(t\right)>=\frac{\Lambda }{{\mu }_0}-\frac{{\mu }_0+{\mu }_1}{{\mu }_0}<I\left(t\right)>-\frac{{\mu }_0+\mu }{{\mu }_0}<Q\left(t\right)>+\varphi \left(t\right),$$ (42)

where

$$\begin{array}{cc}& \varphi \left(t\right)=\frac{1}{{\mu }_0}[-\frac{S\left(t\right)-S\left(0\right)}{t}-\frac{I\left(t\right)-I\left(0\right)}{t}-\frac{Q\left(t\right)-Q\left(0\right)}{t}\hfill \\ & +\frac{{\eta }_1}{t}{\int }_0^{t}Sd{B}_1\left(s\right)+\frac{{\eta }_2}{t}{\int }_0^{t}Id{B}_2\left(s\right)+\frac{{\eta }_3}{t}{\int }_0^{t}Qd{B}_3\left(s\right)].\hfill \end{array}$$ (43)

From the last equation of system (40) we have

$$\frac{Q\left(t\right)-Q\left(0\right)}{t}={\gamma }_1<I\left(t\right)>-({\mu }_0+\mu +\sigma )<Q\left(t\right)>+\frac{{\eta }_3}{t}{\int }_0^{t}Qd{B}_3\left(s\right),$$ (44)

which implies

$$<Q\left(t\right)>=\frac{1}{({\mu }_0+\mu +\sigma )}({\gamma }_1<I\left(t\right)>-\frac{Q\left(t\right)-Q\left(0\right)}{t}+\frac{{\eta }_3}{t}{\int }_0^{t}Qd{B}_3\left(s\right)),$$ (45)

we thus obtain

$$\underset{t\to \infty }{\lim }<Q\left(t\right)>=0\text{a.s},$$

consequently, (42) implies

$$\underset{t\to \infty }{\lim }<S\left(t\right)>=\frac{\Lambda }{{\mu }_0}\text{a.s}.$$

which proves the result. □

6. Case Study and Numerical simulation

6.1. Case study of Khyber Pakhtunkhwa, Pakistan

As other provinces of Pakistan, the Khyber Pakhtunkhawa province is also effected by covid-19 virus. So we fit our model to the real data of Khyber Pakhtunkhawa (Pakistan) covid-19 cases from 9th April to 2nd June 2020. We use Matlab minimization technique and consider the following initial value in which E(0) and Q(0) are estimated while the remaining values are taken from [24] and Table 1

$$\begin{array}{ccc}\hfill S\left(0\right)& =& 35,525,047,\hfill \\ \hfill E\left(0\right)& =& 15000,\hfill \\ \hfill I\left(0\right)& =& 10,485,\hfill \\ \hfill Q\left(0\right)& =& 18000,\hfill \\ \hfill R\left(0\right)& =& 2973.\hfill \end{array}$$

Table 1.

Parameters value

Notation	Value	References
Λ	0.028	[24]
β	0.2	Estimated
μ0	0.011	[24]
μ1	0.2	Estimated
γ	0.06	[24]
σ	0.3	Estimated
μ	0.5	[24]

In Figure 1 the total cases of covid-19 has been depicted from 9th April to 2nd June 2020, which becomes one month and 24 days. In Figure 2 we fitted the real data with the infected class of our covid-19 model which clearly shows the appropriateness of behavior of the infected class. Figure 3 shows long time behavior of the covid-19 cases vs time (months). We can see that the data is accurately fit to the model curve and further, one can observe that the cases with time on long term behavior grows exponentially. This case could be alarming that the incidence may increases further in the coming months if the government not applied the proper optimal strategies.

6.2. Numerical Simulation

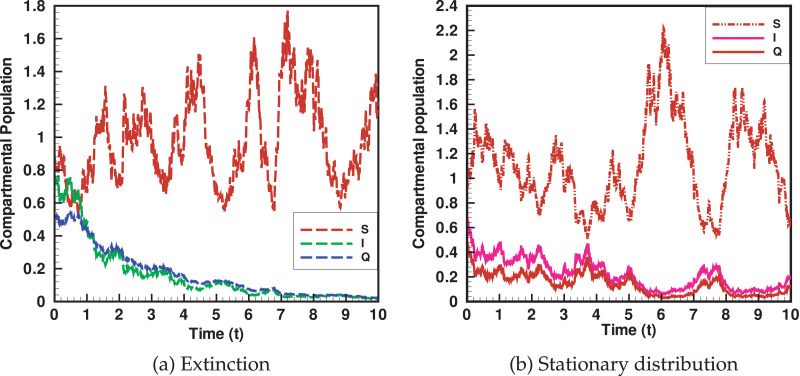
In the current section, we shall perform the numerical simulation of the developed coronavirus stochastic epidemic model. The well know stochastic Runge-Kutta (RK) method for the purposes of numerical findings will be used. This analysis will verify our derived analytical results and will show the influence and effect of noise intensity. We assume the numerical value of the parameters with biological feasibility to verify the extinction result are as: $\Lambda =0.3,$ $\beta =0.5,$ ${\mu }_0=0.2,$ ${\mu }_1=0.2,$ ${\gamma }_1=0.3,$ $\sigma =0.2,$ $\mu =0.1,$ while the numerical values for the intensity of white noise are supposed to be ${\eta }_1=0.5,$ ${\eta }_2=0.4$ and ${\eta }_3=0.2$. Moreover, we also assume some initial sizes of populations densities i.e., $\left(S\right(0)=0.9,I(0)=0.7,R(0)=0.5)$ and units of time 0-10. The long-term predictions and behavior of the model is presented in Fig. 4 . More, precisely Fig. 4a represent the dynamics of susceptible, infected and quarantined population. The dynamics of susceptible population is shown by red dashed line, while the infected with corona virus and quarantine are respectively represented by green dashed and blue dashed lines. Clearly we noted that the disease will extinct i.e., the infection of novel corona virus vanishes exponentially with increasing the value of white noise intensity. However there will be always susceptible population in the case of extinction. In a similar fashion, we assume the following parameter value and the strong effect of white noise to show the permanence or stationary distribution i.e., $\Lambda =0.5,$ ${\mu }_0=0.2,$ $\beta =0.6,$ ${\gamma }_1=0.3,$ ${\mu }_1=0.2,$ $\sigma =0.1,$ $\mu =0.2,$ ${\eta }_1=0.5,$ ${\eta }_3=0.7,$ and ${\eta }_2=0.6$ while the initial population sizes will be taken as above. The simulation carried out for this are presented in Fig. 4b. Again the three trajectories in Fig. 4b, which represent the dynamics of susceptible (red dashed), infected (purple solid) and quarantined population (red solid), which show that the model maintain the persistence i.e., there will be always susceptible, infected and quarantine individuals. Hence it could be noted from the simulation analysis that the white noise intensity have a great influence on the dynamics of the disease: as when the value of the white noise intensity increases the infection will decreases, while on the other hand if the value of the white noise intensity decrease, the infection will increases.

Fig. 4.

The graphical results show the extinction and stationary distribution of the COVID-19 epidemic.

7. Conclusion

The novel COVID-19 is one of the severe disease in the world and till today there is no proper treatment. It could be also noted that majority of real world phenomenon are not simply deterministic, and contain randomness. With the help of stochastic theory, we developed a model for the novel COVID-19 keeping in view the characteristic of the disease to investigate the transmission dynamics with changing population environment. By adopting the idea of stochastic Lyapunov functions theory, the existence and positivity are shown. We established a suitable stochastic Lyapunov function to perform the above activity. The extinction as well as the stationary distribution have been further discussed to find the conditions that how to extinct the disease. It could be noted that the there is a great influence of noise intensity on the COVID-19 transmission. Clearly it has been observed, that the extinction of COVID-19 infected individuals increases with increasing the noise strength, while decreases disease persisting. All the above analytical findings are supported graphically with the help of numerical simulation and therefore concluded that the work reveals stochastic analysis is a better approach to study the dynamics of infectious disease particularly novel COVID-19 etc, because there are many factor which varies time to time and place to place. In future, the model can be further extended by adding an exposed class. One can also fractionalize the model by using Atangana-Baleanu, Caputo or Caputo-Fabrizo operator. Not only this can but researcher may apply optimal control technique to minimize the infected people by choosing suitable optimal control variables.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.