On Restraints in End-Point Protein-Ligand Binding Free Energy Calculations

Abstract

The impact of harmonic restraints on protein heavy atoms and ligand atoms on end-point free energy calculations is systematically characterized for 54 protein-ligand complexes. We observe that stronger restraints reduce the equilibration time and statistical inefficiency, suppress conformational sampling, influence correlation with experiment, and monotonically decrease the estimated loss of entropy upon binding, leading to stronger estimated binding free energies in most systems. A statistical estimator that reweights for the biasing potential and includes data prior to the estimated equilibration time has the highest correlation with experiment. A spring constant of 20 cal mol⁻¹ Å⁻² maintains a near-native energy landscape and suppresses artifactual energy minima while minimally limiting thermal fluctuations about the crystal structure.

Graphical Abstract

The effect of varying spring constants of harmonic restraints on the configuration space sampling and end-point binding free energy estimates of 54 protein-ligand complexes is assessed.

INTRODUCTION

We systematically vary the spring constant for harmonic restraints on backbone heavy atoms and ligand atoms, finding that a spring constant of 20 cal mol⁻¹ Å⁻² maintains a near-native structure and suppresses artifactual energy minima while minimally limiting thermal fluctuations about the crystal structure and reducing end-point entropy estimates to a lesser extent than stronger restraints.

Noncovalent binding free energy calculations, which have wide applications in chemical biology and structure-based drug design, are an important objective in computational chemistry. From the standpoint of statistical mechanics, the most rigorous approaches to these calculations are alchemical pathway techniques¹. Alchemical pathway methods involve simulating a series of thermodynamic states between bound and unbound states. They are referred to as “alchemical” because intermediate states are not necessarily physically meaningful. In the unbound state, the species may either be physically separated or decoupled in a way such that they do not interact with each other. As reviewed by Mobley and Klimovich², many scientists including Roux et. al.^3–18 have contributed to developing both classes (decoupling or physical separation) of calculations. An accumulating number of examples^19–26 have demonstrated the ability of alchemical pathway methods to accurately reproduce experimental binding free energies and provide mechanistic insight into binding processes.

Because of the computational expense required to simulate alchemical pathways, methods based on simulating the end points — the bound (and sometimes unbound) states that bookend the pathway — are widely used in the molecular modeling community. We summarized the history of end-point methods in a recent article²⁷. Here, we will focus on variants of the most prominent approach: Molecular Mechanics/Poisson-Boltzmann Surface Area (MM/PBSA)^{28, 29}. In MM/PBSA, the enthalpy of binding is estimated using the average potential energy of the solvated species. MM/PBSA has multiple variants in which the potential energy is based on different force fields³⁰. The most popular of these is the Molecular Mechanics/Generalized Born Surface Area (MM/GBSA) method, which uses a faster continuum dielectric implicit solvent model.

In MM/PSBA and its variants, the average difference between the potential energy of the complex and individual binding partners is evaluated either from three independent trajectories or, more commonly, a single trajectory of the complex. These approaches are based on different theoretical principles. Calculations using a single trajectory are based on a first-order expansion of an exponential average²⁷. Unfortunately, the single-trajectory approach can often be statistically biased. Exponential averages of potential energy differences can suffer from finite-sample bias if the important configuration spaces of the sampled and targeted thermodynamic states do not overlap³¹. In the case of binding free energies, the bias occurs if the ensemble of conformations accessed by either partner significantly changes upon binding, a common situation in protein-ligand complexes. In contrast to the single-trajectory approach, the use of three independent trajectories is based on estimating absolute partition functions of each species^{28, 29}. Although the three-trajectory approach does not suffer from the same statistical bias, results are noisier and require a greater number of samples to apparently converge. Hence, there have been relatively few studies that employ the three-trajectory approach. For these reasons, the present contribution focuses on the single-trajectory approach.

Notable exceptions to the trend of using single trajectories are from the group of Peter Coveney, who has used sets of multiple short trajectories instead of a single long trajectory to compute binding free energies^32–34. Within a set of trajectories, each is initiated from the same starting configuration but with different initial velocities. Compared to using a single long trajectory, using a set of short trajectories improves the precision, reproducibility, and parallelizability of free energy calculations. As a drawback, short trajectories also limit structural sampling to the vicinity of the initial configuration³². In spite of this shortcoming, Coveney et al. have found that when using multiple short trajectories, free energy calculations based on independent sampling of the complex and of the binding partners outperform those based on sampling of the complex alone. For binding of 12 peptides to a major histocompatibility complex molecule, end-point binding free energy calculations based on three sets of trajectories were more strongly correlated with experiment than those based on a single set of trajectories³³. Wright et al.³⁴ recognized that when computing the binding free energy of multiple ligands to the same protein receptor, the average energy of the protein is constant. For both a diverse and congeneric set of ligands to the bromodomain-containing protein 4, they found that free energies computed with sets of trajectories for the ligand and the complex were better correlated with experiment than sets of trajectories for the complex alone³⁴.

In MM/PBSA and its variants, the entropy of binding is estimated via quasiharmonic or normal modes analysis. Unfortunately, both quasiharmonic and normal modes analysis are flawed ways to estimate entropy. Quasiharmonic analysis assumes that atomic fluctuations observed in a molecular dynamics simulation are a multivariate Gaussian resulting from a harmonic energy surface. Normal modes analysis also assumes that the energy landscape is harmonic, but spring constants are obtained from a Hessian matrix instead of inferred from observed samples. The assumptions underlying both methods fall short when degrees of freedom are coupled or the system samples multiple energy minima^{35, 36}. Additionally, normal modes analysis tends to be computationally expensive and numerically unstable^37–39. For these reasons, MM/PBSA calculations often entirely ignore entropy^{40, 41}.

Recently, alternate approaches to calculating the entropy of binding based on an exponential average⁴² or cumulant expansion²⁷ of the interaction energy have been introduced. In Menzer et al.²⁷, we showed that the MM/PBSA enthalpy estimate can be derived as the first order in a cumulant expansion and that entropy may be evaluated with higher-order terms. While the cumulant expansion has been applied in other types of free energy calculations⁴³, our paper was the first, to our knowledge, to apply it to absolute binding free energies and relate it with MM/PBSA. In contrast to normal modes analysis, these approaches consume trivial computing time beyond the simulation and post-processing required for standard MM/PBSA, are numerically stable, and improve (or at least do not deteriorate) correspondence with experiment. A limitation of these methods is that a larger number of samples is required to estimate second- or highe-rorder cumulants and exponential averages than to estimate the mean. For 200 ns of simulation, we found that a second-order cumulant expansion provided a good balance between statistical rigor and numerical stability.

In many of the simulations in Menzer et al.²⁷, sampling issues were exacerbated by motion of the ligand relative to the protein. Within 200 ns of unrestrained simulation starting from a crystal structure, the ligand often assumed a non-native pose or completely dissociated from the protein. Although spontaneous dissociation (and re-association) is expected over a long simulation, the relatively fast ligand motion observed was likely due to limitations of the force field. We found that correspondence with experimental binding free energies was improved by excluding snapshots in which the ligand root mean square deviation (RMSD) from the native pose is greater than 3 Å. Excluding non-native poses is likely helpful because they are unlikely to significantly contribute to the binding free energy. Excluding dissociated poses is essential because they are not part of the bound state.

Harmonic restraints have the potential to circumvent force field issues and improve sampling of near-native poses. Such restraints have yielded similar benefits in at least three previous studies. Raval et al.⁴⁴ assessed the ability of long all-atom molecular dynamics simulations to refine homology models. For 24 proteins selected from a structure prediction challenge, they performed at least 100 microseconds of three types of simulations: unrestrained, initiated from a homology model; unrestrained, initiated from the crystal structure; and restrained to the homology model. Unrestrained simulations initiated from homology models and crystal structures both generally drifted away from the native structure, a fact they attributed to force field (opposed to sampling) error. On the other hand, most of the weakly restrained simulations drew subtly closer to the respective crystallographic configuration. Xue and Skrynnikov⁴⁵ performed simulations of ubiquitin crystals without restraints and with harmonic restraints applied to the ensemble-average structure. They found that the latter led to better reproduction of crystallographic temperature factors and solid-state NMR spectroscopy parameters. Finally, Wall et al.⁴⁶ performed unrestrained and restrained simulations of endoglucanase crystals. The restrained simulations were much more successful at recovering crystallographic positions of solvent.

Apropos to the topic of this paper, harmonic restraints are beneficial to and are routinely used in alchemical pathways for computing binding free energies. In pathways where species are physically separated, harmonic restraints are placed on the distance between binding partners^{6, 47–50}. In both physical separation and decoupling pathways, restraints are usually also placed on the orientation and position of the ligand relative to the protein^{3, 4, 6–8, 13–16, 20, 51–54}. The free energy of imposing restraints on external degrees of freedom (translation and rotation of the ligand) can be computed analytically or by a fast numerical quadrature. The effects of other restraints are removed before the end points of the pathways such that they do not affect binding free energy estimates. These restraints are beneficial because they limit the configuration space of intermediate states, simplifying sampling and reducing equilibration and autocorrelation times within the reduced space.

While restraints can maintain near-native configurations and improve sampling within a reduced configuration space, it is not obvious, a priori, how they should be applied to end-point binding free energy calculations. First, it is not clear which atoms they should be applied to. They could be applied to all protein atoms, protein heavy atoms, backbone atoms, or only α carbons. They could be applied to all ligand atoms or simply to the center of mass. Moreover, it is unclear what spring constant should be used. In an alchemical pathway, multiple thermodynamic states with different restraint levels may be used to release a strong restraint. In an end-point calculation, an excessively strong restraint can truncate the accessible configuration space. For example, in Figure 1, adding a restraint with a spring constant of 2 kcal mol⁻¹ Å⁻² will likely prevent a simulation from accessing the two free energy minima within a reasonable amount of sampling. On the other extreme, a restraint with a spring constant of 2 cal mol⁻¹ Å⁻² will have little influence on the simulation whatsoever. Therefore, spring constants should be selected to balance sampling near a desired configuration with the ability to explore relevant configuration space.

Figure 1:

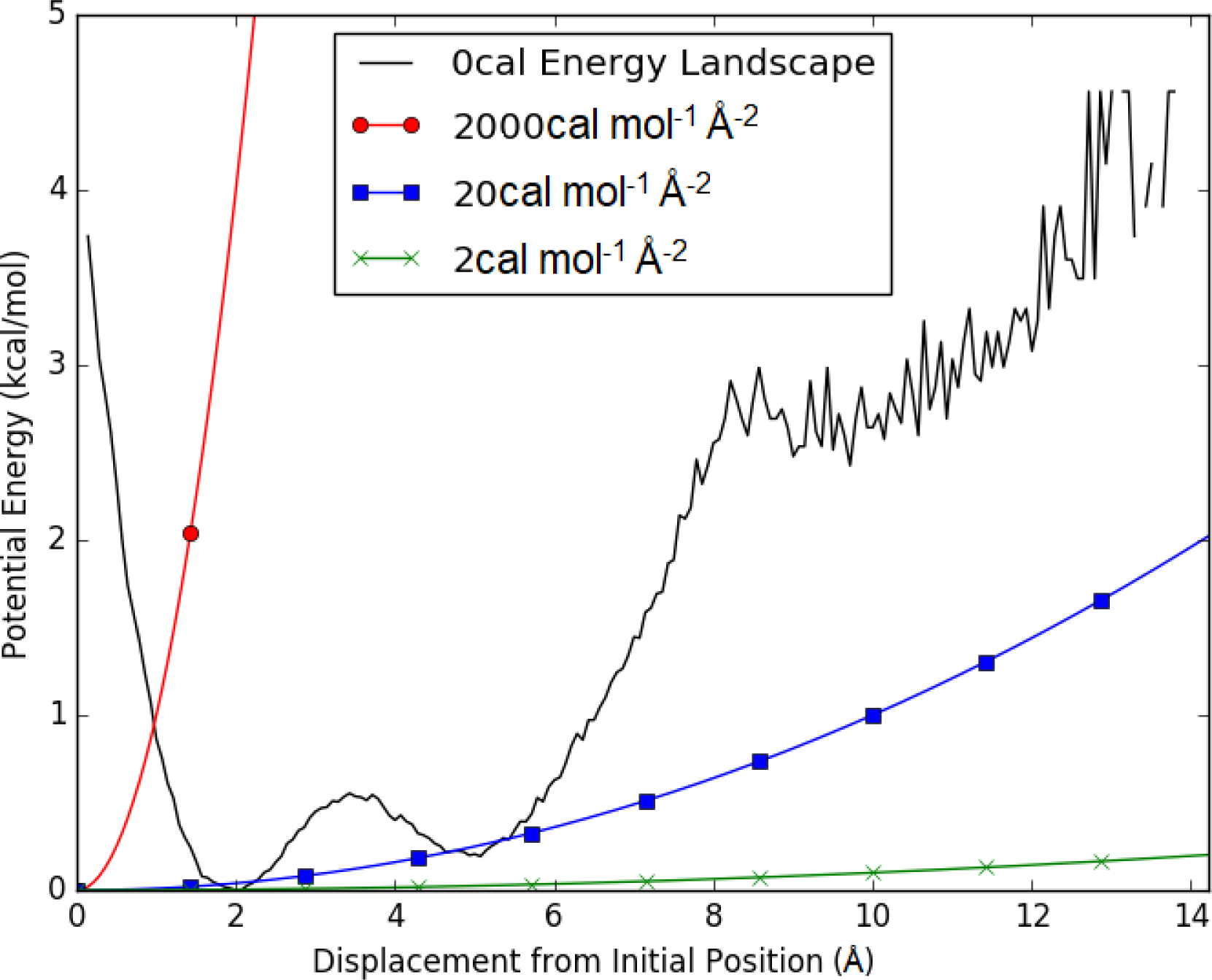
Free energy as a function of displacement from the initial position (black). The displacement is of the second α carbon from an unrestrained simulation based on 4mr4⁵⁵ from the Protein Data Bank. For comparison, the potential energy of harmonic restraints with a spring constant of 2 (green x), 20 (blue squares), and 2000 (red circles) cal mol⁻¹ Ų is shown.

Unfortunately, most of the scientific literature does not provide clear guidance on how to apply harmonic restraints. More often than not, choices of restrained atoms and spring constants are treated as minor technical details that are stated without justification. These choices vary widely across different papers. On the weak end, Raval et al.⁴⁴ used a spring constant of 70 cal mol⁻¹ Å⁻² to restrain α carbon atoms within secondary structure elements to their positions in low-resolution homology models. Wall et al.⁴⁶ used a stronger spring constant of 0.5 kcal mol⁻¹ Å⁻² to restraint protein heavy atoms and all ligand atoms to their crystallographic positions. In a series of simulations used to build a Markov state model of an enzyme-inhibitor binding process, Buch et al.⁵⁶ applied a harmonic restraint of 1 kcal mol⁻¹ Å⁻² to α carbon atoms farther than 9 Å from the binding pocket. In their end-point binding free energy calculations, Duan et al.⁴² used an even stronger spring constant of 10 kcal mol⁻¹ Å⁻² to restrain all atoms.

An important precedent for the principled selection of spring constants was provided by Hamelberg and McCammon⁵². Hamelberg and McCammon⁵² performed alchemical binding free energy calculations of water to two protein-ligand complexes. To determine parameters for a harmonic potential restraining water to the binding site, they simulated the complex and observed fluctuations of the water’s oxygen atom. They subsequently selected spring constants that, according to the equipartition theorem, would reproduce the observed fluctuations. The spring constants were 6.6 kcal mol⁻¹ Å⁻² for a complex of trypsin and benzyldiamine complex and 16.4 kcal mol⁻¹ Å⁻² for a complex of HIV-1 protease and its inhibitor KNI-272.

The equipartition theorem can also inform the selection of spring constants in our more general calculations. The theorem specifies that any degree of freedom with a quadratic energy function has an average energy of $\frac{1}{2}{k}_{B}T$. A harmonic restraint has the form $\frac{1}{2}K{d}^2$, where K is the spring constant and d is the displacement from the restraint center. Hence, if the energy for a displacement from a restraint center is described solely by the restraint, then the root mean square displacement is $\sqrt{\langle d^2\rangle }=\sqrt{\frac{k_{B}T}{K}}$. When K is 0.2, 2, 20, 200, and 2000 cal mol⁻¹ Å⁻², the corresponding $\sqrt{\langle d^2\rangle }$ are 54.6, 17.3, 5.5, 1.7, and 0.5 Å, respectively. Since the system includes other energy terms, equipartition only provides a reasonable estimate of thermal fluctuations in d for the strongest restraints.

In X-ray crystal structures, the extent of thermal fluctuations may be inferred from Debye-Waller factors (also known as B values). The B value of a particular atom is based on thermal fluctuations, experimental error, model error, and lattice error. For well-solved structures, model error will likely contribute very little to B values. While experimental error is impossible to completely discount, structures with small R Merge values will also have small experimental error. Furthermore, when considering protein backbone atoms, the contribution from lattice error is expected to be very low. Thus, by converting B values to spherical fluctuations, a good approximation to thermal fluctuations can be obtained: $\langle d^2\rangle =B/\left(\frac{8}{3}{\pi }^2\right)$ (c.f. Bahar et al.⁵⁷).

As a representative example, consider a structure in the Protein Data Bank: 3mxf⁵⁵. B values for protein backbone atoms are generally between 5 and 20 Ų, with the mean being 9.2 Ų. Thus, we can estimate that under crystallographic conditions, where the temperature is approximately 90 K, $\sqrt{\langle d^2\rangle }$ is generally between 0.44 and 0.87 Å. Assuming that fluctuations are described by a quadratic energy, and scaling them according to the equipartition theorem, $\sqrt{\langle d^2\rangle }$ at 300 K should be between 0.80 and 1.6 Å. Hence, restraints of 2 kcal mol⁻¹ Å⁻² are likely to suppress thermal fluctuations of at least some atoms in the crystal structure. They may have an even more significant effect on fluctuations in solution, which are presumably larger.

In this work, we systematically assess the effects of varying the spring constant from 0.2 to 2000 cal mol⁻¹ Å⁻². Restraints were applied to protein backbone heavy atoms and ligand atoms, a selection that allows side chains to relax. Simulations were performed on 54 protein-ligand complexes that make up a significant subset of systems from Menzer et al.²⁷. All of the systems have both crystal structures and binding affinity data publicly available. Subsequently, they were analyzed to better understand how the spring constant affects the equilibration time and statistical inefficiency, the conformational sampling, the estimated entropy and free energy of binding, and the accuracy of binding free energy estimates compared to experimental data.

METHODS

System Preparation

We performed simulations with most of the systems from Menzer et al.²⁷: eight complexes with the first bromodomain of human bromodomain-containing protein 4 (bromodomains); seven complexes with human phenylethanolamine N-methyltransferase (hPNMT); nine complexes with lysozyme L99A (lysozyme); 17 complexes with mitogen-activated protein kinase kinase kinase kinase 4 (MAP4K4); and 13 complexes from the interaction entropy (IE) data set⁴². The farnesoid X receptor (FXR) data set was excluded because of its high computational cost and poor performance in Menzer et al.²⁷.

Due to the inability to prepare two systems - MAP07 from MAP4K4 and 4dew from IE - using the methods described below, they were excluded from the current study. In these systems there were problems with the file containing the parameters and topology. In both cases remedies were not pursued so as to preserve the consistency of system preparation.

Models were prepared for simulation using the same procedure as in Menzer et al.²⁷, except that protein parameters were from the AMBER⁵⁸ ff14SB (instead of ff14SB.redq) force field. Some key details are that residue protonation and disulfide bond formation was predicted and assigned using PROPKA 3.0^{59, 60} with a pH value of 7.0, as implemented in PDB2PQR 1.9.0⁶¹. The mbondi2 option was used to set atomic radii. Ligands were parametrized with the generalized AMBER force field 2 (leaprc.gaff2)⁶², with AM1BCC^{63, 64} partial charges. Solvent was modeled with OBC2⁶⁵ generalized Born surface area implicit solvent⁶⁶ with a solvent dielectric of 78.5. No cutoffs were used.

Molecular Dynamics Simulation

Seven molecular dynamics simulations were performed for every complex. In one of the simulations, the system was unrestrained. In five others, harmonic restraints were applied to protein backbone heavy atoms and all ligand atoms. The restraint potential was,

$$U_b\left(x,y,z\right)=\frac{K}{2}\left[{\left(x-x_o\right)}^2+{\left(y-y_o\right)}^2+{\left(z-z_o\right)}^2\right]$$ (1)

where K is the spring constant, x_o, y_o, and z_o are the initial x, y, and z positions of each restrained atom, respectively, and x, y, and z are the positions of the atom in the current frame. The spring constants used were K ∈ {0.2, 2, 20, 200, 2000} cal mol⁻¹ Å⁻². Lastly, to compare the convergence when restraints are placed on different atoms, one set of simulations was performed using harmonic restraints with a spring constant of 20 cal mol⁻¹ Å⁻² on all heavy atoms (opposed to heavy atoms in the protein backbone).

Simulations were performed using OpenMM 7.0^{67, 68}. First, systems were minimized for 500 steps without restraints. Then, Langevin dynamics was performed at 300 K with a time step of 2 fs and constraints on bonds involving hydrogen. Restrained simulations were conducted for 50 ns and unrestrained simulations for 200 ns. Harmonic restraints towards the initial positions were implemented with the CustomExternalForce class in OpenMM. Energies were recorded every 2 ps.

Equilibration Detection

The equilibration time and statistical inefficiency of the MD simulations was calculated using the procedure introduced by Chodera et al.⁶⁹. This procedure is based on the effective sample size N_eff = N/g, where N is the number of correlated samples, g = 1 + 2τ_ac is the statistical inefficiency, and τ_ac is the integrated autocorrelation time. For a simulation of length T, the effective sample size for the last T − t_o correlated samples is estimated for various proposed equilibration times, t_o. The equilibration time is the value of t_o that maximizes the effective sample size, $t_o^{*}$, and the statistical inefficiency is the estimate of g at $t_o^{*}$. We used the implementation of the method in detectEquilibration from the timeseries module of pymbar⁷⁰ to analyze the time series of the total potential energy. We chose nskip = 10 and N_eff was estimated every 1 ns of simulation.

Conformational Clustering

To facilitate conformational clustering, MD trajectories were analyzed with principal components analysis (PCA). Trajectory files from all six simulations of each protein-ligand system were concatenated with catdcd⁷¹. Using MDTraj⁷² 1.7.2, snapshots were aligned to minimize the RMSD of all atoms with the first frame. Eigenvalues and eigenvectors of the covariance matrix for all atoms were calculated with ProDy⁷³ 1.8.2.

Snapshots from simulations of every protein-ligand system were clustered using the algorithm described by Rodriguez and Laio⁷⁴. In this algorithm, clusters are defined based on the density of every point. The density of a point is based on how many neighbors — points located within a specified distance cutoff — it has. A cluster center must have a higher density than its neighbors and must be at least a minimum distance away from a point of equal or higher density. Distance matrices were calculated based on the RMSD between all protein α carbons for every pair of frames in combined trajectories. Distance cutoffs were selected such that the average point in the unrestrained simulation was considered to be a neighbor of 1.5% of other points in the unrestrained simulation. The minimum density was set at 100 and minimum distance between cluster centers was set at 1.5 times the distance cutoff. This clustering algorithm has the advantage of grouping together conformations regardless of the cluster shape.

Binding Free Energy Estimation

After simulation, separate trajectories of the ligand and receptor were prepared using VMD 1.9.1⁷⁵. Potential energies for the complex, receptor, and ligand were evaluated with OpenMM 7.0^{67, 68} using the same force field as in the simulation.

Binding free energies were calculated based on trajectories of the complex (single-trajectory mode) using variations of the statistical estimators described in Menzer et al.²⁷. Specifically, we calculated binding free energies: (1) with and without reweighting based on the biasing potential; (2) either discarding or retaining an initial period; (3) with and without a ligand RMSD cutoff of 3 Å; (4) with a first- to fourth-order cumulant expansion or an exponential average. Because they were found to be ineffective in Menzer et al.²⁷, we did not consider an external entropy correction nor normal modes analysis to estimate configurational entropy.

Before describing modifications to the statistical estimators in Menzer et al.²⁷ to account for harmonic restraints, we will introduce some key notation and equations. The noncovalent binding of a receptor, R, and ligand, L, to form a complex, RL, is described by the chemical equation L + R ⟷ RL. The standard binding free energy, $G_{RL}^{\circ }$, is defined as,

$$\Delta G_{RL}^{\circ }=-k_{B}T\text{ln}\left(\frac{C^{\circ }{C}_{RL}}{C_R{C}_L}\right),$$ (2)

in which k_B is Boltzmann’s constant and T is the temperature in Kelvin. C_X is the equilibrium concentration of the species X ∈ {R, L, RL} and C° = 1 M is the standard concentration. The standard binding free energy can be calculated from the free energy of restricting the ligand into the binding site, ΔG_ξ, and of coupling the ligand in the binding site to the receptor, $\Delta G_{RL}^s,\Delta G_{RL}^{°}=\Delta G_{RL}^s+\Delta G_{\xi }$. According to Equation (15) of Menzer et al.²⁷, $\Delta G_{RL}^s$ may be computed by an exponential average,

$$\Delta G_{RL}^s=k_{B}T\text{ln}{\langle e^{\beta \Psi \left(r_{RL}\right)}\rangle }_{RL}$$ (3)

where Ψ(r_RL) = U(r_RL)−U(r_R)−U(r_L) is the interaction energy between the receptor and ligand. r_X for X ∈ {R, L, RL} is the conformation of the species. U(·) is the potential energy of the species, including the solvation free energy, which may be based on a continuum dielectric implicit solvent model. The angular brackets 〈…〉_RL denote an ensemble average of the unbiased complex in implicit solvent.

Because exponential averages may be numerically unstable, it can be helpful to estimate $\Delta G_{RL}^s$ via a cumulant expansion, a power series in β⁴³. As previously described in Equation (16) of Menzer et al.²⁷, the third-order cumulant expansion of Equation (3) is,

$$\Delta G_{RL}^s={\langle \Psi \rangle }_{RL}+\frac{\beta }{2!}{\langle \delta {\Psi }^2\rangle }_{RL}+\frac{{\beta }^2}{3!}{\langle \delta {\Psi }^3\rangle }_{RL},$$ (4)

where Ψ ≡ Ψ(r_RL) and δΨ ≡ Ψ(r_RL) −〈Ψ(r_RL)〉 are used within the brackets for convenience of notation. Assuming that the pressure and volume change negligibly upon ligand binding, the mean interaction energy 〈Ψ〉_RL, which is the first-order cumulant, can be equated with the enthalpy of binding. Higher-order cumulants are estimates of the entropy.

Computing $\Delta G_{RL}^s$ from biased simulations of the complex in implicit solvent is an example of importance sampling. Specifically, Equation (3) may be written as,

$$\begin{gathered} \Delta G_{RL}^s=k_{B}T\text{ln}{〈e^{\beta \Psi \left(r_{RL}\right)}〉}_{RL} \\ =\frac{\int e^{\beta \Psi \left(r_{RL}\right)}{e}^{-\beta \left[U_b\left(r_{RL}\right)-U_b\left(r_{RL}\right)\right]}{e}^{-\beta U\left(r_{RL}\right)}d{r}_{RL}}{\int e^{-\beta \left[U_b\left(r_{RL}\right)-U_b\left(r_{RL}\right)\right]}{e}^{-\beta U\left(r_{RL}\right)}d{r}_{RL}} \\ =k_{B}T\text{ln}\frac{{〈e^{\beta \left[\Psi \left(r_{RL}\right)+U_b\left(r_{RL}\right)\right]}〉}_{RL,b}}{{〈e^{+\beta U_b\left(r_{RL}\right)}〉}_{RL,b}} \end{gathered}$$ (5)

where U_b(r_RL) is the biasing potential on the configuration and the angular brackets 〈…〉_{RL, b} denote an ensemble average of the biased complex in implicit solvent. Both of the expectation values in Equation (5) may be expressed as cumulant expansions. If they are both expanded to the first order, 〈U_b(r_RL)〉_{RL, b} cancels out and the free energy estimate is simply 〈Ψ〉_{RL, b}. Higher-order cumulants lead to expressions distinct from Equation (4).

We also calculated binding free energies based on including or excluding an initial period. The initial period was the smaller of the equilibration time determined by pymbar^{70, 76} or half of the included frames. (If the ligand RMSD cutoff was used, the included frames were those within the cutoff. Otherwise, they were all the frames.) This alternate initial period ensures that even if the equilibration period is long, there is an adequate number of samples available for the free energy calculation.

In addition to the end-point binding free energy calculations, we also estimated the binding free energy based on the interaction energy in a single minimized structure of the complex. Minimization was performed using simulation.minimizeEnergy() with default parameters in the python API for OpenmM 7.0^{67, 68}.

RESULTS

Stronger restraints reduce equilibration time and statistical inefficiency and accelerate convergence

Across all the data sets, the estimated equilibration time is highly dependent on the spring constant (Figure 2). With a spring constant of 20 cal mol⁻¹ Å⁻² or less, most of the estimated equilibration times are a large fraction of the simulation length. In general, as the spring constant is increased, the estimated equilibration time consumes a smaller fraction of the trajectory. At a spring constant of 20 cal mol⁻¹ Å⁻², the estimated equilibration time still consumes the majority of the simulation time in most systems, but in many cases it is significantly shorter. With a spring constant of 2 kcal mol⁻¹ Å⁻², equilibration is almost always very rapid, rarely requiring over 0.1 of the simulation length.

Figure 2:

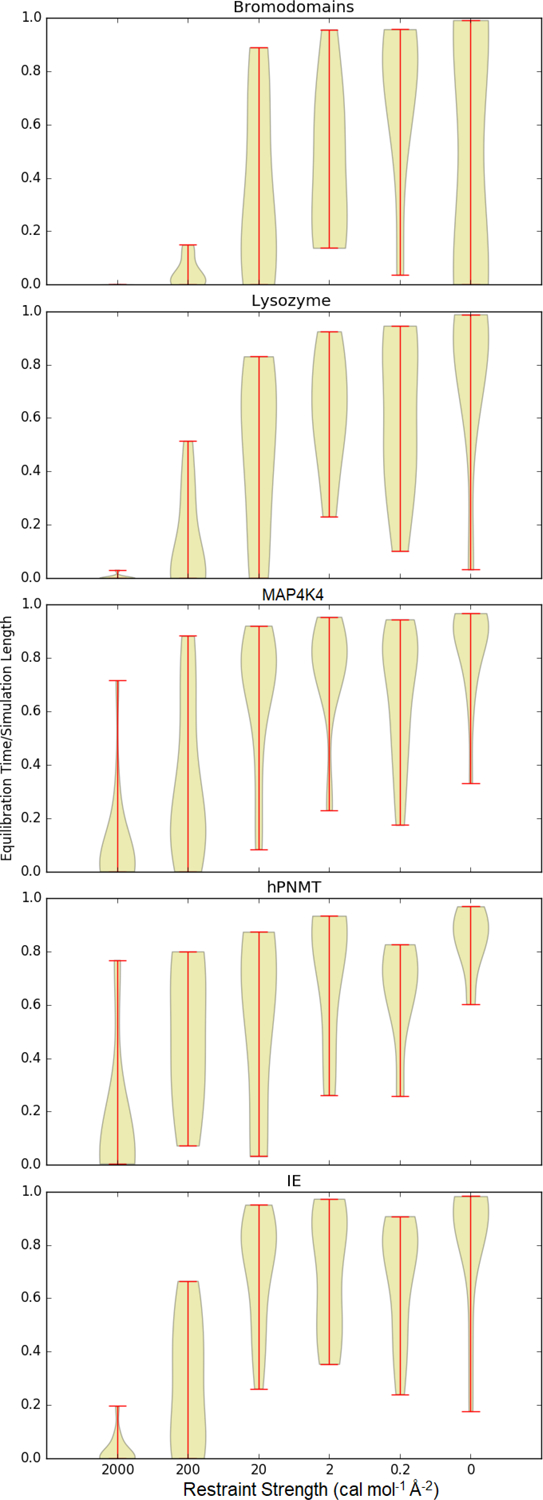
Equilibration times for each system at each spring constant, as a fraction of the total simulation length. This figure is a violin plot, in which the thickness of the colored region is proportional to the number of systems and ends of the lines indicate the range of observations.

The statistical inefficiency is also reduced by a larger spring constant (Figure 3). Overall, the statistical inefficiency is largest for the unrestrained simulation. Many unrestrained simulations of the bromodomains have particularly high statistical inefficiency. The general trend across data sets is that statistical inefficiency gradually decreases as restraints are strengthened. At a spring constant of 2 kcal mol⁻¹ Å⁻², nearly every sample can be considered independent.

Figure 3:

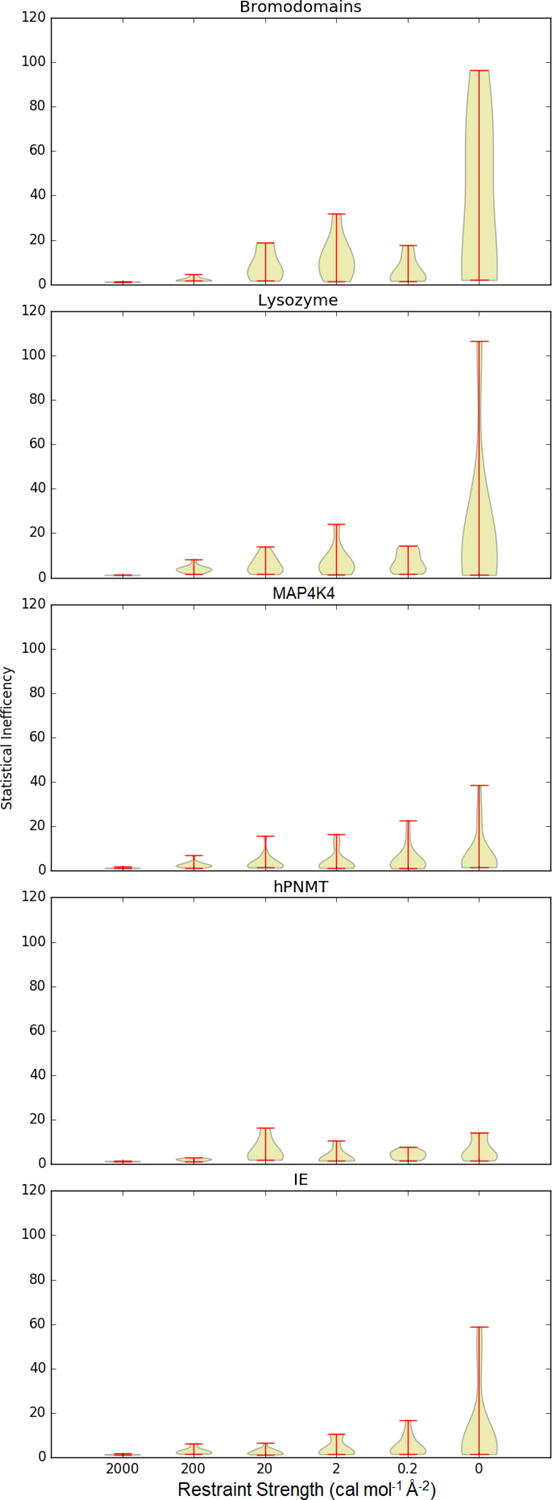
Statistical inefficiency for each system at each spring constant.

Finally, stronger restraints also affect convergence to the final free energy estimate (Figures S1, S2, S3, S4, and S5 of the Supplementary Material.) For spring constants of 20 cal mol⁻¹ Å⁻² and stronger, the root mean square error (RMSE) of the first- and second-order cumulant expansions and exponential average with respect to the final value after 20 ns is within 1 kcal/mol for most and 2 kcal/mol for nearly all data sets. For weaker restraints, the RMSE is often but not always higher after a longer simulation time. The first-order cumulant expansion is more numerically stable than the second-order cumulant expansion and the exponential average, where the RMSE fluctuates more significantly as a function of simulation time. Surprisingly, applying harmonic restraints to all heavy atoms, opposed to backbone heavy atoms, does not accelerate simulation convergence (Figure S6 of the Supplementary Material).

Sufficiently strong restraints suppress configuration space sampling

The RMSD of the protein backbone relative to the crystal structure indicates the extent to which configuration space sampling is suppressed by harmonic restraints (Figure 4). As the spring constant is reduced, the harmonic restraint has a less important role in dictating the observed fluctuations. With at spring constant of 2000 cal mol⁻¹ Å⁻², all the values are only slightly less than 0.5 Å, the RMSD predicted based on the equipartition theorem if the harmonic restraint is the only potential energy term. At 200 cal mol⁻¹ Å⁻² and weaker restraints, the RMSD is significantly less than the equipartition estimate, indicating that other potential energy terms also play an important role in determining the extent of fluctuations. With the restraint of 0.2 cal mol⁻¹ Å⁻², the observed range in RMSD is comparable to the unrestrained simulation, but the mode is lower, at around 2.0 instead of 2.5 Å.

Figure 4: Average RMSD of protein backbone atoms relative to the crystal structure at different restraint strengths.

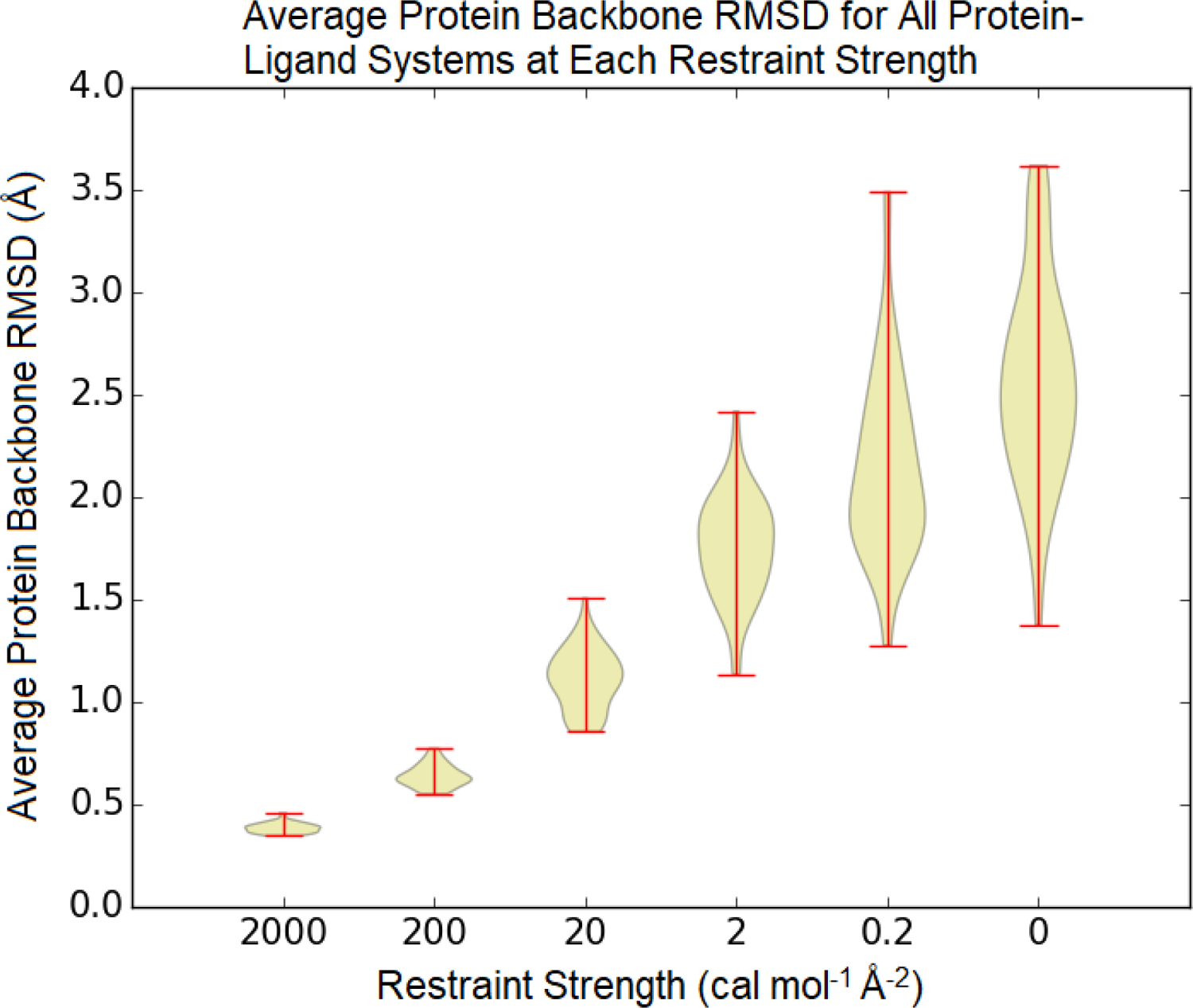
The average was computed based on snapshots after the estimated equilibration time.

Configuration space sampling was also evaluated by the number of clusters (according to the first two principal components) accessed during the simulations (Figure 5). The unrestrained simulations (which are 200 ns long) access the greatest number of clusters. Simulations with restraint of 0.2 cal mol⁻¹ Å⁻² (which are 50 ns long) access slightly fewer clusters. The number of clusters is further reduced as the spring constant is increased from 0.2 and 2 cal mol⁻¹ Å⁻². At spring constants of 20 cal mol⁻¹ Å⁻² and stronger, simulations only access a single cluster. In the majority of cases, the clusters occupied by tightly restrained simulations are a subset of the clusters occupied by the less restrained and unrestrained simulations.

Figure 5:

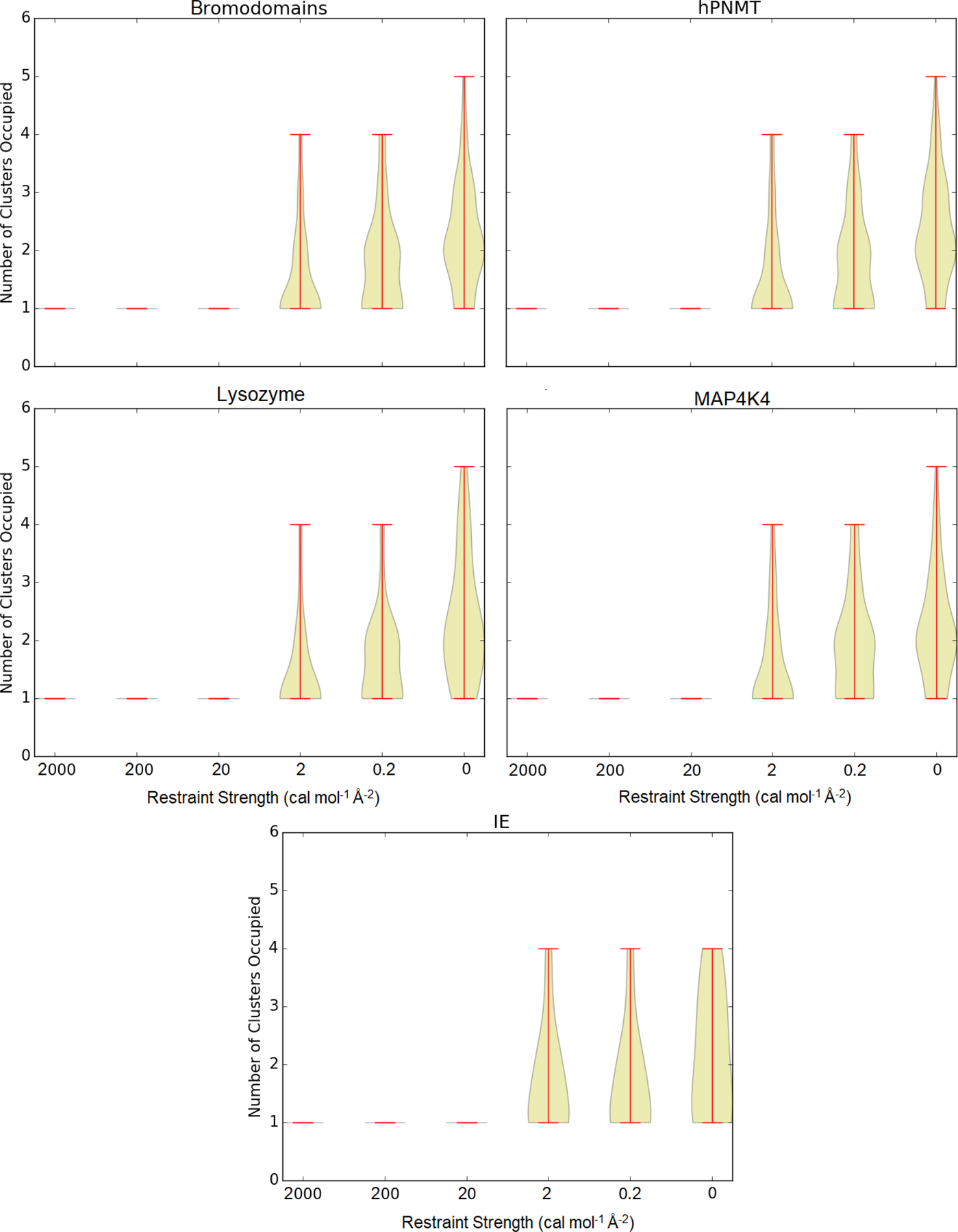
Number of clusters accessed for each system at each restraint energy. The clustering algorithm is described in the Methods section under “Conformational Clustering”.

The two metrics — the average RMSD of the protein backbone and the number of occupied clusters — are closely related to one another (Figure 6). For simulations that occupy a single cluster, the average protein backbone RMSD spans a large range from below 0.5 Å to slightly more than 2.5 Å, with a diminishing number of observations at larger RMSD values. Simulations that occupy more than cluster have a minimum protein backbone RMSD of around 1.5 Å. At an average protein backbone RMSD of 2.0 Å, there are more simulations that occupy multiple clusters than a single cluster. Above 2.5 Å, nearly all simulations occupy multiple clusters.

Figure 6:

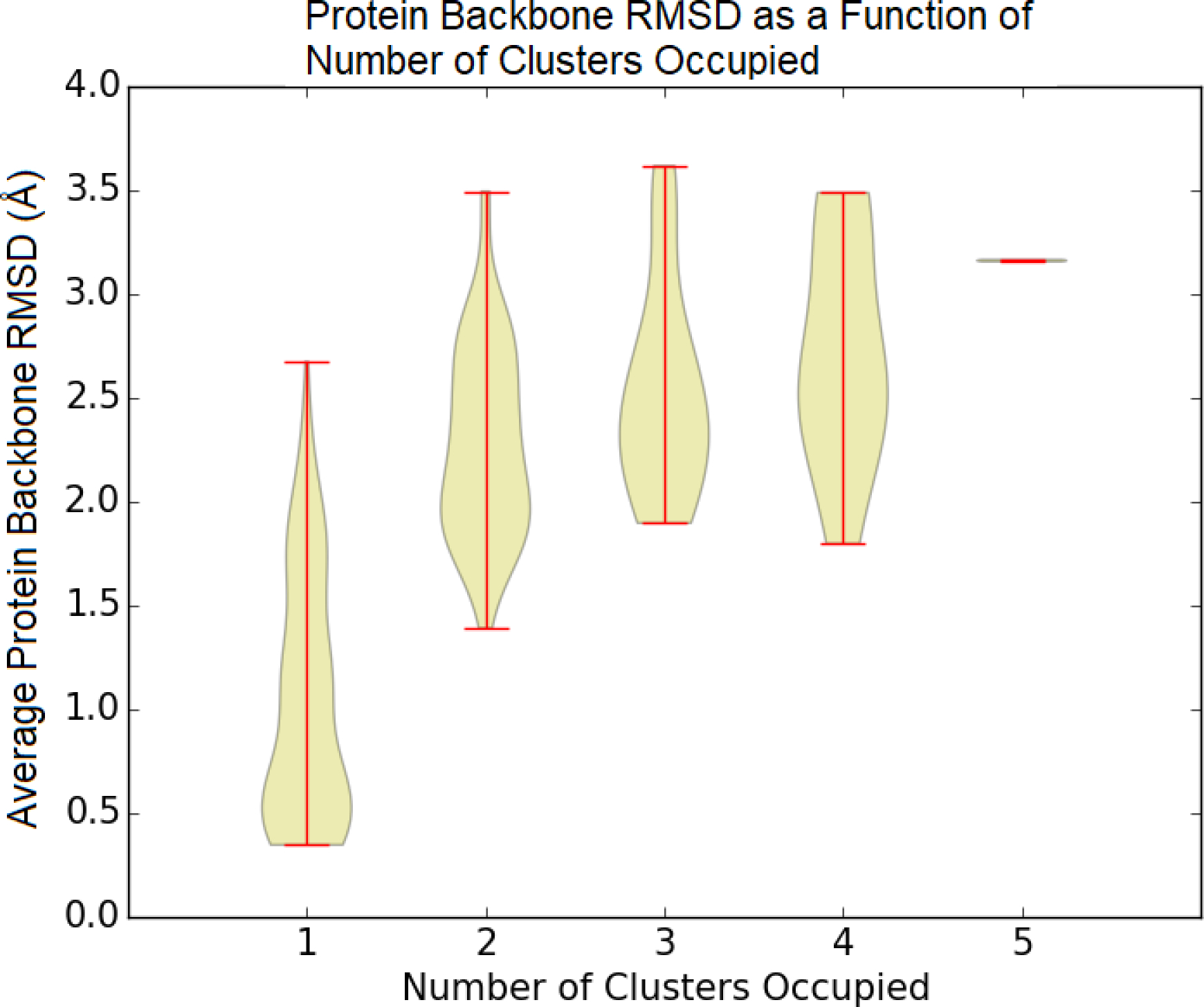
Average RMSD of protein backbone atoms as a function of the number of clusters accessed for every system and every restraint energy.

Numerous factors affect correlation with experiment

As in Menzer et al.²⁷, we systematically considered the influence of statistical estimator options on correlation with experiment. The correlation metrics used were the Pearson R, Spearman ρ, and Kendall τ⁷⁷. The effect of these correlation metrics were ranked for the bromodomains, lysozyme, and MAP4K4 data sets, for which correlation metrics for most estimator options was generally greater than 0.4. Comparing rankings across all estimator options, consideration of the harmonic bias on the weight of each sample (Equation 5) was found to be beneficial (Table S1 of the Supplementary Material), especially with the Spearman ρ and Kendall τ. Using reweighting and comparing rankings against all other estimator options, including the full simulation opposed to discarding an equilibration time was found to provide much better correlation with experiment (Table S2 of the Supplementary Material). Using reweighting and including the full simulation, keeping all snapshots opposed to removing those with the ligand RMSD greater than 3 Å leads to slightly higher correlation with experiment (Table S3 of the Supplementary Material). Finally, the first-order cumulant expansion was found to outrank the second-order cumulant expansion, followed by the exponential average and then higher-order expansions (Table S4 of the Supplementary Material).

Due to the unexpectedly strong performance of the first-order cumulant expansion, we considered the correlation metrics for different data sets as a function of the spring constant (Figures S7, S8, and S9 of the Supplementary Material). This analysis reveals only slight differences in the first- and secon-dorder cumulants and the exponential average. The performance of the third- and fourth-order cumulant expansions strongly fluctuates with the spring constant.

Estimator options for the remaining free energy calculations in this paper were selected based on this systematic comparison. The biasing potential due to harmonic restraints was used to weight averages of the interaction energy (Equation 5). All interaction energies, including those from the estimated equilibration period, were included in the averages. For restrained simulations, no ligand RMSD cutoff was used. For unrestrained simulations, we applied our previous recommendation²⁷ of excluding snapshots with a ligand RMSD greater than 3 Å.

In general, correlation with experiment was maximized at a restraint strength of 20 or 200 cal mol⁻¹ Å⁻² (Figure 7). For the bromodomains, correlation peaked at 200 cal mol⁻¹ Å⁻² and gradually deteriorated with weaker restraint strengths. The performance of lysozyme is fairly stable across restraint strengths but is weaker at spring constants of 2 or 0.2 cal mol⁻¹ Å⁻². It is slightly better for the unrestrained simulation, which is longer. The MAP4K4 data set followed a similar trend as lysozyme. For all systems, the interaction energy of a single minimized structure had similar correlation with experiment as the strongly restrained simulations.

Figure 7: Correlation of estimated binding free energies with experimental values.

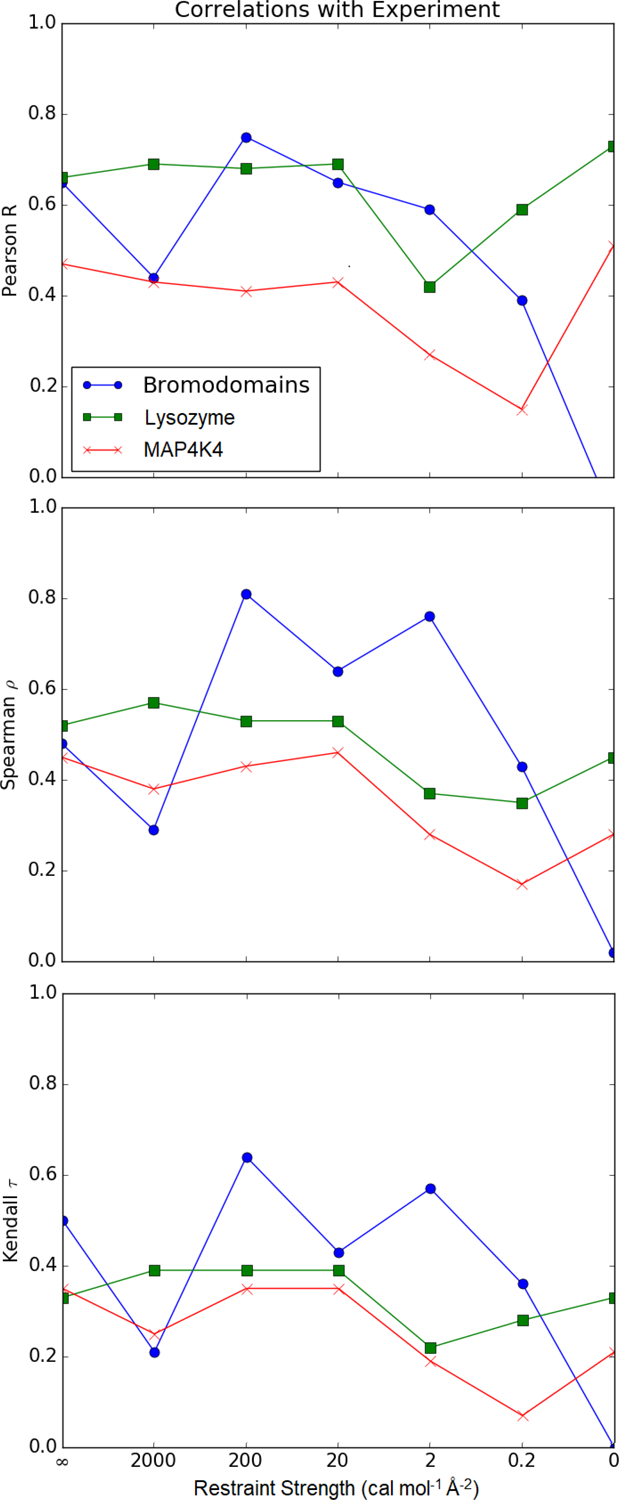
For the Bromodomains, lysozyme, and MAP4K4 data sets, the Pearson R, Spearman ρ, and Kendall τ are plotted for free energy estimates based on a single structure (∞) or a second-order cumulant expansion (all other points). For unrestrained simulations of the bromodomains, the Pearson R, Spearman ρ, and Kendall τ are −0.09, 0.02, and 0.0, respectively.

In addition to correlations, we also considered additional metrics: the adjusted root mean square error (aRMSE) and the slope and intercept of a linear regression (Figure S10 in the Supplementary Material). The aRMSE is,

$$ϵ=\sqrt{\frac{1}{N}\sum _{n=1}^N{\left[x_n-y_n-\left(\overline{x}-\overline{y}\right)\right]}^2},$$ (6)

where the $\overline{x}$ and $\overline{y}$ are the sample mean of x and y, respectively. The aRMSE accounts for systematic deviation between the series and is useful for assessing whether relative binding free energies are accurate. For the lysozyme data set, these metrics are fairly consistent across all restraint strengths, except for a reduction in all quantities at 2 cal mol⁻¹ Å⁻². For the bromodomains data set, estimator performance is steady for spring constants greater than 20 cal mol⁻¹ Å⁻²; the aRMSE is higher for weaker restraints. In the MAP4K4 data set, the aRMSE is particularly high at 20 cal mol⁻¹ Å⁻² but the slope of the linear regression is also closest to zero. The large shift in the statistics at this restraint strength is likely due to a small number of outlier systems.

Stronger restraints reduce entropic contributions to binding

Unsurprisingly, in the vast majority of systems, the estimated entropic contribution to the binding free energy, $-T\Delta \widehat{S}$, is reduced as restraint strength is increased (Figures 8, 9, S4, S5, and S6). Because binding generally leads to a loss in entropy, ΔS < 0, stronger restraints make $-T\Delta \widehat{S}$ a smaller positive quantity. Overall, the trend appears to be monotonic. However, in some systems the estimated entropy of binding for the unrestrained system is contrary to the trend. In these calculations, exclusion of snapshots for which the ligand RMSD is greater than 3 Å likely reduces the estimate of variance of interaction energy, 〈δΨ〉_RL, such that $-T\Delta \widehat{S}$ is smaller.

Figure 8: Comparison of Bromodomain free energy components to the most restrained simulation.

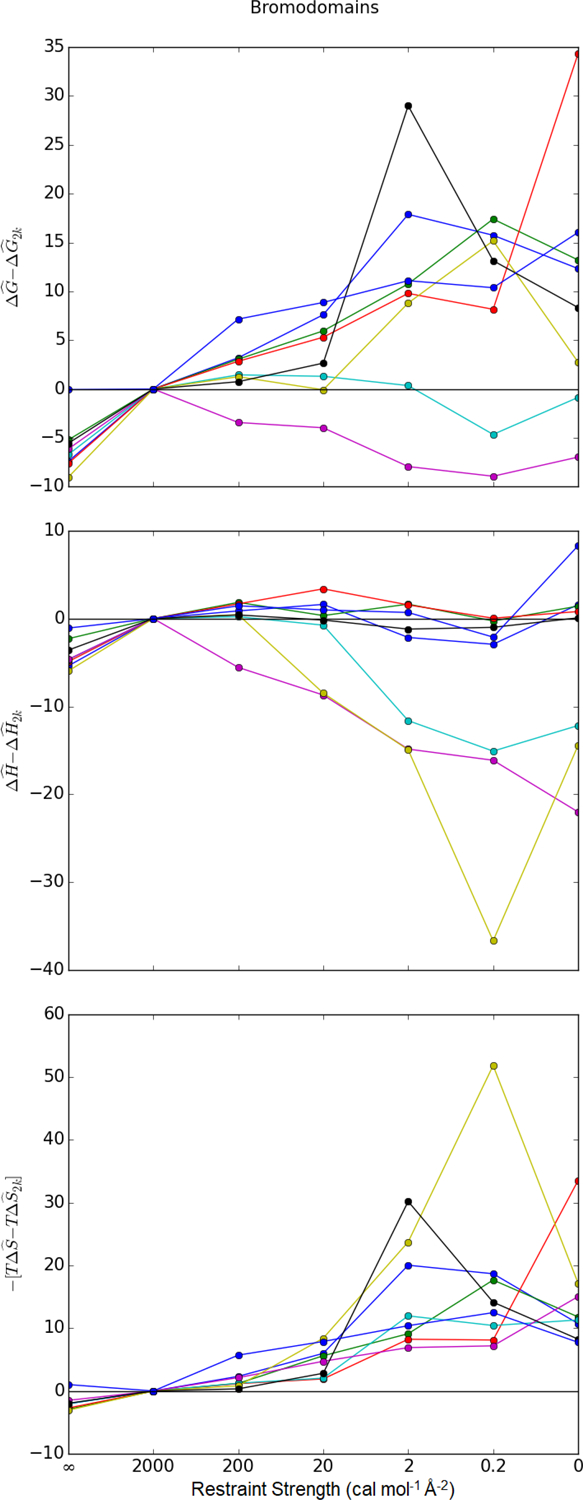
Estimated free energies, enthalpies, and entropies of binding are compared to values estimated with a restraint of 2 kcal mol⁻¹ Å⁻². $\Delta \widehat{X}$ denotes the estimator for the state function X ∈ {G, H, T}. $\Delta {\widehat{X}}_{2k}$ is the estimated value of the quantity from the simulation with a spring constant of 2 kcal mol⁻¹ Å⁻². For most data points, $\Delta \widehat{H}$ is based on the first- and $\Delta \widehat{S}$ and $\Delta \widehat{G}$ on the second-order cumulant expansion. For the data points based on a single minimized structure (∞), $\Delta \widehat{H}$ is the interaction energy and $\Delta \widehat{S}=0$. Similar plots for other data sets are found in Figure 9 and Figures S11, S12, and S13 of the Supplementary Material.

Figure 9: Comparison of MAP4K4 free energy components to the most restrained simulation.

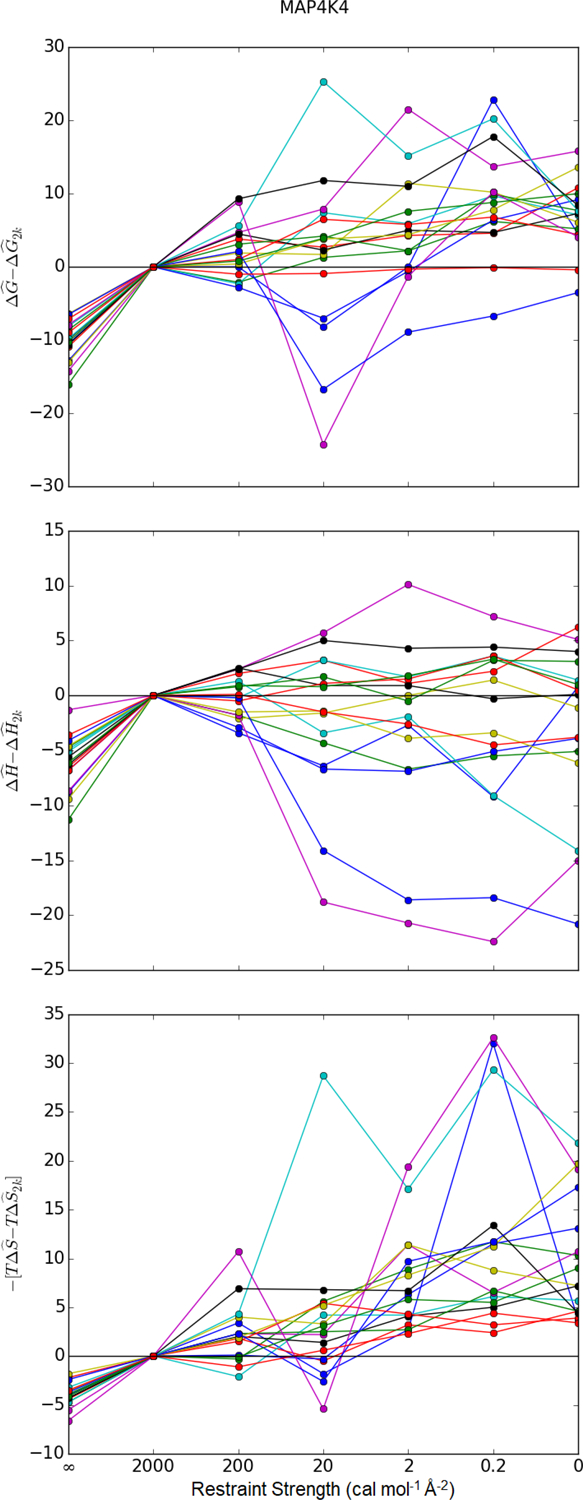
Estimated free energies, enthalpies, and entropies of binding are compared to values estimated with a restraint of 2 kcal mol⁻¹ Å⁻². $\Delta \widehat{X}$ denotes the estimator for the state function X ∈ {G, H, T}. $\Delta {\widehat{X}}_{2k}$ is the estimated value of the quantity from the simulation with a spring constant of 2 kcal mol⁻¹ Å⁻². For most data points, $\Delta \widehat{H}$ is based on the first- and $\Delta \widehat{S}$ and $\Delta \widehat{G}$ on the second-order cumulant expansion. For the data points based on a single minimized structure (∞), $\Delta \widehat{H}$ is the interaction energy and $\Delta \widehat{S}=0$. Similar plots for other data sets are found in Figure 8 and Figures S11, S12, and S13 of the Supplementary Material.

In contrast to the trend in $\Delta \widehat{S}$, the effects of restraints on the estimated enthalpy of binding are inconsistent. In the bromodomains, MAP4K4, and IE data sets, the enthalpy of binding increases in some systems and decreases in others (Figures 8, 9, and S13 of the Supplementary Material). In lysozyme, the binding enthalpy near universally decreases with increased spring constants (Figure S11 of the Supplementary Material). On the other hand, it increases with the spring constant for the entire hPNMT data set (Figure S12 of the Supplementary Material). In all systems, the enthalpy of binding is estimated to be lower for the interaction energy of the minimized structure than for the strongest restraint. The value is lower because it is based on a minimized structure rather than the mean of a configurational distribution.

Combining consistent trends in $\Delta \widehat{S}$ with inconsistency in $\Delta \widehat{H}$ trends, stronger restraints, more often than not, lead to stronger estimated ΔG. The entropic contribution dominates in most of the bromodomains, MAP4k4, and IE data sets (Figures 8, 9, and Figure S13 of the Supplementary Material). In lysozyme, stronger restraints decrease both $\Delta \widehat{H}$ and $-T\widehat{S}$ such that the estimated binding is stronger (Figure S11 of the Supplementary Material). On the other hand, because stronger restraints in the hPNMT data set increase $\Delta \widehat{H}$, they lead to weaker binding free energy estimates in most of the data set (Figure S12 of the Supplementary Material). For all systems, the binding free energy estimate based on the interaction energy of a single minimized structure is nearly always lower than estimates that consider entropy losses.

DISCUSSION

Many systems have force field error

Although crystals are subject to packing forces that are not present in dilute solution, crystal and solution structures are generally consistent. In the context of our calculations, support for this statement comes from the fact that including the initial samples in $\Delta \widehat{G}$ calculations (which are similar to the crystal structure) improves correlation with experiment. If the initial samples were not representative of the experimental energy landscape, they would probably not improve the correlation between $\Delta \widehat{G}$ calculations and experimental binding free energies.

In light of the consistency between crystal and solution structures, molecular simulations of protein systems in dilute solution should sample an ensemble of structures dominated by near-crystallographic structures. Other conformations may be present but less populated. In order for simulations to sample such an ensemble, the energy landscape of the model should have a global minimum similar to the crystal structure. Unfortunately, there are several lines of evidence that in many of the unrestrained and weakly restrained simulations, this is not the case and there is force field error.

One piece of evidence for force field error is the long estimated equilibration time of unrestrained and weakly systems. If the global minimum of an energy landscape resembles the crystal structure, then simulations initiated from near crystal structures should not take long to equilibrate. In many simulations with a spring constant of 20 cal mol⁻¹ Å⁻² or less, however, the estimated equilibration time is a large fraction of the simulation length (Figure 2). In these cases, it is questionable that equilibration has actually occurred. A system can be considered equilibrated when estimated expectation values are independent of initial conditions. In Chodera’s equilibration detection method⁷⁶, including data prior to the estimated equilibration time leads to long autocorrelation times and a smaller effective sample size; the estimated expectation value is perturbed by these early values of the observable (in our case, the total potential energy). If the estimated equilibration time is near the end of the simulated trajectory, then there is a high likelihood that it will continue to change with additional simulation time. If a simulation initiated from near the crystal structure has not equilibrated after 50 ns or 200 ns of simulation, then its energy landscape probably has a different global minimum.

The multiple conformations accessed in unrestrained and weakly restrained systems (Figure 5) are also likely to reflect force field error. In principle, it is possible for the experimental solution ensemble to include multiple conformations. Indeed, multiple conformers have been considered in some binding free energy calculations^78–82. However, the fact that suppressing these non-native conformations with a restraint of 20 cal mol⁻¹ Å⁻² improves the correlation between $\Delta \widehat{G}$ calculations and experimental binding free energies suggests that, for the selected systems, the conformations are force field artifacts.

Finally, shifts in $\Delta \widehat{H}$ as a function of restraint strength also suggest force field error. If a modeled energy landscape is similar to a crystal structure, then changing spring constants should not strongly affect mean interaction energy. In many of the selected systems, however, increasing the restraint strength leads to apparently monotonic shifts in $\Delta \widehat{H}$ (Figures 8, 9, S4, S5, and S6).

More likely than not, the observed force field error is not unique to our calculations. To our knowledge, equilibration time estimates have not been reported in any other end-point binding free energy calculations. (Vosmeer et al.⁸³ reported automated detection of transitions between conformations that contribute to end-point binding free energy estimates). Given that Chodera’s method for automated equilibration detection⁷⁶ is fairly new, this is unsurprising. However, it is probable that most simulations run with the same or a similar force field, including the implicit solvent model, have a modeled energy landscape where the global minimum is distinct from the crystal structure. As most MM/GBSA calculations are based on much shorter simulations, it is likely that many of the simulations have not equilibrated and are still relaxing towards the global minimum of the model. Consequently, estimated ensemble averages are likely to dependent on the starting model. Mobley⁸⁴ has suggested that this problem is widespread in molecular simulation.

A comparison of the average protein backbone RMSD and the number of clusters accessed (Figure 6) suggests that the former may be used to diagnose the presence of non-crystallographic conformations in simulations performed with or without restraints. If the average protein backbone RMSD is below 1.5 Å, then the simulation is sampling within the crystallographic conformation. If it is above 2.0 Å, then there is a good chance that it is sampling non-crystallographic conformational minima that may be artifactual. If it is above 2.5 Å, then it is almost certainly sampling these minima. As a caveat, while we have selected an algorithm that groups together snapshots regardless of cluster shape, this suggestion is likely sensitive to the algorithm used to identify distinct conformations.

Restraints shift global minima towards crystal structures

Fortunately, our results also suggest that sufficiently strong harmonic restraints on protein backbone atoms and ligand atoms can ameliorate force field error and shift global minima towards the crystal structure. This result may be unsurprising, but it is not completely trivial because side chains are unrestrained. Side chain motions could allow access to energy minima distinct from the crystal structure. However, the short estimated equilibration times for highly restrained systems (Figure 2) indicate that little conformational exploration away from the crystal structure is required for equilibration. Moreover, restraints of 20 cal mol⁻¹ Å⁻² or stronger are sufficient to suppress sampling of degrees of freedom that contribute to the largest variance in weakly restrained and unrestrained systems (Figure 5). As discussed above, the additional conformations are likely to be artifactual.

Our present results are consistent with Raval et al.⁴⁴, who found that restraints on an even smaller subset of atoms (α carbons) to homology models were sufficient to make the global minimum of their models more consistent with crystal structures. They also agree with other previously-mentioned papers^{45, 46} which have found that restrained simulations are more consistent with experimental observations than their unrestrained counterparts.

Restraints should be removed from ensemble averages

Given that restraints shift the global minimum towards the crystal structure, it is reasonable to think that they should simply be considered part of the force field. Following this logic, a simple average (e.g. Equation 3) would be used instead of an importance sampling estimator (e.g. Equation 5). We found, however, that importance sampling estimators are more strongly correlated with experiment than simple averages. The stronger performance of importance sampling estimators suggests that the restraints should not be considered part of the force field. This conclusion is reasonable because the harmonic restraints were added without a physical rationale.

A spring constant near 20 cal mol⁻¹ Å⁻² is just about right

Based on our systematic assessment of the effect of restraint strength on equilibration time (Figure 2), statistical efficiency (Figure 3), the number of accessed clusters (Figure 5), correlation with experiment (Figure 7), and contributions to free energy (Figures 8 and 9, and S11, S12, and S13 of the Supplementary Material), we recommend using harmonic restraints with a spring constant around 20 cal mol⁻¹ Å⁻². Spring constants of 2 cal mol⁻¹ Å⁻² or less are too weak. Compared to unrestrained simulations, they have little impact on the equilibration time, statistical inefficiency, number of clusters accessed, and binding free energy. In these simulations, the estimated −TΔS are large and probably unrealistic. On the other hand, a spring constant of 20 cal mol⁻¹ Å⁻² appears to be just right. It reduces the equilibration time and statistical inefficiency in a significant subset of systems, suppresses sampling of likely artefactual conformations, leads to near-peak correlation with experimental ΔG. A spring constant of 200 cal mol⁻¹ Å⁻² may be too strong. Even though it reduces the equilibration time and statistical inefficiency relative to 20 cal mol⁻¹ Å⁻², it further reduces $-T\Delta \widehat{S}$. A spring constant of 2 kcal mol⁻¹ Å⁻² is definitely too strong. Although it leads to a short equilibration time for nearly all systems and low statistical inefficiency for all systems, $-T\Delta \widehat{S}$ is significant suppressed, weakening correlation with experiment. Finally, although using a single minimized structure for binding free energy estimates may not significantly alter correlation with experiment and is comparatively very fast, requiring only seconds to calculate, an entropy loss of zero is not realistic.

Our results are consistent with predicted influences of spring constants on thermal fluctuations based on Debye-Waller factors and the equipartition theorem. The strong suppression of $-T\Delta \widehat{S}$ with a spring constant of 2 kcal mol⁻¹ Å⁻² is consistent with the small root mean square displacement anticipated. With a spring constant of 200 cal mol⁻¹ Å⁻², $\sqrt{\langle d^2\rangle }$ for a purely harmonic system is predicted to be 1.7 Å, which is just at the limit of expected variance around the crystallographic pose. Combined with the unbiased potential, this harmonic restraint still restricts sampling of the energy well. For a purely harmonic system, fluctuations allowed by a restraints with our recommended spring constant, 20 cal mol⁻¹ Å⁻², are much larger than those expected from crystallographic Debye-Waller factors. Although our recommended restraint prevents sampling of additional energy minima, it does not appear to suppress thermal fluctuations about the crystal structure.

CONCLUSIONS AND FUTURE DIRECTIONS

In conclusion, harmonic restraints with a spring constant around 20 cal mol⁻¹ Å⁻² on protein backbone heavy atoms and ligand atoms are a helpful way to maintain a near-crystallographic structure of a protein-ligand complex and perform an end-point binding free energy calculation that apparently converges by around 20 ns of simulation. Using an importance sampling estimator and including initial samples in $\Delta \widehat{G}$ calculations improve correlation with experiment.

Although our simulations were initiated from crystal structures, we selected a restraint procedure that could be relevant to simulations from docked structures. Restraints on protein backbone heavy atoms and ligand atoms allow side chains to relax, which could lead to energetically favorable interactions. A potentially fruitful future direction would be to assess the described procedure for docked structures. It could be helpful to more thoroughly explore other selections of restrained atoms, including all protein heavy atoms, all atoms, or only α carbons.

Other possibly useful directions include: end-point binding free energy calculations based on three trajectories (of the receptor, ligand, and complex) instead of a single trajectory of the complex; end-point calculations of relative binding free energies using restraints, building on Dolenc et al.⁸⁵; explicit solvent simulations; longer simulations to more fully characterize trends in equilibration time; and comparing results of end-point calculations to alchemical (opposed to experimental) ΔG, which would isolate the effect of force field and estimator error when comparing statistical estimators.