Detailed analysis of the high-flux deficiencies of pixel-array detectors leads to a protocol for the measurement of structure factors of unprecedented accuracy even for inorganic materials, and this significantly advances the prospects for experimental electron-density investigations.
Keywords: synchrotron radiation, electron density, hybrid single-photon-counting area detectors, materials science, inorganic chemistry
Abstract
Hybrid photon-counting detectors are widely established at third-generation synchrotron facilities and the specifications of the Pilatus3 X CdTe were quickly recognized as highly promising in charge-density investigations. This is mainly attributable to the detection efficiency in the high-energy X-ray regime, in combination with a dynamic range and noise level that should overcome the perpetual problem of detecting strong and weak data simultaneously. These benefits, however, come at the expense of a persistent problem for high diffracted beam flux, which is particularly problematic in single-crystal diffraction of materials with strong scattering power and sharp diffraction peaks. Here, an in-depth examination of data collected on an inorganic material, FeSb2, and an organic semiconductor, rubrene, revealed systematic differences in strong intensities for different incoming beam fluxes, and the implemented detector intensity corrections were found to be inadequate. Only significant beam attenuation for the collection of strong reflections was able to circumvent this systematic error. All data were collected on a bending-magnet beamline at a third-generation synchrotron radiation facility, so undulator and wiggler beamlines and fourth-generation synchrotrons will be even more prone to this error. On the other hand, the low background now allows for an accurate measurement of very weak intensities, and it is shown that it is possible to extract structure factors of exceptional quality using standard crystallographic software for data processing (SAINT-Plus, SADABS and SORTAV), although special attention has to be paid to the estimation of the background. This study resulted in electron-density models of substantially higher accuracy and precision compared with a previous investigation, thus for the first time fulfilling the promise of photon-counting detectors for very accurate structure factor measurements.
1. Introduction
Accurate X-ray diffraction data are essential for obtaining accurate crystal structures of molecular crystals and extended solids. For the detailed investigation of chemical bonding of materials using the experimental electron-density distribution or the investigation of complex materials with disordered structures, an even higher degree of accuracy and precision is required. The introduction of third-generation synchrotron radiation facilities over the past 20 years has revolutionized X-ray science in terms of beam flux and time resolution of experiments. This increased flux has not always been followed by a similar increase in detection capacity and accuracy, but with modern pixel-array detectors this is rapidly improving (Förster et al., 2019 ▸). One of the most commonly used detector families is the DECTRIS Pilatus, of which the current version, Pilatus3, was released with silicon sensor material in 2012. These are now widely established in macromolecular crystallography, having been used in over 4000 entries in the Protein Data Bank (PDB; Berman et al., 2000 ▸). The specifications of the latest Pilatus3 X with CdTe as sensor material are highly promising for accurate electron-density investigations, mainly due to the high detection efficiency in the high-energy X-ray regime compared with the silicon sensor (Loeliger et al., 2012 ▸). Furthermore, the Pilatus detectors offer a high dynamic range (20-bit counter) and low noise, which should help overcome the perpetual problem of detecting strong and weak data simultaneously. However, to the best of our knowledge, there is no publication available presenting high-resolution data for electron-density analysis collected with a Pilatus3 detector. This article aims to close this gap by providing not only an accurate electron-density investigation using this detector but also a comprehensive survey of the systematic errors that may arise from this family of detectors, as well as describing how to modify the current data collection and processing procedures in order to exploit their full potential.
Current electron-density investigations, whether using synchrotron or laboratory-based X-ray sources, typically use either scintillator-based charge-coupled devices (CCDs) or imaging plates (IPs) for the detection of X-rays. These detectors suffer from accumulation of electronic readout noise, hampering the detection of weak diffraction signals especially for short exposure times. Specific problems regarding the detection of synchrotron radiation have already been discussed in the literature (Coppens et al., 2005 ▸; Jørgensen, 2011 ▸; Schmøkel, 2013 ▸; Hey, 2013 ▸; Jørgensen et al., 2014 ▸). One particularly important issue is the insufficient dynamic range of CCD detectors, which leads to saturation and thus prohibits accurate detection of weak reflections without saturating the detector with the strong reflections simultaneously (Wolf et al., 2015 ▸). A common practice to avoid this effect is to attenuate the primary beam, making it necessary to collect two sets of data: one attenuated, allowing for an accurate estimation of the strong reflections, and another with the full beam to increase the significance of the weak data. This has been especially crucial for cases where lowering the exposure time was technically impossible because the experiments were performed in a shuttered mode. Here, the mechanical opening/closing cycle of the shutter is the speed-determining step. For the final model, these frames would have to be scaled and the data combined, which is not as straightforward as it might appear, as it inherently introduces additional errors (Jørgensen et al., 2014 ▸).
Modern pixel-array detectors employ direct detection single-photon counting, which means that electronic noise is eliminated, and in combination with their larger dynamic range this offers the possibility of detecting both weak and strong reflections in a single exposure. Direct detection means that the incoming photons are converted directly into a charge, in contrast to indirect detection that takes a detour via visible light. The single-photon counting operation uses the proportionality between the energy of the incoming photon and the charge it generates in the sensor layer of the detector (Bergamaschi et al., 2015 ▸). If the detected charge exceeds a threshold, a digital counter is incremented by one and a single photon is counted. The threshold is adjusted so that the counter is only incremented if more than 50% of the generated charge is measured in exactly one pixel. The value of 50% is essential as it prevents double counting in two adjacent pixels. However, this value leads to insensitive pixel corner areas for which the charge cloud is shared between four adjacent pixels; this is called charge sharing (Broennimann et al., 2006 ▸; Kraft et al., 2009 ▸). A benefit of this thresholding is that the electrical (dark) noise of the chip falls below this limit and is very effectively rejected.
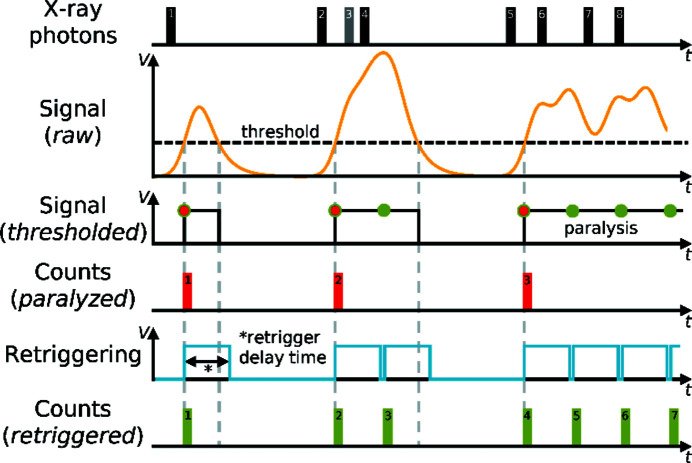
The single-photon counting mode comes with a limitation in the detectable flux (incoming rate of photons), which is due to a pile-up of electric pulses leading to paralyzation and resulting in missed counts (labelled paralyzed in Fig. 1 ▸). The effect of this is that at high photon flux the detector response becomes nonlinear.1 The instant retrigger technology is able to extend the linear response region of the Pilatus detectors by a factor of two (Loeliger et al., 2012 ▸) and eliminates paralyzation. It works by re-enabling the counting circuit after a pre-set interval corresponding to an average pulse length that is dependent on the detector’s threshold energy (labelled Retriggering in Fig. 1 ▸). This retrigger delay time is adjusted to the characteristic pulse shape for a given photon energy and the maximum count rate (measured rate of photons) approaches the retrigger frequency. At high photon flux, usually above several hundred thousand counts per second, the counting loss becomes substantial and a count-rate correction is necessary (Kraft et al., 2009 ▸; Trueb et al., 2012 ▸, 2015 ▸). In Pilatus3 systems, this is based on a look-up table where every pixel’s intensity is corrected when the final image is being written. For this post-processing method to be accurate, a constant flux over the exposure period is essential. However, for the collection of single-crystal diffraction data, the flux on the detector from a Bragg peak is by no means constant over a given time interval, so a count-rate correction based on the average count rate during the frame acquisition is inherently inaccurate. This issue has been mentioned previously in the literature of macromolecular crystallography (Mueller et al., 2012 ▸), but no systematic investigation has been carried out, possibly because the issue becomes considerably more important for high-resolution small-molecule and materials crystallography. This is especially the case for systems with small unit cells and high symmetry in combination with a low crystal mosaicity, which result in a few sharp and highly intense reflections.
Figure 1.
Instant retrigger technology implemented in the DECTRIS Pilatus3 detectors (Trueb et al., 2015 ▸). The black and grey rectangles (1–8) illustrate the individual events of impinging photons. The yellow signal waveform (labelled Signal, raw) shows the associated charge build up in the sensor of the detector, with the threshold indicated with a black dashed line. The black curve (Signal, thresholded) shows the counting of the paralyzable mode (red rectangles, 1–3), whereas the blue curve (Retriggering) shows the re-enabling of the counting circuit after the retrigger delay time, whence the counting of the retriggered mode follows (green rectangles, 1–7). The grey rectangle (3) illustrates a lost photon of a bunch (2–4) whose incoming rate exceeded the inverse of the retrigger delay time (retrigger frequency) and a count-rate correction would be necessary. The figure has been modified and reproduced with permission from Trueb et al. (2015 ▸).
Another important aspect of the data collection is how the reciprocal-space slicing is set up. In wide frames, each reflection is completely sampled on a single frame, which is typically associated with rotations of more than 1°. This was the standard technique for IP detectors where the image read-out time was the bottleneck, and to improve the efficiency of an experiment the scan width was as large as possible without causing spot overlap. Narrow frames became the standard data collection technique when CCD detectors hit the market, because of their much lower read-out time. In this approach, the reflections are sampled over several consecutive frames, with frame widths usually less than half a degree. This rough estimate has its rationale in the reflection’s spread on the detector, resulting from the convolution of the crystal’s mosaicity, the divergence of the incident beam and the wavelength spread of the source. The lower boundary for feasible fine slicing with CCDs is generally well above a tenth of a degree because the read-out noise of the detector accumulates for finer slicing (Pflugrath, 1999 ▸). For pixel detectors with their zero electronic noise and much shorter read-out time, there is again a paradigm shift with this lower boundary vanishing. Systematic approaches to fine slicing have already been carried out for the field of macromolecular crystallography. Previous studies (Mueller et al., 2012 ▸; Casanas et al., 2016 ▸) found an improvement in data quality for macromolecular diffraction data up to a slicing of a tenth of the mosaicity of the crystal. An adoption of these results would easily end in a data collection of multiples of 18 000 frames (e.g. for a 180° ω scan), which is currently unfeasible due to data storage, handling and processing limitations because of missing infrastructure. On the other hand, a possible benefit of fine slicing would be a better approximation to the actual flux of a strong reflection, leading to a better count-rate correction.
Our initial experience with data collected using this type of detector revealed two aspects that introduced systematic bias at the two extremes of the detected intensity scale. Data sets collected at different exposure times or incident fluxes revealed that a change in these experimental conditions led to systematic differences in the acquired data. As this is physically unreasonable, we set out to investigate systematically the origin of and possible solutions for these errors. In this study, we investigate rubrene (5,6,11,12-tetraphenyltetracene) (Hathwar et al., 2015 ▸; Murphy & Fréchet, 2007 ▸) and FeSb2 (Bentien et al., 2006 ▸, 2007 ▸) as representatives of samples with weak and strong scattering power, respectively. We focus on two areas for which highly accurate high-resolution data are required: (i) organic molecules with relatively large unit cells, e.g. molecular electronic materials, where numerous weak and strong reflections are found simultaneously on the images and in particular the accuracy of the weak data is of importance, and (ii) minerals and materials that consist of strongly scattering elements and high symmetry so the scattering of the crystal is largely condensed into few but very strong reflections, such that the very high instantaneous peak flux of a sharp Bragg peak will impose a great challenge on the detector to count the incoming photons accurately. Both systems are of great interest in studies of electron density in materials science (Tolborg & Iversen, 2019 ▸).
The article is structured as follows. Section 2 describes the experimental setup. In Section 3.1, the effects of a systematic error for a strongly scattering sample are presented, Section 3.2 shows how careful modification of current data processing steps is needed to obtain accurate weak intensities, and in Section 3.3 an electron-density model shows the improved quality when using a Pilatus3 X 1M CdTe (P3) detector compared with previous investigations using an IP detector. Conclusions are summarized in Section 4.
2. Experimental
2.1. Experimental information
Data were collected on beamline BL02B1 of the SPring-8 synchrotron in Japan with an X-ray energy of 50 keV (0.2486 Å) and a sample temperature of 20 K or 100 K using a Huber four-circle (quarter χ) goniometer equipped with a Pilatus3 X 1M CdTe (P3) detector. The images were converted to the Bruker .sfrm format (see Section 2.4) and integrated using SAINT-Plus (Bruker, 2013 ▸). The integrated data were processed and corrected using SADABS (Krause et al., 2015 ▸) and subsequently averaged using SORTAV (Blessing, 1997 ▸). An electron-density model was refined against the averaged data using the XD2016 (Volkov et al., 2016 ▸) program following the Hansen–Coppens (Hansen & Coppens, 1978 ▸) multipole formalism. Herein, we use the number of gross residual electrons (egross) (Meindl & Henn, 2008 ▸), the integral of the absolute value of the residual electron density over the unit cell, to determine and compare the quality of refined models, along with R(F 2) and the goodness of fit (GoF). Some of the models include an extinction correction, which is based on the models proposed by Becker & Coppens (1974a ▸,b ▸, 1975 ▸). We here employ an isotropic extinction (Type 1) and assume a Lorentzian mosaic-spread distribution.
2.2. Theoretical calculations
Periodic density functional theory calculations for the experimental geometry (using the P3 model calculated using all data, see below) were performed within the linear combination of atomic orbitals scheme using CRYSTAL14 (Dovesi et al., 2014 ▸). The B3LYP functional (Becke, 1993 ▸; Stephens et al., 1994 ▸) and the POB-TZVP basis set (Peintinger et al., 2013 ▸) were used, and reciprocal space was sampled on a 4 × 4 × 4 mesh in the first Brillouin zone. Theoretical static X-ray structure factors were calculated up to the full experimental resolution as the Fourier transform of the electron density (with the same reflection indices as observed in the experiment), and were employed to derive a theoretical multipole-projected electron-density distribution in XD2016.
2.3. Test crystals
Table 1 ▸ gives general experimental details for the data collections, and Tables 2 ▸–5 ▸ ▸ ▸ give details of exposure times, attenuation degrees and slicing for the different experiments.
Table 1. Experimental details for data collection on rubrene and FeSb2 .
| Name | Space group | Unit-cell dimensions (Å) | Resolution in d spacing (Å) and sin(θ)/λ (Å−1) | Data, measured and unique |
|---|---|---|---|---|
| Rubrene | Cmce | a = 26.7900 (19) | 0.30, 1.67 | 502 029, 26 442 |
| (C42H28) | b = 7.1571 (5) | |||
| c = 14.1540 (11) | ||||
| FeSb2 | Pnnm | a = 5.8415 (3) | 0.30, 1.67 | 42 120, 2509 |
| b = 6.5307 (3) | ||||
| c = 3.1760 (2) |
Table 2. Full data collection for FeSb2 .
| Beam flux (%)† | Temperature (K) | Exposure time (s) | Slicing (°) | Strategy |
|---|---|---|---|---|
| 12 | 20 | 0.2, 0.5, 1.0, 2.0, 4.0 | 0.5 | ‡ |
| 31 | 20 | 0.2, 0.5, 1.0, 2.0, 4.0 | 0.5 | ‡ |
| 65 | 20 | 0.2, 0.5, 1.0, 2.0 | 0.5 | ‡ |
| 100 | 20 | 0.2, 0.5, 1.0 | 0.5 | ‡ |
As a percentage of the maximum beam flux.
180° ω scan at χ = 0.0, 20.0 and 45.0° and 2θ = 0.0, −20.0° (six runs).
Table 3. Slicing experiment for FeSb2 .
| Beam flux (%)† | Temperature (K) | Exposure time (s) | Speed (s per °) | Slicing (°) | Scan width (°) |
|---|---|---|---|---|---|
| 100 | 20 | 0.2 | 2.0 | 0.10 | 90 |
| 100 | 20 | 0.5 | 2.0 | 0.25 | 180 |
| 100 | 20 | 2.0 | 2.0 | 1.00 | 180 |
| 100 | 20 | 4.0 | 2.0 | 2.00 | 180 |
As a percentage of the maximum beam flux.
Table 4. Fine slicing experiment for FeSb2 .
| Beam flux (%)† | Temperature (K) | Exposure time (s) | Speed (s per °) | Slicing (°) | Strategy |
|---|---|---|---|---|---|
| 12 | 100 | 0.10 | 2.0 | 0.05 | ‡ |
| 12 | 100 | 0.20 | 2.0 | 0.10 | ‡ |
| 12 | 100 | 1.00 | 2.0 | 0.50 | ‡ |
| 100 | 100 | 0.01 | 1.0 | 0.01 | ‡ § |
| 100 | 100 | 0.10 | 2.0 | 0.05 | ‡ |
| 100 | 100 | 0.20 | 2.0 | 0.10 | ‡ |
| 100 | 100 | 1.00 | 2.0 | 0.50 | ‡ |
As a percentage of the maximum beam flux.
180° ω scan at χ = 0.0, 20.0 and 45.0° and 2θ = 0.0, −20.0° (six runs).
Due to an experimental error, the data were only collected up to 36° in ω per run.
Table 5. Full data collection for rubrene.
| Beam flux (%)† | Temperature (K) | Exposure time (s) | Slicing (°) | Strategy |
|---|---|---|---|---|
| 100 | 20 | 0.5 | 0.5 | ‡ |
| 100 | 20 | 1.0 | 0.5 | ‡ |
| 100 | 20 | 2.0 | 0.5 | ‡ |
| 100 | 20 | 4.0 | 0.5 | ‡ |
As a percentage of the maximum beam flux.
180° ω scan at χ = 0.0, 20.0 and 45.0°, and 2θ = 0.0, −15.0° (six runs).
2.4. Data processing
The Pilatus images were converted to the Bruker .sfrm format using a custom-made program (the code is available at https://github.com/LennardKrause/) to enable integrating the data using the integration engine SAINT-Plus. The initial processing protocol comprised the profile-fitting routine to maximize the accuracy of weak data (Kabsch, 1988 ▸) and the best-plane background approximation, as it is faster and more robust than the recurrence method (Bruker, 2012 ▸) in reflection background determination. However, we encountered serious issues with the plane background algorithm (see Section 3.2.1). Furthermore, we experienced an ambivalent performance of the profile-fitting routine. Thus, our optimal data integration protocol uses the recurrence algorithm for peak background determination, and a flexible integration box size and simple summation (rather than profile fitting) for intensity extraction.
Additionally, an X-ray aperture mask was prepared for every run to mask dead detector areas, bad pixels and the beam-stop shadow. We tested various solutions to the handling of bad pixels but ended up masking them, as there is no way to reconstruct the value from adjacent pixels. This can mainly be attributed to the extremely narrow detector point-spread function of one pixel, so intensity variations are unpredictable and change dramatically within reflections where the information is needed. The masking approach has the advantage that the integration software will try to reconstruct the reflection profile using average reflection profile information and will only exclude reflections for which too much data is missing (in our case more than 60%). Since this approach relies on average reflection profile information rather than a nearest-neighbour pixel average, it is more reliable and robust.
With the beam-stop shadow included in the aperture masks, an automated generation of an active pixel mask is no longer needed and the automatic generation was thus suppressed. This is of course only useful if there are no other peripheral objects casting shadows on the detector, but it works well for the present setup.
3. Results and discussion
3.1. Persistent systematic errors of strong reflections
As mentioned in the introduction, a challenging case for pixel detectors is a low-mosaic, strongly scattering and highly symmetric sample. As a test case, FeSb2 was used as it is a perfect representative for the aforementioned case. Diffraction data were collected for varying combinations of experimental parameters, covering exposure time, primary beam attenuation factor and frame slicing (Tables 2 ▸–4 ▸ ▸).
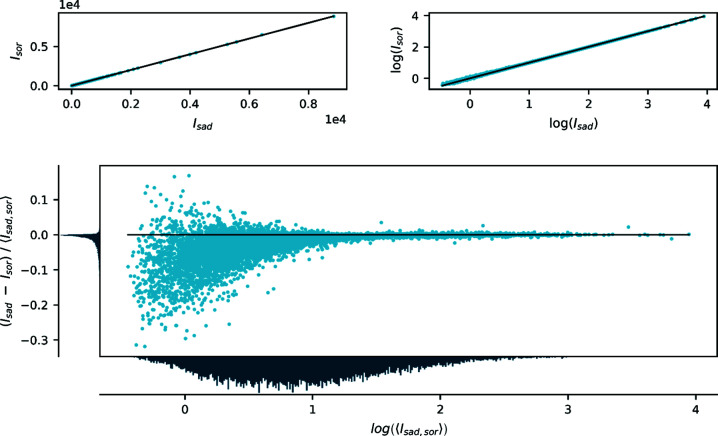
To show systematic trends between two data sets, several descriptors are available. As we aim for an unbiased relative difference between two data sets, where neither can initially be established as the reference point, we propose to employ a visual difference-divided-by-mean approach plotted as a function of (the logarithm of) the mean intensity. In this plot, the allowed values range from −2 to 2 and a complete lack of bias is indicated by values close to zero. The scaling of the data for comparison is arbitrary, as is typically the case for X-ray diffraction data. To supplement this plot, a direct comparison of the intensities of one set versus the intensities of the other set is given on both linear and logarithmic scales.
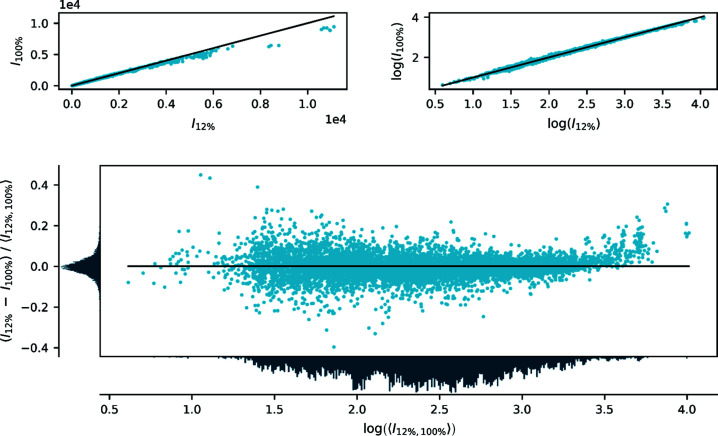
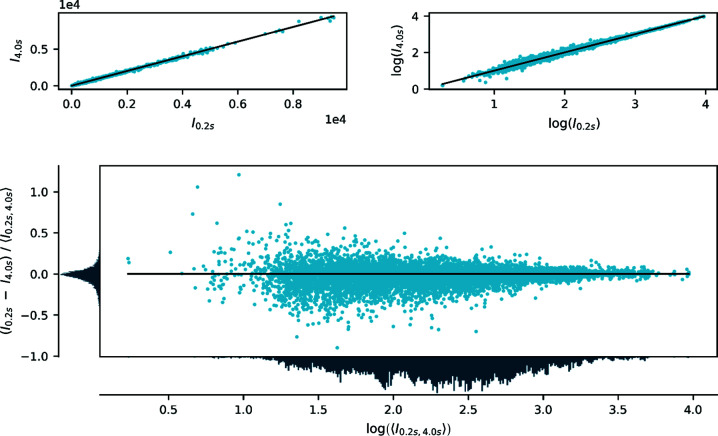
Fig. 2 ▸ shows a comparison of the observed intensities (after scaling and averaging) between data collected with the full incident beam (100%) and a strongly attenuated beam (12%) with the same exposure time of 1.0 s per frame (0.5° per frame). The plot shows that, for the most intense reflections, the integrated intensities are stronger for the attenuated (12%) than for the non-attenuated (100%) data. In contrast, Fig. 3 ▸ shows two data sets collected with the same incident flux (12%) but different exposure times (0.2 and 4.0 s per frame) for which no such trend is evident. For the weak reflections, no systematic differences are observed between the two data sets. A more exhaustive comparison of the different combinations of attenuation degree and exposure time is given in Sections S1, S2 and S4 in the supporting information. These observations indicate that data collected with an identical flux but different exposure times are equivalent within a scale factor accounting for the total number of counts. For data collected with different flux, all but the strongest reflections are also equivalent within a scale factor, whereas the strongest reflections differ significantly. The only possible explanation is that, for the highest flux, the integrated intensities are severely underestimated.
Figure 2.
Comparison of integrated, scaled and averaged diffraction intensities of FeSb2 collected with 12 and 100% of the full beam intensity. The top panels show a direct comparison of intensities on linear (left) and logarithmic (right) scales, and the bottom panel shows the relative difference between the two data sets defined as the difference divided by the mean value as a function of the logarithm of the average intensity. The panels to the left of and below the bottom plot are histograms showing the distribution of data on the two axes. The data are scaled to be similar but the overall scale is arbitrary.
Figure 3.
Comparison of integrated, scaled and averaged diffraction intensities of FeSb2 collected using an attenuation to 12% with exposure times of 0.2 and 4.0 s per frame (with a scan width of 0.5° per frame). The panels are the same as in Fig. 2 ▸.
To rule out that this issue is a result of the data reduction, the precision of the used goniometer on beamline BL02B1 allows us to make a direct comparison of frames acquired from two different experiments and thereby an unprocessed pixel-by-pixel comparison. The individual frames of two experiments with different beam fluxes (65 and 12%)2 are combined to give two images corresponding to full 180° scans and compared in a similar way to the integrated intensities (Fig. S1). The plot shows that the strong data are underestimated for higher flux, similar to what was found for the integrated intensities. Furthermore, no indication of any other bias for the lower intensities was found, meaning that the weak data are accurately reproducible. Thus, the flux-dependent difference in integrated data originates directly from the detector and is not introduced by data processing.
To understand these differences, we need to provide a brief technical discussion of the detector. As mentioned in the Introduction , the effect of a very high flux is a paralyzation of the detector, which is handled in two ways: (i) an instant retrigger technology working in the electronic readout module of the detector, and (ii) a post-processing count-rate correction based on the average total number of photons collected in one pixel. The count-rate correction is based on a Monte Carlo simulation of the detector’s response to a given incoming flux (Trueb et al., 2012 ▸) and is simply a scale factor for each pixel that is based on the total counts in a given pixel. For this post-processing method to be reasonable, a constant flux over the exposure period is important. However, for single-crystal diffraction data, the flux reaching the detector from a narrow Bragg peak is by no means constant over the scan interval, so the number of photons used for the correction corresponds to the average count rate during the frame-acquisition time, and a post-process count-rate correction is a highly inadequate solution. The underlying incoming flux that led to the counted number of photons, and thereby the true correction factor, is unknown. The consequence is an underestimated count-rate correction, leading to systematically under-corrected pixel intensities that manifest experimentally as underestimated strong intensities at high incident flux.
3.1.1. Effect on the electron-density model
This systematic error of only the strong intensities is able to progress unhindered through all the data processing steps, since it affects all reflections within a group of equivalents similarly. Therefore, quality indicators based on groups of equivalent reflections will fail to detect this and the error can manifest itself in the refined model. For strongly scattering crystals, extinction is often an issue which tends to decrease the intensity of the strongest reflections. Thus, a correction for extinction in the refined model might hide the inadequacies of the detector at high flux. To evaluate this experimentally, we have compared a sequence of model refinements against data collected with varying attenuation factors (Table 6 ▸).
Table 6. Refined amount of extinction for different incoming beam flux and exposure times for FeSb2 .
| Beam flux (%)† | Exposure (s) | GoF | Data | Extinction (%) | R(F 2) (%) | egross |
|---|---|---|---|---|---|---|
| 12 | 0.2 | 0.9069 | 2469 | 11.5 | 2.32 | 28.26 |
| 12 | 0.5 | 0.9577 | 2491 | 7.8 | 1.81 | 21.66 |
| 12 | 1.0 | 0.9657 | 2497 | 8.1 | 1.51 | 16.66 |
| 12 | 2.0 | 0.9911 | 2502 | 7.6 | 1.51 | 16.01 |
| 31 | 0.2 | 0.9305 | 2476 | 13.1 | 2.06 | 24.38 |
| 31 | 0.5 | 0.9239 | 2503 | 11.6 | 1.67 | 18.30 |
| 31 | 1.0 | 0.9592 | 2493 | 10.3 | 1.53 | 16.05 |
| 31 | 2.0 | 0.9962 | 2504 | 12.0 | 1.45 | 15.10 |
| 65 | 0.2 | 0.9392 | 2499 | 21.7 | 1.63 | 18.59 |
| 65 | 0.5 | 0.9783 | 2501 | 20.4 | 1.48 | 15.71 |
| 65 | 1.0 | 1.0003 | 2504 | 20.6 | 1.45 | 15.00 |
| 65 | 2.0 | 1.0332 | 2508 | 21.7 | 1.37 | 14.16 |
| 100 | 0.2 | 0.9621 | 2502 | 26.3 | 1.44 | 15.92 |
| 100 | 0.5 | 1.0041 | 2509 | 28.9 | 1.26 | 13.50 |
| 100 | 1.0 | 1.0304 | 2506 | 30.7 | 1.32 | 14.10 |
As a percentage of the maximum beam flux.
Given as the maximum percentage reduction of an individual reflection intensity (always the 120 reflection).
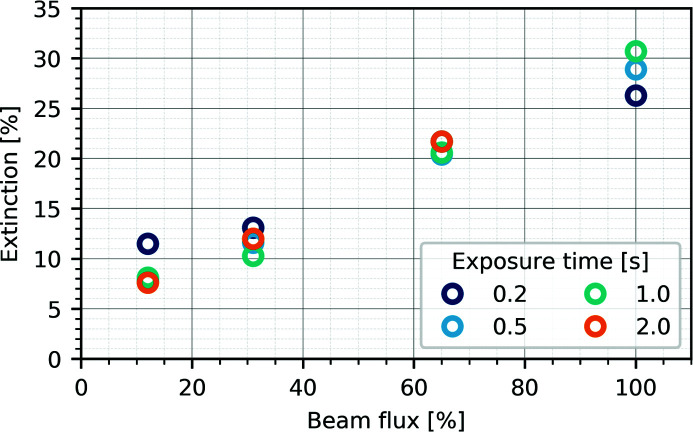
For the data sets collected with different attenuation degrees, we found the degree of extinction to vary between 10 and 25%, given as the maximum reduction of an individual reflection intensity, depending solely on the attenuation degree of the primary beam, whereas the exposure time does not affect the value systematically (see Table 6 ▸ and Fig. 4 ▸).
Figure 4.
Refined amount of extinction reported as the maximum reduction of an individual reflection as a function of the incoming X-ray beam flux and exposure time for FeSb2.
With an included extinction model, the quality indicators clearly benefit from higher flux and longer exposure time, as expected, and this can be attributed to the better counting statistics. As soon as an extinction model is no longer implemented, the picture changes dramatically (Table 7 ▸). The systematic error in the strong reflections now clearly outperforms the benefit of the higher flux and the model quality indicators decrease with increasing incident beam flux. A longer exposure time, however, remains beneficial for the resulting quality of the data (see Sections S1 and S2). This finding underlines the proposed explanation for the error as being solely an issue of the flux of the diffracted beam.
Table 7. Comparison of the quality of FeSb2 models† with and without a refined extinction parameter.
| Beam flux (%)‡ | GoF | Data | Extinction (%)§ | R(F 2) (%) | egross |
|---|---|---|---|---|---|
| 12 | 0.9657 | 2497 | 8.1 | 1.51 | 16.66 |
| 12 | 0.9896 | 2497 | None | 1.76 | 18.56 |
| 31 | 0.9592 | 2493 | 10.3 | 1.53 | 16.05 |
| 31 | 0.994 | 2493 | None | 1.87 | 19.95 |
| 65 | 1.0003 | 2504 | 20.6 | 1.45 | 15.00 |
| 65 | 1.1684 | 2504 | None | 2.43 | 27.14 |
| 100 | 1.0304 | 2506 | 30.7 | 1.32 | 14.10 |
| 100 | 1.5559 | 2506 | None | 3.15 | 36.83 |
Collected with 1.0 s exposure time, using the recurrence background method and without profile fitting.
As a percentage of the maximum beam flux.
Given as the maximum percentage reduction of an individual reflection intensity (always the 120 reflection).
This means that the extinction parameter,3 consisting of an intensity- and an angle-related part, is capable of concealing the systematic error of the count-rate correction. Therefore, even in the model evaluation step, the error is not straightforwardly detectable and could remain unnoticed, as only a large extinction parameter is found. This parameter has been implemented for a completely different purpose, and to rely on it as a correction should be considered highly unsatisfactory. A similar fudge parameter was recently reported for the Rietveld refinement of powder X-ray diffraction where the physically incorrect modelling of preferred orientation and anisotropic strain was able to mimic and completely absorb the underlying effect of thermal diffuse scattering (Zeuthen et al., 2019 ▸).
3.1.2. Estimating the incoming peak flux
The conclusion from the above results must be that the only route to obtain accurate data is to decrease the flux of the incident beam to remain in the linear response region of the detector and thus avoid the count-rate correction entirely. On the other hand, the data quality still benefits from the better statistics of larger total counts. Thus, there are two options available, either to collect all data with an attenuated beam, which comes with a substantial increase in data collection time (here at least tenfold), or to collect two individual data sets, one with the full beam (increasing the statistics of weak reflections) and one with an attenuated beam (obtaining accurate estimates of strong reflections). The second option requires a subsequent scaling of the data, where the incorrect parts of the data (strong reflections with full beam) are selectively excluded.
In either case, in order to find the optimal attenuation degree and which reflections to exclude, knowledge of the flux of the diffracted beam is required. However, this number is not directly available, since the measured intensity in a pixel on a frame is the integral of the diffracted flux over the frame interval, and therefore only the average flux can be obtained directly. In order to retrieve the flux information so it can be used as a diagnostic tool, we propose a reconstruction procedure to estimate the peak flux. Our goal here is not to model the flux of every peak accurately and use this to make a new correction, but rather to utilize the information present in the data to identify if a given reflection is affected by nonlinearity, and to estimate the optimal attenuation degree.
The main assumption in the flux reconstruction procedure is that the flux function f can be described with a Gaussian profile. In this case, the flux in a pixel is given as a function of time, scanning through a reflection:
where I
sum is the total number of photons in a pixel originating from a Bragg peak and corresponds to the time integral of f. The subscript t refers to the fact that these quantities are expressed in units of time. The measured intensity on a frame (Ii) at angle 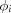 at time ti must then be the integral of this flux function within the time interval of the frame,
at time ti must then be the integral of this flux function within the time interval of the frame,
Since the experiment is performed as a function of rotation angle rather than time, it is convenient to rewrite the integral in terms of the rotation angle 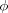 = vt, where v is the scan speed in units of angle per time. Introducing also the width and centre of the flux function in angular space as
= vt, where v is the scan speed in units of angle per time. Introducing also the width and centre of the flux function in angular space as 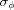 = vσt and
= vσt and 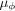 = vμt, the integral can be rewritten as
= vμt, the integral can be rewritten as
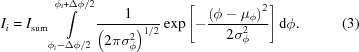 |
As we assume the flux function to be Gaussian, the integral can be represented as the difference between the values of the cumulative normal distribution function,
where
is the cumulative normal distribution and erf(x) is the error function.
The parameters (I
sum, 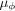 ,
, 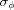 ) entering the expression for the frame intensity (Ii) are directly related to those of the flux function [f(t)], and therefore a least-squares fit of this expression to the intensity profile of a reflection can be utilized to extract the relevant parameters and thus reconstruct the flux profile. Remembering that the fitting is done in angular space, so the width obtained in the fit is
) entering the expression for the frame intensity (Ii) are directly related to those of the flux function [f(t)], and therefore a least-squares fit of this expression to the intensity profile of a reflection can be utilized to extract the relevant parameters and thus reconstruct the flux profile. Remembering that the fitting is done in angular space, so the width obtained in the fit is 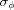 , the peak flux can be calculated as
, the peak flux can be calculated as
In this way, we can estimate the peak flux based on parameters from a fit to the measured frame intensities. One intrinsic drawback is that the estimated flux is based on the frame intensities, which are already affected by nonlinearity and possibly altered by the count-rate correction. However, most data points that contribute to the reconstruction are lower in intensity and are unaffected.
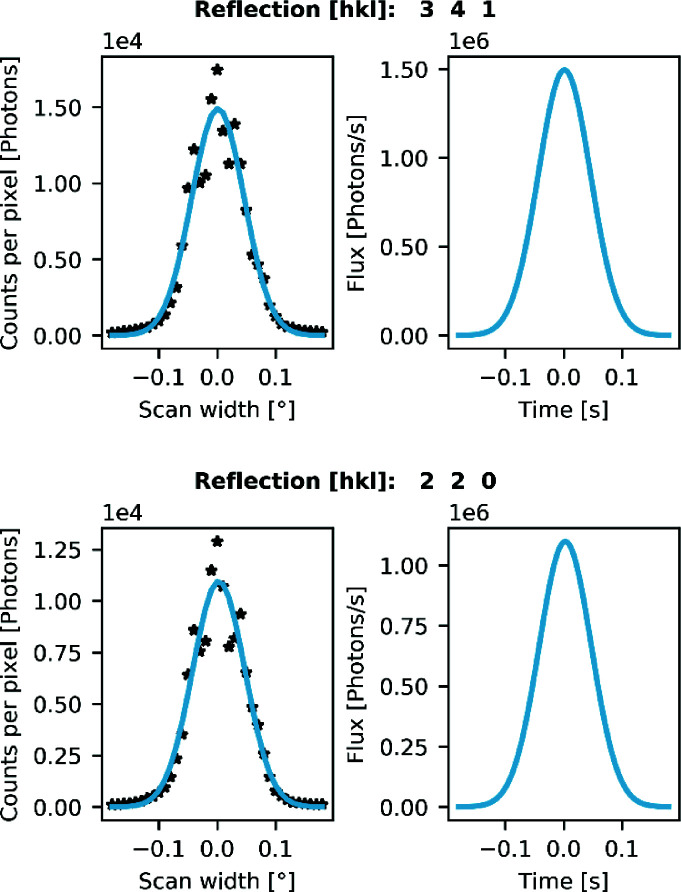
In Fig. 5 ▸, we show a fit to determine the peak flux for some of the reflections that are underestimated for the full flux experiment on a very finely sliced data collection (0.01° per frame). These reflections are labelled in a comparison similar to Fig. 2 ▸ in Fig. S3 of Section S5 in the supporting information. They clearly have a peak flux above 1.0 Mcps (million counts per second) and are thus affected by the nonlinearity. In a standard data collection with a slicing of, say, 0.5° per frame and an exposure time of 1.0 s per degree, the maximum pixel intensities will be approximately 170 000 and 120 000 counts for reflections 341 and 220, respectively. Hence, the intensities are far below the dynamic-range limit of the detector, meaning that the effect could be left unnoticed in this case.
Figure 5.
Flux estimate based on the frame intensities for (top) the 341 reflection and (bottom) the 220 reflection in FeSb2. The left-hand panels show the pixel intensities on the frames in a very fine sliced data collection (0.01° per frame) with the fitted peak profile based on the flux estimation procedure. The right-hand panels show the underlying Gaussian flux function based on the parameters extracted from the fits in the left panel.
Therefore, we propose that, as part of every (accurate) single-crystal diffraction experiment at a synchrotron, a pre-experiment (180° scan) consisting of a fine-sliced data collection at maximum flux should be performed in order to estimate how much attenuation is needed for collecting accurate strong reflections. This can be done very quickly (here in 180 s), as the flux is independent of exposure time, and for the strongest reflections good enough statistics to estimate the flux are already obtained in a short exposure. A rough estimate of the required attenuation degree could also be obtained without the proposed procedure by performing a pre-experiment that is so finely sliced that the flux can be assumed constant for a given pixel during the collection of the frame. However, as evident from Fig. 5 ▸, there are large variations between pixel values in successive frames, much larger than the expected Poisson noise, so the proposed reconstruction procedure should be more robust and reliable.
As mentioned in the Introduction , a finer frame slicing should, in principle, lead to a more accurate count-rate correction as the average count rate in a pixel asymptotically approaches the true instantaneous count rate as the frame width decreases. This is also observed for the present data, where a pixel-by-pixel comparison of two different slicings at full beam (Fig. S1) shows that wider slicing results in lower intensities for the strongest pixels. Thus, extremely fine slicing could be a way of avoiding attenuation of the direct beam, but, in principle, only infinitesimal slicing would yield correct data at high flux. In addition, this ignores any possible inaccuracies of the utilized correction function, which is based on a Monte Carlo simulation of the detector’s response to the incoming flux and intrinsically contains additional errors (Trueb et al., 2012 ▸).
There is another drawback related to fine slicing. If this is to become a viable alternative, data processing must be straightforward, which was not the case for the present fine-sliced data (0.01° per frame). For example, in the inter-frame scaling performed by SADABS, a crucial step in the correction for crystal shape anisotropy, absorption and beam fluctuation (Krause et al., 2015 ▸), the data-to-parameter ratio becomes extremely low and the outcome is at least questionable. In protein crystallography, where these detectors have been successfully used for years, this is less of a problem simply because of the sheer number of reflections on a single frame. An additional, more trivial, problem is the data handling, as single-crystal diffraction beamlines do not yet offer an adequate data management solution. One approach to overcome this issue would be to combine individual frames, not only to reduce the overall data size, but also to improve the data-to-parameter ratio.
3.2. Data processing and its effect on weak reflections
We now turn our attention to the effect of data processing on the final data quality. The currently available software and routines established in laboratories involved in accurate small-molecule and materials crystallography were developed for the previous generation of detector technologies. This means that all steps in the data reduction process must be carefully scrutinized in order to establish an optimal data processing procedure and avoid pitfalls. We decided to use the indexing and integration routines implemented in the APEX3 software suite (Bruker, 2018 ▸). However, the following analysis should be valid for other software packages such as CrysAlisPro (Rigaku Oxford Diffraction, 2018 ▸), as most crystallographic programs fundamentally rely on similar algorithms (with slightly different implementation) for the data integration, handling of outliers, averaging of equivalents and correction of data.
3.2.1. Data integration
In the integration engine SAINT-Plus, reflections are represented as three-dimensional profiles following a coordinate system similar to the one described by Kabsch (1988 ▸). In this coordinate system, every reflection is independent of the diffractometer geometry and appears as if it was acquired taking the shortest path through the Ewald sphere. This transformation allows the use of a global integration box to determine the integration volume, as the resulting reflection profiles are more similar throughout reciprocal space.
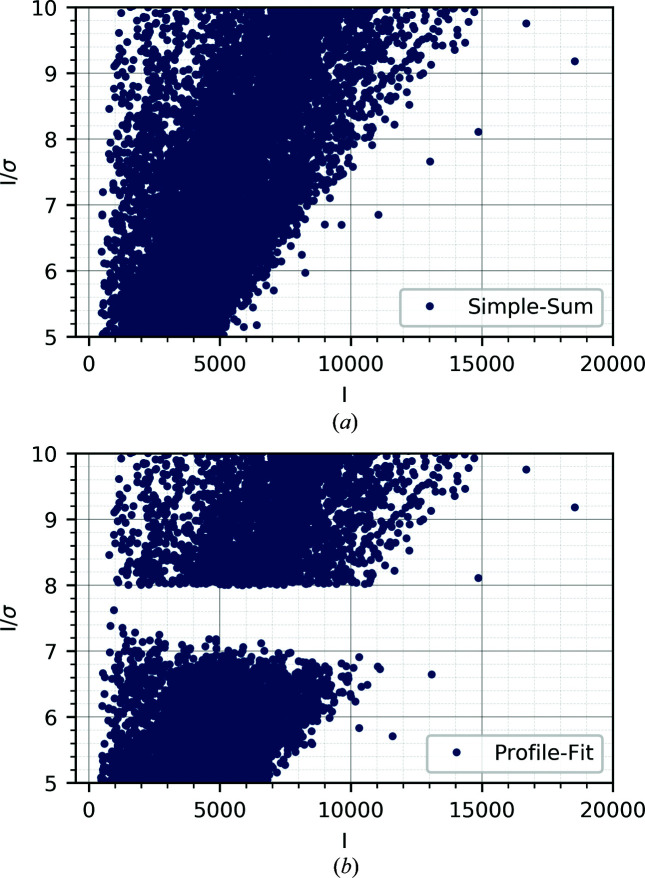
After the determination of the integration box, the next step is to distinguish between signal and background. To find the actual summation volume, a threshold method is used (Kabsch, 1988 ▸) and only those grid points greater than 2% of the profile maximum contribute. The integrated intensity is computed by simple summation over those pixels that lie within the summation volume. For weak reflections and noisy background, this procedure may not be reliable. Instead, it can be assumed that strong and weak reflections have similar normalized profiles, as this allows for a least-squares (LS) fitting approach where the application of learned profiles derived from strong intensities is used to improve the intensity estimate for weaker reflections. The integrated intensity can therefore be determined for every reflection by either of two different techniques: simple summation or LS profile fitting. The LS-fitted intensities are estimated from a fit of the individual reflection profile using the average strong reflections profile collected in a similar detector region. The fitted intensities are on a different scale and, in a post-integration step, the overall scale factor between the two is determined and the LS-fitted intensities are scaled to match the simple-summed intensities. This post-processing seems to be problematic for the P3 data, as a scatter plot of I/σ versus I reveals (Fig. 6 ▸). The figure shows a gap in the data, precisely at the border between LS-fitted and simple-summed intensities. The origin is either in underestimated fitted intensities or in overestimated uncertainties for the scaled data.
Figure 6.
I/σ as a function of I for rubrene (0.5 s exposure, 0.5° slicing). (a) The integrated intensities using the LS profile-fitting procedure (threshold set to 8.0I/σ), and (b) the simple-summed data.
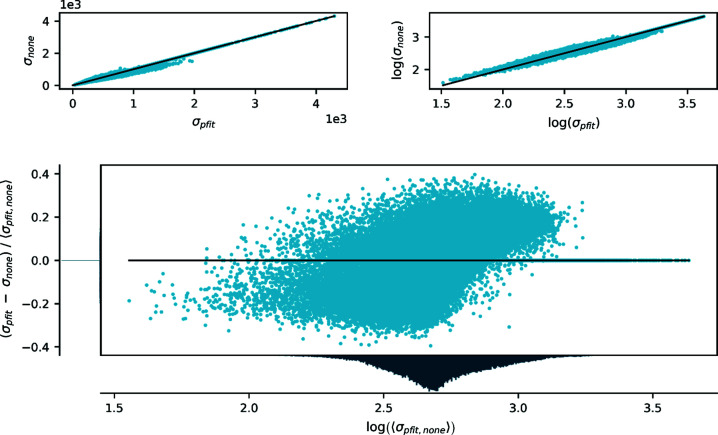
In Fig. 7 ▸, the estimated uncertainties of the integrated intensities are compared for simple-sum and LS-fitting procedures, and we clearly observe a strange pattern, which suggests a flawed scaling of the s.u. values for the LS-fitted data. Similar figures, comparing the intensities, are given in Section S6 in the supporting information and show no systematic differences between the two data sets. This renders the LS-fitting approach less problematic than anticipated, since the final estimated s.u. values are determined in a later step and rely on sample statistics rather than the error estimates provided by the integration software. Thus, this systematic error in the estimated uncertainties should in principle be corrected at a later stage. In the final processing steps, we see no clear preference for either LS-fitted or simple-summed intensities in terms of agreement of equivalent reflections. In terms of model quality no suggestion can be given, simply because the LS-fitted data were beneficial in the case of rubrene but detrimental for FeSb2. Within the scope of this article, the preferred method remains an ad hoc decision.
Figure 7.
Comparison of estimated standard deviations from LS profile fitting and simple summation on rubrene (0.5 s exposure, 0.5° slicing). The panels are as defined in Fig. 2 ▸.
To obtain reliable integrated intensities, especially for weak reflections, a good background estimation and subtraction must be performed. In SAINT-Plus, two options are available, a recurrence background method and a best-plane background. The recurrence method, as described by Howard (1982 ▸), uses a frame averaging procedure, in which the background estimate is updated for every frame over the complete integration process. This approach provides a statistical benefit, with the multiple-frame averaging preserving synchrotron-specific variations, e.g. beam fluctuations. The initial background is refined in subsequent passes over the first several frames. In the best-plane approach, the background is determined on the basis of LS fitting of a plane to the background region around individual peaks. For the constant background produced by the P3, the recurrence method should be beneficial because of the better statistics, but in cases with inhomogeneous background over the data collection, e.g. in high-pressure experiments using diamond anvil cells, or when other equipment casts shadows onto the detector, an individual background estimation as in the best-plane background method may be necessary.
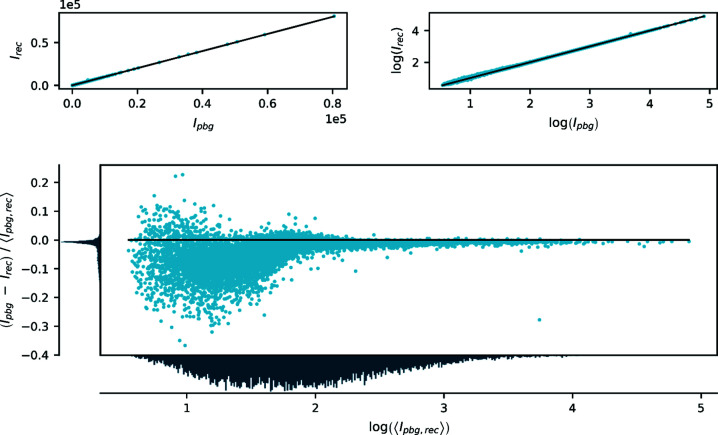
In Fig. 8 ▸, a comparison of the intensities resulting from the two different background estimation methods is given. A large discrepancy is visible, especially for the weakest reflections. From a more thorough analysis (see Section S7 in the supporting information for details), it is evident that systematic differences between exposure times appear only for the best-plane background method. In conclusion, the best-plane background approximation has difficulties handling the low background level of the P3 data and significantly underestimates the intensities of weak reflections, as a direct comparison with data integrated using the recurrence method shows. Fig. S9 in the supporting information shows a similar comparison for data sets with artificially increased intensity and noise, which leads to the same results and excludes systematic errors between the different exposure times as a possible source of the differences.
Figure 8.
Comparison of integrated intensities with best-plane background (pbg) and recurrence background (rec) for rubrene (1.0 s exposure, 0.5° slicing). The panels are the same as in Fig. 2 ▸.
Thus, important points to consider in data integration are the use of LS fitting, which leads to irregular uncertainties, and background estimation, for which the best-plane background as implemented in SAINT-Plus has problems with very weak background levels. We therefore recommend the use of recurrence background methods for Pilatus data.
3.2.2. Data reduction
Careful processing of the integrated data is important for the quality of the resulting data. Here, we draw attention particularly towards outlier rejection and the averaging of equivalent reflections. Several effects, including dead detector areas, defective pixels, the beam stop and additional peripheral shadowing, can result in systematic underestimations of single reflections and may affect and bias a whole group of equivalents. This can generally be handled by outlier rejection, but problematic cases may arise for groups of equivalents measured with a low multiplicity, for which outliers might be concealed behind poor statistics. All these effects are present independent of the detector type, but as the current data reduction implementation in SAINT-Plus is tested for detectors with much higher noise levels, we investigate these steps in detail in order to find possible issues.
SADABS was employed to determine incident-beam scale factors, spherical-harmonic coefficients of the diffracted beam paths and a first stage of gross outlier rejection. It is known that the integration routines of area-detector data highly underestimate the standard uncertainty for strong reflections (Waterman & Evans, 2010 ▸). This leads to a pronounced bias toward strong intensities in the scaling and parameter determination steps of the data processing. To reduce this bias, the parameterized weighting scheme provided within SADABS was used with an initial g value of 0.04 to adjust the uncertainties of strong reflections and thereby lower their influence. The weighting scheme is given as
Here, σ(I)2 is the uncertainty determined by SAINT-Plus and 〈I〉 refers to the mean intensity of a set of equivalents. This expression affects the uncertainties of all reflections but increases with intensity.
In outlier rejection, a similar problem arises as a rejection criterion based on 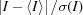 is too rigorous and overly dependent on reasonable initial estimates for the uncertainties. Here, the initial estimates of the uncertainties lead to a significant number of false rejections, especially for strong equivalent intensities, substantially reducing the multiplicity of these sets and thereby rendering the resulting average intensity prone to bias and highly sensitive towards the utilized outlier rejection protocol. To minimize this bias, an adjustment similar to the weighting scheme in the parameter determination was made. Individual intensities were only rejected when their difference from the mean intensity of symmetry-equivalent reflections 〈I〉 exceeded more than four times their adjusted s.u.:
is too rigorous and overly dependent on reasonable initial estimates for the uncertainties. Here, the initial estimates of the uncertainties lead to a significant number of false rejections, especially for strong equivalent intensities, substantially reducing the multiplicity of these sets and thereby rendering the resulting average intensity prone to bias and highly sensitive towards the utilized outlier rejection protocol. To minimize this bias, an adjustment similar to the weighting scheme in the parameter determination was made. Individual intensities were only rejected when their difference from the mean intensity of symmetry-equivalent reflections 〈I〉 exceeded more than four times their adjusted s.u.:
Averaging of sets of equivalent reflections was subsequently performed using either SADABS or SORTAV following individual protocols. The scaling, correction and rejection steps were identical. For averaging using SADABS the following error model was applied:
Here, the individual standard deviations were determined by refining K per run and g only once, globally from all data. The averaging in SORTAV was based on corrected intensities from SADABS and a suppressed error model (K and g fixed to 1.0 and 0.0, respectively), meaning that the input σ values were essentially those from SAINT-Plus. The basic difference between SADABS and SORTAV is that SADABS introduces an error model, which tries to make χ2 unity over the full intensity range with few adjustable parameters, whereas SORTAV makes χ2 unity for each set of equivalent reflections by adjusting the estimated uncertainty to match the deviations between equivalent reflections (Jørgensen et al., 2012 ▸). Attention is drawn to the fact that the final averaged intensities obtained from SADABS are systematically lower than those from SORTAV for the weakest reflections, as seen in Fig. 9 ▸.
Figure 9.
Comparison of the averaged intensities processed with either SADABS (sad) or SORTAV (sor) for rubrene (1.0 s exposure, 0.5° slicing). The panels are the same as in Fig. 2 ▸.
A study of weak intensities obtained with a P3 detector shows a positively skewed distribution for which negative outliers are exceptionally rare (see Section S9 in the supporting information), which might impose difficulties on the employed averaging algorithm. A stricter outlier down-weighting implementation in SADABS may thus reduce the influence of primarily positive intensities as outliers and result in lower averaged estimates, whereas SORTAV incorporates these intensities, shifting the result to larger averaged intensities. To test this, artificial data following a Poisson distribution were simulated and subsequently averaged using SADABS and SORTAV (Section S10 in the supporting information). This clearly shows a systematic error in the averaging of weak intensities for SADABS, which is not present for SORTAV. Moreover, models derived from SORTAV-averaged data result in better overall agreement factors and a more normal distribution of errors (Section S11 in the supporting information). Thus we recommend the use of SORTAV for averaging of equivalent reflections for Pilatus data.
3.3. Final model quality compared with high-quality IP data
Data on rubrene were previously collected on the same beamline (BL02B1) of the SPring-8 synchrotron in 2014 at 35.0 keV using a cylindrical IP detector that the P3 data can be compared with (Hathwar et al., 2015 ▸). In order to rationalize the overall quality of the data, models derived from two different data treatment approaches are now investigated and their residual density indicators are compared.
In the first approach, a more conservative strategy with a strict focus on significance was used, with an I/σ(I) cutoff of 3.0 and a truncated resolution at 0.35 Å. This is common practice in electron-density investigations to avoid the fitting of noise, but excluding those observations introduces a systematic bias where the included very weak reflections are more prone to being overestimated (Henn & Meindl, 2015 ▸). However, for the Pilatus data it seems beneficial not to exclude any measured intensities as they tend to improve the statistical quality indicators, normal-probability and scale-factor plots (Zavodnik et al., 1999 ▸), and only have a minor negative influence on the R(F 2) and egross values (the gross number of residual electrons). Consequently, a second strategy was designed which uses all available data (including negative intensities) and a higher resolution. Models derived from both sets of data are compared in Table 8 ▸ and selected experimental details and parameters are reported.
Table 8. Comparison of IP (35 keV) and P3 (50 keV) data collected on rubrene with an exposure time of 8.0 s.
| Resolution (Å) | I/σ cutoff | I cutoff | Detector | Data used (theoretical†) | R(F 2) (%) | GoF | egross (e) |
|---|---|---|---|---|---|---|---|
| 0.35 | 3 | 0 | IP | 12 690 (17 690) | 1.93 | 1.035 | 35.1 |
| P3 | 14 190 (17 695) | 1.54 | 1.205 | 22.5 | |||
| 0.33 | −3 | −3 | IP | 19 289 (21 004) | 2.31 | 1.018 | 79.2 |
| P3 | 19 389 (21 000) | 1.66 | 1.112 | 39.1 | |||
| 0.30 | −3 | −3 | IP | 26 169 (27 807) | 2.93 | 1.017 | 127.2 |
| P3 | 26 442 (27 802) | 1.87 | 1.029 | 59.0 |
The maximum numbers of reflections up to a given resolution differ slightly for IP and P3 data because of subtle changes in the unit-cell parameters.
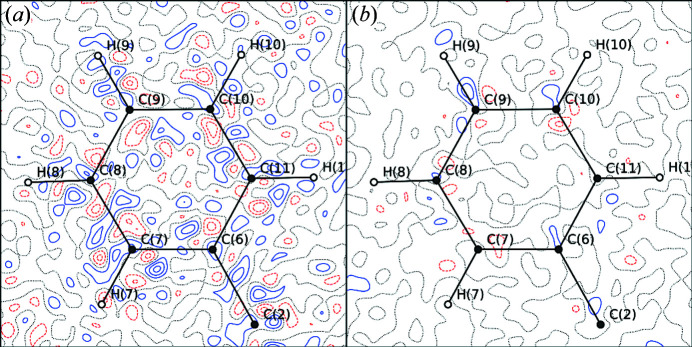
The difference in the used data for the two detectors shows the higher significance for P3 as fewer reflections have been subjected to the I/σ(I) exclusion. Regardless of the higher number of used data, both R(F 2) and egross are lower, indicating a higher accuracy of the weak P3 data. Moreover, the inclusion of higher-resolution and less-significant data shows an overall positive impact on the GoF, especially for the P3 data, and it ends up close to unity. The decrease in the GoF and less pronounced increase in egross show that the accuracy of the merged intensities and their estimated standard deviations is higher for P3 data, and this is also reflected in the residual density maps shown in Fig. 10 ▸ and the fractal dimension plots seen in Fig. S20 in the supporting information. A plot of the ratio of the observed and calculated structure factors versus the resolution underlines this finding and shows a significant deviation for the high-resolution data only for the IP (Section S12 in the supporting information). This comparison shows the exceptional quality of the very weak data in particular, which allows for resolution regimes far beyond 0.45 Å even for organic compounds.
Figure 10.
Residual density contour maps (level of 0.05 e Å−3) of rubrene showing the differences between the models derived from either (a) IP or (b) P3 data using a significance cutoff in I/σ(I) of 3 and truncated resolution (1.43 Å−1). Maps for models derived from all data can be found in Fig. S24 in the supporting information.
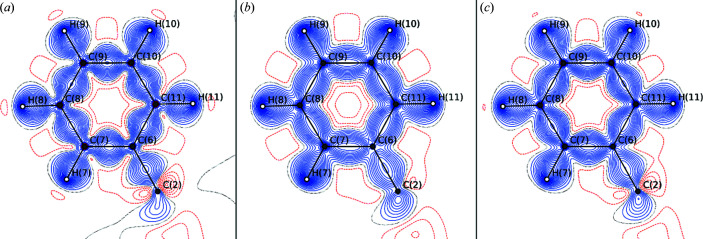
To assess the influence of the data quality on the modelled density we compare the IP and P3 experimental results with a model derived from state-of-the-art periodic density functional theory calculation (Fig. 11 ▸). Despite the similarity, it is noteworthy that the qualitative agreement of the deformation density between theory and P3 is better than that for the IP data. Thus, the improved data quality also seems to result in more accurate model densities.
Figure 11.
Deformation density contour maps (level of 0.05 e Å−3) of rubrene for models derived from data using a significance cutoff in I/σ(I) of 3 and truncated resolution (1.43 Å−1). The deformation density is shown for (a) the IP data, (b) the multipole projected theoretical data and (c) the P3 data. Maps (including the Laplacian) for models derived from all data can be found in Section S12 in the supporting information.
4. Conclusions
In this article, we have demonstrated that the Pilatus3 X CdTe detector family is capable of producing single-crystal X-ray data of high quality. The obtained data are well suited for experimental electron-density investigations on both weakly scattering organic crystals and heavy-element materials. A major benefit of this type of detector is the high quality of the weak data which enables much-increased resolution ranges, especially for weakly scattering organic compounds. The long-lasting problem of overexposed images due to insufficient dynamic range is finally eliminated. These benefits, however, come at the expense of a persistent problem for high diffracted beam flux, particularly problematic in single-crystal diffraction of materials with strong scattering power and sharp diffraction peaks. A systematic examination of collected data reveals this issue to be a systematic difference in strong intensities for different incoming beam fluxes, and the implemented count-rate correction is shown to be inadequate for sharp diffraction peaks. The only currently viable solution to this problem is to collect the strongest reflections with a properly attenuated beam. In this respect, it should be stressed that all data presented herein were collected on a bending magnet beamline at a third-generation synchrotron radiation facility, so undulator and wiggler beamlines, and fourth-generation synchrotron radiation facilities with higher X-ray flux, will be even more prone to this systematic error.
Since the scattering power of protein crystals is orders of magnitude weaker, the presented systematic errors might not be a major problem in macromolecular crystallography. However, with the flux delivered by a third-generation undulator beamline, especially at a lower energy (∼10 keV), we would expect that the diffracted beam flux could be high enough to cause underestimated strong reflections in some unfavourable cases. Refinement of an extinction parameter would absorb the error, similar to the case presented herein. However, as this is not a common protocol for protein data collection, it may result in noisy residual density maps and underestimated displacement parameters, although we do not expect this to have led to wrong structure determinations.
The next generation of single-photon-counting pixel detectors utilizing high frame rates (e.g. Eiger2) will make ultrafine-sliced experiments possible and should in principle improve the performance of the count-rate correction, as well as eliminating the dead time. Experiments using this detector family will reveal if ultra-fine slicing overcomes the current flux limitation.
The currently available data processing and integration routines, despite their age, turned out to be capable of handling the low-background images and high-multiplicity data sets surprisingly well. However, it required the use of the recurrence background estimation in SAINT-Plus and not too strict outlier rejection criteria in the averaging of equivalent reflections.
With regard to averaging, now that it is possible to observe very weak reflections experimentally, their handling needs additional attention, since the question of how to average these reflections adequately remains unanswered, and subsequent investigations of their statistical distribution need to be carried out (e.g. through Monte Carlo simulations of detector response at low count rates).
Supplementary Material
Crystal structure: contains datablock(s) I. DOI: 10.1107/S1600576720003775/kc5106sup1.cif
Structure factors: contains datablock(s) I. DOI: 10.1107/S1600576720003775/kc5106Isup2.hkl
Additional figures and tables. DOI: 10.1107/S1600576720003775/kc5106sup3.pdf
Plots of exposure time at constant attentuation. DOI: 10.1107/S1600576720003775/kc5106sup4.pdf
Plots of attenuation at constant exposure time. DOI: 10.1107/S1600576720003775/kc5106sup5.pdf
Additional XD files for FeSb2. DOI: 10.1107/S1600576720003775/kc5106sup6.zip
Additional XD files for rubrene. DOI: 10.1107/S1600576720003775/kc5106sup7.zip
CCDC reference: 1990530
Acknowledgments
Affiliation with the Center for Integrated Materials Research (iMAT) at Aarhus University is gratefully acknowledged. The synchrotron experiments were performed at SPring-8 on BL02B1 with the approval of the Japan Synchrotron Radiation Research Institute (JASRI) as a Partner User (Proposal Nos. 2018A0078, 2018B0078 and 2019A0159). We thank Aref Mamakhel and Karl F. F. Fischer for providing the single-crystal samples. The assistance during synchrotron experiments of Nikolaj Roth, Emil Damgaard-Møller, Emil A. Klahn, Hidetaka Kasai and Bjarke Svane is gratefully acknowledged. We thank Marcus Müller (DECTRIS) for providing technical information. The theoretical calculations were performed at the Center for Scientific Computing, Aarhus.
Funding Statement
This work was funded by Danmarks Grundforskningsfond grant DNRF93. Danish Agency for Science and Higher Education grant DANSCATT. Villum Fonden grant 12391.
Footnotes
We note that this paralysis effect should not be confused with the detector read-out time (dead time), which for this detector is 0.95 ms to read out a full image, during which the detector is completely inactive.
For the unattenuated experiment, all images are offset by one pixel due to a small deviation in the detector 2θ angle. This does not affect integrated intensities, but hinders a direct pixel-by-pixel comparison of the images.
An extinction parameter x (as implemented in the program SHELXL; Sheldrick, 2015 ▸) is refined by least squares, where the calculated structure factor (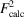 ) is multiplied as
) is multiplied as 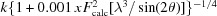 , k being the scale factor, λ the wavelength and 2θ the scattering angle.
, k being the scale factor, λ the wavelength and 2θ the scattering angle.
References
- Becke, A. D. (1993). J. Chem. Phys. 98, 5648–5652.
- Becker, P. J. & Coppens, P. (1974a). Acta Cryst. A30, 129–147.
- Becker, P. J. & Coppens, P. (1974b). Acta Cryst. A30, 148–153.
- Becker, P. J. & Coppens, P. (1975). Acta Cryst. A31, 417–425.
- Bentien, A., Johnsen, S., Madsen, G. K. H., Iversen, B. B. & Steglich, F. (2007). EPL Europhys. Lett. 80, 17008.
- Bentien, A., Madsen, G. K. H., Johnsen, S. & Iversen, B. B. (2006). Phys. Rev. B, 74, 205105.
- Bergamaschi, A., Cartier, S., Dinapoli, R., Greiffenberg, D., Jungmann-Smith, J. H., Mezza, D., Mozzanica, A., Schmitt, B., Shi, X. & Tinti, G. (2015). J. Instrum. 10, C01033.
- Berman, H. M., Westbrook, J., Feng, Z., Gilliland, G., Bhat, T. N., Weissig, H., Shindyalov, I. N. & Bourne, P. E. (2000). Nucleic Acids Res. 28, 235–242. [DOI] [PMC free article] [PubMed]
- Blessing, R. H. (1997). J. Appl. Cryst. 30, 421–426.
- Broennimann, Ch., Eikenberry, E. F., Henrich, B., Horisberger, R., Huelsen, G., Pohl, E., Schmitt, B., Schulze-Briese, C., Suzuki, M., Tomizaki, T., Toyokawa, H. & Wagner, A. (2006). J. Synchrotron Rad. 13, 120–130. [DOI] [PubMed]
- Bruker (2012). SAINT-Plus Integration Engine Reference. Version 8.30A. Bruker AXS Inc., Madison, Wisconsin, USA.
- Bruker (2013). SAINT-Plus Integration Engine. Version 8.38A. Bruker AXS Inc., Madison, Wisconsin, USA.
- Bruker (2018). APEX3. Version 2018.7-2. Bruker AXS Inc., Madison, Wisconsin, USA.
- Casanas, A., Warshamanage, R., Finke, A. D., Panepucci, E., Olieric, V., Nöll, A., Tampé, R., Brandstetter, S., Förster, A., Mueller, M., Schulze-Briese, C., Bunk, O. & Wang, M. (2016). Acta Cryst. D72, 1036–1048. [DOI] [PMC free article] [PubMed]
- Coppens, P., Iversen, B. & Larsen, F. K. (2005). Coord. Chem. Rev. 249, 179–195.
- Dovesi, R., Orlando, R., Erba, A., Zicovich-Wilson, C. M., Civalleri, B., Casassa, S., Maschio, L., Ferrabone, M., De La Pierre, M., D’Arco, P., Noël, Y., Causà, M., Rérat, M. & Kirtman, B. (2014). Int. J. Quantum Chem. 114, 1287–1317.
- Förster, A., Brandstetter, S. & Schulze-Briese, C. (2019). Philos. Trans. A Math. Phys. Eng. Sci. 377, 20180241. [DOI] [PMC free article] [PubMed]
- Hansen, N. K. & Coppens, P. (1978). Acta Cryst. A34, 909–921.
- Hathwar, V. R., Sist, M., Jørgensen, M. R. V., Mamakhel, A. H., Wang, X., Hoffmann, C. M., Sugimoto, K., Overgaard, J. & Iversen, B. B. (2015). IUCrJ, 2, 563–574. [DOI] [PMC free article] [PubMed]
- Henn, J. & Meindl, K. (2015). Acta Cryst. A71, 203–211. [DOI] [PubMed]
- Hey, J. (2013). PhD thesis, University of Göttingen, Germany.
- Howard, A. J. (1982). Computational Crystallography, edited by D. Sayre, pp. 29–40. Oxford: Clarendon Press.
- Jørgensen, M. R. V. (2011). PhD thesis, Aarhus University, Denmark.
- Jørgensen, M. R. V., Hathwar, V. R., Bindzus, N., Wahlberg, N., Chen, Y.-S., Overgaard, J. & Iversen, B. B. (2014). IUCrJ, 1, 267–280. [DOI] [PMC free article] [PubMed]
- Jørgensen, M. R. V., Svendsen, H., Schmøkel, M. S., Overgaard, J. & Iversen, B. B. (2012). Acta Cryst. A68, 301–303. [DOI] [PubMed]
- Kabsch, W. (1988). J. Appl. Cryst. 21, 916–924.
- Kraft, P., Bergamaschi, A., Broennimann, Ch., Dinapoli, R., Eikenberry, E. F., Henrich, B., Johnson, I., Mozzanica, A., Schlepütz, C. M., Willmott, P. R. & Schmitt, B. (2009). J. Synchrotron Rad. 16, 368–375. [DOI] [PMC free article] [PubMed]
- Krause, L., Herbst-Irmer, R., Sheldrick, G. M. & Stalke, D. (2015). J. Appl. Cryst. 48, 3–10. [DOI] [PMC free article] [PubMed]
- Loeliger, T., Bronnimann, C., Donath, T., Schneebeli, M., Schnyder, R. & Trub, P. (2012). Proceedings of the Nuclear Science Symposium/Medical Imaging Conference (NSS/MIC), pp. 610–615. Anaheim: IEEE.
- Meindl, K. & Henn, J. (2008). Acta Cryst. A64, 404–418. [DOI] [PubMed]
- Mueller, M., Wang, M. & Schulze-Briese, C. (2012). Acta Cryst. D68, 42–56. [DOI] [PMC free article] [PubMed]
- Murphy, A. R. & Fréchet, J. M. (2007). Chem. Rev. 107, 1066–1096. [DOI] [PubMed]
- Peintinger, M. F., Oliveira, D. V. & Bredow, T. (2013). J. Comput. Chem. 34, 451–459. [DOI] [PubMed]
- Pflugrath, J. W. (1999). Acta Cryst. D55, 1718–1725. [DOI] [PubMed]
- Rigaku Oxford Diffraction (2018). CrysAlis PRO. Rigaku Oxford Diffraction Ltd, Abingdon, England.
- Schmøkel, M. S. (2013). PhD thesis, Aarhus University, Denmark.
- Sheldrick, G. M. (2015). Acta Cryst. C71, 3–8.
- Stephens, P. J., Devlin, F. J., Chabalowski, C. F. & Frisch, M. J. (1994). J. Phys. Chem. 98, 11623–11627.
- Tolborg, K. & Iversen, B. B. (2019). Chem. Eur. J. 25, 15010. [DOI] [PubMed]
- Trueb, P., Dejoie, C., Kobas, M., Pattison, P., Peake, D. J., Radicci, V., Sobott, B. A., Walko, D. A. & Broennimann, C. (2015). J. Synchrotron Rad. 22, 701–707. [DOI] [PMC free article] [PubMed]
- Trueb, P., Sobott, B. A., Schnyder, R., Loeliger, T., Schneebeli, M., Kobas, M., Rassool, R. P., Peake, D. J. & Broennimann, C. (2012). J. Synchrotron Rad. 19, 347–351. [DOI] [PMC free article] [PubMed]
- Volkov, A. P. M., Macchi, P., Farrugia, L. J., Gatti, C., Mallinson, P., Richter, T. & Koritsanszky, T. (2016). XD2016 – A Computer Program Package for Multipole Refinement, Topological Analysis of Charge Densities and Evaluation of Intermolecular Energies from Experimental and Theoretical Structure Factors, https://www.chem.gla.ac.uk/~louis/xd-home/.
- Waterman, D. & Evans, G. (2010). J. Appl. Cryst. 43, 1356–1371. [DOI] [PMC free article] [PubMed]
- Wolf, H., Jørgensen, M. R. V., Chen, Y.-S., Herbst-Irmer, R. & Stalke, D. (2015). Acta Cryst. B71, 10–19. [DOI] [PubMed]
- Zavodnik, V., Stash, A., Tsirelson, V., de Vries, R. & Feil, D. (1999). Acta Cryst. B55, 45–54. [DOI] [PubMed]
- Zeuthen, C. M., Thorup, P. S., Roth, N. & Iversen, B. B. (2019). J. Am. Chem. Soc. 141, 8146–8157. [DOI] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Crystal structure: contains datablock(s) I. DOI: 10.1107/S1600576720003775/kc5106sup1.cif
Structure factors: contains datablock(s) I. DOI: 10.1107/S1600576720003775/kc5106Isup2.hkl
Additional figures and tables. DOI: 10.1107/S1600576720003775/kc5106sup3.pdf
Plots of exposure time at constant attentuation. DOI: 10.1107/S1600576720003775/kc5106sup4.pdf
Plots of attenuation at constant exposure time. DOI: 10.1107/S1600576720003775/kc5106sup5.pdf
Additional XD files for FeSb2. DOI: 10.1107/S1600576720003775/kc5106sup6.zip
Additional XD files for rubrene. DOI: 10.1107/S1600576720003775/kc5106sup7.zip
CCDC reference: 1990530