Catalytic Site pK_a Values of Aspartic, Cysteine, and Serine Proteases: Constant pH MD Simulations

Abstract

Enzymatic function and activity of proteases is closely controlled by the pH value. The protonation states of titratable residues in the active site react to changes in the pH value, according to their pK_a, and thereby determine the functionality of the enzyme. Knowledge of the titration behavior of these residues is crucial for the development of drugs targeting the active site residues. However, experimental pK_a data are scarce, since the systems’ size and complexity make determination of these pK_a values inherently difficult. In this study, we use single pH constant pH MD simulations as a fast and robust tool to estimate the active site pK_a values of a set of aspartic, cysteine, and serine proteases. We capture characteristic pK_a shifts of the active site residues, which dictate the experimentally determined activity profiles of the respective protease family. We find clear differences of active site pK_a values within the respective families, which closely match the experimentally determined pH preferences of the respective proteases. These shifts are caused by a distinct network of electrostatic interactions characteristic for each protease family. While we find convincing agreement with experimental data for serine and aspartic proteases, we observe clear deficiencies in the description of the titration behavior of cysteines within the constant pH MD framework and highlight opportunities for improvement. Consequently, with this work, we provide a concise set of active site pK_a values of aspartic and serine proteases, which could serve as reference for future theoretical as well as experimental studies.

Introduction

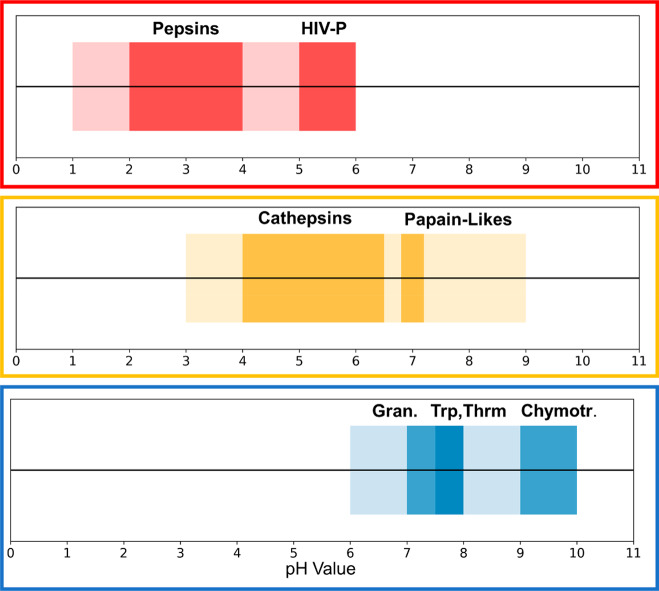
Proteases catalyze the cleavage of peptide bonds, a ubiquitous reaction in the whole biosphere. Indeed, 2–3% of all human genes code for proteases or protease inhibitors.¹ The function of the proteases is manifold. Processes from signaling cascades over digestion to programmed cell death are based on proteolytic processing.² Consequently, the physiological environments where proteases need to operate are very diverse as well, including vastly different ranges of acidity. For example, digestive proteases in the stomach at a pH of 2.0 have to catalyze the same reaction as proteases of the blood coagulation cascade at a pH of 7.4 and proteases in the gut at basic conditions.^3,4 An overview of the various activity profiles of aspartic, cysteine, and serine proteases is shown in Figure 1.^5,6 Taken together, these three families cover a broad pH range in terms of activity. While aspartic proteases are active in the acidic range, cysteine proteases cover the mild acidic to neutral range and finally serine proteases are mostly found active at neutral to slightly alkaline conditions.³⁻⁷

Figure 1.

Overview of the pH-dependent activity profiles of aspartic (red), cysteine (yellow), and serine (blue) proteases. Together these three families cover a broad pH span, ranging from very acidic, over neutral, to mildly basic pH values. The ranges of major subfamilies are highlighted in a darker shade of the respective color.

The major distinctions between these three families in terms of catalysis can be found in their active site architecture. The catalytic center of aspartate proteases consists of an aspartic dyad, of which one aspartate acts as a base and the other one as an acid during catalysis.^3,8,9 For this purpose, it is imperative that the dyad is in a monoprotonated state when the protease is active. In cysteine proteases on the other hand, a cysteine and a histidine constitute the active site, which form an ion pair, i.e., the cysteine is in its thiolate form, while the imidazole side chain of the histidine is protonated and therefore positively charged.^7,9,10 In contrast, serine proteases show a catalytic triad motif, consisting of an aspartate, a histidine, and a serine, of which only the aspartate is negatively charged, while the histidine and serine are ionized intermediately during catalysis.^4,9 In summary, the nature and arrangement of the active site residues are decisive for the pH-dependent activity ranges of the different protease families shown in Figure 1.

Different pH values or changes thereof lead to changes in the protonation states of titratable residues within a protein.¹¹⁻¹⁴ How a titratable residue reacts to different pH values is determined by its pK_a value.^9,15 The so-called intrinsic pK_a value of a titratable residue, i.e., the pK_a of the isolated amino acid, is perturbed by the complex electrostatic environment formed by its surrounding residues within a protein to the so-called macroscopic or apparent pK_a value.^9,16 Intrinsic pK_a values of the various titratable amino acids commonly found in proteins can be rigorously approximated by small peptides (e.g., of the form acetyl-GXG-amide), which are easy to measure directly (commonly by NMR) and readily available in the literature.¹⁶ However, within the complex environment of a protein, the direct determination of pK_a values can be very challenging or even impossible.¹⁶

All of the aforementioned active site residues, except serine, are titratable in the pH range of 0 to 10, in which also the discussed proteases are active.⁹ Thus, the titration states of the active site residues depend directly on the pH. In consequence, the pH determines whether or not the enzyme is active, since a well-defined protonation state configuration is imperative for activity.

As discussed above, the macroscopic pK_a values determine how the titratable residues in the active site react to a specific pH value, which in turn depends on the electrostatic environment they encounter and therefore on the structure of the active site itself. The pK_a values of the active site residues are thus decisive for inhibitor design and mechanistic investigations. However, the experimental determination of these pK_a values is extremely difficult, which is reflected by the low number of available pK_a values in the literature. In consequence, computational tools, which can reliably predict such pK_a values are of utmost importance. Over the last decades a multitude of such prediction tools have emerged, most of which can be generally divided into two groups.¹⁷ The group of static methods, e.g., PROPKA¹⁸ or H++,¹⁹ predicts pK_a values based on single or multiple static structures of a protein. In contrast, dynamic methods such as the family of constant pH molecular dynamics (cpHMD) methods use an ensemble of structures for protonation state predictions.²⁰ It is well-established that proteins in solution are inherently flexible, meaning they relentlessly fluctuate between diverse conformational states of varying probabilities.²¹⁻²⁵ Consequently, the structural environment around titratable residues is continuously changing and the protonation state ensemble is inevitably linked to conformational rearrangements. The cpHMD approach offers the unique opportunity to account for this intricate interplay of conformation and protonation. The approach not only incorporates a diverse set of conformations into the pK_a prediction itself, but also allows capturing how a protein structurally adapts to different pH values.²⁰

Most of the different cpHMD approaches can be attributed to two main groups, based on the treatment of the protonation states. On the one hand, protonation states can be treated discretely, and all titratable protons are explicitly defined at each titratable group and if not active are only present as ghost particles. The simulation is periodically interrupted, and the protonation state changes are attempted based on a Metropolis criterion.²⁶⁻³⁰ On the other hand, protonation states can be sampled along a continuous titration coordinate λ.^31,32 Similar to the concept of thermodynamic integration,³³ if λ is 0, the respective residue is protonated and if λ is 1, it is deprotonated; all states in between are unphysical. As in typical simulations only a small number of frames would meet this criterion, usually a cutoff is employed to maximize the number of analyzable frames. Recently, Radak et al. presented a hybrid nonequilibrium MD/Monte Carlo approach,³⁴ based on the works of Roux³⁵ and Stern.²⁸ Here, equilibrium MD is performed with fixed protonation states. Periodically, a nonequilibrium switch is attempted, sampling in the protonation and conformation space. Whether or not the switch is accepted is determined via a Metropolis Criterion. If the switch is indeed accepted, equilibrium MD continues with the new protonation state from the final conformation of the switch. If not, the simulation reverts back to the conformation before the switch attempt. This approach is implemented in the NAMD package.³⁶ For a more in-depth discussion of the various techniques, we point the reader to the respective works.^{26−32,34,35}

In this work we use cpHMD simulations to titrate the active site residues of selected proteases of the aspartic, cysteine, and serine protease families. We focus on the methods implemented in the AMBER software package.³⁷ We use primarily the Monte Carlo³⁸ (MC)-based cpH approach, as implemented in AMBER, with discrete protonation states, specifically the most recent variant by Roitberg and co-workers utilizing explicit solvent.³⁰ On the other hand, we also make use of the continuous cpHMD approach, which was also recently implemented in AMBER by Shen and co-workers.³²

Both aforementioned approaches of cpHMD have been combined with enhanced sampling techniques like replica exchange MD (REMD³⁹) and accelerated MD (aMD⁴⁰) in order to achieve efficient sampling of conformations and protonation states.^{29,30,32,41−44} The recent implementations of cpHMD on graphics processing units (GPUs) dramatically increased calculation speed. Hence, it is possible to capture dynamics at slower time scales with continuous trajectories at feasible computational costs. Here we use single pH cpHMD simulations, as they can be run easily in parallel with an arbitrary number of GPUs and show acceptable convergence behavior.⁴⁵

We apply this workflow to a set of 9 representative proteases from three of the four main largest protease classes distinguished by the catalytic mechanism.⁴⁶ On the basis of relevance in drug discovery and differences in pH-dependent activity profiles, we selected representative proteases from the aspartate, cysteine, and serine protease families. We excluded the family of metalloproteases, as for this family, the protonation/deprotonation events in the active site are closely linked to the coordinating ion. In order to capture this effect, a sophisticated description of the electrostatics and polarizability of the ion would be necessary, which is not possible for the force fields used within the cpHMD framework.

For the selected proteases we efficiently capture reliable protonation state ensembles. In addition to reference pK_a values, we provide atomistic insights to rationalize the origin of the strongly varying activity profiles.

Methods

System and Simulation Setup

All systems were prepared with the program MOE (molecular operating environment)⁴⁷ from X-ray structures, which are available in the PDB. The respective PDB codes are summarized in Table S1 in the Supporting Information. All crystal waters, agents, and ligands were removed if any were present. If multiple chains were present in the entry, the chain with the highest quality and sequence coverage was chosen based on the full PDB validation report.

The LEaP module of AmberTools 19³⁷ was used to add missing hydrogens and create topology and starting coordinate files. The AMBER ff99SB⁴⁸ force field coupled with the necessary modifications for constant pH MD simulations was used.^27,30 The GB radii of the titratable oxygens of aspartate were reduced to 1.3 Å as suggested by Swails et al.³⁰ All systems were placed in a truncated octahedral TIP3P water box with a minimum wall distance of 10 Å.⁴⁹

Furthermore, the cysteine protease papain was simulated using the GB-Neck2 implicit solvent model with the appropriate GB radii.⁵⁰ As there were no reference energies available for cysteine for this implicit solvent model, reference energies were derived as suggested in the AMBER manual.³⁷ For the derivation of partial charges and force field parameters of deprotonated, i.e., negatively charged serine, the structure was prepared with MOE and the needed parameters subsequently derived with Gaussian 16⁵¹ and the antechamber framework of AmberTools19.³⁷ Partial charges were derived with the RESP⁵² procedure.

Before production simulations, all systems were equilibrated with an elaborate protocol developed in our group.⁵³

All simulations were carried out with the pmemd module of AMBER 18, making use of both the CPU and the GPU implementation.³⁷ Calculations were carried out on the Vienna Scientific Cluster (VSC3 and VSC4) and on our in-house GPU cluster.

The Langevin thermostat⁵⁴ with a collision frequency of 5 ps^–1 was used to keep a constant temperature of 310 K, as was the Berendsen barostat⁵⁵ with a relaxation time of 2 ps to keep atmospheric pressure. The SHAKE⁵⁶ algorithm was used to restrain all bonds involving hydrogens, enabling the use of a 2 fs time step. Long range electrostatics were treated with the particle-mesh Ewald method⁵⁷ (PME), and a nonbonded cutoff of 8 Å was used. All systems were simulated at pH values from 0.0 to 10.0 (0.0 to 14.0 for papain) with a 0.5 spacing. For all MC-based cpHMD simulations, protonation state changes were attempted every 200 steps, followed by 200 steps of solvent relaxation after a successful attempt. For the GB calculations within the cpHMD framework, a salt concentration of 0.1 was used. For aspartic proteases, the two aspartates comprising the catalytic dyad were selected to titrate. For serine proteases, the aspartate and the histidine of the catalytic triad were selected to titrate. For the cysteine protease papain, two approaches were tested. On the one hand, both the cysteine and the histidine of the catalytic center were selected to titrate, and on the other hand, only the cysteine was titrated, while keeping the histidine in its doubly protonated, i.e., positively charged form. Frames were collected every 1000 frames. All simulations were run for 100 ns per pH value, resulting in 2.1 μs of aggregate simulation time per system.

For papain, the system was prepared following the procedure described by Shen and co-workers⁵⁰ and was simulated using the recent implementation of continuous cpHMD in AMBER 18.^32,45,50 In brief, CHARMM⁵⁸ with the CHARMM22 all-hydrogen force field⁵⁹ was used to add missing hydrogens, terminal cappings, set up the titratable groups, and perform initial minimizations. Hereafter, the minimized structure was prepared with LEaP using the AMBER ff14SB⁶⁰ force field with the necessary modifications for continuous cpHMD.³² The GB radius of the titratable sulfur was set to 2.0 Å as suggested by Shen and co-workers.⁵⁰ The subsequent simulations were carried out with the same settings as described above. For the continuous cpHMD specific settings, a mass of 10 amu was used for the lambda particles, a friction coefficient of 5 ps^–1 was used for the titration integrator, and the forces of the lambda particles were updated every step.

Analysis

All analyses were performed using cpptraj⁶¹ and pytraj from AmberTools 19,³⁷ combined with in-house python scripts. Analysis of the continuous cpHMD data was done with a python script provided by Shen and co-workers.⁶² Structural representations were created with PyMol.⁶³

Titration data from MC-based cpHMD simulations was analyzed with the cphstats program from AmberTools 19.³⁷ As the titrations of the catalytic residues were strongly coupled, titration curves were obtained by fitting the average number of total protons as was shown previously by Roitberg and co-workers for the HIV-1 protease (eq 1).⁶⁴ Setups in which only one residue was titrated were fitted to the modified Hill equation (eq 2).

1

2

Shifts in pK_a values were evaluated using capped tripeptide (acetyl-GXG-amide) pK_a values as published by Platzer and McIntosh as reference.¹⁶ Convergence of pK_a values was evaluated by monitoring the cumulative averages of the pK_a predictions.

To profile protonation state transition probabilities between the strongly active site residues in aspartate proteases, we set up a 4-state model based on the possible protonation state combinations of the respective titrated residues and calculated transition matrices based on these models, as we previously showed.⁶⁵ The matrices were then visualized as network plots, in which circle sizes denote state probabilities and arrow sizes transition probabilities.

Results

Chymotrypsin in Apo and Bound Form

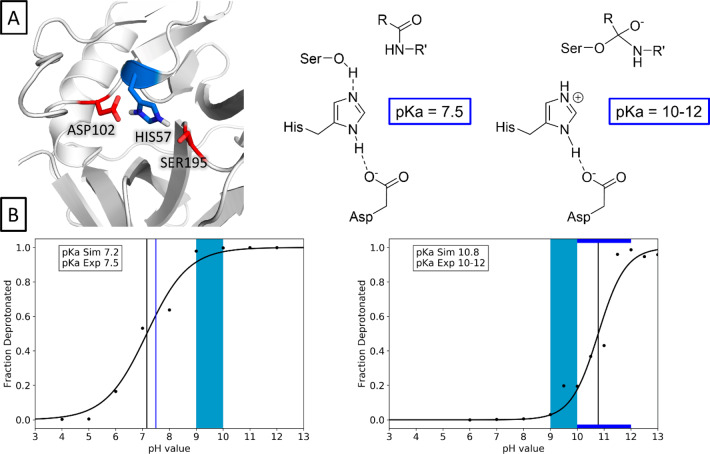
In order to benchmark the robustness of the applied constant pH MD simulation approach, we aimed to reproduce the pK_a change of the catalytic histidine associated with the activation of chymotrypsin described by Lin et al.⁶⁶

We used the apo enzyme as a model for the encounter complex of the protease and the peptide-compound as shown in Figure 2A. With a predicted pK_a value of 7.16, we closely reproduce the literature pK_a value of 7.5 (Figure 2B). We modeled the negatively charged complex of protease and peptide by simply deprotonating the catalytic serine residue, thereby introducing an additional negative charge (see Figure 2A). For this system, we find a pK_a value of 10.78, which is in line with the experimentally determined pK_a range of 10–12.

Figure 2.

Prediction of the pK_a shift of the catalytic HIS57 of chymotrypsin upon formation of the negatively charged complex. Complex structure and schematic representation are shown in the upper panel, titration curves obtained for the apo enzyme (left) and the complex (right) are shown in the lower panel. The light blue area denotes the active region of the enzyme, while experimental (blue), and predicted (black) pK_a values are shown as lines.

Serine Proteases

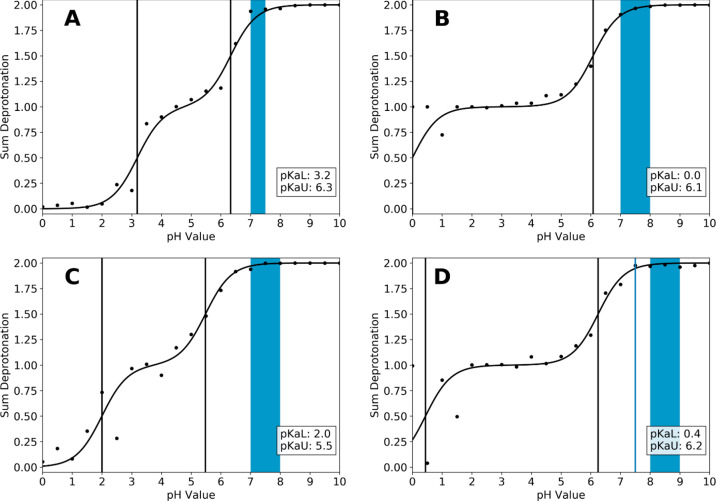
For the serine protease family, elastase, trypsin, granzyme B and chymotrypsin were considered. Reported activity ranges and experimental pK_a values (only available for chymotrypsin) are summarized in Table 1. Side chain pK_a values of the catalytic aspartate and histidine residues were determined with single pH constant pH MD simulation as described in the method section. Reported activity profiles and predicted pK_a values are summarized in Figure 3.

Table 1. Summary of Serine Proteases Which Were Considered in This Study^a.

protease	pH activity range	experimental pKa values
elastase	7–7.5	ND
trypsin	7–8	ND
granzyme B	7–8	ND
chymotrypsin	8–9	7.5

^aActivity ranges reported in literature and available experimental pK_a values are given.

Figure 3.

Titration curves and predicted pK_a values of the serine proteases elastase (A), trypsin (B), granzyme B (C), and chymotrypsin (D), which were considered in this study. Activity ranges reported in the literature are shown as colored boxes (Table 1). Experimental (only available for chymotrypsin) and predicted pK_a values are shown as blue and black lines, respectively.

As can be seen from Figure 3, all four systems show a similar titration behavior. In each system an acidic and a considerably higher, near neutral pK_a value were captured, which span a broad pH range in which a monoprotonated state is stable. While the upper pK_a value is at or near 6.0 for all systems, clear differences can be seen for the lower pK_a value. While for trypsin and chymotrypsin the lower pK_a is very acidic (below 1), this is less pronounced in elastase and granzyme B. For the latter, the titrations of the two active site residues appear to be coupled stronger and the pK_a differences are smaller compared to the other two systems (5.8 and 6.1 vs 3.1 and 3.5).

Furthermore, the upper pK_a value of 6.2 found here for chymotrypsin deviates more from the reported pK_a of 7.5 than the one reported for the isolated titration of the active site histidine described above (7.2).

The convergence analysis shows that all upper pK_a values converged after 50–60 ns. The lower pK_a values show a slower convergence, especially for granzyme B and chymotrypsin (see Figure S2 in the Supporting Information). This is in line with the titration curves in Figure 3, which show that the predictions are more noisy at lower pH values.

In relation to the respective active pH ranges, we find that for all systems the active range is located at pH values higher than both pK_a values, i.e., in a range where both residues are unprotonated.

Aspartic Proteases

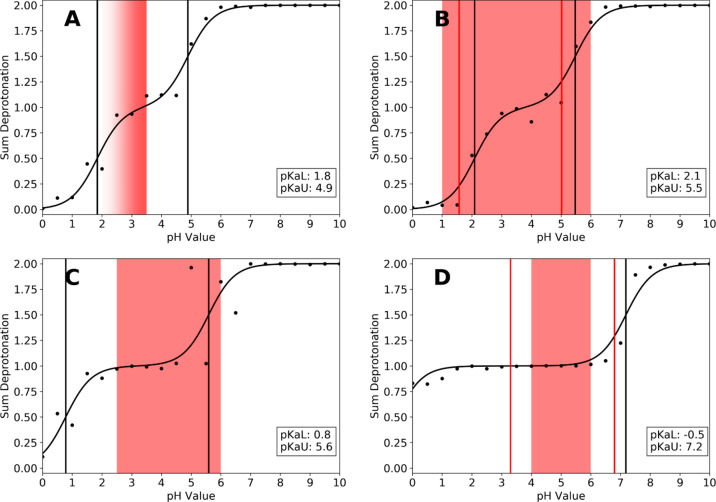
We selected a set of 4 aspartic proteases with varying pH activity ranges and experimental titration information, as summarized in Table 2. Side-chain pK_a values of the active site aspartate residues were predicted with single pH constant pH simulations as described in the Methods section. The calculated titration curves and respective predicted pK_a values are summarized in Figure 4.

Table 2. Summary of Aspartic Proteases Which Were Considered in This Study^a.

protease	pH activity range	experimental pKa values
chymosin	<3.5	ND
pepsin5	1–6 (optimum at 3.5)	1.57; 5.02
cathepsin D67	2.5–6.0	ND
HIV-protease 168−70	4.0–6.0	3.1–3.7; 4.9–6.8

^aExperimental activity ranges and available pKa values are given.

Figure 4.

Titration curves and predicted pK_a values of the aspartate proteases chymosin (A), pepsin (B), cathepsin D (C), and HIV-1 protease (D), which were considered in this study. Activity ranges reported in the literature are shown as colored boxes (Table 2). Experimental (if available) and predicted pK_a values are shown as red and black lines, respectively.

As can be seen from Figure 4, our approach closely reproduces the available experimental pK_a values of pepsin and the HIV-protease I. Furthermore, the calculated pK_a values envelop the experimentally determined active range of the respective protease (shown as colored boxes in Figure 4).

Both systems show notable pK_a shifts for both aspartates away from the free amino acid pK_a value (3.86 for aspartate¹⁶), with the effect being more pronounced in the HIV-protease. In both systems, one pK_a value is shifted more toward acidic and one toward more basic pK_a values compared to the free amino acid. Especially in pepsin, the titration curves appear to be strongly coupled, with practically no gap between the titrating regions, whereas in the HIV-protease, a monoprotonated state is stable for a broad pH range (pH 2.0 to pH 6.0). Consequently, the gap between the pK_a values is much smaller in pepsin (ΔpK_a = 3.4), compared to the HIV-protease (ΔpK_a = 7.7). In both cases, the experimentally determined active range of the respective protease is located between the two pK_a values, i.e., in the monoprotonated region. While for pepsin the reported active region somewhat exceeds both experimental and predicted pK_a values, the reported pH optimum of 3.5 is indeed located at the very center of the calculated titration curve.

Also for chymosin and cathepsin D, for which no experimental pK_a information is available, titration curves and pK_a values could be estimated. The calculated pK_a values show the same trend as already observed for pepsin and the HIV-protease I. Chymosin shows a strongly coupled titration behavior, similar to that of pepsin, with a small pK_a gap of 3.1. The activity maximum is reported to be below pH 3.5, which again lies at the very center of the monoprotonated region of the titration curve. Cathepsin D, on the other hand, shows a titration behavior similar to the HIV-protease I, in that the gap between the pK_a values is larger (4.8) and a monoprotonated state is stable over a longer pH range (pH 2 to 4). The reported activity range again lies in this pH region, below the upper pK_a value.

The convergence analysis of the predicted pK_a values shows that again all pK_a values converge within the 100 ns of simulation time. Most of the upper pK_a values again converge faster than their lower counterparts (see Figure S2 in the Supporting Information).

State and Transition Analysis

To characterize the transition paths and state distributions of the strongly coupled titrations seen for the aspartic proteases, we performed protonation state transition analyses. The active site titrations are modeled as a 4-state-system, based on the protonation states of the two aspartic residues (see Table 3). States 0 and 3 represent the fully deprotonated and fully protonated states, respectively, whereas states 1 and 2 both represent a monoprotonated state but distinguish which aspartate is protonated. Hereby all 4 variants of a protonated aspartate defined in the cpHMD framework are condensed into one state. The resulting transition matrices are visualized as network plots with circle and arrow sizes corresponding to state and transition probabilities, respectively.

Table 3. State Definitions Used for the Protonation State Transition Analyses of the Aspartic Proteases^a.

state number	ASP A	ASP B
0	0	0
1	0	1
2	1	0
3	1	1

^aProtonation states are denoted as 0 (deprotonated) or 1 (protonated).

We find that all proteases follow a similar, pH-dependent pattern in terms of state populations and transition probabilities. In Figure 5, the results for selected pH values of the pepsin simulations are shown exemplary. The analysis for all pH values can be found in the Supporting Information (Figure S1). We find that at very low or very high pH values, the fully protonated (state 3) or deprotonated (state 0) states are dominantly populated, respectively. Transitions to other, very sparsely, populated states do occur but are rare. At moderately acidic pH values, after the first titration has occurred, states 1 and 2, i.e., the monoprotonated states, increase in population until a near uniform distribution of all four states is reached. As the pH further increases, first state 3 and consecutively also states 1 and 2 diminish as state 0 becomes more and more populated. Furthermore, we note that primarily single state transitions occur, which correspond to transitions over the edges in the network plots in Figure 5. However, also transitions over the diagonal are visible, which correspond to both aspartates changing their protonation state at the same time. However, these transitions are very rare.

Figure 5.

Protonation state transition analysis performed for pepsin shown as network plots at selected pH values. Circle sizes and arrow thickness corresponds to state populations and transition probabilities, respectively.

Cysteine Proteases

For the family of cysteine proteases, experimental pK_a values are available for a number of systems,⁹ all of which show a very strong acidic shift of the active site cysteine residue away from its tripeptide pK_a value of 8.5. The pK_a values of active site cysteine residues have been reported to be extremely challenging to predict, with most of the available prediction tools failing to predict experimentally determined pK_a shifts and even predicting shifts into the wrong direction.⁷¹ Here, we selected papain as a test system, which shows a strong acidic shift of the active site cysteine of −5.2 pK_a units (from 8.5 down to 3.3).⁹

We used single pH constant pH MD simulations to predict the active site pK_a value, as described in the Methods section. The resulting titration curves and pK_a values are shown in Figure 6A. Clearly, our approach not only mispredicts the pK_a value of CYS25 but also does not capture the acidic pK_a shift at all. As can be seen from the titration curve in Figure 6A, CYS25 does not titrate at all in the pH range, which was used for the aspartic and serine proteases and only starts to titrate at a pH as high as 12.0.

Figure 6.

Titration of papain active site residues CYS25 and HIS159 with MC based constant pH MD with implicit solvent models GB^OBC (A) and GB-Neck2 (B), cpH REMD with the GB^OBC model (C) and continuous cpHMD (D). Experimental pK_a value of CYS25 of 3.3 could not be reproduced with any approach, with the simulations using the GB^OBC model (A and C) showing no titration at all.

In order to analyze the source of these erroneous predictions, we repeated the simulations utilizing different implicit solvent models and GB-radii for the sulfur, as was suggested recently by Shen and co-workers.^32,50 To do this, we had to derive the reference energies for cysteines, which are necessary for the cpHMD workflow, since they were not yet available for the GB-neck 2 model and different GB radii (see Figure 6B). Furthermore, we employed the constant pH replica exchange (cpH REMD) technique, which is implemented in AMBER. This approach was shown in multiple works to increase both protonation state and conformational sampling (see Figure 6C). Finally, we also repeated the simulations utilizing the recent implementation and setup of continuous cpHMD in AMBER by Shen and co-workers (see Figure 6D).

While the titration curves in both Figure 6B (GB-Neck2 implicit solvent model) and Figure 6D (continuous cpHMD) show notable improvements in the titration prediction of the active site cysteine, the predicted pK_a values (8.75 and 9.80, respectively) are close to the pK_a value of free cysteine (8.5) and the strong acidic shift, which was observed in experiments, could not be captured. In contrast to this, no benefit in terms of pK_a prediction could be achieved with the cpH REMD setup compared to single pH simulations.

Discussion

We use single constant pH MD simulations to predict the active site pK_a values of various members of the aspartic, serine, and cysteine protease families. We further investigate the molecular origins which could explain the observed differences in the pH activity ranges within the individual families.

Chymotrypsin Apo and Bound

As structural data of substrate-bound complexes are limited, we simulated all proteases in their apo-state. Nevertheless, we recognize that the presence of a substrate, especially with charged residues, in the active site might influence the pK_a values of titratable active site residues. For chymotrypsin, experimental pK_a values for both the apo enzyme as well as for various trifluoro-peptidyl complexes are available (see Figure 2A).^9,66 To assess, how well our approach can capture such changes in the active site, we predicted the pK_a value of the apo enzyme as well as for the modified enzyme. We approximated the peptide-bound form with a simple negatively charged serine (see Figure 2A). While this is a drastic simplification, we presume that in terms of pK_a shift potential the additional negative charge in the active site represents the most decisive aspect. As there is no high-quality structural data of these complexes available, we assume that the error introduced by this simplification is smaller, compared to the inaccuracies resulting from modeling the rather large complex into the binding site. The validity of our approximation is supported by the pK_a values we obtain from our simulations as shown in Figure 2B. With an unsigned error of 0.32 pK_a units, we closely reproduce the reported pK_a value of the free enzyme. For the complexes, we find a strong basic shift for the active site histidine. This shift can be directly attributed to the additional charge on the serine residue. The experimental pK_a values for the bound enzyme range from 10 to 13 depending on the complexed peptide. Our predicted pK_a of 10.8 is perfectly in line with these results. This indicates that despite the simplified representation of the bound state, we still capture the strongest perturbation driving the pK_a shift, which is indeed the additional negative charge.

Aspartate Proteases

In Figure 4, we summarize predictions and experimental references for the family of aspartate proteases. As can be seen from Figure 4B,D, our approach closely reproduces the available experimental pK_a values of pepsin and the HIV-1 protease.^5,68−70 Notably, in both systems one pK_a value is predicted to be shifted into the acidic and the other one into the basic direction, compared to the tripeptide reference values of aspartate. Our calculations reproduce these shifts for both proteases. Furthermore, we find that the experimentally reported activity range lies between the two respective pK_a values.

These findings are consistent with the mechanistic picture of a monoprotonated catalytic dyad in active aspartic proteases. To make an example with our predicted pK_a values, following this argument, pepsin should quickly become inactive if the pH falls below 2.1 or rises above 5.5. Indeed, pepsin is reported to be active between pH 1 and pH 6, i.e., in the pH range where a monoprotonated state is predicted to be stable (see Figure 4B). A similar picture can be found for the HIV-1 protease (Figure 4D). Also here the experimental pH range from 4 to 6, in which the enzyme is found active, lies between the predicted pK_a values of −0.5 and 7.2. In contrast to pepsin, the lower pK_a value was predicted to be extremely acidic in our simulations compared to the experimental pK_a values (3.1 or 4.9 depending on the reference). Roitberg and co-workers studied the influence of ligand binding on the active site pK_a values of the HIV-1 protease and predicted pK_a values of 1.29 and 7.32 for the apo enzyme.⁶⁴ While their upper pK_a value is very close to ours (7.32 to 7.2), the lower pK_a value they find is still less acidic than the one we find (1.29 to −0.5). However, both times the lower pK_a is found to be clearly more acidic than in the experiment. With a pK_a difference of 7.7 pK_a units, the pH range, in which a monoprotonated catalytic dyad is stable, is very broad in our simulations. Interestingly, the enzyme is reported to be active in only a small pH window at mildly acidic conditions (pH 4 to 6), thereby using only a portion of the pH range which would be possible from a mechanistic point of view. However, the activity itself is a very complex parameter, which depends not only on the pH value and protonation states, but also on the respective substrate, the exact assay conditions, and the fold stability of the enzyme toward extreme pH values. The fact, that the reported activity range of pepsin somewhat exceeds the margins given by the pK_a values (regardless if predicted or experimental) can also be explained by this argument.

Our findings for chymosin and cathepsin D (see Figures 4A,C, respectively) are in line with the arguments made for pepsin and the HIV-1 protease. At the time of writing this manuscript, no experimental pK_a values from direct titration experiments but only activity profiles were available in the literature for chymosin and cathepsin D. Chymosin was reported to be most active at and slightly below pH 3.5, indicated by the fading color of the panel in Figure 4A. The titration curve we obtain shows a lower pK_a value at 1.8, followed by a small plateau at pH 3.5, which means that a monoprotonated state is predicted to be stable right at the reported most active pH. The loss of activity at higher pH values can be attributed to the second aspartate starting to titrate around pH 4.0 (predicted pK_a of 4.9), thereby inactivating the enzyme. Cathepsin D on the other hand, shows a titration behavior similar to the HIV-1 protease, in that the difference between the two pK_a values is more than 1 pK_a unit larger than in chymosin or pepsin. In consequence, also the plateau between the two pK_a values is broader and a monoprotonated configuration is stable over a broader pH range. Cathepsin is reported to be mostly active at pH values from 2.5 to 6.0, depending on the assay conditions and the substrate. This fits very well with the pK_a values we find for the catalytic dyad (0.8 and 5.6, respectively), as they suggest a stable monoprotonated state over the reported active pH range. Shen and co-workers reported calculated pK_a values of cathepsin D of 2.9 and 4.7, which in turn narrows the range in which a monoprotonated state is predicted to be stable.⁶⁷ Intriguingly, the only available experimental pK_a values of 4.1 and >5 are significantly higher than the predictions of Shen and co-workers and this study. Furthermore, this would suggest that a monoprotonated form is only stable at pH values above 4.1, which stands in contrast to the reported active ranges. However, as the reported experimental pK_a values do not stem from a dedicated titration study, but were estimated from kinetic profiles, it is possible that they are limited by the employed assay conditions.

To evaluate the potential errors of our pK_a values stemming from the discontinuities of the titration curves (see Figure 4), we reran the simulations for cathepsin D and pepsin using the pH-REMD approach implemented in AMBER. As can be seen from Figure S3 in the Supporting Information, for pepsin no notable change was found for the lower pK_a value, while the error of the upper pK_a value compared to the experiment increased by a small margin. On the other hand, for cathepsin D, both pK_a values come closer together, with especially lower pK_a showing a higher value than in our single pH simulations. As expected, with the REMD approach, the discontinuities disappear for both systems. However, as the overall picture does not change and the resulting pK_a values are very similar for both methods, we observe no indication that the discontinuities significantly contribute to the deviation from the experimental values.

While the differences in upper pK_a value are small for chymosin, pepsin, and cathepsin D (4.9, 5.5 and 5.6), they differ significantly from the upper pK_a of the HIV-1 protease (7.2). As all proteases were simulated in their apo form, we conclude that structural differences of the enzymes themselves must be a source of this difference. We have previously shown, that within the constant pH framework and the used force fields, proximal charges and to a lesser degree H-bonds have the biggest potential of perturbing pK_a values.⁶⁵ However, there are no positively charged residues close enough to the active site aspartates to form ion pairs in any of the studied enzymes. Hence, we calculated the average number of H-bonds formed by the catalytic dyad to proximal residues with polar side chains for each pH value. As can be seen from Figure 7, the HIV-1 protease forms around 1 H-bond with neighboring residues before the first titration, after which this number increases to around 4 H-bonds. In contrast to that, pepsin and cathepsin D can form 2.5 H-bonds on average in their doubly negative form and chymosin fluctuates around 3 H-bonds on average. This suggests, that the negative charges in chymosin, pepsin, and cathepsin D are stabilized by an H-bond network with neighboring residues, which is not present in the HIV-1 protease. This in turn could explain the notable shift of the upper pK_a value for the HIV-1 protease, as the number of stabilizing H-bonds drastically increases to 4 H-bonds on average, as soon as the dyad is monoprotonated. The increase in the average number of H-bonds after the first titration is visible for all studied systems, albeit less pronounced compared to the HIV-1 protease. This can be attributed to the special structural arrangement of the catalytic aspartates, which enables the formation of H-bonds between the aspartates when at least one is protonated and thus further stabilizes the monoprotonated state. This is in line with the discussion above and supported by the experimental activity ranges, which report maximum activity of the respective proteases in these regions.

Figure 7.

Average number of hydrogen bonds formed by the catalytic dyads of chymosin (A), pepsin (B), cathepsin D (C), and HIV 1 protease (D).

Due to the spatial vicinity, the titration behavior of the two active site aspartates is expected to be strongly coupled. We thus profile the effect of this coupling by performing a transition analysis based on the possible protonation state combinations of the catalytic dyad. We illustrate this behavior for pepsin in Figure 5, with a focus on the pH region in between the two apparent pK_a values. Here, the state populations indeed suggest primarily a monoprotonated form of the dyad, as is expected from the titration curves. At pH 4.0, all states are almost equally populated with a high number of edge (i.e., single proton) transition between all states. However, at the flanking pH values of 3.0 and 5.0, we note a certain preference in terms of which aspartate is protonated. On the one hand, this could point to a simple convergence issue and could be resolved by extending the simulations; on the other hand, this could mean, that protonation on one aspartate is indeed more stabilized than on the other. To exclude a convergence issue, we extended the simulations to 200 ns per pH, i.e., doubling the simulation time per pH value. However, the state distributions are remarkably stable and do not change significantly with longer simulation time. Furthermore, it is intriguing that single state transitions (transitions over the edges in Figure 5) are far more frequent than both residues changing their protonation state in the same step (diagonal transitions in Figure 5). This is especially interesting for the transition between states 1 and 2 which corresponds to both residues swapping the proton. As both residues are directly interacting with each other, the overall change for the system would be very small; however, the deprotonation of one residue and the protonation of the other in the next step is clearly favored.

Serine Proteases

For serine proteases except chymotrypsin, no reliable active site pK_a values could be found in the literature at the time of the writing of this manuscript. Therefore, the quality of the pK_a prediction is evaluated based on the reported activity profiles of the respective protease. As already stated above, for these systems we did not titrate the whole catalytic triad but only the catalytic aspartate and histidine. Serine is generally not considered titratable in the investigated pH range from 0 to 10.

As can be seen in Figure 3, all studied systems show a similar titration behavior, in that a quite acidic pK_a value below 1.0 and a near neutral pK_a value is predicted for the titrated residues. In relation to the reported active pH ranges, we find for all studied systems that both pK_a values are below the reported active ranges. This means that both residues are in their deprotonated form, i.e., aspartate is negatively charged, while the histidine is neutral. This is well in line with the mechanism of serine proteases, in which a neutral histidine is strongly polarized by the neighboring aspartate and in consequence abstracts a proton from the catalytic serine, which in turn enacts the nucleophile attack on the substrate. It is therefore imperative for activity, that the histidine is in its neutral form and the aspartate is negatively charged. This is reflected in our predicted pK_a values for all studied systems.

While the upper pK_a values for all studied systems are relatively similar and all lie within the error margin of our cpHMD approach of ±1 pK_a units, significant differences in the lower pK_a values can be identified. In the case of trypsin and chymotrypsin (Figure 3B,D), the respective lower pK_a values corresponding to the titration of the catalytic aspartate are located below 1, clearly separating them from the upper pK_a values which are around 6. In contrast, the titrations of elastase and granzyme B (Figure 3A,C) appear to be much more coupled, with a separation of around 3 pK_a units. This difference can be attributed to differences in the H-bond network, which the catalytic aspartate can form with neighboring residues. In detail, a tyrosine residue (Y94, chymotrypsin numbering), which is conserved in trypsin and chymotrypsin and represents a potential H-bond partner for the catalytic aspartate, is mutated to tryptophan in elastase. This loss of interaction could potentially destabilize the deprotonated, i.e., negatively charged form of the catalytic aspartate and in turn lead to an elevated apparent pK_a value. This hypothesis is supported by an H-bond analysis, shown in Figure 8. Clearly, the catalytic aspartate in trypsin (Figure 8C) forms 1 H-bond more on average than the respective aspartates in elastase (Figure 8A) and granzyme B (Figure 8B). Interestingly, the same shift cannot be seen so clearly for chymotrypsin (Figure 8D). We surmise, that while the interaction is not recognized as such by the employed metric, the polar interaction of the side chain is still present and will perturb the apparent pK_a value of the catalytic aspartate.

Figure 8.

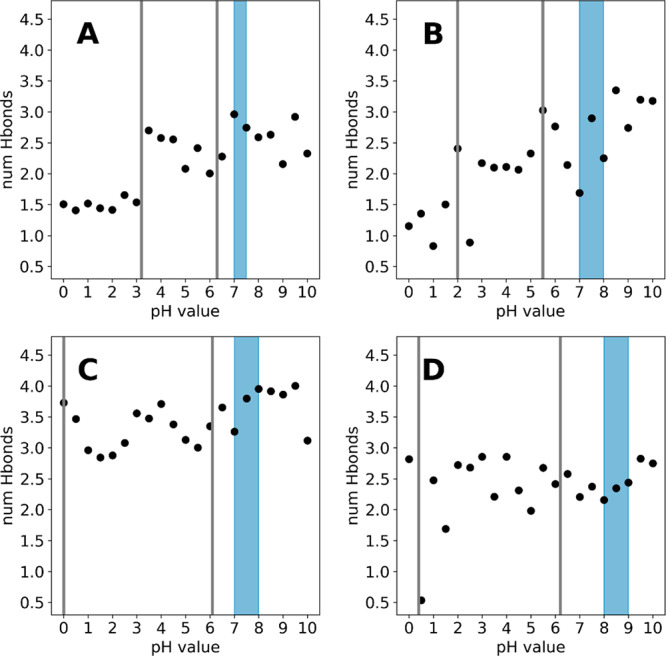
Average number of hydrogen bonds formed by the catalytic aspartate of elastase (A), granzyme B (B), trypsin (C), and chymotrypsin (D).

Cysteine Proteases

Compared to serine proteases, in which the catalytically active serine gets deprotonated intermediately during the reaction and directly attacks the substrate, the catalytic cysteine in papain and other cysteine proteases forms an ion pair with a neighboring histidine residue even in the apo state of the enzyme.^9,72 Since the tripeptide pK_a value of cysteine of 8.5¹⁶ suggests a protonated form at physiological and especially at acidic conditions, a strong perturbation of the cysteine pK_a value is necessary in order to facilitate the ion pair formation. Indeed, for papain and papain-like proteases like caricain and ficin strongly perturbed pK_a values as low as 3.3, 2.9, and 2.5, respectively, have been reported in the literature.^9,72 This strong shift of more than 5 pK_a units is generally attributed to the aforementioned ionic interaction with the neighboring histidine. However, common prediction tools are reportedly unable to capture these strong shifts in the aforementioned systems and strongly mispredict the respective cysteine pK_a values.⁷¹

As can be seen from Figure 6, unfortunately also our approach falls short in predicting the pK_a shift of the catalytic cysteine of papain (experimental pK_a of 3.3). Indeed, with the implicit solvation model, which was successfully used for the other families, no clear titration of cysteine could be observed in the pH range from 0.0 to 14.0 (see Figure 6A). In an effort to pinpoint the source of this erroneous behavior, we switched the used implicit solvent to the most recent GB-Neck 2 model, coupled with the increase of the GB radius of sulfur to 2.0 Å as suggested recently by Shen and co-workers.⁵⁰ This had the notable effect that we now capture a titration of cysteine, resulting in a pK_a value of 8.7 (see Figure 6B). However, the strong acidic shift is still not captured. Furthermore, we repeated the simulations using a replica exchange protocol in order to allow for a coupling of the pH values, but also this did not improve the prediction (Figure 6C). To exclude a deficiency of the MC-based constant pH framework, we reran the simulation with the recent implementation of the continuous constant pH approach in AMBER by Shen and co-workers, following their suggested setup for the treatment of cysteines.⁵⁰ However, as can be seen from Figure 6D, while we capture a titration of the cysteine, we still are not able to predict the strong acidic shift. We would like to note here, that while this manuscript was under revision, Shen and co-workers published a broad benchmark study predicting cysteine pKa values against experimental reference. With refined parameters, they were able to very accurately reproduce even strong pKa shifts (i.e., in papain). We would like to refer the interested reader to their publication.⁷⁴

We see a few possible reasons why the correct pK_a values or at least an acidic shift could not be predicted. First, the predicted pK_a values might correspond to a limited and strongly biased protonation state ensemble, stemming from insufficient conformational sampling. As the time scales, which can be covered in standard MD simulations, are generally several orders of magnitude below the time scales on which the experimental reference values are measured on, it could be possible that we only observe a very small fraction of the experimental conformational space. As the observed protonation state ensemble is closely linked to the conformational ensemble, also the apparent pK_a values we obtain will in turn only correspond to this small sub-ensemble. Large conformational changes, which happen at much slower time scales, might severely alter the underlying conformational ensemble and in turn also the predicted pK_a values. However, we deem this scenario to be very unlikely, as the prediction errors are extensive both in terms of the actual value as well as in the shift direction. Furthermore, this would also mean that the crystal structure and conformations close to it would represent an almost negligible part of the conformational ensemble at slower time scales. Thus, we surmise that a systematic error in the titration prediction is the source of the erroneous cysteine pK_a predictions.

Second, failing to capture the perturbation-effect itself could lead to a complete misprediction of the pK_a values. However, as discussed above, the main perturbation of the pK_a of CYS25 in papain comes from the ionic interaction with HIS159, an interaction that is generally well captured within the cpHMD framework.⁶⁵ To rule out a possible effect of the titration of HIS159, we reran the simulation, not allowing HIS159 to titrate and keeping it in its positively charged form (data not shown). As this did not change the pK_a prediction of CYS25, we presume that also this scenario is not the definitive error source.

Third, the description of the sulfur and its titration in the context of partial charges could be problematic. Since the titration of the reference compounds works without any issues, we presume that the description of the sulfur or the titration itself is not a problem when an isolated cysteine is considered but rather arises when the cysteine is located in a complex, i.e., protein environment. Shen and co-workers recently used the continuous constant pH MD implementation to successfully reproduce the pK_a value of the creatin kinase.⁵⁰ As the cysteine pK_a values in kinases are generally perturbed less than the ones found in proteases like papain,⁹ this could mean that only very strong perturbations are not captured correctly. This could be linked to the strong polarizability of sulfur, an effect that is neglected in all tested cpHMD approaches, as no polarizable force fields are used.⁷³ We therefore presume that either a more sophisticated description of the electrostatics of sulfur or the incorporation of polarizable force fields would significantly improve the prediction. The aforementioned approach by Radak et al. as implemented in the program NAMD holds great promise in this regard due to its modular implementation with generally no prior assumption of the used force field.³⁴

Conclusion

We apply constant pH MD simulations to provide pK_a estimations for active site residues of a set of 9 different proteases. While the constant pH MD framework has been successfully applied to protease systems before, to our knowledge no study was published yet, which systematically predicts and summarizes active site pK_a values of multiple protease families.

We find that our predictions are consistent with the available experimental pK_a values and are in sound agreement with the strongly varying pH activity profiles of aspartic and serine proteases. All titrated active site residues show substantial shifts away from the tripeptide pK_a values. The applied sampling strategy successfully captures this behavior, highlighting the benefits of dynamic pK_a prediction tools compared to static algorithms. The approach also allows us to depict the strongly coupled titration behavior found for some of the studied systems, which we show in detail for pepsin. Furthermore, we find pH-dependent H-bond networks which could explain the varying protonation and thus pH activity profiles. We presume the discussed residues as promising starting points, e.g., for protein engineering efforts toward tailored pH activities. However, we also clearly identify limitations of the methodology in terms of treating the strongly polarizable sulfur. Nevertheless, as the field of cpHMD simulations is rapidly progressing, we see these findings as an opportunity to enhance the reliability of this method even further.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jcim.0c00190.

• Summary of the PDB codes used to generate the starting structures for the simulations, transition analysis for pepsin on all simulated pH values, convergence analysis of all calculated pK_a values, titration curves for pepsin and cathepsin D obtained with cpH-REMD (PDF)

The authors declare no competing financial interest.