Experimental Phasing of MicroED Data Using Radiation Damage

Graphical Abstract

SUMMARY

We previously demonstrated that microcrystal electron diffraction (MicroED) can be used to determine atomic-resolution structures from vanishingly small three-dimensional crystals. Here, we present an example of an experimentally phased structure using only MicroED data. The structure of a seven-residue peptide is solved starting from differences to the diffraction intensities induced by structural changes due to radiation damage. The same wedge of reciprocal space was recorded twice by continuous-rotation MicroED from a set of 11 individual crystals. The data from the first pass were merged to make a “low-dose dataset.” The data from the second pass were similarly merged to form a “damaged dataset.” Differences between these two datasets were used to identify a single heavy-atom site from a Patterson difference map, and initial phases were generated. Finally, the structure was completed by iterative cycles of modeling and refinement.

In Brief

Demonstration of experimental phasing with the cryoEM method MicroED. Data collected from two passes over the same crystals are subtracted. Differences are caused by radiation damage, and used to identify a single zinc site. Initial phases are calculated at 2.5Å, extended to 1.4-Å resolution, and the structure is built manually.

INTRODUCTION

Microcrystal electron diffraction (MicroED) is an cryoelectron microscopy (cryoEM) method that determines atomic-resolution structures from vanishingly small three-dimensional crystals (Shi et al., 2013). The crystalline sample is exposed to the electron beam in diffraction mode under cryogenic conditions. Data are collected using a fast camera as a movie as the crystal is continuously rotating on a fixed axis (Nannenga et al., 2014). Continuous-rotation MicroED and similar techniques have been used by several laboratories worldwide to determine structures of previously unknown proteins, protein complexes, ion channels, peptides, small molecules, and inorganic material (Clabbers et al., 2017; Gemmi et al., 2015; Gruene et al., 2018; Jones et al., 2018, 2019; de la Cruz et al., 2017; Liu and Gonen, 2018; Palatinus et al., 2015, 2017; Rodríguez et al., 2015; Wang et al., 2018; Xu et al., 2018; Yonekura et al., 2015).

To date, all structures determined by MicroED were phased either by molecular replacement (MR) or ab initio direct methods. Direct methods are only applicable to crystals whose diffraction intensities extend to very high resolution; in practice to 1.2Å or better (Morris and Bricogne, 2003; Sawaya et al., 2016). Crystals that do not diffract to these resolutions can often be phased by MR if a homologous structure is available (McCoy et al., 2007; Scapin, 2013). In cases where no search model is available and diffraction is worse than 1.2Å, phases must be recovered by other means. Phasing in electron crystallography of two-dimensional protein crystals and three-dimensional inorganic materials have been previously demonstrated using imaging (Henderson and Unwin, 1975; Henderson et al., 1990; Zou et al., 2003); however, to our knowledge no examples of successful experimental phasing have been reported using only MicroED data from three-dimensional crystals of biological material.

Interpreting a density map in terms of an atomic model is the final step of crystallography analysis. To generate a density map into which the atomic model is built, both the structure factor amplitudes and phases are required. Amplitudes are proportional to the square root of the reflection intensities, which are measured to sufficient accuracy by modern detectors, but the phase information is lost in MicroED measurements just as in X-ray crystallography, giving rise to what is known as the “phase problem”(Rhodes, 1993; Taylor, 2003). The inability to directly measure the phase can be circumvented by using the phases from a homologous structure in MR (McCoy et al., 2007; Rossmann, 1990). For sufficiently small molecules, diffracting to very high resolution, phases can be calculated ab initio (Hauptman, 1986; Sheldrick, 2007). For macromolecules without a sufficiently similar, known structure, the phases must be determined experimentally by calculating the phase of each structure factor from the diffraction intensities. In X-ray crystallography, the anomalous scattering of heavy atoms results in measurable differences between the intensities of Friedel mates I_hkl and I_-h-k-l (Guss et al., 1988). These differences allow for the determination of the heavy-atom substructure of the protein using single or multiple anomalous dispersion (SAD or MAD) (Hendrickson, 1991; Rice et al., 2000). The heavy-atom phases are then used to generate initial phases of the protein structure, and initial density maps may be generated. Electrons do not undergo this type of anomalous scattering (Parthasarathy, 1961), so this approach is not feasible with MicroED.

Before the widespread availability of tunable synchrotron sources necessary for SAD/MAD experiments, it was common to use heavy metal phasing approaches to solve the phase problem (Green et al., 1954; Perutz, 1956). Here the protein is crystallized in its “native form” and these crystals are then soaked in heavy atoms, such as lead, tungsten, or platinum, to yield a “derivative.” Data would be collected from both the native and derivative crystals, resulting in two sets of scattering amplitudes. Because the heavy atoms scatter X-rays more strongly than the lighter protein atoms, the difference in amplitudes between the two otherwise identical structures would allow for the location of the heavy atoms and generation of initial protein phases. This technique is known as (single or multiple) isomorphous replacement (SIR/MIR) (Crick and Magdoff, 1956) because it requires that the lattice of the native and the derivative crystals are the same (isomorphous). However, soaking heavy atoms into proteins can often destroy the crystal or change the unit cell. Such non-isomorphism precludes calculating a meaningful difference map, and renders location of heavy atoms impossible, preventing structure determination altogether. Isomorphous replacement is effective in X-ray scattering but not so much with electron scattering. The difference in electron scattering between light and heavy atoms is much smaller in comparison, leading many to suggest that the SIR/MIR approach would be considerably more difficult using electron diffraction (Ceska and Henderson, 1990).

Radiation damage from the X-ray beam has been used to generate initial phases without having to modify protein crystals (Nanao and Ravelli, 2006; Ravelli et al., 2003, 2005; Thorn et al., 2012). This has been named radiation-induced phasing (RIP) (Nanao et al., 2005). Here, the exposure to the X-ray beam resulted in changes to specific parts of the protein, such as the breaking of disulfide bonds (Galli et al., 2015; Ravelli et al., 2005). Partitioning the data into a damaged and undamaged set allows location of these sites, using methods analogous to those used in anomalous dispersion or isomorphous difference experiments. The RIP approach to generating initial phases avoids the complication of crystallizing the sample under different conditions or soaking heavy metals into the delicate protein crystals. Non-isomorphism is also a much lesser concern because the two datasets are collected from the same crystal. Despite this, the RIP has not been widely adopted by the protein crystallography community, with only a handful of PDB entries being solved using this method. This low use is likely due to the widespread availability of MR models (McCoy et al., 2007), automatic structure solution pipelines (Panjikar et al., 2005; Rodríguez et al., 2009; Terwilliger et al., 2009), and relative ease of selenomethionine (SeMet) derivatization (Hendrickson et al., 1990).

Here, we demonstrate that radiation damage from exposure to the electron beam can be used to generate initial phases in MicroED experiments when combined with a metal. Two sweeps of continuous-rotation MicroED data were collected from 11 crystals of a seven-residue polypeptide (~900 Da). Crystals of this peptide could only be grown in the presence of zinc acetate, and a single zinc atom incorporated into the asymmetric unit (Hattne et al., 2018). We denote the merged, first-pass data as the “low-dose” dataset. The merged data from the second pass we refer to as the “damaged” dataset. The difference in the amplitudes between these two datasets was calculated and used to identify the zinc site in the unit cell. The full atomic model was iteratively built out from the initial phases from this single heavy-atom solution.

RESULTS

The diffraction images used to initially determine the structures PDB: 6CLI and PDB: 6CLJ were integrated and truncated to 2.5-Å resolution (Hattne et al., 2018). 6CLI corresponds to the structure of the peptide GSNQNNF after an average exposure of 0.17e⁻Å⁻², and 6CLJ corresponds to the same structure after an exposure of 0.5 e⁻Å⁻². The structure factor amplitudes from the latter, damaged dataset were subtracted from the amplitudes from the former, low-dose dataset. Amplitudes for each reflection were used to calculate a difference dataset, and isomorphous difference Patterson maps were calculated for the difference dataset (Figure 1). At 2.5-Å resolution, 11 peaks >3σ were found in the native Patterson map of the low-dose dataset. None of these peaks correspond to locations of atoms in the known structure. Scaling coefficients (DSCA values in SHELXC) were screened over the range of 1.05–0.8. Isomorphous difference Patterson maps were calculated for each value, and the peaks >3σ were noted. In the isomorphous difference Patterson, a single peak was found that came in and out of the significance cutoff of 3σ between DSCA values of 0.97 and 0.81, with the highest value at a scaling factor of 0.85 (Figure 1). Using this scaled difference dataset, a difference Fourier was calculated using the phases from 6CLI to identify where the signal was being generated. A strong peak (>6σ) was identified in the difference Fourier map that corresponded to the location of the zinc (Figure 1). Using the scaling value of 0.85, the highest peak was used to place a single zinc atom. The single-atom solution was refined, and initial phases were generated at 2.5-Å resolution (Figure 2). The location of the refined zinc site from this solution was correct and was within 0.2Å of the previously refined location of the zinc in 6CLI (Hattne et al., 2018).

Figure 1. Differences between the Low-Dose and Damaged Datasets at 2.5-Å Resolution.

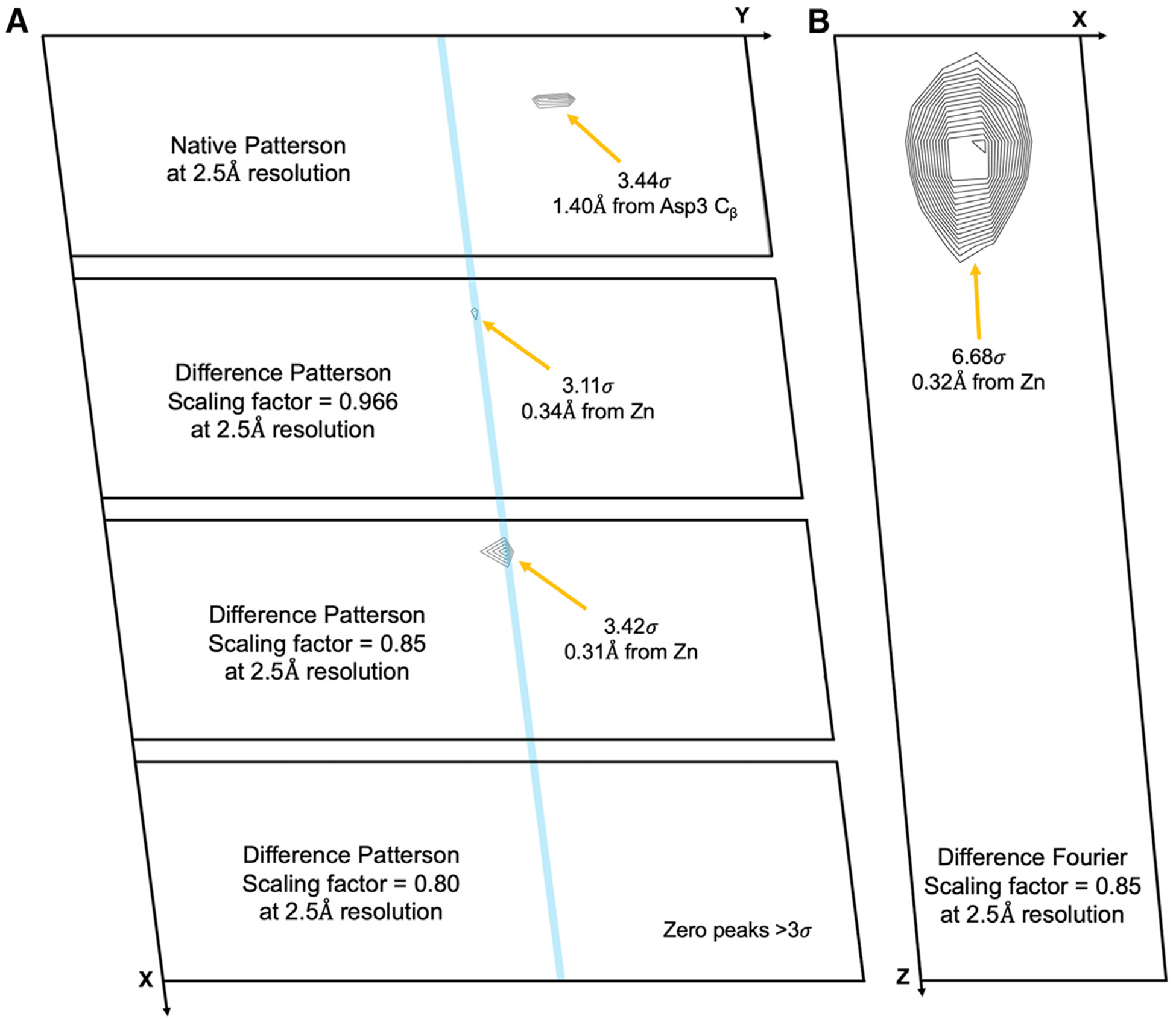
(A) Patterson maps for the native (top), and isomorphous differences at scaling factors 0.966 (top middle), 0.85 (bottom middle), and 0.8 (bottom). Blue line indicates the plane of the zinc atom shared between plots. (B) Difference Fourier map at 2.5-Å resolution using a scaling factor of 0.85. Patterson maps are displayed at the z = 22 slice. Difference Fourier map is displayed at the y = 22 slice. All slices are displayed with a 3σ cutoff and have contour steps at the 0.1σ level. Peaks and their corresponding locations are indicated by arrows.

Figure 2. Locating the Heavy-Atom Substructure and Building Out the Structure.

(A) Fourier difference maps between the damaged and undamaged structure of GSNQNNF using the phases of 6CLI at 2.5-Å resolution contoured at 3σ level (top). Initial phases generated at 2.5-Å resolution (middle), and the map using the initial phases extended to 1.4-Å resolution (bottom). (B) Density maps at 1.0σ contour starting from the initial phases (top) with structures of intermediate building steps until the final structure was completed at step 34 (bottom). All density maps are 2F_o-F_c maps contoured at 1.0σ and carved at 2-Å around the atomic centers.

The zinc site from the isomorphous difference Patterson map was used to calculate initial phases, and an initial density map was generated for the solution at 2.5Å (Figure 2). We calculated the accuracy of our solution using the weighted mean phase error (wMPE). This is a measure of the difference between the known phases of the final structure (6CLI), and those calculated during the solution process. Here, 0° would correspond to the perfect reproduction of the known phases, with 90° being completely random (Lunin and Woolfson, 1993). The initial solution from this single site corresponded to a wMPE of 55°. Structures in macromolecular X-ray crystallography are routinely determined from starting phases of even 70°−80° (De La Fortelle and Bricogne, 1997; Nanao et al., 2005). Here, poor density was present around the zinc atom and in the surrounding areas of the structure (Figure 2).

Building the structure at 2.5Å was too difficult owing to the limited number of unique reflections from this crystal (n = 114). The number of unique reflections increased by phase extension to 1.4-Å resolution (n = 704). The initial maps from the single zinc site were too poor to build complete residues directly into such densities automatically. Attempts at improving the density maps using automated density-modification or phase-improvement algorithms commonly used in X-ray crystallography were not successful at either 2.5-Å or 1.4-Å resolution, as judged by the increase of the wMPE (Table 1). Instead, building out the structure was done by adding single atoms manually into the initial density map.

Table 1.

MicroED Data from Low-Dose and Damaged Datasets

Phasing		Resolution (Å)	14.0–2.5
		No. of reflectionsa	114
		No. of sites identified	1
		Initial wMPE (°)	55
		wMPE after phase extension to 1.4 Å (°)	50
	Parameter	Low-Dose (0.17 e− Å−2)	Damaged (0.5 e− Å−2)
Refinement	Resolution range (A)	14.0–1.40 (1.51–1.40)	13.97–1.40 (1.51–1.40)
	Space group	P1	P1
	Unit cell (a, b, c) (Å)	4.88, 14.17, 17.62	4.85, 14.15, 17.43
	(α, β, γ) (°)	83.60, 84.98, 83.31	83.70, 85.43, 82.96
	Total no. of reflections	6,026 (1,308)	6,202 (1,445)
	Multiplicity	8.4 (8.5)	8.7 (9.3)
	Completeness (%)	77.2 (78.5)	78.1 (79.0)
	Mean l/σ(l)	8.5 (6.6)	8.7 (6.7)
	Rmeas	0.22 (0.28)	0.21(0.29)
	CC½	0.97 (0.94)	0.98 (0.96)
	R1 (%)	22.2	24.3
	Rcomplete (%)	28.9	32.2

^aReflections shared between both datasets.

We initially built individual atoms into peaks in the density that appeared to satisfy typical interatomic distances around the initial zinc site and its symmetry mates. In each round, one to three carbon atoms were placed manually at full occupancy with atomic displacement parameters of 0. New maps were generated without further refining the atom positions. If the new maps did not improve the density and the wMPE, these atoms were discarded and others were tested similarly. We initially built out both hands of the heavy-atom solution until one hand displayed a more clearly defined map. After 20 rounds of single-atom building, almost all of the individual atoms were placed (Figure 2). From here, density for entire amino acids was clear, and individual atomic species were reassigned to create residues. The remainder of the steps refined the structure after adding restraints.

The final structure was completed in 34 rounds of manual building and modeling (Figure 2 and Table 1). This solution was used to re-refine the damaged dataset at 1.4-Å resolution to similar statistics (Table 1) as previously determined (Hattne et al., 2018). The all-atom root-mean-square deviation between known and the experimentally phased structure was 0.071Å.

We chose to validate our structure using R_complete rather than the traditional R_free typically used in macromolecular crystallography (Brünger, 1992; Luebben and Gruene, 2015). Given the limited number of unique reflections (Table 1), assigning a fraction of them to a test set would make building an accurate model more difficult and it would not serve as an accurate validation of the structure. Although we have many observations with high redundancy in our data (Table 1), the total numbers of unique reflections for each of these structures at 1.4-Å resolution were only 704 after merging. For calculating R_complete, the data from the final refinement was divided into 10 datasets, each with-holding approximately 70–80 reflections for the free set. Each dataset was then refined using small perturbations to the initial model. Cross-validations between the individual datasets gave the final R_complete. This approach allowed us to refine and build the model using all the reflections. R_complete has been shown to accurately validate refinements without bias for both small-molecule and macromolecular datasets (Clabbers et al., 2019).

DISCUSSION

We demonstrate that radiation damage combined with a metal site can be used to generate initial experimental phases for MicroED data and that this information can be used to build a structure solution. The structure of GSNQNNF from these initial phases at 2.5Å was ultimately built and determined at 1.4Å. This was initiated by locating a single zinc atom from differences in diffraction amplitudes at 2.5-Å resolution. At this resolution, identifying atomic locations from the native Patterson map was impossible. However, locating the single zinc site by other means may be possible. This is consistent with past reports demonstrating that resolutions of 1.2Å are required for direct methods solutions of MicroED and X-ray data (Hauptman, 1986; Morris and Bricogne, 2003; Sawaya et al., 2016; Sheldrick, 2007). The initial phases in our analysis were determined by locating a single zinc atom that was particularly susceptible to radiation damage. The sensitivity of this zinc atom to damage in MicroED was noted in previous studies by the increasing temperature factor at increasing exposures (Hattne et al., 2018). From these initial observations, we hypothesized that radiation damage would allow us to locate this zinc atom in a difference dataset calculated between the low-dose dataset and the damaged dataset. Indeed, in real space, the difference showed a relatively strong signal for zinc (>6σ level at 2.5Å) (Figures 1 and 2).

RIP is similar to an isomorphous replacement experiment using native and derivative datasets (Ravelli et al., 2005). The heavy atom, or derivative, dataset in our experiment corresponds to the low-dose dataset. The native dataset corresponds to the damaged dataset, because the zinc would have been ionized and removed from the lattice (Hattne et al., 2018; Nave, 1995). Rather than adding a heavy atom to a native dataset as is customary in isomorphous replacement, radiation damage reduces the contributions of the natively present atoms, such that it gradually disappears as the measurement progresses. Whereas the native dataset in an isomorphous replacement measurement has less scattering power than the derivative, the low-dose dataset in RIP scatters stronger than that which has seen a higher exposure to the electron beam. In RIP, the difference between the atoms of these datasets manifests as a reduction of occupancy and/or an increase of B factor in the damaged structure. Indeed, our final solutions demonstrated that the atomic displacement of the zinc in the low-dose dataset refined to a value of 3Ų, whereas it was 5Ų in the damaged structure, both at full occupancy. Displacement of the zinc is facilitated by reduced coordination to the surrounding atoms. The displacement factors for the coordinating acetate oxygen also increased from 0.08 to 0.8Ų, from 1.69 to 5.46Ų for the coordinating oxygen on the glycine, and from 0.87 to 2.39Ų for the N terminus of the peptide. Although these coordinating atoms also increased in displacement factors, the zinc generated a considerably larger difference because it is a heavier atom.

We initially demonstrated the location of the zinc atom from differences in the intensities of the low-dose dataset and the damaged dataset. All attempts to improve the initial phases using density-modification or phase-improvement software failed. Only manually placing model atoms into the density improved the wMPEs and/or visible density. The difficulty in improving the initial phases is to be expected, as these crystals have very low solvent content (~20%) that would greatly reduce the applicability of density-modification approaches (Cowtan, 2010; Terwilliger, 2000).

This peptide only crystallized in the presence of a zinc atom that is present in the final model (Hattne et al., 2018). Although we did not perform a heavy metal soaking experiment per se, our approach can be thought of as a combination of both RIP and SIR phasing: damage allowed us to locate a zinc site, and the fact that it was a heavy atom gave enough signal to begin building the model. Future studies may find that this also applies to negatively charged residues that are also particularly susceptible to damage (Hattne et al., 2018). However, the phasing power from a small number of light-atom sites, such as oxygen, may not be sufficient to begin building an atomic model. We suspect that multiple sweeps of data can be collected, each with progressively more damage to the structure to find additional sites of specific damage. Examining the limits of RIP using MicroED data is an exciting avenue for future research and development.

We were able to demonstrate a structure solution from MicroED data using experimentally determined initial phases. It may now be possible to solve structures by collecting multiple datasets on the same crystals with different levels of exposure. The later datasets would have more damage manifested in the structure. This would change the integrated intensities, and initial phases may be generated from these differences. Here we could monitor the progress of phase improvement because the final structure of this peptide was known (Hattne et al., 2018). Picking the correct hand of an SIR/SAD solution typically relies on inspecting the maps from both hands after density modification (Wang, 1985). Because density-modification procedures in electron diffraction are poor (Gonen et al., 2005; Wisedchaisri and Gonen, 2011), we were unable to accurately assess phase improvement from visually inspecting the initial maps. For now, it is required to build out both hands of the solution until a clear answer is found. Nevertheless, we show that locating accurate positions of heavy atoms and building a correct model starting from experimentally determined initial phases is feasible using MicroED data. Future improvements to density modification and automatic building routines tailored to MicroED data may lead to automated structure solution pipelines that X-ray crystal-lographers currently enjoy.

STAR★METHODS

LEAD CONTACT AND MATERIALS AVAILABILITY

This study did not generate new unique reagents. Further information and requests for resources and reagents should be directed to and will be fulfilled where reasonable by the lead contact, Tamir Gonen (tgonen@g.ucla.edu).

METHOD DETAILS

Data Analysis and Processing

MicroED data from PDB entries 6CLI and 6CLJ were integrated with XDS (Kabsch, 2010a) to a maximum resolution of either 2.5 or 1.4Å (Hattne et al., 2018), scaled and merged in XSCALE (Kabsch, 2010b), and converted to SHELX format in XDSCONV(Kabsch, 2010b). Patterson maps were calculated using either the native or isomorphous difference Patterson tool in the computational crystallography toolbox (cctbx)(Grosse-Kunstleve et al., 2002). Slicing of the Patterson and Fourier maps for visualization was done using MAPSLICER (Winn et al., 2011). Calculating the Patterson vectors from the known structure was done using VECTORS (Winn et al., 2011). Peaks in the Patterson or Fourier maps >3σ were identified using PEAKMAX (Winn et al., 2011). Difference datasets were prepared in SHELXC (Sheldrick, 2010) with varying DSCA values. The zinc site was identified using only the isomorphous difference Patterson map peak as indicated in Figure 1. Generation of initial phases for the low-dose and damaged datasets were calculated in SHELXE without the free lunch algorithm or solvent flipping (Sheldrick, 2002). Identification of the single zinc site was successful using DSCA parameters between 0.97 and 0.81 as judged by the ability to identify the known peak in the Patterson map at the 3σ level or higher. The highest value for the peak was found at a DSCA of 0.85. This value was also correlated to the strength of the peak at the zinc location in the Fourier difference map in ANODE (Thorn and Sheldrick, 2011). Interestingly, this DSCA value resulted in both the strongest peak in the Fourier difference and Patterson map, and ultimately yielded the lowest initial wMPE. Model building was conducted in COOT (Emsley and Cowtan, 2004) and subsequent refinements of the models was performed using SHELXL (Sheldrick, 2015) using electron scattering factors (Peng, 1999). Fourier difference maps were generated in ANODE using the difference datasets from SHELXC at the specified resolutions and DSCA values (Thorn and Sheldrick, 2011). R_complete was calculated as described (Luebben and Gruene, 2015). All atom RMSD values were calculated in Pymol (Schrödinger, 2014). Figures were generated in PY-MOL (Schrödinger, 2014), and arranged in PowerPoint.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

No experimental models were used in this study.

QUANTIFICATION AND STATISTICAL ANALYSIS

Number values appearing in Table 1 were given by the total number of reflections. No other statistical tests were used in this manuscript.

DATA AND CODE AVAILABILITY

The atomic coordinates have been deposited in the Protein Data Bank under ID codes 6VHB and 6VHC. Density maps have been deposited in the Electron Microscopy Data Bank under ID codes EMD-21202 and EMD-21203.

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited Data
Atomic coordinates and structure factors, GSNQNNF after 0.17e/Å2 at 1.01 Å resolution	(Hattne et al., 2018)	PDB: 6CLI
Atomic coordinates and structure factors, GSNQNNF after 0.50e/Å2 at 1.01 Å resolution	(Hattne et al., 2018)	PDB: 6CLJ
Atomic coordinates and density map of GSNQNNF at 1.4A resolution after 0.17e/Å2 exposure with initial phases determined by radiation damage (Table 1 low-dose)	This paper	PDB: 6VHB; EMDB: EMD-21202
Atomic coordinates and density map of GSNQNNF at 1.4 Å resolution after 0.50e/Å2 exposure used to generate initial phases using radiation damage (Table 1 damaged)	This paper	PDB: 6VHC; EMDB: EMD-21203
Software and Algorithms
TVIPS tools	(Hattne et al., 2015)	N/A
XDS	(Kabsch, 2010a)	RRID:SCR_015652
XSCALE	(Kabsch, 2010b)	RRID:SCR_015652
Phaser	(McCoy et al., 2007)	RRID:SCR_014219
Phenix.refine	(Afonine et al., 2012)	RRID:SCR_014224
PyMol	(Schrödinger, 2014)	RRID:SCRJ)00305
SHELXC	(Sheldrick, 2010)	RRID:SCR_014220
SHELXE	(Sheldrick, 2002)	RRID:SCR_014220
SHELXL	(Sheldrick, 2015)	RRID:SCR_014220
ANODE	(Thorn and Sheldrick, 2011)	RRID:SCR_014220
MAPSLICER	(Winn et al., 2011)	RRID:SCRJ)07255
PEAKMAX	(Winn et al., 2011)	RRID:SCR_007255
COOT	(Emsley and Cowtan, 2004)	RRID:SCR_014222

Highlights.

• Demonstration of experimental phasing with MicroED

• Initial phases from radiation damage, Patterson pinpoints damage site

• Damage to structure after two passes of data collection

• Potential method for experimental phasing of larger macromolecules