Higher-order analysis of probabilistic long-term loss under nonstationary hazards

Highlights

• •An efficient and novel approach to derive higher-order statistical moments of the discounted long-term loss.
• •Higher-order analysis to aid decision-making and optimal structural design of civil infrastructure.
• •Large uncertainty associated with the stochastic occurrence and magnitude of hazards.
• •An integrated framework for long-term loss assessment under stationary and nonstationary hazards.

Abstract

Quantification of hazard-induced losses plays a significant role in risk assessment and management of civil infrastructure subjected to hazards in a life-cycle context. A rational approach to assess long-term loss is of vital importance. The loss assessment associated with stationary hazard models and low-order moments (i.e., expectation and variance) has been widely investigated in previous studies. This paper proposes a novel approach for the higher-order analysis of long-term loss under both stationary and nonstationary hazards. An analytical approach based on the moment generating function is developed to assess the first four statistical moments of long-term loss under different stochastic models (e.g., homogeneous Poisson process, non-homogeneous Poisson process, renewal process). Based on the law of total expectation, the developed approach expands the application scope of the moment generating function to nonstationary models and higher-order moments (i.e., skewness and kurtosis). Furthermore, by employing the convolution technique, the proposed approach effectively addresses the difficulty of assessing higher-order moments in a renewal process. Besides the loss analysis, the mixed Poisson process, a relatively new stochastic model, is introduced to consider uncertainty springing from the stochastic occurrence rate. Two illustrative examples are presented to demonstrate practical implementations of the developed approach. Ultimately, the proposed framework could aid the decision-maker to select the optimal option by incorporating higher-order moments of long-term loss within the decision-making process.

Introduction

In recent decades, the devastating effects that hazards have on societies worldwide have intermittently raised the attention of governments and the public to hazard risk assessment and management. For civil infrastructure, various hazards (e.g., earthquakes, hurricanes, and progressive deterioration) may impair structural functionality, thus resulting in severe consequences. The hazard-induced consequences are commonly measured in terms of financial losses (e.g., repair cost), social losses (e.g., downtime, deaths), and environmental losses (e.g., carbon dioxide emissions). Due to various sources of uncertainty, the accumulated losses can be aggravated over the service life of civil infrastructure. Hence, the quantification of long-term loss of civil infrastructure subjected to hazards is of significant importance to aid the decision-maker to mitigate potential losses and enhance preparedness [1,2].

Uncertainty quantification plays a significant role in long-term loss assessment. There are large uncertainties associated with the frequency and magnitude of hazards [3,4]. In previous studies, stationary models (e.g., homogeneous Poisson process) have been widely used to characterize the probabilistic behavior of hazards. Nowadays, studies show strong evidence that hazard arrivals may follow nonstationary behavior [5]. For instance, the renewal process is proposed to model the earthquake arrivals, in order to incorporate the time-varying energy accumulation of the fault [6,7]. Such time-dependent trends are also identified in other hazards, such as more frequent hurricane landfalls under climate change [8], increased wind speeds [9], extreme precipitation [10], and sea level rise [11]. In addition to natural hazards, the progressive deterioration of structural systems is also stochastic and time-variant [12]. Given the time-dependent trend of hazards, a general framework is needed to evaluate the long-term loss of civil infrastructure under both stationary and nonstationary models. This concern is discussed and addressed in this paper.

The analytical formulation of long-term loss is essential for risk assessment and management. Although numerical modeling is accessible, simulations are usually computationally expensive and time-consuming. Low-order moments (i.e., expectation and variance) of long-term loss based on stationary stochastic models have been investigated by previous studies [13,14]. Based on the homogeneous Poisson process, an analytical formulation of the expected life-cycle cost of buildings under single and multiple hazards was presented by Wen and Kang [15]. Recently, several studies assessed the long-term loss (e.g., mean and variance) of civil infrastructure under nonstationary processes. For instance, Yeo and Cornell [16] proposed analytical expressions for the expected loss caused by earthquakes using homogeneous and non-homogeneous Poisson models. Wang et al. [17] computed the mean and variance of hurricane-induced damage loss using the non-homogeneous Poisson process. Lin and Shullman [18] assessed the risk of New York City being damaged by hurricanes and surge flooding in a nonstationary environment. To simplify the computational process, the nonstationary Poisson model was converted into a stationary one in these studies. Additionally, the long-term loss is limited to Poisson models and the first two moments.

In addition to Poisson processes, recent studies proposed some new nonstationary models for the loss assessment. For instance, Pandey and Van Der Weide [19] used a stochastic renewal process with Brownian Passage Time distribution to formulate the expectation and variance of the discounted damage cost of a structure under earthquakes. The derivations were based on the renewal decomposition properties of renewal processes. The renewal model was also used to evaluate the lifetime resilience and cost of structural systems considering progressive deterioration [12]. Although the renewal approach provides an alternative option to assess the loss under nonstationary hazards, it cannot be applied to other stochastic models, such as the non-homogeneous Poisson process. Meanwhile, higher-order moments are not taken into account in previous studies.

Though the minimum expected loss has been widely used as a standard decision criterion, it is only suitable for risk-neutral decision makers. This criterion cannot cope with different attitudes [20]. Goda and Hong [21] indicated the structural design based on the expected life-cycle cost may not be optimal, and stated the need for statistical moments (e.g., variance, skewness, and kurtosis) of the cost. Furthermore, the mean-variance criterion is sufficient only when the utility function within the decision-making process is quadratic or the investment return (e.g., loss represents a negative return) follows a normal distribution [22].

Higher-order moments, i.e., skewness and kurtosis, measure asymmetry and tail conditions of the distribution with respect to the long-term loss. In risk management, large skewness and kurtosis of loss imply heavy tail risks. Such undesired risks are associated with low-probability events with disastrous consequences, e.g., credit risk crisis [23] and COVID-19 pandemic [24]. Higher-order moments are required when risk preferences of decision makers are considered, e.g., in the stochastic dominance criteria [20,25]. For instance, a decision maker with the absolute risk-averse attitude prefers positive skewness and small kurtosis of the investment return, as highly skewed data with large kurtosis indicate an increased likelihood of extreme losses [26]. Different decision results may be obtained due to the exclusion of these moments. Therefore, the assessment of higher-order moments of long-term loss is necessary. These moments can be used to aid the decision-making and optimal structural design of civil infrastructure by considering different attitudes.

To the best knowledge of the authors, mathematical expressions of higher-order moments of long-term loss have not been developed for Poisson and renewal models. In this paper, a novel approach based on the moment generating function is developed to formulate the higher-order moments of long-term loss of civil infrastructure subjected to hazards. In this context, the long-term loss refers to hazard-induced financial losses in a long time interval. In addition to the loss analysis, a new stochastic model of the mixed Poisson process is presented to take the uncertainty springing from stochastic occurrence rate into consideration. This new model has been recently introduced in hurricane landfall simulations [27] and rainfall occurrence models [28] to consider environmental variability.

Overall, this paper develops an integrated framework to assess the probabilistic long-term loss under stationary and nonstationary hazards. Higher-order moments of the loss are formulated based on moment generating functions for the homogeneous Poisson, non-homogeneous Poisson, mixed Poisson, and renewal processes. The merits, application scope, and limitations of the proposed method are explained and discussed. Two illustrative examples are presented to demonstrate implementations of the approach. The remainder of the paper is organized as follows. The subsequent two sections introduce the model setup for long-term loss and the moment generating function-based approach. Then, two case studies are presented to interpret the applications. The last section summarizes major outcomes and conclusions.

Stochastic models of hazards and long-term loss

Hazard arrivals are commonly modeled as a stochastic process using historical observations. For instance, the homogeneous Poisson process is widely used to model the earthquake recurrence [29,30]. The occurrence of hurricanes could also be represented by the homogeneous Poisson process based on historical records [31,32]. In addition to using historical data, the future projection of hazard arrivals requires the consideration of variability in hazard characteristics [4,33]. Various non-stationary models are developed to capture such variability. For instance, the renewal process is used to incorporate the time-dependent characteristics of ground motion activities for long-term seismic forecasting [34]. The non-homogeneous and mixed Poisson processes are utilized to model the occurrence of hurricanes in a changing climate [35,36]. In this section, theoretical descriptions and notations of four typical stochastic models (i.e., homogeneous Poisson process, renewal process, non-homogeneous Poisson process, and mixed Poisson process) are presented. Based on stochastic models, the long-term loss is formulated.

Stationary arrival process

As one of the most classical stationary models, the homogeneous Poisson process is adopted for stationary hazard arrivals and illustrated by using two different models: the homogenous Poisson and renewal processes.

Homogeneous Poisson process

A homogeneous Poisson process is an arrival process with stationary increments. It has a constant occurrence rate λ. The occurrence rate is defined as the number of hazard events within the time unit (e.g., per year), which is also known as the intensity function. A homogeneous Poisson process can be denoted by the number of occurrence {N(t _int), t _int > 0} with the time interval (0, t _int]. The expected number of hazard arrivals can be expressed as E[N(t _int)] = λt _int with N(0) = 0. The probability of having n number of arrivals within the time interval t _int is

$$\mathrm{P}[N\left(t_{\text{int}}\right)=n]=\frac{{\left(\lambda t_{\text{int}}\right)}^n\exp (-\lambda t_{\text{int}})}{n!},n=0,1,2,\cdots$$ (1)

Poisson renewal process

The homogeneous Poisson process can be alternatively described as a renewal process. A renewal process is a counting process, in which the inter-arrival times are independently identically distributed. For instance, over the period (0, t _int], arriving times of hazards are a series of non-negative random variables {T₁, T₂, …, T_k}. Inter-arrival times can be denoted as {W₁, W₂, …, W_k}. By the definition, the arriving time is the summation of inter-arrival times, T_k = W₁ + W₂ + … + W_k. When the inter-arrival time follows an exponential distribution, a renewal process becomes a homogeneous Poisson process, also known as a Poisson renewal process. The probability density function of the inter-arrival time W gives

$$f_W\left(x\right)=\lambda \exp (-\lambda x)$$ (2)

Nonstationary arrival process

The stationary occurrence rate is an idealized assumption and a realistic rate can be time-dependent and stochastic. Herein, three typical examples of nonstationary processes are provided: the non-Poisson renewal process, non-homogeneous Poisson process, and mixed Poisson process. In this context, a process is considered as ‘nonstationary’ when the occurrence rate is not constant.

Non-Poisson renewal process

The occurrence of hazards could be time-dependent. For instance, after an earthquake, there can be a long period before the next earthquake, in which the accumulated elastic strain energy is released by the fault. By considering such time-dependent characteristics, a non-Poisson process can be used to model the occurrence of earthquakes over a long period of time [37,34]. In the nonstationary renewal processes, different probabilistic models of inter-arrival times are used to quantify the time-dependent characteristics. For instance, several distributions of the inter-arrival time are provided in earthquake engineering, including lognormal [38], gamma [39], and Brownian Passage Time distribution [34].

Non-homogeneous Poisson process

Another nonstationary model used for the long-term loss assessment is the non-homogeneous Poisson process, with a time-dependent occurrence rate. A renewal process is not necessarily limited to the exponentially distributed inter-arrival times, while the Poisson process is not subjected to the time-independent occurrence rate. For instance, the non-homogeneous Poisson process can be used to model hurricane landfalls in a changing climate [18,35]. The frequency of hurricanes may increase due to the impact of the warming climate. For this process, the occurrence rate is time-varying, e.g., λ(t). The expected number of hazard arrivals over the time interval (0, t _int] can be computed as

$$E\left[N\right(t_{\text{int}}\left)\right]={\int }_0^{t_{\text{int}}}\lambda \left(t\right)dt$$ (3)

The probability of having n number of arrivals within the time interval (0, t _int] is computed as

$$\mathrm{P}[N\left(t_{\text{int}}\right)=n]=\frac{{\left({\int }_0^{t_{\text{int}}}\lambda \left(t\right)\mathit{dt}\right)}^n\exp (-{\int }_0^{t_{\text{int}}}\lambda \left(t\right)\mathit{dt})}{n!},n=0,1,2,\cdots$$ (4)

Mixed Poisson process

In the homogeneous and non-homogenous Poisson processes, the occurrence rate is restricted to a deterministic intensity function (i.e., either a constant λ or the time-dependent λ(t)). However, the deterministic function may not be sufficient to capture the uncertainty in a long-term trend. The mixed Poisson process, which covers the uncertainty within intensity function, is receiving increased attention in the hazard model and should also be evaluated. For instance, Xiao et al. [27] suggested using a stochastic intensity function to model hurricane occurrence when considering seasonal variability, based on the recorded hurricane activities along the U.S. Gulf and Atlantic coasts between 1900 and 2010.

The mixed Poisson process is known as a special case of the cox process. A cox process is a Poisson process, in which the occurrence rate is a stochastic process (denoted as {G(t _int), t _int > 0}). A cox process becomes a mixed Poisson process when the rate is a random variable, e.g., {G(t _int)} = Λ. Given the rate Λ, increments in the mixed Poisson process stay stationary [40]. However, these increments are no longer independent, as the number of arrivals relies on the distribution of Λ. Herein, the stochastic rate Λ is assigned to follow a gamma distribution with shape parameter α and rate parameter β. The rate Λ is continuous with a probability density function g(x). Hence, the probability density function of the gamma distributed rate Λ ~ Γ(α, β) can be assessed as

$$g\left(x\right)=\frac{{\beta }^{\alpha }{x}^{\alpha -1}}{\Gamma \left(\alpha \right)}{e}^{-\beta x}$$ (5)

Consequently, the probability of having n number of arrivals within the time interval (0, t _int] is

$$\mathrm{P}(N\left(t_{\text{int}}\right)=n)={\int }_0^{\infty }{e}^{-x{t}_{\text{int}}}\frac{{\left(x{t}_{\text{int}}\right)}^n}{n!}\frac{{\beta }^{\alpha }{x}^{\alpha -1}}{\Gamma \left(\alpha \right)}{e}^{-\beta x}dx$$ (6)

Long-term loss model

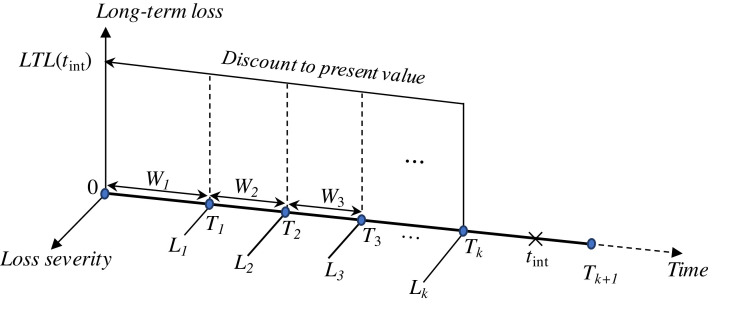
Based on the stochastic models, the long-term loss of civil infrastructure subjected to hazards can be formulated. The time interval (0, t _int] is defined as the service life of civil infrastructure. During the time interval, hazard arrivals are modeled as a stochastic process and the total number of hazard events is N(t _int) = n with N(0) = 0. The arriving time and inter-arrival time of the kth event can be defined as T_k and W_k, respectively. The arriving time T_k equals the sum of inter-arrival times, i.e., T_k = W₁ + W₂ + … + W_k, as described previously. L is the loss severity. L_k refers to the financial loss due to structural damage/failure under the kth hazard event. The loss severity L_k and the inter-arrival time W_k are assumed to be independent. The long-term loss, denoted as LTL(t _int), is the hazard-induced financial loss of civil infrastructure subjected to hazards within the investigated period t _int. The loss is discounted to the present value using a monetary discount rate r, as indicated in Fig. 1 . The long-term loss LTL(t _int) gives

$$LTL\left(t_{\text{int}}\right)=\sum _{k=1}^{N\left(t_{\text{int}}\right)}{L}_k{e}^{-r{T}_k}$$ (7)

Fig. 1.

Long-term loss model by considering discounting and hazard arrival process.

The long-term loss LTL(t _int) is related to the stochastic models of the hazard. For instance, if a homogeneous Poisson process is implemented for loss assessment, the inter-arriving time W_k follows an exponential distribution and the number of arrivals N(t _int) has a Poisson distribution. These parameters are different under different models.

Analytical analysis of long-term loss

This section introduces the theoretical fundamentals of the proposed moment generating function-based approach. Analytical derivations of moment generating functions and statistical moments of long-term loss under the homogeneous Poisson process, non-homogeneous Poisson process, mixed Poisson process, and renewal process are presented. The merit, capability, and limitations of the developed approach are also discussed.

Higher-order analysis using moment generating function

The moment generating function uniquely dictates the probability distribution of a random variable. This property can be adopted to formulate probability distributions of random variables. For instance, random variables will have the same probability distributions if they have identical moment generating functions. Another property of the moment generating function is that raw moments (e.g., mean, second moment) can be obtained by taking derivatives [40,41]. This property is utilized to formulate statistical moments of long-term loss in this paper.

For a random variable X, its moment generating function about η (η ∈ ℝ) is defined as Φ_X(η)

$${\Phi }_X\left(\eta \right)=E\left[e^{\eta X}\right]$$ (8)

The first two raw moments of X can be obtained by taking the first and second derivatives of the moment generating function at zero

$${{\Phi }_X}^{\prime }\left(\eta \right)=\frac{d}{d\eta }E\left[e^{\eta X}\right]=E\left[\frac{d}{d\eta }{e}^{\eta X}\right]=E\left[X{e}^{\eta X}\right]\Rightarrow {{\Phi }_X}^{\prime }\left(0\right)=E\left[X\right]$$ (9)

$${{\Phi }_X}^{″}\left(\eta \right)=\frac{d}{d\eta }E\left[X{e}^{\eta X}\right]=E\left[X^2{e}^{\eta X}\right]\Rightarrow {{\Phi }_X}^{″}\left(0\right)=E\left[X^2\right]$$ (10)

Similarly, the mth-order moment can be assessed by taking the mth derivative at zero

$${\Phi }_X^{\left(m\right)}\left(0\right)=E\left[X^m\right],m\ge 1$$ (11)

Based on this concept, the key to derive higher-order moments of long-term loss LTL(t _int) is to compute its moment generating function ${\Phi }_{LTL\left(t_{\text{int}}\right)}$.

Moment generating function for homogeneous Poisson case

With respect to the homogeneous Poisson case, the moment generating function of long-term loss can be derived in terms of a compound Poisson process. By conditioning on the number of arrivals (i.e., N(t _int) = n) with the Poisson distribution, the moment generating function of long-term loss ${\Phi }_{LTL\left(t_{\text{int}}\right)}$ can be evaluated using the law of total expectation

$${\Phi }_{\mathit{LTL}\left(t_{\text{int}}\right)}\left(\eta \right)=E\left[{e^{\eta }}^{\mathit{LTL}\left(t_{\text{int}}\right)}\right]=E[\exp \left(\eta \sum _{k=1}^{N\left(t_{\text{int}}\right)}{L}_k{e}^{-r{T}_k}\right)|N\left(t_{\text{int}}\right)=n]=e^{-\lambda t_{\text{int}}}+\sum _{n=1}^{\infty }E\left[\exp (\eta \prod _{k=1}^n{L}_k{e}^{-r{T}_k})\right]\left[\frac{{\left(\lambda t_{\text{int}}\right)}^n}{n!}{e}^{-\lambda t_{\text{int}}}\right]=\exp (-\lambda t_{\text{int}})+\exp (-\lambda t_{\text{int}})\sum _{n=1}^{\infty }{\left[{\Phi }_L\left(\eta e^{-r{s}_k}\right)\right]}^n\left[\frac{{\left(\lambda t_{\text{int}}\right)}^n}{n!}\right]=\exp \left[\lambda {\int }_0^{t_{\text{int}}}[{\Phi }_L\left(\eta e^{-\mathit{rs}}\right)-1]\mathit{ds}\right]$$ (12)

in which Φ_L refers to the moment generating function of loss severity L. The derivation of Φ_L requires the information with respect to the probabilistic distribution of loss severity. Previous studies indicated that the probabilistic loss severity can be modeled by the exponential distribution [42,43]. Herein, the loss severity L is assumed to follow an exponential distribution L ~ EXP(θ), with the mean E[L] = 1/θ. By substituting Φ_L into Eq. (12), the moment generating function of long-term loss ${\Phi }_{LTL\left(t_{\text{int}}\right)}$ under the homogeneous Poisson process gives

$${\Phi }_{LTL\left(t_{\text{int}}\right)}\left(\eta \right)=\exp \left[\lambda {\int }_0^{t_{\text{int}}}[\frac{\theta }{\theta -\eta e^{-rs}}-1]ds\right]={\left(\frac{\theta -\eta e^{-r{t}_{\text{int}}}}{\theta -\eta }\right)}^{\frac{\lambda }{r}}$$ (13)

By taking the first and second derivatives at zero, the expectation and variance of long-term loss can be obtained as

$$E\left[LTL\left(t_{\text{int}}\right)\right]={\Phi }_{LTL\left(t_{\text{int}}\right)}^{\prime }\left(0\right)=\frac{\lambda }{\theta r}\left(1-e^{-r{t}_{\text{int}}}\right)$$ (14)

$$Var\left[LTL\left(t_{\text{int}}\right)\right]={\Phi }_{LTL\left(t_{\text{int}}\right)}^{″}\left(0\right)-{\left({{\Phi }^{\prime }}_{LTL\left(t_{\text{int}}\right)}\left(0\right)\right)}^2=\frac{\lambda }{{\theta }^{2}r}\left(1-e^{-2r{t}_{\text{int}}}\right)$$ (15)

Likewise, the mth order moment can be assessed using Eq. (11). The expressions of skewness and kurtosis are associated with the third and fourth-order raw moments. For instance, the skewness u ₃ and kurtosis u ₄ are

$$u_3=\frac{E\left[LT{L}^3\left(t_{\text{int}}\right)\right]-3\mu {\sigma }^2-{\mu }^3}{{\sigma }^3}$$ (16)

$$u_4=\frac{E\left[LT{L}^4\left(t_{\text{int}}\right)\right]-4\mu E\left[LT{L}^3\left(t_{\text{int}}\right)\right]+6{\mu }^{2}E\left[LT{L}^2\left(t_{\text{int}}\right)\right]-3{\mu }^4}{{\sigma }^4}$$ (17)

in which μ refers to the expected long-term loss E[LTL(t _int)] and σ is the standard deviation of LTL(t _int). Consequently, skewness and kurtosis of long-term loss can be obtained

$$u_3=\frac{2\lambda r^{1/2}(1-e^{-3r{t}_{\text{int}}})}{{(\lambda -\lambda e^{-2r{t}_{\text{int}}})}^{3/2}}$$ (18)

$$u_4=\frac{(6r+3\lambda )+(6r-3\lambda )e^{-2r{t}_{\text{int}}}}{\lambda (1-e^{-2r{t}_{\text{int}}})}$$ (19)

From Eqs. (18) and (19), it shows that for the investigated case the skewness and kurtosis of long-term loss are not affected by θ. Hence, the skewness and kurtosis under the homogeneous Poisson process are independent of the exponentially distributed loss severity. When other distributions are used for the loss severity, the higher-order moments may be affected.

Moment generating function for non-homogeneous Poisson case

The same technique can be used for the non-homogeneous model by applying the law of total expectation. For the non-homogeneous Poisson process, the expected number of arrivals Q(t _int) becomes

$$Q\left(t_{\text{int}}\right)=E\left[N\right(t_{\text{int}}\left)\right]={\int }_0^{t_{\text{int}}}\lambda \left(t\right)dt$$ (20)

Given the number of arrivals, the moment generating function of long-term loss can be derived as

$${\displaystyle {\Phi }_{\mathit{LTL}\left(t_{\text{int}}\right)}\left(\eta \right)}={\displaystyle \exp (-Q\left(t_{\text{int}}\right))+\sum _{n=1}^{\infty }E[\prod _{k=1}^n{\Phi }_L\left(\eta e^{-r{T}_k}\right)|N\left(t_{\text{int}}\right)=n]\mathrm{P}(N\left(t_{\text{int}}\right)=n)}={\displaystyle \exp (-Q\left(t_{\text{int}}\right))+\exp (-Q\left(t_{\text{int}}\right))\sum _{n=1}^{\infty }{\int }_0^{t_{\text{int}}}{\int }_{s_1}^{t_{\text{int}}}\cdots {\int }_{s_{n-1}}^{t_{\text{int}}}\prod _{k=1}^n\left[\lambda \left(s_k\right){\Phi }_L\left(\eta e^{-r{s}_k}\right)\right]d{s}_n\cdots d{s}_1}={\displaystyle \exp \left[{\int }_0^{t_{\text{int}}}\lambda \left(s\right)[{\Phi }_L\left(\eta e^{-\mathit{rs}}\right)-1]\mathit{ds}\right]}$$ (21)

The detailed derivations of Eqs. (12) and (21) are shown in Appendix A. If a linear function is used for the increasing occurrence rate, e.g., λ(t _int) = λ ₀(1 + ct _int), the moment generating function becomes

$${\Phi }_{LTL\left(t_{\text{int}}\right)}\left(\eta \right)=\exp \left[{\int }_0^{t_{\text{int}}}{\lambda }_0(1+cs)[{\Phi }_L\left(\eta e^{-rs}\right)-1]ds\right]$$ (22)

in which λ ₀ is the initial stationary occurrence rate and c refers to an annual increase rate of hazard occurrence. For the given linear rate function, the moment generating function may not be differentiable at zero. Under this circumstance, the moments can be computed by taking derivatives and finding limits by approaching zero. Accordingly, the raw moments can be computed as

$$E\left[LT{L}^m\left(t_{\text{int}}\right)\right]=\underset{\eta \to 0}{\lim }\left(\frac{d^m{\Phi }_{LTL\left(t_{\text{int}}\right)}\left(\eta \right)}{d{\eta }^m}\right)$$ (23)

Moment generating function for mixed Poisson case

As mentioned before, the mixed Poisson process has a stochastic occurrence rate Λ. Though the random variable Λ affects the probability of the number of arrivals, the inter-arrival times are not influenced by time. Hence, the derivation of the moment generating function for the mixed Poisson case is similar to that for the homogeneous case, as shown in Eq. (12). The deterministic rate in the homogeneous model is switched to the stochastic random variable, e.g., λ = E[Λ] and λ ² = E[Λ²]. Therefore, the moment generating function of long-term loss under the mixed Poisson model gives

$${\Phi }_{LTL\left(t_{\text{int}}\right)}\left(\eta \right)={\Phi }_{\Lambda }\left[{\int }_0^{t_{\text{int}}}[{\Phi }_L\left(\eta e^{-rs}\right)-1]ds\right]$$ (24)

For the illustrative purpose, the random variable Λ follows a gamma distribution Λ ~ Γ(α, β), as shown in Eq. (5). The loss severity L remains the exponential distribution L ~ EXP(θ). The moment generating function of the gamma distributed rate is

$${\Phi }_{\Lambda }\left(x\right)={\left(\frac{\beta }{\beta -x}\right)}^{\alpha }$$ (25)

Substituting Eq. (25) into Eq. (24), the moment generating function of long-term loss gives

$${\Phi }_{LTL\left(t_{\text{int}}\right)}\left(\eta \right)={\beta }^{\alpha }{\left[\beta -\frac{1}{r}\ln \left(\frac{\theta -\eta e^{-r{t}_{\text{int}}}}{\theta -\eta }\right)\right]}^{-\alpha }$$ (26)

According to Eq. (26), the moments of long-term loss under a mixed Poisson process can be assessed.

Higher-order moments for renewal case

For some stochastic models, properties of the models can be used to formulate the moment generating functions. In this section, statistical moments of long-term loss under a renewal process are assessed by incorporating the renewal function and convolution technique. Under this scenario, the provided derivations are based on a general renewal process and the probability distribution of the inter-arrival time W is not specified. The formulation of moment generating function of long-term loss remains the same as presented before

$${\Phi }_{LTL\left(t_{\text{int}}\right)}\left(\eta \right)=E\left[{e^{\eta }}^{LTL\left(t_{\text{int}}\right)}\right]=E\left[\prod _{k=1}^{N\left(t_{\text{int}}\right)}{\Phi }_L\left(\eta e^{-r{T}_k}\right)\right]$$ (27)

According to the renewal theorem [40],Eq. (27) can be written as

$${\Phi }_{LTL\left(t_{\text{int}}\right)}\left(\eta \right)={\int }_{t_{\text{int}}}^{\infty }d{F}_W\left(s\right)+{\int }_0^{t_{\text{int}}}{\Phi }_L\left(\eta e^{-rs}\right){\Phi }_{LTL(t_{\text{int}}-s)}\left(\eta e^{-rs}\right)d{F}_W\left(s\right)$$ (28)

where F_W indicates the cumulative distribution function of the inter-arrival time. Consequently, the moments of long-term loss under the renewal process can be obtained by taking derivatives of Eq. (28) at zero. The mth-order derivative of the moment generating function gives

$$\begin{array}{ccc}\hfill {\displaystyle \frac{d^m{\Phi }_{\mathit{LTL}\left(t_{\text{int}}\right)}\left(\eta \right)}{d{\eta }^m}}& =& {\Phi }_{\mathit{LTL}\left(t_{\text{int}}\right)}^{\left(m\right)}\left(\eta \right)\hfill \\ & =& \sum _{k=0}^{m-1}\left(\begin{array}{c}{\displaystyle m}\hfill \\ {\displaystyle k}\hfill \end{array}\right){\int }_0^{t_{\text{int}}}{e}^{-\mathit{mrs}}{\Phi }_L^{(m-k)}\left(\eta e^{-\mathit{rs}}\right){\Phi }_{\mathit{LTL}(t_{\text{int}}-s)}^{\left(k\right)}\left(\eta e^{-\mathit{rs}}\right)d{F}_W\left(s\right)\hfill \\ & & +{\int }_0^{t_{\text{int}}}{e}^{-\mathit{mrs}}{\Phi }_L\left(\eta e^{-\mathit{rs}}\right){\Phi }_{\mathit{LTL}(t_{\text{int}}-s)}^{\left(m\right)}\left(\eta e^{-\mathit{rs}}\right)d{F}_W\left(s\right)\hfill \end{array}$$ (29)

When η equals zero, the mth-order moments of long-term loss is

$$\begin{array}{c}E\left[LT{L}^m\left(t_{\text{int}}\right)\right]=\sum _{k=0}^{m-1}\left(\begin{array}{c}m\\ k\end{array}\right)E\left[L^{m-k}\right]{\int }_0^{t_{\text{int}}}{e}^{-mrs}{\Phi }_{LTL(t_{\text{int}}-s)}^{\left(k\right)}\left(0\right)d{F}_W\left(s\right)\\ +{\int }_0^{t_{\text{int}}}{e}^{-mrs}{\Phi }_{LTL(t_{\text{int}}-s)}^{\left(m\right)}\left(0\right)d{F}_W\left(s\right)\end{array}$$ (30)

The convolution technique and the renewal function are used to solve Eq. (30). The renewal function refers to the expected number of events in a renewal process. Based on the cumulative distribution function of the inter-arrival time F_W, a defective distribution function can be defined as [44]

$$D\left(t_{\text{int}}\right)=D_{mr}\left(t_{\text{int}}\right)={\int }_0^{t_{\text{int}}}{e}^{-mrs}d{F}_W\left(s\right)$$ (31)

The convolution power of Eq. (31) can be rewritten using the renewal function Θ. The summed i-fold convolution power gives

$$\sum _{i=1}^{\infty }{D}^{*i}\left(t_{\text{int}}\right)={\int }_0^{t_{\text{int}}}{e}^{-mrs}d\sum _{i=1}^{\infty }{F}_W^{*i}\left(s\right)={\int }_0^{t_{\text{int}}}{e}^{-mrs}d\Theta \left(s\right)$$ (32)

where * is a convolution operator. Substituting Eqs. (31) and (32) into Eq. (30), the mth-order moment can be formulated as follows

$$\begin{array}{ccc}\hfill E\left[LT{L}^m\left(t_{\text{int}}\right)\right]& =& \sum _{k=0}^{m-1}\left(\begin{array}{c}m\\ k\end{array}\right)E\left[L^{m-k}\right]{\Phi }_{LTL}^{\left(k\right)}\left(0\right)*D\left(t_{\text{int}}\right)+{\Phi }_{LTL}^{\left(m\right)}\left(0\right)*D\left(t_{\text{int}}\right)\hfill \\ & =& \sum _{k=0}^{m-1}\left(\begin{array}{c}m\\ k\end{array}\right)E\left[L^{m-k}\right]{\Phi }_{LTL}^{\left(k\right)}\left(0\right)*\sum _{i=1}^{\infty }{D}^{*i}\left(t_{\text{int}}\right)\hfill \\ & =& \sum _{k=0}^{m-1}\left(\begin{array}{c}m\\ k\end{array}\right)E\left[L^{m-k}\right]{\int }_0^{t_{\text{int}}}{e}^{-mrs}{\Phi }_{LTL(t_{\text{int}}-s)}^{\left(k\right)}\left(0\right)d\Theta \left(s\right)\hfill \\ & =& \sum _{k=0}^{m-1}\left(\begin{array}{c}m\\ k\end{array}\right)E\left[L^{m-k}\right]{\int }_0^{t_{\text{int}}}{e}^{-mrs}E\left[LT{L}^k(t_{\text{int}}-s)\right]d\Theta \left(s\right)\hfill \end{array}$$ (33)

The first four moments of long-term loss can be effectively obtained by using this recursive equation, i.e., Eq. (33). This recursive equation is validated by comparing the first two moments with the results provided by Pandey and Van Der Weide [19], in which the analytical expressions of the mean and variance using the regenerative property were provided. The moments of long-term loss assessed by Eq. (33) are based on a general renewal process. The loss under renewal processes with different probabilistic models of the inter-arrival times can be computed by employing different renewal functions. The implementation of renewal function circumvents complicated derivations starting from a stochastic process.

The homogeneous Poisson process, as a typical renewal process, has a renewal function defined as dΘ(s)/ds = λ. Consequently, the mth-order moment of long-term loss under the homogeneous Poisson model is

$$E\left[LT{L}^m\left(t_{\text{int}}\right)\right]=\lambda \sum _{k=0}^{m-1}\left(\begin{array}{c}m\\ k\end{array}\right)E\left[L^{m-k}\right]{\int }_0^{t_{\text{int}}}{e}^{-mrs}E\left[LT{L}^k(t_{\text{int}}-s)\right]ds$$ (34)

The expectation and variance of the long-term loss are assessed

$$E\left[LTL\left(t_{\text{int}}\right)\right]=\frac{E\left[L\right]\lambda }{r}\left(1-e^{-r{t}_{\text{int}}}\right)$$ (35)

$$Var\left[LTL\left(t_{\text{int}}\right)\right]=\frac{E\left[L^2\right]\lambda }{2r}\left(1-e^{-2r{t}_{\text{int}}}\right)$$ (36)

The third and fourth-order moments obtained from the renewal function are also validated by comparing with the values computed using the moment generating function, as shown in Eqs. (14) and (15).

Summary of the moment generating function-based approach

In summary, the developed moment generating function-based analytical approach can effectively evaluate the higher-order moments of long-term loss under different stochastic models. Based on the law of total expectation, the proposed approach expands the application scope of the moment approach, which was formerly used for the homogeneous Poisson model only. Using the convolution technique, the higher-order moments of loss under a renewal process are successfully derived from the developed approach. Identifying the distribution type of loss severity is not necessary under the renewal condition. During the computational process, if the limit function of the moment generating function is difficult to solve, the raw moments can be assessed using Eq. (23). The developed approach is validated by Monte Carlo simulation and more details are shown in illustrative examples. Some of the derivations may not be applicable to stochastic processes without Poisson properties, e.g., when inter-arrival times are not independent identically distributed. Additionally, by considering the mathematical definition, the moment generating function may not exist due to divergent integrals. These issues should be carefully considered during the application process.

Apart from the loss assessment, higher-order moments can be used to compute the long-term reliability [45]. For instance, skewness was involved in the third-order moment method to assess the long-term reliability of reinforced concrete structures under chloride-induced corrosion [46]. Reliability analysis involving skewness and kurtosis was also conducted in Lu et al. [47]. Another application of the moment generating function is that statistical moments can be used if there is insufficient information. For instance, Zhao and Lu [48] used statistical moments to describe probabilistic characteristics of random variables.

Applications: illustrative examples

Two illustrative examples are presented to demonstrate the feasibility and applicability of the developed framework. The first example focuses on the computation of loss severity. The long-term seismic loss of the investigated bridge under seismic hazard is computed using the renewal model. The second example aims to identify the impact of climate variability on the hurricane-induced loss by using different stochastic processes. The homogeneous, non-homogeneous, and mixed Poisson processes are used to model the hurricane arrivals.

Seismic loss evaluation under renewal process

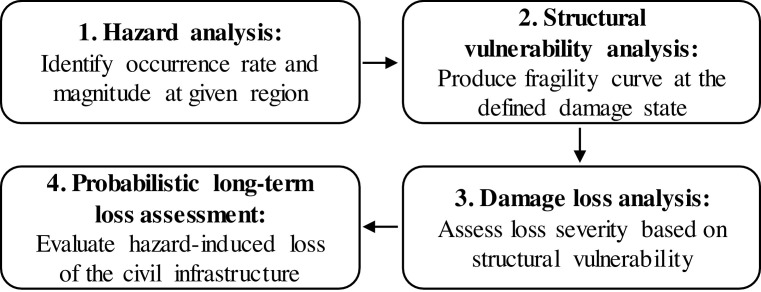
According to the mathematical derivations provided in the previous section, there need several inputs for the long-term loss assessment, including the occurrence rate of hazard, monetary discount rate, time interval, and the statistical moments of loss severity under the investigated hazard scenario. Generally, the loss assessment of civil infrastructure under seismic hazards consists of four components, as shown in Fig. 2 , including hazard analysis, vulnerability analysis, damage loss estimation, and long-term loss assessment. The loss severity is an essential element. This example aims to compute the loss severity of a reinforced concrete bridge under the seismic hazard. The recurrence of earthquakes is modeled as a renewal process.

Fig. 2.

Framework of probabilistic long-term loss assessment of civil infrastructure.

Based on the Gutenberg-Richter law, the occurrence rate of earthquakes can be assessed by the recurrence relationship between earthquake frequency and intensity, as follows [49]

$${\log }_{10}{\lambda }_m=A_m-B_{m}m$$ (37)

in which λ_m is the annual rate of earthquakes greater than magnitude m in the given region and A_m and B_m are coefficients based on analysis of historical records. In this model, a minimum magnitude is considered as 5.5 for the fault. Given this minimum magnitude, coefficients A_m and B_m in Eq. (37) are 3.94 and 0.89, respectively [50]. The annual occurrence rate of earthquakes exceeding a magnitude of 5.5 is computed as 0.1109.

Subsequently, vulnerability analysis is performed to quantify the performance of the bridge under seismic hazard. The distance and the shear wave velocity over the top 30 m at the investigated site are specified as 5 km and 480 m/s, respectively. The exceedance probability of peak ground acceleration is obtained by adopting a ground motion prediction model provided by Boore et al. [51]. The peak ground acceleration follows a lognormal distribution with the expectation of 0.417 and the standard deviation of 0.282.

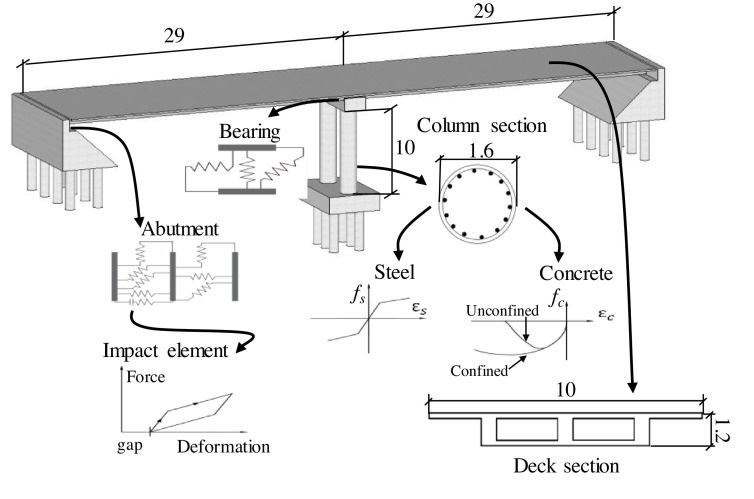
A finite element model of a typical two-span continuous reinforced concrete bridge is established using the software OpenSees [52] to assess the structural performance, as shown in Fig. 3 . This 58 m bridge has a box girder with a height of 1.2 m and a width of 10 m and two circular 10 m high columns with a diameter of 1.6 m. The compressive strength of the concrete is 26 MPa and the yield strength of the reinforcement is 470 MPa. The longitudinal reinforcement ratio for the concrete columns is 1.01%.

Fig. 3.

A three-dimensional bridge model (unit: meter).

Five damage states of the bridge are specified as no damage, slight, moderate, major, and complete, according to HAZUS [53]. The seismic demand is the curvature ductility of the bridge column obtained from the finite element model. For each damage state, the limit of curvature ductility μ has been classified as μ < 1.29, 1.29 ≤ μ < 2.10, 2.10 ≤ μ < 3.52, 3.52 ≤ μ < 5.24, and μ ≥ 5.24, respectively [54]. The required curvature ductility can be attained through a nonlinear time history analysis. A total of 80 ground motion records are used for the regression analysis to assess the response of the bridge [55,56]. The fragility curve provides the probability of the seismic demand D exceeding the capacity C. The fragility function can be expressed as

$$P\left[D\ge C|PGA\right]=Z_{\varphi }\left[\frac{\ln \left(S_D/S_C\right)}{\sqrt{{\beta }_D^2+{\beta }_C^2}}\right]=Z_{\varphi }\left[\frac{\ln \left(PGA\right)-[\ln \left(S_C\right)-\ln \left(A\right)]/B}{\sqrt{{\beta }_D^2+{\beta }_C^2}/B}\right]$$ (38)

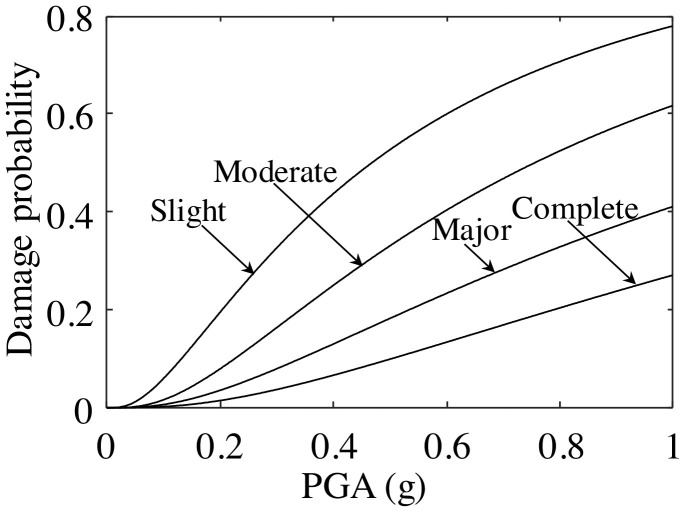
where Z_ϕ refers to the standard normal cumulative distribution function; S_D and S_C represent the median of seismic demand and capacity, respectively; and β_D and β_C refer to the logarithmic standard deviation of demand and capacity, respectively. From the regression relationship, the value of A is 2.8869 and the value of B is 1.0702. Accordingly, the seismic fragility curves of four different damage states considering curvature ductility are obtained, as shown in Fig. 4 .

Fig. 4.

Fragility curves associated with four damage states.

Given the structural vulnerability, the loss severity is the product of the repair cost of the damaged bridge and the conditional probability that the bridge is in a specified damage state under the given intensity measure [57]. The cost of rebuilding equals the unit price times the length and width of the bridge, in which the unit price of bridge rebuilding is taken as 2306 USD/m² [58,59]. The repair cost of the bridge being in different damage states can be evaluated as a fraction of the rebuilding cost through repair ratios. Repair ratios of 0, 0.03, 0.25, 0.75, and 1 are used for none, slight, moderate, major, and complete damage, respectively [60]. Subsequently, the loss severity equals the summation of loss associated with all possible damage states. The expectation, standard deviation, the third, and the fourth-order moments of loss severity are sampled and computed as 1.5631 × 10⁵ USD, 1.7790 × 10⁵ USD, 2.9487 × 10¹⁶, and 1.9239 × 10²², respectively.

Given the loss severity, the long-term seismic loss under a Poisson renewal model can be calculated by Eq. (34). The value of the occurrence rate is 0.1109. The monetary discount rate is defined as 3%. The service life of the investigated bridge is assumed as 75 years. Consequently, the expectation, standard deviation, coefficient of variation, skewness, and kurtosis of the long-term loss of the bridge are 5.1692 × 10⁵ USD, 3.2016 × 10⁵ USD, 0.62, 1.11, and 4.69, respectively.

Hurricane-induced long-term loss considering climate change

The occurrence of hurricanes can be modeled as a stochastic process using the observation data [61,32]. For instance, a homogeneous Poisson process can be used to model hurricane arrivals in a stationary environment [61]. However, stochastic models using historical observations only may not be sufficient to project future scenarios, as the variability in characteristics of hazards is not considered [33]. In recent decades, hurricane arrivals in a changing environment considering the effects of climate change and variability have been modeled by the non-homogeneous and mixed Poisson models [18,31]. This example aims to assess the impact of climate change and variability on the hurricane-induced loss, from a long-term perspective.

The homogeneous Poisson process is widely used to model hurricane arrivals in a stationary environment, which assumes a constant occurrence rate λ based on historical observations [61,32]. This rate is typically determined by dividing the total number of hurricane landfalls by the observation period [61]. Recent studies observe the increasing trend on hurricane frequency in the warming climate [62]. For such scenarios, the non-homogeneous Poisson process with an increasing occurrence rate, i.e., λ(t _int), could be used to predict the increase in the number of hurricane arrivals [35,18].

In a changing environment, in addition to the potential increasing trend, the occurrence of hurricanes can be significantly influenced by climate variability. Climate variability refers to variations in the mean state and characteristics of climate [63]. Previous studies stated the importance of considering the occurrence rate as a random variable in the Poisson process (i.e., the mixed Poisson process) for future hurricane predictions. For instance, Elsner and Bossak [31] projected the occurrence rate of the U.S. hurricane landfalls using the mixed Poisson model. Villarini et al. [36] assessed changes in hurricane frequency using the mixed Poisson process, by modeling the dependence of hurricane occurrence on different climate indices. In this example, a gamma distributed stochastic rate is utilized [31].

The long-term loss analysis is performed on a multi-span simply supported girder bridge [64]. The bridge has six spans equally distributed with a length of 146 m. This type of bridge is most susceptible to the deck unseating damage [65]. The given annual occurrence rate of hurricane λ ₀ is 0.245 for the investigated area in the stationary environment (i.e., with a homogeneous Poisson process). The rate is determined by counting the total number of 27 hurricane landfalls in the investigated region from 1900 to 2100, i.e., λ ₀ = 27/110 per year [17]. The expected loss severity E[L] is 1.283 million USD [64]. The detailed computation of λ ₀ and loss severity under hurricane hazards can be performed according to the process shown in the earthquake example. The monetary discount rate r is 2% for the long-term evaluation [66]. The loss severity follows an exponential distribution.

In a stationary environment, the occurrence of hurricanes is modeled as a homogeneous Poisson process, with a rate of λ = λ ₀ throughout the lifetime. In a changing climate, the non-homogeneous Poisson process is adopted and the occurrence rate is assumed to follow a linear increasing relationship λ(t _int) = λ ₀(1 + ct _int), in which c refers to an annual increase rate of hurricane landfalls [35]. The annual increase rate of 0.2% indicates that the number of hurricanes is increased by 20% in the next century [8,35]. The mixed Poisson process is also adopted to compute the long-term loss of the bridge under hurricanes considering climate variability. Herein, the parameters within the stochastic occurrence rate Λ ~ Γ(α, β) are based on the information presented in Elsner and Bossak [31]. The rate has a mean of E[Λ] = λ ₀ (the same value as the rate in the homogeneous model) and the gamma parameters are assumed as Λ ~ Γ(0.49, 2). Given more information (e.g., climate information), the parameters used in the non-homogenous and mixed Poisson processes can be upgraded and the relevant results would be computed.

Using Eqs. (13),(21), and (26), the expectation, standard deviation, coefficient of variation, skewness, and kurtosis of the long-term loss under the homogeneous, non-homogeneous, and mixed Poisson processes are obtained for the investigated bridge, as shown in Table 1 . When the service life reaches 150 years, the expected long-term loss of bridge under the non-homogeneous Poisson model is approximately increased by 5.0% in the changing climate. As a relatively small increase in the occurrence rate is assumed in this example, the loss results with respect to the non-homogeneous model do not show large differences from those of the homogeneous model.

Table 1.

Long-term loss of the bridge under homogeneous, non-homogeneous, and mixed Poisson processes.

Poisson model	Lifetime (years)	Mean (106 USD)	Standard deviation (106 USD)	Coefficient of variation	Skewness	Kurtosis
Homogeneous	75	12.2099	4.3773	0.36	0.61	3.54
Non-homogeneous		12.9048	4.4686	0.35	0.59	3.51
Mixed		12.2099	17.9835	1.47	2.86	15.27
Homogeneous	150	14.9343	4.4849	0.30	0.57	3.49
Non-homogeneous		16.1929	4.5941	0.28	0.55	3.46
Mixed		14.9343	21.8010	1.46	2.86	15.26

According to Table 1, all skewness values are positive (right skewed), which indicates a longer tail on the right side of the distribution of long-term loss. Homogeneous and non-homogeneous models are moderately skewed (skewness between 0.5 and 1), while the mixed model is highly skewed (skewness greater than 1). Meanwhile, all kurtosis values are greater than 3, indicating that all the tails are heavier and longer than a normal distribution. For the case using the mixed Poisson process, the expected loss is the same as that using the homogeneous Poisson process, but the standard deviation, skewness, and kurtosis are much larger, which indicated potential heavy tail risks. Special attention should be paid to this aspect within the decision-making process.

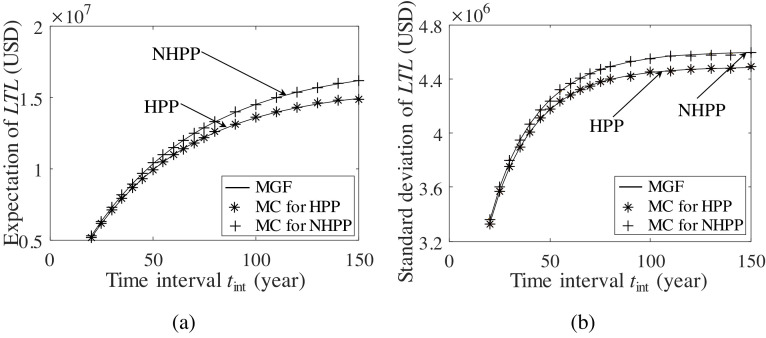
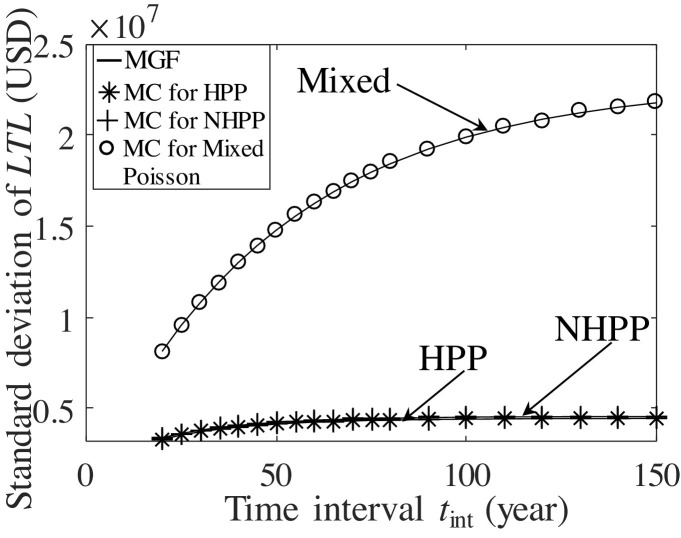
The proposed analytical method is validated by the Monte Carlo simulation. In the simulation approach, the homogeneous model is generated using the exponentially distributed inter-arrival times, while a non-homogeneous process is simulated using the thinning method [67]. The mixed Poisson process is simulated based on the stochastic occurrence rate [68]. The results of the mean and standard deviation of the long-term loss under the homogenous and non-homogeneous models are indicated in Fig. 5 . Fig. 6 shows the standard deviation of long-term loss of the investigated bridge under different hurricane occurrence models. The loss under the mixed Poisson process has the largest dispersion, as the mixed model involves large uncertainties of climate variability, compared with the other two Poisson models. In the figures, the comparison between the analytical and simulation results is also provided. A good agreement among the results indicates the accuracy and effectiveness of the proposed analytical method. Compared with the analytical approach, the simulation of a single run with respect to an assigned lifetime takes about one to two hours. The simulation was conducted on a computer with Intel Core i7–6700 CPU (4 core, 3.40 GHz, 16 GB RAM) and Intel HD Graphics 530 GPU. In this example, the simulation approach is time-consuming and computationally expensive.

Fig. 5.

(a) Expectation and (b) standard deviation of hurricane-induced long-term loss under homogeneous (HPP) and non-homogeneous model (NHPP) by moment generating function (MGF) method and Monte Carlo (MC) simulation.

Fig. 6.

Standard deviation of hurricane-induced long-term loss under homogeneous (HPP), non-homogeneous (NHPP), and mixed Poisson model by moment generating function (MGF) method and Monte Carlo (MC) simulation.

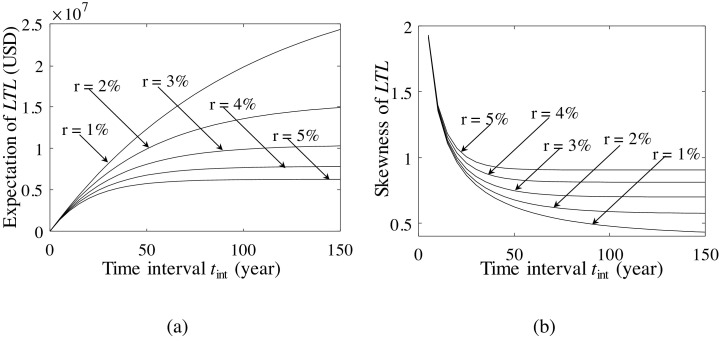
A parametric study is developed to measure the sensitivity of long-term loss to the monetary discount rate and variability of loss severity. A series of incremental monetary discount rates from 1% to 5% is considered for the homogeneous Poisson model. Fig. 7 (a) illustrates that the expected long-term loss decreases rapidly with the increase of the monetary discount rate. The same trend is also observed for the standard deviation of long-term loss. However, the tendency is opposite with respect to the skewness and kurtosis. Fig. 7(b) shows that skewness increases with the discount rates. Hence, appropriate predictions of the monetary discount rate are significant for long-term loss estimation.

Fig. 7.

(a) Expectation and (b) skewness of the long-term loss considering different monetary discount rates.

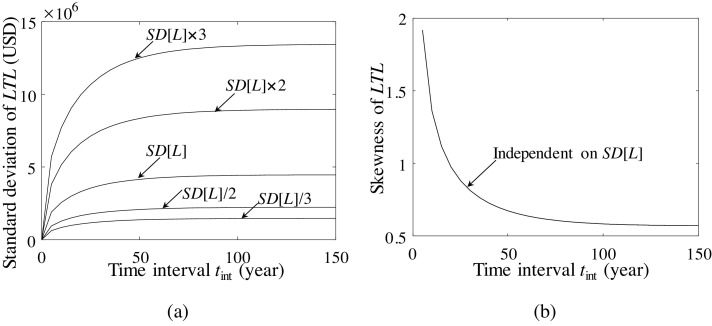
The loss severity is another key input for the loss assessment, as its mean E[L] and standard deviation SD[L] are associated with large uncertainty in hazard characteristics and climate environments. The impact of the variability of loss severity on the long-term loss is assessed. The long-term loss with the initial standard deviation SD[L] is taken as the reference value. The long-term loss under the other four cases with triple, double, one-half, and one-third SD[L] is assessed. The associated standard deviations are presented in Fig. 8 (a). It shows that the dispersion of long-term loss is significantly enlarged with the increase of loss severity. However, the skewness of long-term loss is not influenced, as shown in Fig. 8(b). From Eqs. (18) and (19), the skewness and kurtosis are independent of the exponentially distributed loss severity.

Fig. 8.

(a) Impact of the variability of loss severity on the long-term loss considering identical expectation E[L] with different standard deviations of loss severity SD[L]and (b) the effect of variability of loss severity on the skewness of long-term loss.

In the illustrative examples, structures are assumed to be fully restored to the pre-hazard stage. This assumption is commonly used in the loss assessment [14,15,69]. The level of restoration usually depends on many factors, e.g., the acceptable level of structural performance, investment, and tradeoffs between appropriate performance levels and investment. Further studies are needed to incorporate different restoration models.

Conclusions

This paper develops a novel moment generating function-based analytical approach to assess the long-term loss under both stationary and nonstationary hazards. Higher-order moments of long-term loss under four stochastic models are assessed, including the homogeneous Poisson process, non-homogeneous Poisson process, mixed Poisson process, and renewal process. The proposed approach is applied to two illustrative examples to assess the loss severity and the long-term loss incorporating parametric studies. The analytical approach is validated by the Monte Carlo simulations. With a satisfactory agreement of the results, the effectiveness and accuracy of the proposed approach are validated. Following conclusions are drawn:

• 1.The moment generating function-based approach is proposed for the higher-order analysis of long-term loss. By using the law of total expectation, the developed approach successfully expands the application scope of the moment generating function. Explicit expressions of moment generating functions are presented for the homogeneous, non-homogeneous, and mixed Poisson processes. When the derivations of moment generating functions are complex, e.g., in a renewal process, properties of the stochastic process can be utilized. The renewal function and the convolution technique are used to derive moments under the renewal model. A new stochastic model of the mixed Poisson process is introduced, which is associated with a random variable for the rate function. Statistical moments of long-term loss under this new model are also effectively assessed using the moment generating function.
• 2.The long-term loss of the investigated civil infrastructure under different stochastic occurrence models of hazard is computed. In particular, the homogeneous Poisson, non-homogeneous Poisson, and mixed Poisson processes are investigated. The impact of climate change and variability on hurricane-induced loss is assessed. Due to the stochastic occurrence rate within the mixed Poisson process, the relevant standard deviation, skewness, and kurtosis of long-term loss are much larger than those associated with other models. In addition, the long-term loss is sensitive to the change of loss severity and monetary discount rate. Appropriate evaluations of these parameters are required for the loss assessment.
• 3.Apart from the loss assessment, statistical moments can be used to assess the long-term reliability. Moments can also be used to describe probabilistic characteristics of random variables. Some of the derivations may not be applicable to stochastic processes without Poisson properties. The moment generating function may not exist due to divergent integrals.
• 4.Future studies are needed to incorporate different restoration models by considering the level of structural restoration. A further study may evaluate the statistical moments of loss with limited information, e.g., with a few observations. The application of higher-order moments in the decision-making process needs to be investigated in future studies.

CRediT authorship contribution statement

Yaohan Li: Conceptualization, Methodology, Software, Writing - original draft. You Dong: Visualization, Investigation, Writing - review & editing, Validation, Supervision. Jing Qian: Investigation, Software.

Appendix A. Moment generating function

The derivation of the moment generating function of long-term loss under the homogeneous and non-homogeneous Poisson models in Eqs. (12) and (21) is presented. Following the notations described in Section 3, the moment generating function of the long-term loss is

$${\Phi }_{\mathit{LTL}\left(t_{\text{int}}\right)}\left(\eta \right)=E\left[{e^{\eta }}^{\mathit{LTL}\left(t_{\text{int}}\right)}\right]=E\left[\prod _{k=1}^{N\left(t_{\text{int}}\right)}{\Phi }_L\left(\eta e^{-r{T}_k}\right)\right]$$ (A1)

According to the properties of moment generating functions [70], the Eq. (A1) can be expressed as

$$\begin{array}{ccc}\hfill {\Phi }_{LTL\left(t_{\text{int}}\right)}\left(\eta \right)& =& \exp (-\lambda t_{\text{int}})+\sum _{n=1}^{\infty }E\left[\exp (\eta \prod _{k=1}^n{L}_k{e}^{-r{T}_k})|N\left(t_{\text{int}}\right)=n\right]\mathrm{P}(N\left(t_{\text{int}}\right)=n)\hfill \\ & =& \exp (-\lambda t_{\text{int}})+\sum _{n=1}^{\infty }E\left[\prod _{k=1}^n{\Phi }_L\left(\eta e^{-r{T}_k}\right)|N\left(t_{\text{int}}\right)=n\right]\left[\frac{{\left(\lambda t_{\text{int}}\right)}^n}{n!}{e}^{-\lambda t_{\text{int}}}\right]\hfill \\ & =& \exp (-\lambda t_{\text{int}})\hfill \\ & & +\sum _{n=1}^{\infty }\left\{{\int }_0^{t_{\text{int}}}{\int }_{s_1}^{t_{\text{int}}}\cdots {\int }_{s_{n-1}}^{t_{\text{int}}}\prod _{k=1}^n{\Phi }_L\left(\eta e^{-r{s}_k}\right)f_{T_1,\dots ,T_n}(s_1,\dots ,s_n|N\left(t_{\text{int}}\right))d{s}_n\cdots d{s}_1\right\}\frac{{\left(\lambda t_{\text{int}}\right)}^n}{n!}{e}^{-\lambda t_{\text{int}}}\hfill \end{array}$$ (A2)

Eq. (A2) requires the joint probability density function of the arriving times T ₁, T ₂, …, T_k. The loss severity is independent of the number of arrivals N(t _int). Hence, for the homogeneous Poisson process, the conditional joint probability density function of the arriving times T ₁, T ₂, …, T_k given N(t _int) = n can be represented by

$$f_{T_1,T_2,\dots ,T_n}((s_1,s_2\dots ,s_n)|N\left(t_{\text{int}}\right)=n)=n!·\frac{1}{t^n}$$ (A3)

in which 0 < s ₁ < s ₂ < … < s_n ≤ t _int. The result shown in Eq. (A3) can be alternatively explained by the order statistics [40,70]. Given N(t _int) = n, the arriving time can be expressed by a sequence of independently identically uniformly distributed random variables {U ₁, U ₂, …, U_n}

$$((T_1,T_2\cdots ,T_n)|N\left(t_{\text{int}}\right)=n)\stackrel{d}{=}(t_{\text{int}}{U}_1,t_{\text{int}}{U}_2,\cdots ,t_{\text{int}}{U}_n)$$ (A4)

where $\underset{\_}{\underset{\_}{d}}$ refers to that the same probability distribution is maintained on both sides. Random variables U ₁, U ₂, …, U_n have a uniform distribution over (0, 1). Consequently, substituting Eq. (A3) into Eq. (A2), the moment generating function of long-term loss can be rearranged as

$$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle {\Phi }_{\mathit{LTL}\left(t_{\text{int}}\right)}\left(\eta \right)-\exp (-\lambda t_{\text{int}})}\hfill \\ {\displaystyle =\sum _{n=1}^{\infty }\{{\int }_0^{t_{\text{int}}}{\int }_{s_1}^{t_{\text{int}}}\cdots {\int }_{s_{n-1}}^{t_{\text{int}}}\prod _{k=1}^n{\Phi }_L\left(\eta e^{-r{s}_k}\right)\left(\frac{n!}{t^n}\right)d{s}_n\cdots d{s}_1\}\left[\frac{{\left(\lambda t_{\text{int}}\right)}^n}{n!}{e}^{-\lambda t_{\text{int}}}\right]}\hfill \\ {\displaystyle =\exp (-\lambda t_{\text{int}})\sum _{n=1}^{\infty }{\lambda }^n{\int }_0^{t_{\text{int}}}{\int }_0^{s_n}\cdots {\int }_0^{s_2}\prod _{k=1}^n{\Phi }_L\left(\eta e^{-r{s}_k}\right)d{s}_1\cdots d{s}_n}\hfill \end{array}\end{array}$$ (A5)

Within the period of (0, t _int], the right-hand side of Eq. (A5) is noted as Ω. Taking derivatives on both sides with respect to t _int, the Eq. (A5) gives

$$\begin{array}{ccc}& & \frac{d}{d{t}_{\text{int}}}{\Phi }_{LTL\left(t_{\text{int}}\right)}\left(\eta \right)=-\lambda \exp (-\lambda t_{\text{int}})-\lambda \exp (-\lambda t_{\text{int}})\Omega +\exp (-\lambda t_{\text{int}}){\Omega }^{\prime }\hfill \\ & & =-\lambda \exp (-\lambda t_{\text{int}})(1+\Omega )+\exp (-\lambda t_{\text{int}}){\Omega }^{\prime }=-\lambda {\Phi }_{LTL\left(t_{\text{int}}\right)}\left(\eta \right)+\exp (-\lambda t_{\text{int}}){\Omega }^{\prime }\hfill \\ & & =-\lambda {\Phi }_{LTL\left(t_{\text{int}}\right)}\left(\eta \right)\hfill \\ & & +\lambda {\Phi }_L\left(\eta e^{-rs}\right)\exp (-\lambda t_{\text{int}})\left[1+\sum _{n=1}^{\infty }{\lambda }^n{\int }_0^{t_{\text{int}}}{\int }_0^{s_n}\cdots {\int }_0^{s_2}\prod _{k=1}^n{\Phi }_L\left(\eta e^{-r{s}_k}\right)d{s}_1\cdots d{s}_n\right]\hfill \\ & & =-\lambda {\Phi }_{LTL\left(t_{\text{int}}\right)}\left(\eta \right)+\lambda {\Phi }_L\left(\eta e^{-rs}\right){\Phi }_{LTL\left(t_{\text{int}}\right)}\left(\eta \right)\hfill \end{array}$$ (A6)

By solving this linear differential equation Eq. (A6), the moment generating function can be obtained as

$${\Phi }_{LTL\left(t_{\text{int}}\right)}\left(\eta \right)=\exp \left[\lambda {\int }_0^{t_{\text{int}}}[{\Phi }_L\left(\eta e^{-rs}\right)-1]ds\right]$$ (A7)

For the non-homogeneous Poisson process, the conditional probability density function of arriving times is

$$f_{T_1,T_2,\dots ,T_n}((s_1,s_2\dots ,s_n)|N\left(t_{\text{int}}\right)=n)=\frac{n!}{Q^n\left(t_{\text{int}}\right)}\prod _{k=1}^n\lambda \left(s_k\right)$$ (A8)

where Q(t _int) is the expected number of hazard events [71], as indicated in Eq. (20). Following a similar computation procedure as shown in Eq. (A2), the moment generating function can be expressed as

$$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle {\Phi }_{\mathit{LTL}\left(t_{\text{int}}\right)}\left(\eta \right)}\hfill \\ {\displaystyle =\exp (-Q\left(t_{\text{int}}\right))}\hfill \\ {\displaystyle +\sum _{n=1}^{\infty }\{{\int }_0^{t_{\text{int}}}{\int }_{s_1}^{t_{\text{int}}}\cdots {\int }_{s_{n-1}}^{t_{\text{int}}}\prod _{k=1}^n{\Phi }_L\left(\eta e^{-r{s}_k}\right)f_{T_1,\cdots ,T_n}(s_1,\cdots ,s_n|N\left(t_{\text{int}}\right))d{s}_n\cdots d{s}_1\}\left[\frac{Q^n\left(t_{\text{int}}\right)}{n!}{e}^{-Q\left(t_{\text{int}}\right)}\right]}\hfill \\ {\displaystyle =\exp (-Q\left(t_{\text{int}}\right))+\exp (-Q\left(t_{\text{int}}\right))\sum _{n=1}^{\infty }{\int }_0^{t_{\text{int}}}{\int }_0^{s_n}\cdots {\int }_0^{s_2}\left[\lambda \left(s_k\right){\Phi }_L\left(\eta e^{-r{s}_k}\right)\right]d{s}_1\cdots d{s}_n}\hfill \end{array}\end{array}$$ (A9)

Taking derivatives at two sides of Eq. (A9), the moment generating function of long-term loss associated with the non-homogeneous Poisson process can be expressed as

$${\Phi }_{LTL\left(t_{\text{int}}\right)}\left(\eta \right)=\exp \left[{\int }_0^{t_{\text{int}}}\lambda \left(s\right)[{\Phi }_L\left(\eta e^{-rs}\right)-1]ds\right]$$ (A10)