Parallelization of CPPTRAJ Enables Large Scale Analysis of Molecular Dynamics Trajectory Data

Abstract

Advances in biomolecular simulation methods and access to large scale computer resources have led to a massive increase in the amount of data generated. The key enablers have been optimization and parallelization of the simulation codes. However, much of the software used to analyze trajectory data from these simulations is still run in serial, or in some cases many threads via shared memory. Here we describe the addition of multiple levels of parallel trajectory processing to the molecular dynamics simulation analysis software CPPTRAJ. In addition to the existing OpenMP shared-memory parallelism, CPPTRAJ now has two additional levels of message passing (MPI) parallelism involving both across-trajectory processing and across-ensemble processing. All three levels of parallelism can be simultaneously active, leading to significant speedups in data analysis of large data sets on the NCSA Blue Waters supercomputer by better leveraging the many available nodes and its parallel file system.

INTRODUCTION

Over the past decade, computational simulations have become increasingly faster thanks to improved hardware (such as the use of GPUs^1–4), the availability of high-performance computing clusters (such as the Blue Waters Petascale Resource and those available from XSEDE), and specialized computational resources (such as the Anton machines from D. E. Shaw⁵). This has led to the generation of longer molecular dynamics trajectories, i.e. the time sequence of 3D positional coordinate frames (and sometimes velocities, forces, and unit cell data as well). In addition, ensemble methods that generate multiple trajectories in a single run such as replica exchange molecular dynamics⁶ have become increasingly popular for generating data with well-converged properties.⁷ These factors, combined with the fact that these improvements also allow simulations of increasingly larger systems, means that at the time of publication of this article, the size of the data generated from a single simulation can range from hundreds of gigabytes to multiple terabytes. As a result, for many projects the bottleneck is no longer in generating the data, but instead reading the data and analyzing it.^8,9 In order to keep pace with this explosion of data, analysis software must be made more efficient.

Currently there is a wide variety of software available for the analysis of molecular dynamics (MD) trajectory data. While many MD data analysis tools do not function in parallel, there are a few exceptions. VMD¹⁰ makes use of OpenMP/CUDA to accelerate certain calculations,¹¹ and has some support for certain MPI-parallelized analyses via the TCL/TK interface (for example calculating the solvent-accessible surface area for residues and performing molecular dynamics flexible fitting¹²). Both MDAnalysis¹³ and MDTraj¹⁴ have certain types of analysis that are OpenMP-accelerated (for example the MDAnalysis.lib.distances module in MDAnalysis and the RMSD calculation in MDTraj). MDTraj can also parallelize trajectory processing for calculations in which frames are independent (such as surface area calculation) via the IPython parallel toolkit,¹⁵ while MDAnalysis can parallelize trajectory processing by making use of the Python multiprocessing module or mpi4py¹⁶ to distribute calculations over multiple cores, although this requires additional coding on the part of the user to implement. It should also be noted that some analysis can also be parallelized via tools like GNU Parallel¹⁷ or the xargs command, although this only works if the separate analysis tasks are completely independent.

CPPTRAJ¹⁸ is a program designed to analyze MD simulation data, and can process molecular dynamics trajectory formats from many popular MD software packages such as Amber,¹⁹ NAMD,²⁰ Gromacs,²¹ and CHARMM.²² CPPTRAJ is currently the main analysis software for Amber, and is freely available both as part of AmberTools (http://ambermd.org) and via a GitHub repository that provides access to the latest versions of the code in-between the yearly AmberTools releases (https://github.com/Amber-MD/cpptraj). As of version 16 and beyond, CPPTRAJ now contains three levels of parallelism: 1) Across-ensemble parallelism, where an ensemble of trajectories is divided among MPI processes (also referred to as ranks in this manuscript), 2) Across-trajectory parallelism, where a single trajectory is divided among MPI ranks, and 3) OpenMP parallelism, where time consuming Actions are divided among OpenMP threads. Although across-ensemble and OpenMP parallelism have been present in earlier versions of CPPTRAJ, they can now both be active as the same time as the novel across-trajectory parallelism. An aspect that facilitates usage is that existing CPPTRAJ scripts require no modification to be used in parallel (although it is recommended that ensemble processing scripts add one command solely to improve efficiency, discussed below). This parallelization allows CPPTRAJ to read, write, and process large trajectories much faster while leveraging HPC resources more efficiently. In this manuscript, we will describe in detail new parallel functionality in the current version of CPPTRAJ and its application to accelerating data analysis on the NCSA Blue Waters supercomputer.

Across-trajectory Parallelism

A molecular dynamics trajectory records the 3D positional coordinates (and sometimes also velocities, forces, and/or unit cell data) of a system as it evolves over time. A trajectory frame represents the system at a single time point. Trajectory processing Runs, in which trajectory frames have one or more calculations performed on them, have been parallelized in CPPTRAJ by dividing all frames from all input trajectories as evenly as possible among ranks.

$$Frames\_on\_rank=\left(\frac{TotalFrames}{Nranks}\right)+\left(int\right)\left(Rank<\left(TotalFrames\%Nranks\right)\right)$$

Here Frames_on_rank is the total number of frames the individual MPI process will process during the Run, TotalFrames is the total number of input trajectory frames for the entire Run, Nranks is the number of MPI processes (ranks), Rank is the rank of the individual MPI process, and the ‘%’ represents the modulo operator, which returns the remainder of the division of the two operands. The (int) serves to convert the result of the boolean less-than ‘<’ operator to an integer (1 for true, 0 for false). Stated plainly, if a given MPI process’s rank is less than the remainder of the total number of frames divided by the number of MPI processes, the total number of frames for that rank to handle is increased by 1, otherwise the total to handle is just the total number of frames divided by the number of ranks. This effectively spreads any remainder frames over as many ranks as possible and ensures that the maximum difference of frames to handle between any two ranks is 1. Because the frame division depends on knowing the number of frames to be read in ahead of time, reading of trajectories where the number of frames is not known is not supported in parallel. Figure 1 provides a few examples of how the reading of input trajectory frames is divided across ranks in CPPTRAJ.

Figure 1.

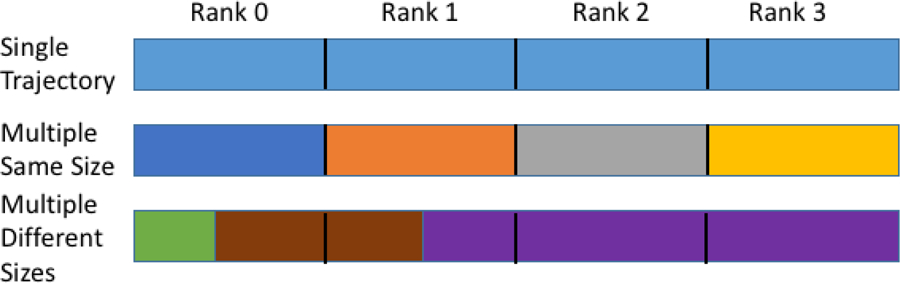
Three examples of how frames are divided among MPI ranks (4 in this example) in across-trajectory parallelism in CPPTRAJ. Each colored rectangle represents a trajectory file; black lines indicate where the previous rank stops reading and the next rank begins reading. Example 1: a single large trajectory. Example 2: four trajectories of the same size. Example 3: three trajectories of various sizes.

Currently all trajectory formats supported by CPPTRAJ can be read in parallel. Trajectory reading does not actually make use of any MPI routines; instead, file seeking is used to position each MPI process at the correct starting frame. However, out of necessity (i.e. to avoid problems due to file locks, etc) trajectory writes do make use of MPI routines for writing to single output trajectory files, so there are some restrictions on which formats are supported for writing in parallel. Currently supported formats for parallel write are NetCDF (via the Parallel NetCDF library²³), Amber ASCII coordinates, Amber ASCII/NetCDF restarts, CHARMM trajectories (DCD), and Gromacs TRR. CPPTRAJ can also write Mol2/PDB files in parallel, but only if writing each frame to a separate file (no MPI routines are used). Although in principle it is possible to write a single PDB/Mol2 file in parallel, this design choice was made because for multiple MPI processes to properly write to a single file in parallel using MPI file routines in the same manner that CPPTRAJ reads trajectories (i.e. independently divided into sections), the final output file size must be known so that each rank knows where to initially position itself. This in turn requires that the size of an individual trajectory frame is known, which can be challenging for the PDB and Mol2 formats since they also include topology information and can be prone to fixed-width text fields overflowing (particularly the PDB format).

When processing trajectories, CPPTRAJ can perform various calculations (e.g. a distance calculation) and/or manipulations (e.g. removing specified atoms); these are collectively referred to as Actions. Since Actions were initially envisioned as acting on a single frame at time, most Actions in CPPTRAJ required no modification to be used in parallel – in general these are Actions in which the result of calculation on any frame does not depend on calculation results from any other frame or a reference state; examples are the distance, angle, and dihedral calculations.

Once a Run has completed, any Data Sets (i.e. data that has been derived from trajectory frames during a Run such as the distance between two atoms) that have been generated by such Actions are consolidated on the master process (rank 0); in CPPTRAJ this is referred to as “syncing” the Data Sets to the master. The end result is that after a trajectory processing Run, only the master has a complete copy of each Data Set. Syncing is accomplished in the following manner. First, an internal consistency check is made to ensure that the number of sets that need to be synced on each rank is the same. Next, the size of each Data Set to be synced on each non-master rank is sent to the master so that 1) the master will know how much space to allocate for each set (i.e. so only one reallocation per Data Set on the master needs to occur) and 2) the master will know how much data each other rank will be attempting to send. Finally, for each Data Set to be synced, each non-master rank sends its data to the master in rank order. Since this consolidation happens separately from Actions, any new Action added to CPPTRAJ in the future which calculates quantities that do not depend on other frames or reference data will effectively be parallelized with no additional work. In practice, we have found that the sync phase is relatively fast; usually no more than 1% of the total Run time.

Once Data Sets have been synced, the master writes to a Data File. Data File writes are currently not performed in parallel since this made it much simpler to use the existing code, and it was found that for the majority of trajectory processing runs, Data File writes take up only a very small fraction of the total run time.

Figure 2 shows an example of the performance benefit from across-trajectory parallelization for calculating the coordinate RMSD of 1293 atoms for a trajectory with 881,372 frames total using the first frame as a reference. Up to 2 MPI processes per node (PPN), the speedup remains near ideal at 6x for 6 ranks (Figure 2, black and red lines) – this is because once initial set up is completed there is no need for the individual ranks to communicate with each other during trajectory processing. As the number of PPN is increased beyond two, the efficiency falls off. A maximum speedup of 11.6x was achieved using 24 ranks spread across two nodes versus 1 rank on a single node. While the speedup is still significant, it is not particularly efficient. The reason is likely that as the number of ranks per node is increased, the input/output (I/O) for each node becomes saturated; more ranks are competing for a fixed amount of I/O bandwidth.

Figure 2.

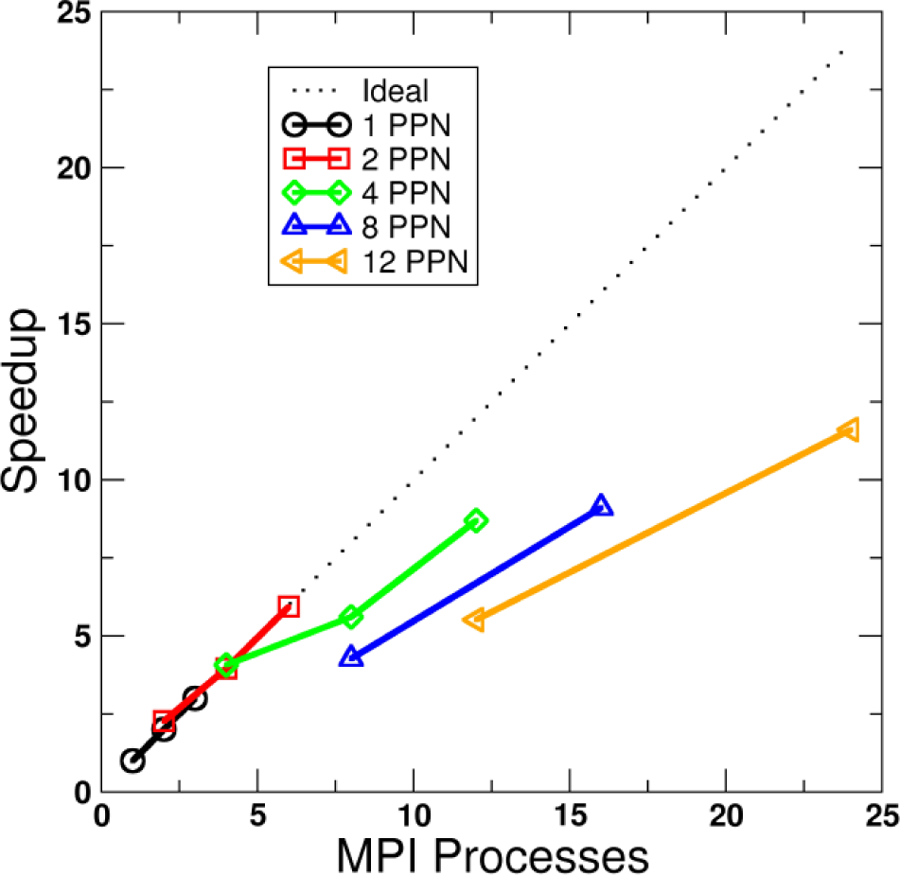
Speedup versus number of MPI processes for across-trajectory parallelization of an RMSD calculation (1293 atoms, 881,372 frames). Each line represents a different number of processes per node (PPN). Raw timing for 1 node, 1 PPN is 590 s. Calculations run on the Ember cluster, CHPC at University of Utah (Westmere 2.8 GHz, dual socket six-core nodes, NFS-mount file storage).

In order to further examine this phenomenon, we examined in more detail the timings for each phase of parallel trajectory processing Runs (trajectory read, action, data write, data sync) using the slightly more CPU- and data-intensive hydrogen bond calculation. Figure 3 shows the speedup relative to 1 PPN for individual Run phases versus number of PPN for hydrogen bond analysis using 16 processes in each case. Runs for each value of PPN were repeated 10 times, and input trajectory files were staged to new locations prior to each Run to prevent any caching of the trajectory files in memory. Detailed timings can be found in Supporting Information.

Figure 3.

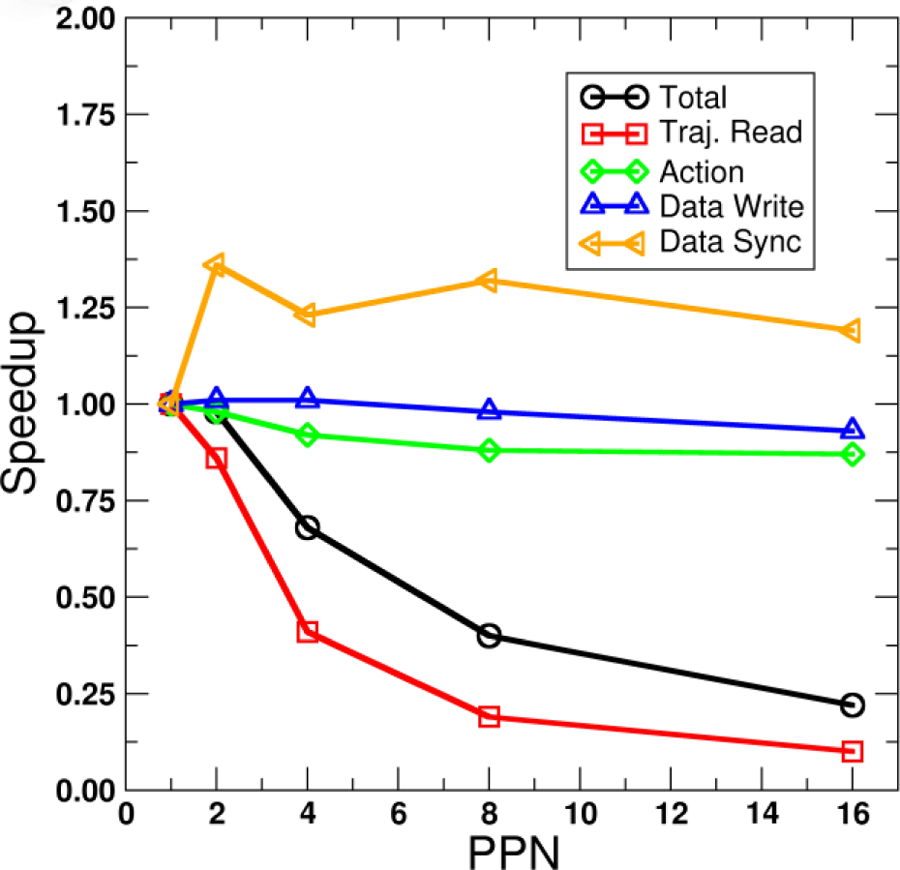
Speed up versus number of MPI processes per node (PPN) for across-trajectory parallelization of a hydrogen bond calculation (375 acceptor atoms, 371 acceptor/donor sites, 440 solute hydrogens, 18000 frames) using 16 MPI processes. Each line represents timings for different parts of the trajectory processing Run (total time, trajectory read, the hydrogen bond action, data file write, and data set sync). Raw timings for 1 PPN (16 nodes): Total=22.62±0.86 s, Traj. Read=8.27±1.12 s, Action=2.35±0.06 s, Data Write=9.14±0.06 s, Data Sync=0.08±0.01 s. Calculations run on the LoBoS cluster, NIH (Haswell 2.4 GHz dual socket eight-core nodes, NFS-mount file storage).

As the number of PPN increases from 1 (16 nodes) to 16 (1 node), trajectory reading slows down, with the most significant drop occurring from 2 PPN to 4 PPN. This leads to the total processing time becoming slower; however, the slowdown in trajectory reading from 1 PPN to 2 PPN is compensated somewhat by a speedup in Data Set syncing, leading to similar overall run times for 1 PPN and 2. Action and data file write timings are relatively unaffected by increasing the number of PPN. Ultimately it appears that there is a maximum number of MPI ranks per node that can be used for across-trajectory parallelization (specifically trajectory reading in parallel) to remain efficient. However, the remaining CPU cores need not remain idle. They could for example be put to use in speeding up individual actions via OpenMP, discussed later.

Almost all functionality present for serial Runs is present for across-trajectory parallel Runs with a few exceptions. One restriction to note is that unlike serial processing mode, parallel processing mode does not support reading trajectories corresponding to different topologies, i.e. all input frames must correspond to a single topology; the topology describes how the system coordinates are organized into atoms, residues, and molecules, and may include other information such as bonds, angles, and dihedrals. This design choice was made for two reasons. The first reason is that it ensures all ranks will process frames at roughly the same rate (since each coordinate frame is guaranteed to be the same size) and so will finish at about the same time, reducing the potential for ranks to be idle. The second reason is it guarantees that Action setup will occur only once, eliminating any further need for any communication between ranks that may be required when setting up for a new topology, allowing ranks to process the trajectory independently. Another important restriction is that in order to properly write out trajectories in parallel, the number of input frames must be known ahead of time so that each rank knows where to position itself in the output trajectory file. This means that reading of trajectories where the number of frames is not known ahead of time (e.g. Amber ASCII trajectories that are BZIP2 compressed) or using Actions that change the number of output frames (e.g. filter) are not supported in parallel.

Some Actions require more setup and/or consolidation steps either in addition to or in place of Data Set synchronization in order to function properly in parallel. By and large these changes do not significantly increase the communication required between ranks as they involve either a one-time communication (e.g. an MPI broadcast or reduce) before or after the trajectory processing Run, or an alternative means of Data Set synchronization. Thus, these Actions perform and scale similar to those using Data Set synchronization. A more in-depth discussion of such Actions and the design elements needed to effectively parallelize them can be found in the Supporting Information. In addition, other Actions simply cannot be easily or effectively parallelized; an example of this is the molecular diffusion calculation, since determination of the mean-squared displacement of a molecule in each frame requires full knowledge of the position of the molecule at all previous frames. An error message is printed for these Actions if run in parallel.

Ensemble Trajectory Processing

Most common implementations of enhanced sampling methods like replica exchange molecular dynamics⁶ involve generating ensembles of trajectories in parallel from effectively independent MD simulations run in parallel, with each member of the ensemble generating a single and separate trajectory. As the ensembles exchange information, for example a change in temperature, Hamiltonian or other property, choices can be made as to how to output and sort the resulting trajectories. The easiest way to handle this is to have each independent ensemble instance output its own “replica” trajectory while keeping track of the associated state variables (temperature, Hamiltonian, etc) that may have changed. The alternative is a “coordinate” trajectory which follows the coordinates at a particular state, for example a particular temperature or particular Hamiltonian.

Like PTRAJ before it, CPPTRAJ is able to extract frames at a target Hamiltonian (e.g. a specific pH or temperature) from “unsorted” coordinate trajectories to “sorted” replica trajectories in the following manner. The input ensemble can either be explicitly specified, or the user provides the “lowest” (i.e. first) member trajectory of the ensemble and all other member trajectories of the ensemble are scanned for and opened based on that file name, using the simple scheme that each trajectory file must end in a monotonically increasing numerical suffix of fixed width. Next, the first frame of each ensemble trajectory is read, and the frame matching the target are selected for further processing. This is repeated for all frames.

While this approach succeeds at extracting all frames for the replica of interest, it is inefficient if one wants to analyze the frames for any or all other ensemble members: obtaining frames for additional replicas requires one or more additional passes over the original trajectory ensemble. A keyword was later added to the trajectory output command wherein an ensemble of output trajectories sorted by replica could be obtained from an “unsorted” ensemble of coordinate trajectories, but this could only be done on a per-ensemble basis (i.e. multiple input ensembles could not be concatenated into a single output ensemble) and no other calculations could be performed on the sorted frames.

Since version 13, CPPTRAJ has had the ensemble command, which enables an entire ensemble of trajectories to be processed at once. The ensemble command can be used in place of the normal trajin (read input trajectory) command. If this is done, CPPTRAJ will enter an ensemble processing mode, whereby any Actions will automatically be run on the entire sorted ensemble instead of just a single target member of the ensemble. In addition, any output trajectories (from the trajout command) will be written for every member of the ensemble. A graphical explanation of the difference between standard replica trajectory processing (trajin remdtraj) and ensemble trajectory processing, as well as an example of input for an ensemble processing Run is given in the Supporting Information. The trajectory files that comprise the ensemble can either be explicitly specified or searched for automatically if the files use a common naming scheme (more details are in Supporting Information). The trajectory files that make up the ensemble do not have to be the same format, but they do have to correspond to a single topology and contain information that can be used to sort (e.g. replica temperatures, replica indices, etc).

Note that sorting of an ensemble of trajectories is not always required. This is the case for example when running Hamiltonian REMD in Amber or standard (i.e. non-fast) temperature REMD in CHARMM, since the trajectories are written by Hamiltonian (i.e. they are already trajectories sorted by replica). For these cases, the nosort keyword should be specified to the ensemble command since CPPTRAJ does not know a priori how an ensemble of trajectories was generated and will try to sort them by default. Beyond its utility in processing trajectories from Hamiltonian REMD simulations, the nosort keyword allows any collection of trajectories to be processed in parallel. As with sorted ensemble processing, the trajectories do not need to be in the same format. The only limitation is that the number of frames processed will only be as large as the shortest trajectory. Also, since sorting does not need to be performed, communication between nodes is not required which improves efficiency. Example input for an ensemble Run with no sorting is given in the Supporting Information.

While it is possible to perform ensemble trajectory processing in CPPTRAJ on a single CPU, it was parallelized via MPI in version 14 to take advantage of multi-core systems and parallel file systems. In this initial implementation, a single MPI rank handled a member of the trajectory ensemble. Frames were sorted by being communicated to the rank that represents their sorted position, at which point they are processed. While this approach can be very communication-intensive which limits its efficiency, it can still provide significant speedup in terms of real time over running in serial (see Table 1). In addition, any data generated when ensemble is run in parallel (such as the RMSD data in the above example) is written to separate files instead of to the same file.

Table 1:

Comparison of serial vs parallel ensemble (8, 60, or 192 members) processing in CPPTRAJ for a typical post-processing run (strip solvent atoms, write the sorted ensemble). Run on NCSA Blue Waters using 8, 60, or 192 nodes, 1 process per node, with the trajectory data stored on a Lustre parallel file system.

# Replicas	# Frames	Serial Time (s)	Parallel Time (s)	Speed up
8	60,000	25,672	3,910	6.57x
60	100	2,859	65	43.98x
192	1,000	2,507	42	59.69x

A practical example of the usage of parallelized ensemble analysis is when processing large ensembles of trajectories (such as those generated by multi-dimensional REMD simulations^7,24) that have been generated on a remote resource but are to be analyzed on another (e.g. a local) resource. Typically, only part of the actual system will be required for analysis, such as the solute in an explicitly solvated system. Using MPI-enabled CPPTRAJ in ensemble mode one could sort, strip, and re-image an ensemble of trajectories in parallel, then transfer the now more compact ensemble for further analysis.

Improved Parallelization of Processing Trajectory Ensembles on Blue Waters

The initial implementation of parallel ensemble processing had two major drawbacks. The first was the requirement that the number of ranks used to process the ensemble had to be equal to the number of replicas (ensemble members), that is to say one could only use 1 process per replica (PPR). The second was that during setup, each rank would have to access each trajectory in the ensemble, i.e. if processing 192 replicas, each rank would have to initially open all 192 files (36864 total file opens); this was extremely inefficient and scaled very poorly. The latest version of CPPTRAJ allows across-trajectory parallelism to be combined with ensemble parallelism, so that multiple ranks can be used to process each member of the ensemble. This is done by dividing all MPI processes into two sets of orthogonal communicators, termed TrajComm and EnsembleComm. Each TrajComm communicator is responsible for reading a single member of the ensemble in parallel, while each EnsembleComm communicator is responsible for sorting frames across the ensemble. In addition, ensemble setup has been rewritten so that each member of the ensemble is set up by a single rank (the master rank of each TrajComm), making setup much more efficient at high replica counts. For example, if processing a 192 file ensemble with 384 MPI processes (2 PPR) there would be 192 TrajComm communicators, each with 2 ranks (dividing each ensemble member trajectory into two), and 2 EnsembleComm communicators, each with 192 ranks. During setup, each member of the ensemble is only accessed by the master rank of the corresponding TrajComm (192 total file opens). Note that in order to implement the optimized setup, a new command, ensemblesize, must be specified so that CPPTRAJ knows the total size of the ensemble prior to the setup phase and can set up the ensemble MPI communicator appropriately.

In certain cases, these improvements to parallel ensemble processing can result in a speedup far beyond what is expected, as illustrated in the following example. Figure 4 shows timings for an ensemble post-processing run on NCSA Blue Waters (Cray XE6 nodes) of a test system (192 replicas, 7622 atoms, 30000 frames) in which the ensemble of trajectories (NetCDF format) is sorted, stripped of all solvent atoms, centered and re-imaged on the remaining atoms, and written to output trajectories also in NetCDF format. For all tests, each replica was run on a single node; only the number of ranks per node was increased. From Figure 4 one can see the importance of modifying the ensemble setup so that only 1 rank is ever accessing a trajectory file as opposed to the previous setup method where every rank accessed every trajectory file. When using the old setup method, going to 4 MPI processes per replica results in a slowdown compared to using 2 PPR.

Figure 4.

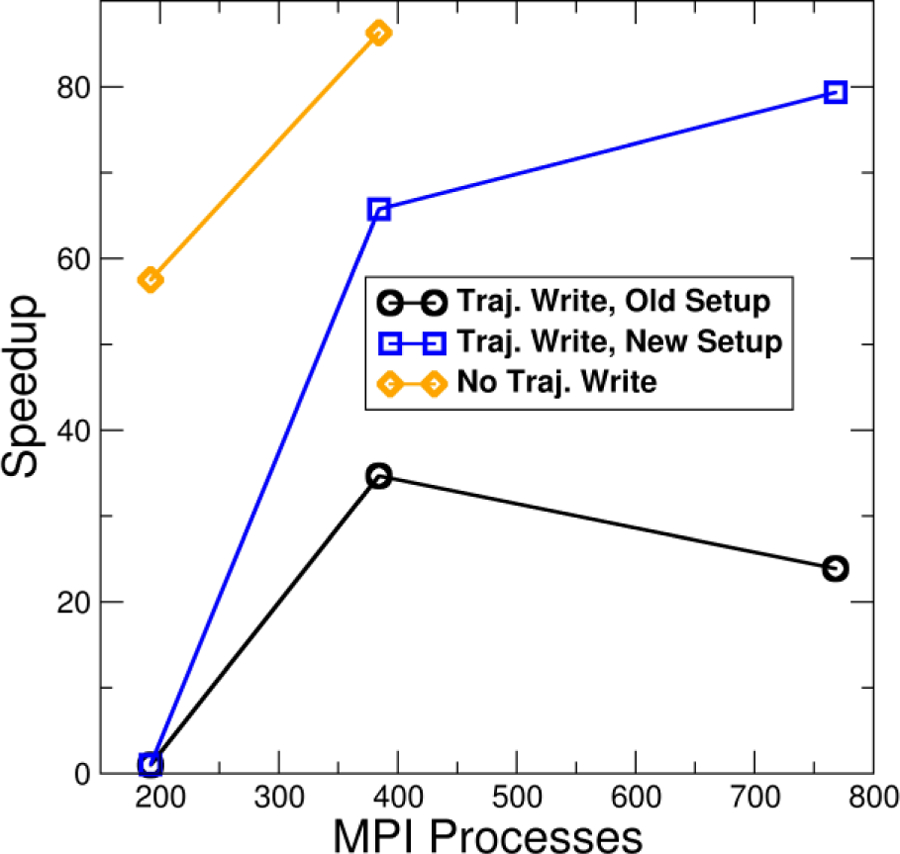
Speed up versus number of MPI processes for a post-processing ensemble run of a test system (192 replicas, 7622 atoms, 30000 frames) consisting of stripping solvent molecules, re-imaging the remaining atoms, and optionally writing output trajectories. All tests were run on 192 nodes. Black line with circles: old setup where each MPI process accessed each member of the ensemble during setup; output trajectories written. Blue line with squares: new setup where only the master MPI process for each ensemble member performs setup; output trajectories written. Orange line with diamonds: new setup, do not write output trajectories. Calculations run on NCSA Blue Waters XE6 nodes.

By far the most time-consuming part of this process is writing the sorted and stripped ensemble of trajectories (which takes 6564 s using 1 PPR), as evidenced by the time needed when trajectories are not written (120 s). Surprisingly, when more than 1 PPR was used, the ensemble processing run sped up by several orders of magnitude (taking only 105 s) instead of scaling linearly. Initially it was thought that this might be due to the use of parallel NetCDF write routines in the case of more than 1 PPR as opposed to the standard NetCDF write routines which are used when there is only 1 PPR. To test this, a modified version of CPPTRAJ was created which forced the use of parallel NetCDF write routines for 1 PPR. While this did result in a moderate speedup (about 1.25x), it was nowhere near the speedup for 2 PPR (63x) or 4 PPR (75x).

In order to better understand the reasons for the unexpectedly large speedup when using more than 1 PPR, we analyzed I/O patterns for the 1 PPR and 4 PPR ensemble processing runs using the Darshan²⁵ HPC I/O characterization tool available on Blue Waters; some of the results from this analysis are shown in Figure 5 – the full results are provided as Supporting Information. The I/O access patterns of the 1 PPR and 4 PPR runs are markedly different. When using 1 PPR, the read and write access patterns are very similar: there are roughly similar numbers of read and write operations, about half of which are sequential (i.e. the next access takes place at a higher offset than where the previous access left off) and practically none are consecutive (i.e. the next access is immediately adjacent to the previous access), most of which range in size from 1 to 4 MB. When using 4 PPR the read access patterns are similar; however, there are far more write operations than read operations, most of which are sequential but some of which are consecutive, and the sizes are much smaller (most are less than 100 bytes).

Figure 5.

Counts of I/O sizes (left column) and I/O operation types (right column) as measured using the Darshan I/O analysis tool of two parallel ensemble processing runs. Top row: 1 process per replica (PPR). Bottom row: 4 PPR. Sizes are in bytes.

Essentially, it appears that when using more than 1 PPR, file writes are being broken into much smaller pieces. Since I/O operations are typically blocking, this may allow the Cray Gemini interconnect on Blue Waters to interact in a more efficient manner with the underlying Lustre file system, as a smaller write will likely have less impact on execution time if it is held up for some reason. It remains unclear what precisely at the system level is causing this change in I/O access patterns; this will be explored in future studies. In short, when running CPPTRAJ on systems with parallel file systems it may be worth it to test performance using multiple MPI processes per node.

In CPPTRAJ versions before 15, one limitation of ensemble processing is that it used a separate Data Set list during a trajectory processing run, meaning subsequent Actions or Analyses could not directly use any data generated during an ensemble run. Instead, data had to be written out to Data Files during the ensemble processing and read back in with a subsequent readdata command. As of version 15 this limitation has been removed, with the one caveat that when ensemble processing occurs with MPI each ensemble member (i.e. rank) can only access the data it has processed. Development is currently underway to more effectively parallelize subsequent Analyses.

Hybrid MPI+OpenMP Parallelism

As previously mentioned, for CPPTRAJ there is usually a limit to how many MPI processes per node can be used for across-trajectory parallelization before efficiency starts to fall off. One can actually make better total use of computational resources by using only as many MPI ranks for trajectory parallelization as is efficient (in our experience, typically up to the number of sockets on the node), then using the remaining CPU cores to parallelize Actions for individual frames using OpenMP threads. As a simple example, consider calculating the oxygen-oxygen radial distribution function (RDF) for 12 water molecules (144 distance calculations per frame) from a single MD trajectory consisting of 10 frames being run on a system consisting of two 6-core CPUs. One could use two MPI processes to parallelize the trajectory read (5 frames per rank), and each rank could use six OpenMP threads to parallelize the RDF calculation (each thread would handle 24 distances per frame). Information on which Actions currently benefit from OpenMP parallelization is given in the Supporting Information.

Figure 6 shows an example of the performance benefit from hybrid MPI+OpenMP across-trajectory parallelization for calculating the RDF of 15022 waters using the water oxygen atom only (15022 × 15022 distances per frame), 100 frames total. With MPI only (i.e. the first 4 ranks process 5 frames while the remaining ranks process 4), the maximum speedup obtained versus a single rank is 15.7x. However, if the trajectory read is divided among 2 MPI processes while the remaining CPU cores are used by the RDF calculation via OpenMP threads, the maximum speedup achieved is 18.7x.

Figure 6.

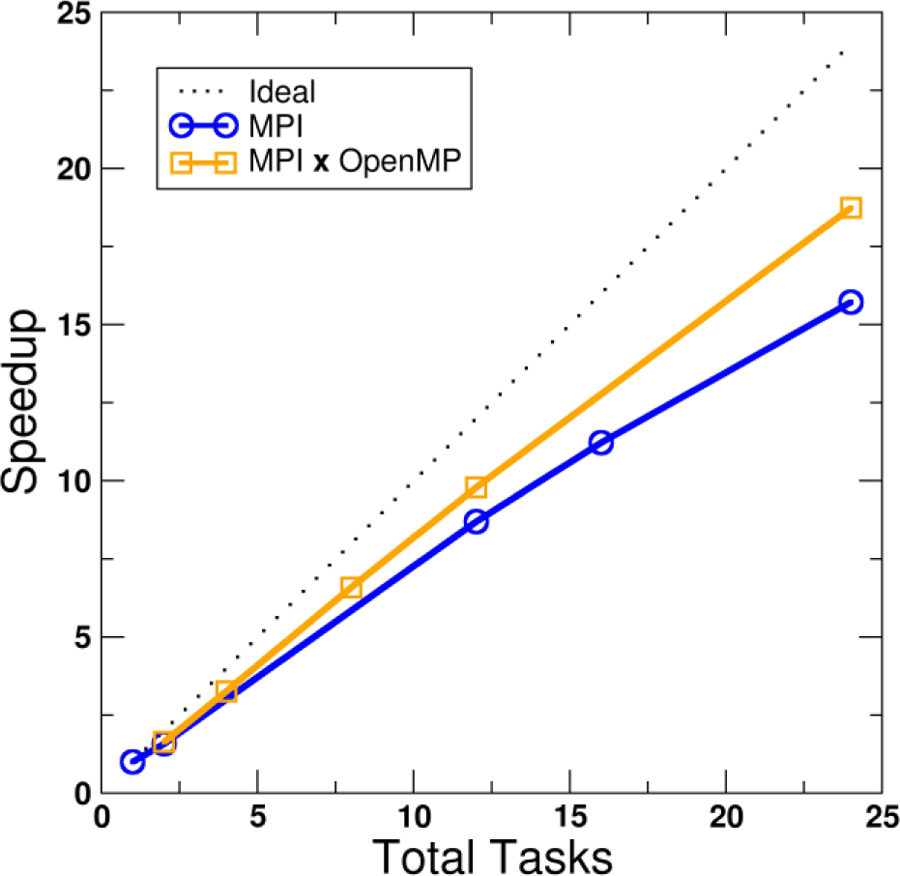
Speedup versus number of tasks for both MPI only and hybrid MPI+OpenMP parallelization of an RDF calculation (15022 water oxygen atoms, 100 frames) for 1 or 2 nodes. Raw timing for 1 node, 1 task (i.e. serial) is 2541 s. Calculations run on the Ember cluster, CHPC at University of Utah (Westmere 2.8 GHz, dual socket six-core nodes).

Figure 7 shows an example of the speedup possible with ensemble, across-trajectory, and OpenMP parallelism active at the same time using NCSA Blue Waters. Two typically time-consuming commands were chosen: radial, which calculates the radial distribution function of selected atoms, and closest, which retains only a specified number of the closest solvent molecules to specified solute; both commands require many distance calculations per frame. The test system is a 192 member multi-dimensional REMD run (Hamiltonian dimension 8, temperature dimension 24) of the r(GACC) tetranucleotide with 2497 TIP3P solvent molecules (full details for this simulation have been published elsewhere²⁴). The radial command was run on 2000 frames and the closest command was run on 10000 frames. For both commands 2 MPI processes were used per replica, 1 replica per node; only the number of OpenMP threads was increased. At 8 OpenMP threads the closest command achieves a maximum speedup of 4.6x and the radial command achieves a maximum speedup of 7.1x versus 1 OpenMP thread. While the scaling of the radial command in this case is much better than the closest command, increasing the number of cores does improve the overall speed of the calculation while leaving fewer idle cores.

Figure 7.

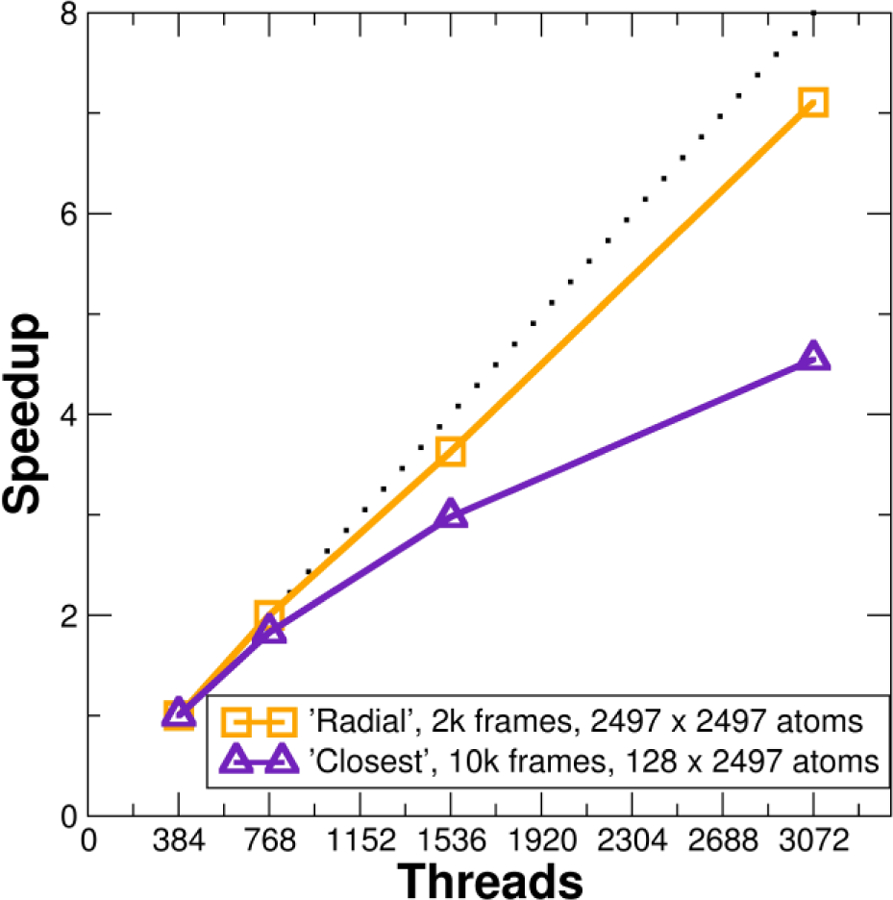
Speedup versus number of threads for hybrid MPI+OpenMP ensemble and across-trajectory parallelization of the radial and closest commands on 192 replica ensemble of r(GACC) with 2497 water molecules (10119 atoms total). The radial command calculated the RDF for 2497 water oxygens, while the closest command was used to determine the closest 89 solvent molecules to solvent. Both commands used 1 node per replica (NPR), 2 MPI processes per node (PPN). Raw timing for radial (1 OpenMP thread) is 1540 s. Raw timing for closest (1 OpenMP thread) is 422 s. Calculations run on NCSA Blue Waters XE6 nodes.

One important caveat for hybrid MPI+OpenMP runs that should be mentioned is that it may sometimes require additional configuration on the part of the user to ensure that OpenMP threads and MPI processes are being spaced efficiently among the available processors. For example, on Blue Waters OpenMP threads needed to be explicitly mapped so that there was one thread per floating point unit on each AMD Bulldozer processor. For the Mvapich2 MPI distribution (http://mvapich.cse.ohio-state.edu) it may be necessary to set the MV2_ENABLE_AFFINITY environment variable to 0 in order to set the correct affinity for threads. How to run hybrid MPI+OpenMP jobs efficiently will vary from resource to resource, and users are encouraged to benchmark carefully.

CONCLUSIONS

Given the ever-increasing amount of data that can be generated from MD simulations, it is critically important that the tools responsible for analyzing this data are able to keep up. The MD data analysis software CPPTRAJ has been modified to contain three levels of parallelism: at the level of individual Actions (via OpenMP), reading and writing across individual trajectories (via MPI), and across ensembles of trajectories (also via MPI). Crucially, no modification is necessary to existing CPPTRAJ scripts in order to take advantage of this parallelism. All three levels of parallelism can be active at the same time which allows CPPTRAJ to make more efficient use of HPC resources in terms of leaving fewer idle CPU cores per node during a trajectory processing run. The trajectory parallelization scheme has been constructed so that it will be simple to integrate with other types of parallelization that may occur at the level of individual Actions (such as offloading calculations to a GPU or Intel PHI) and the developers are continuing to explore options for further enhancements to calculation speed and efficiency.