Research on COVID-19 based on ARIMA model^Δ—Taking Hubei, China as an example to see the epidemic in Italy

Abstract

COVID-19 has spread throughout the world; various forecast models have been used to predict the development of the pandemic. The number of new cases from the outbreak to zero has gone through a complete cycle in Hubei, China, on lockdown over coronavirus. So, we created the time series ARIMA models for new cases and new deaths daily during this period. Moreover, these models have been used in Italy, which has the same population conditions and on lockdown as Hubei, in order to predict the epidemic in Italy in the next ten days and provide a theoretical basis for the development of pandemics in some countries in the future.

Introduction

As acute infectious pneumonia, COVID-19 seriously affects human life and health. Due to its infectiousness and general susceptibility to the crowd, its transmission speed is relatively fast [1], [2]. So far, there was no specific treatment for COVID-19. Moreover, in more severe cases, its infection may lead to pneumonia, severe acute respiratory syndrome, renal failure, and even death [2], [3], thus increasing its social harm.

At present, the domestic new cases in 31 provinces are basically zero, and overseas pandemics are in the outbreak stage. Looking at the overall epidemic situation in China, Hubei was a severely affected area, and the number of new cases from the outbreak to 0 has gone through a complete independent cycle, and the development was a typical representative. Therefore, we could establish ARIMA models for the daily number of new cases and new deaths in this cycle to observe the development trends of the epidemic. These models were then applied to countries with similar characteristics to Hubei, China, to study its follow-up epidemic development. Observing overseas epidemic countries, Italy and Hubei can be used for reference in terms of population (Italy 60.317 million [4], Hubei 59.27 million [5]) and state management (Italy locked down on 2020.3.10 [6], Hubei locked down on 2020.1.27 [7]). Therefore, in this article, Italy is selected as the research object. The study participants applied the ARIMA models based on the new cases and new deaths in Hubei to Italy to observe its subsequent epidemic situation.

Methods [8]

ARIMA, namely the Box–Jenkins model, and is the most common time series prediction model in the statistic model. It regards the data sequence formed by the prediction object over time as a random sequence. It analyzes a portion of the data in the sequence to obtain specific parameters that describe the mathematical model of the sequence to achieve time series modeling. And use the remaining data in the sequence to validate the validity of the model. The validated model can be used to predict the subsequent values of the data series.

According to whether the data show evidence of stationary in the different parts of regression, the ARIMA model has three basic types: moving average (MA) model, autoregressive (AR) model, and autoregressive integral moving average model (ARIMA).

A non-seasonal ARIMA model is generally denoted Arima (p,d,q). If the series is the stationary series, ARIMA model can be expressed as:

$$y_t=\sum _{i=1}^p{a}_i{y}_{t-i}+\sum _{j=1}^q{\delta }_j{\epsilon }_{t-j}$$ (1)

In the formula, p means the autoregressive parameter, q means the moving average order, y _t means the model parameter to be estimated. When the sequence is unstable, it should be stabilized by logarithmic and difference disposal. d is the number of times when the sequence becomes stationary through difference disposal.

For a stable sequence formed by a single observation indicator, calculating the autocorrelation functions (ACF) and partial autocorrelation functions (PACF) and their graphs to determine the parameter values of the model. If the PACF is truncated and the ACF is trailing, then the stationary sequence fits the autoregressive model AR. If the PACF is trailing and the ACF is truncated, the stationary sequence fits the moving average model RA. In other cases, the ARIMA model is recommended.

The process of ARIMA modelling includes four steps: data stabilization, parameters estimation, diagnostic checking, validation and evaluation. Among them, we use 70% of the entire data for modelling and use the remaining 30% of the data for model validation.

Firstly, data stabilization: The primary condition for ARIMA modelling is that the predicted sequence must meet the smoothing condition, which means the individual values fluctuate around the series mean. For non-stationary time series, the smoothing process is to take the logarithm of the sequence and make a difference. Therefore, it is necessary to judge the changing trend of the sequence. If heteroscedasticity appears, the logarithmic transformation is required. If there is a certain upward or downward trend, the sequence needs difference disposal. The number of times when the sequence becomes stationary through difference disposal is the value of parameter d.

Then, parameters estimation: After the data stabilization, calculate the ACF and PACF of the d-order difference sequence. The order of the ACF exceeding the confidence boundary lag is q value, and the order of the PACF exceeding the confidence boundary lag is p value.

Thirdly, diagnostic checking: Observe the ACF and PACF of the model residuals. If they are stable, the residuals at this time is white noise. Check the value of R² to determine the degree of fit of the model.

Finally, validation and evaluation: Apply the built model to predict the remaining 30% of the data, and use the parameter Mean Absolute Error (MAE) as the evaluation criterion. The expression of the MAE is formula (2):

$$\text{MAE}=\frac{1}{n}\sum _{i=1}^n|x_i-{\overline{x}}_i|$$ (2)

In the formula, x is the actual value at time point i, ${\overline{x}}_i$ is the predicted value at time point i, and n is the number of predictions.

ARIMA model construction is performed using the SPSS for Windows software package (ver.25.0, IBM).

Data description

The data, used to model and validate the ARIMA, were derived from the daily number of confirmed new cases and new deaths of COVID-19 cases in Hubei, China, from 2020.1.27 (Hubei, China announced on lockdown) to 2020.3.17 (the new confirmed case was zero) [9]. Italy lockdown since 2020.3.10 [10], so the validated models were used to predict the trend of the epidemic of COVID-19 in Italy.

Results

Use the first 70% (2020.1.27 to 2020.3.2) data of the number of COVID-19 infected in Hubei, China to model, and use the last 30% (2020.3.3 to 2020.3.17) data to validate.

Data stabilization

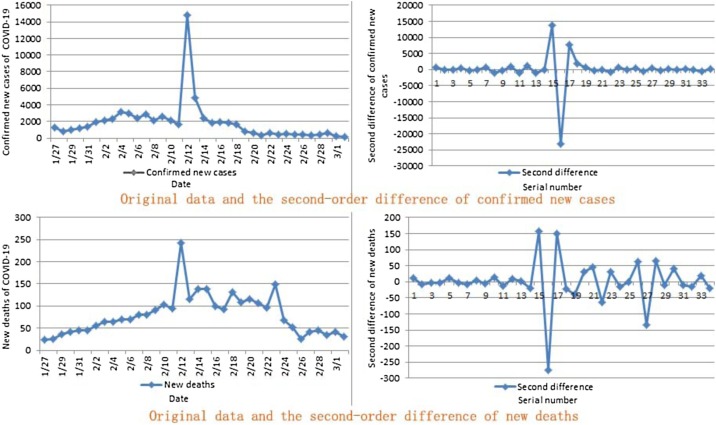
The original data (confirmed new cases and new deaths, left) of Hubei, China used for modelling and the data stabilized (right) are shown in Fig. 1 .

Fig. 1.

Original data and the second-order difference.

In the original data in Fig. 1, the increase of 2.15–2.17 was dramatical, mainly due to the increase in a large number of clinically diagnosed cases. In the second-order difference in Fig. 1, the data sequence (confirmed new cases and new deaths) tended to be stable, which met the requirements of ARIMA modelling.

Parameters estimation

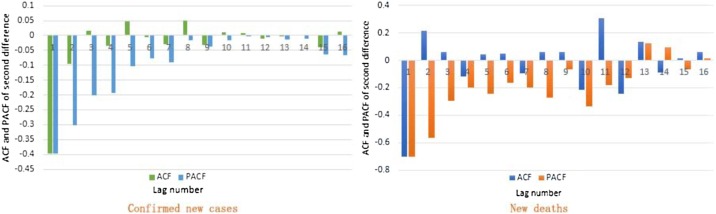
After the second-order difference, the data series of confirmed new cases and new deaths were stationary, the parameter d = 2 in the ARIMA models. The ACF and PACF of the second-order difference sequence were obtained, as shown in Fig. 2 .

Fig. 2.

ACF and PACF of the second-order difference.

In the confirmed new cases, the ACF diagram and PACF diagram of the second-order difference sequence showed that the correlation values did not exceed the significant boundary (0.5), so the ARIMA model was selected as ARIMA (0, 2, 0).

Moreover, in the new deaths, the order of the ACF exceeding the confidence boundary lag was 1, and the order of the PACF exceeding the confidence boundary lag was 2, so the ARIMA model was selected as ARIMA (2, 2, 1).

Diagnostic checking

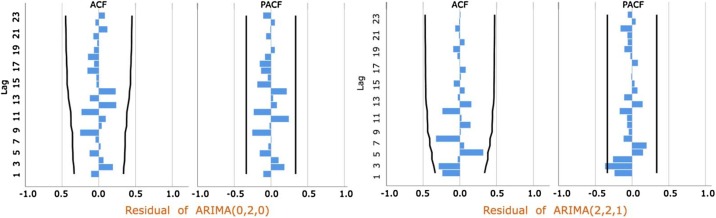
The ACF and PACF of the model residuals showed that the values of all ACF and PACF of the residual sequence were stable. So, the residual sequence no longer contained non-random components that could be extracted. The residual at this time was white noise, and the fitting effect was good. R ² of ARIMA (0, 2, 0) is 0.956. R ² of ARIMA (2, 2, 1) is 0.823. The fitting degrees were good (as shown in Fig. 3 ).

Fig. 3.

ACF and PACF of residual sequence.

Validation and evaluation

The model validation used the remaining 30% of the data. Using MAE as the evaluation criterion, the calculated MAE result of confirmed new cases was 18.1, which was kept within 20. The MAE of new deaths was 5.2, which was kept in single digits.

Trend of the epidemic in Italy

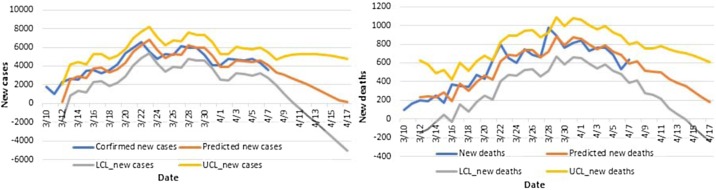
Using the models established by Hubei data, starting from Italy's lockdown, to predict the development of new confirmed cases and new deaths in Italy in the next ten days. The results showed in Fig. 4 . Among them, Confirmed new cases indicated that new cases of COVID-19 were confirmed in Italy from 2020.3.10 to 2020.4.7; Predicted new cases indicated that ARIMA model predicted new cases of COVID-19 in Italy from 2020.3.10 to 2020.4.17; LCL_new cases indicated that ARIMA model predicted the lower 95% confidence interval (CI) for COVID-19 cases in Italy from 2020.3. 10 to 2020.4.17; UCL_new cases indicated that the ARIMA model predicted the upper 95% CI for COVID-19 cases in Italy from 2020.3.10 to 2020.4.17. The definitions of new deaths, predicted new deaths, LCL_new deaths and UCL_new deaths are the same as above.

Fig. 4.

ARIMA models fitting curve in Italy.

It can be seen from Fig. 4 that the actual values of confirmed new cases and new deaths in Italy all fall within the 95% CI of the predicted values. New cases will decrease in the next ten days. The number of new deaths in the next ten days tends to be stable and decreases slightly.

This study uses the complete periodic data of the development of the COVID-19 epidemic in Hubei, China, to establish the ARIMA models. And study participants use these models to predict the development of the Italian epidemic in the next 10 days. The models fit well and are more suitable for short-term prediction. However, with the development of the epidemic situation, the data sequence constantly changes, and the model will also change accordingly. At the same time, the cause and development trend of the COVID-19 epidemic situation are not yet clear. Therefore, the prediction results should be comprehensively considered according to the actual situation.

Funding

This work is supported by Natural Science Foundation of Beijing Municipality, China (7202016).

Conflicts of interest

The authors declare no conflict of interest.