A neural representation of naturalistic motion-guided behavior in the zebrafish brain

SUMMARY

All animals must transform ambiguous sensory data into successful behavior. This requires sensory representations that accurately reflect the statistics of natural stimuli and behavior. Multiple studies show that visual motion processing is tuned for accuracy under naturalistic conditions, but the sensorimotor circuits extracting these cues and implementing motion-guided behavior remain unclear. Here we show that the larval zebrafish retina extracts a diversity of naturalistic motion cues, and the retinorecipient pretectum organizes these cues around the elements of behavior. We find that higher-order motion stimuli, gliders, induce optomotor behavior matching expectations from natural scene analyses. We then image activity of retinal ganglion cell terminals and pretectal neurons. The retina exhibits direction-selective responses across glider stimuli, and anatomically-clustered pretectal neurons respond with magnitudes matching behavior. Peripheral computations thus reflect natural input statistics, whereas central brain activity precisely codes information needed for behavior. This general principle could organize sensorimotor transformations across animal species.

eTOC blurb

Glider stimuli connect motion estimation algorithms to higher-order statistics of natural visual environments. Yildizoglu et al. use behavior and brain-wide imaging to show that gliders induce optomotor responses in larval zebrafish, with multiple visual processing stages extracting motion cues and organizing them by their behavioral relevance.

INTRODUCTION

All animals need to react to changes in their environment. Many changes involve relative motion between the animal and its surroundings [1], making visual motion detection a crucial sensory task [2]. Spatially localized motion signals could indicate a salient object in the visual environment, such as a predator or prey [3–8], which may engage dedicated escape or hunting maneuvers [9–12]. Spatially coherent global motion typically indicates that the animal is moving within its environment, and animals thereby exhibit a variety of stabilization responses to whole-field motion [13–15]. To generate appropriate actions to visual motion stimuli, the animal must accurately estimate motion cues from light signals and route these motion signals through the central brain to the motor circuits that are required to generate the matched elements of behavior [16–19]. However, the circuits and computations that link sensation to action remain largely unknown. For example, although studies in humans and non-human primates have uncovered a variety of computational cues that brains use to infer whole-field motion from noisy sensory inputs [20–22], the extent to which these motion percepts rely on distinct versus common neural circuits is still debated [23,24].

Interestingly, what we do know about the principles, algorithms, and circuits of visual motion processing is remarkably conserved across both vertebrate and invertebrate brains [25–27]. An appealing hypothesis to explain these observations is that each animal species has individually adapted its motion processing strategy to reflect the commonly shared statistics of behaviorally relevant natural sensory environments [28–30]. The fundamental idea that visual information processing is adapted to natural scene statistics has provided quantitative and conceptual insights into diverse visual phenomena [31–37]. In the context of motion processing, this hypothesis has been most thoroughly developed for a class of complex motion stimuli called gliders [20,38,39]. It’s worth noting several key results about gliders before addressing their computational logic. First, gliders are perceptually relevant for at least primates and insects [20,39]. Second, the fly’s directional pattern of glider selectivity emerges in performance-optimized models of whole-field velocity estimation in natural environments [40,41]. Finally, flies extract glider signals early in their visual system, whereas primate glider processing involves the visual cortex [38–40]. This raises the interesting possibility that diverse animal brains have converged on useful algorithmic solutions to shared computational goals, despite differences in the implementation at the level of neural circuits.

An algorithmic description of visual motion estimation must discern when and how the brain interprets spatiotemporal patterns of light as motion. This is challenging to achieve because the space of possible stimuli is too large to sample exhaustively, and only a small fraction of stimuli will induce motion percepts. Furthermore, natural images and movies are notoriously difficult to parametrize because of their intricate statistical content [42–45]. Glider stimuli approach this problem by characterizing motion estimation algorithms in the mathematically complete basis of spatiotemporal correlations [20,26,46–48]. Each glider stimulus is designed to account for the fact that motion induces many different spatiotemporal correlations across the visual field [46,49,50]. By artificially isolating correlations that co-occur during real-world motion [44], gliders can flexibly reveal the contributions of various computational cues to motion perception. For example, odd-ordered glider stimuli measure basis elements that are explicitly asymmetric with respect to ON/OFF stimuli, and this property has been used to show that ON/OFF asymmetric neural processing is highly relevant to fly behavior [40,41,47]. Similar stimuli and correlation computations are also relevant for depth perception and texture perception [51,52].

Here we introduce the larval zebrafish as a teleost model for unraveling the neural mechanisms of glider-induced behavior in a vertebrate brain. It is known that larval zebrafish respond behaviorally to phi, reverse-phi, and non-Fourier motion stimuli [53], which are well-known precursors to glider stimuli [20]. We begin by showing that zebrafish also exhibit directional-responses to third-order glider stimuli, thereby implicating light-dark asymmetric visual motion processing in zebrafish behavior [40,41,46]. Importantly, larval zebrafish are small and optically translucent, which permits brain-wide functional imaging at cellular resolution [54,55]. Recent work shows that several motion-guided stabilization behaviors critically require a central brain area called the pretectum [56–58]. The pretectum spatially integrates visual signals from several classes of retinal ganglion cells [57,59–61] and interconnects with multiple visual and motor pathways [61,62]. This functional multiplexing is reflected in substantial response heterogeneity [56,57,60], although the relative contributions of inputs to the pretectum and within-pretectum computations in shaping the responses of individual pretectal neurons is unclear [61]. By combining retinal and pretectal imaging, here we show that there are retinal ganglion cells that are direction selective across glider stimuli, and that pretectal neurons refine this representation to precisely match the patterns that we observed behaviorally. These data suggest that retinal motion processing is tailored to the demands of naturalistic stimuli, whereas the pretectum provides a flexible code for those visual motion stimuli that drive stabilization behaviors.

RESULTS

Zebrafish optomotor turning is tuned to the temporal frequency of moving gratings.

The optomotor response is an innate behavior that counteracts relative motion between the animal and its environment, such that leftward motion causes a persistent leftward turn bias (Figure 1A). The canonical Hassenstein-Reichardt correlator (HRC) detects visual motion through spatiotemporal correlations in the stimulus and accurately predicts the turning magnitudes of many animals to moving sinusoidal gratings [25,26,49,63]. The spatiotemporal structure of such a drifting sine grating can be intuitively characterized by its spatial wavelength and velocity (Figure 1B, front faces). However, the HRC predicts that the relevant notion of grating speed for turning optomotor behavior is the temporal frequency of motion [64,65] (Figure 1B, right faces), which combines the grating’s wavelength and speed to encode how the stimulus oscillates temporally. For example, the two moving gratings in Figure 1B have the same temporal frequency despite differences in their velocity and spatial wavelength.

Figure 1. Optomotor turning response of larval zebrafish follows the predictions of canonical models of visual motion.

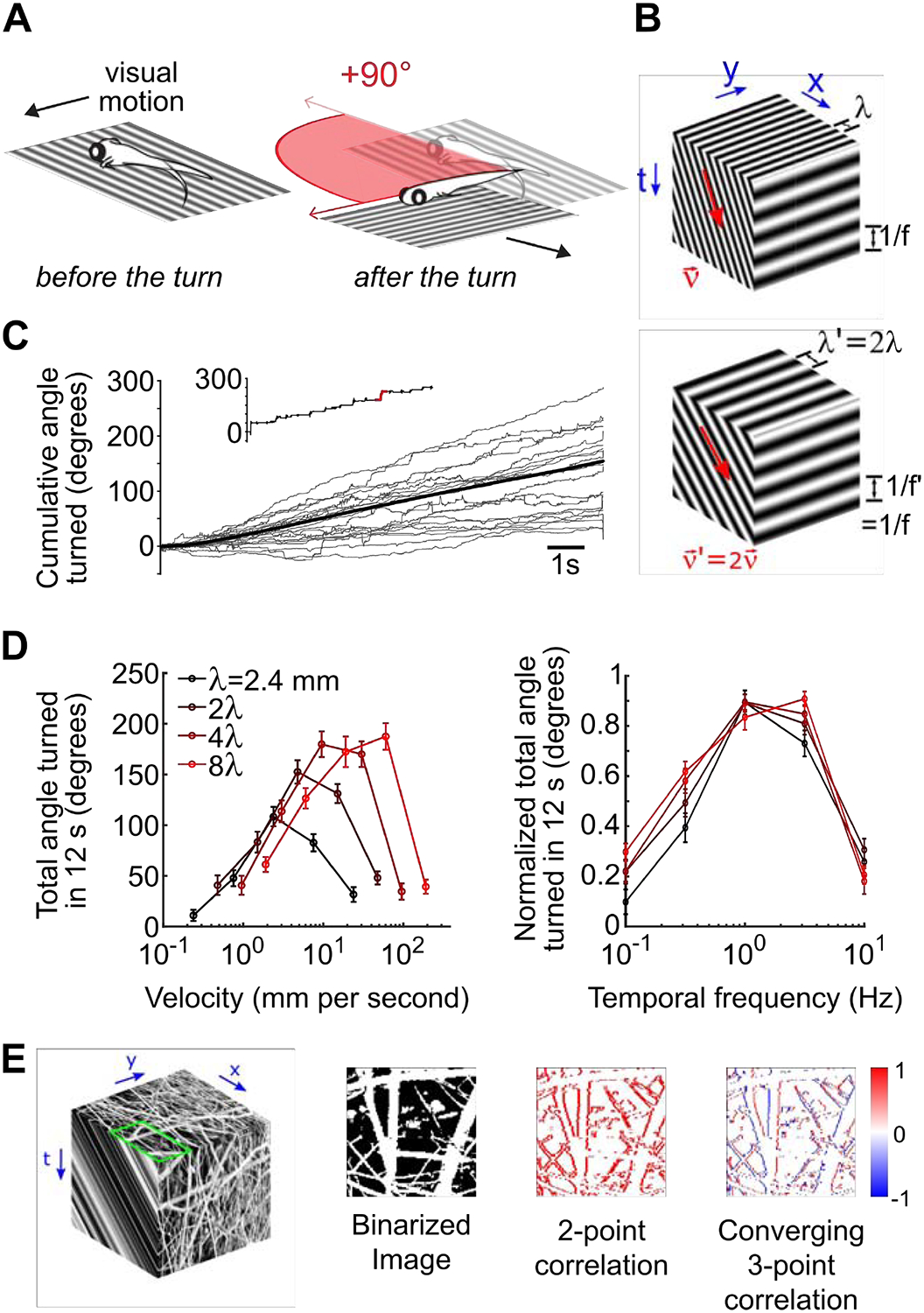
A) Schematic of freely-swimming closed loop experiment in which the stimulus is locked to the fish’s body axis. A turn of 90 degrees is depicted in red. In this panel, and all subsequent panels, positive angles denote leftwards turns. B) Space-time representation of the rightward motion of a 2D sine grating. The spatial structure of sine grating is shown on the top face of the cube. Two quantities are sufficient to describe sine-grating motion, for example the velocity (ν) and wavelength (λ), and the direction and speed of the motion can be inferred from correlations in space and time (front face). However, the canonical HRC model predicts that motion perception is tuned to the temporal frequency of the moving grating (side face). Note that interplay between the velocity and wavelength of the sine grating permits the same temporal structure to occur with different velocity and wavelength parameters (compare the top and bottom cubes). C) The cumulative angle turned as a function of time (full trial = 12 s) is quantified. Individual trials for an example leftward motion stimulus appear in light grey, the trial average is shown in black, and the inset highlights an individual trial with the left turn depicted above. D) Fish-averaged total angle turned during the 12s trial, for multiple velocity and wavelength combinations (N=40 fish) (left). The same data were peak normalized before averaging and plotted against temporal frequency (right), as calculated from each combination of wavelength and velocity. Error bars show standard errors of mean. E) Left: Similar to B. An example natural image selected from van Hateren’s natural image dataset (image number: 598) [35] (top face). We used the luminance-calibrated image to simulate constant velocity rightward motion (front face). For demonstrative purposes only, we contrast equalized the images shown by replacing the luminance of each pixel with the intensity rank of the pixel in the image. Note that the motion consists of both moving light and dark edges. Center-left: To simplify the pattern of motion signals, we binarized the contrast of the natural image around the mean. Center-right: We computed second-order motion cues by multiplying pairs of spacetime pixels whose spatial and temporal offsets matched the speed of motion (1 pixel per time step). By subtracting left-oriented cues from right-oriented cues, we obtained a directional motion signal that indicated rightward motion at each edge location. In particular, note that the signal is positive or zero everywhere. Right: We also computed a third-order motion cue by multiplying three spacetime pixels whose spatial and temporal offsets again matched the speed of motion, now in a temporally converging triangular pattern (see the rightmost column of Fig. 2A). The directional motion signal now depended on whether the moving edge was light or dark, with positive signals resulting from rightward-moving light edges, and negative signals coming from rightward-motion dark edges.

We first tested whether zebrafish optomotor responses to laterally drifting gratings are temporal frequency tuned. We measured optomotor responses in freely swimming zebrafish presented with closed-loop whole-field motion stimuli whose orientation was locked to the fish’s body axis (Figure 1A, STAR Methods). As expected, zebrafish consistently turned in the direction of stimulus motion through a series of discrete swim bouts (Figure 1C). The magnitude of these turning responses was inconsistently tuned to the velocity of motion (Figure 1D, left). For example, zebrafish responded to faster stimulus velocities when the wavelength of the grating was longer. However, we found a universal temporal frequency tuning curve when we plotted the max-normalized response magnitudes as a function of temporal frequency (Figure 1D, right), similarly to what has been reported in flies [64–66]. Therefore, turning responses of larval zebrafish validate a core prediction of the HRC and support the notion that zebrafish detect motion using local spatiotemporal correlations in the stimulus.

Natural image motion contains higher-order correlations.

Natural images are highly intricate [35] (Figure 1E, top face), and their motion involves higher-order spatiotemporal correlations that go beyond the second-order cues detected by the HRC [41,44,46]. We illustrated these higher-order correlations by simulating rightward motion of a binarized natural image (Figure 1E, left, center-left). Positive second-order motion cues reliably indicated rightward motion at each vertical edge within the image (Figure 1E, center-right). Third-order motion cues also appeared at each edge, but the sign of the response was opposite for light and dark edges (Figure 1E, right). Taken together, second and third-order motion cues thus jointly encode the direction and contrast polarity of each moving edge [39]. Interestingly, both invertebrate and vertebrate brains encode motion in an edge-type selective manner [25,26], and sensitivity to third-order motion cues contributes to this selectivity in flies [39,40]. Such encoding could be immediately useful for distinguishing between moving light and dark objects in the natural environment [44]. Moreover, visual motion estimators can use the edge-type specificity afforded by third-order motion cues to more accurately estimate the velocity of whole-field motion in light-dark asymmetric natural environments [40,41,47]. Accordingly, multiple animals exhibit behavioral motion responses to third-order correlations [20,39], and we next asked whether larval zebrafish are among them.

Glider stimuli induce optomotor responses in larval zebrafish

We used a stimulus set consisting of a single pair of laterally drifting sine gratings (Figure 2A, first column), uncorrelated non-directional noise (Figure 2A, second column), and spatiotemporally correlated glider stimuli that were designed to isolate visual cues that predict leftward or rightward motion in natural environments [39,41] (Figure 2A, remaining columns). Note, however, that the spacetime orientation of the glider stimulus (Figure 2A, top vs. bottom rows) need not match the direction of the motion cue [20,39]. Each glider was defined to enforce a particular second- or third-order correlation over space and time (STAR Methods, Figure S1A). For example, positive second-order correlations simply translate binary spatial patterns by one pixel per time step (Figure 2A, third column), whereas negative second-order correlations also invert the contrasts of the translated patterns (Figure 2A, fourth column). These two stimulus types are examples of phi and reverse-phi motion that were instrumental towards establishing several canonical models for visual motion estimation [22,49,53,67]. Third-order glider stimuli construct triangles in spacetime (Figure 2A, fifth through eighth columns) and average away all second-order cues that could be detected by canonical models. Although these stimuli may appear unnatural, they have experimentally useful properties. Firstly, they generate motion responses in several animals [20,38,39]. Secondly, they provide experimental support for models that enhance visual motion estimation by accounting for natural light-dark asymmetries [40,41]. Finally, they provide a rigorous mathematical framework for decomposing visual motion estimates [26,41,46].

Figure 2. Larval zebrafish perceive glider stimuli as motion.

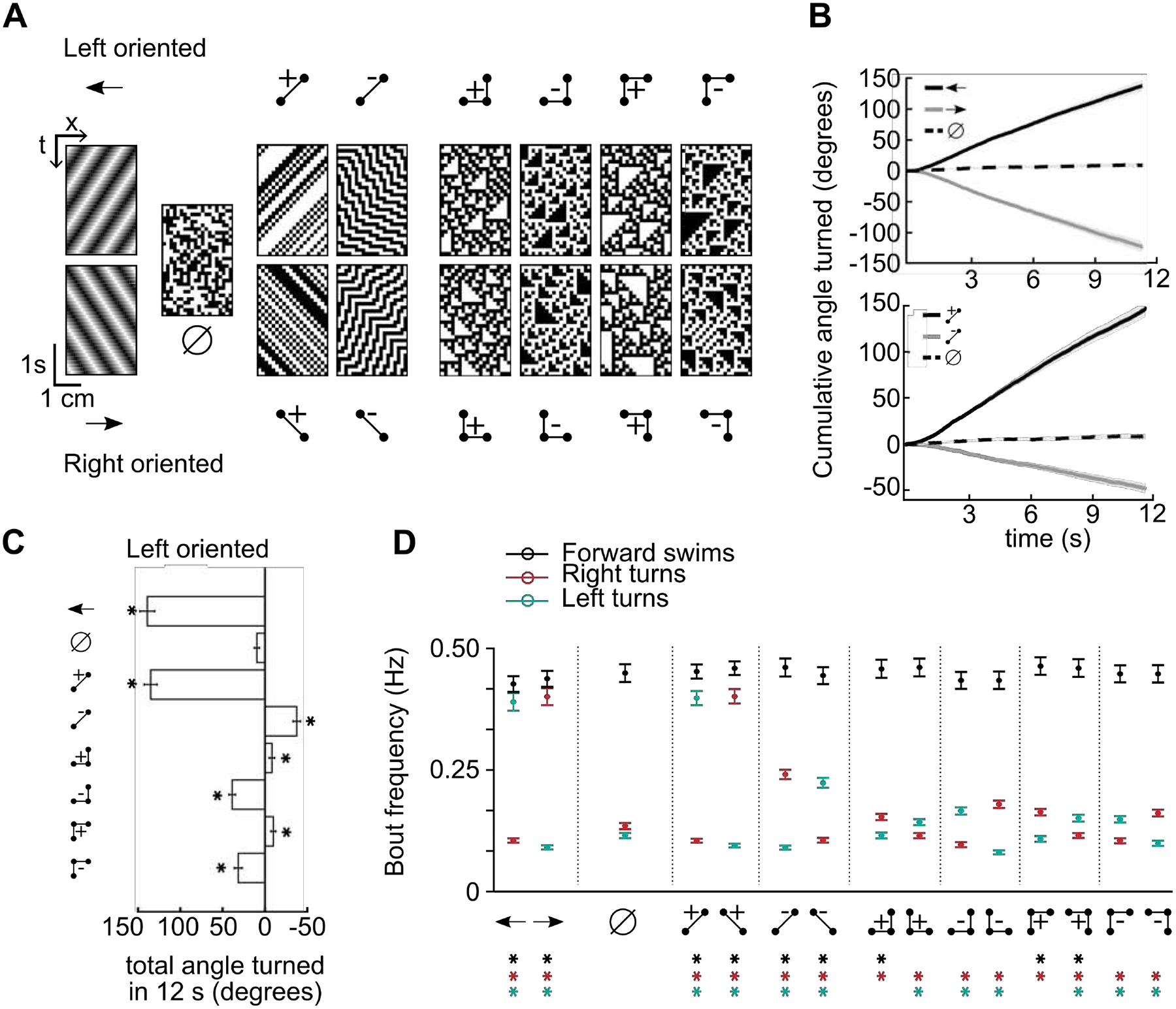
A) Example spacetime diagrams of the 15 stimuli presented in our experiments. Ball and stick diagrams illustrate the correlation structure enforced within the associated spacetime diagrams, the empty set symbol (∅) denotes a spatiotemporally uncorrelated stimulus, and the arrow icons indicate standard leftward or rightward motion of sinusoidal grating stimuli. The directional stimuli were divided into left oriented (top row) and right oriented (bottom row) varieties, based on the displacement direction of the constituent points (STAR Methods). B) Fish-averaged mean turning responses quantified as the cumulative angle turned (N = 120 fish). Shaded error bars represent the standard errors of the mean. Fish responded weakly to uncorrelated stimuli and turned in the motion direction for drifting sine gratings (top). The positive left oriented two-point glider induced turning responses similar to leftward grating motion, whereas the negative left oriented two-point glider induced turning opposite to the stimulus orientation (bottom). C) Total angle turned during the complete 12 s trial for each non-directional or left oriented stimulus. Responses to each glider stimulus, including 3-point gliders, were significantly different from uncorrelated stimulus responses (all p<10–5, Wilcoxon test). Note that the direction of left oriented glider responses depended on the pattern and parity (correlation sign) of the glider. D) Bout-specific zebrafish behavior for the 15 stimuli, quantified as fish-averaged frequencies of forward swimming bouts, leftward turning bouts, and rightward turning bouts over a 12 second trial (N = 120 fish, STAR Methods). Error bars are standard errors of the mean. Asterisks denote significant differences compared to uncorrelated stimulus responses (p<0.05, Wilcoxon test). See also Figure S1.

We first quantified the behavior as the average cumulative angle turned during the 12 s of stimulus presentation (Figure 2B). We used the uncorrelated stimulus to measure a possible turning bias in the population of fish, and leftward and rightward gratings caused fish to change their turning by similar magnitudes in the expected directions (Figure 2B, top). The magnitude and direction of turning responses to positive two-point gliders were closely matched to gratings, and reverse-phi stimuli caused fish to turn against the stimulus orientation (Figure 2B, bottom) [53]. Each third-order glider stimulus caused a weak but highly significant directional turning response (Figure 2C, Figure S1B). Interestingly, positive and negative three-point gliders induced turns in opposite directions (compare fifth and sixth rows of Figure 2C, or the seventh and eighth rows), despite these stimuli being simply related to each other by contrast inversion (Figure2A). Moreover, the signs and relative magnitudes of these turning responses matched those predicted by performance-optimized models and those previously measured in fruit flies [39,41] (Figure S1C). These directionalities also match neuronal recordings in dragonfly and macaque [38]. Thus, glider stimuli are motion illusions that probe naturalistic motion computations across the animal kingdom.

Larval zebrafish swim in a sequence of discrete bouts, and optomotor stimuli modulate several elements of behavior that combine to generate the total angle turned [57,68,69]. We thus further dissected the behavior into bout frequencies associated with forward swims, right turns, and left turns (Figure 2D, Figure S1D). Compared to uncorrelated noise, every stimulus increased bout frequencies in the induced turning direction, and many also decreased turn frequencies in the opposite direction. Although forward swim bouts were less strongly modulated by our lateral motion stimuli, positively correlated three-point gliders usually increased forward swim frequencies and induced relatively weak turning behavior.

Neuronal responses to glider stimuli are lateralized by turning direction

We next sought to characterize brain-wide neuronal responses to glider stimuli. We achieved this by measuring fluorescent calcium responses in transgenic zebrafish expressing a genetically encoded calcium indicator pan-neuronally (Tg:elavl3:GCaMP6f) [70] in a head-fixed and tail-free preparation under a two-photon microscope (Figure 3A–B, STAR Methods). This allowed us to monitor neuronal activity and swimming behavior simultaneously, which is important because the frequency of head-restrained behavior may differ from that of freely-swimming larvae. We automatically detected neuronal regions of interest (ROIs) using previously published methods [58] (STAR Methods). The direction-selectivity of zebrafish neurons to drifting sine gratings is highly lateralized, with the left/right brain primarily responding to leftward/rightward motion [57,71]. Here we reproduced this finding (Figure 3C, Figure S2A) and further observed a similar pattern for positive two-point glider stimuli (Figure 3D, Figure S2A). Interestingly, neuronal responses in the hindbrain (Hb) and cerebellum (Ce) were visually indistinguishable between two-point glider stimuli and drifting gratings, which is consistent with the notion that these regions generate the motor outputs similarly elicited by either type of stimulus (Figure 2D). However, two-point glider stimuli recruited responses in the optic tectum (OT) that drifting gratings did not (Figures 3A, C, D, Figure S2A). Importantly, visual responses in the pretectum (Pt) were similar for both stimulus types, which is consistent with the hypothesis that the pretectum is a critical visual area underlying the zebrafish optomotor response [57].

Figure 3. Neuronal responses in the pretectum are anatomically lateralized and direction-selective for glider stimuli.

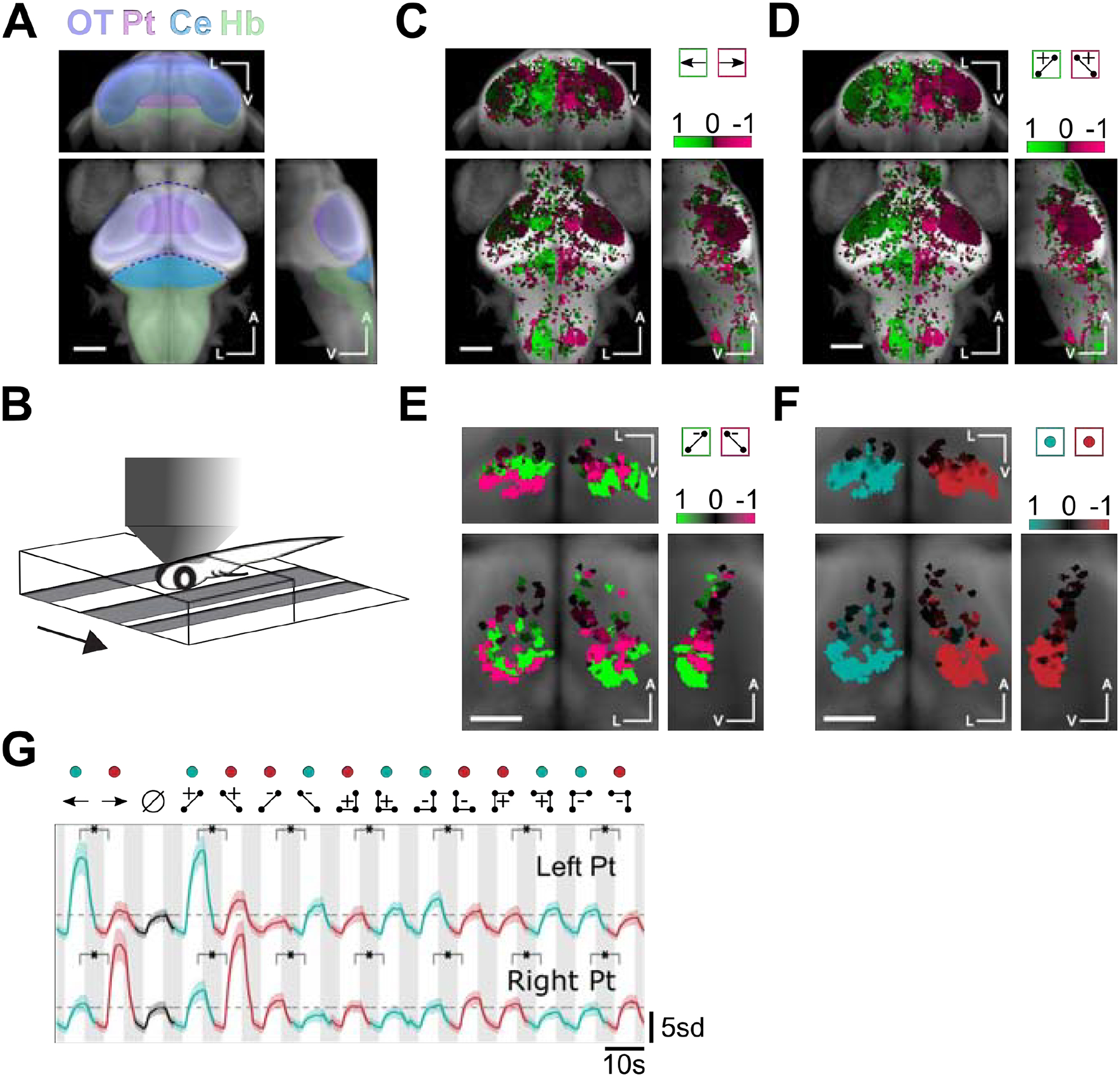
A) Whole-brain anatomical map from a reference brain (constructed from a confocal stack of Tg(elavl3:GCaMP6f) 7dpf larva), on which all subsequent ROI selectivity maps were overlaid. Brain structures referred to in the text are highlighted (approximate locations). OT: Optic Tectum, Pt: Pretectum, Ce: Cerebellum, Hb: Hindbrain. B) Schematic of 2-photon imaging setup in which the larva was head-embedded in agarose but free to move its tail. We presented visual motion stimuli from below, and the behavior could be tracked while imaging the neural activity. C) Whole-brain direction selectivity map moving sine gratings, revealing left preferring (green) and right preferring (magenta) regions (30778 ROIs from 11 fish). D) Whole-brain direction selectivity maps for two-point glider stimuli. E) Pretectum direction selectivity maps for negative 2-point glider stimuli. Direction-selectivity in the ventral (dorsal) pretectum was opposite (matched) to the orientation of positive 2-point glider stimuli (559 ROIs from 11 fish). F) Pretectum direction selectivity maps comparing all stimuli driving leftward turning (green) to those driving rightward turning (red). Direction-selectivity in the pretectum was lateralized in a manner that matched the direction of the turning behavior. For each set of maps, we show coronal (center of triplet), transverse (top of triplet), and right sagittal projections (right of triplet). A indicates the anterior-posterior axis, V the ventral-dorsal axis, and L the left-right axis. Scale bars are 0.1 mm in C, D, B and 0.05 mm in E, F. G) Mean z-scored fluorescence responses of ROIs in the left (N = 840 ROIs) versus right pretectum (N = 991 ROIs). Each mean was direction-selectivity for each directional pair of stimuli, and directional preferences matched the behavioral turning directions. Shaded error bars represent SEM. Green and red colored dots signify visual stimuli driving left turning and right turning, respectively. Horizontal dashed lines mark the peak average responses during the uncorrelated stimulus presentation. Asterisks indicate that all comparisons were significant at the p = 0.01 level (Wilcoxon test). See also Figure S2.

We thus focused on how the pretectum visually represented glider stimuli. Both sides of the pretectum responded to negative two-point glider stimuli (Figure 3E, Figure S2B). The more posterior/ventral sub-region preferred opposite orientations for the negative and positive two-point gliders, whereas the more anterior/dorsal sub-region showed a matched orientation preference. The response pattern seen in the posterior/ventral sub-region was consistent with the hypothesis that neurons in the left/right pretectum prefer stimuli that drive leftward/rightward turning. Indeed, when we defined a directional index that quantified how strongly individual ROIs preferred stimuli driving leftward versus rightward turning, we found that the left/right pretectum strongly preferred stimuli driving leftward/rightward turning (Figure 3F, Figure S2B). The pretectal pattern of direction selectivity was also apparent in hindbrain responses (Figure S2C), and 3-point glider maps similarly showed lateralization that reflected the directionality of turning behavior (Figures. S2D, E). Note that the left/right-oriented negative 2-point gliders contain long-range positive two-point correlations that would drive leftward/rightward turning if isolated [50]. In light of this fact and the results above, we predict that the anterior/dorsal sub-region of pretectum contains neurons that prefer long-range motion cues. By averaging visually activated ROI responses in the left versus right pretectum, we found that this direction-selectivity was observed for every pair of glider stimuli (Figure 3G). This lateralized pattern was absent in the optic tectum and less prevalent in cerebellar and hindbrain neurons (Figure S2F). However, pretectum-like tuning for glider stimuli may be preserved within cerebellar and hindbrain subregions that are anatomically and functionally downstream of pretectum.

AF5/6 contains direction-selective retinal signals

The pretectum receives both direction-selective and non-directional inputs from the retina [56,57,59,61], so we next sought to determine whether direction-selectivity for glider stimuli is already present in the retinal output. In zebrafish, retinal ganglion cell (RGC) axons arborize in ten distinct arborization fields (AFs), with each AF conveying information from a sub-population of RGCs [59,72]. To precisely measure retinal responses, we imaged transgenic SyGCaMP6s fish that selectively express the fluorescent calcium indicator GCaMP6s in retinal ganglion cell synapses under the islet-2b promoter [61,73,74] (Figure 4A, STAR Methods), and we adapted our segmentation routine to detect bouton-scale ROIs (Figure 4B, STAR Methods). Each of AF5, AF6 and AF10 have been shown to contain direction-selective signals, but neuropil ablation experiments found that only processes near AF5 and AF6 affected optomotor behavior [57,61,75]. We thus imaged a field-of-view that does not contain AF10 to achieve high-resolution imaging of the remaining AFs, which are much smaller than AF10. With this technique, we were able to measure visually responsive fluorescent signals in most arborization fields (Figure 4B), but AF1, AF2, and AF3 were too ventral for high-fidelity imaging in our setup. Furthermore, fluorescent signals in AF7 were not visually modulated during our experiment. We thus focus all subsequent analyses on AF4, AF5, AF6, AF8, and AF9. In addition, we merged AF5 and AF6 in the analysis because we only detected a few ROIs in AF5, the response properties of these ROIs were similar to nearby AF6 (Figure S3A), and direction-selective retinal signals do not seem to respect the AF5/6 boundary [61].

Figure 4. The retina computes direction selective glider responses.

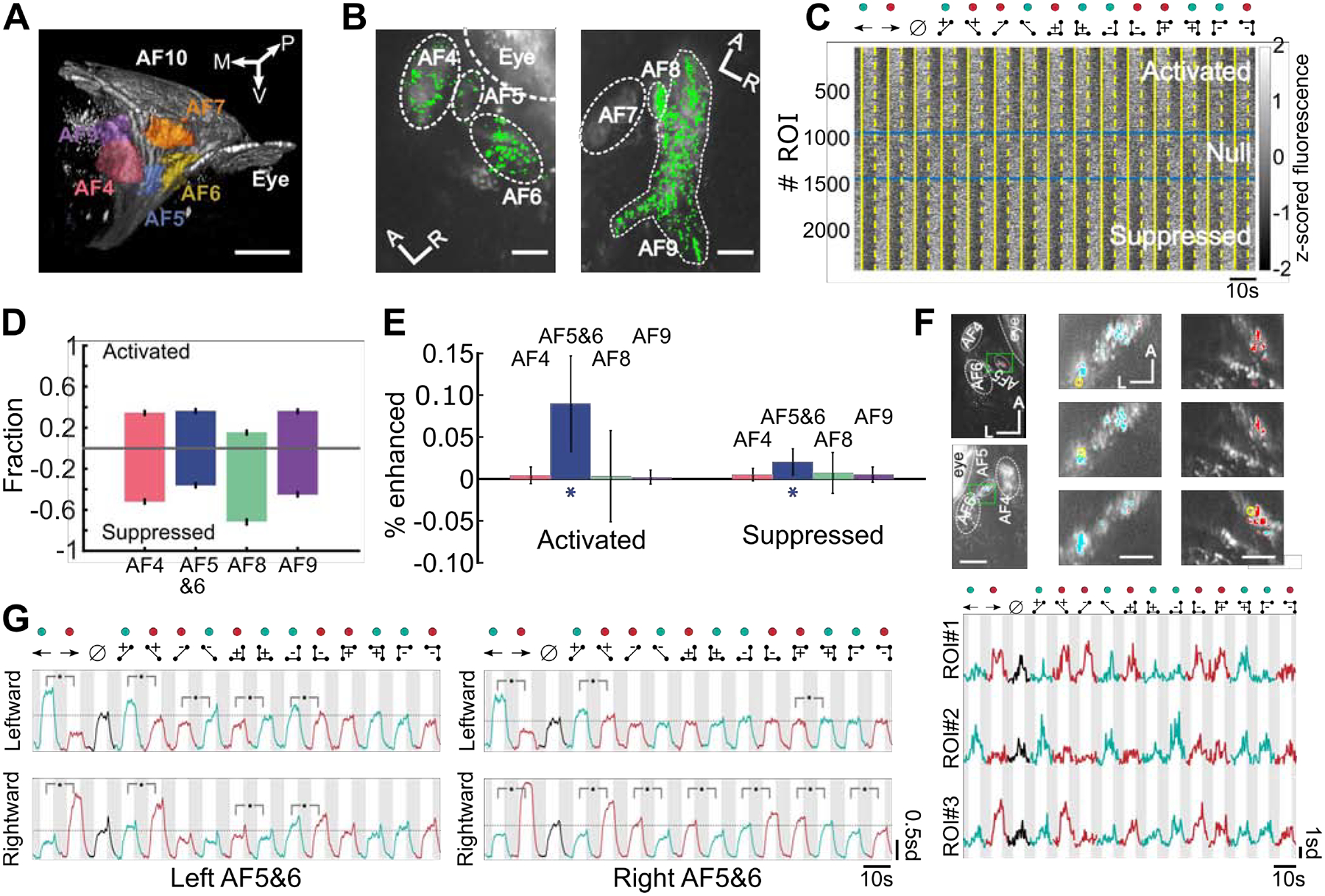
A) Geometry of the how retinal axons arborize in the central zebrafish brain. Here we show a projected view of a 3D reconstruction of the left hemisphere arborization fields (AFs) using retinal-labeled Tg:Islt2b:SyGCAMP6s zebrafish (7dpf). Each color highlights a single AF. AF8 is hidden behind AF7 in this view. Since AF5 and AF6 were difficult to distinguish and functionally similar (Figure S3A), we merged them into AF5&6 for most figure panels. Auto-fluorescence artifacts from the eye were masked prior to other data analyses (STAR Methods). P indicates the anterior-posterior axis, V the ventral-dorsal axis, and M the medial-lateral axis. Scale bar is 50 μm. B) Example planes showing ROIs identified with our imaging and segmentation routines. We extracted many ROIs from most AFs, but we did not observe functional responses in AF7. A and L indicates the anterior-posterior and left-right axes. Scale bar is 20 μm. C) Individual retinal ROIs were consistently activated or suppressed by visual stimuli across the stimulus conditions. We display fluorescence responses from a randomly selected subpopulation of 2500 ROIs (out of 270,596). The ROIs were sorted by the significance of their selectivity for stimulus-on versus stimulus-off periods across all stimuli (Wilcoxon test). Solid and dashed yellow lines indicate the start and end of stimulus presentation periods respectively. Blue lines mark the p-value thresholds (p=0.05) used to define the activated and suppressed ROI populations. D) More retinal ROIs were activated and suppressed than expected by chance, and the fraction of ROIs activated or suppressed varied across the AFs. Error bars represent standard error of the mean, and confidence intervals were estimated by assuming Poisson variability in counting statistics (N= AF4:62173, AF5&6:59450, AF8:5676, AF9:73722 ROIs). E) The number of retinal ROIs that were direction-selective for drifting gratings was only above chance levels in AF5&6, as assessed by a shuffle test (STAR Methods). In particular, error bars represent estimated 95% confidence intervals and excluded the chance level of 0 in AF5&6 only. F) Top: Leftmost column represents two example planes showing a region encompassing AF5 and AF6. ROIs preferring leftward (rightward) gratings are colored cyan (red). Panels in the middle/rightmost columns are from left/right side of the brain. The green boxes in the leftmost panels indicate subregions rotated and shown at higher-resolution to the right. A indicates the anterior-posterior axis, and L indicates the left-right axis. Scale bars, left column: 30 μm, all the other columns: 5 μm. Bottom: Z-scored fluorescence traces of the three example ROIs circled in yellow at top. Each ROI was identified by its direction-selectivity to drifting grating stimuli, but they also showed direction-selective responses to 2-point and 3-point glider stimuli. G) Mean z-scored fluorescence traces of all ROIs direction-selective for leftward or rightward drifting gratings in the left or right AF5&6. The directional stimulus pairs marked with asterisks were significantly different at the p=0.01 level (one tailed Wilcoxon test). All other directionally-paired stimuli did not show statistically significant differences. N=240 ROIs (top left), 330 (bottom left), 234 (top right), 449 (bottom right). See also Figure S3.

Visual motion stimuli increased the fluorescence of some ROIs and decreased the fluorescence of others (Figure 4C), so we first separated ROIs into an activated population that was significantly activated by a positive 2-point motion stimulus, a suppressed population that was significantly suppressed, and a null population that did not respond (STAR Methods). Activated and suppressed populations were both present in all AFs (Figure 4D), and we assessed the direction selectivity of the activated and suppressed populations of each AF separately. We found that most ROIs did not exhibit strong selectivity in any AF, but AF5&6 ROIs showed significantly more direction-selective responses to drifting gratings than would be expected by chance (Figure 4E, STAR Methods), consistent with previous results [61]. We also found that direction-selective responses to positive 2-point glider stimuli, negative 2-point glider stimuli, and 3-point glider stimuli were enhanced only in activated AF5&6 ROIs (Figure S3B–D). We decided to focus on ROIs identified as direction-selective based only on responses to laterally drifting gratings. This choice allowed us to assess whether canonically direction-selective retinal ganglion cells also show direction-selectivity to gliders.

Retinal direction-selectivity includes glider stimuli

We found activated direction-selective ROIs sparsely distributed within AF5/6 and near the AF5/6 boundary (Figure 4F, top). Interestingly, the direction-selectivity of many individual ROIs to drifting gratings generalized to also endow direction-selectivity for positive 2-point gliders, negative 2-point gliders (reverse-phi), and each 3-point glider configuration (Figure 4F, bottom). Moreover, example ROIs preferring rightward moving gratings also preferred glider stimuli associated with rightward turning (Figure 4F, bottom, rows 1 and 3), and ROIs preferring leftward moving gratings also preferred glider stimuli driving leftward turning (Figure 4F, bottom, row 2). However, not all activated direction-selective ROIs exhibited patterned glider responses. For example, the average response of all leftward-selective ROIs in the left AF5&6 showed the aforementioned selectivity pattern (Figure 4G, top-left), but the leftward-selective mean in the right AF5&6 showed weaker glider modulation and did not show significant direction-selectivity to 3-point gliders (Figure 4G, top-right). A similar pattern was seen for rightward-selective ROIs (Figure 4G, bottom), now with the right AF5&6 showing stronger glider selectivity. In contrast, the weaker direction-selectivity for gratings observed in suppressed AF5&6 ROIs (Figure 4E) did not generalize to other stimulus pairs (Figure S3E), and both hemispheres also contained non-directional ROIs (Figure S3F). These results show that the larval zebrafish retina extracts direction-selective signals for higher-order motion stimuli and suggest that multiple direction-selective populations might be distinguishable with gliders. Nevertheless, retinal ROIs responded with magnitudes that imperfectly matched the stimuli’s motion strength and behavioral relevance. For example, the vast majority (~95%) of activated direction-selective ROIs in AF5&6 showed significant responses to non-directional uncorrelated noise. We thus hypothesized that pretectal processing would refine retinal inputs to construct a visual representation more appropriate for driving optomotor behavior.

Modeling pretectal neurons as a threshold-linear integration of behavioral outcomes

To determine whether individual pretectal neurons coded for behavioral outcomes induced by glider stimuli, we modeled each ROI’s activation as a threshold-linear combination of several behavioral predictors (Figure 5A, STAR Methods). In particular, three predictors were derived from the mean behavioral frequencies of leftward turning, rightward turning, and forward swimming, and a fourth predictor represented non-specific stimulus drive (Figures 2D, 5A). These models typically explained a large fraction of the neuronal response variance in the pretectum but not in AF5&6 (Figure 5B). We could improve model fits in AF5&6 by accounting for its precise response kinetics (Figure S4A, B), but this elaborated model form continued to fit pretectum ROIs better (Figure S4B). We found accurate model fits occurred throughout the pretectum (Figure 5C), and the model traces successfully captured pretectal responses to both classical motion and third-order glider stimuli (Figure 5D, Figure S4D). The model fits beautifully revealed many direction-selective neurons that precisely tracked the magnitude by which various stimulus correlations increased the frequencies of leftward or rightward turning (Figure 5D, traces 1–2). Other neurons exhibited response patterns that resembled a combination of turning and forward swimming behaviors (Figure 5D, traces 3–4).

Figure 5. Individual pretectum neurons represent visual motion stimuli according to their effect on optomotor behaviors.

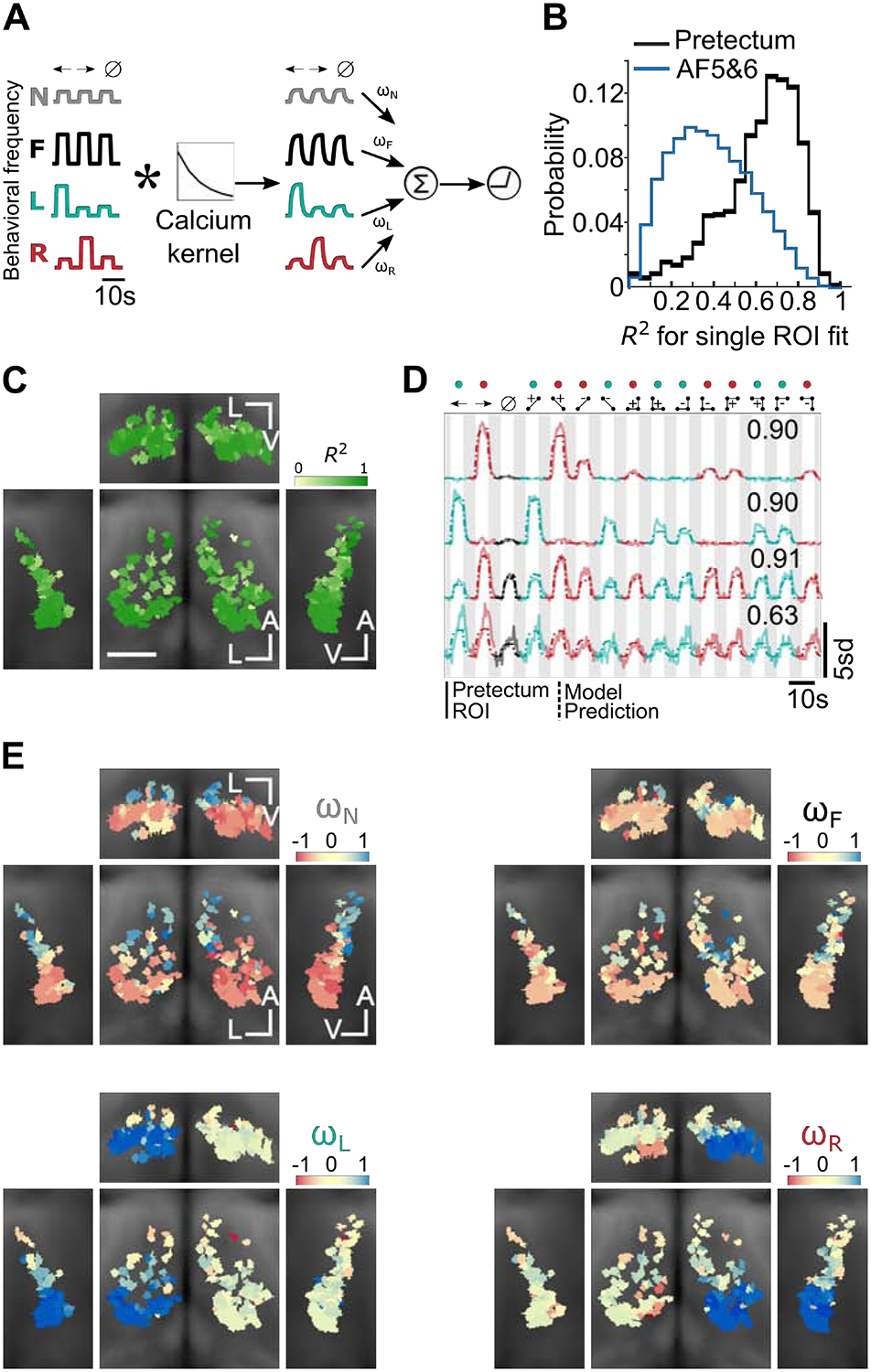
A) Schematic of the model architecture (STAR Methods). Mean behavior regressors were first convolved with a temporal kernel that emulated measurable responses in our calcium imaging experiment. The regressors were then combined as a weighted sum, and a final thresholding step captured the non-negativity of the measured pretectal responses. We use N, F, L and R to denote the Non-specific stimulus-on regressor, the Forward swim frequency regressor, and the Left/Right turn frequency regressors (STAR Methods). For compactness, we illustrate the procedure for the first three stimuli only. B) Distribution of R-squared values (fraction of variance explained by the model) for all ROIs. Note that when the responses of AF5&6 units were fitted similarly, the fraction of variance explained was shifted towards smaller values, compared to the pretectum case. C) R-squared maps showing that the quality of model fits was comparable throughout the pretectum. As in Figure 3, we show coronal (center), transverse (top), left sagittal (left), and right sagittal projections (right) overlaid on anatomical maps (grayscale). A indicates the anterior-posterior axis, V the ventral-dorsal axis, and L the left-right axis. Scale bar is 0.05 mm. D) Example traces for four pretectum ROIs, together with associated model fits and R-squared values. The first two example ROIs show pretectal neurons that respond to glider stimuli with magnitudes closely matching the behavioral turning frequencies induced by the stimuli. The final two ROIs show that other pretectal neurons responded relatively non-selectively to glider stimuli. E) Weight coefficient maps for the four regressors used in the model. ROIs utilizing the L or R regressors were localized to the left or right pretectum, respectively. ROIs receiving positive drive from the N or F regressors were localized to the anterior pretectum. All graphical conventions match panel C. See also Figures S4 and S5.

As anticipated by Figure 3D, neurons in the pretectum were anatomically organized according to their behavioral correlates (Figure 5E). Most obviously, the neurons strongly influenced by the pattern of leftward and rightward turning were respectively localized in the left and right pretectum (Figure 5E, bottom, Figure S4C). We also found a clear organization along the anterior-posterior axis, with turn-associated neurons located more caudally (Figure 5E, bottom, Figure S4C), and the neurons positively associated with forward swimming or non-specific stimulus drive located more rostral (Figure 5E, top, Figure S4C). These coefficient maps are reminiscent of the direction selectivity maps in Figure 3, and the model fits of individual ROIs only had large positive turning weights when the ROI also had high direction selectivity (data not shown). Despite these strong correlations between pretectal neuron activity and mean behavioral outcomes, pretectal activity was not instructive and could occur without behavioral output. For example, during the 5 second stimulus presentation, head-embedded larval zebrafish often responded directionally to drifting gratings and positive two-point gliders (Figure S4E) but not to reverse-phi or 3-point glider stimuli (Figure S4F). Therefore, the pretectal responses to reverse-phi and 3-point glider stimuli must be gated downstream of the pretectum, perhaps by competitive processing in the hindbrain or cerebellum [57,61,76–79]. Overall, we thus hypothesize that the pretectum integrates direction-selective retinal inputs (Figure S5) to construct a behavior-ready code that can be easily readout by downstream motor centers.

DISCUSSION

Visual motion influences a wide variety of ethological behaviors, so evolution demands that visual systems accurately estimate motion from naturalistic patterns of input. Canonical models of visual motion estimation in both flies and primates suppose that pairwise correlations between light signals provide the fundamental cues of elementary motion detection [22,49], and here we found temporal frequency tuning in zebrafish behavior that mimicked model predictions and fly behavior [64,65]. Nevertheless, pairwise motion estimates have limited accuracy for complex naturalistic stimuli [28,39]. Fortunately, the rich statistics of natural motion [44,45] imply that a variety of higher-order spatiotemporal cues can help [29,41,46,47]. In this study, we discovered that third-order cues robustly elicit motion-guided behaviors in larval zebrafish, with patterns that strikingly match those of flies [39]. Interestingly, basic statistics of natural visual scenes are shared across a wide range of visual environments [36,80], and the visual systems of multiple species, including fruit flies, dragonflies, larval zebrafish, macaques, and humans, have found ways to incorporate second, third, and higher-order correlations into their motion processing algorithms [20,38,39,53,81,82]. The observed directionalities of zebrafish and fly turning behaviors agree with the hypotheses of prior theoretical work that calculated how flies should combine low-order correlational cues to best estimate the velocity of whole-field motion [41]. Thus, the algorithms of visual motion estimation are strikingly convergent across the animal kingdom, and natural sensory statistics provide a valuable guide for understanding these algorithms. Since prior models were built from the statistics of natural terrestrial environments, it will be interesting to determine whether any predictions change for the underwater environments experienced by zebrafish [37,83].

Understanding how these algorithms are implemented within visual systems can provide additional insight into the logic and mechanisms of neuronal computation. Direction-selectivity arises in the retina of many vertebrate species, including rabbits, mice, and zebrafish [74,84,85]. However, not all motion cues are present in the earliest direction-selective cells [40,86], and which motion cues are computed in the retina versus central brain remains unclear [87,88]. Here we used functional calcium imaging of retinal ganglion cell axon terminals to show that the zebrafish retina computes direction-selective motion signals for reverse-phi stimuli and three-point glider stimuli. The pattern of direction-selectivity precisely matched the directionality of optomotor turning behavior. Interestingly, the fly’s earliest direction-selective neurons also respond to reverse-phi stimuli with a directionality matched to behavior [50,67]. Fly researchers have recognized that this response pattern is inconsistent with a naïve neuronal implementation of the HRC’s multiplication operation [67], yet it can emerge from a motion energy model [89], a spatially distributed implementation of the HRC [67], or a biophysically realistic neuron model [90]. On the other hand, the correct directional-preferences for third-order glider stimuli only emerge in flies after separate ON-edge and OFF-edge motion signals are combined [40,91]. This suggests that AF5&6 encode both ON-edge and OFF-edge motions. Our results generally support the hypothesis that the elementary motion signals needed for the zebrafish optomotor response are computed in the retina [53,57]. Since the directionality of glider behavior can be predicted from the demands of accurate motion estimation with natural scenes [41], this suggests that the retina’s algorithms for motion processing are tailored to the structure of natural sensory environments. Furthermore, the direction-selective signatures associated with whole-field motion are targeted specifically to AF5 and AF6 [61], which have previously been shown to causally affect optomotor responses to drifting grating stimuli [57]. We were thus able to link a naturalistic retinal computation to behavior, via specific retinal projection patterns in the central brain.

Retinal signals do not project directly to the hindbrain motor centers generating behavior [59,72], and our data support the emerging view that the pretectum is a midbrain visual area that integrates and refines visual motion cues in support of several stabilization behaviors [56,57,60,61]. For example, the pretectum has been shown to binocularly integrate several directions of visual motion information in a manner that recapitulates the magnitudes and latencies of optomotor behaviors [57,92,93]. Here we extend this argument and suggest that the pretectum also integrates direction-selective retinal signals to represent more complex motion cues, including those in reverse-phi and glider stimuli, with magnitudes that facilitate behavior. We further hypothesize that this functional organization will underlie optomotor responses to second-order motion stimuli [53,75], and these properties generally make the pretectum well-suited to process higher-order motion cues that require long-range nonlinear integration of local motion signals [21,24]. Overall, this results in a representation that closely correlates with the behavioral outcomes induced by a diversity of visual motion stimuli [57,76]. This representation is anatomically organized into lateralized populations of neurons with similar directional tuning, which could permit ipsilateral long-range connections from the pretectum to lateralized hindbrain nuclei associated with turning behaviors. More generally, the afferents and efferents of the pretectum are varied and numerous [62], which might permit the pretectum to flexibly influence multiple behaviors.

Our data support the idea that the retina extracts multiple features of naturalistic visual stimuli, whereas central brain areas integrate and refine these features according to their relevance for specific behaviors [56,57,71,94,95]. This idea is likely to generalize across species and visually-guided behaviors. Mice have dozens of functionally distinct RGC types [84]. In larval zebrafish, many anatomically distinct RGCs project contralaterally to ten AFs [59,72]. The non-uniformity of these projections could easily route visual features to their appropriate targets. For instance, RGCs in AF7 specifically respond to natural and artificial prey stimuli [3], which in turn drive prey-capture related circuitry in the optic tectum [5]. Moreover, AF6, AF8, and AF9 process dark looming and dimming stimuli [7], with AF9 being even more strongly activated by bright looming and luminance increases, and these retinal responses could drive escape behaviors via visual processing in the optic tectum [17]. Finally, optomotor and optokinetic responses combine several behavioral motifs, and AF4, AF5, AF6, AF9, and the pretectum have each been implicated in some of their aspects [56,57,61,96]. Future work is needed to more fully identify the functional mapping of retinal features to specific AFs, downstream brain regions, and resultant behaviors.

Visual motion estimation is a computation that all animals need to perform [1]. By comparing the solutions of evolution to this problem, we can better understand similarities and differences between neural circuits. Similarities point to evolutionary convergence. For example, light-dark asymmetries are fundamental to glider processing [41,46], and the neural implementation of glider processing in both flies and primates involves a separation of signals into ON-edge and OFF-edge channels [39,40]. Our current results suggest that ON/OFF separations within the vertebrate retina might be utilized to generate responses to glider stimuli in zebrafish [25,26,97]. Differences are also important, as they could reveal multiple implementations of common computational algorithms. For example, many circuit architectures may extract glider signals [38,40,41,89]. Furthermore, prior work implicates the primate cortex in glider processing [38,39], but our current data suggest that in the zebrafish these signals are present in the retina. This suggests that vertebrate brains have explored multiple strategies for visual processing. For example, some species may have highly specific feature detectors in the retina while others may rely on more generic retinal representations [87,88]. Similarly, saliency maps guiding attention may occur in variable brain regions across vertebrate species [98]. Such species-level differences could provide hints into how subtle evolutionary and ethological factors impact neural computation [38,39,98,99]. Here we have taken important steps towards establishing the larval zebrafish as a powerful system for comparative studies of the neural computations underlying visual motion processing. We anticipate that the unique possibilities afforded by brain-wide imaging in this behaving vertebrate will play crucial roles in comparative studies that address complex aspects of motion-guided behavior and decision making.

STAR METHODS

RESOURCE AVAILABILITY

Lead Contact

Further information and requests for materials, data and code should be directed to and will be fulfilled by the Lead Contact, Ruben Portugues (ruben.portugues@tum.de).

Materials Availability

This study did not generate new unique reagents.

Data and Code Availability

The [datasets/code] supporting the current study have not been deposited in a public repository because of their large size but are available from the corresponding author on request.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Animals

All experiments were performed with 6–7 days post fertilization (dpf) zebrafish larvae, which were maintained at 28°C on a 14hr light/10hr dark cycle. Behavioral experiments were done with Tuepfel long-fin (TL) wild type strain. The nacre transgenic zebrafish lines Tg(elavl3:GCaMP6f+/+) [77] and Tg(Islt2b:Gal4,UAS:SyGCaMP6s+/+) [61,100] were used for wholebrain/pretectal and AF imaging experiments, respectively. All animal experimental procedures were approved by the Max Planck Society and the local government (Regierung von Oberbayern).

METHOD DETAILS

Free-swimming behavioral experiments

Larvae were placed in a 10 cm Petri dish, on a clear acrylic support covered with a diffusive screen, and illuminated from below using an array of IR LEDs. Freely swimming larvae were tracked using a high speed Mikrotron camera (200 fps) and an IR band-pass filter. The visual stimuli were presented from below on a 12 cm by 12 cm region of the screen, covering the area of the dish completely, and using an Asus P2E microprojector. Closed loop motion stimuli were generated with custom written LabView software. The fish’s orientation and position were continuously monitored, and the stimulus was updated such that the stimulus pattern was always oriented perpendicularly to the fish’s body axis [69].

One stimulus was presented during each 12 second trial and there was no inter-trial interval. For the sine grating tuning data shown in Figure 1D, twenty trials were presented within each stimulus set corresponding to all stimulus conditions. For the glider data shown in Figure 2, fifteen trials were needed to show the full stimulus set. Stimuli were randomized within each set of trials. Datasets for sine-grating tuning and glider stimuli were collected through independent experiments from different sets of fish. Whenever the zebrafish left a user-defined region near the center of the dish, we drove the zebrafish back to the center of the dish using a concentric OMR stimulus. Each experiment was limited to be at most 2 hours. In the sine-grating tuning experiments, we uniformly spaced five temporal frequencies on a logarithmic axis at 10 ^ (−1, −0.5, 0, 0.5, 1) Hz. Thus, the velocities used for each spatial period were: 2.4 mm (0.24, 0.75, 2.4, 7.5, 24 mm/s); 4.8 mm (0.48, 1.5, 4.8, 15, 48 mm/s); 9.6 mm (0.96, 3, 9.6, 30, 96 mm/s); 19.2 mm (1.9, 6, 19, 60, 190 mm/s). We computed the max-normalized response magnitudes in Figure 1D by scaling the measured tuning curve of each individual zebrafish to have a maximal value of 1 before averaging. The velocity of the drifting sine gratings in the glider experiments (spatial period 10 mm) was 10 mm/s. Contrast was 100% (darkest and lightest pixels possible) in all stimuli and was not gamma-corrected for the projector.

Behavioral analyses were performed with custom written MATLAB software. We detected the onset and offsets of individual bouts of behavior by finding times where the fish’s distance changed by at least 0.3 mm. By comparing the position and orientation of the fish before and after the bout, we associated each bout with an angle turned. We calculated bout-frequency vs bout angle histograms for directional and non-directional stimuli, and the cut-off values for identification of forward swims, leftward turns, or rightward turns were set based on these distributions (Figure S1D). Histograms were computed by binning bout angles into 1-degree bins.

Glider stimulus construction

Motion induces spatiotemporal correlations in visual stimuli, and each glider stimulus was constructed to enforce a specific correlation amongst two or three spatiotemporally separated pixels [20,38,39]. We represented each glider pattern as a signed ball and stick diagram (e.g. Figure 2A) that defines the update rule by which each pixel is assigned its contrast value of +1 or −1 (white or black) (Figure S1A). For example, the simplest glider patterns enforced positive or negative correlations between two pixels (Figure 2A, third and fourth columns). Denoting the binary contrast value of the i-th pixel at time t by C_i(t), the 2-point update rules were each of the form C_i(t)C_i+Δ(t + δ) = P, where Δ was the displacement between the pixels, δ was the frame duration, and P was the parity of the glider pattern (i.e. sign of the correlation). Consequently, each pixel value was determined by multiplying an adjacent pixel value at the previous time step by P (either 1 or −1). Note that the sign of Δ specifies the orientation of the glider pattern. Also note that each stimulus was randomly initialized with a seed row (i.e. initial stimulus pattern) and seed column (i.e. contrast source at the left or right stimulus boundary). In the case of 3-point gliders, the update rules were C_i(t)C_i+Δ(t)C_i+Δ(t + δ) = P and C_i(t)C_i(t + δ)C_i+Δ(t + δ) = P for the converging and diverging types, respectively. Again, the sign of Δ specifies the orientation of the glider pattern, and each stimulus was randomly seeded with one row and column of the stimulus. Lastly, to generate the uncorrelated noise stimuli each pixel was randomly chosen to be black or white, independent of the rest of the pixels. For all stimuli, pixel sizes were defined by |Δ| = 1.31 mm and δ = 90 ms. Importantly, when integrated over space and time, each glider pattern has vanishing components for the other types of correlational structures. Thus, each of the 3-point gliders excluded 2-point correlations as well as the other 3-point correlations. Additionally, all stimuli were equiluminant in time and space, and each point in spacetime had the same variance. More discussion of glider stimuli is available in several related publications [20,38,39].

Functional imaging

Larvae were embedded in 1.5–2% agarose in 3.5 cm Petri dishes placed onto an acrylic platform covered with a light-diffusing screen [58]. Neural activity was recorded with a custom-built two-photon microscope. A Ti-Sapphire laser tuned to 905 nm (Spectra Physics Mai Tai) was used for excitation. Larval brains were imaged while being presented with visual stimuli from below (pixel size 1.31 mm, presented 5 mm below the fish) at 60 fps using an Asus P2E microprojector and a red long-pass filter (Kodak Wratten No.25), which allowed simultaneous imaging and visual stimulation. Visual stimuli (5 cm by 5 cm) were generated with custom written Labview software. Imaging experiments were done to acquire three different datasets specific for whole-brain, pretectum, and AF regions. Frames were acquired at 2.8 Hz with pixel sizes 0.85 μm (whole-brain), 0.45 – 0.85 μm (pretectum) and 0.3 – 0.45 μm (AFs), depending on the field of view covered. We showed each stimulus once per plane during pretectum/whole-brain imaging experiments and three times per plane in AF imaging experiments. Imaging planes were separated by 1 μm steps, and 300, 60, and 30–60 planes were needed to cover the imaging volume probed during whole-brain, pretectal, and AF imaging experiments, respectively. This small step size implies that single neurons often appeared in several consecutive imaging planes. Each stimulus was presented for 5 s, with 5 s of gray screen presented between stimuli. The fifteen stimuli were presented in randomized order. Since the stimulus encoding was not gamma-corrected for the projector, gray was equally spaced between white and black in RGB units, which roughly match the units of “perceptual brightness” experienced by humans. Consequently, the total physical luminance level increased during stimulus presentation but was matched across glider stimuli.

Head-embedded behavior quantification

In the subset of fish where we simultaneously tracked tail movements and neuronal signals, agarose around the tail was removed with a fine scalpel. In these experiments, larvae were illuminated from above with IR light emitting diodes (850 nm) and tracked from below at 200 fps with an infrared-sensitive charge-coupled device camera (Pike F032B, Allied Vision Technologies). Custom Labview software was used to track the position of eleven points evenly spaced between the base and tip of the tail [58]. The tail trace is then calculated as the sum of the angles of the ten segments. We detected bout onsets and offsets under head-embedded conditions as time points where the difference between the two consecutive points along the tail trace exceeds 3 degrees. We then computed a bout asymmetry index by temporally integrating the mean-subtracted tail trace over the full duration of the bout (Figures S4E, F). Therefore, a positive value indicates that the position of the tail was overall above its mean value, as expected for a leftward turn [68], and negative values likewise indicate rightward turns.

Image processing and ROI detection

All image analyses and anatomical registrations were done as in [58]. In brief, each frame within a trial was first aligned to the average image of that plane to correct for the fish’s movements or the drift, and then all z-planes were aligned to each other. Auto-fluorescence from the eye was discarded by masking out this region in all planes. We then automatically detected ROIs using local correlations, as described in previously published methods [58]. The fluorescence time series of every voxel was correlated with the fluorescence time series of the neighboring 26 voxels in 3D. This generated a stimulus-agnostic anatomical map of local correlation values, based only on the time-varying activity of the voxels. This correlation map was then used to seed an ROI growing algorithm, which starts with the voxel with maximum local correlation and sequentially adds neighboring voxels if their correlation with the ROI exceeds a threshold. The algorithm stops if no neighboring voxels exceed the correlation threshold, or if the ROI’s size reaches a size limit. Note that this method also discards ROIs if their size is too small. We adjusted the ROI size parameters depending on whether we sought neuronal ROIs (min = 50 voxels, max = 1000 voxels) or axonal ROIs in the retinal neuropil (min = 1 voxel, max = 50 voxels). The ROI growing algorithm was then repeated starting at the voxel with the next highest local correlation. After the ROIs have been segmented, their total fluorescence response is defined as the sum of the fluorescence responses of all individual voxels that comprise the ROI.

For AF imaging experiments, we made three modifications to this ROI detection routine to compensate for the decreased number of voxels that constitute the ROI. First, we increased the accuracy of local correlation map by first concatenating the activity across all three trials. Second, ROIs in the AF imaging experiments were built in 2D, because puncta are expected to be too small to span multiple planes. Finally, we replaced the trial-concatenated total fluorescence response by the trial-averaged total fluorescence response, which helped suppress noise in these anatomically small ROIs.

In the whole-brain experiments, anatomical stacks of individual fish were aligned to a reference brain using the Computational Morphometry Toolkit [101]. The reference brain was obtained by summing the fluorescence of GCaMP6f, and each fish’s stack was aligned via an affine transformation followed by a non-rigid one. Individual ROIs from each fish were then registered onto the reference brain via these transformations. Correspondence of salient anatomical features between the reference brain and registered brain was used to assess the registration’s precision.

We defined several preference indices to assess the features that determine the direction-selective patterns seen in the zebrafish brain (Figure 3, Figure S2, annotation based on the Z-Brain atlas [71]). Each index compared the mean z-scored fluorescence responses of visually activated ROIs to a set of “leftward” and “rightward” stimuli. In Figures 3C–E, and Figures S2A, B-left, E, the directionality of the stimulus was determined by its orientation. In Figure 3F and Figure S2B-right, C, D, the directionality of the stimulus was determined by the turning direction it elicited. In all cases, the selectivity index was defined as the difference between the leftward and rightward responses divided by their sum. We represented this 3D direction-selective information in several 2D maps by mean-projecting over voxels in the brain (Figure 3C, D, Figures S2A, C–E) or the pretectum (Figures 3E, F, Figure S2B). Direction-selectivity scores were low in the whole-brain projections because the averages included many non-selective ROIs. We thus enhanced the contrast by raising the selectivity scores to the power of 0.2, and we scaled the color axes in each whole-brain map to reflect selectivity scores relative to the maximum value in that map. On the other hand, color axes in pretectum maps quantitatively corresponded to the mean direction-selective index.

QUANTIFICATION AND STATISTICAL ANALYSIS

Statistical analysis of AF data

Stimulus activated and suppressed populations of ROIs were determined using one-sided Wilcoxon tests comparing the responses during stimulus on and stimulus off periods for all 15 stimuli. Out of 270,596 ROIs, 93,194 were identified as activated, 127,110 as suppressed, and the remaining 50,292 ROIs had no significant stimulus-related modulation. The p-value threshold of 0.05 was used to divide the ROIs into the three groups. Since the total luminance increased during stimulus presentation, many of these responses likely reflect canonical coding of light level by ON and OFF retinal ganglion cells.

Figure 4E and Figure S3B estimated direction-selectivity based on ROI responses to pairs of directional stimuli. We used a shuffle analysis to examine whether each ROI responded differently to leftward and rightward stimulus variants. In particular, for each ROI we shuffled the directionality labels of the six responses (i.e. from three left trials and three right trials), such that every possible correct and incorrect labeling of the trial types was considered. The mean differences between each set of three pseudo-right and three pseudo-left responses were calculated. This resulted in 10 possible trial groupings, one of which corresponds to the true directionality labels. ROIs where the largest magnitude difference corresponded to the true trial labels were identified as direction selective (29,830 direction-selective ROIs across all AFs). Thus, the false positive rate was at most 1/10 or 10%. The “% enhanced” metric plotted in Figure 4E and Figure S3B estimated this false positive rate, and corrected for it, by finding the number of statistically significant directional ROIs in each individual AF and subtracting the mean number of ROIs whose largest difference magnitude corresponded to each of the 9 incorrect labels. We normalized this quantity by dividing by the total number of ROIs in the AF. Note that this “% enhanced” metric would be 1 if every ROI in the AF had statistically significant direction-selectivity and would average to 0 if the AF had no true direction-selective ROIs. We assessed whether the “% enhanced” metric was statistically nonzero by first computing the standard deviation of the number of ROIs whose largest difference magnitude was each of the 9 incorrect labels, and then multiplying the result by 1.96 to assess significance at the p = 0.05 level.

Figure S3D assessed direction-selectivity by pooling ROI responses across 3-point glider stimuli, with directionality labels assigned based on the directionalities of turning behavior. Here there were 24 trials, and it was impractical to assess difference magnitudes for every possible shuffling of the trial labels. We instead generated 999 randomly shuffled labels and assessed direction-selectivity at the p = 0.05 level by checking whether the difference magnitude of the true directionality labels was within the top 5% of the shuffle distribution (Figure S3C). The large number of possible labels made it difficult to estimate the false-positive rate from the data, so the “% enhanced” metric in Figure S3D simply subtracted an assumed false positive rate of 5% from the fraction of ROIs that were direction-selective. Note that this “% enhanced” metric would be 0.95 if every ROI in the AF had statistically significant direction-selectivity and would average to 0 if the AF had no true direction-selective ROIs. To assess whether this “% enhanced” metric was statistically nonzero, we assumed variability dominated by counting statistics and computed the standard deviation of a binomial distribution whose success probability was 0.05 and whose sample size matched the number of activated ROIs in the AF. As before, we multiplied the standard deviation by 1.96 to assess significance at the p = 0.05 level. All statistical analysis was performed with custom written scripts in MATLAB.

Model fitting

We used calcium responses from 1531 activated pretectal ROIs (collected from 26 fish) and 7649 activated AF5&6 ROIs (31 fish) in model fitting. Each activity trace was normalized to have unit variance and shifted to have zero median during interstimulus intervals. Each activity trace was a 420-dimensional vector, because the frame rate was 2.8 Hz, and each stimulus and interstimulus interval was 5 seconds. R-squared values were used to assess the goodness of fit. All analyses were done with custom written scripts in MATLAB.

As depicted in Figure 5A, we used several behaviorally derived regressors to predict the activity trace of each activated ROI in pretectum and AF5&6. Let’s index the stimulus conditions as μ = 1, …,15, and let T^μ denote the set of frame numbers when stimulus μ was present. Note that the frame rate and stimulus duration imply that each T^μ has 14 elements. To construct the regressors, we began by constructing four step functions that encode one stimulus-independent predictor and three different behaviorally derived predictors (Fig. 5A, left). In particular,

$$A_1(t)={\sum }_{\mu =1}^{15}{\chi }_{T^{\mu }}(t),$$

$$A_2(t)={\sum }_{\mu =1}^{15}{F}^{\mu }{\chi }_{T^{\mu }}(t),$$

$$A_3(t)={\sum }_{\mu =1}^{15}{L}^{\mu }{\chi }_{T^{\mu }}(t),$$

$$A_4(t)={\sum }_{\mu =1}^{15}{R}^{\mu }{\chi }_{T^{\mu }}(t),$$

where t = 1,…,420 indexes the frame number,

$${\chi }_{T^{\mu }}(t)=\left\{\begin{array}{ll}1\hfill & ,t\in T^{\mu }\hfill \\ 0\hfill & ,t\notin T^{\mu }\hfill \end{array}\right\}$$

are indicator functions, and F^μ, L^μ, and R^μ are the frequencies of forward swimming, leftward turning, and rightward turning in stimulus condition μ, as measured during free swimming conditions (Fig. 2D). These four regressors were then convolved with an exponential calcium kernel, f(t) = e^−t/τ for t ≥ 0, to emulate the effects of calcium imaging with GCaMP6f (τ = 400 ms [70])

$$B_i(t)=\left(f*A_i\right)(t)$$

(Fig. 5A, middle). Finally, each predictor was normalized to produce a unit variance regressor,

$$X_i(t)=\frac{B_i(t)}{\text{Std}\left(B_i(t)\right)},$$

where i = 1,…,4 and Std(v) denotes the standard deviation across elements of vector v (Fig. 5A, right). Note that each regressor exponentially approaches zero during each interstimulus interval.

Denote the time-dependent activity trace of neuron j as y^(j)(t). In Figure 5, we modeled each ROI as a threshold-linear combination of the four regressors defined above,

$${\widehat{y}}^{(j)}(t)=g\left({\sum }_{i=1}^4{\omega }_i^{(j)}{X}_i(t)\right),$$

where ${\widehat{y}}^{(j)}(t)$ denotes the model’s estimated activity for ROI j, ${\omega }_i^{(j)}$ are weighting coefficients for the effect of regressor i on ROI j, and g(x) = max(x, 0) is a threshold-linear function. We optimized the weights for each ROI by minimizing the squared difference between the model and the data (solved with the quasi-Newton method).

$${\omega }^{(j)}={\text{argmin}}_w\left[{\sum }_t{\left(y^{(j)}(t)-g\left({\sum }_{i=1}^4{w}_i{X}_i(t)\right)\right)}^2+{\lambda }^{(j)}{\sum }_{i=1}^4{w}_i^2\right],$$

where λ^(j) is an ROI-specific parameter that determines the strength of L2 regularization. Nonzero values of λ^(j) help reduce overfitting, and we chose λ^(j) for each cell by leave-one-out cross validation over all 15 stimuli. In particular, let Γ^μ be the union of T^μ, the last 7 frames of the interstimulus interval preceding it, and first 7 frames of the interstimulus interval following it. Then

$${\lambda }^{(j)}={\text{argmin}}_{\lambda }\left({\sum }_{\mu =1}^{15}{\mathcal{L}}^{(j,\mu )}(\lambda )\right),$$

where

$${\mathcal{L}}^{(j,\mu )}(\lambda )={\sum }_{t\in {\Gamma }^{\mu }}{\left(y^{(j)}(t)-g\left({\sum }_{i=1}^4{w}_i^{(j,\mu )}(\lambda )X_i(t)\right)\right)}^2,$$

$$w^{(j,\mu )}(\lambda )={\text{argmin}}_w\left[{\sum }_{t\notin {\Gamma }^{\mu }}{\left(y^{(j)}(t)-g\left({\sum }_{i=1}^4{w}_i{X}_i(t)\right)\right)}^2+\lambda {\sum }_{i=1}^4{w}_i^2\right].$$

To minimize over λ, we empirically tested all values of λ between 0 and 10 in increments of 0.1.

In Figures S4 and S5, we performed the exact same model fitting procedures using different sets of regressors. In Figure S4, we used four behaviorally derived regressors that accounted for the precise kinetics of the GCaMP6f fluorescence response in pretectum and AF5&6. We first estimated separate response waveforms for pretectum and AF5&6 by averaging ROI responses to the uncorrelated stimulus. In particular, let ${\tilde{y}}^{(j)}(t)$ be the total fluorescence response of ROI j throughout the uncorrelated stimulus presentation and the interstimulus interval that follows it. Note that if the uncorrelated stimulus was the last stimulus presented to ROI j, then the subsequent interframe interval was only 7 frames. In this case, we substituted the first 7 frames of the trial for missing frames of ${\tilde{y}}^{(j)}(t)$. Thus, ${\tilde{y}}^{(j)}(t)$ is a 28-dimensional vector. Then the average waveforms in pretectum and AF5&6 are denoted

$$M_{\text{Pt}}(t)=\frac{1}{N_{\text{Pt}}}{\sum }_{j\in \left\{\text{Pt}\right\}}{\tilde{y}}^{(j)}(t)$$

and

$$M_{\text{AF}}(t)=\frac{1}{N_{\text{AF}}}{\sum }_{j\in \left\{\text{AF}\right\}}{\tilde{y}}^{(j)}(t),$$

where is {Pt} and {AF} are the sets of ROIs in pretectum and AF5&6, and N_Pt and N_AF are the number of ROIs in pretectum and AF5&6. Finally, let t^μ = 8 + 28(μ − 1) denote the onset frame of stimulus μ in y^(j)(t). Then the four behavioral regressors become

$$X_{1,C}(t)={\sum }_{\mu =1}^{15}{\sum }_{t^{\prime }=1}^{28}{M}_C\left(t^{\prime }\right){\delta }_{t^{\prime }}^{t-t^{\mu }+1},$$

$$X_{2,C}(t)={\sum }_{\mu =1}^{15}{F}^{\mu }{\sum }_{t^{\prime }=1}^{28}{M}_C\left(t^{\prime }\right){\delta }_{t^{\prime }}^{t-t^{\mu }+1},$$

$$X_{3,C}(t)={\sum }_{\mu =1}^{15}{L}^{\mu }{\sum }_{t^{\prime }=1}^{28}{M}_C\left(t^{\prime }\right){\delta }_{t^{\prime }}^{t-t^{\mu }+1},$$

$$X_{4,C}(t)={\sum }_{\mu =1}^{15}{R}^{\mu }{\sum }_{t^{\prime }=1}^{28}{M}_C\left(t^{\prime }\right){\delta }_{t^{\prime }}^{t-t^{\mu }+1},$$

where C is a stand-in for Pt or AF, and

$${\delta }_j^i=\{\begin{array}{ll}1\hfill & i=j\hfill \\ 0\hfill & i\ne j\hfill \end{array}$$

is the Kronecker delta-function.

In Figure S5, we fit pretectal ROI responses in terms of retinal regressors. Here the six regressors were simply taken to be the mean fluorescent responses of: (i) all leftward selective ROIs in left AF5&6; (ii) all non-directional ROIs in left AF5&6; (iii) all rightward selective ROIs in left AF5&6; (iv) all leftward selective ROIs in right AF5&6; (v) all non-directional ROIs in right AF5&6; and (vi) all rightward selective ROIs in right AF5&6. Note that the four directional regressors are plotted in Figure 4G, and the others are plotted in Figure S3F.

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Experimental Models: Organisms/Strains
Zebrafish: wild-type Tupfel long-fin	N/A	ZFIN ID: ZDB-GENO-990623-2
Zebrafish: Tg(UAS:syGCaMP6s)mpn156	[61]
Zebrafish: Tg(isl2b:Gal4-VP16, myl7:TagRFP)zc65	[100]	ZFIN ID: ZDB-FISH-150901-13523
Zebrafish: Tg(elavl3:GCaMP6f)	[77]	ZFIN ID: ZDB-ALT-180201-1
Software and Algorithms
MATLAB (data analysis)	MathWorks	https://www.mathworks.com/products/matlab.html
Computational Morphometry Toolkit (anatomical registration)	[101]	https://www.nitrc.org/projects/cmtk/
Other
Z-Brain atlas (anatomical reference)	[71]	https://engertlab.fas.harvard.edu/Z-Brain/

Highlights.

• Higher-order glider motion stimuli elicit optomotor responses in larval zebrafish.

• Gliders recruit brain-wide activity lateralized by the induced turning direction.

• Direction-selective retinal ganglion cells respond directionally to glider stimuli.

• Behavioral patterns precisely predict neuronal response magnitudes in pretectum.