Abstract
This decision analytical model study examines the feasibility of using pool testing to identify patients with coronavirus disease 2019 (COVID-19) in a setting with limited testing availability.
Introduction
Specimens from patients with suspected coronavirus disease 2019 (COVID-19) undergo real-time reverse transcriptase–polymerase chain reaction (RT-PCR) testing for qualitative severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) RNA detection. The high demand for SARS-CoV-2 RT-PCR tests during the COVID-19 pandemic has resulted in local shortages, prompting researchers to consider pool testing strategies.1
Pool testing strategies build on testing a pooled sample from several patients: if the results from the pool test are negative, all patients in the pooled sample are declared not to have COVID-19; if the results of the pool are positive, each patient sample is tested individually. The pooled testing strategy is appealing, particularly when test availability is limited. However, any test sensitivity less than 100% bears the risk of a false-negative result for the entire pool. To support informed decision-making regarding the implementation of pool testing for COVID-19, we have developed a probabilistic model to estimate the risk of false negatives considering 3 determining factors: COVID-19 prevalence, test sensitivity, and patient pool size.
Methods
This decision analytical model study did not require institutional review board review because it used simulation-based research, per Common Rule 45 CFR §102 (e). This study followed the Strengthening the Reporting of Empirical Simulation Studies (STRESS) reporting guideline.
We considered a 2-stage pool testing2,3 in the presence of imperfect testing, in which p is prevalence, Se is test sensitivity, and Sp is specificity. We assumed that the probability of a true-positive result pool test equals Se, the probability of a false-positive result equals 1 − Sp, test Se and Sp would be unaffected by the number of patients in a pool (k), and all tests are identically distributed. Let Z be a random variable denoting the number of tests needed to complete the pooling strategy. Let N be the total number of patients, then there are N/k subgroups, each with k members. Assuming independent Bernoulli trials, let Pk be the probability of having at least 1 positive test in k patients. If 1 patient of the subgroup has RT-PCR results positive for SARS-CoV-2, then there will be (k + 1) tests necessary; otherwise, only 1 test will be needed. The expected number of tests for each subgroup with k patients is (k + 1)Pk + (1 − Pk). Then, for N/k subgroups, the expected number of tests needed is E(Z) = (N/k)[(k + 1)Pk + (1 − Pk)] = (N/k)[kPk + 1], in which Pk = (1 − Sp)(1 − p)k + Se(1 − (1 − p)k), which incorporates the effects of test sensitivity and specificity. The optimal pool size is achieved for k that minimizes E(Z). To characterize the pooled test strategy, we define efficiency of the pool as Ef = E(Z)/N = [kPk + 1]/k and expected number of false negatives (ENFN) as kp(1 − S2e) This method does not include a dilution effect on the pooling strategy sensitivity, PS = S2e, as a function of pool size, where S2e provides the upper bound of the pooling sensitivity.
Results
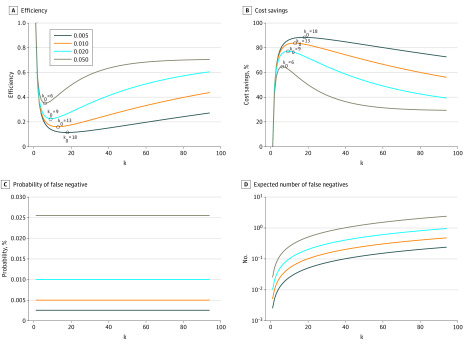
For demonstration purposes, we reported the results for a typical number of RT-PCR tests for 94 patients, a specificity of 100%, a prevalence from 0.001% to 40%, and sensitivities from 60% to 100% (Table). Mathematical simulations showed that a pool testing strategy was an improvement over individual testing for a prevalence less than 30% and that the optimal pool size, k0, was approximately 1 + 1/√(pSe),p ∈ (0.1%, 30%). For a realistic scenario, such as a sensitivity of 70% and prevalence of 1%, the optimal strategy required 13 patients per subgroup. With this optimal pool size, only 16% as many tests would be required by subgroup tests than by individual tests. The Figure shows test efficiency, cost savings, probability of false negatives, and the expected number of false negatives for k and p.
Table. Optimal Pool Size and Corresponding Efficiency, Probability of False Negative, Savings, and Expected Number of False Negatives With Respect to Prevalence and Test Errors for a Pool of 94 Patients.
| Prevalence | K | Ef | Cost savings | False negative | |
|---|---|---|---|---|---|
| Probability | Estimated No. | ||||
| Sensitivity: 1 | |||||
| 0.0001 | 94 | 0.02 | 98 | 0 | 0 |
| 0.001 | 32 | 0.06 | 93.72 | 0 | 0 |
| 0.01 | 11 | 0.20 | 80.44 | 0 | 0 |
| 0.02 | 8 | 0.27 | 72.58 | 0 | 0 |
| 0.05 | 5 | 0.43 | 57.38 | 0 | 0 |
| 0.1 | 4 | 0.59 | 40.61 | 0 | 0 |
| 0.2 | 3 | 0.82 | 17.87 | 0 | 0 |
| 0.3 | 3 | 0.99 | 0.97 | 0 | 0 |
| 0.4 | 1 | 1.00 | 0 | 0 | 0 |
| Sensitivity: 0.95 | |||||
| 0.0001 | 94 | 0.02 | 98.05 | <0.01 | <0.01 |
| 0.001 | 33 | 0.06 | 93.88 | <0.01 | <0.01 |
| 0.01 | 11 | 0.19 | 80.97 | <0.01 | 0.01 |
| 0.02 | 8 | 0.27 | 73.32 | <0.01 | 0.02 |
| 0.05 | 5 | 0.42 | 58.51 | <0.01 | 0.02 |
| 0.1 | 4 | 0.58 | 42.33 | 0.01 | 0.04 |
| 0.2 | 3 | 0.80 | 20.31 | 0.02 | 0.06 |
| 0.3 | 3 | 0.96 | 4.25 | 0.03 | 0.09 |
| 0.4 | 94 | 0.96 | 3.94 | 0.04 | 3.67 |
| Sensitivity: 0.9 | |||||
| 0.0001 | 94 | 0.02 | 98.09 | <0.01 | <0.01 |
| 0.001 | 34 | 0.06 | 94.05 | <0.01 | 0.01 |
| 0.01 | 11 | 0.19 | 81.49 | <0.01 | 0.02 |
| 0.02 | 8 | 0.26 | 74.07 | <0.01 | 0.03 |
| 0.05 | 5 | 0.40 | 59.64 | 0.01 | 0.05 |
| 0.1 | 4 | 0.56 | 44.05 | 0.02 | 0.08 |
| 0.2 | 3 | 0.77 | 22.75 | 0.04 | 0.11 |
| 0.3 | 94 | 0.91 | 8.94 | 0.06 | 5.36 |
| 0.4 | 94 | 0.91 | 8.94 | 0.08 | 7.14 |
| Sensitivity: 0.85 | |||||
| 0.0001 | 94 | 0.02 | 98.14 | <0.01 | <0.01 |
| 0.001 | 35 | 0.06 | 94.22 | <0.01 | 0.01 |
| 0.01 | 11 | 0.18 | 82.01 | <0.01 | 0.03 |
| 0.02 | 8 | 0.25 | 74.81 | 0.01 | 0.04 |
| 0.05 | 6 | 0.39 | 60.82 | 0.01 | 0.08 |
| 0.1 | 4 | 0.54 | 45.77 | 0.03 | 0.11 |
| 0.2 | 3 | 0.75 | 25.19 | 0.06 | 0.17 |
| 0.3 | 94 | 0.86 | 13.94 | 0.08 | 7.83 |
| 0.4 | 94 | 0.86 | 13.94 | 0.11 | 10.43 |
| Sensitivity: 0.8 | |||||
| 0.0001 | 94 | 0.02 | 98.19 | <0.01 | <0.01 |
| 0.001 | 36 | 0.06 | 94.39 | <0.01 | 0.01 |
| 0.01 | 12 | 0.17 | 82.58 | <0.01 | 0.04 |
| 0.02 | 9 | 0.24 | 75.59 | 0.01 | 0.06 |
| 0.05 | 6 | 0.38 | 62.14 | 0.02 | 0.11 |
| 0.1 | 4 | 0.53 | 47.49 | 0.04 | 0.14 |
| 0.2 | 4 | 0.72 | 27.77 | 0.07 | 0.29 |
| 0.3 | 94 | 0.81 | 18.94 | 0.12 | 10.15 |
| 0.4 | 94 | 0.81 | 18.94 | 0.14 | 13.54 |
| Sensitivity: 0.75 | |||||
| 0.0001 | 94 | 0.02 | 98.23 | <0.01 | <0.01 |
| 0.001 | 37 | 0.05 | 94.57 | <0.01 | 0.02 |
| 0.01 | 12 | 0.17 | 83.15 | <0.01 | 0.05 |
| 0.02 | 9 | 0.24 | 76.42 | 0.01 | 0.08 |
| 0.05 | 6 | 0.37 | 63.47 | 0.02 | 0.13 |
| 0.1 | 5 | 0.51 | 49.29 | 0.04 | 0.22 |
| 0.2 | 4 | 0.69 | 30.72 | 0.09 | 0.35 |
| 0.3 | 94 | 0.76 | 23.94 | 0.13 | 12.34 |
| 0.4 | 94 | 0.76 | 23.94 | 0.18 | 16.45 |
| Sensitivity: 0.7 | |||||
| 0.0001 | 94 | 0.02 | 98.28 | <0.01 | <0.01 |
| 0.001 | 39 | 0.05 | 94.76 | <0.01 | 0.02 |
| 0.01 | 13 | 0.16 | 83.73 | 0.01 | 0.07 |
| 0.02 | 9 | 0.23 | 77.25 | 0.01 | 0.09 |
| 0.05 | 6 | 0.35 | 64.79 | 0.03 | 0.15 |
| 0.1 | 5 | 0.49 | 51.33 | 0.05 | 0.26 |
| 0.2 | 4 | 0.66 | 33.67 | 0.10 | 0.41 |
| 0.3 | 94 | 0.71 | 28.94 | 0.15 | 14.38 |
| 0.4 | 94 | 0.71 | 28.94 | 0.20 | 19.18 |
| Sensitivity: 0.6 | |||||
| 0.0001 | 94 | 0.02 | 98.37 | <0.01 | 0.01 |
| 0.001 | 42 | 0.05 | 95.15 | <0.01 | 0.03 |
| 0.01 | 14 | 0.15 | 84.98 | 0.01 | 0.09 |
| 0.02 | 10 | 0.21 | 79.02 | 0.01 | 0.13 |
| 0.05 | 7 | 0.32 | 67.61 | 0.03 | 0.22 |
| 0.1 | 5 | 0.45 | 55.43 | 0.06 | 0.32 |
| 0.2 | 5 | 0.60 | 39.66 | 0.13 | 0.64 |
| 0.3 | 94 | 0.61 | 38.94 | 0.19 | 18.05 |
| 0.4 | 94 | 0.61 | 38.94 | 0.26 | 24.06 |
Abbreviations: Ef, efficiency; K, optimal pool size.
Figure. Operating Characteristics of Pooled Testing Stratified by Prevalence.
k indicates the number of patients in a pool; and k0 (circles), the optimal pool size at which maximal cost-savings was achieved for various prevalence levels. These examples assumed a test sensitivity of 70%.
Discussion
This decision analytical model study found that pool testing efficiency varied with prevalence, test sensitivity, and patient pool size. Therefore, pool testing may be considered as an alternative, especially in circumstances of limited SARS-CoV-2 test availability and a COVID-19 prevalence less 30%. One potential limitation of pool testing is that the false-negative rate may increase owing to dilution of positive samples. The mean viral load of more than 1.5 × 104 RNA copies per mL in nasal swabs4 spikes within the first week after clinical onset and reaches 1.5×107 RNA copies per mL.5 In our example with an optimal pool size of 13 patients, high-sensitivity RT-PCR assays with a lower detection limit of more than 1100 RNA copies per mL will detect SARS-CoV-2 in pooled samples. If sensitivity of the test at hand is a concern, test swabs can be collected and eluted into 1 virus transportation medium container, thereby increasing reliability. However, this requires re-collecting individual samples if a pool tests positive. The mathematical underpinning of the proposed method is generic and can be applied to other infectious diseases.6
References
- 1.Yelin I, Aharony N, Shaer Tamar E, et al. Evaluation of COVID-19 RT-qPCR test in multi-sample pools. Clin Infect Dis. Published online May 2, 2020;ciaa531. doi: 10.1093/cid/ciaa531 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Dorfman R. The detection of defective numbers of large populations. Ann Math Stat. 1943;14:436-440. doi: 10.1214/aoms/1177731363 [DOI] [Google Scholar]
- 3.Johnson NL, Kotz S, Wu X. Inspection Errors for Attributes in Quality Control. Chapman and Hall Ltd; 1991. doi: 10.1007/978-1-4899-3196-2 [DOI] [Google Scholar]
- 4.Wang W, Xu Y, Gao R, et al. Detection of SARS-CoV-2 in different types of clinical specimens. JAMA. 2020;323(18):1843-1844. doi: 10.1001/jama.2020.3786 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Zou L, Ruan F, Huang M, et al. SARS-CoV-2 viral load in upper respiratory specimens of infected patients. N Engl J Med. 2020;382(12):1177-1179. doi: 10.1056/NEJMc2001737 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Zenios SA, Wein LM. Pooled testing for HIV prevalence estimation: exploiting the dilution effect. Stat Med. 1998;17(13):1447-1467. doi: [DOI] [PubMed] [Google Scholar]