Abstract

A systematic study of the thermodynamic stability of various Cu(II) complexes with aminoguanidine (AG) is performed, together with the study of its secondary antioxidant activity. Calculations have been carried out at the M05(SMD)/6-311+G(d,p) level of theory using water as the solvent. The results obtained indicate that AG is capable of forming a wide array of stable coordination compounds with Cu(II) under physiological pH conditions, and it possesses some degree of secondary antioxidant activity when coordinating to copper. The most thermodynamically stable complex can slow down 2.8 times the first step of the Haber–Weiss cycle (from 7.71 × 109 to 2.80 × 109 M–1 s–1) and slightly reduce the potential damage that the formation of •OH radicals can cause. The results of this research add to previous knowledge on this molecule, which could be used as a potential glycation inhibitor.
1. Introduction
Glycation (or nonenzymatic glycosylation) is a natural process in which sugars in the bloodstream attach to nucleophilic groups present in proteins, lipids, or DNA, forming harmful new molecules. Usually, the nucleophilic groups attack the carbonyl groups in the sugars, forming a Schiff base intermediate, which eventually becomes an Amadori compound after a series of intramolecular rearrangement reactions. These Amadori compounds may further react to form advanced glycation end products (AGEs).1,2 While some of these AGEs are harmless, others are highly reactive and may lead to Alzheimer’s disease,3 eye diseases,4 or cancer, among others. Thus, it is of interest to find new drugs that might inhibit this process. The main mechanisms to inhibit glycation are believed to be the scavenging of carbonyl and radical species (which increase the formation of AGEs) and the chelation of metal ions such as Cu(II) and Fe(III).5 These cations, ubiquitous in the human body and most organisms, catalyze the autoxidation of Amadori compounds. Therefore, their chelation and immobilization would slow down glycation.
The reduction of Cu(II) and Fe(III) can lead to the formation of very reactive •OH radicals through a sequence of reactions known as the Haber–Weiss cycle.6 Focusing on the reduction of Cu(II), these reactions are shown in eq 1. Complexes of Cu(II) and Fe(III) with antioxidants can sometimes slow down the rate constant of the reduction process of these cations and reduce the potential damage caused by •OH radical formation in the second step of this reaction sequence (known as the Fenton reaction). When this happens, these compounds are said to have secondary antioxidant activity. Some glycation inhibitors could exhibit secondary antioxidant activity but this has not yet been investigated from a kinetic point of view.
| 1 |
Various glycation inhibitors have been studied both theoretically and experimentally, including aminoguanidine (AG), pyridoxamine, LR-74, metformin, carnosine, tenilsetam, or pioglitazone.7−10 AG has already been investigated (under the name pimagedine) as a drug for the treatment of diabetic nephropathy.11 Previous research has explored some of the complexes that AG, pyridoxamine, ascorbic acid, and a model Amadori compound can form with Cu(II) and Fe(III) ions.12,13 Furthermore, the reactions between glycation inhibitors (namely, pyridoxamine, its analogues, and metformin) and carbonyl species (such as ribose, glucose, other sugars, or methylglyoxal) have been examined on a theoretical basis, as well as experimentally.14−17
A previous study of the Cu(II) complexes with AG was performed at the B3LYP(CPCM)/6-31+G(d) level of theory in water using one of the neutral conformations of AG.13 Four complexes were reported, two with one AG molecule and two with two AG molecules acting as ligands. In both cases, the two square planar complexes were reported to be more stable than their octahedral variations. Gibbs free energy changes were reported at the 1 atm reference state relative to the isolated Cu2+, AG, and H2O species involved in each case; pH was not taken into account.
Ramis et al.18 recently investigated the thermodynamics and kinetics of the free-radical scavenging activity (primary antioxidant activity) of AG, focusing on its reactions with the methoxy and hydroperoxyl radicals in polar and nonpolar environments under physiological pH conditions at the M05-2X(SMD)/6-311+G(d,p) level of theory. This paper reports that the most stable form of AG in aqueous solution is protonated. Furthermore, it shows that the ability of AG to scavenge free radicals takes place exclusively via hydrogen atom transfer and that it seems to depend on the polarity of the environment, exhibiting larger rate constants in nonpolar media. The effectiveness of AG as a free radical scavenger was found to be moderate.
To properly compare the effectiveness of AG as a glycation inhibitor by the three main suggested mechanisms of action [the scavenging of carbonyl and radical species and the chelation of metal ions such as Cu(II) and Fe(III)], quantitative thermodynamic and kinetic results at the same (or equivalent) level of theory must be obtained. Following our kinetic study of the free radical scavenging activity of AG,18 we have decided to perform a more in-depth study of its metal chelating activity with respect to Cu(II) ions in aqueous solution at physiological pH. We are also interested in investigating the secondary antioxidant activity of AG with respect to Cu(II) ions from a kinetic point of view.
In the present work, we have studied the thermodynamic stability of thirty complexes of AG with Cu(II) in aqueous solution at physiological pH. Complexes with protonated AG and with the four neutral forms of AG in aqueous solution at physiological pH have been considered, with one or two (neutral or protonated) AG species as ligands. A selection of complexes are further investigated to quantitatively explore the secondary antioxidant activity of AG.
2. Computational Details
Calculations were performed with the Gaussian 09 software package.19 All the structures were fully optimized and characterized at the M05(SMD)/6-311+G(d,p) level of theory, including solvent effects (water) by means of the SMD solvation method20 in both geometry optimizations and frequency calculations. M05 is a hybrid meta functional that has been shown to be highly accurate for metallic interactions.21 The M06 hybrid meta functional, which is an improvement over the M05 functional, is also recommended for applications in transition metal chemistry.22 Given that the recent study of the free-radical scavenging activity of AG was performed at the M05-2X(SMD)/6-311+G(d,p) level of theory,18 it was decided to choose the M05 functional with the same basis set as the closest best method choice for comparisons. The ultrafine integration grid was also used in the calculations.
The absolute standard Gibbs free energies (G0) and enthalpies (H0) at 298.15 K of the different species considered in this study, together with their Cartesian coordinates and structures, can be found in the Supporting Information document. Using eq 2 and the corresponding G0 values of reactants and products, the standard Gibbs free energy change (ΔGf0) for the reaction of forming a complex from its infinitely-separated ligands and solvated central ion was calculated. The formation constant (Kf) of each complex was calculated using eq 3.
| 2 |
| 3 |
Rate constants (k) were calculated by means of the conventional transition state theory using eq 4. The standard Gibbs free energy of activation (ΔG≠) was estimated applying Marcus theory.23,24 This energy, known as the single electron-transfer activation barrier (ΔGSET≠), was calculated using eq 5, where ΔGSET is the standard Gibbs free energy of reaction and λ is the reorganization energy, calculated with eq 6.
| 4 |
| 5 |
| 6 |
In eq 6, ΔESET is the nonadiabatic difference between the single-point energy calculations of reactants and vertical products.
The Kimball–Collins theory25 was applied to calculate the apparent rate constant kapp when the values of the rate constants were in the diffuse-limited regime (k > 1 × 108 M–1 s–1), making use of eq 7.
| 7 |
The value of kD can be obtained employing eq 8. This is the steady-state Smoluchowski rate constant for an irreversible diffusion-controlled bimolecular reaction.26
| 8 |
In eq 8, R is the reaction distance (taken as the sum of the radii of the two reactants assuming spherical shape), NA is Avogadro’s constant, and DAB is the mutual diffusion coefficient of the reactants, computed as the sum of DA and DB. Each of these values can be found by means of the Stokes–Einstein27,28 approach, as described in eq 9.
| 9 |
In this equation, kB is the Boltzmann constant; T is the absolute temperature; η is the viscosity of the solvent (8.91 × 10–4 Pa s for water); and αAorB is the radius of the solute (A or B), assuming it is spherical.
This methodology has been effectively used to study the secondary antioxidant activity of lipoic and dihydrolipoic acids with respect to both Cu(II) and Fe(III).29,30 The diffusion corrections and apparent rate constant calculations have been previously applied in the kinetic study of various hydrogen-atom transfer reactions.31−33
3. Results and Discussion
The pKa of AG at 298.15 K in aqueous solution is 11.5.34 Thus, at physiological pH 7.40, AG is mostly protonated. Nevertheless, complexes were studied with both protonated and neutral AG to compare their stabilities. Neutral AG has four different conformers depending on the cis/trans position of the imine hydrogen and the hydrazine moiety. Figure 1 displays the structures of these conformers, labeled in the order of stability (A, B, C, and D) as well as the structure of protonated AG, AGH+. The nitrogen atoms have been labeled to facilitate understanding of their coordination points in the copper complexes that they form. For simplicity purposes, the AG conformers have been named using the acronyms AGA, AGB, AGC, and AGD; and the AGH acronym is used for protonated AG. Note that in previous research (see ref (13)), only the complexes of copper with AGD were evaluated.
Figure 1.

Forms of AG considered in this study (on the left, the four conformers of AG in stability order; on the right, protonated AG, AGH+).
Complexes of Cu(II) ions, similar to those of Pt(II) and Pd(II), have been shown to favor square planar geometry, while Cu(I) complexes are known to be linear.35 Several AG-containing complexes have been synthesized using copper, platinum, and palladium (among others), all showing square planar geometry in which AGD coordinates through the N2 and N4 positions (see Figure 1).36−38 For both platinum and palladium, complexes containing one and two AG ligands have been prepared. In the case of the complexes containing two ligands, the AGD molecules coordinate in a nonsymmetrical fashion.37 Ni(II) can display a wide range of coordination numbers and stereochemistry. Structural studies of [Ni(AG)2H2O]SO4 have shown that the AG ligands coordinate to form a square planar environment. The apical positions are then occupied by water molecules, leading to an octahedral geometry; these water molecules coordinate in such a way that one coordination unit contains one water molecule.38 Octahedral and pyramidal complexes containing Cu(II) were attempted in the present study, as copper is known to form complexes with these geometries with some ligands (e.g., dimethylglyoxime and nitrite). Nevertheless, these became square planar after optimization.35
3.1. Complexes of Cu(II) with Protonated AG
In contrast to neutral AG, the protonated molecule has only one conformer. Moreover, there are only two possible coordinating nitrogen atoms: N2 and N4. Other potential complexes were attempted without reaching stable species. The formation of these complexes refers to the equilibrium shown in eq 10. In this equilibrium, as well as in equilibria that will appear later on in this paper, the reactant 2AGH+ (when x = 2) refers to the lowest Gibbs free energy dimer between two protonated AG species. Similarly, the product identified as (4 – n)H2O refers to the most thermodynamically stable cluster of (4 – n) water molecules, with n = 0, ..., 4 depending on the coordination of AGH+ to Cu(II). In this approach, the same number of species exists in the reactant and product sides, and no reference state conversions are needed. Four complexes with one and two protonated AG species were optimized, and their structures are shown in Figure 2. Table 1 displays their ΔGf°, Kf, and log Kf values. These complexes are endergonic.
| 10 |
Figure 2.
Optimized geometries of complexes of Cu(II) with AGH+ in aqueous solution (bond distances in Å).
Table 1. Standard Gibbs Free Energy Change (ΔGf°) and Formation Constant (Kf, log Kf) for the Chelation of Cu(II) with AGH+ (as per eq 10) in Aqueous Solution at 298.15 Ka.
| complex [Cu(AGH)x(H2O)n](2+x)+ |
 (kcal/mol) (kcal/mol) |
||||
|---|---|---|---|---|---|
| [1] [Cu(AGH)2]4+ (N2, N4) | 26.1 | 2.71 × 10–5 | –4.57 | ||
| [2] [Cu(AGH)2(H2O)2]4+ (N4) | 10.3 | 1.58 × 10–2 | –1.80 | ||
| [3] [Cu(AGH)(H2O)2]3+ (N2, N4) | 13.8 | 3.89 × 10–3 | –2.41 | ||
| [4] [Cu(AGH)(H2O)3]3+ (N4) | 7.6 | 4.75 × 10–2 | –1.32 |
Coordinating atoms in the organic ligand are shown in parentheses for each complex.
The two most stable complexes, [4] and [2], with ΔGf° values of 7.6 and 10.3 kcal/mol, respectively, have one or two AGH+ species as a monodentate ligand coordinating only with the hydrazine nitrogen (N4). This is a coordination site for each of the four complexes and there are two reasons to rationalize this behavior. First, N4 is the most negatively charged (most basic) nitrogen atom; hence, it is the strongest coordinating site. Second, when N2 is not coordinating, the positive charge is delocalized between N1, N2, N3, and the carbon atom, which makes the guanidine moiety totally planar. However, this planarity is lost, and the complex becomes less stable, if N2 becomes a coordinating site. This explains why complexes [1] and [3], in which one or two AGH+ species act as a bidentate ligand, are of much lower thermodynamic stability than the complexes in which AGH+ is monodentate [4] and [2]. Moreover, the complexes with two AGH+ ligands, [1] and [2], are less stable than their counterparts with one AGH+ ligand [3] and [4].
The positive charge of the AG cation, in addition to reducing the coordinating ability of the nitrogen atoms, may lead to electrostatic repulsions with Cu2+ and help explain the instability of these complexes. This effect is especially noticeable in the bidentate complexes in which N2 has a positive partial charge.
3.2. Complexes of Cu(II) with AG
The four conformers of unprotonated AG were used to calculate various complexes with Cu(II), with one or two AG molecules present acting either as monodentate or bidentate ligands, all of them displaying square planar geometry. The structures of the seven 1:1 and the nineteen 1:2 complexes calculated are shown in Figures 3 and 4, respectively. The thermodynamic data related to the formation of these complexes, following the reaction shown in eq 11 in which the most thermodynamically stable form of unprotonated AG is used as reactant species, are shown in Table 2. The calculated complexes are all exergonic.
Figure 3.
Optimized geometries of the 1:1 complexes of Cu(II) with AG in aqueous solution (bond distances in Å).
Figure 4.
Optimized geometries of the 1:2 complexes of Cu(II) with AG in aqueous solution (bond distances in Å).
Table 2. Standard Gibbs Free Energy Change (ΔGf°) and Formation Constant (Kf, log Kf) for the Chelation of Cu(II) with AG (as per eq 11) in Aqueous Solution at 298.15 Ka.
| complex [Cu(AG)x(H2O)n]2+ |
 (kcal/mol) (kcal/mol) |
||||
|---|---|---|---|---|---|
| [5] [Cu(AGA)(H2O)2]2+ (N1, N2) | –4.0 | 8.84 × 102 | 2.95 | ||
| [6] [Cu(AGA)(H2O)3]2+ (N2) | –11.7 | 3.64 × 108 | 8.56 | ||
| [7] [Cu(AGB)(H2O)2]2+ (N1, N4) | –3.9 | 6.95 × 102 | 2.84 | ||
| [8] [Cu(AGB)(H2O)3]2+ (N2) | –10.6 | 5.76 × 107 | 7.76 | ||
| [9] [Cu(AGC)(H2O)2]2+ (N1, N4) | –4.1 | 9.91 × 102 | 3.00 | ||
| [10] [Cu(AGC)(H2O)3]2+ (N2) | –11.7 | 3.48 × 108 | 8.54 | ||
| [11] [Cu(AGD)(H2O)2]2+ (N2, N4) | –21.9 | 1.10 × 1016 | 16.04 | ||
| [12] [Cu(AGA)2]2+ (N1, N2) | –7.4 | 2.65 × 105 | 5.42 | ||
| [13] [Cu(AGA)2]2+ (mirror im., N1, N2) | –7.1 | 1.48 × 105 | 5.17 | ||
| [14] [Cu(AGA)2(H2O)2]2+ (N2) | –24.8 | 1.47 × 1018 | 18.17 | ||
| [15] [Cu(AGB)2]2+ (N1, N4) | –7.6 | 3.53 × 105 | 5.55 | ||
| [16] [Cu(AGB)2]2+ (mirror im., N1, N4) | –7.3 | 2.35 × 105 | 5.37 | ||
| [17] [Cu(AGB)2(H2O)]2+ (N1, N4, N2′) | –15.8 | 3.98 × 1011 | 11.60 | ||
| [18] [Cu(AGB)2(H2O)2]2+ (N2) | –24.1 | 4.82 × 1017 | 17.68 | ||
| [19] [Cu(AGC)2]2+ (N1, N4) | –7.7 | 4.40 × 105 | 5.64 | ||
| [20] [Cu(AGC)2]2+ (mirror im., N1, N4) | –7.5 | 3.12 × 105 | 5.49 | ||
| [21] [Cu(AGC)2(H2O)]2+ (N1, N4, N2′) | –16.1 | 6.70 × 1011 | 11.83 | ||
| [22] [Cu(AGC)2(H2O)2]2+ (N2) | –24.5 | 8.52 × 1017 | 17.93 | ||
| [23] [Cu(AGD)2]2+ (N2, N4) | –40.8 | 8.24 × 1029 | 29.92 | ||
| [24] [Cu(AGD)2]2+ (mirror im., N2, N4) | –40.9 | 9.91 × 1029 | 30.00 | ||
| [25] [Cu(AGD)2(H2O)]2+ (N2) | –31.0 | 4.87 × 1022 | 22.69 | ||
| [26] [Cu(AGD)2(H2O)2]2+ (N2) | –22.1 | 1.52 × 1016 | 16.18 | ||
| [27] [Cu(AGA)(AGD)]2+ (N1, N2, N2′, N4) | –25.1 | 2.48 × 1018 | 18.39 | ||
| [28] [Cu(AGB)(AGD)]2+ (N1, N4, N2′, N4) | –24.2 | 5.28 × 1017 | 17.72 | ||
| [29] [Cu(AGC)(AGD)]2+ (N1, N4, N2′, N4) | –25.8 | 8.86 × 1018 | 18.95 | ||
| [30] [Cu(AGC)(AGD)]2+ (mirror im., N1, N4, N2′, N4) | –24.4 | 7.58 × 1017 | 17.88 |
Coordinating atoms in the organic ligand are shown in parentheses for each complex; when two AGs are in different conformations or have different coordinating atoms, these are distinguished using a prime (′).
Only AGC has two possible coordination areas involving two N atoms (N1 and N2, N1 and N4), and these were both studied. The complexes coordinating with N1 and N2 broke during the optimization step, indicating that AGC can only bond in a bidentate fashion using N1 and N4. This is most likely due to the constrained geometry when AGC coordinates by N1 and N2.
Three monodentate ([6], [8], and [10]) and four bidentate ([5], [7], [9], and [11]) 1:1 complexes were optimized. In the monodentate complexes, coordination always involves the N2 atom of AG, which is the most negatively charged. The bidentate complexes containing AGA, AGB, and AGC ([5], [7], and [9]) are much less exergonic than their monodentate counterparts by 6.7–7.7 kcal/mol, whereas the one containing AGD ([11]), which has no monodentate equivalent, is the most exergonic complex, with a ΔGf0 value of −21.9 kcal/mol. This is to be expected, as AGA, AGB, and AGC lose planarity and resonance when coordinating in a bidentate fashion. Moreover, AGB and AGC cannot coordinate via the most negatively charged nitrogen (N2) in the bidentate complexes, which makes them slightly less stable than the AGA complex. In the most thermodynamically stable 1:1 complex, [11] [Cu(AGD)(H2O)2]2+, AGD coordinates to copper by N2 and N4, without breaking the planarity and resonance of the guanidine moiety.
Regarding the 1:2 complexes, several coordination combinations were considered, with both AG molecules of the same conformation being bidentate, monodentate, or mixed (one bidentate and the other monodentate). In the situation in which both AG molecules act as bidentate ligands, two possibilities were explored, one of which processes a quasi-plane of symmetry that goes through the central copper ion without making contact with the ligands. This type of 1:2 complex is shown in Table 2 as “mirror im.”. In most cases, these complexes were slightly less stable (with negligible differences of 0.3 kcal/mol or less) than their original counterparts. Some 1:2 complexes involving different AG conformations (both acting as bidentate ligands) were also optimized.
With AGA, three 1:2 complexes were calculated ([12], [13], and [14]), while with AGB ([15], [16], [17], and [18]), AGC ([19], [20], [21], and [22]), and AGD ([23], [24], [25], and [26]), four coordination compounds were obtained. With each AGA, AGB, and AGC, by far, the most stable 1:2 complex is the one in which the two AG molecules act as monodentate ligands via the N2 atom ([14], [18], and [22]) with ΔGf0 values between −24.1 and −24.8 kcal/mol. The mixed combination optimized for AGB and AGC, in which one AG is bidentate and the other is monodentate ([17], [21]), showed a thermodynamic stability intermediate between the full bidentate and the full monodentate combination.
| 11 |
Similar to what was found with the 1:1 complexes, the presence of AGD in the 1:2 complexes significantly increases their thermodynamic stability, especially when both AGD molecules act as bidentate ligands. Complexes [23] and [24] are the most stable of all the AG complexes considered, with ΔGf0 values close to −41 kcal/mol. When one of the AGD molecules and even more, when the two become monodentate in [25], its stability drops significantly and even more, when the two become monodentate in [26]. Complexes [25] and [26] have ΔGf values of −31 and −22 kcal/mol, respectively. When both AGD molecules are monodentate ligands, the thermodynamic stability of the complex is slightly lower than the analogue 1:2 complexes with the other AG conformations.
Given that the AGD conformation leads to the most stable 1:2 complexes in which both AG species act as bidentate ligands, combinations involving AGD and each of the other AG forms (both acting as bidentate ligands) were also explored. The four complexes calculated ([27], [28], [29], and [30]) have ΔGf0 values in the −24.2 and −25.8 kcal/mol range. These complexes are less stable than [23] and [24], in which only AGD is present, but their thermodynamic stability is significantly greater than the ones that contain only AGA, AGB, or AGC as bidentate ligands (with ΔGf values in the −7.1 to −7.6 kcal/mol range).
Because the thermodynamic stability of the 1:2 bidentate AGD complexes [23] or [24] is almost twice that of the 1:1 bidentate AGD complex [11], it could be inferred that the second AGD molecule stabilizes the complex twice as much as would two water molecules. Another important observation is that the stability of the complexes studied with different AG conformations is not related to the thermodynamic stability order of these conformers (see Figure 1). In fact, the least stable conformer AGD leads to the most thermodynamically stable complexes with Cu(II).
Regarding structural parameters, distances between the copper ion and the ligands are usually above 2.0 Å, and in some cases, above 2.1 Å (usually with the water molecules). However, this distance is reduced to less than 2.0 Å when the coordinating atom is N2.
Given that at physiological pH in aqueous solution AG is protonated, our thermodynamic calculations must take into account the deprotonation Gibbs free energy of AG under these conditions (ΔGdep) for the dissociation equilibrium shown in eq 12. The sequence of eqs 13 to 16 illustrates the calculation of ΔGdep. The resulting value (5.6 kcal/mol), which is the thermodynamic cost of forming neutral AG under these conditions, was added to the calculated ΔGf° values reported in Table 2 for each complex. The new thermodynamic data, which refers to the equilibrium shown in eq 17 (the sum of eqs 11 and 12), are shown in Table 3.
| 12 |
| 13 |
| 14 |
| 15 |
| 16 |
| 17 |
Table 3. Standard Gibbs Free Energy Change
( ) and Formation Constant
(
) and Formation Constant
( ,
,  ) for the Chelation of Cu(II) with AG (as
per eq 17) in Aqueous
Solution at 298.15 K, Taking into Account the ΔG° to Form AG from AGH+ at Physiological
pHa.
) for the Chelation of Cu(II) with AG (as
per eq 17) in Aqueous
Solution at 298.15 K, Taking into Account the ΔG° to Form AG from AGH+ at Physiological
pHa.
| complex [Cu(AG)x(H2O)n]2+ |
 (kcal/mol) (kcal/mol) |
||||
|---|---|---|---|---|---|
| [5] [Cu(AGA)(H2O)2]2+ (N1, N2) | 1.6 | 7.02 × 10–2 | –1.15 | ||
| [6] [Cu(AGA)(H2O)3]2+ (N2) | –6.1 | 2.89 × 104 | 4.46 | ||
| [7] [Cu(AGB)(H2O)2]2+ (N1, N4) | 1.7 | 5.52 × 10–2 | –1.26 | ||
| [8] [Cu(AGB)(H2O)3]2+ (N2) | –5.0 | 4.58 × 103 | 3.66 | ||
| [9] [Cu(AGC)(H2O)2]2+ (N1, N4) | 1.5 | 7.87 × 10–2 | –1.10 | ||
| [10] [Cu(AGC)(H2O)3]2+ (N2) | –6.1 | 2.76 × 104 | 4.44 | ||
| [11] [Cu(AGD)(H2O)2]2+ (N2, N4) | –16.3 | 8.75 × 1011 | 11.94 | ||
| [12] [Cu(AGA)2]2+ (N1, N2) | 3.8 | 1.67 × 10–3 | –2.78 | ||
| [13] [Cu(AGA)2]2+ (mirror im., N1, N2) | 4.1 | 9.34 × 10–4 | –3.03 | ||
| [14] [Cu(AGA)2(H2O)2]2+ (N2) | –13.6 | 9.25 × 109 | 9.97 | ||
| [15] [Cu(AGB)2]2+ (N1, N4) | 3.6 | 2.23 × 10–3 | –2.65 | ||
| [16] [Cu(AGB)2]2+ (mirror im., N1, N4) | 3.9 | 1.48 × 10–3 | –2.83 | ||
| [17] [Cu(AGB)2(H2O)]2+(N1, N4, N2′) | –4.6 | 2.51 × 103 | 3.40 | ||
| [18] [Cu(AGB)2(H2O)2]2+ (N2) | –12.9 | 3.04 × 109 | 9.48 | ||
| [19] [Cu(AGC)2]2+ (N1, N4) | 3.5 | 2.78 × 10–3 | –2.56 | ||
| [20] [Cu(AGC)2]2+ (mirror im., N1, N4) | 3.7 | 1.97 × 10–3 | –2.71 | ||
| [21] [Cu(AGC)2(H2O)]2+ (N1, N4, N2′) | –4.9 | 4.22 × 103 | 3.63 | ||
| [22] [Cu(AGC)2(H2O)2]2+ (N2) | –13.3 | 5.38 × 109 | 9.73 | ||
| [23] [Cu(AGD)2]2+ (N2, N4) | –29.6 | 5.20 × 1021 | 21.72 | ||
| [24] [Cu(AGD)2]2+ (mirror im., N2, N4) | –29.7 | 6.25 × 1021 | 21.80 | ||
| [25] [Cu(AGD)2(H2O)]2+ (N2, N4, N2’) | –19.8 | 3.08 × 1014 | 14.49 | ||
| [26] [Cu(AGD)2(H2O)2]2+ (N2) | –10.9 | 9.59 × 107 | 7.98 | ||
| [27] [Cu(AGA)(AGD)]2+ (N1, N2, N2′, N4) | –13.9 | 1.56 × 1010 | 10.19 | ||
| [28] [Cu(AGB)(AGD)]2+ (N1, N4, N2′, N4) | –13.0 | 3.33 × 109 | 9.52 | ||
| [29] [Cu(AGC)(AGD)]2+ (N1, N4, N2′, N4) | –14.7 | 5.59 × 1010 | 10.75 | ||
| [30] [Cu(AGC)(AGD)]2+ (mirror im., N1, N4, N2′, N4) | –13.2 | 4.78 × 109 | 9.68 |
Coordinating atoms in the organic ligand are shown in parentheses for each complex; when two AGs are in different conformation or have different coordinating atoms, these are distinguished using a prime (′).
When ΔGdep is taken into account, the nine bidentate complexes containing only one or two AGA, AGB, and AGC molecules become endergonic ([5], [7], [9], [12], [13], [15], [16], [19], and [20]). Thus, it is apparent that AGA, AGB, and AGC will not form very stable complexes unless they act as monodentate ligands in 1:2 complexes ([14], [18], and [22]) or as bidentate ligands when AGD is also present ([27], [28], [29], and [30]). The most thermodynamically stable 1:1 and 1:2 complexes have ΔGf0 values of −16.3 and −29.7 kcal/mol, respectively. Of the thirty coordination compounds investigated between AG and Cu(II), the four most stable complexes are [23], [24] > [25] > [11], and all involve AGD.
The previous study of Cu(II) complexes with AG,13 which was performed at the B3LYP(CPCM)/6-31+G(d) level of theory in water, reported two square planar complexes which happen to coincide with our complexes [11] (the most stable 1:1 complex) and [23] (the most stable 1:2 complex, if ignoring a slight variation from it into complex [24]). Gibbs free energy changes were reported at the 1 atm reference state relative to the isolated Cu2+, AG, and H2O species involved in each case (having a complex formation equilibrium with different number of species in the reactant and product sides), and pH was not taken into account. The ΔG° values reported for the formation of complexes [11] and [23] were −136.7 and −147.4 kcal/mol, respectively.13 Our calculated ΔG° values at physiological pH are −16.3 and −29.6 kcal/mol, respectively (see Table 3). The two approaches lead to very different complex formation constants. Given these significant differences, the procedure followed to study the thermodynamics of the formation of the Cu(II) complexes with a model Amadori compound and ascorbate as reported in ref (13), should be revisited.
3.3. Kinetic Calculations with Copper Complexes
AG is said to have secondary antioxidant activity if, by forming a complex with Cu(II), it can slow down the initial step (the copper-catalyzed Haber–Weiss reaction) of the reaction sequence shown in eq 18 and reduce the potential damage caused by •OH radical formation in the second step (the Fenton reaction).
| 18 |
Twelve Cu(II) complexes with AG/AGH+ were selected, and kinetic calculations were performed for their reduction to Cu(I), as well as for the first reaction of the scheme shown in eq 18, which is used as reference for comparison. The calculated rate constants (k, kD, and kapp), together with the ΔG° and ΔG≠ values for each reaction considered in aqueous solution at 298.15 K, are shown in Table S2 of the Supporting Information section. The reactions have been listed in decreasing order of k. The five reactions that lead to the smallest k and kapp values, those from complexes [24], [23], [25], [29] and [11], are shown in Table 4.
Table 4. Standard Gibbs Free Energy of Reaction (ΔG°, kcal/mol) and Activation (ΔG≠, kcal/mol), and the Apparent Rate Constant (kapp, M–1 s–1) for the Initial Reaction of the Haber–Weiss Cycle with the AG-Copper Complexes That Lead to the Slowest Reduction Reactions Relative to the Reference Reaction in Aqueous Solution at 298.15 Ka.
| reaction | ΔG0 | ΔG≠ | kapp |
|---|---|---|---|
| [Cu(H2O)4]2+ + O2•– → [Cu(H2O)2]+·2H2O + O2 | –32.6 | 0.2 | 7.71 × 109 |
| [11][Cu(AGD)(H2O)2]2+ + O2•– → [38][Cu(AGD)(H2O)]+·H2O + O2 | –20.0 | 1.8 | 7.47 × 109 |
| [29][Cu(AGC)(AGD)]2+ + O2•– → [39][Cu(AGC)(AGD)]+ + O2 | –18.2 | 2.2 | 7.40 × 109 |
| [25][Cu(AGD)2(H2O)]2+ + O2•– → [40][Cu(AGD)2]+·H2O + O2 | –19.2 | 2.8 | 7.02 × 109 |
| [23][Cu(AGD)2]2+ + O2•– → [41][Cu(AGD)2]+ + O2 | –11.1 | 4.1 | 3.49 × 109 |
| [24][Cu(AGD)2]2+ + O2•– → [42][Cu(AGD)2]+ + O2b | –11.6 | 4.3 | 2.80 × 109 |
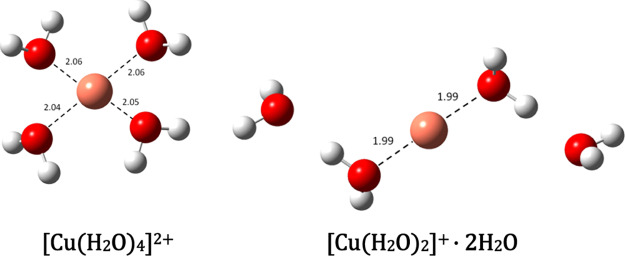
Starting from the optimized Cu(II) complex with AG in each case considered, a corresponding Cu(I) complex was obtained. The structures of the Cu(I) complexes that lead to the reactions with the smallest k (and kapp) values are shown in Figure 5 with a clear indication of the Cu(II) complex to which they are related. The structures of the other Cu(I) complexes referred to in Table S2 are shown in Figure S1 of the Supporting Information section. The calculated structures of the hydrated copper ions in aqueous solution, which participate in the reference reaction, are shown in Figure 6.
Figure 5.
Optimized geometries of the Cu(I) complexes with AG in aqueous solution that appear in Table 4 (indicating the Cu(II) complex used as the starting point in each case; bond distances in Å).
Figure 6.
Optimized geometries of the most stable hydrated Cu(II) and Cu(I) complexes in aqueous solution (bond distances in Å).
To explore the relationship between the thermodynamic stability of the Cu(II) complexes and the kinetics of their reduction to Cu(I), representatives of the calculated Cu(II) complexes of different groups were considered (see Table S2). These complexes are exergonic with the exception of [4] (the most stable complex with AGH+ and the only one considered from this group), [9], [19], and [20]. All the calculated Cu(I) complexes with AG/AGH+ are linear with coordinating bond distances of 1.90–2.01 Å, slightly shorter than the bond distances found in the corresponding Cu(II) complexes from which they were optimized. In all cases the most negatively charged coordinating atom in AG remains coordinated to Cu(I).
With the exception of the [4] → [31] reduction reaction that has a k of 5.50 × 1012, all the reactions studied have smaller rate constants (going from 3.02 × 1012 to 4.32 × 109; units are always M–1 s–1) than the reference reaction involving the hydrated Cu(II) and Cu(I) ions (with a k of 4.37 × 1012). However, after diffusion corrections are taken into account, all apparent rate constants (kapp) are in the order of 109 and the spread is greatly simplified with values from 2.80 × 109 to 7.96 × 109; with the reference reaction having a kapp of 7.71 × 109, which shows that AG possesses some degree of secondary antioxidant activity. This is more clearly shown for the 1:2 doubly-bidentate complexes [24] and [23] with kapp values of 2.80 × 109 and 3.49 × 109, respectively. These two reactions have kapp values that are 2.8 and 2.2 times smaller than that of the reference reaction. All other reactions have a negligible effect of the kinetics of the Cu(II) to Cu(I) reduction reaction.
All the reactions were calculated to be exergonic (see Table S2), with ΔG° values from −11.1 to −33.4 kcal/mol, while the ΔG° of the reference reaction is −32.6 kcal/mol. The calculated ΔG≠ values went from 0.1 to 4.3 kcal/mol, with 0.2 kcal/mol being the corresponding value of the reference reaction. In general, the less exergonic the reduction reaction and the larger its ΔG≠ value, the smaller is its rate constant (k and kapp) and the larger the reduction in k relative to the reference reaction.
Three 1:1 complexes with AG were included in the kinetic study: two bidentate complexes, [9] and [11], and a monodentate one, [10]; [11] is by far the most thermodynamically stable complex of the three. Despite the stability of [9] and [10] being quite different (see Table 3), the resulting values for [9] → [32] and [10] → [33] are quite similar for both k (3.02 × 1012 and 2.61 × 1012, respectively) and kapp (7.67 × 109 and 7.82 × 109, respectively). On the other hand, reaction [11] → [38] exhibits a considerably lower k value of 3.03 × 1011 (one order of magnitude lower), but its kapp is only marginally smaller, 7.47 × 109. Higher concentrations of AG would be needed to favor the formation of the 1:2 complexes which are the only ones able to show some secondary antioxidant activity.
3.4. Biological Implications and Discussion of Previous Work
Experimental studies have shown that desirable glycation inhibitors should be: (1) good radical scavengers, (2) good metal chelators at physiological pH conditions, and (3) good carbonyl scavengers.5 A recent kinetic study of the radical scavenging activity of AG with respect to •OCH3 and •OOH at the M05-2X(SMD)/6-311+G(d,p) level of theory revealed that the radical scavenging activity of AG was more effectively relative to •OCH3 radicals with hydrogen-atom transfer rate constants in nonpolar solvents being the largest in the range from 4.68 × 105 to 6.40 × 107 M –1 s–1. The most exergonic of these reactions had a ΔG° of −22.4 kcal/mol.18
The current study of the Cu(II) metal chelating activity of AG, at an equivalent level of theory [M05(SMD)/6-311+G(d,p)] and applying a similar methodology for the kinetic calculations, shows that the formation of the most thermodynamically stable complex in aqueous solution under physiological pH conditions has a ΔG° of −29.7 kcal/mol, and that once formed, it can be reduced to a Cu(I) complex at a rate of 2.80 × 109 M–1 s–1. AG has some secondary antioxidant character. Even though its action in this manner seems to be more relevant than its action as a radical scavenger, none of these mechanisms seem to be particularly successful for AG as a glycation inhibitor. Previously reported stability comparisons with the Cu(II) complexes that Amadori compounds and ascorbate can form need to be revisited.13
The previously made claim18 that the scavenging of reactive carbonyl species should be the main mechanism of action of AG as a glycation inhibitor should be backed up by a proper kinetic study with rate constant calculations at a comparable level of theory. The previously reported calculations for the mechanism of the reaction between AG and methylglyoxal were performed with the PBE functional and the DNP basis set employing explicit water molecules, but rate constants were not calculated.39
4. Conclusions
It has been shown that AG is capable of forming a wide array of stable complexes with Cu(II) at physiological pH in aqueous solution. Even though protonated AG (AGH+) is the most stable aqueous form of AG under physiological pH conditions, it forms remarkably unstable complexes with Cu(II). In addition, despite this molecule having four distinct conformers, only one of them (labeled AGD in this study) forms highly stable coordination compounds; being the most stable complexes, the ones containing two chelating AGD molecules acting as bidentate ligands in a way that the planarity of the coordinating system is not lost.
Moreover, the most stable complexes, identified as [23] and [24] in this study, can reduce up to 2.2–2.8 times the rate constant of the first step of the Haber–Weiss cycle and slightly diminish the potential damage that the formation of •OH radicals can cause. When diffusion corrections are taken into account, all other complexes have an almost negligible effect on the kinetics of the Cu(II) to Cu(I) reduction process. Higher concentrations of AG would be needed to favor the formation of the 1:2 complexes which are the only ones able to show some secondary antioxidant activity. The twelve reduction reactions studied show that in general, the less exergonic the reduction reaction is, the larger is its ΔG≠ value, the smaller is its rate constant, and the larger is the reduction in k relative to the reference reaction.
In summary, it can be stated that AG exhibits some degree of secondary antioxidant activity, as it can slow down the first step of the Haber–Weiss cycle, but the rate constant reduction for the Cu(II) to Cu(I) process is not sufficiently large as to be able to inhibit this process. However, it is likely that some of the Cu(II)–AG complexes could scavenge the subsequently formed •OH radical in the second step of this process via hydrogen-atom transfer and/or single-electron transfer reactions. The results of this investigation add to current knowledge about AG and its potential to act as a glycation inhibitor. However, more research is needed in order to completely elucidate the biochemical behavior of AG.
Acknowledgments
We gratefully acknowledge the financial support received from the Natural Sciences and Engineering Research Council of Canada (NSERC). G.G.-D. acknowledges the funding received from the Undergraduate Research Experience Award Program (UREAP) at Thompson Rivers University (TRU), R.R. acknowledges his PhD scholarship granted by the Spanish MECD within the FPU program (FPU16/00785), and N.M.-D. acknowledges a Visiting Professorship Award from the Universitat de les Illes Balears. We would also like to thank Information Technology Services at TRU.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.0c01175.
Cartesian coordinates, absolute enthalpies and Gibbs free energies of the different species considered in this study at the M05(SMD)/6-311+G(d,p) level of theory in water at 298.15 K, standard Gibbs free energy of reaction (ΔG°, kcal/mol) and activation (ΔG≠, kcal/mol), and various rate constants (k, kD and kapp, M–1 s–1) for the initial reaction of the Haber–Weiss cycle (with and without copper complexation with AG or AGH+) in aqueous solution at 298.15 K, and optimized geometries of Cu(I) complexes with AG and AGH+ in aqueous solution with a clear indication of the Cu(II) complex to which they are related (PDF)
Author Contributions
§ R.R. contributed to this paper while visiting TRU as a graduate student for two months in 2018.
The authors declare no competing financial interest.
Supplementary Material
References
- Thorpe S. R.; Baynes J. W. Maillard reaction products in tissue proteins: new products and new perspectives. Amino Acids 2003, 25, 275–281. 10.1007/s00726-003-0017-9. [DOI] [PubMed] [Google Scholar]
- Ulrich P.; Cerami A. Protein glycation, diabetes, and aging. Recent Prog. Horm. Res. 2001, 56, 1–22. 10.1210/rp.56.1.1. [DOI] [PubMed] [Google Scholar]
- Münch G.; Mayer S.; Michaelis J.; Hipkiss A. R.; Riederer P.; Müller R.; Neumann A.; Schinzel R.; Cunningham A. M. Influence of advanced glycation end-products and AGE-inhibitors on nucleation-dependent polymerization of β-amyloid peptide. Biochim. Biophys. Acta, Mol. Basis Dis. 1997, 1360, 17–29. 10.1016/s0925-4439(96)00062-2. [DOI] [PubMed] [Google Scholar]
- Stitt A. W. The maillard reaction in eye diseases. Ann. N.Y. Acad. Sci. 2005, 1043, 582–597. 10.1196/annals.1338.066. [DOI] [PubMed] [Google Scholar]
- Colzani M.; De Maddis D.; Casali G.; Carini M.; Vistoli G.; Aldini G. Reactivity, selectivity, and reaction mechanisms of aminoguanidine, hydralazine, pyridoxamine, and carnosine as sequestering agents of reactive carbonyl species: a comparative study. ChemMedChem 2016, 11, 1778–1789. 10.1002/cmdc.201500552. [DOI] [PubMed] [Google Scholar]
- Haber F.; Weiss J. Über die Katalyse des Hydroperoxydes. Naturwissenschaften 1932, 20, 948–950. 10.1007/bf01504715. [DOI] [Google Scholar]
- Price D. L.; Rhett P. M.; Thorpe S. R.; Baynes J. W. Chelating Activity of Advanced Glycation End-product Inhibitors. J. Biol. Chem. 2001, 276, 48967–48972. 10.1074/jbc.m108196200. [DOI] [PubMed] [Google Scholar]
- Rahbar S.; Natarajan R.; Yerneni K.; Scott S.; Gonzales N.; Nadler J. L. Evidence that pioglitazone, metformin and pentoxifylline are inhibitors of glycation. Clin. Chim. Acta. 2000, 301, 65–77. 10.1016/s0009-8981(00)00327-2. [DOI] [PubMed] [Google Scholar]
- Ortega-Castro J.; Adrover M.; Frau J.; Donoso J.; Muñoz F. Chelating power of LR-74, a new AGE-inhibitor. Chem. Phys. Lett. 2008, 465, 120–125. 10.1016/j.cplett.2008.09.027. [DOI] [Google Scholar]
- Casasnovas R.; Ortega-Castro J.; Donoso J.; Frau J.; Muñoz F. Theoretical calculations of stability constants and pKa values of metal complexes in solution: application to pyridoxamine-copper(II) complexes and their biological implications in AGE inhibition. Phys. Chem. Chem. Phys. 2013, 15, 16303–16313. 10.1039/c3cp50840d. [DOI] [PubMed] [Google Scholar]
- Kline Bolton W.; Abdel-Rahman E. Pimagedine: a novel therapy for diabetic nephropathy. Expert Opin. Invest. Drugs 2002, 11, 565–574. 10.1517/13543784.11.4.565. [DOI] [PubMed] [Google Scholar]
- Ortega-Castro J.; Frau J.; Casasnovas R.; Fernández D.; Donoso J.; Muñoz F. High- and low-spin Fe(III) complexes of various AGE inhibitors. J. Phys. Chem. A 2012, 116, 2961–2971. 10.1021/jp210188w. [DOI] [PubMed] [Google Scholar]
- Ortega-Castro J.; Adrover M.; Frau J.; Donoso J.; Muñoz F. Cu2+ complexes of some AGEs inhibitors. Chem. Phys. Lett. 2009, 475, 277–284. 10.1016/j.cplett.2009.05.074. [DOI] [Google Scholar]
- Ortega-Castro J.; Adrover M.; Frau J.; Salvà A.; Donoso J.; Muñoz F. DFT studies on Schiff base formation of vitamin B6 analogues. Reaction between a pyridoxamine-analogue and carbonyl compounds. J. Phys. Chem. A 2010, 114, 4634–4640. 10.1021/jp909156m. [DOI] [PubMed] [Google Scholar]
- Adrover M.; Vilanova B.; Muñoz F.; Donoso J. Pyridoxamine, a scavenger agent of carbohydrates. Int. J. Chem. Kinet. 2007, 39, 154–167. 10.1002/kin.20223. [DOI] [Google Scholar]
- Adrover M.; Vilanova B.; Muñoz F.; Donoso J. Inhibition of glycosylation processes: the reaction between pyridoxamine and glucose. Chem. Biodivers. 2005, 2, 964–975. 10.1002/cbdv.200590074. [DOI] [PubMed] [Google Scholar]
- Solís-Calero C.; Ortega-Castro J.; Frau J.; Muñoz F. Scavenger mechanism of methylglyoxal vy metformin. A DFT study. Theor. Chem. Acc. 2015, 134, 48–62. 10.1007/s00214-015-1649-z. [DOI] [Google Scholar]
- Ramis R.; Casasnovas R.; Mariño L.; Frau J.; Adrover M.; Vilanova B.; Mora-Diez N.; Ortega-Castro J. A density functional theory study of the free-radical scavenging activity of aminoguanidine. Comparison with its reactive carbonyl compound and metal scavenging activities. Int. J. Quantum Chem. 2019, 119, e25911 10.1002/qua.25911. [DOI] [Google Scholar]
- Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Mennucci B.; Petersson G. A.; Nakatsuji H.; Caricato M.; Li X.; Hratchian H. P.; Izmaylov A. F.; Bloino J.; Zhen G.; Sonnenberg J. L.; Hada M.; Ehara M.; Toyota K.; Fukuda R.; Hasegawa J.; Ishida M.; Nakajima T.; Honda Y.; Kitao O.; Nakai H.; Vreven T.; Montgomery J. A. Jr; Peralta J. E.; Ogliaro F.; Bearpark M.; Heyd J. J.; Brothers E.; Kudin K. N.; Staroverov V. N.; Keith T.; Kobayashi R.; Normand J.; Raghavachari K.; Rendell A.; Burant J. C.; Iyengar S. S.; Tomasi J.; Cossi M.; Rega N.; Millam J. M.; Klene M.; Knox J. E.; Cross J. B.; Bakken V.; Adamo C.; Jaramillo J.; Gomperts R.; Stratmann R. E.; Yazyev O.; Austin A. J.; Cammi R.; Pomelli C.; Ochterski J. W.; Martin R. L.; Morokuma K.; Zakrzewski V. G.; Voth G. A.; Salvador P.; Dannenberg J. J.; Dapprich S.; Daniels A. D.; Farkas O.; Foresman J. B.; Ortiz J. V.; Cioslowski J.; Fox D. J.. Gaussian 09, Revision B.01; Gaussian Inc.: Wallingford, CT, 2010.
- Marenich A. V.; Cramer C. J.; Truhlar D. G. Universal solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B 2009, 113, 6378–6396. 10.1021/jp810292n. [DOI] [PubMed] [Google Scholar]
- Zhao Y.; Schultz N. E.; Truhlar D. G. Exchange-correlation functional with broad accuracy for metallic and nonmetallic compounds, kinetics, and noncovalent interactions. J. Chem. Phys. 2005, 123, 161103–161106. 10.1063/1.2126975. [DOI] [PubMed] [Google Scholar]
- Zhao Y.; Truhlar D. G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. 10.1007/s00214-007-0310-x. [DOI] [Google Scholar]
- Marcus R. A. Electron transfer reactions in chemistry. Theory and experiment. Rev. Mod. Phys. 1993, 65, 599–610. 10.1103/revmodphys.65.599. [DOI] [Google Scholar]
- Marcus R. A. Transfer reactions in chemistry. Theory and experiment. Pure Appl. Chem. 1997, 69, 13–30. 10.1351/pac199769010013. [DOI] [Google Scholar]
- Collins F. C.; Kimball G. E. Diffusion-Controlled Reaction Rates. J. Colloid Sci. 1949, 4, 425–437. 10.1016/0095-8522(49)90023-9. [DOI] [Google Scholar]
- Smoluchowski M. v. Versuch einer mathematischen Theorie der Koagulationskinetik kolloider Lösungen. Z. Phys. Chem. 1917, 92U, 129–168. 10.1515/zpch-1918-9209. [DOI] [Google Scholar]
- Einstein A. Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen. Ann. Phys. 1905, 322, 549–560. 10.1002/andp.19053220806. [DOI] [Google Scholar]
- Stokes G. G.Mathematical and Physical Papers; Cambridge University Press: Cambridge, 1903; Vol. 3. [Google Scholar]
- Castañeda-Arriaga R.; Alvarez-Idaboy J. R.; Mora-Diez N. Theoretical study of copper complexes with lipoic and dihydrolipoic acids. RSC Adv. 2016, 6, 107924–107932. 10.1039/c6ra23553k. [DOI] [Google Scholar]
- Monreal-Corona R.; Ippolito A. A.; Biddlecombe J. R.; Mora-Diez N.. Theoretical Study of the Iron Complexes with Lipoic and Dihydrolipoic Acids:Exploring Secondary Antioxidant Activity, submitted. [DOI] [PMC free article] [PubMed]
- Castañeda-Arriaga R.; Mora-Diez N.; Alvarez-Idaboy J. R. Modelling the Chemical Repair of Protein Carbon-Centered Radicals Formed via Oxidative Damage with Dihydrolipoic Acid. RSC Adv. 2015, 5, 96714–96719. 10.1039/c5ra20618a. [DOI] [Google Scholar]
- Castañeda-Arriaga R.; Domínguez-Castro A.; Lee J.; Alvarez-Idaboy J. R.; Mora-Diez N. Chemical Repair of Protein Carbon-Centred Radicals: Long-Distance Dynamic Factors. Can. J. Chem. 2016, 94, 1119–1126. 10.1139/cjc-2016-0230. [DOI] [Google Scholar]
- Ramis R.; Casasnovas R.; Ortega-Castro J.; Frau J.; Álvarez-Idaboy J. R.; Mora-Diez N. Modelling the repair of carbon-centred protein radicals by the antioxidants glutathione and Trolox. New J. Chem. 2019, 43, 2085–2097. 10.1039/c8nj05544k. [DOI] [Google Scholar]
- Koskinen M.; Mutikainen I.; Tilus P.; Pelttari E.; Korvela M.; Elo H. Structure of aminoguanidine hemioxalate. Implications for the synthesis of amidinohydrazones. Monatsh. Chem. 1997, 128, 767–775. 10.1007/bf00807087. [DOI] [Google Scholar]
- Greenwood N. N.; Earnshaw A.. Chemistry of the Elements, 2nd ed.; Butterworth-Heinemann, 1997. [Google Scholar]
- Boldyrev V. V.; Tukhtaev R. K.; Gavrilov A. I.; Larionov S. V.; Savel’eva Z. A.; Lavrenova G. G. Combustion of nickel and copper nitrate complexes of hydrazine derivatives as a method for manufacturing fine-grained and porous metals. Russ. J. Inorg. Chem. 1998, 43, 302–305. [Google Scholar]
- Aitken D. J.; Albinati A.; Gautier A.; Husson H.-P.; Morgant G.; Nguyen-Huy D.; Kozelka J.; Lemoine P.; Ongeri S.; Rizzato S.; Viossat B. Platinum(II) and Palladium(II) Complexes withN-Aminoguanidine. Eur. J. Inorg. Chem. 2007, 2007, 3327–3334. 10.1002/ejic.200600998. [DOI] [Google Scholar]
- Devi R. G. Synthesis and characterization of cationic Ni complexes with aminoguanidine as chelating bidentate ligand. Asian J. Res. Chem. 2016, 9, 378–384. 10.5958/0974-4150.2016.00058.4. [DOI] [Google Scholar]
- Solís-Calero C.; Ortega-Castro J.; Hernandez-Laguna A.; Muñoz F. DFT study of the mechanism of the reaction of aminoguanidine with methylglyoxal. J. Mol. Model. 2014, 20, 2202. 10.1007/s00894-014-2202-z. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.