Proton-Coupled Electron Transfer from Tyrosine in the Interior of a de novo Protein: Mechanisms and Primary Proton Acceptor

Abstract

Proton-coupled electron transfer (PCET) from tyrosine produces a neutral tyrosyl radical (Y^•) that is vital to many catalytic redox reactions. To better understand how the protein environment influences the PCET properties of tyrosine, we have studied the radical formation behavior of Y₃₂ in the α₃Y model protein. The previously solved α₃Y solution NMR structure shows that Y₃₂ is sequestered ∼7.7 ± 0.3 Å below the protein surface without any primary proton acceptors nearby. Here we present transient absorption kinetic data and molecular dynamics (MD) simulations to resolve the PCET mechanism associated with Y₃₂ oxidation. Y₃₂^• was generated in a bimolecular reaction with [Ru(bpy)₃]³⁺ formed by flash photolysis. At pH > 8, the rate constant of Y₃₂^• formation (k_PCET) increases by one order of magnitude per pH unit, corresponding to a proton-first mechanism via tyrosinate (PTET). At lower pH < 7.5, the pH dependence is weak and shows a previously measured KIE ≈ 2.5, which best fits a concerted mechanism. k_PCET is independent of phosphate buffer concentration at pH 6.5. This provides clear evidence that phosphate buffer is not the primary proton acceptor. MD simulations show that one to two water molecules can enter the hydrophobic cavity of α₃Y and hydrogen bond to Y₃₂, as well as the possibility of hydrogen-bonding interactions between Y₃₂ and E₁₃, through structural fluctuations that reorient surrounding side chains. Our results illustrate how protein conformational motions can influence the redox reactivity of a tyrosine residue and how PCET mechanisms can be tuned by changing the pH even when the PCET occurs within the interior of a protein.

Introduction

Protein redox chemistry is at the heart of many biologically important processes such as photosynthesis, respiration, and nitrogen fixation. The large oxidoreductase class of enzymes uses a range of organic molecules and metallocofactors for catalytic and long-range electron transfer (ET) reactions.¹⁻⁷ Some oxidoreductases use tyrosine (Y), tryptophan (W), cysteine, glycine, and possibly methionine as high potential one-electron redox mediators.⁷⁻¹⁸ Y and W are of particular interest because these residues can form spatially organized chains in which high potential, one-electron oxidizing equivalents are moved over large distances.¹⁴⁻¹⁸ Gray and Winkler have even suggested that Y/W-based radical transfer (“hole hopping”) pathways may be quite common and potentially serve as an important protective mechanism against oxidative damage.^17,18 Under physiological conditions, ET from Y is typically coupled to proton transfer (PT) in a proton-coupled electron transfer (PCET) reaction, resulting in the formation of a neutral radical species.^8,10,19−23 The thermodynamics and kinetics involved in radical formation and decay in these amino acids have direct implications for biocatalytic multistep ET/PCET processes. Thus, the study of such processes is important for (i) understanding how proteins effectively and functionally move highly oxidizing holes over large distances and (ii) directing the design of more effective biomimetic catalysts for applications such as the production of solar fuels.²⁴⁻²⁷

Due to the complexity and size of many enzymes, it is extremely challenging to experimentally resolve the thermodynamic and kinetic behavior of a single amino-acid residue. Simplified biomimetic molecular systems that contain Y or W, but lack a protein scaffold, have proven useful in shedding light on PCET kinetics and mechanisms of radical formation in aqueous buffer.²⁸⁻⁴³ However, the thermodynamics, kinetics, and mechanisms of Y radical formation may not necessarily reflect the behavior that would be observed for Y in a protein environment. The α₃X family of model proteins bridges the gap between small-molecule model systems and enzymes by providing a well-defined protein environment wherein the formation of a single amino-acid radical can be experimentally resolved.⁴⁴ Thus, the α₃X proteins provide a unique opportunity to study PCET quantitatively in a protein environment.

The α₃X model protein system is based on a 65-residue, single-stranded three-helix bundle (α₃) with a buried, redox-active residue (X₃₂) at position 32 (Figure 1, α₃Y). Tyrosine (Y₃₂),^45,46 tryptophan (W₃₂),^47,48 and a number of unnatural amino acids such as mercaptophenols,^49,50 fluorotyrosines (F_nY₃₂, where n = 2 or 3),^51,52 and aminotyrosine⁵³ have been placed in position 32. Structural studies using circular dichroism spectroscopy and solution nuclear magnetic resonance (NMR) spectroscopy have shown that the α₃X proteins remain thermodynamically stable and well-folded in the pH range of ∼5–10.^44,45,48,49 A key advantage of the α₃X system is that residue 32 can be reversibly oxidized and reduced.⁵⁴ This property has allowed the determination of true thermodynamic reduction potentials () for Y₃₂, W₃₂, and a range of Y analogues incorporated at site 32.^48,50−54 Pourbaix diagrams that map 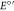of Y₃₂ and W₃₂ as a function of pH were obtained from protein film square-wave voltammograms collected between pH 5.5 and 10.^48,52 The slopes of the Y₃₂ and W₃₂ vs pH plots were consistent with a 1e^–/1H⁺ redox process where oxidation is coupled to the release of a proton to give Y₃₂^• and W₃₂^•, respectively. The α₃Y and α₃W proteins were also interrogated by transient absorption (TA) spectroscopy upon oxidation by flash-quench generated [Ru(bpy₃)]³⁺ (bpy = 2,2′-bipyridine).^46,48 Transient spectra confirmed the formation of the neutral radical species (Y₃₂^• and W₃₂^•) when α₃Y and α₃W were oxidized. From TA kinetic studies, the PCET rate constants of Y₃₂^• and W₃₂^• formation at pH 5.5 and 8.5 were determined. In α₃Y, a significant kinetic isotope effect was observed at both pH 5.5 and 8.5, suggesting that proton transfer is participating in the rate limiting step. PCET was tentatively proposed to proceed by either a concerted or stepwise proton-first (PTET) mechanism with water as the proton acceptor.⁴⁶

Figure 1.

The α₃Y protein is composed of a single chain of 65 amino acids: GSR(1)--LGGGG-Y(32)-LGGGGE-, where helices 1, 2, and 3 are shown in , , and , respectively. The protein ensemble structure of α₃Y (PDB ID 2MI7)⁴⁶ shows very little structural deviation in the 32 lowest energy states and is consistent with a globally stable and well-defined protein.

The present work significantly extends the previous studies of tyrosine radical formation in α₃Y by refining several mechanistic details concerning the formation of the Y₃₂^•. Although it was evident from the previous study⁴⁶ that PT is involved in the rate limiting step of radical formation, it was unclear if Y₃₂ oxidation proceeded by a concerted PCET or stepwise PTET mechanism, what the primary proton acceptor was, and how the mechanism was affected by pH. With the additional pH dependent radical formation kinetics data presented herein, we are able to resolve distinct mechanistic regimes of PCET in Y₃₂. We also report kinetic data for Y₃₂^• formation as a function of buffer concentration. The obtained results clearly eliminate buffer, and point to H₂O, as the primary proton acceptor for Y₃₂. Finally, the solution NMR structure of α₃Y shows that Y₃₂ is situated in the hydrophobic core of the protein (Figure 1). The buried Y₃₂ residue exhibits an effective solvent accessible surface area of zero (0.2 ± 0.2%). A residue depth analysis showed that the atoms associated with Y₃₂ and with its aromatic side chains have an average depth of 7.7 ± 0.3 and 8.1 ± 0.4 Å, respectively.⁴⁶ Based on the static α₃Y structure, it was thus unclear how water gained access in order to accept the phenolic proton released from Y₃₂ upon oxidation. To resolve this conundrum, we present molecular dynamics (MD) simulations that illustrate how structural fluctuations in the protein ensemble facilitate the proton transfer step in PCET. These combined results provide a detailed mechanistic framework that will contribute to the overall understanding of Y-based redox chemistry in enzymes.

Materials and Methods

Sample Preparation

α₃Y was expressed and purified as described previously.⁴⁵ Lyophilized protein was dissolved in phosphate buffer, KP_i (KH₂PO₄ from Sigma Life Science ≥99.0% purity, K₂HPO₄ from ACROS Organics 99+% purity), containing 40 mM KCl (Alfa Aesar 99.0–100.5% purity). In experiments where kinetics was measured as a function of buffer concentration, the solutions were prepared with the following concentrations: [KP_i] = 20–460 mM, [α₃Y] = 391–486 μM, [[Ru(bpy)₃]Cl₂] (bpy = 2,2′-bipyridine) = 26–65 μM, and [[Co(NH₃)₅Cl]Cl₂] = 4 mM. In experiments where kinetics was measured as a function of pH, solutions were prepared to the following concentrations: [KP_i] = 20–40 mM, [α₃Y] = 391–907 μM. 40 mM KP_i was used to minimize pH fluctuations upon decomposition of [Co(NH₃)Cl]Cl₂, which generates NH₃ upon quenching of *[Ru(bpy)₃]Cl₂ (* denotes excited species). Control experiments were carried out in the absence of α₃Y, where [[Ru(bpy)₃]Cl₂] = 26–65 μM and [[Co(NH₃)₅Cl]Cl₂] = 3–4 mM. Concentrations of α₃Y, [Ru(bpy)₃]Cl₂, and [Co(NH₃)₅Cl]Cl₂ were determined spectrophotometrically using a UV/vis spectrometer (Agilent 8453 diode array or Cary 50) using the following extinction coefficients: α₃Y (ε₂₇₇ = 1490 M^–1 cm^–1),⁴⁴ [Ru(bpy)₃]Cl₂ (ε₄₅₂ = 14600 M^–1 cm^–1),⁵⁵ and [Co(NH₃)₅Cl]Cl₂ (ε₅₃₂ = 52 M^–1 cm^–1).⁴⁸ In all experiments, photosensitizer and quencher solutions were prepared separately and mixed under dark conditions to prevent formation of [Ru(bpy)₃]³⁺ and subsequent initiation of PCET prior to flash-quench experiments. The solution pH was adjusted with 0.1–1 M NaOH and 0.1–1 M HCl and measured using a Metrohm 654 pH meter and a calibrated Metrohm LL Biotrode pH-electrode.

Transient Absorption Methods

The transient absorption (TA) setup has been described previously.⁴⁶ In short, the sample was excited using a Nd:YAG laser (Quantel, BrilliantB) with the laser light passed through an OPO that was tuned to 460 nm. The probe light was directed at a right angle to the excitation light and was provided by a 150 W unpulsed Xe lamp that was passed through a monochromator (Applied Photophysics, pbp Spectra Kinetic Monochromator 05-109) prior to reaching the sample. The monochromator was selected for either 410 or 450 nm light, with 2–3 mm slit openings and 4.65 nm/mm bandpass giving fwhm = 9.3 and 13.95 nm, respectively. A second monochromator was placed after the sample and directed the probe light to the detector (PMT, Hamamatsu R928). The signal was digitized using an Agilent Technologies Infiniium digital oscilloscope (600 MHz). TA traces were produced within the Applied Photophysics LKS software package.

Samples were contained in a 4 × 10 mm cuvette where the probe light was led through the 10 mm path length. Oxygen was excluded from the sample during measurement by first gently purging the solution with high purity Ar for 10 min prior to measuring and then by maintaining a positive pressure of Ar during flash photolysis. TA experiments were carried out at 22–23 (±1) °C.

A change of ca. 0.1–0.8 pH units was observed for individual samples used during flash photolysis with larger changes occurring in samples having lower buffer concentrations. The pH of analyzed solutions was measured before and after the flash photolysis experiments. The range of pH values during a given flash photolysis experiment and the average pH were calculated from a linear interpolation of the change in pH as a function of the number of laser flashes supplied to the sample. The first 10 shots were not used for fitting; these traces were not reproducible due to the presence of an impurity that is rapidly consumed under oxidizing conditions (Figure S1).⁴⁶ Each sample received ca. 30 laser shots, and 10–26 laser shots were averaged to obtain kinetic traces from which rate constants were extracted. The power of each laser shot was 9–12 mJ. Approximately 1–6 μM [Ru(bpy)₃]³⁺ was formed per shot. Data were analyzed using Matlab version 2018b.

Computational Methods

The solution NMR structure for α₃Y served as the starting point for all simulations and was obtained from the Protein Data Bank (PDB code: 2MI7).⁴⁶ As the NMR ensemble includes 32 structures, both the last conformer and the medoid (i.e., the most representative of the ensemble average, conformer 19) were selected. Independent simulations starting with each of these structures are referred to as “Traj. 1” and “Traj. 2”, respectively. Each initial protein structure was solvated with explicit TIP3P⁵⁶ water in a periodic rectilinear box. The net positive charge of the protein at pH 7.0 was neutralized with Cl^– ions, followed by adding Na⁺ and Cl^– ions to achieve a salt concentration of ∼150 mM. After the careful equilibration procedure described in the Supporting Information, a 1 μs MD trajectory in the canonical (NVT) ensemble was propagated for each initial structure. This simulation procedure was conducted with two different force fields, CHARMM36⁵⁷ and AMBER ff14SB.⁵⁸ The results with these two force fields exhibit the same qualitative trends, but the CHARMM force field is known to slightly overstabilize helical structures.⁵⁹⁻⁶¹ Therefore, the AMBER ff14SB simulations are featured in the main text, while the analogous CHARMM simulations are discussed in the Supporting Information. The root-mean-square deviations (RMSDs) for the backbone C_α atoms relative to the initial structure were computed to confirm the structural stability over the 1 μs trajectories (Figure S6). The root-mean-square fluctuations (RMSFs) of the C_α positions per residue were also computed to identify the most flexible regions of the protein (Figure S6). A hydrogen-bonding analysis for Y₃₂ was also conducted over all of the trajectories.

Results and Discussion

Radical Formation Kinetics of Y₃₂

The kinetics of Y₃₂ oxidation was investigated between pH 5.7 and pH 9.0. This pH range was chosen on the basis that there is no significant change in the α-helical content, global stability, and tertiary structure of α₃Y.^45,46Figure 2A summarizes the processes that occur during laser flash photolysis under the conditions used here. [Ru(bpy)₃]²⁺ is excited and then oxidatively quenched by the sacrificial quencher [Co(NH₃)₅Cl]Cl₂ (k_q = 9 × 10⁸ M^–1 s^–1)⁴⁶ to form [Ru(bpy)₃]³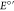⁺ (([Ru(bpy)₃]^3+/2+) = 1260 mV vs NHE). [Ru(bpy)₃]³⁺ subsequently oxidizes Y₃₂; this oxidation is coupled to proton loss, which yields Y₃₂^•. The Y₃₂ Pourbaix diagram provides an 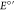(pH 7.0) value of 986 ± 3 mV for the neutral tyrosine Y₃₂(O^•/OH) redox pair and a pH independent E° value of 749 mV for the tyrosinate Y₃₂(O^•/O^–) redox pair (see ref (52), Table S2, for a Nernst analysis of the α₃Y Pourbaix diagram).^48,52

Figure 2.

(A) The mechanism of Y₃₂–O^• generation by laser flash-quench photolysis. (B) Single TA traces collected at pH 6.5 in 20 mM KP_i buffer. Purple circles represent data recorded at 410 nm, shown with a black line fit. The dark gray solid line shows the Y₃₂^• component of the fit, and the light gray line shows the [Ru(bpy)₃]²⁺ bleach component of the fit. Green circles represent data collected at 450 nm with a black line fit to a single exponential decay. Blue dots represent data collected at 410 nm in the absence of α₃Y.

Figure 2B shows TA kinetic traces obtained from an α₃Y-containing sample at 450 nm (green) and 410 nm (purple). The bleach at 450 nm is due to the depletion of [Ru(bpy)₃]²⁺ as a result of oxidative quenching with [Co(NH₃)₅Cl]Cl₂ (step 2, Figure 2A) that produces [Ru(bpy)₃]³⁺. Y₃₂ oxidation by [Ru(bpy)₃]³⁺ (corresponding to step 3 in Figure 2A) replenishes [Ru(bpy)₃]²⁺, as indicated by the recovery to the prepulse baseline of the TA signal at 450 nm. Both [Ru(bpy)₃]²⁺ and Y₃₂^• absorb at 410 nm, resulting in a bleach after the laser flash that grows to a positive signal as [Ru(bpy)₃]²⁺ recovers and Y₃₂^• is formed. On a slower time scale, Y₃₂^• dimerizes following second-order kinetics, as shown through fluorescence measurements.⁴⁶ Kinetic traces collected at 410 nm were therefore fit to a model of pseudo-first-order formation followed by second-order decay. The fitting routine used to extract the pseudo-first-order rate constants (k_obs) associated with radical formation is described in detail in the Supporting Information, page S5.⁶² Second-order PCET rate constants were calculated from k_PCET = k_obs/[α₃Y]. The yield of Y₃₂^• formation ranged from 0.52 to 0.75, which is consistent with previous observations.⁴⁶

The irreversible quenching produces Co²⁺(aq), NH₄⁺(aq), and Cl^–(aq).⁶³ The Co²⁺ ions formed in the quenching event (step 2, Figure 2A) react to generate Co-oxides. These complexes scatter light and exhibit broad absorption spectra in the UV and visible regions (Supporting Information of ref (46)). The blue trace in Figure 2B was collected in the absence of α₃Y. The slow increase observed after the laser flash is due to reduction of [Ru(bpy)₃]³⁺ by water, Co²⁺ (aq), and Co-oxides formed under oxidizing conditions.⁴⁶ We note that it is critical to minimize exposure to probe light when measuring on the ms to s time scale. A monochromator was placed before the sample to filter probe light centered at 450 and 410 nm. A control experiment in the absence of protein confirmed that the reduction of [Ru(bpy)₃]³⁺ by side reactions is significantly slower than the observed rate constants in the presence of α₃Y. Control experiments using α₃X with redox inactive phenylalanine at position 32 have previously shown similar slow kinetics.⁴⁶ As PCET rates associated with Y₃₂^• formation are significantly faster than Co-oxide formation, kinetic traces obtained in the presence of the protein can be attributed solely to Y₃₂^• formation (Figure S2). Additional control experiments without α₃Y also confirmed that Co-oxide formation does not increase with buffer concentration (Figure S3).

PCET Rate Constants as a Function of pH and Buffer Concentration

Bimolecular rate constants for oxidation of Y₃₂ by [Ru(bpy)₃]³⁺ were determined at pH values from 5.7 to 9.0 using kinetics from ns laser flash photolysis, Figure 3. The data shows a steep pH dependence at high pH where a 10-fold increase in rate constant per pH unit is observed. The pH dependence is weaker below ca. pH 7.5. The phenomena giving rise to the observed trend in PCET rate constants (k_PCET) are discussed below.

Figure 3.

Rate constants of PCET versus pH for α₃Y (black circles). Solid black squares represent data from ref (46). The purple solid line is a fit to eq 2, where k_YOH = 2.6 × 10⁴ M^–1 s^–1 and k_YO^– = 1.4 × 10⁸ M^–1 s^–1 (R² = 0.87). The dashed lines show the pH independent and pH dependent terms of the fit. Vertical error bars correspond to ± one standard deviation. Horizontal error bars correspond to the change in pH over the course of the flash photolysis experiment.

The fractions of tyrosine and tyrosinate (f_YOH and f_YO^–, respectively) change with pH, and k_PCET can be expressed as a sum of these fractions multiplied by their respective oxidation rate constants (k_YOH and k_YO^–):

1

f_YOH is close to unity (>0.99) throughout the pH 5.7–9.0 range studied and can therefore be treated as independent of pH. f_YO^– can be approximated as 10^pH–pKa from the Henderson–Hasselbalch equation, thus obtaining the following relation:

2

k_PCET as a function of pH was fit to eq 2, using an apparent pK_a of 11.3 for Y₃₂,⁴⁴ shown in purple (solid line, Figure 3). The fit resulted in k_YOH = 2.6 × 10⁴ M^–1 s^–1 and k_YO^– = 1.4 × 10⁸ M^–1 s^–1.

The equilibrium concentration of deprotonated Y₃₂ at pH 8–9 is similar to, or even lower than, that of [Ru(bpy)₃]³⁺ created in one flash (roughly 0.25 μM compared to 1–6 μM, respectively, for each species at pH 8). Still TA kinetics from pH 8–9 showed single exponential behavior (pseudo-first-order conditions), suggesting that f_YO^– is constant during the experiment. This means that the equilibrium between protonated and deprotonated Y₃₂ is fast on the time scale of Y₃₂ oxidation in these experiments (ca. 0.5 s), and the PCET mechanism dominating at pH > 8 is a rapid pre-equilibrium PT with subsequent ET. Rate-limiting PT, or concerted PCET, to OH^– or buffer species can be excluded (see the Supporting Information, page S8). The observed increase in k_PCET at pH > 8 is due to the increasing equilibrium fraction of tyrosinate (f_YO^–). From the rate constants determined for protonated and deprotonated Y₃₂, we note that the difference in reactivity between the tyrosinate/tyrosine forms of α₃Y and freely solvated phenolate/phenol in aqueous solution is small, within experimental accuracy. With [Ru(bpy)₃]³⁺ as oxidant in both cases, k_YO^–/k_YOH ≈ 5000 (from eqs 1 and 2) for Y₃₂, and the corresponding ratio for phenolate/phenol is k_PhO^–/k_PhOH ≈ 9000.⁶⁴ Even if both rate constants are about 10 times smaller for the protein, the ratios are similar and of the same order of magnitude. ET from Y₃₂ is expected to be slower than ET from phenol due to a greater electron donor–acceptor distance and a lower diffusion rate constant. The near identical k_YO^–/k_YOH and k_PhO^–/k_PhOH ratios suggest that there is no additional kinetic obstacle for proton transfer from Y₃₂, despite its average location of 7.7 ± 0.3 Å inside the protein.

At pH < 7.5, the PCET oxidation of protonated Y₃₂ (k_YOH) is the dominant contribution to k_PCET. A significant kinetic isotope effect (KIE = 2.5 ± 0.5) was observed for PCET rate constants at pH 5.5, from which an ETPT mechanism can be excluded.⁴⁶ With the extended pH dependent data (Figure 3), PTET can also be excluded. The observed pH dependence of k_YOH is much weaker than the factor of 10 per pH unit predicted for a PTET mechanism with OH^–, HPO₄^2–, or PO₄^3– as proton acceptor. Thus, we can now establish that the oxidation of the neutral Y₃₂ in α₃Y by external [Ru(bpy)₃]³⁺ proceeds as a concerted PCET mechanism. Even a concerted PCET with OH^–, HPO₄^2–, or PO₄^3– as primary proton acceptor would have given a 10-fold increase in rate constant per pH unit, following the first-order dependence on the proton acceptor concentration. This prediction seems to exclude those species.

To confirm that no buffer species were directly involved in the reaction, k_PCET for Y₃₂ was measured in pH 6.5 phosphate buffer with concentration ranging from 20 to 460 mM (Figure 4). If phosphate acts as the primary proton acceptor at pH < 7.5, k_PCET is expected to increase with the phosphate concentration in the buffer. At pH 6.5, approximately 17% of the buffer exists in the HPO₄^2– form (H₂PO₄^– pK_a = 7.2), which means that [HPO₄^2–] was varied from 3.3 to 76 mM (20-fold increase). pH 6.5 was chosen for two reasons. First, the Co-oxide formation is slow enough that concentrations of α₃Y could be kept to <500 μM without kinetic interference from the Co-oxide reactions. Second, at pH 6.5, only 0.002% of Y₃₂ is in its deprotonated form, indicating that k_YOH ≫ k_YO^– × 10^pH–pK_a, thus ensuring that PCET from protonated Y₃₂ dominates. The PCET rate constants for Y₃₂ as a function of buffer concentration are compared to PCET rate constants previously reported for a covalently linked ruthenium photosensitizer–tyrosine model complex,³² Ru–Y (chemical structure in Figure S5). PCET rate constants for Ru–Y are given in Figure 4 (black squares); PCET proceeds with an intramolecular ET, and therefore, the rate constants are of first order. Ru–Y exhibits a buffer independent region at low phosphate concentrations (<1 mM) and a region that is first order in phosphate concentrations above 10 mM, indicating that phosphate (HPO₄^2–) acts as the primary proton acceptor only at high enough concentrations of buffer and that water is the primary proton acceptor at low buffer concentrations.³² In contrast, k_PCET in Y₃₂ is clearly independent of [KP_i] even at higher phosphate concentrations (Figure 4, purple circles), showing that phosphate is not the primary proton acceptor in the oxidation of Y₃₂. Thus, the absence of viable proton acceptors nearby Y₃₂ in α₃Y and the exclusion of OH^– and buffer species strongly suggest that water (H₂O) is the primary proton acceptor in the concerted PCET reaction of α₃Y (k_YOH).

Figure 4.

PCET rate constants measured in phosphate buffer. Error bars are shown when the error is larger than the marker. The left y-axis represents first-order rate constants for Ru–Y, and the right y-axis, second-order rate constants for α₃Y. Black squares show data collected for Ru–Y in pH 7 phosphate buffer with a fit to the data using k_obs = k_b + f_b[buffer]k_b³² (dashed black line). Purple circles show data for α₃Y collected in pH 6.5 phosphate buffer with a linear, constant value fit to the data (solid purple line).

From a thermodynamic perspective, HPO₄^2– is a much better proton acceptor than water (H₃O⁺, pK_a = 0 per definition). Despite the thermodynamic advantage of PT to phosphate, the strongly distance dependent PT step requires that the proton acceptor penetrates the protein to get near the Y₃₂ OH group. The finding that buffer does not act as a proton acceptor suggests that the HPO₄^2– or PO₄^3– do not come in close enough contact with Y₃₂. This could be due to their larger size compared to water, as well as their negative charge.

The kinetic data are, however, not completely independent of pH below 7.5 where it deviates from the fit. Having excluded buffer dependence, another possible reason for the pH dependence of k_YOH is that the global surface charge of the protein changes with pH. α₃Y and α₃W have an isoelectric point of ∼8, as shown by isoelectric gel electrophoresis.⁴⁸ As the pH increases, amino acid residues become negatively charged, until the isoelectric point is reached and the protein has an overall neutral charge. For comparison, the oxidation of α₃W was assigned to an ET-limited ETPT mechanism at pH 5.5 and 8.5⁴⁸ where PCET rate constants should be pH independent. PCET rate constants for α₃W increased by a factor of 1.3 between pH 5.5 and 8.5, corresponding to a factor of 1.1 increase per pH unit.⁴⁸ α₃Y and α₃W have the same protein sequence with the exception of site 32 and similar three-helix bundle solution structures.^46,48 The protein surface charge interactions with [Ru(bpy)₃]³⁺ should therefore be nearly identical for α₃Y and α₃W. Inclusion of a 1.1 factor increase per pH unit to the otherwise pH independent term k_YOH only marginally improves the fit of pH dependent PCET rate constants for α₃Y (Figure S4). Thus, the change in electrostatic interaction between α₃Y and [Ru(bpy)₃]³⁺ does not explain the weak pH dependence observed at pH < 7.5. We note that a similarly weak dependence of the concerted PCET reaction for aqueous Ru–Y has been reported,⁴¹ but a theoretical explanation is still lacking.

The weak pH dependence for k_PCET at low pH, where k_YOH dominates, could be due to protein conformational motions. Increasing the pH may favor conformational motions that permit water access to Y₃₂ to a greater extent. Although studying the dependence of protein conformational motions on pH is challenging, MD simulations can provide more general insights into equilibrium conformational motions of the protein and surrounding water. Herein, MD simulations were performed to investigate the possible influence of protein motions on the PCET reactivity of Y₃₂, particularly focusing on water accessibility.

Protein Molecular Dynamics Simulations

The solvent accessibility of Y₃₂ in α₃Y was explored through 1 μs MD simulations. Although the α₃ protein scaffold was designed to sequester Y₃₂,⁴⁴ these simulations show that H₂O can reach the Y₃₂ site through structural fluctuations in nearby side chains. This phenomenon was observed for two different starting structures and two different force fields, suggesting that Y₃₂ is able to briefly hydrogen bond to water. In the solution NMR structure, surrounding nonpolar side chains occlude water access to Y₃₂ (Figure 5A). Using the AMBER ff14SB force field, MD simulations revealed protein conformations in which the side chain of L₁₂ had rotated, forming a small void that transiently allowed water access and hydrogen-bonding interactions with Y₃₂ (Figure 5B). Similar conformations were observed with the CHARMM36 force field and are shown in Figure S7. An additional conformation sampled with the AMBER ff14SB force field, in which Y₃₂ has rotated to face outward, and the hydrophobic side chains have repacked the core, is shown in Figure S8. The prevalence of these transient side chain fluctuations and the associated hydrogen bond between Y₃₂ and water is force field dependent, and thus, the probability of sampling these conformations cannot be established definitively from these simulations.

Figure 5.

Illustration of side chain motions observed in an MD trajectory propagated with the AMBER ff14SB force field. (A) The starting structure from the α₃Y solution NMR structure.⁴⁶ (B) A configuration from the MD trajectory in which two water molecules transiently reside within hydrogen-bonding distance to Y₃₂. The backbone is depicted as tubes, and the residues occluding water access in panel A or bordering the water channel in panel B are depicted as spheres.

The water occupancy around Y₃₂ was analyzed by computing the hydration number around Y₃₂. Here the hydration number is defined as the number of water molecules with the oxygen atom within 3.0 Å of the Y₃₂ hydroxyl oxygen. The average hydration number for Y₃₂ was computed to be 0.49 and 0.35 for Traj. 1 and Traj. 2, respectively. These fractional values of the average hydration number indicate that, in a majority of the sampled protein configurations, Y₃₂ is hydrogen bonded to either no water molecules or one water molecule (Figure 6). Two water molecules were within 3.0 Å of the Y₃₂ hydroxyl group for a small number of configurations (Figure 6). The hydrogen-bonding interaction of the Y₃₂ hydroxyl group with water was analyzed by defining a hydrogen bond according to the criteria of a heavy atom distance less than or equal to 3.0 Å and a donor–hydrogen–acceptor angle greater than or equal to 135°. The percentage of a given trajectory with Y₃₂ forming at least one hydrogen bond to a water molecule was computed to be 38.2 and 27.7% for Traj. 1 and Traj. 2, respectively. The differences between these percentages and the average hydration numbers arise from the configurations with Y₃₂ simultaneously hydrogen bonded to two water molecules. Y₃₂ is also observed to hydrogen bond to the backbone carbonyl oxygen atoms of L₁₂ and L₅₈, the carbonyl of V₉, or the carboxylate of the nearby E₁₃ (Table 1). For a majority of the MD trajectories, these hydrogen bonds within the protein form when Y₃₂ is not hydrogen bonded to water, although simultaneous hydrogen-bonding interactions are possible (Figure S8). The analogous breakdown of hydrogen bonds for the trajectories propagated with the CHARMM36 force field is given in Table S3.

Figure 6.

Histograms of hydration number for MD trajectories propagated with the AMBER ff14SB force field.

Table 1. Hydrogen-Bonding Interactions Involving Y₃₂ for MD Trajectories of α₃Y Propagated with the AMBER ff14SB Force Field.

	V9:O	E13:Oε1,ε2	L58:O	L12:O	WAT:Oa
Traj. 1	54.1%	24.0%	5.12%		38.2%
Traj. 2	39.38%	21.56%	3.98%	3.32%	27.7%

^aThe numbers reported reflect the sum of the hydrogen-bonding interactions with Y₃₂ acting as a H-bond acceptor or donor and can include contributions from multiple water molecules.

For the hydrogen bonds between Y₃₂ and water or E₁₃, the donor–acceptor distance fluctuates and samples shorter distances that would enable proton transfer. Specifically, the MD trajectories propagated with the AMBER ff14SB force field sampled hydrogen bond donor–acceptor distances in the range 2.5–2.75 Å for around 10% of the trajectory, indicating that proton transfer could occur in either case (Figure 7). However, the distributions of distances sampled during the MD trajectories differ between water and E₁₃, with water sampling shorter distances more frequently, as reflected by the percentages in Table 1 and the distributions in Figures 7 and S9.

Figure 7.

Histograms of O–O distances between the hydroxyl oxygen of Y₃₂ and the closest water molecule (A) and the hydroxyl oxygen of Y₃₂ and the closest carboxylate oxygen of E₁₃ (B) for the first MD trajectory (Traj. 1) propagated with the AMBER ff14SB force field.

The hydrogen bonding between Y₃₂ and water is significantly less prevalent for the trajectories propagated with the CHARMM36 force field (Table S3 and Figure S10), most likely due to overstabilization of the compact α-helix. Y₃₂ was observed to be significantly more flexible for the trajectories propagated with the AMBER force field compared to those propagated with the CHARMM force field, as indicated by the Y₃₂ RMSFs given in Table S4. Because of this diminished flexibility, when Y₃₂ is not hydrogen bonded to water, it hydrogen bonds only to the backbone carbonyl oxygen atoms of L₁₂ and L₅₈ for the trajectories propagated with the CHARMM36 force field (Table S3). Despite the quantitative differences observed for the two different force fields, all of the trajectories exhibited the same qualitative trends. In particular, all of the trajectories illustrate that Y₃₂ can become accessible to water through rotations and fluctuations of the surrounding nonpolar side chains.

The interaction between the −OH group of Y₃₂ and the E₁₃ carboxylate group observed with the AMBER ff14SB force field could result in proton transfer to E₁₃, which is deprotonated in the MD simulations. α₃Y may not be structurally well-defined at pH values below the pK_a of E₁₃ (∼4.3) which hinders us from determining rate constants in a pH range where E₁₃ is protonated to rule out this residue as a potential proton acceptor. The E₁₃ interaction has not been sampled with the CHARMM36 force field, which may be due to its overstabilization of helical structures. At present, it is not possible to determine which force field represents the experimental conditions more accurately. Despite these differences between the two force fields, the formation of the water cavity is observed with both of them.

General Discussion

Tyrosine becomes strongly acidic upon oxidation, resulting in a deprotonated neutral radical.¹⁹ The deprotonation mechanism can vary depending on the surroundings. To activate buried Y residues for redox chemistry, enzymes have evolved the placement of an internal proton acceptor within hydrogen-bonding distance. Such an acceptor can act to shuttle the proton back and forth upon redox cycling of the tyrosine (e.g., the Y_Z–histidine and Y_D–histidine pairs in PSII).^11,65 In other cases, proton channels with several acid/base groups connect the PCET reaction with proton transport to or from the bulk solvent. For Y residues close to the protein surface, Brønsted bases in solution, such as water itself, may act as the primary proton acceptor. Water assisted PCET has recently been suggested to facilitate radical transfer between the α and β subunits in E. coli ribonucleotide reductase (RNR).⁶⁶ In RNR, radical transfer occurs reversibly over >32 Å⁶⁷ between a network of Ys where each radical transfer step is likely a concerted PCET mechanism. The radical transfer chain crosses over the α and β subunits of the protein where the distance between the donating and accepting tyrosines is >5 Å. Water is found between the subunits and is believed to aid the radical transfer. There is still much to learn about single water molecules or small water clusters acting as proton acceptors in PCET reactions, and RNR is not the only case reported thus far.⁶⁸

The α₃Y kinetic data and MD simulations presented in this report have shed light on the radical formation process. Y₃₂ is occluded from solvent by nonpolar side chains and residues on average 7.7 ± 0.3 Å below the protein surface. The Y₃₂ pocket is composed of hydrophobic residues that cannot act as proton acceptors. Our MD simulations show that protein fluctuations can transiently form a cavity in the protein that allows water to approach within hydrogen-bonding distance of the Y₃₂ side chain. Within the time scale of our simulations, Y₃₂ interacts with one water molecule at a time, although for a small number of configurations, two water molecules were within 3 Å of the Y₃₂ oxygen. It is likely that such water molecules serve as the primary proton acceptor. In a later step, the proton would then be transferred further to bulk water. The small size of the cavity is likely the reason that phosphate buffer (HPO₄^2–/PO₄^3–) cannot compete as the primary proton acceptor. It should be noted that one of the force fields used in the MD simulations also suggests the possibility of E₁₃ as a potential proton acceptor, which will be further examined in future studies.

Conclusions

The rate constants of Y₃₂^• formation have been determined as a function of pH and buffer concentration. The PCET mechanism is most likely a combination of PTET via Y₃₂^– (dominating at high pH) and concerted PCET (dominating at low pH) with water as the primary proton acceptor across the entire pH range studied. Our results show how the rate constants and PCET mechanism of a buried Y residue can be influenced by the protein environment in combination with the solution pH. The primary proton acceptor is either water or a glutamate (E₁₃) located ≥6.7 Å from Y₃₂ in the NMR structure. Molecular dynamics simulations show that water access to Y₃₂ is facilitated by structural fluctuations of nearby side chains, forming a transient cavity. It should be noted that, while the cavity allowing for water access was seen in all trajectories using two different force fields, the E₁₃ interaction was only seen with one force field (AMBER ff14SB). Local protein fluctuations allow for approach of the primary proton acceptor to form a transient hydrogen bond with Y₃₂. This enables rapid oxidation of Y₃₂ in spite of its location 7.7 ± 0.3 Å from the protein surface.

The α₃X family of proteins strikes a balance between small model systems and enzymes, making it ideal for mechanistic and quantitative PCET studies. The α₃X model proteins are structurally well-defined and exhibit the characteristic cooperative behavior of natural proteins. At the same time, the α₃X proteins provide unambiguous kinetic and thermodynamic details of PCET that are highly challenging and often not possible to obtain from the natural enzyme systems. Our results clearly illustrate the importance of protein conformational motions in mediating PCET. Future PCET studies on the α₃X model system will address how radical formation is affected by modulating the microenvironment of the radical site including solvent exposure and hydrogen-bonding interactions. Such studies can provide key insights into PCET amino acid radical behavior in natural systems.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacs.0c04655.

• Additional TA kinetics, data fitting routines, tabulated rate constants, kinetic derivations, computational details, and additional analysis of MD trajectories (PDF)

The authors declare no competing financial interest.