Abstract
Recent research has advanced infectious disease forecasting from an aspiration to an operational reality. The accuracy of such operational forecasting depends on the quantity and quality of observations available for system optimization. In particular, for forecasting systems that use combined mechanistic model-inference approaches, a broad suite of epidemiological observations could be utilized, if these data were available in near real time. In cases where such data are limited, an in silica, synthetic framework for evaluating the potential benefits of observations on forecasting accuracy can allow researchers and public health officials to more optimally allocate resources for disease surveillance and monitoring. Here, we demonstrate the application of such a framework, using a model-inference system designed to predict dengue, and identify the type and quality of observations that would improve forecasting accuracy.
Keywords: Infectious disease model, Infectious disease forecasting, Vector-borne disease, Disease surveillance data, Dengue, Zika, Mosquito-borne disease
1. Introduction
Both statistical and process-based infectious disease forecasting approaches rely heavily on disease surveillance. Observations of past and present disease activity are used to optimize model systems prior to generating a forecast (Shaman et al., 2013), and this optimization is critical for producing accurate and calibrated predictions. From this vantage, an idealized surveillance system for vector-borne disease would include frequent, high-quality observations of disease dynamics in both the human and vector populations. Measurements would include prevalence and incidence, as well as immune status, in the human population, and vector infection rates, longevity, and abundance for the vector population. However, current vector-borne disease surveillance systems are frequently limited to passive surveillance of human incidence (Beatty et al., 2010). These incomplete observations reduce the accuracy of vector-borne disease forecasting (Yamana et al., 2016).
Traditionally, surveillance of Aedes mosquitoes has consisted primarily of monitoring for the presence of mosquito larvae and pupae inside households (Organization WH., 2003). However, these indicators have not been consistently associated with adult mosquito density or of disease incidence (Chang et al., 2015; Lin and Wen, 2011; Bowman et al., 2014; Sivagnaname and Gunasekaran, 2012; Focks, 2004). In a recent systematic review, Bowman et al. (2014) found only four studies reporting positive correlations between larval and adult Aedes indices and dengue transmission. More recently, measures of adult vector abundance and infection rates have been incorporated into disease surveillance systems and used to improve understanding of the spatiotemporal risk of disease transmission (Fournet et al., 2018; Medeiros et al., 2018; Peña-García et al., 2016; da Cruz Ferreira et al., 2017; Wu et al., 2016). Several studies have incorporated mosquito surveillance data into early warning or forecast systems for disease outbreaks (Sanchez et al., 2006; DeFelice et al., 2017; Shi et al., 2015; Kilpatrick and Pape, 2013; Davis et al., 2017; Hu et al., 2006). However, few have sought to quantify the value of surveillance data in predicting future disease risk. Kilpatrick and Pape (2013) quantified the value of mosquito abundance and infection rates at different temporal and spatial scales as predictors in regression models of West Nile Virus. Davis et al. (2017) used environmental predictors along with mosquito infection rates to forecast West Nile Virus and noted an improvement in forecast once mosquito data became available, but did not compare forecasts with and without these data.
Another type of relevant data that may soon become more widely available is the susceptibility of a population to a given disease. The transmission dynamics of vector-borne diseases are known to be shaped in part by a population’s previous exposure to the pathogen (Reich et al., 2013; Yamana et al., 2017; Barbazan et al., 2002; Endy et al., 2002; Laneri et al., 2015). Currently, such information for vector-borne disease has generally been limited to seroprevalence surveys conducted at isolated research sites (Endy et al., 2010). However, with the rapid improvement and availability of diagnostic tests, such testing may soon become feasible (Auerswald et al., 2019; Emmerich et al., 2013). For example, a recent study suggested that routine seroprevalence surveys could be implemented in a network of major cities across Brazil to improve dengue forecasting capabilities (Lowe et al., 2016).
The value of incorporating additional observations into a model-inference forecast system can be explicitly assessed using a synthetic testing framework. This strategy assumes perfect knowledge of the modeled system, which is considered to be the “truth”. Synthetic observations are then drawn from this “truth” and assimilated by the model-filter system in order to optimize the model and predict future incidence (i.e. the future truth).
In numerical weather prediction and related fields, there is a large body of work built around the framework of synthetic testing of observations (e.g., Zhang et al., 2006; Zhang et al., 2004; Arnold and Dey, 1986; Kuo et al., 1985; Atlas, 1997). Carefully designed experiments, sometimes referred to as Observing System Simulation Experiments (OSSE), have allowed researchers and government agencies to evaluate the effects of proposed observation systems on weather predictions. Such experiments are critical for motivating and justifying the deployment of costly new observation platforms such as satellite-mounted temperature sounders (Arnold and Dey, 1986).
Here, we apply a synthetic testing framework to an infectious disease system and explore the effects of data availability and quality on vector-borne disease forecast accuracy using a process-based model. Specifically, we compared forecast accuracy for different levels of data uncertainty, and quantified the changes in accuracy when simulated vector surveillance data were additionally assimilated into a model-inference forecasting system. We also examined the effects of reducing uncertainty in the prior distribution of human susceptibility. Finally, we tested whether reducing uncertainty of some model parameters affects forecasting accuracy. The described synthetic testing approach can be used to inform decision-making when designing or adjusting disease surveillance systems.
2. Methods
2.1. Disease transmission model
In this study, we use a Susceptible-Exposed-Infectious-Recovered (SEIR) model structure for the human population, coupled with a Susceptible-Exposed-Infectious (SEI) model structure for the vector population (Supplemental Fig. 1). Adaptations of this model form have been used to simulate a number of mosquito-borne diseases, including dengue (Manore et al., 2014), Zika (Manore et al., 2017; Kucharski et al., 2016), Chikungunya (Manore et al., 2014; Manore et al., 2017), and Malaria (Chitnis et al., 2006). Here, we use the model to simulate dengue fever, transmitted by Aedes mosquitoes.
The model equations are as follows:
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
SH, EH, IH, RH and NH refer to the number of susceptible, exposed, infectious, recovered, and total humans, respectively. SM, EM and IM are the proportion of the mosquito population that are susceptible, exposed or infectious, respectively. The model parameters are defined in Table 1. The model is run deterministically.
Table 1.
Model parameters and state variables.
| Parameter / State variable | Units | Distribution of initial values | |
|---|---|---|---|
|
| |||
| α M | 1 / Extrinsic incubation period | days−1 | Uniform [1/14,1/7] |
| α H | 1 / Intrinsic incubation period | days−1 | Uniform [1/7,1/4] |
| γ | 1 / Human infectious period | days−1 | Uniform [1/12,1/4] |
| ϕ | Mosquito death rate | days−1 | Uniform [1/30,1/3] |
| BH | Mosquito to human transmission rate | - | Uniform [0,5] |
| BM | Human to mosquito transmission rate | - | Uniform [0,1] |
| P | Fraction of human infections reported | - | Uniform [0,1] |
| SH | Number of susceptible humans | Humans | Uniform [0, .95*N] |
| EH | Number of exposed humans | Humans | 0 |
| IH | Number of infectious humans | Humans | Exponential [mean = 5] |
| RH | Number of recovered humans | Humans | NH -SH - EH - IH |
| SM | Proportion of mosquitoes that are susceptible | - | 1 |
| EM | Proportion of mosquitoes that are exposed | - | 0 |
| IM | Proportion of mosquitoes that are infectious | - | 0 |
Observed human incidence is given by the number of newly infected humans, EH, times the fraction of infections reported, p:
| (8) |
2.2. Ensemble adjustment Kalman Filter (EAKF)
The above model of disease transmission was coupled with the EAKF, a data assimilation method (Anderson, 2001) that uses observations to iteratively optimize model parameters and state variables over the course of a disease outbreak in a prediction-update cycle. Here, the model-filter system employs an ensemble of 300 simulation replicates with parameters and state variables randomly initialized using values drawn from the prior distributions indicated in Table 1. The prediction step uses the dengue transmission model to propagate each ensemble member forward in time until one or more observations are available. In the update step, the EAKF algorithm (see Anderson, 2001 for full algorithm details) uses Bayes’ rule to assimilate new observations by adjusting the ensemble members such that their mean and variance match the posterior mean and variance, given a prescribed observational error variance. This error is a function of the magnitude of disease incidence, as described below in Eq. (9).
Following each update step, the model-filter system is integrated through time to the next observation and the update is repeated. A forecast is generated when the ensemble of updated parameter and state variable estimates—the posterior—is propagated forward through the remainder of the season without further updating, thus producing an ensemble of future disease incidence trajectories. The central idea is that the ensemble of simulations, having been iteratively optimized with observations during the prior weeks is better aligned to generate a credible forecast of future incidence. Here, the trajectories are used to provide forecasts of the following target metrics:
The timing of the outbreak peak (peak week)
Peak observed incidence
Total observed incidence
Number of cases reported in the next 1 through 4 weeks
2.3. Experimental setup
We used the disease transmission model to generate 20 disease outbreaks of varying magnitudes and 1-year duration (Supplemental Fig. 2). Each of these model realizations provides a time series of ‘true’ values for all parameters and state variables at each time-step. We then used the synthetic truths to generate observations by adding noise to the true values of the observed variables; observations were drawn from a normal distribution with mean equal to the synthetic truth and variance as described below. We used a model time-step of one day, and the sampling resolution of observations was set to every seven days.
We modeled observational error variance as a function of the magnitude of disease incidence, using the formula (Shaman and Karspeck, 2012):
| (9) |
Where Xj represents the observation at time j (ObsH for the number of infected humans and IM for the fraction of infectious mosquitoes), a represents a constant baseline noise, and the fractional component represents a magnitude-dependent error. We set the values of a and b to 1000 and 5, respectively, for observations of ObsH. Observations of IM used values of 10−5 and 5, respectively, for a and b. Adjusting for modeled population size, a represents a standard deviation of one order of magnitude higher for mosquito observations compared to human observations, reflecting greater uncertainty in mosquito observations. Model sensitivity to these parameter settings was tested by altering the values a and b (see below).
For each synthetic truth, we generated ten time series of observations by taking ten random draws around the truth (Fig. 1). We then used the model-filter system to estimate parameters and forecast outbreak characteristics for each set of ‘synthetic’ observations. The data assimilation process was repeated ten times for each set of observations, each time using a new set of initial conditions for the ensemble members and producing 51 weekly forecasts. For each weekly forecast, the EAKF was sequentially applied to observations from week 1 through k, and then the optimized model was used to forecast the remainder of the year from weeks k+1 through 52. The result was 100 sets of parameter estimates and forecasts for each synthetic truth. When comparing the performance of the model-filter system, the primary measure of accuracy for each test case is the mean absolute error (MAE) of the seven forecast targets (peak week, peak incidence, total incidence, and 1through 4-week ahead incidence) over all 2000 simulations (20 truths × 100 sets of forecasts per truth) and 51 weeks of forecasts. We also compared mean absolute relative error (MARE) for peak incidence and total incidence, to account for differences in outbreak intensity.
Fig. 1. Box plots of high, medium and low variance observations of human incidence for one synthetic truth.
The modeled “truth” is shown in pink. The observations drawn from this “truth” fall within the range denoted by the box and whiskers; the boxes indicate 25th and 75th percentile values, the dashed whiskers extend to the most extreme observations, apart from outliers, which are shown as red crosses. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article).
In addition to analyzing mean errors, we ranked the accuracy of the forecasts and posterior estimates at each forecasting week and compared the accuracy of the mean rankings. We performed the Friedman test followed by a Nemenyi test to assess statistically significant differences between mean forecast rankings. The Friedman test is a nonparametric test of differences in the ranking of each trial that assesses whether any of the trial conditions consistently outperformed the other conditions. The Nemenyi test is a post-hoc assessment of statistically significant differences in rankings between each pair of trial conditions.
2.3.1. Quality of observations
We investigated the effect of data quality by varying the magnitude of error added to the truth when generating synthetic observations. This was achieved by altering parameters a and b in Eq. (9). We tested three values of b for synthetic observations of ObsH: 5, 10 and 20 (Fig. 1). For synthetic observations of IM, we compared a low-variance case with a = 10−6 and b = 20, and a high-variance case with a= 10−5 and b= 5.
2.3.2. Number of observational data streams
Dengue surveillance systems generally measure disease incidence in humans; however, mosquito surveillance can provide information about the circulating virus. We investigated the effect of assimilating observations of mosquito infection rates by comparing forecasts in which the model-filter system incorporates observations of human incidence, ObsH alone, to forecasts using observations of IM in addition to ObsH.
To incorporate observations of IM, the update step of the EAKF is performed twice in order to sequentially adjust the ensemble in response to the two observed variables. Observational noise is set to the default parameters for a and b (listed above).
2.3.3. Initial susceptibility
The proportion of a population that is susceptible to a disease at the beginning of an outbreak plays an important role in shaping disease transmission dynamics. We tested whether knowledge of population susceptibility prior to an outbreak would improve model performance. This was achieved by altering the prior distribution of human susceptibility used to initialize the model-filter system. We first tested a naïve case, allowing susceptibility to range from 0 to 95% of the total population. We then constrained initial susceptibility by restricting the prior distribution to a certain percentage around the initial value of the synthetic truth. We tested 4 levels of restriction, representing varying quality estimates of population susceptibility: 50%, 25% and 10% of the full range, centered around the truth, and a fourth case where each ensemble member was initialized with the true value of initial susceptibility. These simulations used two observational data streams (ObsH and IM).
2.3.4. Prior distribution of parameters
We tested the effect of narrowing the prior distributions for each of the model parameters. For each of the parameters, we conducted a set of simulations where the prior distribution for that parameter was restricted to 25% of the full range listed in Table 1, centered around the true value used to the generate the synthetic outbreak being modelled.
3. Results
3.1. Quality of observations
Forecast error decreased as the observational error for human incidence decreased (Table 2). Pairwise differences in forecast rankings were statistically significant (p < 0.001), with the exception of Hhigh vs Hlow in forecasts of human incidence 3- and 4-weeks ahead (Supplemental File 1). Forecast MAE and MARE decreased with observational error of mosquito incidence for all metrics except total incidence (Table 2). However, mean forecast rankings of peak incidence and incidence 4-weeks ahead were not significantly different between high and low mosquito observational error (Table 3). Forecast rankings followed a consistent pattern, with high-variability observations leading to the worst rankings and low-variability observations leading to best rankings (Fig. 2).
Table 2. Forecast MAE for Test Cases comparing quality of observations and number of observational streams.
Mean absolute relative error is shown in parentheses for Peak Incidence and Total Incidence. X1 through X4 indicate forecasts of incidence 1 through 4 weeks into the future. Hhigh,Hmedium and Hlow are test cases using only observations of human incidence, with high, medium and low error, respectively. Hhigh,Mhigh and Hhigh,Mlow are test cases using high-variance observations of human incidence along with high and low variance observations of mosquito infection rates, respectively.
| Test case | Peak week | Peak Incidence | Total Incidence | X1 | X2 | X3 | X4 |
|---|---|---|---|---|---|---|---|
|
| |||||||
| Hhigh | 3.7 | 5959 (.48) | 43187 (0.40) | 1424 | 1997 | 2605 | 3062 |
| Hmedium | 3.6 | 5229 (.44) | 37969 (0.36) | 1252 | 1845 | 2483 | 2973 |
| Hlow | 3.5 | 4699 (.41) | 35748 (0.34) | 1129 | 1735 | 2400 | 2919 |
| Hhigh,Mhigh | 3.3 | 5166 (.46) | 40588 (0.39) | 1049 | 1594 | 2263 | 2844 |
| Hhigh,Mlow | 2.9 | 4880 (.43) | 41686 (0.39) | 845 | 1300 | 1961 | 2623 |
Table 3. Mean Freidman ranking of forecast metrics for test cases comparing quality of observations and number of observational streams.
Values in bold font indicate the top-ranking test case for each forecast metric. More than one top ranking test case is possible if ranks are not significantly different. See Supplemental File 1 for pairwise p-values of Friedman ranks.
| Test case | Peak week | Peak Incidence | Total Incidence | X1 | X2 | X3 | X4 |
|---|---|---|---|---|---|---|---|
|
| |||||||
| HHigh | 3.61 | 3.19 | 3.01 | 3.01 | 3.01 | 3.00 | 3.01 |
| Hmedium | 3.32 | 3.09 | 3.06 | 3.06 | 3.08 | 3.04 | 3.05 |
| Hlow | 2.91 | 2.95 | 2.97 | 2.96 | 2.96 | 2.99 | 3.00 |
| Hhigh,Mhigh | 2.60 | 2.88 | 2.97 | 2.99 | 2.98 | 3.00 | 2.97 |
| Hhigh,Mlow | 2.56 | 2.89 | 3.00 | 2.98 | 2.97 | 2.97 | 2.97 |
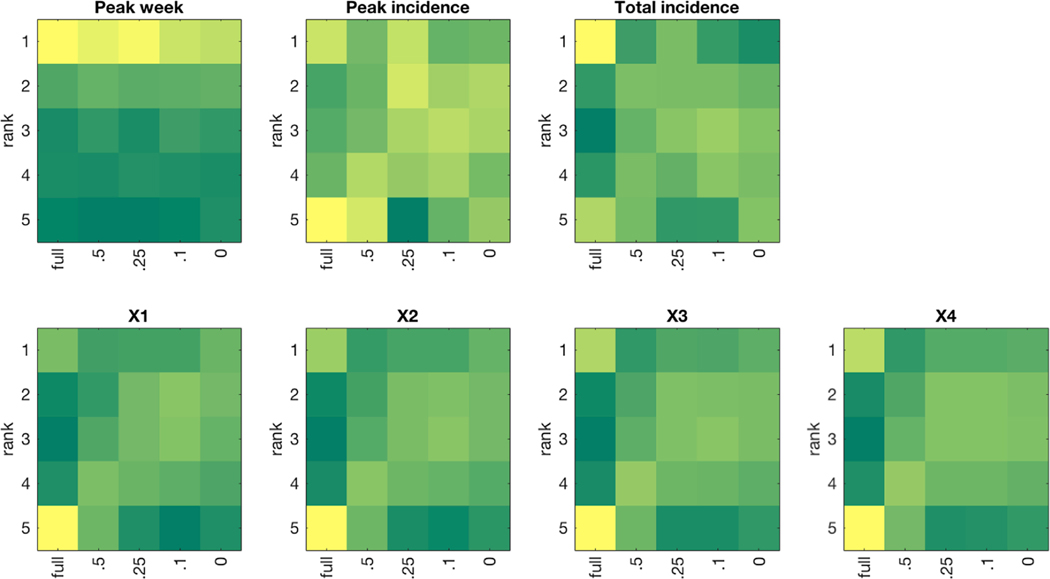
Fig. 2. Heatmap of forecast ranking for each target metric when varying the quality of observations and number of observational streams.
Dark green indicates a small number of forecasts whereas dark yellow indicates a large number of forecasts. Tied ranks were assigned the minimum rank value. On the x-axis, H refers to human observations and M refers to mosquito observations. The subscripts H, M, and L refer to high, medium, and low variance, respectively.
3.2. Number of observational data streams
Forecast MAE and MARE decreased for all targets when the model-filter system incorporated observations of mosquito infection rates in addition to high-variability observations of human incidence (Table 2). The addition of mosquito observations consistently produced better ranking forecasts (Fig. 2), which in turn led to significant improvement in mean rankings for most forecast metrics (Table 3; Supplemental File 1). For the levels of observational error we tested, we observed a larger improvement in peak week and 1- through 4- week ahead forecast accuracy from adding mosquito observations than from decreasing the error of human observations (Table 2). The same was true for the mean ranking of peak week, peak incidence and 4-week ahead forecasts; for the other metrics, incorporating mosquito observations and improving human incidence observations led to similar mean rankings, i.e. not statistically significant different (Table 3).
3.3. Initial susceptibility
Constraint of the range of initial human susceptibility increased forecast MAE for all metrics except peak incidence (Table 4). However, constraint of initial susceptibility to 25% of the full range provided a small advantage in Friedman rankings for all forecast metrics except total incidence (Table 5); initial ranges lower than 25% did not provide additional improvement. Conversely, the 0% range test case had the largest MAE in 1- through 4- week ahead forecasts, despite being tied for the best mean rankings.
Table 4. Forecast MAE for test cases varying initial human susceptibility.
Mean absolute relative error is shown in parentheses for Peak Incidence and Total Incidence. ×X1 through X4 indicate forecasts of incidence 1 through 4 weeks into the future.
| Range of initial human susceptibility | Peak week | Peak incidence | Total incidence | X1 | X2 | X3 | X4 |
|---|---|---|---|---|---|---|---|
|
| |||||||
| full range (control) | 3.3 | 5171 (.45) | 39288 (.38) | 1040 | 1578 | 2262 | 2868 |
| 0.5 | 3.4 | 5162 (.40) | 45969 (.37) | 1166 | 1741 | 2411 | 2994 |
| 0.25 | 3.4 | 4810 (.38) | 42559 (.36) | 1106 | 1686 | 2358 | 2929 |
| 0.1 | 3.5 | 4953 (.38) | 43694 (.36) | 1171 | 1782 | 2476 | 3046 |
| 0 | 3.5 | 5108 (.39) | 45468 (.37) | 1210 | 1822 | 2516 | 3092 |
Table 5. Mean Freidman ranking of forecast metrics for test cases varying initial human susceptibility.
Values in bold font indicate the top-ranking test case for each forecast metric. More than one top ranking test case is possible if ranks are not significantly different. Asterisks indicate mean rankings that are statistically significant improvements over the control case.
| Test case | Peak week | Peak Incidence | Total Incidence | X1 | X2 | X3 | X4 |
|---|---|---|---|---|---|---|---|
|
| |||||||
| full range (control) | 2.34 | 3.05 | 2.93 | 3.09 | 3.07 | 3.07 | 3.07 |
| 0.5 | 2.34 | 3.09 | 3.04 | 3.05* | 3.06 | 3.08 | 3.09 |
| 0.25 | 2.33* | 2.85* | 2.93 | 2.97* | 2.96* | 2.95* | 2.94* |
| 0.1 | 2.46 | 3.00* | 3.00 | 2.94* | 2.95* | 2.95* | 2.94* |
| 0 | 2.53 | 3.01* | 3.09 | 2.94* | 2.95* | 2.95* | 2.95* |
The discrepancy between MAE and ranking is explained in Fig. 3 and Supplemental Fig. 3, which show that while forecasts using the full range of initial susceptibility frequently produced the best-ranking forecast, they also had many of the worst ranking forecasts. Providing a narrower initial prior for susceptibility at 25% of the full range (or less than 25%, for the 1- through 4-week ahead metrics) produced more conservative, mid-ranking forecasts and an overall advantage in mean rankings. These contrasting findings indicate that while constraint of initial susceptibility increased forecast MAE on average, it led to greater consistency in forecast quality.
Fig. 3. Heatmap of forecast ranking for each target metric when varying initial human susceptibility.
Dark green indicates a small number of forecasts whereas dark yellow indicates a large number of forecasts. Tied ranks were assigned the minimum rank value.
3.4. Prior distribution of parameters
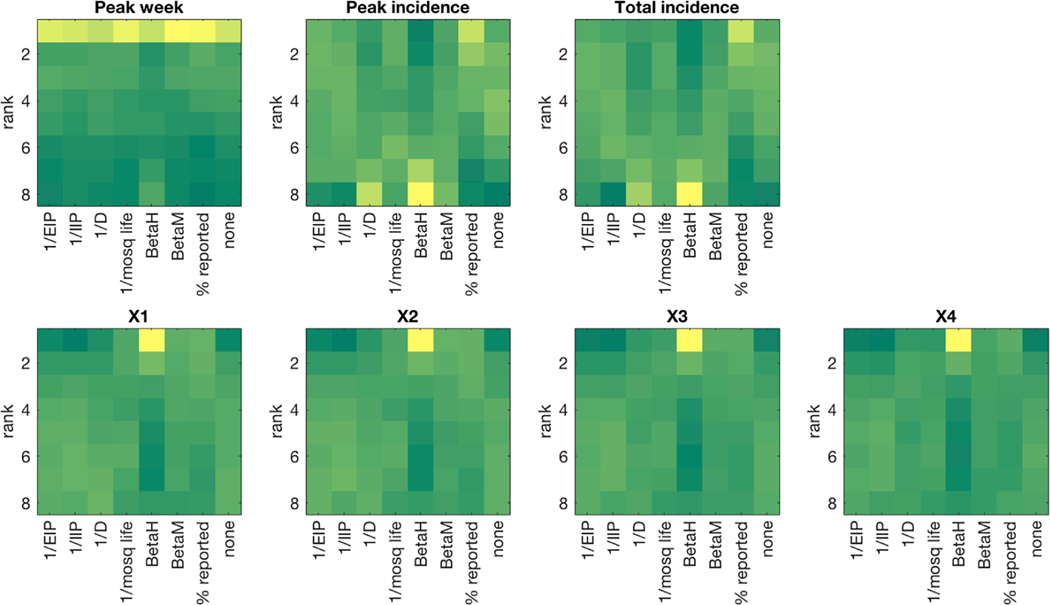
The effect of narrowing the prior distribution of model parameters varied by target metric and parameter (Tables 6 and 7). Narrowing prior estimates of p, the percentage of infectious cases reported led to decreased MAE and MARE in all forecast metrics (Table 6), and the top Friedman ranking for the seasonal forecast metrics (Table 7). Forecasts of peak week were also slightly but significantly improved by constraining αM, φ and BM. Forecasts of peak and total incidence were degraded when parameters other than p were constrained. Forecasts of one- to four-week ahead incidence were improved by narrower prior estimates for all parameters except αM and αH (Table 7). Constraining BH led to con-flicting results; this trial had the highest MAE and MARE for all metrics (Table 6) and the worst mean ranking for seasonal forecast metrics, but had the best ranking for 1- to 4-week ahead incidence (Table 7). The 1- to 4-week ahead forecasts from this trial were most frequently the best-ranking forecast (Fig. 4), but were also prone to large errors.
Table 6. Forecast MAE for test cases with narrowed prior distribution of parameters.
Mean absolute relative error is shown in parentheses for Peak Incidence and Total Incidence.
| Parameterbeingconstrained | Peak week | Peak Incidence | Total Incidence | X1 | X2 | X3 | X4 |
|---|---|---|---|---|---|---|---|
|
| |||||||
| None (control) | 3.3 | 5171 (.45) | 39288 (.38) | 1040 | 1578 | 2262 | 2868 |
| αM | 3.2 | 5184 (.46) | 39420 (.38) | 1051 | 1592 | 2256 | 2829 |
| αH | 3.3 | 5241 (.46) | 39776 (.39) | 1051 | 1605 | 2291 | 2877 |
| γ | 3.4 | 6091 (.46) | 43308 (.40) | 1125 | 1590 | 2170 | 2662 |
| ϕ | 3.3 | 5522 (.48) | 41493 (.41) | 1028 | 1472 | 2032 | 2577 |
| BH | 3.7 | 6361 (.55) | 46920 (.41) | 1294 | 1926 | 2640 | 3177 |
| BM | 3.3 | 5555 (.45) | 41538 (.40) | 1005 | 1481 | 2100 | 2678 |
| p | 3.1 | 4635 (.37) | 34465 (.31) | 970 | 1475 | 2154 | 2785 |
Table 7. Mean Freidman ranking of forecast metrics for test cases with narrowed prior distribution of parameters.
Values in bold font indicate the top-ranking test case for each forecast metric. More than one top ranking test case is possible if ranks are not significantly different. Asterisks indicate mean rankings that are statistically significant improvements over the control case.
| Parameter being constrained | Peak week | Peak Incidence | Total Incidence | X1 | X2 | X3 | X4 |
|---|---|---|---|---|---|---|---|
|
| |||||||
| None (control) | 3.43 | 4.25 | 4.23 | 4.63 | 4.65 | 4.68 | 4.70 |
| αM | 3.31* | 4.33 | 4.35 | 4.64 | 4.67 | 4.69 | 4.71 |
| αH | 3.50 | 4.37 | 4.33 | 4.67 | 4.69 | 4.71 | 4.72 |
| γ | 3.55 | 4.83 | 4.85 | 4.65 | 4.60* | 4.55* | 4.51* |
| ϕ | 3.31* | 4.50 | 4.54 | 4.49 | 4.48* | 4.50* | 4.52* |
| BH | 4.06 | 5.14 | 5.21 | 4.12* | 4.10* | 4.04* | 3.96* |
| BM | 3.26* | 4.61 | 4.59 | 4.43* | 4.42* | 4.43* | 4.45* |
| p | 3.07* | 3.98* | 3.89* | 4.38* | 4.38* | 4.40* | 4.43* |
Fig. 4. Heatmap of forecast ranking for each target metric for test cases with narrowed prior distribution of parameters.
Dark green indicates a small number of forecasts while dark yellow indicates a large number of forecasts. Tied ranks were assigned the minimum rank value.
4. Discussion and conclusion
The approach presented here demonstrates how a model-inference forecasting framework can be used to draw conclusions regarding the benefits of acquiring specific types of information. Policy makers designing a disease surveillance system or considering whether to improve existing systems can test the expected impact of each type of data on forecasting accuracy, thus facilitating an informed assessment of the costs and benefits of the proposed sample.
In this idealized setting, we have shown that improvements in observational data streams can improve the ability to forecast infectious disease outbreaks. While the magnitudes of observed effects are dependent on the specifics of the observations being tested, we demonstrate the following general effects:
Forecasts improve as observational error decreases.
Inclusion of observations of vector infection rates provided a large improvement in predictive accuracy over human observations alone.
Reducing uncertainty in model parameter values can improve forecast skill, particularly for 1- to 4-week ahead targets.
Obtaining a more accurate estimate of the percentage of human cases reported presents an opportunity to make large gains in forecast accuracy.
Interestingly, reducing uncertainty in initial human population susceptibility did not clearly improve forecast accuracy. This may indicate that the model-filter system performed better when individual ensemble members were allowed to sample from a broader state-space. A similar effect was noted by our group during forecast of the 2014 West African Ebola outbreak (not published). Likewise, Lauer et al. (2018) found that estimated susceptibility was not selected for inclusion in a statistical forecasting model of Dengue hemorrhagic fever in Thailand. As the sampling required to establish population susceptibility would be quite expensive, this finding suggests that for current forecasting systems, such efforts may be unwarranted.
While we found that the inclusion of vector infection rates led to improvements in forecast accuracy, we note that there are many logistical and political challenges in establishing an effective vector surveillance system, as recently reviewed in Fournet et al. (Fournet et al., 2018). In quantifying the improvements that could be gained by such data, policy makers can better assess whether the benefits outweigh these challenges.
The study has some limitations. We assume the model provides a perfect representation of disease transmission dynamics; clearly, this assumption is flawed, as the model, which greatly simplifies disease transmission dynamics, is highly mis-specified. For instance, we neglect the effects of seasonality, the interactions between dengue serotypes, and heterogeneous mixing of model populations. The dynamics of vector-borne disease transmission can vary widely depending on the disease in question, as well as local factors such as climate and disease endemicity. For example, in some locations, a rainfall or temperature driven model would be more appropriate than the form we have used here. We therefore do not generalize our conclusions for all locations or diseases. This analysis presents a simple framework for determining the relative value of different types of information in a disease forecasting system. In practice, operational use of this approach would leverage actual observations of human incidence and vector surveillance. The framework can also be adapted to other, more sophisticated disease systems and forecasting models of disease transmission.
Supplementary Material
Acknowledgments
Funding
The research is supported by grant nos. GM110748 and ES009089 from the US National Institutes of Health, and contract HDTRA1–15-C-0018 from the Defense Threat Reduction Agency of the US Department of Defense. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
Footnotes
Declaration of Competing Interest
J.S. and Columbia University declare partial ownership of SK Analytics. T.Y consulted for SK Analytics.
Appendix A. Supplementary data
Supplementary material related to this article can be found, in the online version, at doi:https://doi.org/10.1016/j.epidem.2019.100359.
References
- Anderson JL, 2001. An ensemble adjustment Kalman filter for data assimilation. Mon. Weather. Rev 129 (12), 2884–2903. [Google Scholar]
- Arnold CP Jr, Dey CH, 1986. Observing-systems simulation experiments: past, present, and future. Bull. Am. Meteorol. Soc 67 (6), 687–695. [Google Scholar]
- Atlas R, 1997. Atmospheric observations and experiments to assess their usefulness in data assimilation (gtSpecial IssueltData assimilation in Meteology and oceanography: theory and practice). J. Meteorol. Soc. Jpn 75 (1B), 111–130. [Google Scholar]
- Auerswald H, Klepsch L, Schreiber S, Hülsemann J, Franzke K, Kann S, et al. , 2019. The dengue ED3 dot assay, a novel serological test for the detection of denguevirus type-specific antibodies and its application in a retrospective seroprevalence study. Viruses. 11 (4), 304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barbazan P, Yoksan S, Gonzalez J-P, 2002. Dengue hemorrhagic fever epidemiology in Thailand: description and forecasting of epidemics. Microbes Infect. 4 (7), 699–705. [DOI] [PubMed] [Google Scholar]
- Beatty ME, Stone A, Fitzsimons DW, Hanna JN, Lam SK, Vong S, et al. , 2010. Best practices in dengue surveillance: a report from the Asia-Pacific and Americas Dengue Prevention Boards. PLoS Negl. Trop. Dis 4 (11), e890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bowman LR, Runge-Ranzinger S, McCall P, 2014. Assessing the relationship between vector indices and dengue transmission: a systematic review of the evidence. PLoS Negl. Trop. Dis 8 (5), e2848. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang F-S, Tseng Y-T, Hsu P-S, Chen C-D, Lian I-B, Chao D-Y, 2015. Re-assess vector indices threshold as an early warning tool for predicting dengue epidemic in a dengue non-endemic country. PLoS Negl. Trop. Dis 9 (9), e0004043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chitnis N, Cushing JM, Hyman J, 2006. Bifurcation analysis of a mathematical model for malaria transmission. SIAM J. Appl. Math 67 (1), 24–45. [Google Scholar]
- da Cruz Ferreira DA, Degener CM, de Almeida Marques-Toledo C, Bendati MM, Fetzer LO, Teixeira CP, et al. , 2017. Meteorological variables and mosquito monitoring are good predictors for infestation trends of Aedes aegypti, the vector of dengue, chikungunya and Zika. Parasit. Vectors 10 (1), 78. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davis JK, Vincent G, Hildreth MB, Kightlinger L, Carlson C, Wimberly MC, 2017. Integrating environmental monitoring and mosquito surveillance to predict vector-borne disease: prospective forecasts of a west nile virus outbreak. PLoS Curr. 10.1371/currents.outbreaks.90e80717c4e67e1a830f17feeaaf85de9:ecurrents.outbreaks.90e80717c4e67e1a830f17feeaaf85de. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeFelice NB, Little E, Campbell SR, Shaman J, 2017. Ensemble forecast of human West Nile virus cases and mosquito infection rates. Nat. Commun. 8, 14592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Emmerich P, Mika A, Schmitz H, 2013. Detection of serotype-specific antibodies to the four dengue viruses using an immune complex binding (ICB) ELISA. PLoS Negl. Trop. Dis 7 (12), e2580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Endy TP, Nisalak A, Chunsuttiwat S, Libraty DH, Green S, Rothman AL, et al. , 2002. Spatial and temporal circulation of dengue virus serotypes: a prospective study of primary school children in Kamphaeng Phet, Thailand. Am. J. Epidemiol 156 (1), 52–59. [DOI] [PubMed] [Google Scholar]
- Endy TP, Yoon I-K, Mammen MP, 2010. Prospective cohort studies of dengue viral transmission and severity of disease. In: Rothman AL (Ed.), Dengue Virus. Springer Berlin Heidelberg, Berlin, Heidelberg, pp. 1–13. [DOI] [PubMed] [Google Scholar]
- Focks DA, 2004. A Review of Entomological Sampling Methods and Indicators for Dengue Vectors. World Health Organization, Geneva. [Google Scholar]
- Fournet F, Jourdain F, Bonnet E, Degroote S, Ridde V, 2018. Effective surveillance systems for vector-borne diseases in urban settings and translation of the data into action: a scoping review. Infect. Dis. Poverty 7 (1). 10.1186/s40249018-0473-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu W, Tong S, Mengersen K, Oldenburg B, 2006. Rainfall, mosquito density and the transmission of Ross River virus: a time-series forecasting model. Ecol. Modell. 196 (3–4), 505–514. [Google Scholar]
- Kilpatrick AM, Pape WJ, 2013. Predicting human West Nile virus infections with mosquito surveillance data. Am. J. Epidemiol. 178 (5), 829–835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kucharski AJ, Funk S, Eggo RM, Mallet H-P, Edmunds WJ, Nilles EJ, 2016. Transmission dynamics of Zika virus in island populations: a modelling analysis of the 2013–14 French Polynesia outbreak. . PLoS neglected tropical diseases 10 (5), e0004726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuo Y-H, Skumanich M, Haagenson PL, Chang JS, 1985. The accuracy of trajectory models as revealed by the observing system simulation experiments. Mon. Weather. Rev 113 (11), 1852–1867. [Google Scholar]
- Laneri K, Paul RE, Tall A, Faye J, Diene-Sarr F, Sokhna C, et al. , 2015. Dynamical malaria models reveal how immunity buffers effect of climate variability. Proc. Natl. Acad. Sci 112 (28), 8786–8791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lauer SA, Sakrejda K, Ray EL, Keegan LT, Bi Q, Suangtho P, et al. , 2018. Prospective forecasts of annual dengue hemorrhagic fever incidence in Thailand, 2010–2014. Proc. Natl. Acad. Sci 115 (10), E2175–E2182. 10.1073/pnas.1714457115 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin C-H, Wen T-H, 2011. Using geographically weighted regression (GWR) to explore spatial varying relationships of immature mosquitoes and human densities with the incidence of dengue. Int. J. Environ. Res. Public Health 8 (7), 2798–2815. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lowe R, Coelho CA, Barcellos C, Carvalho MS, Catao RDC, Coelho GE, et al. , 2016. Evaluating probabilistic dengue risk forecasts from a prototype early warning system for Brazil. Elife. 5, e11285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manore CA, Hickmann KS, Xu S, Wearing HJ, Hyman JM, 2014. Comparing dengue and chikungunya emergence and endemic transmission in A. Aegypti and A. Albopictus. J. Theor. Biol. 356, 174–191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manore CA, Ostfeld RS, Agusto FB, Gaff H, LaDeau SL, 2017. Defining the risk of Zika and chikungunya virus transmission in human population centers of the eastern United States. PLoS Negl. Trop. Dis. 11 (1), e0005255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Medeiros AS, Costa DM, Branco MS, Sousa DM, Monteiro JD, Galvão SP, et al. , 2018. Dengue virus in Aedes aegypti and Aedes albopictus in urban areas in the state of Rio Grande do Norte, Brazil: Importance of virological and entomological surveillance. PLoS One 13 (3), e0194108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Organization WH, 2003. Guidelines for Dengue Surveillance and Mosquito Control. WHO Regional Office for the Western Pacific, Manila. [Google Scholar]
- Peña-García V, Triana-Chávez O, Mejía-Jaramillo A, Díaz F, Gómez-Palacio A, Arboleda-Sánchez S, 2016. Infection rates by dengue virus in mosquitoes and the influence of temperature may Be related to different endemicity patterns in three colombian cities. Int. J. Environ. Res. Public Health 13 (7), 734. 10.3390/ijerph13070734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reich NG, Shrestha S, King AA, Rohani P, Lessler J, Kalayanarooj S, et al. , 2013. Interactions between serotypes of dengue highlight epidemiological impact of cross-immunity. Journal of the Royal Society, Interface / the Royal Society 10 (86), 20130414. 10.1098/rsif.2013.0414. Epub 2013/07/05. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanchez L, Vanlerberghe V, Alfonso L, del Carmen Marquetti M, Guzman MG, Bisset J, et al. , 2006. Aedes aegypti larval indices and risk for dengue epidemics. Emerging Infect. Dis. 12 (5), 800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shaman J, Karspeck A, 2012. Forecasting seasonal outbreaks of influenza. Proc. Natl. Acad. Sci 109 (50), 20425–20430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shaman J, Karspeck A, Yang W, Tamerius J, Lipsitch M, 2013. Real-time influenza forecasts during the 2012–2013 season. Nat. Commun. 4, 2837. 10.1038/ncomms3837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi Y, Liu X, Kok S-Y, Rajarethinam J, Liang S, Yap G, et al. , 2015. Three-month real-time dengue forecast models: an early warning system for outbreak alerts and policy decision support in Singapore. Environ. Health Perspect. 124 (9), 1369–1375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sivagnaname N, Gunasekaran K, 2012. Need for an efficient adult trap for the surveillance of dengue vectors. Indian J. Med. Res 136 (5), 739. [PMC free article] [PubMed] [Google Scholar]
- Wu Y, Ling F, Hou J, Guo S, Wang J, Gong Z, 2016. Will integrated surveillance systems for vectors and vector-borne diseases be the future of controlling vector-borne diseases? A practical example from China. Epidemiol. Infect. 144 (9), 1895–1903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamana TK, Kandula S, Shaman J, 2016. Superensemble forecasts of dengue outbreaks. J. R. Soc. Interface 13 (123), 20160410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamana TK, Qiu X, Eltahir EA, 2017. Hysteresis in simulations of malaria transmission. Adv. Water Resour. 108, 416–422. [Google Scholar]
- Zhang F, Meng Z, Aksoy A, 2006. Tests of an ensemble Kalman filter for mesoscale and regional-scale data assimilation. Part I: perfect model experiments. Mon.Weather. Rev. 134 (2), 722–736. [Google Scholar]
- Zhang F, Snyder C, Sun J, 2004. Impacts of initial estimate and observation availability on convective-scale data assimilation with an ensemble Kalman filter. Mon. Weather. Rev. 132 (5), 1238–1253. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.