The impact of COVID-19 on the degree of dependence and structure of risk-return relationship: A quantile regression approach

Highlights

• •Impact of COVID-19 on degree and structure of risk-return dependence is examined.
• •Interaction among Google Search Index for coronavirus (GSIC) and returns is examined.
• •COVID-19 changed the dependence and structure of risk-return relationship.
• •The GSIC-return dependence is asymmetric with a stronger effect in lower tail.

Abstract

This paper examines the impact of the novel coronavirus (COVID-19) on the degree and structure of risk-return dependence in the US. The results from quantile regression (QR) indicate a left-tailed asymmetric dependence structure of sectoral returns with market portfolio. Following the COVID-19 outbreak, degree of dependence among returns and market portfolio have increased in the higher quantiles. Further, the outbreak has converted left-tailed dependence into a right-tailed dependence. Interaction among Google Search Index for coronavirus (GSIC) and returns also examined. Findings reveal an asymmetric GSIC-return dependence that is significant in tails.

1. Introduction

In the last couple of months, world markets’ have been hit by an invisible enemy, the novel coronavirus (COVID-19). The economic activity has suddenly stopped. According to scholars, such diseases can have long-lasting effects on economic wealth (e.g. Fogli and Veldkamp, 2013; Goodell, 2020). Yet, initial impact of more than 20% loss on financial markets’ value have been observed.

The COVID-19 shock can affect stock markets via two important channels. First, value of common stocks, theoretically, equals to the present value of expected cash-flows (Aurori and Nguyen, 2010; Azimli, 2020). Due to its spreading patterns and mortality rate, future economic and policy outcomes are highly uncertain. This has made future cash-flow of corporations highly unpredictable. Second, increased uncertainty affects required rate of return by investors and thus current market value of stocks. Some industries have totally stopped (e.g. transportation, entertainment, hotels and restaurants and retailing) while others still operate to meet basic needs (e.g. communication, consumption goods and pharma). As a result, there has been a sudden shift in investment and consumption patterns. Such a shift can have important implications on central linearity assumption of models’ standard to the asset pricing literature.

For instance, Hu (2006) and Koenker (2005) revealed significant impact of crisis on the structure of linear dependence among random variables used to model risk-return relationship. According to Bae et al. (2003), such periods can be characterized by non-linear shifts and cannot be modelled by relying on conditional mean function. Quantile regression (QR) approach enables the examination of risk-return relationship at different points (i.e. quantiles) of the dependent variable, y, depending on the conditional median function (see, for instance, Baur. (2013)). The QR has two major advantages to model risk-return behavior during such events over standard models. Firstly, no distributional assumptions about residuals must be made and the QR is robust to outliers (Baur and Schulze, 2005). Secondly, QR can show non-linear properties of dependence among variables and it can provide a broader picture about the impact of shocks on the behavior of entire distribution of y (Yu et al., 2003).

This study adopts the QR regression based methodology suggested by Baur (2013) to examine the impact of COVID-19 on the degree of dependence and structure of risk-return relationship. Accordingly, a market-based factor model (i.e. CAPM) is augmented with a proxy that accounts for structural shocks and change in dependence. In addition, Google Search Index for coronavirus (GSIC) is included into the model to proxy overall uncertainty and investor attention fueled by the COVID-19 outbreak. Online search trends have proved to work in predicting pricing and trading patterns of financial assets (e.g. Bijl et al., 2016; Kissian et al., 2011; Takeda and Wakao, 2014; Urquhard, 2018).

2. Data and model

2.1. Data and sample

This paper uses daily returns of 10 major sectors of the US1 . The main co-variates include returns on market portfolio, proxied by daily S&P500 (SP) returns and daily Google Search Index for coronavirus. The data spans from 1/1/2020 to 31/03/2020. Return data is obtained from Yahoo Finance (finance.yahoo.com) and web based search index is from Google (trends.google.com). The summary statistics for variables are reported in Table 1 . Notably, mean returns for all the industries and SP are negative with high standard deviations. The differences between median and mean values are large. All returns are leptokurtic indicating extreme values in tails with either right- or left-skewed distributions that are not normal according to Jarque-Bera statistics. These results indicate tail events in returns and thus justify the use of QR.

Table 1.

Summary statistics.

	Obs.	median	mean	SD	min	max	Skew.	Kurto.	JB	Prob.
Market (S&P500)	64	-0.12	-0.36	3.58	-11.98	9.38	-0.15	5.23	13.55	0.000
Cons. discretionary	64	-0.09	-0.39	3.23	-12.08	8.64	-0.70	6.01	29.31	0.000
Cons. staples	64	-0.02	-0.14	3.04	-9.24	8.41	0.18	5.04	11.41	0.003
Health care	64	-0.17	-0.21	3.17	-9.99	7.57	0.09	4.41	9.44	0.008
Industrials	64	-0.09	-0.53	3.87	-11.45	12.75	0.04	5.41	15.52	0.000
Information tech.	64	-0.00	-0.21	4.07	-13.91	11.39	-0.06	5.43	15.81	0.000
Materials	64	-0.28	-0.48	3.69	-11.44	11.63	-0.09	5.20	13.01	0.001
Real estate	64	0.07	-0.33	4.02	-16.55	8.63	-0.84	6.50	40.24	0.000
Utilities	64	0.26	-0.24	4.09	-11.54	13.11	0.28	5.33	15.38	0.000
Financials	64	-0.20	-0.62	4.46	-13.99	13.23	0.09	5.64	18.74	0.000
Energy	64	-0.65	-0.94	5.35	-20.08	16.31	-0.55	6.50	35.94	0.000

Note: JB indexes Jarque-Bera test of normality.

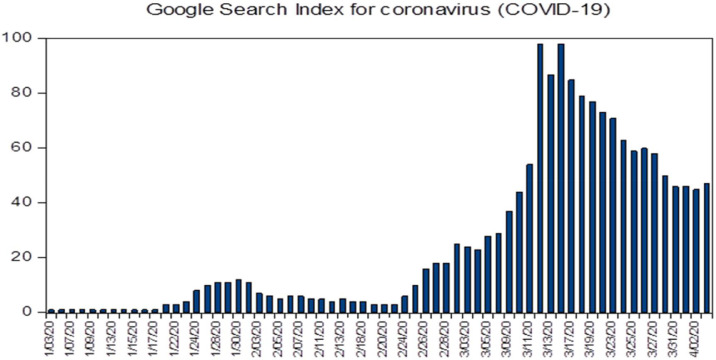
Fig. 1 plots Google searches for coronavirus in the US. It is clearly observable that the index peaks on 12th of March, one day prior the declaration of national emergency by the president Trump. In addition, on 11th of March, the virus has declared as pandemic by World Health Organization and on the same day travel from Europe to the US has been restricted. Breakpoint unit root test of S&P500 series indicated a structural break on 12th of March 2020. Accordingly, this date is used to measure structural impact of COVID-19 outbreak on risk-return relationship.

Fig. 1.

Google search trend for coronavirus in the US.

2.2. Model

This paper employs panelized QR of Koenker and Basset (1978) to model risk-return relationship in the US during COVID-19 outbreak. Possible impacts of lagged industry returns’ and lagged extreme values neutralized following Koenker (2004) and Peng et al. (2018). In addition, methodology of Baur (2013) adopted to measure the impact of COVID-19 outbreak on degree of dependence and structure of risk-return relationship. Consider a panel QR model as follows:

$$Q_{R_{\left(t,i\right)}}\left(\tau |X|\right)={\alpha }_i+\beta \left(\tau \right)R_{\left(t-1,i\right)}+\gamma \left(\tau \right)R_{\left(t-1,i\right)}I\left(\left|R_{\left(t-1,i\right)}\right|>R^q\right)+\theta \left(\tau \right)S{P}_t+\delta \left(\tau \right)S{P}_t{D}_{COVID}+\mathrm{Y}\left(\tau \right)GSI{C}_t+b\left(\tau \right)GSI{C}_{\left(t\right)}{D}_{COVID}$$ (1)

where Q(τ|•) denotes a conditional quantile function, R _t,i is return of industry i at day t, R _{t − 1, i} is return on industry i at day t-1, I(|R _{t − 1, i}| > R^q) is an indicator variable equals to 1 if return on industry i at day t-1 exceeds threshold level, selected as 95th percentile of unconditional distribution, and zero otherwise. First two terms are to neutralize the impact of prior industry returns on results. The SP_{t, i} is return on S&P500 index on day t and GSIC_t is Google search index for coronavirus at day t. Finally, the D_COVID is a dummy variable intended to measure change in structure and degree of dependence of risk-return relationship during the outbreak. It equals to 1 following 12 March 2020. The δ and b measure average change in degree of dependence of industry returns given SP and GSIC during D _COVID. If these coefficients are greater than zero, there is an increase in dependence following the outbreak and vise-versa. Finally, if δ(τ) and b(τ) varies across quantiles, there is a change in the structure of dependence.

The QR method of Koenker and Basset (1978) provides the estimates of the degree of dependence conditional on each quantile (Baur, 2013). It can reveal any type of structure of dependence such as symmetric (e.g. a u-shaped structure or an inverted u-shaped structure) and asymmetric with a left-tail or a right-tail structure of dependence. For example, if the coefficient estimates (i.e. degree of dependence) for each quantile τ is equal, the structure of dependence is said to be constant. If the estimates are equally high in the tails with lower values in the intermediate quantiles, there is a symmetric u-shaped dependence. If the coefficient estimates monotonically increase from the lower quantiles to the upper quantiles, there is an asymmetric dependence structure with a right-tail dependence. If the coefficient estimates monotonically decrease from the lower quantiles to the upper quantiles, there is an asymmetric dependence structure with a left-tail dependence. According to Baur (2013), there is no need to determine an ad hoc structure for QR since the type of structure is an outcome of the piecewise estimation process of dependence across all quantiles. Therefore, QR offers a more comprehensive picture for any type of structure while accounting for non-linearities and asymmetries. A dummy variable (i.e. D _COVID) is used to investigate the degree and structure of dependence in normal times and during the pandemic. The test of significance of any type of structural change in any of the quantile is captured by the significance test of δ and b in Eq. 1.

3. Results

This section presents results of the QR as specified in Eq. (1). Table 2 reports the average coefficient estimates for 10 industries for selected quantiles. Table displays the coefficients of θ, δ, ϒ and  b which are the main focus of the study.

Table 2.

Estimation results.

Panel A: Coefficients for SP index (θ) and SP index and COVID dummy interaction (θ).
	θ	p(θ)	δ	p(δ)
0.025	1.024***	0.000	-0.022	0.882
0.050	1.042***	0.000	0.104	0.130
0.075	0.996***	0.000	0.121*	0.082
0.100	0.972***	0.000	0.086	0.441
0.150	1.002***	0.000	0.039	0.553
0.200	1.022***	0.000	0.020	0.7213
0.250	1.012***	0.000	0.056	0.679
0.500	0.972***	0.000	0.040	0.435
0.750	0.974***	0.000	0.137***	0.006
0.800	0.975***	0.000	0.130*	0.08
0.850	0.965***	0.000	0.169**	0.016
0.900	0.944***	0.000	0.180**	0.012
0.925	0.904***	0.000	0.116	0.173
0.950	0.880***	0.000	0.285***	0.001
0.975	0.870***	0.000	0.281***	0.000
Panel B: Coefficients for GSIC index (ϒ) and GSIC index and COVID dummy interaction (b).
	ϒ	p(ϒ)	b	p(b)
0.025	-0.044***	0.000	-0.003	0.803
0.050	-0.056***	0.000	0.018*	0.098
0.075	-0.045***	0.000	0.010	0.428
0.100	-0.044***	0.000	0.013	0.310
0.150	-0.027**	0.023	0.006	0.583
0.200	-0.017**	0.025	-0.000	0.966
0.250	-0.013**	0.022	0.000	0.949
0.500	-0.005	0.378	0.003	0.655
0.750	0.018**	0.043	-0.007	0.427
0.800	0.022**	0.017	-0.008	0.394
0.850	0.027***	0.002	-0.007	0.435
0.900	0.031***	0.000	-0.004	0.707
0.925	0.032**	0.031	0.003	0.883
0.950	0.032***	0.002	0.017	0.374
0.975	0.027***	0.004	0.029**	0.016

Notes: The Quantile Regression (QR) estimation result for selected quantiles.

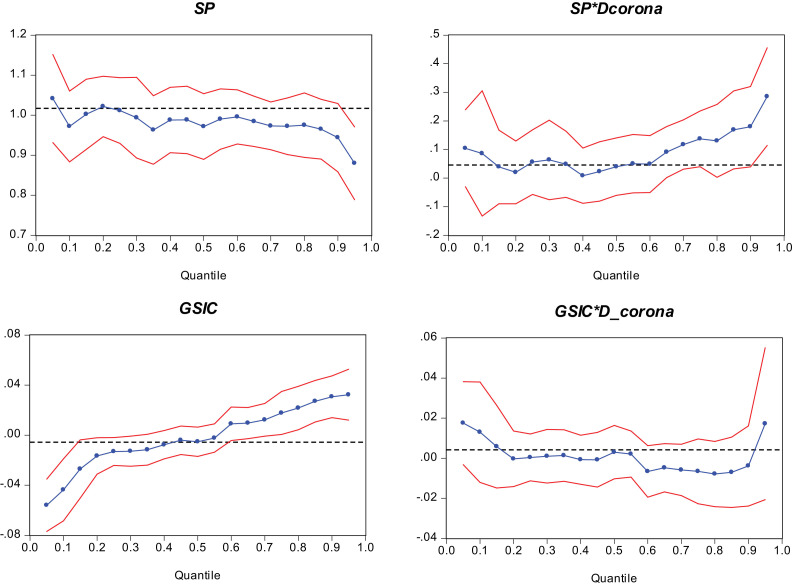
Panel A reports average coefficient loadings of SP (θ) in Column 2 and an interaction term comprised of SP index and COVID-19 dummy (δ) in Column 4 for selected quantiles (Column 1). The results show a left-tailed asymmetric dependence structure with differing degree of dependence among SP and industry returns. The θ estimates show an asymmetric dependence that is larger in lower tail (1.024) compared to the upper tail (0.870). The mid-point (median) estimation is 0.972. The estimates for the COVID effect revel an asymmetric U-shape that can be characterized by right-tail dependence with higher values in tails and lower values around the mid-point. It is important to note that parameter δ measures marginal change of dependence among SP and industry returns relationship. Aggregate effect in the COVID-19 period can be obtained by adding estimates of θ and δ. Based on this, the degree of dependence between industry returns and SP considerably increased in higher quantiles for the selected period. Positive δ estimates in the right-tail indicate increased co-movement among returns. The results show a change in structure of dependence as well due to the asymmetric change in the degree of dependence for some quantiles. The COVID-19 outbreak converted the left-tailed dependence into a right tailed dependence. Accordingly, there exist an increased co-movement in the upper quantiles. This finding is in line with Baur (2013) related to the behavior of stock returns during crisis in emerging markets, degree of dependence increased in upper tail but there is no change in the lower tails. The right-tailed asymmetric structure of dependence during outbreak cannot be explained by margin calls, liquidations and wealth constraints which are normally seen as lower tail behavior.

Panel B reports average coefficient loadings of GSIC (ϒ) in Column 2 and an interaction term comprised of GSIC and COVID-19 dummy (b) in Column 4. The results show an S-shaped asymmetric dependence structure that is negative and stronger in the lower quantiles and positive and relatively weaker in the higher quantiles. For instance, the estimates of ϒ for the 2.5% quantile and 5% quantile are -0.044 and -0.056, respectively. While, the estimates of ϒ for the 95% quantile and 97.5% quantile are 0.037 and 0.027, respectively. These patterns indicate tail dependence in returns-GSIC relationship that is stronger in the left-tail. The median estimation is -0.005 and insignificant, justifying prior predictions of the paper about linear dependence models. Overall, increased attention towards coronavirus has negative and higher effects on industries in the lower tail of distribution but positive and lower effects on industries in the upper tail of distribution. Increased attention of investors could have been triggered a selling wave for losers whereas it triggered demand for winners. These findings are noteworthy since this relationship cannot be captured by the standard linear models that depend on conditional mean function. The estimates for δ is only significant at 97.5% quantiles. Accordingly, except for the highest tail, the interaction term of GSIC-_DCOVID cannot affect the degree and structure of dependence between GSIC and industry returns.

The patterns documented in Table 2 are also illustrated graphically in Fig. 2 for visual aid. The vertical axis in each graph represents dependence measured by parameter estimates and horizontal axis represents quantiles.

Fig. 2.

Quantile Regression (QR) estimates. Notes: The blue solid line with circles plots quantile estimates along with red dashed-lines of 95% pointwise confidence interval. Finally, the black dashed line represents OLS estimate given the conditional mean function. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.).

4. Conclusion

This study uses a QR approach to measure the impact of COVID-19 on the dependence of industry returns and the structure of the risk-return relationship. The paper also examines the relationship among GSIC and stock returns to measure the implications of investor attention and return relationship. Overall, results indicate a left-tailed asymmetric dependence structure of industry returns with market portfolio in normal times. Following the COVID-19 outbreak, degree of dependence between returns and market portfolio has increased in the higher quantiles, lowering the benefits of diversification. The COVID-19 outbreak also converted the left-tailed dependence into a right tailed dependence, indicating a shift in the structure of risk-return relationship. In addition, the GSIC-return relationship revealed an asymmetric pattern, lower tails influenced negatively and almost twice as much compared to the upper tails which influenced positively from increased search activity. Except for the highest tail, the COVID-19 outbreak cannot influence the degree or structure of this S-shaped return-GSIC dependence.

These results have important economic implications. First, market reaction to COVID-19 in terms of change in dependence and structure of risk-return relationship follows a contagion like patterns and show similarities to that of 2008 crisis documented by prior literature. Second, S-shaped return-GSIC dependence indicated that investors’ attention towards extreme losers and/or extreme winners around such shifts. This relationship is not significant on and around median. The asymmetric dependence could be related to investors’ risk aversion behavior around catastrophe events. Finally, understanding risk-return relationship during the outbreak may help investors to respond quickly and manage their portfolios.

Author statement

The only contributor of this article is Asil Azimli.