Abstract
The recent worldwide outbreak of the novel coronavirus disease 2019 (COVID-19) opened new challenges for the research community. Machine learning (ML)-guided methods can be useful for feature prediction, involved risk, and the causes of an analogous epidemic. Such predictions can be useful for managing and intercepting the outbreak of such diseases. The foremost advantages of applying ML methods are handling a wide variety of data and easy identification of trends and patterns of an undetermined nature.In this study, we propose a partial derivative regression and nonlinear machine learning (PDR-NML) method for global pandemic prediction of COVID-19. We used a Progressive Partial Derivative Linear Regression model to search for the best parameters in the dataset in a computationally efficient manner. Next, a Nonlinear Global Pandemic Machine Learning model was applied to the normalized features for making accurate predictions. The results show that the proposed ML method outperformed state-of-the-art methods in the Indian population and can also be a convenient tool for making predictions for other countries.
Keywords: Machine Learning, Progressive, Partial Derivative, Linear Regression, Nonlinear, Global Pandemic, Kuhn-tucker
1. Introduction
The widespread outbreak of Coronavirus disease 2019 (COVID-19) created by Severe Acute Respiratory Syndrome Coronavirus 2 (Sars-CoV-2) has caused devastation to human populations. Following its emergence in the Wuhan City in China, it has been a continuing process of latest new cases and mortalities. What makes it more frightening is the intensity of the virus and yet unknown mechanism. The current plan of action has been to slow its spread via social distancing and the rush to produce state-of-the-art expeditious diagnostic kits in addition to medications.
No reasonable plan has been proposed to halt spread of COVID-19 pandemic that started in China in late 2019 and has since created panic in millions of people globally through illness, recession, and finally an exponential mortality rate. Multiple regression analysis [1] was designed with the objective of designing the trend of the with respect to COVID-19-induced death rates in India. Both global and local data pertaining to COVID-19 and related outcomes were obtained. Prediction accuracy using multiple regression analyses remains at the core of the paper.
An artificial intelligence-based (AI) prediction was used in to detect cluster cases [2]. In addition, predictions about its spread were also made by analyzing all previous data. AI works in a skillful manner to impersonate human intelligence. Besides, it possesses the advantages of comprehending and demonstrating the progress of a making a vaccine for COVID-19. With this information, genuine screening, analyzing, predicting, and current patient tracking with potentialities of future patient analysis were also made thus contributing accurate predictions.
Note that multiple regressions in addition to the conditional posteriors and the cluster class depend on the correlation of upper and lower limit variables. However, we are focused on the negligible arrangements, but unfortunately, the correlative variables cannot be systematically combed out. Several researchers have proposed AI-algorithms and correlative inferences to overcome this problem [1,2]. These algorithms do not scale globally to big data problems, and the correlation evaluation still depends on point estimates of limit variables.
We overcome these problems by proposing a Progressive Partial Derivative Linear Regression (PPDLR) model and acquiring coarse-grained predictive grouping using a Nonlinear Global Pandemic Machine Learning (NGPML) model. In this work, we proposed the Partial Derivative Regression and Nonlinear Machine Learning (PDR-NML) method for early prediction of the pandemic outbreak of COVID-19 in India based on the available data.
1.1. Goals
The goals of this work are listed below.
-
•
To design computationally efficient and normalized features using PDRL model.
-
•
To present a robust and precise prediction of COVID-19, using a NGPMLmodel.
-
•
The proposal is compared with existing methods used on an extensive testbed of COVID-19 in an Indian dataset. Experimental results show that the proposed method significantly outperforms the existing methods in terms of both prediction time and accuracy.
1.2. Organization
This paper has been organized as follows. In Section 2, machine learning, deep learning and optimization models accommodated for early prediction of the novel Coronavirus has been reviewed in detail. In Section 3, the design of the proposed PDR-NML method is described. In Sections 4 and 5, the experimental results and conclusions of the work are described, respectively.
2. Related works
The outbreak of the worldwide pandemic COVID-19 has put the entire human community at risk for contracting the virus and the resulting sustaining economic damage. Due to this, the largest economies are in the stressed state with the highest rate of infectivity and disease transmissibility. Also, because of the increasing number of cases seen over the last several months and its successive stress on the administrative and healthcare professionals, some prediction models are highly required to predict the frequency and number of occurrences in the near future.
In one study, a data-driven long short-term memory (LSTM) estimation method was used for prominent prediction [3]. Pieces of evidence were collected using the Kaplan-Meier curve to derive independent biomarkers for better arriving at better clinical outcomes [4]. A review on the universal content, biomedicine, formation, clinical analysis, diagnosis, therapy and benchmarks of COVID-19 with reference to India is presented in [5]. An update connected to the pandemic outbreak of COVID-19 is discussed in [6].
Continuation of the COVID-19 pandemic due to the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) is a matter of worldwide concern. Several environmental aspects, such as air pollution, smoking, and pre-existing conditions, such as hypertension, diabetes mellitus, and cardiac- and respiratory-related illnesses cause a significant increase in the gravity of COVID-19. The influence of rheumatic-like arthritis was studied in [7].
An objective model for efficient prediction of the prolongation of COVID-19 with the aid of a straightforward and robust method was proposed in [8]. Risk prediction long short-term memory-based neural network was designed in [9]. An optimization Bayesian-base framework was designed with the purpose of predicting country-specific viral networks.
A review of COVID-19 together with the perceptions of the virus, the feedbacks from host cells, and the therapeutic options for lessening the cytokine storm is presented in [10]. A survey on the use of blockchain along with AI was proposed in another study in order to shield against this novel Coronavirus [11].
The acceptance of wearable devices empowers a new viewpoint for halting this contagious disease. In one study, a framework was presented on the basis of the heart rate and sleep data acquired from those devices with the purpose of predicting the epidemic trend of COVID-19 in disparate countries and cities [12]. The importance and significance of the country-wide lockdown implemented in Italy for a total of 60 days were examined in [13].
A novel type of vaccine design with the aid of reverse vaccinology using machine learning for preventing the spread of COVID-19 is presented in [14]. A follow-up study conducted in six different Asian countries with close contact or unknown contact history was designed in [15]. A study of sex-specific differences was conducted with 168 severely ill patients [16], and the results were monitored to see their effects on the novel Coronavirus. A case study for swift categorization of this pandemic Coronavirus using ML with the aid of genomic signatures was proposed in [17].
A multivariate prediction model was investigated in [18] on the basis of the parameters involving current viral transmission and clinical values to reproduce pandemic-related directions in 16 countries from different latitudes and productive classes. With the increase in usage of social media, stress-related problems are said to be the most prevalent issues. In-depth analysis with multivariate logistic regressions to study the correlation between social media and stress owing to novel Coronavirus is discussed in [19]. Mathematical predictions using Monte Carlo simulations and Gauss error function is presented in [20] to analyze the outbreak of the pandemic COVID-19 in Italy.
Motivated by the above facts and findings, the main objective of this study was to describe a novel method for predicting trends in the pandemic outbreak of COVID-19 in Tamilnadu, India using big data acquired from the COVID-19 dataset, acquired from Kaggle. Two major findings from this study were obtained: (1) a PPDLR detection method was developed to identify normalized features reflected by population samples and (2) a NGPMLP model was proposed for making early predictions about outbreaks.
3. Partial derivative regression and nonlinear machine learning for COVID-19 outbreak prediction
The approach to the precise outbreak prediction models is crucial for acquiring information about the probable spread and outcomes of pandemic diseases. Governments and other research organizations depend on predictions from these models to recommend new strategies for evaluating the efficiency of the enforced policies and therefore controlling the spread of disease. A novel PDR-NML method was designed in our study for predicting upcoming cases in a timely and accurate manner.
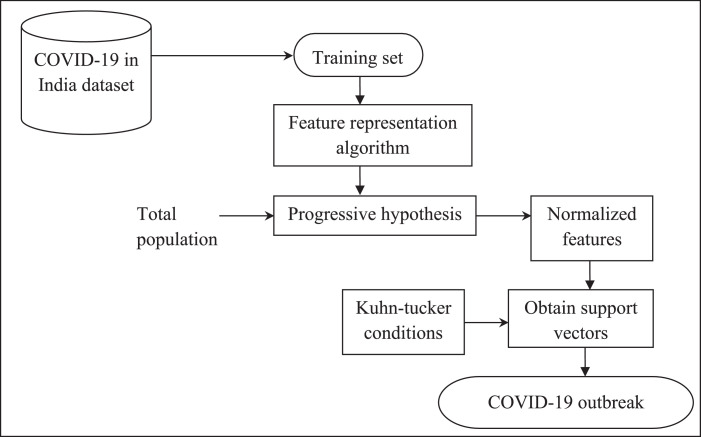
Two steps were involved in the design of the PDR-NML method, including a search for the best parameters in the big data dataset by applying the PPDLR model and NGPML model. Fig. 1 shows the block diagram of the PDR-NML method.
Fig. 1.
Block diagram of Partial Derivative Regression and Nonlinear Machine Learning (PDR-NML) method.
The proposed method analysis was based on a publicly available COVID-19 Indian database, Kaggle, containing the new confirmed daily case reports for the states and union territories of India. On the basis of the released data, we attempted to evaluate the average values of the epidemiological parameters, for example, the basic generative number ‘G 0’, the case mortality rate ‘EM’, and case recovery rate ‘ER’ proportions.
In addition, by scaling the specifications of the Exposed Affected Cured Dead (EACD) model to adapt the detailed big data, mathematical formulas were first designed. Second, normalized features were obtained by means of a progressive hypothesis. Finally, outbreak predictions were made by applying Kuhn–Tucker conditions to the support vector values. The detailed description of the proposed PDR-NML method is given below.
3.1. Progressive Partial Derivative Linear Regression model
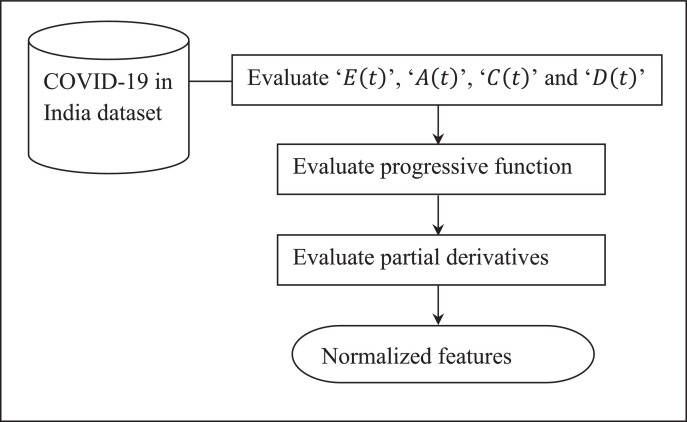
We assume that all the features are not associated with the prediction variable. The data contain four main analyses for the pandemic risk prediction of a country. They are number of exposed people, number of affected people, number of cured, and number of dead. These values are first evaluated followed by selecting the best parameter using the PPDLR model. Fig. 2 illustrates the flow diagram.
Fig. 2.
Block diagram of Progressive Partial Derivative Linear Regression model.
Let us represent ‘E(t)’, ‘A(t)’, ‘C(t)’, and ‘D(t)’ as the number of exposed, affected, cured, and dead people, respectively, at time ‘t’ over the population size ‘N’. For our analysis, we assumed that the total number of the population remained constant. Based on the demographic data for the states and union territories of Indi, the distinct EACD model is written as shown below:
| (1) |
| (2) |
| (3) |
| (4) |
From the above Eqs. (1)–(3), ‘EI’, ‘ER’, ‘EM’ correspond to the estimation of infected rate, estimation of recovery rate, and estimation of mortality rate, respectively. In addition, ‘E(t)’, ‘A(t)’, ‘C(t)’, and ‘D(t)’ refer to the number of exposed, affected, cured and dead patients at time interval ‘t’. Let us represent ‘’, ‘’ and ‘’ as the reported new cases of affected, cured, and dead cases at time ‘t’. The progressive number of cases at time ‘t’ can then be represented as shown below:
| (5) |
Given a novel Coronavirus disease dataset (big data) of variables ‘(pi, qi)’ in which ‘pi’ refers to the describing variable and ‘qi’ refers to the dependent variable that differs as ‘pi’ does (with ‘pi ∈ Si’ being the samples tested and ‘qi ∈ A, R or D’ being the affected/recovery/dead cases), a linear representation for arriving at the association between the describing and the dependent variable is expressedis Eq. (6):
| (6) |
After assuming that ‘Q’ is continuously correlated to ‘P’ with a negligible error value ‘ɛi’, the next step is to evaluate the parameters ‘α’ and ‘β’ as in Eq. (7):
| (7) |
The above equation is to be reduced to obtain the best feasible approximation for our pandemic prediction model and that is performed by associating the first partial derivatives of the above Eq. (7) and can be mathematically written as shown below:
| (8) |
| (9) |
Resolving the organization of equation for ‘α’ and ‘β’ results in the following equations as shown below:
| (10) |
| (11) |
The pseudo code representation of the progressive partial derivative linear feature representation (PPDLFR) is given below.
As given in the Algorithm 1 , the objective is obtain computationally efficient normalized features using the PPDLFR. The novel Coronavirus disease dataset (for example, big data dataset) includes eight different files: (1) AgeGroupDetails, (2) HospitalBedsIndia, (3) ICMRTestintDetails, (4) ICMRTestingLabs, (5) IndividualDetails, (6) StatewiseTestingDetails, (7) Covid_19_india, and (8) population_india_census2011. In addition, the eight files consist of 61 different columns, and as all the 61 different columns are of least importance in the prediction, the normalized features should be obtained in a computationally efficient manner. This process is performed in our study by applying first partial derivatives for each progressive case.
Algorithm 1.
Progressive Partial Derivative Linear feature representation.
| Input: Dataset ‘DS’ time interval, ‘t’, population size, ‘N’, samples tested, ‘’ |
| Output: computationally efficient normalized features: ‘’ |
| 1: Begin |
| 2: For each population size, ‘N’ |
| 3: Evaluate number of exposed ‘E(t)’ persons using Eq. (1). |
| 4: Evaluate number of affected ‘A(t)’ persons using Eq. (2). |
| 5: Evaluate the number of cured ‘C(t)’ persons using Eq. (3). |
| 6: Evaluate number of dead ‘D(t)’ persons using Eq. (4). |
| 7: Measure progressive number of cases at time ‘t’ using Eq. (5). |
| 8: Associate describing and dependent variable using Eq. (6). |
| 9: Evaluate first partial derivatives with respect to ‘α’ using Eq. (8). |
| 10: Evaluate first partial derivatives with respect to ‘β’ using Eq. (9). |
| 11: Measure ‘α’ and ‘β’ using Eqs. (10) and (11). |
| 12: Return (α) |
| 13: End for |
| 14: End |
3.2. Nonlinear Global Pandemic Machine Learning model
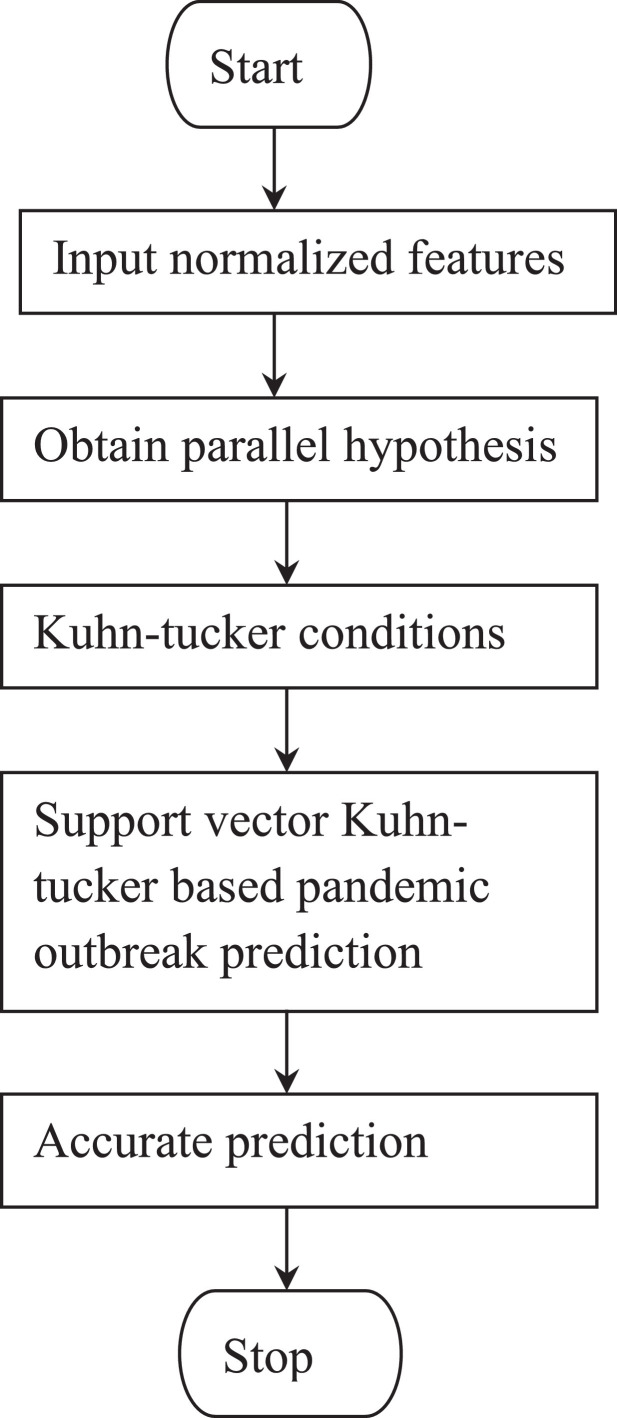
With the identified computationally efficient normalized features from the COVID-19 dataset, the second and final step in the design of the proposed method consists of the outbreak prediction. In this work, global pandemic predictions are made by means of the Nonlinear Global Pandemic Machine Learning (NGP-ML) model. According to the analysis mentioned above, the NGP-ML model for making global pandemic predictions in big data dataset isshown in Fig. 3 .
Fig. 3.
Flow diagram of Nonlinear Global Pandemic Machine Learning model.
First, the input and output of the NGP-ML model for the big data dataset are obtained. The sample test and results are treated as the input and output of the NGP-MP prediction model. Next, the normalized sample (features) ‘’ in which‘xi’ represents the ‘’ of the pandemic features and ‘yi’ represents the output ‘’ of the pandemic features, ‘’, is obtained with the objective being the design of maximum margin hyperplane:
| (12) |
From the above Eq. (12), ‘w’ and ‘b’ refer to the normal vector and class boundary of the ‘x’ hyperplane, respectively. Two parallel hypotheses are said to exist and can bewritten as shown below:
| (13) |
| (14) |
The above Eqs. (13) and (14) iindicates that any value on or above this boundary is of one class with a label of ‘1’ or ‘’. Next, the design parameters of the NGO-ML, such as ‘PΔZ(t)’, ‘ɛ’, and kernel function ‘K(p, p′)’ are selected. Finally, an optimization problem is formulated based on Kuhn-Tucker conditions as shown iin the next series of equations:
| (15) |
| (16) |
| (17) |
| (18) |
| (19) |
From the above Eqs. (15)–(19), ‘wi’ represents the normal vector to hyperplane, ‘pi’, ‘qi’ represents the sample test and output test values, respectively, and ‘b’ refers to the boundary value. In addition, ‘Lp’ and ‘NF’ correspond to the normalized features (obtained from linear feature representation). The pseudo code representation of the NGP-MLP is given below:
As given in the Algorithm 2 , the objective is to obtain an accurate prediction for pandemic disease, COVID-19. With this objective, support vectors are first designed for the acquired normalized features, and then the Kuhn–Tucker conditions are generated. With these conditions, the regression function is tested with the aid of the test dataset. If the expected prediction accuracy is achieved, the prediction model of the development index can be obtained. Otherwise, the parameters are altered and calibrated based on the kernel function and design parameters.
Algorithm 2.
Nonlinear Global Pandemic Machine Learning prediction.
| Input: normalized features ‘’ |
| Output: Precise and early prediction |
| 1: Initialize progressive number of cases ‘PΔZ(t)’, error value ‘ɛi’, kernel function ‘K(p, p′)’ |
| 2: Begin |
| 3: For each normalized feature ‘’ |
| 4: Obtain maximum margin hyperplane using Eq. (12). |
| 5: Repeat |
| 6: Evaluate Kuhn-Tucker conditions using Eqs. (15)–(19) |
| 7: Until (prediction accuracy evolved) |
| 8: End for |
| 9: End |
4. Experimental setup
The proposed method PDR-NML was implemented using the JAVA libraries in Hadoop. To assess the applicability of the proposed method, the method was applied to a benchmark dataset Indian COVID-19 dataset obtained from https://www.kaggle.com/sudalairajkumar/covid19-in-india. This dataset possesses information acquired from the states and union territories of Indiaon a daily basis in which the state-level data can be obtained from Ministry of Health and Family Welfare and individual-level data is obtained from the COVID-19 India database.
On the other hand, individual-level details are acquired from IndividualDetails.csv file, the population at the state level is obtained from population_india_census2011.csv file, and the number of COVDI-19 tests run on a daily basis is obtained from ICMRTestingDetails.csv file. The number of hospital beds in each state is acquired from the HospitalBedsIndia.csv file. The experimental evaluation was carried out on certain factors, such as prediction accuracy and prediction time with respect to a number of samples collected at different time intervals.
5. Discussion
In this section, the analysis of the results for two different parameters, prediction time and prediction accuracy for the outbreak of pandemic Coronavirus in India, is discussed and a comparison is made with the proposed PDR-NML and existing methods, multiple regression analysis [1], and AI-based prediction [2]. For a fair comparison, data is acquired from the COVID-19 in India dataset from Kaggle.
5.1. Performance comparison of prediction time
The time taken to predict the outbreak of Coronavirus disease is referred to as the outbreak prediction time. The faster the outbreak prediction time is indicates the faster the prevention of the spread of the COVID-19 disease can occur.
| (20) |
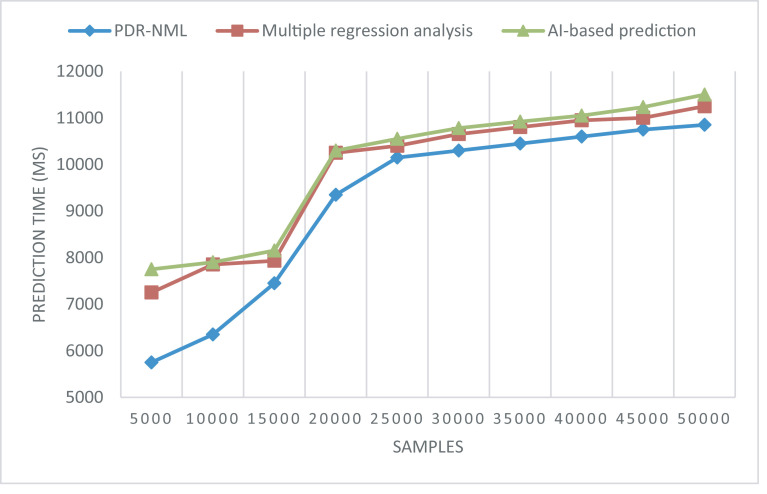
From the above Eq. (20), the prediction time ‘Ptime’ is made based on the samples collected ‘Si’ and the time consumed for prediction ‘Time [Prediction]’. Fig. 4 provides the prediction time results for PDR-NML, multiple regression analysis [1], and AI-based prediction [2] methods. This figure illustrates the outbreak prediction time for Coronavirus in India with 50,000 different samples or from the rural population collected from Tamilnadu State over a period of time. In addition, different ages between 40 and 49 was also considered as a criterion for making a prediction. With an increasing number of samples or populations, the Coronavirus prediction time in Tamilnadu State was observed using three different methods: (1) PDR-NML, (2) multiple regression analysis, and (3) AI-based prediction methods. With 5000 samples considered for experimentation, the time for prediction using PDR-NML was found to be 5750 msec, 7250 msec using the multiple regressions, and 7750 msec using AI-based prediction methods.
Fig. 4.
Graphical representation of prediction time.
From the results, it can be inferred that the prediction time for the samples or the population inflicted with pandemic Coronavirus was found to be reduced using the PDR-NML when compared to the linear regression or AI-based prediction. This difference occurred because of the application of the PPDLR model. By applying this model, the best parameters required for prediction were found by means of partial derivatives and progression functions, resulting in normalized features. With the resulting normalized features and avoidance of the robust features present in the Indian COVID-19 dataset, the prediction time is comparatively lessusing PDR-NML by 7% compared to linear regression and 9% compared to the AI-based prediction.
5.2. Performance comparison of prediction accuracy
Accuracy refers to the quality or state of being correct or precise. In our work, pandemic disease prediction accuracy refers to patients who have Corona symptoms and are being detected based on the assumption that the patient has the virus. This process is expressed in Eq. (21):
| (21) |
From the above Eq. (21), the prediction accuracy ‘Pacc’, can be made based on the samples collected ‘Si’ and the correctly predicted samples ‘SCP’. The prediction accuracy is measured in terms of percentage (%).
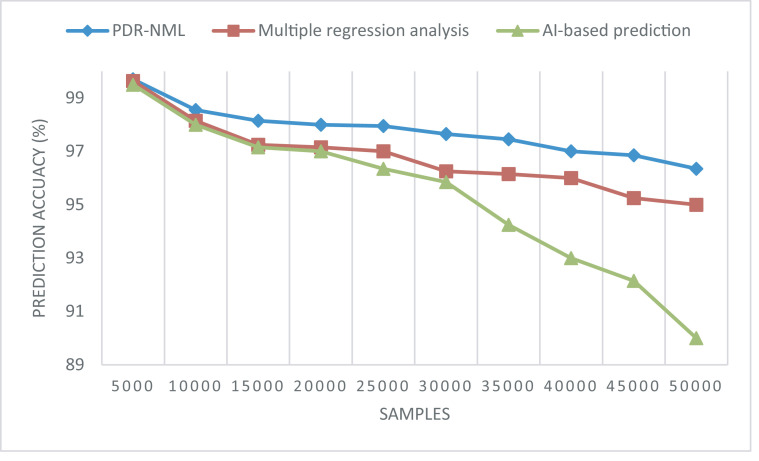
Prediction accuracy is indicated as the association between the samples or persons detected with disease and the actual people with Coronavirus disease. Fig. 5 provides the prediction accuracy results for PDR-NML, multiple regression analysis [1], and AI-based prediction [2] methods. This figure shows the graphical representation of prediction accuracy for the outbreak of Coronavirus in Tamilnadu with the samples acquired from the urban population. For simulations, the age group between 50 and 59 in addition to new cases are considered to evaluate the prediction accuracy. The samples were obtained from different time periods and different ICMR testing labs. A higher prediction of being detected with Coronavirus indicates how well a binary classification precisely detects a condition. In other words, it is the percent ratio of correct predictions among the total number of cases examined.
Fig. 5.
Graphical representation of prediction accuracy.
From the simulations performed for 5000 patients, 4985 patients were correctly predicted as such by using the PDR-NML method, 4982 using linear regression, and 4975 using AI-based prediction. Prediction accuracy improvement was found using the proposed PDR-NML method with the application of the NGP-MLP algorithm. By applying this algorithm, normalized features essential for prediction were first obtained. With the normalized features as input, Kuhn–Tucker conditions were applied using the maximum margin hyperplane that aids in predicting the precise results. This step in turn improves the prediction accuracy using the PDR-NML method by 2% compared to the linear regression and 3% compared to the AI-based method.
6. Conclusion
The worldwide SARS-CoV-2 pandemic has become the foremost national security affair for several nations. Improvement of precise prediction methods for the outbreak is crucial for understanding of this outbreak and effects of this contagious disease. With the elevated extent of unpredictability and shortfall of decisive data, normal and usual models have resulted in shallow validity for long term prediction. This study presents a PDR-NML model for a timely and precise prediction of COVID-19. Two different models were employed, namely, the PPDLR for normalizing the features required for timely prediction and PDLFR for robust and accurate predictions. By integrating the overall learning model, we also learned that other than the AI model, for most of the cases, ML performed well for data analysis. The method can be utilized for predicting COVID-19
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- 1.Ghosal S., Sengupta S., Majumder M., Sinha B. Linear Regression Analysis to predict the number of deaths in India due to SARS-CoV-2 at 6 weeks from day 0 (100 cases - March 14th 2020) Diabetes Metab Syndr. 2020;14:311–315. doi: 10.1016/j.dsx.2020.03.017. Mar. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Vaishya R., Javaid M., Khan I.H., Haleem A. Artificial Intelligence (AI) applications for COVID-19 pandemic. Diabetes Metab Syndr. Apr 2020;14:337–339. doi: 10.1016/j.dsx.2020.04.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Tomar A., Gupta N. Prediction for the spread of COVID-19 in India and effectiveness of preventive measures. Sci Total Environ. Apr 2020;728 doi: 10.1016/j.scitotenv.2020.138762. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Yanga A.P., Liub J., Taoc W., Lib H. The diagnostic and predictive role of NLR, d-NLR and PLR in COVID-19 Patients. Int Immunopharmacol. Apr. 2020;84 doi: 10.1016/j.intimp.2020.106504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Kaushik S., Kaushik S., Sharma Y., Kumar R., Yadav J.P. The Indian Perspective of COVID-19 Outbreak. VirusDis. Apr 2020 doi: 10.1007/s13337-020-00587-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Gabutti G., d’Anchera E., Sandri F., Savio M., Stefanati A. Coronavirus: update related to the current outbreak of COVID-19. Infect Dis Ther. 2020;9:241–253. doi: 10.1007/s40121-020-00295-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Misra D.P., Agarwal V., Gasparyan A.Y., Zimba O. Rheumatologists’ perspective on coronavirus disease 19 (COVID-19) and potential therapeutic targets. Clin Rheumatol. 2020;39:2055–2062. doi: 10.1007/s10067-020-05073-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Petropoulos F., Makridakis S. Forecasting the novel coronavirus COVID-19. PLoS ONE. 2020;15(3) doi: 10.1371/journal.pone.0231236. March 31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Pal R., Sekh A.A., Kar S., Prasad K.Dilip. Neural Network Based Country Wise Risk Prediction of COVID-19. IEEE Access. Mar 2020 doi: 10.1371/journal.pone.0231236. [DOI] [Google Scholar]
- 10.Zhou G., Chen S., Chen Z. Advances in COVID-19: the virus, the pathogenesis, and evidence-based control and therapeutic strategies. Front Med. Mar 2020;14:117–125. doi: 10.1007/s11684-020-0773-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Nguyen DC., Ding M., Pathirana PN., Seneviratne A. Blockchain and AI-based Solutions to combat coronavirus (COVID-19)-like epidemics: a survey. Creative Commons CC, IEEE Access. Apr. 2020 doi: 10.20944/preprints202004.0325.v1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Zhu G., Li J., Meng Zi, Yu Yi, Li Y., Tang X., et al. Learning from large-scale wearable device data for predicting epidemics trend of COVID-19. Discrete Dyn Nat Soc. May 2020;2020:1–9. doi: 10.1155/2020/6152041. [DOI] [Google Scholar]
- 13.Chintalapudi N., Battineni G., Amenta F. COVID-19 virus outbreak forecasting of registered and recovered cases after sixty day lockdown in Italy: a data driven model approach. J Microbiol Immunol Infect. 2020;53(3):396–403. doi: 10.1016/j.jmii.2020.04.004. Apr. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Ong E., Wong M.U., Huffman A., He Y. COVID-19 coronavirus vaccine design using reverse vaccinology and machine learning, the preprint server for biology. Mar. 2020 doi: 10.1101/2020.03.20.000141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Lan F.-Y., Wei C.-F., Hsu Y.-T., Christiani D.C., Kales S.N. Work-related COVID-19 transmission in six Asian countries/areas: a follow-up study. PLoS One. 2020;15(5) doi: 10.1371/journal.pone.0233588. May 19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Meng Y., Wu P., Lu W., Liu K., Ma Ke, Huang L., et al. Sex-specific clinical characteristics and prognosis of coronavirus disease-19 infection in Wuhan, China: a retrospective study of 168 severe patients. PLoS Pathog. 2020;16(4) doi: 10.1371/journal.ppat.1008520. April 28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Randhawa G.S., Soltysiak M.P.M., El Roz H., de Souza C.P.E., Hill K.A., Kari L. Machine learning using intrinsic genomic signatures for rapid classification of novel pathogens: COVID-19 case study. PLoS One. 2020;15(4) doi: 10.1371/journal.pone.0232391. April 24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Chowdhury R., Heng K., Shawon Md.S.R., Goh G., Okonofua D., Ochoa-Rosales C., et al. Dynamic interventions to control COVID-19 pandemic: a multivariate prediction modelling study comparing 16 worldwide countries. Eur J Epidemiol. 2020;35:389–399. doi: 10.1007/s10654-020-00649-w. May. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Gao J., Zheng P., Jia Y., Chen H., Mao Y., Chen S., et al. Mental health problems and social media exposure during COVID-19 outbreak. PLoS One. 2020;15(4) doi: 10.1371/journal.pone.0231924. April 16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ciufolini I., Paolozzi A. Mathematical prediction of the time evolution of the COVID-19 pandemic in Italy by a Gauss error function and Monte Carlo simulations. Eur Phys J. 2020;135 doi: 10.1140/epjp/s13360-020-00383-y. Apr. [DOI] [PMC free article] [PubMed] [Google Scholar]