Impact of media reports on the early spread of COVID-19 epidemic

Highlights

• •The multiple correlation analyses show the strong relations between media reports and the number of new hospital notifications for COVID-19 epidemic.
• •The impact of individual behavior changes (media impact) on the COVID-19 epidemic is embed into the transmission probability.
• •Nonlinear least squares estimation is used to identify the best-fit parameter values in the model from the observed data.
• •Uncertainty and sensitivity analyses determine key parameters during early phase of COVID-19 epidemic outbreak.
• •Main results show that, for mitigating epidemic COVID-19, the media publicity should be focused on how to guide people’s behavioral changes by experts, and the management departments and designated hospitals of the COVID-19 should take effective quarantined.
• •measures.

Abstract

Media reports can modify people’s knowledge of emerging infectious diseases, and thus changing the public attitudes and behaviors. However, how the media reports affect the development of COVID-19 epidemic is a key public health issue. Here the Pearson correlation and cross-correlation analyses are conducted to find the statistically significant correlations between the number of new hospital notifications for COVID-19 and the number of daily news items for twelve major websites in China from January 11th to February 6th 2020. To examine the implication for transmission dynamics of these correlations, we proposed a novel model, which embeds the function of individual behaviour change (media impact) into the intensity of infection. The nonlinear least squares estimation is used to identify the best-fit parameter values in the model from the observed data. To determine impact of key parameters with media impact and control measures for the later outcome of the outbreak, we also carried out the uncertainty and sensitivity analyses. These findings confirm the importance of the responses of individuals to the media reports, and the crucial role of experts and governments in promoting the public under self-quarantine. Therefore, for mitigating epidemic COVID-19, the media publicity should be focused on how to guide people’s behavioral changes by experts, and the management departments and designated hospitals of the COVID-19 should take effective quarantined measures, which are critical for the control of the disease.

1. Introduction

Due to the rapid outbreak of human infections with the emerging COVID-19 virus, people of most countries are now concerning about its possible risks. By the end of 4 April 2020, the COVID-19 virus has infected more than 900,000 people and died at least 46,000 in all over the world. However, since the randomness of population mobility and uncertainty of control measures, methods of predicting COVID-19 and then preventing and controlling the disease for public health departments remain unclear.

Recently, many studies have been done to predict the spread of COVID-19 virus, and the potential risk factors associated with the COVID-19 transmission have been estimated (Tang et al., 2020, Tang et al., 2020, Tang et al., 2020, Wang et al., 2020, Chen et al., 2020, Li, 2020, Benjamin Maie, 2020, Peng et al., 2020, Wu et al., 2019, You et al., 2020, Zeng et al., 2020, Zhou, 2020, Peng et al., 2020, Kucharski et al., 2020, Hellewell et al., 2019, Guan et al., 2020, Backer et al., 2019, Chen et al., 2019, Huang et al., 2020, Li et al., 2020, Zhu et al., 2019, Lu et al., 2020). The works (Tang et al., 2020, Tang et al., 2020, Tang et al., 2020, Wang et al., 2020, Chen et al., 2020, Li, 2020, Benjamin Maie, 2020, Peng et al., 2020, Wu et al., 2019, You et al., 2020, Zeng et al., 2020, Zhou, 2020, Peng et al., 2020, Kucharski et al., 2020, Hellewell et al., 2019) developed ordinary/stochastic/delay/partial differential equations and neural network models, calculated basic or effective reproduction number, and predicted the development trend of COVID-19 epidemic, and also evaluated the effectiveness of control measures, and obtained that how the government and the public should take preventive and control measures to effectively control the epidemic situation in the situation of expensive treatment costs and resource shortage. The studies (Guan et al., 2020, Backer et al., 2019, Chen et al., 2019, Huang et al., 2020, Li et al., 2020) analyzed the individual epidemiology and clinical symptoms, determined the epidemiological characteristics, contact history, and calculated the distribution characteristics of gender and age, incubation period, epidemic doubling time and the basic reproductive number, and showed that COVID-19 epidemic spreads rapidly by human-to-human transmission, and it is necessary to implement the measures to prevent or reduce transmission for the populations at risk. Besides, the literatures (Zhu et al., 2019, Lu et al., 2020) employed the unbiased sequencing, next-generation sequencing of samples, phylogenetic analysis, structural analysis, homology modelling and so on, and analyzed the genomic characterisation and epidemiology, and indicated that COVID-19 is a novel human-infecting coronavirus.

Further, media reports can inform the public about the severity of the epidemic and what preventive and control measures should be taken. Media reports on the infection dynamics will have profound psychological impacts on the public and so that people take individual behavior changes, such as wearing face masks, hand-washing, home quarantine, avoiding public transport and other crowded places(Yan et al., 2016, Yan et al., 2018, De Silva et al., 2009). Existing approaches have focused largely on modeling the media impact on emerging infectious disease prevention and control, and then exploring how media impact affect the number of infected individuals at different disease stages (exposed, infected, hospitalized and dead) (Cui et al., 2008, Collinson and Heffernan, 2014, Li and Cui, 2009, Liu et al., 2007, Sun et al., 2011, Yan et al., 2016, Yan et al., 2018). Besides, when the emerging infectious disease COVID-19 epidemic starts, the number of daily news items relevant to the disease is high; On the other hand, media reports have a great impact on the epidemic in the early stage of emerging infectious diseases (Yan et al., 2016).

However, how do media reports and individuals’ behaviour changes affect the dynamical development of COVID-19 epidemic during the outbreak? Therefore, the main aim of this paper is to address the following issues: (1) whether the number of news items relevant to the COVID-19 is correlated to the COVID-19 infection in the early stage? (2) how strong is this correlation? (3) how does individuals’ behaviour changes affect on the trend of the COVID-19 outbreak during the events? and (4) what is the impact of various control measures on the COVID-19 epidemic?.

To address those questions, we obtain the number of daily (new) hospital notifications, and the accumulated number of hospital notifications for infected and death of COVID-19 from the Chinese Center for Disease Prevention and Control (CDC) and Municipal Health Commissions (MHCs) in all provinces/provincial municipalities in China, and we obtain the number of daily news items relevant to the COVID-19 epidemic from twelve major websites, as showed in Fig. 1, Fig. 2, Fig. 3, Fig. 4 . To determine the strength of the correlation between the number of daily news items and the number of daily (new) hospital notifications, the Pearson correlation and cross-correlation analyses are conducted (Huang et al., 2011, Taylor, 1990, William, 2006). Then, we establish modified SEIR-type models, which incorporate the function of the behaviour change rate into the intensity of infection. The nonlinear least squares estimation is employed to find the best-fit parameter values to the observed data. At last, we assess the impact of individual behavior changes and the effectiveness of control measures by uncertainty and sensitivity analyses.

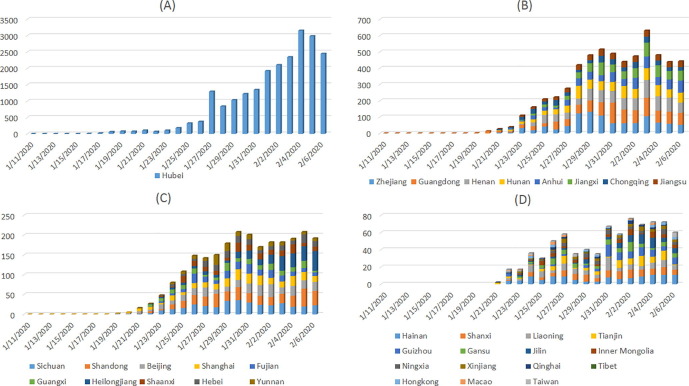
Fig. 1.

The number of new hospital notifications for all provinces/provincial municipalities in mainland China, Hong Kong, Macao and Taiwan from January 11th to February 6th 2020.

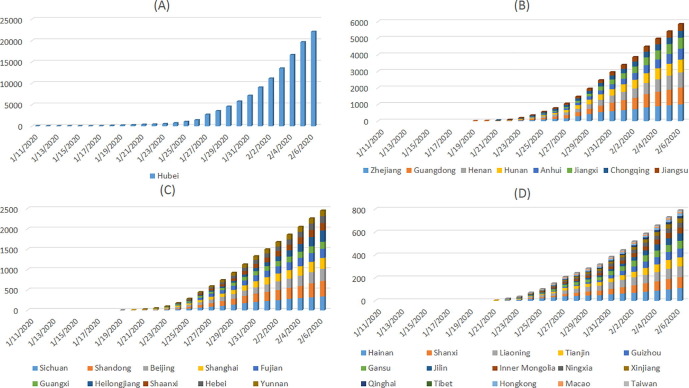
Fig. 2.

The accumulated number of hospital notifications all provinces/provincial municipalities in mainland China, Hong Kong, Macao and Taiwan from January 11th to February 6th 2020.

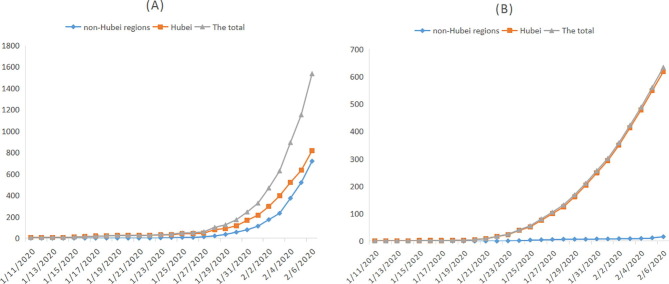
Fig. 3.

The accumulated number of cured cases and death cases for Hubei province and non-Hubei regions from January 11th to February 6th 2020.

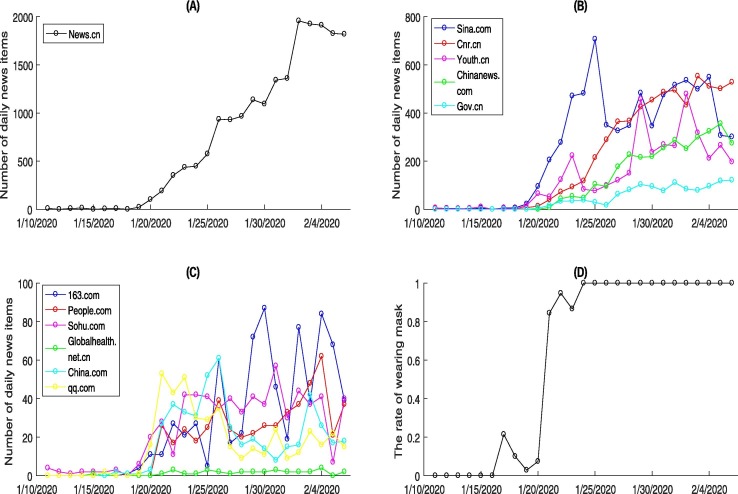
Fig. 4.

The the number of daily news items from the twelve popular sources during January 11th to February 6th 2020: (A)–(C). (D) The rate of wearing masks from January 11th to February 6th 2020.

2. Collection and distribution characteristics of reported COVID-19

2.1. Data collection

Data regarding daily laboratory-confirmed cases of COVID-19 in this study are obtained from the CDC and MHCs in all provinces/provincial municipalities in mainland China (including 23 provinces, 4 municipalities, and 5 autonomous regions), Hong Kong, Macao and Taiwan, from January 11th to February 6th 2020 (The Chinese Center for Disease Prevention and Control, 2020, The Municipal Health Commissions, 2020). A confirmed case is diagnosed according to the World Health Organization (WHO) interim guidance(WHO, 2020). The data of each province/provincial municipality including the number of new hospital notifications, the accumulated number of hospital notifications, the number of cured cases and death cases, tracking close contacts, releasing close contacts, the number of clinical condition (cured cases, mild symptoms, severe cases, critical illness, death), as shown in Fig. 1, Fig. 2, Fig. 3 and Table 1 . The case information at the individual level are achieved from MHCs and news reports of all cities, which includes the age, gender, place of household registration, present address, place of diagnosis, whether or not had history of residence or contact in Wuhan, whether or not had contact history of other cities, whether or not had contact history of confirmed cases, time of initial episode, time of first visit hospital, clinical condition and so on, as shown in Table 2 .

Table 1.

The distribution characteristics of COVID-19 on February 6th 2020.

Province	The number of hospital notifications						Total close contacts
	total cured	mild	severe	critical	total death	total	Tracking	Removing
Hubei	817	16675	3161	841	618	22112	101599	37542
Guangdong	68	830	85	34	1	1018
Zhejiang	98	836	51	21	0	1006	22270	7441
Henan	68	768	48	27	3	914	19555	3356
Hunan	91	624	57	0	0	772	19031	9141
Anhui	34	625	0	6	0	665	14235
Jiangxi	45	558	58	0	0	661	16631	5102
Chongqing	24	340	29	16	2	411	13066	5627
Jiangsu	38	365	4	1	0	408	7876	1994
Shandong	31	320	22	6	0	379	12007	6474
Sichuan	37	287	0	19	1	344	8392	1166
Beijing	33	248	0	15	1	297
Heilongjiang	8	238	28	0	3	277	7144	3273
Shanghai	25	225	10	8	1	269
Fujian	15	190	11	8	0	224	6150	2508
Shaanxi	11	165	8	0	0	184	8309	3088
Guangxi	17	140	9	6	0	172	8008	3909
Hebei	16	140	14	0	1	171	5916	487
Yunan	7	98	16	2	0	123	3281	2631
Hainan	8	86	15	0	2	111	2570	1367
Shanxi	12	74	6	4	0	96	2710	1511
Liaoning	5	81	7	1	0	94	1710	797
Tianjin	2	41	28	7	1	79	599	70
Guizhou	6	60	4	6	1	77	1045	369
Gansu	9	50	5	3	0	67	2433	1138
Jilin	4	56	3	1	1	65	2073	825
Inner Mongolia	0	43	5	2	0	50	1289	195
Ningxia	1	41	1	0	0	43	1818	595
Xinjiang	0	30	7	2	0	39	2392	0
Qinghai	3	14	1	0	0	18	384	39
Tibet	0	1	0	0	0	1
Hongkong	1	22	0	0	1	24
Macao	5	5	0	0	0	10
Taiwan	1	15	0	0	0	16

Table 2.

The statistical description for the COVID-19 data at the individual level on February 6th 2020.

Province	Sex			Age					lived or contact history of the infection
	Male	Female	Unknown	0 $\sim$ 5	6 $\sim$ 17	18 $\sim$ 59	$\sim$60	Unknown	Wuhan	other cities	confirmed cases	unknown
Hubei			22112					22112	11618	0	0	10494
Guangdong	145	141	732	7	13	203	57	738	250	18	2	748
Zhejiang	461	467	78	9	18	764	154	61	243	58	369	336
Henan	385	320	209	9	17	581	96	211	282	0	122	510
Hunan	262	202	308	3	6	329	66	368	74	9	9	680
Anhui	266	206	193	2	14	392	57	200	228	49	12	376
Jiangxi	201	159	301	2	2	269	53	335	59	13	18	571
Chongqing	73	64	274	1	5	110	32	263	37	0	17	357
Jiangsu	203	161	44	1	10	281	64	52	74	29	1	304
Shandong	206	128	45	12	12	275	46	34	113	29	109	128
Sichuan	91	86	167	0	5	150	23	166	82	5	0	257
Beijing	147	150	0	11	9	203	74	0	148	0	68	81
Heilongjiang	36	42	199	1	1	43	11	221	13	6	35	223
Shanghai	140	129	0	0	0	0	0	269	116	8	84	61
Fujian	8	12	204	0	0	6	1	217	34	0	0	190
Shaanxi	104	80	0	3	5	141	35	0	93	1	42	48
Guangxi	72	80	20	4	6	114	26	22	91	11	0	70
Hebei	89	61	21	2	8	117	22	22	111	34	1	25
Yunan	45	43	35	1	9	58	20	35	77	3	2	41
Hainan	44	37	30	1	2	47	31	30	74	3	0	34
Shanxi	14	10	72	0	1	15	3	77	29	0	2	65
Liaoning	24	15	55	0	25	10	1	58	7	6	7	74
Tianjin	44	35	0	0	1	58	20	0	39	8	27	5
Guizhou	38	39	0	1	7	54	12	3	20	25	2	30
Gansu	30	31	6	1	0	39	9	18	39	12	0	16
Jilin	37	25	3	0	3	49	7	6	18	0	27	20
Inner Mongolia	8	9	33	0	0	16	1	33	2	0	15	33
Ningxia	15	12	16	0	1	20	6	16	14	2	0	27
Xinjiang	4	1	34	0	0	5	0	34	6	0	0	33
Qinghai	10	1	7	0	3	14	0	1	12	3	0	3
Tibet	1	0	0	0	0	1	0	0	1	0	0	0
Hongkong	12	12	0	0	0	11	13	0	11	0	5	8
Macao	3	7	0	0	1	7	2	0	7	0	3	0
Taiwan	1	6	9	0	0	3	2	11	8	0	0	8

We also obtain the daily news items related to the COVID-19 epidemic from twelve major popular websites in China: news.cn (xinhua net), sina.com, cnr.cn (Chinese Radio Network), youth.cn, Chinanews.com, gov.com (Central People’s Government of the People’s Republic of China), 163.com, people.com, sohu.com, globalhealth.net.cn, China.com, qq.com, by using the key word Chinese character of ’Xinguanfeiyan’ included in the news item title, from January 11th to February 6th 2020 (Xinhua Net, 2020, sina, 2020, China National Radio, 2020, Youth.cn, 2020, News China, 2020, Central People’s Government of the People’s Republic of China, 2020, News, 2020, People.com, 2020, Sohu, 2020, Globalhealth.net.cn, 2020, China.com, 2020, QQ.com, 2020). This is shown in Fig. 4(A-C). Besides, we collect the rate of wearing masks from the totally 30 news videos relevant to the COVID-19 (such as CCTV videos, qq.com videos et al.) in Wuhan from January 11th to 23rd 2020. As Wuhan adopted the lock down policy on the 23rd, and stipulated that everyone must wear a mask when going out, therefore, we assume that the rate of wearing masks is 1 from January 24th to February 6th 2020, as shown in Fig. 4(D).

2.2. Distribution characteristics of reported COVID-19

Fig. 1 shows that the peak time of new hospital notifications is: (A) February 4th to 5th, (B) January 29th to 31st and February 2nd to 4th, (C) January 29th to 31st and February 4th to 6th, (D) January 31st and February 2nd to 5th. It is related to the control measures taken. Since Wuhan was locked down on January 23rd, and before that, more than 5 million people left Wuhan and went to all parts of the country. At this time, some of them may have been infected. After a incubation period of 3–10 days, they were diagnosed from January 29th to 31st. Therefore, cities in other provinces except Hubei first broke out from January 29th to 31st. This can be confirmed by individual detailed data released by MHC and media reports in various provinces. In addition, during this period, people in the incubation period will transmit the virus to close contacts, resulting in another small outbreak on February 2nd to 6th. It can be seen from Fig. 2 that the accumulated number of hospital notifications in most provinces shows an exponential growth pattern. Besides, the accumulated number of cured cases and death cases also show an exponential growth pattern in Hubei province and China, as shown in Fig. 3. The rate of cured in non–Hubei regions higher than that of Hubei after February 3. Most of the deaths occurred in Hubei during the study.

From Table 1, we can obtain that a total of 31209 cases infected with COVID-19 were confirmed by laboratory tests in China on February 6th 2020. These provinces with the accumulated number of hospital notifications more than 400 on February 6th 2020 are Hubei (account for about 70.88%), Guangdong (3.26%), Zhejiang (3.22%), Henan (2.93%), Hunan (2.47%), Anhui (2.13%), Jiangxi (2.12%), Chongqing (1.32%), Jiangsu (1.31%), respectively. These 10 provinces/provincial municipalities/special administrative regions with the highest accumulated cure rate on February 6th 2020 are: Macao (50.00%), Qinghai (16.67%), Gansu (13.43%), Shanxi (12.50%), Hunan (11.79%), Beijing (11.11%), Sichuan (10.76%), Guangxi (9.88%), Zhejiang (9.74%), Hebei(9.36%). The accumulated cure rate of Hubei is 3.69%. It is noted that there is only one 34-year-old male case lived in Wuhan in Tibet, and he is still hospitalized on February 6th 2020, so we will not analyze the epidemic situation in Tibet in the whole study. Provinces with accumulated number of death cases more than 2 are: Hubei (mortality 2.79%), Hainan (1.80%), Heilongjiang (1.08%), Chongqing (0.49%), Henan (0.33%). Fortunately, there are 20 provinces/provincial municipalities/special administrative regions with zero deaths during the study period. The provinces that severe cases account for more than 10% of number of hospitalized patients are: Tianjin (36.84%), Xinjiang (17.95%), Hubei (15.29%), Hainan (14.85%), Yunnan (13.79%), Heilongjiang (10.53%), Inner Mongolia (10.00%). The provinces that critical illness account for more than 5% of number of hospitalized patients are: Tianjin (9.21%), Guizhou (8.57%), Sichuan (6.21%), Beijing (5.70%), Gansu (5.17%), Xinjiang (5.13%).

These provinces where accumulated number of hospital notifications account for more than 5% of the total number of tracking close contacts are: Hubei (21.76%), Tianjin (13.19%), Guizhou (7.37%), Liaoning (5.50%), Jiangsu (5.18%). These results show that the average diagnosis rate in these provinces is relatively higher. Conversely, the provinces with smallest rate of that are: Xinjiang (1.63%), Guangxi (2.15%), Shaanxi (2.21%), Ningxia (2.37%), Gansu (2.75%), Hebei (2.89%), which indicate the control measures in these provinces are relatively more strict. Provinces with more than 50% of the total number of tracking close contacts removed are: Yunnan (80.19%), Shanxi (55.76%), Shandong (53.92%), Hainan (53.19%), and which means the epidemic situation in these provinces has been gradually alleviated.

The statistical description for the collected data at the individual level is shown in Table 2. Considering the lack of data in the individual level, we analyze provinces with the missing data less than 30% in the following. For gender indicators, 18 regions are selected and the proportion of male in the known individuals is 53.63%. The statistical description of the proportion of male are: mean (52.34%), minimum (30%), lower quartile (49.46%), median (53.18%), upper quartile (56.40%), maximum (61.68%). For age indicators, 18 regions are selected and the distribution characteristics (the total number of infection individuals, proportion) are: 0 $\sim$ 5 (57, 1.40%), 6 $\sim$ 17 (125, 3.07%), 18 $\sim$ 59 (3205, 78.65%), $⩾$60 (688, 16.88%). In particular, there are five regions with no missing data for age. Their age distribution characteristics (the total number of infection individuals, proportion) are as follows: 0 $\sim$ 5 (14, 2.36%), 6 $\sim$ 17 (16, 2.69%), 18 $\sim$ 59 (420, 70.71%), $⩾$60 (144, 24.24%). Besides, these provinces selected with high proportion of individuals (who have lived in Wuhan or contacted with Wuhan’s people) in the known individuals are: Qinghai (80.00%), Gansu (76.47%), Hebei (76.03%), Macao (70%), Beijing (68.52%), Shaanxi (68.38%), Shanghai (55.77%), Tianjin (52.70%). (See Table 3) .

Table 3.

Pearson correlation analysis between the number of daily news items and the number of new hospital notifications of COVID-19 in China from January 11th to February 6th 2020.

	y	$y_1$	$x_1$	$x_2$	$x_3$	$x_4$	$x_5$	$x_6$	$x_7$	$x_8$	$x_9$	$x_{10}$	$x_{11}$	$x_{12}$
y	1
$y_1$	0.993**	1
$x_1$	0.974**	0.949**	1
$x_2$	0.646**	0.583**	0.737**	1
$x_3$	0.948**	0.905**	0.966**	0.747**	1
$x_4$	0.767**	0.716**	0.838**	0.739**	0.817**	1
$x_5$	0.976**	0.947**	0.968**	0.711**	0.981**	0.808**	1
$x_6$	0.919**	0.885**	0.916**	0.707**	0.947**	0.832**	0.957**	1
$x_7$	0.763**	0.723**	0.808**	0.626**	0.783**	0.796**	0.763**	0.760**	1
$x_8$	0.806**	0.776**	0.864**	0.825**	0.829**	0.683**	0.793**	0.738**	0.736**	1
$x_9$	0.569**	0.494**	0.678**	0.882**	0.716**	0.687**	0.629**	0.651**	0.610**	0.782**	1
$x_{10}$	0.562**	0.509**	0.642**	0.801**	0.665**	0.562**	0.618**	0.596**	0.601**	0.804**	0.740**	1
$x_{11}$	0.280	0.231	0.413*	0.724**	0.396*	0.322	0.320	0.287	0.386*	0.690**	0.603**	0.616**	1
$x_{12}$	0.097	0.066	0.215	0.556**	0.174	0.267	0.135	0.183	0.269	0.493**	0.539**	0.437*	0.766**	1

Significance of correlation coefficient different from zero: ** represents $p<0.01$, * represents $p<0.05$.

3. Data analysis

In the following, y and $y_1$ denote the number of new hospital notifications in China and Hubei province, respectively. For the number of daily news items from each source, we use $x_1$ for news.cn, $x_2$ for sina.com, $x_3$ for cnr.cn, $x_4$ for youth.cn, $x_5$ for Chinanews.com, $x_6$ for gov.com, $x_7$ for 163.com, $x_8$ for people.com, $x_9$ for sohu.com, $x_{10}$ for globalhealth.net.cn, $x_{11}$ for China.com, $x_{12}$ for qq.com, respectively. To explore the relationships between the number of daily news items and the number of new hospital notifications for COVID-19 in China and Hubei province during the specified period, the Pearson correlation (Huang et al., 2011, Taylor, 1990) and the cross-correlation analyses (Huang et al., 2011, William, 2006) methods are used.

3.1. Pearson correlation analysis

We conduct the Pearson correlation analysis to determine the association between the number of daily news items and the number of new hospital notifications from January 11th to February 6th 2020. These results are summarized in Table 2. We conclude that the number of daily news items from website of news.cn ($x_1$), cnr.cn ($x_3$), youth.cn ($x_4$), Chinanews.com ($x_5$), gov.com ($x_6$), 163.com($x_7$) and people.com ($x_8$) are statistically significantly highly correlated with the number of new hospital notifications (y and $y_1$) over the study period according to the labeling systems roughly categorized (low or weak correlations ($|\gamma |⩽0.35$), moderate correlations ($0.36⩽|\gamma |⩽0.67$) and strong/high correlations ($0.68⩽|\gamma |⩽1.0$)(Taylor, 1990)). And the number of daily news items of sina.com ($x_2$), sohu.com ($x_9$) and globalhealth.net.cn ($x_{10}$) are moderately correlated with y and $y_1$. Among these seven popular websites, the number of daily news items of news.cn is most closely correlated with the number of new hospital notifications ($r_{x_{1}y}=0.974,r_{x_1{y}_1}=0.949,p<0.01$), while the correlation for globalhealth.net.cn is relatively weak ($r_{x_{10}y}=0.562,r_{x_{10}{y}_1}=0.509,p<0.01$).

Besides, Table 2 also shows that most of these websites have statistically significant high or moderate correlations in terms of reporting the COVID-19 infection dynamics. In particular, we notice that $x_1$ are highly correlated to $x_2,x_3,x_4,x_5,x_6,x_7,x_8$ and $x_9$, while $x_{10}$ is moderately correlated to $x_1$. We also notice the high or moderate correlation pairs except for $(x_1,x_{12}),(x_3,x_{12}),(x_4,x_{12}),(x_5,x_{11}),(x_5,x_{12}),(x_6,x_{11}),(x_6,x_{12})$ and $(x_7,x_{12})$.

To identify time lags between the daily reported news and the daily hospital notifications, cross-correlation analysis is also necessary despite Pearson correlation analysis can reveal the statistically significant correlation between them.

3.2. Cross-correlation analysis

Cross-correlation is a spectral analysis technique that can be used to provide qualitative insights on the casual temporal interaction between the number of daily news items and the number of new hospital notifications of COVID-19. To reveal the range of the cross-correlation coefficients and to identify the specific value of time lags where these coefficients achieve their maximum values, in what follows, the data of the China and Hubei province are used. This information is critical to fitting the data to our proposed dynamic models in order to illustrate the media impact(see more details in literature (Yan et al., 2016)).

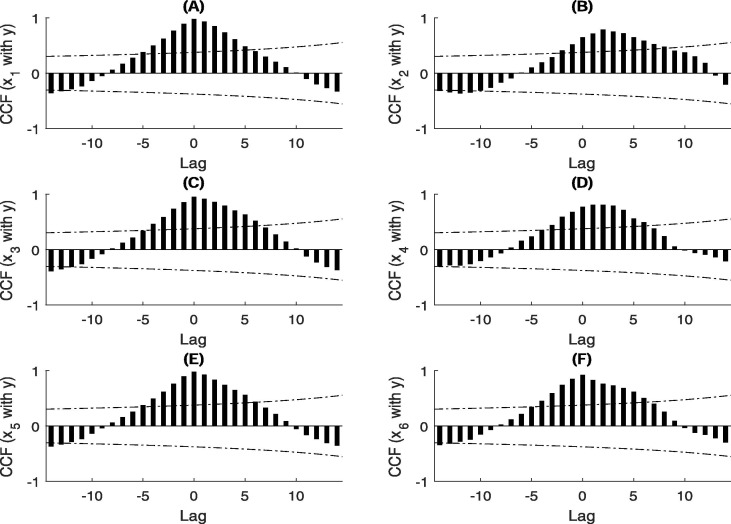
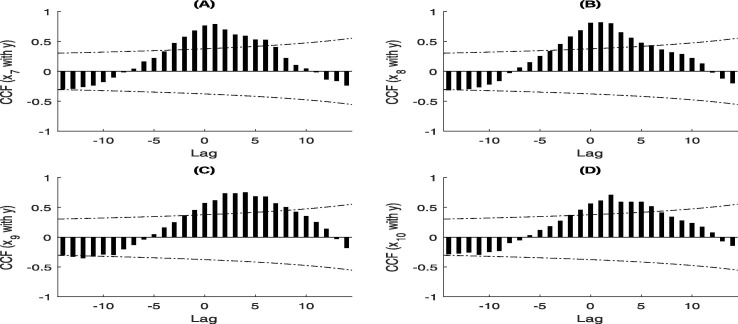
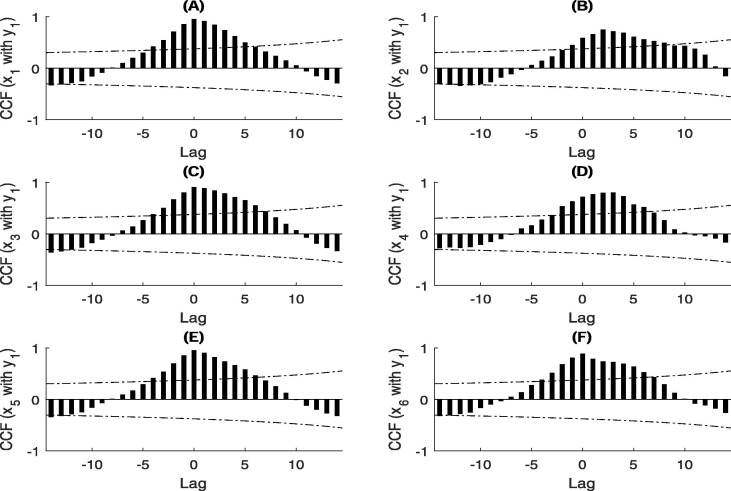
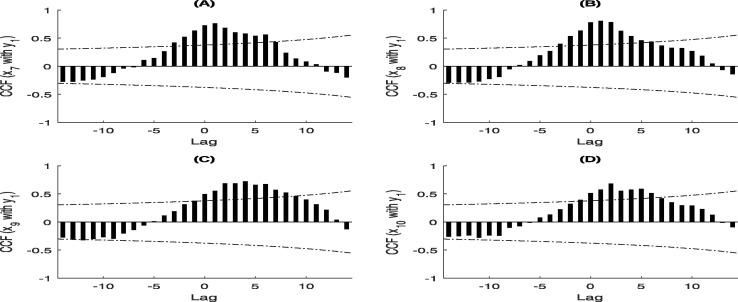
We calculate the cross-correlation function (CCF) between the number of daily news items of each website and the number of new hospital notifications in China. The results are summarized in Fig. 5 and Fig. 6 . We observe that there are statistically significant cross-correlation between the number of daily news items at the sites $x_1,x_2,x_3,x_4,x_5,x_6,x_7,x_8,x_9,x_{10}$ and the number of new hospital notifications y at lags ranging from −5 to 5 days, −3 to 8 days, −4 to 6 days, −3 to 6 days, −5 to 5 days, −4 to 6 days, −3 to 6 days, −3 to 5 days, −1 to 8 days, −1 to 6 days, respectively (see Fig. 5 and Fig. 6). Therefore, there exists a feedback relationship (for $k\ne 0$) and a contemporaneous relationship (for $k=0$) between the number of daily news items at $x_1,x_2,x_3,x_4,x_5,x_6,x_7,x_8,x_9,x_{10}$ and the number of new hospital notifications, and the relation is linear in the range of time lags. We observe that the local maximal cross correlation coefficient exceeds 0.7 (highly correlated) occur at the time lags of 0, 2, 0, 1, 0, 0, 1, 1, 4, 2 days (Fig. 5 and Fig. 6), respectively. Other cross-correlation results (for example, the number of daily news items of each website and the number of new hospital notifications in Hubei province ($y_1$)) can be found in Supplementary Fig. A.1, Fig. A.2.

Fig. 5.

Cross-correlation coefficients between the number of daily news items and the number of new hospital notifications of COVID-19 in China from January 11th to February 6th 2020. The two dotted lines in the graphs represent the upper and lower confidence bounds of 95% confidence intervals.

Fig. 6.

Cross-correlation coefficients between the number of daily news items and the number of new hospital notifications of COVID-19 in China from January 11th to February 6th 2020. The two dotted lines in the graphs represent the upper and lower confidence bounds of 95% confidence intervals.

Fig. A.1.

Cross-correlation coefficients between the number of daily news items and the number of new hospital notifications of COVID-19 in Hubei province from January 11th to February 6th 2020. The two dotted lines in the graphs represent the upper and lower confidence bounds of 95% confidence intervals.

Fig. A.2.

Cross-correlation coefficients between the number of daily news items and the number of new hospital notifications of COVID-19 in Hubei province from January 11th to February 6th 2020. The two dotted lines in the graphs represent the upper and lower confidence bounds of 95% confidence intervals.

4. Model formulation

4.1. SEIRDAH framework

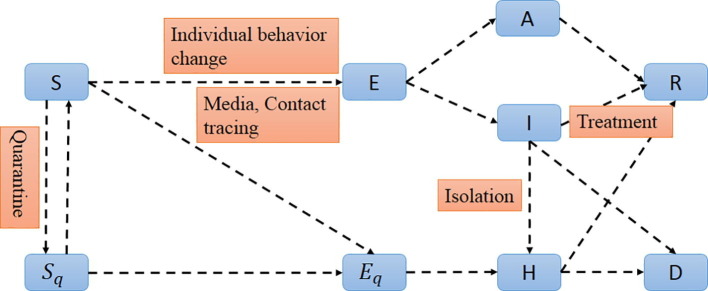
We now incorporate media impact into the general SEIR-type (susceptible-exposed-infective -recovery) epidemiological model, which incorporates appropriate compartments relevant to interventions such as quarantine, isolation and treatment (Tang et al., 2020, Castillo-Chavez et al., 2003). We stratify the susceptible ($S(t)$), exposed ($E(t)$), infectious but not yet symptomatic (asymptomatic) (A), infectious with symptoms (I), hospitalized (H) and recovered (R), the quarantined susceptible ($S_q$), isolated exposed ($I_q$), and isolated infected ($I_q$) compartments in the general SEIR-type model (donated by SEIRDAH model).

Due to media reports lead to individual behavior changes, and based on the model selection results of literature (Yan et al., 2018), the model with rate of behaviour change depicted by an exponential function could fit the observed data best. Therefore, the function of the rate of wearing masks ($e^{-\mathit{kp}(t)}$) is used to describe the impact of individual behavior changes (media) on the COVID-19 epidemic (The rate of wearing masks, $p(t)$, is used to represent the collected data of the wearing masks rate from January 11th to February 6th 2020, as shown in Fig. 4(D)).

Let the individuals expose to the virus is quarantined with a proportion q by contact tracing. If the quarantined individuals are effectively infected, they will move to $E_q$ compartment, $S_q$ compartment otherwise. The individuals who exposed to the virus are missed from the contact tracing with rate $1-q$, can either move to the compartment E or still stay in compartment S, depending on whether they are effectively infected or not. We assume that the base transmission probability is $\beta$ and the contact rate is constant c. Besides, the impact of individual behavior changes (media) on the COVID-19 epidemic ($e^{-\mathit{kp}(t)}$) is embed into the transmission probability. Then, the quarantined individuals, if infected (or uninfected), move to the compartment $E_q$ (or $S_q$) at the rate of $\beta e^{-\mathit{kp}(t)}\mathit{cq}$ (or $(1-\beta e^{-\mathit{kp}(t)})\mathit{cq}$). For those who are not quarantined, they will move to the compartment E at the rate of $\beta e^{-\mathit{kp}(t)}c(1-q)$ if they infected. The infected individuals can be detected and, then, isolated at a rate of ${\delta }_I$ and can also move to the compartment R at the rate of ${\gamma }_I$ due to recovery. The infectious with symptoms individuals I and the quarantined infected individuals H all move to the compartment D at the rate of $\alpha$. And also the asymptomatic individuals are driving the tracking quarantine(Tang et al., 2020). All of these leads to the following SEIRDAH model:

$$\left\{\begin{array}{c}\frac{\mathit{dS}(t)}{\mathit{dt}}=-(\beta e^{-\mathit{kp}(t)}c+\mathit{cq}(1-\beta e^{-\mathit{kp}(t)}))S(t)(I(t)+\theta A(t))+\lambda S_q(t),\hfill \\ \frac{\mathit{dE}(t)}{\mathit{dt}}=\beta e^{-\mathit{kp}(t)}c(1-q)S(t)(I(t)+\theta A(t))-\sigma E(t),\hfill \\ \frac{\mathit{dI}(t)}{\mathit{dt}}=\sigma \rho E(t)-({\delta }_I+\alpha +{\gamma }_I)I(t),\hfill \\ \frac{\mathit{dA}(t)}{\mathit{dt}}=\sigma (1-\rho )E(t)-{\gamma }_{A}A(t),\hfill \\ \frac{{\mathit{dS}}_q(t)}{\mathit{dt}}=\mathit{cq}(1-\beta e^{-\mathit{kp}(t)})S(t)(I(t)+\theta A(t))-\lambda S_q(t),\hfill \\ \frac{{\mathit{dE}}_q(t)}{\mathit{dt}}=\mathit{cq}\beta e^{-\mathit{kp}(t)}S(t)(I(t)+\theta A(t))-S_q(t)E_q(t),\hfill \\ \frac{\mathit{dH}(t)}{\mathit{dt}}={\delta }_{I}I(t)+{\delta }_q{E}_q(t)-(\alpha +{\gamma }_H)H(t),\hfill \\ \frac{\mathit{dR}(t)}{\mathit{dt}}={\gamma }_{I}I(t)+{\gamma }_{A}A(t)+{\gamma }_{H}H(t),\hfill \\ \frac{\mathit{dD}(t)}{\mathit{dt}}=\alpha I(t)+\alpha H(t)\text{.}\hfill \end{array}\right)$$ (1)

The diagram of the model (1) are showed in Fig. A.3. The more detailed definitions of variables and parameters for model (1) are provided in Table 4 .

Fig. A.3.

Diagram of the model (1) for simulating the COVID-19 infection. Interventions including media report, individual behavior change, intensive contact tracing followed by quarantine and isolation are indicated.

Table 4.

Initial conditions and parameter values for model (1).

Initial values	Description	Estimated value	Mean	Std	Source
$S(0)$	Initial susceptible population	11081000			(Health Commission of Hubei Province, 2020)
$E(0)$	Initial exposed population	105.1			(Tang et al., 2020)
$I(0)$	Initial symptomatic infected population	27.679			(Tang et al., 2020)
$A(0)$	Initial asymptomatic infected population	53.839			(Tang et al., 2020)
$S_q(0)$	Initial quarantined susceptible population	763			data
$E_q(0)$	Initial quarantined exposed population	1.1642			(Tang et al., 2020)
$H(0)$	Initial quarantined infected population	34			data
$R(0)$	Initial recovered population	6			data
$D(0)$	Initial death population	1			data
Parameter	Description	Estimated value	Mean	Std	Source
k	the behavior change constant	$5.0147\times {10}^{-13}$	$4.7644\times {10}^{-13}$	$9.4098\times {10}^{-14}$	LS
$\beta$	Probability of transmission per contact	$1.8681\times {10}^{-8}$	$1.8682\times {10}^{-8}$	$2.3218\times {10}^{-12}$	LS
c	Contact rate	22.1690	19.8110	2.7445	LS
q	Quarantined rate of exposed individuals	$3.1363\times {10}^{-7}$	$1.2489\times {10}^{-7}$	$1.0564\times {10}^{-7}$	LS
$\theta$	Contact rate regulatory factor for asymptomatic infected individuals	$4.5503\times {10}^{-11}$	0.0417	0.0661	LS
$\lambda$	Rate at which the quarantined uninfected contacts were released into the wider community	1/14			(Tang et al., 2020)
$\sigma$	Transition rate of exposed individuals to the infected class	1/7			(World Health Organization (WHO), 2020)
$\rho$	Probability of having symptoms among infected individuals	0.7966	0.8392	0.0663	LS
${\delta }_I$	Transition rate of symptomatic infected individuals to the quarantined infected class	0.0909	0.0932	0.0062	LS
${\delta }_q$	Transition rate of quarantined exposed individuals to the quarantined infected class	0.0239	0.0312	0.0323	LS
$\alpha$	Disease-induced death rate	0.0024	0.0025	0.0002	LS
${\gamma }_I$	Recovery rate of symptomatic infected individuals	0.4325	0.4098	0.0376	LS
${\gamma }_A$	Recovery rate of asymptomatic infected individuals	0.2080	0.1780	0.0475	LS
${\gamma }_H$	Recovery rate of quarantined infected individuals	0.1729	0.1529	0.0452	LS

4.2. Parameter estimation and model fitting

The population of Wuhan is around 11081000 inhabitants (Health Commission of Hubei Province, 2020), hence, we set $S(0)=11081000$. By January 11th 2020, 6 patients recovered and were discharged from the hospital leading to $R(0)=6$; 763 individuals were quarantined leading to $S_q(0)=763$; and 1 patient were death leading to $D(0)=1$. The accumulated number of infected case on January 11th 2020 is 41, and we set quarantined infected population $H(0)=34$. The quarantined individuals were isolated for 14 days, thus $\lambda =1/14$, then we carry out the uncertainty and sensitivity analyses for this parameter value. According to WHO(World Health Organization (WHO), 2020), the incubation period of COVID-19 is about 7 days, hence $\sigma =1/7$.

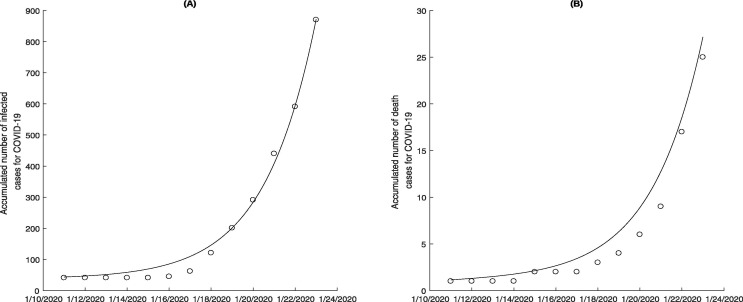
We obtain other unknown parameter values by fitting data on the accumulated number of infected cases and the accumulated number of death cases of COVID-19. To do so, we utilized the nonlinear least-square (NLES) method in Matlab to fit the aforementioned real data sets which correspond to the model solution time series, i.e. $C(t)$ and $D(t)$, where $C(t)$ follows the $\mathit{dC}(t)/\mathit{dt}={\delta }_{I}I(t)+{\delta }_q{E}_q(t)$, as shown in Fig. 7 . The estimated parameter values are listed in Table 4. Besides, we achieve the mean values and standard deviations of the unknown parameters by stochastic simulation technique.

Fig. 7.

Model fitting for the accumulated number of hospital notifications for infected and death of COVID-19 from January 11th to 23th 2020.

5. Uncertainty and sensitivity analyses

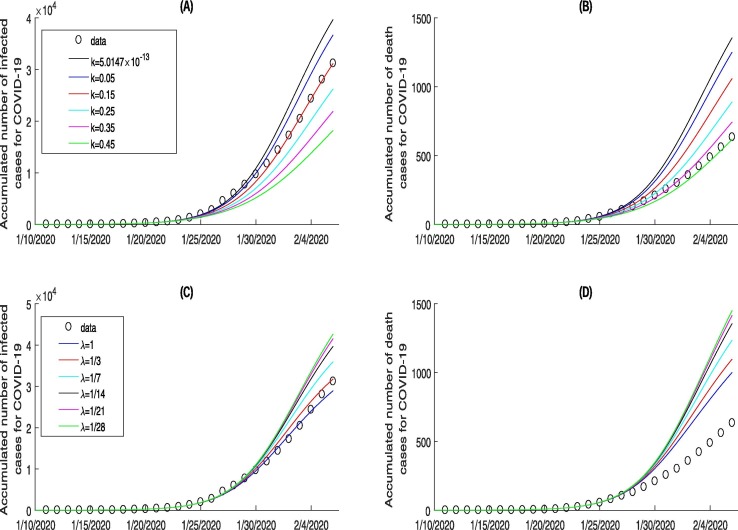
Predictions of model (1) for the accumulated number of infected cases and death cases from January 24th to February 6th 2020 for different behaviour change constant are shown in Fig. 8 (A) and (B). From the observed data, we note that the epidemic of COVID-19 is becoming more and more serious, and a more reasonable explanation is that, during the Spring Festival, people returning home had led to the spread of the epidemic from Wuhan (urban concentrations) to vast provinces/provincial municipalities.

Fig. 8.

Sensitivity analyses of key parameter k and $\lambda$ related to the individual behaviour change and the quarantined duration of uninfected contacts individuals on the COVID-19 infected cases and deaths cases from January 11th to February 6th 2020, where the baseline value $k=5.0147\times {10}^{-13}$ and $\lambda =1/14$.

However, if people kept their behaviour as it was over a period of time, i.e., the behaviour change constant from January 24th to February 6th is $k=5.0147\times {10}^{-13}$, very small and almost zero, which will lead to a significant increase in the accumulated number of infected cases and death cases, and result in an increase of the estimated accumulated number of infected cases and death cases by February 6th by 27.19% and 113.97%. Furthermore, as a result of media reports and lock down measures during the Spring Festival, the behaviour change constant could become lager, i.e., $k=0.15$, the estimated accumulated number of infected cases of COVID-19 is almost the same as the reported cases, and the estimated accumulated number of death cases increased by 40.57%. While the behaviour change constant reaches to 0.45 (i.e. $k=0.45$), the estimated accumulated number of infected cases will largely reduced, and decreased by 41.62%, and the estimated accumulated number of death cases is almost the same as the reported cases by February 6th. All these results confirm that the media reports and then individual behaviour change greatly contribute to the prevention and control of the emerging infectious diseases COVID-19.

The effects of quarantined duration of uninfected contacts individuals $\lambda$ on infections with COVID-19 are shown in Fig. 8(C) and (D), from which we can see that the estimated accumulated number of infected cases and deaths cases significantly increases as quarantined duration increases. This suggests that infection may occur during quarantined for COVID-19. From Fig. 8(C) and (D), we can see that when the quarantined duration is 3 days, the estimated the accumulated number of infected coincides with the real data, which also shows the management departments and designated hospitals of the COVID-19 have taken strong and effective quarantined measures in the later period.

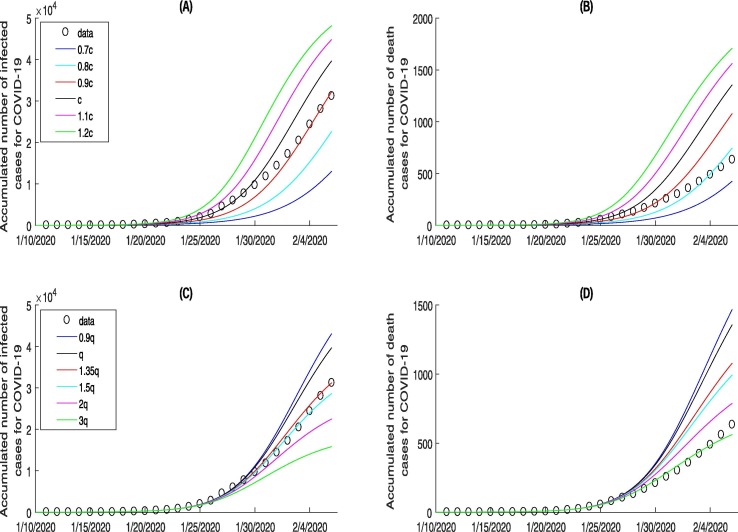
The effects of the parameters c on COVID-19 infection are shown in Fig. 9 (A) and (B). It implies that the less the contact rate, the less the estimated accumulated number of infected cases and deaths cases is. In particular, estimated accumulated number of infected cases and deaths cases by February 6th 2020 can be controlled at around 13076 and 427, and decreased by 58.10% and 32.59% if the contact rate c decreased by 30% ($0.7c$); while increased by 54.27% and 169.34% if the contact rate c increased by 20% of the baseline ($1.2c$). Fig. 9(A) and (B) indicate the effectiveness of reducing contact rate and the crucial role of experts in promoting people’s home quarantined. Furthermore, when the number of contacts is equal to $0.9c$, the estimated accumulated number of infected cases coincides with the real data, which also shows that, to a certain extent, people listened to the expert’s advice and the related management departments’ call to take measures of home quarantined.

Fig. 9.

Sensitivity analyses of key parameter c and q related to the contact rate and quarantined rate of exposed individuals on the COVID-19 infected cases and deaths from January 11th to February 6th 2020, where the baseline value $c=22.169$ and $q=3.1363\times {10}^{-7}$.

Fig. 9(C) and (D) show the variation in accumulated number of infected cases and deaths cases with quarantined rate of exposed individuals q. It follows from Fig. 9(C) and (D) that the larger quarantined rate of exposed individuals, the less estimated accumulated number of infected cases and deaths cases are. This indicates the effectiveness of increasing the quarantined intensity for the exposed individuals. When the quarantined rate is equal to $1.35q$, estimated accumulated number of infected cases is exactly consistent with the real data, which also shows that strong quarantined measures has been taken for the exposed population in the later period.

6. Discussion and conclusions

Media reports play increasingly important roles in the outbreak of the COVID-19 epidemic, which can be used to provide the public with information about the dynamic situation of the epidemic and the effective prevention and control measures proposed by experts.

It follows from the Pearson correlation and the cross-correlation analyses that the number of daily news items at the ten most popular websites (news.cn, sina.com, cnr.cn, youth.cn, Chinanews.com, gov.com, 163.com, people.com, sohu.com, globalhealth.net.cn) are highly/moderately correlated with the number of new hospital notifications during the period. All of these confirm that not only the number of daily news items had impact on the disease control (in terms of the number of new hospital notifications), but also the disease dynamics statistics (in terms of new hospital notifications) affected the news coverage. That is because the outbreak resulted in substantially increasing media coverage, which in turn helped increase the population awareness and alter their behaviors for a better implementation of mitigation.

The individual behaviour change constant k, the rate of quarantined duration of uninfected contacts individuals $\lambda$, the contact rate c, quarantined rate of exposed individuals q all markedly affect the outbreak of epidemic COVID-19. In particular, the estimated accumulated number of infected cases will controlled at around 18219, and decreased by 41.62% if the behaviour change constant k reaches to 0.45 (i.e. $k=0.45$); or increased by 15.23% if the rate of quarantined duration of uninfected contacts individuals $\lambda$ increased to 1/7 (i.e. quarantined duration decreased to 7 days); or decreased by 49.29% if the quarantined rate of exposed individuals q increased to $3q$.

There are three possible reasons for effects of quarantined duration of uninfected contacts individuals $\lambda$ on infections. Firstly, due to the limited medical resources, such as isolation wards and beds, many quarantined contact individuals are together. The infected contact individuals may transmit the virus to the uninfected contact individuals, making them infected. Secondly, since the limited number of medical staffs, a medical staff needs to care for multiple quarantined contact individuals at the same time. In this process, the medical staff may transmit the virus from the infected contact individuals to the uninfected contact individuals, making them become infected. Lastly, because the medical staffs may be asymptomatic infected, but also have to nurse a number of quarantined contact individuals, and passed the virus to the uninfected contact individuals in this process, making them infected. This further shows that it is not the longer the quarantined duration of uninfected contacts individuals, the better, but it is necessary for strategic and effective quarantine. From the Fig. 8(C) and (D), we can see that when the quarantined duration is 3 days, the estimated the accumulated number of infected coincides with the real data, which also shows the management departments and designated hospitals of the COVID-19 have taken strong and effective quarantined measures in the later period.

In addition, comparing Fig. 8 (B and D) and Fig. 9 (B and D) with Fig. 8 (A and C) and Fig. 9 (A and C), we can see that, under the same control measures (red line), when the estimated accumulated number of infected cases exactly coincides with the real data, the real accumulated number of deaths cases is far lower than its estimated value. There are two possible reasons. On the one hand, due to doctors in each COVID-19-designated hospital are trying their best to treat patients with different schemes (such as traditional Chinese medicine treatment, Western medicine treatment, integrated treatment of Chinese and Western Medicine), the treatment rate is higher, and thus the number of deaths is reduced. On the other hand, since the implementation of the management department’s strong policy of ”early detection, early diagnosis, early treatment and early isolation”, and the establishment of more designated hospitals and more shelter hospitals, the infected can receive treatment when the initial stage of infection is relatively light, and, therefore, the number of deaths is greatly reduced.

This study has several limitations. Firstly, The cross-correlation analysis results indicate there are time lags between the number of daily news items and the number of new hospital notifications. However, considering the time lags of the media reports in the model (1) will undoubtedly increase computational cost and computational complexity, and we will address the effects of these important factors on the emerging infectious disease in near future. Secondly, we have assumed the exposed individuals do not to infect others in our model(1). However, if the exposed (latent) individuals are assumed to infect others, even if infectivity is very low, it will certainly affect the severity of the epidemic.

This study presents a novel methodology through using cross-correlation analysis and embedding the function of individual behavior changes (media impact) into the SEIR-type model, showed that combining statistical analysis with a mathematical model are beneficial for analyzing media impacts. It demonstrated that the media reports and these control measures affect the accumulated number of hospital notifications by reducing the transmission rate (increasing the individual behaviour change constant), the contact rate and quarantined duration of uninfected contacts individuals, and also increasing the quarantined rate of exposed individuals. All these results confirmed the importance of the responses of individuals to the media reports, and the crucial role of experts and governments in promoting the public under self-quarantine. Therefore, for mitigating COVID-19 epidemic, the media publicity should be focused on how to guide people’s behavioral changes by experts, and the management departments and designated hospitals of the COVID-19 should take effective quarantined measures, which are critical for the control of the disease.

CRediT authorship contribution statement

Qinling Yan: Conceptualization, Methodology, Writing - original draft. Yingling Tang: Data curation. Dingding Yan: Data curation. Jiaying Wang: Data curation. Linqian Yang: Data curation. Xinpei Yang: Data curation. Sanyi Tang: Conceptualization, Writing - review & editing.

Declaration of interest

The authors declare no conflict of interest.

Appendix A.

Figs. Fig. A.1, Fig. A.2, Fig. A.3 .