Learning Hemodynamic Effect of Transcranial Infrared Laser Stimulation Using Longitudinal Data Analysis

Abstract

Transcranial infrared laser stimulation (TILS) is a promising noninvasive intervention for neurological diseases. Though some experimental work has been done to understand the mechanism of TILS, the reported statistical analysis of data is quite simple and could not provide a comprehensive picture on the effect of TILS. This study learns the effect of TILS on hemodynamics of the human brain from experimental data using longitudinal data analysis methods. Specifically, repeated measures analysis of variance (ANOVA) is first applied to confirm the significance of the TILS effect and its characteristics. Based on that, two parametric mixed-effect models and non-parametric functional mixed-effect model are proposed to model the population-level performance and individual variation of this effect. Interpretations on the fitted models are provided, and comparison of the three proposed models in terms of fitting and prediction performance is made to select the best model. According to the selected model, TILS increases the concentration of oxygenated hemoglobin in the brain and this effect sustains even after the treatment stops. Also, there is considerable variation among individual responses to TILS.

I. Introduction

PHOTOBIOMODULATION is a noninvasive intervention that uses low-level laser to achieve beneficial therapeutic outcomes [1]. Though photobiomodulation has been applied in clinical practices for over 40 years for reduction of pain and inflammation since the first observation of its medical benefits in 1967, it was recently found to be potentially useful for various brain disorders and neurological diseases, such as stroke and Parkinson’s disease [2–4]. From then on, brain photobiomodulation has gained much attention. One form of brain photobiomodulation is transcranial infrared laser stimulation (TILS). Previous studies demonstrated that TILS can improve cognitive, emotional and executive functions and reduce depression symptoms [5–8].

TILS results from photon absorption by cytochrome-c-oxidase, an enzyme within mitochondria in cells, which triggers a chain of complex reactions and eventually leads to an increase in energy metabolism in the brain [9]. Though much preclinical work has been done to explore the underlying biochemical mechanism of TILS, its fundamental principle is still not fully clear so that skepticism about its clinical performance exists [10]. To understand the mechanism of TILS, Wang et al. conducted human in vivo experiments quantifying TILS-triggered changes in cerebral hemodynamics near the stimulation/treatment site [9]. In their study, hemodynamic responses were measured at a number of time points during and after treatment from a placebo group and a TILS group. At each time point, the mean responses of the two groups were compared using two-sample t-test. The test results confirmed that TILS caused significant hemodynamic changes, namely, increases in oxygenated hemoglobin concentration. Their simple statistical analysis provides a reliable tool for establishing the significance of TILS’s population-level performance. However, the time effect of TILS during and after treatment was ignored as the t-test was applied to each time point separately. In addition, only the mean of individual responses to TILS was considered, while the variation among individuals, which is critical for assessing the treatment performance as well, is not clear. The same problems exist in statistical analysis in other studies of TILS such as those about cognition [5, 8] and electrophysiology [11] of the human brain.

In this study, we propose to learn the effect of TILS on hemodynamics of the human brain through longitudinal data analysis. Our proposed methods model the time effect of TILS during and after treatment. Also, both the population-level performance and variation among individuals are considered in order to learn the individual-level uncertainty as well as the expected average therapeutic outcome of TILS. Specifically, three longitudinal data analysis methods are used. First, repeated measures ANOVA is applied to confirm significance of the difference caused by TILS over placebo and the time effect and individual variation of the TILS treatment, as motivation to the following modeling. Then two parametric mixed-effect models are proposed to characterize the population-level effect of TILS as a function of time and its individual variation. Furthermore, a non-parametric functional mixed-effect model is proposed to address problems of the parametric mixed-effect models. Performance of the models will be compared and interpretation of the selected model will be given. The contribution of this study is to provide a set of useful statistical learning methods for analyzing noisy cerebral hemodynamic data in photobiomodulation experiments. Those methods are able to reveal the underlying mechanism of the treatment effect with quantification of individual variation.

The remainder of this paper is organized as follows. Section II introduces the photobiomodulation experiment and data. Section III presents the methods used to analyze the data. Section IV shows the model estimation results and compares the proposed models in fitting and prediction. Section V concludes this study and discusses its limitations.

II. Experiment and Data

The data used in this study were collected from the experiments conducted by Wang et al. [9]. The experimental setup is shown in Fig. 1(a). A total of 11 healthy participants with an average age of 31 were recruited from local community. They underwent two separate experiments: the placebo treatment on their right forehead, followed by the TILS treatment on the same location. A 1064-nm continuous wave laser device was used for both types of treatment. The laser power was controlled at 3.4 W for the TILS treatment. For the placebo treatment, the power was tuned down to 0.1 W, and the laser aperture was further covered by a black cap to ensure that no laser was delivered to the subject. A single-channel broadband near-infrared spectroscopy (bb-NIRS) system was used to measure changes in the concentration of oxygenated hemoglobin (ΔHbO) in the brain during the experiments. The bb-NIRS consists of a tungsten halogen lamp as light source, a miniature spectrometer as detector, an “I’-shaped probe holder to hold two optical fiber bundles connecting to the light source and detector for acquisition of the experimental data.

Fig. 1.

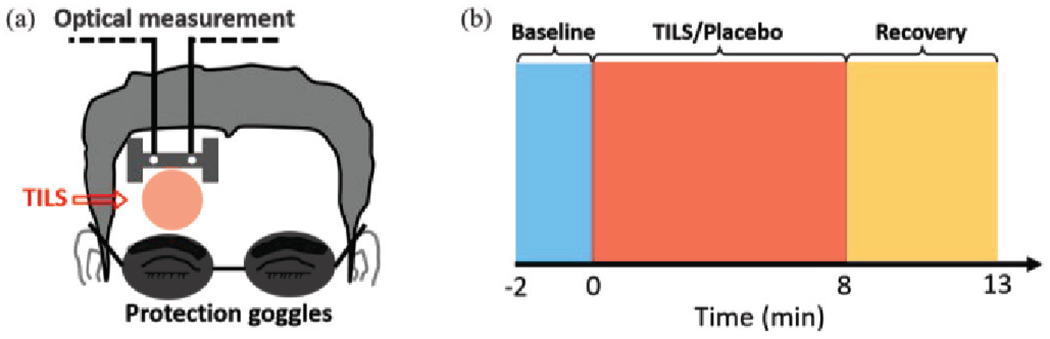
(a) Setup of the TILS/placebo treatment experiments and (b) data acquisition scheme.

Each experiment lasted a period of 15 minutes, as shown in Fig. 1(b), divided into three stages: pre-treatment (first 2 minutes), treatment (next 8 minutes) and recovery (last 5 minutes). In the pre-treatment stage, neither placebo nor TILS was applied so that the baseline of oxygenated hemoglobin (HbO) can be measured for each participant. The treatment stage consists of eight 1-min cycles, 55-s laser on and 5-s laser off per cycle. Spectral data were collected during the 5-s laser-off periods, and then converted to ΔHbO from the baseline [12]. In the recovery stage, the treatment discontinued but data were collected following the same format. The participants were blinded for the placebo and TILS treatments.

Fig. 2 shows the ΔHbO measurements of the placebo group and the TILS group. We denote the data using the following notations. Let y_hij be the ΔHbO of participant i in group h at time t_j, where h = 0 (placebo) or 1 (TILS), i = 1, … , N_h, j = 1, … , n. In this dataset, the two groups have equal number of participants, N₀ = N₁ = 11, and the number of measured time points in each session is n = 13.

Fig. 2.

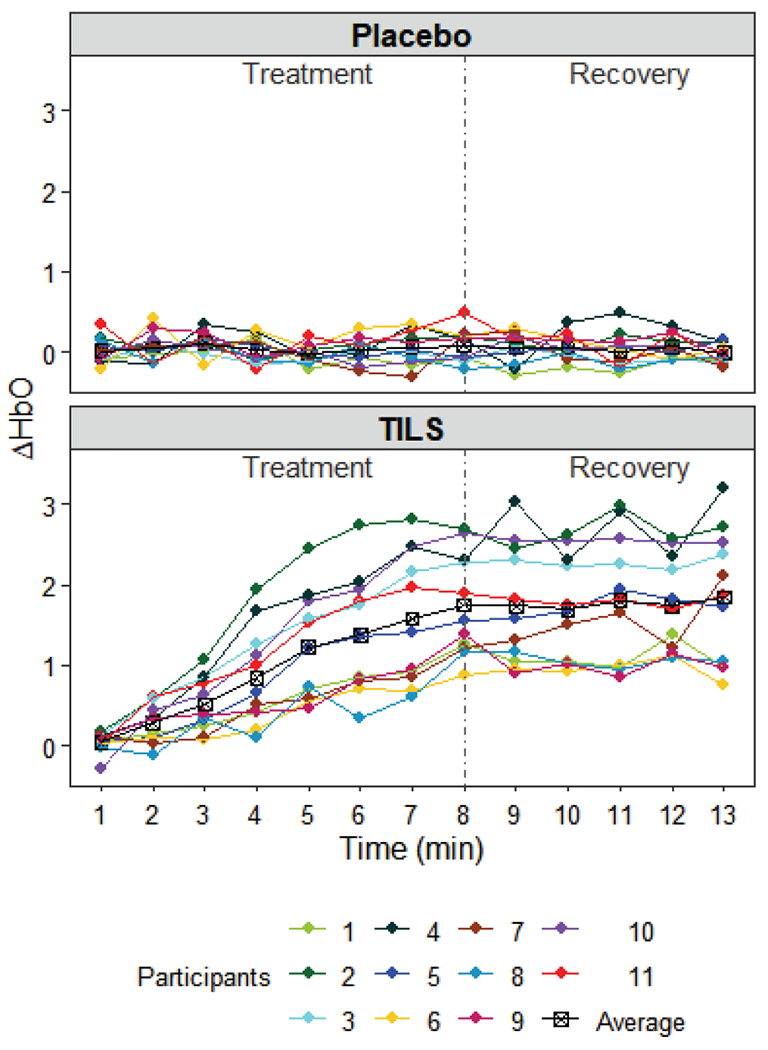
Data collected from the placebo group and TILS group.

III. Methods

A. Repeated Measures ANOVA

We first test if group (TILS vs. placebo), time and individuals cause variation in the ΔHbO measurements before formal, finer modeling of the TILS effect. If the difference between groups is negligible, the effectiveness of TILS at the population-level will be declined. This indicates that modeling the effect of TILS does not make much sense. Time may also play a role in the variation of ΔHbO data. When the time effect is significant, it means that the effect of TILS is time-varying, and thus it should be modeled as a function of time. In addition, individual differences of the participants in their responses to the treatment may help explain the variation in ΔHbO too. If this difference is significant, it should be taken into account in the modeling. The above three aspects can be tested all at once using repeated measures ANOVA [13].

The repeated measures ANOVA is based on the following point-wise model

$$y_{hij}=\mu +{\gamma }_h+{\tau }_j+{\left(\gamma \tau \right)}_{hj}+{\pi }_{i\left(h\right)}+e_{hij},$$ (1)

where μ is the grand mean, γ_h is the group effect, τ_j is the time effect, (γτ)_hj is the interaction effect of group and time, π_i(h) is the individual difference component for participant i in group h, and e_hij is the random eror. In general, it is assumed that π_i(h), and e_hij are independently normally distributed, ${\pi }_{i\left(h\right)}\sim N(0,{\sigma }_{\pi }^2)$, and $e_{hij}\sim N(0,{\sigma }_e^2)$. It is also required that ${\Sigma }_{h=0}^1{\gamma }_h=0$, ${\Sigma }_{j=1}^n{\tau }_j=0$, ${\Sigma }_{h=0}^1{\Sigma }_{j=1}^n{(\gamma \tau )}_{hj}=0$ to make all effects in the model differentiable [6]. The ANOVA table is shown in Table 1. Using the data in Fig. 2, the mean sum-of squares are obtained: MS_G = 107.9045, MS_T = 2.1862 , MS_GT = 2.2242, MS_S(G) = 2.1294, and MSE = 0.0585. The hypothesis tests and results about the three types of effect of interest in this study are given as follows.

TABLE I.

Repeated measure ANOVA table

Source	Degrees of freedom	Sum-of-squares	Mean sum-of-squares
Group	1	$S{S}_G=n\underset{h=0}{\overset{1}{\Sigma }}{N}_h{\left({\overline{y}}_h\mathrm{..}-{\overline{y}}_{\dots }\right)}^2$	$M{S}_G=S{S}_G$
Time	n − 1	$S{S}_T=N(\underset{j=1}{\overset{\mathrm{n}}{\Sigma }}{\left({\overline{y}}_{\mathrm{..}j}-{\overline{y}}_{\dots }\right)}^2)$	$M{S}_T=\frac{S{S}_T}{n-1}$
Group×Time	n − 1	$S{S}_{GT}=n\underset{h=0}{\overset{1}{\Sigma }}\underset{j=1}{\overset{n}{\Sigma }}{N}_h{\left({\overline{y}}_{h,j}-{\overline{y}}_{h\mathrm{..}}-{\overline{y}}_{\mathrm{..}j}+{\overline{y}}_{\dots }\right)}^2$	$M{S}_{GT}=\frac{S{S}_{GT}}{n-1}$
Individuals in Group	N* − 2	$S{S}_{S\left(G\right)}=n\underset{h=0}{\overset{1}{\Sigma }}\underset{i=1}{\overset{N_h}{\Sigma }}{\left({\overline{y}}_{hi\cdot }-{\overline{y}}_{h\cdot \cdot }\right)}^2$	$M{S}_{S\left(G\right)}=\frac{S{S}_{S\left(G\right)}}{N-2}$
Residuals	(N − 2) × (n − 1)	$SSE=\underset{h=0}{\overset{1}{\Sigma }}\underset{i=1}{\overset{N_h}{\Sigma }}\underset{j=1}{\overset{n}{\Sigma }}{\left(y_{hij}-{\overline{y}}_{h.j}-{\overline{y}}_{hi.}+{\overline{y}}_{h\cdot \cdot }\right)}^2$	$MSE=\frac{SSE}{\left(N-2\right)\times \left(n-1\right)}$
Total	Nn − 1	$S{S}_y=\underset{h=0}{\overset{1}{\Sigma }}\underset{i=1}{\overset{N_h}{\Sigma }}\underset{j=1}{\overset{n}{\Sigma }}{\left(y_{hij}-{\overline{y}}_{\dots }\right)}^2$	$M{S}_y=\frac{S{S}_y}{Nn-1}$

^*${\Sigma }_{h=0}^1{N}_h=N$ denotes the total number of participants in the experiment.

1). Group effect hypothesis test

H₀: γ₀ = γ₁ = 0 vs. H_a not both γ₀ and γ₁ are zeros. Under H₀, $F_0=\frac{M{S}_G}{M{S}_{S(G)}}$ follows F distribution with degrees of freedom 1 and (N − 2). The computed p-value is smaller than 0.0001 so the null hypothesis is rejected at the typical level of significance such as 0.05. The test result indicates that the effect of TILS is significant in this experiment so modeling this effect is meaningful.

2). Time effect hypothesis test

H₀: τ₁ = ⋯ = τ_n = 0 vs. H_a: not all of τ₁, … , τ_n are zeros. Under H₀, $F_0=\frac{M{S}_T}{MSE}$ follows F distribution with degrees of freedom (n − 1) and (N − 2)(n − 1). The null hypothesis is rejected as the p-value is smaller than 0.0001. This indicates that the value of ΔHbO depends on time, which suggests to model the effect of TILS as a function of time. To find out the source of the rejection, we apply this test to data in the treatment stage and recovery stage separately. The p-value is smaller than 0.0001 for the treatment stage and 0.586 for the recovery stage, meaning that the time effect results from the treatment stage.

3). Individual effect hypothesis test

$$H_0:{\sigma }_{\pi }^2=0vs.H_a:{\sigma }_{\pi }^2\ne 0$$

Under H₀, $F_0=\frac{M{S}_{S(G)}}{MSE}$ follows F distribution with degrees of freedom (N − 2) and (N − 2)(n − 1). Again, the null hypothesis is rejected as the p-value is smaller than 0.0001, which means that the participants respond to the treatment differently. This result necessitates the quantification of individual variation in the TILS effect.

In summary, the above test results motivate us to model the effect of TILS on the concentration of oxygenated hemoglobin in the human brain. In the modeling, time should be involved as the TILS effect is found to be time-varying. The variation of individual responses should also be taken into account. The following sections provide two types of models that satisfy the requirements. Note that only the data of the TILS group (shown in the lower panel of Fig. 2) will be used in the modeling, and thus the subscript h will be dropped in the notations hereafter.

B. Parametric Mixed-effect Model

Parametric mixed-effect models is a popular class of models for longitudinal data analysis [14, 15]. A general parametric mixed-effect model can be written in the following hierarchical form [16]

$${\text{Level}-1:y}_{ij}=f\left(t_j;{\theta }_i\right)+e_{ij},$$ (2a)

$$\text{Level}-2:{\theta }_i=\beta +u_i.$$ (2b)

Here the Level-1 model assumes that y_ij, the ΔHbO of participant i at time t_j, depends on a parametric function f of time with parameter θ_i and random error e_ij. e_ij is assumed to follow a normal distribution $N(0,{\sigma }_e^2)$. The Level-2 model further defines the parameter θ_i as combination of a constant β, called fixed effect, and a random variable u_i. called random effect. It is assumed that $u_i\sim N(0,{\sigma }_u^2)$.

Note that the model in Eq. (2a) is a point-wise model. The continuous versions of the notations are y_i(t), f(t; θ_i), etc. Intuitively, the responses of participant i at different time points form a curve y_i(t) as shown in Fig. 2. The shape of the curve is determined by θ_i and varies from one participant to another as clearly seen from the figure. Thus, β represents the population-level, or baseline, shape of the curve, while u_i represents the difference of participant i from the baseline.

Once the form of Leve-1 model is determined, the unknown parameters β , σ_e and σ_u can be estimated using the expectation-maximization (EM) algorithm [17] or Bayesian methods [18]. The EM algorithm is used in this study for convenience. Then $f(t;\widehat{\beta })$ can be interpreted as the population-level effect of TILS, and ${\widehat{\sigma }}_u^2$ represents the individual variation of the TILS effect. It deserves to mention that the selection of the Level-1 function f(t; θ) is subjective and often relies on domain knowledge. Without such knowledge about the TILS effect, here we propose two specific forms of Eq. (2a) according to the shape of the average curve in the lower panel of Fig. 2.

1). Model I:

Based on the increasing trend of the average curve during the treatment stage, we assume that the Level-1 model has a quadratic form

$$\text{Level}-1:f\left(t_j:{\mathit{\theta }}_i\right)={\theta }_{1i}{t}_j^2+{\theta }_{2i}{t}_j+{\theta }_{3i}+e_{ij},$$ (3a)

$$\text{Level}-2:\{\begin{array}{c}{\theta }_{1i}={\beta }_1+u_{1i},\\ {\theta }_{2i}={\beta }_2+u_{2i},\\ {\theta }_{3i}={\beta }_3+u_{3i}.\end{array}$$ (3b)

In the Level-1 model, f is a quadratic function of time with three parameters θ_1i, θ_2i, θ_3i. When θ_1i is negative, the curve of participant i first increases monotonically when 0 ≤ t ≤ $-\frac{{\theta }_{2i}}{2{\theta }_{1i}}$ and then decreases, and the increase/decrease rate is controlled by θ_1i. All the three parameters contribute to the highest value that the curve can achieve. In the Level-2 model, each parameter contains a fixed effect and a random effect which allows much flexibility to fit individual curves. The random effects are assumed to be independent and norm ally distributed $u_{1i}\sim N(0,{\sigma }_{u_1}^2)$, $u_{2i}\sim N(0,{\sigma }_{u2}^2)$, $u_{3i}\sim N(0,{\sigma }_{u_3}^2)$. The independence assumption is made for convenience in estimation and easy interpretation.

2). Model II:

Alternatively, it is reasonable to assume that the baseline response has an exponential trend and achieves a plateau eventually. The model is of the following form

$$\text{Level}-1:f\left(t_j;{\mathit{\theta }}_i\right)={\theta }_{1i}+{\theta }_{2i}\left(1-e^{-{\theta }_{3i}\left(t_j-1\right)}\right)+e_{ij},$$ (4a)

$$\text{Level}-2:\{\begin{array}{c}{\theta }_{1i}={\beta }_1+u_{1i},\\ {\theta }_{2i}={\beta }_2+u_{2i},\\ {\theta }_{3i}={\beta }_3+u_{3i}.\end{array}$$ (4b)

Fig. 3 shows an illustration of the Level-1 function f(t; θ) in Eq. (4a). It has an increasing trend starting from θ₁ at t₁ = 1 and reaches a plateau of height θ₁ + θ₂ when t is large. θ₃ reflects the speed of increase before reaching the plateau. The Level-2 model of Model II is the same as in Model I, where each parameter contains a fixed effect and a random effect.

Fig. 3.

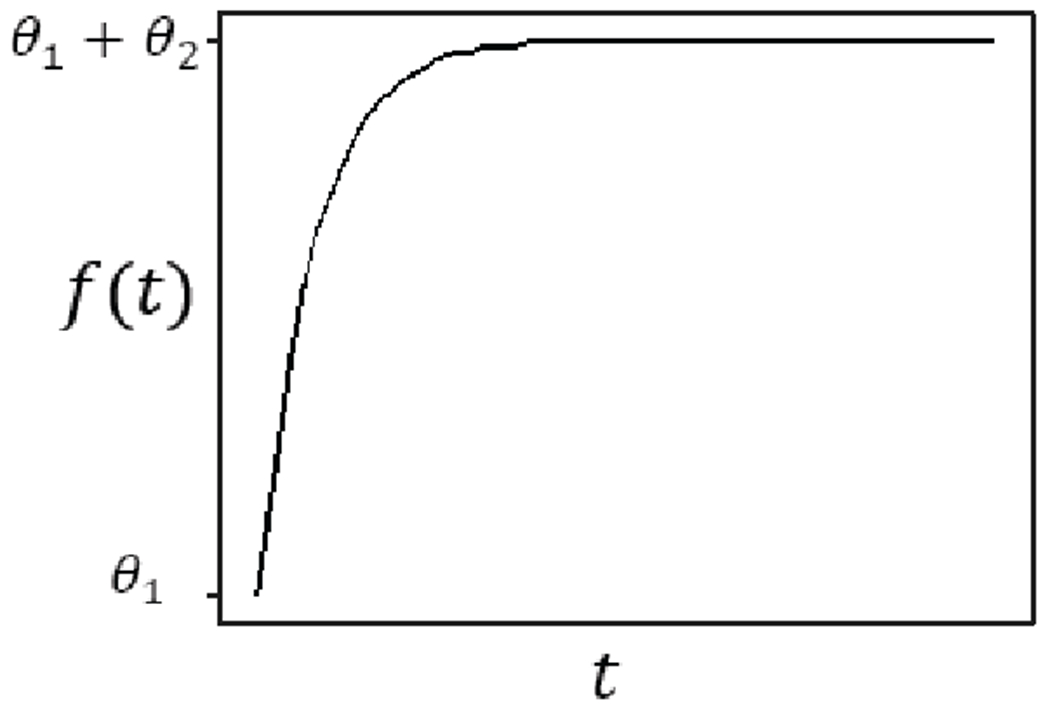
Illustration of Level-1 model in Model II.

C. Functional Mixed-effect Model

Unlike the parametric mixed-effect model, the functional mixed-effect model uses a nonparametric approach and is thus free of selection of function forms [19]. The model (Model III) can be written as below

$$y_{ij}=\beta \left(t_j\right)+{\alpha }_i\left(t_j\right)+e_{ij},$$ (5)

where $e_{ij}\sim N(0,{\sigma }_e^2)$. Here we assume that both β(t) and α_i(t) are smooth functions of time, and thus the estimate ${\widehat{y}}_i(t)$ is also a smooth curve. The random errors e_ij are independent among individuals and time points. The random effects {α_i(t₁), α_i(t₂), … , α_i(t_n)} ~ N(0, Σ_α). Intuitively, β(t) represents the population-average curve that tells the overall trend of the TILS effect, while α_i(t) is the individual-specific deviation from the population curve.

In this study, we model β(t) and α_i(t) using smoothing splines. Specifically, for participant i, the estimates $\widehat{\beta }(t)$ and ${\widehat{\alpha }}_i(t)$ balance the fitting accuracy and smoothness by minimizing a penalized residual sum of squares

$$\left\{\widehat{\beta }\left(t\right),{\widehat{\alpha }}_i\left(t\right)\right\}=argmin{\Sigma }_{j=1}^n{\left[y_{ij}-\beta \left(t_j\right),{\alpha }_i\left(t_j\right)\right]}^2+{\lambda }_{\beta }{\int }_{t_1}^{t_n}\beta ″{\left(t\right)}^{2}dt+{\lambda }_{\alpha }{\int }_{t_1}^{t_n}{\alpha }_i^{″}{\left(t\right)}^{2}dt.$$ (6)

In Eq. (6), λ_β and λ_α are smoothness parameters of the curves. The estimation can be made using the sme algorithm in R [20] where the two smoothness parameters are selected by the corrected Akaike Information Criterion (AIC) and the estimates of β(t) and α_i(t) are obtained by EM algorithm.

IV. Results

In this section, we first show the estimation results of the three proposed models, and then compare them in terms of fitting and prediction performance. The best model will be chosen based on the comparison.

A. Model Estimation

1). Model I:

The fitted population-average curve (i.e., $f(t;\widehat{\mathit{\beta }})$, where $\widehat{\mathit{\beta }}=[{\widehat{\beta }}_1,{\widehat{\beta }}_2,{\widehat{\beta }}_3]$), and individual curves (i.e., $f(t;{\widehat{\mathit{\theta }}}_i)$, where ${\widehat{\mathit{\theta }}}_i=\left[{\widehat{\theta }}_{1i},{\widehat{\theta }}_{2i},{\widehat{\theta }}_{3i}\right]$), of Model I are shown in Fig. 4 with the parameter estimates given in Table 2. The fitted population-average curve shows an overall increasing trend till around the 11^th minute. The fitted individual curves show similar trend and match with the data well. According to Table 2, the estimated variances of random effects are considerably large, indicating that individual variation of the TILS effect is significant. A corresponding fact is that the shapes of individual curves in the right panel of Fig. 4 vary a lot from each other.

Fig. 4.

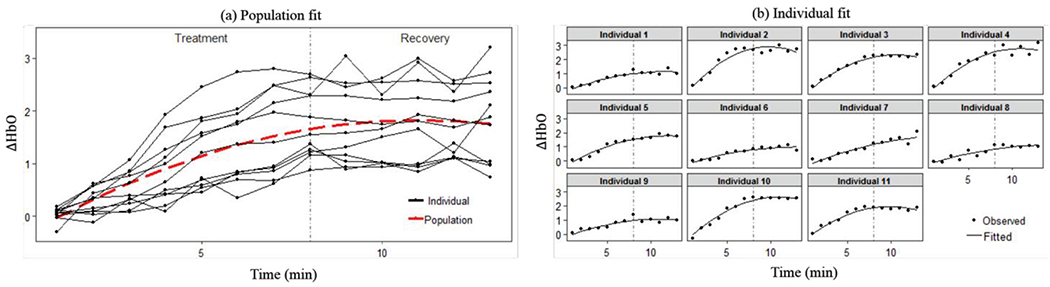
Population and individual fitting of Model I.

TABLE II.

Estimates of parameters in parametric mixed-effect models

Parameter	Model I	Model II
β1	−0.0183	−0.0913
β2	0.4052	2.2300
β3	−0.4181	0.2078
σu1	0.0103	0.0443
σu2	0.1857	0.6847
σu3	0.1340	0.0849
σe	0.1904	0.1990

The interpretation of the fitted Model I is that in general, the change in oxygenated hemoglobin concentration in the brain increases as the TILS treatment continues. When the treatment stops, the change remains increasing and then starts to decrease, meaning that the effect of TILS lasts but gets weaker with time.

2). Model II:

The fitted population-average curve and individual curves of Model II are shown in Fig. 5. The population-level effect keeps increasing without reaching a plateau during the whole experiment period. The fitted individual curves show similar trend and match with data well. According to Table 2, the estimates of variance components are considerably large and similar to those of Model I.

Fig. 5.

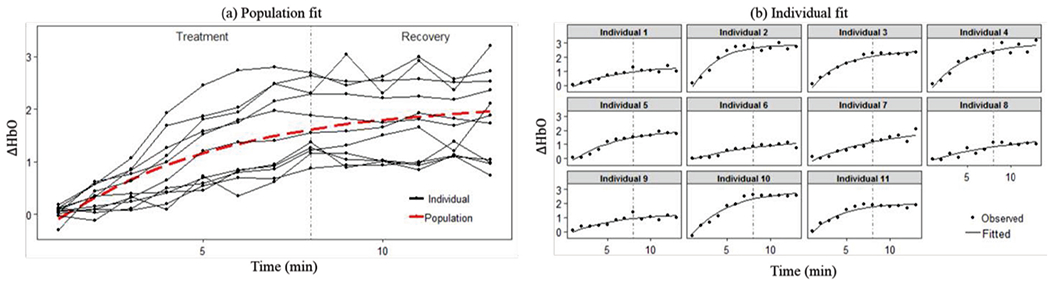
Population and individual fitting of Model II.

The interpretation of the fitted Model II is that the change in oxygenated hemoglobin concentration keeps increasing during the treatment stage and recovery stage, meaning that the TILS effect sustains for quite long time after the treatment stops. This is a little different from the interpretation of the fitted Model I where ΔHbO starts to decrease in the recovery stage. Such a difference is possible when different model forms are used in the parametric mixed-effect model.

3). Model III:

The estimated population-level effect $\widehat{\beta }(t)$ and random effects ${\widehat{\alpha }}_i(t)$ of Model III are given in Fig. 6. In Fig. 6(a), the population-level effect exhibits monotonic increase during the whole experiment period with a decreasing rate in the recovery stage. In Fig. 6(c), we could observe that for all participants, the observed values (black dots) fall close to the individual fits, which indicates good fitting performance. Also, the fitted individual curves do not have similar shapes but vary a lot from each other, which is different from those from parametric mixed-effect models shown in Figs. 4 and 5. To provide some intuition on the fitting, Fig. 6(b) shows the population fit, individual fit and the estimated random effect of a single participant as an example. It can be seen clearly that the individual fit (black solid line) is a combination of the population effect and random effect.

Fig. 6.

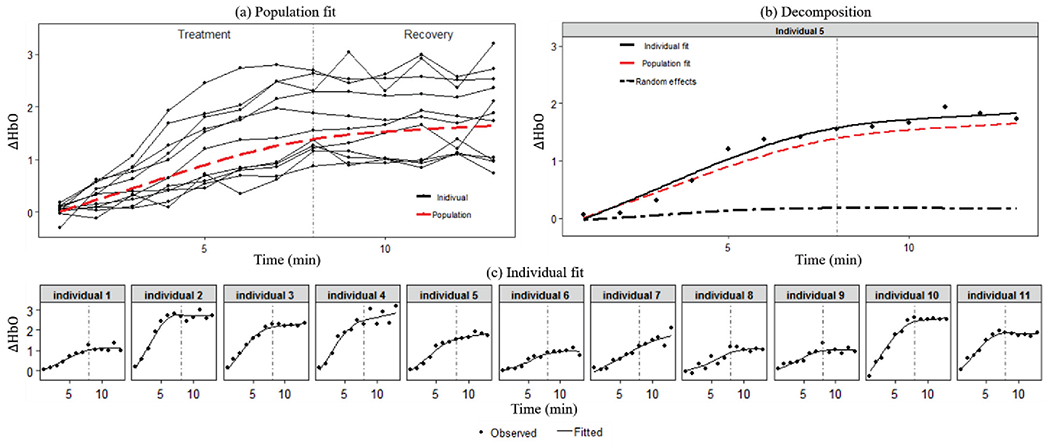
Population and individual fitting of Model III.

The interpretation of the fitted Model III is that TILS causes increasing change in the oxygenated hemoglobin concentration in the brain, and this effect sustains in the recovery stage after the treatment stops with a weakened rate. The individual variation among participants is significant as shown in the fitted individual curves. Especially, their behaviors in the recovery stage are very different, some keeping increasing, some reaching a constant, and some going downward.

B. Model Comparison

1). Fitting performance:

Table 3 lists the residual sum of squares and log likelihood of the three models, which measure how well each model fits the data. It is clear that Model III has the best fitting performance, with the smallest residual sum of squares and largest log likelihood. This is consistent with the visual impression of fitting performance in Figs. 4–6. The two parametric models perform similarly in fitting.

TABLE III.

Comparison of fitting performance of proposed models

Model	Residual sum of squares	Log likelihood
Model I (Eq. (3))	4.508246	1.361531
Model II (Eq. (4))	4.977247	−3.189774
Model III (Eq. (5))	3.135987	147.9451

We also compare the fitted variance patterns of the models. Let V(y) be the variance of the response ΔHbO. For parametric mixed-effect models, the variance is determined by both the Level-1 model and Level-2 model, and thus the resulting structure of variance is often complex. Here we derive the variance of Model I as an example (the variance of Model II is similar). The variance of ΔHbO in Model I is below

$$\begin{gathered} V\left(y\right)=Var\left(f\left(t;\mathit{\theta }\right)\right)+Var\left(e\right) \\ =t^3\left(2{\sigma }_{u_1}^2{\sigma }_{u_2}^2\rho \left(u_1,u_2\right)\right)+t^2\left({\sigma }_{u_1}^2+2{\sigma }_{u_1}^2{\sigma }_{u_3}^2\rho \left(u_1,u_3\right)\right)+t\left({\sigma }_{u_2}^2+2{\sigma }_{u_2}^2{\sigma }_{u_3}^2\rho \left(u_2,u_3\right)\right)+{\sigma }_{u_3}^2+{\sigma }_e^2. \end{gathered}$$ (7)

In contrast, the variance of Model III is determined by the random effect α(t) and random error

$$V\left(y\right)=Var\left(\alpha \left(t\right)\right)+Var\left(e\right).$$ (8)

Fig. 7 shows the variance patterns of data and the fitted models. Sample variance of all observations at each time point is used to represent the variance of data and the fitted variance is obtained based on Eqs. (7)–(8). Again, Model III performs much better in fitting the variance pattern of data. The variance of Model I has a near-linear shape not matching with the data.

Fig. 7.

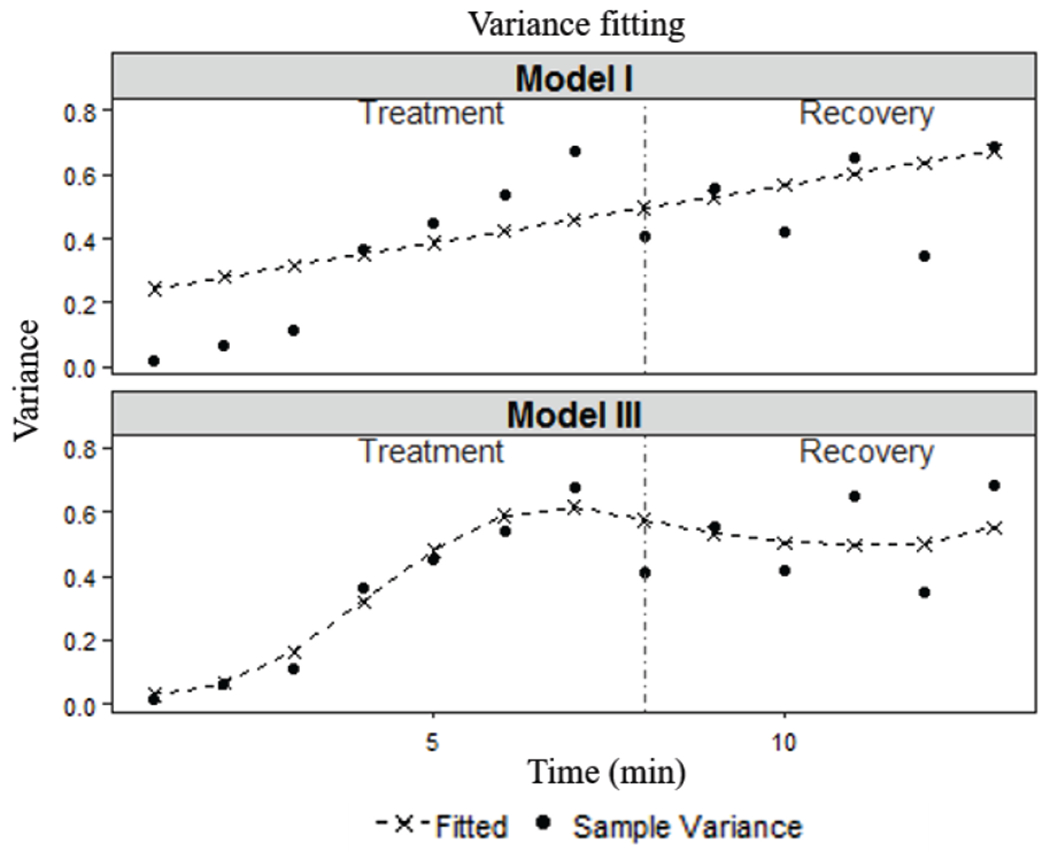
Comparison of fitted variance patterns.

2). Prediction performance:

Prediction at individual level can be made based on the estimated fixed effect and random effect in the model. If the subject does not have any historical data, the prediction is just the estimated population value. Here we compare the prediction performance of Models I, II and III through the following cross validation procedure. First, we split the data into a training set and a testing set. Specifically, the testing set is created by randomly selecting N_test observations from the data (totally 13×11=143 observations), and the remaining data form the framing set. Each model is estimated using the framing set and then the estimated model is used to predict values in the testing set. The performance of prediction is measured by the mean squared error (MSE), which is the mean of squared differences between the predicted values and actual observations. To be robust to sample size in the tiaining/testing set and variation in data splitting, five different sizes of the testing set N_test = {1, 5, 10, 20, 30} are considered, and given each size, 100 runs are conducted and the average prediction error is computed. For a specific example, given N_test = 5, 5 observations are randomly selected from the data to be the testing set and the remaining 138 observations are the training set. The MSE of predictions of the testing set based on the model fitted using the training set will be calculated. This process will repeat 100 times, and the prediction error for this N_test value is the average of the 100 MSEs.

The results are shown in Fig. 8. Model III outperforms the other two models with the smallest prediction error in all scenarios. Between the two parametric models, Model I exhibits relatively better prediction performance than Model II in most scenarios. To further confirm the conparison results, two-sample t-tests are conducted between the 100 MSEs of Model I vs. Model III (H₀: err_I ≤ err_III) and Model II vs. Model III (H₀: err_II ≤ err_III) given each size of testing data. All the p-values are smaller than 0.05, which validates that Model III performs better than Model I and Model II.

Fig. 8.

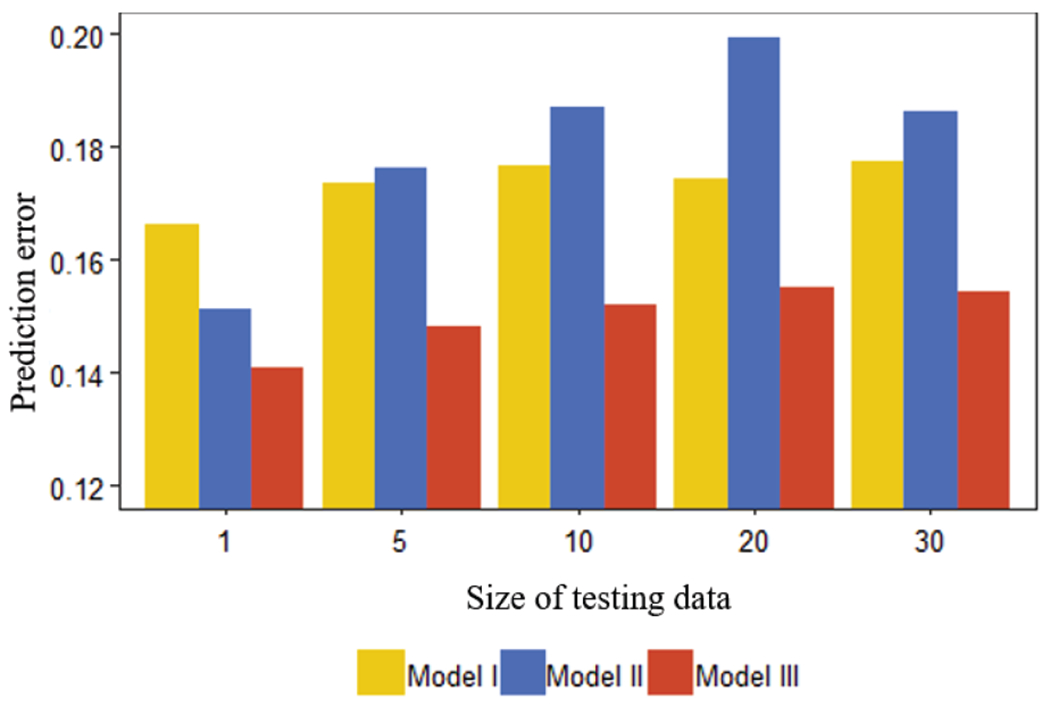
Comparison of prediction performance.

C. Selected Model

Based on the above comparison, the functional mixed-effect model is selected as it has the best fitting and prediction performance. The estimated Model III in Fig. 6 suggests that the change in oxygenated hemoglobin concentration increases as time goes on and sustains even after TILS stops. Also, the individual variation in the TILS effect is large. These findings are useful information to related researchers toward a better understanding of the mechanism of TILS. They will also guide future research in this field. For example, further studies are needed to investigate how long the effect of TILS can sustain in the recovery stage, how the maximum change of HBO depends on individual factors, and how to adjust the dose of treatment (i.e., laser power) to make the maximum change at desired level. Ultimately, such knowledge will enable clinicians to design the TILS treatment for each individual patient according to his/her conditions and needs.

V. Conclusion and Discussion

In this study, we learn the effect of TILS treatment on the concentration of oxygenated hemoglobin in the human brain from experimental data by using three longitudinal data analysis methods. The result of repeated measures ANOVA shows that the TILS effect is significant. We then propose two parametric mixed-effect models and a functional mixed-effect model to characterize the effect of TILS. The functional mixed-effect model is selected through comparison of fitting and prediction performance. Estimation results of the selected model produce meaningful interpretations about the population effect of TILS and individual variation.

This study has some limitations which should be addressed in future research. First, although the proposed methods are effective, accuracy of the results is limited by the small sample size of the data used. The experiment only involved 11 participants, which may not be able to reflect the hue pattern of the population and heterogeneity among individuals well. In our future research, we will conduct larger-scale experiments with more participants and update the conclusions based on the new data. Using the larger dataset, we will also study other response variables such as concentration of deoxygenated hemoglobin and total hemoglobin to generate more comprehensive understanding on the hemodynamic effect of TILS. Another limitation is that characteristics of participants such as age, gender, education level, etc., were not collected in this study. When such data become available in the future, we will incorporate them in the statistical modeling in appropriate ways. This will improve the prediction performance of the proposed methods at individual level and build a foundation for personalized TILS treatment.