Selective Manipulation of Biomolecules with Insulator-Based Dielectrophoretic Tweezers

Abstract

Insulator-based dielectrophoretic (iDEP) trapping, separating, and concentrating nanoscale objects is carried out using a non-metal, unbiased, mobile tip acing as a tweezers. The spatial control and manipulation of fluorescently-labeled polystyrene particles and DNA were performed to demonstrate the feasibility of the iDEP tweezers. Frequency-dependent iDEP tweezers’ strength and polarity were quantitatively determined using two theoretical approaches to DNA, which resulted in a factor of 2 ~ 40 differences between them. In either approach, the strength of iDEP was at least 4-order of magnitude stronger than the thermal force, indicating iDEP was a dominant force for trapping, holding, and separating DNA. The trapping strength and volume of the iDEP tweezers were also determined, which further supports direct capture and manipulation of DNA at the tip end.

Introduction

Manipulation and isolation of target biomolecules in a complex medium have gained special attention due to their central role in disease screening and diagnostics^1-4. Among many biomolecule manipulation methods, force-based dielectrophoresis (DEP) has been widely used to trap, separate, and manipulate a variety of nanoscale objects including proteins and cells suspended in the medium, based on either their size or polarizability^5-8. In principle, traditional DEP techniques utilize the geometry of metal electrodes to create non-uniform electric fields (Figure 1a), which induces motion of polarizable objects from the medium to regions of strong electric fields by either attracting (positive DEP, pDEP) or repelling (negative DEP, nDEP) them^{9, 10}. The electrokinetic-driven, selective trapping and separating of target objects from the medium to the electrodes have been demonstrated previously using DNA^{11, 12}, cancer cells^{1, 6}, and bacteria^{13, 14} along with microfluidic configurations.

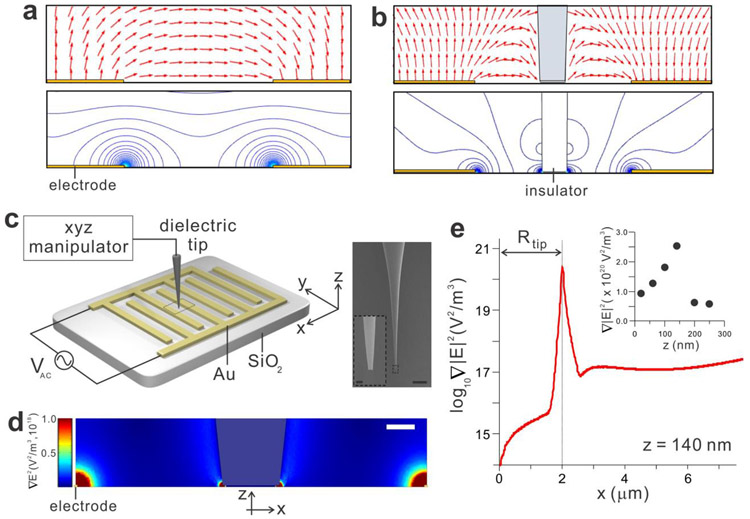
Figure 1.

Insulator-based dielectrophoretic (iDEP) tweezers. (a) Electric field lines (red arrow) and contour plot of the field created by the metal electrodes. (b) Deformation of the field by the insulating obstacle in the center generates the additional iDEP trap. (c) Schematic diagram of the device and zoomed-in SEM images of the insulating tip controlled by the xyz manipulator. The scale bars are 500 μm and 2 μm (inset). (d) The distribution and the strength of the electric field gradient around the tip calculated by the finite element COMSOL simulation, predicting the strong field gradient at the electrode edges and the tip end. The scale bar is 5 μm. (e) The line profile of the electric field gradient along the x-axis at the tip height z of 140 nm, showing a very sharp peak of the field gradient at the rim of the tip. The inset presents the peak values of the field gradient’s strength as function of z.

Alternatively, insulator-based DEP (iDEP) or electrodeless DEP techniques have been developed to trap target objects with insulating obstacles rather than metal electrodes^{8, 15, 16}, eliminating potential fouling, electrolysis, and joule heating issues caused by the applied high electric field at the metal electrodes of the traditional DEP method. In these devices, a constriction or channel in an insulating material deforms the electric field in a conducting solution, creating a high electric field gradient with a local maximum (Figure 1b). Thus, the insulating obstacles can trap target objects including DNA and cells^{8, 17}. Moreover, iDEP provides a non-uniform electric field over the entire depth of the channel, increasing the effective trapping area without the issues^{8, 16}. The advantage of iDEP is that it can be easily fabricated and integrated with microfluidic systems in order to improve detection efficiency and enhance biomolecule mixing, separation, and concentration, which is not possible with other manipulation techniques such as optical and magnetic trapping^{12, 18}.

Although several DNA manipulation techniques have been improved and used to measure DNA unzipping¹⁹, hybridization²⁰, and digestion of DNA by λ-exonuclease²¹, no effective methods have been developed for spatial control of DNA. For instance, fixed-position-based approaches such as atomic force microscope (AFM), micropipette, and optical tweezers, and fixed-force-based approach such as a magnetic trap allow limited control of DNA, since DNA ends are fixed at the beads, AFM and micropipette cantilevers, and glass surfaces^{22, 23}. Furthermore, those techniques suffer from the high force noise and drift associated with high bandwidth of the cantilevers and bead size^{23, 24}. Thus, three-dimensional control of DNA using conventional manipulation techniques including DEP and iDEP methods is not feasible.

For the spatial manipulation capabilities such as picking up, repositioning, and releasing, several nanoscale metallic tip-based DEP methods have been introduced. For example, conductive AFM probe tips^25-28 and nanoscale pipette tips coated with metal^{11, 29, 30} have been used to create the non-uniform electric field and field gradient at the end of the tip, demonstrating as an alternative technique for manipulating biomolecules and biopolymers. However, the metallic tip-based DEP methods in which a working principle is the same as the traditional DEP suffer from the drawbacks associated with unavoidable and electrochemical reactions at the metal DEP electrodes¹⁵.

To overcome this limitation, we demonstrate insulator-based, electrodeless, mobile DEP tweezers that provide spatial control and manipulation of biomolecules without the issues of fouling and electrolysis. In this work, we used non-metal, unbiased tips that squeeze the electric field in the medium and create a strong, localized field and its gradients at the end of the tip. Thus, the tip acts like iDEP tweezers capable of three-dimensional trapping, placing, and releasing biomolecules such as DNA. Furthermore, this technique eliminates the complex fabrication of DEP devices such as coaxial or triaxial nanoscale tips, and the requirements of specialized operating instruments like AFM.

Results

Modeling of the electric fields and the field disturbance.

Our iDEP tweezers exploit the interdigitated electrode array which has proven to be quite useful for dielectrophoretic separation in previous studies^31-33. The device consists of planar gold electrode arrays defined by the standard optical lithography technique on a SiO₂ substrate, similar to our previous work^{31, 34} (Figure 1c, see Experimental Section for details) and an insulator tip controlled by an xyz manipulator between a pair of interdigitated electrodes.

The strength of the electric field intensity gradient ∇E² in the proximity of the tip was examined using the COMSOL Multiphysics. Figures 1d and 1e depict the spatial distributions of ∇E² over and across the electrodes when an external AC voltage V_ac (7 V_pp, f = 50 kHz) is applied between two electrodes. Without the tip, the strong ∇E² were formed only at the sharp electrode edges due to the inhomogeneity of the electric field created by the external AC voltage, which agrees with our previous experimental observations^{31, 35}. In the presence of the tip between the two electrodes, an additional strong ∇E² around the tip end was created (Figure 1d and Figure S1). The insulator tip deformed the electric field in the conducting solution and generated inhomogeneous field gradients with a local maximum surrounding it, suggesting strong DEP at the tip end (F_DEP ∝ ∇E²).

The distribution of ∇E² along the x-axis demonstrates that ∇E² increases near the tip and maximizes at the tip edge (Figure 1e). Compared to the flat surface of the tip end, the edge line of the tip end is highly disordered, which produces additional non-uniform electric field distribution. The ∇E² peak sharply drops to the relatively flat ∇E² along the x-axis, demonstrating that the effective iDEP site is physically smaller than the tip. The effective trapping volume at the tip depends on the tip diameter because the distribution and centration of ∇E² around the tip varies with the tip dimension (Figure S2). Therefore, the unbiased insulator tip producing an additional localized iDEP trap is able to serve as a spatially mobile and remotely tunable biomolecule tweezers, in order to trap, relocate, and release the nanoscale objects.

Fluorescence imaging of the sub-micron particles with the iDEP tweezers.

To demonstrate the feasibility of the iDEP tweezers in relation to transport and mobility, we initially examined the polystyrene particles (Figure 2 and Figure S3). First, the capability of traditional DEP acting on the particles was measured in the absence of the tip (Figure 2a-2c). In the absence of both AC voltage and the tip, the particles were freely diffusive in the buffer (Figure 2a). When the low frequency AC voltage (5 V_pp, f = 20 kHz) was applied, the particles were attracted to the electrode edge due to the positive DEP (pDEP, Figure 2b). In contrast, the high frequency AC voltage (5 V_pp, f = 2 MHz) repelled the particles, so the particles were accumulated in the center between the two electrodes, where the electric field gradient is minimum (nDEP, Figure 2c). These frequency-dependent, bipolar DEP results were in excellent agreement with the classical Maxwell-Wagner (MW) theory^{9, 10}, where the Clausis-Mossotti (CM) factor and the cross over frequency f_co of 0.7 MHz allow for the estimation of the frequency dependent F_DEP polarity (Figure S4).

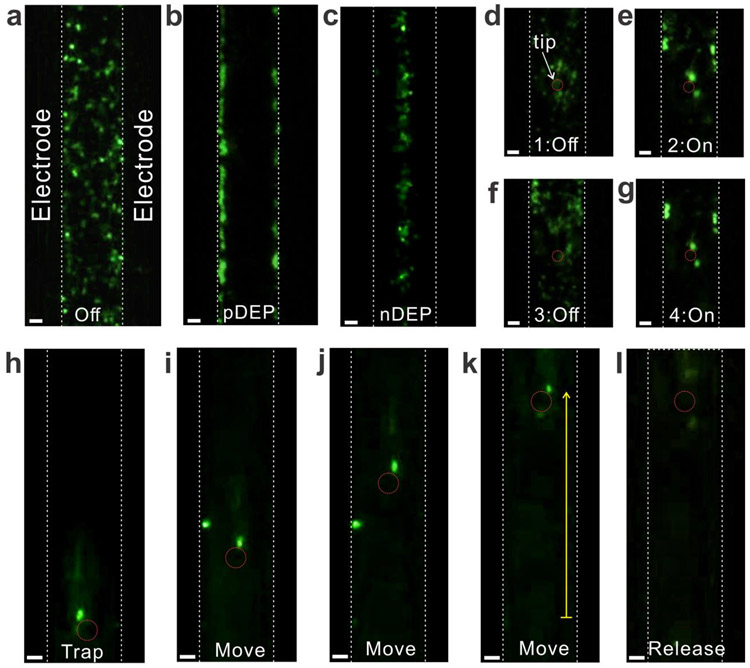
Figure 2.

The iDEP manipulation of fluorescently labeled polystyrene nanoparticles. (a)-(c) DEP acting on the nanoparticles without the tip: (a) No AC field between the electrodes; (b) Low-frequency AC voltage (5 V, 20 kHz) attracts the nanoparticles to the electrodes (pDEP); and (c) High-frequency AC voltage (5 V, 2 MHz), in contrast, repels the nanoparticles to the center of the electrodes (nDEP). (d)-(g) In the presence of the tip, the nanoparticles were trapped around the tip when the AC voltage was applied (5 V, 20 kHz), and the trapped nanoparticles were instantly released from the tip after turning the AC voltage off. (h)-(l) The iDEP tweezers trap the nanoparticles, hold them while repositioning, and release them by turning off the AC voltage (5 V, 20 kHz). The yellow arrow is 80 μm. All scale bars are 5 μm.

Next, the particle trapping at the tip placed in the center of two electrodes was investigated. Figures 2d - 2g demonstrate a series of measurements regarding the trapping of the particles at the tip by turning on and off the AC voltage between the electrodes. By turning on the pDEP trap bias, the particles were attracted to the high electric field near the tip and trapped at the tip end (Figure 2e). The trapped particles were immediately released and diffused away from the tip after turning off the pDEP trap bias (Figure 2f). When the trap bias was reapplied, the particles were trapped again in similar fashion at the tip (Figure 2g). Such trapping and releasing of particles were reproducible.

After trapping particles, the tip was spatially manipulated. Figures 2h - 2k are a sequence of images that show the motion of the tip and particles along the y-axis (yellow arrow). During the tip manipulation, the position and shape of the trapped particles were almost identical without further interferences from the electrodes. Following the repositioning of the tip and particles, the trap bias at the electrodes was turned off (Figure 2l). The particles were immediately released from the trap and freely diffused away from the tip. Thus, the iDEP at the tip is strong enough to trap and hold the particles while repositioning, in order to use the tip as nanoscale mobile tweezers. Please note that the particles drawn into the pDEP trap at the electrode were not shown in Figures 2h - 2k because some electrodes have smooth edges. Although the particles were still trapped on the electrodes, the particles on the Au electrodes could not be seen by the objective placed under the devices.

Spatial manipulation of DNA with the iDEP tweezers.

Following the examination of the particles with the iDEP tweezers, we further investigated the capability of the iDEP tweezers in manipulating DNA (Figure 3 and Figure S5). Compared to the particles, prediction of DEP strength and f_co, determining polarity of DEP for DNA is very complicated^{11, 36}. Several models including the CM factor^{7, 27}, quantitative measurement of the DNA polarizability α^37-40, and the counterion fluctuation (CIF)^{11, 36, 41} have been proposed to estimate DEP strength and polarity acting on DNA (see the discussion section for further details). Although f_co is not exactly defined in those models, the polarity of DEP could be reversed at reasonably separated upper and lower frequency limit.

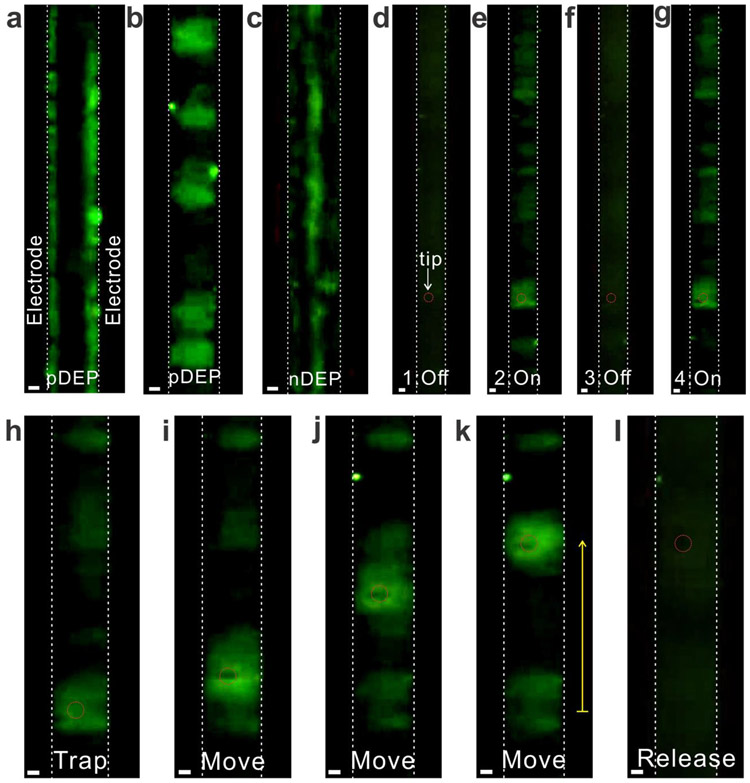
Figure 3.

Spatial manipulation of DNA using the iDEP tweezers. (a)-(c) DEP acting on DNA without the tip: (a) Low-frequency AC voltage (7 V, 50 kHz) strongly attracts DNA to the electrodes (strong pDEP); (b) By increasing the frequency of AC voltage (7 V, 200 kHz), DNA were trapped in the middle of two electrodes, forming the DNA clouds (weak pDEP); and (c) High-frequency AC voltage (7 V, 10 MHz) repels DNA to the center of the electrodes (nDEP). (d)-(g) In the presence of the tip, the iDEP tweezers picked up DNA around the tip under the weak pDEP condition (7 V, 200 kHz), and trapped DNA were immediately released from the tip after turning the AC voltage off. (h)-(l) The iDEP tweezers trap DNA, hold them while repositioning, and release them by turning of the applied AC voltage (7 V, 200 kHz). The yellow arrow is 70 μm. All scale bars are 5 μm.

Similar to the particle manipulation, we first examined bipolar DEP acting on DNA (Figures 3a - 3c). When a low frequency AC voltage was applied (7 V_pp, f = 50 kHz), DNA was attracted to the edge of electrodes (Figure 3a). After increasing the frequency of the applied AC voltage (7 V_pp, f = 200 kHz), DNA moved off from the electrode and trapped between two electrodes, forming stretched-DNA clouds (Figure 3b). Such DNA cloud observation at the interelectrode gaps by the weak pDEP trap agrees with previous observation with the DNA plasmid^{36, 38}. At a sufficiently high frequency (7 V_pp, f = 10 MHz), the DNA was repelled from the electrodes and aligned at the center of the two electrodes (Figure 3c). Therefore, the low and high frequency AC voltages yield both pDEP and nDEP on DNA, suggesting bipolar CM factors.

By placing the tip between a pair of interdigitated electrodes, the utility of the iDEP tweezers in trapping DNA was subsequently examined (Figures 3d - 3g). When the bias of pDEP trap (7 V_pp, f = 200 kHz) was turned on, DNA was attracted to the tip, forming a broad, cloud-like structure surrounding the tip. Compared to the particles which are solid spheres, DNA is a long polymer chain, so the structure of DNA varies under different environments (e.g., pH, ionic strength, force acting on DNA). Thus, such broadening could be attributed to the stretched structure of DNA^{40, 42}. When the pDEP trap vanished by turning off the applied AC bias, the DNA clouds completely disappeared around the tip, indicating that the iDEP tweezers can instantly trap and release DNA without any permanent attachment at the tip or damage due to the direct contact of the metal electrodes applied at a high AC voltage.

Finally, the trapped DNA was manipulated by moving the tip along the y-axis (Figure 3h - 3k). The DNA clouds initially formed around the tip, and followed the direction of the moving tip. Throughout the manipulation, the volume and shape of the clouds were almost identical. These results suggest that our iDEP tweezers can tightly hold DNA, and that the trapping strength is consistent in the devices. Such capabilities are prerequisite for the precise measurements of protein properties and activities while controlling and manipulating proteins²⁴. Following the repositioning the DNA clouds, the AC bias of the pDEP trap was turned off. DNA were completely released from the tip as shown in Figure 3l. Such trapping and manipulating of DNA with iDEP tweezers were reproducible with both homogeneous DNA (48,502 base pairs) and nonhomogeneous mixed DNA containing 6 fragments from 3,550 – 21,226 base pairs (Figure S6).

Discussion

Taken together, results from fluorescence imaging of the sub-micron particles and DNA demonstrate the effective control and manipulation of objects using the iDEP tweezers. In principle, our iDEP tweezers enable us to manipulate nanoscale particles (R > 11 nm) by comparing them to the competing thermal force (F_th = k_BT/2R)^{7, 43}. Here, we briefly discuss the physical mechanisms of the iDEP of DNA to guide design rules for creating effective iDEP tweezers for general use of other biomolecule control and manipulation measurements.

Depending on the dielectric responses of the objects and the surrounding medium, the external fields induce an instantaneous force F_DEP = ¼α∇∣E∣² acting on the objects with the effective polarizability α of the object, which is associated with the frequency-dependent CM factor^{9, 10}. For the spherical particles, spatially asymmetric force due to the inhomogeneous field gradient in the medium drives the movement of the polarized particles either by attracting or repelling them from the medium to regions of strong electric fields, such as the electrode edge or the tip end. Such frequency-dependent CM factors, polarizability, and DEP are in excellent agreement with many experimental observations and computational simulations, ours included^{1, 31}.

Unlike the dielectric particles, precise identification of α values for DNA and the influence of DEP on DNA are not understood⁴⁴, since DNA is not a spherical particle but rather a long biopolymer where the negative charges of DNA are fixed at the backbone. Taking into account the DNA shape, the real part of α values of DNA could be estimated using either the traditional CM factor approach^{7, 27}, the recent CIF model^{11, 36, 41}, or experimental measurements^37-40. By assuming the stretched DNA as ellipsoid, the axis-dependent α of the CM factor model is given by α = 6vε_mRe[K], where $K=\frac{{\epsilon }_p^{\ast }-{\epsilon }_m^{\ast }}{3\left[L_n\right({\epsilon }_p^{\ast }-{\epsilon }_m^{\ast })+{\epsilon }_m^{\ast }]}$, L_n, V, ε_m*, and ε_p* are the complex CM factor, depolarizing factor, volume of the particle, and complex permittivity of the medium and particle, respectively⁴⁵. The polarizability values found from the CM factor model were 6.53 × 10⁻²⁸ Fm² at f = 50 kHz, 2.87 × 10⁻²⁸ Fm² at f = 200 kHz, and −2.59 × 10⁻³¹ Fm² at f = 10 MHz, which yielded the DEP strength of 41.5 nN at f = 50 kHz, 18.3 nN at f = 200 kHz, and nDEP −16.5 pN at f = 10 MHz under constant AC voltage (7 V_pp) (see Experimental Section for details).

Alternatively, the CIF model, in which the redistribution of counterions surrounding DNA under the AC fields is responsible for the movements of DNA, enables an estimate of the total polarizability given by $\alpha =\frac{z^2{q}^2{L}_s^2{n}_{cc}{A}_{st}}{12k_{B}T}\frac{l_{DNA}}{L_s}$, where z, q, L_s, n_cc, A_st, l_DNA, k_B, and T are the valence of counter ion, the electric charge, the subunit length, the number of condensed counter ions, the stability factor of the ionic phase, the contour length of DNA, the Boltzmann constant, and the temperature, respectively^{11, 36}. The total polarizability of the CIF model varies from 1.52 × 10⁻²⁹ to 1.52 × 10⁻²⁸ Fm² depending on the dielectric increment ∆ε values (see Experimental Section for details)^{41, 46}. For the 48,502bp DNA, the polarizability per base pair yields values from 3.12 × 10⁻³⁴ to 3.12 × 10⁻³³ Fm²/bp, which agree with those determined by the experiment measurements and are within the range quoted in the literature^{37, 47}. Thus, the CIF model predicts the DEP strength of 0.962 ~ 9.62 nN. Unfortunately, the CIF model does not allow the reasonable estimation of both pDEP and nDEP since the α values were remarkably insensitive to the frequency range, with only a 3-fold difference for a frequency that differs by 10³-fold^{38, 46}.

Although previous DEP measurements with DNA have demonstrated the pDEP trap around the electrode or obstacles, no experiments have discussed nDEP, or the strength of nDEP that was simply assumed to be identical to pDEP with the reversed sign (i.e., nDEP = −∣pDEP∣)⁴⁸. However, the observations of both pDEP and nDEP rely on the experimental limitations associated with either the DEP operating parameters (e. g., AC voltage, frequency, buffer, DNA fragment and concentration) or the design of the DEP device.

In addition to the polarity of DEP from those models, there is disagreement about the magnitude of DEP between them. First, the strength of pDEP, compared to the nDEP values obtained by the CM factor calculation, is substantially increased by almost three orders of magnitudes. The overestimation of pDEP is originated by the ellipsoidal assumption of DNA in which the effective polarization is different along each axis. In particular, a prolate spheroid or highly elongated (needle-shaped) object tends to align itself with its longest axis parallel to the external fields regardless of positive or negative DEP⁹, which resulted in highly asymmetric CM factor values at a low frequency regime (Figure 4). Such alignment behavior of the DNA could further lead to stretching them between two electrodes under the weak pDEP as shown in Figure 3b. Second, the pDEP values estimated from the two approaches differ by nearly a factor of 2 ~ 40. This difference is attributed to the assumption of DNA as a rigid rod in the CM factor model, which enhances its polarizability in a longitudinal direction and increases subunit length L_s in the CIF model.

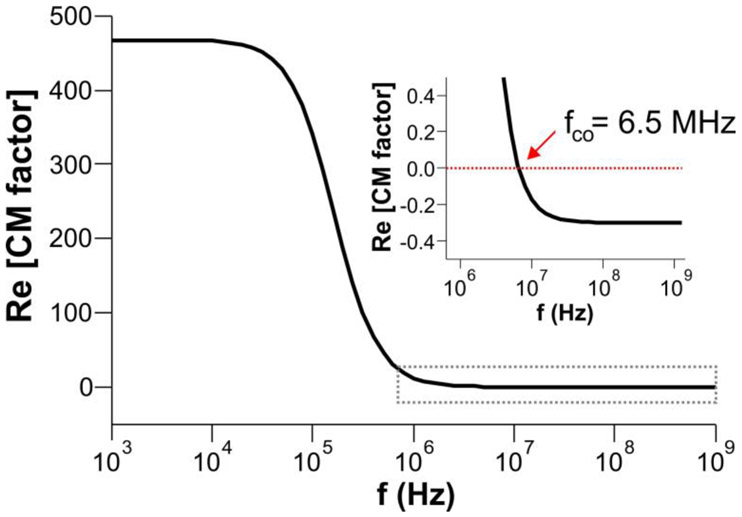
Figure 4.

Asymmetric, frequency dependent real part of the CM factor assuming DNA as an ellipsoidal particle. The inset shows the negative values of the CM factor at f > f_co, which lead to negative DEP. In calculating this plot, the following parameters were used: a = b = 2 nm, c = 22 μm, ε_p = 8ε_o, ε_m = 78ε_o, σ_p = 1 S/m, σ_m = 5×10⁻⁴ S/m (see Supporting Information for details).

The CM factor calculation allows us to estimate f_co = 6.5 MHz and bipolar DEP (Figure 4), which conforms our experimental observations of pDEP and nDEP behaviors. Despite such valuable information from the CM factor model, the charge redistribution under the AC fields is inapplicable to DNA because the negative charges are fixed to the DNA backbone. While the CIF model considers the counterion fluctuation and its contribution to the polarizability of DNA under the AC fields, the polarity and frequency-dependence of nDEP cannot be derived from the model. Thus, further studies are needed to address the polarization mechanism for DNA under the influence of the non-uniform AC fields.

In any case, the theoretical evaluation of the DEP must be stronger than the thermal force F_th = k_BT/2R_H, driving the Brownian motion of particles with a hydrodynamic radius R_H at room temperature T, due to its interference with the DEP manipulation⁷. Using the worm-like chain model⁴⁹, the radius of gyration (R_g ≈ 1.54R_H) of DNA was estimated to be 606 nm, which resulted in F_th of 5.23 fN. These results also suggest a minimum strength of ∇E² of 8.08 × 10¹⁶ V²/m³ at the trapping site to overcome the thermal diffusion (see Experimental Section for details). Thus, the theoretical predictions of pDEP, nDEP, and ∇E² (Figures 1b-1c) from both models are at least 4 orders of magnitude larger than F_th and the minimum requirement of ∇E² for trapping and spatial manipulation of DNA at the tip as demonstrated in Figure 3.

Finally, the effective volume and trapping pattern of DNA are examined. The effective trapping distance from the tip end to the end of the trapped particles and DNA was measured to be approximately 3 – 8 μm, depending on the direction of the measurements. Considering the R_H of 393 nm and the contour length of 22 μm, the trapping distance and pattern suggest that the individual DNA is neither randomly coiled nor perfectly stretched. Instead, the DNA could be partially stretched under the AC fields, forming widely spread cloud structures around the tip end (Figure 3). Such cloud effects due to the partial stretching of DNA trapping was also observed when the pDEP conditions were changed (Figure 5). After increasing the frequency from 80 kHz to 200 kHz of the applied AC voltage (9 V_pp), DNA formed like clouds between two electrodes. In general, high frequency lowers the strength of DEP due to the decrease of the frequency-dependent CM factor in the CM factor model (Figure 4) and the total polarizability of the DNA in the CIF model^{40, 47} and the experimental observations^{38, 46}. Thus, the DNA cloud effects could be partially stretched DNA molecules due to the weak pDEP, which has been also previously observed^{36, 38}. The experimental observation of the DNA trapping pattern manifests the strong dependence of DNA’s α value on the frequency of the AC fields.

Figure 5.

Frequency dependent DEP and the DNA trapping pattern. (a) The low-frequency AC voltage generates strong pDEP, attracting DNA to the electrode (9 V, 80 kHz). (b) After increasing the frequency of the AC voltage (9 V, 120 kHz), DNA experiences slightly reduced pDEP, which causes the trapped DNA to partially move off from the electrode. (c) After further increasing the frequency of the AC voltage (9 V, 200 kHz), the DNA were fully stretched between the electrodes, indicating a significant dependence of the DEP strength and the DNA polarizability on the frequency of the applied AC voltage. The scale bar is 10 μm.

Conclusion

By linking an insulator tip and conventional dielectrophoretic method, we have demonstrated that our iDEP-based molecular tweezers can trap, carry, reposition, and release the sub-micron particles and DNA. The technique allows a simple and effective separation in a fluid environment without potential issues such as fouling, electrolysis, and joule heating associated with traditional metal-based DEP methods. We have compared two polarization models of DNA, and demonstrated that either model could not fully describe iDEP behaviors of DNA. However, the strength of iDEP tweezers estimated by both models was strong enough to overcome the competing forces acting on a particle or DNA in a fluid, including thermal force and viscos drag. These results enable other researchers to design and determine operating parameters to successfully perform iDEP-based manipulation experiments with a range of biomolecules and biopolymers.

Experimental Section

Device fabrication and measurement setup.

The interdigitated electrode arrays are prepared by the standard optical lithography technique on a SiO₂ substrate as described previously³¹. The width of electrodes, gaps between the electrodes, and the height of the electrodes were 16 μm, 25 ~ 40 μm, and 140 nm, respectively. The insulator tips were made from glass rods (Harvard Apparatus, 1.0 mm diameter, 75 mm length) and fabricated by a two end pulling method using a micropipette puller (MicroData Instrument), placed between two gold electrodes, and manipulated through an xyz manipulator (Miller Design & Equipment) while trapping, moving, and releasing biomolecules. The external AC voltage between the electrodes was applied by a commercial function/arbitrary waveform generator (Agilent 33220A). These devices were mounted on a low-power fluorescent microscope (OMFL600), and all experiments were performed in either a PBS or TE buffer without evaporation while measuring. All images and videos were recorded through a CCD camera and analyzed using the ImageJ software.

DNA labeling and preparation.

The iDEP tweezer capability was tested with the polystyrene particles and DNA. The fluorescently labeled polystyrene particles with a diameter of 500 nm were purchased from Phosphorex (λ_Ex = 460 nm, λ_Em = 500 nm). A 5 μl of the particle solution diluted into 0.001× PBS buffer was deposited on the devices before DEP measurements. The double-stranded λ-DNA fragments (48,502 base pairs and mix of 3,550 – 21,226 base pairs, New England Biolab) were purchased and labeled with YOYO-1 (λ_Ex = 491 nm, λ_Em = 509 nm, Thermo Fisher Scientific) at a ratio of five base pairs per YOYO-1 molecule in a 0.01× TE buffer prior to use. Similar to the polystyrene particle measurements, a 5 μl of the labeled DNA solution was deposited on the devices before the manipulation experiments.

COMSOL simulation.

The distribution of the electric fields and the electric field gradients across the electrodes and the tips were calculated using commercial finite element software, COMSOL Multiphysics 5.3a (COMSOL, Inc.). To set-up COMSOL simulations, the interdigitated electrodes and the insulator tip along with the buffer layer were drawn to scale using AutoCAD software (Autodesk) and imported into COMSOL software. The AC/DC electric current module and frequency domain studies were used to calculate electric fields and the electric field gradients. A buffer solution (σ_m= 10⁻³ S/m and ε_m = 78ε_o for 0.001× PBS buffer, σ_m= 5 × 10⁻⁴ S/m and ε_m = 78ε_o for 0.01× TE buffer) was filled over the electrodes as used in the experiments. The sinusoidal potential of 7 V peak to peak at 50 ~ 200 kHz was applied to the electrodes. Finally, the device geometry was meshed with customized mesh. The electrodes and the tip were meshed by extremely fine, free triangular meshes with a maximum element size of 300 nm and a minimum element size of 1 nm. We used a swept mesh on the buffer volume with the maximum element size of 1 nm, the minimum element size of 0.01 nm, the curvature factor of 0.6, and the resolution of narrow regions of 9, in order to increase the number of elements in the mesh, thereby providing better accuracy.

The CM factor calculation.

The complex CM factor is given by $K\left(\omega \right)=\frac{{\epsilon }_p^{\ast }-{\epsilon }_m^{\ast }}{3\left[A\right({\epsilon }_p^{\ast }-{\epsilon }_m^{\ast })+{\epsilon }_m^{\ast }]}$ , where ε_p^* and ε_m^* are the complex dielectric constant of the particle and medium associated with conductivity σ (i.e., ε* = ε - iσ/ω), and A is the depolarization factor (0 ≤ A ≤ 1), respectively. For the spherical particle case (A = 1/3), the real part of the CM factor is expressed as $\text{Re}\left[K\right(\omega \left)\right]=\frac{{\omega }^2({\epsilon }_p-{\epsilon }_m)({\epsilon }_p+2{\epsilon }_m)+({\sigma }_p-{\sigma }_m)({\sigma }_p+2{\sigma }_m)}{{\omega }^2({\epsilon }_p+2{\epsilon }_m{)}^2+({\sigma }_p+2{\sigma }_m{)}^2}$. The CM factor can be a positive or negative value depending on the AC field frequency, determining the DEP direction and strength as shown in Figure S4. DEP can be calculated by F_DEP = πR³ε_mRe[K(ω)]∇E², where R (= 250 nm) is the radius of the particle and of ∇E² (= 1.30 × 10²⁰ V²/m³) is the strength of the field gradient. Thus, the strength of F_DEP at f = 20 KHz and f = 2 MHz is estimated to be 2.2 nN and −1.6 nN, respectively. For the prolate spheroids (a = b < c), the real part of CM factor is expressed as $Re\left[K\right(\omega \left)\right]=\frac{3{\omega }^2({\epsilon }_p-{\epsilon }_m)(A{\epsilon }_p-A{\epsilon }_m+{\epsilon }_m)+3({\sigma }_p-{\sigma }_m)(A{\sigma }_p-A{\sigma }_m+{\sigma }_m)}{9{\omega }^2(A{\epsilon }_p-A{\epsilon }_m+{\epsilon }_m{)}^2+9(A{\sigma }_p-A{\sigma }_m+{\sigma }_m{)}^2}$, where A (parallel to the electric field) has an analytical solution of $A=\frac{1-e^2}{2e^3}\left[\log \left(\frac{1+e}{1-e}\right)-2e\right]$ with the eccentricity of the spheroid $e=\sqrt{1-b^2∕c^2}$. By assuming the minor axis a = b = 2 nm and major axis c = 22,000 nm^{50, 51}, the depolarizing factor A of DNA can be calculated to be 2.13 × 10^-4. DEP of the prolate spheroids is given by F_DEP = 2πabcε_mRe[K(ω)]∇E², where of ∇E² is 2.54 × 10²⁰ V²/m³. Thus, the strength of F_DEP is calculated to be 41.5 nN (f = 50 kHz), 18.3 nN (f = 200 kHz), and −16.5 pN (f = 10 MHz).

The CIF model for DNA.

In this model, the counterions can move freely along the macromolecular “subunit lengths” under the influence of an external electric field^{11, 36}. Total polarizability is given by ${\alpha }_{CIF}=\frac{z^2{q}^2{L}_s^2{n}_{cc}{A}_{st}}{12k_{B}T}\frac{l_{DNA}}{L_s}$, where z, q, Ls, n_cc, A_st, l_DNA, k_B, and T are the valence of counterion, the electric charge, the subunit length of DNA, the number of condensed counterions, the stability factor of the ionic phase including mutual repulsion between fixed charges on the backbone and the effect of Debye screening, the contour length of DNA, the Boltzmann constant, and the temperature, respectively. A_st is given by $A_{st}=\frac{1}{1-2(z\xi -1)\text{ln}\left(K_{s}b\right)}$, where ξ, K_s, and b are charged density parameter $\xi =\frac{q^2}{4\pi {\epsilon }_m{k}_{B}Tb}$, reciprocal of the Debye screening length $K_s=\sqrt{\frac{N_{AV}{q}^2}{{\epsilon }_m{K}_{B}T}\left(C_i{z}^2+\frac{C_p}{\xi }\right)}$, and the average distance between charged sites for the DNA double helix (b = 0.173 nm). Also, $C_i=\frac{{\sigma }_m}{q\mu N_{AV}}$ and $C_p=\frac{2C_{DNA}}{M{W}_{bp}{10}^{-3}}$ are the concentration of ions surrounding DNA and concentration of the phosphate group. Using q = 1.6 × 10⁻¹⁹ C, T = 298 K, ε_m = 78ε₀, N_AV = 6.02 × 10²³ (Avogadro number), z = 1, σ_m = 5 × 10⁻⁴ S/m, × = 8 × 10⁻⁸ m²V⁻¹s⁻¹ (ion mobility), C_DNA = 0.12 μg/μl (DNA concentration), MW_bp = 649 Da/bp (molecular weight per base pair), A_st is estimated to be A_st = 0.029. The subunit length L_s is given by $L_s=\sqrt{\frac{9\Delta \epsilon }{\pi {\epsilon }_m(z\xi -1)A_{st}{N}_{AV}{C}_{p}b}}$ , where ∆ε is the dielectric increment. With Δε = 1 ~ 10 experimentally determined with various DNA^{41, 46}, L_s is estimated to be 1.02 × 10⁻⁷ ~ 3.23 × 10⁻⁷ m. Using the number of condensed counter ions $n_{cc}=\frac{{\varphi }_c{L}_s}{z\cdot b}$ and a fraction of condensed counter ions ${\varnothing }_c=1-\frac{1}{z\xi }$, α_CIF is estimated to be 1.51 × 10⁻²⁹ ~ 1.51 × 10⁻²⁸ Fm². For the 48,500 bp DNA, the total polarizability divided by the DNA base pairs α_CIF/bp lies between 3.12 × 10⁻³⁴ ~ 3.12 × 10⁻³³ Fm²/bp. Finally, the strength of F_DEP = ¼α_CIF∇E² is estimated to be 0.962 ~ 9.62 nN.

Thermal fluctuation of DNA using the worm-like chain model.

The thermal force is given by F_th = k_BT/2R_H, where k_B, T, and R_H are Boltzmann constant, temperature, and a hydrodynamic radius of DNA. In the worm-like chain model⁴⁹, the radius of gyration R_g of DNA is given by $R_g=\sqrt{\frac{1}{3}PL}$, where P (= 50 nm) is persistence length of DNA and L (= 22,000 nm) is the contour length of YOYO-1 labeled DNA. R_g is estimated to be 606 nm. Using the relationship of R_H = R_g/1.54, the R_H is estimated to be 393 nm. Finally, F_th is calculated to be 5.23 fN. By equating F_th with F_DEP, the strength of the field gradient ∇E² = 4F_th/α is calculated to be 3.20 × 10¹³ ~ 8.08 × 10¹⁶ V²/m³ with the lower and upper limit of estimated α values from both the CM factor and CIF models.