Mathematical modeling of the ‘inoculum effect': six applicable models and the MIC advancement point concept

ABSTRACT

Antimicrobial treatment regimens against bacterial pathogens are designed using the drug's minimum inhibitory concentration (MIC) measured at a bacterial density of 5.7 log₁₀(colony-forming units (CFU)/mL) in vitro. However, MIC changes with pathogen density, which varies among infectious diseases and during treatment. Incorporating this into treatment design requires realistic mathematical models of the relationships. We compared the MIC–density relationships for Gram-negative Escherichia coli and non-typhoidal Salmonella enterica subsp. enterica and Gram-positive Staphylococcus aureus and Streptococcus pneumonia (for n = 4 drug-susceptible strains per (sub)species and 1–8 log₁₀(CFU/mL) densities), for antimicrobial classes with bactericidal activity against the (sub)species: β-lactams (ceftriaxone and oxacillin), fluoroquinolones (ciprofloxacin), aminoglycosides (gentamicin), glycopeptides (vancomycin) and oxazolidinones (linezolid). Fitting six candidate mathematical models to the log₂(MIC) vs. log₁₀(CFU/mL) curves did not identify one model best capturing the relationships across the pathogen–antimicrobial combinations. Gompertz and logistic models (rather than a previously proposed Michaelis–Menten model) fitted best most often. Importantly, the bacterial density after which the MIC sharply increases (an MIC advancement-point density) and that density's intra-(sub)species range evidently depended on the antimicrobial mechanism of action. Capturing these dependencies for the disease–pathogen–antimicrobial combination could help determine the MICs for which bacterial densities are most informative for treatment regimen design.

The bacterial density at which an antimicrobial's MIC increases sharply (an MIC advancement-point density) is linked to the antimicrobial mechanism of action, with the complete MIC-density relationship most often captured by a Gompertz or logistic model.

INTRODUCTION

Effective antimicrobial treatment regimens for bacterial diseases are essential for prudent use of existing antimicrobial drugs as a limited resource (Toutain, del Castillo and Bousquet-Mélou 2002; Papich 2014). Antimicrobial treatment regimens are designed by projecting the pharmacodynamics against the pathogen population at the infection site using several different paramaters, the most common being the antimicrobial's minimum inhibitory concentration (MIC) measured in vitro at a bacterial density of 5.7 log₁₀(colony-forming units (CFU)/mL) (i.e. 5 × 10⁵ CFU/mL)" (Lees and Shojaee Aliabadi 2002; Toutain, del Castillo and Bousquet-Mélou 2002; Levison 2004; Mueller, de la Pena and Derendorf 2004; Garcia 2010; Papich 2014; CLSI 2015). Values of the MIC and other pharmacodynamic parameters are assumed to remain constant throughout treatment (Lees and Shojaee Aliabadi 2002; Blondeau et al. 2004; Levison 2004; Mueller, de la Pena and Derendorf 2004; Toutain and Lees 2004; McClary et al. 2011; Papich 2014). However, pathogen density (number of viable bacteria per g or mL) at the infection site varies among pathogen–disease combinations and individuals, e.g. densities 3–9 log₁₀(CFU/mL) are reported in human soft tissue and intraabdominal infections (Chastre et al. 1995; Konig, Simmen and Blaser 1998; Smith 2000; Sheppard et al. 2003; Mastroeni et al. 2009) and 3.7–8.5 log₁₀(CFU/mL) in cerebrospinal fluid of humans with meningitis (Feldman 1976). During treatment, pathogen density at the infection site can fluctuate in response to the antimicrobial concentration, but overall decreases until the infection is eradicated by the treatment (also known as the bacteriological cure) and/or the host immune responses (Read, Day and Huijben 2011; Ankomah and Levin 2014). Importantly, an antimicrobial's MIC changes with the bacterial population density (Brook 1989; Burgess and Hall 2004; LaPlante and Rybak 2004; Bidlas, Du and Lambert 2008; Udekwu et al. 2009). Accounting for the changes could enable optimizing treatment regimens to maximize the bacteriological cure probability while minimizing antimicrobial drug use (Regoes et al. 2004; Meredith et al. 2015).

The term inoculum effect (IE) has been used historically for the MIC–bacterial density relationships (Brook 1989; Burgess and Hall 2004; LaPlante and Rybak 2004; Bidlas, Du and Lambert 2008; Kesteman et al. 2009; Singh et al. 2009; Udekwu et al. 2009). It is believed to have been reported first in vitro in 1945 (Kirby 1945) and in vivo in 1952 (Eagle 1952). Currently, the phenomenon is considered as a bacterial collective antibiotic tolerance response to antimicrobial exposure (Meredith et al. 2015). The phenomenon is documented in vitro for bactericidal and bacteriostatic antimicrobial drugs in Gram-negative and Gram-positive bacterial species, including Enterobacteriaceae, staphylococci and streptococci (Tilton, Lieberman and Gerlach 1973; Chantot, Bryskier and Gasc 1986; Bryskier 1998; Butler 2001; Butler et al. 2001; Thomson and Moland 2001; Tam et al. 2009; Udekwu et al. 2009). Few mathematical models have been investigated for reflecting the antimicrobial MIC–bacterial density relationships. It has been proposed that a Michaelis–Menten model could reflect these relationships, based on data for several antimicrobials and one Staphylococcus aureus strain (Udekwu et al. 2009). We hypothesized it is unlikely that a single model accurately captures the MIC–density relationships across pathogen–antimicrobial combinations, and that the variety of the relationship's mathematical forms has not been elucidated. The objective of this study was to compare the MIC–density relationships and mathematical models capturing those for exemplar Gram-negative (Escherichia coli and non-typhoidal Salmonella enterica subsp. enterica) and Gram-positive (Streptococcus pneumonia and S. aureus) pathogens and focusing on antimicrobials with bactericidal activity against these (sub)species (which will further be abbreviated as species).

MATERIALS AND METHODS

Bacterial isolates

Four isolates from humans and animals of each E. coli, S. enterica subsp. enterica (further—S. enterica), S. aureus and S. pneumoniae were used. The isolates were classified as susceptible to the antimicrobial drugs studied. A convenience sample size (n = 4 isolates per species) was chosen in the absence of prior data on between-isolate variability in the MIC–bacterial density relationships for the antimicrobials and species. The E. coli and S. enterica isolates were obtained from farm-animal feces during field studies by the Kansas State University faculty in 2014–16. The S. enterica isolates were of serotypes Anatum, Bovismorbificans, Give and Typhimurium (serotyped by the US National Veterinary Services Laboratories, Ames, IA). The S. aureus isolates obtained from a skin swab, biopsy and blood samples from domestic animals in 2016 were provided by the Kansas State Veterinary Diagnostic Laboratory. The S. pneumoniae isolates of serotypes 3 and 19A (serotyped by the US Centers for Disease Control and Prevention) were provided by the CDC and obtained from human blood samples between 2003 and 2009.

Antimicrobials

High purity ceftriaxone, ciprofloxacin, gentamicin, linezolid, oxacillin and vancomycin forms (Sigma-Aldrich, Inc., St. Louis, MO, U.S.) were used. Stock drug solutions were prepared accounting for the form potency. The stock solutions of ceftriaxone, gentamicin, oxacillin and vancomycin (10 mg/mL) were prepared by dissolving the drug powder in sterile distilled water; of ciprofloxacin (10 mg/mL) by dissolving the powder in 0.1 N hydrochloric acid solution; and of linezolid (10 mg/mL) by dissolving the powder in dimethyl sulfoxide. The stock solutions were aliquoted, stored at −20°C, and used within 3 months, except for ciprofloxacin stock solutions, which were stored at 4°C and used within 2 weeks. Before each experiment, a stock solution aliquot was diluted to a working solution of desired drug concentration in sterile distilled water.

Determination of antimicrobial MIC for different bacterial densities

Each isolate was incubated overnight at 37°C on tryptic soy agar with 5% sheep blood (BAP, Remel^TM, Lenexa, KS, USA). For an isolate of E. coli, S. enterica or S. aureus, bacterial colonies from the BAP plate were suspended in 9 mL of cation-adjusted Mueller-Hinton broth (Ca-MHB, BBL^TM, Sparks, MD, USA) to visually match the 0.5 McFarland turbidity standard. The suspension was serially diluted in Ca-MHB to each of the expected bacterial densities 10⁸, 5 × 10⁷, 10⁷, 10⁶, 10⁵, 10⁴, 10³ and 10² CFU/mL. The densities were confirmed by serially diluting an aliquot of each of the 10⁸, 10⁵ and 10² dilutions in a sterile 0.9% saline solution, directly plating the dilutions in duplicate on BAP, incubating the plates at 37°C aerobically for 18–24 h (until colonies were visible) and counting the bacterial colonies (Regoes et al. 2004). For an isolate of S. pneumoniae, bacterial colonies from the BAP were suspended to the expected bacterial density ∼1 × 10⁸–5 × 10⁸ CFU/mL in 9 mL of Ca-MHB with 5% (v/v) lysed horse blood (Innovative Research, Inc., Novi, MI, USA). (For each S. pneumoniae isolate, a preparatory experiment was performed to determine the required colony number.) The suspension was serially diluted in Ca-MHB with 5% (v/v) lysed horse blood to the expected densities 10⁸ to 10² CFU/mL, as for the other bacterial species, and the densities similarly confirmed.

A sterile 96-well plate (Corning, Inc., Lowell, MA, USA) was used for one bacterial isolate and one starting drug concentration. A plate row (12 wells) was used for one bacterial density; each well in the row contained 100 µL of the isolate suspension of that density. Eight rows each contained the isolate suspension of one of the 10⁸, 5 × 10⁷, 10⁷, 10⁶, 10⁵, 10⁴, 10³, and 10² CFU/mL densities. The starting drug concentrations (in different plates) were 1500, 1000, 25 and 20 mg/L for all the antimicrobials and species, except linezolid for which those were 1000, 500, 50 and 40 mg/L for S. aureus and S. pneumoniae. Of the starting drug concentration solution, 100 µL was loaded into each well in column 1, the bacterial and antimicrobial solutions in column 1 pipetted 10 times, after which 100 µL of each well were loaded from column 1 to column 2 and the pipette tips replaced; this was repeated for columns 2–11. Thus, each starting drug concentration and 10 of its sequential 2-fold dilutions were tested against each density of the bacterial isolate. Column 12 was the positive control of visible isolate growth in the absence of antimicrobial. The plates were incubated at 37°C aerobically for 18–24 h; the MIC for each density of the isolate was read as the lowest drug concentration inhibiting visible population growth from that density. The experiment for each isolate and each of four starting drug concentrations was performed in duplicate on different dates. For each density of the isolate, if the duplicate MIC readings were within one 2-fold drug dilution apart, the lowest reading was the result recorded. If the duplicate MIC readings were further apart, a third replicate was performed and the lowest MIC of the readings within one 2-fold drug dilution apart from two of the three replicates was the result recorded.

Mathematical modeling of antimicrobial MIC–bacterial density relationships

The experimental data were transformed to log₂(MIC) and log₁₀(CFU/mL) to enable a comparative evaluation of the MIC–density relationship forms (Figs 1 and 2). Each of six candidate non-linear models was fitted to the transformed data for a representative isolate for each of the antimicrobial–bacterial species combinations. This included the Michaelis–Menten model proposed earlier based on data for several antimicrobials and one S. aureus strain (Udekwu et al. 2009). Each model had at most four parameters to capture the log₂(MIC) vs. log₁₀(CFU/mL) curves. Candidate models with more parameters (e.g. see (Andrews 1968; Muhammad et al. 2017)) were not considered, to avoid model overfitting given the limited number of observations per individual antimicrobial–bacterial species combination.

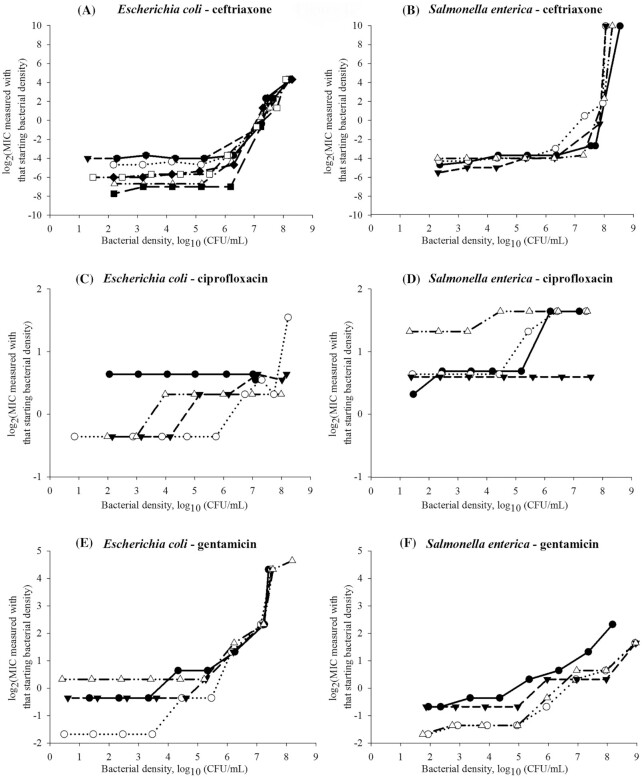
Figure 1.

Experimental data on the antimicrobial's minimum inhibitory concentration (MIC) dependency on the bacterial density for Gram-negative Escherichia coli (n = 4 isolates except for ceftriaxone n = 8 isolates) and non-typhoidal Salmonella enterica subsp. enterica (n = 4 isolates). Each symbol is used to denote a distinct isolate of the bacterial species.

Figure 2.

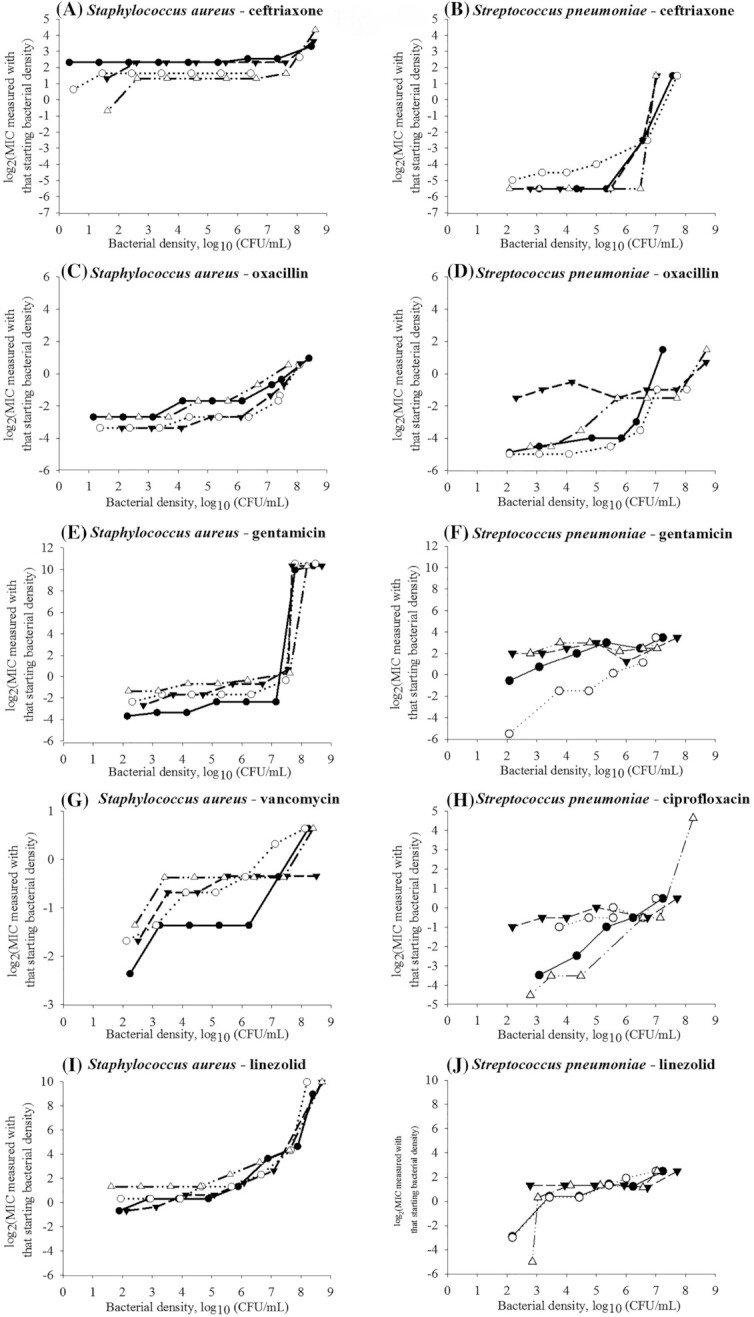
Experimental data on the antimicrobial's minimum inhibitory concentration (MIC) dependency on the bacterial density for Gram-positive Staphylococcus aureus (n = 4 isolates) and Streptococcus pneumoniae (n = 4 isolates). Each symbol is used to denote a distinct isolate of the bacterial species.

The investigated six models are detailed below. We defined y = log₂(MIC) and x = log₁₀(CFU/mL) bacterial density.

A Michaelis–Menten model was formulated by:

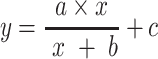(1)

where

• a + c—projects maximum y at high bacterial densities;

• b—projects x at which a half maximum y ((a + c) × 0.5) is reached;

• c—projects minimum y at low bacterial densities.

The Michaelis–Menten models, however, do not reproduce sigmoid curves, such as those observed for the log₂(MIC) vs. log₁₀(CFU/mL) relationships (Figs 1 and 2). The Hill-function models, which are also used to describe antimicrobial pharmacodynamics against bacterial populations, can capture such behavior (Goutelle et al. 2008; Czock et al. 2009; Stefan and Le Novere 2013). Assuming the Hill coefficient value  , a Hill-function model was formulated by:

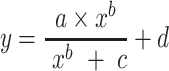(2)

where

• —projects maximum y at high bacterial densities;

• b—reflects steepness (steepness of an increase in y with an increase in x) and shape of sigmoid function;

• c—projects x^b at which a half maximum y (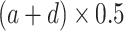) is reached;

• d—projects minimum y at low bacterial densities.

A logistic model can also capture a sigmoid curve and was formulated by:

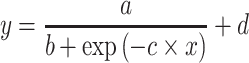(3)

where

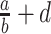• —projects maximum y at high bacterial densities;

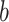• —represents a shift for the location of 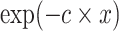at which a half maximum y 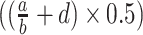is reached;

• c—reflects steepness of sigmoid function;

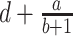• —projects minimum y at low bacterial densities.

Depending on the sigmoid curve shape, a Gompertz model might better capture the shape than Hill or logistic models (Keller et al. 2002; Peleg and Corradini 2011). A Gompertz model was formulated by:

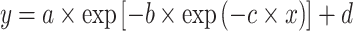(4)

where

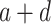• —projects maximum y at high bacterial densities;

• b—represents a shift for the location of 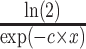at which a half maximum y (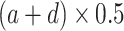) is reached;

• c—reflects steepness of sigmoid function;

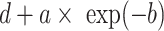• —projects minimum y at low bacterial densities.

A von Bertalanffy model can also capture a sigmoid curve (Fabens 1965; Maino and Kearney 2017) and was formulated by:

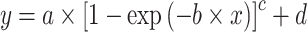(5)

where

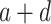• —projects maximum y at high bacterial densities;

• b—reflects steepness of sigmoid function;

• c—reflects shape of sigmoid function;

• d—projects minimum y at low bacterial densities.

Exponential models are used for the bacterial population growth (Karslake et al. 2016). We included a bi-exponential model defined as a multilinear approximation of an exponential function:

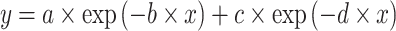(6)

where

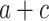• —projects minimum y

• b and d—adjust steepness of sigmoid function in approaching maximum y (i.e. control x at which the maximum y is projected).

Each model was fitted using the least-squares method by regressing y on x for a representative isolate for the antimicrobial-bacterial species combination, with the ‘trust-region’ algorithm that efficiently handles large sparse and small dense problems in searching the parameter space (Shultz, Schnabel and Byrd 1985). Model parameter values minimizing the mean squared error between the predicted and observed y values across the bacterial densities tested were estimated; model iterations were terminated if the tolerance 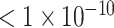change in the mean squared error between successive iterations was met or after 500,000 iterations. No boundaries were imposed on the parameter values except for keeping the value positive or negative per model structure. Using the estimated parameter values, the model projections were generated for the bacterial densities 10¹–10¹² (CFU/mL). Relative fit of the six models (with the parameter values estimated as above) to the representative-isolate data was evaluated with the adjusted coefficient of determination R² (a larger adjusted R² indicated a better model fit) and Akaike's information criterion (AIC) obtained using the log-likelihood function penalized by the number of parameters (a smaller AIC indicated a better model fit).

The density x at which there was the maximum positive change in the y slope was considered as the model-based estimate of the MIC advancement-point density (AP). It was identified using the curvature (Sternberg 2012; Stewart 2015) of the projected yvs.x curve, defined as:

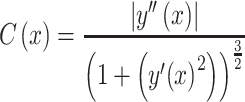(7)

From which the AP estimate was:

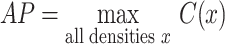(8)

The curvature equations for the six models are included in the online supplementary material. The modeling was implemented in MATLAB® R2019b (MathWorks Inc., Natick, MA, USA). Because of the limited number of isolates (n = 4) tested per bacterial species, statistical evaluations of the intra-species variability and relative magnitudes of the intra- vs. inter-species variabilities in the MIC–density relationships within or between antimicrobials were not performed.

RESULTS AND DISCUSSION

We determined and compared the MIC–bacterial density relationships for two Gram-negative (E. coli, non-typhoidal S. enterica) and two Gram-positive (S. aureus, S. pneumoniae) bacterial species and bactericidal antimicrobials from these drug classes: β-lactams (oxacillin and ceftriaxone), fluoroquinolones (ciprofloxacin), aminoglycosides (gentamicin) and glycopeptides (vancomycin) (Kohanski et al. 2007; Lobritz et al. 2015). We added the bacteriostatic oxazolidinone linezolid as one of newest antimicrobials introduced to tackle infections by strains resistant to older antimicrobials (Dresser and Rybak 1998; Swaney et al. 1998). For an antimicrobial, the MIC–density relationship curve varied among the bacterial species; likewise, for a species, it varied among the antimicrobials (Figs 1 and 2). These results agreed with earlier in vitro data, e.g. for Haemophilus influenzae type b isolates a stronger IE is observed for the β-lactams penicillin and ampicillin than for chloramphenicol (Feldman 1976). For a S. aureus strain, the IE is strongest for the β-lactam oxacillin, followed by the aminoglycoside gentamicin, and lowest for the glycopeptide vancomycin and oxazolidinone linezolid (Udekwu et al. 2009). Based on our results, for a given antimicrobial–species combination, the MIC–density relationship could be similar across isolates (n = 4 tested per combination) classified as susceptible to the antimicrobial (Figs 1 and 2, Table 1).

Table 1.

Location and between-isolate range of the antimicrobial's MIC advancement-point bacterial density (AP), after which the MIC sharply increased, observed for each of the antimicrobial–bacterial (sub)species combinations.

	The antimicrobial drug MIC's AP observed across n = 4 isolates of the bacterial (sub)species, log10(colony forming units (CFU)/mL)
Mechanism of antibacterial action: antimicrobial drug	Escherichia coli	Non-typhoidal Salmonella enterica subsp. enterica	Staphylococcus aureus	Streptococcus pneumoniae
Inhibiting cell-wall synthesis:
Ceftriaxone	5.2–6.3 (range 1.1)	6.2–7.3 (range 1.1)	6.4–7.6 (range 1.2)	5.0–6.5 (range 1.5)
Oxacillin			3.2–4.1 (range 0.9)	3.5–5.5 (range 2.0)
Vancomycin			4.5–7.4 (range 2.9)
Inhibiting DNA replication:
Ciprofloxacin	3.0–5.7 (range 2.7)	3.3–5.2 (range 1.9)		2.2–4.0 (range 1.8)
Inhibiting protein synthesis:
Gentamicin	4.6–5.5 (range 0.9)	4.4–5.0 (range 0.6)	6.7–7.6 (range 0.9)	2.1–2.8 (range 0.7)
Linezolid			4.6–5.7 (range 1.1)	2.2–2.9 (range 0.7)

Mathematical modeling of antimicrobial MIC–bacterial density relationships

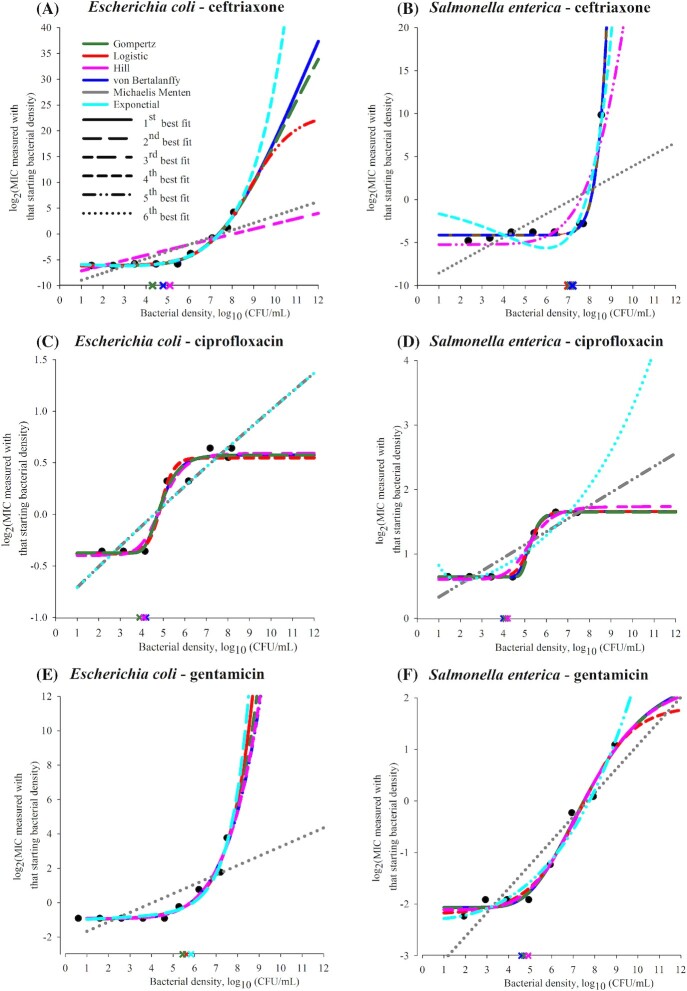
Six mathematical models were compared in fitting the MIC–density relationship curve for a representative isolate for each of the antimicrobial–bacterial species combinations (the model parameter values and fit statistics are given in Supplementary Table S1, see the online supplementary material). The candidate models were chosen based on the observed log₂(MIC) vs. log₁₀(CFU/mL) curves (Figs 1 and 2), and were based on the exponential, logistic, Gompertz, von Bertalanffy, Hill and Michaelis–Menten functions. The logistic model most often fitted best or close to best to the observed relationship curves, followed closely by the Gompertz and von Bertalanffy models (Figs 3 and 4, and Supplementary Table S4, see online supplementary material). However, the MIC's AP estimates obtained by the curvature analysis of the curves projected from the fitted models were most often within the observed AP ranges (Table 1) for the Gompertz model (Supplementary Table S4). The model fit and predictive performance for antimicrobials with different mechanisms of action and individual bacterial species are detailed in Supplementary Tables S2 and S3, respectively, see the online supplementary material.

Figure 3.

Predictions of candidate mathematical models of the log₂(MIC) vs. log₁₀(CFU/mL) density relationship curve for each tested antimicrobial for a representative isolate of Gram-negative Escherichia coli or non-typhoidal Salmonella enterica subsp. enterica. In each panel, the experimental data for the representative isolate for the bacterial (sub)species and antimicrobial combination are shown by black circles. Each of six candidate models was fitted to the data using the least-squares method. Best-fit parameter values for each of the six models were estimated and used to make the model predictions of log₂(MIC) for 1–12 log₁₀(CFU/mL) bacterial densities. The predictions are shown by lines: blue—von Bertalanffy, dark green—Gompertz, red—logistic, pink—Hill, gray—Michaelis–Menten and cyan—exponential model. The line increment indicates the relative fit of the six models (each with best-fit parameter values) to the data for the representative isolate. Specifically, predictions of the model with highest adjusted R² are shown by a solid line; predictions of the other models are shown in order of decreasing adjusted R² of the model by long dashed, short-long dashed, short dashed, dashed-dotted-dotted, and dotted lines. The cross shows the MIC advancement-point density estimated using the curvature analysis of the predicted curve for each of the three models with highest adjusted R²; the cross is of the same color as the line showing the curve predicted by the model.

Figure 4.

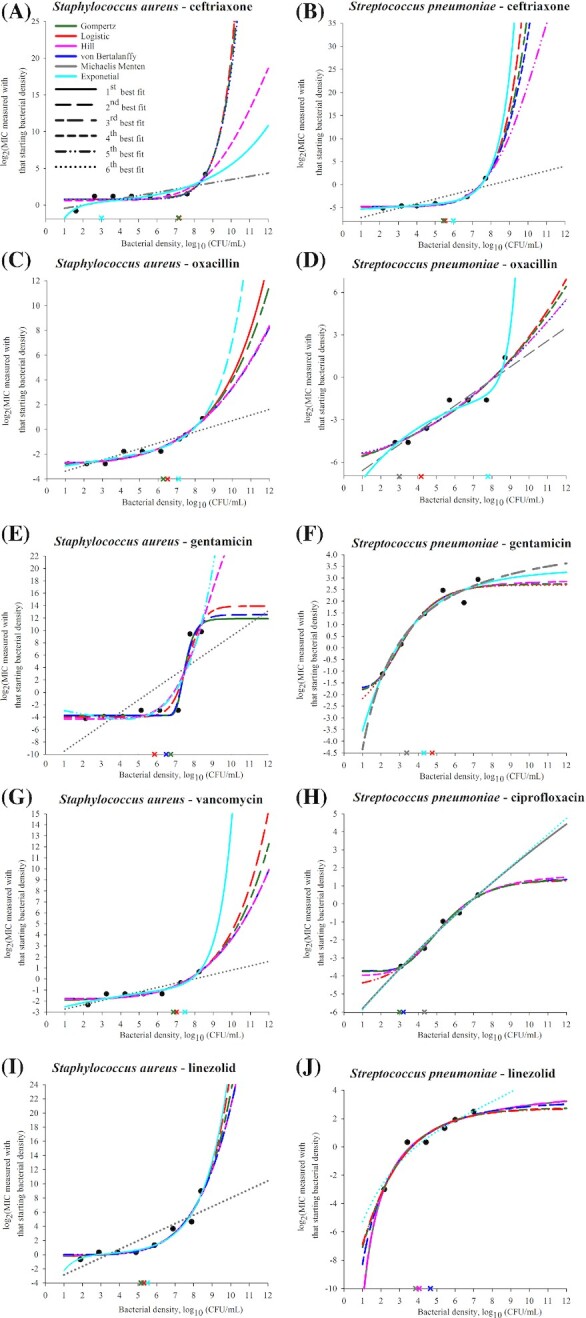
Predictions of candidate mathematical models of the log₂(MIC) vs. log₁₀(CFU/mL) density relationship curve for each tested antimicrobial for a representative isolate of Gram-positive Staphylococcus aureus or Streptococcus pneumoniae. In each panel, the experimental data for the representative isolate for the bacterial (sub)species and antimicrobial combination are shown by black circles. Each of six candidate models was fitted to the data using the least-squares method. Best-fit parameter values for each of the six models were estimated and used to make the model predictions of log₂(MIC) for 1–12 log₁₀(CFU/mL) bacterial densities. The predictions are shown by lines: blue—von Bertalanffy, dark green—Gompertz, red—logistic, pink—Hill, gray—Michaelis-Menten and cyan—exponential model. The line increment indicates the relative fit of the six models (each with best-fit parameter values) to the data for the representative isolate. Specifically, predictions of the model with highest adjusted R² are shown by a solid line; predictions of the other models are shown in order of decreasing adjusted R² of the model by long dashed, short-long dashed, short dashed, dashed-dotted-dotted, and dotted lines. The cross shows the MIC advancement-point density estimated using the curvature analysis of the predicted curve for each of the three models with highest adjusted R²; the cross is of the same color as the line showing the curve predicted by the model.

The ‘classical’ microbiological methods used did not allow reproducible (within one 2-fold drug dilution) MIC measurements at the densities beyond ∼8.5–8.7 log₁₀(CFU/mL). We conjuncture that similar goodness-of-fit of multiple models to a log₂(MIC) vs. log₁₀(CFU/mL) curve was due to the limited observation of the relationship curve. The models captured the curve's observed part; it is uncertain which model would capture the relationship for a wider density range. This is demonstrated theoretically by the model predictions for the densities 10¹–10¹² (CFU/mL) in Figs 3 and 4. Identifying mathematical models that capture the MIC–bacterial density relationship could reveal the relationship's clinically important specifications, including the density after which the MIC increases sharply, which we term the MIC AP, the steepness of the subsequent MIC increase, and whether and at which density an inflection (deceleration in the MIC increase) occurs or the MIC levels-off. For example, predictions of two ‘best-fit’ models for higher-than-tested bacterial densities diverged in some (Fig. 4A, C and D) but not in other (Figs 3C and 4J) cases. The divergent predictions showed the oxacillin MIC would increase steeper at high densities of S. aureus or S. pneumoniae (Fig. 4C and D), or the gentamicin MIC would level-off at a higher value for S. pneumoniae (Fig. 4F), if the relationship follows an exponential rather than logistic model. A ceiling prediction example is that the gentamicin MIC for S. aureus was projected to level-off from ∼8 log₁₀(CFU/mL) (Fig. 4E) but the ceftriaxone MIC to not level-off until >12 log₁₀(CFU/mL) (Fig. 4A).

Location and intra-bacterial species range of the antimicrobial MIC's AP

Antimicrobial treatment regimens are currently designed utilizing the MIC for the density 5.7 log₁₀(CFU/mL). Such a regimen would likely achieve bacteriological cure only if these conditions are true: (i) the antimicrobial MIC's AP across the antimicrobial–susceptible pathogen strains is > 5.7 log₁₀(CFU/mL) (e.g. 6–8 log₁₀(CFU/mL) for the β-lactam ceftriaxone in E. coli, S. enterica and S. aureus, Figs 1A and B and 2A); and (ii) the pathogen density at the infection site(s) is below the AP. A regimen designed utilizing the MIC for the density 5.7 log₁₀(CFU/mL) would less likely achieve bacteriological cure if the MIC's AP is lower (e.g. for gentamicin in E. coli and S. enterica, Fig. 1E and F, and linezolid in S. aureus, Fig. 2I) and the pathogen density at the infection site(s) reaches the AP. The full MIC–density curve and AP have not been considered in the design and interpretation of in vivo experiments. For example, that clinical efficacy of a β-lactam treatment regimen for an experimental infection is apparently not sensitive to the inoculum density for E. coli or Klebsiella spp. (Craig, Bhavnani and Ambrose 2004) but is sensitive for Streptococcus pyogenes (Stevens, Yan and Bryant 1993) could be because the AP densities differ for these antimicrobial–bacterial species combinations (i.e. whether the compared inocula densities were below and/or above the MIC's AP for each combination). For illustration, the ceftriaxone MIC's AP for S. enterica (Fig. 1B) is ≥1 log₁₀(CFU/mL) higher than for S. pneumoniae (Fig. 2B).

Both how consistent the MIC's AP location was among bacterial species and its intra-species between-isolate range apparently depended on the antimicrobial's mechanism of action (Figs 1 and 2, Table 1). The AP location was relatively consistent across the species for an antimicrobial that disrupts bacterial cell-wall synthesis (for the mechanisms see (Waxman, Yocum and Strominger 1980; Waxman and Strominger 1983; Watanakunakorn 1984; Espedido and Gosbell 2012)). For the β-lactam ceftriaxone the AP was at medium-to-high densities (5.2–6.3 log₁₀(CFU/mL) in E. coli, 6.2–7.3 log₁₀(CFU/mL) in S. enterica, 6.4–7.6 log₁₀(CFU/mL) in S. aureus, and 5.0–6.5 log₁₀(CFU/mL) in S. pneumoniae) (Table 1). For the β-lactam oxacillin, the location was at lower densities (3.2–4.1 log₁₀(CFU/mL) in S. aureus and 3.5–5.5 log₁₀(CFU/mL) in S. pneumoniae). The AP location was also relatively consistent across the species for the fluoroquinolone ciprofloxacin that inhibits bacterial DNA replication (Sanders 1988; Hooper 1999; Espedido and Gosbell 2012), and was at lower densities (3.0–5.7 log₁₀(CFU/mL) in E. coli, 3.3–5.2 log₁₀(CFU/mL) in S. enterica, and 2.2–4.0 log₁₀(CFU/mL) in S. pneumoniae). In contrast, the AP location varied widely among the species for the aminoglycoside gentamicin and oxazolidinone linezolid which inhibit bacterial protein synthesis (Mingeot-Leclercq, Glupczynski and Tulkens 1999; Livermore 2003; Espedido and Gosbell 2012). The gentamicin MIC's AP occurred at 4.6–5.5 log₁₀(CFU/mL) in E. coli and 4.4–5.0 log₁₀(CFU/mL) in S. enterica, while it occurred at 6.7–7.6 log₁₀(CFU/mL) in S. aureus and 2.1–2.8 log₁₀(CFU/mL) in S. pneumoniae. The linezolid MIC's AP occurred at 4.6–5.7 log₁₀(CFU/mL) in S. aureus but at 2.2–2.9 log₁₀(CFU/mL) in S. pneumoniae.

In terms of the intra-bacterial species range of the MIC's AP among isolates (n = 4 tested) (Figs 1 and 2, Table 1), comparatively wide ranges were observed for antimicrobials disrupting bacterial cell-wall synthesis. For the β-lactam ceftriaxone the range was 1.1–1.5 log₁₀(CFU/mL) in E. coli, S. enterica, S. aureus and S. pneumoniae; and for vancomycin in S. aureus it was 2.9 log₁₀(CFU/mL). For example, the range of 1.5 log₁₀(CFU/mL) corresponds to the ceftriaxone MIC's AP from 5.0 to 6.5 log₁₀(CFU/mL) across S. pneumoniae isolates. For ciprofloxacin that inhibits bacterial DNA replication, the MIC's AP ranges were also wide (2.7 log₁₀(CFU/mL) in E. coli, 1.9 log₁₀(CFU/mL) in S. enterica, and 1.8 log₁₀(CFU/mL) in S. pneumoniae) (Table 1). In contrast, the AP ranges intra-species were narrow, <1 log₁₀(CFU/mL), for antimicrobials inhibiting bacterial protein synthesis. For the aminoglycoside gentamicin the range was 0.6–0.9 log₁₀(CFU/mL) in E. coli, S. enterica, S. aureus and S. pneumoniae. For the oxazolidinone linezolid, the range was 1.1 log₁₀(CFU/mL) in S. aureus and 0.7 log₁₀(CFU/mL) in S. pneumoniae.

The differences in the overall location and intra-species range of the MIC's AP among antimicrobials with different modes of action could relate to IE mechanisms. For example, for antimicrobials disrupting bacterial cell-wall synthesis, the IE is attributed to reduced availability of the target membrane proteins due to a reduced population growth (Stevens, Yan and Bryant 1993) and to accumulation of drug-degrading enzymes (Craig, Bhavnani and Ambrose 2004) at high bacterial densities. For antimicrobials inhibiting bacterial protein synthesis, the IE is attributed to a population growth instability due to the drug-induced ribosome degradation (Tan et al. 2012). Drug loss due to binding to non-target bacterial structures is proposed as a general mechanism of the IE (Udekwu et al. 2009).

Our results suggest that clinical significance of the IE in a bacterial pathogen likely systematically varies among antimicrobial drug classes depending on the mechanism of action, which determines the MIC's AP and its intra-bacterial species variability. We observed this for bacterial strains susceptible to the antimicrobials. Mathematical models of the MIC–bacterial density relationships could capture such clinically relevant specifications as the MIC'S AP density and steepness and ceiling of the subsequent MIC increase. Such models should be considered for optimizing antimicrobial treatment regimens.

AUTHOR CONTRIBUTIONS

V.V.V. conceived and designed the study. J.R.S. and X.W. performed the experiments. M.J.-D. performed the modeling. J.R.S. and V.V.V. interpreted the microbiological results and M.J.-D., J.R.S. and V.V.V. interpreted the modeling results. V.V.V. and J.R.S. wrote the manuscript and M.J.-D. contributed.

Conflict of interest None declared.