Using a dependent schedule to measure risky choice in male rats: Effects of d-amphetamine, methylphenidate, and methamphetamine

Abstract

Risky choice is the tendency to choose a large, uncertain reward over a small, certain reward, and is typically measured with probability discounting, in which the probability of obtaining the large reinforcer decreases across blocks of trials. One caveat to traditional procedures is that independent schedules are used, in which subjects can show exclusive preference for one alternative relative to the other. For example, some rats show exclusive preference for the small, certain reinforcer as soon as delivery of the large reinforcer becomes probabilistic. Therefore, determining if a drug increases risk aversion (i.e., decreases responding for the probabilistic alternative) is difficult (due to floor effects). The overall goal of this experiment was to use a concurrent-chains procedure that incorporated a dependent schedule during the initial link, thus preventing animals from showing exclusive preference for one alternative relative to the other. To determine how pharmacological manipulations alter performance in this task, male Sprague Dawley rats (n = 8) received injections of amphetamine (0, 0.25, 0.5, 1.0 mg/kg), methylphenidate (0, 0.3, 1.0, 3.0 mg/kg), and methamphetamine (0, 0.5, 1.0, 2.0 mg/kg). Amphetamine (0.25 mg/kg) and methylphenidate (3.0 mg/kg) selectively increased risky choice, whereas higher doses of amphetamine (0.5 and 1.0 kg/mg) and each dose of methamphetamine impaired stimulus control (i.e., flattened the discounting function). These results show that dependent schedules can be used to measure risk-taking behavior and that psychostimulants promote suboptimal choice when this schedule is used.

Risky choice is the tendency to choose a large, uncertain reinforcer over a small, certain reinforcer, and is often measured with probability discounting tasks. Typically, the probability of earning the large, uncertain reinforcer decreases across the session (e.g., Montes, Stopper, & Floresco, 2015; St Onge, Chiu, & Floresco, 2010; St Onge & Floresco, 2009; Stopper, Green, & Floresco, 2014; Yates, Batten, Bardo, & Beckmann, 2015; Yates et al., 2016), although the probability can increase across the session (St Onge et al., 2010; Yates et al., 2016; Yates, Prior, et al., 2018). During each block of trials, subjects are exposed to forced-choice trials, in which only one lever is presented, and free-choice trials, in which both levers are presented. Each free-choice trial is an example of an independent schedule of reinforcement (i.e., a response on either lever advances the session to the next trial). As discussed by Beeby and White (2013), using independent schedules poses two challenges. First, the relative frequency of small, certain and large, uncertain reinforcers is allowed to vary in each session. For example, when the large, uncertain and small, certain reinforcers are both made available with a probability of 1, the large, uncertain reinforcer will be presented at a much higher frequency relative to the small, certain reinforcer (due to rats selecting this option more frequently). Thus, preference for the large, uncertain reinforcer could occur simply because it occurs more frequently. Related to the first caveat, independent schedules allow subjects to show exclusive preference for one alternative relative to the other (i.e., when both alternatives are certain, subjects will show near exclusive preference for the large, uncertain reinforcer). Although forced-choice trials are designed to allow subjects to sample between alternatives, there is no guarantee that animals respond during a forced-choice trial for an alternative they do not prefer; this occurs because limited holds are often implemented in probability discounting tasks (i.e., subjects have to respond within a certain amount of time or the trial ends). For example, some subjects may refuse to respond for the large, uncertain reinforcer during forced-choice trials at lower probabilities. Thus, they never experience this contingency of reinforcement during these blocks of trials.

One way to control for the limitations discussed above is to use a dependent schedule (Stubbs & Pliskoff, 1969). In a dependent schedule, the alternative that allows the subject to advance the session to the next trial is predetermined. For example, on the first trial, responding on the lever associated with the small, certain reinforcer allows the subject to advance the trial. Responses on the lever associated with the large, uncertain reinforcer are recorded but have no programmed consequences. On the second trial, responding on the lever associated with the small, certain reinforcer has no programmed consequences, whereas responding on the lever associated with the large, uncertain reinforcer advances the session (see Figure 1 for a schematic of the dependent schedule used in the current experiment). Dependent schedules have been used to study sensitivity to delayed reinforcement, often in the form of a concurrent-chains procedure (Aparicio, Hughes, & Pitts, 2013; Aparicio, Elcoro, & Alonso-Alvarez, 2015; Aparicio, Hennigan, Mulligan, & Alonso-Alvarez, in press; Beeby & White 2013; Maguire, Rodewald, Hughes, & Pitts, 2009; Pitts, Cummings, Cummings, Woodstock, & Hughes, 2016; Pope, Newland, & Hutsell, 2015; Ta, Pitts, Hughes, McLean, & Grace, 2008; Yates, Gunkel, et al., 2018). In a concurrent-chains schedule, each trial is composed of an initial link and a terminal link. Responses during the initial link allow subjects access to one of two terminal links. Although responses during the terminal link allow subjects to receive reinforcement, preference is actually measured by calculating the responses during the initial link.

Figure 1.

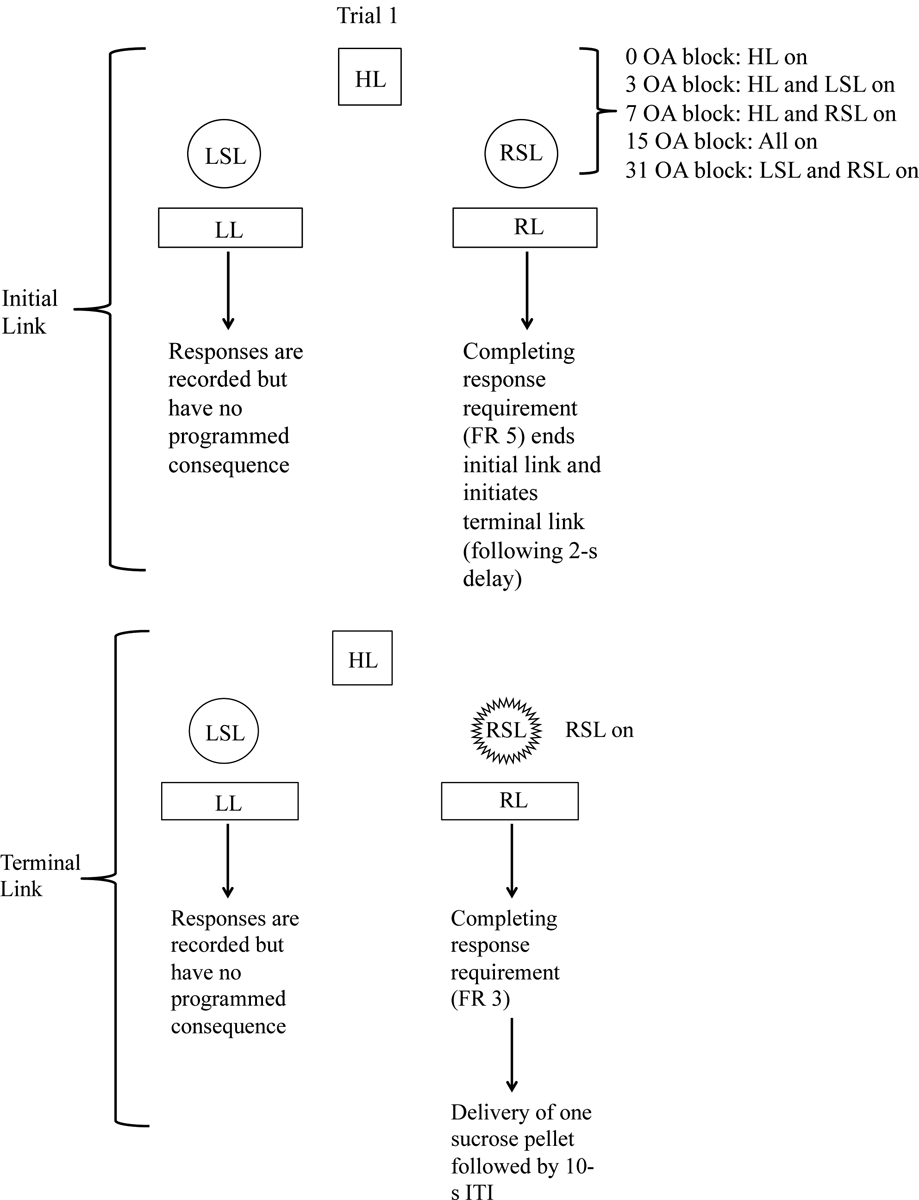
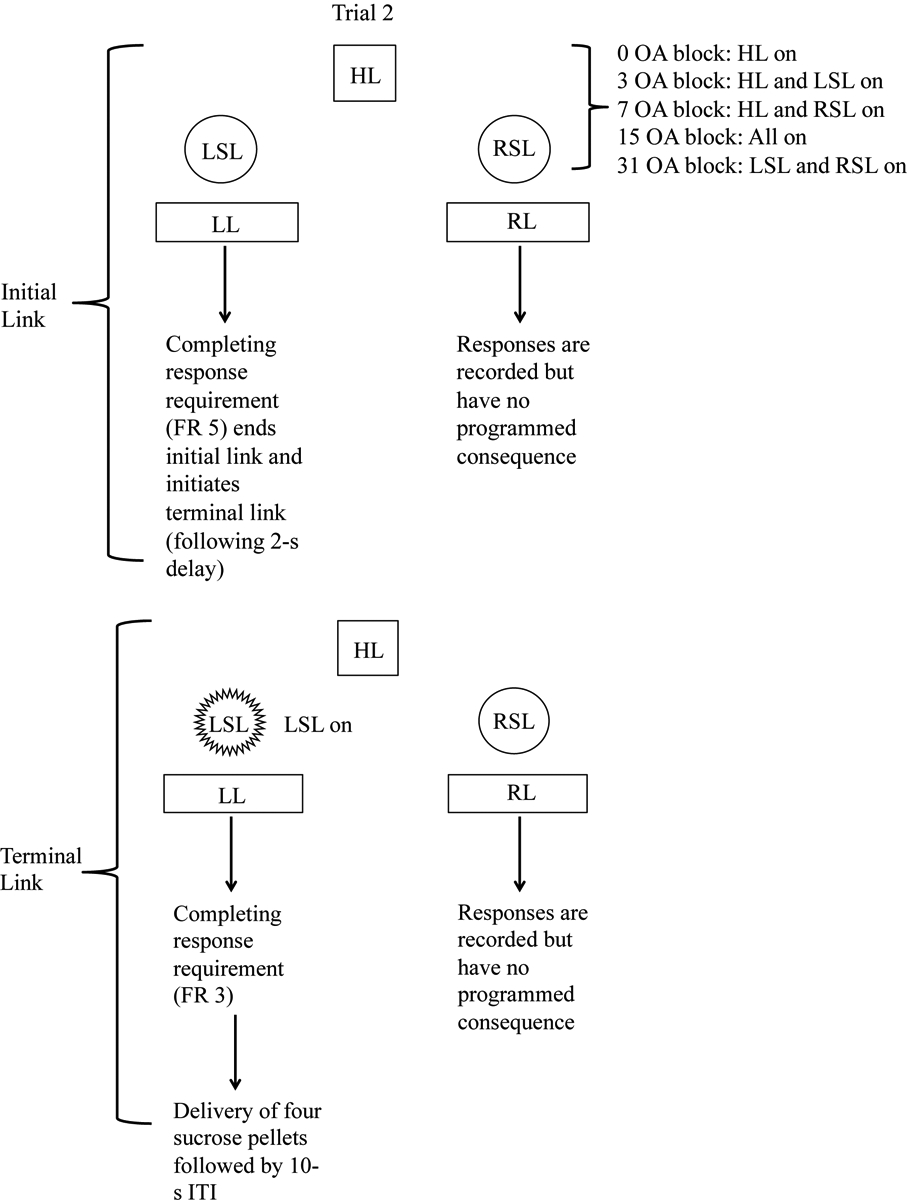
Schematic illustrating two trials in the concurrent-chains procedure for one rat. For this particular rat, the left lever is associated with the large, uncertain reinforcer, and the right lever is associated with the small, certain reinforcer. During the initial link, the lever that allows the rat to advance to the terminal link is determined by the program (this is the dependent schedule). In trial 1, responses on the left lever are recorded during the initial link but have no programmed consequence. In this case, the rat has to complete the response requirement (FR 5) on the right lever to end the initial link. After a 2-s delay, the terminal link begins. Responses on the left lever are recorded but have no programmed consequence. Completing the response requirement (FR 3) on the right lever results in delivery of one sucrose-based pellet. In trial 2, responses on the right lever during the initial link are recorded but have no programmed consequences. The rat has to respond on the left lever to advance to the terminal link. During the terminal link, responses on the right lever are recorded but have no programmed consequences. Completing the response requirement on the left lever results in probabilistic delivery of four sucrose-based pellets. For each rat, the active lever (i.e., the lever that ends the initial link and the lever that leads to reinforcement) is pseudo-randomized across trials, such that each lever leads to reinforcement on an equal number of trials (5 trials each per block; 25 total trials across the session). Abbreviations: HL = house light; ITI = inter-trial interval; LL = left lever; LSL = left stimulus light; OA = odds against (note: odds against = [1/probability]-1); RR = right lever; RSL = right stimulus light.

Dependent schedules have been used to measure the neurochemical basis of impulsive choice. Primarily, these studies have tested psychostimulant drug effects on choice controlled by several dimensions of reinforcement, such as delayed reinforcement and reinforcement magnitude. The drugs d-amphetamine and methylphenidate decrease sensitivity to reinforcement delay (Pitts et al., 2016; Ta et al., 2008) and reinforcement amount (Maguire et al., 2009; Pitts et al., 2016). While dependent schedules have been used to assess the neurochemical basis of delayed reinforcement (i.e., impulsive choice), they have not been used to study the neurochemical basis of probability discounting. At least one study has incorporated dependent schedules to examine sensitivity to probabilistic reinforcement (Kyonka & Grace, 2008), although in this experiment probability to reinforcer magnitude was set at either 100% or 50%, and reinforcer magnitude and reinforcer delay were manipulated with probabilistic reinforcement.

Overall, the major goal of the current experiment was to apply a dependent schedule (via a concurrent-chains procedure) to a probability-discounting task that is commonly used in behavioral pharmacology studies (e.g., Montes et al., 2015; St Onge et al., 2010; St Onge & Floresco, 2009; Stopper et al., 2014; Yates et al., 2015; Yates et al., 2016). We tested three different psychostimulant drugs in the current procedure. d-Amphetamine was chosen because it is commonly used in measures of risky choice (e.g., Orsini, Willis, Gilbert, Bizon, & Setlow, 2016; Simon, Gilbert, Mayse, Bizon, & Setlow, 2009; St Onge et al., 2010; St Onge & Floresco, 2009). Methylphenidate and methamphetamine were included because these drugs have been used in commonly used delay-discounting tasks (e.g., Adriani et al., 2004; Evenden & Ryan, 1996; Pardey, Kumar, Goodchild, & Cornish, 2012; Paterson, Wetzler, Hackett, & Hanania, 2012; Pitts & Febo 2004; Richards, Sabol, & de Wit, 1999; Siemian, Xue, Blough, & Li, 2017; Slezak & Anderson, 2011; Tanno, Maguire, Henson, & France, 2014; van Gaalen, van Koten, Schoffelmeer, & Vanderschuren, 2006; Wade, de Wit, & Richards, 2000) as well as in concurrent-chains procedures (Maguire et al., 2009; Pitts et al., 2016; Ta et al., 2008) but have not been tested in probability discounting. Also, using these drugs is important as they are known to have high abuse potential in both pre-clinical (Baladi, Nielsen, Umpierre, Hanson, & Fleckenstein, 2014; Balster & Schuster, 1973; Collins, Weeks, Cooper, Good, & Russell, 1984; Harrod, Dwoskin, Crooks, Klebaur, & Bardo, 2001; Marusich & Bardo, 2009; Munzar, Baumann, Shoaib, & Goldberg, 1999; Pickens, 1968) and clinical populations (Reynolds, Strickland, Stoops, Lile, & Rush, 2017; Rush, Essman, Simpson, & Baker, 2001; Rush, Stoops, Lile, Glaser, & Hays, 2011; Stoops, Glaser, Fillmore, & Rush, 2004; see Stoops, 2008 for a review) and are known to alter risky decision making in humans (e.g., Campbell-Meiklejohn et al., 2012) or alter neural circuits related to risky decision making (Bischoff-Grethe et al., 2017; Ersche et al., 2005; Kohno, Morales, Ghahremani, Hellemann, & London, 2014). The results of the current experiment can provide further insights in how psychostimulants affect choice between reinforcers that differ in magnitude and probability, which may allow us to better understand the relationship between risky decision making and substance abuse.

Method

Animals

Eight male, Sprague Dawley rats were obtained from Envigo (Indianapolis, IN) and arrived to the laboratory weighing between 200–224 g (66 days of age upon arrival). They were acclimated to an animal housing room and handled for six days before any behavioral testing began. The housing room was maintained on a 12:12-h cycle (lights on at 630 h), and rats were tested in the light phase (approximately 1400–1600 h). Rats were tested during the light phase because most studies assessing the neurochemical basis of risky decision making during this phase (see Jenni, Larkin, & Floresco, 2017; Orsini et al., 2016; Simon et al., 2011; Yates et al., 2015; Yates et al., 2016 for recent examples). Rats were individually housed in clear polypropylene cages (51 cm long × 26.5 cm wide × 32 cm high) with metal tops containing food and a water bottle. Rats were restricted to approximately 10 g of food each day but had ad libitum access to water. All experimental procedures were carried out according to the Current Guide for the Care and Use of Laboratory Animals (USPHS) under a protocol approved by the Northern Kentucky University Institutional Animal Care and Use Committee (Protocol #: 2017–04; Contribution of Glutamate NR2B Subunit to Risky Choice and Amphetamine Reward).

Apparatus

Eight operant-conditioning chambers (28 × 21 × 21 cm; ENV-008; MED Associates, St. Albans, VT) located inside sound attenuating chambers (ENV-018M; MED Associates) were used. The front and back walls of the chambers were made of aluminum, while the side walls were made of Plexiglas. There was a recessed food tray (5 × 4.2 cm) located 2 cm above the floor in the bottom-center of the front wall and was located between the levers. Each lever (4.8 × 0.55 × 1.9 cm) was located 2.1 cm above the floor and required a force of 0.245 N to depress. An infrared photobeam was used to record head entries into the food tray. A 28-V white stimulus light (2.54 cm diameter) was located 6 cm above each response lever. A 28-V white house light was mounted in the center of the back wall of the chamber. A nosepoke aperture was located 2 cm above the floor in the bottom-center of the back wall (the aperture was never used in the current experiment). All responses and scheduled consequences were recorded and controlled by a computer interface. A computer controlled the experimental session using Med-IV software.

Drugs

d-Amphetamine sulfate (0, 0.25, 0.5, 1.0 mg/kg; s.c.), methylphenidate hydrochloride (0, 0.3, 1.0, 3.0 mg/kg; i.p.), and methamphetamine hydrochloride (0, 0.5, 1.0, 2.0 mg/kg; s.c.) were purchased from Sigma Aldrich (St. Louis, MO) and were prepared in 0.9% NaCl (saline). The doses were calculated based on salt weight. Each drug was injected at room temperature in a volume of 1 ml/kg. Each drug was administered 15 min prior to the session, and each drug was administered in a counterbalanced order. Specifically, some rats started with injections of amphetamine, some started with injections of methylphenidate, and some started with injections of methamphetamine. Within an individual drug, doses were administered randomly (i.e., some rats received vehicle first, some received the low dose first, etc.). Rats received each dose of a particular drug before receiving injections of the next drug. The doses and pre-session treatment time (15 min) were chosen based on previous research (Baarendse & Vanderschuren, 2012; Perry, Stairs, & Bardo, 2008; Pitts & Febbo, 2004; Richards et al., 1999; van Gaalen et al., 2006; Wooters & Bardo, 2011).

Procedure

For two sessions, rats received magazine training, in which 20 food pellets (45 mg dustless precision pellets; product F0021; Bio-Serv, Frenchtown, NJ) were non-contingently delivered into the food tray according to a variable-time 30 s schedule of reinforcement. Following magazine training, rats received three sessions of lever-press training. Each session began with illumination of the house light. A head entry into the food tray resulted in presentation of one lever; each lever was presented pseudo-randomly, with no more than two consecutive presentations of the same lever. A response on the extended lever (fixed ratio [FR] 1) resulted in delivery of one food pellet. Following a response on the extended lever, the house light was extinguished, and the lever was retracted for 5 s. After 5 s, the house light was illuminated. Each lever-press training session ended after a rat earned 40 reinforcers or after 30 min, whichever came first.

Rats received five sessions of magnitude discrimination training. Similar to lever-press training, each session consisted of 40 trials, and the beginning of each trial was signaled by illumination of the house light. A head entry into the food tray extended one of the levers (the order of presentation between the two levers was pseudo-randomized, with no more than two consecutive presentations of the same lever). Responses on one lever resulted in immediate delivery of one pellet, whereas responses on the other lever resulted in immediate delivery of four pellets (the lever associated with the large magnitude reinforcer was counterbalanced across rats). Unlike lever-press training, a variable interval (VI) schedule of reinforcement was used during magnitude discrimination training, and this interval increased during each session (VI 2 s, VI 4 s, VI 8 s, VI 16 s, VI 30 s). Following completion of the response requirement on either lever, the house light was extinguished, and the lever was retracted for the remainder of the trial. A VI schedule was used because we initially conducted a pilot study, in which we tested rats in a discounting procedure using concurrent VI-30 s schedules of reinforcement. Rats were not given any drug injections during the VI testing. Following 42 sessions of the concurrent VI testing, rats were tested in the experiment proper (see below).

A dependent schedule was used to assess risky choice. Specifically, a variant of a concurrent-chains procedure was used (see Figure 1 for a schematic of the procedure; Aparicio et al., 2013; Aparicio et al., 2015; Aparicio et al., in press; Beeby & White, 2013; Pope et al., 2015; Yates, Gunkel, et al., 2018). Each session consisted of five blocks of 10 trials (50 total trials; note: each rat completed all 50 trials following each dose of each drug, with the exception that two rats failed to complete a single trial following administration of the highest dose of methamphetamine) and began with illumination of one of several stimuli (first block of trials: house light; second block: house light and left stimulus light; third block: house light and right stimulus light; fourth block: house light and both stimulus lights; fifth block: both stimulus lights only). On each trial, rats had to initiate the extension of both levers by breaking a photo beam in the food tray. In contrast to most discounting procedures, there were no forced-choice trials (i.e., both levers were extended on every trial). During the first component of the trial (the initial link), completing the response requirement (FR 5 schedule) on one lever resulted in (a) the stimuli turning off, (b) the retraction of both levers, and (c) the initiation of a 2-s delay to the terminal link (the next component of the trial). Responses on the other lever were recorded but had no programmed consequences. Similar to previous research examining dependent schedules within the context of delay discounting (Aparicio et al., 2013; Aparicio et al., 2015; Aparicio et al., in press; Beeby & White, 2013; Pope et al., 2015; Yates, Gunkel, et al., 2018), the lever that allowed the rat to advance to the terminal link was pseudo-randomized across trials (this is the dependent schedule). For example, during the first trial, the right lever may be designated as “active” for some rats. As such, completing the response requirement on the right lever would result in completion of the initial link; however, if a rat responded on the left lever, they would not advance to the terminal link until they completed the response requirement on the right lever. Similar to a previous experiment using concurrent FR schedules during the initial link (Pope et al., 2015), we did not incorporate a change-over delay (COD).

During the terminal link, both levers were extended into the operant chamber, but only responses (FR 3) on the active lever (the same lever as designated during the initial link) led to reinforcement. Responses on the other lever were recorded but had no programmed consequences. The stimulus light above the active lever was illuminated during the terminal link. For half of the rats, the left lever was associated with delivery of a small, certain reinforcer (1 pellet), and the right lever was associated with delivery of a large, probabilistic reinforcer (4 pellets). For half of the rats, the contingencies of reinforcement were reversed. The levers associated with the small and large magnitude reinforcers were the same as during magnitude discrimination training and were held constant for an individual rat across the entire experiment. Both levers were made available during the terminal link because this allowed us to determine if psychostimulant administration altered perseverative responses during this component. Averaged across all trials in a block, the proportion of responses on this lever should be 0.5 during the terminal link. Values above 0.5 indicate perseverative responding on the lever associated with the large, uncertain reinforcer, whereas values below 0.5 indicate perseverative responding on the lever associated with the small, certain reinforcer. The odds against obtaining the large reinforcer increased across the session (0, 3, 7, 15, 31, resulting in corresponding probabilities of 100, 25, 12.5, 6.25, 3.125%). On each individual trial within a block of trials, the probability of receiving the large, uncertain reinforcer was the same (e.g., during the 3.125% block, the probability of receiving the large, uncertain reinforcer was always set to 0.3125). Following completion of the terminal link, the stimulus light above the active lever was extinguished, and a 10-s intertrial interval (ITI) occurred. The next trial began upon completion of the ITI. In total, rats received 43 sessions.

Statistical Analyses

We calculated the number of lever presses emitted for the large, uncertain reinforcer on trials in which the small, certain reinforcer was made available (LR choice responses), and we calculated the number of lever presses emitted for the small, certain reinforcer when the large, uncertain reinforcer was made available (SS choice responses). After calculating these two values, we calculated the proportion of responses for the large, uncertain reinforcer with the following calculation: LR proportion = LR choice responses/(LR choice responses + SS choice responses). Figure 2 shows how LR choice responses and SS choice responses were derived.

Figure 2.

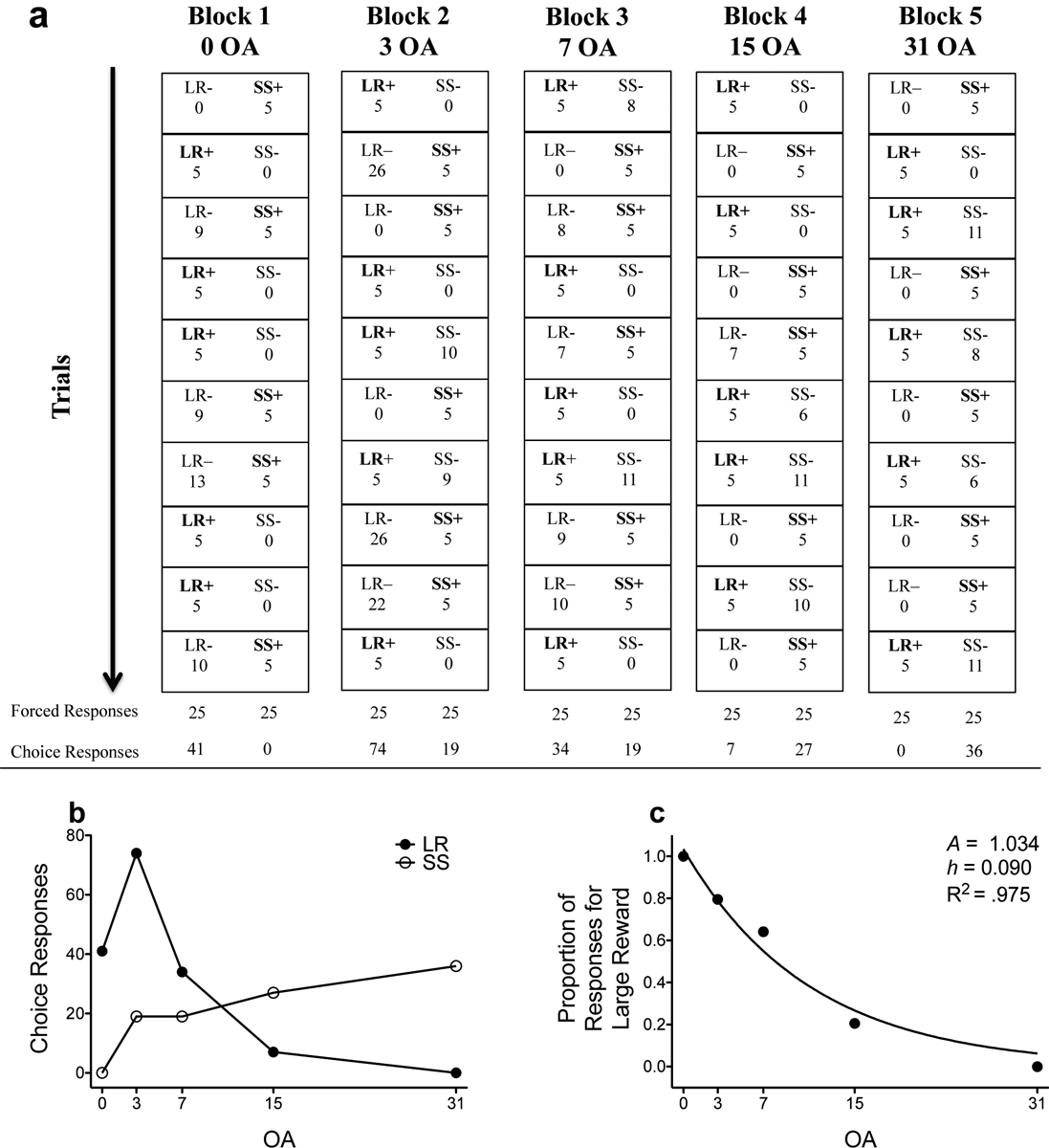
Example session from subject 503 during the initial link of the concurrent chains procedure (dependent schedule component) following administration of vehicle (for methylphenidate). (a) Trial-by-trial (rows) and block-by-block (columns) breakdown during the dependent schedule, where the right lever is associated with the small, certain reinforcer, and the left lever is associated with the large, uncertain reinforcer. Within each trial, only one reinforcer is scheduled, represented by bolded text with (+) sign. The number below LR/SS labels represents the number of responses made on that lever (note: LR = large, risky reinforcer; SS = small, safe reinforcer). Numbers that are under bolded labels with (+) signs represent forced responses (i.e., rats have to respond on this lever to advance from the initial link to the terminal link). Numbers that are under un-bolded labels with (−) signs represent choice responses (i.e., responses on this lever are not necessary to advance the trial to the terminal link). (b) Graphical representation of the number of choice responses for the LR and the SS across blocks as a function of odds against (OA). (c) Graphical representation of the proportion of responses for the LR based upon LR and SS choice responses; the line indicates the best fit of the exponential discounting function. The A and h parameter estimate, as well as R², are listed on the figure. Note: figure is adapted from Beckmann et al. (in press).

Probability discounting during baseline sessions.

For simplicity, the proportion of responses for the large, uncertain reinforcer was averaged across sessions 1–3, 21–23, and 41–43. For these three blocks of sessions, the exponential discounting model was fit to each individual subject via nonlinear mixed effects modeling (NLME) using the NLME package in R (Pinheiro, Bates, DebRoy, & Sarkar, 2007). The exponential model is defined as V = Ae^(-hθ), where V refers to the subjective value of the large, uncertain reinforcer, A refers to discriminability of reinforcer magnitudes (i.e., intercept of the function), h refers to sensitivity to probabilistic reinforcement (i.e., slope of the function), and θ refers to odds against (note: odds against = [1/probability]-1; Rachlin, Raineri, & Cross, 1991). The NLME models defined probability as a fixed, continuous within-subjects factor, session block as a fixed, nominal within-subjects factor, and subject as a random factor. Specifically, the A and h parameter estimates were allowed to vary across subjects. Statistical significance was defined as p < .05. Significant effects were probed using contrasts in R.

Drug effects on discounting.

Similar to baseline sessions, the exponential discounting function was fit to individual subject data via NLME. The NLME models defined probability as a fixed, continuous within-subjects factor, dose as a fixed, nominal within-subjects factor, and subject as a random factor (with A and h parameter estimates being allowed to vary across subjects). Separate NLME models were used for each drug. Statistical significance was defined as p < .05. Significant effects were probed using contrasts in R.

Proportion of responses during the terminal link.

The proportion of responses for the large magnitude reinforcer was analyzed with LME models, with dose and probability as fixed, nominal within-subjects factors and subject as a random factor. Statistical significance was defined as p < .05.

Response rates.

Response rates were analyzed with linear mixed effects (LME) models, with trial component (initial link vs. terminal link) as a fixed, nominal within-subjects factor, reinforcer (small, certain vs. large, uncertain) as a fixed, nominal within-subjects factor, dose as a fixed, nominal within-subjects factor, and subject as a random factor. Statistical significance was defined as p < .05.

Results

For simplicity, the results of each analysis are presented in Table 1. The results of these analyses will be briefly described below.

Table 1.

Results of the inferential tests used to analyze A and h parameter estimates derived from the exponential discounting function and nonreinforced responses during the terminal link.

Probability Discounting Results
Baseline
Parameter	DF	F	p
A	2, 107	4.824	.010
h	2, 107	24.017	< .001
Amphetamine
Parameter	DF	F	p
A	3, 145	4.556	.004
h	3, 145	5.650	.001
Methylphenidate
Parameter	DF	F	p
A	3, 145	0.704	.551
h	3, 145	3.006	.032
Methamphetamire
Parameter	DF	F	p
A	3, 137	9.315	< .001
h	3, 137	8.001	< .001
Nonreinforced Responses During Terminal Link Results
Amphetamine
Factor	DF	F	p
Dose	3, 133	0.202	.895
Trial Block	4, 133	4.184	.003
Dose × Trial Block	12, 133	1.0647	.395
Methylphenidate
Factor	DF	F	p
Dose	3, 133	6.210	< .001
Trial Block	4, 133	6.860	< .001
Dose × Trial Block	12, 133	0.893	.555
Methamphetamine
Factor	DF	F	p
Dose	3, 125	0.859	.465
Trial Block	4, 125	1.507	.204
Dose × Trial Block	12, 125	0.267	.993
Response Rate Results
Amphetamine
Factor	DF	F	P
Trial Component (TC)	1, 105	125.847	< .001
Dose (D)	3, 105	15.094	< .001
Reinforcer (R)	1, 105	2.413	.123
TC × D	3, 105	1.890	.136
TC × R	1, 105	0.349	.556
D × R	3, 105	0.647	.587
TC × D × R	3, 105	0.349	.790
Methylphenidate
Factor	DF	F	P
Trial Component (TC)	1, 105	186.123	< .001
Dose (D)	3, 105	4.349	.006
Reinforcer (R)	1, 105	17.599	< .001
TC × D	3, 105	0.528	.664
TC × R	1, 105	2.394	.125
D × R	3, 105	0.948	.420
TC × D × R	3, 105	0.396	.756
Methamphetamine
Factor	DF	F	P
Trial Component (TC)	1, 103	122.370	< .001
Dose (D)	3, 103	25.097	< .001
Reinforcer (R)	1, 103	2.695	.104
TC × D	3, 103	3.238	.025
TC × R	1, 103	0.062	.804
D × R	3, 103	1.559	.204
TC × D × R	3, 103	0.801	.496

Probability Discounting

Baseline.

Figure 3a shows the raw proportion of responses for the large, uncertain reinforcer during baseline training. Recall that inferential statistics were not conducted for the raw proportion of responses for the large, uncertain reinforcer. A parameter estimates (e.g., discriminability of reinforcer magnitudes) significantly increased across training (Fig. 3b). Similarly, h parameter estimates (e.g., sensitivity to probabilistic reinforcement) significantly increased across blocks of trials (Fig. 3c). These results show that, with repeated training, rats learned to prefer the large, uncertain reinforcer when its delivery was certain, but they became more sensitive to probabilistic reinforcement.

Figure 3.

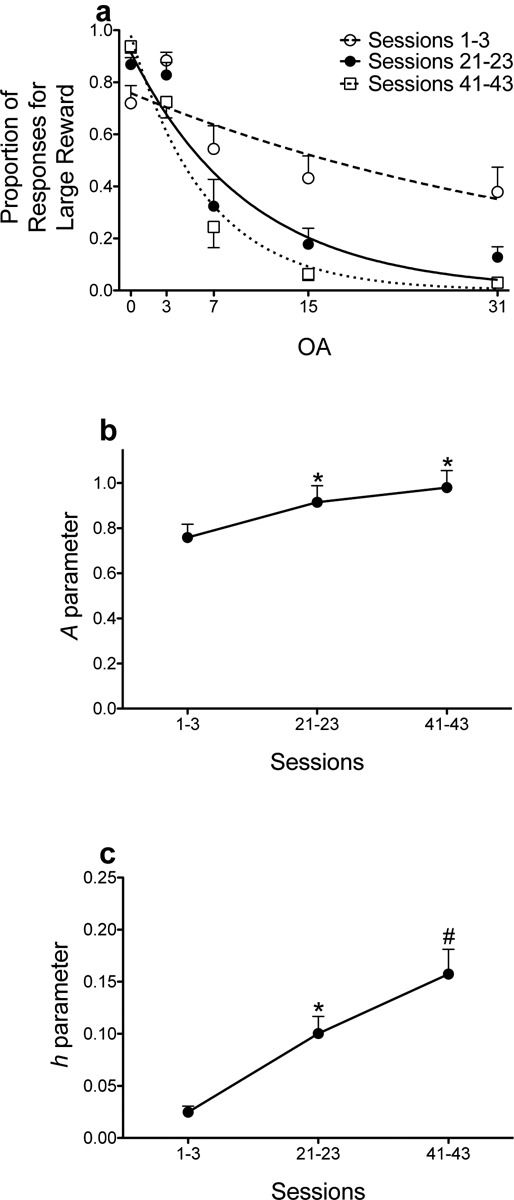
Mean (±SEM) proportion of responses for the large, uncertain reinforcer as a function of odds against (OA) averaged across sessions 1–3, sessions 21–23, and sessions 41–43 (a). Lines are NLME-determined best fits of the exponential discounting function. Mean (±SEM) A (b) and h (c) parameter estimates across the sessions depicted in panel a. *p < .05, relative to sessions 1–3. #p < .05, relative to sessions 1–3 and sessions 21–23.

Effects of psychostimulant drugs on probability discounting.

Panels a–c of Figure 4 show the raw proportion of responses for the large, uncertain reinforcer following administration of amphetamine, methylphenidate, and methamphetamine. Note that we did not analyze these data; instead, we applied the exponential discounting function to these data via NLME. Following vehicle treatments, rats responded less for the large, uncertain reinforcer as a function of the odds against receiving reinforcement (i.e., as probabilities decreased within the session). When delivery of the large, uncertain reinforcer was certain, rats primarily selected that alternative relative to the small, certain reinforcer (> 90%). Amphetamine (0.5 and 1.0 mg/kg) significantly decreased discriminability of reinforcer magnitudes (A parameter estimates; Fig. 4d), and each dose of amphetamine decreased sensitivity to probabilistic reinforcement (h parameter estimates; Fig. 4g). Methylphenidate did not alter discriminability of reinforcer magnitudes (Fig. 4e), but the highest dose (3.0 mg/kg) decreased sensitivity to probabilistic reinforcement (Fig. 4h). Each dose of methamphetamine significantly decreased discriminability of reinforcer magnitudes (Fig. 4f) and decreased sensitivity to probabilistic reinforcement (Fig. 4i).

Figure 4.

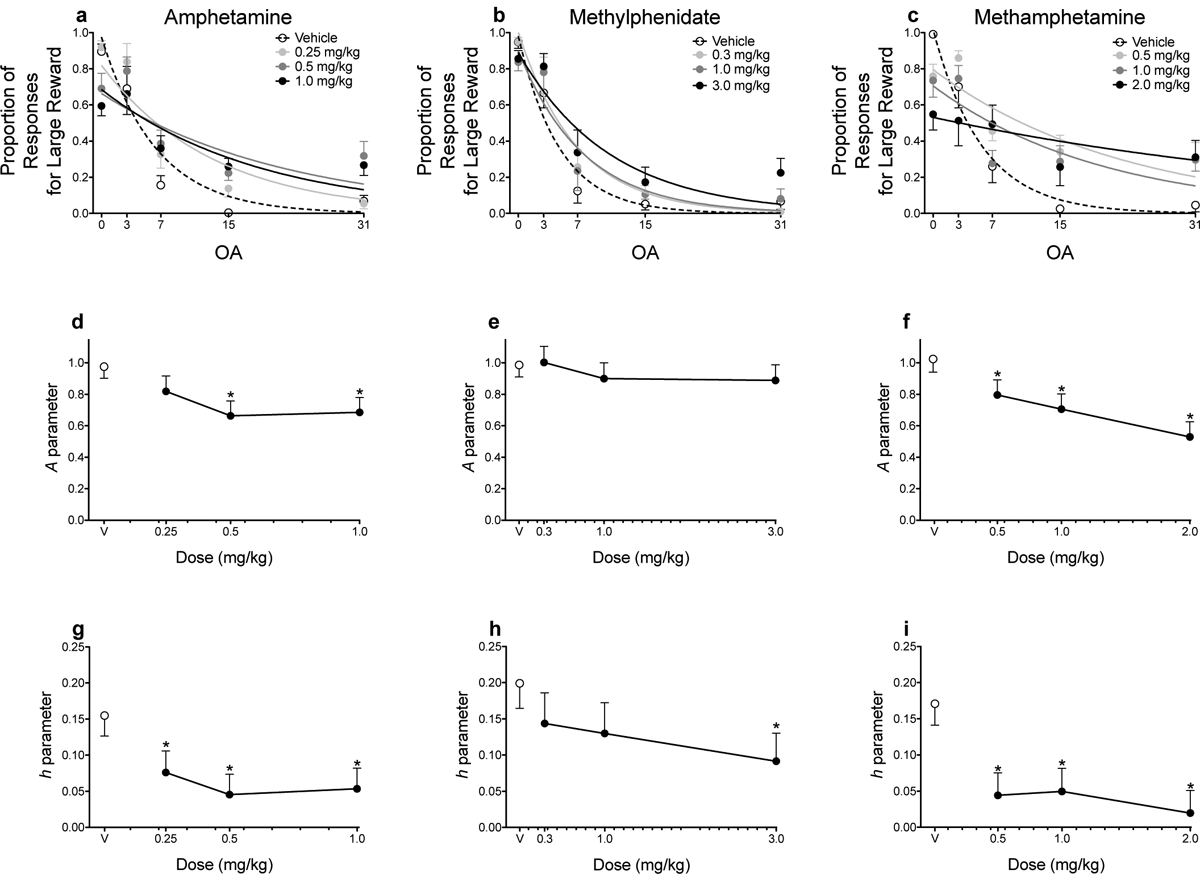
Mean (±SEM) proportion of responses for the large, uncertain reinforcer during the initial link as a function of odds against (OA) across each dose of amphetamine (a), methylphenidate (b), and methamphetamine (c). Lines are NLME-determined best fits of the exponential discounting function. Mean (±SEM) A parameter estimates derived from the exponential function across each dose of amphetamine (d), methylphenidate (e), and methamphetamine (f). Mean (±SEM) h parameter estimates derived from the exponential function across each dose of amphetamine (g), methylphenidate (h), and methamphetamine (i). *p < .05, relative to vehicle. Note: in panels d-i, V = vehicle.

Effects of Psychostimulant Drugs on Non-reinforced Responses During the Terminal Link

Table 2 shows non-reinforced responses during the terminal link. Overall, rats showed more perseverative responding on the lever associated with the small, certain reinforcer when the odds against receiving reinforcement was 15 and 31 (i.e., the proportion of responses during this component were lower than 0.5), although this effect was not statistically significant for rats treated with methamphetamine. Neither amphetamine nor methamphetamine altered non-reinforced responses; however, methylphenidate (3.0 mg/kg) increased perseverative responding on the lever associated with the small, certain reinforcer. This alteration in perseverative responding was most pronounced when the odds against receiving the large, uncertain reinforcer were low.

Table 2.

Mean (±SEM) non-reinforced responses during the terminal link following administration of each psychostimulant drug.

Amphetamine
Dose	0 OA	3 OA	7 OA	15 OA#	31 OA#
0 mg/kg	0.502 (0.002)	0.500 (0.000)	0.500 (0.000)	0.494 (0.006)	0.500 (0.003)
0.25 mg/kg	0.518 (0.011)	0.500 (0.000)	0.484 (0.011)	0.498 (0.002)	0.488 (0.012)
0.5 mg/kg	0.531 (0.027)	0.522 (0.018)	0.494 (0.023)	0.453 (0.025)	0.451 (0.023)
1.0 mg/kg	0.517 (0.016)	0.545 (0.035)	0.513 (0.045)	0.457 (0.045)	0.457 (0.038)
Methylphenidate
Dose	0 OA	3 OA	7 OA	15 OA#	31 OA#
0 mg/kg	0.514 (0.010)	0.500 (0.000)	0.500 (0.000)	0.496 (0.004)	0.476 (0.014)
0.3 mg/kg	0.520 (0.011)	0.500 (0.000)	0.507 (0.007)	0.496 (0.004)	0.485 (0.013)
1.0 mg/kg	0.516 (0.011)	0.535 (0.024)	0.525 (0.028)	0.473 (0.016)	0.459 (0.022)
3.0 mg/kg*	0.495 (0.008)	0.502 (0.002)	0.456 (0.028)	0.441 (0.034)	0.424 (0.031)
Methamphetamine
Dose	0 OA	3 OA	7 OA	15 OA	31 OA
0 mg/kg	0.506 (0.003)	0.500 (0.000)	0.500 (0.000)	0.500 (0.000)	0.496 (0.004)
0.5 mg/kg	0.519 (0.013)	0.509 (0.009)	0.493 (0.016)	0.476 (0.033)	0.475 (0.041)
1.0 mg/kg	0.558 (0.031)	0.523 (0.016)	0.523 (0.031)	0.486 (0.036)	0.513 (0.018)
2.0 mg/kg	0.519 (0.078)	0.538 (0.040)	0.491 (0.032)	0.467 (0.032)	0.510 (0.031)

^*p < .05, relative to vehicle (main effect of dose).

^#p < relative to the 0 OA block (main effect of trial block).

Effects of Psychostimulant Drugs on Response Rates

Table 3 shows response rates following administration of each psychostimulant. Overall, response rates were higher during the terminal link relative to the initial link, regardless of which drug was administered. Amphetamine (0.5 and 1.0 mg/kg) and methamphetamine (each dose) significantly decreased response rates. For methamphetamine, the decreased response rate was more pronounced during the terminal link relative to the initial link (trial component × reinforcer interaction). Although there was main effect of dose following methylphenidate administration, none of the doses significantly altered response rates relative to vehicle.

Table 3.

Mean (±SEM) response rates (responses/s) on the levers associated with the large magnitude and small magnitude reinforcers during the initial and terminal links following psychostimulant administration.

Amphetamine
Dose	Initial Link - Large Reinforcer	Initial Link - Small Reinforcer	Terminal Link - Large Reinforcer#	Terminal Link - Small Reinforcer#
0 mg/kg	1.195 (0.066)	1.728 (0.129)	2.859 (0.264)	3.072 (0.407)
0.25 mg/kg	1.055 (0.107)	1.262 (0.118)	2.703 (0.320)	3.189 (0.406)
0.5 mg/kg*	0.792 (0.063)	0.932 (0.094)	2.001 (0.388)	1.938 (0.399)
1.0 mg/kg*	0.609 (0.070)	0.779 (0.088)	1.867 (0.422)	1.701 (0.514)
Methylphenidate
Dose	Initial Link - Large Reinforcer	Initial Link - Small Reinforcer^	Terminal Link - Large Reinforcer#	Terminal Link - Small Reinforcer#^
0 mg/kg	1.140 (0.122)	1.666 (0.203)	2.282 (0.258)	3.294 (0.329)
0.3 mg/kg	1.255 (0.087)	1.557 (0.064)	2.880 (0.322)	3.304 (0.389)
1.0 mg/kg	0.978 (0.085)	1.216 (0.145)	2.502 (0.317)	2.834 (0.298)
3.0 mg/kg	1.009 (0.098)	1.106 (0.141)	2.027 (0.293)	2.780 (0.308)
Methamphetamine
Dose	Initial Link - Large Reinforcer	Initial Link - Small Reinforcer	Terminal Link - Large Reinforcer#	Terminal Link - Small Reinforcer#
0 mg/kg	1.255 (0.134)	1.616 (0.109)	2.772 (0.221)	3.658 (0.348)
0.5 mg/kg*	0.750 (0.098)	0.757 (0.134)	2.076 (0.307)	2.412 (0.388)
1.0 mg/kg*	0.699 (0.194)	0.905 (0.321)	2.183 (0.333)	2.158 (0.431)
2.0 mg/kg*	0.416 (0.094)	0.517 (0.120)	1.362 (0.372)	1.082 (0.275)

^*p < .05, relative to vehicle (main effect of dose).

^#p < .05, relative to the terminal link (main effect of trial component).

^{^}p < .05, relative to the large, uncertain reinforcer (main effect of reinforcer).

Discussion

The current study shows that a dependent schedule can be used to measure probability discounting, as rats responded less for the probabilistic reinforcer as the odds against obtaining that reward alternative decreased across the session. In traditional discounting paradigms (e.g., Cardinal & Howes, 2005; Evenden & Ryan, 1996), rats often show exclusive preference for one alternative relative to the other at certain probabilities/delays. For example, when both reward alternatives are certain, rats most often choose the large, uncertain reinforcer. When the probability of obtaining the large, uncertain reinforcer is low, some rats show exclusive preference for the small, certain option. Thus, the graded discounting functions depicted in previous studies are often the result of averaging across rats. Dependent schedules often produce graded discounting functions (e.g., Aparicio et al., 2013, Aparicio et al., 2015, Aparicio et al., in press). In the current experiment, rats still showed relatively steep discounting, but the discounting functions generated with this procedure were more graded compared to our previous work using independent schedules (e.g., Yates et al., 2016; Yates, Prior, et al., 2018; see Figure 5; also, see Figure 2c for a representative discounting curve generated for an individual subject). Concerning drug effects, higher doses of amphetamine (0.5 and 1.0 mg/kg) and each dose of methamphetamine (0.5–2.0 mg/kg) impaired stimulus control, whereas a lower dose of amphetamine (0.25 mg/kg) and the highest dose of methylphenidate (3.0 mg/kg) selectively increased risky choice.

Figure 5.

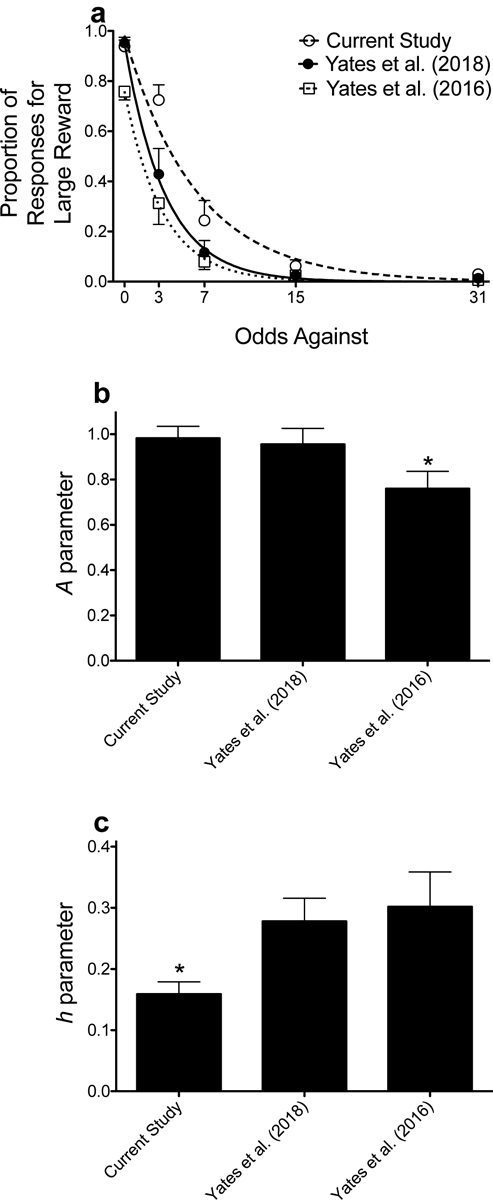
Mean (±SEM) proportion of responses for the large, uncertain reinforcer as a function of odds against (OA) in the current experiment and in two of our previous studies (Yates et al. 2016; Yates, Prior, et al. 2018) (a). Lines are NLME-determined best fits of the exponential discounting function. Mean (±SEM) A (b) and h (c) parameter estimates across the experiments depicted in panel a. *p < .05, relative to the current experiment and the Yates, Prior, et al. (2018) study (b), and relative to the Yates, Prior, et al. (2018) and the Yates et al. (2016) studies (c).

Most studies assessing the neurochemical basis of risky choice have analyzed drug effects on probability discounting performance by conducting two/three-way ANOVAs on the raw proportion of responses for the large, uncertain reinforcer. Using ANOVA to analyze drug effects on discounting procedures (whether probability discounting or delay discounting) is not ideal for several reasons. One major weakness is decreased power (due to the numerous pairwise comparisons that need to be made following significant interactions). For example, St Onge and Floresco (2009) report that amphetamine significantly increases risky choice, but this effect is only observed after averaging across each dose. When each individual dose is subsequently analyzed, there are no significant effects. By using NLME, we are able to show that amphetamine significant alters h (0.25–1.0 mg/kg) and A (0.5 and 1.0 mg/kg) parameter estimates. The finding that amphetamine (0.25 mg/kg) increased risky choice without altering discriminability of reinforcer magnitudes is similar to previous research conducted by Floresco and colleagues (St Onge et al., 2010; St Onge & Floresco, 2009). Furthermore, the finding that a higher dose of amphetamine (1.0 mg/kg) increased risky choice while simultaneously decreasing discriminability is somewhat similar to what St Onge and Floresco (2009) observed with this dose. Although St Onge and Floresco (2009) did not apply quantitative analyses to their data, their results show that amphetamine (1.0 mg/kg) decreased responding for the large, uncertain reinforcer when its delivery was certain (~95% following vehicle and ~85% following amphetamine; note: the lack of a statistically significant effect observed in the St Onge and Floresco (2009) study may be due to the use of ANOVA on these data).

The effects of methamphetamine on probability discounting performance were somewhat similar to those observed with amphetamine. However, each dose of methamphetamine increased risky choice while impairing discriminability of the two reward alternatives. We need to note that we may have observed a selective alteration in h parameter estimates if we had used lower doses of methamphetamine (e.g., 0.25 mg/kg); however, previous research has shown that a lower dose of methamphetamine (0.3 mg/kg) does not affect responding in a choice procedure (Pitts & Febo, 2004). Considering amphetamine and methamphetamine have similar pharmacokinetic properties, such as dopamine release in the striatum and elimination rates (Melega, Williams, Schmitz, DiStefano, & Cho, 1995), and have similar mechanisms of action (see Sulzer, Sonders, Poulsen, & Galli, 2005 for a review), the somewhat concordant results observed across these drugs were not surprising. Importantly, the effects of amphetamine and methamphetamine do not appear to be due to alterations in response rate. Although amphetamine (0.5 and 1.0 mg/kg) significantly decreased response rates for both the large, uncertain and small, certain reinforcers, methamphetamine did not significantly alter response rates.

The pattern of responding observed following amphetamine (0.5 and 1.0 mg/kg) and methamphetamine (0.5–2.0 mg/kg) administration may be influenced, at least in part, to a combination of carry-over effects and perseverative responding. One limitation to probability discounting tasks is that they typically decrease the probability of obtaining the large, uncertain reinforcer across the session (e.g., Cardinal & Howes, 2005; St Onge & Floresco 2009; Yates et al., 2015). Because each session ends with the lowest probability, subjects, particularly when treated with higher doses of psychostimulants, may start the next session by responding as if they are still in the final block of the preceding session (e.g., they respond as if the probability of earning the large, uncertain reinforcer is lower than it actually is). This carry-over effect may account for the decreased responding for the large, uncertain reinforcer when its delivery is certain. Once the subject learns that delivery of the large, uncertain reinforcer is certain, they continue to perseverate on this lever during the duration of the session. This perseverative responding may account for the increased responding for the large, uncertain reinforcer that is observed in these subjects at lower probabilities, even though it is more optimal for subjects to respond for the small, certain reinforcer. There is evidence that drugs such as amphetamine increase perseverative-like responding in probability discounting (St Onge et al., 2010). Considering that non-reinforced responses during the terminal link were not altered by amphetamine/methamphetamine, one may argue that the drug effects observed in the current study are unrelated to perseverative responding. As discussed in Yates, Gunkel, et al. (2018), there is one caveat to this argument. Because rats had to break a photobeam in the food tray to extend the levers in the chamber during the initial link, they were equidistant to each lever at the beginning of each trial. During the terminal link, the levers extended into the chamber, regardless of where the rat was located. In this event, rats may have stayed in the same location following completion of the initial link and then responded on the lever directly in front of them during the terminal link. Thus, one cannot rule out the possibility that the effects of amphetamine (0.5 and 1.0 mg/kg) and methamphetamine (0.5–2.0 mg/kg) observed in the current study are due to alterations in perseverative responding. To control for drug-induced perseverative responding, one can either (a) run separate groups of rats in which one group is experiences increasing probabilities during the session and another group experiences decreasing probabilities during the session or (b) randomize the order in which probabilities are presented. Randomizing trial blocks has been incorporated in delay discounting (e.g., Aparicio et al., 2013; Aparicio et al., 2015; Pope et al., 2015) but is rarely used in probability discounting (but see St Onge et al., 2010, in which they used a pseudo-randomized schedule).

Whereas higher doses of amphetamine (0.5 and 1.0 mg/kg) and each dose of methamphetamine (0.5 mg/kg) impaired discriminability of reinforcer magnitude, methylphenidate (3.0 mg/kg) selectively increased risky choice without altering discriminability. These results are consistent with those obtained with humans, in which methylphenidate is known to increase gambling-like behavior in a task in which participants choose between accepting an incurred loss of money or accepting a gamble that can either avoid the incurred loss or double it (Campbell-Meiklejohn et al., 2012). Although we did not observe a decrease in A parameter estimates following methylphenidate administration, this may due to the use of lower doses (0.3–3.0 mg/kg) in the current experiment. Theoretically, we may have observed impairment in discriminability of reinforcer magnitude if we had used a higher dose of methylphenidate (10.0 mg/kg). However, higher doses of methylphenidate (up to 17.0 mg/kg) do not appear to impair discriminability of reinforcer magnitude in delay discounting (Pitts & McKinney, 2005).

The results of the current experiment are somewhat similar to those using dependent schedules to assess the effects of psychostimulants on sensitivity to delayed reinforcement. In the current experiment, amphetamine decreased sensitivity to probabilistic reinforcement and, at higher doses, decreased discriminability of reinforcer magnitudes (i.e., rats responded less for the large, uncertain reinforcer, even when its delivery was certain). Ta et al. (2008) found that amphetamine decreases sensitivity to delayed reinforcement, and Maguire et al. (2009) observed decreases in sensitivity to reinforcement amount following amphetamine administration. However, although methylphenidate selectively decreased sensitivity to probabilistic reinforcement in the current experiment, Pitts et al. (2016) found that methylphenidate decreases sensitivity to delayed reinforcement and sensitivity to reinforcer amount. This discrepancy may due to the species used across experiments (rat in the current experiment; pigeon in Pitts et al., 2016) or may be due to procedural differences. In the current experiment, the probability of receiving reinforcement decreased within a session. Pitts et al. (2016) randomized the delays to reinforcement across sessions. Also, in the current experiment, we used concurrent FR 5/FR 5 schedules of reinforcement as opposed to concurrent variable interval schedules of reinforcement.

Because we used concurrent FR schedules during the initial and terminal links, one important caveat needs to be discussed. In a concurrent-chains procedure, the use of FR schedules can be problematic because they do not control the rate at which animals enter the terminal link, even when dependent schedules are used. By using concurrent FR schedules, terminal link entry rate and preference for one alternative are confounded. For example, when the odds against receiving the large, uncertain reinforcer are 0, rats typically will allocate most (if not all) of their responding on trials in which the lever associated with this alternative is “active”. Conversely, on trials in which the lever associated with the small, certain reinforcer is “active”, rats will initially respond on the lever associated with the large, uncertain reinforcer before responding on the lever associated with the small magnitude reinforcer. Therefore, the time it takes to enter the terminal link increases for these trials. This in turn increases the amount of time that passes before the animal receives reinforcement. Research has shown that as the time spent in the initial link for one alternative increases, preference for that alternative will decrease (see Grace, 1994 for a discussion). Appendix 1 presents representative data for one subject following amphetamine injections to further illustrate this point. In order to prevent this limitation, concurrent variable interval or random interval schedules can be used, as they control the rate at which subjects enter each terminal link even when response rate changes (e.g., Aparicio et al., 2015; Beeby & White, 2013; Maguire et al., 2009; Ta et al., 2008).

Despite the limitations of using concurrent FR schedules, one interesting observation is that psychostimulants decrease sensitivity to delayed and probabilistic reinforcement in similar manners. The current results mirror the results obtained in delay and probability discounting tasks that do not incorporate dependent schedules (Floresco & Whelan, 2009; St Onge & Floresco, 2009; van Gaalen et al., 2006; Winstanley, Dalley, Theobald, & Robbins, 2003). Considering psychostimulants shift delay discounting and probability discounting functions in the same direction, this raises the question of whether “impulsive choice” and “risky choice” reflect dissociable constructs or if they describe a similar underlying behavioral mechanism (Myerson & Green, 1995; Rachlin et al., 1991). In the case of delayed reinforcement, the finding that psychostimulant drugs decrease sensitivity to delayed reinforcement can be interpreted as a decrease in impulsive choice; however, when these drugs decrease sensitivity to probabilistic reinforcement (i.e., shift the discounting function in the same direction as in delay discounting), the drug effects are now interpreted as increases in risky choice. Fully understanding how drugs affect multiple dimensions of choice (e.g., delay, probability, magnitude, etc.) can help us develop better treatments for those with disorders characterized by excessive impulsivity (e.g., attention-deficit/hyperactivity disorder) and/or excessive risk (e.g., pathological gambling and substance use disorders).

In conclusion, we are able to show that a dependent schedule can be used to measure probability discounting in rats. This procedure provides an advantage over traditional measures of probability discounting (e.g., Cardinal & Howes, 2005; St Onge et al., 2010; St Onge & Floresco, 2009; Yates et al., 2016) as it prevents sensitivity to probabilistic reinforcement/reinforcer magnitude to be confounded by preference (e.g., Beeby & White, 2013; Pope et al., 2015). Additionally, we show that psychostimulants promote suboptimal choice in this task, as rats respond more on the lever associated with probabilistic reinforcer even when the expected value for this alternative is lower than responding on the other lever, and in the case of amphetamine (0.5 and 1.0 mg/kg) and methamphetamine (0.5–2.0 mg/kg), they decrease preference for the large, uncertain reinforcer when its delivery is certain. This procedure can be used to further assess the neurochemical basis of probability discounting and be applied to other measures of risky choice, such as the risky decision task RDT (e.g., Simon et al., 2009; Orsini et al., 2016). Considering the data generated from the RDT appear to follow an exponential function, dependent schedules, in conjunction with NLME analyses, can be used to determine if pharmacological manipulations increase/decrease sensitivity to reinforcement coupled to punishment and/or discriminability of reinforcer magnitudes.

Public Significance Statement:

Probability discounting is often used to measure risky choice in rodents; however, probability discounting tasks often incorporate independent schedules of reinforcement, which allow subjects to show exclusive preference for one alternative. By using a dependent schedule, we are able to measure risky choice while simultaneously controlling for reinforcer frequency. The psychostimulant drugs amphetamine and methylphenidate increase risky choice, whereas methamphetamine impairs discriminability of reinforcer magnitude.

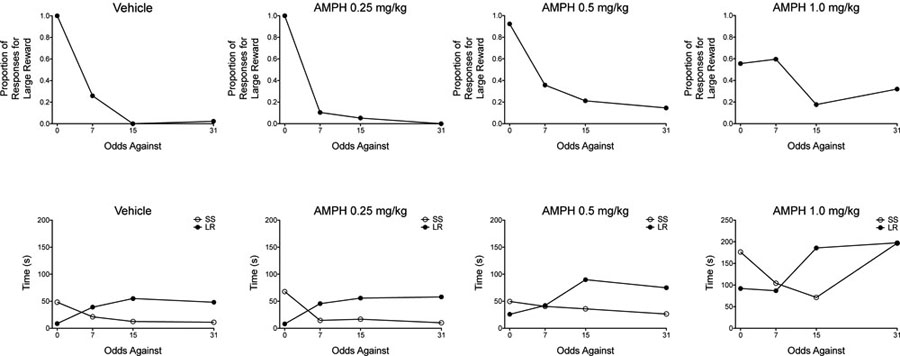
Appendix 1: Time Spent During Initial Links and Preference for Each Alternative

To illustrate the issues of using concurrent FR schedules of reinforcement in concurrent-chains procedures, we have plotted the proportion of choices for the large, uncertain reinforcer for one subject (Subject 501) following administration of each dose of d-amphetamine (see top row of the figure provided below for the raw proportion of responses), and we have plotted the time spent in each initial link (LR+ trials vs. SS+ trials; see Figure 2 of manuscript for a description of LR+ and SS+ trials) following each dose of amphetamine (see bottom row of figure provided below). Due to a programming error, we were unable to extract the time spent in each initial link during the second block of trials (3 odds against). Thus, we only plotted data for blocks of trials (0, 7, 15, and 31 odds against) in which we could extract these data. Under vehicle conditions, as preference for the large, uncertain reinforcer decreases across blocks of trials, the time spent in the initial link associated with this alternative increases. Conversely, the time spent in the initial link associated with the small, certain reinforcer decreases across the session. Overall, as the dose of amphetamine increases, the time spent in each initial link increases (amphetamine decreased overall response rates); however, amphetamine appears to cause a larger percentage increase in the time spent in the initial link associated with the small, certain reinforcer relative to the time spent in the initial link associated with the large, uncertain reinforcer. This may (at least partially) account for the increased preference for the large, uncertain reinforcer that is observed following amphetamine administration.