Modeling immune cell behavior across scales in cancer

Abstract

Detailed, mechanistic models of immune cell behavior across multiple scales in the context of cancer provide clinically relevant insights needed to understand existing immunotherapies and develop more optimal treatment strategies. We highlight mechanistic models of immune cells and their ability to become activated and promote tumor cell killing. These models capture various aspects of immune cells: (a) single‐cell behavior by predicting the dynamics of intracellular signaling networks in individual immune cells, (b) multicellular interactions between tumor and immune cells, and (c) multiscale dynamics across space and different levels of biological organization. Computational modeling is shown to provide detailed quantitative insight into immune cell behavior and immunotherapeutic strategies. However, there are gaps in the literature, and we suggest areas where additional modeling efforts should be focused to more prominently impact our understanding of the complexities of the immune system in the context of cancer.

This article is categorized under:

• Biological Mechanisms > Cell Signaling

• Models of Systems Properties and Processes > Mechanistic Models

• Models of Systems Properties and Processes > Cellular Models

A better understanding of immune cell response in tumors requires multiscale modeling of intracellular signaling, multicellular interactions, and spatial and whole‐body dynamics.

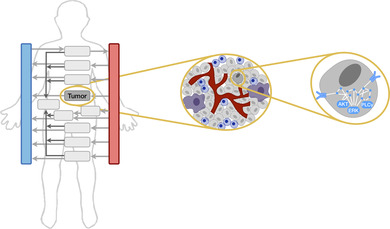
1. INTRODUCTION

1.1. Overview of cancer immunotherapy and associated challenges

Cancer immunotherapy, a treatment that aims to use a patient's own immune system to kill cancer cells, has emerged as a promising anticancer modality. Although immunotherapy in the context of cancer is not a new concept, it has garnered more attention in the past decade (Oiseth & Aziz, 2017), with new cancer‐specific immunotherapeutic drugs being approved by the US FDA (Fesnak, June, & Levine, 2016; Ribas & Wolchok, 2018). Moreover, immunotherapy is highly regarded as a scientific breakthrough (Couzin‐Fankel, 2013), and the field was prominently recognized with the 2018 Nobel Prize in Physiology or Medicine awarded to Dr. James Allison and Dr. Tasuku Honzo for research leading to the development of immune checkpoint inhibiting drugs.

Despite some great successes with cancer immunotherapy, there remain several challenges that must be overcome. These include predicting the response to treatment, identifying and increasing the number of patients who will respond to immunotherapy, and enhancing those responses. Each of these challenges requires a detailed understanding of the biological processes that mediate immune cell activation and directed killing of cancer cells. These processes involve complex networks of biochemical reactions, numerous molecular species that influence interactions between tumor and immune cells, and events that happen over a range of different time and spatial scales.

1.2. Overview of the body's immune response

One aspect that contributes to the complexity of understanding the immune response is the fact that there are multiple types of immune cells, and each plays a unique role in targeting and killing cancer cells (Pandya, Murray, Pollok, & Renbarger, 2016). The body has both innate and adaptive immune responses, which are mediated by specific cells (Figure 1). The body's innate immune response rapidly acts to kill foreign cells and against antigens recognized by receptors on host immune cells such as Toll‐like receptors (TLRs; Brennan & Gilmore, 2018). This response is mediated by cells that engulf and kill foreign cells via lysosomal enzymes (such as neutrophils, monocytes, and macrophages), as well as natural killer (NK) cells, which promote cell killing by secreting cytotoxic factors. The adaptive immune response targets specific antigens and establishes immunological memory. Adaptive immunity is mediated by antigen‐presenting cells (APCs such as B cells, macrophages, and dendritic cells, DCs) and T cells. T cells are further distinguished as CD8+ and CD4+, cytotoxic and effector cells, respectively. In addition, CD4+ can differentiate into more specialized cells: T helper cells (including Th1, Th2, Th9, and Th17), T regulatory (Treg) cells, follicular helper T (Tfh) cells (Luckheeram, Zhou, Verma, & Xia, 2012). This differentiation depends on the cytokines, antigens, and APCs present in their microenvironment. The innate and adaptive immune responses are cell type‐dependent; however, some entities, such as DCs and macrophages, can promote both—mediating the innate response through phagocytosis and promoting adaptive immunity by functioning as APCs (Pandya et al., 2016).

Figure 1.

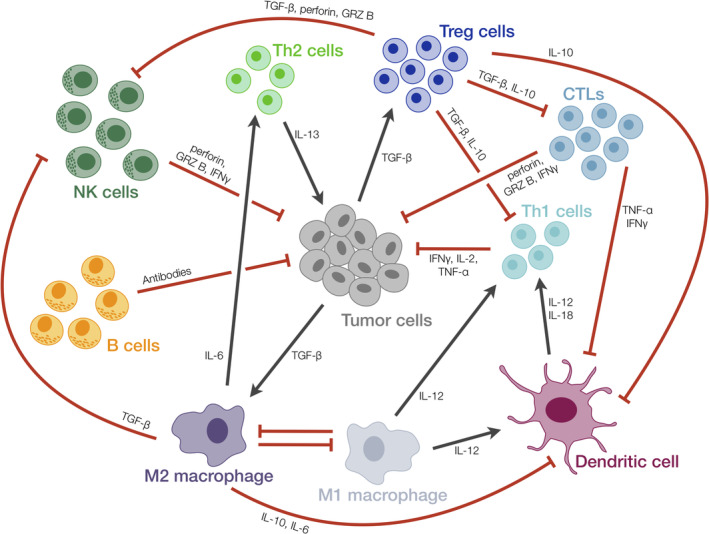
Schematic of interactions between tumor cells and different immune cell populations. Tumor and immune cells interact in various ways: certain immune cells impede tumor cell proliferation and survival, whereas others lead to a pro‐tumor environment by directly targeting tumor cells or inhibiting activation of other immune cells. Gray arrows: activating interaction; Red bars: inhibiting interaction; Dashed line: macrophage polarization

In addition to the many cell types that facilitate the immune response, intracellular signaling is required to activate the cells. This signaling is mediated by certain soluble factors secreted by immune cells, as well as ligands secreted by or presented on the surface of tumor cells. These ligands promote autocrine and paracrine signaling. Intracellular signaling leading to cell activation happens more rapidly than their killing effects. This means that it is important to consider the dynamics of and the mechanisms that promote the immune response. Moreover, space is a key consideration in cell activation, deployment to the peripheral lymphoid organs for antigen‐mediated differentiation, infiltration of the immune cells into the tumor, and tumor cell killing. Given the complexities of these events, which occur over time and space, it is difficult to fully understand and exploit the body's immune response to eradicate a tumor.

1.3. Tools to understand the immune response

A systems‐level approach consisting of predictive computational modeling and robust experimental measurements across scales provides tools to understand the immune system and propel the development of effective immunotherapies (Szeto & Finley, 2019). With many recent large‐scale studies at both the single‐cell level and across the tumor as a whole, there is now an unprecedented amount of data that characterizes the tumor–immune landscape. Of note, Thorsson and coworkers analyzed data from the Cancer Genome Atlas (TCGA, which contains more than 11,000 samples across 33 cancer types) to identify six emergent immune subtypes (Thorsson et al., 2018). In addition, researchers have analyzed the tumor–immune landscape in specific cancer types; for example, in breast (Bao et al., 2019), colorectal (Zhang et al., 2018), head and neck (Mandal et al., 2016), lung adenocarcinoma (Lavin et al., 2017), and prostate (Zhao et al., 2019) cancers. In addition, several groups have applied experimental tools to explore the dynamics of immune cells and their signaling pathways, including using microscopy, microfluidic devices, and mass spectrometry‐based proteomics (Chylek et al., 2014; Friedmann, Bozem, & Hoth, 2019; He et al., 2015; Hui et al., 2017; Junkin et al., 2016; Xue et al., 2015).

Computational modeling makes it possible to account for the complex and multiscale nature of immune cell activation and tumor–immune interactions. Several research groups, including our own, have demonstrated that mathematical modeling complements preclinical and clinical studies of immunology and immunotherapy. The models provide a framework to generate novel hypotheses as to which pathways to target for enhanced immune activation. As such, computational modeling complements experimental studies and can leverage the large datasets being generated. Given the complexity of tumor–immune interactions, a range of modeling approaches have been applied to study their interactions. This includes deterministic differential equation models, as well as stochastic agent‐based modeling. Ordinary differential equation (ODE) models describe how a continuous state variable (i.e., species' concentration or the number of a particular type of cell) changes with time. Partial differential equation (PDE) models are used to predict how a state variable changes with respect to both time and space. Alternatively, agent‐based models (ABMs) are used to simulate the discrete behavior of a population of cells that arises from a network of interactions that follows a set of defined rules. Each approach has its advantages and can be used to answer particular biological questions related to tumor–immune interactions, including intracellular signaling, cell–cell interactions, and whole‐body dynamics.

1.4. Goals of this review

While the application of modeling in the context of tumor–immune interactions has been the focus of multiple reviews (Cappuccio, Tieri, & Castiglione, 2016; Eftimie, Gillard, & Cantrell, 2016; Konstorum, Vella, Adler, & Laubenbacher, 2017; G. E. Mahlbacher, Reihmer, & Frieboes, 2019), here, we specifically present examples of mechanistic models of immune cells and their interactions with tumor cells. The review is comprised of three parts, organized according to the scale being modeled (Figure 2): (a) Single cells: signaling networks in individual immune cells, (b) Multicellular: interactions between tumor and immune cells, and (c) Multiscale: simulations across space and different levels of biological organization. Given the importance of accounting for the complex tumor microenvironment, we summarize several published models in the latter two sections. In all cases, we take care to list what experimental data are used for model construction.

Figure 2.

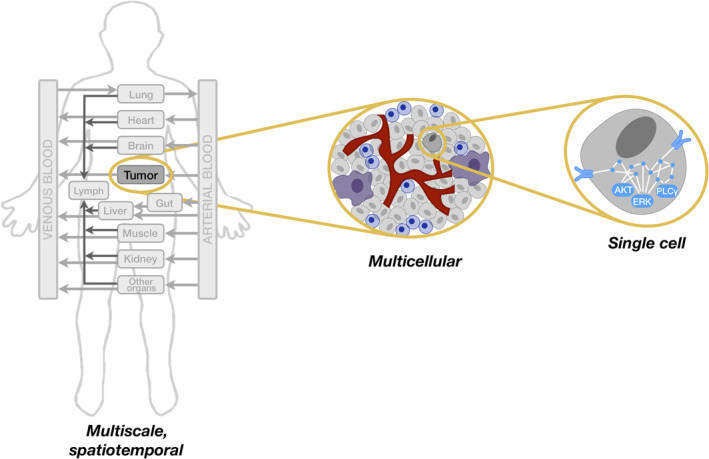
Computational models in cancer encompass multiple aspects of immune cell behavior. Multiscale models can account for spatial effects and represent the whole body. Multicellular models include immune and cancer cells to represent the tumor microenvironment. Models of single cells focus on intracellular signaling networks. AKT, ERK, and PLCγ are intracellular signaling species that mediate immune cell activation

By highlighting specific examples of mathematical models in each of these contexts (Table 1), we demonstrate that detailed, mechanistic models provide a framework to understand immune cell behavior and to exploit that behavior for optimal immunotherapeutic strategies. However, some examples illustrate areas where modeling is not tightly linked to experimental data or do not satisfactorily capture the complexity of tumor–immune interactions. With these issues in mind, we conclude by presenting two opportunities where computational modeling can be improved to have a greater impact in understanding the complexities of the immune system in the context of cancer.

Table 1.

Summary of models highlighted in the main text

Scale	Reference	Type of model	Cell types included
			T cells	NK cells	B cells	Macrophages	DCs	Tumor cells
Single cell	Arulraj et al. (2018)	ODEs	Effector T cells
	Mesecke et al. (2014)	ODEs		•
	Ziegler et al. (2019)	ODEs			•
	Sung et al. (2014)	ODEs				•
Multicellular	Hoffmann et al. (2018)	ODEs		•				•
	Robertson‐Tessi et al. (2012)	ODEs	CTLs, Th, Treg				•	•
	Robertson‐Tessi et al. (2015)	ODEs	CTLs, Th, Treg				•	•
	Arabameri et al. (2019)	ODEs	CTLs, Th, Treg				•	•
	Li et al. (2015)	ODEs	CTLs	•			•	•
	Mahasa et al. (2016)	ODEs	CTLs	•				•
Spatial	Liao et al. (2014a)	PDEs	CTLs					•
	Liao et al. (2014b)	PDEs	CTLs					•
	Gong et al. (2017)	ABM	CTLs					•
	Kather et al. (2017)	ABM	CTLs					•
	Mahlbacher et al. (2018)	PDEs				•		•
	El‐Kenawi et al. (2019)	ABM, PDEs				•		•
Intracellular signaling‐cellular response	Prokopiou et al. (2014)	ABM, PDEs	Naïve T cells					•
	Gao et al. (2016)	ABM, PDEs	Naïve T cells					•
	Girel et al. (2019)	ABM, PDEs	Naïve T cells					•
Multiple tissues	Kim et al. (2018)	ODEs	CTLs				•	•
Systems pharmacology	Milberg et al. (2019)	ODEs	Naïve, Primed, Treg, Effector					•

2. SINGLE CELLS: INTRACELLULAR SIGNALING

2.1. T cells

There are numerous mechanistic models of endogenous T cell signaling, and these models were the focus of our recent review (Rohrs, Wang, & Finley, 2019). Thus, here, we highlight a particular example by Arulraj and Barik, as it relates more specifically to cancer. This study examines early T cell signaling when inhibited by the checkpoint inhibitor, programmed cell death protein 1 (PD‐1; Arulraj & Barik, 2018). PD‐1 is used to prevent autoimmunity, however cancer cells are sometimes able to express its ligand (PD‐L1) to escape the immune system. The authors modeled the early events of T cell receptor (TCR) activation to determine how PD‐1 affects signaling. Upon antigen binding, two components of the TCR, CD3ξ, which transmits the signal to Zap70, and CD28, which transmits the signal to PI3K, become phosphorylated. These two components proceed to phosphorylate downstream signaling molecules with the help of the kinase LCK. LCK also phosphorylates ligated PD‐1, which then binds to the phosphatase Shp2 to dephosphorylate CD3ξ and CD28, inhibiting downstream signaling. The model was calibrated to and validated by various experimental measurements presented by Hui and coworkers, who used a biochemical reconstitution system to identify the primary target of PD‐1 inhibition in T cells (Hui et al., 2017). Arulraj et al. found that CD28 is much more sensitive to PD‐1 inhibition than CD3ξ. Through model simulations, the authors showed that via an indirect path, PD‐1 also dephosphorylates LCK, preventing LCK from activating Zap70, LAT, and Slp76. This result highlights LCK as a potential target for blocking PD‐1 inhibition.

2.2. NK cells

Natural killer cells express stimulatory and inhibitory receptors on their cell surface. Once engaged, the stimulatory receptors induce a cascade of phosphorylation reactions leading to the secretion of cytolytic molecules and targeted cell killing (Figure 3). Mesecke et al. constructed a mathematical model to better understand how the co‐stimulation of opposing signals impacts the NK cell's cytotoxic response (Mesecke et al., 2014). The molecule Vav1 is integral to both pathways, where it is activated by the NKG2D stimulatory pathway and deactivated by the CD94/NKG2A inhibitory pathway. The researchers quantified Vav1 activation via Western blotting and found its dose–response profile is correlated with the percent of tumor cell death measured using a cytotoxicity assay. The researchers then constructed several mathematical models to determine which set of reactions is necessary to qualitatively match their experimental results. Based on model simulations, they observed that the physical association of the Src family kinases (SFK) to the inhibitory receptors is crucial for recapitulating the dose–response profile of Vav1 activation obtained in the experiments. The authors further verified the model prediction via immunoprecipitation of SFK with the activated inhibitory receptor. In total, Mesecke et al. demonstrated that mechanistic models of cell signaling pathways can be applied to determine the essential species and reactions in the signaling network topology. Simulations generated by such data‐calibrated models provide realistic predictions that can be useful for scientists, engineers and clinicians working to improve NK cell activation for immunotherapy.

Figure 3.

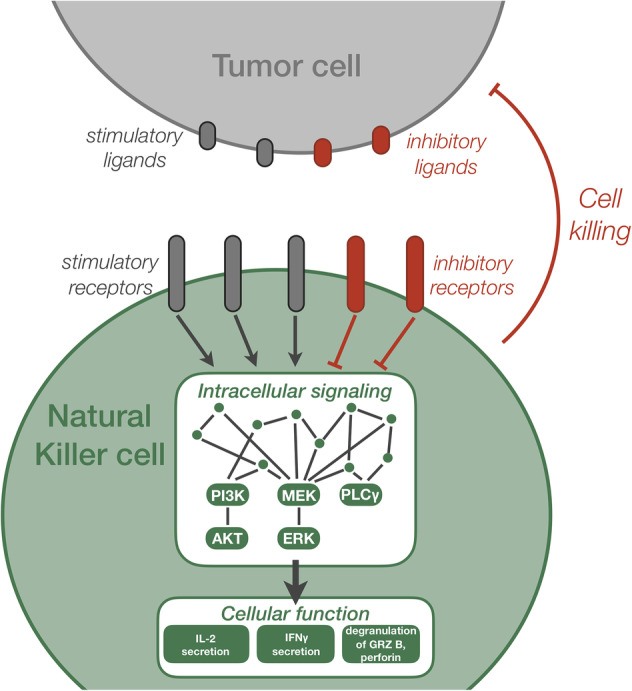
Schematic of natural killer (NK) cell signaling and activation. NK cells express a repertoire of stimulatory and inhibitory receptors. Engagement of the NK cell surface receptors to ligands presented by tumor cells initiates intracellular signaling, including cascades of phosphorylation reactions. In addition, intracellular signaling can be promoted by antibodies that bind to tumor cell receptors and increase engagement of NK cells and tumor cells, termed antibody‐dependent cell‐mediated cytotoxicity (ADCC). The intracellular signaling enables the NK cells to become activated, leading to secretion of cytokines such as IL‐2 and IFN γ, as well as degranulation of granzyme B and perforin. Overall, NK cell activation mediates tumor cell killing. GRZ b: granzyme B; Gray arrows: activating interaction; Red bars: inhibiting interaction

2.3. B cells

B cells are part of the adaptive immune system, where they play a vital role in adaptive immunity in multiple ways: by secreting antibodies against specific antigens, serving as APCs, producing cytokines, and even directly killing tumor cells (Shen, Sun, Wang, Pan, & Ren, 2016). The B cell receptor (BCR) is responsible for activating the B cell upon antigen recognition and is involved in B cell development and differentiation. BCR signaling is not fully understood, particularly in the pathological case of chronic lymphocytic leukemia (CLL), which is characterized by abnormal B cell activation. To address this knowledge gap, Ziegler et al. integrated CLL patient data with mathematical modeling (Ziegler et al., 2019). Specifically, the researchers developed a mechanistic ODE‐based model of BCR activation and applied the model to understand the mechanisms driving constitutive BCR signaling that mediates BCR clustering and the all‐or‐none response to phosphatase inhibition, observations seen in their single‐cell experimental studies. Super‐resolution imaging was used to quantify BCR clustering and generate data for model construction. The model predicted that positive feedback between the kinase Syk and the BCR was needed to induce constitutive activation. The authors confirmed the importance of Syk‐mediated positive feedback experimentally using B cells from CLL patients. Since constitutive BCR signaling involves chronic kinase activity, Ziegler et al. also investigated the role of phosphatases in this scenario. By expanding the model to include the dynamics of the phosphatase SHP1, they found that the threshold for BCR activation is dependent on SHP1 abundance. That is, if SHP1 levels are high, constitutive BCR activation is low due to the dampened effect of the positive feedback motif. This prediction was also validated experimentally using B cells from CLL patients. This work shows that integration of patient data with mechanistic models can yield insights regarding the drivers of disease. Thus, the results can be applied to develop novel therapies to dampen constitutive BCR signaling for patients with CLL.

2.4. Macrophages

Several models of macrophage intracellular signaling have been developed. Overall, the models aim to predict signaling needed to mediate an inflammatory response. These models are applicable in a range of pathological conditions, providing a mathematical framework to probe the behavior of macrophages. For example, the macrophage‐mediated inflammatory response has been modeled in the context of traumatic brain injury (Vaughan, Ranganathan, Kumar, Wagner, & Rubin, 2018), tuberculosis (Fallahi‐Sichani, Schaller, Kirschner, Kunkel, & Linderman, 2010; Ray, Wang, Chan, & Kirschner, 2008), and parasitic or bacterial infection (Figueiredo et al., 2009; Maiti, Dai, Alaniz, Hahn, & Jayaraman, 2015; Sung et al., 2014).

In one example, Sung et al. identified a new feedback loop in NF‐kB signaling mediated by Toll‐like receptor 4 (TLR4) upon LPS stimulation (Sung et al., 2014). Using live, single‐cell imaging of macrophages, the researchers determined that Ikaros, a transcription factor that promotes development of lymphoid cells, rewires NF‐kB signaling. They then incorporated the feedback loop into a mathematical model comprised of ODEs to investigate its effect on NF‐kB signaling dynamics and the cell's ability to respond to different doses of LPS. The model predicted that the positive feedback loop counteracted negative feedback at high LPS doses, enabling a dose‐dependent response. Model simulations suggest that in response to stimulation, macrophages switch the dominance of opposing feedback loops to intricately regulate the transcription factor. This work demonstrates that models of intracellular signaling in macrophages can reveal new insights into the regulatory mechanisms that control the cells' inflammatory responses.

3. MULTICELLULAR: TUMOR–IMMUNE INTERACTIONS

Models of signaling at the cellular level, such as those presented above, can be expanded in two ways to further study immune cell behavior: by incorporating additional cell types and by modeling across scales. The former requires accounting for other types of immune cells, as well as the target cancer. The latter includes embedding a model of intracellular signaling in a cellular framework such that the dynamics of the signaling network drive the cells' behavior, modeling the spatial dynamics of tumor–immune interactions, accounting for multiple tissue compartments in the body, even leading up to whole‐body models. Below, we highlight models that consider these aspects. We note that other cells in the tumor microenvironment contribute to the immune response, such as mesenchymal stromal cells (O'Malley et al., 2018; Poggi, Varesano, & Zocchi, 2018) and cancer associated fibroblasts (Ziani, Chouaib, & Thiery, 2018). However, here, we focus solely on interactions between tumor and immune cells.

While models of intracellular signaling give valuable information about how a cell responds to environmental cues, models of the interactions between different cell types can provide more information about the system as a whole and how perturbations may influence cells' behaviors. Modeling the tumor–immune response at the cellular level can provide information not only on which interactions govern the system, but also allows for exploring potential immunotherapies and combination therapies. Indeed, a natural extension of the models of immune cell signaling described above is to simulate interactions between the immune cells and tumor cells. This includes cells that mediate both adaptive and innate immune responses. In this section, we highlight models that include multiple immune cell types.

Hoffmann et al. developed an ODE‐based model of antibody‐dependent cellular cytotoxicity (ADCC) to understand how the dynamic interactions between tumor and NK cells influence tumor cell killing (Hoffman et al., 2018). ADCC involves administering antibodies that bind to antigens on the surface of tumor cells. NK‐tumor complexes form when NK cells bind to receptors on the tumor cells. When the NK cells sense a high level of antibody on the tumor cell surface, they kill the tumor cells by secreting cytotoxic factors. Data from an in vitro cytotoxicity assay quantifying the amount of NK cell‐mediated tumor cell killing at a single time point provide the basis for this work, where the experimental data informs their perturbation analysis. The authors used the model to demonstrate that NK cell activation and subsequent tumor cell killing occur on separate timescales. On the fast timescale, the system dynamics are entirely governed by NK‐tumor complex formation, and tumor cell killing is negligible. However, on the longer timescale, NK‐tumor complex formation reaches steady state, enabling tumor cell killing. The authors then derived approximate solutions of the model for each timescale and analyzed the approximate solutions to determine how model parameters affect tumor cell killing. Simulations show that the ratio of tumor cell receptor density to initial antibody concentration determines the extent of tumor cell killing, not the ratio of NK cells to tumor cells. When the antibody concentrations are much lower than the concentration of receptors on tumor cells, the number of tumor cells remains constant, since complex formation is below saturating levels. However, as antibody concentration increases relative to the tumor cell receptor concentration, complex formation can reach the maximum density and the number of tumor cells decays exponentially. Based on their simulations, the authors conclude that to maximize NK cell‐mediated tumor cell killing, it is much more important to saturate tumor cells with antibodies than to increase the concentration of NK cells.

Robertson‐Tessi et al. developed an ODE model of the interactions between tumor cells, DCs, CTLs, Th cells, and Treg cells, with IL‐2, IL‐10, and TGF‐β mediating cell‐to‐cell communications (Robertson‐Tessi et al., 2012). The authors assume a well‐mixed system, and thus model a single compartment. However, they include parameters to account for trafficking, including the reduced immune cell numbers arriving at the tumor compared to the total number of immune cells administered in the simulated DC treatment. All model parameters were derived from or set based on in vitro, preclinical, and clinical data from multiple published studies and cancer types. With this model, they examined the immune system's ability to control (maintain the number of tumor cells at a stable steady state or oscillate around a particular size) or remove (completely eliminate) the tumor. The authors expanded their model to examine the effect of chemotherapy on improving the immune response (Robertson‐Tessi et al., 2015). Because chemotherapy kills both tumor cells and Tregs, the amount of TGF‐β in the system is reduced, as fewer tumor and Treg cells are present to secrete this cytokine. This reduction in TGF‐β allows the remaining CTLs to become uninhibited. Thus, model simulations show that direct tumor cell killing is not the only effect of chemotherapy and that without the immune system, chemotherapy would not be able to completely eradicate the tumor. Additionally, several methods of immunotherapy were tested in combination with chemotherapy. Treg depletion, DC therapy, and adoptive T cell transfer were shown to better control tumor size, while TGF‐β blockade together with chemotherapy had a small effect since chemotherapy inherently lead to a reduction of TGF‐β in the system. For each immune‐based therapy simulated, the authors varied tumor growth rate and antigenicity. The simulations predicted that efficacy of the immunotherapy also depends on these tumor‐specific properties, demonstrating the utility of the model for personalized medicine.

Arabameri et al. also constructed a multicellular model that included the same cell types included in the models by Roberston‐Tessi and coworkers (Arabameri et al., 2019). They used the model to examine the effect of combining DC therapy with a drug that inhibits hypoxia‐inducible factors (HIFs), which are produced by the tumor in response to hypoxia. HIFs enhance immunosuppression by promoting Tregs and inhibiting CTLs and Th cells. In the model, HIF increases tumor carrying capacity by promoting angiogenesis, increases the production and inhibitory effect of Tregs, decreases activation and function of CTLs, and increases DC activation of Th1. The model was fit to in vivo tumor growth data, providing parameter estimates for tumor growth, DC‐mediated tumor cell killing, and the effect of HIF. The model predicted that inhibiting HIF while giving DC therapy leads to a larger reduction in tumor size by reducing Tregs and increasing the effect of CTLs. Including DC immunotherapy was found to be successful because it helped to offset the negative effect that the HIF inhibitor has on DCs.

Immune cell activation is not only determined by recognition of foreign agents or antibodies; activation can also occur in response to danger signals, which indicate cell damage. APCs in particular respond to danger signals, and then go on to activate T cells. However, very few mechanistic models of tumor–immune dynamics incorporate such a danger model. Li et al. addressed this issue by constructing a model that includes the dynamics of tumor cells, CD8⁺ T cells, NK cells, DCs, and interleukin‐12 (IL‐12) secretion in response to danger signals such as pathogens, toxins, and LPS (Li & Xu, 2015). Here, model parameter values were taken from previous modeling works and there is no comparison to experimental data. The authors simulated the model and identified three steady states, which represent low, medium, or high tumor density. Interestingly, the low and high tumor density steady states were stable, while the medium tumor density case was unstable. Their analysis suggests a healthy immune system can force the unstable medium tumor toward the low density state. On the other hand, with a depleted immune system, the tumor can grow indefinitely. The model was applied to predict the number of tumor cells for varying initial tumor sizes, with and without chemotherapy. When the initial tumor density is small, the model predicts that a healthy immune system can eliminate the tumor without treatment. However, when the immune system is compromised, even a small tumor cannot be eliminated. In contrast, when the initial tumor density is large, treatment is required even in the presence of a competent immune system. The model was also applied to predict the effects of different chemotherapy dosing strategies. Model predictions showed that the tumor can be successfully eliminated when chemotherapy is given with a shorter interval between doses, compared to treating with the same number of doses, but with a longer time interval between doses. The researchers concluded that a healthy immune system is necessary for chemotherapeutic interventions to completely eradicate the tumor, as chemotherapy alone is insufficient.

While testing potential therapies is a major use of mathematical modeling, it can also be used to learn about the dynamics of how a tumor comes to escape the immune system. Mahasa et al. created a model to examine tumor cells that evolve to become resistant to both NK cells and CTLs (Mahasa, Ouifki, Eladdadi, and de Pillis (2016)). Model parameters were taken from previous modeling works, and the predicted number of tumor cells over time was compared to data from an in vivo mouse study (Diefenbach, Jensen, Jamieson, & Raulet, 2001). The authors specifically applied the model to see how the strength of the immune response influences tumor escape. In their model, the immune cells are able to form complexes with the tumor cells, at which point either the immune cell would kill the tumor cell or the tumor cell would escape and become resistant to that immune cell type. There is also a chance of immune cell death following interaction with a tumor. Resistance to one immune cell type is assumed to cause susceptibility to the other immune cell type, due to changes in the tumor cells' expression of the major histocompatibility complex Class I molecules. Eventually, a population of tumor cells emerges that is resistant to both CTLs and NK cells. Model simulations showed that a strong immune presence (high numbers of immune cells) is able to control tumor growth, whereas a weak immune presence (low numbers of immune cells) leads to tumor escape. The authors performed a sensitivity analysis to determine how sensitive the size of the naïve tumor population (resistant to neither immune cell) was to variability in the model parameters, at different times. Early on, parameters relating to CTL recruitment and binding were found to be influential. At later time points, parameters relating to NK cell survival are influential. These results identify potential immunotherapy targets. Further simulations showed that NK cell immunotherapies may be useful against developing tumors. However, a large number of NK cells is needed to control tumor size; otherwise, NK cell treatment just delays tumor escape.

4. MULTISCALE MODELS

4.1. Accounting for spatial interactions

While ODEs are useful for modeling several cell types and multiple scales, PDEs can provide information about how tumor cells interact spatially with the immune system. Modeling cells as discrete agents also allows for spatial interactions and takes stochastic cellular heterogeneity into account. There are many models that incorporate interactions between tumor and immune cells across space. For a recent review on solely this subject, see Norton, Gong, Jamalian, and Popel (2019). Here, we highlight models that focus on different types of interactions between immune and tumor cells, including PDE models and ABMs.

A study by Liao et al. investigated immune cell migration and examined the potential feasibility of IL‐27, a less toxic member of the IL‐12 family, as an immunotherapeutic agent (Liao et al., 2014a). PDEs were used to model tumor growth, CTL infiltration, and diffusion of IL‐10, IL‐27, and IFN‐γ. Experimental measurements of tumor volume from mouse studies where tumor cells modified to secrete IL‐27 were used to fit the model. With the secretion rate set to zero, the model was used to test two different IL‐27 injection strategies: continuous dose at level F or intermittent dose at a level of 2F. They found that a continuous, lower dose provides more of a benefit, however this advantage decreases as the value of F becomes smaller. However, IL‐27 only slows down tumor growth; it has no lasting effects once therapy is discontinued. In later work, this model was further expanded to include myeloid‐derived suppressor cells and macrophages in order to study the anti‐inflammatory effects of IL‐35 treatment (Liao et al., 2014b).

A spatial model by Gong et al. examines the ability of CTLs to eradicate the tumor when the tumor cells are able to randomly express PD‐L1 in order to suppress the immune system (Gong et al., 2017). The parameter values were specified by adopting values from experimental studies or previous modeling works and were not calibrated to a specific cancer type. The authors modified parameters relating to neoantigen characteristics in order to predict how those properties affect the response to anti‐PD‐1 treatment. Specifically, the authors varied the mutational burden (antigen‐spreading) and the antigen strength (immunogenicity). Together, these parameters influence recruitment of effector T cells to the tumor. Interestingly, the model predicted that at low mutational burden, the tumor continues to grow even with anti‐PD‐1 treatment, independent of the antigen strength. Additionally, the number of tumor cells expressing PD‐L1 is higher compared to the case without treatment. The authors hypothesize that this is due to an increased inflammation stemming from reduced immune suppression. In contrast, anti‐PD‐1 treatment can eliminate tumors with high mutational burden, and the response depends on antigen strength. The model was also used to identify which initial tumor characteristics predict response to treatment, providing insight into potential drug targets. For example, this analysis revealed that sensitizing T cells to IL‐2 (which influences activation of effector T cells) can synergize with anti‐PD‐1 treatment. Overall, the model provides a framework to study immune checkpoint inhibitors and predict possible treatment biomarkers.

Kather et al. constructed a spatial, agent‐based model of tumor cells and T cells (Kather et al., 2017). Here, model parameters were based on histological tumor measurements, taken from other studies, or set based on biological knowledge. An interesting aspect of their model is that they included production of stromal (fibrotic) areas in the tumor as a result of sustained activation of the T cells. The authors applied the model to determine how the stroma can affect interactions between immune cells and tumor cells, for different levels of immune cell recruitment. The model predicted that with high immune cell recruitment, it is possible to control or eliminate the tumor size for high and low stroma levels, respectively. The authors also varied stroma permeability, which affects migration of both immune and tumor cells. In order to reduce tumor growth, the model predicts that higher immune recruitment is needed, otherwise, the tumor would take advantage of the higher permeability to continue to grow. Therefore, it was concluded that although stroma‐reducing therapy has been shown to aid immunotherapy, it can actually be detrimental to treatment if there is not a sufficient immune presence to counteract the increased ability of the tumor to spread.

The dynamic interactions between tumor cells, macrophages, and the tumor microenvironment have also been modeled by various research groups (Eftimie & Eftimie, 2018; Li, Jolly, George, Pienta, & Levine, 2019). Some models include the effects of diffusible factors, such as colony stimulating factor‐1, on macrophage behavior and suggest strategies to block the effects of those diffusible factors and hence influence tumor growth (Knutsdottir, Condeelis, & Palsson, 2016; Knútsdóttir, Pálsson, & Edelstein‐Keshet, 2014; Zheng, Bao, Zhao, Zhou, & Sun, 2018) Other studies model macrophage‐based therapy (Leonard et al., 2016; Owen et al., 2011). Two recent examples simulate the cellular behavior of macrophages in the context of tumor cells and provide mechanistic insight and rationale for immunotherapies that exploit the role of macrophages in tumor growth.

Mahlbacher et al. developed a spatial modeling framework to investigate the role of Tie2‐expressing macrophages (TEMs) in the growth of vascularized tumors (G. Mahlbacher et al., 2018). TEMs are a recently discovered subtype of macrophages whose role in tumor progression is still being investigated. The model includes tumor growth and angiogenesis, M1‐ and M2‐type macrophages, TEMs, cytokine production by macrophages, oxygen diffusion, and cell migration. Tumor growth parameters were calibrated to experimental data, while other model parameters were set to literature values. In the model, cells are represented as discrete entities, and all macrophages differentiate from monocyte precursors. M1 and M2 macrophages negatively and positively affect tumor growth, respectively, while TEMs promote angiogenesis. TEMs also affect M2 differentiation through the secretion of IL‐10. The authors consider several cases that have M1, M2, and TEMs in different combinations to determine their effects on tumor growth. The simulations predict that the tumor growth profiles strongly depend on the relative sizes of the three types of macrophages. Interestingly, the presence of M2 macrophages leads to more tumor growth, with or without TEMs present, and the antitumor effects of TEMs are predicted to be less influential than M1 macrophages. Their results provide a quantitative basis for proposing immunotherapeutic strategies that take advantage of the timescales over which each type of macrophage influences tumor volume.

El‐Kenawi and coworkers combined experimental and modeling studies to better understand how intratumoral acidity influences tumor growth and macrophage phenotype (El‐Kenawi et al., 2019). They first found experimentally that neutralizing tumor acidity reduces the pro‐tumor phenotype of tumor‐associated macrophages in in vitro cell assays, as well as an in vivo model of prostate cancer. The spatiotemporal effects of tumor acidity were further explored using agent‐based modeling. Here, the model parameters were taken from experimental measurements or set based on biologically relevant ranges. The authors performed in silico experiments where they altered the macrophages' ability to sense and respond to pH. Interestingly, tumors were predicted to grow less rapidly in simulations with acidosis‐resistant macrophages, as compared to tumors where acidity influences the polarization of macrophages into a pro‐tumor phenotype. Thus, their results show that acidity affects macrophage behavior and tumor growth and lends support to therapies that modulate the tumor microenvironment by reducing acidity.

4.2. Linking intracellular signaling and cellular response

The dynamics of the signaling reactions in immune cells upon recognition of or stimulation by foreign cells directly influences the immune cells' behavior. Thus, it is important to connect models of intracellular signaling, such as those described in Section 2, with models of cell behavior and cell–cell interactions, such as the models presented in Section 3. This kind of multiscale approach enables quantitative investigations of targeted immunotherapies directed toward specific molecular signaling species or particular signaling networks. Unfortunately, such multiscale models in the context of the tumor–immune interactions are lacking. Therefore, below, we highlight a series of multiscale models that predict T cell maturation and effects in response to viral infection. In these models, the target and immune cells' responses are influenced by intracellular signaling species. Similar multiscale modeling efforts are needed to study tumor–immune interactions.

Modeling work by Crauste and coworkers predicts the progression of CD8+ T cells in murine lymph nodes from naïve precursors to effector cells (Prokopiou et al., 2014). This maturation of the T cells occurs upon interactions with APCs and is mediated by intracellular signaling. Specifically, cellular behavior is controlled by the signaling dynamics promoted by antigen binding to the TCR as well as IL‐2 and Fas‐L binding to their receptors (IL‐2R and Fas, respectively). T cells are present as naïve, preactivated, activated, and effector cells. When APCs remain bound to TCRs for a contact time that exceeds a threshold value, the T cell transitions to a preactivated state. Subsequent T cell maturation depends on threshold values of intracellular signaling species: activated IL‐2R promotes activation of naïve T cells, and Tbet promotes the conversion of activated T cells to effector cells (Kaech & Cui, 2012). In addition, both APCs and T cells are can migrate and die. Death of the APC depends on its intrinsic half‐life, while T cell death is influenced by the cells' intracellular caspase level mediated by Fas‐L signaling. Thus, the model explicitly accounts for how signaling species affect cellular behavior. Model parameters were specified using literature evidence or based on biological insight. The model was implemented using CompuCell3D (Swat et al., 2012), and it consisted of ODEs for the intracellular dynamics, a Cellular Potts model to describe cellular behavior, and PDEs for the dynamics of extracellular species. The authors fit the model to in vivo measurements of T cell counts in murine lymph nodes 3–5.5 days after infection. This initial work established a framework for studying T cell maturation, including molecular‐ and cellular‐level detail.

Crauste et al. expanded on this initial model of T cell maturation in subsequent papers (Barbarroux, Michel, Adimy, & Crauste, 2018; Gao et al., 2016; Girel et al., 2019). The authors applied the model to predict the effects of exogenous IL‐2 levels and the threshold value of the activated IL‐2:IL‐2R complex needed for a preactivated T cell to transition to an activated cell (Gao et al., 2016). Their simulations show that both IL‐2 supplementation and the cells' sensitivity to IL‐2R activation tune the duration of T cell–APC interaction, which directly influences T cell fate and phenotype (the concentrations of intracellular species). Recently, Crauste and coworkers (Girel et al., 2019) built on this model to add memory T cells and the transcription factor Eomesodermin (Eomes), which plays an important role in the formation of memory T cells (Kaech & Cui, 2012). They use the expanded model to study how intracellular heterogeneity (variability in the concentrations of Tbet and Eomes) affects cell division. The model simulations emphasize the impact of heterogeneity on the T cell immune response. Altogether, these studies demonstrate the unique insights gained from a combined molecular and cellular description of the immune cell response.

4.3. Including multiple tissue compartments

Since the human body is a complex interconnected system, modeling the events of only a single tissue can miss vital dynamics influenced by other parts of the body. Some modeling work accounts for multiple tissue compartments. For example, Kim et al. expanded a multi‐compartment ODE‐based model (Köse et al., 2017) to examine the effects of anti‐PD‐L1 therapy (Kim et al., 2018). This model contains three compartments (spleen, blood, and tumor), and accounts for DCs, CTLs, and tumor cells. Although the lymphatic system is involved in the body's immune response, as mature DCs travel to lymphoid organs to activate T cells, the authors simplify their model by only including the blood compartment as a means of allowing DCs to travel to and from the tumor to recruit proliferating CTLs in the spleen. These CTLs then travel through the blood to reach the tumor. Incorporating separate compartments allows for the time delay between DC activation and CTL killing. Anti‐PD‐L1 is modeled by increasing CTL kill rate based on the amount of anti‐PD‐L1 in the system. Many model parameters were fit to preclinical tumor volume measurements and others were taken from previously published mathematical models. The authors applied the model to explore different doses and dosing schedules for anti‐PD‐L1 treatment for a range of tumors. Tumor growth rates and CTL killing rates were randomly sampled, where the parameter ranges were informed by model fitting to in vivo mouse data, and the model predicted what percentage of tumors would become eradicated. Model simulations show that higher doses of anti‐PD‐L1 improve tumor killing to an extent until further increasing the dose no longer increases tumor killing. They also found that giving the same number of doses over a shorter timescale leads to a higher chance of eradication. Since the tumor growth rate and rate of CTL‐mediated killing represent patient‐specific properties, a model such as this can be applied to simulate personalized treatment strategies.

4.4. Applying quantitative systems pharmacology approaches

Multicellular, multiscale models of tumor–immune interactions have been applied to study the systems‐level effects of drug treatments. These approaches, termed quantitative systems pharmacology (QSP), include mechanistic detail of the “system,” which can refer to a pathway, cell, tissue, organ, or whole body (Musante et al., 2017). In comparison, traditional pharmacokinetic/pharmacodynamic models have an empirical or semi‐mechanistic basis. QSP models are increasingly being used as a platform to help inform drug discovery and development and predict the effects of targeted drugs in a virtual patient population, including in the area of cancer immunology (Byrne‐Hoffman & Klinke, 2015). We highlight a recent example below.

Milberg and coworkers developed an ODE‐based QSP model to explore checkpoint blockade therapies in melanoma (Milberg et al., 2019). The authors first fit a minimal physiologically based pharmacokinetic model to clinical trial data for checkpoint blockade therapies. The model included transport between peripheral and central blood compartments, as well as the tumor and tumor‐draining lymph nodes. Multiple cell types were included: naïve CD8+ T cells, primed T cells, Treg cells, effector T cells, myeloid‐derived suppressor cells, tumor cells, monocytes, and APCs. Monocytes differentiate into APCs when educated by tumor cells. T cells become primed and activated upon interaction with APCs and are then able to kill tumor cells. The model was applied to simulate the response of a virtual cohort of patients to various immunotherapies. Several tumor‐specific parameters were varied to represent individual patients. The model was quantitatively and qualitatively validated by comparing to clinical data. Excitingly, the model generated novel predictions for combining multiple checkpoint blockade, providing a mechanistic explanation as to why the ordering of CTLA‐4 and PD‐1 combination therapy. Specifically, their model predicts that administering anti‐PD‐1 first is most effective because initially, anti‐PD‐1 greatly reduces tumor size and the number of antigens for T cell priming, allowing anti‐CTLA‐4 to be more effective when administered second.

5. CONCLUSION

5.1. Opportunities for systems‐level studies of tumor–immune interactions

5.1.1. Better leverage experimental data

Understanding how immune cells become activated and mediate tumor cell killing can greatly enhance cancer immunotherapy. Accomplishing this goal requires predictive computational models, constructed using robust experimental data. A handful of the studies highlighted above use intracellular measurements to specify the model parameters. Others use Western blotting, tumor volume over time, or cytotoxicity assays for model calibration. These data do not provide information at the cellular level, and do not include any spatial insights. In comparison, large genomic studies provide detailed insight into the distinct features of the tumor–immune setting; however, many generate a single snapshot of the tumor and are missing the temporal component, which is a significant aspect of the immune response. Thus, mathematical modeling of the tumor–immune system has not fully taken advantage of the wealth of data being generated. This creates a natural opportunity where systems‐level computational modeling can impact the field of tumor immunology. Modelers must leverage large‐scale data from experimental methods that characterize tumors, such as single‐cell RNA sequencing, mass spectrometry, and mass cytometry. These data are useful during model construction to specify the set of interactions to include in the model and determine parameter values, as well as to test and validate model predictions.

5.1.2. Better represent the multiscale nature of immune response

Immune‐based treatment strategies are often molecularly focused; they target a specific signaling species, diffusible factors, or set of reactions. Therefore, mechanistic models at the molecular scale are particularly useful. Although there are many such models that include detailed intracellular signaling pathways or the secretion of various cytokines that mediate cell killing, these molecular‐scale models are rarely linked to models at the cell‐ or whole‐body level in the context of cancer. The effects of tumor–immune interactions span different spatial and temporal scales, and it is important to have computational models that capture this complexity. Thus, we propose that future efforts in modeling immune cells in tumors should bridge different time and spatial scales. Such a multiscale modeling approach will enable simulations that predict the effects of immunotherapy in a range of patient‐specific settings, generate new testable hypotheses, and complement experimental studies. Overall, computational models of immune cell behavior across scales can increase our fundamental understanding of immune cells and their role in eliminating tumors.

In summary, by leveraging high‐throughput technology to generate rich datasets and building multiscale models that recapitulate the tumor–immune ecosystem, computational modeling can generate novel insight into immune cell activation and provide a platform to aid in the development of effective immunotherapies.

CONFLICT OF INTEREST

The authors have declared no conflicts of interest for this article.

AUTHOR CONTRIBUTIONS

Sahak Makaryan: Writing‐original draft; writing‐review and editing. Colin Cess: Writing‐original draft; writing‐review and editing. Stacey Finley: Resources; supervision; writing‐original draft; writing‐review and editing.

RELATED WIREs ARTICLES

Towards multiscale modeling of the CD8+ T cell response to viral infections

IL7 receptor signaling in T cells: A mathematical modeling perspective

Makaryan SZ, Cess CG, Finley SD. Modeling immune cell behavior across scales in cancer. WIREs Syst Biol Med. 2020;12:e1484 10.1002/wsbm.1484