Parental Age and Offspring Childhood Mental Health: A Multi‐Cohort, Population‐Based Investigation

Abstract

To examine the contributions of maternal and paternal age on offspring externalizing and internalizing problems, this study analyzed problem behaviors at age 10–12 years from four Dutch population‐based cohorts (N = 32,892) by a multiple informant design. Bayesian evidence synthesis was used to combine results across cohorts with 50% of the data analyzed for discovery and 50% for confirmation. There was evidence of a robust negative linear relation between parental age and externalizing problems as reported by parents. In teacher‐reports, this relation was largely explained by parental socio‐economic status. Parental age had limited to no association with internalizing problems. Thus, in this large population‐based study, either a beneficial or no effect of advanced parenthood on child problem behavior was observed.

Since 1995, the mean maternal age at first birth has increased at a rate of .10 years per year in Organisation for Economic Co‐operation and Development countries, and in 2017 exceeded 30 years in the vast majority of these countries (OECD, 2017). Only in Mexico was the mean age of women at childbirth lower than 28 years, and only in eight countries was it between 28 and 30 years of age. Women's reproductive years generally range from about 15 to 45 years (Te Velde, 2002). Within this wide age range some periods are generally considered more suitable to have children than others, but which parental reproductive ages are optimal for offspring physical and mental health has been a matter of debate ever since individuals have engaged in active birth control. Whereas having children at an advanced age was quite common historically, when families tended to be larger (e.g., Desjardins, Bideau, & Brunet, 1994), the current trend to delay childbearing has given rise to public health concerns.

Concerns Regarding Delayed Childbearing

Concerns regarding delayed childbearing are understandable, as a large number of research reports highlight that increased maternal age at childbirth is associated with several adverse consequences, ranging from physical problems, such as increased Body Mass Index (BMI), blood pressure and height (Carslake, Tynelius, Van den Berg, Davey Smith, & Rasmussen, 2017) to psychiatric conditions, such as autism (Lee & McGrath, 2015; Sandin et al., 2012), bipolar disorder (Menezes, et al., 2010), symptoms of depression, anxiety, and stress (Tearne et al., 2016), and poor social functioning (Weiser et al., 2008). More recently, increased paternal age at birth has also been associated with adverse child outcomes, such as stillbirth and cleft palate (see Nybo Andersen & Urhoj, 2017, for a review). In over 40 million live births between 2007 and 2016, having an older father increased the risk of low birthweight, Apgar score, and premature birth (Khandwala et al., 2018). A study of the Danish population, which included 2.8 million persons, found that older fathers are at risk of having offspring with intellectual disabilities, autism spectrum disorders, and schizophrenia (McGrath et al., 2014; see De Kluiver, Buizer‐Voskamp, Dolan, & Boomsma, 2017 for a review).

Several, not mutually exclusive, mechanisms have been proposed to explain the increased physical and mental health risks in offspring of older parents. First, age‐related deterioration of the functioning of women's reproductive organs, such as DNA damage in germ cells, and worse quality of oocytes and placenta, can increase the risk of obstetric and perinatal complications (Myrskylä & Fenelon, 2012). Second, male germline cells undergo cell replication cycles repeatedly during aging, with de novo point mutations accumulating over time (e.g., Jónsson et al., 2017) and the number of de novo mutations in the newborn increasing with higher age of the father at the time of conception (Francioli et al., 2015; Kong et al., 2012). Although weaker than with paternal age, de novo mutations in offspring correlate with maternal age as well (Goldmann et al., 2018; Wong et al., 2016). Third, genomic regions in the male germline may become less methylated with increasing age (Jenkins, Aston, Pflueger, Cairns, & Carrell, 2014) and alter the expression of health‐related genes. Fourth, age effects can be due to selection, with older parents differing from younger ones in characteristics that are relevant for developmental outcomes in their offspring, such as poor social skills. The influence of selection effects can be exacerbated by assortative mating (Gratten et al., 2016). Fifth, being the child of older parents carries the risk of having to cope with parental frailty or losing a parent at a relatively young age (Myrskylä & Fenelon, 2012), and the stress evoked by these experiences may trigger health problems. Most of these mechanisms involve consequences of biological aging. Parenthood at an advanced age is disadvantageous from a biological perspective; except for very young, physiologically immature mothers, younger parents are in a better physical condition.

Possible Benefits of Delayed Childbearing

Whereas the effects of older parental age on children's physical health and psychiatric disorders tend to be predominantly negative, the effects of older parental age on mental health problems with a stronger psychosocial component, such as externalizing and internalizing problems, tend to be more inconsistent. An indication that the negative consequences of high parental age may stretch beyond clinical diagnosis is provided by Tearne et al. (2015, 2016), who found that high maternal age predicted symptoms of depression, anxiety, and stress in daughters, and by Janecka, Haworth, et al. (2017) who reported a negative association between advanced paternal age and social development. In contrast, in several population‐based studies, offspring of older parents, particularly of older mothers, perform better at school and work, score higher on intelligence tests, report better health and higher well‐being, use fewer drugs, and have fewer behavioral and emotional problems than offspring of younger parents (e.g., Carslake et al., 2017; McGrath et al., 2014; Myrskylä & Fenelon, 2012; Myrskylä, Barclay & Goisis, 2017; Orlebeke, Knol, Boomsma, & Verhulst, 1998; Tearne et al., 2015).

While the biology of aging seems to put older parents in an unfavorable position with regard to their offspring's physical and mental health, these contradictory effects of parental age on offspring mental health outcomes might be explained by a psychosocial perspective. Being a child of older parents can have substantial benefits (Lawlor, Mortensen, & Andersen, 2011), as older parents not only are often in a better socioeconomic position than young parents (Bray, Gunnell, & Davey Smith, 2006), thereby providing a more favorable environment for children, they also have greater life experience. Furthermore, older parents display more hardiness (McMahon, Gibson, Allen, & Saunders, 2007) and tend to have less substance use and fewer mental health problems (Kiernan, 1997), hence score higher on parenting factors that promote health and development (Janecka, Rijsdijk, et al., 2017; Kiernan, 1997). In part, positive associations of advanced parental age could be related to selection effects. In young people, substance abuse and related externalizing problems go together with earlier sexual activity (Crockett, Bingham, Chopak, & Vicary, 1996), which increases the probability that intergenerational transmission of externalizing problems occurs at an early parental age (Bailey, Hill, Oesterle, & Hawkins, 2009). Like age‐related parental characteristics that may have negative effects on offspring outcomes, the influence of such selection effects can be exacerbated by assortative mating (Gratten et al., 2016).

In sum, whereas advanced parenthood, particularly advanced paternal age, has primarily been associated with physical health and neurodevelopmental outcomes, such as autism and schizophrenia, advanced parenthood, particularly advanced maternal age, rather seems to predict mental health problems with a stronger psychosocial component, such as externalizing problems. Although it seems plausible that parental age interferes with subclinical problems and traits underlying these conditions, comprehensive evidence from population‐based cohorts is scarce and inconsistent, and more empirical evidence is desirable. Moreover, prior population‐based studies that used continuous measures of mental health problems usually focused on cognitive or behavioral problems (e.g., Carslake et al., 2017; Orlebeke et al., 1998) and, with a few exceptions that require replication in other cohorts (Janecka, Haworth, et al., 2017; Tearne et al., 2015, 2016), rarely included internalizing problems. A final reason to extend the research conducted thus far with this study is the wide variety of populations, designs, and outcomes used, which makes it hard to distinguish between substantive variation in association patterns and sample‐specific artefacts. In short, there is a need for studies that investigate both maternal and paternal age effects on continuously assessed core dimensions of offspring mental health (including internalizing problems) and that use robust analytical methods are suitable for the investigation of increased risk for both young and old parenthood.

The Present Study

We investigated parental age effects on offspring externalizing and internalizing problems around age 10–13 years in four Dutch population‐based cohorts: Generation R (Gen‐R), the Netherlands Twin Register (NTR), the Research on Adolescent Development and Relationships—Young cohort (RADAR‐Y), and the TRacking Adolescents' Individual Lives Survey (TRAILS) (see Table 1). The Netherlands is characterized by a high maternal age at birth, and relatively few teenage pregnancies. In 1950, 1.6% of the children were born to mothers younger than 20 years of age, with a comparable percentage (1.7%) in 1990. In 2016 this number had decreased to 0.6%. In contrast, the percentages of women who gave birth at an age above 40 years were 8.5% in 1950, 1.5% in 1990, and 4.3% in 2016 (Centraal Bureau voor de Statistiek, 2018).

Table 1.

General Cohort Information

Full cohort name	Short name	Website	Birth years	References (DOI)
Generation R	Gen‐R	generationr.nl	2002–2006	https://doi.org/10.1007/s10654-016-0224-9 https://doi.org/10.1016/j.jaac.2012.08.021
Netherlands Twin Register	NTR	tweelingenregister.org	1986–2017	https://doi.org/10.1017/thg.2012.118 https://doi.org/10.1016/j.jaac.2012.10.009
Research on Adolescent Development And Relationships—Young cohort	RADAR‐Y	www.uu.nl/onderzoek/radar	1990–1995	https://doi.org/10.1111/cdev.12547 https://doi.org/10.17026/dans-zrb-v5wp
TRacking Adolescents' Individual Lives Survey	TRAILS	trails.nl	1989–1991	https://doi.org/10.1093/ije/dyu225

As the perception of childhood problems may differ for different informants (Hudziak et al., 2003; Rescorla et al., 2013), we aimed to obtain a comprehensive set of outcome measures of internalizing and externalizing problems through a multiple informant design. The four cohorts provided reports from mothers, fathers, the children themselves, and the children's teachers. The addition of reports from teachers is particularly valuable, because their reports are unlikely to be affected by parental age‐related report biases. We tested both linear and nonlinear effects, to be better able to distinguish effects of older parenthood versus younger parenthood. We tested effects with and without adjusting for child gender and socioeconomic status (SES). SES was included as a covariate to get an impression of the relative importance of socioeconomic factors in explaining parental age effects.

Bayesian evidence synthesis was used to summarize the results over the cohorts. The current era is one of increased awareness of the need for replication research before making scientific claims (see Open Science Collaboration, 2015). Therefore, in this study, the data sets of the four cohort studies were used to evaluate the same set of hypotheses with respect to the relation between parental age and offspring mental health problems. This approach is called Bayesian evidence synthesis (Kuiper, Buskens, Raub, & Hoijtink, 2012).

Method

Participants

The participants in this study came from the Gen‐R, NTR, RADAR‐Y, and TRAILS population cohort studies. Table 2 gives the total sample size and information on parental age for each cohort. The total number of children in each cohort was 4,769 for Gen‐R, 25,396 for NTR, 497 for RADAR‐Y, and 2,230 for TRAILS.

Table 2.

Cohort Descriptive Statistics of Total Sample Size and Parental Age in Current Study

Cohort	N	Maternal age at child's birth child		Paternal age at child's birth child
		Range	M (SD)	Range	M (SD)
Gen‐R	4,769	16.56–46.85	31.68 (4.79)	17.61–68.67	34.24 (5.58)
NTR	25,396	17.36–47.09	31.35 (3.95)	18.75–63.61	33.76 (4.71)
RADAR‐Y	497	17.80–48.61	31.38 (4.43)	20.34–52.52	33.70 (5.10)
TRAILS	2,230	16.34–44.88	29.32 (4.58)	18.28–52.09	31.99 (4.71)

Gen‐R = generation R; NTR = Netherlands Twin Register; RADAR‐Y = Research on Adolescent Development And Relationships—Young cohort; TRAILS = TRacking Adolescents' Individual Lives Survey.

Gen‐R mothers were recruited in the city of Rotterdam during pregnancy. Their partners, and later their children, were also invited to participate. For Gen‐R, participants from the child age‐10 study wave (born between 2002 and 2006) were included if they had complete information on maternal age and a child behavioral problems sum score by at least one informant. When multiple children from one family were present, one sibling was randomly removed (N = 397) to create a sample of unrelated individuals. Mean child age for mother report was: 9.72 (SD = .32), father report: 9.77 (SD = .32), and child self‐report: 9.83 (SD = .36). 71.2% of the Gen‐R sample is Dutch or European. Other ethnic groups are Suriname (6.4%), Turkish (5.3%), and Moroccan (4.2%). Mother's educational level is low (i.e., no education or primary education) for 9%, intermediate (i.e., secondary school, lower vocational training) for 42%, and high (i.e., higher vocational training, university) for 49%. Based on mother reports, 84.5% of the children had nonclinical scores for internalizing problems, 7.1% scored in the borderline category, and 8.4% scored in the clinical category. With respect to externalizing problems, 92.0% scored in the nonclinical category, 3.6% in the borderline category, and 4.5% in the clinical category.

The NTR study recruits new‐born twins from all regions in the Netherlands. Here we included the data on 10‐year‐olds who were born between 1986 and 2008. Children were not included if they had a severe handicap which interfered with daily functioning. Mean child age for mother report was: 9.95 (SD = .51), father report: 9.94 (SD = .50), and teacher report: 9.80 (SD = .58). The children in NTR were mostly born in the Netherlands (99.5%). The remaining 0.5% consisted mainly of other West European nationalities (0.4%). Parents in the NTR were mostly born in the Netherlands (95.7% of fathers and 96.7% of mothers). The NTR genotype database indicates that 2.2% of participants born in the Netherlands have non‐Dutch ancestry. 3.1% of mothers had a low skill occupation (primary education), 11.4% had an occupation that required lower secondary education, 40.3% had an upper secondary educational level, 30.6% had a higher vocational occupation level, and 14.6% worked at the highest (i.e., scientific) level. According to mother reports for internalizing problems, 86.1% of children had a nonclinical score, 5.9% had a borderline score, and 8.0% scored in the clinical range. For externalizing problems, 85.7% scored in the nonclinical range, 6.5% scored in the borderline range, and 7.8% in the clinical range.

The RADAR‐Y sample was recruited in the province of Utrecht and four large cities in the mid–west of the Netherlands. Because the RADAR‐Y study had a focus on delinquency development, children with borderline externalizing behavior problems at age 12 were oversampled. All participants from the first wave of data collection, born between 1990 and 1995, were selected. The mean age of the children at this wave was 13.03 years (SD = .46). The sample consisted mainly of native Dutch (87.9%) children. Remaining participants belonged to the following ethnic groups: Surinam (2.4%), Indonesian/ Moluccan (2.4%), Antillean (1.8%), Turkish (0.4%), and other (4.8%). Mother's educational level is low (i.e., no education or primary education) for 3.2%, intermediate (i.e., secondary school, lower vocational training) for 56.7%, and high (i.e., higher vocational training, university) for 40.1%. According to the children's reports for externalizing problems, 81.6% of the participants had a nonclinical score, 7.2% had a borderline score, and 11.2% scored in the clinical range. Using the cutoff scores for the depression scale as described by Reynolds (2000), 4.0% of the children scored in the subclinical or clinical range of depressive symptoms. Using the cutoff scores for the anxiety scale of Birmaher et al. (1997), 5.3% of the children scored in the subclinical or clinical range for anxiety symptoms.

The TRAILS sample was recruited in the Northern regions of the Netherlands. All participants from the first wave of data collection (born between 1990 and 1991) were selected. The mean age of the children at the first wave was 11.09 (SD = .56). The large majority of participants were Dutch (86.5%), with other participants being Surinam (2.1%), Indonesian (1.7%), Antillean (1.7%), Moroccan (0.7%), Turkish (0.5%), and other (6.9%). Mother's educational level is low (i.e., no education or primary education) for 6.9%, intermediate (i.e., secondary school, lower vocational training) for 66.3%, and high (i.e., higher vocational training, university) for 26.8%. Based on mother‐reported sum‐scores for the internalizing and externalizing scales, TRAILS participants were categorized in a nonclinical, borderline, or clinical category. For internalizing problems, 67.3% of the participants had a nonclinical score, 13.9% had a borderline score, and 18.8% had a clinical score. For externalizing problems, 74.5% had a nonclinical score, 10.2% a borderline score, and 15.4% had a score in the clinical range.

To summarize, the cohorts represented the entire Dutch geographic region across all strata from society. They had a similar distribution of SES. The percentage of participants with parents born in the Netherlands was relatively high in NTR (> 95%), around 87% in Radar‐Y and TRAILS, and relatively low in Gen‐R (< 72%). The percentage of nonclinical behavioral problem scores was lowest in TRAILS.

All studies were approved by central or institutional ethical review boards. The participants were treated in compliance with the Declaration of Helsinki, and data collection was carried out with their adequate understanding and parental consent. All measures in RADAR‐Y were self‐reports. In the other cohorts, children were rated by any combination of: their parents, themselves, or their teachers. Table 3 shows the total number of children in each cohort, and the number of participants with an externalizing and internalizing behavior problem score, as a function of informant (father, mother, teacher, and self).

Table 3.

Total Sample Size and Sample Sizes per Informant per Cohort

(Total sample size)		Gen‐R (N = 4,769)		NTR (N = 25,396)		RADAR‐Y (N = 497)		TRAILS (N = 2,230)
Variable	Informant
Externalizing behavior problems	Child	BPMa	4,010	—	—	YSRb	491	YSRb	2,188
	Mother	CBCLc	4,549	CBCLc	21,921	—	—	CBCLc	1,965
	Father	CBCLc	3,259	CBCLc	14,715	—	—	—	—
	Teacher	—	—	TRFd	12,573	—	—	TCPe	1,925
Internalizing behavior problems	Child	BPMa	4,018	—	—	RADS–2f + SCAREDg	266	YSRb	2,171
	Mother	CBCLc	4,550	CBCLc	21,731	—	—	CBCLc	1,955
	Father	CBCLc	3,259	CBCLc	14,626	—	—	—	—
	Teacher	—	—	TRFd	12,389	—	—	TCPe	1,924

Gen‐R = generation R; NTR = Netherlands Twin Register; RADAR‐Y = Research on Adolescent Development And Relationships—Young cohort.

^aBrief Problem Monitor (BPM; Achenbach, 2011).

^bYouth Self Report (YSR; Achenbach, 1991).

^cChild Behavior Checklist (CBCL; Achenbach, 1991; Achenbach, 2001).

^dTeacher Report Form (TRF; Achenbach, 2001).

^eTeacher Checklist of Psychopathology (TCP). Vignette questionnaire on the basis of the Achenbach Teacher Report Form developed by TRacking Adolescents' Individual Lives Survey (TRAILS).

^fReynolds Adolescent Depression Scale, 2nd ed. (RADS–2; Reynolds, 2000). Excluding anhedonia scale. Standardized before averaged with Screen for Child Anxiety Related Emotional Disorders (SCARED).

^gSCARED (Birmaher, et al., 1997). Standardized before averaged with RADS–2.

Measures

Predictors

Maternal and Paternal Age at Birth. The age of the biological parents at birth of the child was measured in years up to two decimals for each cohort.

Outcomes

Externalizing and Internalizing Problems. In most cohorts, internalizing and externalizing problems were assessed by the parent‐rated Child Behavior Checklist (Achenbach, 1991; Achenbach & Rescorla, 2001), the Youth Self‐Report (YSR; Achenbach, 1991), and the Teacher Report Form (TRF; Achenbach & Rescorla, 2001). These questionnaires contain a list of around 120 behavioral and emotional problems, which can be rated as 0 = not true, 1 = somewhat or sometimes true, or 2 = very or often true in the past 6 months. The broadband scale Internalizing problems includes the syndromes anxious/depressed behavior, withdrawn/depressed behavior, and somatic complaints; the broadband scale Externalizing problems involves aggressive and rule‐breaking behavior. In TRAILS, the Teacher Checklist of Psychopathology (TCP) was developed to be completed by teachers. The TCP contains descriptions of problem behaviors corresponding to the syndromes of the TRF. Teachers rated the TCP on a 5‐point scale (De Winter et al., 2005). In Gen‐R, the YSR was replaced by the Brief Problem Monitor, containing six items for internalizing and seven items for externalizing behavior problems from the YSR. All items were scored on a 3‐point scale. In RADAR‐Y, internalizing behavior problems were assessed by a combined score of the Reynolds Adolescent Depression Scale, 2nd ed. (RADS–2; Reynolds, 2000) and the Screen for Child Anxiety Related Emotional Disorders (SCARED; Birmaher, et al., 1997) questionnaires. The RADS–2 contained 23 items (the subscale anhedonia was deleted) and the SCARED contained 38 items, which were rated on a 4‐point scale (1 = almost never, 2 = hardly ever, 3 = sometimes, 4 = most of the time) and 3‐point scale (1 = almost never, 2 = sometimes, 3 = often), respectively.

Table 3 gives an overview of the rating instruments, the informants for each of the cohorts and the number of children in each cohort for each informant/instrument combination. A sum score was calculated per informant/instrument for the relevant items for externalizing and internalizing problems, respectively. Table 4 shows the mean scores for externalizing and internalizing problems per cohort. The scores for girls and boys are given in Tables S1 and S2, respectively.

Table 4.

Mean and SD for Externalizing and Internalizing Problems

Informant	Cohort	Externalizing	Internalizing	N‐Ext/N‐Int
Child	Gen‐R	1.94 (1.92)	2.15 (2.09)	4,010/4,018
	RADAR‐Y	10.61 (7.15)	−0.04 (0.86)	491/266
	TRAILS	8.68 (6.25)	11.28 (7.41)	2,188/2,171
Mother	Gen‐R	3.92 (4.91)	4.86 (5.05)	4,549/4,550
	NTR	5.61 (6.12)	4.68 (5.07)	11,086/10,986
	TRAILS	8.40 (7.03)	7.85 (6.20)	1,965/1,955
Father	Gen‐R	3.99 (4.91)	4.58 (4.72)	3,259/3,259
	NTR	4.66 (5.41)	3.56 (4.24)	7,420/7,374
Teacher	NTR	3.28 (5.88)	4.41 (4.96)	6,536/6,446
	TRAILS	0.44 (0.77)	0.99 (1.12)	1,925/1,924

For NTR one child per family was selected to compute means and SDs. For instruments, see Note Table 3. Gen‐R = generation R; NTR = Netherlands Twin Register; RADAR‐Y = Research on Adolescent Development And Relationships—Young cohort; TRAILS = TRacking Adolescents' Individual Lives Survey.

Covariates

SES and child gender. In Gen‐R, SES was defined as a continuous variable (principal component) based on parental education and household income. In NTR, SES was a five‐level ordinal variable based on occupational level. In TRAILS, SES was a three‐level ordinal variable based on parental education, parental occupational status, and household income. In RADAR‐Y SES was a dichotomous variable based on parents' occupational level. Child gender was coded as male = 0 and female = 1.

Missing Data and Data Imputation

Missing Data

For externalizing problem behavior, 15.9% of the child self‐reports were missing for Gen‐R, whereas for RADAR‐Y and TRAILS these percentages were 1.2% and 1.9%, respectively. For mother‐reported data, 4.6% were missing for Gen‐R, 13.7% for NTR, and 11.9% for TRAILS. For father‐reported data, 31.7% were missing for Gen‐R and 42.1% for NTR. For teacher‐reported data, 50.5% were missing for NTR and 13.7% for TRAILS. For internalizing problem behavior, the percentages were similar, except for child‐reported data in RADAR‐Y, where 46.4% was missing. For the predictor variables, age mother and age father, 0.3% and 1.3%, were missing for NTR, 0.0% and 14.4% for Gen‐R, 0.4% and 9.7% for RADAR‐Y, and 5.1% and 25.0% for TRAILS, respectively. For SES, the percentage of missing values was always below 3.0%, except for Gen‐R, where 22.3% was missing. For child gender, all cohorts had complete information.

Please note that the higher percentage for missing teacher‐ and father‐reported data of NTR is due to the fact that NTR did not collect teacher‐reported data at the initiation of the study and that NTR had not collected father‐reported data in multiple birth years due to financial constraints. The higher percentage of missing self‐reported data of internalizing problem behavior for RADAR‐Y is caused by the fact that not all subscales on which the internalizing problem behavior score was based were collected from all participants.

Data Imputation

Missing data were handled by means of multiple imputation (Van Buuren, 2012; Schafer & Graham, 2002). When multiple imputation is used, the missing values are repeatedly (in this study 100 times) imputed, that is, replaced by values that are plausible given the child's scores that are not missing, resulting in 100, so‐called, completed data sets. Subsequently, each completed data set is analyzed (e.g., using a multiple regression) and the 100 analyses are summarized such that the fact that “artificial data” are created by imputation is properly accounted for. Multiple imputation proceeds along three steps:

Determine which variables are to be used for imputation

The variables used for imputation have to be chosen such that conditional on these variables the missing data are believed to be missing at random (MAR; van Buuren, 2012), that is, whether or not a score is missing does not depend on the missing value (Schafer & Graham, 2002). Unless missingness is planned, the variables causing the missingness remain unknown to the researcher. What is often done in practice is that variables are chosen that are expected to be good predictors of the variables containing missing values. One can argue with respect to which and how many variables to use, but there is no way to test whether MAR is achieved, and MAR is an assumption.

The imputation model included the outcome variables externalizing and internalizing behavioral problems per informant, total behavioral problems, SES, child gender, age of the child, age of the father, and age of the mother. In some cohorts, other variables were present that could also contribute to the imputation. Specifically, parent psychopathology (in Gen‐R) and total number of siblings (in NTR) contributed to the imputation model. Variables functioned only as predictors when a correlation of at least .10 with the imputed variable was present. Since the NTR data set contained twins, the imputation process differed from that of the other cohorts. The imputation for NTR was done for each family instead of each participant, so that the same value for SES, age father, and age mother was obtained for both twins. The imputation of missing data was done for informants available in each cohort. So, for example, when a cohort had no teacher‐reported data, teacher data were not imputed.

Generate imputed data matrices

The R package MICE (Multiple Imputation by Chained Equations; Van Buuren & Groothuis‐Oudshoorn, 2011) was used to create 100 imputed data matrices. MICE uses an iterative procedure in which sequentially each variable is imputed conditional on the real and imputed values of the other variables. Continuous variables were imputed by predictive mean matching. Categorical variables were imputed using logistic regression (see Van Buuren & Groothuis‐Oudshoorn, 2011). Success of the imputation was evaluated by checking the events logged by the software, and by checking convergence plots for a lack of trends and proper mixing of the imputation chains.

Analyze each imputed data set as desired and pool the results

In this study, each of the 100 imputed data sets was analyzed using multiple regression or cluster linear regression. The results, for each regression coefficient, were 100 estimates and 100 SEs of the estimate. As may be clear, each of the standard errors was too small because they are partly based on artificial imputed data. This was accounted for by properly pooling the results using Rubin's rules (see Van Buuren, 2012). The variance over the 100 estimates reflects the uncertainty in the estimate due to missing values (in each of the 100 completed data sets different values are imputed). In Rubin's rules the variance of the 100 estimates is used to increase the standard errors such that they properly account for the fact that part of the data is imputed. Gen‐R, TRAILS, and RADAR‐Y used the “pool” function of MICE in R for summarizing the effects of the 100 separate imputed data sets, whereas NTR used the pooling option of Mplus instead of R, to appropriately take into account the family clustering of the twins in the same analysis. Both pooling methods are based on the principles as explained here. The pooled estimates and standard errors were the main outcomes of the analyses after imputation.

Analytical Strategy: Bayesian Evidence Synthesis

The process of Bayesian evidence synthesis consists of four steps: (a) creating exploratory and confirmatory data sets; (b) generating competing hypotheses using exploratory analysis; (c) quantifying the support for each of the competing hypotheses using Bayesian hypothesis evaluation; and (d) Bayesian evidence synthesis, that is, summarizing the support resulting from each study into the overall support for the competing hypotheses in the data from the four cohort studies.

Exploration and Confirmation

As was elaborated in the introduction, diverse results regarding the relation between parental age and child problem behavior have been found in the literature, with increased parental age both positively and negatively related to child problem behavior. In the same vein, there may be a quadratic effect and if there is, increased child problem behavior may be present at high and low parental age. Since research is indecisive, especially for the nonclinical studies reviewed in this article, the data resulting from each of the cohorts were split randomly into two parts containing the same number of children: an exploratory part, which was used to generate a set of competing hypotheses; and a confirmatory part, which was used to quantify the support in the data for each of the hypotheses considered. Since the NTR data set consisted of twins, the cross‐validation data sets were split based on family ID for this cohort, to ensure independent data sets. Multiple imputation was applied separately to the exploratory and confirmatory part of the data. Having an exploratory and confirmatory data set avoids the so‐called “double dipping,” that is, using the same data to generate and evaluate hypotheses. Here a hypothesis survived if it: (a) emerged from the exploratory analyses and (b) was supported by the confirmatory analyses. The process of generating hypotheses is explained next.

Generating Hypotheses using Exploratory Analyses

The exploratory half of the data resulting from each of the four cohorts was used to generate hypotheses with respect to the relation between child problem behavior and parental age. First, for each cohort separately, linear regression analyses were conducted to regress internalizing and externalizing problem behavior as evaluated by child, mother, father, and teacher (see Table 3 for the informants that were present per cohort) on paternal and maternal age and age squared (both with and without child gender and SES as covariates). Parental age was mean‐centered to obtain the linear effect at the mean age of the samples and to reduce the correlation between the linear and quadratic terms. For Gen‐R, RADAR‐Y, and TRAILS, the analyses were conducted in R (R Core Team, 2017). For the NTR twin‐data, cluster linear regression analyses were conducted in Mplus version 8.0 (Muthén & Muthén, 1998–2017). All analyses were repeated with SES and child gender as covariates. This rendered, for each combination (e.g., predicting externalizing problems as rated by the mother from mother age and age squared) an estimate of both the linear and quadratic effect for each of the cohorts that included the informant of interest. These estimates and the corresponding p‐values provided information with respect to whether the linear and nonlinear effects were expected to be negative, zero, or positive. To interpret the strength of relations, the variables in the exploratory analyses were all standardized. The results of the regression analyses were translated into so‐called informative hypotheses (Hoijtink, 2012), that is, hypotheses that represent expectations with respect to the state of affairs in the populations from which the data of the four cohorts were sampled. An example of such an informative hypothesis is: H₁: β < 0. That is, the regression coefficient is negative. Informative hypotheses go beyond the traditional null hypothesis (here H₀: β = 0) by stating explicitly which relations between variables are expected. Often the null is added to the set of hypotheses under consideration to protect against unjustified claims that the effect specified by an informative hypothesis exists. Another hypothesis that can be added besides the informative hypotheses is the alternative hypothesis H_a: β. That is, there are no restrictions on the regression coefficient. The alternative hypothesis is used to protect against choosing the best of a set of inadequate informative hypotheses. For example, H₀: β = 0, and H₁: β < 0 constitute the set of hypotheses supported by the exploratory parts of the data, but both are inadequate in the confirmatory data. Instead, another unspecified hypothesis (β > 0) describes the confirmatory data best. In this case the Bayesian approach (specified next) will prefer the alternative hypothesis, H_a: β, over the informative hypotheses H₀ and H₁. Using informative hypotheses, the exact same hypotheses could be evaluated in all cohorts, even when cohorts used different measurement instruments for the same concepts. Not requiring the exact same measurement instruments is an important benefit of Bayesian evidence synthesis over classical meta‐analyses.

Confirmatory Bayesian Hypotheses Evaluation

Once a set of competing informative hypotheses had been formulated (including the traditional null and alternative hypotheses), the empirical support for each pair of hypotheses was quantified using the Bayes factor (BF; Kass & Raftery, 1995). The BF is the ratio of the marginal likelihood of two competing hypotheses. Loosely speaking, the marginal likelihood of a hypothesis is the probability of that hypothesis given the data. Consequently, a BF comparing H₁ with H_a of, for example, five indicates that the support in the data for H₁ is five times larger than for H_a. The BF as the ratio of two marginal likelihoods implies that the fit (how well does a hypothesis describe the data set at hand) and the specificity (how specific is a hypothesis) of the hypotheses involved are accounted for (Gu, Mulder, & Hoijtink, 2018). To give an example, if β = −2, H₁: β < 0, and H_a: β, both have an excellent fit, but H₁: β < 0 is more specific than H_a: β (anything goes), and as a result, the BF will prefer H₁ over H_a. Note that the size of the BF is related to sample size. If the precision of the evidence in the data for a hypothesis increases as a result of a larger sample, the BF for that hypothesis will increase as well. The BF implemented in the R package Bain (Gu et al., 2018) was used to evaluate informative hypotheses in the context of (cluster) multiple linear regression models.

Assuming that a priori each hypothesis is equally likely to be true, the BFs were transformed in so‐called posterior model probabilities (PMPs), that is, the support in the data for the hypothesis at hand given the set of hypotheses under evaluation. PMPs have values between 0 and 1 and sum to 1 for the hypotheses in the set under consideration. For example, if PMP H₀ = .05, PMP H₁ = .85, and PMP H_a = .10, then it is clear that H₁ receives the most support from the data, because it has by far the largest PMP. Thus, the result of the confirmatory Bayesian hypotheses evaluation were PMPs for each hypothesis and for each informant by each of the cohorts that had ratings by this informant. The next step was to apply Bayesian evidence synthesis.

Bayesian Evidence Synthesis

Bayesian evidence synthesis was used to summarize the support for the hypotheses of interest over the four cohort studies. Bayesian evidence synthesis (Kuiper et al., 2012) can be illustrated using the set of hypotheses: H₀: β = 0, H₁: β < 0, and H_a: β. In the context of this article, these hypotheses are incompletely specified. The complete specification would be H₀: β₁ = 0 for NTR, H₁: β₁ < 0 for NTR, and H_a: β₁ for NTR, and analogously for the other three cohort studies. This specification highlights that the support for the hypotheses depends on the cohort study at hand. Bayesian evidence synthesis can then be used to determine support for a set of hypotheses:

• H₀: H₀ for NTR & H₀ for TRAILS & H₀ for Gen‐R & H₀ for Radar‐Y

• H₁: H₁ for NTR & H₁ for TRAILS & H₁ for Gen‐R & H₁ for Radar‐Y

• H_a: H_a for NTR & H_a for TRAILS & H_a for Gen‐R & H_a for Radar‐Y

that is, the regression coefficient is zero in the populations corresponding to each of the four cohort studies, the regression coefficient is smaller than zero in the populations corresponding to each of the four cohort studies, and there is not prediction with respect to the regression coefficient in the populations corresponding to each of the four cohort studies. If for a specific set of hypotheses only two or three cohorts contain the necessary variables, the hypotheses can be adjusted accordingly. Like for each individual study, the support for these composite hypotheses was quantified using PMPs.

If a hypothesis emerges from the exploratory analyses of the data corresponding to the cohort studies and is supported by the confirmatory analyses of the data corresponding to the cohort studies, then there is evidence that this hypothesis provides an adequate description of the relation between child problem behavior and parental age, that is, in general, independent of the specific cohort studies used to evaluate this hypothesis. With the methodological approach elaborated in this section and applied in the remainder of this article, the increased awareness of the need for replication studies before making scientific claims is explicitly addressed.

Results

Exploratory Analyses

The results of the exploratory analyses (see Supporting Information) generally showed a negative relation between mean‐centered parental age and externalizing problems accompanied by a positive quadratic coefficient, implying that the negative relation with age at the mean declined across age (see Table S3 and Figure S1). This model explained about 1.9% of the total variance in externalizing problems with maternal age and 1.2% with paternal age. For internalizing problems, the relation with parental age was less apparent: about 0.5% of the total variance was explained by maternal age, and about 0.2% was explained by paternal age. In analyses including the covariates SES and gender, the relation with age diminished, but remained significant (Tables S4 and S5). Higher SES was related to fewer externalizing problems, and boys showed more externalizing problems than girls. In general, no relation between parental age and internalizing problems was observed (see Tables S6–S8, and Figure S1).

Our interpretation of the exploratory results led to the following set of competing informative hypotheses with respect to the relation between parental age (mean‐centered), as indicated by a linear (i.e., β₁) and a quadratic (i.e., β₂) coefficient, and child problem behavior:

• H₁: β₁ = 0, β₂ = 0. Age does not have a linear or quadratic relation.

• H₂: β₁ < 0, β₂ = 0. Age has a negative linear relation, there is no quadratic relation.

• H₃: β₁ < 0, β₂ > 0. Age has a negative linear relation, and a positive quadratic relation.

• H_a: β₁, β₂. The coefficients can have any value.

On the basis of the exploratory results, we expected most evidence for H₂ or H₃ in analyses with parental age predicting externalizing problems, and most evidence for H₁ in analyses with parental age predicting internalizing problems. Since the exploratory results did not show a positive linear or a negative quadratic relation between age and behavioral problems, the hypotheses do not include these features. However, we remained open to other options by including the alternative hypothesis H_a that imposes no constraints on the parameters, and accordingly claims that anything can be true. H_a receives the most support if none of the specified informative hypotheses provides an adequate description of the confirmatory part of the data from each of the four cohorts. In this manner, we avoided that the best hypothesis out of the set of H₁, H₂, and H₃, is an implausible hypothesis.

Confirmatory Analyses

Tables S9–S14 contain the confirmatory unstandardized regression coefficients. These are the results per cohort that generated the relative support for the competing informative hypotheses as will be presented in the next paragraph. We will discuss the underlying results briefly. Similar to the exploratory data, the results showed negative relations across cohorts between parental age and externalizing problems. However, in the confirmatory data, the quadratic coefficients from the cohorts were less often significantly different from zero than in the exploratory data. The model with a linear and quadratic coefficient for parental age explained on average about 1.1% of the total variance in externalizing problems with maternal age and 0.9% with paternal age as a predictor. With respect to internalizing behavior problems, the model with maternal age explained on average about 0.4% of the total variance, and paternal age explained on average about 0.3%. Figure 1 visualizes the relation between age and behavioral problems using the first imputation of the confirmatory part of Gen‐R and NTR, respectively. The figure presents a plot of data for internalizing and externalizing problems. As a result of centering, the linear effect that we investigated is the effect at the mean age around 29–32 years for mothers and 32–34 years for fathers (see Table 2 for mean parental age per cohort). The results presented in the figures were representative for all other analyses and cohorts.

Figure 1.

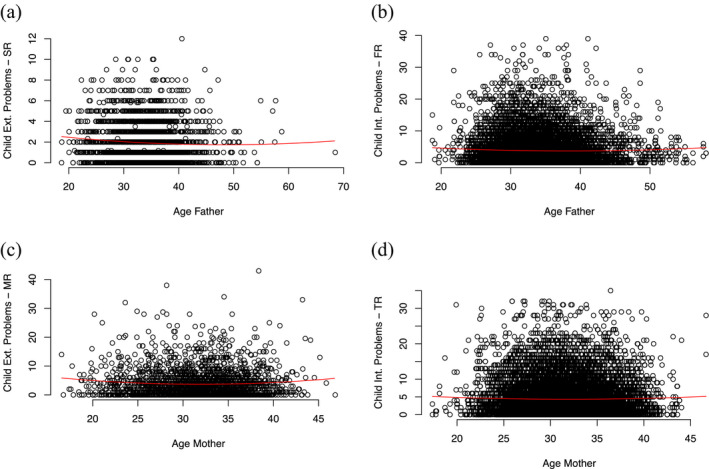
Confirmatory results for parental age in relation to problem behavior as represented in generation R (Gen‐R) and Netherlands Twin Register (NTR). (a) Gen‐R child‐reported externalizing problems in relation to paternal age. (b) NTR father‐reported internalizing problems in relation to paternal age. (c) Gen‐R mother‐reported externalizing problems in relation to maternal age. (d) NTR teacher‐reported internalizing problems in relation to maternal age. [Color figure can be viewed at wileyonlinelibrary.com]

Parental Age and Externalizing Behavior Problems

The PMPs concerning the relation between parental age and externalizing problems are presented in Table 5. The table only shows PMP scores for those cohorts that included the associated informants (see Table 3 for an overview of informants per cohort). As shown in Table 5, for parent‐reported externalizing behavior problems, Gen‐R yielded most evidence for H₁ (i.e., no relation with parental age); NTR mostly supported H₂, (i.e., the relation with parental age is linear and negative) as did TRAILS, but for mother‐reported externalizing behavior problems predicted by paternal age, NTR yielded most support for H₃ (i.e., the relation with parental age follows a negative linear trend including a positive quadratic factor). The combined results for mother‐reported externalizing behavior problems predicted by father age showed substantial support (PMP = .53 and .45, respectively) for H₂ and H₃. For father‐reported externalizing behavior problems predicted by father age and for parent‐reported externalizing behavior problems predicted by mother age, the combined results provided most support for H₂: the relation with parental age is linear and negative, in other words, higher parental age is associated with less externalizing behavioral problems. For teacher‐reported externalizing behavior problems predicted by paternal age, TRAILS and NTR combined yielded most evidence for H₁ (i.e., no relation with parental age) closely followed by H₂. When maternal age was included, most support was found for H₂: the relation with parental age is linear and negative. For child‐reported externalizing behavior problems, the results were mixed across cohorts (Gen‐R preferred H₂ or H₃, RADAR‐Y H₃ or H₁, and TRAILS H₁). After combining the results from the three cohorts, however, most support was obtained for H₁, that is, no relation with parental age.

Table 5.

Posterior Model Probabilities for Parental Age Predicting Externalizing Problems

Informant	Cohort	Age father				Age mother
		H1	H2	H3	Ha	H1	H2	H3	Ha
Child	Gen‐R	.23	.56	.16	.05	.22	.18	.49	.13
	RADAR‐Y	.28	.02	.49	.22	.43	.07	.38	.12
	TRAILS	.86	.13	.00	.01	.83	.15	.02	.01
	All	.98	.02	.00	.00	.93	.02	.04	.00
Mother	Gen‐R	.90	.07	.02	.01	.82	.04	.10	.05
	NTR	.00	.02	.74	.24	.00	.89	.09	.03
	TRAILS	.18	.74	.06	.02	.00	.88	.09	.03
	All	.00	.53	.45	.02	.00	.97	.03	.00
Father	Gen‐R	.65	.22	.10	.03	.60	.19	.17	.04
	NTR	.00	.49	.38	.13	.00	.93	.05	.02
	All	.00	.73	.25	.02	.00	.95	.05	.00
Teacher	NTR	.55	.41	.03	.01	.29	.60	.09	.02
	TRAILS	.48	.31	.16	.05	.00	.73	.21	.06
	All	.67	.32	.01	.00	.00	.96	.04	.00

Numbers in italic font represent the highest posterior model probability per cohort. Numbers in bold font represent the highest meta‐analytic results. Gen‐R = generation R; NTR = Netherlands Twin Register; RADAR‐Y = Research on Adolescent Development And Relationships—Young cohort; TRAILS = TRacking Adolescents' Individual Lives Survey.

Table 6 shows the results after inclusion of the covariates as predictors of externalizing problems. After adjusting for SES and gender, all cohorts yielded substantial evidence for H₁ with respect to child‐ and teacher‐reported externalizing problem behavior. This meant a shift especially for the child‐reported problem behavior by Gen‐R, and the teacher‐reported problem behaviors by both NTR and TRAILS. For parent‐reported problem behavior, some cohorts provided most support for H₁ (Gen‐R for all parent‐reports, and TRAILS for paternal age predicting mother‐reported problem behavior), others for H₂ (TRAILS and NTR), and NTR for H₃ in mother‐reported problem scores related to paternal age. By including covariates in the model, Gen‐R and TRAILS mainly handed in support on H₂, whereas in NTR the support for H₂ increased at the expense of support for H₃. When combining evidence for the parent reports, most support was still found for H₂, that is, there is a linear inverse relation between parental age and externalizing problem behavior.

Table 6.

Posterior Model Probabilities for Parental Age Predicting Externalizing Problems After Correction for Impact Covariates

Informant	Cohort	Age father				Age mother
		H1	H2	H3	Ha	H1	H2	H3	Ha
Child	Gen‐R	.62	.33	.04	.01	.83	.10	.05	.02
	RADAR‐Y	.36	.02	.42	.19	.53	.08	.29	.10
	TRAILS	.88	.11	.00	.01	.89	.09	.02	.01
	All	1.00	.00	.00	.00	1.00	.00	.00	.00
Mother	Gen‐R	.96	.03	.00	.00	.97	.02	.00	.01
	NTR	.00	.31	.52	.17	.00	.95	.04	.01
	TRAILS	.67	.31	.01	.01	.30	.63	.05	.02
	All	.00	.99	.01	.00	.00	1.00	.00	.00
Father	Gen‐R	.88	.10	.02	.00	.92	.06	.01	.00
	NTR	.02	.84	.11	.04	.00	.96	.03	.01
	All	.15	. 84	.02	.00	.00	.99	.01	.00
Teacher	NTR	.79	.20	.01	.00	.68	.28	.03	.01
	TRAILS	.87	.11	.02	.00	.60	.32	.07	.02
	All	.97	.03	.00	.00	.81	.18	.00	.00

Numbers in italic font represent the highest posterior model probability per cohort. Numbers in bold font represent the highest meta‐analytic result. Gen‐R = generation R; NTR = Netherlands Twin Register; RADAR‐Y = Research on Adolescent Development And Relationships—Young cohort; TRAILS = TRacking Adolescents' Individual Lives Survey.

Parental Age and Internalizing Behavior Problems

With regard to internalizing problems (the results are presented in Table 7), the cohorts generally found most evidence for H₁ for multiple informants, except for mother‐reported internalizing problems reported by maternal age in NTR. All combinations of studies rendered most support for H₁, which means that the hypothesis that there is no relation between parental age and internalizing problems was best supported by the set of studies.

Table 7.

Posterior Model Probabilities for Parental Age Predicting Internalizing Problems

Informant	Cohort	Age father				Age mother
		H1	H2	H3	Ha	H1	H2	H3	Ha
Child	Gen‐R	.91	.08	.01	.00	.86	.09	.04	.01
	RADAR‐Y	.84	.09	.05	.03	.81	.16	.02	.01
	TRAILS	.96	.04	.00	.00	.93	.06	.01	.00
	All	1.00	.00	.00	.00	1.00	.00	.00	.00
Mother	Gen‐R	.58	.25	.14	.04	.35	.25	.33	.08
	NTR	.69	.26	.04	.01	.26	.72	.01	.01
	TRAILS	.94	.05	.00	.00	.81	.17	.02	.01
	All	.99	.01	.00	.00	.71	.29	.00	.00
Father	Gen‐R	.43	.42	.11	.03	.48	.36	.13	.03
	NTR	.96	.04	.00	.00	.95	.05	.00	.00
	All	.96	.04	.00	.00	.97	.03	.00	.00
Teacher	NTR	.99	.01	.00	.00	.99	.01	.00	.00
	TRAILS	.85	.06	.07	.02	.24	.15	.49	.12
	All	1.00	.00	.00	.00	.99	.01	.00	.00

Numbers in italic font represent the highest posterior model probability per cohort. Numbers in bold font represent the highest meta‐analytic results. Gen‐R = generation R; NTR = Netherlands Twin Register; RADAR‐Y = Research on Adolescent Development And Relationships—Young cohort; TRAILS = TRacking Adolescents' Individual Lives Survey.

After including the covariates SES and gender (Table 8), all results still suggested the most support for H₁ for the impact of parental age on internalizing problem behavior, irrespective of the cohort and informant. Consequently, combining the results from the various cohorts provided overwhelming support for H₁, that is, there is no evidence for a relation between parental age and child internalizing problem behavior.

Table 8.

Posterior Model Probabilities for Parental Age Predicting Internalizing Problems After Correction for Impact Covariates

Informant	Cohort	Age father				Age mother
		H1	H2	H3	Ha	H1	H2	H3	Ha
Child	Gen‐R	.77	.21	.02	.01	.82	.09	.07	.02
	RADAR‐Y	.86	.07	.04	.03	.86	.11	.02	.01
	TRAILS	.97	.03	.00	.00	.95	.04	.00	.00
	All	1.00	.00	.00	.00	1.00	.00	.00	.00
Mother	Gen‐R	.88	.11	.01	.00	.93	.05	.01	.00
	NTR	.88	.11	.01	.00	.70	.29	.00	.00
	TRAILS	.96	.04	.00	.00	.91	.08	.01	.00
	All	1.00	.00	.00	.00	1.00	.00	.00	.00
Father	Gen‐R	.88	.09	.02	.01	.90	.08	.01	.00
	NTR	.96	.03	.00	.00	.96	.04	.00	.00
	All	1.00	.01	.00	.00	1.00	.01	.00	.00
Teacher	NTR	.99	.01	.00	.00	.99	.01	.00	.00
	TRAILS	.94	.04	.02	.01	.83	.06	.08	.03
	All	1.00	.00	.00	.00	1.00	.00	.00	.00

Numbers in italic font represent the highest posterior model probability per cohort. Numbers in bold font represent the highest meta‐analytic results. Gen‐R = generation R; NTR = Netherlands Twin Register; RADAR‐Y = Research on Adolescent Development And Relationships—Young cohort; TRAILS = TRacking Adolescents' Individual Lives Survey.

Discussion

Parental Age and Externalizing Problems

We found evidence for a negative linear relation between parental age and externalizing problems as reported by parents. That is, older parents have children with less externalizing behavior problems. There was also evidence for a negative linear relation between maternal age and externalizing problems as reported by teachers. For teachers, this finding was partly explained by SES. However, the relation between parental age and parent‐reported externalizing problems persisted after adjusting for SES, so the favorable effect of parental age is not solely due to SES.

Parental Age and Internalizing Problems

Parental age seemed unrelated to child internalizing problem behavior, especially when accounting for SES. Tentatively, older parenthood might be associated with both high and low vulnerability to develop internalizing problems. On the one hand, older parents may have a lower probability of internalizing problems because they are less likely to have a background characterized by deprivation and social instability (Robson & Pevalin, 2007), known to be related to internalizing problems such as anxiety and depression. On the other hand, internalizing problems can increase the probability of older parenthood, by hampering engagement in and consolidation of romantic relationships (Manning, Trella, Lyons, & Toit, 2010; Sandberg‐Thoma & Kam Dusch, 2014). Possibly, both processes play a role, and their joint influence results in a lack of net result.

Sociodemographic Factors as a Potential Explanation

The relatively consistent beneficial effect of advanced parenthood for childhood externalizing problems may seem unexpected, given mixed findings from earlier research on more common mental health problems (De Kluiver, Buizer‐Voskamp, Dolan, & Boomsma, 2017; McGrath et al., 2014). The beneficial effect of advanced parental age could have more than one explanation. Older and younger parents have different parenting styles. For example, there is evidence that older mothers use less frequent sanctions towards their children, are more sensitive to the child's needs and provide more structure (Trillingsgaard & Sommer, 2018). Older parents may also tend to appraise a specific problem level as less disturbing than younger parents, and older parents might be more patient and are capable of setting limits, thus feeling more equipped to handle externalizing behaviors. The positive impact of higher quality parenting by older parents is expected to be more relevant to externalizing problem behavior than to autism and schizophrenia, where a disadvantageous impact of increased parental age has been established.

Previous studies provided evidence indicating that offspring of older parents are, in several respects, more affluent than those with younger parents (e.g., Carslake et al., 2017; McGrath et al., 2014; Myrskylä & Fenelon, 2012; Orlebeke et al., 1998; Tearne et al., 2015). The finding that the negative relation of parental age and externalizing problems became weaker when SES was taken into account, indicates that the relatively high SES of older parents, or SES‐related selection effects (Robson & Pevalin, 2007) at least partly explained why their children have a decreased probability of externalizing problems. Myrskylä, Barclay and Goisis (2017) argued that there are indeed important socio‐demographic pathways associated with delayed parenthood in more recent birth cohorts. Older mothers tend to have better health behaviors during pregnancy, for example, with respect to smoking during pregnancy, which is an established risk factor for offspring externalizing problems (Dolan et al., 2016).

Furthermore, parents who have externalizing behavior problems themselves may be higher in risk taking and may have children at a younger age. Hence, externalizing behavior problems may be transmitted especially by younger parents and less by older parents. This idea is in line with the unclarity about a relation between ADHD and advanced paternal age (De Kluiver et al., 2017; McGrath et al., 2014).

From a biological point of view, advanced parenthood seems mostly disadvantageous, but socio‐demographic factors might compensate (or even more than compensate) for the biological disadvantages related to reproductive aging when it comes to mental health problems. Older mothers from more recent birth cohorts are more socioeconomically advantaged, and happier after childbearing. The observation that older parents have offspring with fewer externalizing problems, tended to disappear when SES was taken into account. This shows that demographic factors can indeed compensate for the biological disadvantages.

Earlier Versus Later Birth Cohorts

In the 1950s and 1960s the number children born to mothers over the age of 40 was larger than in 2016. For offspring born during the 1960s, Saha, Barnett, Buka, and McGrath (2009) found a negative association between maternal age and externalizing behavior problems, but in contrast to our results, they observed a positive association between maternal age and internalizing problems, and a positive association between paternal age and externalizing behavior problems. The study differed in several important aspects from the current one. All offspring were born during the 1960s, whereas in our study, all offspring were born after 1980. The age at which fathers and mothers have children has increased in the last 20 years. In the Saha et al. study average maternal and paternal ages were 24.8 and 28.4, respectively, whereas in our samples average maternal‐ and paternal ages were around 31 and 33 years. Older mothers from earlier birth cohorts tended to have low levels of education and their offspring had many older siblings (Myrskylä, Barclay & Goisis, 2017). In later birth cohorts, older mothers had higher education than younger mothers and their offspring had fewer older siblings. Thus, the family resources are spread less thinly across siblings than in earlier times. This may be the reason that our results differ from some of the findings of Saha et al. (2009). As argued by Myrskylä, Barclay and Goisis (2017), as well, being a parent during the 1960s differs from being a parent in the 1980s, and children born during the 1980s and later might benefit from positive changes in the macroenvironment.

Informant Effect

We used a multi‐informant design (i.e., mother, father, teacher, child) to investigate parental age effects on behavioral problems. Most questionnaires belonged to the same system Achenbach System of Empirically Based Assessment (ASEBA), but they do not necessarily capture the exact same construct, as different informants observe the children in different contexts. It is well‐established that correlations between different types of informants are modest at the most (Achenbach, McConaught, & Howell, 1987; Renk & Phares, 2004), and it is generally recommended to involve multiple informants to assess child and adolescent psychopathology (Jensen et al., 1999). Consistent with the notion that different informants provide partly nonoverlapping information, the results in this study depended on the choice of informant, since, as opposed to parent‐reported problems, child‐reported externalizing problems were not predicted by parental age. Conceivably, this different outcome for child‐reported problems is due to a limited ability of 10‐year‐old children to report reliably and validly on their externalizing behaviors. It is less likely that the associations with parent‐reports are caused by reporter bias because, as teacher‐reports also provided support for an association with maternal age. Thus, the choice of informant is not an arbitrary one, and may influence the associations that are found. Obviously, the parent and teacher sample sizes were also substantially larger than the sample size for child‐reports. Additionally, the largest study with child reports (i.e., TRAILS) used a shortened version of the YSR, which could cause lower reliability and validity of child‐reports.

Strengths of the Current Article

This article adopted an analysis strategy that used the data of multiple cohort studies to evaluate the same set of hypotheses. First, the data of each cohort study were divided into two parts: an exploratory part and a confirmatory part. Second, the exploratory part was used to generate a set of competing informative hypotheses. Third, the confirmatory part was used to compute the support in each cohort for the hypotheses entertained and to combine studies by means of Bayesian updating to compute overall results (Kuiper et al., 2012). This analysis strategy had a number of advantages. In the exploratory analyses data snooping or even p‐hacking is allowed, because this part of the data is only used to generate a set of competing informative hypotheses and not to evaluate these hypotheses. In contrast, the confirmatory part of each data set is only used to evaluate this set of informative hypotheses to the traditional null and alternative hypotheses, which should, especially in ages of replication crisis, publication bias and questionable research practices, increase the credibility of our results. The interested reader is referred to the Supporting Information where we highlight why exploratory analyses may lead to incorrect interpretations, even with large samples, and that cross‐validation can prevent this from happening. In addition, with traditional null hypothesis significance testing, we would not have been able to quantify the support for the null hypothesis (p‐values cannot be used to “accept” the null‐hypothesis), which appeared an important hypothesis in our study. BFs and PMPs are not used to reject or not reject the null‐hypotheses, they are used to quantify the support in each of the cohorts for the hypotheses entertained. Furthermore, combining studies using Bayesian updating enabled us to quantify the relative evidence with respect to multiple hypotheses using the data from multiple cohorts. Again, in ages of replication crisis, it is valuable to base conclusions on data from multiple cohorts that can all be used to address the same research question.

Limitations

Although the study has a number of methodological strengths, there are also limitations. First, the study focused on children's externalizing and internalizing behavior problems and did not examine other outcomes that may be positively associated with parental age, such as physical health problems and neurodevelopmental conditions. Second, children's behavior problems were only assessed during early adolescence. Thus, the study could not investigate the possibility that the direction or magnitude of the associations may vary at different points in development. For example, previous research suggesting a negative association between parental age and individuals' well‐being has focused on late adolescents and young adults (e.g., Tearne et al., 2016, Weiser et al., 2008). Third, a tiny percentage of the parents were under the age of 20 at the time of the child's birth. Although this reflects societal changes in the Netherlands, it would be important to note that some results may not replicate in other populations that have higher percentages of teenage pregnancies. This may be especially relevant when interpreting the lack of an association between parental age and children's internalizing behavior problems in this study.

Conclusion

The analytic strategy applied to large cohorts showed us a beneficial association between advanced parental age and externalizing problem behavior, whereas for internalizing problem behavior there was no beneficial association with parental age. We found no evidence for a harmful effect of advanced parenthood.

Authors Contributions

M.A.J. Zondervan‐Zwijnenburg, S.A.M. Veldkamp and H.J.A. Hoijtink designed the data analysis protocol, supervised its execution, summarized the outcomes. S.A.M. Veldkamp, M.A.J. Zondervan‐Zwijnenburg, H.J.A. Hoijtink, A.J. Oldehinkel, and D.I. Boomsma wrote the manuscript. S.A.M. Veldkamp, A. Neumann, S. Barzeva, S. Nelemans, and M.A.J. Zondervan‐Zwijnenburg contributed to the exploratory analysis design and analyzed data. A. Neumann and H. Tiemeier contributed to Gen‐R data‐collection. C.E.M. Van Beijsterveldt and D.I. Boomsma, contributed to the NTR data collection. A.J. Oldehinkel contributed to the TRAILS data collection. S. Nelemans, S. Branje, and W.H.J. Meeus contributed to the Radar‐Y data collection. All authors read, reviewed, revised, and approved the manuscript. All analysis scripts and access to the data are available on request from each cohort (Gen‐R, A. Neumann: a.neumann@erasmusmc.nl; TRAILS, S. Barzeva: s.a.barzeva@umcg.nl; RADAR‐Y, S. Nelemans: s.a.nelemans@uu.nl; NTR, S.A.M. Veldkamp: s.a.m.veldkamp@vu.nl).

Supporting information

Figure S1 . Exploratory Results for Parental Age in Relation to Problem Behavior as Represented in Generation R and Netherlands Twin Register

Figure S2 . Netherlands Twin Register Mother‐Reported Externalizing Problems in Relation to Parental Age. Exploratory Results

Figure S3 . Netherlands Twin Register Mother‐Reported Externalizing Problems in Relation to Parental Age. Confirmatory Results

Table S1 . Mean and SD for Externalizing and Internalizing Problems of Girls

Table S2 . Mean and SD for Externalizing and Internalizing Problems of Boys

Table S3 . Parental Age Predicting Externalizing Problems From Exploratory Results

Table S4 . Age Father and Covariates Predicting Externalizing Problems From Exploratory Results

Table S5 . Age Mother and Covariates Predicting Externalizing Problems From Exploratory Results

Table S6 . Exploratory Results for Parental Age Predicting Internalizing Problems

Table S7 . Age Father and Covariates Predicting Internalizing Problems From Exploratory Results

Table S8 . Age Mother and Covariates Predicting Internalizing Problems From Exploratory Results

Table S9 . Parental Age Predicting Externalizing Problems From Confirmatory Results

Table S10 . Age Father and Covariates Predicting Externalizing Problems From Confirmatory Results

Table S11 . Age Mother and Covariates Predicting Externalizing Problems From Confirmatory Results

Table S12 . Confirmatory Results for Parental Age Predicting Internalizing Problems

Table S13 . Age Father and Covariates Predicting Internalizing Problems From Confirmatory Results

Table S14 . Age Mother and Covariates Predicting Internalizing Problems From Confimatory Results