Probing the Molecular Mechanism of Rifampin Resistance Caused by the Point Mutations S456L and D441V on Mycobacterium tuberculosis RNA Polymerase through Gaussian Accelerated Molecular Dynamics Simulation

Rifampin is the first-line antituberculosis drug, with Mycobacterium tuberculosis RNA polymerase as the molecular target. Unfortunately, M. tuberculosis strains that are resistant to rifampin have been identified in clinical settings, which limits its therapeutic effects. In clinical isolates, S531L and D516V (in Escherichia coli) are two common mutated codons in the gene rpoB, corresponding to S456L and D441V in M. tuberculosis.

ABSTRACT

Rifampin is the first-line antituberculosis drug, with Mycobacterium tuberculosis RNA polymerase as the molecular target. Unfortunately, M. tuberculosis strains that are resistant to rifampin have been identified in clinical settings, which limits its therapeutic effects. In clinical isolates, S531L and D516V (in Escherichia coli) are two common mutated codons in the gene rpoB, corresponding to S456L and D441V in M. tuberculosis. However, the resistance mechanism at the molecular level is still elusive. In this work, Gaussian accelerated molecular dynamics simulations were performed to uncover the resistance mechanism of rifampin due to S456L and D441V mutations at the atomic level. The binding free energy analysis revealed that the reduction in the ability of two mutants to bind rifampin is mainly due to a decrease in electrostatic interaction, specifically, a decrease in the energy contribution of the R454 residue. R454 acts as an anchor and forms stable hydrogen bond interaction with rifampin, allowing rifampin to be stably incorporated in the center of the binding pocket. However, the disappearance of the hydrogen bond between R454 and the mutated residues increases the flexibility of the side chain of R454. The conformation of R454 changes, and the hydrogen bond interaction between it and rifampin is disrupted. As result, the rifampin molecule moves to the outside of the pocket, and the binding affinity decreases. Overall, these findings can provide useful information for understanding the drug resistance mechanism of rifampin and also can give theoretical guidance for further design of novel inhibitors to overcome the drug resistance.

INTRODUCTION

Tuberculosis has plagued humans for thousands of years and threatens human health. The WHO announced in 1993 that the tuberculosis epidemic had become a “global health emergency” (1) and launched the Global Tuberculosis Control Program in 2006. However, with the increasing cases of HIV-associated tuberculosis (2) and multidrug-resistant tuberculosis (MDR-TB) (3), progress in the prevention and treatment of tuberculosis has been substantially undermined. To date, tuberculosis remains the leading cause of death among infectious diseases and kills an estimated 1.4 million people each year (4).

Rifampin is the cornerstone of the combination of four drugs (rifampin, isoniazid, pyrazinamide, and ethambutol) used for the treatment of tuberculosis (5). Rifampin, which targets Mycobacterium tuberculosis RNA polymerase (RNAP), inhibits the transcription process of M. tuberculosis and prevents the synthesis of bacterial RNA and protein (6). M. tuberculosis RNAP is composed of five subunits (α₂ββ′δ). The β subunit, encoded by rpoB, is the rifampin-binding domain. However, with the long-term use of rifampin, the inhibitory effect of rifampin is impaired by mutation of rpoB. Studies have shown that most rifampin-resistant strains have mutations in the 81-bp core region of rpoB, which is defined as the rifampin resistance-determining region (RRDR) (7). In clinical isolates, S456L and D441V are two common mutations in the RRDR, accounting for more than 50% in the rifampin-resistant isolates (8, 9). Here, S456L and D441V are numbered in the M. tuberculosis system and correspond to S531L and D516V in the Escherichia coli numbering system, respectively. In addition, two mutants were demonstrated to exhibit high-level rifampin resistance (10).

Currently, the emergence and spread of rifampin-resistant tuberculosis (RR-TB) as well as MDR-TB are still a serious threat to public health (4). However, the resistance mechanism of rifampin is still unclear at the atomic level. Specific resistance mechanisms will provide theoretical guidance for the design of new antituberculosis drugs. Unfortunately, traditional experimental methods cannot uncover the atomic-level drug resistance mechanism. Previously studies (11–13) have shown that molecular dynamics (MD) simulation is a robust computational technique to shed light on the mechanism of drug resistance caused by point mutations in drug targets.

Despite the remarkable advances in computer technology, the sampling is still a key factor to influence if MD simulations can reveal the real structural transition process (14). A Gaussian accelerated molecular dynamics (GaMD) (15) approach can reduce the energy barriers by adding a boost potential [$\Delta V\text{(}\overrightarrow{r}\text{)}$] to smooth the potential energy surface and thus accelerate conformation transitions between the different low-energy states (16), which could capture the events that are not available in the conventional experimental methods. Unlike other enhanced sampling methods, such as metadynamics (17) and adaptive biasing force (ABF) (18), GaMD does not require predefined collective variables (CVs). In addition, the added boost potential follows Gaussian distribution, which allows the reweighting of simulations through cumulant expansion to the second order (15) to obtain the original free-energy landscape profiles. This “unconstrained” enhanced sampling approach has been successfully used to analyze protein folding (19), protein-ligand binding (20), and membrane proteins (21, 22) as well as large biomolecules (23, 24).

In this study, 1-μs GaMD simulations following 100-ns conventional molecular dynamics simulations were performed on the wild type and two mutants with the mutations mentioned above to decipher the molecular mechanism of rifampin resistance. Based on the obtained trajectories, the binding free energy between rifampin and M. tuberculosis RNAP for each system was determined based on the molecular mechanics–generalized Born surface area (MM-GBSA) method. Then, detailed binding mode analysis and dynamic network analysis were performed to uncover the drug resistance mechanism from the perspective of structure. Overall, the present study characterizes the mechanism of rifampin resistance caused by two point mutations, S456 and D441, at the atomic level, which will be valuable for future design of new drugs against MDR-TB and RR-TB.

RESULTS

The decrease in the energy contribution of R454 residue is an important reason for the weakened binding affinity of rifampin.

First, the convergences of MD simulations were assessed according to the root mean square deviations (RMSDs) of the binding pocket (Fig. 1) (residues within 5 Å around the ligand) and the heavy atoms of rifampin relative to the initial structure. As shown in Fig. 2, the fluctuations of all simulations were relatively stable and reached equilibrium at ∼600 ns. Figure 2a shows that the value of RMSDs of the residues in the binding pocket are similar for wild-type (WT) and D441V systems (∼1 Å), while the value for the S456L system (∼1.5 Å) is slightly higher. From the RMSD of WT M. tuberculosis RNAP, it can be seen that the separated β subunit structure is relatively stable during the simulation process and the fluctuation is very small, further indicating that it is reasonable to extract only the β subunit as the initial structure for the MD simulation. Additionally, the RMSDs of ligand indicate that the fluctuation of rifampin tends to be stable after ∼250 ns for all systems (Fig. 2b).

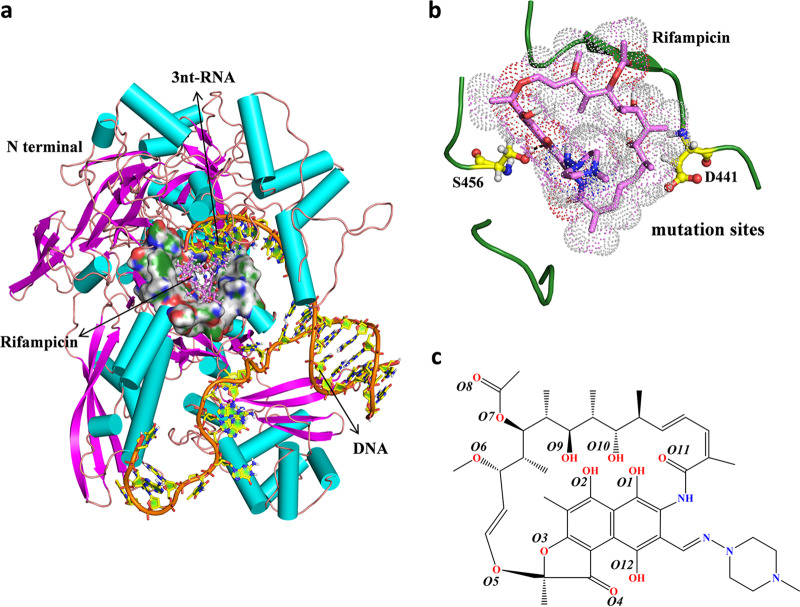
FIG 1.

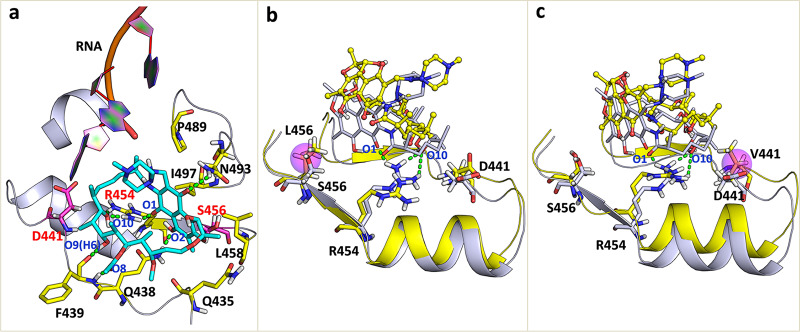
(a) Overall structure of the M. tuberculosis RNAP complex with rifampin and DNA/RNA. The protein and DNA/RNA are shown as cartoons, and the binding pocket is shown as a surface representation. Rifampin is shown as pink sticks. (b) The mutated residues analyzed in this study are labeled. S456 and D441 are shown as yellow sticks. (c) Chemical structure of rifampin.

FIG 2.

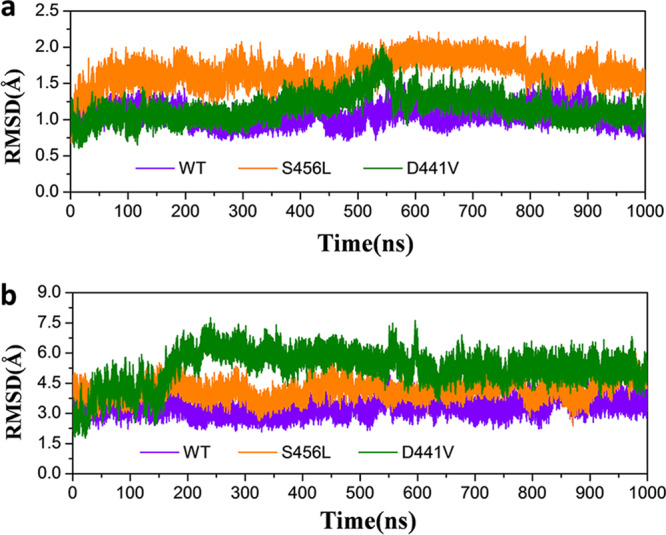
(a) Evolution over time of the RMSD values of the active pocket residues within 5 Å of rifampin in the three systems studied. (b) Evolution over time of the RMSD values of the heavy atoms of rifampin in the three systems studied.

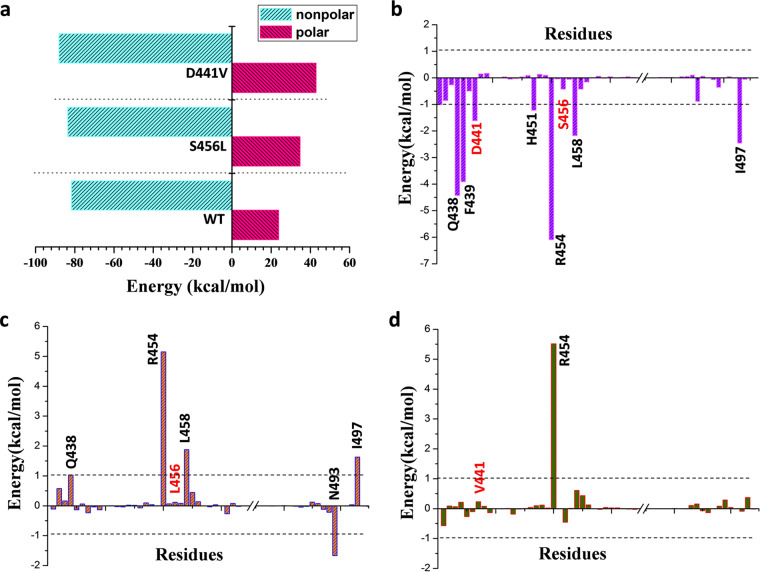
For each system, we extracted 1,000, 2,000, and 4,000 snapshots from last 200-ns trajectory to obtain the average binding free energy. The binding free energies of S456L (−48.96 kcal/mol) and D441V (−45.18 kcal/mol) mutants decreased noticeably compared to that of the WT (−57.97 kcal/mol) (Table 1), which is consistent with the previous experimental data (MIC). The histogram in Fig. 3a reflects the polar and nonpolar energy contribution changes in wild-type M. tuberculosis RNAP and the two mutants. It can be seen that the contribution of polar energy is unfavorable to the binding of rifampin, especially in the S456L and D441V mutants. The calculated electrostatic interaction contributions in gas (ΔE_ele) of WT, S456L, and D441V are, respectively, −71.68 kcal/mol, −54.84 kcal/mol, and −42.88 kcal/mol (Table 1), indicating that the contribution of electrostatic interaction in mutants decreased markedly compared with that in wild-type M. tuberculosis RNAP, which is the main reason for the decrease in polar energy contribution. In contrast, in the mutants, the contribution of nonpolar energy is slightly greater, mainly because of the increase of van der Waals (ΔE_vdw) energy (Table 1). In summary, the contribution of electrostatic interaction undergoes the most obvious change, suggesting that two mutations disrupted the direct electrostatic interaction between rifampin and M. tuberculosis RNAP.

TABLE 1.

Calculated average binding free energy based on 1,000, 2,000, and 4,000 snapshots from the last 200-ns trajectory and contributions of different energy terms

Contribution	Mean value (kcal/mol) ± SD for:
	WT	S456L	D441V
ΔEele	−71.68 ± 0.18	−54.84 ± 0.23	−42.88 ± 0.15
ΔEvdw	−73.26 ± 0.09	−74.86 ± 0.11	−78.88 ± 0.10
ΔEMMa	−144.94 ± 0.18	−129.69 ± 0.27	−121.76 ± 0.16
ΔGSA	−8.48 ± 0.01	−8.82 ± 0.01	−9.22 ± 0.01
ΔGGB	95.45 ± 0.13	89.55 ± 0.16	85.80 ± 0.14
ΔGsol	86.97 ± 0.13	80.74 ± 0.16	76.58 ± 0.13
ΔGpolarb	23.76 ± 0.11	34.71 ± 0.14	42.92 ± 0.10
ΔGnonpolarc	−81.74 ± 0.05	−83.68 ± 0.04	−88.10 ± 0.05
ΔHbind	−57.97 ± 0.11	−48.96 ± 0.15	−45.18 ± 0.10
MIC (mg/liter)d	0.25–0.5	>8.0	>8.0

^aΔE_MM = ΔE_ele + ΔE_vdw.

^bΔG_polar = ΔE_ele + ΔG_GB.

^cΔG_nonpolar = ΔE_vdw + ΔG_SA.

^dIn vitro activity of rifampin against wild-type and rifampin-resistant Mycobacterium tuberculosis.

FIG 3.

(a) Energy contributions of total nonpolar and total polar interactions of WT M. tuberculosis RNAP and the studied mutants. (b) Spectrum of energy contributions of key residues to the binding of rifampin in WT M. tuberculosis RNAP. (c and d) The difference in per-residue energy contribution (ΔG_mut − ΔG_wt) for the S456L (c) and D441V (d) mutant M. tuberculosis RNAPs relative to the wild type.

The decomposition of binding free energy was further used to characterize the key residues for rifampin binding in the WT system. As shown in Fig. 3b, the residues Q438, F439, D441, H451, R454, L458, and I497 have a free energy contribution of more than 1 kcal/mol. In order to find out which key residues’ energy contributions were affected by the mutations, the profiles of the difference in the per-residue energy contribution (ΔG_mut – ΔG_wt) between the mutants and WT were plotted in Fig. 3c and d. For the S456L mutant, the energy contribution of residues Q438, R454, L458, and I497 decreased noticeably (Fig. 3c), especially that of R454, which was most obviously reduced. For the D441V mutant, only the energy contribution of the R454 residue decreased significantly (Fig. 3d). Interestingly, the energy contributions of the two mutated residues did not change significantly. In summary, R454 is the key residue for rifampin binding, and the reduction of its energy contribution is also a key factor for the decrease of rifampin binding affinity in mutation systems.

Comparison of detailed binding mode reveals the relationship between the structural and energetic change.

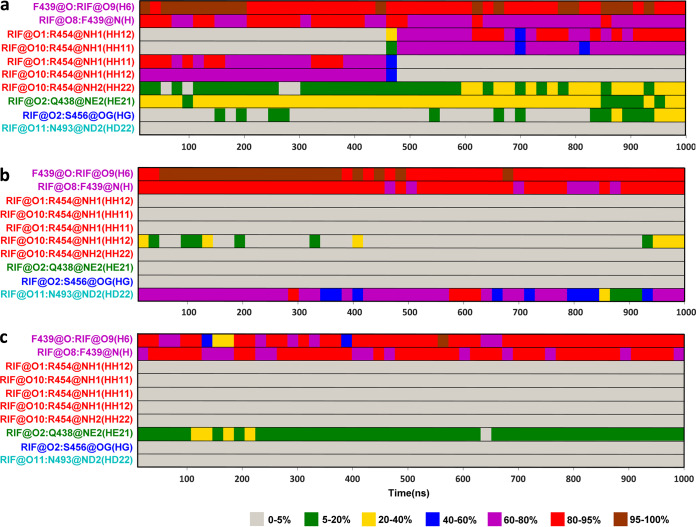
It is well known that hydrogen bond interactions play a key role in the binding of ligand receptors. Therefore, the dynamic changes in hydrogen bonds formed between rifampin and M. tuberculosis RNAP during the simulations were detected and plotted in Fig. 4 and also in Fig. S1 in the supplemental material. Figure 4 shows the hydrogen bond occupancy formed between rifampin and M. tuberculosis RNAP during the simulations. The hydrogen bonds are thought to be formed when the distance between two related heavy atoms is less than 3.5 Å and the angle between the acceptor, hydrogen, and donor atoms is larger than 120°. In the process of calculating the hydrogen bond occupancy, all frames in the entire trajectory were divided into 50 parts on average—that is, each part corresponds to 20 ns—and then the occupancy probability of a hydrogen bond in each part was calculated. Figure S1 displays the corresponding distances between two heavy atoms forming a hydrogen bond versus simulation time. It can be seen that the changes in the atomic distances during the simulation are consistent with the results of hydrogen bond occupancy calculations. In the wild-type system (Fig. 4a), it can be seen that the F439 residue’s backbone O atom as a hydrogen bond acceptor formed the hydrogen bond with the H-6 atom of rifampin, while its backbone N atom acted as a donor to form the stable hydrogen bond with the O-8 atom of rifampin. Moreover, the side chain of the R454 residue formed the hydrogen bonds with the O-1 and O-10 atoms of rifampin. The conformation of R454 rearranged at about 480 ns, where the position of side chain changed to form more stable hydrogen bonds with rifampin. The occupancy of these hydrogen bonds is more than 60% during MD simulation, which is the key interaction for rifampin binding. In addition, the H atom of the amino group on the side chain of Q438 as a donor could form the hydrogen bond with the O-2 atom of rifampin, and this hydrogen bond occupancy rate is 20% to 40%. The S456 residue also could form a partial hydrogen bond with rifampin in the last 150 ns. In any case, the formation of these hydrogen bonds indicated that the residues Q438, F439, and R454 made a large energy contribution to the binding of rifampin (Fig. 3b). However, in the S456L mutant, the formation of hydrogen bonds between rifampin and the residues R454, Q438, and S456 disappeared completely (Fig. 4b). In the D441V mutant, the hydrogen bonds formed between rifampin and R454, and S456 residues also disappeared completely, while the Q438 residue’s hydrogen bond occupancy exhibited a small decrease (Fig. 4c). The destruction of these hydrogen bonds reduced the corresponding residues’ energy contribution, especially that of the R454 residue (Fig. 3c and d).

FIG 4.

Hydrogen bond occupancy formed between rifampin and M. tuberculosis RNAP during MD simulations. (a) WT; (b) S456L; (c) D441V.

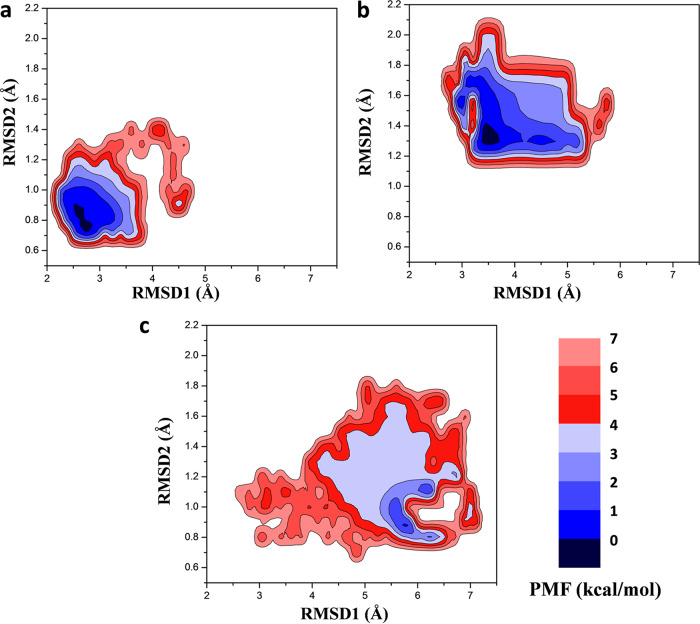
To uncover the relationship between the energetic change and conformational change for the residues in the binding pocket, we used the structure located at the lowest energy state in free energy landscape as the representative conformation to show the specific binding mode of rifampin for different systems. First, the free-energy profiles were recovered based on the trajectory of 900-ns production MD simulations. The boost potential $\Delta V\text{(}\overrightarrow{r}\text{)}$ applied in GaMD simulations of all three systems followed Gaussian distribution (see Fig. S2). Three two-dimensional (2D) potential of mean force (PMF) profiles (Fig. 5) were calculated using the RMSD of the heavy atoms of the ligand and the RMSD of the active pocket residues within 5 Å of rifampin. The PMF profiles obtained indicated that the conformational states of the WT and mutant systems underwent dynamic changes during 0- to 900-ns GaMD simulations and finally stabilized in one state. Compared to the WT system, the mutant systems tended to have larger conformational distributions.

FIG 5.

2D potential of mean force (PMF) profiles constructed based on the RMSDs of the heavy atoms of ligand and the active pocket residues within 5 Å of rifampin in WT (a), S456L (b), and D441V (c) systems.

The detailed binding modes of rifampin with M. tuberculosis RNAP are pictured in Fig. 6a (WT) and Fig. S3 (S456L and D441V). Figure 6a shows the hydrogen bond interaction between rifampin and Q438, F439, and R454 described above. In addition, the hydrophobic pocket formed by L458 and I497 residues just accommodated the naphthalene ring of rifampin and produced a hydrophobic interaction with rifampin. Therefore, L458 and I497 residues also have a large energy contribution for the binding of rifampin. Furthermore, H451 and D441 residues were close to the rifampin and could provide a van der Waals energy contribution (Fig. 3b). In order to obtain a more intuitive observation of the conformational changes of rifampin and the binding pocket, we superposed the representative conformation of the S456L and D441V mutants with WT M. tuberculosis RNAP (Fig. 6b and c, respectively). From the superposition of the binding pocket, it can be seen that the conformation of rifampin undergoes a clear change in the mutants, especially in the S456L mutant. As shown in Fig. 6b and Fig. S3, the naphthalene ring of rifampin turned to the outside of the binding pocket in the S456L mutant, which caused the naphthalene ring to leave the hydrophobic pocket formed by L458 and I497. The increase in the distance between rifampin and the I497 and L458 residues led to a decrease in the hydrophobic contribution of the I497 and L458 residues (Fig. 3b). Additionally, the hydrogen bond between O2 and Q438 was also impaired due to the flipping of naphthalene ring. However, this flipping enhanced the interaction of rifampin with the N493 residue by forming a hydrogen bond between the amino hydrogen of N493 and O11 on the naphthalene ring (Fig. 4b). Therefore, the energy contribution of N493 increased compared to that of the WT (Fig. 3b). In addition, it can be seen that the position of the side chain of R454 had a slight movement (Fig. 6b), and the proper angle and distance of hydrogen bond formation were destroyed. For the D441V mutant, the position of rifampin changed slightly, which allowed rifampin to remain incorporated in the pocket in a manner similar to that of the wild type (Fig. 6c and Fig. S3). Therefore, the energy contributions of key residues did not change much, except for that of R454. Similar to that in the S456L mutant, the conformation of the R454 residue also changed.

FIG 6.

(a) Detailed binding mode of rifampin with WT M. tuberculosis RNAP. (b and c) Superposed structures of S456L and D441V mutants (yellow cartoons) relative to the WT M. tuberculosis RNAP (white cartoon). The mutated residue (L456 or V441) is highlighted by a magenta circle. Rifampin is displayed by different representations in the mutants (sphere-stick model) and the wild type (stick model) to show its displacements more clearly. The green dashed lines represent the hydrogen bond interactions formed between rifampin and M. tuberculosis RNAP.

Dynamic network analysis uncovers the reason for the conformational change of the R454 residue.

Energetic analysis revealed that the key role of the R454 residue is in the binding of rifampin. The energy contribution of R454 is the highest (−6.10 kcal/mol) in the WT system, while it was reduced by approximately 5.3 kcal/mol in two mutant systems (Fig. 3). From the above analysis results, it can be determined that the main reason for the decrease is the movement of the side chains of R454 residues in the mutants, further destroying the hydrogen bond between R454 and rifampin. The dynamic changes of the interaction between rifampin and R454 during the simulations are shown in the movies in the supplemental material.

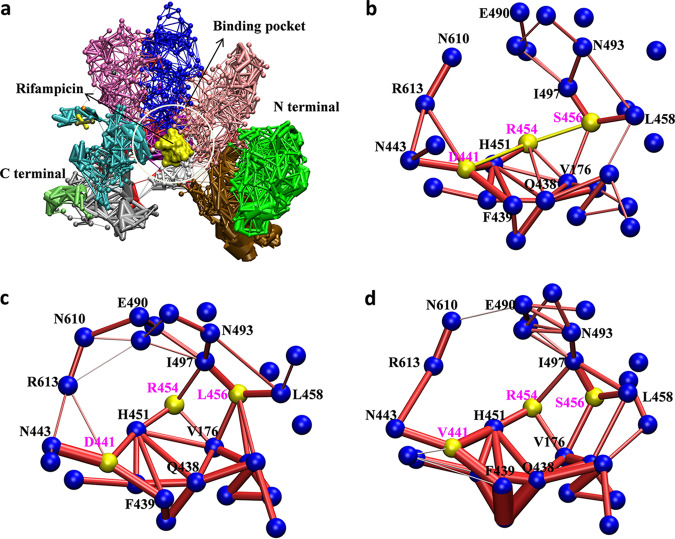
Why does the position of the side chain of the R454 residue change in the mutants? To further understand the reason, dynamic interaction network analysis for each system was performed. Here, 10,000 snapshots were extracted from the last 200-ns trajectory for each system to carry out the dynamic network analysis. As shown in Fig. 7, one node represents a residue and the edge between two nodes represents the total interaction between two residues. In WT system, the R454 residue is located in the center of the binding pocket, interacting with five surrounding residues, including S456, D441, H451, Q438, and V176. There is a salt bridge interaction between the positively charged amino group on the R454 side chain and negatively charged carboxyl group on the D441 side chain (Fig. 7b). However, the interaction network was different in the mutants. According to Fig. 7c and d, there were similar changes in the S456L and D441V mutants. First, the number of residues that interact with R454 was lower in the mutants. Mutation at two sites both impaired the interaction between R454 and residues S456, D441, and Q438, which increased the flexibility of the R454 residue’s side chain. In addition, the new interaction formed between R454 and I497 stabilized R454 in a new conformation that prevented the hydrogen bond interactions between it and rifampin, thereby changing the position of rifampin.

FIG 7.

Dynamic network analysis for WT and mutant systems. (a) Overview of the residue interaction network of M. tuberculosis RNAP. Rifampin is shown as a surface representation in yellow. The differently colored domains represent different network communities. (b to d) Interaction network diagram for the residues around the binding pocket of rifampin. The blue nodes represent the C_α atoms of residues, and the red bars between nodes represent their interactions. The thickness of the bar indicates the strength of the interaction. The nodes and bars for residues S456, R454, and D441 are in yellow. (b) WT; (c) S456L; (d) D441V.

DISCUSSION

In this work, GaMD simulation was used to reveal the resistance mechanism of rifampin due to the point mutations S456L and D441V encoded in the rpoB gene. The results show that the energy contribution differences of two mutated residues in the wild type and mutants are subtle. Therefore, these two mutations do not directly affect the binding ability of rifampin, but they indirectly affect the interaction of other residues, such as R454, with rifampin. In the wild-type system, R454 anchored rifampin to the binding pocket by forming a stable hydrogen bond with rifampin. However, when the mutation S456L or D441V occurred, the original polar residues (Ser and Asp) were replaced by nonpolar residues (Leu and Val), disrupting the key salt bridge and hydrogen bond interactions of R454 with the original polar residues. As a result, the conformation of R454 was rearranged, destroying the formation of the hydrogen bond between it and rifampin. Then, the weakened interaction between rifampin and R454 caused rifampin to move to the outside of the pocket, and the interaction between M. tuberculosis RNAP and rifampin was reduced.

Based on the resistance mechanism detected here, it appears that the hydrogen bonds especially relevant to the R454 residue are very important in the binding of rifampin. The formation of hydrogen bonds between R454 and rifampin is significantly affected by the S456L or D441V mutation, which is also the main reason for the reduced affinity of rifampin for the target. Therefore, to enhance the binding affinity between the molecule and target, it is important to design the molecule to reconstruct the hydrogen bonding interaction between it and the R454 residue. For example, the distance between the O-1 or O-10 atom and the side chain of R454 can be reduced by extending the length of the side chain where O-1 and O-10 are located, so that the hydrogen bonding interaction can be formed again and the molecule may be stably anchored again in the center of the binding pocket.

In summary, we explored the resistance mechanism of rifampin at the molecular level, which could not be done in traditional experiments. Therefore, it is meaningful to investigate the mechanism of molecular resistance through theoretical calculations. Gaussian accelerated simulation can enhance the sampling process of macromolecules, which can reveal the conformational transformation process more realistically. From the calculation of binding free energy, we learn that the reduced binding affinity for the mutants studied here is mainly due to the loss of the direct electrostatic interaction contributions. The decomposition of binding free energy characterizes some key residues for rifampin binding, such as Q438, F439, R454, I497, and others. For the two mutants studied here, the energy contribution of R454 decreased most obviously. The dynamic network analysis shows that the mutation of these two residues destroyed their interactions with R454 and changed the conformation of R454, leading to the disappearance of the hydrogen bond between rifampin and R454. As a result, the binding position of rifampin changed greatly in the two mutants. Therefore, the binding affinity of M. tuberculosis RNAP for rifampin was reduced in the two mutants and resulted in the emergence of drug resistance. Here, we determined the detailed change in binding mode due to S456L or D441V mutation. The resistance mechanism revealed here provides a theoretical basis for the resistance of rifampin and can inform the design of new inhibitors to overcome drug resistance of M. tuberculosis.

MATERIALS AND METHODS

System preparation.

The wild-type structure of M. tuberculosis RNAP with rifampin was obtained from the Protein Data Bank (PDB ID 5UHC) (25). The whole enzyme system (∼3,826 residues) is composed of five subunits (α₂ββ′δ). Through careful analysis of the full crystal structure, we found that each subunit is relatively independent in structure, and the connection between them is loose. Furthermore, the aim of this study was to explore the effect of mutations in the binding pocket (lying on the β subunit) on rifampin binding affinity. Thus, other subunits should have small effects on rifampin binding. Considering the feasibility of the simulation, here, only the β subunit was extracted and used. In addition, there were also studies that extracted only the structural parts of functional regions for molecular dynamics simulation studies (26). The 3D structures of S456L and D441V M. tuberculosis RNAP mutants were modeled using the PyMOL program by replacing specific residues in the wild-type M. tuberculosis RNAP (WT). The overall structure is shown in Fig. 1a. The mode of binding of rifampin to M. tuberculosis RNAP is depicted in Fig. 1b. Rifampin is a macrocyclic amide molecule, as shown in Fig. 1c. The macrocycle of rifampin has a naphthalene ring attached to a stereo fatty acid chain to further form a bridged ring. In addition, the N-methyl piperazine ring is linked to the naphthalene ring.

Conventional molecular dynamics simulations.

Three complexes of rifampin with WT M. tuberculosis RNAP and two mutants, S456L and D441V, were used as the initial structures for the conventional molecular dynamics (cMD) simulations. First, the LEaP module in Amber18 (27) was employed to add the hydrogen atoms of protein. Gaussian 09 (28) was used for the electrostatic potential calculation and optimization of the ligand at the Hartree-Fock 6-31G* level. The partial charges were calculated with the restrained electrostatic potential (RESP) (29–31). In addition, the proteins and nucleic acids were parameterized using the ff14SB force field (32). The ligand was parameterized using the GAFF force field (33). Then, the complexes were immersed in the explicit TIP3P (transferable intermolecular potential with 3 points) (34) water box, which extends 10 Å from the solute surface, and the periodic boundary conditions (PBC) were applied to avoid edge effects. Finally, the counterions (Na⁺) were added to neutralize the system. Detailed information about the simulation is provided in Table S1.

All simulations were performed in Amber18. First, energy minimization was performed for each system to eliminate atomic collisions. Afterwards, each system was heated gradually from 0 to 310 K under the NVT ensemble. Four equilibration steps were performed to adjust the density of water with the solutes restrained. The particle mesh Ewald (PME) system (35) was employed to treat the long-range electrostatic interactions, and the SHAKE (36) algorithm was employed to constrain all bonds involving hydrogen atoms. Finally, 50-ns unconstrained cMD simulations were performed for each system under the NPT ensemble.

Gaussian accelerated molecular dynamics simulation.

Gaussian accelerated molecular dynamics (GaMD) simulation enhances the conformational sampling of biomolecules by adding a harmonic boost potential to smooth the potential energy surface of the systems (15). When the system potential [V($\overrightarrow{r}$)] is lower than a defined threshold energy (E), a boost potential [$\Delta V\text{(}\overrightarrow{r}\text{)}$] is added as

$$\Delta V\text{(}\overrightarrow{r}\text{) =}\frac{\text{1}}{\text{2}}\text{κ}{\left[E-V\text{(}\overrightarrow{r}\text{)}\right]}^2,V\text{(}\overrightarrow{r}\text{) <}E$$

where κ is the harmonic force constant. Therefore, the modified system potential [$\Delta V*\text{(}\overrightarrow{r}\text{)}$] is given by

$$\Delta V*\text{(}\overrightarrow{r}\text{) =}V\text{(}\overrightarrow{r}\text{) +}\frac{\text{1}}{\text{2}}\text{κ}{\left[E-V\text{(}\overrightarrow{r}\text{)}\right]}^2,V\text{(}\overrightarrow{r}\text{) <}E$$

Otherwise, when the system potential is above the threshold energy, the boost potential is set to zero and the modified system potential is

$$V*\text{(}\overrightarrow{r}\text{) =}V\text{(}\overrightarrow{r}\text{),\hspace{1em}}V\text{(}\overrightarrow{r}\text{)}>E$$

In this work, the final structures of cMD were used as the initial structures for GaMD simulations. During GaMD simulations, 50-ns cMD simulations with no boost potential were first performed to collect the statistics, including the maximum, minimum, average, and standard deviation values (V_max, V_min, V_av, and σ_V) of the system potential, which is used for the calculation of the acceleration parameters in GaMD. After that, 100-ns GaMD equilibration simulations were performed to update the acceleration parameters. Finally, 900-ns dual-boost GaMD production simulations were performed for each system. The system threshold energy (E) was set as V_max. The atomic coordinate trajectory was saved every 5 ps.

MM-GBSA calculation.

As an important indicator for judging the binding affinity of ligands and receptors, the MM-GBSA method (37, 38) has been widely used to calculate the binding free energy of ligands and receptors. In this work, we extracted multiple snapshots from an equilibrated MD trajectory. For each snapshot, the free energy is calculated for each molecular species (complex, protein, and ligand). The binding free energy is computed as the difference:

$$\Delta G_{\text{bind}}\text{=}{G}_{\text{complex}}-G_{\text{receptor}}-G_{\text{ligand}}$$

Each of them can be estimated by the following equations:

$$G\text{=}{E}_{\text{gas}}+G{}_{\text{sol}}\hspace{0.17em}-\mathit{TS}$$

E_gas is the gas phase energy and includes the bond, angle, and torsion as well as the Coulomb and van der Waals energies. In the MM-GBSA method, the solvation free energy (G_sol) is calculated as follows:

$$G{}_{\text{sol}}=G{}_{\text{GB}}+G{}_{\text{SA}}$$

$$G_{\text{SA}}\text{= γ * SASA + β}$$

where G_GB was calculated by solving the GB equation. The dielectric constants for solute as well as solvent were set to 1.0 and 80.0, respectively (39). G_SA was estimated by the solvent-accessible surface area (SASA) determined using a water probe radius of 1.4 Å. The surface tension constant γ was set to 0.0072 kcal/(mol·Å²), and β was set to 0 kcal/mol (40). T and S are the temperature and the total solute entropy, respectively. The entropy contributions can be estimated by normal mode analysis. However, here, we did not calculate the entropy contributions, since our aim was not to obtain the absolute Gibbs energy. In addition, previous studies (26, 41) proved that it is sufficient to compare the binding abilities of receptors and ligands without the calculation of entropy.

Calculation of potential of mean force.

First, we examined the boost potential distributions for all GaMD simulations. Then, the PyReweighting tool kit (42) was used to reweight the GaMD simulations for calculating the potential of mean force (PMF) profiles based on the product GaMD simulations. Here, two-dimensional PMF profiles were constructed using the root mean square deviations (RMSDs) of the heavy atoms of the ligand and the residues of the binding pocket. Last, the original free energy landscape was recovered by cumulant expansion to the second-order method. The PMF was generated as follows:

$$\mathrm{\Delta }G(\text{rmsd}1,\text{rmsd}2)=-{\kappa }_{B}T\ln \hspace{0.17em}\rho (\text{rmsd}1,\text{rmsd}2)$$

where T and κ_B represent the temperature of MD simulations and the Boltzmann constant, respectively. rmsd1 and rmsd2 represent the RMSDs of the ligand and the residues of the binding pocket, respectively. ρ(rmsd1, rmsd2) is the normalized joint probability. The cutoff value was set at 10 for reweighting of GaMD simulations on each system.

Dynamic network analysis.

The analysis of the conformation transition for the residues within the binding pocket is pivotal for the interpretation of the resistance mechanism. For this purpose, we used the dynamic network analysis method to resolve the discrepancy of binding pocket between the wild type and the mutants. Here, the center of the residues’ C_α atom was treated as a node. The edge distance (d_ij) between two nodes was defined as follows:

$$d_{\mathit{ij}}\text{=}-\text{log(|}{C}_{\mathit{ij}}\text{|)}$$

where C_ij represents the pairwise correlations calculated by the Carma program (43). Finally, the residue interaction networks were constructed in the VMD program (44).