Predicting Clinical Effects of CYP3A4 Modulators on Abemaciclib and Active Metabolites Exposure Using Physiologically Based Pharmacokinetic Modeling

Abstract

Abemaciclib, a selective inhibitor of cyclin‐dependent kinases 4 and 6, is metabolized mainly by cytochrome P450 (CYP)3A4. Clinical studies were performed to assess the impact of strong inhibitor (clarithromycin) and inducer (rifampin) on the exposure of abemaciclib and active metabolites. A physiologically based pharmacokinetic (PBPK) model incorporating the metabolites was developed to predict the effect of other strong and moderate CYP3A4 inhibitors and inducers. Clarithromycin increased the area under the plasma concentration‐time curve (AUC) of abemaciclib and potency‐adjusted unbound active species 3.4‐fold and 2.5‐fold, respectively. Rifampin decreased corresponding exposures 95% and 77%, respectively. These changes influenced the fraction metabolized via CYP3A4 in the model. An absolute bioavailability study informed the hepatic and gastric availability. In vitro data and a human radiolabel study determined the fraction and rate of formation of the active metabolites as well as absorption‐related parameters. The predicted AUC ratios of potency‐adjusted unbound active species with rifampin and clarithromycin were within 0.7‐ and 1.25‐fold of those observed. The PBPK model predicted 3.78‐ and 7.15‐fold increases in the AUC of the potency‐adjusted unbound active species with strong CYP3A4 inhibitors itraconazole and ketoconazole, respectively; and 1.62‐ and 2.37‐fold increases with the concomitant use of moderate CYP3A4 inhibitors verapamil and diltiazem, respectively. The model predicted modafinil, bosentan, and efavirenz would decrease the AUC of the potency‐adjusted unbound active species by 29%, 42%, and 52%, respectively. The current PBPK model, which considers changes in unbound potency‐adjusted active species, can be used to inform dosing recommendations when abemaciclib is coadministered with CYP3A4 perpetrators.

Abemaciclib is an oral cyclin‐dependent kinase (CDK) 4 and 6 inhibitor approved for the treatment of hormone receptor–positive, human epidermal growth factor 2–negative advanced or metastatic breast cancer.1, 2, 3 The pharmacokinetics of abemaciclib has been characterized in patients and in healthy subjects, with no significant differences between groups.4 Following oral administration, abemaciclib is almost completely absorbed with a time of observed maximum plasma concentration of about 6 to 8 hours.1, 5 Abemaciclib is highly bound to plasma proteins, with a fraction unbound in plasma (fu) of 0.0557. Abemaciclib is extensively distributed to tissues, with a systemic volume of distribution at steady state (Vd_ss) estimated to be 724 L in the absolute bioavailability study. The mean half‐life and systemic clearance (CL) of abemaciclib are 29.3 hours and 24 L/h, respectively.6 Following oral administration of a 200‐mg dose, the oral bioavailability of abemaciclib is 45%.6

In vitro and human disposition studies have demonstrated that abemaciclib is extensively metabolized via cytochrome P450 (CYP)3A4, but not CYP3A5, in liver to multiple active metabolites.5 These oxidative metabolites are present in significant concentrations in plasma and accounted for approximately 45% of total plasma radioactivity in the human mass balance study.5 Metabolites M2 and M20 are formed from abemaciclib by CYP3A4, and metabolite M18 can be formed by CYP3A4 from either M2 or M20.5 The active metabolites are either eliminated unchanged in bile or further metabolized by CYP3A4 or via sulfate conjugation and eliminated via biliary excretion.5 Clinical drug interaction studies with the CYP3A4 inhibitor clarithromycin and inducer rifampin demonstrated the extensive involvement of CYP3A4 metabolism of abemaciclib.5 Because the patient population for abemaciclib may include individuals taking other medications that can be inhibitors or inducers of CYP3A4, the primary objective of this study was to predict the pharmacokinetics (PK) of a single dose of abemaciclib and its active metabolites (M2, M18, and M20) in the presence of known moderate and strong CYP3A4 inhibitors and inducers using physiologically based pharmacokinetic (PBPK) modeling.

Methods

Clinical Studies With Abemaciclib

All clinical studies used for modeling were approved by the respective institutional review boards or independent ethics committees, and all subjects who participated in the studies provided written informed consent. The studies were conducted in accordance with the principles of the Declaration of Helsinki and consistent with good clinical practices. A description of the clinical studies can be found in the supplemental information.

Simulation Strategy

A scheme of the overall simulation strategy is shown in Figure 1A. Briefly, multiple models were developed and/or verified including models for abemaciclib and its 3 active metabolites, and the CYP3A4 inducers (efavirenz, modafinil, bosentan, and rifampicin) and inhibitors (ketoconazole, itraconazole, clarithromycin, diltiazem, and verapamil). The abemaciclib and metabolites models were built using both physicochemical and biological in vitro data as well as data from the absolute bioavailability study and the human radiolabel disposition study. The fractions formed and metabolized via CYP3A4 for abemaciclib and metabolites models were furthered optimized using the results from the rifampicin and clarithromycin interaction studies.

Figure 1.

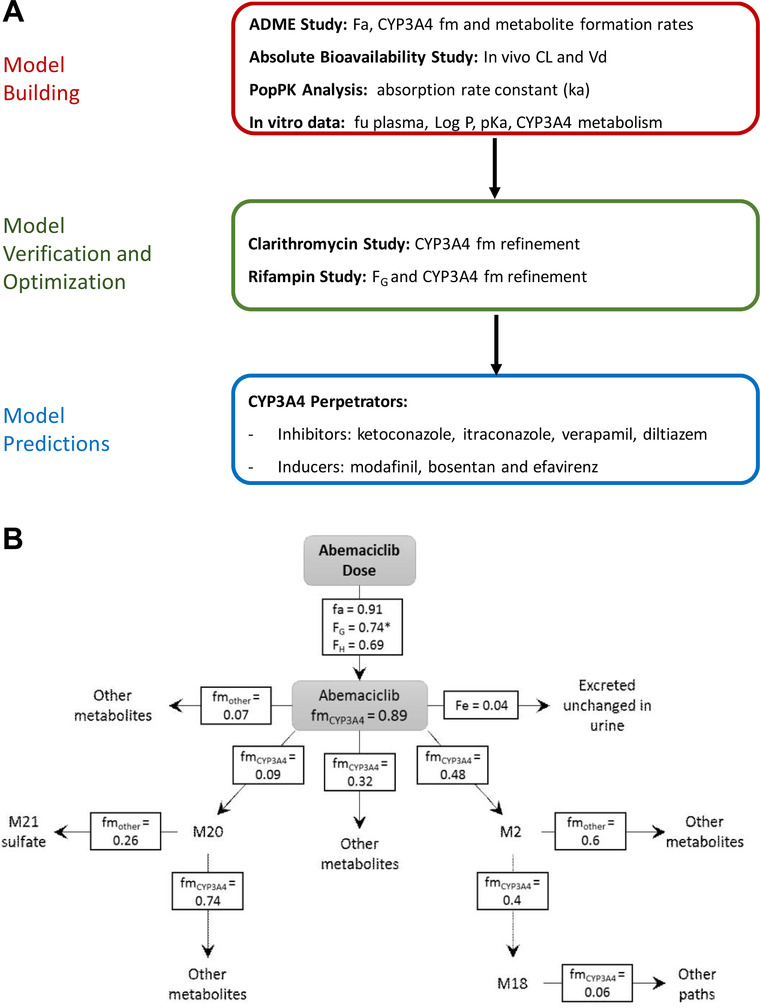
A, Simulation strategy. B, Proposed disposition scheme for abemaciclib and active metabolites after a 200‐mg dose. *F_G was set to 1 for a 50‐mg dose of abemaciclib. ADME indicates absorption, distribution, metabolism, and excretion; CL, clearance; Fa, fraction absorbed; Fe, fraction eliminated; F_G, fraction escaping first‐pass metabolism in the gut; F_H, fraction escaping first‐pass metabolism in the liver; fm, fraction metabolized by CYP3A4; fu, fraction unbound; ka, absorption rate constant; pKa, acid dissociation constant; PopPK, population pharmacokinetics; Vd, volume of distribution.

Software

Simcyp version 14 (Sheffield, UK) was used to develop and/or verify the pharmacokinetics of abemaciclib, 3 active metabolites (M2, M18, and M20), ketoconazole, itraconazole, clarithromycin, diltiazem verapamil, rifampin, efavirenz, bosentan, and modafinil. These models were used to simulate and predict drug‐drug interactions between 200 mg abemaciclib and the various inhibitors and inducers, including those that have not been studied in human clinical trials.

Input Data

The input parameters to the PBPK models are summarized in Table 1.

Table 1.

PBPK Input Parameters for Abemaciclib and Active Metabolites in Healthy Volunteers

Abemaciclib
Molecular weight (g/mol)	506.6
LogP	3.36	Measured
pKa 1 (basic)	7.95	Measured
pKa 2 (basic)	4.48	Measured
Blood‐to‐plasma ratio	0.84	Measured in vitro
fu plasma	0.0557	Measured in vitro [18]
ka (h−1) (%CV)	0.2 (60)	PopPK analysis
Fa	0.91	Estimated from mass balance study
hPeff (10−4 cm/s)	2.46	Predicted from HBD and PSA (Simcyp v14)
fu,gut	0.7	Manually fitted to obtain FG = 0.75 match observed F = 0.45
Qgut (L/h)	10.1	Predicted (Simcyp)
Polar surface area (Å2)	71.4	Predicted, in‐house QSAR model
Number of hydrogen bond donors	1	Predicted, in‐house QSAR model
Vdss (L/kg)	8.93	ABA study (IV administration)
CL systemic (L/h)	24	ABA study (IV administration)
CL renal (L/h)a	1.0	Estimated from mass balance study
CLint CYP3A4 p1 (µL/[min/pmol isoform])b	0.634	Back‐calculated from IV CL of ABA Study and fm values from 14C study using the retrograde model in Simcyp
CLint CYP3A4 p2 (µL/[min/pmol isoform])c	0.117
CLint CYP3A4 p3 (µL/[min/pmol isoform])d	0.576
CLint HLM (µL/[min/mg protein])	9.733

M2
Molecular weight (g/mol)	478.55
cLogP	3.66	Predicted (Prism)
pKa (basic)	9.19	Predicted (Chemaxon)
fu plasma	0.081	Measured in vitro
Blood‐to‐plasma ratio	0.836	Predicted (Simcyp)
Vdss (L/kg) minimal PBPK model	12. 1	Fitted manually to approximate Cmax
CLint CYP3A4 (µL/[min/pmol isoform])e	0.487	Fitted manually based on interaction with rifampin
CLint HLM (µL/[min/mg protein])	100

M20
Molecular weight (g/mol)	522.6
cLogP	2.78	Predicted (Prism)
pKa (basic)	8.37	Predicted (Chemaxon)
Blood‐to‐plasma ratio	0.67	Predicted (Simcyp)
fu plasma	0.021	Measured
Vdss (L/kg) minimal PBPK model	1.24	Fitted manually to approximate Cmax
CLint CYP3A4 (µL/[min/pmol isoform])	0.444	Fitted manually based on interaction with rifampin
CLint HLM (µL/[min/mg protein])	21.369	Fitted manually based on interaction with rifampin

M18
Molecular weight (g/mol)	494.5
cLogP	2.35	Predicted (Prism)
pKa (basic)	9.19	Predicted (Chemaxon)
Blood‐to‐plasma ratio	0.664	Predicted (Simcyp)
fu plasma	0.034	Measured in vitro
Vdss (L/kg) minimal PBPK model	2.5	Fitted manually to approximate Cmax
CLint CYP3A4 (µL/[min/pmol isoform])	0.197	Fitted manually based on interaction with rifampin
CLint HLM (µL/[min/mg protein])	423.210	Fitted manually based on interaction with rifampin

ABA indicates absolute bioavailability study; CL_int, intrinsic clearance; cLogP, calculated octanol/water partition coefficient; C_max, maximum plasma concentration; F, absolute bioavailability; F_a, fraction absorbed; F_G, fraction of the dose that escapes first‐pass gut metabolism; fm, fraction metabolized; fu, fraction unbound; fu,gut, fraction unbound of drug in the enterocyte; fu plasma, fraction unbound in plasma; HBD, hydrogen bond donor; HLM, human liver microsomes; hPeff, predicted human effective permeability; IV, intravenous; k_a, absorption rate constant; pKa, acid dissociation constant; PBPK, physiologically based pharmacokinetics; PopPK, population pharmacokinetic studies; PSA, polar surface area; Qgut, hybrid term that includes villous blood flow and permeability through the enterocyte; QSAR, quantitative structure‐activity relationship; Vd_ss, volume of distribution at steady state.

^aRenal clearance estimated as 4% of systemic clearance based on radioactivity recovery in urine in the mass balance study (NCT01913314).⁵

^bp1 is the CYP3A4‐mediated clearance pathway that forms M2.

^cp2 is the CYP3A4‐medited clearance pathway that forms M20.

^dp3 is the CYP3A4‐mediated clearance pathway that forms metabolites not included in this model.

^eCYP3A4‐mediated clearance pathway that forms M18.

Simulation Assumptions

Absorption

The fraction of 200 mg abemaciclib absorbed (Fa) from the intestine after an oral dose was calculated using equation 1:

$$\mathrm{Fa}=1-\left(\frac{\%\mathrm{of}\mathrm{parent}\mathrm{in}\mathrm{feces}}{\%\mathrm{of}\mathrm{dose}\mathrm{recovered}}\right)$$ (1)

where the percentage, of parent in feces, determined in the ¹⁴C study, was 6.76 and the percentage of dose quantified was 75.4% (total radioactivity recovery was 84%). Therefore, the Fa was determined to be 0.91. The Fa and the absorption rate constant (Table 1) were input into the first‐order absorption model within Simcyp.

Distribution

A full PBPK model was selected for the parent compound, and minimal PBPK models were selected for the metabolites. The tissue composition–based model (method 2) implemented in Simcyp as proposed by Rodgers et al7, 8, 9, 10 was selected to predict the volume of distribution of abemaciclib at steady state. The tissue‐to‐plasma partition coefficient scalar was adjusted to 2.5 to match the observed Vd_ss, calculated by noncompartmental analysis from intravenous (IV) data in the ABA study.6 The Vd_ss of the 3 active metabolites was estimated manually, while clearance was kept fixed (see elimination section), based on the assumption that volume is the primary factor driving the metabolites’ peak pasma concentration (C_max).

First‐Pass Hepatic Extraction

The fraction of a 200‐mg oral dose of abemaciclib escaping first‐pass metabolism in the liver (F_H) was calculated according to equations (2), (3), and 4, by first calculating the IV blood clearance (CL_B,iv):

$${\mathrm{CL}}_{\mathrm{B},\mathrm{iv}}=\frac{{\mathrm{CL}}_{\mathrm{iv}}}{\mathrm{B}:\mathrm{P}}$$ (2)

where CL_iv was the IV plasma clearance (24 L/h) and B:P was the blood to plasma concentration ratio (0.84). The CL_B,iv was used to calculate the hepatic extraction ratio (E_H):

$${\mathrm{E}}_{\mathrm{H}}=\frac{\mathrm{C}{\mathrm{L}}_{\mathrm{B},\mathrm{iv}}}{\mathrm{Q}}$$ (3)

where Q was the hepatic blood flow, assumed to be 80 L/h.¹¹ Finally, F_H was calculated from E_H:

$${\mathrm{F}}_{\mathrm{H}}=1-{\mathrm{E}}_{\mathrm{H}}$$ (4)

resulting in a calculated F_H of 0.64.

First‐Pass Gut Extraction

The fraction of a 200‐mg oral dose of abemaciclib escaping first‐pass metabolism in the gut (F_G), was calculated according to equation 5:

$${\mathrm{F}}_{\mathrm{G}}=\frac{\mathrm{F}}{{\mathrm{F}}_{\mathrm{H}}\times \mathrm{Fa}}$$ (5)

where the absolute bioavailability (F) was 0.45, F_H was 0.64, and Fa was 0.91, giving an F_G value of approximately 0.77.

It should be noted that when abemaciclib is dosed at 50 mg, the dose‐normalized abemaciclib exposure is higher than when it is dosed at 200 mg. The difference is thought to represent a lower gut extraction (and higher F_G) at 50 mg than at 200 mg rather than a difference in the intrinsic clearance, absorption, or any other parameter. This possibility is further considered in the Discussion.

Metabolism and Elimination

In order to calculate the fraction of abemaciclib metabolized by CYP3A4 (f_m), equation 6, previously described,12 was rearranged to equation 7:

$$\mathrm{AU}{\mathrm{C}}_{\mathrm{R}}=\frac{1}{\mathrm{A}\times \mathrm{fm}+\left(1-\mathrm{fm}\right)}$$ (6)

$$\mathrm{fm}=\frac{\frac{1}{\mathrm{AU}{\mathrm{C}}_{\mathrm{R}}}-1}{\left(\mathrm{A}-1\right)}$$ (7)

where the area under the concentration time curve (AUC) ratio of inhibited to uninhibited abemaciclib (AUC_R) was 3.37 in the clarithromycin interaction study, and A describes the proportion of CYP3A4 intrinsic clearance in the liver that was inhibited by 500 mg of clarithromycin given orally twice daily for 5 days before the administration of abemaciclib. The parameter A was calculated for clarithromycin using static modeling with IV midazolam as the substrate drug (according to the observed 3.5‐fold increase in midazolam AUC extrapolated to infinity13).

The percentage of the oral abemaciclib dose recovered in feces of the parent compound and the 6 metabolites are listed in Table S2. M1, M2, M20, and M22 are primary metabolites. M21 is a secondary metabolite formed from M20. M18 is a secondary metabolite that could be formed from either M2 or M20. In order to calculate the fraction of metabolites formed, the percentage of analytes recovered in feces was adjusted to 100, assuming the proportion of each metabolite remains constant (Table S2). The fraction of M2 formed from the parent compound was calculated by summing the percentage of M2 and M18 present in feces and dividing by 100. The fraction of M20 formed was calculated by summing the percentages of M20 and M21 recovered in feces and dividing by 100.

In the human mass balance study, 4% of the radioactivity was excreted in urine, and for modeling purposes it was assumed to be parent compound (cold profiling of urine suggests parent is the predominant species in urine). Initial estimates of the systemic clearances of M2 and M20 (CL_met) were calculated from equation 8:

$$\mathrm{C}{\mathrm{L}}_{\mathrm{met}}={\mathrm{f}}_{\mathrm{m},\mathrm{p}-\mathrm{m}}\times \mathrm{C}{\mathrm{L}}_{\mathrm{parent}}\times \frac{\mathrm{AU}{\mathrm{C}}_{0-\infty \mathrm{parent}}}{\mathrm{AU}{\mathrm{C}}_{0-\infty \mathrm{Met}}}$$ (8)

where f_m,p‐m was the fraction of the parent forming each of the metabolites (calculated as described above), CL_parent was the observed systemic (IV) clearance of the parent compound, AUC_0‐∞Met was the observed area under the plasma concentration‐time curve of the metabolite M2 or M20, and AUC_{0‐∞parent} was the observed area under the plasma concentration‐time curve of the parent (from the rifampin interaction study5). M18 can be formed from M2 or M20; however, for modeling purposes it was assumed that it is formed solely from M2 (supported by the observation that M2 is the major route of metabolism). Hence, the systemic clearance of the secondary metabolite M18 (CL_M18) was calculated according to equation 9.14

$$\mathrm{C}{\mathrm{L}}_{\mathrm{M}18}={\mathrm{f}}_{\mathrm{m},2-18}\times \mathrm{C}{\mathrm{L}}_{\mathrm{M}2}\times \frac{\mathrm{AU}{\mathrm{C}}_{0-\infty \mathrm{M}2}}{\mathrm{AU}{\mathrm{C}}_{0-\infty \mathrm{M}18}}$$ (9)

where f_m,2‐18 is the fraction of M2 forming M18, CL_M2 was the systemic clearance of M2 calculated from equation 8, AUC_0‐∞M2 was the observed area under the plasma concentration‐time curve of M2 (from rifampin interaction study), and AUC_0‐∞M18 was the observed area under the plasma concentration‐time curve of M18 (from the human mass balance study).

The fraction of M20 metabolized via CYP3A4 (0.74) was determined by manual fitting to be within 0.8‐ and 1.25‐fold of the observed AUC_0‐∞ in the human mass balance study and the observed AUC_0‐∞ ratio of for M20 in the rifampin interaction study.5 The fraction of M2 metabolized via CYP3A4 (0.4) was similarly fitted to match the AUC_0‐∞ and the AUC_0‐∞ ratios of M2 and M18 in the rifampin interaction study. The fraction of M18 metabolized via CYP3A4 (0.06) was fitted to match the observed AUC_0‐∞ and the AUC_0‐∞ ratio of M18 in the rifampin interaction study. The CL_int values of M2, M18, and M20 were manually optimized within Simcyp to match the observed AUC_0‐∞ of each of the metabolites in both arms of the rifampin interaction study. Renal clearance (1 L/h) was estimated as 4% of systemic clearance, based on the recovered radioactivity in urine in the mass balance study.

Simulation Design

The simulations were all performed with the Simcyp Healthy Volunteer population aged 40 to 65 years, and 80% female to approximate to the clarithromycin and rifampin clinical interaction study populations. All simulations were performed under fasted conditions with 100 virtual individuals (10 trials of 10 individuals each).

Inhibition Simulations

The predictions of the effect of CYP3A4 inhibition by clarithromycin (500 mg twice daily [BID]), diltiazem (120 mg 3 times daily) and its n‐desmethyl metabolite, and verapamil (120 mg 3 times daily) were performed using standard Simcyp v14 library files with modifications described below. Inhibitors were dosed orally for 12 days, and on day 7 a dose of 200 mg of abemaciclib was given 2 hours after the first dose of the inhibitor.

Modifications to Inhibitor Files

The ketoconazole and itraconazole files available in Simcyp version 14 predicted AUC ratios for abemaciclib of 7‐ and 3.8‐fold, respectively. This is significantly lower than would be expected, given that ketoconazole and itraconazole are known strong inhibitors of CYP3A4,15, 16 and a high proportion (>0.89) of abemaciclib metabolism is CYP3A4 mediated. Other authors have addressed the systematic underprediction of CYP3A4 drug‐grug interaction (DDI) with the Simcyp itraconazole and ketoconazole files and described several necessary modifications to the ketoconazole and itraconazole files,17, 18, 19 including the need to incorporate uptake and efflux transporters in the liver to increase the unbound concentration of ketoconazole at the site of inhibition and a considerable decrease in the inhibition constant for itraconazole. Our approach is as follows. The observed AUC ratio of midazolam in the presence of ketoconazole was reported to be 19.20 Assuming an F_G and f_m of midazolam of 0.5 and 0.9,19, 21 respectively, this ratio suggests that ketoconazole completely inhibits CYP3A4 activity in the gut and liver. In order to simulate this complete inhibition, the CYP3A4‐mediated intrinsic clearance of abemaciclib was reduced to 0 in the Simcyp compound file. Similarly, a 90% reduction in CYP3A4 intrinsic clearance by itraconazole was used to reproduce the reported AUC ratio of midazolam in the presence of itraconazole.^11, 22, 23 Therefore, the CYP3A4‐mediated intrinsic clearance was multiplied by 0.1 in the abemaciclib and 3 metabolite files to simulate the itraconazole interaction. The interactions assumptions were verified against midazolam as described in the Model Verification section.

Because the clarithromycin CYP3A4‐mediated interaction was overpredicted, the competitive inhibition of CYP3A4 by clarithromycin was removed, leaving time‐dependent inhibition only as reported in the literature.24 This resulted in improved predictions compared with observed interactions with abemaciclib. The prediction of the clarithromycin‐midazolam interaction was also acceptable and is described in the Model Verification section.

Induction Simulations

The predictions of the effect of CYP3A4 induction by rifampin (600 mg once daily [QD]), modafinil (200 mg QD for 7 days and then 400 mg QD), efavirenz (600 mg QD), bosentan (125 mg BID), were performed using either standard Simcyp library files (efavirenz and rifampin) with a slight modification to the rifampin file as described below or custom files described below (modafinil and bosentan).25, 26, 27 The prediction of the effect of efavirenz (600 mg QD) was performed using the Simcyp v16 library file, implemented in Simcyp v14. The inducers were dosed orally for 12 days, and on day 7, a 200‐mg dose of abemaciclib was given concurrently with the dose of the inducer, except for the interaction with modafinil, where modafinil was dosed QD for 40 days, and abemaciclib was given on day 27 to reproduce dosing schedules from several published clinical trials.28, 29, 30, 31

Modifications to Simcyp Inducer Files

The inhibition of CYP3A4 by rifampin was removed from the model to better replicate the observed interaction with abemaciclib given that rifampin is not a CYP3A4 inhibitor.32 The prediction was verified against the observed interaction with known CYP3A4 substrates (see the Model Verification section).

Inducer Files for Bosentan and Modafinil

The bosentan PBPK model was developed using physicochemical and biological in vitro data and published in vivo data. The model included hepatic and nonhepatic (target‐mediated) clearances as observed at therapeutic bosentan plasma concentrations33 and autoinduction of CYP3A4‐mediated bosentan clearance. These assumptions were verified using bosentan single‐ and multiple‐dose data.34 Active uptake into the liver via organic anion–transporting polypeptides (OATPs) was considered in the model to reproduce in vivo hepatic clearance of bosentan as well as in the calculation of in vitro induction parameters (maximal induction fold and 50% of the maximal induction unbound concentration).35 Because the model was able to accurately predict the autoinduction of bosentan with regard to CYP3A4 metabolism in both the gut and liver, no induction of OATPs by bosentan was necessary in the model. The modafinil induction file was built based on a published model, with minor changes to the input parameters.30, 31 The input parameters for bosentan and modafinil are shown in Table S3.

Abemaciclib Active Species Calculations

Calculations for the prediction of the AUC ratio for the active species are shown in equation 10:

$$\begin{array}{ccc}& & \text{AUC}\text{ratio}\text{active}\text{species}\hfill \\ & & =\frac{\mathrm{AU}{\mathrm{C}}_{\mathrm{parent}\mathrm{In}}+\mathrm{AU}{\mathrm{C}}_{\mathrm{M}2\mathrm{In}}+\mathrm{AU}{\mathrm{C}}_{\mathrm{M}20\mathrm{In}}+\mathrm{AU}{\mathrm{C}}_{\mathrm{M}18\mathrm{In}}}{\mathrm{AU}{\mathrm{C}}_{\mathrm{parent}}+\mathrm{AU}{\mathrm{C}}_{\mathrm{M}2}+\mathrm{AU}{\mathrm{C}}_{\mathrm{M}20}+\mathrm{AU}{\mathrm{C}}_{\mathrm{M}18}}\hfill \end{array}$$ (10)

where AUC has the units nanomole‐hour per liter, and the subscript “in” indicates the AUC of the parent or metabolite when coadministered with the inhibitor or inducer.

To account for protein‐binding and potency differences among the 4 active analytes, the AUCs of parent and metabolites were adjusted according to equations 11 and 12, respectively:

$${\mathrm{AUC}}_{\mathrm{parent}\mathrm{adjusted}}=\mathrm{AU}{\mathrm{C}}_{\mathrm{parent}}\times \mathrm{f}{\mathrm{u}}_{\mathrm{parent}}$$ (11)

where fu_parent is the fraction unbound of parent abemaciclib in plasma, and

$$\begin{array}{ccc}\hfill {\mathrm{AUC}}_{\mathrm{metabolite}\mathrm{adjusted}}& =& \mathrm{AU}{\mathrm{C}}_{\mathrm{metabolite}}\times \mathrm{f}{\mathrm{u}}_{\mathrm{metabolite}}\hfill \\ & & \times \frac{\mathrm{I}{\mathrm{C}}_{50}\mathrm{Parent}}{\mathrm{I}{\mathrm{C}}_{50}\mathrm{Metabolite}}\hfill \end{array}$$ (12)

where fu_metabolite is the fraction unbound of the metabolite(s) in plasma, and half‐maximal inhibitory concentration for parent/metabolite represents the in vitro potency for CDK4/cyclin D1 of each analyte. The mean ± SD CDK4/cyclin D1 half‐maximal inhibitory concentration values were measured in vitro and are as follows: 1.57 ± 0.6 nmol/L for abemaciclib, 1.24 ± 0.4 nmol/L for M2, 1.46 ± 0.2 nmol/L for M18, and 1.54 ± 0.2 nmol/L for M20.³⁶ The adjusted AUC ratios of active species were then calculated as in equation 10.

Results

Abemaciclib Simulations

The proposed disposition of abemaciclib and active metabolites is shown in Figure 1B. The observed and the model‐simulated plasma concentration‐time profiles of abemaciclib and its 3 active metabolites M2, M20, and M18 after a 50‐ and 200‐mg dose of abemaciclib are shown in Figure 2 and Figure 3. The model adequately reproduced the observed concentration profiles of abemaciclib and its metabolites in the control arm of the rifampin and clarithromycin studies. The predicted C_max and AUC_0‐∞ values are all within 0.66‐ and 1.25‐fold of the observed values (Table 2).

Figure 2.

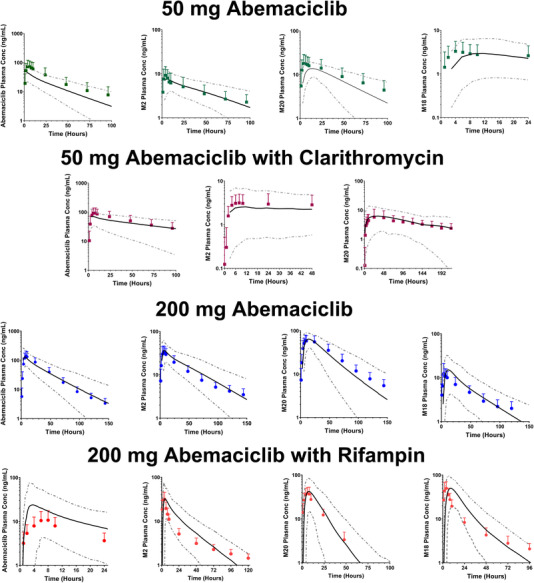
Observed and predicted plasma concentrations for bemaciclib and active metabolites after a 50‐mg dose of abemaciclib alone (green solid squares), a 50‐mg dose of abemaciclib coadministered with 500 mg twice a day clarithromycin (purple solid squares), a 200‐mg dose of abemaciclib alone (blue solid circles), and a 200‐mg dose of abemaciclib coadministered with 600 mg daily rifampin (red solid circles). The solid symbols represent the observed mean concentrations, and the error bars represent the observed SDs. The solid black lines represent the predicted mean concentrations; the dotted gray lines represent the 5th and 95th percentiles.

Figure 3.

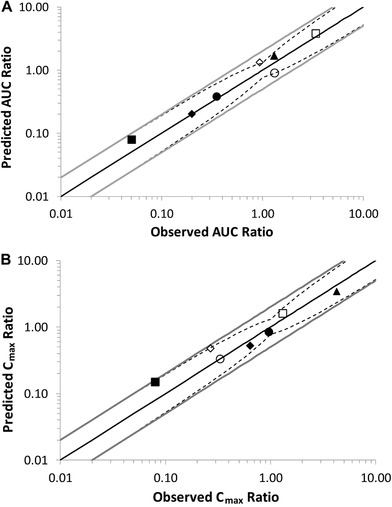
Predicted vs observed (A) AUC ratios and (B) C_max ratios for abemaciclib, M2, M18, and M20 with rifampin and clarithromycin. Open symbols represent the ratios with clarithromycin and solid symbols the ratios with rifampin. Open squares represent abemaciclib + clarithromycin. Open circles represent M2 + clarithromycin. Open diamonds represent M20 + clarithromycin. Open triangles represent M18 + clarithromycin. Closed squares represent abemaciclib + rifampin. Closed circles represent M2 + rifampin. Closed diamonds represent M20 + rifampin. Open triangles represent M18 + rifampin. The solid black lines represent the lines of unity, the solid gray lines represent the 2‐fold limits, and the dotted lines represent the upper and lower limits defined by Guest and collaborators³⁷ using a Δ value of 1.3. AUC indicates area under the plasma concentration–time curve; C_max, peak plasma concentration.

Table 2.

Observed Versus Predicted AUC and C_max Values for Abemaciclib, M2, M20, M18, and Total Active Species After an Oral Dose of 50 mg or 200 mg Abemaciclib

Compound	Parameter	Observed Geometric Mean (%CV)	Predicted Geometric Mean (%CV)	Observed/Predicted
50 mg abemaciclib (control group clarithromycin study)
Abemaciclib	AUC(0‐∞) (ng•h/mL)	2230 (93)	1461 (50)	1.53
	Cmax (ng/mL)	70.0 (73)	46 (48)	1.52
	Tmax (h)a	4.03 (2‐23.78)	3.61 (0.91‐35.26)	1.12
	T½ (h)	28.8 (12.2‐79.2)	25.25 (16.13‐48.99)	1.14
M2	AUC(0‐∞) (ng•h/mL)	509 (75)	457 (41)	1.11
	Cmax (ng/mL)	9.11 (70)	7.78 (40)	1.17
	Tmax (h)a	4.00 (1‐24.50)	5.93 (1.85‐68.55)	0.67
	T½ (h)	60.1 (10.8‐200)	31.25 (21.11‐56.13)	1.92
M20	AUC(0‐∞) (ng•h/mL)	1090 (63)	777 (41)	1.40
	Cmax (ng/mL)	18.1 (66)	14.0 (21)	1.29
	Tmax (h)a	6.00 (2‐24.50)	16.08 (4.46‐63.51)	0.37
	T½ (h)	43.0 (19.7‐94.8)	25.10 (16.74‐49.74)	1.71
M18	AUC(0‐∞) (ng•h/mL)	196 (176)	152 (48)	1.29
	Cmax (ng/mL)	3.53 (61)	2.73 (54)	1.29
	Tmax (h)a	4.00 (1‐74.27)	11.78 (5.67‐63.26)	0.34
	T½ (h)	38.0 (4.18‐151)	30.79 (21.08‐57.26)	1.23
200 mg abemaciclib (control group rifampin study)
Abemaciclib	AUC(0‐∞) (ng•h/mL)	4570 (53)	4449 (50)	1.03
	Cmax (ng/mL)	134 (45)	140 (51)	0.96
	Tmax (h)a	8.00 (4‐24)	3.60 (0.91‐35.26)	2.22
	T½ (h)	25.2 (17.6‐42.7)	25.19 (16.68‐48.92)	1.00
M2	AUC(0‐∞) (ng•h/mL)	1780 (30)	1861 (41)	0.96
	Cmax (ng/mL)	35 (47)	38 (40)	0.92
	Tmax (h)a	6.08 (4‐24)	4.98 (1.75‐60.66)	1.22
	T½ (h)	60.5 (43.1‐123)	31.11 (21.19‐57.21)	1.95
M20	AUC(0‐∞) (ng•h/mL)	3760 (33)	3112 (41)	1.21
	Cmax (ng/mL)	63 (32)	63 (22)	1.00
	Tmax (h)a	10.00 (4‐24)	13.28 (4.31‐56.85)	0.75
	T½ (h)	35.8 (27.2‐58.8)	25.10 (16.74‐49.49)	1.43
M18	AUC(0‐∞) (ng•h/mL)	660 (38)	628 (47)	1.05
	Cmax (ng/mL)	12 (69)	13 (49)	0.92
	Tmax (h)a	6.03 (4‐24)	10.13 (4.95‐53.97)	0.60
	T½ (h)	52.5 (30.9‐91.8)	30.70 (21.14‐56.71)	1.71

AUC_(0‐∞) indicates area under the concentration‐time curve from 0 to infinity; C_max, maximal concentration observed; CV, coefficient of variation; T_max, time of observed C_max; T_½, plasma half‐life.

^aMedian (min‐max).

Interaction Simulations

The observed and the model‐predicted plasma concentration‐time profiles of abemaciclib and active metabolites M2, M20, and M18 when a 50‐mg dose of abemaciclib was coadministered with clarithromycin are shown in Figure 2. The model‐predicted concentration‐time profiles are consistent with observed abemaciclib and metabolites in the presence of clarithromycin. The C_max and AUC_0‐∞ ratios for the interaction are listed in Table 3. The observed and the model‐predicted plasma concentration‐time profiles of abemaciclib and its metabolites M2, M20, and M18 when a 200‐mg dose of abemaciclib was coadministered with rifampin are shown in Figure 2. The models reproduced the observed concentration‐time profiles in the presence of rifampin. These C_max and AUC_0‐∞ ratios for the interaction are also listed in Table 3. Using the criteria published by Guest and collaborators,37 with a Δ value of 1.3 based on the percentage coefficient of variation (CV) of abemaciclib AUC after intravenous dosing, the models were acceptable and able to capture the effect of clarithromycin and rifampin on abemaciclib and active metabolites within the appropriate limits (Figure 3).

Table 3.

Predicted and Observed AUC_(0‐∞) and C_max Ratios for Abemaciclib, M2, M20, M18, and Active Species When Abemaciclib Is Coadministered With Clarithromycin and Rifampin

Compound	Parameter	Observed Geometric Mean (90%CI)	Predicted Geometric Mean (90%CI)	Observed/Predicted
50 mg abemaciclib with clarithromycin
Abemaciclib	AUC(0‐∞) ratio	3.37 (2.85‐3.99)	3.80 (3.50‐4.11)	0.89
	Cmax ratio	1.30 (1.10‐1.52)	1.61 (1.56‐1.66)	0.81
M2	AUC(0‐∞) ratio	1.32 (1.14‐1.53)	0.90 (0.85‐0.95)	1.47
	Cmax ratio	0.33 (0.27‐0.40)	0.33 (0.30‐0.37)	1.00
M20	AUC(0‐∞) ratio	0.94 (0.84‐1.06)	1.32 (1.24‐1.41)	0.71
	Cmax ratio	0.27 (0.21‐0.34)	0.47 (0.43‐0.51)	0.57
M18	AUC(0‐∞) ratio	NCa	0.31 (0.28‐0.34)	NC
	Cmax ratio	NCa	0.13 (0.11‐0.15)	NC
Potency‐adjusted unbound active species	AUC(0‐∞) ratio	2.45	2.47	0.99
200 mg abemaciclib with rifampin
Abemaciclib	AUC(0‐∞) ratio	0.05 (0.04‐0.06)	0.08 (0.07‐0.09)	0.63
	Cmax ratio	0.08 (0.07‐0.09)	0.15 (0.13‐0.17)	0.53
M2	AUC(0‐∞) ratio	0.35 (0.32‐0.38)	0.38 (0.35‐0.41)	0.92
	Cmax ratio	0.96 (0.81‐1.13)	0.84 (0.78‐0.90)	1.14
M20	AUC(0‐∞) ratio	0.20 (0.19‐0.22)	0.20 (0.18‐0.22)	1.00
	Cmax ratio	0.64 (0.56‐0.73)	0.52 (0.47‐0.57)	1.23
M18	AUC(0‐∞) ratio	1.31 (1.18‐1.44)	1.67 (1.59‐1.76)	0.78
	Cmax ratio	4.26 (3.42‐5.31)	3.40 (3.18‐3.64)	1.25
Potency‐adjusted unbound active species	AUC(0‐∞) ratio	0.23	0.28	0.82

AUC_(0‐∞) indicates area under the concentration‐time curve from 0 to infinity; C_max, maximal concentration observed; NC, not calculated.

^aConcentration values of M18 after administration of clarithromycin were below the limit of quantitation of 1 ng/mL.

The predicted C_max and AUC_0‐∞ ratios for a 200‐mg dose of abemaciclib and its active metabolites when coadministered with other CYP3A inhibitors and inducers are listed in Table 4. The model predicted 7.11‐ and 15.7‐fold increases in abemaciclib AUC in the presence of strong CYP3A4 inhibitors itraconazole and ketoconazole, respectively; and, 2.27‐ and 3.90‐fold increases with the concomitant use of moderate CYP3A4 inhibitors verapamil and diltiazem, respectively (Table 4). The model predicted AUC ratios of 0.31, 0.32, and 0.54 in abemaciclib AUC in the presence of CYP3A4 inducers efavirenz, bosentan, and modafinil, respectively (Table 4). The predicted AUC ratios for the potency‐adjusted unbound active species with diltiazem, verapamil, itraconazole and ketoconazole ranged from 1.62 to 7.15 (Table 4). The predicted AUC ratios for the potency‐adjusted unbound active species with efavirenz, bosentan, and modafinil ranged from 0.48 to 0.71 (Table 4).

Table 4.

Predicted AUC_(0‐inf) and C_max Ratios for Abemaciclib, M2, M20, M18, and Active Species After Coadministration of 200 mg of Abemaciclib, Moderate and Strong CYP3A4 Inhibitors, and Moderate Inducers

		Inhibitors, Geometric Mean (90%CI)				Inducers, Geometric Mean (90%CI)
Compound	Parameter	Diltiazem	Verapamil	Itraconazolea	Ketoconazoleb	Efavirenz	Bosentan	Modafinil
Abemaciclib	AUC(0‐∞) ratio	3.90 (3.67‐4.16)	2.27 (2.08‐2.46)	7.11 (6.82‐7.41)	15.7 (14.1‐17.2)	0.31 (0.29‐0.34)	0.32 (0.30‐0.34)	0.54 (0.52‐0.57)
	Cmax ratio	1.90 (1.84‐1.97)	1.63 (1.56‐1.69)	2.17 (2.09‐ 2.25)	2.46 (2.35‐2.58)	0.49 (0.46‐0.52)	0.40 (0.38‐0.42)	0.66 (0.64‐0.69)
M2	AUC(0‐∞) ratio	1.04 (1.00‐1.08)	1.06 (1.04‐1.09)	0.87 (0.81‐0.93)	0	0.58 (0.55‐0.61)	0.80 (0.79‐0.82)	0.84 (0.82‐0.86)
	Cmax ratio	0.42 (0.39‐0.45)	0.61 (0.57‐0.66)	0.24 (0.23‐0.26)	0	0.98 (0.94‐1.01)	1.19 (1.16‐1.22)	1.09 (1.07‐1.11)
M20	AUC(0‐∞) ratio	1.53 (1.46‐1.61)	1.32 (1.26‐1.37)	1.62 (1.48‐1.76)	0	0.42 (0.39‐0.45)	0.59 (0.57‐0.61)	0.70 (0.68‐0.73)
	Cmax ratio	0.57 (0.53‐0.61)	0.75 (0.72‐0.79)	0.38 (0.36‐0.40)	0	0.83 (0.80‐0.87)	0.91 (0.89‐0.94)	0.98 (0.96‐1.0)
M18	AUC(0‐∞) ratio	0.34 (0.31‐0.36)	0.60 (0.55‐0.64)	0.09 (0.08‐0.10)	0	1.57 (1.50‐1.64)	1.40 (1.36‐1.44)	1.30 (1.26‐1.33)
	Cmax ratio	0.12 (0.10‐0.14)	0.33 (0.28‐0.38)	0.03 (0.03‐0.03)	0	2.45 (2.30‐2.62)	2.09 (1.99‐2.20)	1.66 (1.59‐1.73)
Potency‐adjusted unbound active species	AUC(0‐∞) ratio	2.37	1.62	3.78	7.15	0.48	0.58	0.71

AUC_(0‐∞) indicates area under the concentration‐time curve from 0 to infinity; C_max, maximal concentration observed.

^aThe itraconazole interaction was modeled by reducing the CYP3A4‐mediated clearance by 90%.

^bThe ketoconazole interaction was modeled by reducing the CYP3A4‐mediated clearance to 0.

Model Verification

The abemaciclib PBPK model was verified against multiple clinical studies, including studies that were not used in model building (Table S4). All assumptions and conditions used in the inhibition simulations were verified using midazolam as a victim drug. Models of various CYP3A4 inhibitors were qualified by comparing the simulated and observed AUC_0‐∞ and C_max ratios of midazolam in the presence and absence of these inhibitors (Table S5). The models of the strong CYP3A4 inducer, rifampin, qualified by Simcyp.26 The modafinil PBPK model was qualified by comparing the predicted PK parameters after a single and multiple dose with the observed values.30, 31, 38 Furthermore, the observed AUC and C_max ratios of palbociclib,39 triazolam,29 and midazolam30 in the presence and absence of modafinil are within 0.78‐ to 1.14‐fold of the observed values (Table S7).

The bosentan model adequately reproduced the reported PK of bosentan after a single 125‐mg dose in healthy male volunteers.34 The observed over‐predicted ratios of AUC_0‐τ and Cmax are within 1.06 and 1.25 (Table S6). The model also adequately reproduced the reported CYP3A4 autoinduction in bosentan PK after multiple dosing (125 mg BID for 10 days).34 The observed over predicted ratios of AUC_0‐τ and C_max are within 0.97 and 1.12 (Table S6).

Furthermore, the model accurately predicted the gut‐specific CYP3A4 autoinduction of bosentan, which can be calculated with data from the Tracleer (bosentan) clinical pharmacology biopharmaceutics review40 following 5 days of bosentan 125 mg BID in the absence and presence of ketoconazole 200 mg QD. The observed and predicted F_G values for bosentan on day 5 were 0.62 and 0.67. The observed F_G value is calculated from a reported C_max ratio of 1.62 with and without ketoconazole and assuming an F_G of 1.0 in the presence of ketoconazole (calculated using reported data from the Tracleer U.S. Food and Drug Administration clinical pharmacology biopharmaceutics review).40 The predicted F_G is calculated by applying a Qgut model to the PBPK model–predicted CYP3A4 gut intrinsic clearance on day 5.41 The induction of CYP3A4 by bosentan was additionally verified using midazolam, a well‐characterized CYP3A4 substrate. The interactions were simulated using the midazolam model developed and verified by SimcypV14 (Table S7).

Sensitivity Analyses

A sensitivity analysis was conducted to determine the effect of individually changing the f_m by CYP3A4 of abemaciclib (parent), M2, M18, and M20 on the AUC ratio associated with the clarithromycin interaction. A complementary sensitivity analysis was performed to determine the effect of changing individual f_m values on the potency‐adjusted unbound AUC ratios of the active species. Figure 4 shows the effect of changing CYP3A4 f_m on the AUC ratio with clarithromycin of the individual species (abemaciclib, M2, M20, and M18) (Figure 4A). As expected, the AUC ratio of parent drug associated with the clarithromycin interaction was sensitive to changes in the f_m of parent drug because of the high dependence on CYP3A4 for elimination. In contrast, the clarithromycin DDI AUC ratios for the active metabolites were insensitive to changes in f_m because the metabolites are not highly dependent on CYP3A4 for elimination. A similar trend was seen for the effect of changing individual f_m values on the potency‐adjusted unbound AUC ratios for parent drug and active metabolites (Figure 4B). The predicted AUC ratio (ratio with clarithromycin coadministration to no inhibitor control) for total active species was sensitive to parent drug f_m but not the f_m of the individual metabolites for the reasons described previously. Together, these data indicate that the f_m for parent drug has been accurately estimated because suboptimal values would not reproduce the observed extent of DDI with clarithromycin.

Figure 4.

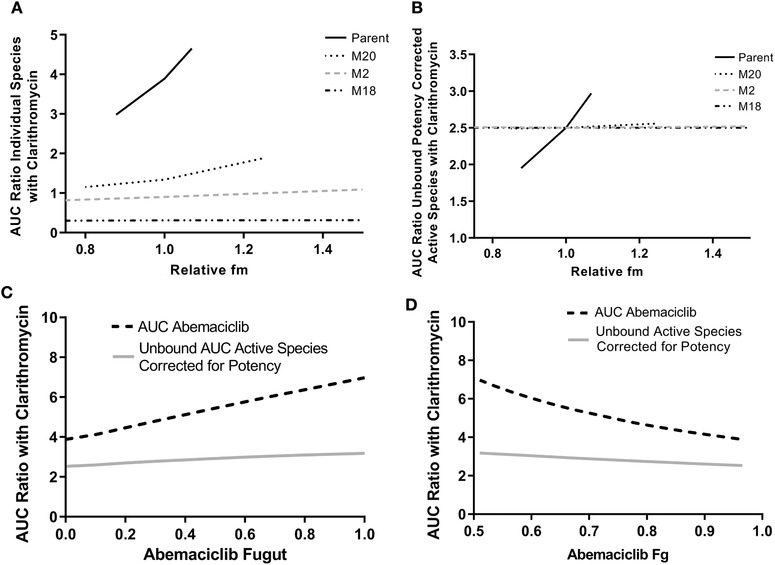
Sensitivity analysis of the effect of CYP3A4 fm and Fg on the AUC ratio with clarithromycin. A, Effect of changes in fraction metabolized via CYP3A4 (fm) of abemaciclib and active metabolites on the individual species AUC ratio with clarithromycin. B, Effect of changes in fraction metabolized via CYP3A4 of abemaciclib and active metabolites on the potency‐adjusted unbound species AUC ratio with clarithromycin. C, Effect of Fugut on the AUC ratio with clarithromycin for abemaciclib alone (black dotted line) and unbound potency‐corrected AUC active species (gray solid line). D, Effect of Fg on the AUC ratio with clarithromycin for abemaciclib alone (black dotted line) and unbound potency corrected AUC active species (gray solid line). AUC indicates area under the plasma concentration–time curve; Fg, fraction escaping first‐pass metabolism in the gut; fm, fraction metabolized by CYP3A4; Fugut, unbound fraction of Fg.

Within the Simcyp framework, the fraction unbound in the gut (fu,gut) is employed to set the desirable value of gut wall availability (F_G) at given values of membrane permeability and CYP3A4 intrinsic clearance in the Qgut model.42 For the abemaciclib PBPK model, the value of F_G for the 50‐mg dose was 0.98 and the corresponding fu,gut was 0.008, whereas for the 200‐mg abemaciclib model, the F_G was 0.74 and the corresponding fu,gut was 0.7. The boundaries of possible fu,gut values are therefore established by the observed DDIs with clarithromycin and rifampin. Sensitivity analyses were performed to determine the effect of changing F_G and fu,gut on the AUC ratio with clarithromycin of abemaciclib and potency‐corrected unbound active species. As expected, the AUC ratio of abemaciclib is moderately sensitive to changes in fu,gut and F_G over the feasible range, whereas the unbound AUC ratio of active species adjusted for potency is insensitive to changes in fu,gut (Figure 4C and 4D). Misspecification of fu,gut is not expected to significantly influence AUC ratios associated with coadministration of CYP3A4 inhibitors.

Discussion

The use of PBPK modeling to support dosing recommendations for DDI scenarios in regulatory submissions and prescribing labels has increased in recent years as exemplified by recent publications.43, 44, 45 Regulatory acceptance of such PBPK‐driven recommendations appears to have increased concurrently, as the models become more robust and can simulate ever more complex scenarios.46, 47 However, various regulatory authorities have also indicated the need for thorough model qualification and testing.48, 49

Early in the development cycle, the metabolic profile of abemaciclib was understood to include a significant CYP3A4 component. Hence, clinical DDI studies were conducted with clarithromycin and rifampin.5 In these studies, abemaciclib AUC ratios of 3.4 and 0.05, respectively, and total active species AUC ratios of 2.5 and 0.23, respectively, were observed, indicating that CYP3A4 did indeed play an important role not just in the metabolism of abemaciclib (f_m = 0.89; Figure 1B) but also in its active metabolites (f_m = 0.1‐0.7; Figure 1B). It would therefore be important to include prescribing recommendations for other types of CYP3A4 modulators (ie, strong and moderate) in the drug label. Fortunately, PBPK modeling allows for the efficient use of the vast amount of clinical knowledge gathered over the last 30 years in multiple drug interaction studies and the translation of the in vitro characteristics (ie, induction and inhibition parameters) of several CYP3A4 perpetrators. This is evident by the high number of applications of this type of modeling by academia, regulatory agencies, and industry.50, 51, 52, 53, 54, 55 A PBPK modeling approach was used to predict the effect of CYP3A4 inhibitors and inducers that have not been tested with abemaciclib but have been tested in the clinic with well‐characterized sensitive CYP3A4 substrates (eg, midazolam, triazolam), for which the used PBPK models have been thoroughly verified. However, in order to have value in accurately predicting CYP3A4‐mediated interactions, the model would need to be unusually complex, incorporating first‐pass elimination by the gut and liver, 3 metabolites, and multiple routes of elimination of the parent compound and the metabolites (CYP mediated and non–CYP‐mediated metabolism and renal elimination).

It was critical to capture both parent and metabolite exposure in the model due to the metabolites having similar potency at CDK4 and CDK6 as the parent. Similar to abemaciclib, each of the metabolites was known to undergo CYP3A4‐mediated metabolism. Although inhibition of CYP3A4 would result in a likely increase in exposure to abemaciclib and a decrease in the formation clearance of metabolites, the elimination clearance of the metabolites would also decrease, resulting in a complex disposition scenario whereby the overall effect on the exposure to total active species can only be understood through the use of an integrated model. Despite the complexity of this task, which involved integrating and reconciling data from multiple studies, high interindividual variability in observed abemaciclib pharmacokinetics, challenges associated with fitting multiple analytes (abemaciclib, M2, M20, and M18), and fitting different dose levels with apparently different absorption characteristics, it was possible to achieve an acceptable and useful match to the observed data. As shown in Figure 2, most of the predicted concentration‐time profiles matched the observed median, and all were within the 90% prediction interval (Figure 2), demonstrating that the current parameter set is well justified and based on sound assumptions. Further, the observed versus predicted ratios ranged from 0.92 for the C_max of M18 after a 200‐mg dose, up to 1.53 for the AUC of abemaciclib after a 50‐mg dose. Although not perfect, the fit of the model predictions to the observed clinical data can certainly be considered acceptable, given the large variability in observed parameters. For example, the AUC of abemaciclib and its metabolites demonstrated observed CV values ranging from 30% to 176%, depending on the analyte and the dose (Table 2). Similarly, observed CV values for C_max ranged from 32% to 73%, depending on analyte and dose. Figure 3 displays the observed versus predicted (1) AUC and (2) C_max ratios for abemaciclib, M2, M18, and M20 when coadministered with clarithromycin or rifampin. The data are within the predictability limits from 2 different methods used to assess the accuracy of the predictions. The first method is the traditional 2‐fold measure, and the second is the method introduced by Guest and collaborators,37 in which the limits are narrower when the ratios are close to 1 and approach the 2‐fold traditional method with larger ratios. For this work, the variability term was taken from the percentage CV in abemaciclib after intravenous administration, as in the approach taken with the variability in midazolam in the aforementioned publication. Figure S1 displays similar plots with a variability term of 1.65 reflective of the larger variability in AUC and C_max observed for the active species after oral administration of abemaciclib. As expected, the predicted and observed AUC ratios are also within the successful prediction these wider limits.

Clarithromycin is designated as a strong inhibitor of CYP3A based on the observed interaction with sensitive substrate midazolam,13 which demonstrated an AUC ratio of 6.32 (Table S5). However, both itraconazole and ketoconazole are known to more strongly inhibit CYP3A4 in both the gut and liver.20, 22, 23 Hence, it was important to demonstrate the potential “worst case” interaction ratios that would result when abemaciclib is dosed with stronger inhibitors. Following qualification of all the inhibitor models against midazolam data taken from the literature, the interaction with abemaciclib was simulated. The resulting AUC ratios with various moderate to strong inhibitors ranged from 2.27 to 15.7 for the parent alone and from 1.62 to 7.15 for the potency‐adjusted unbound total active species (Table 4). Similar differences in the magnitude of the effect of moderate inducers on parent alone compared with total active species demonstrate the importance of considering the total active species. If a dose reduction recommendation were based on the AUC ratio of abemaciclib alone, it could potentially result in patients being under‐ or overdosed.

This PBPK model encompassed several assumptions. First, in the human absorption, distribution, metabolism, excretion ADME study, 85% of the radioactivity was recovered in feces and urine over 336 hours. Given the low amounts of radioactivity recovered at later time points, only feces samples were pooled (up to 216 hours) and profiled using accelerator mass spectrometry for parent and metabolites. Therefore, in this modeling exercise it was assumed that the percentage of the parent excreted in feces calculated from the profiled samples using Equation 1 would have been the same if measured in the total recovered radioactivity. We believe this assumption holds true even for the capsule and tablet formulations, given the high permeability, high solubility, and fast dissolution in stomach pH of abemaciclib. Furthermore, the effect of a high‐fat and high‐calorie meal increased the AUC of abemaciclib and active species by 9%.3

Another important assumption was that CYP3A4 f_m of abemaciclib and the metabolites could be determined using the data from the clarithromycin and rifampin interaction studies. The f_m assumptions in the model could be further verified with other studies. Although, the current model is able to reproduce the known interactions with these 2 perpetrators, and the sensitivity analyses show that changes in f_m do not have a high impact on the AUC of the potency‐corrected unbound active species.

Another assumption of the model is that the partition of abemaciclib and metabolites into the liver is perfusion rate limited. This holds true because abemaciclib and active metabolites have good permeability and are not substrates of hepatic uptake transporters organic cation transporter 1, organic anion–transporting polypeptide 1B1 or 1B3. Therefore, the changes observed in plasma caused by CYP3A4 perpetrators are expected to reflect the changes inside the liver. Given this, we were able to use the plasma AUC and C_max values for the parent and the metabolites, in the presence and absence of rifampin and clarithromycin, to calculate the fractions formed and eliminated via CYP3A4. Although abemaciclib in vitro is a substrate of P‐glycoprotein and breast cancer resistance protein, these intestinal efflux transporters were not incorporated into the model given the high permeability and solubility and the expected lack of an effect of inhibitors of P‐glycoprotein and breast cancer resistance protein on the PK of abemaciclib.56, 57

In addition to facilitating an understanding of optimal prescribing in the presence of CYP3A‐modulators, the approach taken to building the PBPK model led to a deeper understanding of the mechanisms underlying abemaciclib PK and identified some interesting characteristics. For example, the bioavailability of abemaciclib appears to be different with 50‐ versus 200‐mg doses. This difference is thought to reflect a difference in F_G and was further confirmed with population analyses conducted throughout development. These analyses showed that hepatic intrinsic clearance and absorption were not dependent on dose, whereas F_G was shown to change with dose.4 Further, no difference in the fraction absorbed was expected between dose levels due to the compound having high predicted human effective jejunal permeability (2.46 × 10⁻⁴ cm/s), fast dissolution in the stomach, and a lack of precipitation.

A comparison of AUC‐based metabolite:parent ratios (Table S1) between the clarithromycin study conducted at 50 mg and 2 studies conducted at 200 mg (rifampin interaction and ABA studies) reveals approximately 2‐fold higher ratios in the 200‐mg studies, compared with the 50‐mg study. Hence, there was a greater extent of metabolism at 200 mg, and the observed difference in exposure between doses is therefore the result of metabolic differences and not absorption changes. In addition, there is no change in half‐life between 50 mg and 200 mg (Table S4), which adds further weight to the argument that changes in CL_int or F_H were not the source of the difference in exposure. Therefore, F_G was concluded to be the most likely source of the apparent dose dependency. Unfortunately, there is no crossover study with doses between 50 and 200 mg available to assess different doses in the same individuals with adequate power, so it is not possible to conclude a true dose dependency, only that there is some difference between these 2 studies that leads to a conclusion of a difference in F_G.

The prediction of the DDIs is determined by f_m and F_G. Because there is some degree of computational difficulty in identifying the true value of f_m and F_G, sensitivity analyses were conducted on these parameters. The absolute bioavailability study informs the value of the product of Fa and F_G; however, it does not allow the identification of the individual parameters. Instead, F_G was calculated indirectly by assuming Fa is 0.91 (based on permeability, solubility, and parent drug excreted in feces). As would be expected, altering F_G has the biggest effect on a predicted AUC ratio for abemaciclib but a minimal effect on the total active species bound and unbound (Figure 4B). Another sensitivity analysis was conducted to determine the effect of individually changing the CYP3A4 f_m of abemaciclib (parent), M2, M18, and M20 on the AUC ratio associated with the clarithromycin interaction. As expected (Figure 4), the AUC ratio of parent drug associated with the clarithromycin interaction was sensitive to changes in the f_m of parent drug because of the high dependence on CYP3A4 for elimination. In contrast, the clarithromycin DDI AUC ratios for the active metabolites were insensitive to changes in f_m because the metabolites are not highly dependent on CYP3A4 for elimination.

Conclusions

In conclusion, a complex PBPK model for abemaciclib and active metabolites was developed and verified. The model output demonstrated the importance of considering total active species when using PBPK to determine dose adjustments for molecules with active metabolites. The current PBPK model, which considers changes in unbound potency‐adjusted active species, can be used to inform dosing recommendations to support prescribing practices when abemaciclib is coadministered with inhibitors and inducers of CYP3A4.

Conflicts of Interest

M.M.P., B.L.M., P.K.T., S.D.H., and G.L.D. are all employees and shareholders of Eli Lilly and Company; P.K. is a shareholder of Eli Lilly and Company.

Data Sharing

Lilly provides access to all individual participant data collected during the trials, after anonymization, with the exception of pharmacokinetic or genetic data. Data are available to request 6 months after the indication studied has been approved in the US and EU and after primary publication acceptance, whichever is later. No expiration date of data requests is currently set once data are made available. Access is provided after a proposal has been approved by an independent review committee identified for this purpose and after receipt of a signed data‐sharing agreement. Data and documents, including the study protocol, statistical analysis plan, clinical study report, blank or annotated case report forms, will be provided in a secure data‐sharing environment. For details on submitting a request, see the instructions provided at www.vivli.org.

Supporting information

Supporting Information