Abstract
Human populations display remarkable diversity in language and culture, but the variation is not without limit. At the population level, variation between societies may be structured by a range of macro‐evolutionary factors, including ecological and environmental resources, shared ancestry, spatial proximity, and covarying social practices. Kinship terminology systems are varying linguistic paradigms that denote familial social relationships of kin and non‐kin. Systems vary by the kinds of salient distinctions that are made (e.g., age, gender, generation) and the extent to which different kinds of kin are called by the same term. Here, we explore two kinds of explanations for an observed typology of kin terms for cousins. The first one derives the typology from a learning bottleneck linked to population size. This would lead to a correlation between community size and the type of kinship system. The second one derives it from a set of social practices, particularly marriage and transfer of resources that might shape kinship systems. Using a global ethnographic database of over a thousand societies, we show that marriage rules and shared linguistic affiliation have a significant influence on the type of kinship system found in a society. This remains true if we control for the effect of spatial proximity and cultural ancestry. By combining cognitive and historic approaches to this aspect of kinship, we suggest broader implications for the study of human social cognition in general.
Keywords: Kinship terminology, Social cognition, Semantics, Cross‐cultural analysis, Cultural evolution
Short abstract
Kinship terminologies are basic cognitive semantic systems that all human societies use for organizing kin relations. Diversity in kinship systems and their categories is substantial, but constrained. Rácz, Passmore, and Jordan explore hypotheses about such constraints from learning theories and social pressures, testing the impact of a community‐size driven learning bottleneck against the social coordination demands of different kinds of marriage and resource systems.
1. Background
Social and cultural systems of meaning—such as grammatical categories, marriageable partners, the classifications of the natural world, and religious beliefs—all vary across cultures. While these systems are the products of generations of individuals interacting, they also partly reflect the possibilities of the human mind.
Anthropologists have long recognized the adaptive diversity of human behavior and cognition, and the importance and challenge of incorporating the facts of diversity is now an invigorated concern within the cognitive sciences (Evans, 2010; Henrich et al., 2010; Song et al., 2009). Investigations in domains such as color, space, and the body reveal that perception and expression of conceptual categories varies cross‐culturally (e.g., Malt & Majid, 2013). At the same time, there are systematic cross‐cultural regularities in category structures which may relate to shared human physiology of perception (for example in color categories, see Regier & Kay, 2009). Furthermore, for some domains, cross‐cultural variation in categories can be limited by the need for social coordination between individuals (Boyd et al., 1997). Cognitive constraints may also influence the extent to which any categorical system is free to vary (Kemp & Regier, 2012). A strong case can also be made for the mediating effect of cultural evolutionary processes on category formation. These include shared ancestry of language and culture, processes of diffusion and contact (Dunn et al., 2011; Levinson, 2012), as well as co‐dependencies between cultural categories and aspects of social and ecological environments (Botero et al., 2014).
A long‐standing focus in cognitive anthropology has been the semantic system of kinship: how different cultural groups classify family members using language. In this paper, we explore the interaction of culture and cognition by examining the effects of various cultural characteristics on the structure of kinship terminology systems in a large cross‐cultural sample.
A core example of cognitive effects on cultural evolution comes from recent work which has pointed to the role of speaker group size in shaping linguistic interaction, and, in turn, the complexity of grammar and vocabulary in language (see e.g., Nettle, 2012). These results indicate that languages spoken by large groups will have larger vocabularies of content words (like verbs and nouns) and less complexity in their morphology (so that fewer function‐form pairings of the same word exist). If we can arrange kinship systems along some particular axis of complexity, we have predictions on its correlation with the size of the speaker group.
Alternatively, measures of kinship vocabulary complexity may also be shaped by social practice. The complexity of a kinship system is shaped by its roles as a symbolic system interacting with how practices of family and marriage are organized in a society. These practices, and their instantiation in the meanings of words, may then be largely constrained by shared history as language is transmitted over time.
There is evidence for both group size and social practice affecting language in general and social practice affecting kinship terminology in particular. Our paper breaks new ground in that it compares the effects of group size and social practice on kinship terminology. We intend to demonstrate how a complete understanding of the micro‐level cognitive processes underlying any semantic category system must also be examined in the macro‐level context of cultural history. Some of our cognitive capacities or “gadgets” may themselves be products of a cultural evolution (Heyes, 2018). Similarly, we propose that the adaptive landscape of human social diversity constrains the kinds of social learning our cognitive mechanisms should be equipped to deal with.
1.1. The semantic typology of kinship variation
A kinship terminology system is a cognitive and social category system that is used by speakers of a language to refer to, group together, and distinguish, family members. These terminology sets (here, “kinship systems”) vary cross‐linguistically in structured and constrained ways (Murdock, 1949). Attested kinship systems show parallels with other category systems like color terms; they reflect cognitive pressures in displaying a trade‐off between simplicity and the ability to discriminate. Multiple relatives can be grouped together under one term: for example, an English “aunt” can refer to one’s mother’s or father’s sister. Globally, these extension patterns cover no more than a small space of all possible arrangements (Kemp & Regier, 2012): No language uses the same word to exclusively refer to all one’s grandparents and all one’s younger siblings.
Typological systems that categorize kinship terminology according to some axes of variation were first named by Morgan (1871). Morgan’s typology focuses on the ways in which relatives in own’s own (one) generation were named. The systems that he identified and that Murdock (1949, p. 67) later formalized are attached to the contemporary ethnonyms of paradigm anthropological example communities: Eskimo, Crow, Omaha, Sudanese, Hawaiian, and Iroquois (Fig. 1). Further variations have been identified (e.g., Dravidian, Kachin) and other typological schemes for classifying kinship terminologies proposed, in particular those that concentrate on the terms applied to relatives in one’s parental generation (for discussion, see Parkin, 1997). Here, we take advantage of the large body of literature that has explored the Morgan–Murdock typology of kin terms for cousins and concentrate on these semantic typologies and their global distribution.
Figure 1.
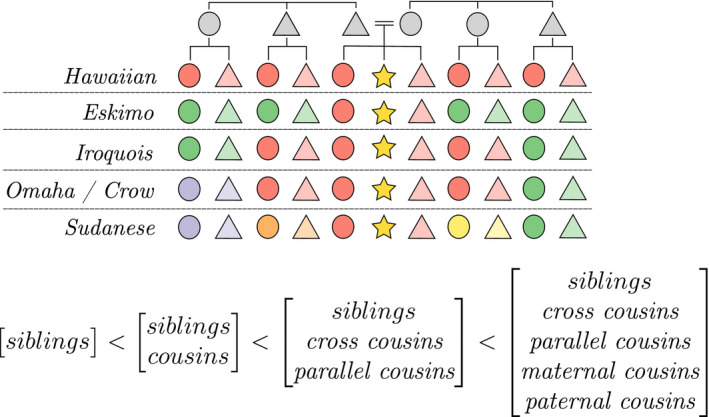
Above: Visual descriptions of the kinship typology. Circles indicate women, triangles indicate men, and the star represents the ego. Colors indicate common terms. Below: Increase in cousin term paradigmatic complexity
Systems of cousin terms can be ranked according to their paradigmatic complexity, that is, the number of distinctions they envelope in a single form. Hawaiian kinship systems use the same words to describe Ego’s siblings and the children of Ego’s parents’ siblings. All relatives in Ego’s generation are therefore called by sibling terms. Eskimo systems introduce a distinction between siblings and cousins: most major European languages such as English belong to this category, as do many in South‐east Asia. Iroquois systems further discriminate parallel cousins (i.e. children of parent’s same‐sex siblings, such as father’s brother’s son) and cross‐cousins (children of parent’s opposite‐sex siblings, such as mother’s brother’s son). Crow and Omaha systems introduce further “skewed” generational distinctions amongst cross‐cousins of one’s matrilineage (Crow) or patrilineage (Omaha), while removing generational distinctions for other cross‐cousins. Sudanese systems, on the whole, add a distinction between maternal‐ and paternal‐ cross‐ and parallel‐cousins, and fully descriptive systems discriminate all eight kinds of cousins by gender and that of connecting relatives.
Moving from Hawaiian to Sudanese, we see an increase in paradigmatic complexity, as more terms are used to describe the same number of relations. This increase is structured in the sense that distinctions comprise an implicational hierarchy (see Fig. 1). This structured variation in cousin terminology is a general aspect of kinship typology. Kinship systems, like other cognitive category systems, are presumed to be inherited through observation, imitation, and instruction. They are subject to small variations in replication, and the success of the variants hinges on two crucial general aspects of cognition—the ease with which the system can be learned and its goodness‐of‐fit in modeling the outside world. We can call the former learning pressure (see Tomasello, 2009) and the latter external social practice (see Bybee & Hopper, 2001).
These pressures tie back to the issues raised in Section 1. A cognitive category system must be learned by the individual, so a combination of salient environmental input (how culture shapes cognition) and various cognitive biases (how cognition shapes culture) will compete in shaping it. The question is (a) what form these biases take and (b) how they map to more general aspects of the social environment.
1.2. Learning pressures, population size, and grammatical complexity
Learning pressure manifests both in the variability of input received by the learner and the learner’s own cognitive biases. Input variability affects category learning on the sound and the word level (Maye & Weiss, 2003; Maye et al., 2002; Rácz et al., 2017). The robustness of category learning is increased if information is distributed across a larger number of contexts. For instance, hearing the same word from multiple speakers makes it easier to recognize, process, and learn that word, although this claim has been called into question (see e.g., Atkinson et al., 2015). At the same time, adult second‐ language learners tend to process language differently from native child learners in that they select for variants of smaller morphological complexity (see e.g., DeKeyser, 2000; Hudson Kam & Newport, 2009). This means that context variability and the ratio of child and adult learners will have a long‐term effect on linguistic complexity (for an alternate account, see Atkinson et al., 2018).
For a given language, both factors correlate with the number of speakers. What follows is that we expect a correlation between linguistic category complexity and the size of the speaker population. Nettle (2012) provides an excellent summary of the evidence on the correlation between population size and linguistic category complexity. He notes (p. 1829) that “[l]anguages of small communities tend to have smaller phonological inventories, longer words and greater morphological complexity than languages spoken in larger communities.” That is, the morphology of “larger” languages tends to have less paradigmatic complexity.
Lupyan and Dale (2010) point to the role of adult learners in the correlation between population size and morphological complexity, arguing that a large ratio of adult learners results in morphologically simpler languages with more lexical marking. This is consonant with the overall picture, summarized by Nettle, that an increase in population size comes together with a decrease in morphological complexity. Bromham et al. (2015), using a sample of Polynesian languages, find that larger populations are more prone to gain new word forms in the basic vocabulary while smaller populations are more prone to lose forms within the same vocabulary. Reali et al. (2018) offer a formal modeling treatment of how a variant’s ease to be learned affects its diffusion in the community, and how this correlates with the size and composition of the community. Sinnemäki and Di Garbo (2018) highlight that, in looking at group size and morphological complexity, the number of adult learners (L2 speakers) does not trivially correlate with population size and that the effect on morphological complexity varies across morphological domains.
Grammatical/morphological complexity in this literature typically refers to paradigmatic complexity, introduced in Section 1. In larger speaker groups, grammatical relations are less likely to be expressed by different forms of the same word (the word’s paradigm) and more likely to be paraphrased by a sequence of words. English has about 340 million native speakers and two forms for each noun. Hungarian has about 13 million native speakers and about 16 forms for each noun. The Hungarian form “házában” (house‐Poss3sg‐loc) translates in English as “in his/her house.” Here, English makes up for paradigmatic complexity with syntagmatic complexity.
While we are not aware of previous cross‐cultural work on kinship complexity and group size, paradigmatic and syntagmatic complexity readily apply to kinship terms. Polish has the term “siostrzenica” to refer to a sister’s daughter which can only be para‐phrased in English (as “niece” does not specify the gender of the parent). Here, again, Polish shows higher paradigmatic complexity, compensated by higher syntagmatic complexity in English.
Larger populations with a large amount of adult learners and high variability should have kinship systems with lower paradigmatic complexity, using fewer words to describe the same relations. We find support for this when we look at the use of kinship terms and related linguistic practices in specific small communities. For example, in Murrinhpatha in Northern Australia (Blythe, 2013) and in Datooga in Northern Tanzania (Mitchell, 2016), learning kinship terms or kinship‐related practices, such as name avoidance, requires a great extent of familiarity with the kinship relations of the entire local community. Farber (1975) discusses, on a greater scale, how this type of familiarity changes in larger communities with shifts in kinship practice.
Previous research has suggested a number of ways in which population size can influence paradigmatic complexity in language. This includes the ratio of adult learners, input variability, and ease of transmission in the community, all of which are correlated with the size of the overall speaker population. All these arguments can apply to the paradigmatic complexity of kinship systems. The essential point here is that a set of learning biases can mediate the effects of population size, and, as a result, become mainly responsible for variation in kinship systems.
1.3. Social practice
An alternative explanation for the paradigmatic complexity of kinship systems is that these are shaped by the specific social practices that make use of kinship terms; patterns of wealth transfer, marriage, or inheritance. Links between kinship systems and such practices have been extensively documented in the cultural anthropology literature (see for example the Explaining Human Culture database of hypotheses at the Human Relations Area Files & Inc, 22017), based on correlations in the Ethnographic Atlas (Murdock, 1967), the Standard Cross‐Cultural Sample (Murdock & White, 1969), or specific language groups. We provide here some examples to give a flavor of the kinds of associations described in the literature, but these are by no means exhaustive.
Murdock (1947) finds a correlation between the use of Crow and Omaha systems (which discriminate cross‐ and parallel‐cousins on the father’s or the mother’s side, respectively), exogamy (marrying outside the community), and/or unilinear descent (traced on the mother’s or the father’s side). Here, the social pressure comes from distinguishing who is and who is not in one’s matrilineage or patrilineage. Murdock (1949) returns to these findings and adds that a clan system or exogamous moieties also favor Crow/Omaha cousin terms. In both these instances, the kinship systems reflect who may be available for marriage. Coult (1965) finds correlations between, on the one hand, Omaha cousin terms, patrilineal descent, and preferential matrilineal cross‐cousin marriage and, on the other hand, Crow terms, matrilineal descent, and preferential patrilineal cross‐cousin marriage. Iroquois terms (cross‐ and parallel‐cousins are discriminated on both parent’s side) correlate with preferential bilateral cross‐cousin marriage in his sample. We should note that more recent work, relying on more advanced methods, puts at least some of these claims to question, as in the case of Guillon and Mace (2016), whose comparative phylogenetic analysis finds little evidence for the co‐evolution of cousin terms and descent organization in Bantu languages.
Goody (1970) surveys cousin terms and finds a correlation between Hawaiian terms and the prohibition of cross‐cousin marriage. A cross‐cousin will be called “sibling” in a Hawaiian system, so here the semantic system reflects the incest taboo. Iroquois terms are found with preference for cross‐cousin marriage, and it is precisely some cross‐cousins who might be outside one’s lineage and thus available for marriage. Much like Coult, Goody finds a correlation between Omaha, Crow, and Eskimo terms and patrilineal, matrilineal, and bilateral descent, respectively. Köbben et al. (1974) support Goody’s findings on the link between Hawaiian terms and the prohibition of cross‐cousin marriage, and establishes a correlation between Crow/Omaha terms and prohibition of marriage into the line of cross cousins.
The intuition underlying these correlations is that the semantic system reflects social practice. If marriage is permitted to certain types of siblings/cousins, these types should be named separately; emphasis on one line of descent should make distinctions on that line more salient.
1.4. Hypotheses
The broader cognitive literature on category complexity and population size and the anthropology literature on kinship terms and social practice provide us with two hypotheses that are testable against a cross‐cultural sample.
The main source of kinship complexity is speaker group size. Kinship systems vary in paradigmatic complexity. Paradigmatic complexity decreases with an increase in population size. This means that larger or more complex communities will use simpler kinship systems, irrespective of Sprachbund and language family effects.
The main source of kinship complexity is associated social practice. Kinship systems vary in structure. Various cultural practices (such as marriage or inheritance) rely on kinship distinctions. This means that the use of a kinship system will be linked to the presence or absence of these practices across communities: A society with prevalent cousin marriage or a society with asymmetrical patterns of descent and transfer will make more distinctions across siblings and cousins.
2. Methods
We examine the distribution of cousin term systems across 1,291 societies in the D‐PLACE online ethnographic database (d-place.org) (Kirby et al., 2016), largely based on data from the Ethnographic Atlas (Murdock, 1967).1 We work with 936 societies which have available information on kinship systems. The distribution of kinship systems can be seen in Fig. 2. Here, we display the variation in a subset of societies (those from the 12 largest language families represented in D‐PLACE) to visualize the influence of shared linguistic history on kinship diversity.
Figure 2.
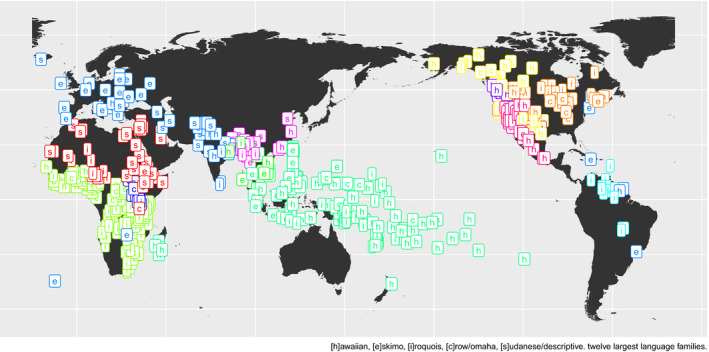
Global distribution of kinship systems across twelve largest language families in D‐PLACE ([H]awaiian, [E]skimo, [I]roquois, [C]row/Omaha, [S]udanese/Descriptive)
2.1. Outcome
Our outcome variable is the complexity of the kinship system which we quantify based on the number of distinctions across cousin terms, as discussed in Section 1.1 (EA027 in the Ethnographic Atlas—for details, see Appendix). We posit the ranking of Hawaiian < Eskimo < Iroquois < Crow/Omaha < Sudanese/Descriptive (see Fig. 1).
This quantification is simplified. For example, many Hawaiian systems make a distinction between Ego’s younger and older siblings/cousins. At the same time, the lack of distinction persists between “sibling” and “cousin” in these systems, such that our ranking still holds.
More complex characterizations of kinship system complexity, such as a calculation of entropy, require systematic kinship term lexical data comparison. We are currently building such a dataset to be publicly available (KinBank, see https://excd.org/research-activities/varikin), but in order to make large global comparisons here we focus on cousin terms.
2.2. Population‐level factors
We have two groups of population‐level factors.
Hypothesis 1 hinges on population size (EA202) and community size (EA031), represented in the Ethnographic Atlas data in D‐PLACE. Population size is defined therein as the size of the ethnic group as a whole. Community size represents an average population of local communities and is equally important as it determines the amount of variation and adult/child learner ratios in the individual learner’s language environment.
However, a large amount of data is missing for population size (27.03%) and community size (46.26%). Other indicators of community size are available: settlement patterns (EA030), the number of jurisdictional levels in the local community (EA032), the number of jurisdictional levels beyond the local community (EA033). The first one captures settlement size and complexity, categorizing societies from migratory bands to complex permanent settlements (pairwise correlation with population size (logged): r = 0.41). The second one focuses on the power hierarchy within settlements, ranging from independent families to clan districts (r = 0.22). The third one pulls focus onto inter‐settlement patterns, ranging from no authority beyond the local community to chiefdoms to complex states (r = 0.58). While subsistence (EA042) is not a direct proxy of population size, different subsistence types will typically support populations of various sizes: Forager populations are generally smaller, and societies that rely on intensive agriculture can be larger (r = 0.44, using numeric subsistence complexity). Following Botero et al. (2014), we combine these factors with population size and community size to estimate social group size and social complexity.
Hypothesis 2 hinges on a set of cultural practices coded in the Ethnographic Atlas data in D‐PLACE. These are the prevalence of cousin marriage (EA023, ranging from complete proscription to the allowance of marriage to first cousins), community marriage patterns (EA015, exogamous, endogamous, or agamous), and descent (EA043, patrilineal, matrilineal, bilateral, ambilineal, or mixed); see the Appendix for details.
2.3. Grouping factors
It is evident from Fig. 2 that the kinship system of a community is highly correlated with the language spoken in the community and the community’s location. For example, groups across the Pacific in the large Austronesian language family mostly have Hawaiian kinship. European languages mostly have Eskimo kinship, including Hungarian, a non‐Indo‐European language. As a consequence, we incorporate language family and geographical proximity in the analysis by adding a grouping factor for language family and one for the named geographic region, both taken from D‐PLACE.
2.4. Data analysis
The dataset is challenging in two ways, both typical for cross‐cultural data. Predictor variables are correlated (e.g., a society with unilineal descent is more likely to permit cousin marriage) and a lot of data are missing—population size and community size are two good examples. Our approach aims to account for these issues without the use of stepwise regression modeling, which increases the likelihood of Type I errors (Flom & Cassell, 2007).
We use a multilevel ordered categorical model to fit on the data (Wood, 2006; Wood et al., 2016) in R (R Core Team, 2016). We use ggplot to create the plots (Wickham, 2009). Our outcome variable is the type of kinship system, ranked by complexity (Hawaiian < Eskimo < Iroquois < Crow/Omaha < Sudanese/Descriptive). An ordered categorical model estimates an intercept for all levels of the outcome variable and assumes that they have a set order.
We fit two hypothesis‐testing models, one using predictors relevant to Hypothesis 1 (population size (logged), community size, jurisdiction, local jurisdiction, settlement patterns, and subsistence) and the other using predictors relevant to Hypothesis 2 (prevalence of cousin marriage, descent, community marriage practice). We do not impute missing data and instead fit each model on the maximum number of societies with available data for all predictors. This leaves us with n = 366 for Model 1 and n = 779 for Model 2). We then remove predictors with −1.5 < z < 1.5 and use a chi‐square test on the difference in scores and degrees of freedom as well as the Akaike Information Criterion for model selection. Subsequently, streamlined models are refit on the maximum number of data available. This procedure is followed to arrive at a best fit for each model.
The predictors from the best fits of the two models—local jurisdiction, subsistence, descent, and cousin marriage—are combined in Model 3. These are predictors that are relevant to testing our hypotheses. We also have evidence of their robustness. Using all possibly relevant predictors would inflate multicollinearity and create a data imputation problem, both of which are largely avoided using our approach.
This model is fit on all societies with data available on all these predictors (n = 743). To check robustness, Model 3 is also refit on data subsets (a) excluding Indo–European societies, (b) excluding the largest 5% of societies, and (c) limiting the dataset to societies in the standard cross‐cultural sample (SCCS; Murdock & White, 1969), albeit using the same predictors derived from the Ethnographic Atlas.
Our justification for (3a) is that many Indo‐European speakers are members of Western, rich, industrialized democracies and these groups tend to be outliers of broader ethnographic variation (Henrich et al., 2010). We have a similar reasoning for (3b)—we use population size to exclude the largest 5% and while population size data are missing for many societies, we expect that, for large societies, it will be more readily available, allowing for our method of exclusion. We use (3c) to render testing more robust, because the SCCS is a widely used sample of human societies that is deliberately stratified by region to minimize the effect of ancestry and diffusion (“Galton’s Problem” and spatial autocorrelation), and the sample was chosen to be representative of human lifeways.
Finally, to explore these relationships at finer resolution than the global level, we take a phylogenetic approach (Blute & Jordan, 2018; Mace & Pagel, 1994). We use language phylogenies (evolutionary trees) of three large representative language families, and a subset of the cultural data used for our models to calculate the phylogenetic signal for a set of traits. By mapping cultural data onto the tips of a language tree, we are able to measure how well a trait is structured by the branching relationships of cultural history. If a trait is primarily vertically inherited from parent to offspring cultural groups, then phylogenetic signal will be high. If traits are subject to cultural borrowing, independent innovation, stochastic change, or rapid contextual change, signal will be low.
3. Results
We quote four models here and discuss one in detail (see Table 1; note that we use zero‐based numbering. We return to robustness checks and high resolution phylogenetic analysis in Section 3.2.
Table 1.
Summary statistics for models
| Model | No. Observations | Cumulative Deviance Explained |
|---|---|---|
| 0 (only grouping factors) | 936 | 0.18 |
| 1 (social complexity) | 807 | 0.19 |
| 2 (social practice) | 841 | 0.23 |
| 3 (combined) | 743 | 0.23 |
Model 0 has no population‐level effects and only contains grouping factors for language family and geographic region. As we can see, this model already explains some amount of variation (18%), underscoring that language family (shared history) and region (spatial diffusion opportunities and shared adaptation) are very important factors in determining the kinship system used in a community. These grouping factors are present in all subsequent models.
Model 1 is fit to determine the relevance of predictors for Hypothesis 1 (i.e., social relevant are jurisdiction on a local level and main mode of subsistence. Population and community size, jurisdiction beyond the local level and settlement patterns are not relevant in predicting kinship system. This can be either because these factors are not directly relevant to kinship complexity, or because too many data are missing for meaningful inference.
Model 2 is fit to determine the relevance of predictors for Hypothesis 2 (social practice affects kinship complexity). The fixed effects that remain relevant are descent and prevalence of cousin marriage. Community marriage patterns are not relevant in predicting the use of a particular kinship system.
The relevant aspects of models 1 and 2 are that both explain some amount of variation in the data, but that the additional explaining power of Model 1 is relatively low—social complexity plays little, if any role.
Model 3 is our combined model. It contains the relevant predictors from Model 1 and Model 2. The summary of the fixed effects can be seen in Table 2. The base levels are “intensive agriculture” for subsistence and “patrilineal” for descent. These are essentially arbitrary, though the plurality of societies are patrilineal.
Table 2.
Summary of the fixed effects, Model 3 (Predictor name, estimated effect, standard error, and z‐value)
| Estimate | SE | z‐value | |
|---|---|---|---|
| (Intercept) | −0.073 | 0.511 | −0.142 |
| local jurisdictional hierarchy | −0.005 | 0.137 | −0.036 |
| subsistence:extensive agriculture | 0.062 | 0.217 | 0.285 |
| subsistence:foraging | −0.149 | 0.276 | −0.540 |
| subsistence:pastoralism | 0.882 | 0.382 | 2.310 |
| cousin marriage | 0.461 | 0.078 | 5.904 |
| descent:matrilineal | −0.115 | 0.243 | −0.473 |
| descent:bilateral or quasi‐lineage | −1.656 | 0.232 | −7.146 |
| descent:duo‐ or ambilineal | −1.100 | 0.301 | −3.656 |
| descent:mixed | −1.456 | 0.384 | −3.789 |
Our proxy of community size, local jurisdictional hierarchy, is not a robust predictor of kinship complexity. Robust predictors (−1.5 > z > 1.5) are subsistence, prevalence of cousin marriage, and descent. Pastoralist societies are more likely to have more complex kinship systems. We had no starting assumptions about pastoralists, so this is a curious result and we return to it in the discussion. Kinship complexity increases with more prevalent cousin marriage. Symmetrical descent systems (such as bilateral or ambilineal ones) are likely to have less complex kinship systems than unilineal (patri‐ or matrilineal) ones.
While model fitting is explicitly designed to avoid multicollinearity, it remains an issue given the nature of the predictors. A post hoc inspection of variance inflation factors (Clifford, 2016) reveals that confidence intervals for the robust predictors can be inflated up to a rate of 2.1–3.01 times. This especially casts a doubt on the effect of pastoralism, which is estimated to be relatively small in the first place. The other predictor estimates are larger and more resilient in the face of possible multicollinearity effects.
Fig. 3 illustrates the global distribution of some of the relevant predictors—descent type, cousin marriage, and subsistence—against kinship system type. It demonstrates the spatial (and historical) clustering of many co‐associations in the ethnographic data. For example, across Northern Africa and the Middle East, we see substantial co‐occurrence of pastoralism, Sudanese/Descriptive kinship systems, and marriage with first cousins. These co‐occurrences are not new observations, and have been attributed as adaptations to unproductive environments in the case of pastoralism (see Pryor, 2005), and in the case of Sudanese kinship, as logical‐linguistic indicators that some relatives are marriageable while others are not. Importantly, our results show that while shared history and environment can account for some co‐occurrence in language and culture between societies, there is further variation left to explain.
Figure 3.
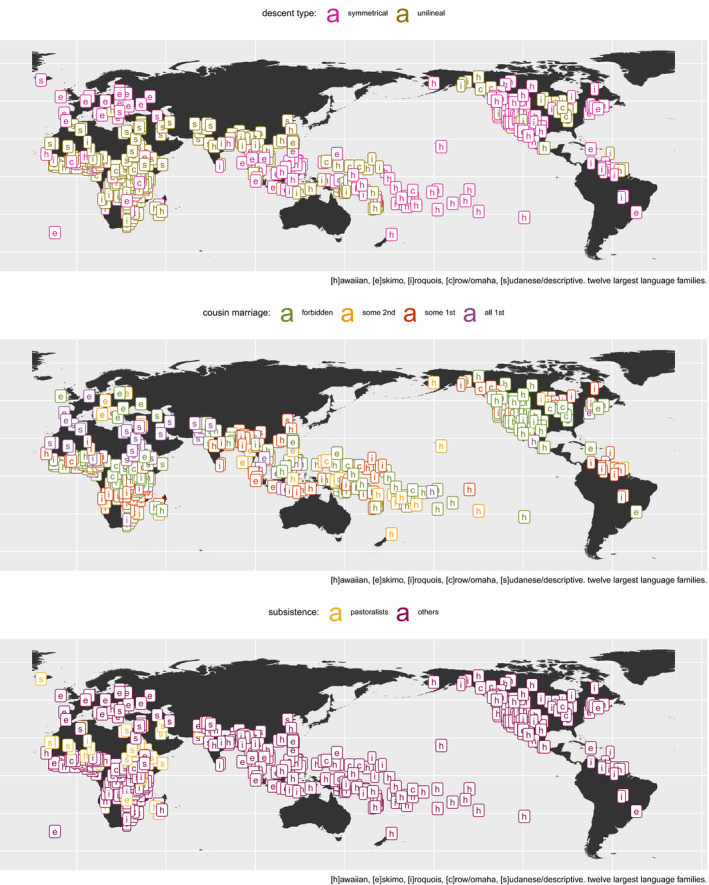
The distribution of social predictors and kinship systems. Panel (a) shows kinship system versus descent category. Symmetrical descent includes societies coded as bilateral or double descent; unilineal includes societies coded as patrilineal or matrilineal. Panel (b) shows cousin marriage practice: forbidden, some 2nd cousins, some 1st cousins, all 1st cousins. Panel (c) divides societies by whether they are pastoralists or not
3.1. Predictions
Fig. 4 shows the predictions of Model 3, aggregated across levels of the predictors, with aggregated estimated standard errors. The model gives a probability for society having each kinship system; these add up to 1. Fig. 4 aggregates the predicted probabilities and standard errors across levels of the predictors.
Figure 4.
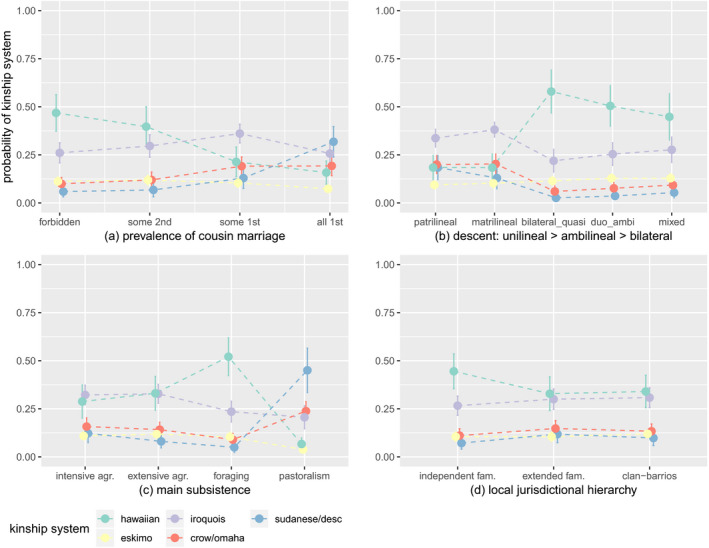
Predictions of the combined model. The ordered outcome categories are Hawaiian < Eskimo < Iroquois < Crow/Omaha < Sudanese/Descriptive. For each panel, we show the probability of any particular kinship system for a given category of (a) cousin marriage (b) main form of subsistence (c) descent system and (d) local jurisdictional hierarchy. (a) Cousin marriage is categorized as (i) all forms forbidden, (ii) some 2nd cousins, (iii) some 1st cousins, (iv) all 1st cousins; (b) subsistence is categorized as (i) intensive and (ii) extensive agriculture, (iii) foraging, and (iv) pastoralism; (c) descent systems are categorized as unilineal/ambilineal/bilateral, and, specifically, as (i) patrilineal, (ii) matrilineal, (iii) bilateral, (iv) ambilineal, (v) mixed; (d) local jurisdictional hierarchy is categorized as (i) independent and (ii) extended families, (iii) clan‐barrios.
For instance, (upper left panel) the likelihood of having a simpler Hawaiian system drops with the increase in the prevalence of cousin marriage. In contrast, the likelihood of having a more complex Sudanese system increases under this condition. One has to bear in mind that the model assumes these systems to be ordered according to complexity.
This means that the subsistence effect is more robust for pastoralists (upper right panel) than for foragers. This is because, in the former case, we see, for example, both a drop in the likelihood of Hawaiian and an increase in the likelihood of Sudanese. Kinship complexity is higher for unilineal than for symmetrical systems, driven by all types except Crow/Omaha and Eskimo (lower left), while, despite the drop in the likelihood of Hawaiian, local political complexity overall does not covary with kinship complexity in this model (lower right).
3.2. Robustness checks and phylogenetic signal
Fitting Model 3 on data (a) after excluding Indo–European‐speaking societies or (b) the largest 5% in terms of population size yields very similar results, except that, in the latter case, the distinction between pastoralists and other subsistence types is diminished.
In terms of (c) comparing the Standard Cross‐Cultural Sample and the Ethnographic Atlas: All 186 societies of the SCCS are present in the Ethnographic Atlas, but only 161 have all the required data, so we fit the model on these societies. This yields similar results on the population‐level predictors: Pastoralists and more prevalent cousin marriage practices are correlated with more complex kinship systems, along with unilineal (as opposed to symmetrical) descent systems. One main difference is that language family and region are no longer significant predictors in this model, which is to be expected given the stratified purpose of the SCCS.
On the whole, our regression analysis finds strong effects of cousin marriage and descent, along with an effect of subsistence (pastoralists/other main sources of subsistence) on the complexity of the kinship system in the societies of the sample. The effects remain robust if we take into consideration the skewing effect of Indo‐European or very large societies, and also remain for the smaller set of societies in the SCCS. However, one simplification of the regression model is that it treats language families as trees with no internal structure, effectively assuming the same distance between all languages that belong to a given family.
In order to test for cultural inheritance using a higher resolution, we use phylogenetic “D” tests to determine if kinship systems display phylogenetic structure (Fritz & Purvis, 2010). A “D” test provides a value to express the extent to which patterns are constrained by the evolutionary relationships between societies (cultural history) or dispersed randomly across the phylogenetic tree. We use language family trees (phylogenies) from D‐PLACE to estimate the D statistic and its associated p‐values for the most common kinship system types in three different language families: Austronesian (85 observations), Bantu (69 observations), and Uto‐Aztecan (22 observations). Because multiple histories might be inferred from any linguistic data set, for each family we test D across 1,000 trees derived using Bayesian phylogenetic inference (Dunn et al., 2011; Gray et al., 2009; Grollemund et al., 2015). Each of these trees represents a slightly different but highly plausible reconstruction of cultural history. We infer a value of D for kinship system types that are seen in more than 10% of societies on the language tree: Eskimo, Hawaiian, and Iroquois systems in Austronesian; Hawaiian, Iroquois, and Omaha systems in Bantu; and Crow, Eskimo, Hawaiian, and Iroquois systems in Uto‐Aztecan.
Across all three families we find that around half of the kinship systems show meaningful phylogenetic signal (i.e., D close to or less than 0) at a fine‐grained local level, demonstrating the importance of shared ancestry in structuring complexity in semantic systems even in closely related languages. The D values can be seen in Table 3.
Table 3.
D‐statistic tests of phylogenetic structuring for terminological types, in three large language families
| Present | D‐Statistic | ||
|---|---|---|---|
| Austronesian (n = 85) | Eskimo | 14 | −0.498 |
| Hawaiian | 48 | 0.659 | |
| Iroquois | 15 | 0.095 | |
| Bantu (n = 69) | Hawaiian | 9 | 0.402 |
| Iroquois | 44 | 0.162 | |
| Omaha | 8 | 0.780 | |
| Uto‐Aztecan (n = 22) | Hawaiian | 16 | −0.596 |
| Iroquois | 4 | −2.336 |
A D‐statistic close to or greater than 1 indicates a random distribution, not structured by the phylogeny. A D statistic close to 0 implies consistency with Brownian motion along the branches of the phylogeny, that is, structuring by descent. D less than 0 implies strong phylogenetic clustering.
4. Discussion
We used multilevel ordered categorical models to account for an axis of kinship system complexity across hundreds of human societies. We tested two hypotheses that emerged from the literature on the correlates of semantic complexity and kinship systems: the effects of speaker group size and cultural practices. Our analysis of the evidence does not support a link between an increase in community size and a decrease in kinship system complexity, but we do find support for the position that kinship systems are co‐determined by specific practices of marriage and descent. In doing so, we also assessed the extent to which spatial proximity and shared ancestry influence our measure of kinship complexity. We found that while both explain some variation at a global scale on a large unstratified data set, detecting these effects is subject to the scale and type of analysis.
Our evidence for both main findings remains robust when we control for the effect of language family and spatial proximity is resilient to multicollinearity, and our analyses do not hinge on the inclusion of data points from large‐population states or Indo‐European societies. This is striking, as large cross‐cultural analyses are inevitably plagued by noise in the data, related to the inherent patchiness and unstructured nature of much ethnographic data. Data on population and community size are difficult to extrapolate from ethnographic sources where a formal census is not available, and they are restricted to a particular time and place foci (Ember et al., 1992). Despite these complexities, our aim was to avoid the methodological pitfalls related to the regression analysis of large sets of covarying factors in incomplete data, such as the use of unprincipled top–down stepwise regression (Flom & Cassell, 2007). Instead, we opted to rely on expert judgment (Galison & Daston, 2007) in choosing a set of factors to compare two plausible hypotheses, adapted to variation in kinship systems, and to see which one explained more variation in our data.
The low predictive power of our models strongly suggests that kinship systems evolve in complex, multifaceted processes which are difficult to capture in a correlational study. While other studies have detected some broad predictive trends in cultural features, such as an association between poorer environment and the presence of a belief in moralizing high gods (Botero et al., 2014), it may be that here the global scope of our analyses masks important regional cultural dynamics of kinship systems. Our tests for phylogenetic signal support this supposition: Different kinship systems show phylogenetic clustering in different language families, echoing the lineage‐specificity found in word‐order studies (Dunn et al., 2011). Ultimately, language family remains the most important predictor of kinship system in our analyses. Given that some large language families such as Indo‐European, Austronesian, and Bantu are associated with Neolithic spread of agricultural technologies (Bellwood, 2005), and that changes in subsistence have been considered to be catalysts for change in social organization (Apostolou, 2010; Ember et al., 1992; Nimkoff, 1965; Walker et al., 2013), we suggest that language–family‐level approaches using comparative phylogenetic methods (Jordan, 2013) may test these coevolutionary hypotheses in future.
While our results suggest that our measure of kinship complexity is determined by specific practices and not by community size or population size, the effect of subsistence on kinship complexity remains an exception. Pastoralists tend to have more complex kinship systems than agriculturalists or foragers. Holden and Mace (2003) discuss the relationship between the emergence of patriliny and cattle ownership in the Bantu. They explain the apparent connection (cattle ownership leads to patriliny) in terms of wealth transfer—herds of cattle need to be held together to defend and inherit, favoring male heirs. This explanation, scaled upwards, could apply to our data. Cattle ownership shapes wealth transfer practices and these, in turn, shape kinship. This means that subsistence should be interpreted as a proxy for social practices rather than a proxy for overall complexity of social organization. Our result on pastoralism should be treated with reservations, however, as it is relatively weak and more sensitive to predictor multicollinearity.
The covariation of kinship systems with specific practices, rather than group size, has implications for the debate on the relationship between linguistic and speaker group complexity. Works such as Nettle (2012) and Reali et al. (2018) point to and formalize broad biases in learning and transmission for aspects of language that covary with group size. These include low‐level, closed sets of function words, like morphology, and higher‐ evel, open sets of content words, like vocabulary.
Kinship systems are closed sets of content words, entwined with social practice. In some cases, kinship is able to “invade” the grammar and be marked on, for example, verb agreement (Blythe, 2013). This means that it is an ideal testing ground for hypotheses on the effects of broad biases and specific practices on language use. Our phylogenetic signal analyses are suggestive: On our measure of complexity, the most complex systems that we tested (Crow, Omaha) are not structured by long‐term shared ancestry and perhaps more liable to change from learning pressures. What we infer from cross‐cultural variation in kinship is that caution is warranted in attributing patterns of cross‐cultural variation to broad biases because these patterns are more likely to be mediated by specific cultural practices. No doubt, these practices are sensitive to group size (exemplified by the difference between pastoralists and other forms of subsistence in Bantu language groups). It is simply to say that a rounded account of explaining cognitive diversity should consider macro (cultural evolutionary) as well as micro (cognition and learning) drivers. Given that kinship is a good example of an intermediate lexical class, these results could be generalized as informative for the broader debate.
The intermediate nature of kinship systems in language invokes the parallel of a separate debate in anthropology and archaeology on the correlation between population size and toolkit size (Aoki, 2018; Henrich, 2004). The major difference is that unlike tools, cultural practices or the specialized vocabulary that goes with them (e.g., kinship words) —and the systems in which they articulate—must be learned by everyone in the community. As a consequence, many of the explanations proposed for the correlation between toolkit size and population size may not be applicable to kinship.
This paper builds on the existing literature on language complexity in general and kinship systems in particular. It is novel in extending arguments on population size and complexity to kinship system and comparing population size and social practice at an unprecedented scale. The results presented here are both larger in scope and more statistically principled than previous work on the correlates of kinship systems, rendering our findings fairly robust. Further, we see our contribution as demonstrating how kinship categories, a key aspect of social cognition, can be approached in a comparative and cultural‐evolutionary manner alongside the standard individual‐level experimental and modeling tools of cognitive science. Further research combining the macro and the micro can help give a well‐rounded account of the constraints on human social categories.
Supporting information
5. Acknowledgments
We thank Joe Blythe, Simon Greenhill, Alice Mitchell, Sean Roberts, Alex Schumacher, and Catherine Sheard, as well as three reviewers for their useful insights which improved this paper. We particularly thank Andrea Bender and Sieghard Beller for their encouragement. This research was funded from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement no. 639291, Starting Grant VARIKIN), and was supported by a Leverhulme Research Fellowship (47690) to F.M.J.
Appendix 1.
Coding of Ethnographic Atlas variables
For details, see https://github.com/petyaracz/RaczPassmoreJordan2018.
| EA Variable | Name | EA Code: Coding Used in Paper | Type in Paper |
|---|---|---|---|
| EA015 | Marriage types | 1,2: endogamous; 3: agamous; 4,5,6: exogamous | Factor |
| EA023 | Cousin marriage | 7,8: 1; 11,12: 2; 1,2,3,4,5,6,9,13: 3; 10, 4 | Ordered |
| EA027 | Cousin type | 4: hawaiian; 3: eskimo; 5: iroquois; 1,6: crow/omaha; 7,2: sudanese/descriptive | Ordered |
| EA031 | Community size | Ordered | |
| EA030 | Settlement patterns | Ordered | |
| EA032 | Local jurisdiction | Ordered | |
| EA033 | Jurisdiction | Ordered | |
| EA042 | Subsistence | 7: intensive agriculture; 5,6,9: extensive agriculture; 4: pastoralism; 1,2,3: foraging | Factor |
| EA043 | Descent type | 1: patrilineal; 6,4: bilateral/quasi‐lineages; 3: matrilineal, 2,5: duolateral/ambilineal; 7: mixed | Factor |
| EA202 | Population size | Numeric |
This article is part of the topic “The Cultural Evolution of Cognition,” Andrea Bender, Sieghard Beller and Fiona Jordan (Topic Editors). For a full listing of topic papers, see http://onlinelibrary.wiley.com/journal/10.1111/(ISSN)1756-8765/earlyview
Note
Code and data available at http://doi.org/10.5281/zenodo.2625861.
References
- Aoki, K. (2018). On the absence of a correlation between population size and "toolkit size" in ethnographic hunter‐gatherers. Philosophical Transactions of the Royal Society B: Biological Sciences, 373(1743), 20170061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Apostolou, M. (2010). Bridewealth as an instrument of male parental control over mating: Evidence from the standard cross‐cultural sample. Journal of Evolutionary Psychology, 8, 205–216.22947792 [Google Scholar]
- Atkinson, M. , Kirby, S. , & Smith, K. (2015). Speaker input variability does not explain why larger populations have simpler languages. PLoS ONE, 10(6), e0129463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Atkinson, M. , Smith, K. , & Kirby, S. (2018). Adult learning and language simplification. Cognitive Science, 42(8), 2818–2854. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bellwood, P. (2005). First farmers: The origins of Agricultural Societies. Malden, MA: Blackwell. [Google Scholar]
- Blute, M. , & Jordan, F. (2018). The evolutionary approach to history: Sociocultural phylogenetics In Hopcroft R. (Ed.), Oxford handbook of evolution, biology, and society (pp. 1:25621-25642). New York: Oxford University Press. [Google Scholar]
- Blythe, J. (2013). Preference organization driving structuration: Evidence from Australian Aboriginal interaction for pragmatically motivated grammaticalization. Language, 89(4), 883–919. [Google Scholar]
- Botero, C. A. , Gardner, B. , Kirby, K. R. , Bulbulia, J. , Gavin, M. C. , & Gray, R. D. (2014). The ecology of religious beliefs. Proceedings of the National Academy of Sciences, 111(47), 16784–16789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boyd, R. , Durham, W. H. , & Richerson, P. J. (1997). Are cultural phylogenies possible In Weingart P., Mitchell S. D., Richerson P. J., & Maasen S. (Eds.), Human by nature: Between biology and the social sciences (pp. 355–384) London: Psychology Press. [Google Scholar]
- Bromham, L. , Hua, X. , Fitzpatrick, T. G. , & Greenhill, S. J. (2015). Rate of language evolution is affected by population size. Proceedings of the National Academy of Sciences, 112(7), 2097–2102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bybee, J. L. , & Hopper, P. J. (2001). Frequency and the emergence of linguistic structure. Amsterdam: John Benjamins. [Google Scholar]
- Clifford, S. (2016). Variance inflation factor for generalized additive models [accessed on April 24, 2016]. Available at https://gist.github.com/samclifford/e1223861931c69ff159c8c680a96c11d.
- Coult, A. D. (1965). Terminological correlates of cross‐cousin marriage. Bijdragen tot de Taal‐, Land‐, en Volkenkunde, 1ste Afl, 120–139. [Google Scholar]
- DeKeyser, R. M. (2000). The robustness of critical period effects in second language acquisition. Studies in Second Language Acquisition, 22(4), 499–533. [Google Scholar]
- Dunn, M. , Greenhill, S. J. , Levinson, S. C. , & Gray, R. D. (2011). Evolved structure of language shows lineage‐specific trends in word‐order universals. Nature, 473(7345), 79–82. [DOI] [PubMed] [Google Scholar]
- Ember, C. R. , Page, H. , O’Leary, T. , & Martin, M. (1992). Computerized concordance of cross‐cultural samples. New Haven, CT: Human Relations Area Files. [Google Scholar]
- Evans, N . (2010). Chapter 23. Semantic typology In Bakker D. (Ed.), The Oxford handbook of linguistic typology (pp. 463-487). Oxford, UK: Oxford University Press. [Google Scholar]
- Farber, B. (1975). Bilateral kinship: Centripetal and centrifugal types of organization. Journal of Marriage and the Family, 37(4), 871–888. [Google Scholar]
- Flom, P. L. , & Cassell, D. L. (2007). Stopping stepwise: Why stepwise and similar selection methods are bad, and what you should use. In NorthEast SAS Users Group Inc 20th Annual Conference: November 11-14, 2007; Baltimore, MD. [Google Scholar]
- Fritz, S. A. , & Purvis, A. (2010). Selectivity in mammalian extinction risk and threat types: A new measure of phylogenetic signal strength in binary traits. Conservation Biology, 24(4), 1042–1051. [DOI] [PubMed] [Google Scholar]
- Galison, P. , & Daston, L. (2007). Objectivity. New York, NY: Zone Books. [Google Scholar]
- Goody, J. (1970). Cousin terms. Southwestern Journal of Anthropology, 26(2), 125–142. [Google Scholar]
- Gray, R. D. , Drummond, A. J. , & Greenhill, S. J. (2009). Language phylogenies reveal expansion pulses and pauses in pacific settlement. Science, 323(5913), 479–483. [DOI] [PubMed] [Google Scholar]
- Grollemund, R. , Branford, S. , Bostoen, K. , Meade, A. , Venditti, C. , & Pagel, M. (2015). Bantu expansion shows that habitat alters the route and pace of human dispersals. Proceedings of the National Academy of Sciences, 112(43), 13296–13301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guillon, M. , & Mace, R. (2016). A phylogenetic comparative study of bantu kinship terminology finds limited support for its co‐evolution with social organisation. PLoS ONE, 11(3), e0147920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henrich, J. (2004). Demography and cultural evolution: how adaptive cultural processes can produce maladaptive losses—The Tasmanian case. American Antiquity, 69(2), 197–214. [Google Scholar]
- Henrich, J. , Heine, S. J. , & Norenzayan, A. (2010). Most people are not weird. Nature, 466(7302), 29–29. [DOI] [PubMed] [Google Scholar]
- Heyes, C. (2018). Cognitive gadgets: The cultural evolution of thinking. Cambridge, MA: Harvard University Press. [Google Scholar]
- Holden, C. J. , & Mace, R. (2003). Spread of cattle led to the loss of matrilineal descent in Africa: A coevolutionary analysis. Proceedings of the Royal Society of London B: Biological Sciences, 270(1532), 2425–2433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hudson Kam, C. L. , & Newport, E. L. (2009). Getting it right by getting it wrong: When learners change languages. Cognitive Psychology, 59(1), 30–66. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Human Relations Area Files, Inc . (2017). World cultures ethnography database. Available at http://hraf.yale.edu/ehc. Accessed August 01, 2017.
- Jordan, F. M. (2013). Comparative phylogenetic methods and the study ofpattern and process in kinship In McConvell P., Keen I., & Hendery R. (Eds.), Kinship systems: Change and reconstruction (pp. 43–58). Salt Lake City, UT: University of Utah Press. [Google Scholar]
- Kemp, C. , & Regier, T. (2012). Kinship categories across languages reflect general communicative principles. Science, 336(6084), 1049–1054. [DOI] [PubMed] [Google Scholar]
- Kirby, K. R. , Gray, R. D. , Greenhill, S. J. , Jordan, F. M. , Gomes‐Ng, S. , Bibiko, H.‐J. , Blasi, D. E. , Botero, C. A. , Bowern, C. , Ember, C. R. , Leehr, D. , Low, B. S. , McCarter, J. , Divale, W. , & Gavin, M. C. (2016). D‐place: A global database of cultural, linguistic and environmental diversity. PLoS ONE, 11(7), e0158391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Köbben, A. J. , Verrips, J. , & Brunt, L. (1974). Lévi‐Strauss and empirical inquiry. Ethnology, 13, 215–223. [Google Scholar]
- Levinson, S. C. (2012). The original sin of cognitive science. Topics in Cognitive Science, 4(3), 396–403. [DOI] [PubMed] [Google Scholar]
- Lupyan, G. , & Dale, R. (2010). Language structure is partly determined by social structure. PLoS ONE, 5(1), e8559. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mace, R. , & Pagel, M. (1994). A latitudinal gradient in the density of human languages in North America. Proceedings of the Royal Society of London, Series B: Biological Sciences, 261(1360), 117–121. [Google Scholar]
- Malt, B. C. , & Majid, A. (2013). How thought is mapped into words. Wiley Interdisciplinary Reviews: Cognitive Science, 4(6), 583–597. [DOI] [PubMed] [Google Scholar]
- Maye, J. , & Weiss, D. (2003). Statistical cues facilitate infants’ discrimination of difficult phonetic contrasts In Proceedings of the 27th annual Boston University conference on language development (vol. 2, pp. 508–518). Boston: Boston University Press. [Google Scholar]
- Maye, J. , Werker, J. F. , & Gerken, L. (2002). Infant sensitivity to distributional information can affect phonetic discrimination. Cognition, 82(3), B101–B111. [DOI] [PubMed] [Google Scholar]
- Mitchell, A. (2016). Words that smell like father‐in‐law: A linguistic description of the Datooga avoidance register. Anthropological Linguistics, 57(2), 195–217. [Google Scholar]
- Morgan, L. H. (1871). Systems of consanguinity and affinity of the human family, vol. 218. Washington, DC: Smithsonian Institution. [Google Scholar]
- Murdock, G. P. (1947). Bifurcate merging, a test of five theories. American Anthropologist, 49(1), 56–68. [DOI] [PubMed] [Google Scholar]
- Murdock, G. P. (1949). Social structure. London: Macmillan. [Google Scholar]
- Murdock, G. P. (1967). Ethnographic atlas: a summary. Ethnology, 6(2), 109–236. [Google Scholar]
- Murdock, G. P. , & White, D. R. (1969). Standard cross‐cultural sample. Ethnology, 8(4), 329–369. [Google Scholar]
- Nettle, D. (2012). Social scale and structural complexity in human languages. Philosophical Transactions of the Royal Society B, 367(1597), 1829–1836. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nimkoff, M. F. (1965). Types of family and the social system and the family In Nimkoff M. F. (Ed.), Comparative family systems (pp. 12–60). Boston, MA: Houghton Mifflin. [Google Scholar]
- Parkin, D. (1997). Kinship: An introduction to the basic concepts. Oxford, UK: Wiley‐Blackwell. [Google Scholar]
- Pryor, F. L. (2005). Economic systems of foraging, agricultural, and industrial societies. Cambridge, UK: Cambridge University Press. [Google Scholar]
- R Core Team . (2016). R: A language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing. [Google Scholar]
- Rácz, P. , Hay, J. B. , & Pierrehumbert, J. B. (2017). Social salience discriminates learnability of contextual cues in an artificial language. Frontiers in Psychology, 8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reali, Florencia , Chater, Nick , & Christiansen, Morten H. (2018). Simpler grammar, larger vocabulary: How population size affects language. Proceedings of the Royal Society B: Biological Sciences, 285(1871), 2017-2586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Regier, T. , & Kay, P. (2009). Language, thought, and color: Whorf was half right. Trends in Cognitive Sciences, 13(10), 439–446. [DOI] [PubMed] [Google Scholar]
- Sinnemäki, K. , & Di Garbo, F. (2018). Language structures may adapt to the sociolinguistic environment, but it matters what and how you count: A typological study of verbal and nominal complexity. Frontiers in Psychology, 9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song, J. , Bender, A. , & Beller, S. (2009). Conditional promises and threats in Germany, China, and Tonga: Cognition and emotion. Journal of Cognition and Culture, 9(1–2), 115–139. [Google Scholar]
- Tomasello, M. (2009). Constructing a language. Cambridge, MA: Harvard University Press. [Google Scholar]
- Walker, R. S. , Beckerman, S. , Flinn, M. V. , Gurven, M. , von Rueden, C. , Kramer, K. L. , Greaves, R. D. , Cordoba, L. , Villar, D. , Hagen, E. H. , Koster, J. M. , Sugiyama, L. , Hunter, T. E. , & Hill, K. (2013). Living with kin in lowland horticultural societies. Current Anthropology, 54(1), 96–103. [Google Scholar]
- Wickham, H. (2009). ggplot2: Elegant graphics for data analysis. New York: Springer. [Google Scholar]
- Wood, S. (2006). Generalized additive models: An introduction with R. Boca Raton, FL: CRC Press. [Google Scholar]
- Wood, S. N. , Pya, N. , & Säfken, B. (2016). Smoothing parameter and model selection for general smooth models. Journal of the American Statistical Association, 111(516), 1548–1563. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials


