Lumbar intervertebral disc characterization through quantitative MRI analysis: An automatic voxel‐based relaxometry approach

Abstract

Purpose

To develop an automated pipeline based on convolutional neural networks to segment lumbar intervertebral discs and characterize their biochemical composition using voxel‐based relaxometry, and establish local associations with clinical measures of disability, muscle changes, and other symptoms of lower back pain.

Methods

This work proposes a new methodology using MRI (n = 31, across the spectrum of disc degeneration) that combines deep learning–based segmentation, atlas‐based registration, and statistical parametric mapping for voxel‐based analysis of T_1ρ and T₂ relaxation time maps to characterize disc degeneration and its associated disability.

Results

Across degenerative grades, the segmentation algorithm produced accurate, high‐confidence segmentations of the lumbar discs in two independent data sets. Manually and automatically extracted mean disc T_1ρ and T₂ relaxation times were in high agreement for all discs with minimal bias. On a voxel‐by‐voxel basis, imaging‐based degenerative grades were strongly negatively correlated with T_1ρ and T₂, particularly in the nucleus. Stratifying patients by disability grades revealed significant differences in the relaxation maps between minimal/moderate versus severe disability: The average T_1ρ relaxation maps from the minimal/moderate disability group showed clear annulus nucleus distinction with a visible midline, whereas the severe disability group had lower average T_1ρ values with a homogeneous distribution.

Conclusion

This work presented a scalable pipeline for fast, automated assessment of disc relaxation times, and voxel‐based relaxometry that overcomes limitations of current region of interest–based analysis methods and may enable greater insights and associations between disc degeneration, disability, and lower back pain.

1. INTRODUCTION

Low back pain (LBP) is the leading cause of disability globally,1 with a 38%2 average lifetime prevalence. Treatments, lost wages, and reduced productivity cost the United States over $100 billion3 every year. Although LBP is widespread, its clinical presentation is complex and its pathophysiology is poorly understood.4 Identifying patients’ pain‐generating structures and determining the appropriate treatment course remains a challenge5, 6: Despite a 6‐fold increase in Medicare expenditures on LBP treatments over 10 years, patient outcomes have not improved. There is an urgent need for the discovery of noninvasive biomarkers that distinguish LBP phenotypes.

A common mechanism for developing LBP is intervertebral disc degeneration, which occurs when disc homeostasis is perturbed by injury or aging.7 A cascade of biochemical and microstructural changes take place, including loss of glycosaminoglycans, disorganization of annular collagen, and dehydration.8 These early‐stage changes precede large‐scale morphological changes that are associated with pain and disability.9 Conventional MRI sequences and grading systems (Pfirrmann10/modified Pfirrmann11) are used to determine the severity of disc degeneration through qualitative assessment of disc morphology and signal intensity of the nucleus and annulus. These methods are limited by moderate interrater reproducibility10 and broad binning of disc phenotypes.12 Quantitative MRI (qMRI) is a powerful tool that is capable of detecting local variations in disc composition; however, its use is limited by coarse, unreliable, and slow manual analyses methods.13, 14, 15, 16, 17

T_1ρ mapping, or spin‐lock imaging, is a qMRI sequence that probes slow interactions between bulk water and extracellular matrix macromolecules by applying a continuous, low‐frequency RF pulse. T₂ mapping, or spin‐spin imaging, is a quantitative sequence that is sensitive to hydrated collagen and its orientation. These sequences create parametric maps that reflect the spatial distribution of biochemical components within an imaged tissue. Both T_1ρ and T₂ relaxation times are strongly positively correlated with hydration and glycosaminoglycan content, and negatively correlated with clinical grades of disc degeneration in human intervertebral disc studies.13, 18, 19, 20, 21, 22, 23 For image analysis, the referenced studies calculate the average T_1ρ and T₂ relaxation times in the whole disc or within user‐defined regions of interest (ROIs): anterior annulus, posterior annulus, and nucleus. The averaging operation performed disregards potentially relevant information about the local distribution of relaxation values, thus decreasing the method’s ability to capture subtle changes in biochemistry. In hip and knee cartilage studies,24, 25 local analysis of T_1ρ and T₂ relaxation times revealed patterns that could differentiate between osteoarthritic patients and healthy patients, whereas these patterns were not detectable with ROI analysis. Additionally, variability in manual ROI placement introduces selection bias in the quantification of relaxation times and limits method scalability.

Although manual ROI methods are common for qMRI analysis, there is longstanding interest in the automation of tools for conventional MRI analysis. For example, intervertebral disc segmentation on sagittal T₂‐weighted images is tackled using computer vision methods including graph‐cuts,26 fuzzy clustering,14 shape modeling,27 and active contours.28 Classical computer vision approaches have been moderately successful in small data sets of healthy patients; however, the handcrafted features they rely on do not generalize well to unseen data or sequences with highly anisotropic voxels. Spinal tissues vary in intensity, volume, shape, and position within the spine, whereas SNR depends on acquisition parameters. This data diversity presents multiple challenges to classical algorithm development. Recent advancements in convolutional neural network architectures and training strategies have enabled the development of algorithms that can learn the general image features needed to accurately segment one or multiple spinal structures, even on small data sets.29, 30

We therefore propose a new analysis pipeline to address current limitations in the sensitivity, reliability, and scalability of quantitative imaging analysis. Unlike ROI‐based approaches, our method combines deep‐learning segmentation and atlas registration to perform analyses voxel‐wise. Our method leverages a recently published convolutional neural network to segment the intervertebral disc and guide the registration. We hypothesize that a voxel‐based relaxometry approach will reveal localized differences in disc biochemical composition among patients, while still correlating strongly with established measures of disc degeneration.

2. METHODS

An overview of the voxel‐based relaxometry pipeline is shown in Figure 1 and consists of three parts: disc segmentation and registration, image fitting, and statistical analysis. Intervertebral discs are segmented automatically, after which the mask for each disc level is used as input into the registration algorithm. The goal of spatial registration is to find a mapping between the input disc mask and a template disc mask (i.e., to find a deformation field that, when applied to the input disc, will create spatial correspondence between the input and the template). This deformation is applied to all images before fitting image intensities to calculate relaxation times. Once all subjects are registered to the same space, statistical analyses are performed at each voxel. Mask‐guided registration was deemed necessary when intensity‐guided registration failed to accurately register the discs, and image similarity metrics were unreliable indicators of registration performance. Disc and vertebra vary in intensity, volume, and positioning among subjects, making these tissues ill‐suited for intensity‐based registration methods (failure mode in Supporting Information Figure S2).

Figure 1.

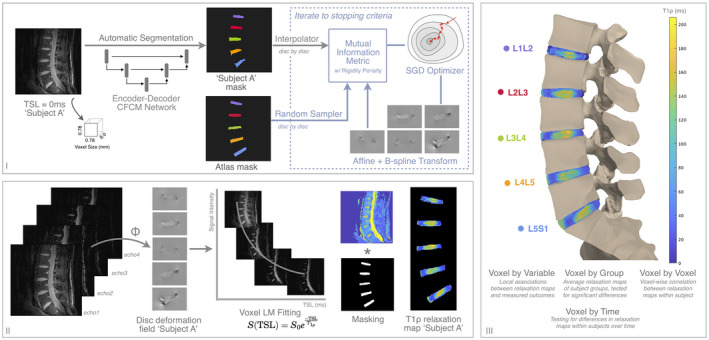
Overview of segmentation (I), registration (I,II), fitting (II), and statistical analysis pipeline for lumbar intervertebral disc characterization with quantitative MRI (qMRI). Once optimized, one or multiple qMRI slices are fed into the 2D segmentation algorithm, after which a single mask or a stack of masks enter the registration procedure. Once deformation fields for each disc are found, they are applied to the various echoes of the qMRI sequence before mono‐exponential fitting. For visualization purposes, the registered T_1ρ relaxation map for subject A is rendered on a spine mesh in step III. If multiple qMRI sequences exist, such as T₂ relaxation maps, the deformation fields found in step I are applied to additional sequences in step II. Details on network implementation are found in Supporting Information Figure S1. Abbreviations: CFCM, coarse‐to‐fine‐context memory; LM, Levenberg‐Marquardt; SGD, stochastic gradient descent; TSL, time spin lock

The approach was developed and evaluated on lumbar spine MR T_1ρ‐weighted images from two studies (study A31 and study B32) in compliance with the institutional review board. Results from data set A and data set B are presented in the text, and color coding of the disc levels is carried throughout all of the figures. Data set A included 16 subjects (10 with documented LBP, 6 controls) scanned at a single time point. The study acquired a single‐slice T_1ρ map (2D fast spin echo) and T₂‐weighted images aiming to quantify the biochemical signature of symptomatic degenerative discs. Data set B consisted of 15 patients with documented LBP scanned at baseline, with 4 returning for a follow‐up scan within a year. The study acquired multislice T_1ρ/T₂ maps (3D spoiled gradient echo), T₂ weighted images, and paraspinal muscle fat‐fraction maps with the goal of identifying MR biomarkers related to pain and disability. Demographic variables, clinical variables, and MR sequences for each data set are detailed in Table 1. Categorical variables in each data set are compared with Fisher’s exact test, while continuous variables are compared with two‐sided t‐tests.

Table 1.

Demographic variables, clinical descriptors, and MR acquisition parameters for lumbar spine data sets

	Number of subjects		Age (y)		Body mass index (kg/m2)		Height (m)		Sex = Female	Is LBP patient	Follow‐up scan
Demographic variables
Data set A	16		41.7 (±11.9)		27.2 (±4.7)		1.77 (±8.6)		4 (25.0%)	10 (62.5%)	–
Data set B	15		48.6 (±13.9)		26.1 (±4.5)		1.71 (±9.4)		9 (60.0%)	15 (100%)	4 (21.1%)
	Pfirrmann		Modified Pfirrmann		Discography + ve discs		Mean VAS/max VAS	IPAQ > 0	ODI	SF36 physical	SF36 mental
Clinical descriptors
Data set A	2.2 (±0.7)		–		6 (60.0%)		–	–	28.3 (±26.4)	42.9 (±12.3)	49.4 (±13.6)
Data set B	–		3.6 (±2.1)		–		6.8 (±1.9)/8.6 (±1.3)	8 (53.3%)	44.9 (±17.5)	–	–
	Scanner	Coil	Sequence name	View	FOV (mm)	Matrix size (x, y)	TR/TE (ms)	TSL (ms), FSL (Hz)	Pixel BW (Hz)	Time (m:s)	Purpose
MR acquisition parameters
Data set A	3T GE Excite Signa	8‐ch CTL spine coil	T1ρ FSE	Sag	200	256 192	2000/80	0/40/80/120, 300	125	6:36	T1ρ relaxometry
			T2 FSE	Sag	200	320 224	5000/70	–	122	2:25	Pfirrmann grading
Data set B	3T GE Discovery MR750w	8‐12‐ch embedded GEM coil	MAPSS T1ρ/T2	Sag	200	256,128	5.7/51	T1ρ 0/10/40/80, 300	488	11:33	T1ρ, T2 relaxometry
								T2 0/12/25/51
			T2 CUBE FSE	Sag	240	160 160	2500/91	–	244	4:13	Modified Pfirrmann grading
			IDEAL IQ	Ax	180	180 180	11/3.9	–	651	6:37	Paraspinal muscle qMR

Continuous variables are described as mean (±SD); categorical variables are listed as number of subjects (percentage of total) or number of discs (percentage of total).

Abbreviations: Ax, axial; BW, bandwidth; ch, channel; FSE, fast spin echo; IPAQ, International Physical Activity Questionnaire; LBP, low back pain; MAPSS, magnetization‐prepared angle‐modulated partitioned‐k‐space SPGR snapshots; Sag, sagittal; SF36, Short Form 36 Health Survey; VAS, visual analog scale for pain.

2.1. Segmentation

Ground‐truth masks for segmentation network training were generated by annotating lumbar discs L1L2‐L5S1 on a single sagittal slice (data set A, fully manual) or multiple sagittal slices of the T_1ρ sequence (data set B, 3D region growing algorithm with manual seeds and manual edits32) with an in‐house spline‐based annotation tool in MATLAB 2018a (MathWorks, Natick, MA). Throughput for manual annotations was about 90 seconds per disc per slice (7.5 minutes per slice).

Data were split per subject, and a 5‐fold cross‐validation strategy was used to train five identical coarse‐to‐fine context memory (CFCM) networks33 with a 80/20 (62 slices/18 slices) train–test division, ensuring that data sets A and B were each represented in the splits. Image preprocessing, network architecture, training, and hyperparameter details are found in Supporting Information Figure S1. Each image was loaded, and an adaptive histogram was equalized to enhance the appearance of local low‐contrast tissues, then normalized to zero mean and unit variance. Unique augmentations were produced every epoch, introducing enough variability to regularize network training. After training each of the five networks, inference was run on an independent test set and segmentations fed into the registration pipeline. To properly evaluate the network’s generalization capability, all segmentation results presented herein were inferred using the single network that never trained on those subject’s slices. For future applications of this pipeline on new T_1ρ‐weighted data, a five‐network ensemble (logits averaging) would be recommended for segmentation inference.

The performance of the segmentation algorithm is evaluated per disc using semantic segmentation metrics (Dice overlap, mean surface distance, percent volume difference, sensitivity, and precision). The 2D version of the metrics is used to analyze single‐segmented slices from data set A, while the 3D version analyzes stacks of segmented slices from data set B. To further evaluate segmentation performance, mean disc T_1ρ and T₂ relaxation times are extracted using the manual segmentation and the inferred segmentation. Biomarker extraction accuracy on each disc is evaluated by comparing manually and automatically extracted mean T_1ρ and T₂ values with Pearson correlation, a paired two‐sided t‐test for differences, and Bland‐Altman analysis for bias. Segmentation performance and biomarker extraction are contextualized with radiological scores for degeneration Pfirrmann/modified Pfirrmann, scored on a 1 to 5 scale and a 1 to 8 scale in terms of increasing degeneration. To examine the effect of changing the segmentation algorithm, three U‐Net variants were trained and evaluated as previously (results in Supporting Information Figures S7‐S9).

2.2. Registration

Inferred segmentations were registered to a lumbar disc atlas using Elastix,35 ElastixFromMatlab wrapper (National Center for Scientific Research/Riverside Research), and MATLAB 2018a. Segmentations were postprocessed, identifying connected components in 2D or 3D larger than 125 voxels and labeling them in the inferior–superior direction (L5/S1 to L1/2). Registration was performed between the inferred disc mask and the atlas disc mask on a disc‐by‐disc basis. A healthy spine mask without gross morphological deformities was selected as the atlas to minimize registration artifacts (another healthy spine and a degenerated spine mask were tested as atlases in robustness experiments presented in Supporting Information Figures S10 and S11). Per disc, the mask is translated to align with the centroid of the atlas disc mask before the two‐step registration. First, a four‐resolution recursive pyramidal affine registration rigidly scales, rotates, and shears the disc mask, providing initialization for the second step. Then, a b‐spline registration elastically deforms the disc segmentation, guided by mutual information with a rigidity penalty term to avoid large local deformations. The two‐step registration maximizes the overlap between the inferred disc mask and the template disc mask while preserving the original topology of the inferred disc. The resulting 2D (data set A) and 3D (data set B) deformation fields are applied to all T_1ρ and T₂ echoes, and a two‐parameter Levenberg‐Marquardt mono‐exponential fitting is performed voxel‐wise to create parameter maps of T_1ρ and T₂ relaxation times in the registered space. B‐spline registration parameters including final grid spacing (2), iterations (200), and rigidity penalty weight (0.77) were selected using Bayesian optimization, a method commonly used for hyperparameter tuning of machine‐learning models. Bayesian optimization performs registration over many iterations, the choice of the next registration parameters informed by the performance of the previous parameters, which are evaluated for all discs by calling the registration pipeline and treating the result of the objective function (Equation 1) as an observation.

$$L=\frac{1}{N}\sum _{i=1}^N\left(1-DS{C}_i+\sigma {(\mathbf{J})}_i\right)$$ (1)

where N is the total number of discs; $DS{C}_i$ is the Dice overlap coefficient $DS{C}_i=\frac{2\ast TP}{2\ast TP+FP+FN}$; and $\sigma {(\mathbf{J})}_i$ is the SD of the determinant of the spatial Jacobian.

The determinant of the Jacobian of the deformation field is a pixel‐wise description of volume changes: expansion (J > 1), compression (0 < J < 1), folding (J < 0), or constant volume (J = 1). Statistics computed across all pixels in the original disc space quantitatively describe the effect of registration. Per disc, Jacobian determinant values are centered around 1, with the SD describing the severity of local expansion and compression. Evaluations of the objective function guide the Bayesian optimizer, maximizing Dice overlap between the inferred disc mask and the atlas mask, while minimizing the SD of the determinant of the Jacobian across all registered discs for all subjects to find the optimal registration parameters. All resulting deformation fields and relaxation maps were checked to ensure that local topology and distribution of relaxation values were preserved after registration.

2.3. Statistical analyses

Four types of voxel‐wise statistics are performed on the registered T_1ρ/T₂ maps from each study. Only voxels meeting threshold criteria (data set A [T_1ρ < 250 ms], data set B [T_1ρ < 200 ms, T₂ < 150 ms]) are included. Missing data at the patient level (e.g., missing questionnaire) or at the disc level (e.g., missing Pfirrmann data) exclude patient maps from the analysis concerning those variables. Voxel‐by‐variable statistics examine local associations between relaxation maps and measured outcomes with Pearson correlation or partial correlation, with adjustments for age, gender, body mass index, and group assignment when relevant. Correlation coefficient maps and P‐value maps are visualized. Voxel‐by‐group statistics compare the average relaxation maps of subjects grouped by demographic or clinical variables (e.g., high disability, low disability) or by group assignment, unpaired t‐test checking for significant differences between groups. The average map for each group and P‐value map is visualized. Voxel‐by‐voxel statistics calculate within‐subject voxel‐wise correlation between two relaxation maps (e.g., T1ρ, T₂). These values are compared with Pearson correlation; correlation coefficient maps and P‐value maps are visualized. Voxel‐by‐time statistics are primarily for testing longitudinal changes in relaxation maps within subjects. Given the low number of follow‐ups, statistical differences between baseline and follow‐up cannot be computed. In larger studies, longitudinal difference maps would be tested for association with changing clinical outcomes or for differences between groups in which baseline, follow‐up, and difference relaxation maps are visualized. Correlation results for data set A are visualized as a single slice on a spine mesh, while correlation results for 3D volumetric data are visualized as two central slices on a spine mesh. All postprocessing and statistical tests were performed using Pingouin (0.2.6), SciPy (1.2.0), and StatsModels (0.9.0) using Python 3.6, with α < 0.05.

3. RESULTS

The data sets used for method development are similarly distributed in age, body mass index, and height (full description in Table 1). Significant differences exist in gender ratios, proportion of LBP patients, Oswestry Disability Index scores, and degenerative grades (Pfirrmann 1: 12%, 2: 54%, 2.5: 8%, 3: 24%, 3.5: 1%, and 4: 1% versus Modified Pfirrmann 1: 8%, 2: 36%, 3: 23%, 4: 3%, 5: 1%, 6: 14%, 7: 10%, and 8: 5%). When data sets A and B are combined, the final data set evenly samples the spectrum of morphologic and symptomatic intervertebral disk disease (IVDD).

Across data sets and degenerative grades, the CFCM networks produced accurate, high‐confidence segmentations of the lumbar discs. Representative segmentations before thresholding probabilities at 0.5 are shown in Figure 2. Predicted probability maps show the network highest uncertainty along disc boundaries, particularly at the anterior and posterior annulus‐ligament interface. Per slice, automatic segmentation of all discs took 0.393 seconds, over 1000 times faster than manual segmentation.

Figure 2.

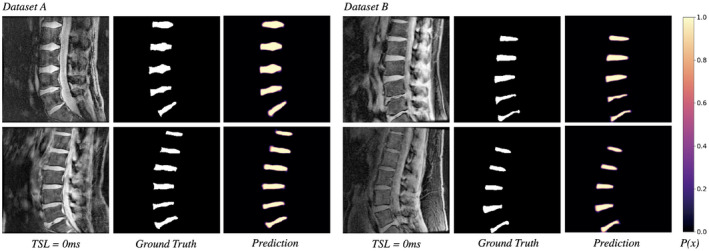
Input qMRI slice, ground‐truth mask, and predicted segmentation probabilities for 4 test subjects: 2 from data set A (left) and 2 from data set B (right). The 2D‐CFCM segmentation network demonstrates consistent performance in both T_1ρ acquisition sequences, across grades of disc degeneration, and spinal morphology without off‐target segmentation predictions. Probabilities are thresholded at 0.5 to create binary masks. Additional segmentation experiments were performed using U‐Net architectures; segmentation results are presented in Supporting Information Figures S7‐S9

Evaluated using segmentation metrics (Table 2), the network produced segmentations with Dice overlap (Dice similarity score [DSC]) consistently above 0.85 and mean absolute surface distance (MSD) less than 1 pixel at all levels, approaching the limit of image resolution. As a metric, DSC is sensitive to the size of the ground‐truth structure, as a single pixel error will disproportionately lower DSC for a small disc compared with a large disc. The lowest performing disc segmentation was L5S1, which is the smallest, most likely to be degenerated and most challenging to manually segment. The highest performing disc was L3L4, which was usually the largest and always centered in the FOV. Volume difference (%VD), sensitivity (Sens), and precision (Prec) between ground truth and network segmentations revealed that the networks were biased toward moderate overestimation of disc volume in data set B (greater number of false‐positive voxels), whereas data set A had slight overestimation and underestimation depending on the disc level. Comparing segmentation metrics against radiological grades of degeneration, the networks showed lower DSC performance in more degenerated discs, whereas MSD and %VD were invariant to degenerative grade, suggesting that lowered performance could be a result of the metric itself (Supporting Information Figure S3). Pooled lumbar spine metrics (n = 88, n = 92) were 0.904, 0.898 DSC; 0.936, 0.236 MSD; +0.07, −3.52 %VD; 0.904, 0.913 Sens; and 0.912, 0.888 Prec, respectively.

Table 2.

Dice similarity score, mean absolute surface distance at disc boundary, percent volume difference, sensitivity, and precision results per disc for each data set (95% confidence intervals in parenthesis)

	L5S1	L4L5	L3L4	L2L3	L1L2
Data set A
DSC	0.871 (0.848, 0.893)	0.916 (0.907, 0.926)	0.932 (0.923, 0.941)	0.915 (0.903, 0.928)	0.883 (0.852, 0.913)
MSD	1.37 (0.976, 1.76)	0.836 (0.748, 0.923)	0.683 (0.596, 0.769)	0.820 (0.687, 0.953)	0.972 (0.716, 0.228)
%VD	2.60 (−6.03, 11.24)	−1.91 (−7.23, 3.40)	0.51 (−3.10, 4.13)	1.19 (−3.18, 5.57)	−2.28 (−11.7, 7.19)
Sens	0.858 (0.824, 0.893)	0.925 (0.902, 0.949)	0.930 (0.910, 0.950)	0.911 (0.883, 0.938)	0.894 (0.843, 0.945)
Prec	0.896 (0.85, 0.942)	0.913 (0.885, 0.941)	0.937 (0.918, 0.956)	0.924 (0.906, 0.943)	0.886 (0.841, 0.931)
Data set B
DSC	0.877 (0.858, 0.897)	0.895 (0.877, 0.914)	0.913 (0.898, 0.928)	0.899 (0.875, 0.922)	0.901 (0.890, 0.912)
MSD	0.300 (0.205, 0.395)	0.265 (0.176, 0.354)	0.186 (0.153, 0.219)	0.215 (0.170, 0.260)	0.215 (0.173, 0.258)
%VD	−1.70 (−8.04, 4.64)	−2.95 (−9.87, 3.95)	−5.25 (−10.5, −0.00)	−4.78 (−10.4, 0.86)	−2.71 (−7.81, 2.37)
Sens	0.886 (0.85, 0.921)	0.909 (0.875, 0.943)	0.937 (0.917, 0.957)	0.92 (0.891, 0.949)	0.914 (0.889, 0.939)
Prec	0.876 (0.846, 0.907)	0.89 (0.858, 0.923)	0.896 (0.866, 0.926)	0.884 (0.85, 0.918)	0.894 (0.869, 0.919)

Performance results for additional segmentation experiments are found in Supporting Information Figures S7 and S8.

Abbreviations: DSC, Dice similarity score; MSD, mean absolute surface distance; Prec, precision; Sens, sensitivity; %VD, percent volume difference.

Manually and automatically extracted mean disc T_1ρ and T₂ relaxation times show strong, significant correlations at all disc levels (Table 3). All disc correlations for data set A T_1ρ were r = 0.995, P = 7.4e‐84, and bias = −0.74 ms (−4.35, 2.87); data set B T_1ρ were r = 0.990, P = 4.1e‐78, and bias = −0.01 ms (−4.36, 4.33); and T₂ r = 0.984, P = 2.5e‐70, and bias = 0.12 ms (−3.55, 3.79), with no trends evident in difference plots (Figure 3). Data set A showed more precise biomarker extraction with a slight bias toward overestimating relaxation times, particularly in L5S1. Data set B had less precise T_1ρ biomarker extraction (as observed with the wider confidence intervals) but produced unbiased estimates of relaxation time. Correlations between manual and automatic T_1ρ times in data set B were stronger than correlations between T₂ times, in all discs except L5S1. The T_1ρ and T₂ biomarker extraction accuracy did not change with increasing degenerative grade and remained within 5 ms of manually extracted values in all but two discs (Supporting Information Figure S4).

Table 3.

Comparison of manually and automatically extracted relaxation values with Pearson correlation coefficient r _coeff and bias measurement per disc for each data set (P‐values, [95% confidence intervals])

	L5S1	L4L5	L3L4	L2L3	L1L2
Data set A
T1ρ r coeff	0.987 (P = 3.0e‐13)	0.998 (P = 3.6e‐20)	0.997 (P = 1.4e‐20)	0.998 (P = 4.5e‐20)	0.995 (P = 1.1e‐14)
T1ρ bias (ms)	−2.0 (−8.16, 4.07)	−0.3 (−2.44, 1.74)	−0.5 (−2.33, 1.21)	0.0 (−2.12, 1.99)	−0.6 (−3.72, 2.34)
Data set B
T1ρ r coeff	0.969 (P = 4.3e‐11)	0.991 (P = 3.7e‐16)	0.990 (P = 5.1e‐16)	0.993 (P = 3.5e‐17)	0.988 (P = 2.6e‐14)
T1ρ bias (ms)	−0.4 (−4.92, 4.01)	0.03 (−4.50, 4.56)	0.0 (−4.41, 4.40)	0.41 (−3.31, 4.15)	0.06 (−4.83, 4.96)
T2 r coeff	0.975 (P = 7.1e‐12)	0.984 (P = 3.8e‐14)	0.983 (P = 6.5e‐14)	0.991 (P = 4.0e‐16)	0.979 (P = 1.6e‐12)
T2 bias (ms)	−0.2 (−3.63, 3.23)	−0.1 (3.86, 3.49)	0.18 (−3.55, 3.92)	0.68 (−2.48, 3.84)	0.10 (−4.18, 4.39)

Biomarker results for additional segmentation experiments are found in Supporting Information Figures S7 and S8.

Figure 3.

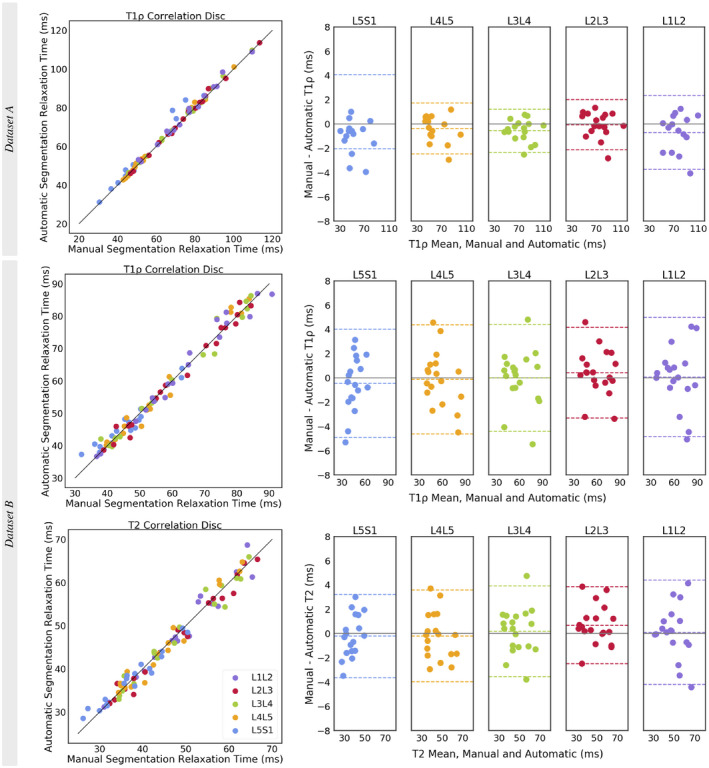
Correlation scatterplot for all discs and Bland‐Altman plots with the 95% limits of agreement (LOAs) for each disc level for comparison of manually and automatically extracted T_1ρ and T₂ relaxation times. In data set A’s L5S1 T_1ρ Bland‐Altman plot, the lower LOA at −8.16 ms was omitted to maintain the same y‐axis range between plots. Biomarker results for data set A are from a single T_1ρ map slice (2D), whereas results from data set B are from a stack of T_1ρ and T₂ map slices (3D)

Qualitatively, the two‐step registration approach successfully morphed the lumbar discs into the atlas space, preserving the spatial distribution of relaxation times in the nucleus and annulus as well as the total distribution of intensity values across the disc; the effect of registration is visualized in Figure 4. Performance was consistent across degenerative grades. Histogram plots of disc intensities show good agreement between the values before and after registration, indicating that deformations were applied smoothly throughout the disc, and disc regions are represented fairly. Disc boundaries, particularly the anterior and posterior disc–ligament interface, showed the most variability in registration accuracy.

Figure 4.

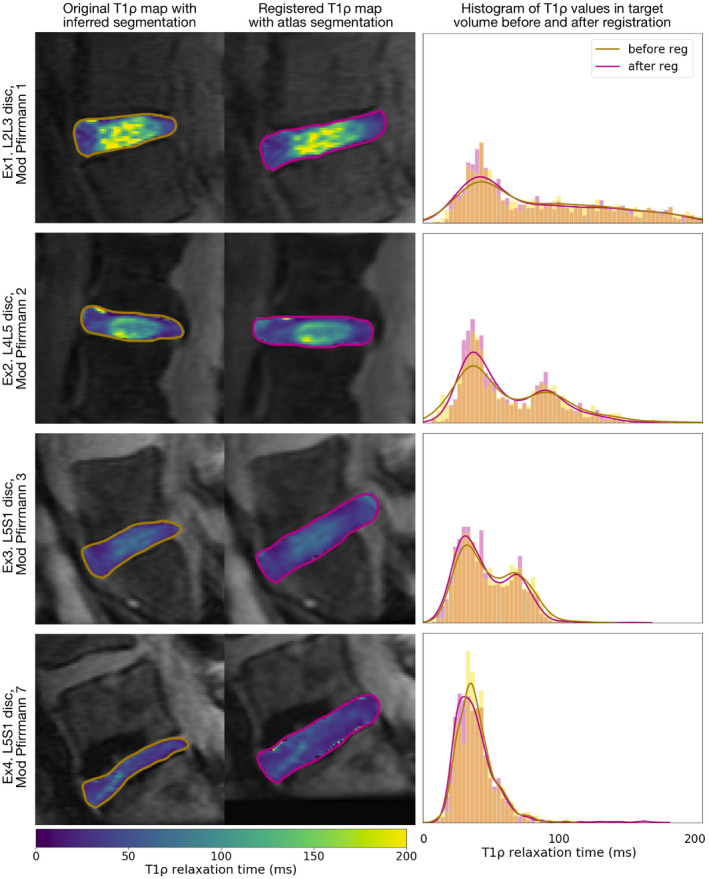
Example T_1ρ maps before and after registration and distribution of T_1ρ relaxation values within the segmented disc before and after registration, from 4 test subjects. The registration process preserves spatial patterns in relaxation maps, with consistent performance across degenerative grades. Histograms show the density and a Gaussian kernel density estimate of T_1ρ relaxation times within the segmented disc before and after registration. Similarity between histograms indicates that the deformation was smooth and even, preserving the relative proportion of nucleus and annulus T_1ρ relaxation times. Additional registration experiments were performed with another healthy spine atlas and a degenerated spine atlas; example maps are presented in the top panel of Supporting Information Figures S10 and S11

Example statistical parametric maps are visualized in Figures 5, 6, 7. Local patterns in relaxation‐time maps show significant associations with radiological grading, as well as clinical measures of disability. Imaging‐based Pfirrmann/modified Pfirrmann degenerative grades were strongly negatively correlated with the T_1ρ maps in both data sets and with the T₂ maps in data set B (Figure 5). Significant correlations are localized to lumbar disc nucleus and inner annulus, with correlation strength and significance increasing in data set A’s lower disc levels (L3‐4 through L5S1), while associations remain consistent across disc levels in data set B. The T₂ correlations were similar, yet not identically distributed, to the T_1ρ correlations, with T_1ρ showing stronger and more significant correlations around the superior and inferior portion of the nucleus. Comparing the correlations of T_1ρ values estimated from the whole‐disc ROI approach, data set A (Pearson r L1L2: −0.15, P = .60; L2L3: −0.458, P = .07; L3L4: −0.516, P = .04; L4L5: −0.741, P = .001; L5S1: −0.772, P = .0005), and data set B (L1L2: −0.670, P = .003; L2L3: −0.660, P = .003; L3L4: −0.715, P = .0008; L4L5: −0.732, P = .0008; L5S1: −0.671, P = .003), the proposed voxel‐based method confirms ROI associations and recovers significant associations in disc subregions not identifiable with ROI methods. For example, in data set A’s L2L3 disc, Pfirrmann grades are weakly and insignificantly correlated with mean whole‐disc T_1ρ values, yet the voxel‐based method reveals a moderate, positive correlation in the inferior region of the nucleus.

Figure 5.

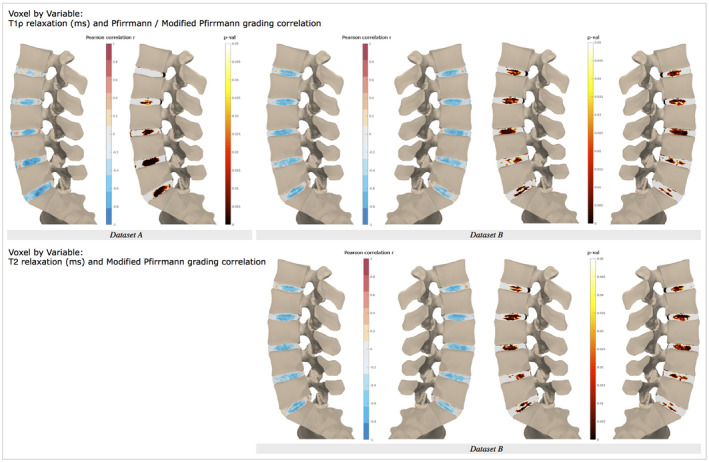
Voxel‐wise associations between T_1ρ and T₂ maps and Pfirrmann/modified Pfirrmann grading. Single‐slice Pearson correlation with 5‐point Pfirrmann grade for data set A (left) and two central slice correlation with 8‐point modified Pfirrmann grade for data set B (right), each shown with corresponding P‐value map. Voxel‐wise associations for additional registration experiments are presented in the bottom panel of Supporting Information Figures S10 and S11

Figure 6.

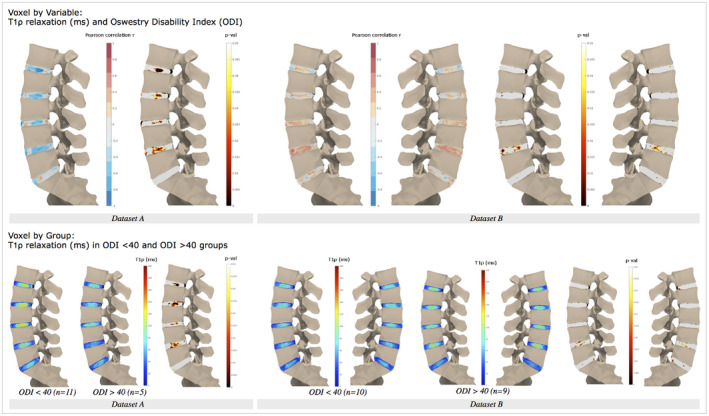
(Top) Voxel‐wise associations between T_1ρ maps and Oswestry Disability Index (ODI) scores. (Bottom) Voxel‐by‐group analysis, mean relaxation T_1ρ maps, and P‐values for minimal/moderate (0‐40 ODI score) and severe disability (> 40 ODI score) groups. The T₂ results for data set B are presented in Supporting Information Figure S5

Figure 7.

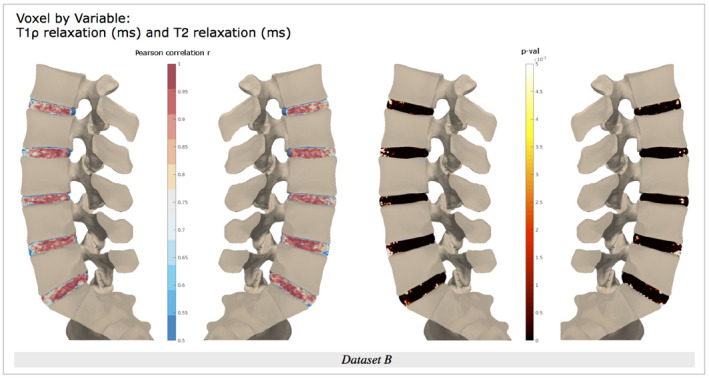
Voxel‐wise associations in data set B between T_1ρ and T₂ maps, with Pearson correlation r map displayed from 0.5 to 1, and P‐value map from P = 0 to P = .005

Interestingly, results with respect to disability measures varied between the two data sets (Figure 6). Data set A shows strong, negative correlations between T_1ρ and Oswestry Disability Index scores, whereas data set B shows weak, positive correlations between the two, particularly in the nucleus–annulus transition region of L4L5. Data set B’s T₂ correlation maps mostly mirror those of T_1ρ (Supporting Information Figure S5); however, positive correlations seen in L4L5 are stronger and have significant voxels clustered in the posterior inner annulus. The trends in data sets A and B appear to be opposite; however, the association between Oswestry Disability Index and T_1ρ is only consistent in data set A, in which negative correlations are stronger and present across multiple lumbar disc levels, with the exception of L5S1, where no relationship is evident. Again, these trends support whole‐disc T_1ρ findings, with the advantage that the voxel‐based method can recover the anatomical location of significant associations: data set A (Pearson r L1L2: −0.800, P = .001; L2L3: −0.650, P = .016; L3L4: −0.620, P = .024; L4L5: −0.674, P = .011; L5S1: −0.231, P = .45) and data set B (L1L2: 0.152, P = .57; L2L3: 0.224, P = .39; L3L4: 0.415, P = .098; L4L5: 0.574, P = .02; L5S1: 0.314, P = .24). Further stratifying patients in data set A by Oswestry Disability Index (minimal/moderate vs. severe disability) and performing a group comparison shows significant differences between the relaxation maps. Average T_1ρ relaxation maps from the minimal/moderate disability group showed clear annulus–nucleus distinction with a visible midline, whereas the severe disability group had lower average T_1ρ values with a homogeneous distribution. Relative to other discs, low and high disability groups in both data sets had low mean relaxation values for the L5S1 disc.

Finally, T_1ρ maps and T₂ maps were highly and significantly positively correlated, as observed with whole‐disc ROI analysis (Pearson r from 0.954 to 0.989, with P < 1e‐10) (Figure 7). However, voxel‐by‐voxel analysis suggests that correlation strength between T_1ρ and T₂ relaxation values is localized: The anterior annulus and near‐endplate regions show weaker correlations than the rest of the disc space, for all lumbar discs. Additionally, correlation values in the center of the disc are heterogeneous, suggesting that the relationship between T_1ρ and T₂ values fluctuates throughout the disc.

4. DISCUSSION

We have demonstrated that the novel pipeline proposed for qMRI analysis of intervertebral discs is feasible and addresses the limitations of conventional analysis methods. The intervertebral disc is a challenging tissue to analyze, due to its deformable structure, lack of anatomical landmarks, and variations in image intensity.

By integrating a convolutional neural network for segmentation into our atlas‐based registration pipeline, we developed a fast, robust, and scalable solution to analyze local patterns in intervertebral disc qMRI.

Merging data sets A and B was necessary for the development of a robust analysis pipeline. Together, the data sets sample the full morphologic and symptomatic IVDD spectrum, including a range of degenerative grades and patient‐reported outcomes such as pain and disability. Similarity in T_1ρ image contrast and image prescription enabled the merging of these data sets for 2D‐segmentation method development and validation. However, differences in acquisition parameters (spin‐lock pulse duration, spin‐lock frequency, and voxel size) prevented joint registration and statistical analysis of relaxation maps. Given the limited sample size of each data set, the appearance of common trends in T_1ρ correlation maps demonstrated face validity of our analysis pipeline. Trends in T₂ correlation maps were similar but not identical to T_1ρ maps, demonstrating the feasibility of integrating multiple, potentially complementary qMRI sequences into the analysis pipeline.

Our training strategy helped the CFCM segmentation network learn to reliably segment image slices even with limited training data. The network was prevented from overfitting by aggressively augmenting every training iteration, using large batch sizes with batch normalization, no hyperparameter tuning, and creating data splits by subject. Both contrast and geometric augmentations were chosen to introduce diversity into the images, as disc shape, position, intensity, and texture vary widely between data sets. The choice of network was key in achieving high performance: The memory mechanism in the CFCM learns how to best fuse features to combine local and global context, and had fewer spurious segmentation predictions compared with U‐Net.33 State‐of‐the‐art disc segmentation performance in the T₂ 2015 challenge and the IVD3M 2018 challenge are Dice scores of 0.918 and 0.907, respectively. We believe the performance of our segmentation network is competitive with and more generalizable than other published disc segmentation methods, although a direct comparison is not possible due to differences in data sets and annotation methods. Data sets provided by disc segmentation challenges29, 30 have more training data (576 segmented slices from 8 subjects in IVD3M) but are only trained on images from volunteers with healthy discs.

There are several reasons why the segmentation performance in our data set decreased in discs with severe IVDD. First, manual segmentations are less reliable; loss of nucleus glycosaminoglycans, annular collagen, and dehydration lead to a decrease in disc volume. In turn, these changes are reflected in shorter tissue relaxation times and lower disc signal intensity on the T_1ρ‐weighted images, obscuring the boundary at the interface of the annulus and spinal ligaments, which compounds with partial‐volume artifacts on edge slices. Second, there are fewer training examples of severely degenerated discs, and many degenerative phenotypes exist. Healthy discs are often surrounded by normal presenting anatomy, while severe IVDD is associated with fattier vertebral bone marrow, narrowed spinal canal, and even signal voids due to the vacuum phenomena.36 Finally, Dice coefficient and percent volume difference are sensitive to segmented tissue size, and given the smaller disc volume in severe IVDD, single pixel errors disproportionately affected these results.

Our results demonstrate that errors in disc segmentation were not propagated to errors in biomarker extraction. Segmentation is performed on the first echo of the mapping sequence, and relaxation times are calculated from the mono‐exponential fit of all acquired echoes. Errors by the segmentation network represent a small fraction of the total disc area, thereby not significantly skewing the mean. Error pixels may also contain intensity values that do not have high enough SNR for mono‐exponential fitting or produce relaxation values outside of a feasible range, neither of which are included in the calculation of mean relaxation times. Even in the worst‐performing disc (L5S1 in data set A), the mean disc T_1ρ errors ranged from −8 ms to 4 ms. Calculation of mean disc relaxation times from automatic segmentations is an intermediate output to validate the segmentation portion of the pipeline. However, our automatic segmentation method is a viable alternative to ROI‐based analysis, as it is significantly faster (0.393 seconds/slice compared with our 7.5‐minute/slice manual, 12‐second/slice average for submissions to the T₂ disc segmentation challenge30) and more reliable than manual segmentation.

The automatic segmentation network provides masks that are necessary to guide registration. Mutual information‐guided atlas registration is successful in other tissues, but intensity‐based methods fail to register intervertebral discs (Supporting Information Figure S2). We hypothesize that this issue arises with cases of severe degeneration, in which intensity signals from normal presenting anatomy are absent. The disc mask allows for good initialization of the registration algorithm and calculation of overlap metrics for Bayesian optimization of registration parameters. Our proposed objective function is designed to maximize registration accuracy while preventing significant deformations that would perturb the local distribution of relaxation values. This highlights the flexibility of our proposed pipeline, with automatic parameter tuning for application to other data sets or different atlases.

Local distribution of relaxation values was preserved throughout the registration procedure, even with alternate segmentation methods and atlas selection, thus demonstrating the success of the full analysis pipeline. Recent studies have recognized the limitations of coarse ROI methods and have attempted to address this problem with smaller ROIs increasing the time, complexity, and bias introduced. In a group of healthy discs, our method’s average relaxation maps show distinctive regions corresponding to the annulus, nucleus, and disc midline; the patterns recovered in a fully data‐driven manner without introducing user bias. Additionally, our voxel‐based method showed greater sensitivity to small, significant associations within the disc such as that were washed out with whole‐disc ROI averaging. Our proposed statistical parametric mapping method still performs an averaging procedure, on a voxel scale. This will show common trends within the studied group, but it is not ideal for the identification of focal lesions.37 High‐intensity zones, for example, would only be identified if they co‐localized for a large group of patients. In voxel‐by‐group analysis, the maximum and SD maps could potentially identify these clusters.

Different physiological loading demands explain variations in geometry, biochemical, and microstructural composition between disc levels. A level‐specific atlas was used for registration, as it is inappropriate to pool relaxometry results from all discs. Relationships between relaxation values at different disc levels may reveal important associations with clinical outcomes. Additionally, the strength of the relationship between T_1ρ and T₂ relaxation times was highly spatially dependent, indicating that each of these biomarkers may reveal differences in local biochemistry, which are observed in human disc specimens.38

The limitations of this work are discussed in two parts: the pipeline and data set. As a pipeline, segmentation network training and registration optimization impose upfront computational and time costs. However, once these sections have been optimized to the target task, processing time is faster than manual ROI analysis methods. As for the data set, one or two 8‐mm sagittal qMRI slices do not fully capture biochemical composition of the intervertebral disc. Both data set A and data set B reported that SNR prevented the acquisition of thinner slices, although recent developments may address this limitation.

Finally, low sample size prevented meaningful interpretation of associations with patient‐reported outcomes. Associations between T_1ρ and disability were strongly negative and significant in data set A, yet were not visible in data set B, indicating that the studies were underpowered. Similarly, associations with muscle data extracted from data set B did not reach statistical significance (Supporting Information Figure S6). A greater sample size is necessary to power proper statistical analysis, adjusting for multiple comparisons and demographic/clinical confounders, and to enable feature extraction for IVDD characterization.

Image statistics can be defined in voxels, clusters, or peaks. Voxel‐wise inference examines whether the t‐statistic (or F‐statistic) is within a predefined threshold at each voxel, to reject the null hypothesis at that voxel (high spatial specificity). Cluster‐wise inference defines a t‐statistic threshold and minimum cluster size, to reject the null hypothesis of the whole cluster, indicating that activity is somewhere within the cluster (high sensitivity, low spatial specificity). Peak‐wise inference identifies local maxima in t‐statistics greater than a predefined threshold (high spatial specificity). To correct inferences for multiplicity, corrections on P‐values with familywise error rate (Bonferroni correction, random field theory) and false discovery rate controlled the procedures.

There are several promising applications of our analysis method. Broadly, the main motivation of this work was to develop an automatic pipeline for lumbar intervertebral disc characterization, creating a fast, reliable, and robust tool to aid mechanistic disease research of IVDD. Applied to a larger clinical imaging data set, our approach could be used for LBP phenotyping: selecting patient cohorts for clinical trials, matching patients to effective treatments, or tracking treatment effects over time. ReSPINE, a randomized clinical trial for mesenchymal stem cell therapy for IVDD, is underway in Europe, and qMRI will be acquired over four time points. Our proposed pipeline could provide automatic, reliable processing of qMRI to follow subtle changes in spine biochemistry through statistical parametric mapping. Finally, there is value for researchers validating new quantitative pulse sequences or compressed‐sensing schemes, to reliably compare the voxel‐based patterns extracted by both methods. Application to other registration tasks and data sets is straightforward, given the flexibility of our method.

5. CONCLUSIONS

This work proposes a novel methodology that combines deep learning–based segmentation, atlas‐based registration, and statistical parametric mapping for automatic analysis of quantitative spine imaging, addressing current methods’ issues with sensitivity, reliability, and scalability. Evaluation of the segmentation method demonstrates that performance is robust and shows excellent agreement with manual methods of biomarker extraction across the spectrum of morphologic and symptomatic IVDD. Despite the limited data available for method development, the voxel‐based relaxometry pipeline reveals local trends in disc qMRI values, which were significantly associated with clinical measures of degeneration and disability in two independent data sets. Future research directions include applying the proposed framework on larger spine qMRI data sets to investigate LBP phenotypes for pathophysiological research, clinical cohort selection, and treatment monitoring.

Supporting information

FIGURE S1 Ground‐truth segmentations were saved as 256 × 256 binary masks (one 2D mask per slice). The final data set for network training included 38 scans from 31 unique patients, with a total of 80 segmented slices. A 2D coarse‐to‐fine context memory (CFCM) segmentation network (Tensorflow 1.4, Python 3.6) was trained end‐to‐end using full image slices (256 × 256) as a single‐channel input. The CFCM network replaces the decoding path in a classic encoder‐decoder with a convolutional long‐short‐term‐memory unit that serves as a memory mechanism to fuse different feature scales and receptive fields, while the encoding path is a ResNet34. Aggressive online augmentations were applied to every batch: rotation (in‐plane: −20 to 20º), elastic deformations (1 to 3 points, σ 6 to 12), and localized Gaussian brightening (image intensity scaled with Gaussian kernel σ 3, with −100 to 100 x,y shift). Images underwent adaptive histogram equalization (sklearn v. 0.15, kernel size = 32, clip limit = 0.01, histogram bins = 256) and zero mean, unit variance normalization. Xavier initialization was used for network weights, trained for 8000 epochs with Dice loss,34 batch size = 20, and Adam optimizer (learning rate 1e‐6, epsilon 1e‐8) on a single Nvidia TitanX GPU, saving the last checkpoint for inference on the test set

FIGURE S2 Example failure mode in image‐guided registration: unsuccessful disc localization and boundary registration: original image before registration (left), image after intensity‐based registration with atlas segmentation contours in white (middle), image after proposed disc‐by‐disc mask‐based registration with atlas segmentation contours in pink (right)

FIGURE S3 Dice similarity score (DSC), mean absolute surface distance (MSD) at disc boundary, and percent volume difference results for each data set, color‐coded by disc. Segmentation performance is plotted against Pfirrmann and modified Pfirrmann radiological grades

FIGURE S4 Comparison of manually and automatically extracted T_1ρ, T₂ relaxation values for each data set, color‐coded by disc. Biomarker extraction performance plotted against Pfirrmann and modified Pfirrmann radiological grades

FIGURE S5 (Top) Voxel‐wise associations between T₂ maps and Oswestry Disability Index (ODI) scores. (Bottom) Voxel‐by‐group analysis, mean relaxation T₂ maps, and P‐values for minimal/moderate (0‐40 ODI score) and severe disability (> 40 ODI score) groups

FIGURE S6 Voxel‐wise associations between T_1ρ maps and paraspinal muscle (psoas, multifidus, erector spinae) fat fraction for data set B. Fat fraction calculated using manual segmentations of each muscle group, using decomposed fat and water images fat/(fat + water), averaged across the whole muscle

FIGURE S7 Segmentation and biomarker extraction performance for UNet architecture with 64 base filters. Connected component threshold was increased to 200 voxels (from 125 voxels) to remove spurious segmentation predictions, after which, automatic disc labeling was successful. With postprocessing, segmentation performance and biomarker extraction was comparable to CFCM network. In data set A, the network consistently underestimated disc volume, whereas disc volume was overestimated in data set B

FIGURE S8 Segmentation and biomarker extraction performance for UNet architecture with 32 base filters. Again, connected component threshold was increased to 200 voxels (from 125 voxels) to remove spurious segmentation predictions, after which, automatic disc labeling was successful. With postprocessing, segmentation performance and biomarker extraction was slightly lower than CFCM and U‐Net with 64 base filters. When evaluated on the whole pipeline, patterns extracted in correlation maps match those in Figure 5

FIGURE S9 Qualitative segmentation performance for U‐Net architecture with 16 base filters (limited expressive capacity). Large, off‐target segmentation predictions, most located near L5S1, led to the failure of an automatic disc labeling process. As a result, disc‐by‐disc segmentation performance and biomarker extraction could not be computed

FIGURE S10 Registration results using a different healthy spine atlas mask (I). Panel II shows example T_1ρ maps before and after registration (same example maps as Figure 4). Local patterns in relaxation times are preserved throughout the disc and the relative proportions of nucleus/annulus relaxation values are maintained. Histograms show the density and a gaussian kernel density estimate of T_1ρ relaxation times within the segmented disc before and after registration. Distributions are similar in all but example 3, where a signal void region decreases the proportion of voxels in the 60‐80ms relaxation range. Panel III shows voxel by variable correlations with Pfirrmann/Modified Pfirrmann grades, showing similar associations and significance patterns to Figure 5 for Dataset A and B

FIGURE S11 I, Registration results using a degenerated spine atlas mask. II, Example T_1ρ maps before and after registration (same example maps as Figure 4). Registration performance is affected by the narrow disc height of the atlas: Examples 1 and 3 undergo significant compression during registration, upper and lower disc boundaries are not well registered, and the center of the disc loses spatial resolution. Additionally, registered discs did not expand to fill the posterior region of the atlas disc (many levels of the atlas contained a disc protrusion). III, Voxel‐by‐variable correlations with Pfirrmann/modified Pfirrmann grades. Despite the limitations in registration, similar (albeit compressed) associations and significance patterns appear in the nucleus (Figure 5); however, significant patterns also appear in the highly unreliable disc protrusion on disc L5S1 of data set B, so results should be interpreted in the context of registration performance

Iriondo C, Pedoia V, Majumdar S. Lumbar intervertebral disc characterization through quantitative MRI analysis: An automatic voxel‐based relaxometry approach. Magn Reson Med. 2020;84:1376–1390. 10.1002/mrm.28210