Exploring the use of molecular dynamics in assessing protein variants for phenotypic alterations

Abstract

With the advent of rapid sequencing technologies, making sense of all the genomic variations that we see among us has been a major challenge. A plethora of algorithms and methods exist that try to address genome interpretation through genotype-phenotype linkage analysis or evaluating the loss of function/stability mutations in protein. Critical Assessment of Genome Interpretation (CAGI) offers an exceptional platform to blind-test all such algorithms and methods to assess their true ability. We take advantage of this opportunity to explore the use of molecular dynamics simulation as a tool to assess alteration of phenotype, loss of protein function, interaction and stability. The results show that coarse-grained dynamics based protein flexibility analysis on 34 CHEK2 and 1719 CALM1 single mutants perform reasonably well for class-based predictions for phenotype alteration and two-thirds of the predicted scores return a correlation coefficient of 0.6 or more. When all-atom dynamics is used to predict altered stability due to mutations for Frataxin protein (8 cases), the predictions are comparable to the state-of-art methods. The competitive performance of our straightforward approach to phenotype interpretation contrasts with heavily trained machine learning approaches, and open new avenues to rationally improve genome interpretation.

Graphical Abstract

Introduction

With the advent of rapid sequencing technologies (Ekblom and Wolf, 2014), we have the advantage of studying a large amount of chromosomal and transcript sequences that shed light on the variations that we have in our genetic makeup. Among these, mutations that occur in the protein coding regions and alter the amino acid sequence are of prime interest as they may lead to loss of function due to loss of catalytic machinery (in case of enzymes), or alteration of stability, structure, dynamics, interaction, or localization. How these alterations affect the immediate spatiotemporal neighborhood of the protein in an organism and cascade to an externally observable phenotypic trait is an extremely challenging question to answer. Indeed, gene interactions observed as epistasis (Starr and Thornton, 2016), canalization (Sato and Siomi, 2010), robustness, or buffering (Hartman, et al., 2001) are known to complicate the translation of genotype to phenotype information. In addition, this paradigm excludes evaluation of complex traits that may arise due to additional contributions from non-coding variants (Boyle, et al., 2017).

Efforts over the past years have improved our understanding of the complexity of addressing a genotype-phenotype relation (Dowell, et al., 2010). The key lies in dissecting the role of conditionally essential and modifier genes in the phenotype trait development. The role of epistasis and genetic interactions are important in here for interpreting the trait(s) in their right context. Genome-wide association studies make an effort in this direction but are limited to estimating the genetic contributions to traits through statistical inference of a genome-wide set of genetic variants. Wherever common variants appear to associate with common or related traits, they are often identified as potential signals (Reich and Lander, 2001). A similar yet synthetic association can also happen through rare variants (Dickson, et al., 2010). Besides, structural (Collins, et al., 2017) and epigenetic variations (Carja, et al., 2017), multiple alleles with additive effect or synergistic interaction add to the complexities that confront our understanding of phenotypic traits.

There is already a plethora of methods available that interpret genotypes for predicting alteration of traits. These methods can largely be grouped into sequence-, structure- and machine learning-based algorithms. The sequence-based algorithms attempt to analyze the alteration of the amino acid properties (Stone and Sidow, 2005), residue conservation through entropy measures (Reva, et al., 2007), position-specific scoring matrices (Ng and Henikoff, 2001), evolutionary trace (Katsonis and Lichtarge, 2017), scoring substitutions and indels in alignments (Choi, et al., 2012) to assess the fitness of a mutation, relying on evolutionary information. Structure-based approaches primarily target assessment of folding and stability effects on protein due to a mutation (Gromiha, 2007). The extent of alteration of the free energy upon mutation of the protein is used to predict its putative effect on the phenotype (George Priya Doss, et al., 2008). The machine learning methods use an assortment of features to train the classifiers using protein properties like sequence conservation, local sequence environment, secondary structure, structural disorder, solvent exposure, functional categorization and so on (Niroula and Vihinen, 2016). They are generic predictors that make phenotype predictions for missense variants in any protein. Their accuracy depends on the dataset(s) used to train the classifier.

It may be noted that it is entirely possible for a mutation to have a limited effect on the protein structure but alter molecular interactions. Incorporation of such interaction information into phenotype assessment pipeline enhance accuracy (Capriotti, et al., 2018). Similarly, alteration-of-localization information of the protein variant would also improve assessing the impact on phenotype (Park, et al., 2011).

A class of methods based on molecular dynamics (MD) simulation has also been used in which mean-square-fluctuation, radius of gyration, solvent accessibility has been analyzed for estimating variation with mutation (Sneha and Doss, 2016). In cases, where ligand binding plays an important role in protein function, its alteration due to mutation has also been widely studied as a measure of phenotypic alteration, especially in the context of MD embedded drug discovery (Gibbs, 2014). MD simulations are based on first principles where protein motions and forces acting on the atoms are determined by Newton’s laws of motion. This largely makes it devoid of biases arising out of prior information which makes it a very attractive tool for the rational understanding of alteration of a phenotype. However, MD simulations are computationally expensive and take a considerable amount of time to yield results. Due to this limitation, long timescale simulations are practically unfeasible for reproducing biological phenomena in the microsecond to the millisecond time interval. Additionally, MD uses generalized potential energy functions that exclude electrostatic polarization effects. Also, since MD simulations reproduce equilibrium dynamics, the results are influenced by the starting energy minimized structure. The description of the explicit solvent environment in the simulations is still quite primitive. Despite these limitations, MD still remains the best tool to sample conformational states and calculate thermodynamic and kinetic parameters of interest from first principles (Lindahl, 2015).

The CALM1 and CHEK2 proteins that we attempt to analyze in the CAGI challenge are dependent on alteration of protein conformation for their activity. For example, CALM1 protein that senses and binds calcium across a wide concentration range through its two lobes is able to bind to target proteins through an allosterically controlled affinity, in which the target proteins modulate the conformation of CALM1 (Jensen, et al., 2018; Tidow and Nissen, 2013). This way the protein is able to interact with diverse targets and show a plethora of binding geometries. Similarly, the checkpoint kinase protein CHEK2 interacts with several proteins in its activated state in response to DNA damage or strand break in the cell. Investigation of CHEK2 phosphorylation of TP53 shows that this activation is allosterically controlled by a novel docking interaction with TP53 (Craig, et al., 2003), which also acts as a specificity inducing mechanism for Ser/Thr kinases in general (Biondi and Nebreda, 2003). These processes involve conformational alteration at the protein-protein docking site maximizing complementary interaction between the kinase and its substrate, thereby enhancing the interaction specificity. Therefore, probing the alteration of structural dynamics, which has key relevance to the function of both CALM1 and CHEK2 is very much pertinent to our present study.

In this paper, we introduce the use of coarse-grained MD as a tool for generic interpretation of loss-of-function upon mutation and extend the inference to predict alteration of a phenotype. This method is based on our previous work (Bhadra and Pal, 2014) which shows a proof of principle that fluctuations in the protein segments obtained from coarse-grained MD can be directly used to screen for molecular function. The full pipeline of the methodology based on the use of our handcrafted Coarse Grained Molecular Mechanics (CGMM) forcefield has been extensively tested (Bhadra and Pal, 2017) and also shown to improve protein function annotation (Das, et al., 2017). By participating in the Critical Assessment of Genome Interpretation 2018 (CAGI) for the first time, we have subjected our methodology to blind tests for assessing function alteration due to mutation. We have predicted for three test cases where a protein structural model was available or could be reliably built and we could rationalize the performance of our method. Because we use coarse-grained dynamics, side-chain modeling was not an issue for model preparation. For one case where more detailed information was necessary for interpretation, we have used all-atom dynamics using CHARMM27 (MacKerell, et al., 2000) forcefield. This has allowed us to explore the use of MD in assessing protein variants for phenotypic alterations in a reasonably comprehensive manner for which we believe the results are both insightful and encouraging.

Methods

The global overview of workflow followed in evaluating phenotype alterations due to variants of CALM1 and CHEK2 proteins, and stability alteration in Frataxin variants is given in Fig. 1. Common to all the workflows for individual proteins is the MD simulation step in coarse-grained and all-atom form. Before submitting the wild-type proteins and the variants for MD simulation, it was essential to prepare them for submission and each case posed its own set of requirements. In each case, wherever required, the wild-type model was first built using the Modeller software (Fiser and Sali, 2003). Thereafter, the variant models were built using the wild-type model by altering the amino acid at the specific site in the tertiary structure.

Figure 1.

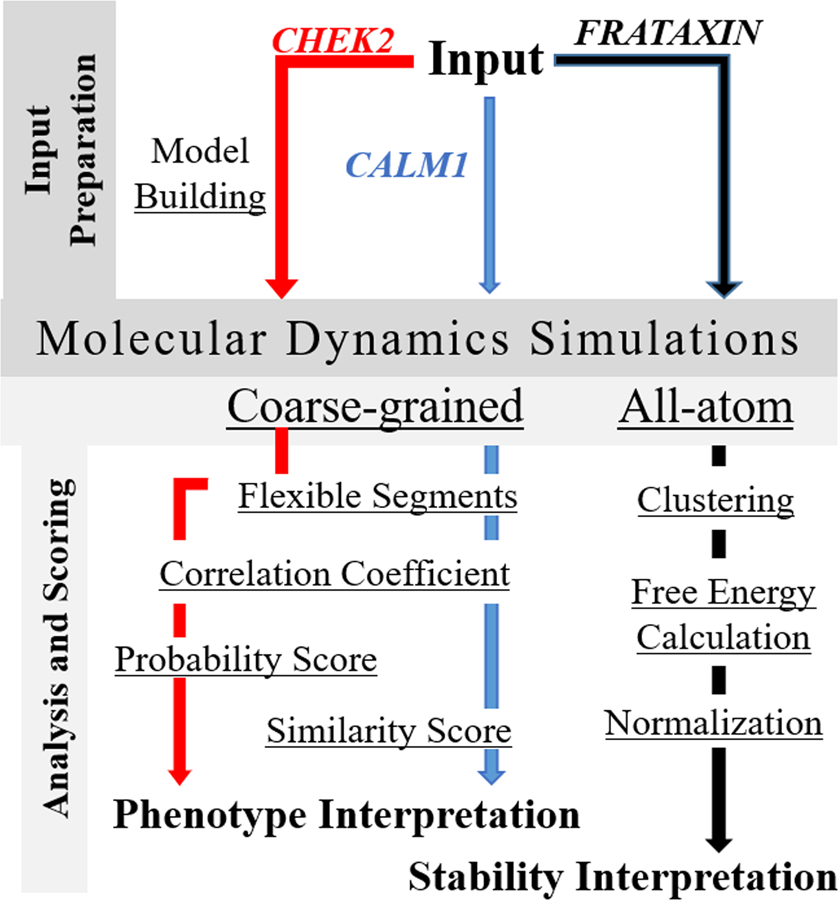
A global overview of the workflow for the Molecular Dynamics based calculation of phenotype alterations due to CHEK2 and CALM1 protein variants, and stability alteration interpretation of the Frataxin protein variants. Calculation of Flexible Segments and Correlation Coefficients are the common steps shared between CHEK2 and CALM1 protein for analyses post MD simulation.

Input Preparation

CHEK2.

We worked with the isoform 9 of the protein, which is of 586 amino acid length for which a complete structure is not available in the Protein Data Bank (PDB, http://www.rcsb.org). Therefore, we took two templates from the PDB and created a single model by multi-chain modeling using Modeller. The templates with PDB identifier (ID): 3I6W and 2CN5 had sequence identities of 99.7% and 99.3%, respectively, with the CHEK2 and corresponding templates segments 92–501, 208–504 span 92–547 segment of the CHEK2 polypeptide sequence. The best structure spanning residues 92–586 with Discrete Optimized Protein Energy Score of −40091 was used for coarse-grained MD simulations. 39 residues at the C-terminal end of CHEK2 is modeled as a loop. For mutant cases located between residue positions 1–91, for which no tertiary structure was available, we performed a secondary structure prediction using YASPIN (Lin, et al., 2005) and identified the secondary structure at the mutation locations. Mutation located within the regular secondary structure segment, such as helix or sheet was deemed as damaging, while others were benign. E→Q mutation was treated as neutral for the segment. We worked on a total of 34 non-synonymous Single Nucleotide Variants (SNVs) available from Genome Wide Association Studies on Latina population with 1000 breast cancer cases and 1000 ancestry-matched controls. Variants in the list were observed between 1–20 times.

CALM1.

It is a 149 amino acid length protein. The coordinates of the protein for the segment 5–149 was available from the PDB with ID: 3CLN, which was used for the MD simulations. The coordinate file had only one subunit, which was taken for the model building to fill in the missing coordinates in the N-terminal region. We had a data set of 1813 SNVs to investigate for which at least three independent barcoded clones were represented, providing internal replicates of the experiment. The analysis is performed on 1719 SNVs because the remaining scores derived from the experiments had negative values corresponding to their trait. MD simulations were run on the wild-type protein and all the mutants except for the ones where the mutation was occurring at the metal binding residue location.

Frataxin.

It is a 210 amino acid long protein of which residues 81–210 represent the mature form. The coordinates for this segment (90–208) was available from the PDB with ID 1EKG, which was used for our calculations. The coordinate file had only one subunit, which was taken for model building to fill in the missing coordinates in the C-terminal region. We had information for 8 non-synonymous variants for which we had to predict alteration of protein stability with respect to the wild-type.

Molecular Dynamics Simulations

Coarse-grained.

We ran the coarse-grained MD simulation on the pseudo-atoms located at the C_α atom position of the protein structure for 1μs with CGMM forcefield (Bhadra and Pal, 2014; Bhadra and Pal, 2017) at 300K temperature using Gromacs software Version 4.6.5 (Van Der Spoel, et al., 2005). The pseudo-atom types supported by the CGMM forcefield is available at cgmm.itp (http://pallab.cds.iisc.ac.in/CGMM/cgmm_download.php). The mass of each pseudo-atom is set to its corresponding accurate amino acid mass. To begin, we make the itp (include topology), gro (molecular structure in Gromacs format) and top (topology file) files using the utility script provided at the above URL. Potential energy functions in a tabulated format are also available here for use in the simulation run. The simulation medium is taken as a vacuum. The protein was subjected to steepest descent energy minimization to remove any overlapping contacts and reduce the maximum force in the system to 100kJ/mol/nm. This was followed by the equilibration step. For equilibration, canonical or NVT (constant number (N), volume (V), and temperature (T)) ensemble was used with Berendsen temperature coupling at 298K. Simulated annealing was used in the equilibration step for 70ps time interval. Then the unconstrained dynamics was run using a 2fs integration time step. Leapfrog method was used as the integrator algorithm. Structures during unconstrained dynamics simulation were recorded every 100ps time in the 1µs long simulation to give a total of 10,000 frames for analyses. Simulations were performed in a 64bit 2.7 GHz processor server and a typical CALM1 MD simulation took about 33 hrs in a single processor, while CHEK2 took about 76 hours. Multi-process jobs were avoided due to unstable behavior.

All-atom.

The MD simulations were run using Gromacs software Version 4.6.5 (Van Der Spoel, et al., 2005) with CHARMM27 (MacKerell, et al., 2000) as forcefield for 1ns at 300K temperature. In each case, we used a cubic box of a specific size with SPC/E (SPC216) water and centered the protein such that it left roughly 10Å distance to the edge of the box. Thereafter we neutralized the system and subjected it to steepest descent energy minimization to remove any overlapping contacts and reduce the maximum force in the system to 1000 kJ/mol/nm. This was followed by NVT equilibration, with a 2fs time step, using modified Berendsen thermostat with a total simulation time of 100ps under a temperature of 300K. Subsequently, the NPT (constant number (N), pressure (P), and temperature (T)) equilibration of 100ps using 2fs time step at 1atm was done using Parinello-Rahman pressure coupling. Structures during unconstrained dynamics simulation were recorded every 10ps to give a total of 101 frames for analyses.

Analyses and Scoring

Flexible Segments.

We obtain the flexible regions of the protein from the simulation trajectory using Root Mean Square Fluctuation (RMSF) estimated from all the frames. These RMSF values are then normalized using the formula [RMSF_norm = (RMSF_{obs –} RMSF_mean)/ σ(RMSF)], where σ = standard deviation of the observed RMSF values. For identifying segments that are flexible, we convert the real number values of RMSF for each residue in the frame into discrete symbols representing specific RMSF ranges. The detailed scheme is described in Bhadra et al. (Bhadra and Pal, 2014). The symbols L, I, H, and G correspond to normalized RMSF ranges of 0–1, 1–2, 2–3, and >3, respectively. On the basis of RMSF_norm profile and the criterion for a flexible region; i.e. the percentage occurrence of a symbol (L >35% or combined G, H and I >14%), we select the flexible regions of the structure.

Correlation Coefficient.

Once the flexible regions of the protein are identified, we embark on matching the flexible regions of the wild-type and the variant to compute a Pearson correlation coefficient (PCC). For this, we first calculate a three‐dimensional (3D) unweighted Autocorrelation Vector (ACV) for individual flexible regions based on residues in each frame. The formula for calculating 3D ACV is (Bhadra and Pal, 2014):

$$3\text{D ACV}=\left[v\mathit{\left(}\mathit{1}\mathit{\right)},v\mathit{\left(}\mathit{2}\mathit{\right)},\dots \mathrm{..}v\mathit{\left(}i\mathit{\right)}\dots \dots v\mathit{\left(}n\mathit{\right)}\right]$$

$$v\left(i\right)={\mathrm{\Sigma }}_{j,k}\delta \left(i\right)P_j{P}_k\hspace{1em}\hspace{1em}where\hspace{0.17em}\delta \left(i\right)=\left\{\begin{array}{cc}1& if\hspace{0.17em}i\le D<\left(i+1\right)dx\\ 0& if\hspace{0.17em}i>D\ge \left(i+1\right)dx\end{array}\right\}$$

In here, P_j and P_k are the properties or weights associated with the atoms j and k, separated by a distance D = [(i+1) dx - (i) dx]. Note that in our case each atom is, in fact, a pseudo-atom placed at the Cα atom position representing an amino acid in the polypeptide chain. The dimension of the 3D ACV is n, where n = d_max/dx; d_max being the distance between two farthest atoms in the concerned protein segment and dx is the step size, which is 2Å in our case. Each flexible segment yields an ACV, and these are compared for a pair of proteins to obtain a PCC value using 11 frames (each at 100 ns apart) available from the MD trajectory. For the CHEK2 case study, we use 11 × 11 = 121 PCC values from the ACVs for each pair of proteins where 50% of them must have a PCC of >0.90 and 25% must be >0.95 or Euclidean Distance $\left(\text{ED}=\sqrt{{\left(x-50\right)}^2+{\left(y-25\right)}^2}\right)$ value <15, to screen a match for similarity in function between the two proteins (in this case, wild-type and the mutant). For the CALM1 case study, we have relaxed the screening condition slightly to increase the coverage. The criteria to screen from 121 PCC values from the ACVs for each pair of proteins is accordingly relaxed to 50% must have a PCC of >0.80 and 25% must be >0.85 or ED value <15, to screen a match for similarity in function between the two proteins.

Probability score for CHEK2.

The filtered wild-type protein and the variant-pair are sent for a similarity score calculation defined as a ratio of the number of flexible regions in mutated protein (a) and wild-type (b): Similarity Score = a/b. It may be noted, that the Similarity score caters to comparing proteins through matching flexible protein segments that may contribute to similar function. However, mutations in the protein always have a context-based effect at a given site. If the mutation is in the ligand binding site of a protein, there is a higher chance of mutation being damaging to protein function. Consequently, one can prioritize the sites to investigate as per the question asked. In the context of CHEK2 isoform 9 protein, which is a kinase protein, ATP binding activity is of the highest importance. Therefore, the mutations given for CHEK2 were classified to be near or far away from the ATP binding site. We found one segment (412–421) near this site which was flexible and could affect the ATP binding of the protein thereby altering or hindering its biological function. Since the mutations at different site alter the flexibility of protein segments of different sizes, while evaluating for effects of alteration of ATP binding, we chose only the common segment of 412–421 for all proteins for comparison. The premise used for evaluation was that higher the similarity of the variant protein to the wild-type, the lesser is its chance to be present in cancer patients. Some previous experimental values for the effect of CHEK2 variants to be damaging or benign for cancer patients were already available from Calvez-Kelm et al. (Le Calvez-Kelm, et al., 2011) and Desrichard et al. (Desrichard, et al., 2011). Our scores calculated for the mutants were mapped to the identical cases reported in these papers (Table 1). This allowed us to segregate the range of the scores corresponding to benign, damaging, or neutral. The ranges were mapped to: <70 Damaging, 70–80 Neutral, and >80 Benign for scores, and >0.5 Damaging, 0.5 Neutral, and <0.5 Benign for the corresponding probabilities.

Table 1.

Available classification of CHEK2 mutant phenotypes used in our study for defining the ranges of similarity scores and probability values

Mutation	Reference result*	Our Similarity Score	Our Probability Score	Our Result
p.L555V	Benign	81.25	0.4	Benign
p.I491S	Benign	87.5	0.3	Benign
p.I200T	Benign	63.15	0.6	Damaging
p.I491V	I491S is Benign	100	0.0	Benign
p.I264V	I264M is Possibly Damaging	68.42	0.6	Damaging
p.R562L	Possibly Damaging	57.89	0.6	Damaging
p.D481Y	Possibly Damaging	57.89	0.6	Damaging
p.E282K	Possibly Damaging	73.68	0.5	Neutral
p.R223C	Possibly Damaging	100	0.0	Benign
p.R180Q	Possibly Damaging	47.36	0.7	Damaging
p.P527L	Possibly Damaging	0	1.0	Damaging
p.T519M	Possibly Damaging	68.4	0.7	Damaging
p.R389H	Possibly Damaging	0	1.0	Damaging
p.R160G	Possibly Damaging	87.5	0.3	Benign

^*Calvez-Kelm et al. (Le Calvez-Kelm, et al., 2011) and Desrichard et al. (Desrichard, et al., 2011)

Similarity Score for CALM1.

At first, the Similarity score is calculated in the same manner as in CHEK2 using the formula (Similarity Score = a/b) as above. For the metal binding residues, if upon mutation the covalent structure of the protein is getting changed, we did not run the simulation and directly inferred from the fact that if the metal is bound with a side chain of an amino acid and that side chain is getting changed; that is, upon the amino acid getting mutated, the metal will not be able to bind, and the whole structure will become unstable and dissimilar to wild-type.

Clustering and free energy calculation for Frataxin.

After finishing with all the MD simulations, we cluster the frames on the basis of their RMSF using the g_cluster command of the Gromacs utilities. The RMSF threshold is set such that we obtain only 2 clusters. We assumed that the cluster which had the higher number of frames is the one having the more stable structures, while the one which had a lower number of structures is the one that is less stable. These two states were assumed to represent the folded and unfolded states, respectively for the purpose of our calculations. In the third step, we select one representative structure from the cluster that is closest to the cluster centroid and use it for free energy calculation using the g_mmpbsa (Kumari, et al., 2014) method. This method gives 3 types of energies: molecular mechanics potential energy, apolar and polar energy. The free energy is calculated by summing up all the three energies. The unfolding free energy is the difference between the unfolded and the folded state (ΔG). Correspondingly, we calculate another ΔG value by taking the variant protein. We estimate the ΔΔG by taking the difference between the variant ΔGs and wild-type.

Normalization of ΔΔG values.

Normalization is performed retrospectively from the available experimental information. This normalization step is necessary because the folded and the unfolded states assumed in our method are representative cases only, and an exhaustive unfolding simulation will be computationally expensive. We apply a simple linear transformation {Normalized ΔΔG = [(0.09 * predicted ΔΔG) – 1.5]} to the obtained values such that the predicted centroid value of the ΔΔGs coincides with the centroid of the experimental values. The predicted ΔΔG values used by us excludes the constant solvent contributions to the free energy value.

Prediction Performance Assessment

We use two types of evaluation metrics, one based on values and other categorical, namely the class prediction. For evaluating based on values, we use (i) PCC, (ii) Root Mean Square Error (RMSE), and (iii) Absolute Mean Error (MAE) with reference to the experimental data. PCC = cov(X,Y)/σ_xσ_y, where X and Y are the two variables between which we want to compute the correlation coefficient. Cov is covariance between the variables and σ their standard deviation.

$\text{RMSE}=\sqrt{\frac{{\sum }_{i=1}^N{(X_{i,pred}-X_{i,exp})}^2}{N}}$, where X_i,pred is predicted value at i^th position and X_i,exp is experimental value at i^th position and N is the total number of data points.

$\text{MAE}=\frac{{\sum }_{i=1}^N\left(X_{i,pred}-X_{i,exp}\right)}{N}$, where X_i,pred is predicted value at i^th position and X_i,exp is experimental value at i^th position and N is the total number of data points.

PCC is used to estimate the linear relationship between the prediction and experiments. RMSE is a measure indicating how close the predictions are to the experimental data points. MAE depicts the difference between the experimental and predicted values.

Receiver Operating Characteristic (ROC) curve is a graphical measurement for analyzing the classification ability of a method. It is a curve between True Positive Rate (TPR = TP ÷ Total Positives) and False Positive Rate (FPR = FP ÷ Total Negatives) at different thresholds (T). TP and FP are generated as part of the four measures that form the confusion matrix.

• True Positive (TP) are the cases where both predicted and experimental values are positive.

• True Negative (TN) are the cases where both predicted and experimental values are negative.

• False Positive (FP) are the cases where the experimental value is negative, but the method predicts it as positive.

• False Negative (FN) are the cases where the experimental value is positive, but the method predicts it as negative.

Thresholds (T) are the different cut-off values used for the demarcation of the predicted value into positive and negative class. ROC shows the trade-off between specificity (TPR) and sensitivity (FPR) of the method. The area under the ROC curve (AUC) is a measure of how well a binary classification method is performing.

For class-based evaluation, the following evaluation metrics are used: Accuracy and F1 score.

Accuracy (Acc = (TP+TN)/(TP+TN+FP+FN)) is the fraction of predictions our model got right. It is measured by the number of correct predictions made divided by the total number of predictions made.

F1 score (F1 = 2 × Precision × Recall / (Precision + Recall)) is also a measure of the accuracy of the method but it uses precision and recall for the assessment. Precision (TP/ (TP+FP)) is defined as the fraction of correct positive prediction to the total positive prediction made, which indicates the relevancy of the method. Recall (TP/ (TP+FN)) is defined as the fraction of correct positive prediction and total positive cases.

Class definitions for each challenge are as follows:

Frataxin: variants are divided into two classes based on threshold values, ΔΔG ≥ −2.0 (or −1.0) kcal/mol (class label 0, stable) and ΔΔG < −2.0 (or −1.0) kcal/mol (class label 1, unstable).

CHEK2 and CALM1: variants are also divided into two classes based on threshold values, probability ≤ 0.5 (class label 0) and probability > 0.5 (class label 1). In CHEK2, the class label 0 correspond to Benign, and class label 1 Cancerous. In CALM1, the class label 0 correspond to Deleterious and class label 1 Benign. Although another class called “Neutral” was also given in CHEK2 experimental data, only one data point was available there and therefore it was not considered for defining an additional class. Moreover, it is somewhat arbitrary to put a specific threshold to distinguish a “Neutral” mutation from “Benign” or “Deleterious”.

Results

The submissions made for the CAGI challenge can be grouped into two parts, one where there is functional interpretation, and second where the interpretation is restricted to assessing loss-or-gain of stability due to a point mutation. Submissions for CHEK2 and CALM1 are for the former category and submission for Frataxin is for the latter. The results are reasonably good for all. Below we describe the results and attempt to analyze the performance of the method.

CHEK2.

Figure 2 shows the scatter diagram of predicted probability values for CHEK2 marked against each mutant case. The experimental values are available in the categorical form (red color represents cancerous, green the benign, and black the neutral mutations), where we have merged neutral class to benign, as it had only one data point. It can be seen from Figure 2 that our method is able to discriminate between the mutants, and the Accuracy obtained is 0.62 and the F1 score 0.71, which is a reasonable performance of precision and recall. The same obtained from a machine learning based tool Polyphen (Adzhubei, et al., 2013) is higher at 0.73 for Accuracy and 0.78 for the F1 score. In the region 1–91 with 4 mutations, we could predict only one correctly.

Figure 2.

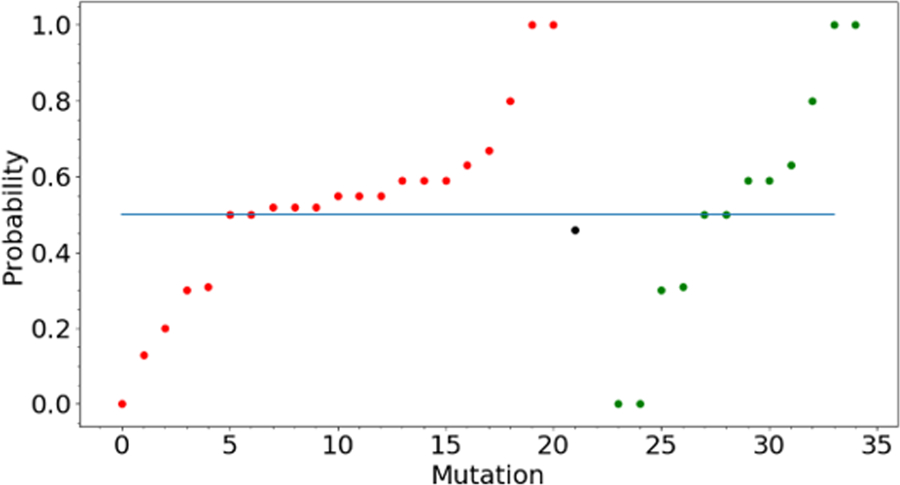
Scatter plot showing various probability values predicted for different mutants of CHEK2. The color code represents the various classes of data points; viz, Red=Cancer, Black=Neutral, Green=Benign. A predicted value of 1 means Cancerous, 0.5 means Neutral and 0 means Benign. Only one data point is present in the Neutral class and therefore merged with the Benign class for performance evaluation of our method.

It may be noted that in the experimental data 24, 6, 2, 1, 1 mutants with 1, 2, 3, 4, 17 replicate experiments, respectively were available for evaluation. Since a minimum of three replicates is necessary for confident interpretation, one can divide the analysis into two parts where we have sufficient data and otherwise. The former had only one case that showed all benign observations and the other two cases did not show unambiguous cancer or benign state. If we take this information into the background while calculating Accuracy of our predictions, in the 24 cases where only one replicate information is present, we could predict correctly in 14 cases (58% cases accurate; F1 score 0.68), for 6 cases with two replicates we predict 4 cases correctly (66% accurate, F1 score 0.8) and in 2 cases with three replicates we predict one correctly. For one case with 4 replicates, 2:2 were cancerous:benign. We have predicted a probability 0.46 for this case which is close to 0.5 ideally expected for the Neutral case. For a single case where 17 replicates are present, we predict it correctly with a probability of 0.55.

If we look at the results in terms of a linear trend between predicted probabilities and observed occurrence values, the overall PCC is poor due to anti-correlating predictions on 18% data (Table 2). Otherwise, for 82% of the data, we have a reasonable PCC of 0.47, which is improved to 0.73 for 68% of the data. The corresponding RMSE and MAE values are reasonable given the low number of replicates in the experiments, as outlined above. The performance of the method can also be seen from the ROC plot (Fig. 3A) showing an AUC of 0.77 for 75% of the data, consistent with the trends presented in Table 2.

Table 2.

Performance of our method shown on partitioned and complete data

	|ScorePredicted - ScoreExpt.|	PCC	Data (%)	RMSE	MAE
CHEK2 (34 cases)
1.	≤0.25	0.98	20.5	0.11	0.07
2.	≤0.50	0.73	67.6	0.34	0.29
3.	≤0.75	0.47	82	0.42	0.36
4.	≤1.00	0.02	100	0.54	0.45
CALM1- ALL (1719 cases)
1.	≤0.25	0.79	50	0.14	0.12
2.	≤0.50	0.58	67.1	0.22	0.18
3.	≤0.75	0.32	80.6	0.33	0.25
4.	≤1.00	−0.024	100	0.49	0.38
CALM1- Excluding Zeros (1274 cases)
1.	≤0.25	0.59	65.3	0.14	0.12
2.	≤0.50	0.33	85	0.21	0.17
3.	≤0.75	0.09	97.3	0.3	0.23
4.	≤1.00	0.03	100	0.32	0.245
Frataxin (8 cases)*
1.	≤1.75	1	25	0.67	0.65
2.	≤3.25	0.9	62.5	1.65	1.49
3.	≤4.875	0.83	75	2.11	1.84
4.	≤6.5	0.6	100	3.52	2.89

^*Scores for Frataxin are ΔΔG values

Figure 3.

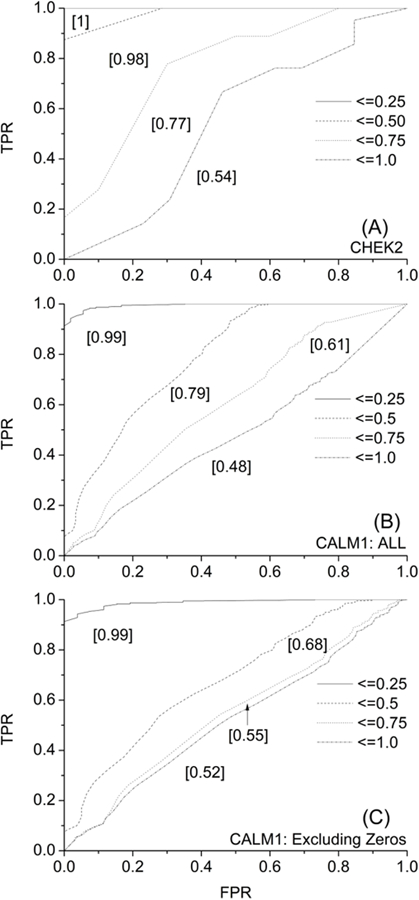
ROC curves for predictions made on CHEK2 (A) and CALM1 (B-C) variants. There are four curves (solid, dash, dot, dot-dash) in each plot corresponding to top 25%, 50%, 75%, and 100% of the MAE-sorted data. The area under the curve for each curve is indicated in square brackets [].

CALM1.

Figure 4 shows the distribution of predicted and experimental classification values of CALM1. The distribution is shown in 2 parts, “All” (Fig. 4 A–B) and “Excluding Zeros” (Fig. 4 C–D). We submitted all the data to the CAGI5 competition as was mandated, even though we could not perform MD simulations for all, and therefore not able to make predictions for those cases (reported “Zero” as their value). These cases have been removed from our evaluation to show the actual performance of the method. Distribution of experimental and predicted values are better aligned after removing “Zero” entries. When we take the difference between the predicted and observed data points in “All” and “Excluding Zeros” cases, we see that we have the highest bars close to zero, indicating good prediction for a large number of cases (Fig. 4 E–F). A closer look at Table 2 reveals that about 20% and 15% of the predictions in “All” and “Excluding Zeros” dataset are anti-correlating due to which the overall PCC for the results are poor. Otherwise, for about two-thirds of all the data, we get a reasonable PCC of around 0.6. The corresponding RMSE and MAE values are within 0.22 and 0.18, respectively. Together with these observations and the bell-shaped nature of the distribution observed in Fig. 4 E–F, one can argue that our method’s performance is reasonably good. These performance trends are also reflected from the ROC plots (Fig. 3 B–C).

Figure 4.

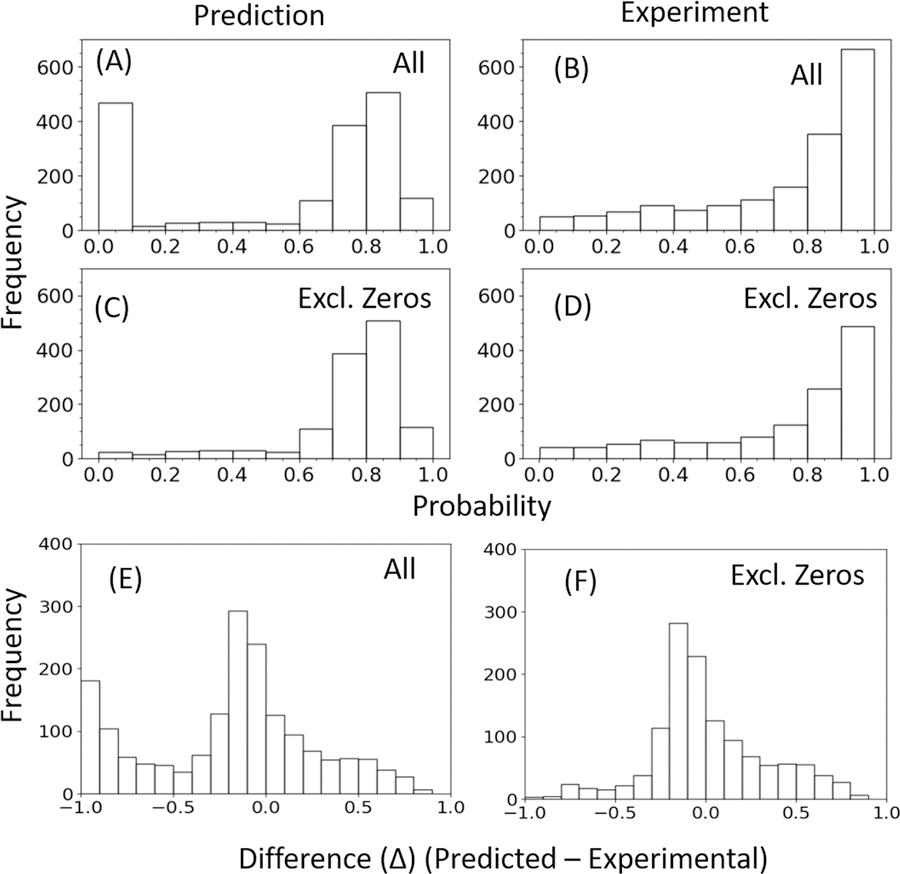
Comparison of the distributions of CALM1 predictions with its experimental data based on probability. Two sets of diagrams are given, one in which all data points are included “All” (A-B) and other in which “Zero” (C-D) data points are excluded. “Zero” data points correspond to no prediction cases. The difference between the data points in (A) and (C) are given in (E), and the difference in data points in (B) and (D) are given in (F), as histograms.

If we evaluate based on Deleterious and Benign classes using the F1 score, then we get a value of 0.72 (All) and 0.84 (excluding Zeros). The accuracy of the method is 0.59 (All), which improves to 0.73 when we exclude the “Zero” cases. If we compare our results to a popular phenotype classifier like Polyphen then it gives a lower Accuracy of 0.52 (All) and 0.49 (excluding Zeros). The F1 scores are 0.66 (All) and 0.63 (excluding Zeros).

Frataxin.

Figure 5 and Table 3 shows the comparison between the experimental and predicted values of ΔΔG. On the basis of experimental results, values are divided into two parts, unstable and stable at the threshold of ΔΔG = −2.0 kcal/mole or −1.0 kcal/mol. Lesser the ΔΔG value, lesser stable is the mutant. In the graph, stable mutations are shown in green while unstable mutations are shown in red. As shown in the graph, our method is able to distinguish between stable and unstable mutations. We are predicting for 3 stable mutations and 3 unstable mutations correctly at the threshold of ΔΔG > −2.0 kcal/mol. While at the threshold ΔΔG > −1.0 kcal/mol, we are predicting correct classes for 5 out of 8 variants (Table 3).

Figure 5.

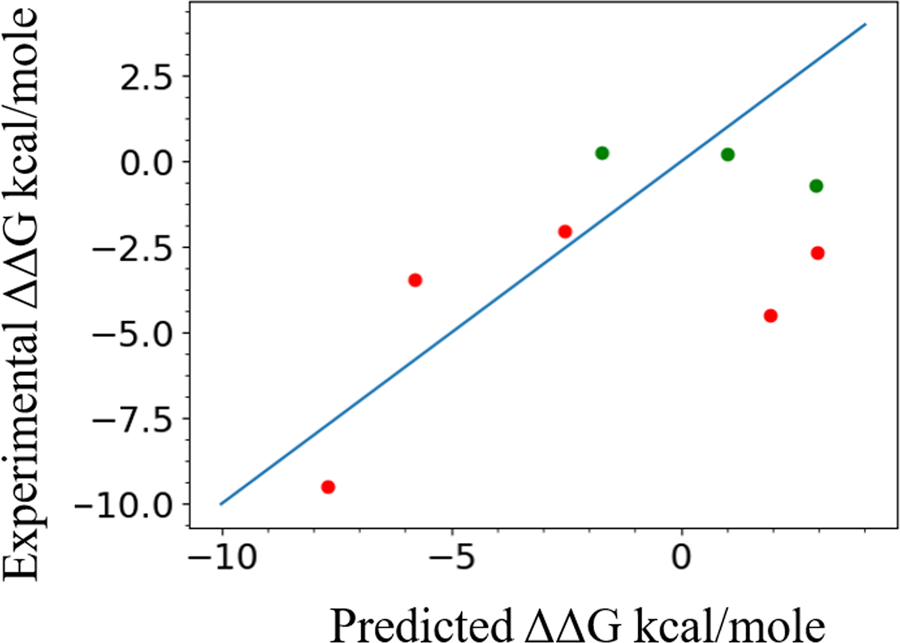
Graph showing the linear correlation between the Frataxin normalized ΔΔG values predicted by our method and compared to their experimental values. Data points greater than −1.0 kcal/mol are marked in green and others in red. Ideal predictions would be along the diagonal line.

Table 3.

Classification of Frataxin stability values

	Variant	ΔΔG (Exp.)	ΔΔG (Raw)	ΔΔG (Norm.)	Class 1† Exp	Class 1† Pred.	Class 2‡ Exp.	Class 2‡ Pred.
1.	D104G	0.26	−2.5	−1.7	0	0	0	1
2.	A107V	0.22	28.1	1.02	0	0	0	0
3.	F109L	−2.65	49.8	3.0	1	0	1	0
4.	Y123S	−4.48	38.3	1.9	1	0	1	0
5.	S161L	−3.44	−47.7	−5.8	1	1	1	1
6.	W173C	−9.54	−68.8	−7.7	1	1	1	1
7.	S181F	−2.04	−11.6	−2.5	1	1	1	1
8.	S202F	−0.69	49.1	2.9	0	0	0	0

A threshold of −2.0 kcal/mol^† and −1.0 kcal/mol^‡ is used to create classes. Label 0 means mutant is stable and 1 otherwise.

Using value-based analysis, PCC between predicted and experimental data is found to be 0.6, with RMSE and MAE being 3.52 and 2.89, respectively, showing the closeness between the predicted and experimental values (Table 3). A comparative evaluation using the Fold-X server (Schymkowitz, et al., 2005) returned PCC: 0.77, RMSE: 2.24, MAE: 1.62. The same values for I-mutant server (Capriotti, et al., 2005) are PCC: 0.76, RMSE: 3.13, MAE: 2.24. On performing classification-based analysis using a threshold of −1.0 kcal/mol, Accuracy for our method was found to be 0.63 and F1 score 0.67 showing good precision and recall. A similar analysis at threshold −2.0 kcal/mol shows Accuracy 0.75 and F1 score 0.75, indicating improved precision and recall. The Accuracy given by Fold-X and I-mutant were 0.75 and 0.63, respectively for classification threshold of ΔΔG > −1.0 kcal/mol, and 0.63 and 0.63 for threshold ΔΔG > −2.0 kcal/mol. The F1 score for Fold-X and I-mutant were 0.8 and 0.57 for threshold ΔΔG > −1.0 kcal/mol, and 0.57 and 0.57 for threshold ΔΔG > −2.0 kcal/mol.

Discussion

It is the first time “Protein Flexibility” has been used as a primary predictor in a CAGI challenge for blind tests. Our approach demonstrates the straightforward use of MD simulation to understand the alteration of phenotype or protein stability. These are linked to protein function which in turn is intimately linked to protein flexibility. Function requires interaction with another molecule, which in turn requires the protein to be able to change its conformation. This rearrangement could be of various degrees; however, a perturbation that changes the flexibility affects how this rearrangement is realized, therefore directly affecting the function. MD in our case is simply a tool to estimate this flexibility and its alteration due to mutation. If one were to look at previous attempts of estimating alteration of function, protein feature based studies have used measures like hydrophobic burial (or burial of charge), backbone strain, overpacking, secondary structure and electrostatic interactions (Teng, et al., 2008). All these features are tied to protein conformational dynamics in varying degrees and likely to get perturbed in case of a mutation. Consistent with this underlying concept we explore the use of MD in studying phenotypic alteration. The basic premise exploits the fact that any alteration of the protein that changes its dynamics such that it can perturb the function and/or interaction is likely to have phenotypic consequences.

Conformational flexibility has been previously used by existing pathogenic variant callers as one of the many other features (Ancien, et al., 2018; Pejaver, et al., 2017). B-Factor values of atomic coordinates in crystal structures (Sun, et al., 2019), NMR order parameters (Torchia, 2015) or fluctuation calculated from an alignment of multiple X-ray structures or NMR derived ensembles allows straightforward estimates on flexibility. Conformational flexibility estimated through MD has also been used as one of the many features in predicting for effects of a missense mutation (Ponzoni and Bahar, 2018), but not in a direct manner as us. We look at altered flexibility; therefore, if any protein segment, including non-flexible segment, if altered in flexibility, those effects are accounted for. The approach is powerful as it does not rely on any evolutionary information and can be obtained from first principles such that its application can be done on novel proteins with no or limited homology information. The minimum requirement is only the availability of a structural model of the protein in consideration.

The importance of the protein in the functional network is another key aspect to judge the extent of the downstream cascading effects that it might produce to alter a phenotype. In general, one can expect the alteration of essential proteins, including those forming hub and bridge to maximally affect the phenotype, provided the function/interaction is truly altered by the mutation. Any mutation that does not alter interaction or function owing to their remote location from the site of activity, will have limited or no bearing on the alteration of phenotypes. However, it is possible that such mutations that globally destabilize proteins, especially those occurring in protein core, may alter function although they may be remote from the actual functional site (Yue, et al., 2005). This primarily affects the protein’s overall fitness (i.e., the ability to do its function) owing to lowered free energy (i.e., stability) due to mutation (Tokuriki and Tawfik, 2009). However, increase in the stability could also be a cause of disease, even though the protein’s fitness is not altered (Chiang, et al., 2016; Li, et al., 2004). Therefore, approaches that assess both global and local features to estimate protein properties stand a better chance to correctly predict altered phenotypes. Protein flexibility used as a measure by us to screen for altered phenotypes in this study appears to encapsulate features that are both global and local in nature.

Looking specifically at our application on CHEK2, we already know it to be a key hub protein regulating the G2/M cell-cycle checkpoint and maintaining the genome integrity, forms a functional linkage clique with a host of other important proteins like ATM, ATR, CDC25C/CDC25A, MRE11A, RAD50, H2AFX TP53BP1, TP53, and BRCA1 (Szklarczyk, et al., 2015). Since the phenotype to evaluate in CAGI challenge is cancer and the CHEK2 is a kinase, we focussed on screening the alteration of dynamics around the ATP binding site (412–421), as phosphorylation is known to be one of the most important activities in cancer pathway. This allowed us to avoid evaluating other parts of this large 586 length protein that may have limited or no consequence for the phenotype alteration in question. Understandably, a better knowledge of the parts of the protein that has a contribution to phenotype alteration would allow us to improve the results. Notwithstanding, the present results are reasonable, based on a simple rational premise compared to the heavily trained state-of-the-art machine learning methods, like Polyphen, whose results are only marginally superior to ours. This fact is further corroborated from predictions for CALM1, also a hub protein, and shown to be a rescue phenotype, suggesting its important role in cell viability. In this case, our predictions are superior to Polyphen, and it can be rationalized to the measure of flexibility-based similarity that we use to assess the phenotype alteration here. The improved performance can be attributed to using all parts of the protein for score estimation, as we found all protein segments to be involved in some activity or the other with relevance to cell viability. This contrasts with the focussed assessment we make for CHEK2, although it vindicates our presumption that alteration of the ATP binding site has a key consequence for cancer pathogenesis.

One of the key steps of our methodology common to both CHEK2 and CALM1 phenotype prediction is finding the Correlation Coefficient. This step is based on comparing frames from the MD trajectory using 3D ACV. Currently, we implement unweighted 3D ACV for finding matches. This means that we only evaluate the alteration of the flexibility of a protein segment ignoring its chemical consequences. If we use weighted 3D ACV, the alteration of the flexibility information will incorporate chemical consequences alongside, which is more relevant for phenotype alteration assessment.

Protein-protein interaction required for signaling, recognition, and transport events are key activities contributing to a phenotype. Similarly, protein-ligand binding is a key activity that could also be the principal contributor to a phenotype. However, one can counter that probing protein conformational dynamics is not the same as probing its interaction and vice versa. A closer look reveals that the conformational dynamics of a protein directly affects its interaction potential. For example, the fluctuation of the protein molecule during dynamics alters its atomic packing, and with a mutation, this packing is also altered and may affect protein-protein interaction when such a site is in the mutation neighborhood (Naganathan, 2019). Conformational dynamics is also known to alter the hydration shell of a protein, and water hydration is known to play a key role in binding thermodynamics of protein complexes (Chong and Ham, 2017). Similarly, conformation dynamics can affect ligand binding affinity when the opening/closing of the binding groove gets altered by mutation (Seo, et al., 2014). By checking for the alteration of flexibility between wild-type and mutant using MD, we implicitly check for alteration of protein-protein and protein-ligand binding activity. Since protein-protein and protein-ligand interaction are context specific and spatiotemporal in nature, it is practically not feasible to gather knowledge over all such interactions possible in a cell. Alteration of flexibility assessed through MD simulations could provide an alternative way to quantitatively judge how such interactions may be affected thereby altering a phenotype.

Looking at the Frataxin predictions, we can clearly see that our method performs equally well compared to others, although being simplistic in approach. All-atom simulation using CHARMM27 forcefield was appropriate compared to coarse-grained MD because CGMM forcefield lacks electrostatics-based nonbonded potential functions essential for the method used by us to estimate free energy change. Moreover, the use of the all-atom model ensures more sensitive computation of free energies compared to the pseudo-atom based coarse-grained model. It can be argued that the free energy change estimates can be further improved if we had performed more sampling of states by increasing the simulation time to microseconds. A key challenge, however, is the normalization of the free energy estimates, such that it is comparable to the experimental values. More research is needed in this direction through the improvement of forcefield parameters.

Conclusion

We described new applications of MD based prediction of altered phenotypes of CHEK2 and CALM1 protein and presented an estimate of altered free energy on mutation for Frataxin protein. The results are competitive to the existing methods, despite being simplistic and straight forward in nature. The CAGI challenge has offered a unique opportunity to consider further ideas to improve our method through the lessons learned from this edition of the challenge and to better assess protein variations. The mechanism(s) relating stability-flexibility-function/interaction-phenotype is complex and our goal is to understand this further.