3D Printed Electrically-Driven Soft Actuators

Abstract

Soft robotics is an emerging field enabled by advances in the development of soft materials with properties commensurate to their biological counterparts, for the purpose of reproducing locomotion and other distinctive capabilities of active biological organisms. The development of soft actuators is fundamental to the advancement of soft robots and bio-inspired machines. Among the different material systems incorporated in the fabrication of soft devices, ionic hydrogel–elastomer hybrids have recently attracted vast attention due to their favorable characteristics, including their analogy with human skin. Here, we demonstrate that this hybrid material system can be 3D printed as a soft dielectric elastomer actuator (DEA) with a unimorph configuration that is capable of generating high bending motion in response to an applied electrical stimulus. We characterized the device actuation performance via applied (i) ramp-up electrical input, (ii) cyclic electrical loading, and (iii) payload masses. A maximum vertical tip displacement of 9.78 ± 2.52 mm at 5.44 kV was achieved from the tested 3D printed DEAs. Furthermore, the nonlinear actuation behavior of the unimorph DEA was successfully modeled using analytical energetic formulation and a finite element method (FEM).

1. Introduction

Since the early 1500s, when Leonardo da Vinci explored the possibility of human flight by observing and attempting to imitate birds, the concept of “biomimetics” – the ability to emulate nature and living organisms – has inspired a plethora of scientific discoveries and engineering innovations that have led to novel materials, mechanisms, and devices [1, 2]. Among these efforts is the development of “soft robots” with the purpose of reproducing locomotion, morphing structures, and emulating other distinctive capabilities of active biological organisms [3–6]. The field of soft robotics is primarily enabled by advances in the development of soft materials with properties commensurate to their biological counterparts.

In recent years, ionic hydrogel–elastomer hybrids, which are formed by laminating layers of hydrogels and elastomers together, have attracted vast attention owing to their favorable characteristics. Specifically, elastomers are resilient materials with low elastic modulus (~ 0.1 MPa to ~100 MPa), high failure strains (> 300% strain) [7], and resistance to extreme environmental conditions such as changes in temperature [8]. Moreover, ionic hydrogels are soft, transparent, conductive materials which employ ions as the charge carriers as opposed to electrons in conventional electrode components. It has been demonstrated that such hydrogels remain functional at high voltages (above 10 kV) and high frequencies (above 10 kHz), and can exhibit large stretchability (area strain of 167%) with high transmittance and low sheet resistance [9]. Furthermore, the combination of these two materials has been found to be analogous to human skin, with the elastomer replicating the epidermis layer, and the ionic hydrogel mimicking the dermis layer, including signal transfer via ions as part of the natural sensing mechanism [10, 11]. Such ionic hydrogel–elastomer hybrids have been used in development of soft devices and stretchable electronics including sensors [11–14], actuators [9, 15], mechanical energy harvesting devices [16], electroluminescent skins [17, 18], electrical interconnects [19], flexible circuit boards, and stretchable microfluidic chips [10].

Conventional methods used for the fabrication of soft devices typically involve post-processing steps, or manual assembly of the parts. Recent advances in extrusion-based, direct ink writing (DIW) approaches for multi-material 3D printing allow for the incorporation of various functional layers in high density and with fine features in the fabrication process, thus paving a path for the facile creation of soft robots with complex geometries and integrated functionalities [20]. It has been demonstrated previously that hydrogel and elastomer precursors can also be employed in a DIW process for fabricating functional soft sensors [12, 13]. To date, the work reported here is the first demonstration of 3D printing ionic hydrogel–elastomer hybrids for fabricating electrically-driven bending actuators.

In this study, we successfully demonstrate the 3D printing of unimorph dielectric elastomer actuators (DEAs) with a silicone-based dielectric layer and ionic hydrogel electrodes. Dielectric elastomers (DE) are types of electroactive polymers (EAPs) that form transducer devices when laminated between two compliant electrodes. When a high electric field is applied to the device in actuation mode, the DE layer exhibits in-plane expansion and compression along its thickness. In the unimorph configuration, the device resembles a cantilever in which the unit DEA structure is attached to a stiffer passive layer. Upon the application of high electric fields, the in-plane expansion of the dielectric layer is translated to an out-of-plane bending motion due to the restriction imposed by the passive layer (Fig. 1(a), left) [21, 22]. After optimizing the individual material compositions for performance and printability, and overcoming their incompatibilities using effective surface engineering strategies, we 3D printed the layered structure of the unimorph DEAs via the DIW technique. We evaluated the actuation performance of the 3D printed devices in response to applied (i) ramp-up electrical input; (ii) cyclic electrical loading; and (iii) payload masses. Furthermore, we performed analytical modeling and finite element method (FEM) simulations of the device performance to acquire a better understanding of the mechanics of the nonlinear actuation behavior of the unimorph DEAs.

Figure 1.

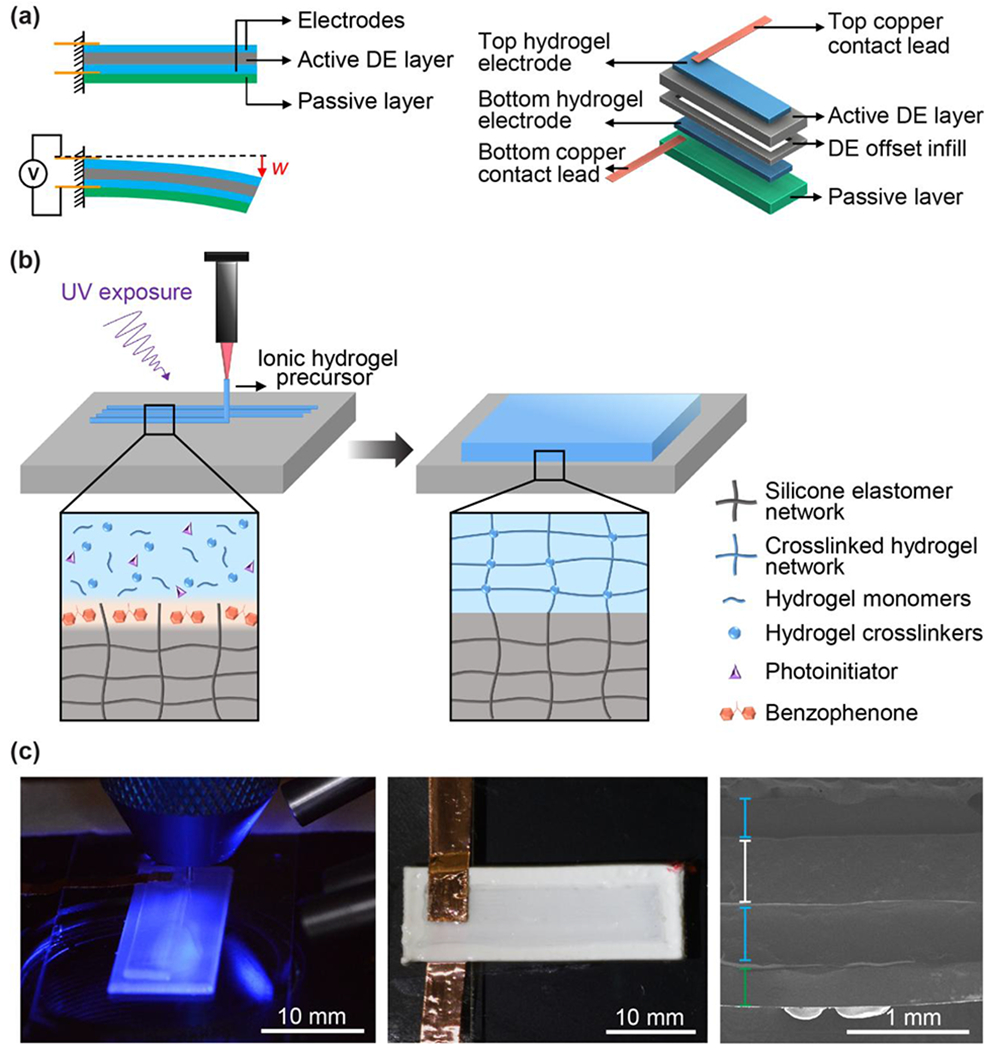
(a) Schematic of a bending unimorph dielectric elastomer actuator (left) and exploded view of the DEA device and different constituent material layers (right). (b) Schematic of depositing hydrogel on the surface of silicone-based layer treated with BP under UV light exposure. (c) Printing of the ionic hydrogel on the passive layer after surface treatment with BP and under UV light (left), final 3D printed DEA (middle), and SEM image of the DEA cross section (right). The green, blue, and white markers denote the passive layer, hydrogel electrodes, and dielectric layer, respectively. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

2. Materials and methods

2.1. Material preparation

The first step in developing the unimorph DEA is tailoring and optimizing the individual material compositions for the electrodes, the active dielectric elastomer, and the passive layer in order to satisfy printability and device performance requirements. To manipulate the selected materials in the DIW process, careful consideration of the rheological properties of the inks (viscosity, yield stress, and viscoelastic moduli) is required. Specifically, the selected ink materials should exhibit shear thinning behavior, a property attributed to non-Newtonian fluids, which results in a decrease in the viscosity of a fluid under applied shear strains. The shear thinning behavior facilitates the flow of the ink materials through the deposition nozzle due to a decrease in the viscosity under the imposed shear rates during the printing process, while sustaining the shape of the printed inks after deposition onto the substrate [23]. In addition, the ink materials should preferably require no post-processing steps, in an effort to maintain a comprehensive fabrication process on the printer platform, thus simplifying the process.

Combining low and high molecular weight polymers for formulating the composition of ionic hydrogels and other materials, including silicones, has been demonstrated to be a viable strategy for modifying their rheological properties, thus rendering them suitable for use in the DIW process [12, 13]. In these material systems, the high molecular weight polymer is used to modify the viscosity and yield stress of the ink [12, 13], while the crosslinking of the low molecular weight polymer dictates the material elasticity [12].

Here, we adopted a similar strategy to formulate the composition of the main components of the device. Following optimization, the composition of the UV curable, ionic hydrogel used for the compliant electrodes consisted of 7.9 wt.% acrylamide (AAm) as the monomer, 3.16 wt.% polyacrylamide (PAM, Mol. Wt.=5,000,000) as the rheology modifier, 21.48 wt.% lithium chloride (LiCl) for ion induction, 0.13 wt.% N,N’-Methylenebisacrylamide (MBAA) as the crosslinking agent, 0.08 wt.% Irgacure 1173 as the photoinitiator, and 37.6 wt.% ethylene glycol (EG) along with 29.64 wt.% ultrapure water as the solvents. The hygroscopic properties of LiCl used in this formulation improved the water retention of the hydrogel, thus increasing its longevity and preventing dehydration that could inhibit its performance as an electrode in the DEA [24].

The final composition of the active dielectric layer in this study included 20 wt.% barium titanate (BaTiO₃) nanoparticles (<100 nm, cubic) in a UV curable silicone matrix comprising high molecular weight silicone sealant (Loctite® 5039™ Nuva-Sil®) and a two-part silicone elastomer (Wacker SEMICOSIL® 912 as the base and ELASTOSIL® CAT UV as the catalyst with a 10:1 mixing ratio) at a 1:1 weight ratio. Silicone elastomer was utilized due to its relatively fast and stable electromechanical response, low mechanical loss [25, 26], and availability in a wide range of viscosities, curing rates, and mechanical properties. Furthermore, BaTiO₃ particles possess a high dielectric constant that can range from 500 to 6900 at room temperature depending on the synthesis method, and levels of purity, density, and grain sizes [27]. Thus, the inclusion of BaTiO₃ in a silicone matrix yields an elastomeric composite material with an enhanced dielectric property and electromechanical sensitivity [28–31].

Finally, we used a UV curable, one-part silicone sealant (Loctite® 5084™ Nuva-Sil®) as the passive layer due to its higher stiffness (relative to the dielectric elastomer), non-corrosiveness, and facile printability. The 3D printing of the individual materials was optimized based on the nozzle tip diameter, extrusion pressure, and printing speed (details in Supporting Information, SI, Table S1).

2.2. Unimorph DEA fabrication

The fabrication of the DEA device required the stacking of different material layers (Fig. 1(a), right) in the DIW process, followed by post-deposition crosslinking and curing of each layer prior to the deposition of subsequent layers. One of the main challenges that should be addressed during the device fabrication process was the integration of the different materials and overcoming their incompatibilities. This issue arose from the fact that silicone-based materials are hydrophobic, and the hydrogel ink is hydrophilic. Therefore, effective surface engineering strategies should be incorporated in the device fabrication process in order to overcome the surface dewetting that results from the weak interactions between the hydrogel droplet and the underlying silicone layer.

For this purpose, we employed a method that entailed the chemical treatment of the silicone surface and took advantage of the UV element present in the fabrication process. This method involved the application of benzophenone (BP) photoinitiator, which has been used to activate elastomer surfaces in UV assisted polymer grafting and was shown to improve the interfacial bonding of elastomer/hydrogel hybrids [10]. As illustrated in Fig. 1(b), upon the treatment of the elastomer surface with BP and exposure to UV light, the BP molecule generates radical sites that can separate a hydrogen atom from the elastomer [32–34]. The hydrogel monomer, acrylamide in this case, will then react with the generated radicals, leading to graft polymerization and chemical bonding of the hydrogel to the elastomer surface [32–34]. During device fabrication, we treated the surface of the 3D printed silicone structures with aliquots of l0 wt.% BP solution in acetone. After the absorption of BP, the surface of silicone was dried using nitrogen gas and the subsequent hydrogel layers were printed while the entire structure was exposed to UV light. This method resulted in the deposition of hydrogel films with uniform surfaces on the silicone layer with improved interfacial bonding (Fig. 1(c), Fig. S1, SI Movie 1).

In order to facilitate the testing of DEA actuation performance, copper tape pieces were integrated into the device structure to function as electrical contact leads. The bottom electrical lead was inserted during the printing process, prior to depositing the bottom hydrogel electrode. The top electrical lead was attached to the upper surface of the hydrogel layer after completing the printing process of the device. The final 3D printed DEA (Fig. 1(c)) had dimensions of ca. 30 × 10 × 1.6 mm³ (L × W × H). The thicknesses of the passive layer, DE layer, and hydrogel electrodes were approximated as 300 μm, 500 μm, and 380 μm, respectively, based on SEM images of the device cross section (Fig. 1(c), right).

2.3. Analytical and finite element modeling

Most of the modeling efforts provided in the literature for predicting the deformation response of nonlinear soft devices tend to apply linearized approaches, which are applicable only in restrictive conditions, such as small displacements [35]. Thus, linear models are inaccurate when the deflection amplitudes are higher than the thicknesses of the structures [36]. The modeling approach in this study encompasses both the material and kinematic nonlinearities through the implementation of the energy formulation instead of the common force-balance method, which can become cumbersome for nonlinear systems [36]. In other words, the material and kinematic nonlinearities are the impetuses for the mathematical development to capture the important energetics of the device [35]. The energy formulation is an attractive approach for predicting the device actuation and response characteristics due to electrical and mechanical loads experienced simultaneously by the device. Additionally, the Rayleigh-Ritz method can be employed in conjunction with the energy formulation to obtain a solution for the deflection in the beam-like device [36]. Details of the model derivation are presented in the supporting information. Briefly, the DEA device was treated as a cantilever nonlinear Euler-Bernoulli beam (Fig. S2). The general assumptions were: (i) static equilibrium; (ii) no slip occurs between the layer interfaces; (iii) isotropic behavior in each material layer; and (iv) zero strain at the neutral axis.

To account for the materials nonlinearities, the hyperelastic constitutive laws were incorporated into the derivations using the Neo-Hookean material model. Thus, the predictive actuation response included nonlinearities stemming from (i) the electro–hyperelastic coupling in the dielectric elastomer layer, and (ii) the hyperelastic behavior of the hydrogel and passive layers.

In order to capture the geometric nonlinearities due to the high kinematics (physical flexibility) of the device, third-order terms were included in the strain energy development using the Taylor series expansion. If w represents the transverse displacement of the device during deflection, the normalized curvature (κ) can be defined as a function of the spatial derivatives (w′ and w″) of w as follows [35]:

$$\kappa =w^{″}+\frac{1}{2}{w}^{″}{w^{\prime }}^2$$ (1)

The Rayleigh-Ritz method was employed in which an assumed solution was directly substituted into the energy expressions [36, 37]. Mathematically, w, can be expressed as a summation of functions from a complete, orthogonal, sufficiently differentiable function set. The advantage of using the Rayleigh-Ritz method is that a function needs to satisfy only the kinematic boundary conditions. The approximate solutions were assumed in the form:

$$w\left(x\right)=q\psi \left(x\right)$$ (2)

where the trial functions, ψ, are known independent comparison functions to denote the mode shapes (curvature due to deflection) of the beam and q represents the generalized coordinates.

The constitutive relation for the entire DEA system can be modeled similar to piezoelectric devices [38], which can be generally expressed as follows [39]:

$$\left[\begin{array}{c}\mathit{D}\\ \mathit{ϵ}\end{array}\right]=\left[\begin{array}{cc}{e}^{\sigma }& d^d\\ d^c& s^{\mathbb{E}}\end{array}\right]\left[\begin{array}{c}\mathbb{E}\\ \mathit{\sigma }\end{array}\right]$$ (3)

where electric displacement, strain, applied electric field and stress vectors are denoted by vectors D, ϵ, $\mathbb{E}$, and σ, respectively. The dielectric layer material constants include the dielectric permittivity at a constant stress σ(e^σ), the electric displacement per unit stress at a given electric field (d^d), strain per unit electric field at a known stress (d^c), and the elastic compliance at a constant electric field $\mathbb{E}(s^{\mathbb{E}}$). It should be noted that d^c and d^d are numerically identical [39].

Using 1-axis and 2-axis notations to represent the planar directions, and the 3-axis to denote the direction along the thickness of the device, the axial stress (σ₁₁) – which includes the contribution of the electromechanical strain (Λ) and axial strain (ε ) – can be simplified as:

$${\sigma }_{11}=E_{11}\left[{\epsilon }_{11}-\Lambda \right]$$ (4)

where E₁₁ represents the elastic modulus of the DE. The electromechanical strain, Λ, of the DE layer with thickness t in response to applied voltage V can be defined as [36, 38]:

$${\Lambda }^{}=d_{31}\left(\frac{V}{t^{}}\right)=\nu \frac{{ϵ}_o{ϵ}_r^{}}{E_{11}^{}}{\left(\frac{V}{t^{}}\right)}^2$$ (5)

The Poisson ratio, vacuum permittivity, and relative dielectric permittivity are ν , ϵ_o, and ϵ_r, respectively.

Finally, the potential energy of the DEA with length L and cross section area A can be expressed as follows [36]:

$$P=\frac{1}{2}\underset{0}{\overset{L}{\int }}\left[\begin{array}{cc}{\epsilon }_{}& \kappa \end{array}\right]\left[\begin{array}{cc}EA& E{I}_c\\ E{I}_c& E{I}_b\end{array}\right]\left[\begin{array}{c}{\epsilon }_{}\\ \kappa \end{array}\right]dx-\underset{0}{\overset{L}{\int }}\left[\begin{array}{cc}{F}_{\Lambda }& M_{\Lambda }\end{array}\right]\left[\begin{array}{c}{\epsilon }_{}\\ \kappa \end{array}\right]dx$$ (6)

where, EA, EI_c, EI_b, F_Λ, and M_Λ are the extensional stiffness, coupling stiffness, bending stiffness, induced force and bending moment, respectively. After substituting the assumed solution into P and applying the Euler–Lagrange method for a static condition, the governing equation for the DEA transverse displacement as a function of the generalized coordinates becomes:

$$k_{nb}{q}_2^3-k_{n\Lambda }{q}_2^2+k_{lb}{q}_2=Q_{2,int}+Q_{2,ext}$$ (7)

where, k_lb, k_nΛ, and k_nb represent the coefficients due to linear bending stiffness, nonlinear electromechanical strain, and nonlinear kinematic bending stiffness, respectively. The generalized internal, Q_int, and external, Q_ext, forces are due to the electrical potential, and external loads, respectively. The blocking force can also be defined as [36]:

$$F_{bl}=\Lambda EA$$ (8)

The DEA actuation was also simulated using Abaqus FEM software to predict the device deflection due to a voltage ramp-up input and applied tip mass and gravitational loads. Further details on the FEM simulation are presented in the SI.

3. Results and discussion

3.1. Material characterization

The shear thinning behavior of the ionic hydrogel and the dielectric elastomer inks was confirmed by performing viscometry tests on material precursors in the uncured state (Fig 2(a)). The shear thinning behavior for both materials occurred at shear rates above 0.1 s⁻¹, which facilitated their extrusion through the deposition nozzles. Specifically, during extrusion from nozzles with specified diameters and printing speeds (Table S1), the hydrogel and DE inks experienced shear rates of ca. 78.19 s⁻¹, and 111.85 s⁻¹, at which the exhibited apparent viscosities were 3.20 Pa·s, and 21.93 Pa·s, respectively (see SI for details). The shear yield stress, σ_y, along with the storage (G’) and loss (G”) moduli of the inks, were obtained by performing oscillatory rheometry on the materials (Fig. 2(b)). The hydrogel and DE inks exhibited yield stresses of ~ 51 Pa and 253 Pa, respectively. It is important to point out that both G’ and G” remained constant below the yield values; however, beyond the yield points, both materials experienced a drop in G’ and G”. Manipulating the yield behavior of the inks provided two key fabrication advantages: (i) a decrease in the storage modulus beyond the yield point improved the controllability of the ink extrusion; and (ii) an increase in storage modulus (G’ reached values of ~ 69 Pa and 1034 Pa, for hydrogel and DE inks, respectively) at shear stresses below the yield values facilitated the shape retention of the printed materials after their deposition on the substrate [40].

Figure 2.

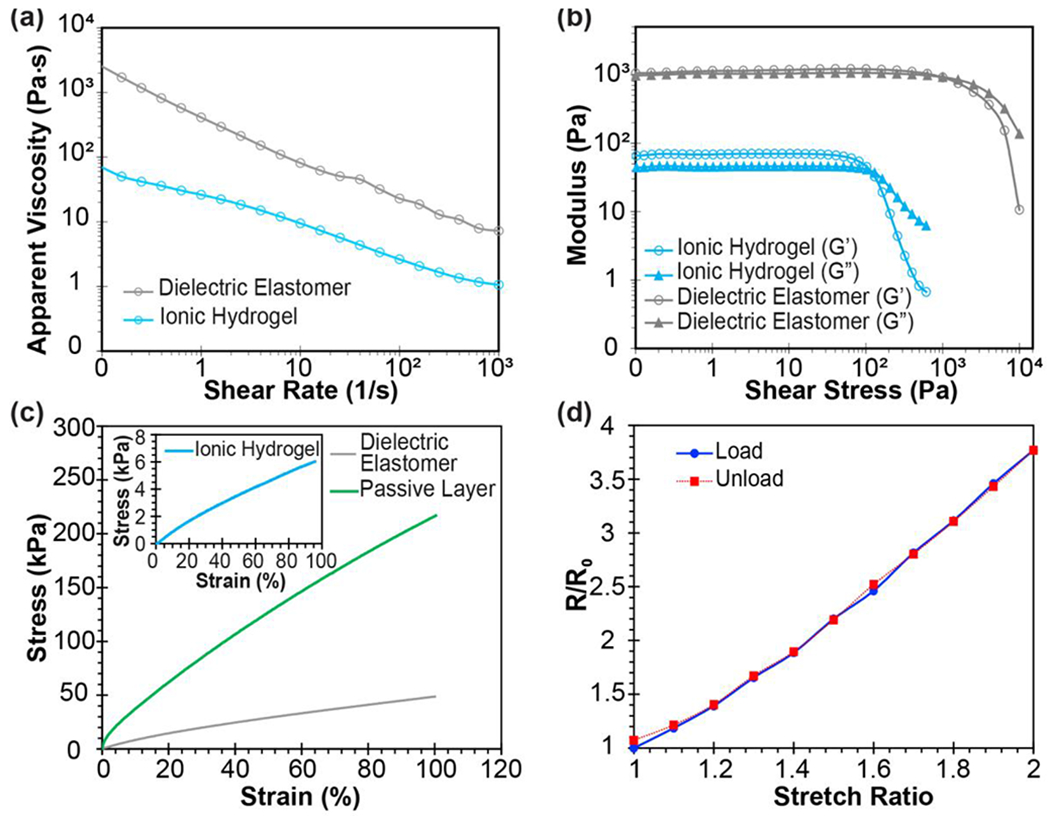
(a) Viscometry and (b) oscillatory rheology data including the storage modulus (G’) and loss modulus (G”) of the ionic hydrogel electrode and the silicone/BaTiO₃ dielectric layer. (c) Stress-strain plots of the three components. (d) Changes in resistance of the ionic hydrogel at different stretch ratios for loading and unloading cycles.

To evaluate the overall performance of the device components, mechanical and electrical characterizations were conducted, consisting of uniaxial tensile tests of the three materials (ionic hydrogel, DE layer, and passive layer), and studying the changes in resistance of hydrogel electrodes with applied strains. The uniaxial tensile tests were performed to ensure that the hydrogel electrodes were compliant to the dielectric layer, and the passive layer had a higher stiffness compared to the dielectric layer to yield out-of-plane motion (Fig. 2(c)). All materials exhibited a non-linear hyperelastic behavior. The elastic modulus of the passive layer, silicone dielectric elastomer, and ionic hydrogel electrodes at 100% strain were estimated as 167.57 ± 36.27 kPa, 39.82 ± 7.15 kPa, and 8.77 ± 3.00 kPa, respectively.

We examined the effect of uniaxial stretching on the changes in resistance of 3D printed ionic hydrogel electrodes in loading and unloading tests (Fig. 2(d)). The increase in the resistance of the hydrogel with increasing stretch ratio was consistent with the expected trend of R/R₀ = λ² for a conductive material with resistivity independent of applied stretch, where R₀ and R represent the resistance before and after stretching the hydrogel λ times its initial length, respectively [9]. In addition, no significant hysteresis was observed in the changes in resistance during loading and unloading cycles.

3.2. Device performance characterization

The actuation performance of the 3D printed DEA was investigated in three different cases, including applied (i) ramp-up electrical input, (ii) cyclic electrical loading, and (iii) payload masses. For this purpose, one end of the device was anchored to a rigid structure, while the other end was unconstrained and free to deflect. The input voltage was delivered to the device via a custom-built electrical setup (Fig. S3) connected to the copper leads. The application of high voltage stimulated the out-of-plane motion of the device. The vertical displacement of the free end of the device was obtained by analyzing the recorded actuation performance using a video analysis and modeling software (Tracker, see SI for more details). First, we evaluated the performance of the DEAs in response to slowly ramping-up voltages (250 V/10 s) (Fig. 3(a), Movie S2). As shown in Fig. 3(b), the DEA tip displacement was found to exhibit a quadratic relationship with the applied voltage. A maximum vertical tip displacement of 9.78 ± 2.52 mm (n=3) at ~5.44 kV was achieved, which was more than six times the thickness of the device.

Figure 3.

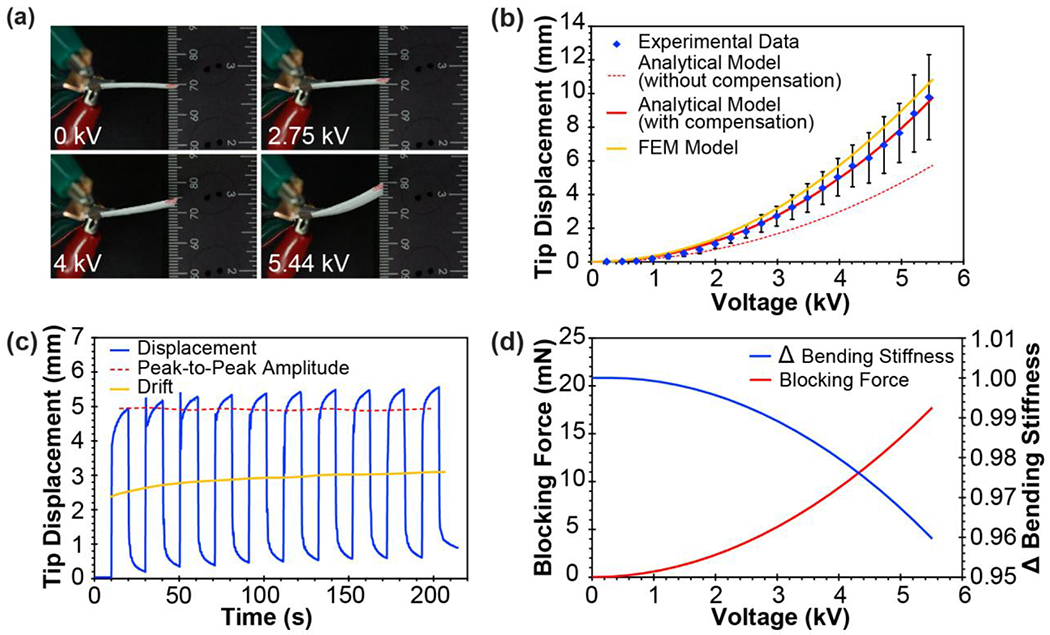
(a) Stills of device actuation performance at different applied voltages. (b) Experimental results during voltage ramp-up and their comparison with analytical and FEM simulation. Error bars represent standard deviation of the n samples that did not breakdown up to a specific level of the applied voltage. Specifically, n is equal to 5, 4, and 3 for voltage ranges of 0-4.21 kV, 4.47-4.96 kV, and 5.2-5.44 kV, respectively. (c) DEA performance in response to square wave voltage input with an amplitude of 4 kV and frequency of ~ 0.05 Hz. (d) Estimation of DEA blocking force and change in (Δ) bending stiffness as a function of applied voltage using the analytical model.

We also tested the repeatability and time-dependence of the device performance by applying a cyclic electrical load via a square-wave input voltage with a constant amplitude of 4 kV (Fig. 3(c), Movie S3). The results showed that the DEAs exhibited a time-dependent response to step changes in the applied voltage from 0 to 4 kV (and vice versa), which was found to be consistent with previous reports on the performances of unimorph DEAs [22, 38]. A rise time of 1.85 s was approximated for the device response at a frequency of 0.05 Hz. In addition, a slight drift in the device displacement over consecutive cycles of stimulation was observed, which was more prominent at the beginning and diminished after the first few cycles. These time-dependent characteristics of DEA performance have been attributed to the relaxation behavior of dielectric elastomers [41, 42], and the electrical dynamics of the device during capacitive charging and discharging [25, 43]. Nevertheless, the peak-to-peak amplitude of the DEA displacement remained consistent over the actuation cycles, confirming the repeatability of the device performance. Furthermore, we investigated the effect of oscillatory inputs on the deflection amplitude and rise time of the device (Fig. S4). The effect of changes in frequency on device displacement was found to be trivial for frequencies below 0.1 Hz, while the rise time decreased with an increase in frequencies in this range. For oscillation frequencies above 0.1 Hz, a significant decrease in the device deflection and a relatively constant rise time were observed.

In order to verify the behavior of the DEA, we simulated the actuation performance in response to an applied ramp-up voltage via analytical and FEM models. Both models illustrated similar quadratic relationships seen in the experimental results between the DEA tip displacement and the input voltage, as shown in Fig. 3(b). The analytical deflection results were ~41% below the experimental values. This noticeable deviation between the experimental and analytical results could be attributed to the following factors. First, the modeling was conducted for static conditions; thus, the time-dependent response and the relaxation behavior of the DEA were not considered. Second, the transverse shear effect was ignored in the analytical model due to simplifying assumptions in the non-linear Euler–Bernoulli beam theory [44]. Finally, variations in the material properties, such as density and elastic modulus, and potential variabilities in each layer during the fabrication process may affect controlling the overall geometry and structural stiffness of the device, which will contribute to the deviations between the experimental and modeling results. In designing electromechanical transducers, it is required to include a compensation factor to account for these variabilities [36]. Thus, by comparing the analytical model with the experimental results, a compensation factor with a value of ~1.65 was used, which yielded an excellent fit with the experimental data (Fig. 3(b)). The values for E and d₃₁ of the DE layer were then obtained using the model with the compensation factor and were implemented in the FEM simulation. The FEM predictions were in good agreement with the experimental results and remained within one standard deviation of the experimental data.

The bending stiffness and blocking force of the device were estimated as functions of the input voltage (Fig. 3(d)). The blocking force increased due to an increase in V, reaching a value of 17.27 mN at ~5.44 kV, while the restoring bending stiffness decreased as V increased (Fig. 3(d)). Thus, the device became more compliant when the voltage increased. Using the approximation $\frac{F_{\mathrm{bl}}w}{\mathrm{2m}}$ [45, 46] (where m represents the mass of the device), a maximum energy density of ca. 0.13 J kg⁻¹ and efficiency of ca. 30 % were estimated for the unimorph DEA.

Finally, we evaluated the DEA load lifting capacity by mounting payload masses of 0.04, 0.08, and 0.12 g on the tip of the device and obtaining the displacement of the tip mass against gravity upon the application of voltages ranging from 0.250 to 5 kV (Fig.4, Movie S4). At an input voltage of 5 kV, increasing the tip mass from 0 to 0.12 g reduced the maximum tip deflection from 2.80 to 0.85 mm. We also compared the experimental data for the DEA performance in response to an applied payload mass with results obtained from FEM. In general, the FEM simulations were consistent with the experimental trends and were in good agreement for tip masses with values of 0, 0.04, and 0.08 g (Fig. 4(b)). For the case with a tip mass of 0.12 g, a higher deviation between the experimental and FEM maximum displacement was observed. A possible explanation involves the relative shift in the radius of gyration due to the mounting of the increased mass on the tip of the device.

Figure 4:

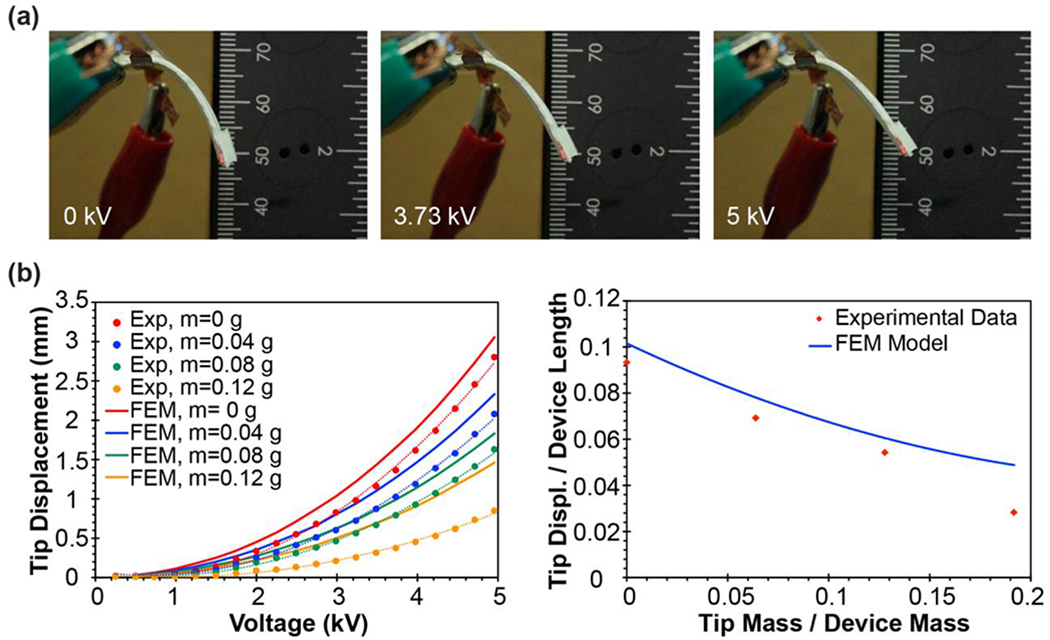
(a) Stills of DEA performance in lifting a tip payload mass of 0.04 g at different applied voltages. (b) Effect of different tip mass values on device performance and comparison with FEM simulation (left), and plot of normalized maximum tip displacement as a function of normalized tip mass for experimental and FEM results (right).

4. Conclusions

In summary, we demonstrated the 3D printing of soft dielectric elastomer actuators that are capable of generating bending modes of motion. The observed actuation performance suggests the promise of 3D printing hydrogel–elastomer hybrids as soft actuators, thus paving the path for 3D printing self-sensing, soft robotic systems with complex geometries and functionalities that harness the dual sensing/actuation capabilities of dielectric elastomers. This self-sensing capability could be employed for closed-loop feedback control of soft robots without the need for additional optical or electromechanical sensors, and could be of particular interest for mimicking the proprioception abilities of natural muscle, enabled by strain-sensitive neurons that provide a sense of spatial position and motion [47].

Several strategies can be incorporated with the goal of improving the performance of the current devices to achieve higher spatial range and temporal rate of actuation at lower applied electric fields, thus broadening their range of applications in various fields, including but not limited to soft robotics. For instance, given that the device performance is more sensitive to variations in the thickness of the active DE layer, decreasing the thickness of this layer (for example via using finer nozzles during the printing process) could enhance the device deflection (Fig. S5), but entails a tradeoff via an increase in the probability of dielectric breakdown. Hence, surface modification of the barium titanate nanoparticles could be considered to improve the dielectric properties and electromechanical strength of the DE/BaTiO₃ composites [48]. Furthermore, stacking multiple layers of active DE membranes, which is readily achievable using a 3D printing process, can be employed as a method to enhance the device actuation performance. In the long term, the outcomes of this work can serve as stepping stones for the freeform fabrication of untethered mechanical systems and soft robots, with implications in artificial life and programmable matter, mechanically-driven morphogenesis, and smart prosthetics.