The ability to represent recursive sequences is early developing and found across cultures, but is not unique to human thought.
Abstract
The question of what computational capacities, if any, differ between humans and nonhuman animals has been at the core of foundational debates in cognitive psychology, anthropology, linguistics, and animal behavior. The capacity to form nested hierarchical representations is hypothesized to be essential to uniquely human thought, but its origins in evolution, development, and culture are controversial. We used a nonlinguistic sequence generation task to test whether subjects generalize sequential groupings of items to a center-embedded, recursive structure. Children (3 to 5 years old), U.S. adults, and adults from a Bolivian indigenous group spontaneously induced recursive structures from ambiguous training data. In contrast, monkeys did so only with additional exposure. We quantify these patterns using a Bayesian mixture model over logically possible strategies. Our results show that recursive hierarchical strategies are robust in human thought, both early in development and across cultures, but the capacity itself is not unique to humans.
INTRODUCTION
Recursion is a computational capacity that allows one to embed elements within elements of the same kind (1). It is thought to be the key feature of human syntax (2, 3) and has been implicated in the learning of a number of uniquely human concepts such as language (2), complex tool use (4, 5), music (6), social cognition (5), and mathematics (3, 7). The universality of recursion among human languages is hotly debated (8–10). The capacity for recursion is hypothesized to be uniquely human, or even the sole difference that separates humans from nonhuman animals (1, 3, 11); however, little comparative empirical work supports this claim.
Representations of discrete sequential representations, a precursor for language-like hierarchy and recursion, have been studied in both humans and nonhuman animals. Extensive studies have shown that infants and nonhuman animals have the capacity to represent transitional probabilities (e.g., that B is likely to follow A) (12), ordinal sequences (e.g., A1A2A3) (13, 14), chunk sequences (i.e., group sequences that happen together and represent them as a whole) (15–17), and abstract algebraic patterns (e.g., AAA versus AAB) (11, 18–21). While these kinds of patterns may be important for some sequential processing in language, the hierarchical structures of language require richer computational capacity (2, 11).
Motivated by context-free grammars as a simple model in linguistics, some empirical work has explored learning of symbol systems that are naturally captured with center-embedded recursion via phrase structure rules such as the language AnBn (the set of strings {ab, aabb, aaabbb, ...}) (22, 23). This language mirrors some of the dependency relations found in human language (2). Unfortunately, empirical tasks using AnBn fail to provide a strong test of recursive hierarchical structure since nonrecursive strategies exist to succeed in the paradigm. For example, the recursion task by Fitch and Hauser tested to see if adult humans and tamarin monkeys could differentiate between artificial grammars that follow an AnBn pattern (22). They found that humans could discriminate these languages, while the monkeys could not, a result used to argue for species differences (11, 24). However, this experiment failed to provide a strong test of recursion because there was no dependency between the As and the Bs (25). For example, in the sentence “The cat[A1] the dog[A2] chased[B2] ran[B1],” each of the two “A” phrases (“The cat[A1]” and “the dog[A2]”) must be appropriately matched to the “B” phrases (“chased[B2]” and “ran[B1],” respectively). Such dependencies are not present in AnBn strings themselves, leaving the possibility that subjects could have used nonrecursive strategies to judge grammaticality or discriminate stimuli that satisfy the rule from those that do not (26, 27). This same generic flaw has been seen in other studies arguing for recursive abilities in birds (23, 28, 29). Subsequent experiments have extended this task in humans to include the critical test trials for what most people would consider essential for having recursion. In these, subjects are presented with a violation of the AnBn artificial grammar that is a violation not because of the number of As or Bs, or the order of the As versus Bs, but rather the dependency structure (e.g., A1A2A3B3B1B2). Such studies found that using similar methods to Fitch and Hauser (22), humans did not distinguish these trials as violations of the grammar and thus were most likely using alternative strategies like counting or tracking A-B switches (26, 27). A separate line of research has aimed at showing that recursive abilities could be learned from associative learning (30). However, this work lacks the critical comparison that allows one to differentiate between an associative learning strategy and an abstract recursive rule learning strategy: open-ended transfer trials (31). On a similar line of research, one recent study in human infants used a habituation task to show that there were differences in infant event-related potential (ERP) signals in response to sequences that did not match the learned center-embedded strings (32). However, this work lacks the critical comparison of generalization to new, nontrained lists. Last, one recent study has shown that monkeys and older preschool children can be explicitly taught to use a mirror grammar (a grammar in which at the end of the first half of the sequence, the sequence is repeated in reverse order) to solve a spatial sequencing problem (33), but it is unclear what processes underlie this ability. It is also unclear whether humans and nonhuman primates spontaneously generalize according to recursive structures over new, never before seen, combinations of elements when other strategies are available.
Here, we test whether U.S. adults, Tsimane’ adults who lack formal mathematics and reading abilities, 3- to 4-year-old children, and nonhuman primates can learn to produce center-embedded sequences and transfer this ability to novel stimuli. Our experimental design is motivated to address the primary shortcomings of previous work, namely, the lack of dependency between sequential elements, the existence of other possible strategies, and the need for comparison not only across species but across human groups to provide compelling evidence of universality (34). In addition, the current study uses a generation task to assess subjects’ spontaneous transfer to novel lists and allows us to measure the sequences they generate relative to all other possible responses in an open-ended transfer task. This allows us to examine alternative strategies in subjects’ responses that could emerge through associative representations, such as representing transitional probabilities or ordinal sequences. Each of these alternative strategies predicts different response patterns compared with center embedding on the open-ended transfer trials. A transitional probability strategy could be used to represent a trained list by representing which items have been presented next to each other in training. However, this type of strategy would break down with new combinations of items and would only preserve previously seen item-to-item transitions but would lack the overall structure of center-embedded lists. Similarly, an ordinal strategy could be used to represent center-embedded training lists, as it could with any stable sequence of random items. However, an ordinal strategy would be evident in subjects’ responses on novel transfer trials, particularly in the frequency of “crossing errors” in which subjects respond “A1A2B1B2.” In previous studies, these errors could not be measured because the studies lacked dependencies between the As and Bs in the AnBn grammar (22, 23). In the current study, each strategy is directly compared to the strategy of center embedding in the subjects’ data. Last, we model the results of the experiment using a Bayesian data analysis that allows us to infer subjects’ likely strategies and noise parameters while respecting the clustered structure of our behavioral design.
RESULTS
Center-embedded sequence generation in adults, children, and monkeys
Subjects were first trained on a sequence generation task (Fig. 1A and movie S1). Participants were presented with four brackets in random locations and had to touch them in a specific order to receive positive feedback (Fig. 1B). Subjects were trained on two lists until they reached the training criterion of 70% correct (Fig. 1C). These training lists were consistent with a center-embedded structure but did not require subjects to learn the center-embedded nature of the lists. They could be encoded as two arbitrary lists of items (e.g., A -> B -> C -> D). Previous studies have shown that both children and monkeys can represent lists or arbitrary items that do not contain any internal dependencies or underlying structure (35). Once trained to criterion, a novel list, which was composed only of the center two elements from each of the training lists, was randomly mixed into training trials (Fig. 1D). Subjects received positive feedback regardless of the order produced on the transfer trials. These transfer trials were aimed at seeing whether the underlying center-embedded structure of the training lists was represented and then generalized to new combinations of items even when this was not required to represent or reproduce the training lists. Subjects from all groups reached criterion on the training lists and remained above chance on the training lists throughout testing (chance = 8%; mean: U.S. adults = 97%, Tsimane’ adults = 91%, children = 60%, monkeys = 68%).
Fig. 1. Task design and stimuli.

(A) Monkeys, children, U.S. adults, and Tsimane’ adults complete the sequence generation task. Subjects were required to touch the images in a center-embedded order. (B) A sample training trial is shown. Subjects were trained to order two training lists in which the pictures had to be touched in a specific center-embedded order (C) and were tested on a third transfer list that was rewarded regardless of the sequence generated (D). Photo credit: S.F., Harvard University.
The critical test trials examined how subjects generalized elements from separate training lists (e.g., “(“, “)” and “[“, “]”), which had not been observed together. These test items occupied overlapping ordinal positions in the training lists (both open brackets were always in the second position, and both close brackets were always in the third position, e.g., “{ () }” or “{ [] }”). Thus, an ordinal strategy would produce an equal mix of center-embedded structures (e.g., “( [] )”) and nonembedded, crossed structures (e.g., “( [) ]”) because it could just place the items near the beginning or the end based on where they were in training. In addition, if subjects rely on an associative chain strategy (i.e., ordering the stimuli in a way that maximizes the previous sequential orders from the training trials), then subjects would produce tail-embedded orders, “[ ] ( )” or “( ) [ ].” Thus, a bias to produce more center-embedded than crossed or tail-embedded responses during generalization reflects a hierarchical tendency that subjects bring to the task. On these transfer trials, subjects received positive reinforcement regardless of which sequence they generated.
Our results (Fig. 2) show that all human groups were more likely to order the novel transfer stimuli in a center-embedded structure than chance [binomial (two tailed): U.S. adults, 224/240, P < .001; Tsimane’ adults, 157/251, P < .001; U.S. children, 217/500, P < .001; monkeys, 47/180, P < .001; chance = ~8%]. Across all trials, the only sequences that were produced more often than chance were center-embedded, crossed, and tail-embedded structures (see fig. S1). Although the monkeys had a higher number of trials that did not fall in these categories, there was no systematic pattern among them as each structure was produced less often than chance (1/24). These groups all produced center-embedded responses much more systematically than chance would predict, which shows a bias to produce these structures. Moreover, to test between a center-embedded strategy and an ordinal strategy (or knowing the open brackets come first and the close brackets come after), we measured whether subjects were more likely to match the close brackets in the correct order to form a correct center-embedded structure than to mismatch the close brackets to form a non–center-embedded, crossed structure. We found that all human groups were more likely to produce correctly center-embedded structures [binomial (two tailed): U.S. adults, 224/240, P < .001; Tsimane’ adults, 157/213, P < .001; U.S. children, 217/301, P < .001]. This bias to generalize the center-embedded structure suggests that subjects induced from the training data that the sequences were hierarchically/recursively structured, rather than just extracting the ordinal positions. In contrast, although monkeys had more center-embedded responses than chance, the number of center-embedded responses was not significantly greater than the number of crossed responses [binomial (two tailed): 47/97, P = .66]. This suggests that the first strategy monkeys used was a nonrecursive ordinal strategy (i.e., using the average position from the training lists). Thus, exposure to only two sample center-embedded lists did not lead to the spontaneous transfer of a recursive strategy to novel stimuli in monkeys. Monkeys performed better than human children on the training trials that were mixed in during the testing session (68 versus 60%), so their failure to spontaneously generalize the recursive rule was not due to low training acquisition or to misunderstanding the general task. However, the question of whether monkeys can represent and transfer a hierarchical recursive structure remained open.
Fig. 2. The proportion of center-embedded, crossed, and tail-embedded responses on transfer trials for monkeys, children, U.S. adults, and Tsimane’ adults.
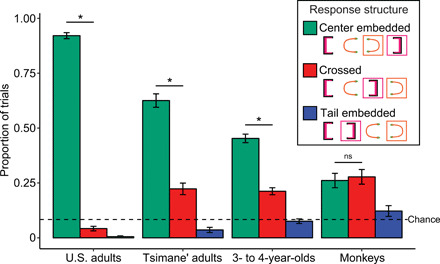
Error bars represent the SE of the proportion. ns, not significant. * represents a significant difference (P < 0.05) between center-embedded responses and crossed responses using a two-tailed binomial test.
Center-embedded sequence generation in monkeys with additional exposure
The failure of monkeys in experiment 1 could be due to a capacity difference between humans and monkeys, or it could also be due to differences in the amount of evidence each group needs to infer these types of complex center-embedded structures. To test if this is truly a capacity difference as some have suggested (2, 22), we gave monkeys additional exposure to center-embedded lists and retested their ability to transfer to a novel list. If it is truly a capacity difference, then no amount of exposure to center-embedded lists should lead to transfer to a novel list. This training and testing procedure followed the same general design as experiment 1. The same monkeys from experiment 1 were exposed to two additional novel center-embedded training lists. Once trained on these lists, we introduced a novel transfer list to test what strategy was learned and applied to the novel list. With these additional data, monkeys ordered the novel transfer list in a center-embedded fashion more than chance [binomial (two tailed): 49/200, P < .001; see Fig. 3A] and more than crossed responses (binomial: 49/68, P < .001), suggesting that monkeys did not use a purely ordinal strategy.
Fig. 3. With additional exposure, monkeys show generalization performance similar to that of children.
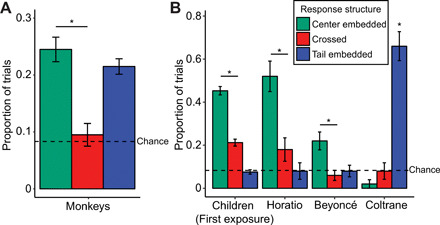
(A) The proportion of center-embedded, crossed, and tail-embedded responses for monkeys on transfer trials after training on two additional lists. (B) A comparison between the average performance of children on the first exposure and individual monkeys tested after the additional training. Error bars represent the SE of the proportion. * represents a significant difference (P < 0.05) between center-embedded responses and crossed responses using a two-tailed binomial test.
To further investigate the strategies used by individual monkeys, we looked at the responses of each animal individually. Two of three monkeys had significantly more center-embedded response structures than crossed, suggesting they used a center-embedded strategy [binomial (two tailed): Horatio, 26/35, P < .01; Beyoncé, 22/28, P < .01]. The third monkey, Coltrane, had at or below chance levels of responding in both center-embedded and crossed responses (center embedded, 2%; crossed, 8%). Instead, he was more likely to order them in a tail-embedded way, suggesting that he used an associative chain strategy (e.g., “( ) [ ]” ; binomial: 33/50, P < .001). When compared with the performance of children, both monkeys who produced center-embedded sequences were within the range (<2 SDs) of human children (Fig. 3B).
Generalization to novel stimuli in monkeys
We next tested whether monkeys could generalize the recursive rule to completely novel stimuli. Although the previous experiment showed that two of the monkeys did not just use an associative chain solution to order the novel list, it is possible that they could have used a combination of associative chain solution paired with an associative ordinal solution to keep open brackets at the beginning and close brackets at the end of the list (e.g., the first and second choices are based on an ordinal strategy because open brackets were rewarded for being early in the lists; the third choice switches to an associative strategy between two of the trained base pairs, which would create a paired center; and then, the last item is again selected because of an ordinal strategy). To examine this, we tested subjects using novel bracket stimuli that they had never been exposed to and, thus, could not have used an associative chain process (the items were never shown together before so there is no chance to extract the transitional probabilities). In this task, monkeys were given two novel sets of brackets and were rewarded regardless of their response for the first five trials of a novel list. After the first five transfer test trials, monkeys were rewarded only for center-embedded responses (e.g., “{ < > }” or “< { } >”). Once a subject reached 7 of 10 correct, they immediately were shown a new transfer list and rewarded regardless of the response for the first five trials. Critically, these training lists were structured analogously to experiment 1 so that training reinforced the overall structure, but not the way to generalize on novel combinations of items. This process repeated for 30 lists per monkey.
Overall, monkeys made more center-embedded responses than crossed responses on transfer trials [Fig. 4; binomial (two tailed); overall, 135/244, P = .05). This effect was largely driven by one monkey who was significantly above chance on the generalization trials (Beyoncé: 34/50, P < .01; Horatio: 45/88, P = .46; Coltrane: 56/106, P = .31), which is an existence proof that it is at least within the capacity of a monkey to deploy a recursive hierarchical sequencing strategy and generalize it to stimuli that it had never seen before. In addition, our Bayesian analysis of these data revealed that the recursive strategy was higher than the prior in all three monkeys, which further supports this conclusion (see Supplemental Results and fig. S4 for the Bayesian analysis of these data). Previous studies have suggested that center-embedded sequencing could be a by-product of associative learning mechanism (30). However, the transfer of the abstract center-embedded structure without prior exposure to the stimuli used further suggests that the transfer is not due to an associative mechanism, but rather a representation of the recursive structure required by the task. Furthermore, this suggests that it is possible for a monkey to learn to abstract and generalize this structure to completely novel instances using new, never before seen items.
Fig. 4. The proportion of center-embedded, crossed, and tail-embedded responses for monkeys on the generalization to novel lists.
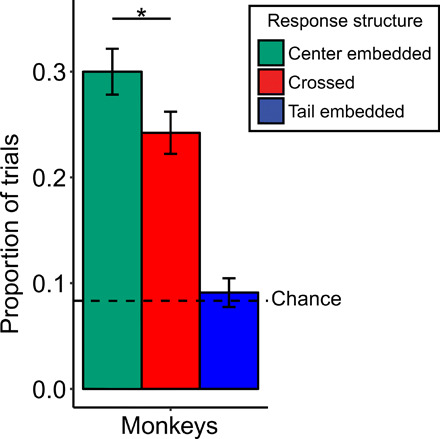
Error bars represent the SE of the proportion. * represents a significant difference (P < 0.05) between center-embedded responses and crossed responses using a two-tailed binomial test.
Bayesian analysis of strategies
Many responses cannot be classified as center embedded, tail recursive, or crossing. Three percent of the responses from U.S. adults, 12% from Tsimane’ adults, 25% from U.S. children, and about half of monkeys’ responses do not fall cleanly into one of those categories (e.g., the bars in Figs. 2 and 3 do not add up to one). The previous analyses focused on the relative proportion of crossing and center-embedded responses as a gauge of a participant’s learning and did not examine these other responses. To better understand the entire set of responses, we implemented a model that formalized the space of all logically possible responses under a simple noise process. Using this model, we performed a Bayesian data analysis (36) to jointly infer the strategies used by each participant in the task to make each response, as well as their noisiness (e.g., miss-presses, memory error) in implementing those strategies, and group-level parameters quantifying the distribution of responses in each species and population. This permits us to test a large variety of different response patterns and processes and to quantify the degree to which subjects respond recursively while incorporating these other factors. Previous works investigating the strategies used by participants (both human and nonhuman) have often failed to test for the possibility of other nonrecursive strategies (22, 23), and when other strategies are systematically tested, these alternative nonrecursive strategies are shown to be used (37). Thus, this analysis is aimed at understanding the underlying processes that produced the center-embedded structures in our task (see Supplementary Materials and Methods and fig. S2 for the complete model details). For this analysis, we used the results from experiment 2 for the monkeys and those from experiment 1 for the human subjects. We chose this set of data because in experiment 1, the monkeys showed a clear failure to transfer the overall structure to the transfer list, and experiment 2 was the most closely matched to experiment 1 in human subjects. We also ran the full Bayesian models on experiments 1 and 3 (see figs. S3 and S4)
Figure 5 shows the probability that individuals in each group were using a recursive strategy, both at the group level and for each individual in a group. The prior probability of using a strategy on a given trial was 1 of 12 (≈0.08) for each of the 12 strategies. Each group was inferred to be more likely using a recursive strategy than was a priori expected, as each group’s probability of using a recursive strategy was inferred to be very likely greater than 1 of 12. The maximum a posteriori estimates for each group’s probability of using a recursive strategy rank in order from U.S. adults as the highest [mean = 0.82, Credible Interval (CI) = 0.72 to 0.89], followed by Tsimane’ adults (mean = 0.41, CI = 0.31 to 0.52), U.S. kids (mean = 0.27, CI = 0.19 to 0.34), and then monkeys (mean = 0.22, CI = 0.12 to 0.34). The individual probabilities of using a recursive strategy, however, tell a more subtle story: The relatively low-average recursive strategy use by monkeys is heavily driven by a single monkey who had near-zero probability mass on the correct recursive strategy and was instead inferred to have been using an “open, matched-close, open, matched-close” strategy. However, the monkey inferred to use a recursive strategy most often (Beyoncé) had a mean probability of recursive strategy use of 0.48 (CI = 0.21 to 0.70), higher than 67% of human participants (76% of U.S. kids and 52% of Tsimane’ adults).
Fig. 5. The probability of using a recursive strategy for each group (red) and each individual in that group (black), using a Bayesian data analysis that allowed strategies to vary by individual and population.
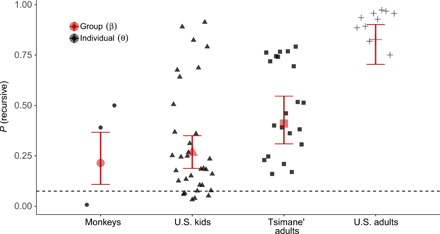
The dotted line represents the prior. Error bars around the group means represent the 95% credible interval.
Inferred noisiness in responding
The Bayesian model included a by-participant noise parameter that specified the probability that any given bracket choice a participant made was unintended. We made the simplifying assumptions that (i) a mistake changes the intended bracket to one of the other three brackets at random and (ii) that each mistake is independent of other mistakes. Although memory capacity could be one source of this noisiness, this noise model is not designed to account for every possible source of error separately, of which there are many (e.g., inattention, memory failure, mis-presses). Rather, this model was designed to be a general catch for responses that were unlikely to have been generated intentionally, without respect to their exact causes.
The analysis also revealed large differences between groups in the inferred error rate over trials, where the error rate is defined as the probability of making an error on one or more bracket choices in a trial. Monkeys were inferred to have the highest levels of error, followed by U.S. kids, Tsimane’ adults, and then U.S. adults. These differences are substantial: Monkeys had an error rate of 0.075 on any given bracket choice, which corresponds to an error rate over trials of 0.24 (CI = 0.19 to 0.28). This is over 70% higher than the error rate of U.S. kids (mean = 0.14, CI = 0.12 to 0.16), 80% higher than Tsimane’ adults (mean = 0.13, CI = 0.09 to 0.17), and 260% higher than U.S. adults (mean = 0.09, CI = 0.06 to 0.13). Figure 6A shows the probability that individuals in each group made an error on a given trial (see the Supplementary Materials for complete model results).
Fig. 6. The effects of noise and memory errors on generating center-embedded structures.
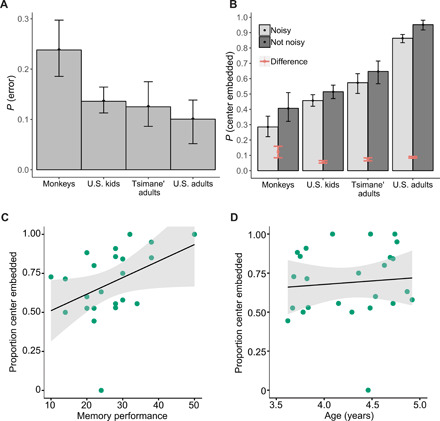
(A) The probability each group made an error implementing their strategy at least once in a trial, according to the results of the Bayesian analysis. (B) The probability each group generates center-embedded responses, with noise included in the model (light gray) and excluded from it (dark gray). The red bars represent the difference in center-embedding rates with and without noise for each group (i.e., the difference in the height of the bars). The error bars around the means in both (A) and (B) represent the 95% credible intervals. (C) Working memory performance, as measured by a forwards-digit task, was correlated with the proportion of center-embedded responses. (D) Age was not correlated with the proportion of center-embedded responses. The shaded regions represent 95% confidence intervals in (C) and (D).
The differing levels of noise between groups can explain some of the difference in their ability to correctly and consistently center embed. We compared the model’s predictions with and without the noise parameters, holding the other inferred parameters constant, to determine the effect of noise on each group’s performance. The results, displayed in Fig. 6B, show that monkeys would center embed with probability of 0.38 (CI = 0.30 to 0.47) if they implemented their intended strategies correctly, compared with their previous rate of 0.26. This 46% increase in the rate of center-embedded responses is substantially higher than the increase for kids (13%), Tsimane’ adults (22%), and U.S. adults (10%). The absolute differences in center embedding between monkeys and the other groups would also diminish. For instance, the difference in rates of center embedding between monkeys and U.S. kids (removing U.S. kids’ errors as well) would drop 41% from 0.17 (CI = 0.14 to 0.19) to 0.10 (CI = 0.06 to 0.13).
Memory constraints on recursive processing
We also looked at individual differences in the children’s sequence generation on the transfer list. Children were given a forwards-digit-span memory task where the experimenter would say a sequence of numbers and the participant would then repeat the sequence back to the experimenter. Only children who had a significantly higher than chance number of center-embedded and crossed responses were included in the correlation (n = 25). In addition, two subjects were excluded from this working memory correlation because they did not complete the memory task. We found a strong correlation between working memory and the proportion of center-embedded responses compared with crossed responses, such that children who performed better on the working memory task were more likely to produce center-embedded sequences (R2 = 0.17, P = 0.05; see Fig. 6C). In contrast, we found little to no relation between the proportion of center-embedded sequences and age (R2 = 0.008, P = 0.68; see Fig. 6D). In a multiple regression including centered and scaled age and working memory score, we found that working memory had a marginally significant effect over and above age (working memory score: β = 0.11, P = 0.058; age: β = −0.03, P = 0.62). When the outlier (>2 SDs away from the mean proportion of center-embedded responses) is excluded, the significance of the correlation between the proportion of center-embedded responses and working memory score (but not age) is increased (working memory: β = 0.09, P = 0.04; age: β = −0.004, P = 0.91). This suggests that the differences among children may be due in part to differences in working memory, which supports the hypothesis that subjects used a memory taxing recursive strategy (e.g., a pushdown stack). In addition, in U.S. children, we found that the inferred probability of making an error in the Bayesian analysis was correlated with their memory performance (Spearman ρ = −0.36, P < 0.05; see fig. S5). These data provide evidence that one of the limiting factors in representing recursive structures is working memory capacity.
DISCUSSION
Our results show the natural tendency of humans to spontaneously infer an abstract hierarchical structure when representing sequences. Subjects were exposed to two sequences, which contained an underlying center-embedded structure. These lists were ambiguous in how they should be represented. One could represent them as two arbitrary lists, a capacity that has been attested in both human children and monkeys (35), or they could spontaneously extract the underlying hierarchical structure of the training stimuli. We found that all human groups tested regardless of age, cultural, or educational experiences extracted and then generalized the internal center-embedded structure of the training lists to generate a novel instance of a center-embedded structure. This was not due to previous exposure to bracket-like stimuli because the Tsimane’ adults, preschool children, and monkeys, who lack formal mathematics and reading training, had never been exposed to such stimuli before testing. The Tsimane’ adults’ performance shows that formal education is not needed to represent and generate recursive sequences. In addition, by the age of 3.5 years old, human children already have the ability to represent the abstract rule and spontaneously generate novel recursive sequences. These data support the theory that humans have a bias to infer hierarchical structures from sequential data, also known as “dendrophilia” (25).
Our data also provide evidence that nonhuman animals can represent and generate novel sequences with a recursive, hierarchical, and center-embedded structure. Although, the abstract hierarchical structure was not the first strategy used, with additional exposure, two of three monkeys learned to generalize and create novel center-embedded sequences. These results are convergent with prior results showing that monkeys and preschool children can be taught to use a mirror grammar (33), one part of the center-embedded data structure (a unit consisting of two pairs embedded inside of another like unit) shown to be represented here. In addition, some research has suggested that center-embedded recursion could come about through ordinal position or associative chain learning (30). However, each of these strategies predicted a pattern of results that was disconfirmed by our analyses. Instead, our data suggest that monkeys have the capacity to come to understand an abstract hierarchical grouping. The ability of monkeys to generate center-embedded recursive sequences suggests that recursive processing may not be limited to humans, as has been claimed (3). Instead, our results provide evidence that working memory constraints may be one cause of differences in recursive abilities between monkeys, human children, and human adults. Although our results show that monkeys can generate recursive sequences, it is still unknown how widespread this capacity is at the population level. To measure the generalizability of this capacity to populations, future research would need to measure the heterogeneity of this capacity across many nonhuman subjects. Last, it is still an open question whether this ability to represent center-embedded sequences could generalize to larger sequences with multiple center embeddings and possibly enable the type of theoretically infinite combinatorial capacity in language. However, because of the high memory demands that multiple embeddings require, even human adults have difficulty representing multiple center embeddings in language (38). It is possible that the same computations used to represent one embedding could be used for multiple embeddings if the memory demands are decreased. Future work should test for this possibility in both human and nonhuman populations.
MATERIALS AND METHODS
Participants
Sample sizes for human subjects were designed to match the amount of data collected between groups based on the number of task trials that subjects from each group could reasonably complete.
U.S. adult participants were 10 adults (mean age = 22.6, SD = 1.0, 1 male). Participants were undergraduate students recruited from the University of Rochester River Campus. All guidelines and requirements of the University of Rochester’s Research Subjects Review Board were followed for participant recruitment and experimental procedures.
U.S. children participants were 50 children (mean age = 4.1 years, SD = 0.51 years, age range = 3.1 to 5.0 years, 22 male). Participants were recruited through the Kid Neuro Lab at the University of Rochester. All guidelines and requirements of the University of Rochester’s Research Subjects Review Board were followed for participant recruitment and experimental procedures. U.S. children completed the Test of Early Mathematics Ability (TEMA-3) (39), the Test of Auditory Comprehension of Language (TACL-4) (40), and a memory task in which they repeated a set of one to four numbers back to the experimenter. Note that data from children who did not reach high performance on the training lists are not informative because failures on training trials signal that they did not understand the task. Children were excluded because performance on the training trials did not meet the criteria of 3 of 5 trials correct on the training lists after 20 trials per training list (n = 15), failure to remain significantly above chance (at least 15% accuracy, chance = 4%) on the check trials in the testing session (n = 1), or experimenter error (n = 1). This exclusion rate is well within the normal range for tasks of this difficulty with children of this age range.
Tsimane’ adult participants were 37 adults (mean age = 32.4 years, SD = 15 years, 10 male). Participants were recruited from Tsimane’ communities near San Borja, Bolivia. All guidelines and requirements of the University of Rochester’s Research Subjects Review Board were followed for participant recruitment and experimental procedures. Interpreters were provided by the Centro Boliviano de Investigación y de Desarrollo Socio Integral. Subjects had a range between 0 and 12 years of formal education taught at the local village (mean = 4.2 years). As with other populations, we excluded Tsimane’ adults who did not reach performance of three correct in any five-trial period during the training lists on training trials (n = 16). Exclusions are expected for populations with little or no formal education and for whom psychology experiments with outsiders are extremely unusual.
Nonhuman primate subjects were three adult rhesus macaques (two males), who were socially housed. This sample size was chosen because it was the maximum number of animals that were available for testing. This number of subjects is sufficient for the purpose of the study because it allowed us to collect a large number of trials per subject and because each trial consisted of an open-ended response. Although this small number of subjects cannot measure the prevalence on a population level, it is sufficient to test for an existence proof of whether the capacity to represent recursive sequences is possible in a nonhuman animal. Two animals received food and water ad libitum as approved by the University of Rochester Committee on Animal Resources and veterinary staff. One animal was kept on an ad libitum food and water-restricted diet as approved by the University of Rochester Committee on Animal Resources and veterinary staff. All animal care procedures were in accordance with an Institutional Animal Care and Use Committee protocol. All monkeys had prior experience with sequencing tasks using photographs and geometric shapes.
Procedure
The procedure was designed to accommodate a wide variety of subjects. Sample sizes and the number of trials per subject were chosen to match the total amount of usable transfer trial data collected on the basis of the number of task trials subjects in each population could complete. More U.S. children and Tsimane’ adults were tested using a smaller number of trials compared with U.S. adults and monkeys who can complete many more trials in any given session.
U.S. adults, children, and monkeys all completed the task on touch screen monitors. To begin a trial, subjects would start a trial by touching the start stimulus, a white box. Then, the four stimuli pictures would be randomly placed on the monitor. Subjects were required to touch the stimuli in the correct order. When an item was pressed, it flashed and gave auditory feedback to cue that the touch was registered. Items remained on the screen after being touched but were unable to be activated again for 2 s to help decrease accidental double clicking. During training trials, if the first choice of a trial was correct, the subject heard positive auditory feedback (a ding) and continued onto the next choice until either the trial was completed correctly or an incorrect item was selected. If an incorrect item was selected during a training trial, subjects immediately received auditory feedback (a buzzer) and a 2-s time-out screen. If a training trial was correctly completed, subjects received positive auditory feedback (a chime). For the Tsimane’ adults, verbal feedback was given (“OK” for a correct touch, “wrong” for an incorrect touch, and “good” for a correct trial). In addition, monkeys received a small food or juice reward for correct trials. There was a 2-s intertrial interval before the start of the next trial regardless of accuracy. During transfer trials, each trial continued until the end of the trial, and subjects received positive feedback regardless of the response.
Prior research has shown that nonindustrialized populations including the Tsimane’ group show a disadvantage with computerized testing procedures compared with manual presentations (41). To eliminate these issues, Tsimane’ adults were presented with stimuli printed on laminated 4″ by 4″ index cards. At the start of each trial, the stimuli were shuffled and randomly placed in front of the subject. Subjects would respond by touching the index cards. On training trials, verbal feedback was given (“OK” for a correct touch, “wrong” for an incorrect touch, and “good” for a correct complete trial). For transfer trials, only the “OK” verbal cue was used to indicate they had touched a picture and no verbal feedback was given at the end of the trial regardless of a response. The testing sessions were video recorded and coded by two researchers for reliability. The stimuli, instructions, and randomization were the same as all U.S. subjects.
Training phase
To keep the task consistent across subject groups, verbal instruction was kept to a minimum. At the start of the training session, subjects were told, “You will see four images. You will need to touch them in order.” U.S. adults received no additional instruction. For each training list, Tsimane’ adults and U.S. children were shown an example of how a trial works with the experimenter touching the training list in the correct order while saying, “It goes, this one, this one, this one, and then this one.” Although this procedure could not be used for monkeys, they had previously been trained to order sets of random images and, thus, were used to the structure of the task before testing.
All subjects received training on two center-embedded lists (see Fig. 1C) before the testing session began. Each list consisted of four bracket images, “{ ( ) }” and “{ [ ] }”, respectively. These training images were selected to give cues to link the base pairs (type/color of the brackets) and the order within the base pairs (left/right facing brackets and a colored box around the close brackets). Previous research has shown that in order for adults to represent true center-embedded sequences (and differentiate between center-embedded and “crossed” errors), they first need to learn what the base pairs are. In the past, this has been accomplished via both having a perceptual cue to the base pairs (phonetic features) and training on two-item lists in order for subjects to learn the base pairs (42). To eliminate the two-item training phase, we chose to just use perceptual cues to indicate the base pairs. In addition, there needs to be a cue to the order within the pairs or which falls in the “A” set and in the “B” set in the AnBn grammar. As with the base pairs, in the past, this has been indicated with both perceptual features (22, 42) and two-item training. We used the perceptual features of the direction of the bracket and a border around the close brackets to eliminate the need for two-item training, which would increase the possibility of using associative strategies (30). A border was used around the close brackets as an extra indicator to the order within a pair as to eliminate the need to differentiate stimuli just based on the direction they were rotated.
Subjects were trained on one training list until they met the criterion [U.S. adults: 7 of 10 correct; Tsimane’ adults and U.S. children: 3 of 5 correct; monkeys: 7 of 10 correct (1 monkey) and 70% correct for two consecutive, 200 trial training sessions (2 monkeys)]. The goal of testing monkeys was to test if it was within the capacity of a nonhuman animal to transfer the recursive structures to novel lists. It is possible that failure could be due to undertraining of the training sequences or overtraining of the sequences (which could push monkeys to rely on less computationally complex ordinal rules). Thus, we wanted to be sure that failure (or success) was not due to one specific training procedure. Subjects were then trained on the second list to the same criterion before moving onto testing sessions. Monkeys took on average 1368 trials per training list (Horatio: 800 per list, Coltrane: 800 per list, Beyoncé: 2504 per list).
Experiment 1
After completion of the training phase, a percentage of transfer trials were randomly intermixed within the training trials (U.S. adults, Tsimane’ adults, U.S. children, and one monkey: 50%, two monkeys; 5%). Because this type of procedure has never been used to test nonhuman primates, we varied the percentage of transfer trials to make sure that the percentage of transfer trials did not affect the results. All monkeys in experiment 1 showed similar, nonsignificant results on the transfer trials regardless of the percentage of transfer trials. These transfer trials were nondifferentially reinforced such that subjects received positive feedback regardless of response or no feedback for the Tsimane’ adults. The transfer trials consisted of the inner brackets from each of the two training lists. They had never been presented together before in a single trial. Transfer responses that contained a repeated touch of the same image were allowed but excluded from analysis because they were rare and no individual repeat error happened more often than 1% of the time in any group.
Experiment 2: Additional exposure
To test if monkeys could use a recursive strategy with additional exposure, after the initial testing phase, monkeys received training on two additional center-embedded lists. These lists were composed of completely novel sets of bracket images, which were different colors and shapes than the brackets in experiment 1. The structure of these additional training lists matched the initial training such that the first list was two sets of two bracket images (total of four). The second list consisted of the same outside bracket images and two novel bracket images for the center. As in the initial training phase, subjects were first trained to 70% correct on each training list (one monkey: 70% correct for two sessions, two monkeys: 7 of 10 correct). This took an average of 1795 trials per list. We chose to vary the training criteria between monkeys as to balance any possibility of over- or undertraining the training lists.
After training, subjects were shown transfer trials (one monkey: 50%, one monkey: 7%, one monkey: 100% transfer trials) that consisted of the two sets of center brackets presented in the training lists. Again, the percentage of transfer trials was varied to make sure there was no effect of the percentage of transfer trials. Because of the novelty of the task, there was no strong a priori reason to choose a specific percentage of probe trials. Instead of limiting the type of testing, we chose to vary the percentage of probe trials between the monkeys. We saw no systematic evidence of transfer trial percentage, such that the two monkeys who had a significant number of center-embedded responses received the smallest and largest percentage of transfer trials. These transfer list brackets had never been presented together before the transfer trials. Subjects received positive feedback regardless of the order chosen in transfer trials.
Experiment 3: Generalization to novel stimuli
To test if monkeys could generalize the recursive rule to completely novel stimuli, we tested their transfer to four item lists that they had never seen in training. To do this, we created 30 novel transfer lists. Monkeys were presented with one of the novel lists at a time. The first five trials the monkey received of a novel list were nondifferentially reinforced. Monkeys received positive feedback regardless of their response. This allowed us to see what strategy they used for lists in which they had never seen any of the items before. After five transfer trials, monkeys received differential reinforcement such that they received positive feedback only for center-embedded responses (e.g., either “{ < > }” or “< { } >”). Once subjects correctly ordered 8 of 10 trials in a row, subjects immediately moved onto another novel transfer list and repeated this procedure—5 nondifferentially reinforced transfer trials, followed by training to 8 of 10 correct. This procedure was repeated for a total of 30 novel transfer lists. The subjects averaged 157 trials to reach criterion for each list. The data presented in Fig. 4 only included the first five nondifferentially reinforced transfer trials from each of the novel lists.
Supplementary Material
Acknowledgments
We thank S. Carey and S. Dehaene for the comments on the manuscript. We thank T. Gibson, R. Godoy, T. Huanca, S. Alonzo, J. Jara-Ettinger, R. Futrell, D. N. Anez, S. Hiza Nate, and the Grand Consejo for field research support. We thank C. Lussier, K. Blakely, K. Brown, E. Prentiss, S. Koopman, A. Haslinger, A. Arre, Y. Qiu, G. Bueno, Y. Huang, S. Robinson, J. Yurkovic, K. Csumitta, M. Mullen, G. Schwartz, and A. O’Donnel for laboratory research support. Funding: This work is supported by the National Science Foundation (DRL1459625; to J.F.C.), the National Science Foundation Division of Research on Learning (1760874; to S.T.P.), the National Institute of Health (R01-HD064636; to J.F.C.), the James S. McDonnell Foundation (to J.F.C.), the Alfred P. Sloan Foundation (to J.F.C.), and the University of Rochester. Author contributions: S.F., S.T.P., and J.F.C. developed the study concept and contributed to the study design. S.F. collected the data. S.F., S.C., S.T.P., and J.F.C. performed the data analysis. S.C. and S.T.P. developed and performed the Bayesian analysis. All authors wrote the manuscript, discussed the results, and commented on the manuscript. Competing interests: The authors declare that they have no competing interests. Data and materials availability: All data have been made public (https://github.com/Sferrigno/RecursiveSequenceGeneration). All Bayesian model code has been made public (https://github.com/samcheyette/monkey_recursion_final). All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials. Additional data related to this paper may be requested from the authors.
SUPPLEMENTARY MATERIALS
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/26/eaaz1002/DC1
REFERENCES AND NOTES
- 1.Pinker S., Jackendoff R., The faculty of language: What's special about it? Cognition 95, 201–236 (2005). [DOI] [PubMed] [Google Scholar]
- 2.N. Chomsky, Syntactic Structure (Mouton, 1957). [Google Scholar]
- 3.Hauser M. D., Chomsky N., Fitch W. T., The faculty of language: What is it, who has it, and how did it evolve? Science 298, 1569–1579 (2002). [DOI] [PubMed] [Google Scholar]
- 4.N. I. Badler, R. Bindiganavale, J. C. Bourne, M. S. Palmer, J. Shi, Parameterized action representation for virtual human agents. in Embodied Conversational Agents, J. Cassell, J. Sullivan, S. Prevost, E. Churchill, Eds. (MIT Press, Cambridge, MA, 2000), pp. 256–284. [Google Scholar]
- 5.R. Jackendoff, Language, Consciousness, Culture: Essays on Mental Structure (MIT Press, 2007). [Google Scholar]
- 6.Lerdahl F., Jackendoff R., An overview of hierarchical structure in music. Music Percept. 1, 229–252 (1983). [Google Scholar]
- 7.Piantadosi S. T., Tenenbaum J. B., Goodman N. D., Bootstrapping in a language of thought: A formal model of numerical concept learning. Cognition 123, 199–217 (2012). [DOI] [PubMed] [Google Scholar]
- 8.Everett D., Cultural constraints on grammar and cognition in Pirahã: Another look at the design features of human language. Curr. Anthropol. 46, 621–646 (2005). [Google Scholar]
- 9.Nevins A., Pesetsky D., Rodrigues C., Pirahã exceptionality: A reassessment. Language 85, 355–404 (2009). [Google Scholar]
- 10.Futrell R., Stearns L., Everett D. L., Piantadosi S. T., Gibson E., A corpus investigation of syntactic embedding in Pirahã. PLOS ONE 11, e0145289 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Dehaene S., Meyniel F., Wacongne C., Wang L., Pallier C., The neural representation of sequences: From transition probabilities to algebraic patterns and linguistic trees. Neuron 88, 2–19 (2015). [DOI] [PubMed] [Google Scholar]
- 12.C. R. Gallistel, The Organization of Learning (MIT Press, Cambridge, MA, 1990). [Google Scholar]
- 13.Brannon E. M., Terrace H. S., Ordering of the numerosities 1 to 9 by monkeys. Science 282, 746–749 (1998). [DOI] [PubMed] [Google Scholar]
- 14.Brannon E. M., The development of ordinal numerical knowledge in infancy. Cognition 83, 223–240 (2002). [DOI] [PubMed] [Google Scholar]
- 15.Saffran J. R., Aslin R. N., Newport E. L., Statistical learning by 8-month-old infants. Science 274, 1926–1928 (1996). [DOI] [PubMed] [Google Scholar]
- 16.Hauser M. D., Newport E. L., Aslin R. N., Segmentation of the speech stream in a non-human primate: Statistical learning in cotton-top tamarins. Cognition 78, B53–B64 (2001). [DOI] [PubMed] [Google Scholar]
- 17.Heimbauer L. A., Conway C. M., Christiansen M. H., Beran M. J., Owren M. J., Visual artificial grammar learning by rhesus macaques (Macaca mulatta): Exploring the role of grammar complexity and sequence length. Anim. Cogn. 21, 267–284 (2018). [DOI] [PubMed] [Google Scholar]
- 18.Marcus G. F., Vijayan S., Rao S. B., Vishton P. M., Rule learning by seven-month-old infants. Science 283, 77–80 (1999). [DOI] [PubMed] [Google Scholar]
- 19.Saffran J., Hauser M., Seibel R., Kapfhamer J., Tsao F., Cushman F., Grammatical pattern learning by human infants and cotton-top tamarin monkeys. Cognition 107, 479–500 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Wang L., Uhrig L., Jarraya B., Dehaene S., Representation of numerical and sequential patterns in macaque and human brains. Curr. Biol. 25, 1966–1974 (2015). [DOI] [PubMed] [Google Scholar]
- 21.Sonnweber R., Ravignani A., Fitch W. T., Non-adjacent visual dependency learning in chimpanzees. Anim. Cogn. 18, 733–745 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Fitch W. T., Hauser M. D., Computational constraints on syntactic processing in a nonhuman primate. Science 303, 377–380 (2004). [DOI] [PubMed] [Google Scholar]
- 23.Gentner T. Q., Fenn K. M., Margoliash D., Nusbaum H. C., Recursive syntactic pattern learning by songbirds. Nature 440, 1204–1207 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Penn D. C., Holyoak K. J., Povinelli D. J., Darwin's mistake: Explaining the discontinuity between human and nonhuman minds. Behav. Brain Sci. 31, 109–130 (2008). [DOI] [PubMed] [Google Scholar]
- 25.Fitch W. T., Toward a computational framework for cognitive biology: Unifying approaches from cognitive neuroscience and comparative cognition. Phys. Life Rev. 11, 329–364 (2014). [DOI] [PubMed] [Google Scholar]
- 26.Perruchet P., Rey A., Does the mastery of center-embedded linguistic structures distinguish humans from nonhuman primates? Psychon. Bull. Rev. 12, 307–313 (2005). [DOI] [PubMed] [Google Scholar]
- 27.de Vries M. H., Monaghan P., Knecht S., Zwitserlood P., Syntactic structure and artificial grammar learning: The learnability of embedded hierarchical structures. Cognition 107, 763–774 (2008). [DOI] [PubMed] [Google Scholar]
- 28.Corballis M. C., Recursion, language, and starlings. Cognit. Sci. 31, 697–704 (2007). [DOI] [PubMed] [Google Scholar]
- 29.Abe K., Watanabe D., Songbirds possess the spontaneous ability to discriminate syntactic rules. Nat. Neurosci. 14, 1067–1074 (2011). [DOI] [PubMed] [Google Scholar]
- 30.Rey A., Perruchet P., Fagot J., Centre-embedded structures are a by-product of associative learning and working memory constraints: Evidence from baboons (Papio Papio). Cognition 123, 180–184 (2012). [DOI] [PubMed] [Google Scholar]
- 31.Poletiek F. H., Fitz H., Bocanegra B. R., What baboons can (not) tell us about natural language grammars. Cognition 151, 108–112 (2016). [DOI] [PubMed] [Google Scholar]
- 32.Winkler M., Mueller J. L., Friederici A. D., Männel C., Infant cognition includes the potentially human-unique ability to encode embedding. Sci. Adv. 4, eaar8334 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Jiang X., Long T., Cao W., Li J., Dehaene S., Wang L., Production of supra-regular spatial sequences by macaque monkeys. Curr. Biol. 28, 1851–1859.e4 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Henrich J., Heine S. J., Norenzayan A., Most people are not WEIRD. Nature 466, 29 (2010). [DOI] [PubMed] [Google Scholar]
- 35.Terrace H. S., McGonigle B., Memory and representation of serial order by children, monkeys, and pigeons. Curr. Dir. Psychol. Sci. 3, 180–185 (1994). [Google Scholar]
- 36.A. Gelman, J. B. Carlin, H. S. Stern, D. B. Rubin, Bayesian Data Analysis (CRC press, Boca Raton, FL, 2014). [Google Scholar]
- 37.Ravignani A., Westphal-Fitch G., Aust U., Schlumpp M. M., Fitch W. T., More than one way to see it: Individual heuristics in avian visual computation. Cognition 143, 13–24 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Gibson E., Linguistic complexity: Locality of syntactic dependencies. Cognition 68, 1–76 (1998). [DOI] [PubMed] [Google Scholar]
- 39.H. Ginsburg, A. J. Baroody, TEMA-3: Test of Early Mathematics Ability (Pro-ed.), (2003).
- 40.E. Carrow-Woolfolk, Test for Auditory Comprehension of Language (DLM Teaching Resources, Allen, TX, 1985). [Google Scholar]
- 41.Gibson E., Jara-Ettinger J., Levy R., Piantadosi S., The use of a computer display exaggerates the connection between education and approximate number ability in remote populations. Open Mind 1, 159–168 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Bahlmann J., Schubotz R. I., Friederici A. D., Hierarchical artificial grammar processing engages Broca's area. Neuroimage 42, 525–534 (2008). [DOI] [PubMed] [Google Scholar]
- 43.Blei D. M., Ng A. Y., Jordan M. I., Latent dirichlet allocation. J. Mach. Learn. Res. 3, 993–1022 (2003). [Google Scholar]
- 44.Hoffman M. D., Gelman A., The no-U-turn sampler: Adaptively setting path lengths in Hamiltonian Monte Carlo. J. Mach. Learn. Res. 15, 1593–1623 (2014). [Google Scholar]
- 45.Salvatier J., Wiecki T. V., Fonnesbeck C., Probabilistic programming in Python using PyMC3. PeerJ Comput. Sci. 2, e55 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/26/eaaz1002/DC1


