Abstract
Objective
The goals of this study were to 1) specify the factor structure of the Uniform Dataset 3.0 Neuropsychological Battery (UDS3NB) in cognitively unimpaired older adults, 2) establish measurement invariance for this model, and 3) create a normative calculator for factor scores.
Methods
Data from 2,520 cognitively intact older adults was submitted to confirmatory factor analyses and invariance testing across sex, age, and education. Additionally, a subsample of this dataset was used to examine invariance over time using one-year follow up data (n = 1,061). With the establishment of metric invariance of the UDS3NB measures, factor scores could be extracted uniformly for the entire normative sample. Finally, a calculator was created for deriving demographically-adjusted factor scores.
Results
A higher order model of cognition yielded the best fit to the data χ2(47) = 385.18, p < .001, CFI = .962, TLI = .947, RMSEA = .054, SRMR = .036. This model included a higher order general cognitive abilities factor, as well as lower order processing speed/executive, visual, attention, language, and memory factors. Age, sex, and education were significantly associated with factor score performance, evidencing a need for demographic correction when interpreting factor scores. A user-friendly Excel calculator was created to accomplish this goal and is available in the online supplementary materials.
Conclusions
The UDS3NB is best characterized by a higher order factor structure. Factor scores demonstrate at least metric invariance across time and demographic groups. Methods for calculating these factors scores are provided.
Keywords: Uniform Data Set, neuropsychological tests, factor analysis, cognition, demographic correction, measurement invariance
Introduction
Measurement of Cognitive Decline
The Uniform Data Set (UDS) neuropsychological battery from the National Alzheimer’s Coordinating Center is in its third revision (Weintraub et al., 2018) and has already generated considerable clinical research interest. It has been cross-validated with existing measures (Monsell et al., 2016) and normative data on over 3,000 healthy older adults (Weintraub et al, 2018) has been published. Additionally, discrepancy scores and derived measures have been created (Devora, Beevers, Kiselica, & Benge, 2019). A critical next step toward the promulgation of this battery is addressing core psychometric questions pertinent to its interpretation and use.
Factor analytic studies in particular are critical to address these questions and provide evidence for construct validity. Construct validity is established by an accumulation of findings that a measure captures a phenomenon of interest, most commonly by testing whether measures function as predicted by theory (Cronbach & Meehl, 1955). Factor analysis assesses the extent to which directly observed variables load onto latent factors, as well as the relationships among those factors. Thus, it provides direct evidence for construct validity and is now considered a standard practice in measure validation (Thompson & Daniel, 1996). Ethical guidelines and professional standards emphasize the need to utilize tests with empirical evidence of construct validity, such that factor analytic studies are necessary if the UDS neuropsychological battery is to be implemented in practice (American Educational Research Association, American Psychological Association, National Council on Measurement in Education, & Joint Committee on Standards for Educational and Psychological Testing, 2014).
In addition, factor analysis allows for data reduction. The UDS 3.0 neuropsychological battery (UDS3NB) includes 21 individual cognitive scores in its published normative calculator, as well as a host of available item-level data and derived or discrepancy indices that can be calculated from the core tests (Devora et al., 2019; Weintraub et al., 2018). These observed scores likely tap shared and overlapping constructs of interest to clinical researchers (e.g., memory as a single value as opposed to five scores that could be used to assess this construct in the battery). Factor analytic processes allow for exploration of the variance common across observed measures and the extraction of indices less impacted by measurement error that constitute fairly pure representations of domains of interest (Thompson, 2004). Factor scores thus may allow for fewer variables to be employed across studies, increasing the power to detect findings and allowing a common language of cognitive factors to be utilized.
Applying a Latent Variable Approach to the UDS Battery
Factor analytic methods have been applied to past versions of the UDS. For instance Hayden and colleagues (2011) conducted an exploratory factor analysis (EFA) of the UDS 2.0 neuropsychological test battery, followed by a series confirmatory factor analyses (CFA). They found evidence for a four-factor structure, including memory, attention, executive functioning, and language domains. Subsequently, this group found evidence that patterns of performance on these factor scores predicted conversion to dementia in the UDS sample; that is, individuals with poor performance across all factors were at greater risk for developing dementia than those who performed well across cognitive domains (Hayden et al., 2014).
Since this work, the UDS neuropsychological battery has been updated in several important ways for the release of version 3.0 (Monsell et al., 2016; Weintraub et al., 2018; Weintraub et al., 2009). First, the Wechsler Memory Scales-Revised Logical Memory and Digit Span (Wechsler, 1987) subtests have been replaced with the Craft Story (Craft et al., 1996) and Number Span tests, respectively. Second, the Boston Naming Test (Goodglass, Kaplan, & Barresi, 2000) has been replaced with the Multilingual Naming Test (Ivanova, Salmon, & Gollan, 2013). Third, a measure of visuoconstruction and visuospatial recall, the Benson Figure (Possin, Laluz, Alcantar, Miller, & Kramer, 2011), and a letter fluency task have been added. Fourth, the psychomotor coding task has been removed. These changes necessitate reconsideration of the factors that are measured by the revised battery.
In addition, alternative, and as yet untested, conceptualizations of the UDS factor structure require examination. For example, higher order models of cognition, including a general cognitive factor, may be more accurate models of neuropsychological functioning. (Jensen, 1998; Wechsler, 2008). Indeed, one study indicated that the UDS 2.0 neuropsychological measures covary highly and tend to load on a unitary factor (Gavett et al., 2015). This finding suggests that both unitary and multi-factor models of the UDS 3.0 need to be explored. Additionally, it will be important to examine the most commonly supported model of cognition, the higher order model, which includes a superordinate general factor and subordinate specific factors (Reeve & Blacksmith, 2009; Schneider & McGrew, 2018).
The Importance of Normative Factor Scores
Establishing the factor structure of the UDS3NB is important to provide evidence of construct validity and allow for data reduction. However, this knowledge of is limited utility if factor scores cannot be extracted and interpreted. Thus, another important step toward making the UDS3NB a user-friendly clinical and research tool will consist of establishing a method for deriving factor scores and understanding what they mean for individuals. This goal is particularly important when considering the increased focus on identifying individuals in pre-clinical or prodromal stages of cognitive decline (Jack et al., 2018). Indeed, many current clinical trials are specifically recruiting individuals in these early stages of neurodegenerative disease (Cummings, Lee, Ritter, Sabbagh, & Zhong, 2019) where frank cognitive impairments are lacking, though subtle transitional cognitive declines may exist (Jack et al., 2018; Kiselica, Kaser, & Benge, in preparation; Kiselica, Webber, & Benge, under review). The development of normative data for factor scores will allow comparison of individual test performances, such that expected versus abnormal scores can be delineated in the earliest stages of neurodegenerative disease. It is also essential to establish that factor scores can be utilized with varied populations within the normative sample by establishing measurement invariance to ensure wide applicability of these metrics.
Current Study
There were three main goals of the current study:
Identify the underlying factor structure of the UDS3NB in sample of cognitively intact individuals. Our a priori hypothesis is that 4 lower order factors (memory, attention, visual/executive, and language) would emerge, as well as a higher-level general cognitive abilities factor.
Establish metric invariance of factor scores across demographic groups (i.e., age, sex, and education) and over time to provide evidence that factor scores can be extracted and applied uniformly in these populations over serial evaluations.
Use a regression-based technique to extract factor scores from the sample, and present a calculator to allow researchers and clinicians to calculate demographically corrected factor scores in their own samples, similar to prior work with the UDS (Devora et al., 2019; Shirk et al., 2011; Weintraub et al., 2018).
Methods
Sample
We requested all available UDS data through the NACC portal on 1/29/19. Data included 39,412 participants from 39 Alzheimer’s Disease Research Centers. Data were collected under the auspices of the IRBs at the respective institutions and were provided in a deidentified format. This study was exempt from IRB review, given that it consisted of secondary analyses of deidentified data. The research was completed in accordance with the Helsinki Declaration.
The sample was restricted to English speaking individuals (n = 36,134) given that several measures used for analyses were language-based. Next, the sample was reduced to individuals who received the UDS 3.0 at their initial visit (n = 6,042), which included data collected from 03/2015 through 12/2018, because this study focused specifically on the factor structure of the UDS 3.0. The dataset was then reduced to those individuals diagnosed as cognitively normal (n = 2,520) in keeping with prior research using the UDS (Devora et al., 2019; Shirk et al., 2011; Weintraub et al., 2018), as well as common practice in publishing normative data (e.g., Wechsler, 2008).
Classification of cognitive status was based on UDS consensus decision, as well as the Clinical Dementia Rating (CDR) Dementia Staging Instrument ®, a reliable and valid clinical interview for staging the severity of cognitive and functional declines among individuals with neurodegenerative diseases (Fillenbaum, Peterson, & Morris, 1996; Morris, 1993, 1997). The CDR has a global rating scale that divides patients into cognitively normal (0), MCI/mild dementia (.5), and dementia (>.5) stages. Thus, individuals needed a CDR score of zero to be included in the analyses. Finally, we utilized a subset of these participants with available one-year follow up data to investigate invariance of the UDS3NB factor structure over time (n = 1,061). Descriptive statistics for these samples are provided in Table 1.
Table 1.
Descriptive Statistics for Raw Scores of Study Variables for the Total and Longitudinal Samples
| Demographic variables | Total Sample (n = 2,520) | Longitudinal Sample (n = 1,061) |
|---|---|---|
| Age: M (SD) | 68.33 (10.26) | 68.82 (10.55) |
| Education: M (SD) | 16.39 (2.50) | 17.04 (7.55) |
| % Female | 65.10% | 64.10% |
| % White | 78.60% | 78.60% |
| Cognitive Variables | M (SD) | M (SD) |
| Benson Figure Copy | 15.58 (1.31) | 15.51 (1.34) |
| Benson Figure Recall | 11.50 (2.90) | 11.71 (2.87) |
| Trailmaking Test part A | 31.21 (12.25) | 40.50 (12.02) |
| Trailmaking Test part B | 80.32 (38.42) | 81.50 (44.42) |
| Letter Fluency | 24.47 (9.72) | 29.75 (8.51) |
| Number Span Forward | 8.34 (2.30) | 8.39 (2.39) |
| Number Span Backward | 7.12 (2.20) | 7.22 (2.22) |
| Vegetable Naming | 14.89 (4.04) | 15.07 (3.95) |
| Animal Naming | 21.63 (5.58) | 21.99 (5.46) |
| Multilingual Naming Test | 30.12 (2.00) | 30.43 (1.87) |
| Craft Story Immediate Recall | 21.90 (6.45) | 22.64 (6.25) |
| Craft Story Delayed Recall | 19.08 (6.53) | 19.99 (6.49) |
Measures
Measures in the UDS 3.0 battery are described in detail elsewhere (Besser et al., 2018; Weintraub et al., 2018). In brief, the UDS 3.0 includes 1) the Craft Story (Craft et al., 1996), a measure of immediate and delayed recall of orally presented story information (though both verbatim recall and thematic unit scores can be calculated, verbatim recall points were used for the current study); 2) the Benson Figure, which includes a figure copy trial and a delayed figure recall trial (Possin et al., 2011); 3) Number Span Forwards and Backwards (total score used for the current study); 4) the Multilingual Naming Test (MINT), a confrontation naming test (Gollan, Weissberger, Runnqvist, Montoya, & Cera, 2012; Ivanova et al., 2013); 5) letter (F- and L-words) and semantic fluency (animals and vegetables) tasks; and 6) Trailmaking Test parts A and B, which evaluate simple number sequencing and letter-number sequencing, respectively (Partington & Leiter, 1949).
Analyses
Confirmatory factor analyses
The Lavaan program (Rosseel, 2012) in R (RStudio Team, 2015) was used to conduct CFAs. All cognitive variables were z-scored before model entry. Global model fit was examined using the χ2, comparative fit index (CFI), Tucker-Lewis Index (TLI), root mean square error of approximation (RMSEA), and the standardized root mean residual (SRMR). Improved model fit is suggested by a lower (and ideally non-significant) chi-square value, CFI and TLI values closer to one (>.90 for acceptable fit and >.95 for good fit), and RMSEA and SRMR values closer to zero (<.08 for acceptable fit and <.05 for good fit, respectively; Hooper, Coughlan, & Mullen, 2008; Hu & Bentler, 1999). Changes in CFI (>.01; Cheung & Rensvold, 2002), RMSEA (>.015; Chen, 2007), TLI (>.05; Little, 1997), and SRMR (>.03; Chen, 2007) indicated superior fit when evaluating fit between models.
Three potential models were examined:
A unitary model, wherein all cognitive variables loaded onto a single factor, and residual covariances were allowed between Trailmkaing parts A and B, as well as between animal and vegetable fluency, to account for method variance.
A four-factor correlated model that included memory, attention, processing speed/executive functioning, and language domains, consistent with previous findings with the UDS 2.0 (Hayden et al., 2011). The memory factor was composed of Craft Story immediate and delayed recall scores, as well as the Benson Figure delayed recall score. Next, the attention factor included the two Number Span variables. The executive functioning variable included Trailmaking parts A and B, as in the Hayden and colleagues paper (2011). Additionally, the Benson Figure copy was added to this factor, given research suggesting that complex visuoconstruction tasks involve executive skills, such as planning and organization (Possin et al., 2011; Shin, Park, Park, Seol, & Kwon, 2006). Another executive task, letter fluency (Henry & Crawford, 2004; Lezak, Howieson, & Loring, 2012; Varjacic, Mantini, Demeyere, & Gillebert, 2018), was also modeled on the processing speed/executive functioning factor. Finally, the latent language variable was comprised of the two semantic fluency scores, as well as the MINT score. Again, residual covariances were allowed between Trailmkaing parts A and B, as well as between animal and vegetable fluency, to account for method variance.
A higher order model that included the above four first-order factors (specified as orthogonal), as well as a superordinate general cognitive ability factor, composed of the four first-order factors.
After examination of global fit indices, models were respecified to improve fit based upon review of the local pattern of factor loadings and modification indices (Kline, 2011).
Measurement invariance
Measurement invariance was assessed using the Lavaan program (Rosseel, 2012) in R (RStudio Team, 2015) following the procedures of van de Schoot, Lugtig, and Hox (2012). First, the best fitting model was specified across groups to assure that the basic structure of the CFA held and establish configural invariance. Second, the factor structure and factor loadings were held constant across groups to test for metric invariance. This was considered the minimum level of invariance required to establish that factor scores could be extracted uniformly for the normative calculator. Third, the factor structure, loadings, and intercepts were held constant across groups to test for scalar invariance. Finally, the factor structure, loadings, intercepts, and residual variances were fixed to be equal across groups to test for strict invariance.
Each increasingly restrictive model is compared against the previous model to evaluate for changes in fit. Measurement invariance was considered established at the most restrictive level (i.e., configural, metric, scalar, or strict), wherein an unacceptable decrement in fit did not occur when adding additional constraints. Evaluation of invariance was completed by using the RMSEA and CFI rules for interpretation of change in fit described in the previous section. We completed invariance testing for several demographic variables, including sex, age (participants divided into <60, 60–79, and ≥80 age groups), and education (participants divided into groups with ≤12, 13–15, ≥16 years of education). Additionally, measurement invariance for a subsample of participants with one-year follow up data available (n = 1,061) was evaluated to ensure the stability of the factor structure across serial assessments.
Demographic influences and normative calculator
Once the factor structure of the UDS3NB was established and determined to demonstrate metric invariance, we created a calculator for estimating demographically-adjusted scores based on the normative sample. Examination of demographic influences followed the procedures of previous normative evaluations of the UDS 3.0 (Devora et al., 2019; Shirk et al., 2011; Weintraub et al., 2018). Specifically, each factor score was regressed on age, education, and sex (entered as a block) using SPSS 25.0 (IBM Corp., 2017). Regression coefficients from this analysis were then used to create formulas for demographically-adjusted scaled scores. These formulas were then employed in Microsoft Excel to create a user-friendly calculator that would convert raw test data from the UDS 3.0 to a series of normative factor scaled scores for application in research and applied settings. This calculator is available in the online supplementary material.
Results
Confirmatory Factor Analyses
Results of CFA analyses are presented in Table 2. The unitary model was a poor fit to the data. The four-factor correlated model yielded an improvement in fit; however, the overall model fit was inadequate, and there were weak to very strong correlations between the factors (.28 ≤ r ≤ 1.00). Consequently, a higher order structure that captured the common variance across these factors was explored. This higher order model fit the data similarly to the four-factor model, and the difference in model fit fell below recommended thresholds for meaningful change. Given that the higher order model of cognition has long been supported by theory and empirical work and captures meaningful variance among specific factors (Gavett et al., 2015; Reeve & Blacksmith, 2009; Schneider & McGrew, 2018), this model was chosen for respecification.
Table 2.
Model Fit Statistics for Confirmatory Factor Analyses
| Unitary Model | 4-Factor Correlated Model | Higher Order Model | Modified Higher Order Model | |
|---|---|---|---|---|
| (df) χ2, p | (54) 2925.28, <.001 | (48) 507.74, <.001 | (48) 580.25, <.001 | (47) 385.18, <.001 |
| CFI | .677 | .948 | .940 | .962 |
| TLI | .590 | .925 | .918 | .947 |
| RMSEA [90%CI] | .149 | .063 | .067 | .054 |
| SRMR | .137 | .052 | .056 | .036 |
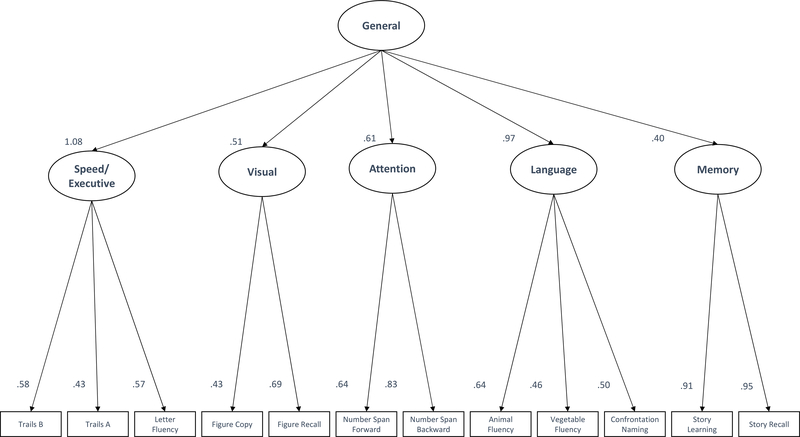
The loadings for the two Benson Figure variables were low (.21 for the figure copy variable loading onto the Speed/Executive factor and .28 for the figure recall variable loading onto the Memory factor). Consequently, the model was respecified to include a separate first-order visual factor. This step resulted in a substantial improvement in model fit (see the Modified Higher Order Model column of Table 2) and guided selection of this model as the optimal factor model (see Figure 1 for a visual representation).
Figure 1.
Best fitting model for factor structure of cognitive measures in the UDS 3.0 Neuropsychological Battery. Standardized factor loadings for each variable are presented to the left of the relevant arrows. All loadings were significant at the p < .001 level.
Measurement Invariance
Results of measurement invariance testing are presented in Table 3. The overall model provided a good fit for both men and women, and there was not a substantial decrease in fit when factor structure and loadings were held constant. However, fit declined to unacceptable levels when factor structure, loadings, and intercepts were held constant based on the change in the CFI and RMSEA (ΔCFI = .025, ΔRMSEA = .025). Thus, there was evidence for metric invariance across sexes.
Table 3.
Model Fit Results for Invariance Testing
| Grouping Variable | χ2 | df | p | Δχ2 | df | p | CFI | ΔCFI | RMSEA | ΔRMSEA | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Sex | Configural | 410.55 | 94 | <.001 | -- | -- | -- | .964 | -- | .053 | -- |
| Metric | 446.45 | 105 | <.001 | 35.90 | 11 | <.001 | .961 | .003 | .052 | .001 | |
| Scalar | 936.92 | 111 | <.001 | 490.47 | 6 | <.001 | .907 | .055 | .078 | .026 | |
| Strict | 978.15 | 117 | <.001 | 41.23 | 6 | <.001 | .903 | .004 | .078 | .000 | |
| Age | Configural | 515.53 | 141 | <.001 | -- | -- | -- | .955 | -- | .057 | -- |
| Metric | 551.25 | 163 | <.001 | 35.72 | 22 | .032 | .953 | .002 | .054 | .003 | |
| Scalar | 757.02 | 175 | <.001 | 205.77 | 12 | <.001 | .930 | .023 | .064 | .010 | |
| Strict | 1067.04 | 187 | <.001 | 310.02 | 12 | <.001 | .894 | .036 | .076 | .012 | |
| Education | Configural | 488.32 | 141 | <.001 | -- | -- | -- | .957 | -- | .055 | -- |
| Metric | 533.93 | 163 | <.001 | 45.62 | 22 | .002 | .954 | .003 | .053 | .003 | |
| Scalar | 574.05 | 175 | <.001 | 40.12 | 12 | <.001 | .951 | .003 | .053 | .000 | |
| Strict | 793.60 | 187 | <.001 | 219.55 | 12 | <.001 | .925 | .026 | .063 | .010 | |
| Time | Configural | 301.62 | 94 | <.001 | -- | -- | -- | .972 | -- | .047 | -- |
| Metric | 310.84 | 105 | <.001 | 9.22 | 11 | .602 | .972 | .000 | .044 | .003 | |
| Scalar | 346.09 | 111 | <.001 | 35.25 | 6 | <.001 | .968 | .002 | .046 | .002 | |
| Strict | 357.51 | 117 | <.001 | 11.42 | 6 | <.076 | .967 | .001 | .045 | .001 | |
Bolded rows indicate the highest level of measurement invariance evidenced by the data.
The overall model also provided a good fit across age groups, and fit remained similar when factor structure and loadings were constrained to be equal across age categories. However, a meaningful decrement in fit was found when factor structure, loadings, and intercepts were held equal based on the CFI (ΔCFI = .023). Therefore, there was evidence for metric invariance across age groups.
The overall model fit well across education categories with no clear decrease in fit when factor structure, loadings, and intercepts were held constant across education groups. However, an unacceptable decrease in fit was noted when residual variances were also held constant. Thus, there was evidence for scalar invariance across education groups.
Finally, we assessed measurement invariance across baseline and one-year follow up visits. The model fit well across time with no decrement in fit when factor structure, loadings, intercepts, and residual variances were constrained to be equal across evaluation points. Hence, there was evidence for strict invariance of the model over time.
Demographic Influences and Normative Calculator
Scores from the general, processing speed/executive, visual, memory, and attention factors were extracted using the regression-based method. Next, each factor score was regressed onto age, sex, and education. As can be seen in Table 4, age demonstrated a significant negative relationship with all cognitive factor scores, whereas education was significantly positively related to all scores. Female sex was significantly associated with better cognitive performance on the general, speed/executive, memory, and language factors. However, sex was not a significant predictor of performance on the visual and attention factors. The impact of demographic variables on cognitive factor scores ranged from small (in the case of attention and memory) to moderate or large (in the case of general abilities, processing speed/executive, visual abilities, and language abilities). The factor score calculator derived from these analyses is found in the online supplementary materials.
Table 4.
Results of Linear Regression of Cognitive Variables on Demographic Variables
| Cognitive Domain | Age | Sex | Education | |||
|---|---|---|---|---|---|---|
| Intercept | Coefficient (SE) | Coefficient (SE) | Coefficient (SE) | R2 | SE of Estimate | |
| General Factor | 1.81*** (0.40) | −0.07*** (0.00) | 0.35*** (0.08) | 0.29*** (0.02) | .20*** | 1.91 |
| Speed/Executive | 0.75*** (0.17) | −0.02*** (0.00) | 0.08** (0.03) | 0.08*** (0.01) | .17*** | 0.68 |
| Visual | 1.05*** (0.10) | −0.01*** (0.00) | −0.02 (0.02) | 0.02*** (0.00) | .08*** | 0.49 |
| Memory | 0.15 (0.27) | −0.02*** (0.00) | 0.32*** (0.06) | 0.10*** (0.01) | .06*** | 1.31 |
| Attention | 0.38 (0.23) | −0.02*** (0.00) | −0.09 (0.05) | 0.09*** (0.01) | .06*** | 1.10 |
| Language | 0.15 (0.16) | −0.02*** (0.00) | 0.23*** (0.03) | 0.09*** (.01) | .12*** | 0.78 |
Note. Male coded as 1, female coded as 2.
p < .05
p < .01
p < .001
Discussion
The goals of the current study were to examine the factor structure of the UDS3NB, establish at least metric invariance of the UDS3NB measures across demographic groups and time, and extract demographically-adjusted factor scores to create a user-friendly Excel calculator.
Factor Structure of the UDS3NB
In contrast research with the UDS2NB, which did not include tests of higher order factor models (Hayden et al., 2011), we found evidence for a higher order model of cognition when using UDS3NB data in a large national sample, consisting of lower order attention, visual, processing speed/executive, memory, and language factors, as well as a higher order general cognitive factor. This finding fits with a wealth of previous research, which suggests that a higher order model of cognition represents the best conceptualization of cognitive abilities (Reeve & Blacksmith, 2009; Schneider & McGrew, 2018). Notably, the addition of a visuconstruction and recall task in the UDS3NB battery resulted in evidence for an additional visual factor not found in the UDS2NB (Hayden et al., 2011).
Measurement Invariance
Once this best fitting structure of cognition was established, we investigated measurement invariance across demographic groups and time. Importantly, at least metric invariance was established for all variables, suggesting that factor scores can be extracted uniformly across sexes, ages, and education levels and in the context of one-year repeated evaluations. However, the level of measurement invariance differed, depending on the variable.
Findings regarding education and time were consistent with past research. Regarding education, we found evidence for scalar invariance. This result suggests that that factor structure, loadings, and intercepts are equivalent across individuals of varying levels of formal education and conforms with the results reported by Rawlings et al. (2016). Similarly, we reported evidence for strict invariance over time, replicating the findings of Hayden et al. (2011) with the UDS2NB. Thus, the measurement characteristics of the UDS3NB variables do not change in serial evaluation evaluations over a one-year time span in unimpaired older adults.
Past research on measurement invariance across sexes and age groups among older adults has been mixed, likely due to differences in the batteries administered and the recruitment criteria used to select participants. For instance, past studies found evidence for scalar (Dowling, Hermann, La Rue, & Sager, 2010), strict (Rawlings et al., 2016), or partial strict invariance (Niileksela, Reynolds, & Kaufman, 2013) across age groups. We did not replicate any of these findings, instead finding evidence for metric invariance, suggesting that loadings were equivalent across age groups but intercepts and residual variances differed. Variables most impacted by age included the memory indicators and memory factor, though allowing these intercepts to vary across demographic groups did not improve the fit of the scalar model: χ2(171) = 743.28, p < .001, CFI = .931, RMSEA = .064.
For sex, there was evidence for metric invariance, suggesting that the factor structure and loadings of the UDS3NB were equivalent for men and women, while intercepts and residual variances differed. Similar results were found in a sample of older adults administered the Atherosclerosis Risk in Communities Neurocognitive Study neuropsychological battery (Rawlings et al., 2016), though other authors have reported strict invariance of cognitive batteries by sex (Blankson & McArdle, 2015). Post-hoc examination of group differences in intercepts revealed that the largest difference occurred on the vegetable naming variable, with the intercept for women being higher than men.1 This finding may reflect gender role differences in involvement in activities requiring knowledge of vegetable names, such as meal planning, grocery shopping, and meal preparation, which have historically been completed more often by women (Harnack, Story, Martinson, Neumark-Sztainer, & Stang, 1998).
Extracted Factor Scores
After demonstrating at least metric invariance across time and demographic groups, we extracted factor scores using a regression-based approach. Extracted factor scores were associated with demographic variables in a manner consistent with prior research. Indeed, cognitive abilities are expected to decline with age (Salthouse, 2010), and all cognitive factor scores were significantly negatively related to age in the normative sample. Similarly, research consistently finds a positive correlation between years of education and cognitive performance (Lenehan, Summers, Saunders, Summers, & Vickers, 2015), and such a relationship emerged as significant for all cognitive factor scores in the normative sample.
Sex differences also emerged on the cognitive factors with female sex being associated with improved performance on the general, speed/executive, memory, and language factors. Consistent with our findings, research on sex differences in cognition tends to support the notion that women perform better than men on verbal memory tests (Ferreira, Santos‐Galduróz, Ferri, & Galduróz, 2014). However, examination of other cognitive domains has yielded mixed results (Duff, Schoenberg, Mold, Scott, & Adams, 2011; Kaplan et al., 2009; Li & Hsu, 2015; Munro et al., 2012; Proust-Lima et al., 2008; Tripathi, Kumar, Bharath, Marimuthu, & Varghese, 2014), likely to due to cultural differences, variations in statistical control, and sample selection factors. Future research using large cross-cultural samples with adequate statistical controls will lead to improved understanding of sex differences in cognitive performance.
An interesting finding regarding demographic impacts on factor scores was that the percentage of variance explained in cognitive performance was higher in our study than in past work using the UDS (Devora et al., 2019). This difference is likely due to the use of factor scores in the current research, which tend to have reduced error variance than raw scores (Thompson, 2004), allowing for improved predictive accuracy.
Importantly, the means of calculating these factor scores for individual patients has been made readily accessible through a user-friendly Excel calculator (available in the online supplementary material). This tool could reduce subjectivity in interpreting UDS3NB data in practice, though it remains to be determined whether factor scores are superior to their constituent scores for assessing cognitive decline. Additionally, given that current research criteria for defining declines prior to mild cognitive impairment suggest accounting for demographics (Jack et al., 2018), the scoring spreadsheet represents an important tool for the research community. Future research may replicate this method with past versions of the UDS to ensure continuity across the batteries and associated datasets.
Limitations
Findings are interpreted in the context of the study’s limitations. One difficulty in calculating factor scores concerns the method of factor extraction. We used a regression-based approach for several reasons. First, the regression-based method is superior to coarse factor score methods, such as summing scaled scores or averaging test scores (DiStefano, Zhu, & Mindrila, 2009; Grice, 2001). Second, this factor score calculation method can be easily understood without advanced statistical knowledge. And third, the regression-based approach can be readily transferred to a user-friendly Excel calculator. This feature eliminates the need for complex and/or expensive statistical software and increases the likelihood of adoption by a broad base of professionals. However, it must be acknowledged that the regression-based method has some disadvantages (e.g., it may fail to replicate orthogonal relationships specified in the original model), such that future research may fruitfully explore alternative means of factor extraction.
A second limitation concerns the variables used to diagnose individuals as cognitively normal in the study. Indeed, while the CDR provides a diagnosis of cognitively normal based on interview data, it is recognized that individuals rated as normal on this scale occasionally demonstrate subtle cognitive impairments on formal testing. This concern is somewhat ameliorated by the simultaneous use of a second criterion to define normality, the UDS consensus diagnosis. Of course, this method has its own limitations, including the possibility of criterion contamination, given that consensus diagnoses in the UDS are based in part on the UDS3NB data. Two important points reduce the concern for criterion contamination. First, consensus raters also based their conclusions on a host of other available information, including patient demographic background, medical history, known dementia risk factors, and data gathered at the clinical interviews with the patients and caregivers. Second, raters did not have access to the factor score data utilized in the current analysis. Still, it will be important to replicate the current findings in an independent sample, in which diagnoses are not based on neuropsychological data.
On a related note, researchers and clinicians are cautioned against utilizing the factor scores in populations with known cognitive impairments. Indeed, concern has been raised in past research about our ability to generalize factor models from normal to clinical populations, as measurement properties may change in these different groups (Delis, Jacobson, Bondi, Hamilton, & Salmon, 2003; Jacobson, Delis, Hamilton, Bondi, & Salmon, 2004). Future research will examine the factor structure of the UDS3NB in clinical samples, as well as the utility of factor scores in these groups.
A final limitation of this research concerns the UDS sample characteristics. Given that the sample includes primarily older, white participants, factor scores may not be as applicable to younger adults and individuals of minority backgrounds. Regarding age, the UDS3NB is simply not designed for data collection in a younger population at this time. It may be modified in the future as attempts to capture the very earliest cognitive signs of neurodegenerative disease emerge, while efforts to expand the diversity of data collection with at Alzheimer’s Disease Research Centers are ongoing.
Conclusions
These limitations are balanced by the manuscripts many strengths, including use of a large national sample to investigate the factor structure of the UDS3NB, comprehensive invariance testing across demographic groups and time, and creation of a user-friendly Excel calculator for deriving demographically-adjusted factor scores. Our findings provide evidence for a higher order factor structure of the UDS3NB and demonstrate an easily accessible means of extracting and demographically correcting factor scores for use in research and applied settings. Future studies will replicate these findings in clinical samples and provide evidence for the psychometric properties of factor scores.
Supplementary Material
Acknowledgements
The NACC database is funded by NIA/NIH Grant U01 AG016976. NACC data are contributed by the NIA-funded ADCs: P30 AG019610 (PI Eric Reiman, MD), P30 AG013846 (PI Neil Kowall, MD), P50 AG008702 (PI Scott Small, MD), P50 AG025688 (PI Allan Levey, MD, PhD), P50 AG047266 (PI Todd Golde, MD, PhD), P30 AG010133 (PI Andrew Saykin, PsyD), P50 AG005146 (PI Marilyn Albert, PhD), P50 AG005134 (PI Bradley Hyman, MD, PhD), P50 AG016574 (PI Ronald Petersen, MD, PhD), P50 AG005138 (PI Mary Sano, PhD), P30 AG008051 (PI Thomas Wisniewski, MD), P30 AG013854 (PI Robert Vassar, PhD), P30 AG008017 (PI Jeffrey Kaye, MD), P30 AG010161 (PI David Bennett, MD), P50 AG047366 (PI Victor Henderson, MD, MS), P30 AG010129 (PI Charles DeCarli, MD), P50 AG016573 (PI Frank LaFerla, PhD), P50 AG005131 (PI James Brewer, MD, PhD), P50 AG023501 (PI Bruce Miller, MD), P30 AG035982 (PI Russell Swerdlow, MD), P30 AG028383 (PI Linda Van Eldik, PhD), P30 AG053760 (PI Henry Paulson, MD, PhD), P30 AG010124 (PI John Trojanowski, MD, PhD), P50 AG005133 (PI Oscar Lopez, MD), P50 AG005142 (PI Helena Chui, MD), P30 AG012300 (PI Roger Rosenberg, MD), P30 AG049638 (PI Suzanne Craft, PhD), P50 AG005136 (PI Thomas Grabowski, MD), P50 AG033514 (PI Sanjay Asthana, MD, FRCP), P50 AG005681 (PI John Morris, MD), P50 AG047270 (PI Stephen Strittmatter, MD, PhD)
Funding: This work was supported by an Alzheimer’s Association Research Fellowship (2019AARF-641693 PI Andrew Kiselica, PhD) and the 2019–2020 National Academy of Neuropsychology Clinical Research Grant (PI Andrew Kiselica, PhD).
Footnotes
Conflicts of Interest: The authors have no conflicts of interest to disclose.
Allowing this intercept to differ across groups led to a substantial improvement in fit of the scalar model: χ2(110) = 558.02, p < .001, CFI = .949, RMSEA = .058. However, fit still remained worse than that of the metric model. Release of the intercept constraint for the variable with the next highest group difference (the MINT) did not result in further improvement in fit, such that further investigation of partial scalar invariance was terminated.
References
- American Educational Research Association, American Psychological Association, National Council on Measurement in Education, & Joint Committee on Standards for Educational and Psychological Testing. (2014). The Standards for Educational and Psychological Testing. Washington, D.C.: AERA. [Google Scholar]
- Besser L, Kukull W, Knopman DS, Chui H, Galasko D, Weintraub S, … Quinn J. (2018). Version 3 of the National Alzheimer’s Coordinating Center’s Uniform Data Set. Alzheimer Disease and Associated Disorders, 32(4), 351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blankson AN, & McArdle JJ (2015). Measurement Invariance of Cognitive Abilities Across Ethnicity, Gender, and Time Among Older Americans. Journals of Gerontology Series B-Psychological Sciences and Social Sciences, 70(3), 386–397. doi: 10.1093/geronb/gbt106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen FF (2007). Sensitivity of goodness of fit indexes to lack of measurement invariance. Structural Equation Modeling: A Multidisciplinary Journal, 14(3), 464–504. [Google Scholar]
- Cheung GW, & Rensvold RB (2002). Evaluating goodness-of-fit indexes for testing measurement invariance. Structural equation modeling, 9(2), 233–255. [Google Scholar]
- Craft S, Newcomer J, Kanne S, Dagogo-Jack S, Cryer P, Sheline Y, … Alderson A (1996). Memory improvement following induced hyperinsulinemia in Alzheimer’s disease. Neurobiology of Aging, 17(1), 123–130. [DOI] [PubMed] [Google Scholar]
- Cronbach LJ, & Meehl PE (1955). Construct validity in psychological tests. Psychological Bulletin, 52(4), 281. [DOI] [PubMed] [Google Scholar]
- Cummings J, Lee G, Ritter A, Sabbagh M, & Zhong K (2019). Alzheimer’s disease drug development pipeline: 2019. Alzheimer’s & Dementia: Translational Research & Clinical Interventions, 5, 272–293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delis DC, Jacobson M, Bondi MW, Hamilton JM, & Salmon DP (2003). The myth of testing construct validity using factor analysis or correlations with normal or mixed clinical populations: Lessons from memory assessment. Journal of the International neuropsychological Society, 9(6), 936–946. [DOI] [PubMed] [Google Scholar]
- Devora PV, Beevers S, Kiselica AM, & Benge JF (2019). Normative data for derived measures and discrepancy scores for the Uniform Data Set 3.0 Neuropsychological Battery. Archives of Clinical Neuropsychology, epublication ahead of print. doi: 10.1093/arclin/acz025 [DOI] [PMC free article] [PubMed] [Google Scholar]
- DiStefano C, Zhu M, & Mindrila D (2009). Understanding and using factor scores: Considerations for the applied researcher. Practical assessment, research & evaluation, 14(20), 1–11. [Google Scholar]
- Dowling NM, Hermann B, La Rue A, & Sager MA (2010). Latent Structure and Factorial Invariance of a Neuropsychological Test Battery for the Study of Preclinical Alzheimer’s Disease. Neuropsychology, 24(6), 742–756. doi: 10.1037/a0020176 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duff K, Schoenberg MR, Mold JW, Scott JG, & Adams RL (2011). Gender differences on the Repeatable Battery for the Assessment of Neuropsychological Status subtests in older adults: Baseline and retest data. Journal of Clinical and Experimental Neuropsychology, 33(4), 448–455. doi: 10.1080/13803395.2010.533156 [DOI] [PubMed] [Google Scholar]
- Ferreira L, Santos‐Galduróz RF, Ferri CP, & Galduróz JCF (2014). Rate of cognitive decline in relation to sex after 60 years‐of‐age: A systematic review. Geriatrics & Gerontology International, 14(1), 23–31. doi: 10.1111/ggi.12093 [DOI] [PubMed] [Google Scholar]
- Fillenbaum G, Peterson B, & Morris J (1996). Estimating the validity of the Clinical Dementia Rating scale: the CERAD experience. Aging Clinical and Experimental Research, 8(6), 379–385. [DOI] [PubMed] [Google Scholar]
- Gavett BE, Vudy V, Jeffrey M, John SE, Gurnani AS, & Adams JW (2015). The δ latent dementia phenotype in the uniform data set: Cross-validation and extension. Neuropsychology, 29(3), 344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gollan TH, Weissberger GH, Runnqvist E, Montoya RI, & Cera CM (2012). Self-ratings of spoken language dominance: A Multilingual Naming Test (MINT) and preliminary norms for young and aging Spanish–English bilinguals. Bilingualism: Language and Cognition, 15(3), 594–615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goodglass H, Kaplan E, & Barresi B (2000). Boston Diagnostic Aphasia Examination Record Booklet. Philadelphia, PA: Lippincott Williams & Wilkins. [Google Scholar]
- Grice JW (2001). Computing and evaluating factor scores. Psychological Methods, 6(4), 430. [PubMed] [Google Scholar]
- Harnack L, Story M, Martinson B, Neumark-Sztainer D, & Stang J (1998). Guess who’s cooking? The role of men in meal planning, shopping, and preparation in US families. Journal of the American Dietetic Association, 98(9), 995–1000. [DOI] [PubMed] [Google Scholar]
- Hayden KM, Jones RN, Zimmer C, Plassman BL, Browndyke JN, Pieper C, … Welsh-Bohmer KA (2011). Factor structure of the National Alzheimer’s Coordinating Centers uniform dataset neuropsychological battery: An evaluation of invariance between and within groups over time. Alzheimer Disease and Associated Disorders, 25(2), 128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hayden KM, Kuchibhatla M, Romero HR, Plassman BL, Burke JR, Browndyke JN, & Welsh-Bohmer KA (2014). Pre-clinical cognitive phenotypes for Alzheimer disease: A latent profile approach. The American Journal of Geriatric Psychiatry, 22(11), 1364–1374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henry JD, & Crawford JR (2004). A meta-analytic review of verbal fluency performance following focal cortical lesions. Neuropsychology, 18(2), 284. [DOI] [PubMed] [Google Scholar]
- Hooper D, Coughlan J, & Mullen M (2008). Structural equation modelling: Guidelines for determining model fit. Journal of Business Research Methods, 6(1), 53–60. [Google Scholar]
- Hu L. t., & Bentler PM (1999). Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Structural equation modeling, 6(1), 1–55. doi: 10.1080/10705519909540118 [DOI] [Google Scholar]
- IBM Corp. (2017). SPSS Statistics 25.0. Armonk, NY. [Google Scholar]
- Ivanova I, Salmon DP, & Gollan TH (2013). The multilingual naming test in Alzheimer’s disease: clues to the origin of naming impairments. Journal of the International neuropsychological Society, 19(3), 272–283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jack CR, Bennett DA, Blennow K, Carrillo MC, Dunn B, Haeberlein SB, … Silverberg N (2018). NIA-AA Research Framework: Toward a biological definition of Alzheimer’s disease. Alzheimers & Dementia, 14(4), 535–562. doi: 10.1016/j.jalz.2018.02.018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jacobson MW, Delis DC, Hamilton JM, Bondi MW, & Salmon DP (2004). How do neuropsychologists define cognitive constructs? Further thoughts on limitations of factor analysis used with normal or mixed clinical populations. Journal of the International neuropsychological Society, 10(7), 1020–1021. [Google Scholar]
- Jensen AR (1998). The g factor: The science of mental ability. Wesport, CT: Praeger Publishers. [Google Scholar]
- Kaplan RF, Cohen RA, Moscufo N, Guttmann C, Chasman J, Buttaro M, … Wolfson L (2009). Demographic and biological influences on cognitive reserve. Journal of Clinical and Experimental Neuropsychology, 31(7), 868–876. doi: 10.1080/13803390802635174 [DOI] [PubMed] [Google Scholar]
- Kiselica AM, Kaser A, & Benge JF (in preparation). An initial empirical operationalization of the earliest stages of the Alzheimer’s Continuum. [DOI] [PMC free article] [PubMed]
- Kiselica AM, Webber TA, & Benge JF (under review). Multivariate base rates of low scores in the Uniform Data Set 3.0 Neuropsychological Battery: Normative data and predictive validity for cognitive decline. [DOI] [PMC free article] [PubMed]
- Kline RB (2011). Principles and practice of structural equation modeling (3rd ed.). New York, NY, US: Guilford Press. [Google Scholar]
- Lenehan ME, Summers MJ, Saunders NL, Summers JJ, & Vickers JC (2015). Relationship between education and age‐related cognitive decline: A review of recent research. Psychogeriatrics, 15(2), 154–162. [DOI] [PubMed] [Google Scholar]
- Lezak M, Howieson D, & Loring D (2012). Neuropsychological assessment (5th ed.). New York, NY: Oxford. [Google Scholar]
- Li C-L, & Hsu H-C (2015). Cognitive function and associated factors among older people in Taiwan: Age and sex differences. Archives of Gerontology and Geriatrics, 60(1), 196–200. doi: 10.1016/j.archger.2014.10.007 [DOI] [PubMed] [Google Scholar]
- Little TD (1997). Mean and covariance structures (MACS) analyses of cross-cultural data: Practical and theoretical issues. Multivariate behavioral research, 32(1), 53–76. [DOI] [PubMed] [Google Scholar]
- Monsell SE, Dodge HH, Zhou X-H, Bu Y, Besser LM, Mock C, … Weintraub S (2016). Results from the NACC Uniform Data Set neuropsychological battery Crosswalk Study. Alzheimer Disease and Associated Disorders, 30(2), 134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morris JC (1993). The Clinical Dementia Rating (CDR): Current version and scoring rules. Neurology, 43(11), 2412. [DOI] [PubMed] [Google Scholar]
- Morris JC (1997). Clinical dementia rating: a reliable and valid diagnostic and staging measure for dementia of the Alzheimer type. International psychogeriatrics, 9(S1), 173–176. [DOI] [PubMed] [Google Scholar]
- Munro CA, Winicki JM, Schretlen DJ, Gower EW, Turano KA, Muñoz B, … West SK (2012). Sex differences in cognition in healthy elderly individuals. Aging, Neuropsychology, and Cognition, 19(6), 759–768. doi: 10.1080/13825585.2012.690366 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Niileksela CR, Reynolds MR, & Kaufman AS (2013). An Alternative Cattell-Horn-Carroll (CHC) Factor Structure of the WAIS-IV: Age Invariance of an Alternative Model for Ages 70–90. Psychological Assessment, 25(2), 391–404. doi: 10.1037/a0031175 [DOI] [PubMed] [Google Scholar]
- Partington JE, & Leiter RG (1949). Partington Pathways Test. Psychological Service Center Journal, 1, 11–20. [Google Scholar]
- Possin KL, Laluz VR, Alcantar OZ, Miller BL, & Kramer JH (2011). Distinct neuroanatomical substrates and cognitive mechanisms of figure copy performance in Alzheimer’s disease and behavioral variant frontotemporal dementia. Neuropsychologia, 49(1), 43–48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Proust-Lima C, Amieva H, Letenneur L, Orgogozo J-M, Jacqmin-Gadda H, & Dartigues J-F (2008). Gender and education impact on brain aging: A general cognitive factor approach. Psychology and Aging, 23(3), 608–620. doi: 10.1037/a0012838.supp [DOI] [PubMed] [Google Scholar]
- Rawlings AM, Bandeen-Roche K, Gross AL, Gottesman RF, Coker LH, Penman AD, … Mosley TH (2016). Factor Structure of the ARIC-NCS Neuropsychological Battery: An Evaluation of Invariance Across Vascular Factors and Demographic Characteristics. Psychological Assessment, 28(12), 1674–1683. doi: 10.1037/pas0000293 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reeve CL, & Blacksmith N (2009). Identifying g: A review of current factor analytic practices in the science of mental abilities. Intelligence, 37(5), 487–494. doi: 10.1016/j.intell.2009.06.002 [DOI] [Google Scholar]
- Rosseel Y (2012). Lavaan: An R package for structural equation modeling and more. Version 0.5–12 (BETA). Journal of Statistical Software, 48(2), 1–36. [Google Scholar]
- RStudio Team. (2015). RStudio: Integrated development for R. Boston, MA: RStudio, Inc; Retrieved from http://www.rstudio.com/ [Google Scholar]
- Salthouse TA (2010). Selective review of cognitive aging. Journal of the International neuropsychological Society, 16(5), 754–760. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schneider WJ, & McGrew KS (2018). The Cattell-Horn-Carroll theory of cognitive abilities In Flanagan DP & McDonough EM (Eds.), Contemporary intellectual assessment: Theories, tests, and issues (4th ed., pp. 73–163). New York, NY: The Guilford Press. [Google Scholar]
- Shin MS, Park SY, Park SR, Seol SH, & Kwon JS (2006). Clinical and empirical applications of the Rey-Osterrieth Complex Figure Test. Nature Protocols, 1(2), 892–899. doi: 10.1038/nprot.2006.115 [DOI] [PubMed] [Google Scholar]
- Shirk SD, Mitchell MB, Shaughnessy LW, Sherman JC, Locascio JJ, Weintraub S, & Atri A (2011). A web-based normative calculator for the Uniform Dataset (UDS) neuropsychological test battery. Alzheimer’s research & therapy, 3(6), 32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson B (2004). Exploratory and confirmatory factor analysis: Understanding concepts and applications. Washington, D.C.: American Psychological Association. [Google Scholar]
- Thompson B, & Daniel LG (1996). Factor analytic evidence for the construct validity of scores: A historical overview and some guidelines: Sage Publications Sage CA: Thousand Oaks, CA. [Google Scholar]
- Tripathi R, Kumar K, Bharath S, Marimuthu P, & Varghese M (2014). Age, education and gender effects on neuropsychological functions in healthy Indian older adults. Dementia & Neuropsychologia, 8(2), 148–154. doi: 10.1590/S1980-57642014DN82000010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- van de Schoot R, Lugtig P, & Hox J (2012). A checklist for testing measurement invariance. European Journal of Developmental Psychology, 9(4), 486–492. doi: 10.1080/17405629.2012.686740 [DOI] [Google Scholar]
- Varjacic A, Mantini D, Demeyere N, & Gillebert CR (2018). Neural signatures of Trail Making Test performance: evidence from lesion-mapping and neuroimaging studies. Neuropsychologia, (115), 78–87. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wechsler D (1987). Wechsler Memory Scale-Revised Manual. San Antonio, TX: The Psychological Corporation. [Google Scholar]
- Wechsler D (2008). Wechsler Adult Intelligence Scale–Fourth Edition (WAIS–IV): San Antonio, TX: The Psychological Corporation. [Google Scholar]
- Weintraub S, Besser L, Dodge HH, Teylan M, Ferris S, Goldstein FC, … Marson D (2018). Version 3 of the Alzheimer Disease Centers’ Neuropsychological Test Battery in the Uniform Data Set (UDS). Alzheimer Disease and Associated Disorders, 32(1), 10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weintraub S, Salmon D, Mercaldo N, Ferris S, Graff-Radford NR, Chui H, … Galasko D (2009). The Alzheimer’s disease centers’ uniform data set (UDS): The neuropsychological test battery. Alzheimer Disease and Associated Disorders, 23(2), 91. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.