A reactive phase against disruptions for designing a proactive platelet supply network

Highlights

• •Proposing a novel mathematical formulation to design a platelet network.
• •Considering lateral transshipment strategy between hospitals.
• •Devising a reactive phase in order to update the planning of the platelet network.
• •Coping with the hybrid risk by utilizing a fuzzy-stochastic programming approach.
• •Applying a real case to evaluate the practicality of the proposed model.

Abstract

Previous studies in blood supply chain network design often follow a commonly used approach in protecting the chain against disruptions, considering the effects of disruptions on the designing phase. However, in many real-world situations, disruptions cannot be adequately measured in advance. Moreover, using disruptions in the designing phase through the common two-stage stochastic programming models impose high costs on the network, since they cannot be updated based on unpredicted disruptions. This paper proposes an updatable two-phase approach which deals with disruptions in the operational phase, not in the strategic design phase. In the first step, called the proactive phase, a nominal platelet supply chain network is designed under operational uncertainty, using the whole-blood collection method. In the event of disruptions, the second step, called the reactive phase, is applied, and the tailored network is updated based on the realized data, using apheresis as the collection mechanism. The operational risks are captured using a fuzzy programming approach in the model. Based on the real data from Fars province of Iran, we compare the performance of the two-phase approach with the commonly used approaches in the literature, resulting in more flexible decisions, and consequently, less conservatism degree rather than the existing approaches.

1. Introduction

Population ageing is a global phenomenon, and almost all countries are experiencing an increased rate of elderly in their population, which is predicted to be near 2.1 billion by 2050 (World Population Ageing 2017). As population ages, the demand for health services and medical interventions increases, and consequently, high health expenditure is borne by society (World population ageing 2013, 2014). Blood transfusions, as a dispensable part of health care services, will be affected by this demographic transition, and blood transfusion rate will grow significantly thereafter. Furthermore, population ageing, particularly donors ageing, will cause a serious shortfall in the blood donor pools, and it is not guaranteed that the higher rate of need for blood transfusion could be met by younger cohort. The drop in donor population and growth of blood demand are of considerable concern for blood centers; therefore, an efficient plan for the management of blood transfusion services is of great significance.

Every efficient health care system needs to have access to sufficient and safe blood transfusion for doing routine medical treatments or surgeries. Blood is typically collected in whole blood form which is separated into various components, including red blood cells, plasma, platelet, and cryoprecipitate. Blood platelets are the most expensive product of whole blood, with the complication of having an extremely short life span of only seven days. Platelets are collected from donors through all aspects of testing, production, storage, and distribution for transfusion usages in hospitals. The platelet transfusion has a broad range of usage in therapies, including chemotherapy and bone marrow transplants, and treatment for peripheral vascular disease and coronary artery disease, as one of the leading causes of death in developing countries (Ensafian and Yaghoubi, 2017). Also, recently, most countries faced an unexpected challenge as coronavirus (COVID-19) outbreak, and the significant number of people around the world have infected with this virus (Choi, 2020, Govindan et al., 2020). COVID-19 has taken the lives of more than 235,000 people as of May 1, 2020 (Worldometers, 2020), and it caused severe social and economic consequences around the globe (Ivanov, 2020). Thus, researchers intend to treat this disease by developing vaccines to protect people from COVID-19. The researchers have discovered that blood and its products can be used to develop Coronavirus vaccines (Chang et al., 2020). Therefore, the efficient supply of blood and platelet can be a critical concern to cope with this situation.

Platelets can be extracted from the whole blood donation or through apheresis procedure. In the whole blood collection method, blood is drawn by phlebotomy from a donor and is collected in a set of bags. There are several bag systems for blood collection, which vary in the number of attached bags. Bag selection depends on the types of needed components. Based on the selected bag, the time and speed of centrifugation are determined; thereafter, the whole blood is separated into the desired products. In the apheresis collection procedure, the whole blood is drawn from the donor, and the specific blood components, such as red blood cells, plasma, or platelet, are extracted from the donor’s blood while the remaining is returned to the donor’s body. An apheresis-derived platelet unit is equivalent to 6–8 whole-blood-derived platelet units. Furthermore, an apheresis-derived platelet has significant advantages compared with the whole-blood-derived platelet, including decreased donor exposure, decreased risk of being infected with the transfusion-transmitted diseases, relative ease of detecting bacterial contamination, and fewer hospital preparations (Van Der Meer, 2012). However, apheresis is high-expense and time-consuming process, and special eligibility criteria are required for apheresis platelet donors. Therefore, most of the donors are unwilling to donate blood through the apheresis method (Ensafian and Yaghoubi, 2017).

Apheresis platelet collection can be conducted in production centers (PCs) and collection-based hospitals, and due to requiring fewer preparations and testing procedures, the collected platelet can be transfused during the collection day (Vassallo and Murphy, 2006); whereby, the collected whole blood undergoes scrutinized testing and screening process, which lasts about two days. This mandatory testing process further exacerbates the perishability issue, and in practice, transfusable whole-blood-derived platelets will have a five-day shelf life after being delivered to hospitals.

Managing platelet inventory has been a critical issue in blood centers due to the dominating characteristics of this product, including extremely short lifetime, demand and supply uncertainty, and multiple ways of collection and fractionation methods. The supply of the platelet is solely dependent on people’s willingness to donate blood, and consequently, it will face uncertainty (Wang and Ma, 2015). In the demand side, although hospitals can estimate platelet demand due to planned surgeries and transfusions, additional demands arise randomly from traumas, accidents, and public health emergencies (Nagurney and Dutta, 2019). The mismatch between demand and supply, which results in wastage or shortage of platelet places a substantial social and economic burden on hospitals and blood centers. These issues have heightened the need to reconsider the platelet inventory management in such a way that the components of blood supply chains (BSCs) interact in a coordinated way to minimize platelet shortage and outdated rate.

Lateral transshipment is a practical strategy that can improve the flexibility of the platelet supply chain (PSC) management. In this strategy, the unused platelet units in a hospital are shared with another hospital to preclude it from facing stock-out situations. Accordingly, the transshipment strategy can enhance supply chain performance while reducing costs (Wang and Ma, 2015).

Supply chains experience disruptions due to natural disasters, such as extreme weather events, floods, and earthquakes, or man-made threats, e.g., explosions, power outages, and political instability (Chiu and Choi, 2016, Xu et al., 2020). Disruptions can affect the capacity of facilities, the number of produced units, number of satisfied demands, and consequently, they are influential in the financial and operational performance of supply chains (Hendricks et al., 2019, Liang et al., 2019). Based on the EventWatch report, 2,629 disruptive events occurred in 2018 which affected 552,950 parts of different supply chains around the world. Also, this report revealed that only 12% of the supply chains that are under the threat of disruptions have provided strategies to deal with (Khan and Perez, 2019). In the same way, BSCs and PSCs are prone to disruptions; since they are related to human lives, special attention should be paid to prevent the serious repercussions of disruptions for such networks. Severe damage to blood infrastructures in Bam earthquake in Iran (2003), damage to blood testing equipment in Great East Japan Earthquake (2011), the strike of blood banking employees in Berhampur and Odisha in India (2018), the power outage in Khorasan transfusion center in Iran (2018), the explosion of Sanaa blood bank in Yemen (2018), financial problems in Kenya blood transfusion service (2019), and disruption in blood supplies in the USA due to bomb cyclone, hurricanes Florence and Michael (2018) are reminders of potential disruptions that can affect the performance of the PSCs. Such unforeseen disruptions occur rarely, and they are different in their types and scales. Besides, there are incomplete or no historical data about them (Hosseini et al., 2019). However, such disruptions do occur; meanwhile, the network is not adequately proper for them. Therefore, managers and decision-makers should take efficient strategies to control the effects of disruptive events. In the recent studies provided by some researchers, such as Samani and Hosseini-Motlagh, 2019, Hosseini-Motlagh et al., 2020a, and (Hosseini-Motlagh et al. 2020b), proactive strategies were proposed to deal with disruptions in BSCs. These strategies, such as redundancy and flexibility in capacities and considering backup facilities in the network, are used to protect the network against disruptions and increase the robustness of the network (Xu et al., 2020). Proactive strategies aim to absorb disruptions and lessen their effects; however, shortages will occur if proactive strategies cannot harness the disruption thoroughly. In these situations, reactive strategies should be implemented to adapt the network and respond to the shortages arisen from disruptive events immediately. To do so, we proposed a two-phase approach by exploiting proactive and reactive strategies to handle uncertainties and production disruptions in PSCs. The main questions of this paper are as follows:

• •How to manage the PSC so that the total costs are minimized and the shortage and outdated rates are reduced?
• •How to manage irregular platelet production stemmed from disruptions?
• •How to exploit multiple collection and fractionation methods of blood to manage the PSC efficiently?
• •How to cope with uncertainties and mitigate their effects on demand and supply mismatch?

This study contributes to the existing literature from several points of view. First, we present an age-based mathematical formulation for designing a PSC network. The model captures the perishability of the platelet and incorporates several blood fractionation methods and uncertainty in demand, supply, and cost. From the modeling point of view, the research provided by Ensafian and Yaghoubi (2017) is the most relevant to our work; however, the structure of the investigated supply chain in this study is different, and this study addresses location and capacity decisions, along with allocation and inventory decisions. Second, we propose a reactive strategy to cope with disruptions that occur in the designed network. Based on the reviewed literature in the field of BSCs, a few studies considered disruption risks in their networks, none of which used reactive strategies to deal with disruptions. In some studies (see, e.g. Hasani and Khosrojerdi, 2016, Ivanov et al., 2016, Zhao et al., 2019), some reactive strategies were proposed; however, these studies are not in the field of BSC and PSC, and the performance and structure of their proposed approach are different in comparison with our proposed reactive strategy. In this strategy, we use a mathematical formulation similar to the model of the first phase in which the blood is collected by the apheresis method. The reasons for using the apheresis collection method in this phase are twofold. First, an apheresis-derived platelet unit equals 6–8 whole-blood-derives platelet units, and a few numbers of donors will be required to meet the demand. Second, the apheresis-derived platelet needs fewer testing and production processes, and consequently, it can meet demands on time under disruptive conditions. Moreover, the lateral transshipment policy is utilized in this phase to improve the performance of the network. Besides, we apply a fuzzy stochastic approach to cope with operational risks (uncertainty in demand, supply, and costs). This approach increases the degree of the complexity of the problem less than other approaches and handles a large number of uncertain parameters. Finally, the proposed two-phase approach is applied to a real case of Fars province, and its results are compared with the results of the most commonly used approaches in the literature. The main contributions of this paper are categorized as follows:

• •Proposing a mixed-integer mathematical programming formulation to design PSC network considering perishability of blood products, several collection and fractionation methods, several disruption scenarios, and uncertainty in parameters such as demand, supply, and cost;
• •Considering lateral transshipment strategy between hospitals;
• •Devising a reactive phase in order to update the planning of the PSC in the event of disruptions;
• •Coping with the hybrid risk stemmed from imprecise parameters and disruptions by utilizing a fuzzy-stochastic programming approach;
• •Applying a real case to evaluate the practicality of the proposed model.

The remainder of the paper is organized as follows. In Section 2, the related literature is reviewed. After that, the problem description is presented in Section 3. The solution approach and a real case study are provided in Section 4 and Section 5. Section 6 represents the results, and finally, the paper is concluded in Section 7.

2. Literature review

In this section, the most relevant recent works in the fields of designing and managing BSCs, especially PSCs, are reviewed. Several review papers have been published which investigate the BSCs from different aspects. Beliën and Forcé (2012) studied the papers related to inventory and management of BSCs, including papers up to 2010, and they classified the papers using different perspectives. In another work, Osorio et al. (2015) published a review paper, including papers up to 2014, in which the papers were categorized based on the echelons of BSCs and decisions related to each echelon were addressed. In the recent work by Pirabán et al. (2019), papers devoted to BSCs, including papers up to 2019, are classified based on several aspects such as network structures, decision makings, processes, inventory management, and data characteristics.

In this paper, we designed a PSC in the first phase. Then, the shortage (including the shortage of the first phase arisen from the fluctuations in platelet demand and supply, along with the shortage due to disruptions) was satisfied by collecting platelet through the apheresis method, and the platelet inventory was managed in the second phase. Therefore, we classified the most relevant papers into two main categories: blood supply chain network (BSCN) design and blood inventory management.

2.1. Blood supply chain network design

Several papers in the literature investigated the BSCN design problem to address optimal decisions over the supply chain. Ramezanian and Behboodi (2017) investigated a BSCN design for locating blood collection facilities considering demand, supply, and cost uncertainties. They analyzed the effect of social aspects such as advertising and donors’ experiences on donors’ behavior and used a robust optimization approach to capture uncertainties. Zahiri and Pishvaee (2017) presented a mixed-integer mathematical model to design a BSCN which locates collection centers (CCs) and PCs. They developed a robust possibilistic approach to capture uncertainties in cost, demand, and supply. Diabat et al. (2019) tailored a supply chain for managing the supply of perishable products in normal and emergency conditions. They proposed a mixed-integer mathematical model to determine optimal location, allocation, and routing decisions. Also, a robust programming approach was employed to cope with uncertainty, and the location of warehouses is determined by solving the model. Eskandari-Khanghahi et al. (2018) proposed a mathematical model to address a PSC network design integrated with sustainability which locates temporary and fixed CCs and PCs. They deployed a fuzzy possibilistic programming approach to handle imprecise parameters and utilized a meta-heuristic algorithm to solve the model.

Heidari-Fathian and Pasandideh (2018) investigated the problem of environmental pollutions in a BSC in which the blood collection facilities are located. A robust optimization approach is applied to the model to capture demand and supply uncertainty, and they exploited the Lagrangian relaxation approach to solve the model. Rahmani (2019) designed a BSCN to address strategic and tactical decisions under uncertainties stemmed from imprecise parameters and disruptions. The optimal location of blood collection facilities is determined by solving the model, and the Lagrangian relaxation algorithm is utilized to solve it.

Osorio et al. (2018b) investigated the impact of centralization on the performance of the BSCN. They suggested a mathematical model that addresses location-allocation and capacity decisions. The model determined the location of CCs, PCs, and distribution centers of blood products, and several collection and separation methods were considered in the model. Samani and Hosseini-Motlagh (2019) designed a BSCN to investigate the effect of disruption and operational risks on the performance of the presented network in which the optimal location of CCs is determined. To avoid supply shortage, they considered backup facilities and utilized a p-robust approach to reduce disruption risks in blood production facilities, and they used a fuzzy robust programming approach to deal with imprecise parameters.

In another work, Samani et al. (2019) presented a multi-objective mathematical model to design a BSCN which locates CCs, PCs, and distribution centers, and they also used a robust optimization approach to cope with uncertainty. Hamdan and Diabat (2019) developed a two-stage stochastic programming approach to manage an integrated red blood cells supply chain considering demand and supply uncertainty. The proposed model seeks to determine optimal locations of temporary blood collection facilities.

Haeri et al. (2020) utilized resiliency measure and motivational social aspects in their proposed mathematical formulation to designing a BSCN in which optimal locations of blood CCs, PCs, distribution centers are determined. They also utilized a robust optimization approach to handle uncertainties. Hosseini-Motlagh et al. (2020b) designed a red blood cell supply chain network considering demand uncertainty and disruption risk, and they also used a robust optimization approach to deal with combinatorial risk. Also, the optimal location of mobile blood centers is determined by solving the model. In another work, Hosseini-Motlagh et al. (2020a) proposed a model to design a BSCN considering hybrid risks arisen from imprecise data and disruptions which locates collection, production, and distribution centers. They investigated the impact of factors such as advertisements, medical credits, and education on donors’ motivation, and they also utilized a robust programming approach to cope with hybrid risks.

2.2. Blood inventory management

Wang and Ma (2015) presented an age-based transshipment policy for managing blood inventory at blood banks during shortage situations. They classified blood products into two groups according to their ages and investigated its impact on the transshipment decision-makings. Osorio et al. (2017) developed a simulation–optimization model in which discrete event simulation is coupled with an integer linear model to evaluate the optimal inventory policy at PCs. The optimization model is used to determine strategic decisions such as the number of donors and the efficient collection methods. Daily operations of blood centers are also determined by the simulation model. Ensafian et al. (2017) presented a mathematical model to manage inventory of platelet at PCs considering demand and supply uncertainty. First, they used a discrete Markov chain model to predict blood supply; then, they exploited a two-stage stochastic programming approach to deal with demand uncertainty.

In another work, Ensafian and Yaghoubi (2017) presented several models for managing the platelet inventory at PCs and hospitals, including a single objective programming model based on LIFO policy to minimize total cost, a single objective model based on FIFO policy to minimize total cost, a bi-objective model to minimize total cost and maximize the freshness of platelet units, and a bi-objective stochastic model to minimize total cost and maximize the freshness of platelet units. Rajendran and Ravindran (2017) proposed a stochastic programming approach to determine an optimal ordering policy for managing platelet inventory at hospitals considering demand uncertainty, cost prioritization, and size of hospitals.

Gilani Larimi et al. (2019) presented a model to manage a PSC which determines the optimal inventory level at PCs and evaluates the discard rate of platelets at PCs based on several factors such as laboratory hygiene and staff errors. They implemented a robust-stochastic approach to hedge against uncertainty, and the Monte Carlo sampling approach was utilized to determine the number of scenarios. Chen et al. (2019) presented a stochastic dynamic programming approach to investigate the impact of joint decision-making on whole blood collection and platelet production and obtain the optimal collection, production, inventory, and disposal policies at PCs. Paul et al. (2019) developed an inventory model for the management of red blood cells supply chain. They employed strategies such as consignment policies and assigning subsidy to encourage hospital authorities to report their demands honestly and without the temptation to exaggerate their needs.

Blood can be collected by whole blood or apheresis donation methods. The apheresis-derived blood products expense more than whole-blood-derived products; however, the efficiency of apheresis-derived products is higher than whole-blood-derived products. Therefore, decision-making about the employment of efficient blood collection methods is of great significance. Most papers only considered whole blood donation, and apheresis donation has been rarely addressed in a few papers such as Ensafian and Yaghoubi, 2017, Ensafian et al., 2017, Osorio et al., 2017, Osorio et al., 2018a, Osorio et al., 2018b, Gilani Larimi et al., 2019, Haeri et al., 2020, and Hosseini-Motlagh et al. (2020a). Moreover, the whole blood can be decomposed through different fractionation processes, each of which yields different component of blood products. A few researchers incorporated this feature into their proposed networks, which can be traced in Osorio et al., 2017, Osorio et al., 2018a, Osorio et al., 2018b, Haeri et al., 2020, and Hosseini-Motlagh et al. (2020a).

A few researchers investigated the effect of disruptions on the BSCNs. For example, Diabat et al. (2019) considered disruptions in distribution centers and paths of the network and used a robust stochastic approach to handle it. Rahmani (2019) addressed disruption in blood facilities, which is dealt with the p-robust approach. Also, Samani and Hosseini-Motlagh (2019) used back up facilities, along with the p-robust approach, to cope with disruption in PCs. Haeri et al. (2020) considered disruption in CCs and handled it by using different resiliency measures. Hosseini-Motlagh et al. (2020a) addressed disruption in blood centers and utilized a possibilistic stochastic robust approach to cope with uncertainty and disruption risks. In another work, Hosseini-Motlagh et al. (2020b) considered disruptions in CCs and used a robust stochastic programming approach to hedge against disruptions.

According to the reviewed papers, proactive approaches are implemented in the proposed BSCs to deal with disruptions, which enables the network to absorb the impacts of disruptions as much as possible; however, these papers did not suggest any strategies if the proposed proactive strategies could not harness the effects of disruptions thoroughly. Therefore, exploiting a reactive strategy to provide an immediate response to the disruption can enhance the resiliency of the network against disruptions. In this paper, we leverage proactive and reactive strategies simultaneously to provide the low vulnerability and high adaptability for the network against disruptions and use apheresis platelets as a back-up plan to respond to occurred shortages due to disruptions, variations in whole blood supplies, and demand fluctuations. Also, we utilize lateral transshipment strategy to facilitate the matching of demand and supply.

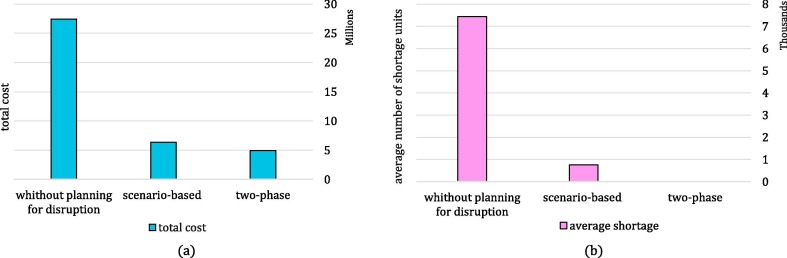
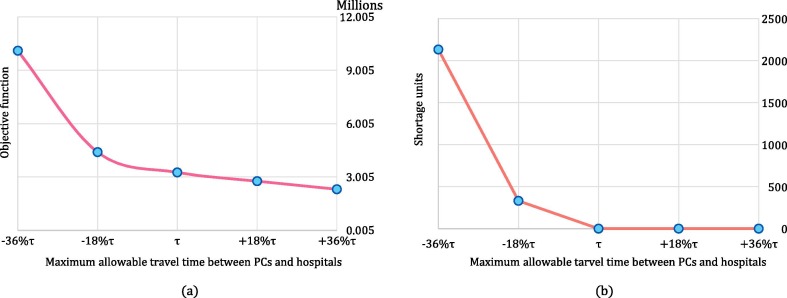
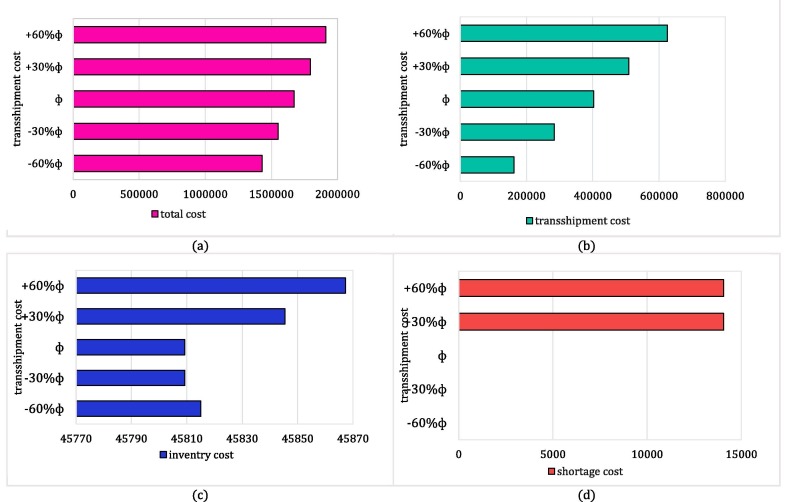
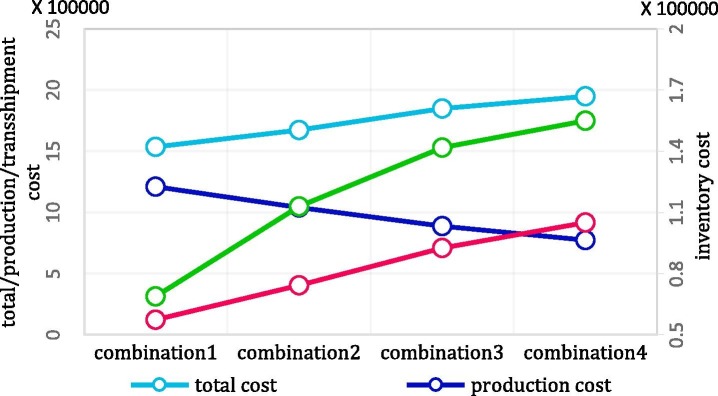
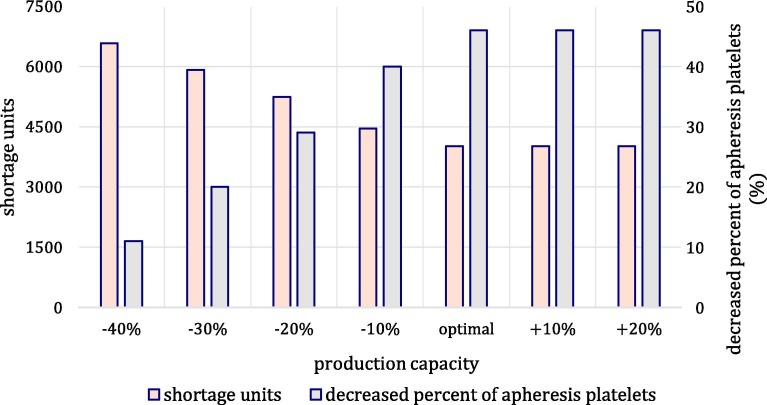
The two-stage stochastic approach is one of the frequently used proactive approaches in the literature to deal with disruptions. We compare the two-stage stochastic approach with the two-phase approach on two measures: cost efficiency and shortage units, in which the two-phase approach outperforms the stochastic approach on both measures. In the two-stage stochastic approach, decision-makers factor in disruption effects on their decision from the beginning of the planning horizon, which leads in more conservative decisions, and consequently, imposes more costs on the network. On the other hand, the stochastic strategy aims to protect the network against disruption. However, there are no alternatives to satisfy the shortages if it cannot harness disruption completely. Hence, the likelihood of shortage occurrence increases in this approach. Hence, we exploit the two-phase approach to design a cost-efficient network that is more resilient against shortages. This comparison is illustrated in more detail in Subsection 6.4.

The main characteristics of BSCN such as types of blood products, hierarchical level of the supply chain, collection method of blood products, planning horizon, time period, modeling approach, uncertainty approach, disruption approach, and lateral transshipment strategy, along with incorporating case study, are investigated in the reviewed papers, which are summarized in Table A1, in Appendix A.

3. Problem description

In this section, the proposed PSC in both proactive and reactive phases is presented, and afterward, the mathematical formulations of these phases are provided.

3.1. Proactive phase

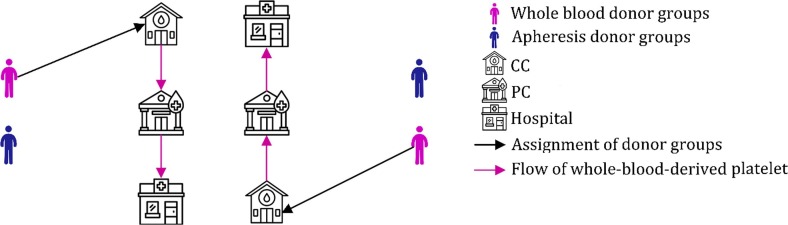
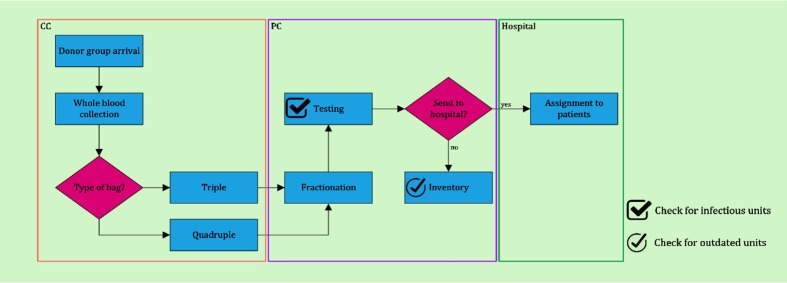
In the first phase, we design a nominal PSC without considering disruptions. To do so, we tailor a network consists of donor groups, CCs, PCs, and hospitals. In this phase, donors refer to CCs to donate their blood. The whole blood is drawn from donors and sent to the PCs. Then, the whole blood is tested strictly to reduce the risk of transfusion-transmitted diseases in PCs. When the test results are determined, the contaminated blood is discarded, and the safe blood decomposes to red blood cells, plasma, platelet, and cryoprecipitate. The procedure of testing, separation, and production lasts for two days; accordingly, the practical lifetime of the platelet will be five days. In PCs, the platelets can either be stored or be transferred to hospitals. Furthermore, several fractionation methods are used in PCs, which yield different proportions of blood products. In the next step, platelets are transferred from PCs to hospitals and are used to satisfy patients’ demands. The effect of disruptions and potential failures on platelet supply is not considered in this phase. In fact, this phase acts based on a proactive manner and the estimation of potential platelet supplies. This is why we have called this phase the proactive phase. The schematic view of the proposed PSC in the first phase is depicted in Fig. 1 .

Fig. 1.

Schematic view of the proposed PSC in the first phase.

The main decisions of this phase are as follows:

• •The optimal location of CCs and PCs and assignment of donor groups to CCs
• •The optimal amount of the collected whole blood in each CC
• •The blood flow between blood facilities
• •Wastage level and optimal inventory level of whole-blood-derived platelet in PCs, and shortage level of whole-blood-derived platelet in hospitals

The following assumptions are considered in the model of proactive phase:

• •Each donor group can be assigned to a CC.
• •The testing and production procedures of the whole-blood-derived platelet last for two days.
• •The discard rates of whole-blood-derived platelet in PCs are constant.
• •Optimal locations of CCs and PCs are selected from the suggested candidate sites.
• •Blood is collected solely by the whole blood collection method.

3.1.1. Mathematical formulation

The mathematical model of the first phase, a mixed-integer linear programming model, is formulated as follows, and notations of the first phase are provided in Appendix B.

Objective function

$$\min z_1=\sum _{e,i,t}\xi .U_{\mathit{ei}}^t+\sum _i\beta .F_i+\sum _{i,t}{\beta }^{\text{'}}.{F\text{'}}_i^t+\sum _{e,i,w,t}{\alpha }_{\mathit{iw}}.{X\text{'}}_{\mathit{eiw}}^t+\sum _{i,j,w,t}{\gamma }_{\mathit{ij}}.P_{\mathit{ijw}}^t+\sum _j\zeta .V_j+\sum _{j,t}{\zeta }^{\text{'}}.{V^{\text{'}}}_j^t+\sum _{i,j,w,t}\vartheta .P_{\mathit{ijw}}^t+\sum _{j,k,g,t}{\eta }_{\mathit{jk}}.{Y\text{'}}_{\mathit{jkg}}^t.D_k^t+\sum _{j,g,t}\theta .R_{\mathit{jg}}^t+\sum _{k,t}\varrho .N_k^t+\sum _{j,t}\mu .W_j^t$$ (1)

The objective function (1) aims to minimize the total cost of the proposed supply chain, including the cost of assigning donor groups to CCs, establishment cost of CCs, the cost of assigned capacity packages to CCs, cost of blood collection from donors according to the utilized collection process, cost of transporting blood units from CCs to PCs, establishment cost of PCs according to the assigned capacities, production cost of platelet in PCs, storage cost of whole blood-derived-platelets in PCs, cost of expired platelet units in PCs, cost of transporting platelet units from PCs to hospitals, and shortage cost of whole-blood-derived platelets in hospitals.

subject to

Donor groups’ assignment constraints

$$\sum _i{U}_{\mathit{ei}}^t\le 1\forall e,t$$ (2)

$$U_{\mathit{ei}}^t.{\chi }_{\mathit{ei}}\le \mathrm{\Delta }.F_i\forall e,i,t$$ (3)

$$X_{\mathit{ei}}^t\le {\mathrm{\Gamma }}_e.U_{\mathit{ei}}^t\forall e,i,t$$ (4)

Constraint (2) guarantees that each donor group can be assigned to one CC. In other words, it is considered that the donors placed in a donor group will refer to the same CC if they want to donate their blood. The accessibility to CC is an important factor in donors’ willingness to donate their blood, and people will refer to a CC to donate their blood if that CC is close enough to them. Thus, we considered a coverage radius for CCs, and Constraint (3) signifies that donor groups can refer to an opened CC if the donor group is placed in the service area of the CC. Constraint (4) assures that the number of collected whole blood units from each donor group in each opened CC cannot exceed the number of potential donors in that donor group.

Flow conservative, capacity, and transportation constraints in CCs

$$X_{\mathit{ei}}^t=\sum _w{X\text{'}}_{\mathit{eiw}}^t\forall e,i,t$$ (5)

$$\sum _e{X\text{'}}_{\mathit{eiw}}^t\ge \sum _j{P}_{\mathit{ijw}}^t\forall i,w,t$$ (6)

$$\sum _e{X}_{\mathit{ei}}^t\le \epsilon .{F\text{'}}_i^t\forall i,t$$ (7)

$$\sum _w{P}_{\mathit{ijw}}^t\le {\upsilon }_{\mathit{ij}}.M\forall i,j,t$$ (8)

$${F\text{'}}_i^t\le F_i.M\forall i,t$$ (9)

Whole blood collected in a CC and sent to a PC for processing can be separated into blood products by different fractionation method depending on the type of bag which is collected. Thus, regarding the different collection processes, Constraint (5) indicates that the number of collected whole blood units from each donor group in each CC is equal to the total amount of collected blood from that donor group through each collection process. Constraint (6) ensures that the output flow in the CC should be less than the input flow in that CC during each period, and Constraint (7) restricts the number of assigned donors to the capacity of the CC. In order to extract platelet from whole blood donation, it should be sent to PCs within a specified time period, and Constraint (8) guarantees that the collected whole blood can be transferred to PCs if the transportation time is in the allowable period. Constraint (9) indicates that the capacity can be assigned to a CC only if that CC is established.

Platelet assignment constraints in PC

$$\sum _j\sum _{g=3}^G{Y\text{'}}_{\mathit{jkg}}^t\le 1\forall k,t$$ (10)

$${Y\text{'}}_{\mathit{jkg}}^t=0\forall j,k,g\le 2,t$$ (11)

$${Y\text{'}}_{\mathit{jkg}}^t\le V_j\forall j,k,g\ge 3,t$$ (12)

Constraint (10) guarantees that the number of whole-blood-derived platelet units delivered to a hospital from any PC is fewer than or equal to platelet demands in that hospital. In other words, the amount of transferred whole-blood-derived platelet to hospitals can equal to the number of platelet units are demanded in hospitals, in which case the demand will be met totally. Also, it can be less than the number of demands, in which case the unsatisfied demands can be satisfied by either stored platelets, apheresis-derived platelets, or transferred platelets from other hospitals. Notably, the age of the transferred platelet to hospitals is more than two days, which is because of the two-day mandatory testing period. Given this two-day gap, platelet units of age one and two cannot be assigned to patients in order to meet demand in hospitals, as shown by Constraint (11). Constraint (12) guarantees that the platelet can be transferred from a PC to a hospital in case of the establishment of that PC.

Production, capacity, and transportation constraints in PCs

$$Q_j^t=0\forall j,t\le 1,2$$ (13)

$$Q_j^t\le \sum _{i,w}{\delta }_w.P_{\mathit{ijw}}^{t-2}.\left(1-\mathrm{\Omega }\right)\forall j,t\ge 3$$ (14)

$$Q_j^t\le \lambda .{V^{\text{'}}}_j^t\forall j,t$$ (15)

$${V^{\text{'}}}_j^t\le V_j.M\forall j,t$$ (16)

$${Y\text{'}}_{\mathit{jkg}}^t.D_k^t\le {\sigma }_{\mathit{jk}}.M\forall j,k,g,t$$ (17)

The procurement and testing process for each transferred whole blood unit to a PC takes two days; consequently, any platelet unit cannot be produced in the first and second periods of the planning horizon, as shown by Constraint (13). Constraint (14) restricts the number of processed whole-blood-derived platelet units in a PC to the number of collected whole blood units in CCs which have been transferred to that PC regarding the two-day production period, and a number of whole blood units will be discarded due to containing infectious agents. Constraint (15) captures the capacity of PCs, and Constraint (16) determines the number of capacity packages allocated to opened PCs. Stored platelets should be agitated continuously to preserve the quality of the platelets. During transportation time, platelets are not agitating for several times, and the quality of platelet units deteriorates considerably, which may compromise the patient’s safety. Thus, the platelet transportation time should be limited, and Constraint (17) guarantees that the platelet is permitted to transfer from PCs to hospitals if the travel time is in the allowable time interval.

Flow conservation in PCs

$$R_{\mathit{jg}}^t=0\forall j,t,g=1,2$$ (18)

$$R_{\mathit{jg}}^t\le {\phi }_{\mathit{jg}}^t-\sum _k{Y\text{'}}_{\mathit{jkg}}^t.D_k^t\forall j,t=1,g\ge 3$$ (19)

$$R_{\mathit{jg}}^t\le {\phi }_{\mathit{jg}}^t-\sum _k{Y\text{'}}_{\mathit{jkg}}^t.D_k^t\forall j,t=2,g=3$$ (20)

$$R_{\mathit{jg}}^t\le {\phi }_{\mathit{jg}}^t+R_{j,g-1}^{t-1}-\sum _k{Y\text{'}}_{\mathit{jkg}}^t.D_k^t\forall j,t=2,g\ge 4$$ (21)

$$R_{\mathit{jg}}^t\le Q_j^t+R_{j,g-1}^{t-1}-\sum _k{Y\text{'}}_{\mathit{jkg}}^t.D_k^t\forall j,t\ge 3,g=3$$ (22)

$$R_{\mathit{jg}}^t\le R_{j,g-1}^{t-1}-\sum _k{Y\text{'}}_{\mathit{jkg}}^t.D_k^t\forall j,t\ge 3,g\ge 4$$ (23)

$${R_{\mathit{jg}}^t=W}_j^t\forall j,g=G,t$$ (24)

Constraints (18)- (24) indicate the balance constraints of the whole-blood-derived platelet in each PC at each period. Constraint (18) shows that the age of all stored whole-blood-derived platelets is more than two days. Constraints (19), (20) calculate the inventory level for platelet with the age of more than three days in the first period and the three-day-old platelet in the second period. Given that there is no produced and stored platelet in the first and second periods, demands should be satisfied by the available platelet in PCs. Constraint (21) calculates the storage level for different ages ($g\ge 4$) during the second period. In the second period, there is no produced platelet. Therefore, the demands should be met by available platelet in the PC and the portion of available platelet in the first period which had been stocked. Constraints (22), (23) update the platelet stock level of distinct ages for $t\ge 3$. In the third and subsequent periods, the platelet is produced, and accordingly, the three-day-old platelet demands can be satisfied by produced platelets, and the demands for the age of more than one day are met by stored platelet in the previous period. Constraint (24) shows that the stored platelet of age $G$ will be expired.

Demand satisfaction constraint in hospitals

$$\sum _{g,j}{Y\text{'}}_{\mathit{jkg}}^t.D_k^t+N_k^t\ge D_k^t\forall k,t$$ (25)

Constraint (25) indicates that the platelet demands will be satisfied by arrived platelet in hospitals; otherwise, they will face a shortage. Also, the structural properties of the model are provided in Appendix C.

Domain of the decision variables

$$U_{\mathit{ei}}^t,F_i,V_j\in \{0,1\}\forall e,i,j,t$$ (26)

$$X_{\mathit{ei}}^t,{X\text{'}}_{\mathit{eiw}}^t,{Y\text{'}}_{\mathit{jkg}}^t,Q_j^t,W_j^t,R_{\mathit{jg}}^t,N_k^t\in {\mathbb{R}}^{+}\forall e,i,j,k,g,w,t$$ (27)

$${F\text{'}}_i^t,P_{\mathit{ijw}}^t,{V^{\text{'}}}_j^t\in {\mathbb{Z}}^{+}\forall i,j,w,t$$ (28)

Finally, constraints (26)- (28) determine the types of decision variables. Fig. 2 depicts the flow diagram of the presented PSC in the first phase.

Fig. 2.

Flow diagram of the PSC in the proactive phase during a period.

After solving the model of the first phase and determining the values of decision variables in this phase, a nominal PSC network was designed. At present, we factor in the effect of the production disruption on the designed network. In this paper, whole disruptions occur in the PCs, and we define several production disruption scenarios regarding the number and location of opened PCs. When a PC is disrupted, it cannot produce platelet units. Therefore, the hospitals which are provided with the disrupted PCs in the designed network in the first phase will face shortages. Besides, the designed network in the first phase may experience shortage due to fluctuations in the platelet demand and whole blood supply, which can be satisfied by apheresis platelet in the second phase. Therefore, the number of shortage stemmed from disruption, along with the shortage of the first phase, will be the demands of the second phase and will be fulfilled by apheresis-derived platelets. In BSC networks, a regular supply of blood is needed to guarantee demand fulfillment. Based on the existing literature in the fields of the BSC (see, e.g. Compernolle et al., 2018, Deelen et al., 2019, Gschwender and Gillard, 2017), the supply shortage barely occurs in the event of disruptions; However, in case of supply shortage, it can be mitigated by postponing elective events, triage patients’ transfusion to avoid inappropriate usage of blood products, and family or replacement donations (Abdella et al., 2018, Gschwender and Gillard, 2017). The effect of disruption on the designed network in the first phase is depicted in Fig. 3 .

Fig. 3.

Schematic view of the designed PSC in the first phase by considering the effect of disruption on the network.

3.2. Reactive phase

In this phase, the designed network in the first phase is adapted to the new situation that arises from disruptions in PCs. We use apheresis-derived-platelet units as a reactive strategy to handle this situation which is implemented in the network coincident with the proactive strategy. Thus, by simultaneous usage of reactive and proactive strategies, the regular demand is fulfilled by whole-blood-derived platelets (as the proactive strategy); at the same time, the shortages due to disruption and fluctuations in whole blood supply and platelet demand are met by apheresis-derived platelets (as the reactive strategy). In other words, most portion of the demands is satisfied by whole-blood-derived platelets, and the remainder of the demands, which cannot be met by whole-blood-derived platelets, is fulfilled by apheresis-derived platelet due to the fact that there are fewer apheresis donors. However, collecting platelet through the apheresis method will be an efficient strategy to handle disruptions due to its high efficiency and time-saving testing procedures. Besides, in addition to handling production disruptions, this strategy can be used to control other types of disruptions, such as demand disruption in which the demand increases. Thus, if whole-blood-derived platelet units cannot meet demand, the reactive strategy is triggered to handle this situation. In fact, these phases complete each other, and they are used simultaneously to cope with shortages efficiently.

In the second phase, the apheresis-derived platelets are collected and distributed among hospitals. This phase is planned based on the reveled portion of uncertain data and outputs in the first phase, such as the number and location of the opened PCs, the amount of sent blood from PCs to hospitals, and the shortage of the first phase. The amount of the sent platelet from disrupted PCs to hospitals in the first phase, along with the shortage of the first phase, is considered as the demands of the second phase under each disruption scenario which are fulfilled by the collected platelet from apheresis donor pools. In this phase, a PSC, including donor groups, PCs, and hospitals, is addressed. The platelet is collected through apheresis machines in PCs and collection-based hospitals. The collected platelet in PCs is stored or sent to the hospitals for transfusion usages. In hospitals, collected platelet units, along with transferred units from PCs, are used to fulfill demands, and remaining units can be stored to be utilized in the next periods. More precisely, the second phase updates the planning of the first phase in reaction to the occurred disruption; therefore, the second phase is named reactive phase. Furthermore, this phase exploits a transshipment strategy, which enables the hospitals to share their inventory resources and reduces the risk of shortages and outdates. Such a combined use of whole blood and apheresis collection methods and lateral transshipment policy can be an efficient way to streamline the matching of platelet demand and supply.

The main decisions of the second phase are as follows:

• •Assignment of donor groups to PCs and hospitals
• •The optimal amount of collected apheresis-derived platelet in each PC and hospital
• •The amount of apheresis-derived platelet transferred from each PC to each hospital
• •The optimal number of apheresis machines in each PC and hospital
• •Wastage level and the optimal inventory level of whole-blood-derived platelets in each PC and hospital, and shortage level in each hospital
• •The optimal amount of transshipped platelet between hospitals

The following assumptions are considered in the model of the proactive phase:

• •Each donor group can be assigned to either a PC or a hospital.
• •Apheresis-derived platelet can be transfused on the collection day.
• •The discard rates of apheresis-derived platelet in PCs and hospitals are constant.
• •The locations of PCs are determined based on the outputs of the first phase.

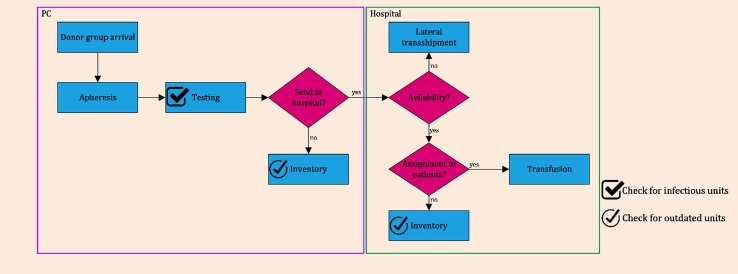
The schematic view of the proposed PSC after applying proactive and reactive strategies is depicted in Fig. 4 .

Fig. 4.

Schematic view of the proposed PSC by applying proactive and reactive strategies.

3.2.1. Mathematical formulation

The mathematical formulation of the second phase is described below, and notations of this phase are provided in Appendix B.

Objective function

$$\min z_2=\sum _{e,j,t,s}{\pi }^s.\xi .U_{\mathit{ej}}^{\mathit{ts}}+\sum _{e,k,t,s}{{\pi }^s.\xi \text{'}.U\text{'}}_{e,k}^{t,s}+\sum _{j,s}{\pi }^s.\psi .F_j^s+\sum _{k,s}{\pi }^s.{\psi }^{\text{'}}.{F\text{'}}_k^s+\sum _{e,j,t,s}{\pi }^s.\alpha .X_{\mathit{ej}}^{\mathit{ts}}+\sum _{e,k,t,s}{\pi }^s.\alpha \text{'}.X_{\mathit{ek}}^{\text{'}ts}+\sum _{j,t,s}{\pi }^s.\vartheta .Q_j^{\mathit{ts}}+\sum _{k,t,s}{{\pi }^s.\vartheta }^{\text{'}}.Q_k^{\text{'}ts}+\sum _{j,g,t,s}{\pi }^s.\theta .R_{\mathit{jg}}^{\mathit{ts}}+\sum _{k,g,t,s}{{\pi }^s.\theta }^{\text{'}}.{R\text{'}}_{\mathit{kg}}^{\mathit{ts}}+\sum _{j,t,s}{\pi }^s.\mu .W_j^{\mathit{ts}}+\sum _{k,t,s}{{\pi }^s.\mu }^{\text{'}}.{W\text{'}}_k^{\mathit{ts}}+\sum _{j,k,g,t,s}{\pi }^s.{\eta }_{\mathit{jk}}.{Y\text{'}}_{\mathit{jkg}}^{\mathit{ts}}.D_k^{\mathit{ts}}+\sum _{k,g,t,s}{\pi }^s.\varrho .N_{\mathit{kg}}^{\mathit{ts}}+\sum _{k,k\text{'}\ne k,g,t,s}{\pi }^s.\varphi .V_{kk\text{'}g}^{\mathit{ts}}$$ (29)

The objective function of this phase, Equation (29), seeks to minimize the total cost of the supply chain, including the cost of assigning donor groups to PCs and hospitals, the cost of apheresis machines in PCs and hospitals, cost of collecting platelet in PCs and hospitals through apheresis method, production, storage, and expiring cost of platelets in PCs and hospitals, cost of shipping apheresis-derived-platelet from PCs to hospitals, cost of apheresis-derived platelet stock-out in hospitals, and transshipment cost of apheresis-derived-platelet units between hospitals.

$$\mathrm{s}\mathrm{u}\mathrm{b}\mathrm{j}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{t}\mathrm{o}$$

Donor groups’ assignment constraints

$$\sum _j{U}_{\mathit{ej}}^{\mathit{ts}}+\sum _k{U\text{'}}_{\mathit{ek}}^{\mathit{ts}}\le 1\forall e,t,s$$ (30)

$$U_{\mathit{ej}}^{\mathit{ts}}.{\chi }_{\mathit{ej}}\le \mathrm{\Delta }.(1-{\mathit{dis}}_j^s)\forall e,j,t,s$$ (31)

$${U\text{'}}_{\mathit{ek}}^{\mathit{ts}}.{\chi \text{'}}_{\mathit{ek}}\le {\mathrm{\Delta }}^{\text{'}}\forall e,k,t,s$$ (32)

$$X_{\mathit{ej}}^{\mathit{ts}}\le U_{\mathit{ej}}^{\mathit{ts}}.{\mathrm{\Gamma }}_e\forall e,j,t,s$$ (33)

$${X\text{'}}_{\mathit{ek}}^{\mathit{ts}}\le {U^{\text{'}}}_{\mathit{ek}}^{\mathit{ts}}.{\mathrm{\Gamma }}_e\forall e,k,t,s$$ (34)

Platelet collection thorough the apheresis method can take place in PCs and collection-based hospitals, and Constraint (30) indicates that each donor group can be assigned to either an undisrupted PC or a hospital regarding their proximity. As mentioned before, people are not willing to refer to centers that are located at a farther distance of them in order to donate their blood. Constraints (31), (32) restrict the service area of PCs and hospitals to their coverage radii, respectively. Constraints (33), (34) limit the number of collected apheresis-derived platelet units from each donor group to the maximum number of eligible apheresis donors of that group.

Production, capacity, and transportation constraints in PCs

$$Q_j^{\mathit{ts}}\le \delta .\left(1-\mathrm{\Omega }\right).\sum _e{X}_{\mathit{ej}}^{\mathit{ts}}\forall j,t,s$$ (35)

$${Q\text{'}}_k^{\mathit{ts}}\le \delta .\left(1-{\mathrm{\Omega }}^{\text{'}}\right).\sum _e{X\text{'}}_{\mathit{ek}}^{\mathit{ts}}\forall k,t,s$$ (36)

$$\sum _e{X}_{\mathit{ej}}^{\mathit{ts}}\le \epsilon .F_j^s\forall j,t,s$$ (37)

$$\sum _g{Y\text{'}}_{\mathit{jkg}}^{\mathit{ts}}.D_k^{\mathit{ts}}\le {\sigma }_{\mathit{jk}}.M\forall j,k,t,s$$ (38)

The platelet collected through the aphresis method can be produced on the collection day, and therefore, the apheresis-derived platelets will be available of each age of 1 to G; consequently, produced apheresis platelet can be available in each period. Constraint (35) captures the number of produced apheresis-derived platelet in a PC at each period regarding the discard rate of platelet, the amount of obtained platelet from a donor, and the number of referred donors to that PC. Constraint (36) determines the number of produced apheresis platelet units in hospitals, and the capacity of each PC is captured by Constraint (37). As mentioned before, the transportation time of platelets should be less than a determined time period due to their specific storage conditions, and Constraint (38) restricts the transportation time of platelet units from PCs to hospitals.

Platelet assignment constraints

$$F_j^s\le M.(1-{\mathit{dis}}_j^s)\forall j,s$$ (39)

$$\sum _{j,g}{Y\text{'}}_{\mathit{jkg}}^{\mathit{ts}}+\sum _g{Z\text{'}}_{\mathit{kg}}^{\mathit{ts}}\le 1\forall k,t,s$$ (40)

$${Y\text{'}}_{\mathit{jkg}}^{\mathit{ts}}.D_k^{\mathit{ts}}\le \epsilon .\delta .F_j^s\forall j,k,g,t,s$$ (41)

$${Y\text{'}}_{\mathit{jkg}}^{\mathit{ts}}.D_k^{\mathit{ts}}\le \delta .\sum _e{X}_{\mathit{ej}}^{\mathit{ts}}\forall j,k,g=1,t,s$$ (42)

$$\sum _e{X\text{'}}_{\mathit{ek}}^{\mathit{ts}}\le \epsilon \text{'}.{F\text{'}}_k^s\forall k,t,s$$ (43)

$${Z\text{'}}_{\mathit{kg}}^{\mathit{ts}}.D_k^{\mathit{ts}}\le \delta .\sum _e{X\text{'}}_{\mathit{ek}}^{\mathit{ts}}\forall k,g=1,t,s$$ (44)

Constraint (39) guarantees that apheresis machines can only be assigned to undisrupted PCs. Constraint (40) illustrates that the number of collected platelet units in a hospital, along with the number of arrived platelets in that hospital, is fewer than or equal to the platelet demands in that hospital. If the number of collected apheresis platelet in a hospital and the number of delivered apheresis platelet to that hospital is fewer than the number of platelet demands in that hospital, the unmet demands can be satisfied by either transferred platelet from other hospitals or stored platelets. Constraints (41), (42) restrict the number of transferred platelet units from PCs to hospitals to the capacity of allocated apheresis machines and to the number of collected platelets in that PC, respectively. Constraint (43) limits the number of referred donors to a hospital to the capacity of available apheresis machines in that hospital, and Constraint (44) restricts the assigned platelet to meet demands in a hospital to the number of collected platelet in that hospital.

Flow conservation in PCs

$$R_{\mathit{jg}}^{\mathit{ts}}\le Q_j^{\mathit{ts}}-\sum _k{Y\text{'}}_{\mathit{jkg}}^{\mathit{ts}}.D_k^{\mathit{ts}}\forall j,g=1,t,s$$ (45)

$$R_{\mathit{jg}}^{\mathit{ts}}\le {\phi }_{\mathit{jg}}^{\mathit{ts}}-\sum _k{Y\text{'}}_{\mathit{jkg}}^{\mathit{ts}}.D_k^{\mathit{ts}}\forall j,g\ge 2,t=1,s$$ (46)

$$R_{\mathit{jg}}^{\mathit{ts}}\le R_{j,g-1}^{t-1,s}-\sum _k{Y\text{'}}_{\mathit{jkg}}^{\mathit{ts}}.D_k^{\mathit{ts}}\forall j,g\ge 2,t\ge 2,s$$ (47)

$$R_{\mathit{jg}}^{\mathit{ts}}=W_j^{\mathit{ts}}\forall j,g=G,t,s$$ (48)

Constraints (45)- (48) are inventory conservation constraints and update the inventory of PCs for different ages and distinct periods. As mentioned before, the apheresis-derived platelet can be used on the collection day. Therefore, we can use the produced platelet in each period to satisfy the one-day platelet demands, as shown in Constraint (45). In other words, when an apheresis platelet is collected, it will change into a one-day apheresis platelet after the production process that can be used to fulfill one-day demands or can be stored to fulfill the needs in next periods. Constraint (46) updates the inventory level of PCs in the first period for the platelets of the age of 2, …, G, in which the demands should be met by the available platelet in PCs. Also, Constraint (47) calculates the inventory levels of PCs for subsequent periods and distinct ages, in which demands are satisfied by the stored platelet of the previous period. The outdated level of platelet in PCs is calculated by Constraint (48).

Flow conservation in hospitals

$${R\text{'}}_{\mathit{kg}}^{\mathit{ts}}\le {Q^{\text{'}}}_k^{\mathit{ts}}+\sum _{k\text{'}\ne k}{V}_{kk\text{'}g}^{\mathit{ts}}-{Z^{\text{'}}}_{\mathit{kg}}^{\mathit{ts}}.D_k^{\mathit{ts}}-\sum _{k\text{'}\ne k}{V}_{k\text{'}kg}^{\mathit{ts}}+N_{\mathit{kg}}^{\mathit{ts}}\forall k,g=1,t,s$$ (49)

$${R\text{'}}_{\mathit{kg}}^{\mathit{ts}}\le {\phi \text{'}}_{\mathit{kg}}^t+\sum _{k\text{'}\ne k}{V}_{kk\text{'}g}^{\mathit{ts}}-{Z^{\text{'}}}_{\mathit{kg}}^{\mathit{ts}}.D_k^{\mathit{ts}}-\sum _{k\text{'}\ne k}{V}_{k\text{'}kg}^{\mathit{ts}}+N_{\mathit{kg}}^{\mathit{ts}}\forall k,g\ge 2,t=1,s$$ (50)

$${R\text{'}}_{\mathit{kg}}^{\mathit{ts}}\le {R^{\text{'}}}_{k,g-1}^{t-1,s}+\sum _{k\text{'}\ne k}{V}_{kk\text{'}g}^{\mathit{ts}}-{Z^{\text{'}}}_{\mathit{kg}}^{\mathit{ts}}.D_k^{\mathit{ts}}-\sum _{k\text{'}\ne k}{V}_{k\text{'}kg}^{\mathit{ts}}+N_{\mathit{kg}}^{\mathit{ts}}\forall k,g\ge 2,t\ge 2,s$$ (51)

$${R\text{'}}_{\mathit{kg}}^{\mathit{ts}}={W\text{'}}_k^{\mathit{ts}}\forall k,g=G,t,s$$ (52)

Constraints (49)- (52) update the inventory level of apheresis-derived platelets for each age and each period in hospitals. The one-day platelet demands can be satisfied by produced platelet in each period, along with transshipped platelet from other hospitals, as shown in Constraint (49). In the first period, the platelet demands with the age of more than one day can be met by available platelet in the hospital as well as transshipped platelet to that hospital from other hospitals, as shown in Constraint (50). Also, Constraint (51) indicates that the platelet inventory and transshipped units from other hospitals are used to fulfill demands for the platelet of the age of more than one day. Constraint (52) calculates the amount of platelet wastage in hospitals.

Transshipment constraints

$$\sum _{k\ne k\text{'}}{V}_{kk\text{'}g}^{\mathit{ts}}\le {Q^{\text{'}}}_{k\text{'}}^{\mathit{ts}}\forall k\text{'}\ne k,g=1,t,s$$ (53)

$$\sum _{k\ne k\text{'}}{V}_{kk\text{'}g}^{\mathit{ts}}\le {\phi \text{'}}_{k\text{'}g}^t\forall k^{\text{'}}\ne k,g\ge 2,t=1,s$$ (54)

$$\sum _{k\ne k\text{'}}{V}_{kk\text{'}g}^{\mathit{ts}}\le {R^{\text{'}}}_{k\text{'},g-1}^{t-1,s}\forall k^{\text{'}}\ne k,g\ge 2,t\ge 2,s$$ (55)

Constraints (53)- (55) determine the maximum allowable amount of platelet of each age in a hospital which can be transshipped to other hospitals. The number of transshipped one-day platelets from a hospital to other hospitals should be less than the number of the produced platelets in that hospitals, as shown by Constraint (53). The reason is that the amount of one-day platelet in each period in a hospital equals the amount of produced platelets in that period at that hospital. In the first period, the maximum amount of platelet of more than one day equals to the available amount of stored platelet, and therefore, the amount of transshipped platelet should be less than this value, as shown by Constraint (54). Constraint (55) does the same for a platelet of more than one day for $t\ge 2$.

Demand satisfaction constraint in hospitals

$$\sum _{k\text{'}\ne k}{V}_{k\text{'}kg}^{\mathit{ts}}+{Z^{\text{'}}}_{\mathit{kg}}^{\mathit{ts}}+\sum _j{Y\text{'}}_{\mathit{jkg}}^{\mathit{ts}}.D_k^{\mathit{ts}}\ge d_{\mathit{kg}}^{\mathit{ts}}\forall k,g,t,s$$ (56)

Constraint (56) guarantees the demand satisfaction for platelets of any age in each period under each disruption scenario, which indicates that demands can be satisfied by transferred units from PCs, collected units in the hospital, or transshipped units from other hospitals. Also, the structural properties of the model are provided in Appendix C.

Domain of the decision variables

$$U_{\mathit{ej}}^{\mathit{ts}},{U\text{'}}_{\mathit{ek}}^{\mathit{ts}}\in \{0,1\}\forall e,j,k,t,s$$ (57)

$$X_{\mathit{ej}}^{\mathit{ts}},{X^{\text{'}}}_{\mathit{ek}}^{\mathit{ts}},{Y^{\text{'}}}_{\mathit{jkg}}^{\mathit{ts}},{Z^{\text{'}}}_{\mathit{kg}}^{\mathit{ts}},Q_j^{\mathit{ts}},{Q^{\text{'}}}_k^{\mathit{ts}},R_{\mathit{jg}}^{\mathit{ts}},{R^{\text{'}}}_{\mathit{kg}}^{\mathit{ts}},W_j^{\mathit{ts}},{W^{\text{'}}}_k^{\mathit{ts}},V_{kk\text{'}g}^{\mathit{ts}},N_{\mathit{kg}}^{\mathit{ts}}\in {\mathbb{R}}^{+}\forall e,j,k,k^{\text{'}},g,t,s$$ (58)

$$F_j^s,{F\text{'}}_k^s\in {\mathbb{Z}}^{+}\forall j,k,s$$ (59)

The domain of decision variables is determined by Constraints (57)- (59). Fig. 5 depicts the flow diagram of the presented PSC in the second phase.

Fig. 5.

Flow diagram of the PSC in the reactive phase during a period.

4. Solution approach

In proposed models, several parameters such as the demand of platelet, the supply of whole blood, the supply of apheresis platelet, and the costs associated with the PSC are considered as imprecise parameters. In this study, a fuzzy stochastic programming approach is utilized to cope with uncertainty. The applied approach in this study is described in the ensuing section.

4.1. The proposed fuzzy stochastic possibilistic approach

Uncertainties are important factors that affect the supply chain design, and they arise from different sources such as lack of information or incomplete data, environmental conditions, and errors in the estimation of indeterminable factors. In practice, even a small amount of uncertainty can significantly affect the performance of supply chains. Accordingly, an appropriate approach should be devised to cope with uncertainty and immunize supply chains against its impacts.

Regarding the amount of available data, uncertainties can be categorized into three types: random, epistemic, and deep uncertainties, whichever should differently be dealt with. Random uncertainties happen when there are sufficient historical data for input parameters, which their patterns can be fitted to future situations. To deal with these types of uncertainties, stochastic programming approaches can be used. Imprecise parameters causing by insufficient knowledge, which can often be estimated based on experts’ opinion, lead to epistemic uncertainties. Fuzzy mathematical programming approaches can be utilized to hedge against these types of uncertainties (Salehi Sadghiani et al., 2015, Zhalechian et al., 2018). Deep uncertainties are related to the lack of knowledge in such a way that only the interval of input parameters can be estimated. In these situations, the convex programming approaches are applied to cope with uncertainties. In the field of BSCs and PSCs, demand and supply, as well as costs of the supply chain, are some critical parameters that are usually tainted with uncertainties. Based on the literature, most of the researchers used stochastic programming approaches or robust scenario-based stochastic programming approaches to deal with such uncertainties. However, these uncertain parameters vary in a wide range, which leads to a high number of scenarios, and consequently, may result in high computational challenges and high numerical complexities. Besides, the needs for sufficient and reliable historical data such that their pattern can be fitted to future situations are conditions, which limit the usage of these approaches in real life-cases within a reasonable time. Therefore, we utilize fuzzy approaches to handle epistemic uncertainties in the proposed PSC. The complexity of this approach is less than other approaches, while it can control a large number of uncertain parameters.

In the proposed PSC, two types of uncertainties exist, including random uncertainty and epistemic uncertainty. Epistemic uncertainty arises from imprecise parameters such as demand, supply, and costs. Also, the uncertainty which stems from disruptions is considered as random uncertainty. Therefore, a fuzzy stochastic programming approach is proposed to deal with this hybrid uncertainty. The required definitions in this section are provided in Appendix D.

4.2. Fuzzy stochastic programming approach

The compact forms of the proposed models for designing the PSC are formulated as follows:

(60)

The presented models are related to the first and second phases of the proposed PSC problem. $A_1,B_1,G_1,A_2,G_2,$and${G\text{'}}_2$ are matrices of the models, which contain deterministic parameters, and moreover, $\stackrel{}{f_1},\stackrel{}{c_1},\stackrel{}{e_1},\stackrel{}{d_1},\stackrel{}{f_2},{\stackrel{}{c_2}}_s$and $\stackrel{}{e_2}$ are fuzzy parameter vectors. $\stackrel{}{f_1}$is related to the opening cost of blood centers and the cost of assigning donors to CCs, and ${\stackrel{}{c}}_1$ is the variable cost of the PSC in the first phase. $\stackrel{}{f_2}$ is related to the cost of assigning donor groups to PCs and hospitals, and ${\stackrel{}{c_2}}_s$ is the operational cost of the PSC during the second phase under scenario $s$. $x_1$ and ${x_2}_s$ are binary decision variables related to the first and second phases, respectively. Also, $y_1$ and ${y\text{'}}_1$ are continuous decision variables of the first phase, and ${y_2}_s$ represents the continuous scenario-based decision variable of the second phase. Disruption scenarios are denoted by $s$, the probability of which is ${\pi }_s$ (${\sum }_s{\pi }_s=1$).

In the model mentioned above, the constraints containing fuzzy parameters are in the form of possibilistic constraints, and credibility measure is exploited to convert them into equivalent crisp forms. Also, to formulate the basic possibilistic chance constraint programming, we use the possibilistic mean value of the objective functions in the presented model. Therefore, the compact form of basic possibilistic chance constraint programming is formulated as follows:

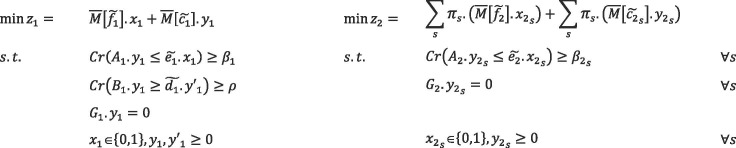(61)

The minimum confidence level of each chance constraints is determined by decision-makers, which is denoted by ${\beta }_1$ and $\rho$ in the first phase. In the second phase, ${{\beta }_2}_s$ represents the minimum confidence level of chance constraints, which is different for each disruption scenario.

We assume that all of the costs of the PSC are trapezoidal LR-fuzzy number as ${\stackrel{}{f_1}}_i={({\underset{\_}{f_1}}_i,{\overline{f_1}}_i,{{\alpha }_1}_i,{{\beta }_1}_i)}_{\mathit{LR}}$, ${\stackrel{}{f_2}}_{\mathit{is}}={({\underset{\_}{f_2}}_{\mathit{is}},{\overline{f_2}}_{\mathit{is}},{{\alpha }_2}_{\mathit{is}},{{\beta }_2}_{\mathit{is}})}_{\mathit{LR}}$, ${\stackrel{}{c_1}}_j{=({\underset{\_}{c_1}}_j,{\overline{c_1}}_j,{{\alpha }_1}_j,{{\beta }_1}_j)}_{\mathit{LR}}$, and ${\stackrel{}{c_2}}_{\mathit{js}}{=({\underset{\_}{c_2}}_{\mathit{js}},{\overline{c_2}}_{\mathit{js}},{{\alpha }_2}_{\mathit{js}},{{\beta }_2}_{\mathit{js}})}_{\mathit{LR}}$. Therefore, the value of the objective function of the first phase, for the solution $\left(x,y\right)$, will be a fuzzy interval as ${\stackrel{}{F}}_1\left(x_1,y_1\right)=\stackrel{}{f_1}.x_1+\stackrel{}{c_1}.y_1$. Likewise, ${\stackrel{}{F_2}}_s\left({x_2}_s,{y_2}_s\right)=\stackrel{}{f_2}.{x_2}_s+{\stackrel{}{c_2}}_s.{y_2}_s$ will be a fuzzy interval for the solution $\left({x_2}_s,{y_2}_s\right)$ under scenario $s$ in the second phase. (Hereafter, ${\stackrel{}{F}}_1\left(x_1,y_1\right)$ is denoted by ${\stackrel{}{F}}_1$; likewise $\underset{\_}{F_1},\overline{F_1},M_1,N_1,{\stackrel{}{F_2}}_s,{\underset{\_}{F_2}}_s,{\overline{F_2}}_s,{M_2}_s,{N_2}_s,\stackrel{}{F_2},\underset{\_}{F_2},\overline{F_2},M_2,N_2$). Based on Definition 1 (in Appendix D), $\stackrel{}{F_1}$, $\stackrel{}{F_2}$, and ${\stackrel{}{F_2}}_s$ will be calculated as follows:

$$\stackrel{}{F_1}={(\sum _i{\underset{\_}{f_1}}_i.{x_1}_i+\sum _j{\underset{\_}{c_1}}_j.{y_1}_j,\sum _i{\overline{f_1}}_i.{x_1}_i+\sum _j{\overline{c_1}}_j.{y_1}_j,\sum _i{{\alpha }_1}_i.{x_1}_i+\sum _j{{\alpha }_1}_j.{y_1}_j,\sum _i{{\beta }_1}_i.{x_1}_i+\sum _j{{\beta }_1}_j.{y_1}_j)}_{\mathit{LR}}={(\underset{\_}{F_1},\overline{F_1},M_1,N_1)}_{\mathit{LR}}$$ (62)

$${\stackrel{}{F_2}}_s={(\sum _i{\underset{\_}{f_2}}_{\mathit{is}}.{x_2}_{\mathit{is}}+\sum _j{\underset{\_}{c_2}}_{\mathit{js}}.{y_2}_{\mathit{js}},\sum _i{\overline{f_2}}_{\mathit{is}}.{x_2}_{\mathit{is}}+\sum _j{\overline{c_2}}_{\mathit{js}}.{y_2}_{\mathit{js}},\sum _i{{\alpha }_2}_{\mathit{is}}.{x_2}_{\mathit{is}}+\sum _j{{\alpha }_2}_{\mathit{js}}.{y_2}_{\mathit{js}},\sum _i{{\beta }_2}_{\mathit{is}}.{x_2}_{\mathit{is}}+\sum _j{{\beta }_2}_{\mathit{js}}.{y_2}_{\mathit{js}})}_{\mathit{LR}}={({\underset{\_}{F_2}}_s,{\overline{F_2}}_s,{M_2}_s,{N_2}_s)}_{\mathit{LR}}$$ (63)

$$\stackrel{}{F_2}={(\sum _{i,s}{\pi }_s.{\underset{\_}{f_2}}_{\mathit{is}}.{x_2}_{\mathit{is}}+\sum _{j,s}{\pi }_s.{\underset{\_}{c_2}}_{\mathit{js}}.{y_2}_{\mathit{js}},\sum _{i,s}{\pi }_s.{\overline{f_2}}_{\mathit{is}}.{x_2}_{\mathit{is}}+\sum _{j,s}{\pi }_s.{\overline{c_2}}_{\mathit{js}}.{y_2}_{\mathit{js}},\sum _{i,s}{\pi }_s.{{\alpha }_2}_{\mathit{is}}.{x_2}_{\mathit{is}}+\sum _{j,s}{\pi }_s.{{\alpha }_2}_{\mathit{js}}.{y_2}_{\mathit{js}},\sum _{i,s}{\pi }_s.{{\beta }_2}_{\mathit{is}}.{x_2}_{\mathit{is}}+\sum _{j,s}{\pi }_s.{{\beta }_2}_{\mathit{js}}.{y_2}_{\mathit{js}})}_{\mathit{LR}}={(\underset{\_}{F_2},\overline{F_2},M_2,N_2)}_{\mathit{LR}}$$ (64)

Also, based on Definition 3 (in Appendix D), the possibilistic mean value of the objective function of the first phase $(F_1)$, the possibilistic mean value of the objective function of the second phase under scenario $s$ (${F_2}_s$), and the weighted possibilistic mean value of the objective function of the second phase ($F_2$) can be stated as follows:

$$F_1=\overline{M}\left(\stackrel{}{F_1}\right)=\sum _i\overline{M}\left({\stackrel{}{f_1}}_i\right).{x_1}_i+\sum _j\overline{M}\left({\stackrel{}{c_1}}_j\right).{y_1}_j=\sum _i\left(\frac{{\underset{\_}{f_1}}_i+{\overline{f_1}}_i}{2}+\frac{{{\beta }_1}_i-{{\alpha }_1}_i}{6}\right).{x_1}_i+\sum _j\left(\frac{{\underset{\_}{c_1}}_j+{\overline{c_1}}_j}{2}+\frac{{{\beta }_1}_j-{{\alpha }_1}_j}{6}\right).{y_1}_j$$ (65)

$${F_2}_s=\overline{M}\left({\stackrel{}{F_2}}_s\right)=\sum _i\overline{M}\left({\stackrel{}{f_2}}_{\mathit{is}}\right).{x_2}_{\mathit{is}}+\sum _j\overline{M}\left({\stackrel{}{c_2}}_{\mathit{js}}\right).{y_2}_{\mathit{js}}=\sum _i\left(\frac{{\underset{\_}{f_2}}_{\mathit{is}}+{\overline{f_2}}_{\mathit{is}}}{2}+\frac{{{\beta }_2}_{\mathit{is}}-{{\alpha }_2}_{\mathit{is}}}{6}\right).{x_2}_{\mathit{is}}+\sum _j\left(\frac{{\underset{\_}{c_2}}_{\mathit{js}}+{\overline{c_2}}_{\mathit{js}}}{2}+\frac{{{\beta }_2}_{\mathit{js}}-{{\alpha }_2}_{\mathit{js}}}{6}\right).{y_2}_{\mathit{js}}\forall s$$ (66)

$$F_2=\overline{M}\left(\stackrel{}{F_2}\right)=\sum _{i,s}{\pi }_s.\overline{M}\left({\stackrel{}{f_2}}_{\mathit{is}}\right).{x_2}_{\mathit{is}}+\sum _{j,s}{\pi }_s.\overline{M}\left({\stackrel{}{c_2}}_{\mathit{js}}\right).{y_2}_{\mathit{js}}=\sum _{i,s}{\pi }_s.\left(\frac{{\underset{\_}{f_2}}_{\mathit{is}}+{\overline{f_2}}_{\mathit{is}}}{2}+\frac{{{\beta }_2}_{\mathit{is}}-{{\alpha }_2}_{\mathit{is}}}{6}\right).{x_2}_{\mathit{is}}+\sum _{j,s}{\pi }_s.\left(\frac{{\underset{\_}{c_2}}_{\mathit{js}}+{\overline{c_2}}_{\mathit{js}}}{2}+\frac{{{\beta }_2}_{\mathit{js}}-{{\alpha }_2}_{\mathit{js}}}{6}\right).{y_2}_{\mathit{js}}$$ (67)

We assume that $\stackrel{}{e_1}={(\underset{\_}{e_1},\overline{e_1},{\gamma }_1,{\delta }_1)}_{\mathit{LR}}$, $\stackrel{}{d_1}={(\underset{\_}{d_1},\overline{d_1},\tau ,\nu )}_{\mathit{LR}}$, and $\stackrel{}{e_2}={(\underset{\_}{e_2},\overline{e_2},{\gamma }_2,{\delta }_2)}_{\mathit{LR}}$. Then, the basic crisp fuzzy stochastic programming formulation can be stated as follows:

5. Case description

To achieve the goal of universal health care coverage, each country should properly provide health care services, such as a safe and sufficient supply of blood products. In Iran, one organization is responsible for blood collection, production, storage, and distribution. For this organization, called the Iranian blood transfusion organization (IBTO), providing safe and adequate blood services is the highest priority. Achieving this goal entails crucial decision-making in the context of transfusion-related activities such as identifying the optimal location of CCs and PCs and the capacity of these centers, determining the optimal blood collection and fractionation methods in blood centers, the optimal assignment of blood to hospitals, and how to hedge against disruptions. There is a main blood transfusion center in each province of Iran, which is in charge of the management of blood supply in that province. This study investigates the problem of designing the PSC in Fars province.

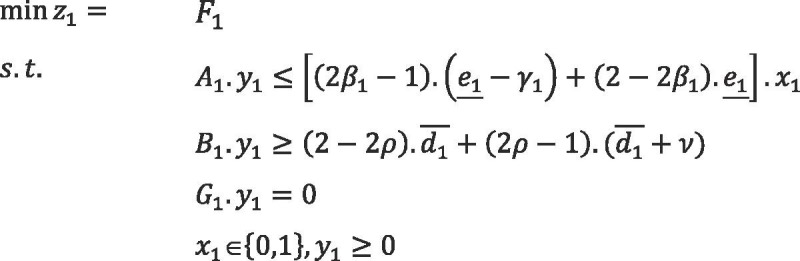(68)

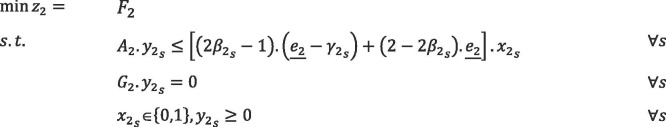(69)

Fars province, with an area of 122,608 km², is located in the southwest of Iran. By population, this province is the 4th largest province of Iran. It consists of 29 counties, the geographic dispersions of which are depicted in Fig. 6 . The number of CCs in this province is not enough, and accordingly, the poor access to CCs is a deterrent factor for blood donations. In Iran, the blood donation rate is 20–29.9 donations of 1000 population, and the scarcity of these resources will impose irreversible consequences like the loss of life (Chegini et al., 2017). Shiraz, the capital of Fars province, is the leader in the field of organ transplantation in Iran which has been identified as the largest liver transplant center in the world in 2015, and many patients referred to Shiraz from other cities of Iran and even foreign countries for transplantation (Malek-Hosseini et al., 2019). Blood transfusion is an indispensable part of these surgeries, and the blood should be provided sufficiently to guarantee the health of patients. According to the above, Fars province has the most transfusion rate in Iran. From an economic viewpoint, IBTO faces challenges in providing transfusion-related equipment, such as blood bags and apheresis machines. Therefore, there is a substantial need for an efficient BSC, specifically the PSC, in Fars province, which is investigated in this study.

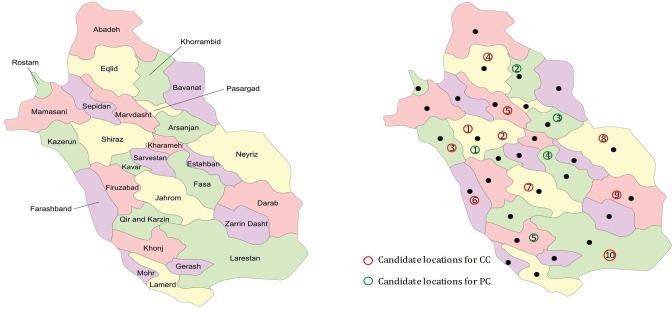
Fig. 6.

Geographic desperation of counties in Fars province and candidate locations of CCs and BCs.

In BSCN design, one of the real challenges is to identify the candidate location for the establishment of blood centers. In this paper, the best candidate location of CCs and PCs are determined according to the experts’ knowledge and viewpoint. Several criteria are influential in selecting the best candidate location for blood centers, such as traffic, population density, and skilled staff. Considering these factors by field experts in the decision-making procedures will improve the utility of the PSC. In this study, the candidate locations for PCs and CCs are determined by close cooperation with experts, which are depicted in Fig. 6.

Based on the IBTO regulation policies, people in the 18–60 age range can donate their blood, which 60% of the population of Fars province place in this age range. On the other hand, based on the documented donation pattern, the average rate of blood donation is estimated at 15% (Mean and Median Age of Iranian Population 2016, 2017). Therefore, it is assumed that almost 9% of the population donate their blood in this study. Furthermore, each county of Fars province by 6% whole blood donation rate and 3% apheresis donation rate is taken into account as donor groups. The population of the counties of Fars province is inserted in Table A2 in Appendix A. The number of platelet supplies is calculated based on population and donation rate of each county; however, the donation rate is uncertain, and accordingly, the supply is considered a fuzzy number.

In this case, the maximum shelf life of platelets is considered seven days, and a two-day mandatory testing process is considered in the production of whole-blood-derived platelets. However, the apheresis-derived-platelets do not require strict testing procedures, and therefore, they can be used on the collection day. Furthermore, a derived platelet by apheresis method is equivalent to 6 whole-blood-derived platelets. As reported by the world health organization (WHO), the discard rate of platelets in the production process is considered 7%.

The demand for platelets by patients in hospitals remains to be uncertain due to unexpected accidents and traumas, along with high perishability of platelets. Therefore, the estimated demand based on historical data is not reliable. Accordingly, demand is presented as fuzzy numbers such that the elements of this fuzzy number are extracted based on experts’ opinions. The geographic coordinates of the main hospitals in Fars province are inserted in Table A3 in Appendix A.

Transportation times between a pair of nodes are calculated based on the distance between these nodes and the average speed of vehicles transferred blood units between the pair of nodes. Transportation costs are also calculated based on the fuel cost and traveled distance between the nodes. The values of other parameters are extracted from IBTO and information on related papers, as shown in Table 1 .

Table 1.

The value of parameters.

Parameters	Value	Unit	Reference
Whole-blood-derived platelet production cost	84	$	Ghandforoush and Sen (2010)
Apheresis-derived platelet production cost	517	$	Jones (2018)
Inventory cost	130	$	Rajendran and Ravindran (2017)
Shortage cost	3250	$	Rajendran and Ravindran (2017)
Outdate cost	650	$	Rajendran and Ravindran (2017)
Apheresis machine price	50′000	$	Apheresis in the Office Setting (2008)
Collection cost	10	$	Real data

6. Computational results

In this section, the inspired data from the real case of the Fars province in Iran are implemented to the proposed two-phase approach. Firstly, we solve the model of the first phase and report the results of the model. Afterward, the entities of the second phase are determined based on the results of the first phase, and then, the results of the second phase are obtained and reported. Furthermore, we use a fuzzy stochastic approach to deal with disruptions in the PSC network, and its results are compared with the results of two-phase approach. Finally, sensitivity analyses are conducted to some important parameters, and managerial insights are extracted from the results. The computational tests of this study were performed by GAMS 25.1.2 using CPLEX solver on a computer with core i7 2.5 GHz and 8 GB of RAM.

6.1. Results of the proactive phase

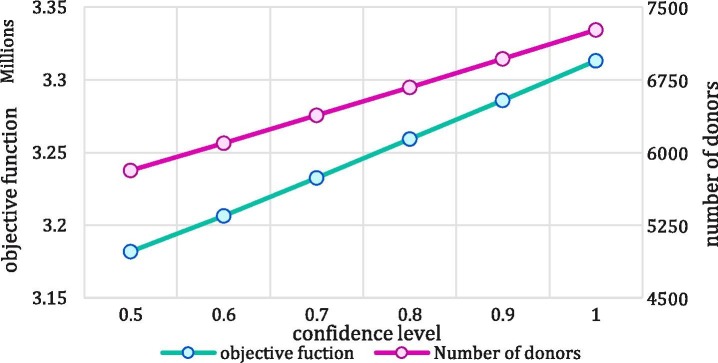
In the first step, the fuzzy model of the first phase is solved, which the results are reported in Table 2 . The total cost of the proposed PSC network in the first phase is 3,259,354.879 $ associated with the collection, production, transportation, and inventory costs. There are no shortage and wastage units, and accordingly, the wastage and shortage costs are equal to zero. The shortage rate of this model is equal to zero, which means that a sufficient number of CCs and PCs are established in optimal locations, which can provide efficient platelet services in demand points. Furthermore, due to the perishability of platelet, a higher amount of collected platelet results in wastages. Accordingly, collecting an optimal number of platelet units will prevent platelet wastage, which leads to cost reduction in the PSC. In this model, the platelet demand and supply and costs are considered as trapezoidal LR-fuzzy numbers, and the confidence level of each chance constraint is determined by 0.8 (${\beta }_1$,${\rho }_1,{\beta }_2$). Notably, the fuzzy form of a given uncertain parameter like $a_i$ is considered as $\left(0.9a_i,1.1a_i,0.05a_i,0.05a_i\right)$. Moreover, the geographic dispersion of the opened CCs and PCs is depicted in Fig. 7 . As shown in this figure, five CCs (1, 2, 5, 7, and 8) and four PCs (1, 2, 4, and 5) are established throughout Fars province. It can be shown that the dispersion of the opened CCs are concentrated in the central part of the Fars province, where the number of populated counties is higher compared to other counties. It can be said that the number of eligible donors is high in this part, and the concentration of CCs in this area is because of this reason. Notably, CCs are not established in some counties. Nevertheless, the lack of CC in a county does not mean that the blood cannot be collected from that county. The reason is that the the collection services can be provided by opened CCs in adjacent counties regarding their coverage radius.

Table 2.

Summary of the results of the first phase.

Objective function($)	Shortage units	Wastage units
3,259,354.879	0	0

Fig. 7.

The opened CCs and PCs throughout Fars province.

Also, the lack of a PC in a county does not mean that the county will face a shortage. The reason is that the platelet can be distributed to the hospital of this county from the opened PCs in other counties regarding the maximum allowable travel time between PCs and hospitals. It can be shown that PCs are dispersed in a wider area than CCs, which leads to facilitate the distribution of platelet units among the hospitals. The amount of collected blood by each bag system (triple or quadruple bag) is reported in Table 3 . Due to the two-day production period, blood is not collected from donors in the last two periods. From 6,981 collected blood units, 49% of them are collected by a triple bag system, and 51% are collected in quadruple bags. It is shown that blood units are not collected in the first period, which means that the demands of the third period are satisfied by available platelet units in PCs.

Table 3.

The number of collected whole blood from each donor group by different bag systems.

Donor groups	Opened CCs	t = 1		t = 2		t = 3		t = 4		t = 5		t = 6
		w = 1	w = 2	w = 1	w = 2	w = 1	w = 2	w = 1	w = 2	w = 1	w = 2	w = 1	w = 2
2	1	0	0	0	0	467	0	0	0	0	0	0	0
5	7	0	0	0	0	0	0	0	0	0	0	0	500
6	1	0	0	360	0	0	0	0	500	0	0	342	25
10	7	0	0	0	0	0	0	0	0	500	105	0	0
10	8	0	0	0	0	0	0	0	0	0	0	37	0
11	5	0	0	0	0	0	0	75	288	182	0	0	0
13	7	0	0	0	0	0	0	0	500	0	0	0	0
17	2	0	0	500	0	0	0	0	500	500	0	0	0
20	2	0	0	0	0	0	500	0	0	0	0	0	0
22	1	0	0	0	0	0	0	0	0	500	0	0	500
28	5	0	0	0	0	0	0	0	0	0	0	0	100

The number of allocated capacity to each opened CC and PC is shown in Table 4 and Table 5 , respectively. It can be said that a large number of donated blood units are collected in CC 1 and CC2 which are enclosed with the most populated counties. Moreover, only one capacity package is assigned to the CC 8, and the blood of donor group 10 is collected in this CC. Due to coverage restriction, this center is established to cover donors who are placed far from the central part of the Fars province to avoid shortage occurrence. Also, the assignment of hospitals to PCs is provided in Fig. A1, in Appendix A.

Table 4.

The number of allocated capacity packages to opened CCs (capacity of each package = 50 units).

Number of allocated capacity packages to opened CCs	t = 2	t = 3	t = 4	t = 5	t = 6
1	4	5	5	5	4
2	5	5	5	5	5
5			4	2	1
7			5	3	5
8					1

Table 5.

The number of allocated capacity packages to opened PCs (capacity of each package = 100 units).

Number of allocated capacity packages to opened PCs	t = 4	t = 5	t = 6	t = 7	t = 8
1	8	9	10	10	8
2			3	1	1
4			5	1	3
5				2	2

Fig. A1.

The assignment of hospitals to PCs in the first phase.

6.2. Disruption scenarios

In the proposed two-phase approach, the model of the first phase is solved, and a nominal schedule is provided during the planning horizon without considering the probable disruptions in PCs. To protect the network against disruptions, a reactive plan is provided to handle the situation more efficiently. In this paper, several disruption scenarios are considered through a different combination of disrupted PCs. Based on the results of the first model, four PCs are established in the Fars province, and accordingly, sixteen disruption scenarios are provided in this paper. It is notable that if a PC is disrupted, it will be entirely out of service, and partial disruption is not considered in this study. The disruption scenarios are provided in Table 6 .

Table 6.

The disrupted PCs under each disruption scenario.

Disrupted PCs	S1	S2	S3	S4	S5	S6	S7	S8	S9	S10	S11	S12	S13	S14	S15	S16
1		✓				✓	✓	✓				✓	✓	✓		✓
2			✓			✓			✓	✓		✓	✓		✓	✓
4				✓			✓		✓		✓	✓		✓	✓	✓
5					✓			✓		✓	✓		✓	✓	✓	✓

6.2.1. Results of the reactive phase

In the second phase, a part of the results of the first phase is the entities of the second phase. The optimal location of PCs is known given the results of the first phase. As said before, sixteen disruption scenarios are considered, the demand of which in the second phase is determined based on the results of the first phase. For instance, in S₆, which PC1 and PC2 are disrupted, the transferred platelets from PC1 and PC2 to hospital $k$, along with the shortage units in that hospital, constitute the demand of hospital $k$ in the second phase. In other words:

$${\left(D_k^{t6}\right)}_{\mathit{second}\mathit{phase}}=\sum _g{\left(\left({Y^{\text{'}}}_{1kg}^{t6}+{Y^{\text{'}}}_{2kg}^{t6}\right).D_k^t.+N_k^t\right)}_{\mathit{first}\mathit{phase}}\forall k,t$$ (70)

Since the number of platelet demands of the second phase is determined based on the results of the first phase, the demand is considered deterministic, while the supply of the platelet and costs are considered as a fuzzy number. The fuzzy form of an uncertain parameter like $a_i$is considered as $\left(0.9a_i,1.1a_i,0.05a_i,0.05a_i\right)$. In addition, the platelet units are collected by the apheresis method in the second phase, and given the different physical conditions for donating apheresis- and whole-blood-derived platelets , the donor pools for these collection methods differentiate with each other. Besides, the reactive strategy is implemented in the network at the beginning of the planning horizon, similar to the proactive strategy. Therefore, the decisions of the second phase are made by considering the effect of all disruption scenarios given the lack of information in the occurred scenario. Summaries of the results of the second phase are inserted in Table 7 , Table 8 , Table 9 , and Table 10 .

Table 7.

Summary of the results of the second phase.

Objective function($)	Average shortage units	Average wastage units
1,673,015.505	0	0

Table 8.

The number of provided apheresis machines under each scenario.

	S1	S2	S3	S4	S5	S6	S7	S8	S9	S10	S11	S12	S13	S14	S15	S16
PCs	0	8	1	2	3	7	10	10	3	3	3	2	8	8	4	0
hospitals	0	1	4	2	2	8	3	4	6	6	9	16	11	14	13	27

Table 9.

Number of donors assigned to PCs in each period under each disruption scenario.

periods	S1	S2	S3	S4	S5	S6	S7	S8	S9	S10	S11	S12	S13	S14	S15	S16
1	0	135	12	40	49	100	176	176	54	60	56	33	141	144	68	0
2	0	154	6	40	47	111	193	193	45	52	57	33	150	160	62	0
3	0	155	5	29	32	122	184	181	34	37	35	35	148	150	40	0
4	0	151	5	27	26	126	178	173	31	31	32	37	148	141	36	0
5	0	129	4	25	18	114	153	142	29	22	23	38	128	114	27	0
6	0	116	4	22	15	102	138	127	25	18	20	38	114	100	23	0
7	0	67	3	8	10	66	75	75	10	12	6	19	73	57	8	0
8	0	30	2	6	6	29	35	35	7	7	4	9	34	26	5	0

Table 10.

Number of donors assigned to hospitals in each period under each disruption scenario.

periods	S1	S2	S3	S4	S5	S6	S7	S8	S9	S10	S11	S12	S13	S14	S15	S16
1	0	9	63	25	15	118	33	30	85	78	73	249	139	127	135	344
2	0	9	60	30	15	117	30	30	90	75	74	264	138	132	134	357
3	0	10	34	35	12	82	44	26	69	46	71	232	98	121	105	309
4	0	8	35	37	11	73	45	23	72	46	69	225	87	119	104	298
5	0	7	24	24	11	49	31	21	48	35	54	172	63	98	78	240
6	0	6	22	20	8	45	25	17	41	30	45	150	55	85	66	210
7	0	4	7	8	6	14	11	11	14	12	25	76	21	44	31	109
8	0	2	3	6	4	7	8	7	9	7	18	38	11	26	20	56

As shown in Table 7, the total costs of the PSC in the second phase are 1,673,015.505$, including collection, production, inventory, transportation costs, and the costs related to platelet transshipment between hospitals. Approximately 60% of the costs are assigned to the procurement process of platelet, and consequently, developing and least developed countries utilize the apheresis method less than developed countries due to the high expense of associated production processes in this method. Furthermore, wastage and shortage do not happen during the planning horizon, and all the demands are satisfied in this phase. Therefore, given the results of the first and second phases, the number of shortage and wastage units in the tailored PSC network is equal to zero under each disruption scenario. In other words, whatever the scenario, not only does the proposed approach provides a sufficient number of platelet units to meet demands, it also avoids platelet expiration.

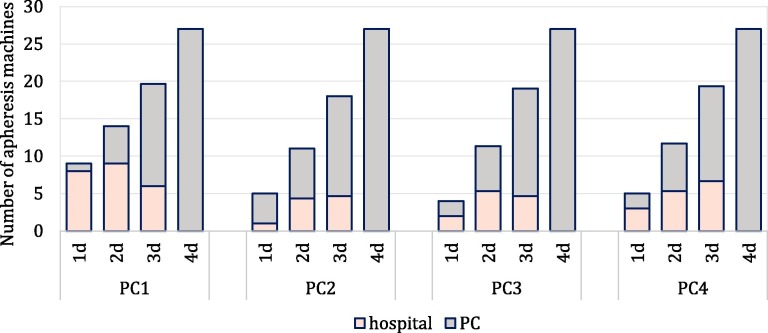
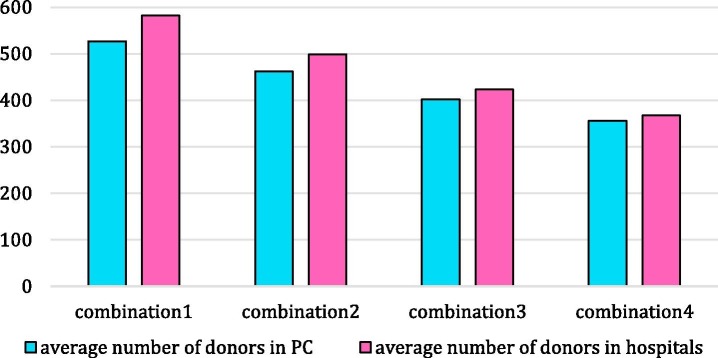
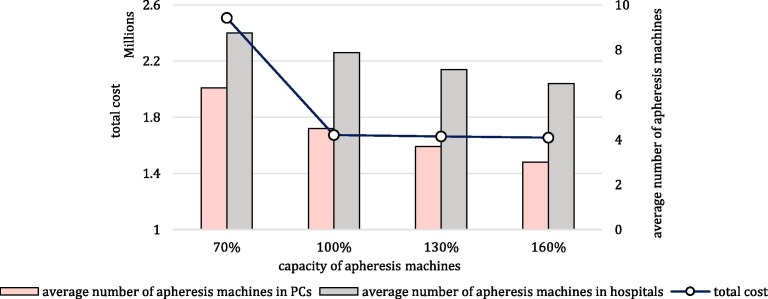
Table 8 shows the number of required apheresis machines in each PC and each hospital under each disruption scenario. Based on the results of first phase, most of the platelet units are produced in PC1 in the first phase, and consequently, more apheresis machines are required if PC1 is out of service. For instance, a higher number of apheresis machines are needed under S₂ (the scenario in which PC1 is disrupted) among the scenarios with one disrupted PC (i.e., S₂, S₃, S₄, and S₅). Furthermore, as the number of disrupted PCs increases, the number of required apheresis machines increases in hospitals than the number of apheresis machines in PCs. The average number of apheresis machines in PCs and hospitals is depicted in Fig. 8 . In this chart, the scenarios are clustered together based on which PC is disrupted. For example, in cluster PC1, the average number of required apheresis machines are depicted in the scenarios in which PC 1 is disrupted, given the number of disrupted PCs. It is evident that all of the apheresis machines are deployed in hospitals in S₁₆, and no apheresis machine is needed under the first disruption scenario in which all PCs work correctly.

Fig. 8.

Number of provided apheresis machines in PCs and hospitals under disruption scenarios (1d: one disrupted PC, 2d: two disrupted PCs, 3d: three disrupted PCs, 4d: four disrupted PCs).

Table 9 and Table 10 show the number of required donors to donate apheresis-derived platelet in PCs and hospitals at each period under each disruption scenario. Given these tables, it is needed to collect platelet from an average of 462 donors in PCs and 499 donors in hospitals under each scenario during the planning horizon, which will survive the life of a multitude of patients. Implementing the proposed two-phase approach in the PSC leads to collecting a sufficient number of platelet units and prevents the probable shortage. It can be said that the average number of assigned donors to hospitals increases in the last scenarios (S₁₂, S₁₃, S₁₄, S₁₅, and S₁₆). As said before, in the last scenario, due to a smaller number of undisrupted PCs, the average number of assigned donors to PCs decreases; however, the capacities of the apheresis machines in undisrupted PCs are used as much as possible to avoid deploying additional apheresis machines in hospitals. Notably, the age of platelet is a crucial factor in the treatment of patients, and it is preferred to transfuse fresh platelets ($g=1,2,3$) to patients during surgeries. Consequently, the consumption rate of platelet in hospitals are different, and the consumption rate of fresh platelet is more than old platelet ($g=4,5,6,7$). The consumption rate of each age group in hospitals is inserted in Table 11 .

Table 11.

The consumption rate of each age group at hospitals.

$\mathit{g}$	1	2	3	4	5	6	7
${\mathrm{\Theta }}_g$	20%	20%	20%	15%	10%	10%	5%

The produced platelet in PCs or hospitals can be used to meet the platelet demand with the age of one day, and the remaining of them can be stored to satisfy the demands with the age of more than one day. Consequently, the number of demands for platelet with the age of more than one day in the next periods affects the number of required platelet to produce. Based on this fact and given the eight-period planning horizon, the average number of required platelet in periods 7 and 8 are relatively smaller than the other periods. Also, the allocation of donors to collection facilities (PCs and hospitals) is determined in this phase, which is illustrated in Fig. 9 for t = 1 and S₈. In this setting, PC1 and PC5 are disrupted, and one donor group assign to each of PC2 and PC4. The produced platelet units in PC2 are transferred to hospital 1, 2, 10, 14, and 20. Also, the collected platelets in PC4 are assigned to hospital 3, 11, 19, and 21, which are in the coverage radius of the associated PC. Moreover, some donor groups are directly referred to hospitals to donate their platelet by apheresis method.

Fig. 9.

Assignment of donor groups to PCs and hospitals, and assignment of PCs to hospitals for ${\mathrm{s}}_8$ and t = 1.

The number of transshipped platelets between hospitals is inserted in Table 12 . The average number of transshipped platelets between hospitals is 288 units throughout the proposed PSC, which satisfies a smaller portion of demands than produced and stored platelet units. In other words, due to assigning high expense for the transshipped platelet, the model prefers to satisfy demand by produced and stored platelet units as much as possible. In the case of shortage situations, the demand is met by transshipped platelet from other hospitals.

Table 12.

Number of transshipped platelets in each period under each disruption scenario.

periods	S1	S2	S3	S4	S5	S6	S7	S8	S9	S10	S11	S12	S13	S14	S15	S16
1	0	0	0	0	0	0	0	0	0	0	0	28	0	0	0	28
2	0	0	182	0	0	209	27	0	182	182	0	306	212	32	182	311
3	0	18	8	0	0	95	79	25	8	8	0	115	98	83	8	119
4	0	82	35	5	0	137	109	97	40	35	5	145	154	128	49	163
5	0	38	3	13	0	41	51	39	15	3	13	54	42	52	16	102
6	0	28	10	11	0	37	36	31	18	11	9	46	40	46	25	72
7	0	0	0	2	0	0	0	0	0	1	0	1	0	0	0	1
8	0	0	0	0	0	0	1	0	0	0	0	0	0	1	0	0

6.3. Sensitivity analyses

Recent studies indicate that the number of disruptive events is increasing, and therefore, designers should employ strategies to protect networks against them (Ivanov et al., 2016, Jalali et al., 2018). When a disruption occurs in a PSC network, some PCs may be out of service, and consequently, hospitals provided by these centers will face shortages. Therefore, if the impact of the disruptions on the network is ignored, the tailored network will not be reliable enough; consequently, the lives of the patients will be threatened and irreparable consequences will be imposed on the network (Mohammadi et al., 2019). In some studies (see, e.g. Haeri et al., 2020, Hosseini-Motlagh et al., 2020a, Hosseini-Motlagh et al., 2020b, Rahmani, 2019, Samani and Hosseini-Motlagh, 2019), proactive approaches have been used to cope with disruption risks. In these cases, networks are designed to be prepared for dealing with disruptions (Choi et al., 2016). Therefore, all decisions are made by considering all of the probable disruptions. For example, a higher number of PCs will be opened, or a higher number of platelet units will be produced at each period in order to hedge against disruptions. This strategy will lead to more conservative decisions and consequently imposes burdensome costs on the network. On the other hand, reactive approaches can be used to protect the network against disruptions. In this paper, a reactive strategy is used in which demands are met by collected platelet through the apheresis method during disruptive events.

Most of the existing studies did not consider the impact of disruptions on the BSC and PSC networks. Among studies that considered the effect of disruptions, many have used a two-stage stochastic approach to deal with uncertainties. To highlight how the occurrence of disruptions impacts the performance of the supply chain and how different strategies work under disruptions, we compared three approaches: 1) without planning for disruptions, 2) using scenario-based approach to cope with disruptions, 3) using two-phase approach to cope wit disruptions. In the first approach, we designed a PSC without considering disruptions, and therefore, the tailored supply chain will encounter a shortage in the event of disruptions. We calculate the average shortage of this approach and take into account the average shortage cost. In the second approach, a scenario-based approach (two-stage stochastic approach) is used to handle disruption in a PSC; 32 scenarios are recognized in this model, given that five candidate locations are considered for PCs in the network. Indeed, the value of the decision variables in the scenario-based approach is an expected value that hedge against all the scenarios.

The number of shortage units and the total costs of these approaches are compared in Fig. 10 . As shown in the figure, the total costs of the PSC significantly decrease in the case of using the two-phase approach, in which the costs decrease by 20% in comparison to scenario-based approach, and the costs reduce approximately 80% than the case that disruption does not take into account. Furthermore, any shortage occurs in the two-phase programming approach, and consequently, the shortage rate of the two-phase approach is significantly lower than the shortage rates of other approaches. Therefore, by considering the disruption in the PSCs, shortage rate and costs decrease remarkably. Finally, among the approaches used to cope with disruptions in this paper, the two-phase approach outperforms other approaches in the context of cost-effectiveness and based on the shortage measure.

Fig. 10.

Comparison between different approaches in the face of disruptions based on (a) total cost and (b) average shortage.

As said before, the fuzzy stochastic approach is utilized to deal with uncertainty in demand, supply, and costs. In this approach, confidence levels of chance constraints are determined based on the decision-makers’ preferences. A conservative decision-maker selects the high value for the confidence level of chance constraints. In Fig. 11 , the effect of different values of the confidence level on the total cost of the first phase and the number of required donors is investigated. As shown in this figure, by increasing the value of the confidence level, the total cost of the objective function increases. In other words, a higher value of the confidence level entails the network to collect platelet from a large number of donors and produce a large number of platelets; consequently, the required number of donors and total costs of the PSC increase.

Fig. 11.

Effect of different confidence level on the total costs and number of required donors in the first phase.

Platelet is an extremely perishable product. Thus, to avoid the expiration of platelet units, maximum allowable transportation times between blood facilities are considered in this model. In Fig. 12 , the impact of different values of maximum travel time between PCs and hospitals ($\tau$) on the total costs and shortage units of the first phase is investigated. As $\tau$ increases, the produced platelet in a PC can be sent to the farther hospitals, and the opened PCs can provide services for a large number of hospitals. Accordingly, the required number of PCs decreases, and consequently, the cost of establishment PCs decreases. Additionally, by reducing the value of $\tau$, the number of shortages will increase. In this case, the coverage radius of the PCs shrinks in such a way that PCs cannot send platelets to some hospitals. Accordingly, the number of shortage units will increase, which leads to an increased total cost.

Fig. 12.

Effect of the different maximum allowable travel time between PCs and hospitals on total cost and shortage units of the first phase.

The lateral transshipment strategy is exploited in this paper to avoid platelet shortage and expiration in hospitals. In Fig. 13 , the impact of the various price of transshipped platelet units on the costs of the network is investigated. It is evident that by raising the price of the transshipped units, the transshipment costs increase; the increased price leads to a reduction in the number of transshipped units; consequently, hospitals will face a shortage, which results in an increased shortage costs. On the other hand, in order to satisfy the shortage, the number of stored units increases, which results in an increasing inventory cost. Finally, the total costs of the supply chain increase.

Fig. 13.

Effect of the various price of transshipped units between hospitals on (a) total cost, (b) transshipment cost, (c) inventory cost, (d) shortage cost in the second phase.

As mentioned before, the different ages of the platelet have different transfusion usages. To evaluate the effect of the platelet age on the number of required donors, various age combinations are inserted in Table 13 . In combinations 1 and 2, a large number of fresh units are required, and in order to satisfy their demands, it is needed to collect platelet from a large number of donors. Accordingly, the number of donors in PCs and hospitals increases, as shown in Fig. 14 .

Table 13.

Different combination of platelet consumption rate in the second phase.

Age	1	2	3	4	5	6	7
combination1	50%	15%	15%	5%	5%	5%	5%
combination2	20%	20%	20%	10%	10%	10%	10%
combination3	10%	10%	20%	20%	20%	10%	10%
combination4	10%	10%	10%	10%	20%	20%	20%

Fig. 14.

Effect of different consumption rate on the number of donors in PCs and hospitals in the second phase.

In combination 3, the consumption rate of the young ($g=3,4,5$) platelet is high, and in combination 4, the consumption rate of the old ($g=6,7$) platelet is higher than fresh ($g=1,2$) and young platelets. Therefore, from combination 1 to combination 4, the consumption rate of fresh platelet decreases, which leads to collecting a lower number of platelet, and consequently, lower production cost. On the other hand, the model seeks to store a higher number of platelet as well as transshipped units in order to satisfy young and old demand. As a result, the transshipment costs and inventory cost increase, and the production costs decrease, and the total cost increases overall. The effect of different consumption rate on the costs of the second phase is depicted in Fig. 15 .

Fig. 15.

Effect of different consumption rate on the costs of the second phase.

The impact of different capacities of apheresis machines on the number of deployed apheresis machines in PCs and hospitals is investigated in Fig. 16 . It is evident that as the capacity of an apheresis machine increases, the number of assigned donors to that machine grows, and consequently, the number of required apheresis machines decreases. Accordingly, the costs paid for the purchase of apheresis machines decrease, which leads to a reduction in total costs.

Fig. 16.

Effect of different capacities on the number of deployed apheresis machines in PCs and hospitals.

The purpose of this study is to design and plan a platelet supply chain network with the aim of minimization the cost of platelet supply chain network in disruptions. Platelet is a high expense product, and its shortage jeopardizes the patients’ lives. Therefore, high costs are considered for per shortage unit of platelet (the shortage cost of a platelet unit is considered 3,250$ in this study). On the other hand, due to the event of unpredictable conditions in platelet supply chains, there is a need to have platelet stocks at all times. However, its wastage should be avoided as much as possible. Thus, the considered cost for every wastage unit is high (the wastage cost of a platelet unit is considered 650$ in this study). Therefore, the model aims to minimize the number of platelet shortage and wastage since their imposed costs are higher than other costs in the model, such as inventory cost, collection cost, and production costs. Accordingly, there are no wastage and shortage units in this study. Moreover, the demand and supply may vary during disastrous conditions, and therefore, we embed demand and supply fluctuations in the model by applying the fuzzy approach, and we also conduct a sensitivity analysis on the confidence level of the first phase to demonstrate its impact on the number of required blood donors. The number of blood donors varies from 5,816 to 7,266 regarding the different value of confidence level. According to the blood donation rate in Iran (20–29.9 donation of 1000 population), this supply fluctuation can be handled easily. Also, based on the extracted historical data and information from the IBTO, we considered constant discard rate for blood in production centers.

6.4. Re-planning the network

In this paper, we designed a PSC, in which the shortages stemmed from disruptions, along with shortages of the first phase, are responded by apheresis platelets reactively. It is noteworthy that apheresis-derived platelets are expensive, and some people are not willing to donate platelet through this method due to its time-consuming process and its possible side effects. Thus, we aim to re-plan designed network in the first phase by implementing some strategies for several purposes: 1) to better protect the network against disruption by decreasing the dependency of the network to reactive strategy, 2) to increase the portion of demands that are fulfilled by whole-blood-derived platelets, 3) to reduce the need for apheresis platelets. To do so, we adjust the capacity of PCs in the designed network in the first phase by using proactive strategies entitled to redundancy and flexibility in the capacities. By using redundancy strategy, we increase production capacities compared with the assigned capacities in the first phase, and by using flexibility strategy, we can re-allocate the assigned capacities to achieve a further reduction in the need for apheresis platelets. To obtain the optimal production capacity, we apply scenarios in the model of the first phase and solve the model for each scenario; then, we achieve the optimal capacity of each disruption scenario, which are inserted in Table 14 . By assigning the capacities according to this table, the average number of platelet shortage units experiences further reduction, and the need for apheresis platelets decreases 50% on average.

Table 14.

Optimal capacity of PCs for producing whole-blood-derived platelets under each scenario.

		3	4	5	6	7	8			3	4	5	6	7	8			3	4	5	6	7	8
S1	1		8	9	10	10	8	S2	2	5	6	5	5	4	4	S3	1		9	9	10	10	9
	2				3	1	1		4		5	9	14	8	7		4				5	2	3
	4				5	1	3		5					1	3		5					1	2
	5					2	2
		3	4	5	6	7	8			3	4	5	6	7	8			3	4	5	6	7	8
S4	1	6	10	10	11	10	8	S5	1	4	9	10	11	10	8	S6	4	1	9	10	14	11	10
	2				3	1	1		2			3	1	1			5					1	3
	5				2	2	4		4		4	6	2	4
		3	4	5	6	7	8			3	4	5	6	7	8			3	4	5	6	7	8
S7	2	10	13	9	13	9	7	S8	2	6	7	5	5	4	4	S9	1	8	10	9	14	10	9
	5			5	5	4	5		4								5				2	2	3
		3	4	5	6	7	8			3	4	5	6	7	8			3	4	5	6	7	8
S10	1	6	10	9	14	10	9	S11	1	9	10	14	10	11	9	S12	5			5	5	4	5
	4								2				4	1	1
		3	4	5	6	7	8			3	4	5	6	7	8			3	4	5	6	7	8
S13	4	9	13	12	14	11	11	S14	2	9	14	8	14	9	8	S15	1	10	13	10	14	11	10

In Fig. 17 , we demonstrate the average number of shortages occurred under disruptions for a various number of production capacities, and we also show the decreased portion of required apheresis platelets in the re-planned network rather than those used in the second phase. It is evident that the number of required apheresis platelet increases as the production capacity decreases. By diminishing the capacity, the number of shortages increases which should be responded by apheresis platelets. Thus, the need for apheresis platelets increases. Besides, it is apparent that the amount of shortage remains stable after achieving the optimal production capacity, and applying redundancy strategy does not affect the number of shortages. The reason is that some hospitals are at the coverage radius of one PC. Thus, if that specific PC is disrupted, the hospitals cannot be provided with undisrupted PCs regardless of how much capacity is assigned to that undisrupted centers. So, the shortage will occur, which cannot be fulfilled by assigning extra capacity. In conclusion, if the capacities are assigned according to Table 14, the network will culminate in the further reduction in shortage units by using redundancy and flexibility strategy, which leads to a decreased number of apheresis platelets.

Fig. 17.

The average number of shortage units and decreased portion of apheresis platelets for different amount of production capacities under disruptions.

7. Conclusions

In this section, the key finding of the study, practical implications, the limitations of the research, and future research avenues are provided.

7.1. Summary of this paper

In this paper, we focus on designing a PSC under uncertainty and disruption risks. To do so, we devise a two-phase approach that exploits proactive strategies to deal with uncertainties and reactive strategies to harness disruptions; therefore, contributing to BSCN literature, which often uses proactive strategies. To address the proposed approach, in the first phase, named the proactive phase, a nominal PSC is tailored under operational risks as demand, supply, and costs uncertainties. The fuzzy approach is used to deal with uncertainty, and the platelet is collected by whole blood donation in this phase. By solving the model of this phase, the location, allocation, and capacity decisions are determined before the real data reveals itself. The impact of disruptions is not considered in the first phase. Therefore, the second phase, named reactive phase, is triggered to harness the impact of disruptive events and update the provided plan in the first phase based on the portion of revealed data. In the reactive phase, the occurred shortages due to disruptions, along with the shortage units of the first phase, are satisfied by collected platelet in PCs and hospitals through apheresis method. Moreover, the stochastic-fuzzy approach is used to deal with disruption and operational (supply and cost) risks. The proposed approach is implemented to a real case of Iran, Fars province, and is compared with the two-stage stochastic approach as a mostly used approach in the literature. Moreover, a series of sensitivity analyses are conducted. The key findings and real-life implications of the proposed approach are provided in the following.

7.2. Key findings and real-life implications

The results demonstrate that the performance of the two-phase approach is significantly enhanced compared with the two-stage approach regarding the quantity of the shortage units and the total cost of the supply chain. The proposed model makes the supply chain resilient to disruptions and shortage, simultaneously. Although all proactive approaches, such as the stochastic approach, aim to protect networks against disruptions, no alternative is considered in these approaches in the case of shortages. The proposed two-phase approach uses apheresis-derived platelets as a reactive strategy to respond to shortage immediately, either shortage are due to lack of sufficient supply of whole-blood-derived platelet or due to disruptive events. The proposed network is capable of absorbing the effects of disruptions efficiently and adapting its plan to enhance the performance of the network; thus, resulting in more resiliency for the network.

The following managerial insights are resulted from implementing the two-phase approach:

• 1)The decision-makers of the PSCs can benefit from proactive and reactive strategies against disruptions and operational risks; as it results in more efficient, cost-effective, and resilient supply chains. Using apheresis-derived platelets can be a proper strategy due to requiring few preparations and testing procedures; thus, it responds more quickly in case of shortages.
• 2)Collecting platelet through the apheresis method in hospitals can be applied for several reasons: first, the platelet production will not entirely depend on PCs. Thus, the supply chain can satisfy demands through apheresis platelet in the case of occurring disruptions in PCs. Second, the shortage will be responded faster.
• 3)Decision-makers can re-plan the proposed network regarding the results of the first and second phases to lessen the efforts needed after disruptive events. (i.e., to lessen the number of collected apheresis platelet after a disruption). Thus, not only can the network harness disruption efficiently, but also it will be less dependent on apheresis-derived platelet. In fact, we made it to be less dependent on this method, since in some countries, the donors are less likely to donate their blood through the apheresis method.
• 4)Considering the service area for blood centers (CCs and PCs) is beneficial from several points of view: 1) This feature leads to the appropriate dispersion of blood centers. Thus, donors’ willingness to donate blood increases due to better access to CCs. 2) This feature enforces the opened centers to disperse throughout the area to cover more donor groups. It leads to collect platelet from different donor groups, and the supply chain will not depend on the limited number of donors. 3) Regarding this feature, the freshness of the platelet will be preserved due to the appropriate distribution of centers. 4) The executives can better manage the network by being aware of the potential services that will be needed to serve the corresponding centers.

7.3. Limitations and future studies

This study, however, is subject to several limitations. The proposed approach can support several types of disruptions, such as partial disruption in PCs and incorporating disruptions in other facilities and network links. Moreover, the number of scenarios in the second phase depends on the number of opened PCs in the first phase. Thus, the number of scenarios may increase dramatically in some cases, in which scenario reduction techniques can be applied. Other research avenues can be suggested, including identifying best candidate location of blood centers using multi-attribute decision making approaches, considering motivational initiatives to encourage blood donation, estimating the platelet supply by considering several types of donors (first-time donors or repetitive donors), considering different platelet extraction methods from whole blood (buffy coat of platelet-rich plasma), monitoring the freshness of platelets by using internet of things-based technologies during transportation processes, applying adjustable robust optimization to the presented PSC, and considering the ineligibility of donors during lockout periods.

CRediT authorship contribution statement

Mohammad Reza Ghatreh Samani: Conceptualization, Writing - review & editing, Methodology, Software. Seyyed-Mahdi Hosseini-Motlagh: Conceptualization, Methodology, Formal analysis, Supervision. Shamim Homaei: Investigation, Writing - original draft, Data curation, Software.

Appendix A. . Tables and figures

See Table A1, Table A2, Table A3 , and Fig. A1 .

Table A1.

Summary of reviewed papers in the context of BSCs.

Reference paper	Types of blood product	Hierarchical level	Collection method	Planning horizon	Modeling approach	Objective function	Uncertainty approach	Time period	Disruption approach	Lateral transshipment	Solution approach	Case study
Wang and Ma (2015)	RBC	inventory	whole blood	tactical, operational	MIP	number of transshipped units	–	multi	–	yes	exact	no
Osorio et al. (2017)	RBC,PLS,PLT,CR	integrated	whole blood, apheresis	strategic	ILP	cost	–	multi	–	no	exact	yes
Ensafian et al. (2017)	PLT	integrated	whole blood, apheresis	strategic, tactical	MILP	cost	Stochastic, robust	multi	–	no	exact	yes
Ensafian and Yaghoubi (2017)	PLT	integrated	whole blood, apheresis	operational, tactical	MILP	cost, freshness	robust	multi	–	no	exact	yes
Rajendran and Ravindran (2017)	PLT	inventory	whole blood	tactical	MILP	ordered platelet units	stochastic	multi	–	no	heuristic	no
Ramezanian and Behboodi (2017)	WB	collection	whole blood	strategic, tactical	MILP	cost	robust	multi	–	no	exact	yes
Zahiri and Pishvaee (2017)	WB,PLS,PLT,RBC	integrated	whole blood	strategic, tactical	MINLP	cost, shortage	robust-fuzzy	multi	–	no	exact	yes
Salehi et al. (2019)	PLS,PLT	integrated	whole blood	strategic, tactical	MILP	cost	stochastic, robust	multi	–	no	exact	yes
Osorio et al. (2018a)	RBC,PLS,PLT,CR	integrated	whole blood, apheresis	strategic	ILP	cost, required donors	stochastic	single	–	no	exact	yes
Diabat et al. (2019)	WB	inventory	whole blood	strategic	MILP	cost, products’ delivery time	robust	multi	–	no	heuristic	no
Eskandari-Khanghahi et al. (2018)	PLT	integrated	apheresis	strategic, tactical	MINLP	cost, environmental effects, social effects	fuzzy	multi	–	no	heuristic	no
Heidari-Fathian and Pasandideh (2018)	RBC,PLS,PLT	integrated	whole blood	tactical	MILP	cost, shortage, greenhouse gas emission	robust	multi	–	no	heuristic	no
Rahmani (2019)	WB	integrated	whole blood	strategic, tactical	MILP	cost	robust	multi	robust	no	heuristic	yes
Fahimnia et al. (2017)	WB	integrated	whole blood	tactical	MILP	Cost, blood delivery time	stochastic	multi	–	no	heuristic	no
Osorio et al. (2018b)	RBC,PLS,PLT,CR	integrated	whole blood, apheresis	strategic	MILP	cost	–	single	–	no	exact	yes
Zahiri et al. (2018)	WB,PLS,PLT,RBC	integrated	whole blood	operational, tactical	MINLP	cost, remaining shelf life	stochastic	multi	–	no	heuristic	no
Samani and Hosseini-Motlagh (2019)	RBC,PLS,PLT	integrated	whole blood	strategic, tactical	MILP	cost	robust-fuzzy	multi	robust	no	exact	yes
Samani et al. (2019)	WB,PLS,PLT,RBC	integrated	whole blood, apheresis	strategic, tactical	MILP	cost, freshness, best candidate locations	robust	multi	–	no	exact	yes
Yousefi Nejad Attari et al. (2019)	WB	collection	whole blood	strategic, tactical	MILP	cost, blood delivery time	stochastic, robust	multi	–	no	exact	yes
Gilani Larimi et al. (2019)	PLT	inventory	whole blood, apheresis	tactical	MILP	cost, service level	stochastic, robust	multi	–	yes	exact	yes
Hamdan and Diabat (2019)	RBC	integrated	whole blood	strategic, tactical	MIP	cost, blood delivery time	Stochastic	multi	–	no	exact	yes
Haeri et al. (2020)	RBC,PLS,PLT,CR	integrated	whole blood, apheresis	strategic, tactical	MILP	cost, social aspect, resiliency	robust	single	robust	no	exact	yes
Hosseini-Motlagh et al. (2020a)	RBC,PLS,PLT,CR	integrated	whole blood, apheresis	strategic, tactical	MIP	cost	fuzzy, stochastic, robust	multi	stochastic	no	exact	yes
Hosseini-Motlagh et al. (2020b)	RBC	integrated	whole blood	strategic, tactical	MILP	cost, number of substituted unites	stochastic, robust	multi	stochastic	no	exact	yes
Chen et al. (2019)	PLT	inventory	whole blood	tactical, operational	MIP	cost	–	multi	–	no	heuristic	no
Paul et al. (2019)	RBC	inventory	whole blood	tactical, operational	MIP	cost	–	single	–	yes	exact	no
This study	platelet	integrated	whole blood, apheresis	strategic, tactical, operational	MILP	cost	stochastic, fuzzy	multi	two-phase	yes	exact	yes

RBC: Red Blood Cells; PLS: Plasma; PLT: Platelet; CR: Cryoprecipitate; WB: Whole Blood; ILP: Integer Linear Programming; MILP: Mixed Integer Linear Programming; MINLP: Mixed Integer Non-Linear Programming; MIP: Mixe d Integer Programming.

Table A2.

Geographic coordinates of counties in Fars province.

No.	County	Population	Longitude	Latitude	No.	County	Population	Longitude	Latitude
1	Shiraz	1,869,001	52.53337958	29.59665708	16	Zarrin Dasht	73,199	54.41901208	28.36092890
2	Marvdasht	323,434	52.79760566	29.86863716	17	Ghir and Karzin	71,202	53.04647208	28.47542630
3	Kazerun	266,217	51.64990935	29.61633016	18	Estahban	68,850	54.05523077	29.12442874
4	Jahrom	228,532	53.56076152	28.50497943	19	Mohr	64,827	52.86973539	27.55087575
5	Larestan	213,930	54.32192349	27.66208440	20	Kharameh	54,864	53.31612468	29.49704731
6	Fasa	205,187	53.64331052	28.94666897	21	Gerash	53,907	54.13573191	27.67477134
7	Darab	201,489	54.55291063	28.75533500	22	Khorrambid	50,522	53.18945494	30.61601411
8	Firuzabad	121,417	52.57127953	28.84452269	23	Bavanat	50,418	53.59014387	30.49227509
9	Mamasani	117,527	51.54732478	30.10706796	24	Farashband	45,459	52.09177727	28.86104080
10	Neyriz	113,291	54.32005647	29.20150707	25	Rostam	44,386	51.52754919	30.24626243
11	Abadeh	100,831	52.64836051	31.16248247	26	Arsanjan	43,725	53.30252089	29.91141944
12	Eqlid	93,763	52.68857018	30.89270422	27	Khonj	41,359	53.43681894	27.88729792
13	Lamerd	91,782	53.18653033	27.34171385	28	Sarvestan	38,114	53.22168282	29.27845111
14	Sepidan	91,049	51.98532882	30.25965241	29	Pasargad	30,118	53.18061412	30.18863338
15	Kavar	83,882	52.68819232	29.21144181

Table A3.

Geographic coordinates of hospitals in Fars province.

No.	Hospital name	Location	Longitude	Latitude	No.	Hospital name	Location	Longitude	Latitude
1	Namazi hospital	Shiraz	52.518777	29.632010	12	Imam Khomeini hospital	Estahban	54.041943	29.123100
2	Faqihi hospital	Shiraz	52.528785	29.626432	13	Amiralmomenin Ali hospital	Gerash	54.137114	27.675728
3	Peymaniye hospital	Jahrom	53.529822	28.517120	14	Vali’e Asr hospital	Arsanjan	53.293701	29.918129
4	Vali’e Asr hospital	Fasa	53.628981	28.934773	15	Vali’e Asr hospital	Eqlid	52.679589	30.873293
5	Imam Reza hospital	Larestan	54.292711	27.653484	16	Vali’e Asr hospital	Khoram bid	53.165653	30.597415
6	Vali’e Asr hospital	Lamerd	53.194670	27.326123	17	Vali’e Asr hospital	Bavanat	53.625971	30.469324
7	Shohada hospital	Neyriz	54.337896	29.191305	18	Imam Hassan hospital	Darab	54.555702	28.743578
8	Vali’e Asr hospital	Kazerun	51.670864	29.637025	19	Imam Baqer hospital	Qir and Karzin	53.044595	28.473824
9	Imam Khomeini hospital	Abadeh	52.628091	31.160395	20	Imam Ja’far Sadiq hospital	Pasargad	53.144167	30.080686
10	Imam Hussein hospital	Sepidan	51.991033	30.237843	21	Khonj hospital	Khonj	53.439648	27.858552
11	Qaem hospital	Firuzabad	52.588281	28.837099	22	Shohada hospital	Sarvestan	53.211563	29.275552

Appendix B. . Notations of the proposed models

Notations of the proactive phase

The following notations are used to formulate the proactive phase mathematical model:

Sets
$e$	Set of donor groups ,$e=\{1,\cdots ,E\}$
$i$	Set of candidate locations for CCs,$i=\{1,\cdots ,I\}$
$j$	Set of candidate locations for PCs,$j=\{1,\cdots ,J\}$
$k$	Set of hospitals,$k=\{1,\cdots ,K\}$
$g$	Set of ages of platelets,$g=\{1,\cdots ,G\}$
$t$	Set of time periods, $t=\{1,\cdots ,T\}$
$w$	Set of fractionation processes,$w=\{1,\cdots ,W\}$
Parameters
${\alpha }_{\mathit{iw}}$	Cost of collecting whole blood from a donor by collection process $w$ in CC $i$
$\xi$	Fixed cost of assigning a donor group to a CC
${\chi }_{\mathit{ei}}$	Distance between donor group $e$ and CC$i$
$\mathrm{\Delta }$	Maximum coverage radius of CCs to serve donors
${\mathrm{\Gamma }}_e$	Maximum number of eligible whole blood donors in donor group $e$
$\beta$	Fixed cost of a CC establishment
${\beta }^{\text{'}}$	Fixed cost of each capacity package added in CCs
${\gamma }_{\mathit{ij}}$	Cost of transporting a whole blood unit from CC $i$ to PC $j$
${\delta }_w$	The number of obtained whole-blood-derived platelet units from a donor by collection process$w$
$\epsilon$	The capacity of each assigned package to CCs
$\rho$	Maximum allowable transportation time between CCs and PCs (hours)
${\upsilon }_{\mathit{ij}}$	1, if transportation time between CC $i$ and PC $j$ is less than or equal to $\rho$; 0, otherwise
$\zeta$	Fixed cost of a PC establishment
${\zeta }^{\text{'}}$	Fixed cost of each package capacity added in PCs
${\eta }_{\mathit{jk}}$	Cost of transporting a whole-blood-derived platelet from PC $j$ to hospital $k$
$\theta$	Inventory cost of a whole-blood-derived platelet unit in PCs
$\vartheta$	The production cost of a whole-blood-derived platelet unit in PCs
$\mu$	Wastage cost of a whole-blood-derived platelet unit in PCs
$\varrho$	Shortage cost a whole-blood-derived platelet unit in hospitals
$\lambda$	The capacity of each package added to PCs
$\tau$	Maximum allowable transportation time between PCs and hospitals (hours)
${\sigma }_{\mathit{jk}}$	1, if transportation time between PC $j$ and hospital $k$ is less than or equal to $\tau$; 0, otherwise
${\phi }_{\mathit{jg}}^t$	The available amount of whole-blood-derived platelet units of age $g$ in PC $j$ at period$t$
$\mathrm{\Omega }$	Discard rate of collected whole blood in PCs
$D_k^t$	Demand for platelet in hospital $k$ at period$t$
$M$	A large number
Decision variables
$U_{\mathit{ei}}^t$	1, if donor group $e$ is assigned to CC $i$ at period $t$; 0, otherwise
$X_{\mathit{ei}}^t$	Number of persons of donor group $e$ whose blood is collected in CC $j$ at period $t$
${X\text{'}}_{\mathit{eiw}}^t$	Number of persons of donor group $e$ whose blood is collected in CC $j$ via collection process $w$ at period$t$
$F_i$	1, if a CC is established in location $i$; 0, otherwise
${F\text{'}}_i^t$	Number of allocated capacity packages to CC $i$ at time period$t$
$P_{\mathit{ijw}}^t$	Number of donors whose blood are collected via collection process $w$ in CC $i$ and will be processed in PC $j$ at time period $t$
$V_j$	1, if a PC is established in location$j$; 0, otherwise
${V^{\text{'}}}_j^t$	Number of allocated capacity packages to PC $j$ at time period$t$
${Y\text{'}}_{\mathit{jkg}}^t$	The proportion of maximum demand for platelet of age $g$ in hospital $k$, which will be satisfied by the transferred whole-blood-derived platelets from PC $j$ at period$t$
$Q_j^t$	Number of processed whole-blood-derived platelet units in PC $j$ at period$t$
$W_j^t$	Wastage level of whole-blood-derived platelet in PC $j$ at period$t$
$R_{\mathit{jg}}^t$	Inventory level of whole-blood-derived platelet of age $g$ in PC $j$ at period$t$
$N_k^t$	Shortage level of platelet in hospital $k$ at period$t$

Notations of the reactive phase

The following sets, parameters, and decision variables are used in the formulation of reactive phase:

Sets
$e$	Set of donor groups,$e=\{1,\cdots ,E\}$
$j$	Set of PCs,$j=\{1,\cdots ,J\}$
$k,k\text{'}$	Set of demand points,$k=\{1,\cdots ,K\}$
$g$	Set of ages of platelet, $g$={1,…,G}
$t$	Set of periods, $t$={1,…,T}
$s$	Set of disruption scenarios, $s$={1,…,S}
Parameters
${\mathrm{\Gamma }}_e$	Maximum number of eligible apheresis donors in donor group $e$
${\chi }_{\mathit{ej}}$	Distance between donor group $e$ and PC$j$
${\chi \text{'}}_{\mathit{ek}}$	Distance between donor group $e$ and hospital$k$
$\mathrm{\Delta }$	Maximum coverage radius of PCs to serve donors
${\mathrm{\Delta }}^{\text{'}}$	Maximum coverage radius of hospitals to serve donors
$\alpha$	Cost of collecting platelet from a donor through the apheresis method in PCs
$\alpha \text{'}$	Cost of collecting platelet from a donor through the apheresis method in hospitals
$\xi$	Fixed cost of assigning a donor group to a PC
$\xi \text{'}$	Fixed cost of assigning a donor group to a hospital
$\delta$	The number of obtained apheresis-derived platelet units from a donor
$\epsilon$	The capacity of each apheresis machine in PCs
$\epsilon \text{'}$	The capacity of each apheresis machine in hospitals
$\psi$	Fixed cost of an apheresis machine in PCs
$\psi \text{'}$	Fixed cost of an apheresis machine in hospitals
${\phi }_{\mathit{jg}}^t$	The available amount of apheresis-derived platelet of age $g$ in PC $j$ at period$t$
${\phi \text{'}}_{\mathit{kg}}^t$	The available amount of apheresis-derived platelet of age $g$ in hospital $k$ at period$t$
$\vartheta$	The production cost of an apheresis-derived platelet unit in PCs
$\vartheta \text{'}$	The production cost of an apheresis-derived platelet unit in hospitals
$\theta$	Inventory cost of an apheresis-derived platelet unit in PCs
$\theta \text{'}$	Inventory cost of an apheresis-derived platelet unit in hospitals
${\eta }_{\mathit{jk}}$	Cost of transporting an apheresis-derived platelet unit from PC $j$ to hospital $k$
$\tau$	Maximum allowable transportation time between PCs and hospitals (hours)
${\sigma }_{\mathit{jk}}$	1, if transportation time between PC $j$ and hospital $k$ is less than or equal to $\tau$; 0, otherwise
$\mu$	Wastage cost of an apheresis-derived platelet unit in PCs
${\mu }^{\text{'}}$	Wastage cost of an apheresis-derived platelet unit in hospitals
$\varrho$	Shortage cost of an apheresis-derived platelet unit in hospitals
$\varphi$	Cost of a transshipped platelet unit to a hospital from another hospital
$\mathrm{\Omega }$	Discard rate of collected apheresis platelet in PCs
$\mathrm{\Omega }\text{'}$	Discard rate of collected apheresis platelet in hospitals
${\pi }^s$	Probability of disruption scenario$s$
$D_k^{\mathit{ts}}$	Demand for platelet in hospital $k$ at period $t$ under scenario $s$
$d_{\mathit{kg}}^t$	Injected apheresis platelet units of age $g$ in hospital $k$ at period$t$
${\mathit{dis}}_j^s$	Disrupted PCs under scenario$s$
$M$	A large number
Decision variables
$U_{\mathit{ej}}^{\mathit{ts}}$	1, if donor group $e$ is assigned to PC $j$ at period $t$ under scenario $s$; 0, otherwise
${U\text{'}}_{\mathit{ek}}^{\mathit{ts}}$	1, if donor group $e$ is assigned to hospital $k$ at period $t$ under disruption scenario $s$; 0, otherwise
$X_{\mathit{ej}}^{\mathit{ts}}$	Number of persons of donor group $e$ whose blood is donated in PC $j$ at period $t$ under scenario$s$
${X\text{'}}_{\mathit{ek}}^{\mathit{ts}}$	Number of persons of donor group $e$ whose blood is donated in hospital $k$ at period $t$ under scenario$s$
${Y\text{'}}_{\mathit{jkg}}^{\mathit{ts}}$	The proportion of maximum demand for platelet of age $g$ in hospital $k$ which will be satisfied by transferred apheresis-derived platelet from PC $j$ at period $t$ under scenario $s$
${Z\text{'}}_{\mathit{kg}}^{\mathit{ts}}$	The proportion of maximum demand for platelet of age $g$ in hospital $k$ which will be satisfied by collected apheresis-derived platelet in that hospital at period $t$ under scenario $s$
$Q_j^{\mathit{ts}}$	Amount of processed apheresis platelet in PC $j$ at period $t$ under scenario$s$
${Q\text{'}}_k^{\mathit{ts}}$	Amount of processed apheresis platelet in hospital $k$ at period $t$ under scenario$s$
$F_j^s$	Number of apheresis machines in PC $j$ under scenario$s$
${F\text{'}}_k^s$	Number of apheresis machines in hospital $k$ under scenario$s$
$V_{kk\text{'}g}^{\mathit{ts}}$	Amount of apheresis-derived platelet of age $g$ delivered to hospital $k$ from hospital $k\text{'}$ at period $t$ under scenario$s$
$N_{\mathit{kg}}^{\mathit{ts}}$	Shortage level of platelet of age $g$ in hospital $k$ at period $t$ under scenario$s$
Intermediate variables
$R_{\mathit{jLg}}^{\mathit{ts}}$	Inventory level of apheresis-derived platelet of age $g$ in PC $j$ at period $t$ under scenario$s$
${R\text{'}}_{\mathit{kg}}^{\mathit{ts}}$	Inventory level of apheresis-derived platelet of age $g$ in hospital $k$ at period $t$ under scenario$s$
$W_j^{\mathit{ts}}$	Wastage level of apheresis-derived platelet in PC $j$ at period $t$ under scenario$s$
${W\text{'}}_k^{\mathit{ts}}$	Wastage level of apheresis-derived platelet in hospital $k$ at period $t$ under scenario$s$

Appendix C. . Structural properties of the proposed model

Model of the proactive phase

In this phase, a mixed-integer linear programming model is developed to design a nominal PSC without considering disruptions, in which the platelet is collected through the whole blood method. The proposed network comprises of donor groups, CCs, PCs, and hospitals. The objective function aims to minimize the costs of the network comprises of cost of assigning donor groups to CCs (${\sum }_{e,i,t}\xi .U_{\mathit{ei}}^t$), cost of opening CCs (${\sum }_i\beta .F_i$), cost of provided blood packages in CCs (${\sum }_{i,t}{\beta }^{\text{'}}.{F\text{'}}_i^t$), cost of collecting blood from donors in CCs (${\sum }_{e,i,w,t}{\alpha }_{\mathit{iw}}.{X\text{'}}_{\mathit{eiw}}^t$), cost of transporting blood from CCs to PCs (${\sum }_{i,j,w,t}{\gamma }_{\mathit{ij}}.P_{\mathit{ijw}}^t$), cost of opening PCs (${\sum }_j\zeta .V_j$), cost of provided capacities in PCs (${\sum }_{j,t}{\zeta }^{\text{'}}.{V^{\text{'}}}_j^t$), cost of platelet production in PCs (${\sum }_{i,j,w,t}\vartheta .P_{\mathit{ijw}}^t$), inventory cost in PCs (${\sum }_{j,g,t}\theta .R_{\mathit{jg}}^t$), wastage cost in PCs (${\sum }_{j,t}\mu .W_j^t$), transportation cost of platelet units from PCs to hospitals (${\sum }_{j,k,g,t}{\eta }_{\mathit{jk}}.{Y\text{'}}_{\mathit{jkg}}^t.D_k^t$), and shortage cost in hospitals (${\sum }_{k,t}\varrho .N_k^t$).

We consider $E$ regions in the determined area, and we also considered the estimated eligible donors of each region as donor groups, in which the maximum eligible donor of each donor group is shown by ${\mathrm{\Gamma }}_e$. The model seeks to determine the optimal number of donors of each donor group and assign them to the opened CCs efficiently. Based on the assumption, all the selected donors of each donor group can refer to one opened CC which is shown by Constraint (2). Also, we consider that each CC has coverage radius, and thus, a CC can serve the donor groups which are in their coverage radius (Constraint (3)). As mentioned before, a number of donors of each donor group can donate their blood, which the number of them cannot be more than the maximum number of donors in each group (Constraint (4)).

In this research, we considered different fractionation methods in PCs. Thus, the collected blood from each donor can be separated by a specific fractionation method in PCs, in which the number of these donors is determined by the ${X\text{'}}_{\mathit{eiw}}^t$. It is obvious that the collected blood from each donor should be separated by one of these fractionation methods in PCs, which is shown by Constraint (5). We know that the input flow to a center should be greater than the output flow in a supply chain network. In the same way, the input flow in the CC, the number of collected blood, should be greater than the number of transferred blood from that CC to PCs (Constraint (6)). Moreover, in this study, the capacity of the blood centers is decision variables and is determined by solving the model. The input flow to a center should be lower than the capacity of that center, which this fact is shown by Constraint (7) for CCs. It is notable that the collected blood should be sent to PCs within eight hours to be able to extract platelet from whole blood. To address this fact, we consider a maximum allowable time between CCs and hospitals, which is shown by Constraint (8). Also, we know that capacities can only be assigned to opened centers, which is shown by Constraint (9) for CCs.

In this study, we considered the age of the platelet. In PCs, platelets can be produced or be stored; thus, the age of the transferred platelet from PCs to hospitals can be different. In order to determine the number of transferred platelets from PCs to hospitals of each age, we defined a decision variable as ${Y\text{'}}_{\mathit{jkg}}^t$, which addresses the portion of transferred platelet from PCs to hospitals based on their age. Constraint (10) that can be replaced by ${\sum }_j{\sum }_{g=3}^G{Y\text{'}}_{\mathit{jkg}}^t.D_k^t\le D_k^t$ shows that the number of arrived platelet unit in hospitals should be less than their demand. The blood units in the PCs should be tested and decomposed to different blood products, which takes two days. All the collected blood should undergo this two-day procedure, so the transferred platelet from PCs to hospitals cannot be one-day and two-day platelets, as shown by Constraint (11). Also, the transshipment of platelet from PCs to hospitals can happen if the PCs are established (Constraint (12)).

Due to the two-day testing process, the age of the produced platelet units in PC should be more than two days, which is shown by Constraint (13). Regarding the used fractionation method in PCs, the number of produced platelet units from one unit of whole blood can be different. Also, a portion of whole blood units in PCs are discarded based on the results of the tests. So, when blood units are transferred to a PC, firstly, they are tested, and the infected units are discarded; then the platelet units are produced regarding the employed fractionation method. In other words, collected blood units in period $t$ are converted into three-day platelets in period $t+3$ (Constraint (14)). It is obvious that platelets can be produced in an opened PC, and capacities can be assigned to opened PCs, which are shown by Constraints (15), (16), respectively. Also, to capture the freshness and quality of platelet units, we consider the maximum allowable time between PCs and hospitals (Constraint (17)).

As mentioned before, the first two days are spent in testing and procurement processes, and the age of the produced platelets is three days; consequently, the age of the stored platelet should be more than two days. (Constraint (18)). The flow conservation in PCs is defined as follows. In the first period, there is no produced platelet, and the demands (${\sum }_k{Y\text{'}}_{\mathit{jkg}}^t.D_k^t$) should be fulfilled by the available platelet units in PCs (${\phi }_{\mathit{jg}}^t$), and the remaining units can be stored ($R_{\mathit{jg}}^t$) (Constraint (19)). In the same way, in the second period, to satisfy demands which should be met by three-day platelets, the available platelet units in PCs can be used (Constraint (20)). While the previous period stocks can be available in the second phase for $g\ge 4$ (Constraint (21)).

From the third period onwards, the produced platelets are available and can be satisfied with the demands which should be met by three-day platelets. Also, they can be stored to be used in the next periods (Constraint (22)). While the demands which should be met by four-day platelets are met by the previous period stocks (Constraint (23)). We considered the maximum age of platelets $G$ days, and therefore, the stored platelet with $g=G$ will be outdated (Constraint (24)). Finally, the received platelet units to the hospitals are used to satisfy the demand, and if the platelet supply is not sufficient, a shortage will occur (Constraint (25)).

Model of the reactive phase

In the second phase, the reactive phase, we aim to satisfy the shortages stemmed from the disruption in PCs, along with shortages due to insufficient supply of the whole blood in the first phase, by collecting apheresis-derived platelets in undisrupted PCs and hospitals. To do so, we defined disruption scenarios and proposed a scenario-based mixed-integer linear programming model, in which the average costs of the network is minimized. The objective function comprises of cost of assigning donor groups to PCs (${\sum }_{e,j,t,s}{\pi }^s.\xi .U_{\mathit{ej}}^{\mathit{ts}}$), cost of assigning donor groups to hospitals (${\sum }_{e,k,t,s}{{\pi }^s.\xi \text{'}.U\text{'}}_{e,k}^{t,s}$), cost of provided apheresis machines in PCs (${\sum }_{j,s}{\pi }^s.\psi .F_j^s$), cost of provided apheresis machines in hospitals (${\sum }_{k,s}{\pi }^s.{\psi }^{\text{'}}.{F\text{'}}_k^s$), collection cost in PCs (${\sum }_{e,j,t,s}{\pi }^s.\alpha .X_{\mathit{ej}}^{\mathit{ts}}$), collection cost in hospitals (${\sum }_{e,k,t,s}{\pi }^s.\alpha \text{'}.{X\text{'}}_{\mathit{ek}}^{\mathit{ts}}$), production cost in PCs (${\sum }_{j,t,s}{\pi }^s.\vartheta .Q_j^{\mathit{ts}}$), production cost in hospitals (${\sum }_{k,t,s}{{\pi }^s.\vartheta }^{\text{'}}.{Q\text{'}}_k^{\mathit{ts}}$), inventory cost in PCs (${\sum }_{j,g,t,s}{\pi }^s.\theta .R_{\mathit{jg}}^{\mathit{ts}}$), inventory cost in hospitals (${\sum }_{k,g,t,s}{{\pi }^s.\theta }^{\text{'}}.{R\text{'}}_{\mathit{kg}}^{\mathit{ts}}$), wastage cost in PCs (${\sum }_{j,t,s}{\pi }^s.\mu .W_j^{\mathit{ts}}$), wastage cost in hospitals (${\sum }_{k,t,s}{{\pi }^s.\mu }^{\text{'}}.W_k^{\text{'}ts}$), cost of transporting platelet units from PCs to hospitals (${\sum }_{j,k,g,t,s}{\pi }^s.{\eta }_{\mathit{jk}}.Y_{\mathit{jkg}}^{\text{'}ts}.D_k^{\mathit{ts}}$), shortage cost in hospitals (${\sum }_{k,g,t,s}{\pi }^s.\varrho .N_{\mathit{kg}}^{\mathit{ts}}$), and transshipping cost between hospitals (${\sum }_{k,k\text{'}\ne k,g,t,s}{\pi }^s.\varphi .V_{kk\text{'}g}^{\mathit{ts}}$).

In this paper, we consider whole blood donor pools and apheresis donor pools separately. Also, we consider that collecting blood through the apheresis method can be carried out in PCs and hospitals in order to reduce the amount of time that patients wait for receipt of platelets. Thus, apheresis donors can referred to either undisrupted PCs or hospitals to donate their blood (Constraint (30)). In order to determine the disrupted PCs in each scenario, we defined a binary matrices (${\mathit{dis}}_j^s$), in which if a PC is disrupted, its elements will be equal to one, and zero otherwise. The assignment of donor groups to undisrupted PCs and hospitals depend on the coverage radius of that PCs and hospitals, which are shown by Constraints (31), (32), respectively. Also, the selected donors of each donor group, which can be assigned to PCs and hospitals, should be less than the potential number of donors in that donor groups (Constraints (33), (34)).

In apheresis methods, the collected platelet can be tested and produced in a short time, and therefore, the collected blood can be used to meet demands in the collection day. For this reason, we proposed apheresis-derived platelet as a reactive strategy to handle the effects of disruptions. Moreover, each apheresis platelet unit equals to 6–8 whole-blood-derived platelet units, and a portion of collected units will be discarded due to infections. According to the above-mentioned, the amount of produced platelet units in PCs and hospitals is calculated according to Constraints (35), (36), respectively. Each apheresis machine can serve a limited number of donors ($\epsilon$) in each period. Therefore, the number of referred donors to PCs and hospitals is limited according to the number of apheresis machines and their relevant capacities, as shown in Constraints (37), (38). Also, we know that apheresis machines can be deployed in undisrupted PCs under each scenario (Constraint (39)).

As the first phase, to determine the number of required platelet unit of each age, we define two decision variables: ${Y\text{'}}_{\mathit{jkg}}^{\mathit{ts}}$, which determines the portion of required platelet units in each PC of each age that should be transferred to hospitals, and ${Z\text{'}}_{\mathit{kg}}^{\mathit{ts}}$, which determines the portion of collected platelet units in each hospital of each age that should be allocated to satisfy platelet demands of each age. Constraint (40) that can be replaced by $\left({\sum }_{j,g}{Y^{\text{'}}}_{\mathit{jkg}}^{\mathit{ts}}+{\sum }_g{Z^{\text{'}}}_{\mathit{kg}}^{\mathit{ts}}\right).D_k^{\mathit{ts}}\le D_k^{\mathit{ts}}$ shows that the number of arrived platelet units in a hospital, along with the number of available platelets in that hospital, should be fewer than its demands. The number of transferred platelet from a PC to a hospital is restricted to the number of apheresis machines in each PC, the capacity of each apheresis machine, and the number of derived platelet units of each donor (Constraint (41)). Also, it is obvious that the number of transferred platelet from a PC to a hospital is restricted to the number of referred donors to that PC and the number of derived platelet units from each donor (Constraint (42)). In the same way, the number of assigned donors to meet demand is restricted, as shown by Constraints (43), (44).

The flow conservation in PCs is defined as follows. The collected platelet by apheresis method can be produced on the collection day, and therefore, the platelet with $g=1$ will be available. Accordingly, the produced platelets in PCs can be used to satisfy the demand which should be met by one-day platelets, and they can also be stored, as shown by Constraint (45). In the first period, to satisfy the demand with $g\ge 2$, we should use the available platelet units in PCs to meet demands, since, there are no previous period stocks ($R_{j,g-1}^{0,s}$ = 0,$\forall g\ge 2$) (Constraint (46)). While, from the first period onwards, previous period stocks will be available and will be used to satisfy demands (Constraint (47)). Also, the stored platelet with the maximum age will be outdated (Constraint (48)).

In this phase, we employed the transshipment strategy, in which the platelet units can be transferred between hospitals. The flow conservation in hospitals is defined as follows. In each period, the produced platelets in that hospital and the transshipped platelet from other hospitals can be used to satisfy the demand with $g=1$, and extra units can also be stored or sent to other hospitals. On the other hand, if the input platelet flow to the hospital is insufficient, a shortage will occur (Constraint (49)). Constraint (50) does the same for demands with $g\ge 2$ in the first period, in which platelets can be satisfied by the available platelet in hospitals instead of ${Q^{\text{'}}}_k^{\mathit{ts}}$, and Constraint (51) also does the same in which platelets can be filled by previous period stocks instead of ${Q^{\text{'}}}_k^{\mathit{ts}}$. Finally, the stored platelet with the maximum age will be outdated (Constraint (52)). In each period, we have a limitation on the number of platelet units that can be sent to other hospitals. In other words, the number of transshipped platelet units is restricted by the available platelet units in the hospital, as shown in Constraints (53)- (55).

In this paper, we defined a parameter as $d_{\mathit{kg}}^{\mathit{ts}}$ based on the historical data from hospitals, which determine the number of transfused platelets to patients of each age. To meet this demand, the input flow to hospitals, including transshipped platelet from PCs, assigned platelet to meet demands in hospitals, and the platelet transshipped from other hospitals, should be more than the number of demands of each age in each hospital (Constraint (56)).

Appendix D. . Definitions for the proposed fuzzy approach

Preliminaries

Definition 1.

An LR-fuzzy number is represented as $\stackrel{}{E}={\left(\underset{\_}{e},\overline{e},\gamma ,\eta \right)}_{\mathit{LR}}$ in which $\gamma$ and $\eta$ are left and right spread of the fuzzy number. If $\lambda$ is a real number, the arithmetic operations on every pair of fuzzy numbers $\stackrel{}{E}={\left(\underset{\_}{e},\overline{e},\gamma ,\eta \right)}_{\mathit{LR}}$ and $\stackrel{}{F}={(\underset{\_}{f},\overline{f},\omega ,\phi )}_{\mathit{LR}}$ will be as follows :

• i.Addition: $\stackrel{}{E}+\stackrel{}{F}={(\underset{\_}{e}+\underset{\_}{f},\overline{e}+\overline{f},\gamma +\omega ,\eta +\phi )}_{\mathit{LR}}$
• ii.Subtraction: $\stackrel{}{E}-\stackrel{}{F}={(\underset{\_}{e}-\underset{\_}{f},\overline{e}-\overline{f},\gamma +\omega ,\eta +\phi )}_{\mathit{LR}}$

$$\mathrm{M}\mathrm{u}\mathrm{l}\mathrm{t}\mathrm{i}\mathrm{p}\mathrm{l}\mathrm{i}\mathrm{c}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}:\lambda .\stackrel{}{E}=\left\{\begin{array}{c}{(\lambda .\underset{\_}{e},\lambda .\overline{e},\lambda .\gamma ,\lambda .\eta )}_{\mathit{LR}}\lambda >0\\ {(\lambda .\underset{\_}{e},\lambda .\overline{e},\lambda .\gamma ,\lambda .\eta )}_{\mathit{LR}}\lambda <0\end{array}\right)$$ (D.1)

Definition 2.

The lower and upper possibilistic mean values of any LR-fuzzy number, which can be explained as optimistic and pessimistic mean values, are respectively defined by the following formulae:

$$M_{\ast }\left(\stackrel{}{E}\right)=2\underset{0}{\stackrel{1}{\int }}\alpha (\inf {\stackrel{}{E}}_{\alpha })d\alpha$$ (D.2)

$$M^{\ast }\left(\stackrel{}{E}\right)=2\underset{0}{\stackrel{1}{\int }}\alpha (\sup {\stackrel{}{E}}_{\alpha })d\alpha$$ (D.3)

which $\inf {\stackrel{}{E}}_{\alpha }$ and $\sup {\stackrel{}{E}}_{\alpha }$ indicate best possible upper bound and lower bound for $\alpha$-level cut of $\stackrel{}{E}$ such that $0<\alpha <1$. Then, we will have

$$M_{\ast }\left(\stackrel{}{E}+\stackrel{}{F}\right)=M_{\ast }\left(\stackrel{}{E}\right)+M_{\ast }\left(\stackrel{}{F}\right)$$

$$M^{\ast }\left(\stackrel{}{E}+\stackrel{}{F}\right)=M^{\ast }\left(\stackrel{}{E}\right)+M^{\ast }\left(\stackrel{}{F}\right)$$

$$M_{\ast }\left(\lambda .\stackrel{}{E}\right)=\left\{\begin{array}{c}\lambda .M_{\ast }\left(\stackrel{}{E}\right)\lambda \ge 0\\ \lambda .M_{\ast }\left(\stackrel{}{E}\right)\lambda <0\end{array}\right)$$

$$M^{\ast }\left(\lambda .\stackrel{}{E}\right)=\left\{\begin{array}{c}\lambda .M^{\ast }\left(\stackrel{}{E}\right)\lambda \ge 0\\ \lambda .M^{\ast }\left(\stackrel{}{E}\right)\lambda <0\end{array}\right)$$ (D.4)

It is proven that the lower and upper possibilistic mean values can be calculated by:

$$M_{\ast }\left(\stackrel{}{E}\right)=\underset{\_}{e}-\gamma /3$$

$$M^{\ast }\left(E\right)=\overline{e}+\eta /3$$ (D.5)

The interval-valued possibilistic mean is a closed interval bounded by possibilistic mean values, which are expectations calculated from the upper and lower distribution functions of the fuzzy number is shown as follows:

$$M\left(\stackrel{}{E}\right)=[M_{\ast }\left(\stackrel{}{E}\right),M^{\ast }\left(\stackrel{}{E}\right)]$$ (D.6)

and we have

$$M\left(\lambda .\stackrel{}{E}+\theta .\stackrel{}{F}\right)=\lambda .M\left(\stackrel{}{E}\right)+\theta .M(\stackrel{}{F})$$ (D.7)

Definition 3.

The arithmetic mean of upper and lower possibilistic mean values of the fuzzy number $\stackrel{}{E}$ is interpreted as the crisp possibilistic mean value of the fuzzy number, i.e.

$$\overline{M}\left(E\right)=\underset{0}{\stackrel{1}{\int }}\alpha .(\inf {\stackrel{}{E}}_{\alpha }+\sup {\stackrel{}{E}}_{\alpha })d\alpha =\frac{M_{\ast }\left(\stackrel{}{E}\right)+M^{\ast }\left(\stackrel{}{E}\right)}{2}=\frac{\underset{\_}{e}+\overline{e}}{2}+\frac{\eta -\gamma }{6}$$ (D.8)

It is proven that:

$$\overline{M}\left(\stackrel{}{E}+\stackrel{}{F}\right)=\overline{M}\left(\stackrel{}{E}\right)+\overline{M}(\stackrel{}{F})$$

$$\overline{M}\left(\lambda .\stackrel{}{E}+\theta .\stackrel{}{F}\right)=\lambda .\overline{M}\left(\stackrel{}{E}\right)+\theta .\overline{M}(\stackrel{}{F})$$ (D.9)

Definition 4.

The possibilistic absolute deviation of an LR-fuzzy number and the possibilistic absolute deviation between any pair of fuzzy numbers are defined as follows, respectively:

$$\upsilon \left(\stackrel{}{E}\right)=\overline{e}-\underset{\_}{e}+\frac{\gamma +\eta }{3}$$ (D.10)

$$\upsilon \left(\stackrel{}{E},\stackrel{}{F}\right)=\frac{1}{2}(\overline{M}\left|\stackrel{}{E}+\stackrel{}{F}-\overline{M}\left(\stackrel{}{E}\right)-\overline{M}(\stackrel{}{F})\right|)$$ (D.11)

Definition 5.

Credibility is a self-dual fuzzy measure which is described based on the possibility and necessity measures as below:

$$Cr\left\{\stackrel{}{E}\le k\right\}=\frac{1}{2}Pos\left\{\stackrel{}{E}\le k\right\}+\frac{1}{2}Nec\left\{\stackrel{}{E}\le k\right\}$$

$$Cr\left\{\stackrel{}{E}\ge k\right\}=\frac{1}{2}Pos\left\{\stackrel{}{E}\ge k\right\}+\frac{1}{2}Nec\left\{\stackrel{}{E}\ge k\right\}$$ (D.12)

Therefore, the credibility measure of any fuzzy number can be reformulated as follows ($k$ is a real number):

$$\mathit{Cr}(\stackrel{}{E}\le k)=\left\{\begin{array}{c}0-\infty <k\le \underset{\_}{e}-\gamma \\ \frac{k-\underset{\_}{e}+\gamma }{2\gamma }\underset{\_}{e}-\gamma \le k\le \underset{\_}{e}\\ \frac{1}{2}\underset{\_}{e}\le k\le \overline{e}\\ \frac{k-\overline{e}+\eta }{2\eta }\overline{e}\le k\le \overline{e}+\eta \\ 1\overline{e}+\eta \le k<+\infty \end{array}\right)$$ (D.13)

$$Cr\left(\stackrel{}{E}\ge k\right)=\left\{\begin{array}{c}1-\infty <k\le \underset{\_}{e}-\gamma \\ \frac{\underset{\_}{e}+\gamma -k}{2\gamma }\underset{\_}{e}-\gamma \le k\le \underset{\_}{e}\\ \frac{1}{2}\underset{\_}{e}\le k\le \overline{e}\\ \frac{\overline{e}+\eta -k}{2\eta }\overline{e}\le k\le \overline{e}+\eta \\ 0\overline{e}+\eta \le k<+\infty \end{array}\right)$$ (D.14)

Fuzzy constraints can be converted to an equivalent crisp form with $\beta$-critical value ($\beta \ge 0.5$) as follows (Farrokh et al., 2018):

$$Cr\left\{\stackrel{}{E}\le k\right\}\ge \beta ⟺k\ge \left(2-2\beta \right)\overline{e}+(2\beta -1)(\overline{e}+\eta )$$

$$Cr\left\{\stackrel{}{E}\ge k\right\}\ge \beta ⟺k\le \left(2\beta -1\right)(\underset{\_}{e}-\gamma )+(2-2\beta )\underset{\_}{e}$$ (D.15)

Appendix E. Supplementary data

The following are the Supplementary data to this article: