Abstract
Motivation
Protein structure and function are essentially determined by how the side-chain atoms interact with each other. Thus, accurate protein side-chain packing (PSCP) is a critical step toward protein structure prediction and protein design. Despite the importance of the problem, however, the accuracy and speed of current PSCP programs are still not satisfactory.
Results
We present FASPR for fast and accurate PSCP by using an optimized scoring function in combination with a deterministic searching algorithm. The performance of FASPR was compared with four state-of-the-art PSCP methods (CISRR, RASP, SCATD and SCWRL4) on both native and non-native protein backbones. For the assessment on native backbones, FASPR achieved a good performance by correctly predicting 69.1% of all the side-chain dihedral angles using a stringent tolerance criterion of 20°, compared favorably with SCWRL4, CISRR, RASP and SCATD which successfully predicted 68.8%, 68.6%, 67.8% and 61.7%, respectively. Additionally, FASPR achieved the highest speed for packing the 379 test protein structures in only 34.3 s, which was significantly faster than the control methods. For the assessment on non-native backbones, FASPR showed an equivalent or better performance on I-TASSER predicted backbones and the backbones perturbed from experimental structures. Detailed analyses showed that the major advantage of FASPR lies in the optimal combination of the dead-end elimination and tree decomposition with a well optimized scoring function, which makes FASPR of practical use for both protein structure modeling and protein design studies.
Availability and implementation
The web server, source code and datasets are freely available at https://zhanglab.ccmb.med.umich.edu/FASPR and https://github.com/tommyhuangthu/FASPR.
Supplementary information
Supplementary data are available at Bioinformatics online.
1 Introduction
Protein side-chain conformations are closely relevant to their biological functions (Miao and Cao, 2016), and therefore the accurate modeling of protein side-chains is of great significance. Protein side-chain packing (PSCP) is an important step in protein structure prediction (Roy et al., 2010; Yang et al., 2015), structure-based protein and enzyme design (He et al., 2018; Huang et al., 2017; Pearce et al., 2019; Shultis et al., 2019) and structure refinement (Chitsaz and Mayo, 2013; Zhang et al., 2011).
Typically, a PSCP method is composed of three components: (i) a rotamer library, (ii) a scoring function and (iii) a searching method (Huang et al., 2020b). Solving a PSCP problem thus involves identifying a set of amino acid conformations from a rotamer library that minimizes the protein folding energy calculated by the scoring function using a searching method. Many programs have been developed to address the PSCP problem, which use different rotamer libraries, scoring functions and searching methods (Cao et al., 2011; Krivov et al., 2009; Lu et al., 2008; Miao et al., 2011; Xu and Berger, 2006). These programs achieved similar performance on side-chain torsion angle prediction by correctly predicting 84–86% of the dihedral angles and 71–75% of the angles for native protein backbones using a widely used tolerance criterion of 40°. The searching algorithms used by these packers can be categorized into two classes: (i) deterministic, such as dead-end elimination (DEE) (Desmet et al., 1992; Goldstein, 1994; Pierce et al., 2000), A* (Leach and Lemon, 1998), linear and integer programming (Kingsford et al., 2005), mixed integer linear programming (Huang et al., 2013a, b; Pantazes et al., 2015), branch-and-bound (Gordon and Mayo, 1999), graph-theoretic algorithm (Canutescu et al., 2003; Samudrala and Moult, 1998), residue-rotamer-reduction (Xie and Sahinidis, 2006) and tree decomposition (Xu and Berger, 2006), and (ii) non-deterministic, such as Monte Carlo (Lu et al., 2008; Miao et al., 2011), simulated annealing (Peterson, 2004) and genetic algorithms (Liu et al., 2002). More attention has been paid to the development of efficient deterministic searching algorithms for PSCP. Among the packing programs, the SCWRL series developed by Dunbrack’s laboratory are the most popular ones due to their accuracy, determinacy and robustness (Canutescu et al., 2003; Krivov et al., 2009). As a consequence, SCWRL4 was incorporated into the first version of our evolution-based de novo protein sequence design program, EvoDesign (Mitra et al., 2013). However, the relatively slow speed of SCWRL4 significantly limits the number of Monte Carlo steps that can be performed during design simulations, and subsequently, SCWRL4 was replaced by a much faster but similarly accurate packer, RASP (Miao et al., 2011), which allows for running more simulation steps within an identical computational time in an updated version of EvoDesign for protein–protein interaction design (Pearce et al., 2019). Although RASP is sufficiently fast for side-chain modeling, its major drawback is that it incorporates a stochastic searching procedure, thus different structure models may be obtained from independent runs. This results in great difficulty tracking the repacked structure models in protein design simulations. Therefore, it is quite desirable to develop a new packing tool that is fast, accurate and deterministic.
To achieve a good balance between accuracy, speed and determinacy, we developed a new method, FASPR, for solving PSCP problems effectively and efficiently. We compared the performance of FASPR with four other state-of-the-art packers, CISRR (Cao et al., 2011), RASP (Miao et al., 2011), SCATD (Xu and Berger, 2006) and SCWRL4 (Krivov et al., 2009), on both native and non-native protein backbones. With the exception of RASP, the other four programs, including FASPR, utilize deterministic searching methods. In the native backbone assessment, the 379 non-redundant experimental structures used to test SCWRL4 were used, while in the non-native backbone assessment, two sets of backbones were utilized: (i) a set of 379 structure models constructed using I-TASSER (Yang et al., 2015) from the sequences extracted from the 379 SCWRL4 test proteins and (ii) 10 sets of 379 structural models obtained by perturbing the main-chains with different variances using the SCWRL4 test proteins, which were constructed by Xu et al. (2019). The results demonstrate that FASPR achieved very high accuracy and the highest speed among all the programs tested on both native and non-native backbones. The advantageous combination of high accuracy, speed and determinacy for modeling the side-chains of both native and non-native backbones makes FASPR a useful tool for protein structure modeling. Except for the standard C/C++ libraries, FASPR is completely independent from any other third-party program or library, making it easy to propagate and be used in different operating systems. Moreover, the source code of FASPR is freely available to the community, allowing users to optimize it for their own needs.
2 Materials and methods
2.1 Overview of the FASPR algorithm
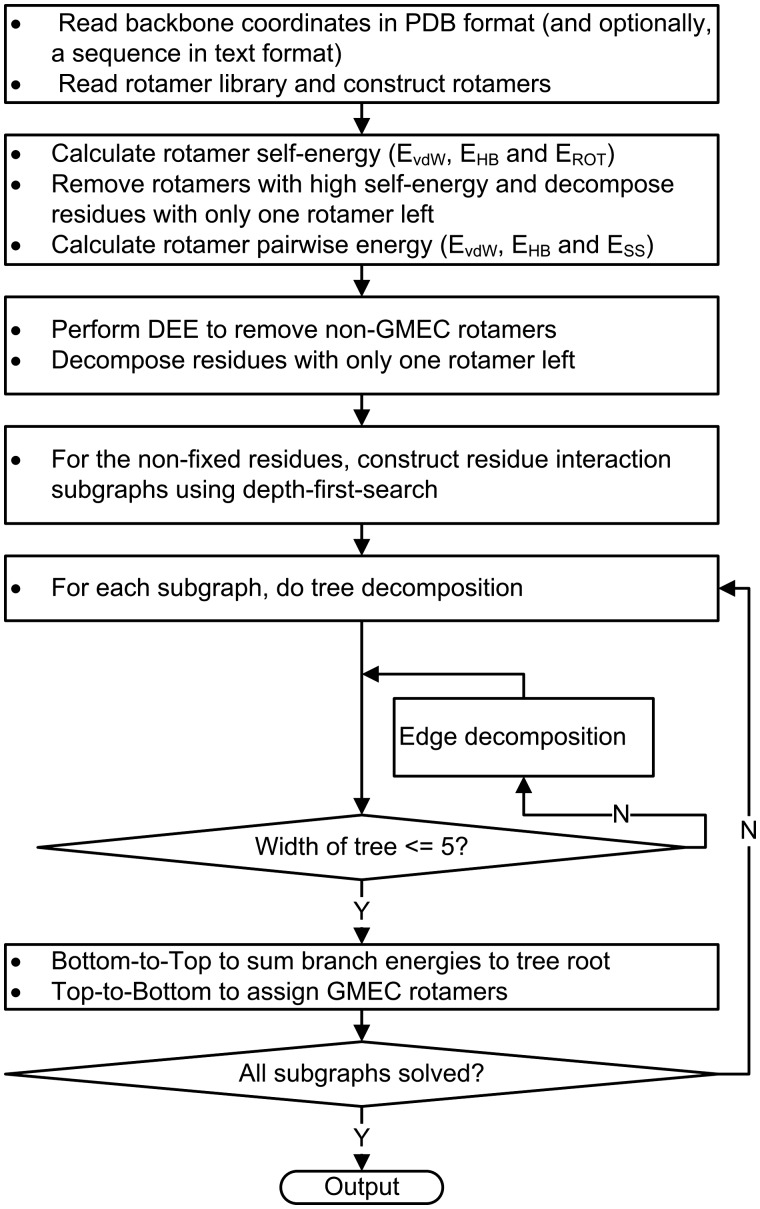
The flowchart of the FASPR algorithm is illustrated in Figure 1. The input is the protein backbone coordinates in PDB format and optionally an amino acid sequence to be packed on the given backbone. When repacking a new sequence, its length must be identical to the number of residues of the provided backbone. FASPR samples the amino acid side-chain conformations from the Dunbrack rotamer library (Shapovalov and Dunbrack, 2011). To construct the side-chain rotamers, there should be no missing main-chain atoms (i.e. N, Cα, C and O). The coordinates of all side-chain atoms are built using the standard topology given in Engh and Huber (1991) and the dihedral angles taken from the Dunbrack rotamer library, and are converted into Cartesian space using the NeRF method (Parsons et al., 2005).
Fig. 1.
Flowchart of the FASPR approach
For each rotamer at a packing position, the self-energy between the rotamer side-chain and the fixed backbone is calculated using an empirical scoring function. The rotamers whose self-energies are higher than a given threshold relative to the lowest self-energy at that position are unlikely to be a part of the global minimum energy configuration (GMEC) and are directly eliminated (see below). After this process, the residues with only one rotamer left are fixed and the side-chain conformation is taken as the retained rotamer. The pairwise energy between rotamer pairs located at different residues is calculated for the unfixed positions. Then Goldstein DEE (Goldstein, 1994) and Split DEE (Pierce et al., 2000) are performed to eliminate the rotamers that cannot be in the GMEC state and similarly the residues with only one rotamers left are fixed. For the remaining unfixed residues, a residue interaction graph is constructed using a depth-first-search approach; the whole graph is in general comprised of one or more separated subgraphs. Each subgraph is subjected to a tree decomposition procedure (Krivov et al., 2009; Xu and Berger, 2006) and exhaustive enumeration of rotamer combinations if the width of the tree is ≤5, otherwise an extra edge decomposition technique is repeated until the width is ≤5 (see below). Once all the subgraphs are solved via tree decomposition, the PSCP solution is obtained and the repacked structure model is generated.
2.2 Rotamer library
FASPR uses the latest version of the Dunbrack rotamer library (Shapovalov and Dunbrack, 2011), which was shown to be the library that is most suitable for PSCP (Huang et al., 2020b). Rare rotamers with probability <1% are excluded and the other rotamers are read until the accumulative probability reaches 97%.
2.3 Scoring function
The FASPR scoring function is comprised of four terms:
| (1) |
where is the total van der Waals energy of non-bonded atom pairs, is the total hydrogen bonding energy, is the total disulfide bonding energy and is a term related to the rotamer frequencies derived from the Dunbrack rotamer library. , and are the energy weights for their corresponding energy terms, where a summary of the energy weights is listed in Supplementary Table S1. The energy terms are mainly adapted from the EvoEF2 force field (Huang et al., 2020a) with some modification to allow for rapid caculation. For example, the solvation energy term is excluded from the FASPR scoring function, hydrogens are not explicitly considered in the orientation-dependent hydrogen bonding term, and the two dihedral angle () terms for disulfide bonding energy scoring are not considered.
The van der Waals energy between atoms and takes the form:
| (2) |
where is the sum of their hard-sphere van der Waals atomic radii, is the combined well-depth for atoms and () and is the distance between atoms and . is defined to be . A total of 18 non-hydrogen atom types were taken from OPUS-Rota (Lu et al., 2008) and the corresponding and values were reoptimized in this work. A summary of the optimized atomic parameters is listed in Supplementary Table S2.
The hydrogen bonding energy between the donor atom () and the acceptor atom () is calculated as:
| (3) |
where is the distance between and , is the angle between the donor-base (), and and is the angle between , and the acceptor-base (). is the optimal hydrogen bond length, which is set to 2.8 Å. and are the optimal and angles centered on atoms and , respectively. The values of and are set to 120° for and atoms in sp2 hybridized states or 109.5° for sp3 hybridized and atoms. The value of is evaluated only if Å and . The amino acid hydrogen bonding donors and acceptors are listed in Supplementary Table S3.
The disulfide bonding energy between two cysteines is calculated as:
| (4) |
where is the distance between sulfur atoms and , is the angle between atoms , and , is the angle between atoms , and and is the torsional angle between atoms , , and . is the optimal disulfide length which is set to 2.03 Å and is the optimal C–S–S angle which is set to 105°. The value of is calculated only if Å and .
The rotamer frequency term is calculated as:
| (5) |
where are the main-chain torsional angles at the -th amino acid position along a protein chain, is a rotamer with the specified type and is the probability for rotamer , which is taken from the Dunbrack rotamer library.
2.4 Searching method
Solving a PSCP problem involves identifying a set of rotamers that makes the folded protein system adopt the GMEC state. FASPR solves PSCP problems using DEE in combination with tree decomposition.
The total energy of the protein system can be calculated as:
| (6) |
where is the energy of the backbone and can be ignored because it is a constant given a fixed backbone, is the number of positions that are placed with rotatable residues (Ala and Gly are excluded because they do not have rotatable non-hydrogen side-chain atoms) and and are the rotamers chosen at positions and , respectively. is the energy between rotamer and the fixed protein backbone, while represents the energy between rotamers and at different positions. and are calculated using Equations (1)–(5) and the rotamer frequency term is only included in the calculation of . To efficiently calculate all the values, we only consider the pairs of residues that are in contact. A pair of residues and is defined to be in contact if the distances between their and atoms satisfy the following conditions: Å and Å, where and are the radii of the side-chain hemispheres for residues and , respectively. A list of the hemisphere radii for all 20 amino acids is given in Supplementary Table S4.
Some rotamers with high self-energies are eliminated since they are very unlikely to be a part of the GMEC structure in reality. For each residue, a rotamer with self-energy higher than 15 kcal/mol relative to the lowest self-energy rotamer is removed; this threshold was determined during the parameter optimization process.
Following this, the Goldstein DEE theorem (Goldstein, 1994) is used to eliminate rotamers that cannot be a part of the GMEC:
| (7) |
which states that rotamer can be eliminated if its contribution to the total energy can be reduced by using an alternative rotamer, .
Subsequently, the Split DEE theorem (Pierce et al., 2000) is used to further eliminate non-GMEC rotamers:
| (8) |
which states that rotamer can be eliminated if, for each splitting rotamer at some splitting position , there exists a rotamer that achieves a lower energy contribution. The Goldstein and Split DEE steps are repeated until no rotamers can be removed.
Next, a residue interaction graph is constructed for the residues that have more than one remaining rotamer. In the graph, vertices represent residues while edges between vertices indicate that at least one rotamer of one residue has a non-zero interaction with rotamers from another residue. Typically, the resulting interaction graph may contain several separated subgraphs with no edges between them. Each of these subgraphs is then subjected to a tree decomposition procedure which was described by Krivov et al. (2009) in detail. The algorithmic complexity of a tree decomposition is exponentially dominated by the width of the tree, which is the size of the largest node minus one. For a given graph, different tree decompositions can be built and the optimal decomposition is the one with the minimum width, which is also called the treewidth. Unfortunately, it is difficult to determine the treewidth of an optimal tree decomposition, which has been proven to be NP-hard (Krivov et al., 2009). In this work, we utilized the minimal-degree approach to carry out tree decomposition, which was proposed by Xu and Berger (2006).
During tree decomposition, the minimum energy rotamer configuration of a subgraph is calculated through a bottom-to-top process to assign the energies from the branch nodes to the root node and a top-to-bottom process to determine the optimal rotamer from the root to the branches via backtracking (Krivov et al., 2009). Sometimes, even with efficient tree decomposition, the calculation still remains intractable because the width of a tree is too large and the actual search for the local solution is done via exhaustive enumeration. When the number of rotamer combinations within a node is sufficiently large, the exhaustive search can be very time-consuming. Since the product is exponentially related to the width of a tree decomposition, a threshold of the width is used to check if the decomposition is easily tractable. In this work, when the width is larger than 5, the edge decomposition technique is utilized to remove edges that can be approximated as the sum over single-residue energies (Krivov et al., 2009). The threshold for decomposing an edge is set to 0.5 kcal/mol and doubled for each iteration of the edge decomposition procedure. After each iteration of edge decomposition, the new width is determined and the tree is enumerated if the width is ≤5, otherwise edge decomposition is repeated. Based on our benchmark, in general two iterations of edge decomposition are sufficient.
2.5 Datasets
Training set. The 100 crystal structures that were used to train SCWRL4 were also used to train FASPR in this work. The PDB IDs of these 100 structures are listed in Supplementary Table S5. It should be noted that the PDB ID 1PS4 has been replaced by 1Q2U in the Protein Data Bank database (Berman et al., 2002). Test set. We evaluated FASPR’s performance on both native and non-native protein backbones. For the native backbone assessment, the 379 experimental structures (DB379) that were used to test SCWRL4 were employed to test FASPR. The PDB IDs of these 379 structures are listed in Supplementary Table S6. Notably, five PDB IDs, 1P6Z, 1YO3, 2DPO, 2O37 and 2PZ4 have been replaced by 3SSW, 5WOF, 3ADO, 4RWU and 3PHS in the Protein Data Bank database (Berman et al., 2002), respectively. We performed two kinds of non-native backbone assessments. In the first non-native backbone test, we used I-TASSER (Yang et al., 2015) to remodel the 379 structures given the corresponding sequences and then repacked the structures based on the modeled main-chain conformations. As shown in Supplementary Table S7, 378 out of 379 models adopted the same global topologies as their native counterparts with TM-score >0.5 (Xu and Zhang, 2010), suggesting that the I-TASSER models are of sufficiently high quality to be used for PSCP assessment on non-native backbones. In the second non-native backbone test, we directly used the 10 non-native test sets compiled by Xu et al. (2019) based on DB379. To be specific, the non-native sets were constructed by using the main-chain torsional angles with their original values multiplied by a modulating factor randomly sampled from a Gaussian distribution for all proteins in DB379. Ten different levels of noise strength were used; the mean values of the Gaussians were 1.0, and the standard deviations were 0.001, 0.003, 0.005, 0.008, 0.01, 0.013, 0.014, 0.015, 0.016 and 0.02. Therefore, each of the 10 non-native test sets contained 379 proteins. The corresponding average main-chain root mean square deviations (RMSDs) between the perturbed structures and the native counterparts at each noise level were 0.21, 0.57, 0.93, 1.48, 1.88, 2.38, 2.55, 2.74, 2.95 and 3.68 Å, respectively. The native structures, I-TASSER models and perturbed backbones are freely available on our website (see Availability and implementation section of the abstract).
Although all the training and test proteins had a high resolution (≤1.8 Å), the side-chains of many residues were still not well defined. The coordinates of some side-chain atoms were missing due to low electron density. Similarly, some atoms had poor coordinates due to high mobility, given the large B-factor values. To eliminate the negative effects of these ill-defined side-chains, Krivov et al. (2009) only took the side-chains with electron density above the 25th percentile to benchmark SCWRL4. In this work, to generate reliable side-chains for training and testing FASPR, we also culled the datasets, but in a slightly different way. Specifically, we defined and calculated the B-factor value of a residue as the arithmetic mean of those of its non-hydrogen atoms. For a residue with missing atoms, its B-factor was arbitrarily set to a large value (i.e. 1000). Only the residues with the average B-factor value below the 75th percentile were used for training and testing. As a result, a total of 43 921 residues were reserved in the test set, where Ala and Gly were excluded. As a comparison, Krivov et al. (2009) collected 45 216 residues for testing SCWRL4 based on the electron density rule. To be consistent, the corresponding 43 921 residues were also used for the assessment on non-native backbones. Krivov et al. (2009) also reported that considering the crystal lattice improved protein side-chain prediction accuracy on the native backbones, but the crystal information was not considered in this study, because it was not available for the I-TASSER models and/or the randomly perturbed main-chains.
2.6 Evaluation criteria
The accuracy of side-chain prediction is usually assessed in terms of dihedral angle deviations and RMSDs between the predicted and native conformations. In previous studies, usually only the and dihedral angles were considered and a dihedral angle was regarded as being predicted correctly if its value was within 40° to that of the native structure (Canutescu et al., 2003; Cao et al., 2011; Krivov et al., 2009; Miao et al., 2011; Xu and Berger, 2006). However, recently we showed that this criterion was relatively loose and good performance could be easily achieved by all the methods (i.e. the success rates for and were above 85% and 70%, respectively), thus underestimating the difficulty of the PSCP problem. Instead, when we used a more stringent criterion (i.e. all predicted angles were within 20° to that of the native structure), the performance of all methods dropped significantly and the prediction accuracy was much lower than the maximum achievable accuracy level (Huang et al., 2020b). In this work, we continued to report the performance, denoted as recovery rate, following this stringent criterion. As a second metric, the RMSD was only calculated for the non-hydrogen side-chain atoms without atom . There are two ways to calculate RMSD among a set of proteins: overall and average RMSD. The overall RMSD is calculated by summing over all of the residues in all of the proteins, while the average RMSD is simply the average value of the sum of RMSDs for each of the proteins from the set. The value of overall RMSD is usually larger than that of average RMSD and was used in this work. The symmetry of residues Asp, Glu, Phe, Arg and Tyr were considered during the diheral angle and RMSD calculations. For residues Asn, Gln and His, their terminal groups were also flipped due to the difficulty of distinguishing different terminal atoms (Cao et al., 2011). Ala and Gly were excluded in the analyses.
In addition to the dihedral angles and RMSDs, we also calculated the steric clashes to examine the quality of models constructed by FASPR as described in the study by Miao et al. (2011). Specifically, two non-bonded atoms were regarded to have a clash if their distance was <60% of the sum of their van der Waals radii taken from the AMBER force field (Case et al., 2005).
2.7 Parameter optimization
In this section, we describe in detail how the parameters were optimized in the FASPR method. The parameters include the energy weights (, and ), the radii and well-depths for the 18 non-hydrogen atom types (see Supplementary Tables S1 and S2), and the self-energy threshold. was set to be amino acid-specific; i.e. it may take different values for different amino acid types. Each parameter was allowed to vary from the lower bound to the upper bound in increments (Supplementary Table S8). Starting from a set of random values, the parameters were first optimized by minimizing the objective function shown in Equation (9), which is calculated from packing the 100 training proteins using a simulated annealing Monte Carlo (SAMC) procedure.
| (9) |
where is the side-chain recovery rate ranging in [0, 1] and is the total number of clashes in the 100 repacked models.
The highest and lowest temperatures were set to kT=100 and 0.01, respectively, and the temperature decreasing factor was set to 0.8. At each temperature, 1000 Monte Carlo steps were performed, where a move was accepted or rejected using the Metropolis criteria (Metropolis and Ulam, 1949). Then three cycles of greedy search were performed to further optimize the parameters using the same objective function, starting from the values obtained via SAMC. In the greedy search, one parameter was changed at a time from its lower to upper bound (Supplementary Table S8), while the other parameters were fixed at their optimal values. If the value of the objective function was improved, then the new parameter was recorded.
2.8 Definition of core and surface residues
It was shown that the side-chain prediction accuracy was quite different for residues located in distinct regions (e.g. core and surface) of a protein (Cao et al., 2011). In this work, the core and surface residues were defined using the same criteria as before (Huang et al., 2020a). Specifically, we defined core residues as those positions that had more than 20 atoms within 10 Å of the atom of the residue of interest, while the surface residues were required to have less than 15 atoms within the same region. The atoms were counted for Gly.
3 Results
3.1 Performance of FASPR on native backbones
We compared FASPR with CISRR, RASP, SCATD and SCWRL4 for side-chain modeling on the representative test set DB379, which was first compiled by Krivov et al. (2009). The results are shown in Table 1. SCWRL4 by default samples subrotamers to enhance PSCP accuracy, and therefore is more time-consuming. To compare with FASPR in an identical conformational space, we also ran SCWRL4 without subrotamer sampling (Table 1, row 6). In general, with the exception of SCATD, the performance of FASPR, CISRR, RASP and the default SCWRL4 were quite comparable. FASPR achieved the highest overall recovery rate of 69.1% and the lowest overall RMSD of 1.457 Å on the whole test set (Table 1, column 2). In the protein core, FASPR achieved slightly lower recovery rates and higher RMSD values than CISRR and the default SCWRL4 (Table 1, column 3), while in the protein surface, FASPR outperformed the other methods in terms of both recovery rate and RMSD (Table 1, column 4). The high accuracy of CISRR for the core residues was probably because CISRR rotates the side-chain conformations to reduce steric clashes, while the default SCWRL4 achieved a high accuracy for core residues due to the effective subrotamer sampling. The accuracy of SCWRL4 decreased somewhat when the subrotamers were disabled, which was much worse than that of FASPR for the residues in all three categories. The side-chain modeling accuracy for each of the 18 amino acid types (Ala and Gly excluded) is listed in Supplementary Table S9. It was shown that, with the exception of SCATD, none of the methods could outperform the others for every residue type in each of the three categories.
Table 1.
Comparison of FASPR with four popular side-chain packing programs on the native structures from DB379, where bold fonts mark the best performer in each category
| Methoda |
recovery rate (%)/RMSD (Å) |
#Clashb | Relative timec | ||
|---|---|---|---|---|---|
| All | Core | Surface | |||
| FASPR | 69.1/1.457 | 80.3/0.983 | 56.8/1.906 | 149 | 1.00 |
| CISRR | 68.6/1.526 | 81.4/0.958 | 54.8/2.022 | 60 | 44.09 |
| RASP | 67.8/1.551 | 78.9/1.067 | 55.5/1.998 | 785 | 1.27 |
| SCATD | 61.7/1.856 | 74.7/1.279 | 48.4/2.318 | 1388 | 4.93 |
| SCWRL4 | 68.8/1.524 | 80.7/0.966 | 55.5/1.991 | 557 | 26.77 |
| SCWRL4v | 67.0/1.620 | 78.9/1.061 | 54.1/2.072 | 232 | 5.11 |
SCWRL4 by default samples subrotamers and thus searches in a larger rotamer space; SCWRL4v runs the SCWRL4 program by disabling the subrotamers sampling with option “-v”. The other PSCP programs also use the Dunbrack rotamer library without sampling subrotamers.
#Clash, the total number of clashes for all the 379 packed structure models.
Reports how much slower on average the other methods are than FASPR. These values were calculated by averaging the ratio of the computational time at each column with respect to the FASPR column in Supplementary Table S10. All the programs were run on the XSEDE Comet server (Towns et al., 2014) using a single CPU [Intel(R) Xeon(R) CPU E5-2680 v3 @ 2.50 GHz].
In addition to the side-chain recovery rate and RMSD, it is also important to evaluate the quality of the repacked structures. Based on our test, CISRR achieved the least number of steric clashes in all the 379 models, probably because CISRR was specifically optimized to minimize the number of clashes by rotamer relaxation rather than maximize the side-chain recovery rate. FASPR yielded 149 clashes (Table 1, column 5), which was greater than that of CISRR but much less than that produced by the other methods. The clashes obtained in this work were different from those reported by Miao et al. (2011), where RASP, CISRR and SCWRL4 had 47, 59 and 411 clashes in the structure models on the DB379 dataset. The great discrepancy of the clashes was obtained for RASP models probably because no rotamer relaxation phase was included as reported for rapid side-chain packing (Miao et al., 2011). As shown by Cao et al. (2011), a rotamer relaxation procedure was very time-consuming.
With respect to the speed, FASPR showed the highest computational efficiency, and overall, FASPR was about 44.09, 26.77, 5.11, 4.93 and 1.27 times faster than CISRR, the default SCWRL4 with subrotamers sampled, SCWRL4 with subrotamers disabled, SCATD and RASP, respectively (Table 1). The computational time for PSCP on the 379 native backbones is shown in Supplementary Table S10. It took only 34.3 s for FASPR to repack all of the 379 test proteins, which was even faster than the previously fastest packer, RASP (Colbes et al., 2017; Miao et al., 2011). To the best of our knowledge, FASPR may be the most efficient packing program developed so far. In addition, compared to RASP, FASPR uses a deterministic searching method, which allows for easy tracking of the repacked structure models in our protein design algorithm, EvoDesign (Pearce et al., 2019), or similar protein design approaches that separately consider the sequence space and rotamer space.
3.2 Performance of FASPR on I-TASSER-modeled backbones
It is important to test the ability of FASPR to perform side-chain modeling on non-native protein backbones, e.g. the predicted models produced by a typical protein structure prediction software. Previous studies demonstrated that PSCP programs can be applied to the protein backbones predicted by homology modeling (Kingsford et al., 2005; Lu et al., 2008), where higher side-chain modeling accuracy was achieved when the sequence identity between the modeled and template structures was higher (Lu et al., 2008).
We evaluated the performance of FASPR for side-chain modeling on the non-native main-chain structures extracted from the 379 I-TASSER models. The results are summarized in Table 2. The side-chain modeling accuracy on the I-TASSER backbones for the 18 amino acids with rotamers is listed in Supplementary Table S11. Compared to the results in Table 1, the overall prediction accuracy in terms of recovery rate dropped by about 10% for all of the methods, indicating that protein backbone conformations significantly impact the accuracy of side-chain prediction. Nevertheless, FASPR still achieved the highest overall side-chain torsion angle recovery rates among all of the programs by correctly predicting 58.0% of the side-chains. FASPR also yielded the second least number of clashes for the I-TASSER backbones, which was only worse than CISRR. These results reveal that FASPR may be more suitable for repacking structural models generated by I-TASSER than the other PSCP programs, demonstrating its usefulness in protein structure prediction.
Table 2.
Comparison of FASPR with four popular side-chain packing programs on the I-TASSER-modeled structures from DB379, where bold fonts mark the best performer in each category
| Method |
recovery rate (%)a |
#Clash | ||
|---|---|---|---|---|
| All | Core | Surface | ||
| FASPR | 58.0 | 70.9 | 44.0 | 397 |
| CISRR | 57.1 | 70.7 | 42.5 | 224 |
| RASP | 55.9 | 68.4 | 42.8 | 1633 |
| SCATD | 52.7 | 66.7 | 38.5 | 2452 |
| SCWRL4 | 57.4 | 71.0 | 42.9 | 893 |
| SCWRL4v | 55.3 | 68.5 | 41.7 | 647 |
The recovery rate was calculated between the 379 repacked models based on I-TASSER main chains and the native structures. Since the I-TASSER models have different main-chain positions compared to the native structures, the side-chain RMSD values were not calculated.
3.3 Performance of FASPR on perturbed backbones
We also tested the performance of FASPR on a series of non-native backbones by randomly perturbing the main-chains of the 379 structures from DB379. Main-chain perturbation was found to be useful in flexible-backbone protein design (Ollikainen et al., 2013; Saunders and Baker, 2005). This kind of non-native backbone is different from the I-TASSER modeled backbones because no energy minimization was performed to generate these main-chains. Ten sets of non-native main-chains were taken from the work by Xu et al. (2019).
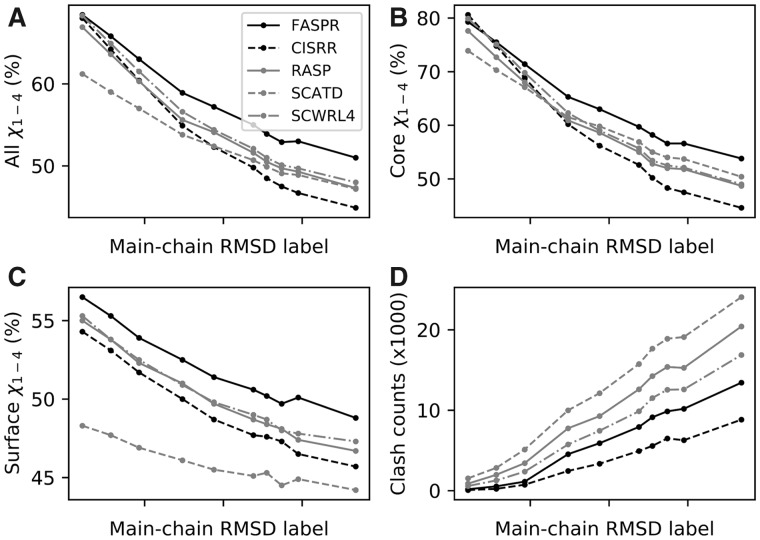
The results are illustrated in Figure 2. The side-chain modeling accuracy on the perturbed backbones for the 18 amino acids with rotamers is listed in Supplementary Tables S12–S21. A summary of the steric clashes produced by different methods for distinct main-chain RMSD levels is listed in Supplementary Table S22. In general, the recovery rate quickly decreased and meanwhile the number of clashes rapidly increased in the repacked structures for all the methods, as the main-chain RMSD increased (Fig. 2). Compared to the other methods, FASPR achieved a good performance in terms of recovery rate at different main-chain RMSD perturbation levels for the residues in all three categories (Fig. 2A–C). For the core residues, the difference between the performances of the five programs was only moderate (Fig. 2B), while for the surface residues, FASPR considerably outperformed the other programs (Fig. 2C). As shown in Fig. 2D and Supplementary Table S22, a large number of clashes were produced in the repacked structures for all the methods when the main-chain RMSD was very large (e.g. >2.38 Å); this was because the non-native backbones were generated by randomly perturbing the native main-chains and the tertiary folds might not be maintained when the RMSD is large. However, the performance on the backbones with small main-chain RMSDs (e.g. <0.93 Å) was to some extent meaningful, as much less steric clashes were obtained. For these low-RMSD backbones, FASPR achieved a good balance between packing accuracy and steric clashes.
Fig. 2.
Comparison of FASPR with four popular side-chain packing programs on the perturbed backbones. The main-chain RMSD values along the X-axis in each subplot are 0.21, 0.57, 0.93, 1.48, 1.88, 2.38, 2.55, 2.74, 2.95 and 3.68 Å, respectively
Most regular proteins possess a globular fold shape with a hydrophobic core and a hydrophilic surface. The state-of-the-art packing algorithms achieved about 20–30% higher recovery rates for packing the core residues than for packing the surface residues on both the native and near-native (e.g. I-TASSER models) structures (Tables 1 and 2), indicating that the I-TASSER models were in well-folded shapes. However, it can be seen that the difference between the recovery rates for the core and surface residues was less than 10% when the main-chain perturbation RMSD was large, e.g. >2.38 Å (Supplementary Tables S17–S21), suggesting that the folds may be destroyed. Therefore, the side-chain modeling results on the perturbed backbones revealed that, for flexible-backbone protein design, the main-chain conformation should not be changed too much so as not to damage the global fold and the designability. It has been suggested that a de novo protein sequence design case may be regarded as successful if the designed sequence can fold into a structure with a global RMSD <2 Å to the template used for design (Bazzoli et al., 2011), and ideally, this may also be an upper limit for the main-chain variation in flexible-backbone protein design.
4 Discussion and conclusion
In this work, we developed a new deterministic method, FASPR, for fast and accurate modeling of protein side-chain conformations. FASPR takes rotamers from the Dunbrack rotamer library (Shapovalov and Dunbrack, 2011). Atomic interactions are calculated using an optimized empirical scoring function that is mainly adapted from the EvoEF2 force field (Huang et al., 2020a) but with modifications to facilitate fast calculation. FASPR utilizes a deterministic searching algorithm, which combines self-energy checks, DEE (Goldstein, 1994; Pierce et al., 2000) and tree decomposition (Xu and Berger, 2006).
As a standard benchmark, the performance of FASPR was first evaluated and compared with four other state-of-the-art PSCP methods (i.e. CISRR, RASP, SCATD and SCWRL4) on a representative set of 379 native backbones. FASPR slightly outperformed CISRR, RASP and SCWRL4 by correctly predicting 69.1% of all the side-chains using a stringent tolerance criterion of 20°, and considerably outperformed SCATD, which only achieved a low recovery rate of 61.7%. FASPR, SCATD and SCWRL4 also utilize DEE and tree decomposition to solve the PSCP problem, and FASPR and SCWRL4 use the same rotamer library (Shapovalov and Dunbrack, 2011) but different scoring functions. Meanwhile, SCATD uses an older rotamer library (Dunbrack and Cohen, 1997) and a simple scoring function which contains only the van der Waals and rotamer probability terms. This comparison suggests that the accuracy of FASPR should be ensured by the optimized scoring function and the state-of-the-art rotamer library. Although FASPR uses similar searching techniques as SCATD and SCWRL4, the architectures of the search engines used by these programs are different. For instance, to enhance the computational efficiency of tree decomposition, Split DEE (Pierce et al., 2000) was introduced to further eliminate the non-GMEC rotamers after the application of the Goldstein DEE theorem (Goldstein, 1994). In practice, we found that Split DEE significantly improved the speed, as it took 0.6 and 1.0 min to pack all of the 379 native structures with and without Split DEE, respectively. To our knowledge, Split DEE has not been implemented in the other four programs. To show the efficiency of FASPR in detail, we listed the number and ratio of rotamers which were eliminated at each searching stage (i.e. self-energy check, Goldstein DEE, Split DEE and tree decomposition) for each of the 379 test cases on native backbones. As shown in Supplementary Table S23, overall self-energy check, Goldstein DEE, Split DEE and tree decomposition eliminated 11.55%, 75.62%, 4.25% and 8.57% of the rotamers, respectively. Alternatively, on average, 10.76 ± 3.19%, 76.97 ± 5.92%, 3.86 ± 3.23% and 8.41 ± 3.25% of the rotamers were eliminated at the four stages, respectively. The relatively low ratio of rotamers eliminated by Split DEE was because it was performed after self-energy check and Goldstein DEE. Nevertheless, we can see from Supplementary Table S23 that Split DEE eliminated more than 10% of the rotamers for many cases. Only two cases, 1HZ6 and 2VC8, can be directly solved by self-energy check and DEE, indicating that the efficiency of FASPR can be attributed to the elaborate collaboration of the four filters. As expected, it took a longer time to pack larger proteins with more rotamers and/or residues (Supplementary Fig. S1); but it was still sufficiently efficient for large proteins (e.g. >500 amino acids). Moreover, it is likely that the prediction accuracy is independent from the size of a protein (Supplementary Fig. S2).
For protein structure prediction and flexible-backbone protein design, the main-chain of a protein scaffold is not native. Therefore, it is of great significance to examine the ability of packing methods to model the side-chains of non-native backbones. To this end, we compared FASPR and the other four packers on the 379 I-TASSER backbones and 10 sets of perturbed backbones derived from DB379. In both kinds of tests, FASPR also performed equivalently or even better than the other methods, although all of them showed reduced performance.
Although FASPR achieved high prediction accuracy, the performance was still far from the maximum accuracy level that can be achieved, due to the inaccuracy of scoring functions and rotamer libraries (Colbes et al., 2017; Huang et al., 2020b). Recently, Xiong et al. (2020) reported that their protein design method, ABACUS2, significantly outperformed SCWRL4 if it was repurposed for PSCP. We also evaluated ABACUS2 on both native and non-native backbones in this work. ABACUS2 indeed outperformed the other PSCP methods including FASPR in terms of recovery rate and the number of steric clashes on both experimental backbones (Supplementary Table S9) and I-TASSER modeled backbones (Supplementary Table S11), but with much longer computational time (Supplementary Table S10). It was mentioned that the improvement of high prediction accuracy of ABACUS2 was due to the combination of a novel Cartesian-space conformer library collected from experimental side-chain coordinates, which is quite different from the Dunbrack rotamer library, and an elaborate statistical scoring function. We also tested ABACUS2 on the perturbed main-chains, and it was shown in Supplementary Tables S12–S21 that ABACUS2 outperformed FASPR only when the main-chain RMSD was sufficiently low (i.e. 0.21 Å), while FASPR significantly outperformed ABACUS2 when the main-chain RMSD was higher (e.g. ≥0.57 Å).
We performed side-chain packing assessment on perturbed backbones as a comparison with a previous study (Xu et al., 2019). However, it should be noted that the perturbed main-chains may form a poor test set to benchmark side-chain repacking methods, because the random structure perturbations applied to generate these main-chains may lead to violations of some basic constraints on the polypeptide backbone conformations. For the perturbed main-chains, ABACUS2 had significantly fewer atomic clashes than the other methods (Supplementary Table S22), but its performance was reduced the most as the perturbation increased (Supplementary Tables S12–S21). The I-TASSER modeled structures constitute a much more reasonable benchmark set to evaluate the ability of different methods to tolerate backbone variations.
Intrinsically disordered proteins (IDPs) are a large and functionally important class of proteins that lack a fixed or ordered three-dimensional (3D) structure (Dunker et al., 2008; Dyson and Wright, 2005). The discovery of IDPs has challenged the paradigm that protein function depends on a fixed 3D structure, where it is commonly thought that proteins fold into the GMEC in the protein folding field. FASPR also followed this principle to determine the side-chain conformations of amino acids. For IDPs, protein dynamics may be more important for modeling their structures and functions. Nevertheless, technically, given a protein backbone, FASPR can be used to pack the side-chains whether or not the protein is an IDP. But since FASPR is not benchmarked on IDPs, the quality of the repacked models cannot be guaranteed. Additionally, since FASPR employs a deterministic searching method, it cannot produce an ensemble of side-chain configurations. For the case where an ensemble of conformations is required, stochastic methods such as EvoEF2 (Huang et al., 2020a, b) can be utilized.
In addition to the high accuracy and speed, another important feature of FASPR is its determinacy. In our last updated version of EvoDesign for de novo protein design, we found that it was difficult to track the packed structure models for a given protein sequence because RASP introduces a stochastic searching procedure for side-chain modeling. In some design cases (e.g. the designed protein has >500 amino acids), the RASP model might not be of good quality in protein design simulations, which can harm the design results. Therefore, RASP has been replaced by FASPR for side-chain modeling in the EvoDesign package. In summary, the combination of high accuracy, speed and determinacy for modeling the side-chains of both native and non-native main-chain conformations makes FASPR a very useful tool for protein structure modeling and protein design.
Supplementary Material
Acknowledgements
The work used the Extreme Science and Engineering Discovery Environment (XSEDE) clusters (Towns et al., 2014), which is supported by the National Science Foundation (ACI-1548562).
Funding
The work was supported by the National Institute of General Medical Sciences (GM083107 and GM116960), the National Institute of Allergy and Infectious Diseases (AI134678) and the National Science Foundation (DBI1564756 and IIS1901191).
Conflict of Interest: none declared.
References
- Bazzoli A. et al. (2011) Computational protein design and large-scale assessment by I-TASSER structure assembly simulations. J. Mol. Biol., 407, 764–776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berman H.M. et al. (2002) The Protein Data Bank. Acta Crystallogr. D, 58, 899–907. [DOI] [PubMed] [Google Scholar]
- Canutescu A.A. et al. (2003) A graph-theory algorithm for rapid protein side-chain prediction. Protein Sci., 12, 2001–2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cao Y. et al. (2011) Improved side-chain modeling by coupling clash-detection guided iterative search with rotamer relaxation. Bioinformatics, 27, 785–790. [DOI] [PubMed] [Google Scholar]
- Case D.A. et al. (2005) The Amber biomolecular simulation programs. J. Comput. Chem., 26, 1668–1688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chitsaz M., Mayo S.L. (2013) GRID: a high-resolution protein structure refinement algorithm. J. Comput. Chem., 34, 445–450. [DOI] [PubMed] [Google Scholar]
- Colbes J. et al. (2017) Protein side-chain packing problem: is there still room for improvement? Brief Bioinform., 18, 1033–1043. [DOI] [PubMed] [Google Scholar]
- Desmet J. et al. (1992) The dead-end elimination theorem and its use in protein side-chain positioning. Nature, 356, 539–542. [DOI] [PubMed] [Google Scholar]
- Dunbrack R.L. Jr., Cohen F.E. (1997) Bayesian statistical analysis of protein side-chain rotamer preferences. Protein Sci., 6, 1661–1681. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dunker A.K. et al. (2008) Function and structure of inherently disordered proteins. Curr. Opin. Struct. Biol., 18, 756–764. [DOI] [PubMed] [Google Scholar]
- Dyson H.J., Wright P.E. (2005) Intrinsically unstructured proteins and their functions. Nat. Rev. Mol. Cell Biol., 6, 197–208. [DOI] [PubMed] [Google Scholar]
- Engh R.A., Huber R. (1991) Accurate bond and angle parameters for X‐ray protein structure refinement. Acta Crystallogr. A, 47, 392–400. [Google Scholar]
- Goldstein R.F. (1994) Efficient rotamer elimination applied to protein side-chains and related spin glasses. Biophys. J., 66, 1335–1340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gordon D.B., Mayo S.L. (1999) Branch-and-terminate: a combinatorial optimization algorithm for protein design. Structure, 7, 1089–1098. [DOI] [PubMed] [Google Scholar]
- He J. et al. (2018) Computational redesign of penicillin acylase for cephradine synthesis with high kinetic selectivity. Green Chem., 20, 5484–5490. [Google Scholar]
- Huang X. et al. (2013. a) Systematic optimization model and algorithm for binding sequence selection in computational enzyme design. Protein Sci., 22, 929–941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang X. et al. (2013. b) A solvated ligand rotamer approach and its application in computational protein design. J. Mol. Model., 19, 1355–1367. [DOI] [PubMed] [Google Scholar]
- Huang X. et al. (2017) Computational design of cephradine synthase in a new scaffold identified from structural databases. Chem. Commun., 53, 7604–7607. [DOI] [PubMed] [Google Scholar]
- Huang X. et al. (2020. a) EvoEF2: accurate and fast energy function for computational protein design. Bioinformatics, 36, 1135–1142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang X. et al. (2020. b) Toward the accuracy and speed of protein side-chain packing: a systematic study on rotamer libraries. J. Chem. Inf. Model., 60, 410–420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kingsford C.L. et al. (2005) Solving and analyzing side-chain positioning problems using linear and integer programming. Bioinformatics, 21, 1028–1036. [DOI] [PubMed] [Google Scholar]
- Krivov G.G. et al. (2009) Improved prediction of protein side-chain conformations with SCWRL4. Proteins, 77, 778–795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leach A.R., Lemon A.P. (1998) Exploring the conformational space of protein side chains using dead-end elimination and the A* algorithm. Proteins, 33, 227–239. [DOI] [PubMed] [Google Scholar]
- Liu Z. et al. (2002) Beyond the rotamer library: genetic algorithm combined with the disturbing mutation process for upbuilding protein side-chains. Proteins, 50, 49–62. [DOI] [PubMed] [Google Scholar]
- Lu M. et al. (2008) OPUS-Rota: a fast and accurate method for side-chain modeling. Protein Sci., 17, 1576–1585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Metropolis N., Ulam S. (1949) The Monte Carlo method. J. Am. Stat. Assoc., 44, 335–341. [DOI] [PubMed] [Google Scholar]
- Miao Z., Cao Y. (2016) Quantifying side-chain conformational variations in protein structure. Sci. Rep., 6, 37024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miao Z. et al. (2011) RASP: rapid modeling of protein side chain conformations. Bioinformatics, 27, 3117–3122. [DOI] [PubMed] [Google Scholar]
- Mitra P. et al. (2013) An evolution-based approach to de novo protein design and case study on Mycobacterium tuberculosis. PLoS Comput. Biol., 9, e1003298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ollikainen N. et al. (2013) Flexible backbone sampling methods to model and design protein alternative conformations. Methods Enzymol., 523, 61–85. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pantazes R.J. et al. (2015) The Iterative Protein Redesign and Optimization (IPRO) suite of programs. J. Comput. Chem., 36, 251–263. [DOI] [PubMed] [Google Scholar]
- Parsons J. et al. (2005) Practical conversion from torsion space to Cartesian space for in silico protein synthesis. J. Comput. Chem., 26, 1063–1068. [DOI] [PubMed] [Google Scholar]
- Pearce R. et al. (2019) EvoDesign: designing protein-protein binding interactions using evolutionary interface profiles in conjunction with an optimized physical energy function. J. Mol. Biol., 431, 2467–2476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peterson R.W. (2004) Improved side-chain prediction accuracy using an ab initio potential energy function and a very large rotamer library. Protein Sci., 13, 735–751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pierce N.A. et al. (2000) Conformational splitting: a more powerful criterion for dead-end elimination. J. Comput. Chem., 21, 999–1009. [Google Scholar]
- Roy A. et al. (2010) I-TASSER: a unified platform for automated protein structure and function prediction. Nat. Protoc., 5, 725–738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Samudrala R., Moult J. (1998) A graph-theoretic algorithm for comparative modeling of protein structure. J. Mol. Biol., 279, 287–302. [DOI] [PubMed] [Google Scholar]
- Saunders C.T., Baker D. (2005) Recapitulation of protein family divergence using flexible backbone protein design. J. Mol. Biol., 346, 631–644. [DOI] [PubMed] [Google Scholar]
- Shapovalov M.V., Dunbrack R.L. Jr. (2011) A smoothed backbone-dependent rotamer library for proteins derived from adaptive kernel density estimates and regressions. Structure, 19, 844–858. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shultis D. et al. (2019) Changing the apoptosis pathway through evolutionary protein design. J. Mol. Biol., 431, 825–841. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Towns J. et al. (2014) XSEDE: accelerating scientific discovery. Comput. Sci. Eng., 16, 62–74. [Google Scholar]
- Xie W., Sahinidis N.V. (2006) Residue-rotamer-reduction algorithm for the protein side-chain conformation problem. Bioinformatics, 22, 188–194. [DOI] [PubMed] [Google Scholar]
- Xiong P. et al. (2020) Increasing the efficiency and accuracy of the ABACUS protein sequence design method. Bioinformatics, 36, 136–144. [DOI] [PubMed] [Google Scholar]
- Xu J., Berger B. (2006) Fast and accurate algorithms for protein side-chain packing. J. ACM, 53, 533–557. [Google Scholar]
- Xu J., Zhang Y. (2010) How significant is a protein structure similarity with TM-score = 0.5? Bioinformatics, 26, 889–895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu G. et al. (2019) OPUS-Rota2: an improved fast and accurate side-chain modeling method. J. Chem. Theory Comput., 15, 5154–5160. [DOI] [PubMed] [Google Scholar]
- Yang J. et al. (2015) The I-TASSER Suite: protein structure and function prediction. Nat. Methods, 12, 7–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang J. et al. (2011) Atomic-level protein structure refinement using fragment-guided molecular dynamics conformation sampling. Structure, 19, 1784–1795. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.