Serpentine: a flexible 2D binning method for differential Hi-C analysis

Abstract

Motivation

Hi-C contact maps reflect the relative contact frequencies between pairs of genomic loci, quantified through deep sequencing. Differential analyses of these maps enable downstream biological interpretations. However, the multi-fractal nature of the chromatin polymer inside the cellular envelope results in contact frequency values spanning several orders of magnitude: contacts between loci pairs separated by large genomic distances are much sparser than closer pairs. The same is true for poorly covered regions, such as repeated sequences. Both distant and poorly covered regions translate into low signal-to-noise ratios. There is no clear consensus to address this limitation.

Results

We present Serpentine, a fast, flexible procedure operating on raw data, which considers the contacts in each region of a contact map. Binning is performed only when necessary on noisy regions, preserving informative ones. This results in high-quality, low-noise contact maps that can be conveniently visualized for rigorous comparative analyses.

Availability and implementation

Serpentine is available on the PyPI repository and https://github.com/koszullab/serpentine; documentation and tutorials are provided at https://serpentine.readthedocs.io/en/latest/.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Chromosomal conformation capture experiments (Hi-C) provide a quantitative way to infer the spatial proximity of DNA segments (Dekker et al., 2002; Lieberman-Aiden et al., 2009). Hi-C relies on deep sequencing to detect and quantify contacts between pairs of DNA segments, genome-wide. These contacts are displayed in a contact map, i.e. a table or matrix reporting the number of events between each pair of loci. The rows and columns of this matrix represent DNA segments of the reference genome, of identical size (in bp). Each entry indicates the contact count between two regions (Fig. 1A, upper panel). The analyses of contact matrices typically involve a normalization step, as well as the identification of specific patterns reflecting functional folding of the genome (for a comparison of available methods, see Forcato et al., 2017). However, experimental variability may influence data analysis in slight yet irreproducible ways. While this does not affect analyses where robust trends are not altered by noise, the quality suffers in poorly covered regions and/or distant regions, limiting accurate comparisons of biological samples. A variety of approaches, taking into account the contact distribution, have been developed to tackle these limitations (Lun and Smyth, 2015; Stansfield et al., 2018). However, these software packages do not consider sparse information. Another option is to bin pixels (i.e. replace groups of pixels by the value of their sum or mean) by fixed-size squares to increase the signal-to-noise ratio in regions with few or no contacts (Lajoie et al., 2015). This is performed uniformly over the entire map, limiting the overall resolution. The result misses out information on dense regions with sufficient coverage to be observed at a higher resolution, and is often insufficient to observe sparser regions.

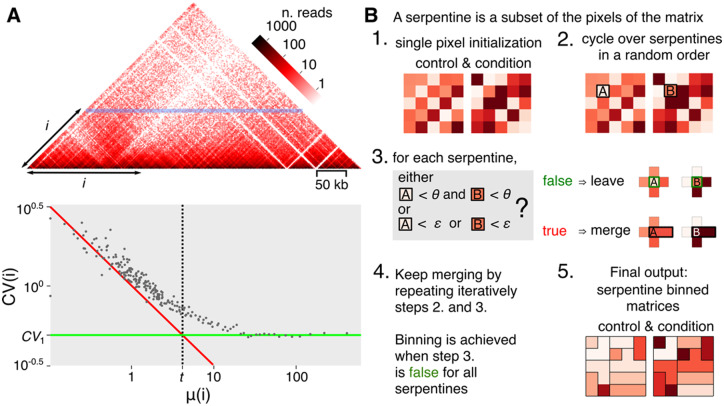
Fig. 1.

Contact matrix and algorithm. (A) Hi-C matrix (S.cerevisiae chromosome V). Since contact matrices are symmetric, only one half is shown. Each pixel of the map corresponds to a pair of coordinates of genomic segments (or bins). The color intensity reflects the frequency of contacts. The horizontal blue line corresponds to one of the diagonals of the contact matrix, with $i$ indicating the distance separating the pairs of segments positioned along that diagonal. At high $i$ values, i.e. for DNA segments separated by large distances, the matrix becomes sparse (white pixels). The lower panel shows the mean and $CV$ for all diagonals (i.e. $i$ values) of the matrix. The resulting scatter-plot reveals a transition that defines two constants: the $CV$ constant ${CV}_1$ (green line, for $\mu >t$) and the mean constant $t$ (dotted line, intersection of green line and the Poisson distribution represented by the red line). Dots at the left of $t$ and over ${CV}_1$ are subject to the effect of sparsity. (B) Algorithm flowchart of serpentine. See main text for detailed description of the workflow. (Color version of this figure is available at Bioinformatics online.)

1.1 Description of the problem

Low or noisy signal ratio is intrinsic to Hi-C contact maps and varies depending on the read coverage, i.e. the sequencing depth of the Hi-C libraries. Indeed, because of the polymer nature of chromosomes, the contact frequency between DNA segments decreases with the genomic distance $i$ separating them by multiple orders of magnitude (Imakaev et al., 2015; Rippe, 2001). As a result, adjacent segments interact much more frequently than distant ones, as shown by the curve describing the mean number of contacts at fixed genomic distance $\mu \left(i\right)$ (Mirny, 2011). The sequencing depth also affects the relative level of variability observed in Hi-C datasets. The coefficient of variation (CV) at fixed genomic distance, $CV\left(i\right)=\sigma \left(i\right)/\mu \left(i\right),$ is a value that at high-enough read coverages reflects the biological variability and locus-specific biases (Muller et al., 2018). Close to the main diagonal of the maps, both the means $\mu$ and SDs $\sigma$ are proportional to the read coverage, resulting in constant CVs: ${CV=CV}_1$ (Fig. 1A, right part of the lower panel). The contributions of the statistical noise become measurable as the coverage decrease, notably in positions distant from the main diagonal where the coverage is influenced by random sampling (e.g. PCR-amplification, sequencing). This results in pixel values following a Poisson distribution, thus: $\sigma =\sqrt{\mu }$. At these levels of coverage, the biological variability is overwhelmed by noise and consequently $CV\propto {\mathrm{\mu }}^{-\frac{1}{2}}$ and $CV>\mathrm{ }{CV}_1$. The transition between low and high-enough coverages can be defined by the threshold $t$ (Fig. 1A, dotted line), with $t=1/{CV}_1^2$, calculated by the intersection between the lines representing constant and coverage-dependent $CV$’s. This divergence signifies that the biological variability is lost due to the sampling process in sparse regions.

1.2 Overview of the proposed approach

To overcome the effects of sparse information across the whole contact map, we developed serpentine binning, a normalization- and assumption-free method that only bins low pixel values (i.e. low-covered regions). It ensures that the resulting coverage values for each bin in the final map are all above a certain threshold. Instead of shaping pixel bins according to a fixed, unique rule, like square-pooling, binning now results from random iterations based on the number of contacts. When applied to sparse regions, it unveils patterns hidden in non-binned matrices, emphasizing the detection of contacts between distant genomic regions in a more statistically significant way.

2 Materials and methods

2.1 Contact map generation

Fastq-sequencing files from yeast Saccharomyces cerevisiae Hi-C DpnII libraries were recovered from public repositories (Patel et al., 2019; Schalbetter et al., 2019), or generated in the lab (SRA accession numbers SRX7554368 and SRX7554369). Raw contact maps were generated and binned using a custom-made python package (https://github.com/koszullab/hicstuff) and the following parameter: hicstuff pipeline -n -t 28 -e DpnII –filter –aligner=bowtie2. Alignment of fastq was done using either the SK1 (Song et al., 2019) or S288C reference genomes (Yue et al., 2017), depending on the strain. Alignments were filtered as described in Cournac et al. (2012) and binned along 2.5 kb sequences (hicstuff rebin –binning =2500 bp). An example of resulting yeast genome intra-chromosomal contact maps is depicted in Supplementary Figure S1.

2.2 Down-sampling of contact maps

Hicstuff provides the ability to downsample the data through the following command line: hicstuff subsample –prop x, where x is the proportion of subsampling.

2.3 Joint serpentine binning

The serpentine-binning algorithm (Fig. 1B) requires two input thresholds $\theta$ and$\mathrm{ }\epsilon$, with $\epsilon <\mathrm{ }\theta$, and two contact maps; typically, an experimental contact map compared to its biological control. The parameters $\theta$ and $\epsilon$ correspond to the coverage thresholds, tunable by the user, that control the minimal number of reads present in each serpentine, in, respectively, each or both matrices. Higher $\theta$ and$\mathrm{ }\epsilon$ values result in more binning. $\theta$ and$\mathrm{ }\epsilon$ are related to the threshold $t$, i.e. the settings of $\theta$ and$\mathrm{ }\epsilon$ and the resulting binning move all the bins from the left side of $t$ (high noise signal ratio; Fig. 1A lower panel) toward the right side of $t$ (low-noise signal ratio). A serpentine is then defined as an irregular geometrical bin, i.e. a subset of connected pixels. At the beginning of the binning process, each pixel is a serpentine. One of those serpentines is then randomly chosen. This defines a pair of serpentines, one on each of the two matrices to be compared (pixel A and B in Fig. 1B, step 2). If both values of the two serpentines are lower than $\theta$, or if a value of any serpentine of the pair is lower than $\epsilon$, then these serpentines are suitable to merge with another serpentine randomly chosen among neighbors (Fig. 1B, step 3). The merging takes place identically in both maps, resulting in a pair of larger serpentines (two pixels or sets of pixels instead of one). In each map, the sum of the pixels is attributed to the newly formed serpentine. The same procedure is applied over all serpentines on the contact matrix in a random order. This procedure is repeated until the total number of serpentines remains constant across two iterations, i.e. when the structure cannot evolve further. The resulting contact maps are then binned serpentine-wise, i.e. each pixel value is replaced with the average value of all pixels belonging to its final serpentine. This average value represents the amount of contacts spread over the regions involved. At the end of the binning, all serpentines have collected enough statistics to greatly reduce sampling effects, but the shape of the serpentines is determined by the randomly chosen 2D paths. To avoid this distortion, the full algorithm is run independently N (N > 4) times. The final binned matrix is the average of the N runs. Of note, the serpentine algorithm described here is applied on two contact matrices, but it can be run on more.

2.4 Mean-deviation plots

From a couple of matrices $M_1$ and $M_2$, and for each $M_1$ and $M_2$ pixel, of same coordinates, the mean $m_{x,y}$ and the ratio $r_{y,x}$ are computed. The mean-deviation (MD) plot is a scatter-plot where each dot maps to a pixel coordinates, and have values of log₂$m_{x,y}$ (respectively log₂$r_{y,x}$ centered on ratio 1) for the x- (respectively y-) axis (Figs 2 and 3, right panels).

Fig. 2.

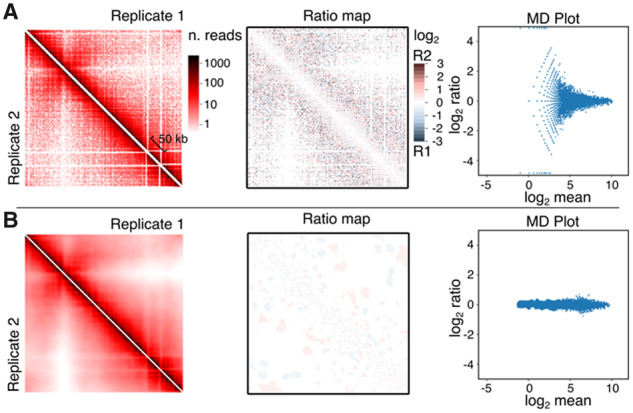
Serpentine analysis using biological replicates of asynchronous yeast cultures. Contact maps of chromosome V, ratio heatmaps and MD plots before (A) (bin =2.5 kb) and after (B), serpentine binning. On the left panels, half of the symmetric matrices are depicted: top right for replicate 1 and bottom left for replicate 2. Center panels show the full symmetric ratio heatmap of the two matrices from the corresponding left panel. See the M&M section for MD plot details

2.5 Generation of ratio heatmaps

Standard contact maps (Figs 2A and 3A and C, left panels) depict raw read counts. Ratio heatmaps (Figs 2A and 3A, center panels) were obtained using the log₂ of $r_{y,x}/f_{y,x}$, with $r_{y,x}$ described above and with $f_{y,x}=\mathit{mean}\left(y\right)/\mathit{mean}\left(x\right)$. Ratios cancel out locus-specific biases. Mask matrices (Figs 4 and 6, right panel) were obtained using the HiCcompare R package (Stansfield et al., 2018). Starting from the two raw square contact matrices to be compared, we applied the statistical model using the functions full2sparse, create. hic.table, hic.loess and hic.compare. This package provides P-value measures that indicate significant $r_{y,x}$ ratios. The corresponding significant coordinates were used to generate an inverted binary mask matrix with significant ratios as transparent pixels and with non-significant ratios as semi-transparent black pixels.

Fig. 4.

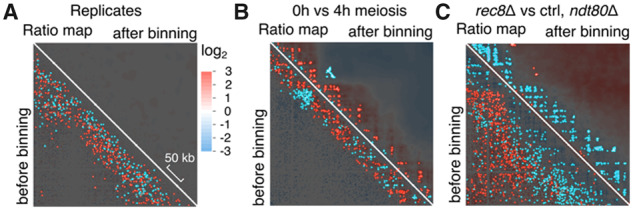
HiCcompare analysis of ratio heatmaps before (bottom left) or after (top right) serpentine binning. Maps and masks obtained using the data from Figure 2 (A) (biological replicates, asynchronous cells) or from Figure 3 (B) (meiosis t=0 and 4 h cells) (C) (pachytene-arrested cells rec8Δ and control). A semi-transparent mask derived from HiCcompare analysis overlays the ratio heatmaps, which highlights the significant ratio determined by HiCcompare (no dark areas)

2.6 Filtering and normalization

Filtering is performed by removing from the matrices all rows/columns with total coverage <3 SDs below the median row coverage. Normalization is performed by iterative correction (ICE) (Imakaev et al., 2012).

2.7 Comparison with binless

Serpentine was compared to binless (Spill et al., 2019) using the data and procedure used as an example in the binless package and accessible at https://github.com/3DGenomes/binless/blob/56c78b3588a708076b9a046759eafa783053aac1/example/rao_HiCall_FOXP1ext_2.3M_optimized_binless_difference.pdf.

3 Results

3.1 Serpentine attenuates noise in poorly covered regions

We first tested serpentine binning on two biological Hi-C replicates of asynchronous populations of S.cerevisiae (Fig. 2). Without serpentine, ratio heatmap unveils strong local variation, with neighboring pixels sometimes presenting opposite log2 ratios, except on the main diagonal (Fig. 2, center panel). MD plot confirms that the variation is highest for low mean coverages (right panel). Altogether, these analyses illustrate the substantial sampling noise that can be observed in poorly covered regions when comparing two Hi-C contact maps. Using the mean-CV plot (Fig. 1A, lower panel) on both replicates, a mean threshold $t\mathrm{ }\approx \mathrm{ }7$ was computed. From this, we used serpentine parameters $\theta \mathrm{ }=70$ and $\epsilon =\mathrm{ }7$. The value of $\theta \mathrm{ }$is 10-fold higher than $t$, in order to strongly fade the noise. Iterations were set to $N\mathrm{ }=\mathrm{ }128$. After serpentine binning, the signal-to-noise ratio globally improves (Fig. 2B, center panel). The MD plot that diverges to infinite values before binning, assumes a cigar-like shape after, showing the pixels’ values in both maps do not display much differences, as expected from biological replicates. Serpentine binning therefore attenuates the noise present in poorly covered regions without creating aberrant patterns that could be interpreted as biological contacts.

3.2 Serpentine enhances patterns related to biological structures in yeast meiosis Hi-C maps

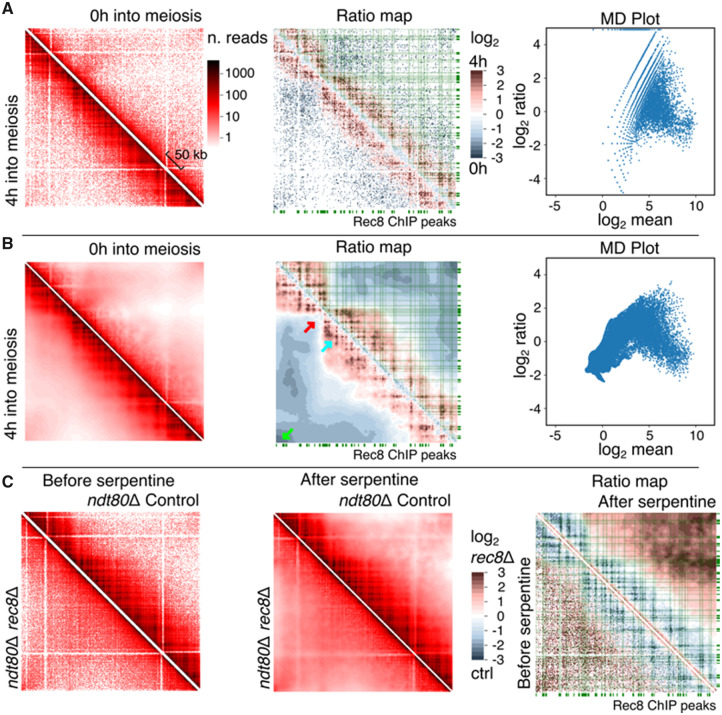
We then tested serpentine binning using highly-covered contact maps generated over prophase I of a S.cerevisiae meiotic time course (Fig. 3 and Supplementary Fig. S2) (Schalbetter et al., 2019). Over progression into prophase, chromosomes first replicate, while undergoing large structural changes, most prominently a loss of centromere clustering (Trelles-Sticken et al., 1999), an increase in compaction (Zickler and Kleckner, 1998), and a loss of telomere–telomere enriched contacts accompanied by vigorous movements (Koszul et al., 2008; Koszul and Kleckner, 2009; Trelles-Sticken et al., 1999). This chromosomal reorganization has been recently studied using Hi-C (Muller et al., 2018; Schalbetter et al., 2019). The ratio of the raw contact maps of pre-meiotic (0 h) cells and cells at 4 h into prophase, when this reorganization has taken place (see Muller et al., 2018 for discussion), results in sparse signal (Fig. 3A). The MD plot (Fig. 3A, right panel) highlights a strong sampling effect (large ratios at small means), as observed for comparison of replicates (Fig. 2A). The application of serpentine binning to the two contact maps at 0 and 4 h into meiosis prophase reduces the variability at low coverages observed in the MD plot (Fig. 3B, right panel). However, this scatter-plot has a curved shape, which is qualitatively different from the one observed for comparison of replicates (Fig. 2B). In addition, the application of serpentine binning improves the direct observation of contact patterns on contact maps at all scales (Fig. 3B). At shorter distances, the centromere shows enriched contacts with both flanking arms, reflecting the loss of insulation of the pericentromeric region resulting from de-clustering (Fig. 3B, red arrow) (Muller et al, 2018). At long distances, one can observe a general drop in contacts that most likely reflects the increase in short-range compaction. However, this drop is stronger at telomeres, which probably reflects the loss of trans-telomere contacts resulting from the dynamics movements they initiate at that stage (Fig. 3B, green arrow) (Koszul et al., 2008).

Fig. 3.

Serpentine analysis comparing contact maps generated during meiosis. Time course at 0 and 4 h, before (A) and after (B) serpentine binning, left, right and central panels are the same as in Figure 2. (C) Serpentine analysis comparing the Rec8 cohesin deletion mutant to control, in a population blocked in pachytene through Ndt80 deletion: before binning, after binning and ratio-maps. The green rectangles along the axis of contact maps correspond to the deposition sites of the cohesin meiotic subunit Rec8. The green lines connect these deposition sites to the diagonal. Green arrow: telomere-telomere contacts. Red arrow: centromere position. Cyan arrow, meiotic loop. (Color version of this figure is available at Bioinformatics online.)

At short- and medium-range distances, a grid-like pattern appears, highlighting discrete positions enriched in contacts. This pattern was strongly enhanced after serpentine binning compared to the raw signal (compare Fig. 3B, cyan arrow, with Fig. 3A). This pattern reflects the formation of cohesin-dependent loops along the chromosome that promote the increase in compaction [see Muller et al. (2018) and Schalbetter et al. (2019) for demonstration and discussion]. In agreement with these past works, those clusters clearly overlap visually with genomic sites enriched in the cohesin subunit Rec8 (Fig. 3B, green lines) and disappear in a rec8 mutant (Fig. 3C) (cells synchronized and arrested in pachytene through a Ndt80 depletion) (Schalbetter et al., 2019).

Altogether, these results show that serpentine binning enhances biologically relevant patterns.

3.3 Serpentine enhances significant structures

To determine the sensitivity of serpentine, we used HiCcompare before and after binning (Stansfield et al., 2018). Significant pixels provided by HiCcompare were used to generate a semi-transparent mask that highlights the regions of significant ratios when overlaid on top of the ratio-maps (Fig. 4). As a negative control, we performed the analysis on biological replicates (Fig. 4A). HiCcompare detected ∼3% and zero significant pixel ratios before and after serpentine binning, respectively, confirming that the process attenuates noise in poorly covered regions without generating aberrant patterns. We then applied HiCcompare on ratio of meiotic contact maps at 0 and 4 h (Fig. 4B). Before serpentine, HiCcompare pointed at ∼2% of significant pixel ratios, with an enrichment in contacts in the vicinity the diagonal (red pixels) and a drop at the centromere (blue pixels). However, those significant pixels were often intermingled, with no obvious pattern emerging from the mask. On the opposite, the ∼1% pixels highlighted as significant by HiCcompare after serpentine binning correspond to larger clusters positioned into a grid-like pattern, with little intermingling. To determine whether these clusters correspond to biologically relevant features, we repeated the analysis with meiotic, ndt80-arrested cells lacking cohesin-mediated loops (rec8 mutant, Fig. 4C). The application of HiCcompare on the ratio of rec8 depleted and control cells contact maps shows 4% significant pixel scattered on the raw ratio, reduced to 2% of discrete, larger clusters after serpentine binning. Furthermore, the overlap between the pixels identified by HiCcompare when comparing progression into meiosis (0 versus 4 h) and the absence of cohesin-mediated loops (rec8 versus control) was of 4% for the maps not treated with serpentine and 46% after serpentine binning (compare Fig. 4B versus C lower and upper right panels).

These results show that serpentine allows programs, such as HiCcompare, to identify relevant biological signals in contact maps, otherwise difficult to distinguish from the noise.

3.4 Serpentine attenuates the effects of low-coverage data

To test the robustness of serpentine binning on poorly covered regions, the counts of contact matrices at t=0 and 4 h into meiosis (see Fig. 3) were subsampled to mimic various sequencing depths (Fig. 5; Materials and methods). As a consequence of down-sampling, the ratio-maps become sparser and sparser before the application of serpentine binning (lower-left part of the matrices). The effect is particularly prominent at long distances from the main diagonal, where coverage is scarce. After serpentine binning (upper-high part of the matrices), matrices display a smoother pattern, while retaining biologically relevant features, i.e. a clear increase in compaction, the presence of loops (though not of all of them), and loss of long-range contacts (Supplementary Figs S3 and S4).

Fig. 5.

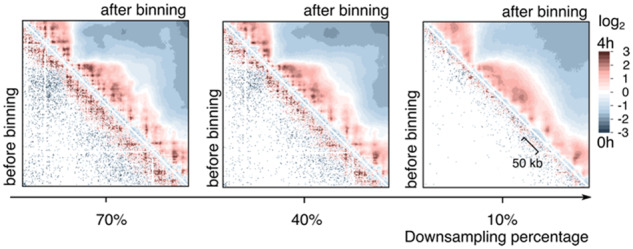
Serpentine analysis on low-coverage data. Same as Figure 3 middle panels, but using the same data downsampled to reduce the global coverage. The percentage of the total initial count kept after down-sampling is indicated below each panel

These results show that serpentine can help identify relevant changes otherwise difficult to see in poorly covered contact maps or regions.

3.5 Evidence of structuration in mouse spermatocytes during meiosis

To assess for serpentine versatility, we tested the binning on contact maps of mouse spermatocytes undergoing meiosis (Fig. 6; raw matrices in Supplementary Fig. S5) (Patel et al., 2019). Changes in contacts intensities were highlighted between cells at the zygotene (a stage of meiotic prophase I) versus premeiosis stages. Notably, in agreement with Patel et al. (2019), the chromatin loops that structure the pre-meiotic (and interphase) chromosomes at short- or medium (<200 kb)-genomic distances vanish upon entry into meiosis. The pattern is clearly visible on the serpentine ratio.

Fig. 6.

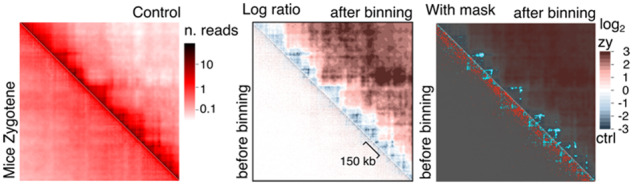
Serpentine applied to mammalian data from (Patel et al., 2019). Comparison of mouse spermatocytes during zygotene stage of meiosis versus control (mice interphase). Data from mouse chromosome II, region 27 700–29 160 (1.46 Mb, 1 kb bins) are depicted. See the previous figures for details

3.6 Serpentine performances

Finally, we benchmarked serpentine binning first by assessing the runtime performance according to matrix complexity (Supplementary Fig. S6A). With a total number of two million reads, in a square matrix of order 200×200 pixels, serpentine binning takes ∼10 s on a PC workstation with 64 GB of RAM and Intel Core i7 processor. Runtime increases as n² [complexity O(n²)], where (n× n) is the order of the input square matrices. We then assessed the runtime performance depending on matrix sparsity (proportion of non-zeros in the contact map, Supplementary Fig. S6B). With a matrix of order 100×100, and a measure of sparsity spanning from 10⁻⁴ to 10⁰, we show that, over 5 independent runs, runtime appears largely independent from this parameter.

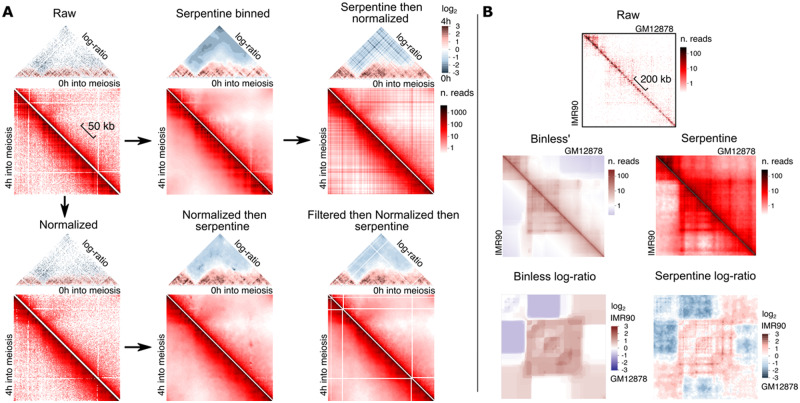
Normalization, notably ICE (Imakaev et al., 2012) and sequential component normalization (SCN) (Cournac et al., 2012) are frequently used to remove locus-specific biases on contact maps. Serpentine binning performed after ICE normalization appears (i) to generate noisier data, (ii) to remove the biological patterns highlighted above (Fig. 3), while (iii) adding new signal in the sparse regions (Fig. 7A, lower row). Even more notable is the effect of ICE normalization performed after serpentine binning (Fig. 7A, upper row); in this case, the appearance of straight lines resembling a checkerboard pattern, visible on both contact maps and the log-ratio map, is artifactual and a consequence of the normalization. Therefore, serpentine is better suited to raw data and does not necessitate prior normalization (see also Discussion).

Fig. 7.

Performances. (A) Influence of ICE iterative normalization (Imakaev et al., 2012), with or without filtering, on Serpentine outcomes. (B) Comparison between log-ratios for binless (left) and serpentine (right), using the binless-provided datasets (IMR90 versus GM12878) for the locus FOXP1 (Chromosome 3, region 7–7.2 Mb)

We compared serpentine with Binless, an image analysis algorithm that enhances contact patterns in Hi-C maps (Spill et al., 2019). We applied serpentine to a binless dataset comparing contacts in the FOXP1 locus (Chromosome 3, region 7–7.2 Mb) between the IMR90 (fetal lung fibroblast) and GM12878 (B-lymphoblast) human cell lines. We reproduced the published log-ratio map using binless (Fig. 7B; URL in Materials and methods). Although Binless uses a very different approach from serpentine, the two methods highlighted the same large-scale patterns. Domains and borders were accurately displayed in both cases and consistent with one another. However, the resolution seemed higher on serpentine ratio-maps, with small-scale patterns clearly distinguishable from the background noise. This would be important when loop-size pattern detection and visualization is required. Overall, we believe that the runtime, absence of normalization pre-processing and high-resolution output of serpentine, will be valuable for contact maps analyses.

4 Discussion

We designed serpentine binning as an intuitive and user-friendly method to highlight differences in contact maps, aggregating statistics in regions of sparsity without diluting regions presenting strong signals independently of coverage. The choice of binning and observation scale is a common problem when visualizing Hi-C data and the most common approach is to perform a simple 2D sum-pooling. We show that serpentine binning removes noise in poorly covered regions without generating aberrant patterns, while enhancing patterns corresponding to biological contacts. Serpentine binning is robust, managing to maintain the emphasis on relevant contacts even in poorly covered datasets or regions.

Normalizing the data using SCN or ICE before serpentine did not improve downstream differential analysis. This is expected. At low coverage, sparse regions in the maps will consist of pixels equal either to 0 or 1. Normalization will transform a pixel =1 into approximately a geometric mean of the coverage of the corresponding row and column. A pixel =0 will remain 0. As a result, the ratio-maps between two matrices obtained that way will contain infinites, not-a-numbers and random values. The application of SCN or ICE will therefore not solve the problem of low statistics of Hi-C data. These algorithms are appropriate when displaying contact maps to cancel loci-specific biases of Hi-C, such as guanine-cytosine content or experimental noise (Cournac et al., 2012). However, generally, when performing ratio-maps over biological conditions, loci-specific biases are the same on both maps; and they cancel each other. As a consequence, SCN or ICE is not required. For all these reasons, we advise against using serpentine after normalization. In addition, after normalization, the meaning of the parameters $\theta$ and$\mathrm{ }\epsilon$ related to coverage is lost, and we did not find an obvious way to relate the serpentine thresholds input before normalization to the pixel values after normalization. On raw contact maps, those parameters can be chosen by measuring the value of $t$ (Fig. 1A). In this article, we adopted a value of $\theta \mathrm{ }$10-fold higher than $t$, and $\epsilon$ equal to $t.$

Serpentine binning can be applied on a single matrix. To do so, the user should use the same contact map as both inputs. In that case, the parameter $\epsilon$ will be ignored while $\theta$ will play the role of the unique coverage threshold. Binning will be performed until all serpentine bins reach that coverage. However, the interest to use the tool this way (on a single map) is not obvious, as loci-specific biases will remain in the serpentine map. Those biases represent most of the variability of contact maps plotted in Figure 1A. As shown in Figure 7A, normalization using SCN or ICE after serpentine should not be done as it will introduces artifacts, a consequence of the fact that normalization is performed row- and column-wise, and not locally. The normalization algorithm introduces a flow of information between positions that can be far apart on the matrix, but on the same row/column, in a way difficult to control. Canonical binning in fixed-size squares spreads the noise or distorted signals uniformly along the whole fixed-size bin. Serpentine binning prior normalization, on the other hand, would make these artifacts prominent. Artifact are visible also when using SCN or ICE normalization prior to serpentine binning, in this case, due to the presence of spikes in lowly covered regions. Spikes are created as a consequence of the division of bins with one or a few aligned reads by a very small normalization factor. Filtering the matrices prior to normalization, in this case, qualitatively helps in reducing the effects of these artifacts, as shown in Figure 7A.

Serpentine is available as an open-access Python package easy to integrate into existing analysis pipelines. Currently, its input consists in relatively dense matrices loaded into memory, with a dataset reasonable upper size being 1500×1500 bins. In the future, this condition may be relaxed by using either sparse structures or by implementing disk-based formats. Sparsity of Hi-C contact maps can also be addressed experimentally through targeted capture protocols that selectively increase the read coverage of regions of interest, reducing complexity (at the expense of genome-wide information).