Abstract
Motivation
Epistasis reflects the distortion on a particular trait or phenotype resulting from the combinatorial effect of two or more genes or genetic variants. Epistasis is an important genetic foundation underlying quantitative traits in many organisms as well as in complex human diseases. However, there are two major barriers in identifying epistasis using large genomic datasets. One is that epistasis analysis will induce over-fitting of an over-saturated model with the high-dimensionality of a genomic dataset. Therefore, the problem of identifying epistasis demands efficient statistical methods. The second barrier comes from the intensive computing time for epistasis analysis, even when the appropriate model and data are specified.
Results
In this study, we combine statistical techniques and computational techniques to scale up epistasis analysis using Empirical Bayesian Elastic Net (EBEN) models. Specifically, we first apply a matrix manipulation strategy for pre-computing the correlation matrix and pre-filter to narrow down the search space for epistasis analysis. We then develop a parallelized approach to further accelerate the modeling process. Our experiments on synthetic and empirical genomic data demonstrate that our parallelized methods offer tens of fold speed up in comparison with the classical EBEN method which runs in a sequential manner. We applied our parallelized approach to a yeast dataset, and we were able to identify both main and epistatic effects of genetic variants associated with traits such as fitness.
Availability and implementation
The software is available at github.com/shilab/parEBEN.
1 Introduction
Recent advances in sequencing technology and data sharing have allowed the rapid accumulation a large amount of genomic data. Modern datasets are often genome-wide and highly dimensional because the feature size is significantly larger than sample size. This complexity has brought genomics researchers to the field of data science. Hence, it is urgent to develop new methods that allow for scalable, robust and efficient analysis of large genomic datasets.
One problem that we address in this study is termed as epistasis. Epistasis is an important yet challenging problem in genetics and genomics. Epistasis is considered as a critical genetic factor that contributes to complex traits, including many quantitative traits. Epistasis can be reflected when the effect of two or more genetic variants or genes combined have an effect, larger or smaller, than the sum of their individual effects (Forsberg et al., 2017). Epistasis among genetic variants or genes can account for an appreciable proportion of the hidden heritability of complex traits (Carlborg and Haley, 2004; Gibson, 2010; Zuk et al., 2012). Epistasis also plays an important role in gene expression and regulation (Carter et al., 2007; Gertz et al., 2010; Gibson, 1996). Previous studies have shown that accounting for epistasis led to better predictions of individual phenotypes (Forsberg et al., 2017) and higher detection power than single-locus analysis (Evans et al., 2006; Marchini et al., 2005; Verhoeven et al., 2010).
Users of high-throughput sequencing technology typically profile genome-wide genetic variants on a relatively low number of biological samples. This practice leads to a challenge in identifying epistasis in large-scale and typically high-dimensional genomic data. Since a high-dimensional dataset usually induces an over-saturated model, this in turn demands efficient and scalable statistical methods to solve the model on a vast search space (Van Steen and Moore, 2019).
A variety computational methods have been developed for epistasis analysis of genomic datasets, which can be classified into model-based and model-free methods. Model-based methods include regression-based methods which perform an exhaustive search for pairwise genetic variants, such as PLINK, BiForce, SNP–SNP interaction and FastEpistasis (Evans et al., 2006; Gyenesei et al., 2012a,b; Purcell et al., 2007; Schüpbach et al., 2010). Some sparse learning methods are also regression-based methods, such as the least absolute shrinkage and the selection operator (Lasso), Fused Lasso and multitask-Lasso (Chen et al., 2012; Lee et al., 2010; Quitadamo et al., 2015; Tian et al., 2014; Tibshirani, 1996; Tibshirani et al., 2005; Wang et al., 2014). These sparse learning/regression-based methods formalize the association problem as an optimization problem with regularization terms. Some aim to find the sets of genetic variants that associated with one or multiple traits for expression quantitative trait loci (eQTL) analysis. Bayesian-based methods, such as the Bayesian Epistasis Association Mapping method, Bayesian inference methods, Bayesian partition methods and BhGLM (Tang et al., 2009; Yi et al., 2011; Zhang and Liu, 2007; Zhang et al., 2010, 2011), usually impute the posterior probability through prior distribution for epistatic effects.
Model-free methods include machine learning methods which developed for epistatic analysis with a theme of data dimensionality reduction and feature selection, such as combinatorial partitioning method (Nelson, 2001), Multifactor Dimensionality Reduction (MDR) (Moore, 2004; Moore et al., 2017), Spatially Uniform ReliefF (Greene et al., 2009) and Epistasis Detector based on the Clustering of relatively Frequent items (Xie et al., 2012) and the Multi-SNP Combination Set Detector based on a combinatorial optimization model (Ding et al., 2015). MDR is a classical nonparameter machine learning method which was designed for the identification of multi-order epistasis in case–control studies. As an extension to MDR, Quantitative Multifactor Dimensionality Reduction (QMDR) (Gui et al., 2013) was developed to identify multi-order epistasis for quantitative traits. QMDR uses t-statistics to construct a score to rank the effects, which means that the higher the t-statistic score, the higher the confidence level of each effect. QMDR is computationally efficient and performs well for epistasis identification. We hence chose QMDR to compare against parEBEN (parallelized EBEN) since QMDR is a classical machine learning method with which parEBEN can be fairly compared and QMDR can quickly identify epistasis for quantitative traits which are the focus of this study.
Another strategy for the identification of epistasis aims to reduce the genomic data dimensionality before applying either model-based or model-free method aforementioned. These strategies include data-driven filtering (Brown et al., 2014; Huang et al., 2013; Lewinger et al., 2013; Shen et al., 2012; Sun et al., 2014), which is based on performing statistical tests to keep the most informative variants (Litvin et al., 2009; Pendergrass et al., 2015; Rönnegård and Valdar, 2012; Sun et al., 2014) and biological filtering, which is based on prior knowledge such as pathway information, protein–protein interactions, gene modules and/or mutation knowledge (New and Lehner, 2019). However, most of these methods cannot handle large genomic datasets and are not scalable. Thus, it is of interest to develop new statistical methods to solve and scale up analyses of epistasis on large-scale genomic data. The Empirical Bayesian Elastic Net (EBEN) method is recently developed for identifying quantitative trait loci (QTL) and epistasis, which has shown to be efficient and highly accurate (Huang et al., 2015; Wen et al., 2017). We choose the EBEN algorithm as it scales well on high-dimensional data and suits our needs for genome-wide epistatic analysis. EBEN moderately enables epistasis analysis by using statistical feature filtering to remove unimportant features, and a coordinate ascent method to estimate the unknown parameters in an over-saturated statistical model (Huang et al., 2015).
In some degree, the EBEN algorithm needs intensive hyperparameter tuning to produce the optimal values of two hyperparameters to obtain the best performance usually through cross-validation. However, the cross-validation in the EBEN algorithm is time-consuming as this exercise sweeps 400 combinations of 2 hyperparameters step-by-step in a serial manner for each subset in n-fold cross-validation (Fig. 2). This procedure significantly affects the scalability of EBEN.
Fig. 2.

The time bottleneck due to the serial nature of the original EBEN algorithm
In this report, we use parallelization to solve the scaling issues around the cross-validation and hyperparameter tuning of EBEN and create parEBEN. Originally, the sequential algorithm was published as an R package, simply named EBEN (Huang, 2015; Huang and Liu, 2016). The original EBEN R package is only implemented in a sequential manner, meaning that the computations of the cross-validation and hyperparameter tuning only run one at a time on a single core of a CPU. We have developed a parEBEN package to allow efficient learning for analysis of epistasis with highly dimensional genomic datasets. We further scale up the parEBEN algorithm by filtering using a matrix multiplication step to narrow down the search space of features in analysis of epistasis. The parEBEN method can speed up the epistasis identification by distributing to multiple processors.
In the following sections, we first describe the pre-computation of the matrix multiplication step, the EBEN algorithm and introduce the parEBEN R package (Ford, 2018). We use simulated and empirical yeast data as examples to demonstrate the performance of our newly developed parallelization method, parEBEN.
2 Materials and methods
In our analysis of epistasis, we aim to build a multi-locus model that includes all main and epistatic terms in the model. Our multi-locus model is different from the single-locus model for epistasis, which has to face the problem of testing for multi-correction. Our methods can handle the high co-linearity problem with the application of the Bayesian prior distribution, shrinkage operator and variable selection strategy. Due to the large number of features, we first apply a matrix multiplication strategy to generate the correlation matrix and pre-filter unrelated features. Once we have narrowed the search space, we use a parEBEN algorithm to accelerate the search for solutions of the model with reduced features.
Our multi-locus model includes all main and epistatic effects but we include a step to first remove unrelated features and prioritize related features. To achieve this, we first apply the matrix multiplication to calculate the correlation matrix for pre-filtering the unrelated features, and then use a parEBEN algorithm that serves as the core algorithm for the estimation of the main and epistatic effects.
The epistasis model is constructed as below, which is summarized by Equation (1) with main and pairwise interaction terms:
| (1) |
Here, y represents a single trait under study, which is an matrix. μ is the mean of the trait. Xp denotes the pth genotype matrix of genetic variants which is N × P with N samples and P genetic variants, and βp denotes the main effect of genetic variants. Xi and Xj denote the genotype vectors of two different genetic variants in N samples. βe denotes the epistasis effect between these two genetic variants Xi and Xj. ε denotes the residual effect that follows the normal distribution . To illustrate our strategy, we rewrite Model (1) as a simplified format which is used in the workflow (Fig. 1).
| (2) |
where and .
Fig. 1.
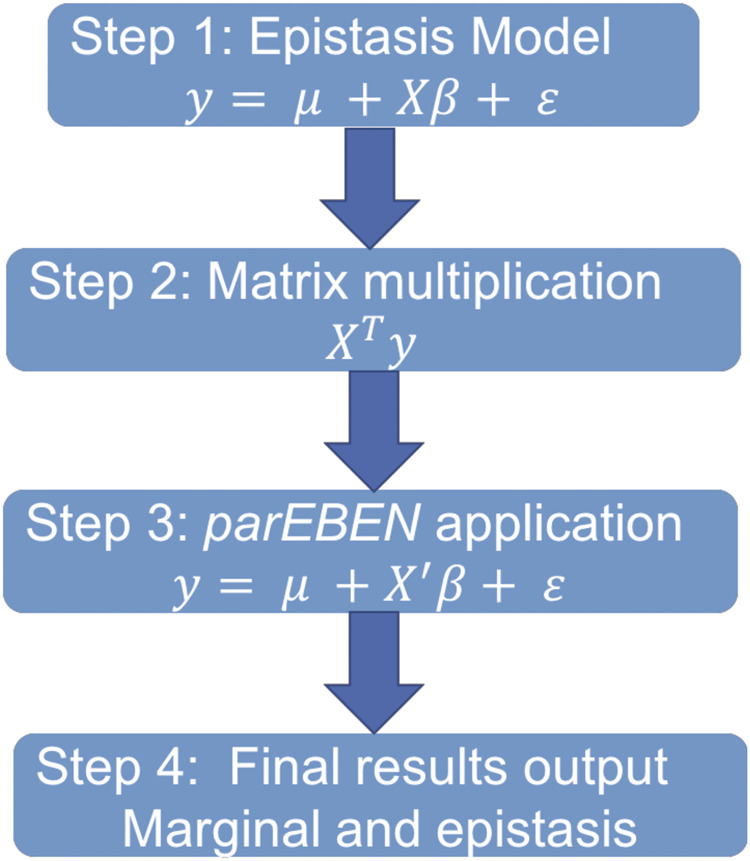
The figure shows the full workflow of our method that combines two strategies for epistasis analysis
This workflow includes two strategies in our method scheme to solve this Model 1. Our strategies combine the matrix multiplication pre-computation step and the parEBEN algorithm, which is proven to greatly improve the genome-wide epistasis analysis using comparative large genomic datasets. Figure 1 illustrates our workflow including the following four steps.
Step 1: we construct the statistical model including main and epistatic effects.
Step 2: a matrix multiplication strategy is applied to quickly pre-compute the correlation matrix between all features and dependent variable and filter features using a pre-specified value.
Step 3: we use the features output from Step 2 to construct the reduced statistical model, and use parEBEN to solve the reduced model.
Step 4: we output the significant main and epistatic features for the final result.
Note that the steps above in our workflow can be run iteratively. In other words, this workflow is flexible to include not only pairwise epistasis analysis (i.e. the nonlinear relationship between two genetic variants regarding their contribution to a trait) but also multi-loci epistasis analysis (i.e. the nonlinear contribution to a trait from more than two genetic variants). With the newly parallelized method as we describe later, our workflow is well posed to conduct multi-locus epistasis analysis in addition to main analysis on large genomic datasets.
3 Algorithm
3.1 EBEN algorithm
We use the EBEN algorithm to identify the main and epistatic effect of the comparative highly dimensional genomic data (Huang et al., 2015). Here, we introduce five main steps of the EBEN algorithm. More details regarding EBEN models can be found in Huang et al. (2015). The first step is the initialization step. We initialize three model parameters, , and . μ denotes the mean trait of population; denotes the initial dependent variable; represents the variance of the model and can be initialized as a very small number (Huang et al., 2015).
Second, EBEN starts with the feature with the highest correlation with the dependent variable, so we initialize the features sets as . Here, N is the number of samples and xi denotes the vector of ith feature in genotype matrix.
In the third step, we calculate the posterior probabilities of unknown model parameters using the posterior distributions of unknown parameters in Equation (3) and the log posterior distribution of in Equation (4), according to their prior distributions (Huang et al., 2015). is the element of which can be calculated through (Huang et al., 2015). In the log posterior probability, Equation (4), sp and qp can be calculated from C, which is the covariance matrix of y calculated by the given in Equation (4):
| (3) |
| (4) |
In the fourth step, we derive the optimal estimate of as in Equation (5) through maximizing (Huang et al., 2015):
| (5) |
Here, r can be calculated according to the sp, qp, λ1 and λ2. From Equation (5), βp will be reduced to zero if the is infinite. During the iterations, the algorithm will find a new according to Equation (6) (Cai et al., 2011):
| (6) |
If is finite, feature p will be kept in the model; otherwise feature p is deleted from the model. Three convergence criteria, (i) not new finite is outputted; (ii) the difference of between consecutive iterations is less than a pre-specified value and (iii) the difference of Euclidean norm between consecutive iterations is less than a pre-specified value. In addition, we will use cross-validations to determine the optimal value of hyperparameters λ1 and λ2 (Equations 7 and 8) to get the best performance (Huang et al., 2015). According to (Huang et al., 2015), the original algorithm of EBEN proposed that the model can be optimized by performing a grid-based search of the two parameters. Specifically, the model is optimized by seeking a solution by decreasing the initial value of λ to 0.001 evenly in 20 steps and decreasing the initial value of v from 1 to 0 by step of 0.05 (Cai et al., 2011; Huang et al., 2015).
| (7) |
| (8) |
where,
| (9) |
In the last step, the algorithm performs a hypothesis test, t-test, using the non-zero coefficients β and covariance matrix C to denote the final significant β corresponding to significant features selected.
3.2 Feature filtering strategy
Due to the comparably large-scale genomic data, we first use a matrix strategy that pre-computes the correlation matrix using fast matrix multiplication to conduct a pre-filtering procedure, which can first narrow down the search space of genomic data. The matrix multiplication accelerates the filtering of the main term and especially the pairwise epistasis term, which is similar to a strategy used in Matrix eQTL (Shabalin, 2012). In Model 1, we calculate the correlation matrix between each feature and the phenotype, which is calculated using Equation (10),
| (10) |
We can have Equation (11) if both the feature X and phenotype Y are standardized,
| (11) |
So, the correlation between features and phenotype can be defined as the inner product (Equation 12).
| (12) |
The inner product will quickly generate the correlation matrix through matrix multiplication , which can be used to pre-filter unrelated features according to the significance level of hypothesis test, and the features will be kept if the corresponding absolute value passes the hypothesis test. From Equations (10) and (12), we can infer that the pre-computing and pre-filtering step as the inner product of matrix manipulation would not affect the correlation between features and phenotype. Through this step, we can also remove the effect of irrelevant features on epistasis identification algorithm. This procedure can accelerate the analysis by narrowing down the number of features and will not affect the epistasis analysis result given that only unrelated features are removed, but related features remain in the epistasis model. For simulation data, we use the P-value = 0.05 as the threshold value for both main effect and epistatic effect. In yeast real data analysis, we implemented the empirically tune threshold value of 0.08 as the threshold value.
3.3 parEBEN method
The EBEN algorithm was developed for handling multicollinearity in generalized linear regression models. It can be used in QTL and epistasis analysis, which is implemented in the EBEN R package. This package includes functions to generate the elastic net for both binomial and Gaussian priors. These functions are efficient and do not require large amounts of computational time. However, the package also includes functions for the cross-validation. While essential, this step is a considerably more complex task. The cross-validation functions perform a sweep to determine hyperparameters and minimize prediction error. More specifically, an n-fold cross-validation sweep is performed to minimize error by trying combinations of two hyperparameters (λ1 and λ2) in a stepped manner (Fig. 2). Experimentally, it has been shown that this can take an extended amount of time, especially on larger datasets (as seen in genomics-based problems). To combat this complexity issue, the parallelization of the cross-validation functions is performed by employing parallel packages in R to accelerate the EBEN algorithm.
We parallelized the EBEN method, and packaged this functionality as an independent package for R named parEBEN. The original EBEN package’s EBelasticNet.GaussianCV function contains logic to halt the sweep of further tests of λ1 for a given λ2 if the current iteration’s MSE is greater than the MSE of the previous iteration plus the standard error of the previous iteration. This means that the original EBEN package may not actually perform the hyperparameter sweep of all 400 iterations (as the algorithm dictates), but only a subset of the combinations of λ1 and λ2. This results in an output of ‘optimal’ parameters that may only be locally optimal rather than globally optimal. It is presumed that this logic was included to speed up the processing time of the Gaussian cross-validation. The binomial cross-validation function of the EBEN package always performs the full search over all 400 iterations of λ1 and λ2.
In our parEBEN package, however, the functionality to perform a local search (as is done in the Gaussian prior version of the EBEN cross-validation function) or a global search is included. If the global search is selected in the parEBEN package, all 400 iterations are tested, regardless of the presence of a locally minimum error.
The level of parallelism for the parEBEN package depends on type of hyperparameter search being performed: local search versus global search. If a global search is performed, each hyperparameter combination of λ1 and λ2 as well as each of the n-folds of the cross-validation is fully distributed to separate compute contexts (processor cores or machines). Specifically, all 400 combinations of λ1 and λ2 are evaluated for each of the n-folds of data.
If a local search is performed, the package will only evaluate a subset of hyperparameter combinations and thus only the n-folds of the data of the cross-validation are parallelized. This is due to the behavior of comparing one iteration against another and stopping the search early if the error is getting worse. Specifically, after a combination of λ1 and λ2 is evaluated, the next combination (using the same λ1 with a different λ2) will be compared to the previous combination. If the current hyperparameter set has a higher error than the previous iteration, the search will cease for that value of λ1 and a new iteration will begin using the next value for λ1. Due to the need to compare a current iteration’s error metric with the previous iteration in the local search, the hyperparameter tuning in this mode cannot be parallelized. Thus, the gain in speed due to parallelism is limited to the number of folds in the cross-validation. In other words, performing an n-fold cross-validation on an n core processor will have a similar overall performance on a processor cores. The consideration of performing a local versus global search greatly depends on the complexity of the data being analyzed. For example, a local search may be sufficient on smaller datasets, especially when the algorithm opts to only test a smaller subset of hyperparameter combinations. When a larger computing environment is available, the global search may be a better option, since this search can scale to a higher degree of parallelism and may produce a smaller error than the local search.
4 Experiments
We first conduct two sets of simulations using the real yeast genomic data to compare the performance of parEBEN against the original serial EBEN package. The simulation results show that parEBEN outperforms EBEN with no negative impact on the detection power and estimates of effects. Next, we analyze the same full yeast genome data using our workflow. Our results are consistent with previous studies. We also compare the computing time of different dimensions of data including various sample sizes and feature numbers between serial EBEN and parEBEN, as shown in Figure 4.
Fig. 4.
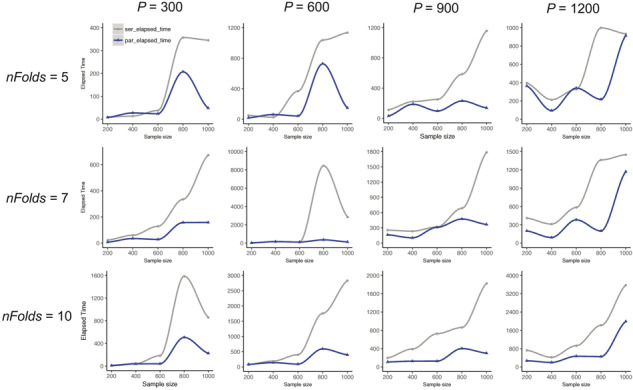
The elapsed times (in seconds) between serial EBEN and parEBEN in Monte Carlo simulation experiments. Three fold numbers 5, 7 and 10 are corresponding to each row, and four sample sizes 300, 600, 900 and 1200 are corresponding to each column. Gray lines denote the elapsed time from serial EBEN; Blue lines denote the elapsed time from parEBEN. (Color version of this figure is available at Bioinformatics online.)
4.1 Simulation experiments
Using the full real yeast data (see Section 4.2) in the first set of simulation experiments (Sim I), we verified our workflow of combining the matrix multiplication step with parEBEN to determine if we can quickly identify the main and epistatic effects with relative power but with no negative effect (as compared to the traditional EBEN). Then, we conducted the second simulation set (Sim II) for comparing the performance between EBEN and parEBEN on various sample sizes, number of features and number of folds in cross-validation. Sim I compares the performance of serial EBEN and parEBEN, looking at the accuracy and efficiency of the whole workflow for identifying epistasis. QMDR (Gui et al., 2013), a representative of classical machine learning methods for fast epistasis analysis on quantitative traits, was chosen to compare and evaluate the efficiency and accuracy of parEBEN. Sim II gives a comprehensive overview of the computing time comparison between EBEN and parEBEN.
Sim I serves to demonstrate the detection power of main and epistasis effects using our workflow, including the first pre-filtering step and parEBEN package. We randomly sample 150 individuals and 283 features from the full real dataset. Four main and four epistasis effects with different heritabilities (5%, 8%, 10% and 15%) are set up along the whole genome. This simulation experiment is replicated 100 times for measuring the statistical power of detection for each effects as well as the computing time for each run of serial EBEN, parEBEN and QMDR.
In Sim II, we randomly select different sample sizes (n = 200, 400, 600, 800 and 1000) and features (P = 300, 600, 900 and 1200) from the full real yeast dataset to conduct different levels of cross-validation folds (n-folds = 5, 7 and 10) to assess the performance of parEBEN. Thus, a total of 60 simulation experiments were run in Sim II.
Sim I was completed on a macOS machine with 16 GB of RAM and an Intel Core i5 CPU. The CPU contains 4 cores at 2.7 GHz with 1 thread per core (for a total of 4 parallelized threads). A 5-fold cross-validation is used for testing both serial EBEN and parEBEN. For QMDR, we set the option for epistasis analysis to be 2 to identify pairwise epistasis between any two genetic features as a focus of this study. The simulation results from Sim I show our strategy of combing the matrix multiplication processing and the application of parEBEN can obtain reasonable detection power of main and epistasis effects even with small heritabilities (Fig. 3) using parEBEN. QMDR can only identify the main and epistatic effects where heritabilities were >10%, even though the computing time of QMDR was significantly lower than serial EBEN and parEBEN (only ∼1.9 s for each run). Moreover, the computing time, an average of 73.8 s for each run, is reduced by about 50% with the application of parEBEN, while it needs an average of 132.36 s of serial EBEN for each run. The timing tests for Sim II are performed on a macOS machine with 32 GB of RAM and an Intel Core i7 CPU. The CPU contains 4 cores at 3.5 GHz with 2 threads per core (for a total of 8 parallelized threads). Both EBEN and parEBEN were installed on R version 3.3.3 using the Intel Math Kernel Library for parallel mathematical computing. The simulation results from Sim II show that a drastic time reduction can be seen in most cases by parallelizing the iterations of the cross-validation over multiple CPU cores or multiple machines of a computing cluster (Fig. 4). For some cases, the elapsed time of parEBEN is almost the same or a little more than serial EBEN, and this might be due to the fold numbers and the cores we use for parallelization procedure. We do not see a significant speed gain if the number of cores we use is larger than or equal to the number of folds when performing a ‘local’ hyperparameter sweep. However, Figure 4 shows the larger deduction for the computing time if we use the larger fold numbers for cross-validation on higher dimensional genomic data. This is also the case when performing a ‘global’ search as there is more opportunity to scale up the processing with parallelization. Note that for some increases sample size, the processing time may decrease, this is due to the trade-off between parallelization and the computational overhead to manage the parallelism. Specifically, if the overhead is equal between two different size datasets, the larger dataset may take slightly less time to process as this is more effective use of the parallel processes. In other words, certain larger datasets may require the same amount of management overhead to parallelize as a smaller dataset, thus offsetting the extra computational work from the larger amount of data. Also, the computing time heavily depends on the structure of data including the ratio between sample size and features, correlation of features, the dropped unrelated features, etc., which can affect the algorithm iterations embedded in the package.
Fig. 3.
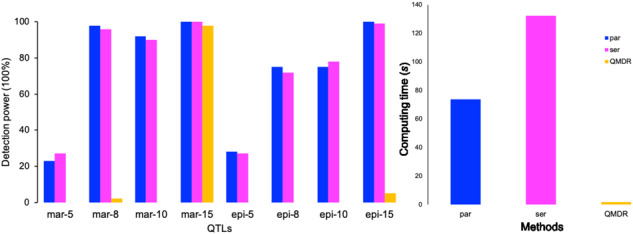
The detection power of main and epistasis with application of matrix multiplication and parEBEN, serial EBEN or QMDR. Blue bars show the detection power for QTL with different heritabilities of parEBEN; Magenta bars show the detection power of QTL with different heritabilities of serial EBEN; Yellow bars show the detection power of QTL with different heritabilities; mar-5 means the main effects with heritability of 5% and epi-5 means the epistatic effect with heritability of 5%. (Color version of this figure is available at Bioinformatics online.)
4.2 Real yeast data
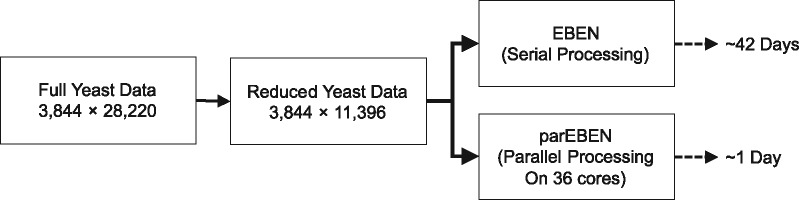
We use a real yeast dataset (Bloom et al., 2015) as an example to demonstrate the real scenario for using our method and parEBEN package. This yeast dataset includes 28 220 SNP genotypes and 4390 segregants and are phenotyped with 20 quantitative traits with two replicates from Bloom et al. (2015). We analyze one phenotype being related to yeast growth trait measured as Zeocin level in this study. In total, 3844 samples are left after removing missing data. After the matrix multiplication filtering step, we have 11 597 features remaining, made of 11 396 main and 201 epistatic effects. For the empirical reduced yeast data, it only takes around 14 h to generate the epistasis estimates with parEBEN, while it takes ∼42 days to obtain the final main and epistasis estimates using EBEN as seen in Figure 5. The computing time shown in Figure 5 is only for the parEBEN portion of the analysis, not including the matrix multiplication step. For the matrix multiplication calculation step, we can use the serial manner script for estimating main effects. We parallelize the script for the matrix multiplication step which is similar to the ‘grid’ search, which means the computing time of the matrix multiplication step depends on the size of the ‘grid’.
Fig. 5.
Computing time comparisons of serial EBEN and parEBEN on the real yeast data
On the real yeast data, our parEBEN workflow successfully identified 31 main effects and 3 epistatic effects associated with Zeocin levels in yeast (Table 1). Specifically, 19 of these main effects and 1 epistasis were previously reported by Bloom et al. (2015) and Forsberg et al. (2017). For example, SNP chrVIII:114 934 with main effect identified in our result has been previously shown to be associated with Zeocin level variation (Forsberg et al., 2017). SNP chrVIII:114 934, which maps to the gene GPA1, was reported to be a hub QTL in a Zeocin involved network. The mapped gene GPA1 was reported to affect the yeast response to mating pheromones, which corresponds to the yeast pheromone response pathway and further affects fitness as measured by Zeocin production in yeast (Bloom et al., 2015; Forsberg et al., 2017; Lang et al., 2009). Another SNP, chrXIII:751 466, associated with Zeocin level was reported to overlap with the refined QTL in an earlier study (Forsberg et al., 2017). In addition, we found an epistatic effect between two SNPs, chrIV:998 484 and chrVIII:100 079 (Fig. 6). It has been reported that (Bloom et al., 2015) SNP chrIV:998 484 had epistatic effects with both chrVIII:118 187 and chrVIII:114 934. We found the SNP chrVIII:100 079 has a high linkage disequilibrium (LD) with both SNPs chrVIII:118 187 and chrVIII:114 934, which R2 values were 0.876 and 0.917, respectively. Moreover, gene TRM8, mapped to SNP chrVIII:100 079, was also reported to be related to the Zeocin level of yeast. Another two genes, GPA1 and STP2, which were mapped to SNPs chrVIII:114 934 and chrVIII:118 187, were reported to affect the Zeocin levels of yeast (Bloom et al., 2015; Forsberg et al., 2017; Lang et al., 2009). These findings help to demonstrate that our identified main and epistatic effects results reflect real biological signals. In addition, these newly identified SNPs with main or epistasis effects on the Zeocin levels of yeast may provide a new candidate pool of potential genetic factors that may impact Zeocin levels in yeast awaiting for further experimental evaluation and validation. In summary, the empirical yeast data demonstrate the reality of identification of epistasis by parallelizing the iterations of the cross-validation over multiple CPU cores or multiple machines of a computing cluster.
Table 1.
Summary of the main and epistatic effects results
| chr1 | position1 | chr2 | position2 | t-Value | P-value | Literature | |
|---|---|---|---|---|---|---|---|
| II | 503 196 | −0.0249 | 2.0147 | 0.0440 | |||
| III | 128 224 | 0.0463 | 2.9652 | 0.0030 | Bloom et al. (2015) | ||
| IV | 1 471 524 | 0.0386 | 3.6806 | 0.0002 | Bloom et al. (2015) | ||
| V | 212 373 | −0.0361 | 1.9957 | 0.0460 | |||
| VII | 842 206 | −0.0387 | 2.3022 | 0.0214 | Bloom et al. (2015) | ||
| VIII | 114 934 | 0.0827 | 2.8283 | 0.0047 | Bloom et al. (2015) and Forsberg et al. (2017) | ||
| X | 92 630 | −0.0308 | 2.0381 | 0.0416 | |||
| X | 123 590 | −0.0411 | 2.0417 | 0.0412 | |||
| X | 383 417 | 0.0250 | 2.1278 | 0.0334 | |||
| X | 549 542 | −0.0487 | 2.3339 | 0.0197 | Bloom et al. (2015) | ||
| XI | 466 269 | −0.0262 | 2.7424 | 0.0061 | |||
| XI | 532 119 | −0.0461 | 2.0182 | 0.0436 | Bloom et al. (2015) | ||
| XI | 579 622 | 0.0273 | 2.3398 | 0.0193 | |||
| XII | 141 390 | 0.0342 | 2.1336 | 0.0329 | Bloom et al. (2015) | ||
| XII | 569 539 | 0.0503 | 2.1966 | 0.0281 | Bloom et al. (2015) | ||
| XIII | 23 620 | 0.0686 | 2.2181 | 0.0266 | Bloom et al. (2015) | ||
| XIII | 24 565 | 0.0956 | 2.7379 | 0.0062 | Bloom et al. (2015) | ||
| XIII | 25 025 | 0.0633 | 2.0706 | 0.0385 | Bloom et al. (2015) | ||
| XIII | 25 638 | 0.0923 | 2.6961 | 0.0070 | |||
| XIII | 49 898 | −0.0633 | 2.4692 | 0.0136 | Bloom et al. (2015) | ||
| XIII | 285 831 | −0.0400 | 4.1116 | 0.0000 | Bloom et al. (2015) | ||
| XIII | 398 491 | −0.0400 | 2.6333 | 0.0085 | Bloom et al. (2015) | ||
| XIII | 618 430 | −0.0404 | 2.6718 | 0.0076 | |||
| XIII | 697 993 | −0.0479 | 1.9661 | 0.0493 | |||
| XIII | 701 244 | −0.0528 | 2.0161 | 0.0439 | Bloom et al. (2015) | ||
| XIII | 751 466 | 0.0723 | 4.0617 | 0.0000 | Bloom et al. (2015) and Forsberg et al. (2017) | ||
| XV | 74 338 | −0.0321 | 2.6910 | 0.0072 | |||
| XV | 309 869 | 0.0233 | 2.5929 | 0.0096 | Bloom et al. (2015) | ||
| XV | 758 119 | 0.0242 | 2.0074 | 0.0448 | |||
| XV | 828 529 | 0.0392 | 2.0774 | 0.0378 | Bloom et al. (2015) | ||
| XVI | 208 747 | 0.0729 | 4.5646 | 0.0000 | Bloom et al. (2015) | ||
| XI | 521 261 | II | 718 018 | 0.0299 | 3.2682 | 0.0011 | |
| VIII | 100 079 | IV | 998 484 | 0.0619 | 5.5940 | 0.0000 | Bloom et al. (2015) |
| VIII | 517 419 | VII | 167 895 | −0.0325 | 3.3301 | 0.0009 |
Note: The first four columns list the significant main and epistatic effects. The rows with one SNP denote main effects, while those with two SNPs represent epistatic effects.
Fig. 6.
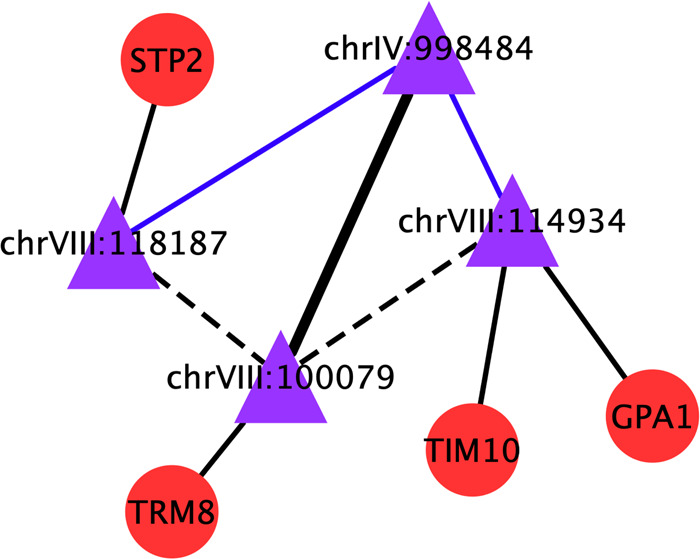
An example of epistasis effects between two SNPs and their mapped genes. Purple triangles denote the SNPs, and red circles denote the genes. The black bold solid line denotes the epistasis identified by our workflow; the blue solid line denotes the interaction verified by other studies; the black dashed line denotes the high LD relationship between two SNPs and the black solid lines denote the genes to which the SNPs map. (Color version of this figure is available at Bioinformatics online.)
In summary, parEBEN performed better in identifying small effect SNPs associated with a quantitative trait comparing with QMDR, which are essential genetic components for the analysis of genetic architecture of complex traits and human diseases. In our Sim I, QMDR can achieve enough power in identifying main and epistatic effects where the heritability in the trait under study is >10%. This observation was supported by an earlier study (Gui et al., 2013), which showed the success rate (power) of QMDR was ∼80% when the heritability was 40% with sample sizes ranging from 400 to 1600. Our parEBEN pipeline can achieve relative power (>20%) even when the heritabilities of main and epistatic effects were 5%. Moreover, numerous studies report that human diseases and complex traits are polygenic traits, which are controlled by minor signals spread across chromosomes (Boyle et al., 2017; Liu et al., 2019). Thus, comparing with a faster method of QMDR, our parEBEN strategy can better dissect the genetic architecture underlying complex traits and human diseases.
5 Discussion
In summary, our newly proposed method of combining the matrix multiplication and parallelization strategies provides a solution to speed up complex analysis like epistasis analyses in mining comparative large biological data. We compared our combined methods against a classical epistasis method named QMDR. Although very fast, QMDR performs well in scenarios where the heritability is relatively high. We ran an additional simulation with data that only includes one main effect and one epistasis effect with large heritability. Results showed that QMDR can reach a similar detection power to parEBEN (Table 2) where the heritability is relatively high. In summary, QMDR can achieve high detection power on effects with large heritability, which is consistent with simulation results in Gui et al. (2013). In real biological settings, effects with small heritability are ubiquitous and are the origins of polygenic inheritance such as height. Therefore, it is important to mine the effects with small heritability in real genetics data where parEBEN shows superior performance.
Table 2.
QMDR simulation results
| Type | Locus1 | Locus2 | Heritability | Power (%) |
|---|---|---|---|---|
| Main | 138 | 0.30 | 100 | |
| Epistasis | 95 | 177 | 0.45 | 95 |
Note: Power means that the detection power for main and epistasis effects.
In our parEBEN workflow, we relieve some computational complexity by first reducing the dimensionality of the genomic data using our matrix multiplication strategy, which converts the simple statistical test method (t-test) for each feature to a single matrix multiplication step for all features, thus accelerating the pre-filtering procedure. We use a pre-specified value as a threshold to filter the features, which is considered to be the significant P-value as 0.01 or 0.05, depending on the sample size and the full distribution of correlation between features and phenotype. This setting can be later improved by changing this static threshold to a hyperparameter that can be tuned in the optimization process of solving the model. We then apply parEBEN as the parameter estimation method to solve the reduced model. By distributing the computational workload of each iteration of the n-fold cross-validation and hyperparameters sweep to individual compute contexts (cores on a single CPU or multiple CPUs in machines in a cluster), a drastic time reduction can be seen with no negative effect on the resulting EBEN model(s).
Our parEBEN package can run on multiple platforms, and all foreach-related methods are supported, such as doParallel (Revolution Analytics and Weston, 2015a), doMPI (Weston, 2017) and doSNOW (Revolution Analytics and Weston, 2015b) over multiple CPU cores or multiple machines of a computing clusters (Microsoft and Weston, 2017). Hence, the genome-wide association analysis and genome-wide QTL mapping analysis of complex biological real datasets can be analysed with the application of this kind of linear regression model using parEBEN due to the reduction of computational time. This allows for larger biological datasets to be analyzed as opposed to limiting the research due to time and computing resource constraints. Thus, parallelizing the cross-validation of the EBEN models will be greatly beneficial in future research using the cross-validated EBEN method.
The parEBEN package and corresponding data for this study is available at https://github.com/shilab/parEBEN.
In future work, we would like to incorporate the covariates such as known and unknown confounders, population structure and the pedigree information into our model to improve the accuracy of our method. We can also extend the current epistasis analysis models to incorporate prior biological resources, such as pathway, gene network and protein–protein interaction, for modeling or predicting a particular trait or phenotype. In addition to quantitative traits, we will extend our model for solving categorical dependent variables that can be applied to many broader biological problems such as the tolerance analysis in plants and the pathological stage analysis in cancer studies. Future enhancements to our parEBEN package will also include additional parallelization capabilities. We will add in further connectivity capabilities to other parallel platforms such as Apache Spark (Zaharia et al., 2016) and will explore the utility of graphics processing unit-based processing to further improve the performance gain of our method.
Acknowledgements
We would like to thank Jonathan Halter from the UNCC Research Computing team for his expert help in cluster configuration, troubleshooting and testing. We acknowledge the support of the Department of Bioinformatics and Genomics and the College and Computing and Informatics at UNC Charlotte.
Funding
This work was supported in part by the National Institutes of Health [R15HG009565 to X.S.].
Conflict of Interest: none declared.
References
- Bloom J.S. et al. (2015) Genetic interactions contribute less than additive effects to quantitative trait variation in yeast. Nat. Commun., 6, 8712. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boyle E.A. et al. (2017) An expanded view of complex traits: from polygenic to omnigenic. Cell, 169, 1177–1186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown A.A. et al. (2014) Genetic interactions affecting human gene expression identified by variance association mapping. Elife, 3, e01381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cai X. et al. (2011) Fast empirical Bayesian Lasso for multiple quantitative trait locus mapping. BMC Bioinformatics, 12, 1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carlborg Ö., Haley C.S. (2004) Epistasis: too often neglected in complex trait studies? Nat. Rev. Genet., 5, 618–625. [DOI] [PubMed] [Google Scholar]
- Carter G.W. et al. (2007) Prediction of phenotype and gene expression for combinations of mutations. Mol. Syst. Biol., 3, 96. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen X. et al. (2012) A two-graph guided multi-task Lasso approach for eQTL mapping. In: International Conference on Artificial Intelligence and Statistics, pp. 208–217.
- Ding X. et al. (2015) Searching high-order SNP combinations for complex diseases based on energy distribution difference. IEEE/ACM Trans. Comput. Biol. Bioinform., 12, 695–704. [DOI] [PubMed] [Google Scholar]
- Evans D.M. et al. (2006) Two-stage two-locus models in genome-wide association. PLoS Genet., 2, e157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ford C.T. (2018) parEBEN: Parallel Implementations of the Empirical Bayesian Elastic Net Cross-validation. R Package Version 0.9.9.
- Forsberg S.K. et al. (2017) Accounting for genetic interactions improves modeling of individual quantitative trait phenotypes in yeast. Nat. Genet., 49, 497–503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gertz J. et al. (2010) Epistasis in a quantitative trait captured by a molecular model of transcription factor interactions. Theor. Popul. Biol., 77, 1–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gibson G. (1996) Epistasis and pleiotropy as natural properties of transcriptional regulation. Theor. Popul. Biol., 49, 58–89. [DOI] [PubMed] [Google Scholar]
- Gibson G. (2010) Hints of hidden heritability in GWAS. Nat. Genet., 42, 558–560. [DOI] [PubMed] [Google Scholar]
- Greene C.S. et al. (2009) Spatially Uniform ReliefF (SURF) for computationally-efficient filtering of gene–gene interactions. BioData Min., 2, 5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gui J. et al. (2013) A simple and computationally efficient approach to multifactor dimensionality reduction analysis of gene–gene interactions for quantitative traits. PLoS One, 8, e66545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gyenesei A. et al. (2012. a) BiForce Toolbox: powerful high-throughput computational analysis of gene–gene interactions in genome-wide association studies. Nucleic Acids Res., 40, W628–W632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gyenesei A. et al. (2012. b) High-throughput analysis of epistasis in genome-wide association studies with BiForce. Bioinformatics, 28, 1957–1964. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang A. (2015) EBEN: Empirical Bayesian Elastic Net. R Package Version 4.6.
- Huang A., Liu D. (2016) EBglmnet: a comprehensive R package for sparse generalized linear regression models. Bioinformatics, pii: btw143. [DOI] [PubMed]
- Huang A. et al. (2015) Empirical Bayesian Elastic Net for multiple quantitative trait locus mapping. Heredity, 114, 107–115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang Y. et al. (2013) eQTL epistasis—challenges and computational approaches. Front. Genet., 4, 51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lang G.I. et al. (2009) The cost of gene expression underlies a fitness trade-off in yeast. Proc. Natl. Acad. Sci. USA, 106, 5755–5760. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee S. et al. (2010) Adaptive multi-task Lasso: with application to eQTL detection. In: Advances in Neural Information Processing Systems, 1306–1314. [Google Scholar]
- Lewinger J.P. et al. (2013) Efficient two-step testing of gene–gene interactions in genome-wide association studies. Genet. Epidemiol., 37, 440–451. [DOI] [PubMed] [Google Scholar]
- Litvin O. et al. (2009) Modularity and interactions in the genetics of gene expression. Proc. Natl. Acad. Sci. USA, 106, 6441–6446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu X. et al. (2019) Trans effects on gene expression can drive omnigenic inheritance. Cell, 177, 1022–1034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marchini J. et al. (2005) Genome-wide strategies for detecting multiple loci that influence complex diseases. Nat. Genet., 37, 413–417. [DOI] [PubMed] [Google Scholar]
- Microsoft and Weston, S. (2017) foreach: Provides Foreach Looping Construct for R. R Package Version 1.4.4.
- Moore J.H. (2004) Computational analysis of gene–gene interactions using multifactor dimensionality reduction. Expert Rev. Mol. Diagn., 4, 795–803. [DOI] [PubMed] [Google Scholar]
- Moore J.H. et al. (2017) Grid-based stochastic search for hierarchical gene–gene interactions in population-based genetic studies of common human diseases. BioData Min., 10, 19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nelson M. (2001) A combinatorial partitioning method to identify multilocus genotypic partitions that predict quantitative trait variation. Genome Res., 11, 458–470. [DOI] [PMC free article] [PubMed] [Google Scholar]
- New,A.M. and Lehner,B. (2019) Harmonious genetic combinations rewire regulatory networks and flip gene essentiality. Nature communications, 10, 1–12. [DOI] [PMC free article] [PubMed]
- Pendergrass S.A. et al. (2015) Next-generation analysis of cataracts: determining knowledge driven gene–gene interactions using Biofilter, and gene–environment interactions using the Phenx Toolkit Pac Symp Biocomput., 495–505. [PubMed] [Google Scholar]
- Purcell S. et al. (2007) PLINK: a tool set for whole-genome association and population-based linkage analyses. Am. J. Hum. Genet., 81, 559–575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quitadamo A. et al. (2015) An integrated network of microRNA and gene expression in ovarian cancer. BMC Bioinformatics, 16, S5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Revolution Analytics and Weston, S. (2015. a) doParallel: Foreach Parallel Adaptor for the ‘Parallel’ Package. R Package Version 1.0.10.
- Revolution Analytics and Weston S. (2015. b) doSNOW: Foreach Parallel Adaptor for the ‘Snow’ Package. R Package Version 1.0.14.
- Rönnegård L., Valdar W. (2012) Recent developments in statistical methods for detecting genetic loci affecting phenotypic variability. BMC Genet., 13, 63. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schüpbach T. et al. (2010) FastEpistasis: a high performance computing solution for quantitative trait epistasis. Bioinformatics, 26, 1468–1469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shabalin A.A. (2012) Matrix eQTL: ultra fast eQTL analysis via large matrix operations. Bioinformatics, 28, 1353–1358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen X. et al. (2012) Inheritance beyond plain heritability: variance-controlling genes in Arabidopsis thaliana. PLoS Genet., 8, e1002839. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun X. et al. (2014) Analysis pipeline for the epistasis search—statistical versus biological filtering. Front. Genet., 5, 106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang W. et al. (2009) Epistatic module detection for case–control studies: a Bayesian model with a Gibbs sampling strategy. PLoS Genet., 5, e1000464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tian L. et al. (2014) Methods for population-based eQTL analysis in human genetics. Tsinghua Sci. Technol., 19, 624–634. [Google Scholar]
- Tibshirani R. (1996) Regression shrinkage and selection via the Lasso. J. R. Stat. Soc., 58, 267–288. [Google Scholar]
- Tibshirani R. et al. (2005) Sparsity and smoothness via the fused Lasso. J. R. Stat. Soc., 67, 91–108. [Google Scholar]
- Van Steen K., Moore J. (2019) How to increase our belief in discovered statistical interactions via large-scale association studies? Hum. Genet., 138, 293–305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Verhoeven K.J. et al. (2010) Epistasis: obstacle or advantage for mapping complex traits? PLoS One, 5, e12264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Z. et al. (2014) Finding alternative expression quantitative trait loci by exploring sparse model space. J. Comput. Biol., 21, 385–393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wen J. et al. (2017) Epistasis analysis of microRNAs on pathological stages in colon cancer based on an Empirical Bayesian Elastic Net method. BMC Genomics, 18, 21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weston S. (2017) doMPI: Foreach Parallel Adaptor for the Rmpi Package. R Package Version 0.2.2.
- Xie M. et al. (2012) Detecting genome-wide epistases based on the clustering of relatively frequent items. Bioinformatics, 28, 5–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yi N. et al. (2011) Hierarchical generalized linear models for multiple groups of rare and common variants: jointly estimating group and individual-variant effects. PLoS Genet., 7, e1002382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zaharia M. et al. (2016) Apache Spark: a unified engine for big data processing. Commun. ACM, 59, 56–65. [Google Scholar]
- Zhang W. et al. (2010) A Bayesian partition method for detecting pleiotropic and epistatic eQTL modules. PLoS Comput. Biol., 6, e1000642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y., Liu J.S. (2007) Bayesian inference of epistatic interactions in case–control studies. Nat. Genet., 39, 1167–1173. [DOI] [PubMed] [Google Scholar]
- Zhang Y. et al. (2011) Bayesian models for detecting epistatic interactions from genetic data. Ann. Hum. Genet., 75, 183–193. [DOI] [PubMed] [Google Scholar]
- Zuk O. et al. (2012) The mystery of missing heritability: genetic interactions create phantom heritability. Proc. Natl. Acad. Sci. USA, 109, 1193–1198. [DOI] [PMC free article] [PubMed] [Google Scholar]