Rapid simulation of viral decontamination efficacy with UV irradiation

Abstract

This paper focuses on viral decontamination by ultraviolet (UV) irradiation technologies. This work develops an efficient and rapid computational method to simulate a UV pulse in order to ascertain the decontamination efficacy of UV irradiation for a surface. It is based on decomposition of a pulse into a group of rays, which are then tracked as they progress towards the target contact surface. The algorithm computes the absorption at the point of contact and color codes it relative to the incoming irradiation. This allows one to quickly quantify the decontamination efficacy across the topology of a structure.

Highlights

• •The pandemic of 2020 has led to a dramatic increase in research of infectious diseases.
• •This paper focuses on decontamination by ultraviolet irradiation technologies
• •Develops an efficient and rapid computational method to simulate a UV pulse to ascertain decontamination efficacy
• •Based on decomposition of a pulse into a groups of rays, which are then tracked and processed
• •The algorithm computes the absorption and color codes it relative to the incoming irradiation

1. Introduction

Viral decontamination based on ultraviolet (UV) technology has become ubiquitous, with many variants now being proposed, in response to the outbreak of COVID-19 in 2020. UV light varies in wavelength from approximately 10 nm to 400 nm, thus making it shorter than visible wavelengths and larger than X-rays. Short wave UV light (UV-c) can damage DNA and sterilize surfaces making it useful in the medical industry. This was first noted in 1878 (Downes and Blunt [1]) when the effect of short-wavelength light killing bacteria was discovered. By 1903 it was known the most effective wavelengths were around 250 nm (UV-c), for which Niels Finsen won a Nobel Prize (for skin-based tuberculosis eradication using UV light). By approximately 1960, the effect that ultraviolet radiation can destroy DNA in living microorganisms was established (see Bolton and Colton [2] for reviews). While many types of decontamination technologies are of interest (see references Anderson et al. [3], Battelle [4], Boyce et al. [5], Card et al. [6], Heimbuch and Harish [7], Heimbuch et al. [8], Ito and Ito [9], Lin et al. [10], Kanemitsu [11], Lindsley et al. [12], Lore et al. [13], Marra et al. [14], Mills et al. [15], Nerandzic et al. [16], Tseng and Li [17] and Viscusi et al. [18]), this paper will focus on UV-c technologies. The literature asserts that UV-c irradiation dose of above 1 $\mathrm{J}∕{\mathrm{cm}}^2$ at 254 nm peak wavelength inactivates SARS-CoV-2 and achieves above a 99% biocidal efficacy on Bacillus subtilis spores.1 However, the literature also presents evidence that it is difficult to ensure that all surfaces are completely decontaminated, due to shadowing effects. Accordingly, this paper focuses on viral decontamination by ultraviolet (UV) irradiation technologies, specifically on developing an efficient and rapid computational method to simulate a UV pulse, in order to ascertain the decontamination efficacy of UV irradiation for a surface.

Remarks

Purely UV-c protocols should be adopted if there is no other choice, but can be a key component of a multistage paradigm involving a combination of decontamination processes such as (1) gas, such as hydrogen peroxide vapor, (2) heat and humidity and (3) UV-c irradiation.

1.1. Objectives

This paper develops an efficient and rapid computational method to simulate a UV pulse in order to ascertain the decontamination efficacy of UV irradiation for a surface. It is based on decomposition of a pulse into a groups of rays, which are then tracked as they progress towards the target contact surface. The algorithm computes the absorption at the point of contact and color codes it relative to the incoming irradiation. This allows one to rapidly quantify the decontamination uncertainty by identifying regions where the absorption is inadequate and serves as a guide for practitioners to ascertain where problems may occur a priori to experiments. Additionally, the reflections are calculated, and can be used in ascertaining safety to bystanders. The interest here is on the absorption of an initially coherent pulse (Fig. 1), represented by multiple collimated (parallel) rays (initially forming a planar wave front), where each ray is a vector in the direction of the flow of energy (the rays are parallel to the initial wave’s propagation vector). We make the following observations:

Fig. 1.

An electromagnetic pulse applied to a surface.

• •It is assumed that the features of the surface to be irradiated are at least an order of magnitude larger than the wavelength of the incident radiation (essentially specular surfaces), therefore “geometrical” ray tracing theory is applicable, and is well-suited for the systems of interest. It is important to emphasize the regimes of validity of such a model are where the surface features are larger than the UV wavelengths. For example, if we were to use UV-rays ($10^{-8}\mathrm{m}\le \lambda \le 4\times 10^{-7}\mathrm{m}$), the features in this analysis would be assumed to possess scales larger than approximately $4\times 10^{-6}\mathrm{m}$. For systems containing features smaller than this, one can simply use the model as a qualitative guide.
• •Ray-tracing is a method that is employed to produce rapid approximate solutions to wave-equations for high-frequency/small-wavelength applications where the primary interest is in the overall propagation of energy.2
• •Ray-tracing methods proceed by initially representing wave fronts by an array of discrete rays. Thereafter, the problem becomes one of a primarily geometric character, where one tracks the changing trajectories and magnitudes of individual rays which are dictated by the reflectivity and the Fresnel conditions (if a ray encounters a material interface).
• •Ray-tracing methods are well-suited for computation of scattering in complex systems that are difficult to mesh/discretize, relative to procedures such as the Finite Difference Time Domain Method or the Finite Element Method.
• •Other high frequency irradiation regimes can also be considered in the same manner, such as X-rays and gamma rays, provided that the scattering target has the appropriate (larger) length-scale. Even in the case where this clear separation of length scales is not present, this model still provides valuable information on the propagation of the beam and the reflected response of the system.

2. Electromagnetic energy propagation

2.1. Beam-ray decomposition

In order to connect the concept of a ray with a pulse/beam, since $\overline{I}$ is the energy per unit area per unit time, we obtain the energy associated with an entire pulse/beam by multiplying the irradiance by the cross-sectional area of an initially coherent beam, $\overline{I}{A}^b$, where $A^b$ is the cross-sectional area of the beam (comprising all of the rays). The energy per unit time (power) for a ray in the pulse/beam is then given by

$$I=\overline{I}{A}^r=\overline{I}{A}^b∕N_r,$$ (2.1)

where $N_r$ is the number of rays in the beam (Fig. 1) and $A^r$ can be considered the area associated with a ray. Essentially, rays are a mathematical construction/discretization of a pulse/beam We refer the reader to Gross [19], Zohdi [20], [21], [22], [23], [24], [25], [26] for details.

2.2. Reflection and absorption of rays

Following a framework found in Zohdi [20], [22], [23], [24], [25], [26] for details, we consider a ray of light incident upon a material interface which produces a reflected ray and a transmitted/absorbed (refracted) ray (Fig. 1), the amount of incident electromagnetic energy per unit time, power ($I_i$), that is reflected ($I_r$) is given by the total reflectance $\mathcal{I}\mathcal{R}\stackrel{\mathrm{def}}{=}\frac{I_r}{I_i}$, where $0\le \mathcal{I}\mathcal{R}\le 1$. $\mathcal{I}\mathcal{R}$ is given by Eq. (2.3), for unpolarized electromagnetic radiation. We have the following observations:

• •The angle between the point of contact of a ray (Fig. 1) and the outward normal to the surface at that point is the angle of incidence, ${\theta }_i$. The classical reflection law states that the angle at which a ray is reflected is the same as the angle of incidence and that the incoming (incident, ${\theta }_i$) and outgoing (reflected, ${\theta }_r$) ray lays in the same plane, and ${\theta }_i={\theta }_r$.
• •The classical refraction law states that, if the ray passes from one medium into a second one (with a different index of refraction), and, if the index of refraction of the second medium is less than that of the first, the angle the ray makes with the normal to the interface is always less than the angle of incidence, where $\hat{n}\stackrel{\mathrm{def}}{=}\frac{v_i}{v_a}=\sqrt{\frac{{ϵ}_a{\mu }_a}{{ϵ}_i{\mu }_i}}=\frac{sin{\theta }_i}{sin{\theta }_a}$, ${\theta }_a$ being the angle of the absorbed ray (Fig. 1), $v_a$ is the propagation speed in the absorbing medium, $v_i$ is the propagation speed in the incident medium, ${ϵ}_a$ is the electric permittivity of the absorbing medium, ${\mu }_a$ magnetic permeability of the absorbing medium, ${ϵ}_i$ is the electric permittivity in the incident medium and ${\mu }_i$ magnetic permeability in the incident medium.
• •Recall, all electromagnetic radiation travels, in a vacuum, at the speed $c\approx 2.99792458\times 10^8\pm 1.1\mathrm{m∕s}$. In any another medium $v=\frac{1}{\sqrt{ϵ\mu }}$ for electromagnetic waves.3
• •
  We define $\hat{n}$ as the ratio of the refractive indices of the ambient (incident) medium ($n_i$) and absorbing medium ($n_a$), $\hat{n}=n_a∕n_i$, where $\hat{\mu }$ is the ratio of the magnetic permeabilities of the surrounding incident medium (${\mu }_i$) and scattering/absorbing medium (${\mu }_a$), $\hat{\mu }={\mu }_a∕{\mu }_i$. Thus, we have

  $$\hat{n}=\frac{n_a}{n_i}=\sqrt{\frac{{ϵ}_a{\mu }_a}{{ϵ}_i{\mu }_i}}\Rightarrow {ϵ}_a{\mu }_a={\left(\hat{n}\right)}^2{ϵ}_i{\mu }_i.$$ (2.2)
• •
  For a pulse of light, the reflectivity $\mathcal{I}\mathcal{R}$ can be shown to be (see [19] for example)

  $$\begin{array}{c}\mathcal{I}\mathcal{R}=\frac{I_r}{I_i}=\frac{1}{2}\left({\left(\frac{\frac{{\hat{n}}^2}{\hat{\mu }}cos{\theta }_i-{({\hat{n}}^2-si{n}^2{\theta }_i)}^{\frac{1}{2}}}{\frac{{\hat{n}}^2}{\hat{\mu }}cos{\theta }_i+{({\hat{n}}^2-si{n}^2{\theta }_i)}^{\frac{1}{2}}}\right)}^2+{\left(\frac{cos{\theta }_i-\frac{1}{\hat{\mu }}{({\hat{n}}^2-si{n}^2{\theta }_i)}^{\frac{1}{2}}}{cos{\theta }_i+\frac{1}{\hat{\mu }}{({\hat{n}}^2-si{n}^2{\theta }_i)}^{\frac{1}{2}}}\right)}^2\right),\hfill \end{array}$$ (2.3)

  where $I_i$ is the incoming irradiance, $I_r$ the reflected irradiance, $\hat{n}$ is the ratio of the refractive indices of the of absorbing ($n_a$) and incident media ($n_i$), where the refractive index is defined as the ratio of the speed of light in a vacuum ($c$) to that of the medium ($v$), where the speed of electromagnetic waves is $c=\frac{1}{\sqrt{{ϵ}_o{\mu }_o}}$, where $ϵ$ is the electric permittivity and $\mu$ is the magnetic permeability.
• •
  We consider applications with non-magnetic media and frequencies where the magnetic permeability is virtually the same for both the incident medium (usually the atmosphere) and the scattering/absorbing medium. Thus, for the remainder of the work, we shall take $\hat{\mu }=1$ (${\mu }_o={\mu }_i={\mu }_a$), thus

  $$\hat{n}=\frac{n_a}{n_i}=\sqrt{\frac{{ϵ}_a{\mu }_a}{{ϵ}_i{\mu }_i}}\Rightarrow {ϵ}_a{\mu }_a={\left(\hat{n}\right)}^2{ϵ}_i{\mu }_i\Rightarrow {ϵ}_a={\left(\hat{n}\right)}^2{ϵ}_i.$$ (2.4)

  This yields

  $$\begin{array}{c}\mathcal{I}\mathcal{R}=\frac{I_r}{I_i}=\frac{1}{2}\left({\left(\frac{{\hat{n}}^{2}cos{\theta }_i-{({\hat{n}}^2-si{n}^2{\theta }_i)}^{\frac{1}{2}}}{{\hat{n}}^{2}cos{\theta }_i+{({\hat{n}}^2-si{n}^2{\theta }_i)}^{\frac{1}{2}}}\right)}^2+{\left(\frac{cos{\theta }_i-{({\hat{n}}^2-si{n}^2{\theta }_i)}^{\frac{1}{2}}}{cos{\theta }_i+{({\hat{n}}^2-si{n}^2{\theta }_i)}^{\frac{1}{2}}}\right)}^2\right).\hfill \end{array}$$ (2.5)
• •Notice that as $\hat{n}\to 1$ we have complete absorption, while as $\hat{n}\to \infty$ we have complete reflection. The total amount of absorbed power by the material is $(1-\mathcal{I}\mathcal{R})I_i$.

The next section supplies the theory underpinning electromagnetic wave propagation and rays.

3. Electromagnetic wave propagation and rays

Following a framework found in Zohdi [20], [21], [22], [23], [24], [25], [26], the propagation of electromagnetic waves in free space can be described by a simplified form of Maxwell’s equations (see Jackson [27], Zohdi [23])

$$\begin{array}{c}\nabla \times \mathit{E}=-{\mu }_o\frac{\partial \mathit{H}}{\partial t},\mathrm{and}\nabla \times \mathit{H}={ϵ}_o\frac{\partial \mathit{E}}{\partial t},\hfill \end{array}$$ (3.1)

where $\nabla \cdot \mathit{H}=0$, $\nabla \cdot \mathit{E}=0$, $\mathit{E}$ is the electric field, $\mathit{H}$ is the magnetic field, ${ϵ}_o$ is the free space permittivity and ${\mu }_o$ is the free space permeability. Using standard vector identities, one can show that

$$\begin{array}{c}\nabla \times (\nabla \times \mathit{E})=-{\mu }_o{ϵ}_o\frac{{\partial }^2\mathit{E}}{\partial t^2},\mathrm{and}\nabla \times (\nabla \times \mathit{H})=-{\mu }_o{ϵ}_o\frac{{\partial }^2\mathit{H}}{\partial t^2},\hfill \end{array}$$ (3.2)

and that

$$\begin{array}{c}{\nabla }^2\mathit{E}=\frac{1}{c^2}\frac{{\partial }^2\mathit{E}}{\partial t^2},\mathrm{and}{\nabla }^2\mathit{H}=\frac{1}{c^2}\frac{{\partial }^2\mathit{H}}{\partial t^2},\hfill \end{array}$$ (3.3)

where the speed of electromagnetic waves is $c=\frac{1}{\sqrt{{ϵ}_o{\mu }_o}}$. All electromagnetic radiation travels, in a vacuum, at the speed $c\approx 2.99792458\times 10^8\pm 1.1\mathrm{m∕s}$. In any another medium, for electromagnetic waves, the propagation speed is $v=\frac{1}{\sqrt{ϵ\mu }}$, where $ϵ$ and $\mu$ are the electric permittivity and magnetic permeability of that medium, respectively.4

3.1. Plane harmonic wave fronts

Now consider the special case of plane harmonic waves, for example of the form

$$\begin{array}{c}\mathit{E}={\mathit{E}}_{o}cos(\mathit{k}\cdot \mathit{x}-\omega t)\mathrm{and}\mathit{H}={\mathit{H}}_{o}cos(\mathit{k}\cdot \mathit{x}-\omega t),\hfill \end{array}$$ (3.4)

where $\mathit{x}$ is an initial position vector to the wave front, where $\mathit{k}$ is the direction of propagation. We refer to the phase as $\varphi =\mathit{k}\cdot \mathit{x}-\omega t$, and $\omega =\frac{2\pi }{\tau }$ as the angular frequency, where $\tau$ is the period. For plane waves, the wave front is a plane on which $\varphi$ is constant, which is orthogonal to the direction of propagation, characterized by $\mathit{k}$. In the case of harmonic waves, we have

$$\begin{array}{c}\mathit{k}\times \mathit{E}={\mu }_o\omega \mathit{H}\mathrm{and}\mathit{k}\times \mathit{H}=-{ϵ}_o\omega \mathit{E},\hfill \end{array}$$ (3.5)

and $\mathit{k}\cdot \mathit{E}=0$ and $\mathit{k}\cdot \mathit{H}=0$. The three vectors, $\mathit{k}$, $\mathit{E}$ and $\mathit{H}$ constitute a mutually orthogonal triad.5 The direction of wave propagation is given by $\frac{\mathit{E}\times \mathit{H}}{\Vert \mathit{E}\times \mathit{H}\Vert }$. Electromagnetic waves traveling through space carry electromagnetic energy which flows in the direction of wave propagation. The energy per unit area per unit time flowing perpendicularly into a surface in free space is given by the Poynting vector $\mathit{S}=\mathit{E}\times \mathit{H}$.

3.2. Natural (random) electromagnetic energy propagation

Since at high-frequencies $\mathit{E}$, $\mathit{H}$ and $\mathit{S}$ oscillate rapidly, it is impractical to measure instantaneous values of $\mathit{S}$ directly. Consider the harmonic representations in Eq. (3.4) which leads to $\mathit{S}={\mathit{E}}_o\times {\mathit{H}}_{o}co{s}^2(\mathit{k}\cdot \mathit{x}-\omega t)$, and consequently the average value over a longer time interval ($\mathcal{T}$) than the time scale of rapid random oscillation,

$$\begin{array}{c}{〈\mathit{S}〉}_{\mathcal{T}}={\mathit{E}}_o\times {\mathit{H}}_o{〈co{s}^2(\mathit{k}\cdot \mathit{x}-\omega t)〉}_{\mathcal{T}}=\frac{1}{2}{\mathit{E}}_o\times {\mathit{H}}_o,\hfill \end{array}$$ (3.6)

leading to the definition of the irradiance

$$\begin{array}{c}I\stackrel{\mathrm{def}}{=}{〈\Vert \mathit{S}\Vert 〉}_{\mathcal{T}}=\frac{1}{2}\Vert {\mathit{E}}_o\times {\mathit{H}}_o\Vert =\frac{1}{2}\sqrt{\frac{{ϵ}_o}{{\mu }_o}}{\Vert {\mathit{E}}_o\Vert }^2.\hfill \end{array}$$ (3.7)

Thus, the rate of flow of energy is proportional to the square of the amplitude of the electric field.

3.3. Reflection and absorption of energy-Fresnel relations

We consider a plane harmonic wave incident upon a plane boundary separating two different materials, specifically vacuum and surface, which produces a reflected wave and an absorbed (refracted) wave (Fig. 1). Two cases for the electric field vector are considered:

• •(1) electric field vectors that are parallel ($\parallel$) to the plane of incidence and
• •(2) electric field vectors that are perpendicular ($\perp$) to the plane of incidence.

In either case, the tangential components of the electric and magnetic fields are required to be continuous across the interface. Consider case (1). We have the following general vectorial representations

$${\mathit{E}}_{\parallel }=E_{\parallel }cos(\mathit{k}\cdot \mathit{x}-\omega t){\mathit{e}}_1\mathrm{and}{\mathit{H}}_{\parallel }=H_{\parallel }cos(\mathit{k}\cdot \mathit{x}-\omega t){\mathit{e}}_2,$$ (3.8)

where ${\mathit{e}}_1$ and ${\mathit{e}}_2$ are orthogonal to the propagation direction $\mathit{k}$. By employing the law of refraction ($n_{i}sin{\theta }_i=n_{a}sin{\theta }_a$) we obtain the following conditions relating the incident, reflected and absorbed components of the electric field quantities

$$\begin{array}{c}{E}_{\parallel i}cos{\theta }_i-E_{\parallel r}cos{\theta }_r=E_{\parallel a}cos{\theta }_a\mathrm{and}{H}_{\perp i}+H_{\perp r}=H_{\perp a}.\hfill \end{array}$$ (3.9)

Since, for plane harmonic waves, the magnetic and electric field amplitudes are related by $H=\frac{E}{v\mu }$, we have

$$E_{\parallel i}+E_{\parallel r}=\frac{{\mu }_i}{{\mu }_a}\frac{v_i}{v_a}{E}_{\parallel a}=\frac{{\mu }_i}{{\mu }_a}\frac{n_a}{n_i}{E}_{\parallel a}\stackrel{\mathrm{def}}{=}\frac{\hat{n}}{\hat{\mu }}{E}_{\parallel a},$$ (3.10)

where $\hat{\mu }\stackrel{\mathrm{def}}{=}\frac{{\mu }_a}{{\mu }_i}$, $\hat{n}\stackrel{\mathrm{def}}{=}\frac{n_a}{n_i}$ and where $v_i$, $v_r$ and $v_a$ are the values of the velocity in the incident, reflected and absorbed directions.6 By again employing the law of refraction, we obtain the Fresnel reflection and transmission/absorption coefficients, generalized for the case of unequal magnetic permeabilities

$$\begin{array}{c}{r}_{\parallel }=\frac{E_{\parallel r}}{E_{\parallel i}}=\frac{\frac{\hat{n}}{\hat{\mu }}cos{\theta }_i-cos{\theta }_a}{\frac{\hat{n}}{\hat{\mu }}cos{\theta }_i+cos{\theta }_a}\mathrm{and}{a}_{\parallel }=\frac{E_{\parallel a}}{E_{\parallel i}}=\frac{2cos{\theta }_i}{cos{\theta }_a+\frac{\hat{n}}{\hat{\mu }}cos{\theta }_i}.\hfill \end{array}$$ (3.11)

Following the same procedure for case (2), where the components of $\mathit{E}$ are perpendicular to the plane of incidence, we have

$$\begin{array}{c}{r}_{\perp }=\frac{E_{\perp r}}{E_{\perp i}}=\frac{cos{\theta }_i-\frac{\hat{n}}{\hat{\mu }}cos{\theta }_a}{cos{\theta }_i+\frac{\hat{n}}{\hat{\mu }}cos{\theta }_a}\mathrm{and}{a}_{\perp }=\frac{E_{\perp a}}{E_{\perp i}}=\frac{2cos{\theta }_i}{cos{\theta }_i+\frac{\hat{n}}{\hat{\mu }}cos{\theta }_a}.\hfill \end{array}$$ (3.12)

Our primary interest is in the reflections. We define the reflectances as

$$\begin{array}{c}\mathcal{I}{\mathcal{R}}_{\parallel }\stackrel{\mathrm{def}}{=}{r}_{\parallel }^2\mathrm{and}\mathcal{I}{\mathcal{R}}_{\perp }\stackrel{\mathrm{def}}{=}{r}_{\perp }^2.\hfill \end{array}$$ (3.13)

Particularly convenient forms for the reflections are

$$\begin{array}{c}{r}_{\parallel }=\frac{\frac{{\hat{n}}^2}{\hat{\mu }}cos{\theta }_i-{({\hat{n}}^2-si{n}^2{\theta }_i)}^{\frac{1}{2}}}{\frac{{\hat{n}}^2}{\hat{\mu }}cos{\theta }_i+{({\hat{n}}^2-si{n}^2{\theta }_i)}^{\frac{1}{2}}}\mathrm{and}{r}_{\perp }=\frac{cos{\theta }_i-\frac{1}{\hat{\mu }}{({\hat{n}}^2-si{n}^2{\theta }_i)}^{\frac{1}{2}}}{cos{\theta }_i+\frac{1}{\hat{\mu }}{({\hat{n}}^2-si{n}^2{\theta }_i)}^{\frac{1}{2}}}.\hfill \end{array}$$ (3.14)

Thus, the total energy reflected can be characterized by

$$\mathcal{I}\mathcal{R}\stackrel{\mathrm{def}}{=}{\left(\frac{E_r}{E_i}\right)}^2=\frac{E_{\perp r}^2+E_{\parallel r}^2}{E_i^2}=\frac{I_{\parallel r}+I_{\perp r}}{I_i}.$$ (3.15)

If the resultant plane of oscillation of the (polarized) wave makes an angle of ${\gamma }_i$ with the plane of incidence, then

$$\begin{array}{c}{E}_{\parallel i}=E_{i}cos{\gamma }_i\mathrm{and}{E}_{\perp i}=E_{i}sin{\gamma }_i,\hfill \end{array}$$ (3.16)

and it follows from the previous definition of $I$ that

$$\begin{array}{c}{I}_{\parallel i}=I_{i}co{s}^2{\gamma }_i\mathrm{and}{I}_{\perp i}=I_{i}si{n}^2{\gamma }_i.\hfill \end{array}$$ (3.17)

Substituting these expression back into the expressions for the reflectances yields

$$\mathcal{I}\mathcal{R}=\frac{I_{\parallel r}}{I_i}co{s}^2{\gamma }_i+\frac{I_{\perp r}}{I_i}si{n}^2{\gamma }_i=\mathcal{I}{\mathcal{R}}_{\parallel }co{s}^2{\gamma }_i+\mathcal{I}{\mathcal{R}}_{\perp }si{n}^2{\gamma }_i.$$ (3.18)

For natural or unpolarized electromagnetic radiation, the angle ${\gamma }_i$ varies rapidly in a random manner, as does the field amplitude. Thus, since

$$\begin{array}{c}{〈co{s}^2{\gamma }_i\left(t\right)〉}_{\mathcal{T}}=\frac{1}{2}\mathrm{and}{〈si{n}^2{\gamma }_i\left(t\right)〉}_{\mathcal{T}}=\frac{1}{2},\hfill \end{array}$$ (3.19)

and therefore for natural electromagnetic radiation

$$\begin{array}{c}{I}_{\parallel i}=\frac{I_i}{2}\mathrm{and}{I}_{\perp i}=\frac{I_i}{2}.\hfill \end{array}$$ (3.20)

and therefore

$$\begin{array}{c}{r}_{\parallel }^2={\left(\frac{E_{\parallel r}^2}{E_{\parallel i}^2}\right)}^2=\frac{I_{\parallel r}}{I_{\parallel i}}\mathrm{and}{r}_{\perp }^2={\left(\frac{E_{\perp r}^2}{E_{\perp i}^2}\right)}^2=\frac{I_{\perp r}}{I_{\perp i}}.\hfill \end{array}$$ (3.21)

Thus, the total reflectance becomes

$$\mathcal{I}\mathcal{R}=\frac{1}{2}(\mathcal{I}{\mathcal{R}}_{\parallel }+\mathcal{I}{\mathcal{R}}_{\perp })=\frac{1}{2}(r_{\parallel }^2+r_{\perp }^2),$$ (3.22)

where $0\le \mathcal{I}\mathcal{R}\le 1$. For the cases where $sin{\theta }_a=\frac{sin{\theta }_i}{\hat{n}}>1$, one may rewrite reflection relations as

$$\begin{array}{c}{r}_{\parallel }=\frac{\frac{{\hat{n}}^2}{\hat{\mu }}cos{\theta }_i-j{(si{n}^2{\theta }_i-{\hat{n}}^2)}^{\frac{1}{2}}}{\frac{{\hat{n}}^2}{\hat{\mu }}cos{\theta }_i+j{(si{n}^2{\theta }_i-{\hat{n}}^2)}^{\frac{1}{2}}}\mathrm{and}{r}_{\perp }=\frac{cos{\theta }_i-\frac{1}{\hat{\mu }}j{(si{n}^2{\theta }_i-{\hat{n}}^2)}^{\frac{1}{2}}}{cos{\theta }_i+\frac{1}{\hat{\mu }}j{(si{n}^2{\theta }_i-{\hat{n}}^2)}^{\frac{1}{2}}},\hfill \end{array}$$ (3.23)

where, $j=\sqrt{-1}$, and in this complex case7

$$\begin{array}{c}\mathcal{I}{\mathcal{R}}_{\parallel }\stackrel{\mathrm{def}}{=}{r}_{\parallel }{\overline{r}}_{\parallel }=1,\mathrm{and}\mathcal{I}{\mathcal{R}}_{\perp }\stackrel{\mathrm{def}}{=}{r}_{\perp }{\overline{r}}_{\perp }=1,\hfill \end{array}$$ (3.24)

where ${\overline{r}}_{\parallel }$ and ${\overline{r}}_{\perp }$ are complex conjugates. Thus, for angles above the critical angle ${\theta }_i^{\ast }$, all of the energy is reflected. Notice that as $\hat{n}\to 1$ we have complete absorption, while as $\hat{n}\to \infty$ we have complete reflection. The amount of absorbed irradiance by the surface is $I_a=(1-\mathcal{I}\mathcal{R})I_i$.

3.4. Reflectivity

To observe the dependency of $\mathcal{I}\mathcal{R}$ on $\hat{n}$ and ${\theta }_i$ we can explicitly write

$$\begin{array}{c}\mathcal{I}\mathcal{R}=\frac{1}{2}\left({\left(\frac{\frac{{\hat{n}}^2}{\hat{\mu }}cos{\theta }_i-{({\hat{n}}^2-si{n}^2{\theta }_i)}^{\frac{1}{2}}}{\frac{{\hat{n}}^2}{\hat{\mu }}cos{\theta }_i+{({\hat{n}}^2-si{n}^2{\theta }_i)}^{\frac{1}{2}}}\right)}^2+{\left(\frac{cos{\theta }_i-\frac{1}{\hat{\mu }}{({\hat{n}}^2-si{n}^2{\theta }_i)}^{\frac{1}{2}}}{cos{\theta }_i+\frac{1}{\hat{\mu }}{({\hat{n}}^2-si{n}^2{\theta }_i)}^{\frac{1}{2}}}\right)}^2\right).\hfill \end{array}$$ (3.25)

We observe:

• •As $\hat{n}\to \infty$, $\mathcal{I}\mathcal{R}\to 1$, no matter what the angle of incidence’s value. We note that as $\hat{n}\to 1$, provided that $\hat{\mu }=1$, $\mathcal{I}\mathcal{R}\to 0$, i.e. all incident energy is absorbed (it is transparent).
• •
  With increasing $\hat{n}$, the angle for minimum reflectance grows larger. As mentioned previously, for the remainder of the work, we shall take $\hat{\mu }=1$ (${\mu }_o={\mu }_i={\mu }_a$), thus

  $$\hat{n}=\frac{n_a}{n_i}=\sqrt{\frac{{ϵ}_a{\mu }_a}{{ϵ}_i{\mu }_i}}\Rightarrow {ϵ}_a{\mu }_a={\left(\hat{n}\right)}^2{ϵ}_i{\mu }_i\Rightarrow {ϵ}_a={\left(\hat{n}\right)}^2{ϵ}_i.$$ (3.26)
• •
  The previous assumption yields

  $$\begin{array}{c}\mathcal{I}\mathcal{R}=\frac{I_r}{I_i}=\frac{1}{2}\left({\left(\frac{{\hat{n}}^{2}cos{\theta }_i-{({\hat{n}}^2-si{n}^2{\theta }_i)}^{\frac{1}{2}}}{{\hat{n}}^{2}cos{\theta }_i+{({\hat{n}}^2-si{n}^2{\theta }_i)}^{\frac{1}{2}}}\right)}^2+{\left(\frac{cos{\theta }_i-{({\hat{n}}^2-si{n}^2{\theta }_i)}^{\frac{1}{2}}}{cos{\theta }_i+{({\hat{n}}^2-si{n}^2{\theta }_i)}^{\frac{1}{2}}}\right)}^2\right).\hfill \end{array}$$ (3.27)

Remark

We now recall Eq. (2.1) connects the concept of a ray with a pulse/beam and observe:

• •Since $\overline{I}$ is the energy per unit area per unit time, we obtain the energy associated with an entire pulse/beam by multiplying the irradiance by the cross-sectional area of an initially coherent beam, $\overline{I}{A}^b$, where $A^b$ is the cross-sectional area of the beam (comprising all of the rays).
• •The energy per unit time (power) for a ray in the pulse/beam is then given by $I=\overline{I}{A}^r=\overline{I}{A}^b∕N_r$, where $N_r$ is the number of rays in the beam (Fig. 1) and $A^r$ can be considered the area associated with a ray.
• •The reflection relation, Eq. (3.25), can then be used to compute changes in the magnitude of the reflected rays (and the amount absorbed), with directional changes given by the laws of reflection.

We refer the reader to Gross [19] and Zohdi [20], [21], [22], [23], [24], [25], [26] for details.

4. Model problem and response trends

From this point forth, we assume that the ambient medium behaves as a vacuum. Accordingly, there are no energetic losses as the rays move through the surrounding medium.

4.1. Tracking of beam-decomposed rays

Starting at $t=0$ and ending at $t=T$, the simple overall algorithm to track rays is as follows, at each time increment:

• 1.Check for intersections of rays with surfaces (hence a reflection), and compute the ray magnitudes and orientation if there are reflections (for all rays that are experiencing a reflection, $I_j^{ref}$, $j=1,2,\dots ,Rays$),
• 2.Increment all ray positions (${\mathit{r}}_j(t+\Delta t)={\mathit{r}}_j\left(t\right)+\Delta t{\mathit{v}}_j\left(t\right)$, $j=1,2,\dots ,Rays$),
• 3.Increment time forward ($t=t+\Delta t$) and repeat the process for the next time interval.

In order to capture all of the ray reflections that occur:

• •The time step size $\Delta t$ is dictated by the offset height of the source. A somewhat ad-hoc approach is to scale the time step size by the speed of ray propagation according to $\Delta t=\xi \frac{\mathcal{H}}{\Vert \mathit{v}\Vert }$, where $\mathcal{H}$ is the height of the source and $0.0001\le \xi \le 0.01$. Typically, the results are insensitive to $\xi$ that are smaller than this range.
• •Although outside the scope of this work, one can also use this algorithm to compute the thermal response by combining it with heat transfer equations via staggering schemes (Zohdi [20], [22], [23]).

4.2. Test surface

The discrete-ray approach is flexible enough to simulate a wide variety of systems. As a test surface, we consider a topology to be irradiated described by $F(x_1,x_2,x_3)=0$. The outward surface normals, $\mathit{n}$, needed during the scattering calculations, are easy to characterize by writing

$$\mathit{n}=\frac{\nabla F}{\Vert \nabla F\Vert }.$$ (4.1)

The components of the gradient are

$$\nabla F=\frac{\partial F}{\partial x_1}{\mathit{e}}_1+\frac{\partial F}{\partial x_2}{\mathit{e}}_2+\frac{\partial F}{\partial x_3}{\mathit{e}}_3.$$ (4.2)

It is advantageous to write the surface in parametric form:

$$F(x_1,x_2,x_3)=G(x_1,x_2)-x_3=0.$$ (4.3)

which leads to

$$x_3=G(x_1,x_2).$$ (4.4)

The gradient becomes

$$\nabla F=\frac{\partial G}{\partial x_1}{\mathit{e}}_1+\frac{\partial G}{\partial x_2}{\mathit{e}}_2-{\mathit{e}}_3.$$ (4.5)

In order to determine whether a ray has made contact with a surface domain, one checks if the $x_3$ component of a ray (${\mathit{r}}_j$) is less that $x_3$ of the surface.

5. Numerical/quantitative examples

We have the following set up for a series of tests:

• •The initial velocity vector for all initially collimated (parallel) rays comprising the beam was $\mathit{v}=(c,0,0)$, where $c=3\times 10^8\mathrm{m∕s}$ is the speed of light in a vacuum.
• •
  We used a parametrized test surface given by

  $$x_3=2+A\left(sin\frac{2{\omega }_1\pi x_1}{L_1}\right)sin\left(\frac{2{\omega }_2\pi x_2}{L_2}\right),$$ (5.1)

  with $L_1=L_2=1$, ${\omega }_1=1.5$ and ${\omega }_2=0.75$, where we vary $A$. We also added a flat cut-off so that the surface had a half-sine wave character (Fig. 3).
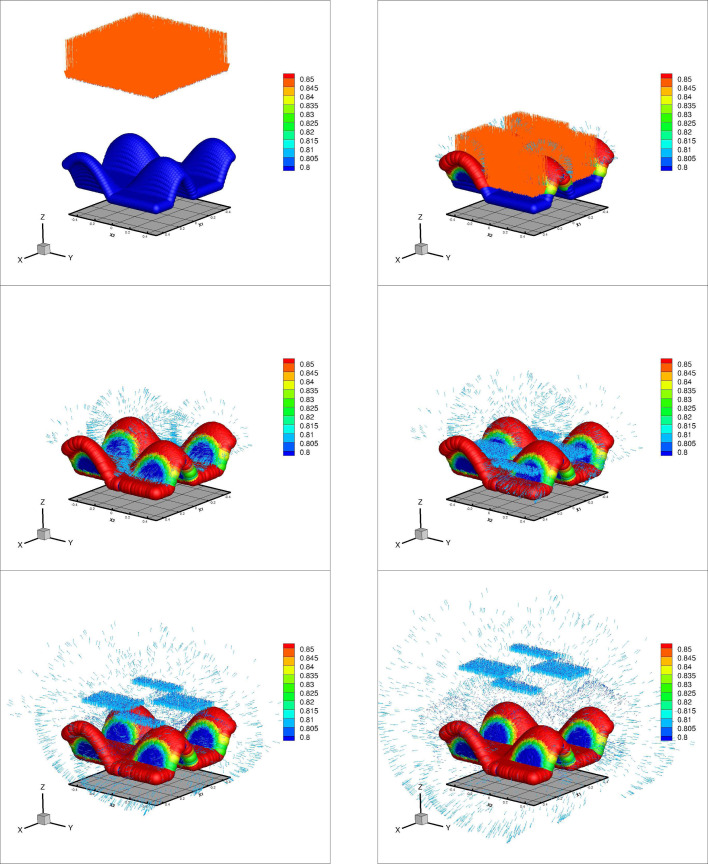
• •The number of rays in the beam were steadily increased from $N_r=100,200,etc$, until the results were insensitive to further refinements. This approach indicated that between approximately $9500\le N_r\le 10000$ parallel rays in rectangular cross-sectional plane of the beam. The rays were randomly placed within the beam (Fig. 1, Fig. 3), to correspond to unpolarized incoming energy, and yielded stable results across the parameter study range.
• • Fig. 3 shows a sequence of frames of the detailed response of a surface to $10000$ rays. Fig. 2 shows a top view. Table 1 shows the steady loss of absorption efficacy with contact surface amplitude oscillation (waviness). The algorithm computes the absorption at the point of contact and color codes it relative to the incoming irradiation. This allows one to quickly quantify the decontamination across the topology of the structure.
• •This approach also allows an analyst to explore nonuniform beam profiles, for example exponential central irradiance decay: $I\left(d\right)=I(d=0)e^{-ad}$, where $d$ is the distance from the center of the initial beam, where in the case of $a=0$, one recaptures a flat beam, $I\left(d\right)=I(d=0)$.8

Fig. 3.

Sequence of frames for a surface with amplitude $A=0.3$ (the amplitude was enhanced by a factor of 20 in graphics to more easily see the effects of the topology on absorption). Colors indicate the absorption, normalized by the incoming radiation level. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Fig. 2.

Top view for a surface with amplitude $A=0.3$. Colors indicate the absorption, normalized by the incoming. radiation level. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Table 1.

The loss of absorption efficacy with contact surface amplitude oscillation (waviness).

Surface amplitude	Average surface absorption
0.0	0.8888
0.1	0.8879
0.2	0.8808
0.3	0.8675
0.4	0.8507
0.5	0.8327
0.6	0.8126
0.7	0.7878
0.8	0.7679
0.9	0.7485
1.0	0.7315

6. Summary and discussion

In closing, the pandemic of 2020 has led to a gigantic increase research in modeling and simulation of infectious diseases. There are numerous aspects associated with this literally epoch-changing event that is now facing humanity, such as (a) Disease propagation, (b) Immune-responses, (c) Logistical responses, (d) Political responses and (e) Decontamination protocols. Because UV-c based decontamination methods are becoming widely used in industry, with many variants being proposed, fast computational analysis and design tools are needed to ascertain their effectiveness. Accordingly, this work developed a discrete-ray model to allow for propagation of energy encountering a surface, based on the decomposition of irradiation into a groups of rays, which are then tracked as they progress towards the target. This facilitates:

• •Quick quantification of the decontamination efficacy across the topology of the structure (color coding the efficacy relative to the incoming irradiation).
• •Parametric studies to the changes in absorption as a function of changes in surface geometry.

The simulations take on the order of one minute on a laptop. This type of approach makes it quite suitable for use in conjunction with mobile decontamination systems and allows provides a simpler alternative to a direct, computationally intensive, discretization of a continuum description using Maxwell’s equations with a Finite Element or Finite Difference method.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.