Circuit mechanisms for the maintenance and manipulation of information in working memory

Abstract

Recently it has been proposed that information in working memory (WM) may not always be stored in persistent neuronal activity, but can be maintained in “activity-silent” hidden states such as synaptic efficacies endowed with short-term synaptic plasticity (STSP). To test this idea computationally, we investigated recurrent neural network (RNN) models trained to perform several WM dependent tasks, in which WM representation emerges from learning and is not a priori assumed to depend on self-sustained persistent activity. We found that STSP can support the short-term maintenance of information provided that the memory delay period is sufficiently short. However, in tasks that require actively manipulating information, persistent activity naturally emerges from learning, and the amount of persistent activity scales with the degree of manipulation required. These results shed insight into the current debate on WM encoding, and suggest that persistent activity can vary markedly between short-term memory tasks with different cognitive demands.

Introduction

Working memory (WM) refers to our ability to temporarily maintain and manipulate information, and is a cornerstone of higher intelligence¹. In order to understand the mechanisms underlying WM, we must resolve the substrate(s) in which information in WM is maintained. It has been assumed that information in WM is maintained in persistent neuronal activity^2–6, likely resulting from local recurrent connections^7,8, and/or cortical to subcortical loops⁹. However, recent experiments reveal that the strength of persistent activity varies markedly between tasks^10–16. This raises two related questions: 1) why does persistent activity vary between tasks, and 2) for those tasks with weak or non-existent persistent activity, where and how is information maintained?

A possible answer to the second question is that information is not necessarily maintained in persistent activity, but can be maintained through short-term synaptic plasticity (STSP). STSP, which is distinct from long-term depression (LTD) and potentiation (LTP), is the process in which pre-synaptic activity alters synaptic efficacies for hundreds or thousands of milliseconds¹⁷. Importantly, modelling studies suggest that STSP can allow networks to maintain an “activity-silent” memory trace of a stimulus, in which short-term information is maintained without persistent activity¹⁸. Recent work in human subjects suggests that information can be mnemonically encoded in a silent, or latent, state, and that information can be reactivated into neuronal activity by probing the circuit^19,20.

While STSP might provide another mechanism for information maintenance, it does not in itself fully account for why the strength of persistent activity varies between tasks. To answer this, we highlight that WM involves not just the maintenance of information, but also its manipulation. Importantly, manipulating information in WM engages the frontoparietal network differently compared to simply maintaining information^21,22. While STSP can support activity-silent information maintenance, it is unknown whether STSP can support activity-silent manipulation of information without persistent activity. If not, then it suggests that the strength of persistent activity reflects the degree of manipulation required by the task.

In this study, we examine whether STSP can support the silent manipulation of information in WM, and whether it could explain the variability in persistent activity between tasks. Unfortunately, it is currently extremely challenging to measure synaptic efficacies in awake behaving mice, and next to impossible in non-human primates. However, recurrent neural network (RNN) models have opened a new avenue to study the putative neural mechanisms underlying various cognitive functions. Crucially, RNNs have successfully reproduced the patterns of neural activity and behavioral output that are observed in vivo, generating novel insights into circuit function that would otherwise be unattainable through direct experimental measurement^23–29.

Here, we train biologically inspired RNNs, consisting of excitatory and inhibitory like neurons³⁰ and dynamic synapses governed by STSP¹⁸, to solve a variety of widely studied WM-based tasks. We show that STSP can support the activity-silent maintenance of information, but that it cannot support the silent manipulation of information. Furthermore, we show that the strength of persistent activity covaries with the degree of manipulation, potentially explaining the observation that persistent activity varies markedly between tasks.

Results

The goal of this study was 1) to determine whether STSP can support activity-silent manipulation of information in WM, and 2) whether STSP can explain the variability in persistent activity observed in different tasks^10–16. We trained RNNs to solve several widely studied WM tasks, which varied in their specific cognitive demands. Furthermore, given that cortical firing rates are relatively low^31,32, either because of metabolic pressure³³ or to facilitate information encoding and read-out^31,32, we added a penalty on high neuronal activity (see Methods: Network training) to encourage networks to solve tasks using low levels of activity.

Network model

We defined neurons in our network as either excitatory or inhibitory³⁰. The input layer consisted of 24 excitatory, direction tuned neurons projecting onto a recurrently connected network of 80 excitatory and 20 inhibitory neurons (Figure 1a, see Methods: Network models). The connection weights between all recurrently connected neurons were dynamically modulated by STSP (see Methods: Short-term synaptic plasticity) using a previously proposed model¹⁸. Connection weights from half of the neurons were depressing, such that pre-synaptic activity decreases synaptic efficacy (Figure 1b, left panels), and the other half were facilitating, such that presynaptic activity increases synaptic efficacy (right panels).

Figure 1. RNN design.

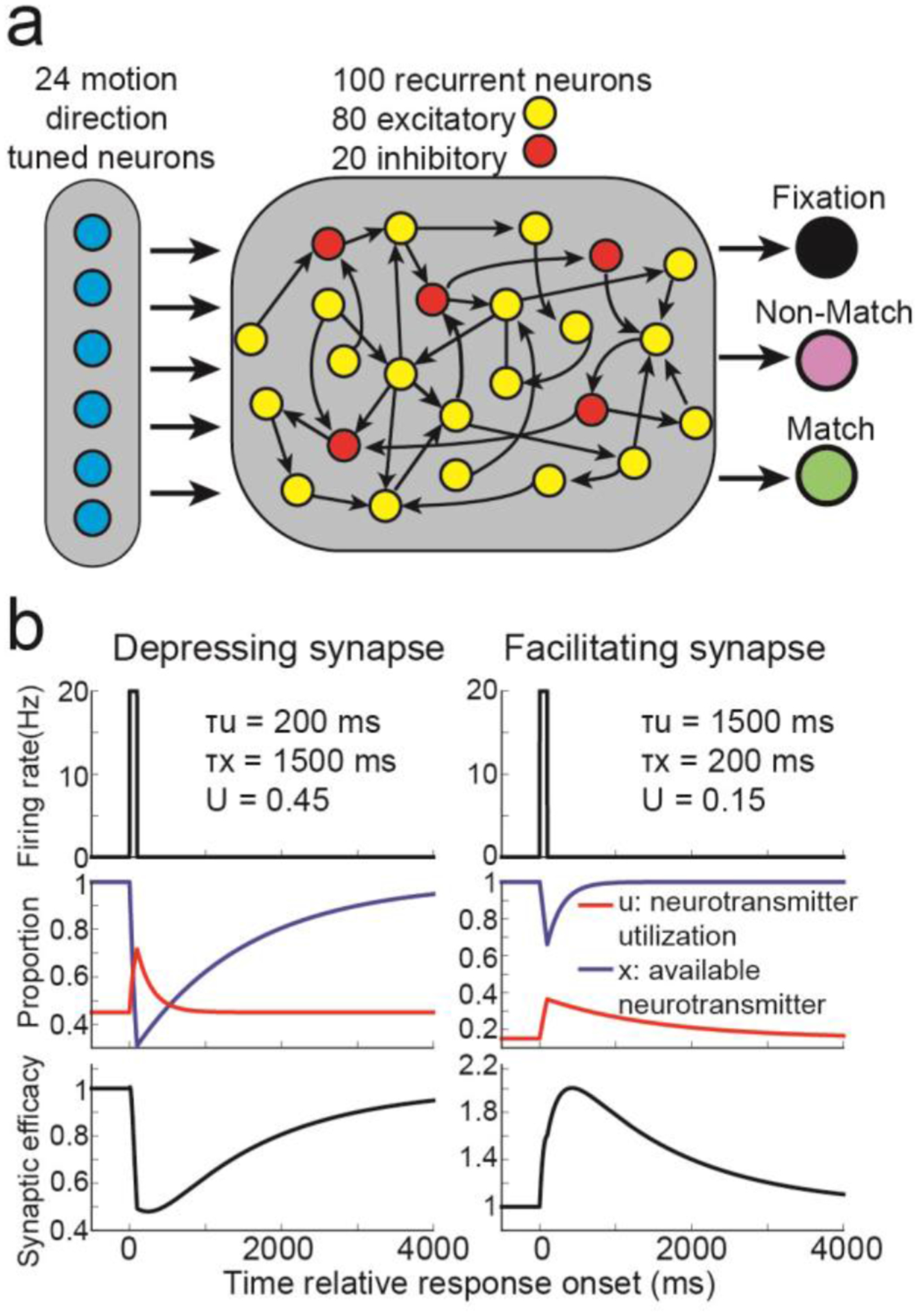
(a) The core rate-based model consisted of 24 motion direction tuned neurons projecting onto 80 excitatory, and 20 inhibitory, recurrently connected neurons. The 80 excitatory neurons projected onto three decisions neurons. (b) For synapses that exhibited short-term synaptic depression (left panels), presynaptic activity (top panel) weakly increases neurotransmitter utilization (red trace, middle panel) and strongly decreases available neurotransmitter (blue trace), decreasing synaptic efficacy (bottom panel). For synapses that exhibited short-term synaptic facilitation (right panels), presynaptic activity strongly increases neurotransmitter utilization and weakly decreases available neurotransmitter, increasing synaptic efficacy.

Given this setup, the synaptic efficacy connecting neuron j to all other neurons at time t is the product between the available neurotransmitter and the neurotransmitter utilization: S_j(t) = x_j(t)u_j(t). Furthermore, the total input into neuron i is ∑_j W_j,iS_jR_j, where W_j,i is the connection weight from neuron j to neuron i, and R_j is the neural activity of neuron j.

Maintaining information in short-term memory

We first examined how networks endowed with STSP maintain information in WM using either persistent neuronal activity or STSP. We trained 20 networks to solve a delayed match-to-sample task (DMS, Figure 2a), in which the networks had to indicate whether sequentially presented (500 ms presentation; 1000 ms delay) sample and test stimuli were an exact match.

Figure 2. Delayed match-to-sample (DMS) task.

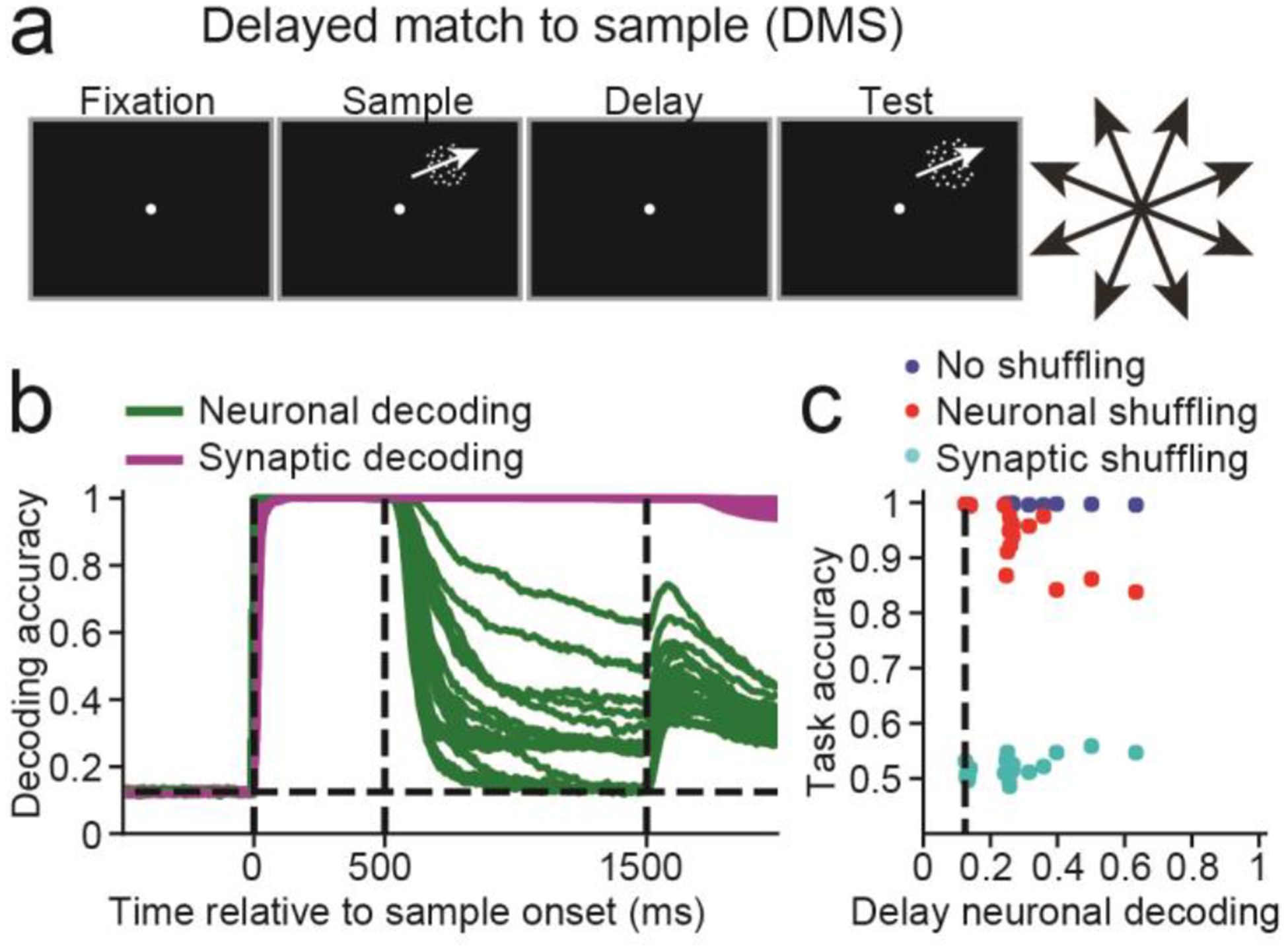
(a) A 500 ms fixation period was followed by a 500 ms sample motion direction stimulus, followed by a 1000 ms delay period and finally a 500 ms test stimulus. (b) Sample decoding accuracy, calculated using neuronal activity (green curves) and synaptic efficacy (magenta curves) for n = 20 networks. The dashed vertical lines, from left to right, indicate the sample onset, offset, and end of the delay period. (c) Scatter plot showing the neuronal decoding accuracy measured at the end of the delay (x-axis) versus the task accuracy (y-axis) for all 20 networks (blue circles), the task accuracy for the same 20 networks after neuronal activity was shuffled right before test onset (red circles) or synaptic efficacies were shuffled right before test onset (cyan circles). The dashed vertical line indicates chance level decoding.

To measure how information was maintained, we decoded the sample direction using 1) the population activity of the 100 recurrent neurons, and from 2) the 100 unique synaptic efficacies modulated by STSP (see Methods: Short-term synaptic plasticity). If, during the delay, we could decode sample direction from synaptic efficacies, but not neuronal activity, it would indicate that STSP allows for activity-silent maintenance of information.

Sample decoding using synaptic efficacies (magenta curves, one for each network) was equal to 1.0 (perfect decoding) for the entire delay across all networks (Figure 2b). In contrast, decoding accuracy using neuronal activity (green curves) decreased to <0.7 for all networks by the end of the delay, and decoding accuracies were near chance levels (0.125) for 6 networks (P>0.05, bootstrap, measured during the last 100ms of delay, see Methods: Population decoding). Thus, the sample was perfectly encoded by synaptic efficacies in all 20 networks, and either weakly, or not encoded at all, in neuronal activity.

Although the decoding accuracies measure how much information is stored in either substrate, it does not address how the network uses either substrate to solve the task. We wanted to 1) measure how networks used information in neuronal activity and synaptic efficacies to solve the task, and 2) how these contributions relate to the neuronal decoding accuracy.

We answered these questions by disrupting network activity or synaptic efficacies during task performance. We simulated each trial starting at test onset using the exact same input activity in three different ways: 1) using the actual neuronal activity and synaptic efficacies taken at test onset as starting points, 2) synaptic efficacies were kept as is, but neuronal activity was shuffled between trials, and 3) neuronal activity was kept as is, but synaptic efficacies were shuffled (but not connection weights) between trials. In other words, given that the total input into the neuron is weight × synaptic efficacy × neuronal activity as defined above, then in 2), we only shuffle neuronal activity, and in 3) we only shuffle synaptic efficacy. We shuffled across all trials to destroy any correlation between the sample motion direction and neuronal activity or synaptic efficacy. In all three cases, we calculated whether the network output indicated the correct choice.

These results are shown in Figure 2c, comparing neuronal decoding accuracy measured at the end of the delay (x-axis) and task accuracy (y-axis). This allows us to relate sample decoding accuracy (which one could measure in neurophysiological experiments) with the causal contribution of neuronal and synaptic WM towards solving the task (which is easy to measure in RNNs, but not in neurophysiological experiments).

Neuronal decoding at the end of the delay was distributed between chance and < 0.7, with task accuracy (calculated without shuffling data) consistently > 0.98 (blue circles). Networks with the strongest persistent activity suffered the greatest performance loss when neuronal activity was shuffled (red circles, Pearson correlation R = −10.80, P<10⁻⁴, n = 20), and suffered the least performance loss when synaptic efficacies were shuffled (cyan circles, R = 0.60, P = 0.005).

For 5 of the 6 networks that solved the task using activity-silent WM, shuffling neuronal activity did not affect task accuracy (P>0.05, permutation test, see Methods: Shuffle analysis). Furthermore, setting activity for all recurrently connected neurons to zero for the last 50 ms of the delay had little effect on performance (Figure S1), confirming that information maintained in synaptic efficacies during the delay, and not neuronal activity, was used to solve the DMS task. Interestingly, analysis of how networks computed the match/non-match suggests that synaptic efficacies prospectively encode the stimulus³⁴, allowing the network to transform the test stimulus into the appropriate match/non-match decision (Figure S2). In Modelling Notes and Figures S2–S4, we discuss the effect of different delay times, and different regularizations of neuronal activity and the connectivity weights.

Manipulating information

Given that STSP can allow networks to silently maintain information in WM, we examined whether it could also allow networks to silently manipulate information. Thus, we repeated the analysis from Figure 2 on 20 networks trained to solve a delayed match-to-rotated (DMRS) sample task, in which the target test direction was rotated 90° clockwise from the sample (Figure 3a). Neuronal decoding accuracy for this task (green curves, Figure 3b) was greater than the DMS task (DMS = 0.27, DMRS = 0.72, t(38) =9.89, P < 10⁻¹¹, two-sided, unpaired, t-test, n = 20, measured during last 100 ms of the delay period), suggesting that more information was maintained in neuronal activity compared to the DMS task. Unlike the DMS task, all 20 networks maintained information in a hybrid manner, with elevated neuronal decoding accuracy at the end of the delay (P<0.05, bootstrap), and shuffling either neuronal activity or synaptic efficacies significantly decreased task accuracy (P<0.05, Figure 3c).

Figure 3. Delayed match-to-rotated sample (DMRS) task.

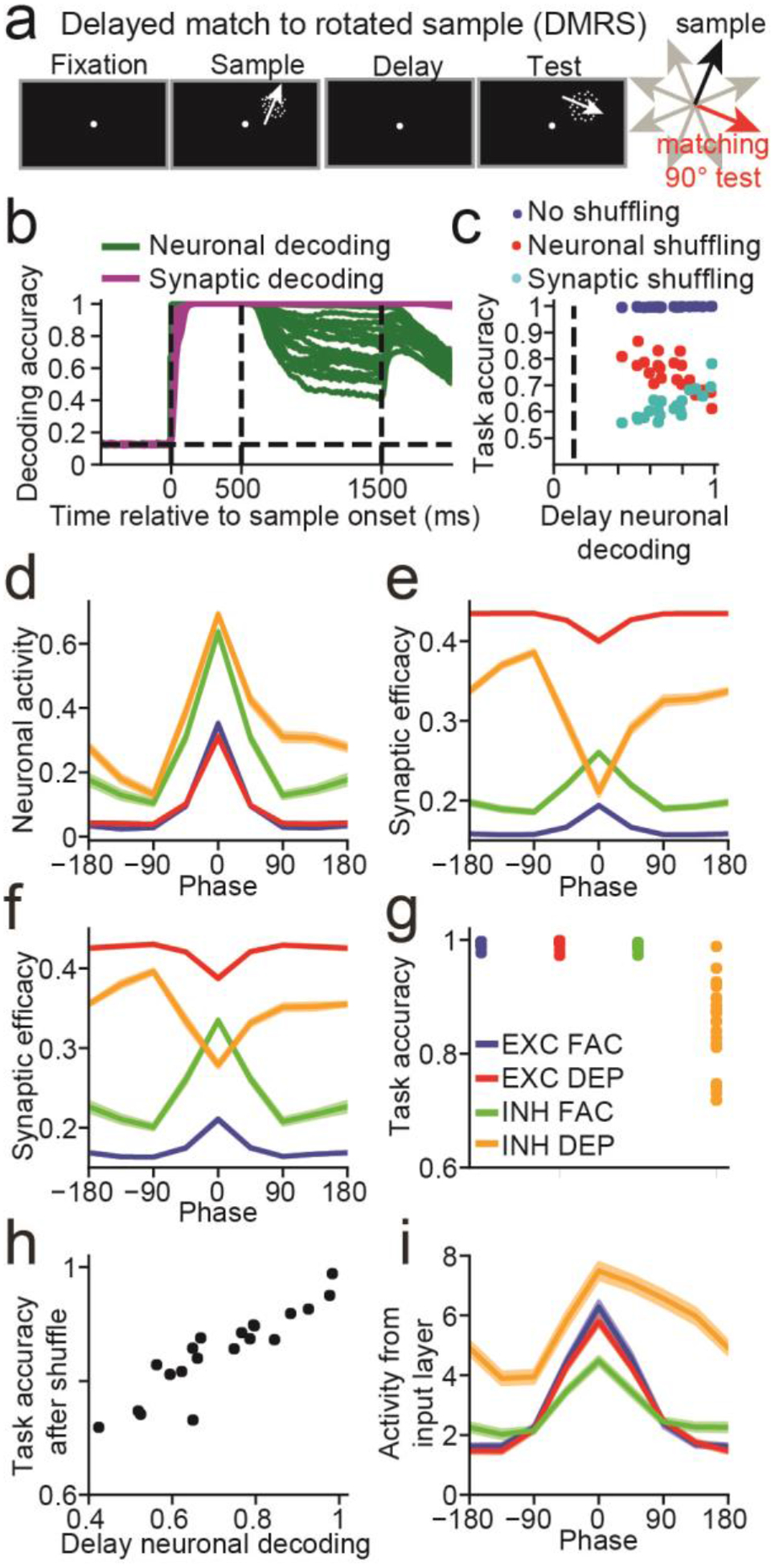
(a) The DMRS task is similar to the DMS task (Figure 2A), except that the target test motion direction was rotated 90° clockwise from the sample direction. (b) Similar to Figure 2b. (c) Similar to Figure 2c. (d) Neuronal sample tuning curves of the four neuronal groups (EXC FAC, blue; EXC DEP, red; INH FAC, green; INH DEP, orange). Neuronal activity was averaged across the entire sample period, and the tuning curves were centered around the sample direction that generated the maximum response (i.e. the preferred direction). The sample tuning curves in panels (e,f,i) are also centered around the same preferred directions. (e) Same as (d), except that synaptic efficacies were used to calculate the tuning curves. (f) Same as (d), except that synaptic efficacies calculated at the end of the delay period were used to calculate the tuning curves. (g) Task accuracy after shuffling synaptic efficacies at the end of the sample period for each of the four neuronal groups. Each dot represents the accuracy from one network. (h) Scatter plot showing the neuronal decoding accuracy measured at the end of the delay (x-axis) against the task accuracy after shuffling the synaptic efficacies of inhibitory neurons with depressing synapses at the end of the sample (y-axis). (i) Tuning curves showing the mean amount of input (input activity × input to recurrent connection weights) each group of neurons receives from the input layer for each direction. (d,e,f,i) Tuning curves are mean values across n = 20 networks. Shaded error bars (which are small and difficult to see) indicate one SEM.

We again found that networks with the strongest delay-period neuronal selectivity suffered the greatest performance loss when neuronal activity was shuffled (Pearson R = −0.72, P < 0.001, n = 20, Figure 3c), and suffered the least performance loss when synaptic efficacies were shuffled (R = 0.81, P < 10⁻⁴).

Although all 20 networks solved the task using persistent activity, we wondered if STSP could still manipulate sample information, and thus sought to understand the networks’ strategies to solve this task. We examined neuronal responses averaged across the sample for all 20 networks from 4 groups of neurons: excitatory with facilitating synapses (EXC FAC), excitatory with depressing synapses (EXC DEP), inhibitory with facilitating synapses (INH FAC), and inhibitory with depressing synapses (INH DEP) (Figure 3d). We found a striking asymmetry for INH DEP neurons: neuronal responses 90° clockwise from the preferred sample direction were significantly greater than responses 90° counterclockwise from the preferred sample direction (difference between 90° clockwise and counterclockwise, EXC FAC = 0.001, t(19) = 0.44, P = 0.67; EXC DEP = 0.002, t(19) = 1.02, P = 0.32; INH FAC = 0.024, t(19) = 2.05, P = 0.054; INH DEP = 0.18, t(19) = 10.90, P < 10⁻⁸, two-sided, paired t-tests).

While this asymmetry in the neuronal response disappeared by the end of the delay (EXC FAC = 0.004, t(19) = 0.71, P = 0.48; EXC DEP = 0.004, t(19) = 0.52, P = 0.61; INH FAC = 0.043, t(19) = 1.55, P = 0.14; INH DEP = −0.001, t(19) = −0.13, P = 0.90, two-sided, paired t-tests), it translated into asymmetric synaptic efficacies for INH DEP neurons, both during the sample (Figure 3e) and throughout the delay (Figure 3f) (EXC FAC (sample, delay) = −0.0001, 0.0008, t(19) = −0.46, 0.81, P = 0.65, 0.43; EXC DEP = −0.0005, −0.001, t(19) = −1.31, −0.94, P = 0.21, 0.36; INH FAC = 0.004, 0.007, t(19) = 2.12, 1.42, P = 0.047, 0.17; INH DEP = −0.060, −0.045, t(19) = −9.81, −9.70, P < 10⁻⁸, 10⁻⁸). Thus, synaptic efficacies for INH DEP neurons were greatest at the start of the test period on trials in which the sample was 90° counterclockwise from their preferred direction. If such a sample is followed by a target test stimulus (90° clockwise from the sample), the total synaptic current (neuronal response × synaptic efficacy) these neurons project to their targets will be at a maximum. In Figure S5, we further analyze how networks computed the match/non-match decision.

The results so far suggest that the asymmetric synaptic efficacies generated during the sample allowed the network generate correct match/non-match decisions. To confirm this, we shuffled synaptic efficacies for all four neuron groups at sample end, and found that the decrease in accuracy after shuffling efficacies for INH DEP neurons (mean accuracy = 0.85) was greater compared to the other three neuron groups (EXC FAC = 0.99, t(19) = −8.41, P < 10⁻⁷; EXC DEP = 0.99, t(19) = −8.74, P < 10⁻⁷; INH FAC = 0.99, t(19) = −8.36, P < 10⁻⁷, paired, two-sided, t-tests, Figure 3g). Furthermore, networks that maintained less information in neuronal activity during the delay were more adversely affected by shuffling synaptic efficacies (Pearson R = 0.91, P < 10⁻⁷, n = 20, Figure 3h).

We hypothesized that the asymmetric tuning of INH DEP neurons emerged via connection weights from the input layer. Thus, we examined tuning curves for the current (neuronal activity × connection weight) neurons receive from the input layer, and found that it was significantly asymmetric for inhibitory and excitatory neurons with depressing synapses (EXC FAC = 0.12, t(19) = 0.90, P = 0.38; EXC DEP = 0.29, t(19) = 4.15, P < 0.001; INH FAC = 0.28, t(19) = 2.06, P = 0.053; INH DEP = 2.62, t(19) = 14.51, P < 10⁻¹¹, two-sided t-tests, Figure 3i) Consistent with above, the asymmetry was greater for INH DEP neurons (P < 10⁻¹⁰ for all comparisons between INH DEP neurons and other neuron groups, two-sided t-tests).

As expected, we find that our results are the mirror image of those in Figure 3 when networks are trained using a 90° counterclockwise rule (Figure S6). We also repeated our analysis on a delayed match-to-category task¹⁶, and found that the networks performed the manipulation (i.e. stimulus categorization) by adjusting connection weights from the input layer (Figure S7). Given the penalty on neuronal activity, our results suggest that networks will manipulate sample stimuli (at least partly) by learning specific connection weights from the input layer if possible.

Manipulating information during the WM delay period

To better understand whether STSP can support silent manipulation, we need to examine tasks in which the network cannot perform the required manipulation through modification of input weights. This could be accomplished by forcing the manipulation to occur after sample offset. We trained networks to solve a delayed cue task (Figure 4a), in which a cue was presented between 500 and 750 ms into the delay, instructing the network whether to use the DMS or DMRS task rule.

Figure 4. Delayed cue task.

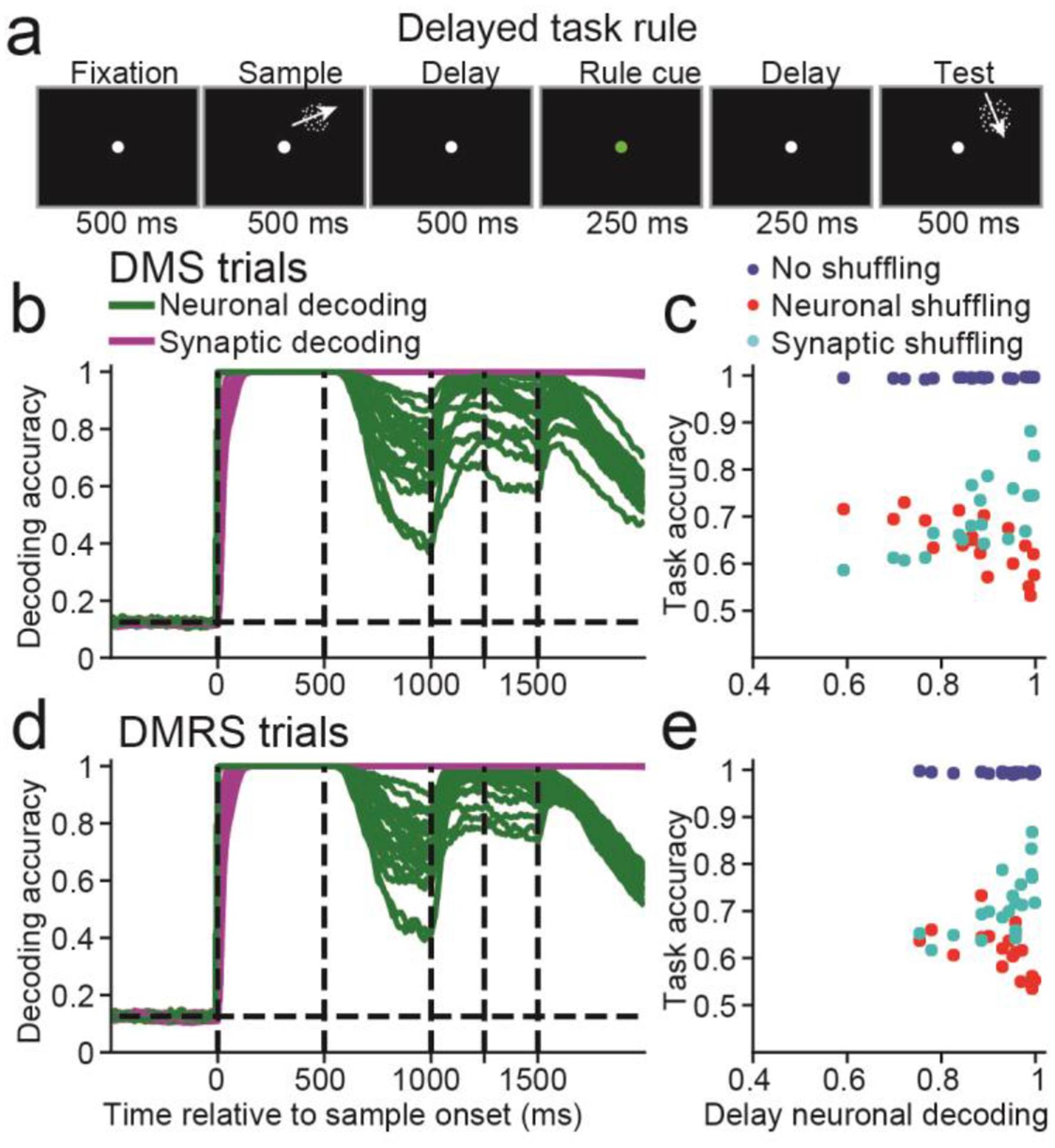
(a) This task was similar to the DMS and DMRS tasks, except that a rule cue from 500 to 750 ms into the delay indicated to the network whether to perform the DMS or the DMRS task. (b) Similar to Figure 2b, calculated using only DMS trials. The dashed vertical lines, from left to right, indicate the sample onset and offset, the rule cue onset and offset, and end of the delay period. (c) Similar to Figure 2c, calculated using only DMS trials. (d-e) Similar to (b-c), except for DMRS trials.

We found neuronal decoding accuracy was always greater than chance (P < 0.05, bootstrap) during the delay for either DMS (green curves, Figure 4b) or DMRS trials (Figure 4d). Thus, these networks manipulate information in WM (at least partly) using persistent activity. This was also true for different delay and rule cue onset/offset times (Figure S8).

Consistent with Figures 2&3, networks with the strongest delay-period neuronal selectivity suffered the greatest performance loss when neuronal activity was shuffled (DMS: Pearson R = −0.73, P< 0.001, n = 20, Figure 4c; DMRS: R = −0.60, P = 0.005, Figure 4e and suffered the least performance loss when synaptic efficacies were shuffled (DMS: R = 0.75, P < 0.001; DMRS: R = 0.64, P = 0.001). Furthermore, shuffling neuronal activity or synaptic efficacies decreased task accuracy (P < 0.05, bootstrap) in all networks for both tasks. Lastly, shuffling synaptic efficacies before rule-cue onset was more deleterious to task accuracy, whereas shuffling neuronal activity after rule-cue offset was more deleterious (Figure S8). Thus, networks required neuronal activity to manipulate information in WM.

Controlling the representation of information

Although STSP did not silently manipulate information during the tasks considered so far, we wondered if it could allow for subtler manipulations in a silent manner. For example, neural circuits in vivo are occasionally required to represent relevant information differently than irrelevant information³⁵. Thus, we trained networks on a task that required controlling how information is represented: the A-B-B-A task³⁶ (Figure 5a). Networks were shown a sample followed by three sequentially presented test stimuli, and had to indicate whether each test matched the sample. Importantly, if a test was a non-match, there was a 50% probability that the test would be repeated immediately. This forces the network to encode sample and test stimuli in different ways: if the sample and test were represented in similar manners, then the network could not distinguish between a test that matched the sample, compared to a repeated non-match.

Figure 5. A-B-B-A and A-B-C-A tasks.

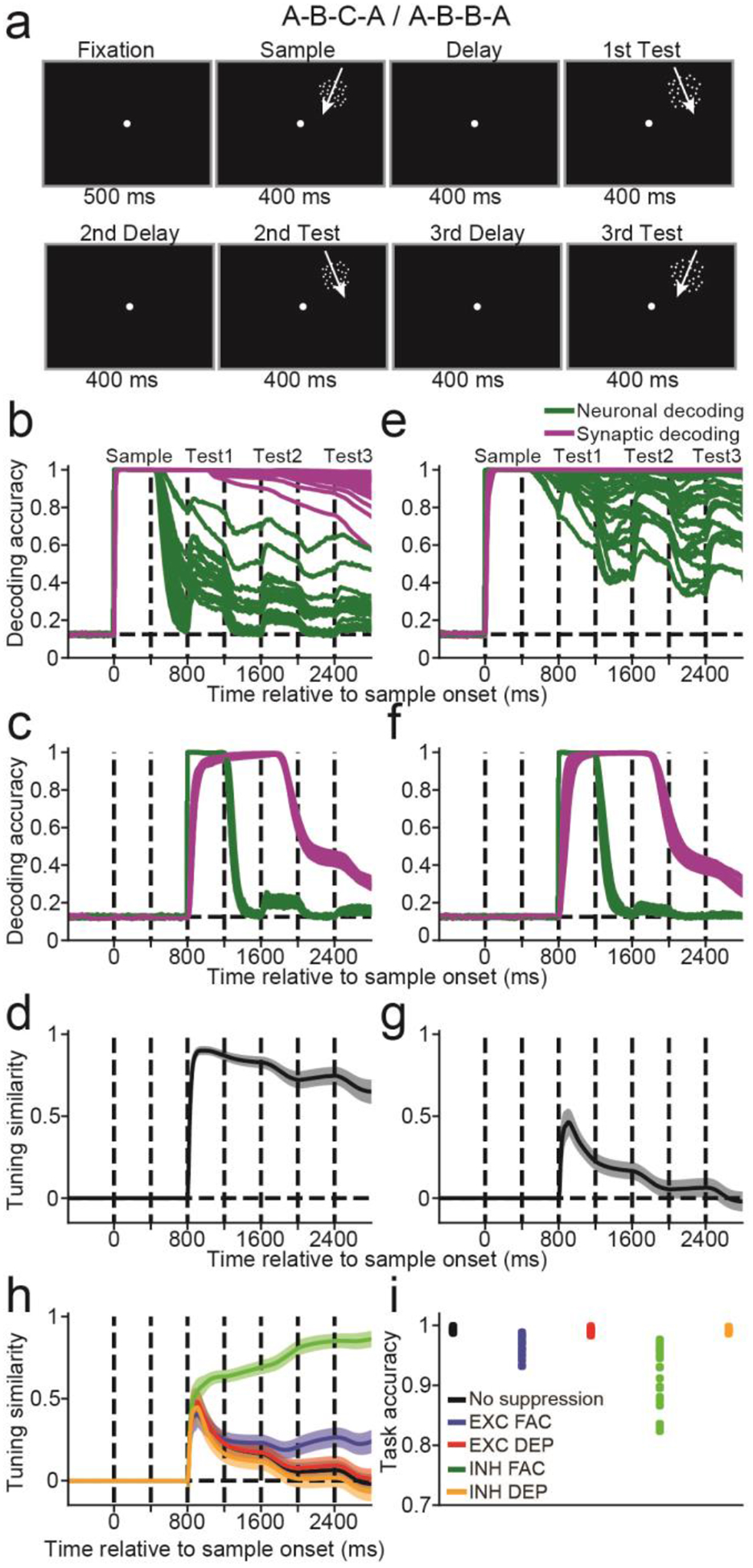
(a) The network was presented with a 400 ms sample stimulus, followed by three 400 ms test stimuli, all separated by 400 ms delays. (b) Similar to Figure 2b, and calculated for the A-B-B-C task. The dashed lines indicate, from left to right, the sample onset, the sample offset, and the test onset and offset for the three sequential test stimuli. (c) Similar to (b), except showing the decoding accuracy of the first test stimulus. (d) The time course of the tuning similarity index (TSI), mean value across n = 20 networks. (e-g) Similar to (b-d), except for the A-B-B-A task. (h) The TSI for the A-B-B-A task after suppressing neuronal activity for 200 ms before the first test onset, from four different neuronal groups (EXC FAC, blue curve EXC DEP, red curve; INH FAC, green curve; INH DEP, orange curve), and with no suppression (black curve). (i) Task accuracy after suppressing activity from the four groups described in (h), and with no suppression (black dots). (d,g,h) TSI curves are mean values across n = 20 networks. Shaded error bars indicate one SEM.

As a control, we also trained networks on an A-B-C-A version of the task, in which non-matching test stimuli were never repeated during a single trial, so that the network was not forced to represent sample and test stimuli in different formats. For the A-B-C-A task, few networks encoded sample information in neural activity throughout the entire trial, as decoding decreased to chance (P>0.05, bootstrap) for 1 of the 20 networks during the last 100 ms of the first delay, 7 of 20 networks during the second delay, and 8 of 20 networks for the third delay (green curves, Figure 5b). In contrast, sample decoding using synaptic efficacies (magenta curves) remained significantly above chance (P<0.05) throughout the entire trial for all networks (values ranging from ~0.6 to 1.0). Note that decoding accuracy appeared relatively lower for this task because of how we performed the calculation (see Modelling Note).

We next asked whether networks maintained test information in WM, which is only behaviorally relevant during test presentation. Neuronal decoding accuracy for the first test (green curves) was perfect (1.0) for all networks during test presentation, before dropping to chance (P>0.05) for all networks by the third delay (Figure 5C). Test decoding using synaptic efficacies (magenta curves) was near perfect (~1.0) for all networks during the later stage of the first test and into the second test presentation. Thus, networks encoded both the sample and first test stimuli during presentation of the second test. This could be problematic if the network had to distinguish between cases where the second test matched the sample vs the first test. However, this was not a problem for the A-B-C-A task, as non-matching test stimuli were never repeated. We confirmed that the networks were under no pressure to represent sample and test stimuli differently using a tuning similarity index (TSI)¹⁰ (Figure 5d, see Methods: Tuning similarity index). As expected, the TSI was >0.7 for the first and second test periods, indicating a similar representation of sample and test information by synaptic efficacies.

We repeated these analyses for the A-B-B-A task, in which subsequent non-matching test stimuli were repeated 50% of the time. In contrast to the A-B-C-A task, sample decoding (green curves, Figure 5e) using neuronal activity in the A-B-B-A task remained above chance (P<0.05, bootstrap) during all three delay periods for all networks. Furthermore, sample decoding using synaptic efficacies (magenta curves) remained close to 1.0 throughout the trial.

Consistent with the A-B-C-A task, decoding the first test using neuronal activity (green curves, Figure 5F) was perfect during test presentation before falling to chance (P>0.05) levels after test offset. In addition, decoding the first test stimulus using synaptic efficacies (magenta curves) was also near perfect for all networks during the later stages of the first test presentation, and into the second test.

We hypothesized that networks must encode the sample and test stimuli in different formats to accurately solve the task. In contrast to the A-B-C-A task (Figure 5d), in which the TSI was 0.78 ± 0.15 (standard deviation) during the second test, the TSI for the A-B-B-A task decreased to 0.11 ± 0.20 (t(38) = 11.72, P < 10⁻¹³, unpaired two-sided, t-test, Figure 5g). Thus, the sample and first test stimuli were encoded in synapses using different formats, potentially allowing networks to distinguish between cases in which subsequent test stimuli match the sample (match) vs earlier test stimuli (non-match).

We hypothesized that persistent activity helped encode the sample and first test stimuli in different formats. Thus, we suppressed neuronal activity from the four neuronal groups for the 200 ms period prior to the first test, and re-calculated the TSI (Figure 5h). Suppressing activity from INH FAC neurons increased the TSI, measured during the second test (0.74 ± 0.17, green curve, t(19) =10.28, P < 10⁻⁸, paired, two-sided, t-test). Furthermore, suppressing INH FAC activity (task accuracy = 0.91) decreased task accuracy more than suppressing any of the other three neuronal groups (task accuracy after suppressing EXC FAC neurons = 0.97, t(19) = −4.97, P < 10⁻⁴; after suppressing EXC DEP neurons = 0.99, t(19) = −6.65, P < 10⁻⁵; after suppressing INH DEP neurons = 0.99, t(19) = −6.58, P < 10⁻⁵, paired, two-sided, t-tests, Figure 5i). Thus, neuronal activity from these neurons likely facilitated the manipulation of information in WM, increasing task performance.

Attending to specific memoranda

Silently-maintained information may be reactivated either by focusing attention towards the memorandum¹⁹ or by probing the neural circuits involved²⁰. We examined how STSP supports maintenance of either attended or unattended information. We trained networks on a dualsample delayed matching task (Figure 6a) similar to Rose et al.¹⁹. Networks were trained to maintain two sample directions (presented simultaneously in two locations) in WM, followed by two successive cues and test stimuli. The cue indicated which of the samples was relevant for the upcoming test. In this setup, stimuli that were not cued as relevant for the first test stimulus could still be cued as relevant for the second test.

Figure 6. Dual delayed match-to-sample task.

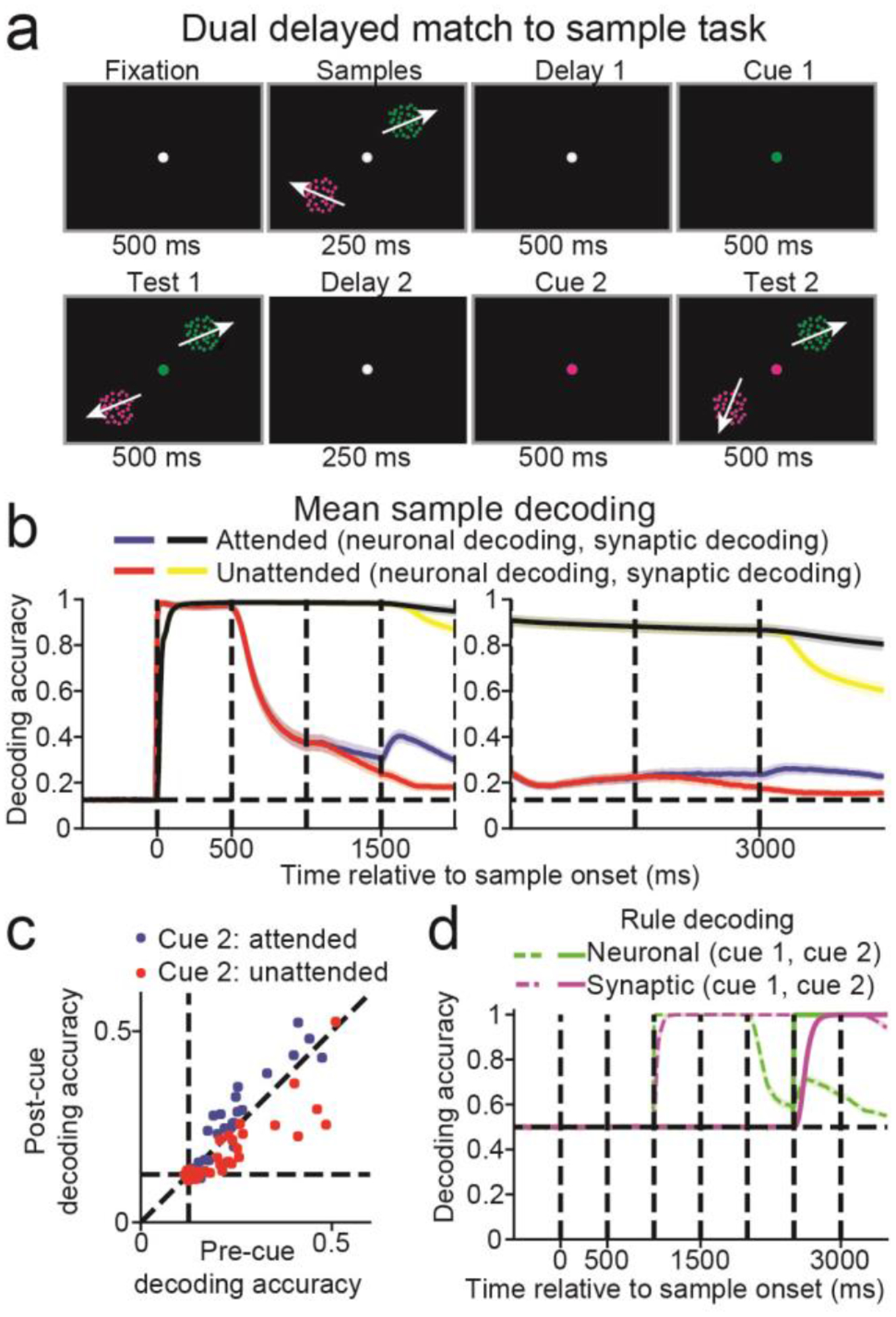
(a) Two sample stimuli were simultaneously presented for 500 ms. This was followed by a 1000 ms delay in which a cue appeared halfway through, and then two simultaneous test stimuli for 500 ms. The cue indicated which of the two sample/test pairs were task-relevant. Another 1000 ms delay and 500 ms test period was then repeated, in which a second cue again indicated which of the two sample/test pairs was task-relevant. (b) Neuronal decoding accuracy for the attended (blue curve) and unattended (red) stimuli, and the synaptic decoding accuracy for the attended (black) and unattended (yellow) stimuli, are shown from trial start through the first test period (left panel), and the second delay and test periods (right panel). Decoding accuracy curves are mean values across n = 20 networks. Shaded error bars indicate one SEM. (c) Scatter plot showing the neuronal decoding accuracy, measured from 100 to 0 ms before the second cue (x-axis) against neuronal decoding accuracy, measured from 400 to 500 ms after second cue (y-axis). Blue dots represent stimuli that were unattended after the first cue, and attended after the second cue, and red dots represent stimuli that were not attended to after the first and second cues. (d) The neuronal (green) and synaptic (magenta) rule decoding accuracy. The dashed lines indicate the decoding accuracy of the first cue, and the solid lines indicate the decoding accuracy of the second cue.

Sample decoding using neuronal activity was greater when the sample was attended (blue curve) than unattended (red curve), during the last 100 ms of the first and second delays (first delay: Figure 6b, left panel, attended = 0.314 ± 0.174 (SD), unattended = 0.261 ± 0.134, t(39) = 4.46, P < 10⁻⁴; second delay: right panel, attended = 0.237 ± 0.131, unattended = 0.185 ± 0.085, t(39) = 5.19, P < 10⁻⁵, paired, two-sided, t-tests). Sample decoding using synaptic efficacies was near perfect (~1.0) for both attended (black curves) and unattended (yellow curves) conditions. Thus, the attended memoranda were more strongly represented in neural activity than unattended memoranda.

The study by Rose et al. found that silently maintained unattended information could be reinstated into neuronal activity after it was attended¹⁹ (although see³⁷). Similarly, we found that neuronal decoding for stimuli that were unattended after the first cue were near chance (P > 0.05, bootstrap, measured in the 100 ms before second cue onset) in 19 out of 40 cases (20 networks × 2 stimuli). However, decoding accuracy increased if the stimulus became the focus of attention (blue circles, Figure 6c, decoding pre-cue = 0.212, post-cue = 0.233, t(39) = 3.11, P = 0.003, paired, two-sided, t-tests), whereas decoding accuracy decreased if the stimulus remained unattended (red circles, decoding post-cue = 0.175, t(39) = −4.16, P < 0.001).

Although neuronal sample decoding was near chance for many networks, the rule cue indicating the relevant stimulus was maintained in neuronal activity across all networks (P <0.05, bootstrap, decoding accuracy for rule cues 1 and 2 are indicated by the dashed green, and solid green curves, respectively, Figure 6d). Thus, while sample information can be silently maintained, allocating attention to either memoranda requires neuronal activity.

Manipulating information and persistent neuronal activity

In this study, persistent activity during the delay was observed in all tasks involving manipulating information. We wondered if the level of manipulation required by the task was correlated with the level of persistent activity. This could be of special interest as varying levels of persistent activity have been observed between different tasks^10–16.

We measured task manipulations based on the similarity between the neuronal response during the early sample period and the synaptic efficacies during the late delay period (see Methods: Task manipulation). To boost statistical power, we included three additional tasks: two were delayed match-to-rotated sample tasks in which the target test direction was 45° (DMRS45) or 180° (DMRS180) clockwise from the sample. The third task was a cross-location DMS task, in which the sample was presented in one location and the test was randomly presented in one of two different locations³⁸. Analysis of this task is shown in Figure S9.

We found that the level of manipulation correlated with the level of persistent activity at the end of the delay (Spearman correlation R = 0.93, P < 0.001, n = 9, Figure 7a). This suggests that tasks requiring greater manipulation require greater persistent activity. However, since the penalty on high neuronal activity could impact how information was encoded, we retrained 20 networks for all tasks with no penalty term, and found the correlation remained (R = 0.92, P < 0.001, Figure 7b). We next wondered whether different task contingencies (e.g. the presence of rule cues, stimulus timing, etc.) affected the correlation. Thus, we ran simulations of all our trained networks performing a standard DMS task, with a 500 ms sample stimulus and 1000 ms delay. The correlation between persistent activity and manipulation remained for networks trained with the penalty on neuronal activity (R = 0.88, P = 0.002, Figure 7c) and for networks trained without (R = 0.82, P = 0.007, Figure 7d). In Modelling Notes and Figures S10–13, we discuss the results when networks are trained using different configurations of STSP. In summary, these results suggest that network models exhibit more persistent neuronal activity when trained on tasks that require more manipulation.

Figure 7. The relationship between manipulation and stimulus-selective persistent activity.

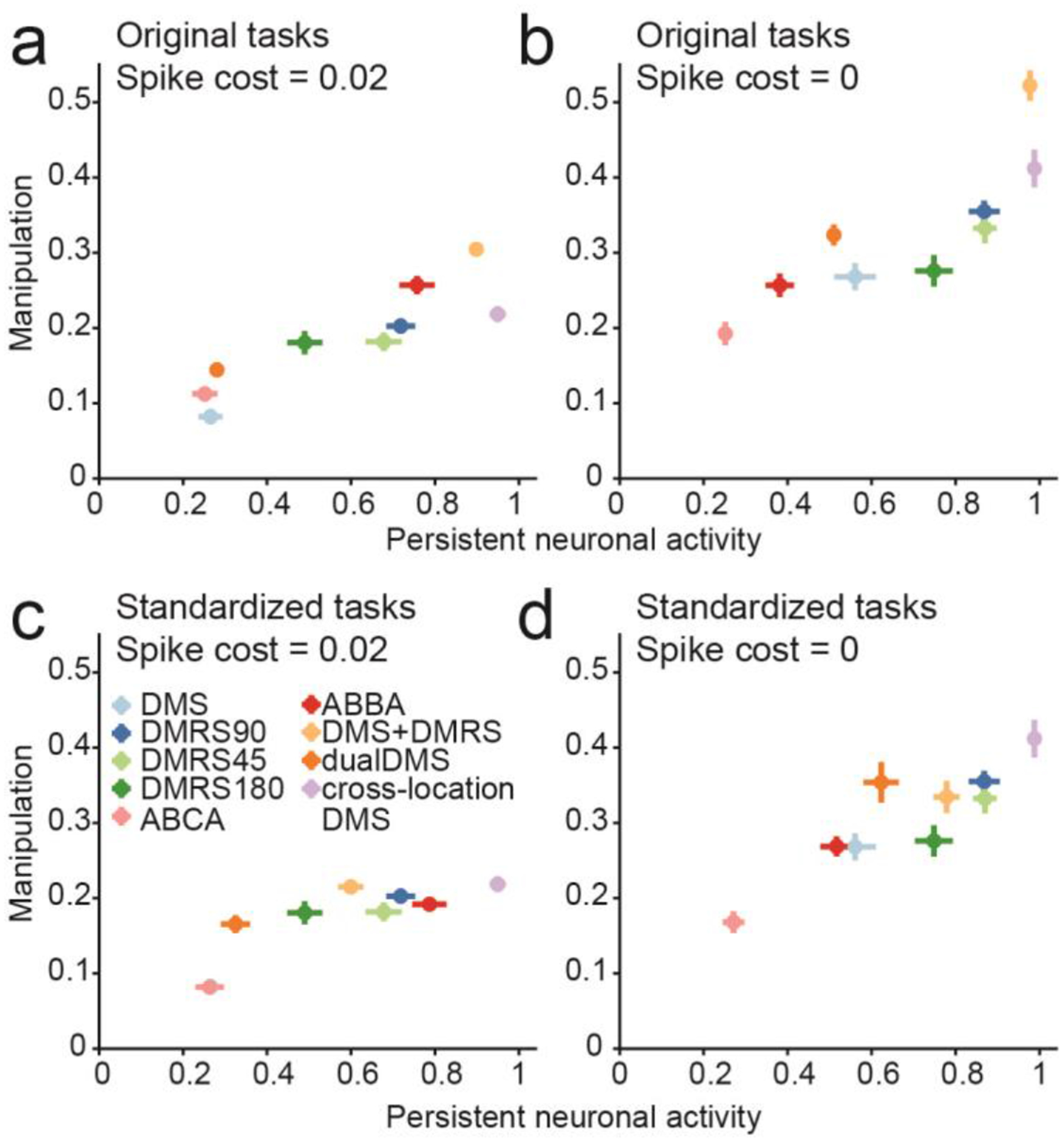
(a) Scatter plot shows the level of persistent neuronal activity, measured as the neuronal decoding accuracy during the last 100 ms of the delay (x-axis), versus the level of manipulation (y-axis). (b) Same as (a), except that networks were trained without the penalty on high neuronal activity. (c) Same as (a), except that persistent activity and task manipulation were measured by presenting all networks with a standard 500 ms motion stimulus followed by a 1000 ms delay. (d) Same as (c), except for networks trained without the penalty on high neuronal activity. (a-d) Center of each dot represents the mean value across n = 20 networks trained on one specific task. Error bars represent one SEM.

Discussion

We examined whether STSP can support the activity-silent manipulation of information, and whether it could help explain previous observations that different tasks evoke different levels of persistent activity. We found that while STSP can silently support the short-term maintenance of information, it cannot support manipulation of information without persistent neuronal activity. Furthermore, we found that tasks that required more manipulation also required more persistent activity, giving insight into why the strength of persistent neuronal activity varies markedly between different tasks.

Variation in persistent neuronal activity in vivo

Over the last several decades, electrophysiology experiments^2–6, and human imaging studies³⁹, have supported the idea that information in WM is maintained in stimulus-selective persistent neuronal activity during memory-delay periods of behavioral tasks. However, this viewpoint has evolved, as various studies now suggest that persistent neuronal activity might not always reflect information maintenance, but can reflect control processes required to manipulate remembered information into appropriate behavioral responses¹⁴.

It is often unclear whether persistent neural activity reflects the maintenance or the manipulation of the stimulus. For example, neural activity in the frontal and parietal cortices mnemonically encodes stimulus location in a memory delayed saccade task^2,4. However, recent studies that have dissociated the stimulus location from the upcoming saccade location have shown that activity in frontal cortex initially encodes the location of the recent stimulus (retrospective code), before its representation shifts towards encoding the planned saccade target (prospective code) later in the delay⁴⁰.

A recent study showed robust persistent activity in the medial superior temporal (MST) area during a motion DMS task³⁸. This initially appears at odds with the results of our current study, and our past work showing little or no persistent activity in the lateral intraparietal area (LIP), an area considered to be downstream of MST, also during a motion DMS task^10,16. However, in this study³⁸, the sample and test stimuli were shown at different retinotopic locations. This forces MST to represent the sample and test stimuli using two different pools of neurons, eliminating the possibility that synaptic efficacy changes through STSP driven by the sample could be directly compared to the test stimulus activity. This also forces the monkey to translate information from the sample location to the location of the test stimulus. Moreover, while we only observed weak delay-period direction encoding in area LIP during the DMS task^10,16, we found that after the monkeys underwent extensive categorization training using the same stimuli, delay-period categorical encoding become highly robust¹⁶. Similarly, we also observed robust persistent neuronal activity in networks models trained on a similar task to the one found in Mendoza Halliday et al. (Figure S9).

In another example, prefrontal cortex (PFC) was shown to mnemonically encode color in a change-detection task when six distinguishable, colors are used⁴¹, but color-selective persistent activity was not evident in PFC when the subject had to detect a change amongst a continuum of 20 colors¹². This suggests that PFC can encode a categorical representation of the stimulus, but not a precise representation of stimulus features.

These studies suggest that tasks that require greater manipulation of the memoranda evoke greater levels of persistent neuronal activity, consistent with the correlation we observe between the level of manipulation and the level of persistent neuronal activity in our network models (Figure 7). These studies are also consistent with a recent human MEG study which also suggests that manipulating information in WM requires the reinstatement of persistent activity⁴².

However, other factors surely play a role in determining the level of persistent activity. For example, task-related factors such as the whether the delay period duration was fixed or random, or whether the network was trained on previous tasks, can affect the nature of persistent activity⁴³. Furthermore, circuit-level properties, such as the connection strength within local circuits^43,44, or the whether nearby neurons are similarly tuned (i.e. functional clustering)¹⁰, can also affect persistent activity.

Going forward, there are several other mechanisms in the brain that potentially support WM, such as oscillatory activity^45,46, or loops between cortical and sub-cortical structures⁴⁷. Future studies will focus on developing RNNs with even greater biological realism, such as networks with spiking neuron models, that can better explore how diverse mechanisms work together in support of maintaining and manipulating information in WM.

Comparison to other artificial neural network architectures

To solve tasks that involve very long temporal delays, long short-term memory (LSTM)⁴⁸ based architectures are typically used. These architectures work by giving networks control over how to maintain and update information. We noticed that RNNs without STSP either failed to solve the task, or required longer training, even with no penalty on neuronal activity (Figure S14). This difficulty was partly because neurons in our networks never connected onto themselves, which can facilitate the information maintenance. STSP facilitated training on our set of WM based tasks with its relatively long time constants. Thus, adding network substrates with long time constants, without necessarily making these time constants flexible, can potentially facilitate learning on tasks with long-term time dependencies. More generally, it highlights how incorporating neurobiologically-inspired features into RNNs is a promising strategy for advancing their capabilities.

Understanding strategies employed by artificial neural networks

A key differentiating feature of RNNs compared to biological networks is that all connection weights and activity is known, facilitating attempts to understand how the network solves various tasks. This has allowed researchers to describe how delayed association in RNNs can be performed by transient dynamics²⁵, how simple dynamical systems consisting of line attractors and a selection vector can underlie flexible decision-making²³, how RNNs can encode temporally-invariant signals^26,27, and how clustering develops when RNNs learn 20 cognitive tasks, in which groups of neurons become functionally specialized for different cognitive processes⁴⁹. Whereas our analyses focused on understanding how RNNs solve single tasks, it will be of interest to examine whether the network strategies persist when the same RNNs are trained on multiple tasks.

In this study, we have taken advantage of this full network knowledge to determine the substrates in which information is maintained in WM (Figures 2–7), how synaptic efficacies can prospectively encode stimuli (Figures 3), how neuronal activity can control how information is represented (Figure 5), and how match/non-match decisions are formed (Figures S2&S5). To provide greater insight into how networks solved each of the tasks, we also show a range of network properties for each task (Figures S15 – S24). Each figure shows an example network that solved one specific task, and provides details of the population activity, the sample, test and match selectivity of all four neuron groups, and the sample encoding stability across time for the entire population and each neuronal subgroup. We observed that information maintained in WM is mostly stable across time (panels i and j). This mostly stable mnemonic encoding might be the result of our network architecture or hyperparameters, and future studies will be required to understand which network factors affect encoding stability.

While modelling studies cannot replace experimental work, they can be advantageous when obtaining the necessary experimental data is not feasible. Thus, modelling can serve as a complement to experimental work, allowing researchers to rapidly generate novel hypothesis regarding neural function that can later be tested when technology better allows for experimental verification. Lastly, the discovery of novel mechanisms found in silico can be fed back into the design of network models, potentially accelerating the development of machine learning algorithms and architectures. We believe that this synergy between experimental neuroscience and neural network modelling will only strengthen in the future.

Methods

Network models

Neural networks were trained and simulated using the Python machine learning framework TensorFlow⁵⁰. Parameters used to define the network architecture and training are given in Table 1. In all tasks, the stimuli were represented as coherent motion patterns moving in one of eight possible directions. However, the results of this study are not meant to be specific to motion, or even visual, inputs, and the use of motion patterns as stimuli was simply used to make our example tasks more concrete.

Table 1.

Hyperparameters used for network architecture and training.

Hyperparameter	Symbol	Value
Learning rate	n/a	0.02
Neuron time constant	τ	100 ms
Time step (training and testing)	Δt	10 ms
Standard deviation of input noise	σin	0.1
Standard deviation of recurrent noise	σrec	0.5
L2 penalty term on firing rates	β	0.02
STSP neurotransmitter time constant	τx	200 ms / 1500 ms (facilitating / depressing)
STSP neurotransmitter utilization	τu	1500 ms / 200 ms (facilitating / depressing)
STSP neurotransmitter increment	U	0.15 / 0.45 (facilitating / depressing)
Number of neurons (input layer, recurrent layer, output layer)	Nin, Nrec, Nout	24, 100, 3
Gradient batch size	Ntrials	1024
Number of batches used to train network	n/a	2000

All networks consisted of motion-direction selective input neurons (whose firing rates are represented as u(t)) that projected onto 100 recurrently connected neurons (whose firing rates are represented as r(t)), which in turn projected onto 3 output neurons (whose firing rates are represented as z(t)) (Figure 2A). Recurrently connected neurons never sent projections back onto themselves.

The activity of the recurrent neurons was modelled to follow the dynamical system^30,49:

$$\tau \frac{dr}{dt}=-r+f\left(W^{\mathit{\text{rec}}}r+W^{in}u+b^{\mathit{\text{rec}}}+\sqrt{2\tau }{\sigma }_{\mathit{\text{rec}}}\zeta \right)$$

where τ is the neuron’s time constant, f(·) is the activation function, W^rec and Wⁱⁿ are the synaptic weights between recurrent neurons, and between input and recurrent neurons, respectively, b^rec is a bias term, ζ is independent Gaussian white noise with zero mean and unit variance applied to all recurrent neurons, and σ_rec is the strength of the noise. To ensure that neuron’s firing rates were non-negative and non-saturating, we chose the rectified linear function as our activation function:f(x) = max(0, x).

The recurrent neurons project linearly to the output neurons. The activity of the output neurons, z, was normalized by a softmax function such that their total activity at any given time point was one:

$$z=g\left(W^{\mathit{\text{out}}}r+b^{\mathit{\text{out}}}\right)$$

where W^out are the synaptic weights between the recurrent and output neurons, and g is the softmax function:

$$g\left(x_i\right)=\frac{\text{exp}\left(x_i\right)}{{\sum }_j\text{exp}\left(x_j\right)}$$

To simulate the network, we used a first-order Euler approximation with time step Δt:

$$r_t=(1-\alpha )r_{t-1}+\alpha f\left(W^{\mathit{\text{rec}}}{r}_{t-1}+W^{in}{u}_t+b^{\mathit{\text{rec}}}+\sqrt{\frac{2}{\alpha }}{\sigma }_{\mathit{\text{rec}}}N(0,1)\right)$$

where $\alpha =\frac{\Delta t}{\tau }$ and N(0,1) indicates the standard normal distribution.

To maintain separate populations of 80 excitatory and 20 inhibitory neurons, we decomposed the recurrent weight matrix, W^rec as the product between a matrix for which all entries are nonnegative, W^rec,+ whose values were trained, and a fixed diagonal matrix, D, composed of 1s and −1s, corresponding to excitatory and inhibitory neurons, respectively³⁰:

$$\begin{gathered} W^{\mathit{\text{rec}}}=W^{\mathit{\text{rec}},+}D \\ D=\left[\begin{array}{ccc}1& & \\ & \ddots & \\ & & -1\end{array}\right] \end{gathered}$$

Initial connection weights from the input layer, projecting to the output layer, and between excitatory neurons were randomly sampled from a Gamma distribution with shape parameter of 0.1 and scale parameter of 1.0. Initial connections weights projecting to or from inhibitory neurons were sampled from a Gamma distribution with shape parameter of 0.2 and scale parameter of 1.0. We note that training networks to accurately solve the tasks appeared somewhat faster when initializing connection weights from a gamma distribution compared to a uniform distribution (data not shown). Initial bias values were set to 0.

Networks consisted of 24 motion direction tuned input neurons per receptive field. All tasks had one receptive field except for the dual DMS task (2 receptive fields) and the cross-location DMS task (3 receptive fields). For the rule switching tasks (i.e. delayed rule and dual DMS tasks), an additional 6 rule tuned neurons were included. The tuning of the motion direction selective neurons followed a Von Mises’ distribution, such that the activity of the input neuron i at time t was

$$u_t^i=\mathit{\text{Aexp}}\left(\kappa \text{ cos}\left(\theta -{\theta }_{\mathit{\text{pref}}}^i\right)\right)+\sqrt{\frac{2}{\alpha }}{\sigma }_{in}N(0,1)$$

where θ is the direction of the stimulus, ${\theta }_{\mathit{\text{pref}}}^i$ is the preferred direction of input neuron i, k was set to 2, and A was set to $\frac{4}{\text{exp}(\kappa )}$ when a stimulus was present (i.e. during the sample and test periods), and was set to zero when no stimulus was present (i.e. during the fixation and delay periods

The 6 rule tuned neurons for the delayed rule and dual DMS tasks had binary tuning, in which their activity was set to 4 (plus the Gaussian noise term) for their preferred rule cue, and 0 (plus the Gaussian noise term) for all other times. The number of rule tuned neurons was arbitrarily chosen, and had little impact on network training.

Network training

RNNs were trained based on techniques previously described^30,49. Specifically, the goal of training was to minimize 1) the cross-entropy between the output activity and the target output, and 2) the mean L2-norm of the recurrent neurons’ activity level. The target output was a length 3 one-hot vector, in which the first element was equal to one for all times except the test period, the second element was one when the test stimulus matched the sample, and the third element was one when the test stimulus did not match the sample. Specifically, the loss function at time t during trial i is

$${\mathcal{L}}_{i,t}=-\sum _{n=1}^{N_{\mathit{\text{out}}}}{m}^i(t)z_n^{\mathit{\text{target}},i}(t)\text{ log }{z}_n^i(t)+\frac{\beta }{N_{\mathit{\text{rec}}}}\sum _{n=1}^{N_{\mathit{\text{rec}}}}{r}_n^2(t)$$

Where β controls how much to penalize neuronal activity of the recurrent neurons, and mⁱ(t) is a mask function. In Figure S3b, we penalized connection weights instead of neuronal activity. The penalty term in this case involved squaring all connections weights between the 100 recurrently connected neurons, taking the mean, and multiplying by β = 2.

To give the network adequate time to form a match or non-match decision, networks had a 50 ms grace period starting at test onset, in which we set the mask function to zero. The mask value was set to 1.0 during the fixation, sample and delay periods, and to 2.0 during the test period(s), in order to encourage networks to learn the correct match/non-match decision. The total loss function is then

$$\mathcal{L}=\frac{1}{N_{\mathit{\text{trials}}}{N}_{\mathit{\text{time}}}}\sum _i^{N_{\mathit{\text{trials}}}}\sum _t^{N_{\mathit{\text{time}}}}{\mathcal{L}}_{i,t}$$

During training, we adjusted all parameters, (Wⁱⁿ, W^rec,+, W^out, W^rec, W^out, h^init), where h^init refers to the initial neuronal activity at time step 0, using the Adam⁵¹ version of stochastic gradient descent. The decay rate of the 1st and 2nd moments were set to their default values (0.9 and 0.999, respectively).

We measured task accuracy as the percentage of time points during the test period(s) (excluding the 50 ms grace period described above) in which the activity of the match output neuron was greater than the activity of the other two output neurons during match trials, and in which the activity of the non-match output neuron was greater than the activity of the other two output neurons during non-match trials. Before test onset, all networks correctly maintained fixation with an accuracy ~100%, and thus was not used in our measure of task accuracy. Task accuracy for all networks in this study was >90%.

Short-term synaptic plasticity

The synaptic efficacy between all recurrently connected neurons was dynamically modulated through short-term synaptic plasticity (STSP). For half of the recurrent neurons (40 excitatory and 10 inhibitory), all projecting synapses were facilitating, and for the other half of recurrent neurons, all projecting synapses were depressing. Following the conventions of Mongillo et al.¹⁸, we modelled STSP as the interaction between two values: x, representing the fraction of available neurotransmitter, and u, representing the neurotransmitter utilization. Presynaptic activity acts to increase the calcium concentration inside the presynaptic terminal, increasing the utilization and the synaptic efficacy. However, presynaptic activity decreases the fraction of neurotransmitter available, leading to decreasing efficacy. These two values evolve according to:

$$\begin{gathered} \frac{dx(t)}{dt}=\frac{1-x(t)}{{\tau }_x}-u(t)x(t)r(t)\Delta t, \\ \frac{du(t)}{dt}=\frac{U-u(t)}{{\tau }_u}+U(1-u(t))r(t)\Delta t \end{gathered}$$

where r(t) is the presynaptic activity at time t, τ_x is the neurotransmitter recovery time constant, τ_u is the calcium concentration time constant, and Δt is the time step (0.01 seconds for our networks). The amount of input the postsynaptic neuron receives through this one synapses at time t is then

$$I(t)=Wx(t)u(t)r(t)$$

where W is the synaptic efficacy before STSP is applied. For depressing synapses, the neurotransmitter recovery time constant was much longer compared to the calcium concentration time constant, whereas the opposite was true for facilitating synapses.

For computational efficiency, these values will be identical for all synapses sharing the same presynaptic neuron. Connections weights from the input layer, and onto the output layer, were not governed by STSP.

Population decoding

Similar to our previous studies^10,16, we quantified the strength of stimulus encoding by measuring how accurately we could decode the motion direction using linear multiclass support vector machines (SVMs). We chose to measure stimulus encoding through linear classifiers since the output neurons of our network are essentially performing linear classification of the population activity in the recurrent layer. In this approach, we trained linear, multiclass SVMs to classify the motion direction using the neuronal activity of the 100 recurrent neurons, or the synaptic efficacies from the same 100 recurrent neurons, at each time point (separated by 10 ms). Training and test data for the classifiers always came from the same time points. The synaptic efficacy values were the product x(t)u(t), where x(t) and u(t) are the time varying values representing the amount of neurotransmitter available, and the neurotransmitter utilization, respectively, as described above.

We measured the classification accuracy using cross-validation, in which we randomly selected 75% of trials for training the decoder and the remaining 25% for testing the decoder. For each of the eight motion directions, we randomly sampled, with replacement, 25 trials to train the decoder (from the 75% of trials set aside for training), and 25 trials to test the decoder (from the 25% of trials set aside for testing). From the 200 trials in the test set (25 time 8 directions), the accuracy was the fraction of trials in which the predicted motion direction matched the actual motion direction.

We used a bootstrap approach to determine statistical significance. We did so by repeated this sampling procedure 100 times to create a decoder accuracy distribution for each time point. The difference was deemed significantly greater than chance if 98 values were greater than chance (equivalent to P < 0.05 for a two-sided test).

For each network, we calculated decoding accuracies using a batch of 1024 trials in which the test motion directions were randomly sampled independently of the sample motion direction. This was in contrast to how we trained the network and measured task accuracy, in which there was always a 50% chance that a test stimulus would match the sample. We note that the pattern of neural and synaptic activity generated by a sample stimulus will be similar to the pattern generated by a matching test stimulus. Thus, if matching test stimuli occur more frequently than chance, our sample decoding accuracy during and after the test stimuli would be artificially elevated.

Shuffle analysis

To measure how network models used information maintained in neuronal activity and in dynamic synaptic efficacies to solve the task, we used a shuffling procedure as follows. At the time point right before test onset (or right before the third test onset for the A-B-C-A/A-B-B-A tasks), we either 1) did not shuffle any activity, 2) shuffled the neuronal activity between trials, or 3) shuffled the synaptic efficacies between trials. We shuffled between trials as opposed to between neurons because neurons can have different baseline activity levels, and shuffling this activity can significantly perturb the network and degrade performance, even if no information is maintained in their activity. We then simulated the network activity for the remainder of the trial using the saved input activity, and measured the performance accuracy by comparing the activity of the three output neurons to the target output activity during the test period. We performed this random shuffling 100 times, and measured the mean performance accuracy for all three conditions. The rationale behind this analysis is that if the network was exclusively using information maintained in neuronal activity to solve the task, then shuffling neuronal activity between trials should devastate performance, while shuffling synaptic efficacies should have little effect. Similarly, if the network was exclusively using information maintained in synaptic efficacies to solve the task, then shuffling synaptic efficacies between trials should devastate performance, while shuffling neuronal activity should have little effect. If the network was using information maintained in both neuronal activity and synaptic efficacies, then shuffling either should lead to significant decreases in performance.

We determined if shuffling either substrate significantly decreased task accuracy for a single network using a permutation test. Specifically, if the task accuracy without shuffling was greater than 98 of the 100 shuffled values, the decrease was deemed significant (equivalent to P < 0.05 for a two-sided test).

We note that note that a priori, there should be no qualitative difference between shuffling neuronal activity and synaptic efficacies. Both substrates are capable of maintaining information, as they both operate as leaky integrators (although the time constant of neuronal activity, 100 ms, is much smaller than the effective time constant of synaptic efficacy, which is 1500 ms). Thus, shuffling either substrate can potentially affect network performance if information needed to solved the task was maintained within that substrate.

Tuning similarity index

We measured the similarity between sample and test stimuli encoding in the A-B-C-A and A-B-B-A tasks (Figure 5), between neuronal and synaptic sample encoding (Figures 7, S11 – S13), and between neuronal sample encoding at different time points (Figures S15 – S24), using a tuning similarity index (TSI) we previously employed to study the relation between functional clustering and mnemonic encoding¹⁰. To calculate this index, we first modelled the neuronal activity or synaptic efficacy for each neuron, z_i(t), as a linear function of the sample or test motion direction, represented by the unit vector d:

$$z_i(t)=d{H}_i(t)+{ϵ}_i(t)$$

where ϵ_i(t) is a Gaussian noise term and the vector H_i(t) relates the stimulus direction to the neuronal activity or synaptic efficacy at time t.

The angle of H_i(t) is the preferred direction of the neuron at time t, and its magnitude indicates the change in neuronal activity or synaptic efficacy from baseline when the stimulus matches the preferred direction of the synapse. Thus, the preferred direction of a neuron, represented as a unit vector, is

$$P{D}_i\left(t\right)=\frac{H_i\left(t\right)}{\Vert H_i\left(t\right)\Vert }$$

We can calculate how well this linear model fit the data for each neuron i and time point t, indicated by w_i(t), by comparing the variance in the residuals with the variance in the synaptic efficacy:

$$w_i(t)=1-\frac{var\left({\widehat{z}}_i(t)-z_i(t)\right)}{var\left(z_i(t)\right)}$$

where the fitted neuronal activity or synaptic efficacy is determined by the linear model:

$${\widehat{z}}_i(t)=\mathit{\text{baseline}}+d{H}_i(t)$$

For the analysis in Figure 5, we calculated the preferred directions and linear model fits for both the sample and the first test motion direction, and then calculated the tuning similarity of each individual neuron as the dot-product between their preferred sample and test motion directions of each neuron, weighted by the geometric mean of their normalized linear model fits:

$$s_i(t)=\sqrt{w_{i,\mathit{\text{sample}}}(t)w_{i,\mathit{\text{test}}}(t)}P{D}_{i,\mathit{\text{sample}}}(t)P{D}_{i,\mathit{\text{test}}}^T(t)$$

Finally, we calculated the tuning similarity index as the sum of the similarity scores for all neurons, divided by the sum of the geometric means of their respective linear model fits:

$$\mathit{\text{TSI}}(t)=\frac{{\sum }_i{s}_i(t)}{{\sum }_i\sqrt{w_{i,\mathit{\text{sample}}}(t)w_{i,\mathit{\text{test}}}(t)}}$$

A value of +1 indicates that neuronal activities or synaptic efficacies are identically tuned to sample and test stimuli, and 0 indicates no correlation between the two.

Task manipulation

We were interested if the level of manipulation required by a task was correlated with the level of persistent activity. In order to measure the level of manipulation required by a task, we reasoned that when tasks do not require manipulation, the network should encode the sample stimulus in fundamentally the same manner during all trial epochs (e.g. early sample vs late delay). In other words, the neural code used to represent the sample stimulus should remain constant across time. One caveat is that for most networks, the sample stimulus was not fully encoded in neuronal activity at the end of the delay (shown by neuronal decoding neuronal accuracies significantly less than 1.0 at the end of the delay in Figures 2–6). However, the sample stimulus was fully encoded in the synaptic efficacies (shown by the synaptic decoding accuracies approximately equal to 1.0 at the end of the delay in Figures 2–6)

Thus, if no manipulation occurs, then the neuronal tuning curve measured during the early sample should look similar to the synaptic tuning curve measured late in the delay (assuming the synapse was facilitating, the synaptic tuning curve would be reflected horizontally for a depressing synapse). We computed the similarity between the neuronal tuning curves measured during the early sample and the synaptic tuning curves measured late in the delay using the same method as described above (see Methods: Tuning similarity index). Specifically, we calculated model fits and preferred directions for neuronal activity measured during the early sample period (50 to 150 ms after sample onset) and for synaptic efficacies measured from 1400 to 1500 ms after sample onset (corresponding to the second delay period for the ABCA and ABBA tasks, and the end of the delay period for all other tasks), and calculated the similarity between these values for each neuron:

$$s_i=Z\sqrt{W_{i,\mathit{\text{early sample}}}{W}_{i,\mathit{\text{late delay}}}}P{D}_{i,\mathit{\text{early sample}}}P{D}_{i,\mathit{\text{late delay}}}^T$$

where Z = 1 for facilitating synapses, and Z = −1 for depressing synapses. This extra term was necessary since increases in neuronal activity will depress the efficacies of depressing synapses. We then calculated the TSI by averaging across all neurons, divided by the sum of the geometric means of their respective linear model fits:

$$\mathit{\text{TSI}}=\frac{{\sum }_i{s}_i}{{\sum }_i\sqrt{W_{i,\mathit{\text{early sample}}}{W}_{i,\mathit{\text{late delay}}}}}$$

We then calculated task manipulation as 1 − TSI

Encoding stability

For the analysis in Figures S15–S24, panel j, we calculated the stability in neuronal encoding as the similarity (TSI) between neuronal sample tuning between different time points:

$$s_i\left(t_1,t_2\right)=\sqrt{w_{i,\mathit{\text{sample}}}\left(t_1\right)w_{i,\mathit{\text{sample}}}\left(t_2\right)}P{D}_{i,\mathit{\text{sample}}}\left(t_1\right)P{D}_{i,\mathit{\text{sample}}}^T\left(t_2\right)$$

We then calculated the mean similarity score for each of the four neuronal subgroups by averaging across all neurons within that subgroup, divided by the sum of the geometric means of their respective linear model fits:

$$\mathit{\text{TSI}}\left(t_1,t_2\right)=\frac{{\sum }_i{s}_i\left(t_1,t_2\right)}{{\sum }_i\sqrt{w_{i,\mathit{\text{sample}}}\left(t_1\right)w_{i,\mathit{\text{sample}}}\left(t_2\right)}}$$

Category tuning index

The category tuning index (CTI), used in Figure S7, measured the difference in synaptic efficacy (averaged across all trials for each direction) for each neuron between pairs of directions in different categories (a between category difference or BCD) and the difference in activity between pairs of directions in the same category (a within category difference or WCD)⁵². The CTI was defined as the difference between BCD and WCD divided by their sum. Values of the index could vary from +1 (which indicates strong binary-like differences in activity to directions in the two categories) to −1 (which indicates large activity differences between directions in the same category, no difference between categories). A CTI value of 0 indicates the same difference in firing rate between and within categories.

Statistics

We trained 20 networks for each task in order to assess the variability between different network solutions. All networks were initialized with different sets of random weights. No statistical methods were used to pre-determine sample sizes but our sample sizes are similar to those reported in a previous publication⁴⁹. We report mean ± standard deviation throughout the paper unless otherwise noted. Error bars in the figures indicate standard error of measurement. We measured correlation using the Pearson correlation coefficient, except for Figures 7 and S11–13, where we used the Spearman correlation coefficient because of the small sample size (n = 9). We used a bootstrap procedure (described in Methods: Population decoding) to determine if decoding accuracy for a single network was significantly greater than chance. We used two-sided t-tests to determine if groups of values across our population of 20 networks were significantly different. The data distribution was assumed to be normal, but this was not formally tested. No data points were excluded from the analyses, since all networks were able to solve the task with satisfactory (> 90%) accuracy. Data collection and analysis were not performed blind to the conditions of the experiments, as this did not apply to our simulations. Data collection and assignment to experimental groups also did not apply, since all networks were equivalent before training.

Reporting Summary

Further information on research design is available in the Nature Research Life Sciences Reporting Summary linked to this article.

Data availability

Data from all trained networks that were analyzed for this study is available from the corresponding author upon reasonable request.

Code availability

The code used to train, simulate and analyze network activity is available at https://github.com/nmasse/Short-term-plasticity-RNN.