Nearest-neighbor parameters for predicting DNA duplex stability in diverse molecular crowding conditions

Significance

The intracellular environment is occupied by a high concentration of various types of biomolecules that lead to a situation known as molecular crowding, which affects important biological reactions such as replication and transcription by altering the stability of nucleic acids. Because intracellular crowded conditions are heterogeneous, a general method is needed to predict the stability of nucleic acids in such conditions. Here, we predicted the stability of DNA duplexes under crowded conditions induced by a large amount of a cosolute at a physiological salt concentration using the nearest-neighbor model. We also extended the parameters for predicting DNA stability under conditions imposed by different cosolutes that mimicked a localized intracellular crowded region.

Abstract

The intracellular environment is crowded and heterogeneous. Although the thermodynamic stability of nucleic acid duplexes is predictable in dilute solutions, methods of predicting such stability under specific intracellular conditions are not yet available. We recently showed that the nearest-neighbor model for self-complementary DNA is valid under molecular crowding condition of 40% polyethylene glycol with an average molecular weight of 200 (PEG 200) in 100 mM NaCl. Here, we determined nearest-neighbor parameters for DNA duplex formation under the same crowding condition to predict the thermodynamics of DNA duplexes in the intracellular environment. Preferential hydration of the nucleotides was found to be the key factor for nearest-neighbor parameters in the crowding condition. The determined parameters were shown to predict the thermodynamic parameters (∆H°, ∆S°, and ∆G°₃₇) and melting temperatures (T_m) of the DNA duplexes in the crowding condition with significant accuracy. Moreover, we proposed a general method for predicting the stability of short DNA duplexes in different cosolutes based on the relationship between duplex stability and the water activity of the cosolute solution. The method described herein would be valuable for investigating biological processes that occur under specific intracellular crowded conditions and for the application of DNA-based biotechnologies in crowded environments.

Intracellular biological processes occur in an environment that is teeming with macromolecular cosolutes such as proteins, nucleic acids, polysaccharides, various ions, and small molecules (1, 2). These cosolutes can vary the physical properties of solutions in terms of water activity, dielectric constant, and viscosity that can subsequently alter the behavior of biomolecules (3). In addition, the steric effects of cosolutes influence their reactivity (4). Nucleic acids (DNA and RNA) are polyelectrolyte chains that are particularly sensitive to the intracellular environment (3). Therefore, understanding the influence of intracellular conditions on nucleic acids is important to consider so that biological processes can be elucidated and related technologies can be developed. Therefore, to predict DNA and RNA stability and thermodynamic parameters in cells is crucial.

The most convenient prediction method is based on the nearest-neighbor (NN) model pioneered by Tinoco and coworkers (5–7), which can predict stability from the base sequence of a duplex DNA, RNA, or RNA/DNA hybrid. The model assumes that the thermodynamic parameters of duplex formation, namely changes in enthalpy (∆H°), entropy (∆S°), and free energy at 37 °C (∆G°₃₇), are the sum of the values of adjacent NN base pairs and helix initiation factors that correspond to the formation of the first base pair in a double helix (8–11). The simplicity and accuracy of the prediction are major advantages of this model. The stability (∆G°₃₇) and melting temperature (T_m) of the recently developed “Hachimoji” DNA and RNA can be also predicted using the NN model, indicating its generality (12). However, since classical NN parameters are determined under conditions of 1 M NaCl, it is difficult to apply them for predictions in intracellular environments populated with highly concentrated macromolecules in lower salt concentrations. Recent attempts to establish NN parameters applicable to physiological conditions have aimed to predict the intracellular stability of duplexes (13–19). Although the ∆G°₃₇ of DNA and RNA duplexes under modified conditions was predicted, such predictions can only be used in a specific condition. Intracellular concentrations of cations and biomolecules might fluctuate (1, 2). Moreover, many intracellular organelles do not have a membrane (20–22), such as the nucleolus that is located within the nucleus where it promotes the transcription of ribosomal DNA (20). Organelles without membranes are generated by liquid–liquid phase separation, indicating that their interior molecular environment differs from that around them. These properties indicate the need to develop a general method for predicting intracellular duplex stability. Therefore, the establishment of generalized NN parameters is required to predict the stability of duplexes in any physiological crowding condition that resembles different salt and crowding environments within a cell.

The present study aimed to determine the ∆H°, ∆S°, and ∆G°₃₇ of 10 possible Watson–Crick NN base pairs and two helix initiation factors for DNA duplexes in the presence of 40 wt% polyethylene glycol with an average molecular weight of 200 (PEG 200) at the physiologically relevant salt concentration of 100 mM NaCl. PEGs have been frequently applied as cosolutes to investigate the structure and stability of nucleic acids under simulated intracellular conditions (23–26). Inertness toward nucleobases, high water solubility, and the availability of many molecular sizes render PEG useful as potential cosolutes to mimic a crowded intracellular environment. We recently showed that the crowding condition imposed by PEG 200 is similar to that of the nucleolus indicated that PEG 200 is a suitable agent for simulating the intracellular environment (27). The determined parameters in our experimental condition contained contributions from both salt (100 mM NaCl) and the crowder (40 wt% PEG 200). Subtraction of NN parameters in the absence of PEG 200 at 100 mM NaCl from our determined NN parameters provided the contribution of the crowder molecule (PEG 200) only in each of the 10 NN pairs and two initiation factors. We subsequently developed NN parameters under diverse molecular crowding conditions based on the relationship between duplex destabilization and water activity under different cosolute conditions. These parameters can be used to predict DNA stability in different cosolute conditions, which resemble the different regions of a cell having totally different crowding environments from each other. These predictions have immense importance in understanding the effects of duplex stability on various biological reactions that occur in different intracellular compartments as well as in the advancement of biotechnological applications such as antisense therapy, gene editing, plasmonics, and nanodevices for drug delivery that focus on duplex hybridization in crowded environments (28, 29).

Results and Discussion

Sequence Design and Thermodynamics of DNA Duplexes in Crowded Environments.

Duplexes of various lengths and base composition are needed to obtain reliable NN parameters. We recently confirmed the validity of the NN model for DNA duplexes in 40 wt% PEG 200 with 100 mM NaCl by showing similar thermodynamic parameters (∆H°, ∆S°, and ∆G°₃₇) and T_m for sequences with identical NN sets (17). However, the sequences were self-complementary, which rendered them insufficient to determine NN parameters. Here, we designed 12 non-self-complementary sequences of various lengths (8- to 16-mer) and NN frequencies, covering all 10 possible NN sets, for the formation of DNA duplexes (SI Appendix, Table S1). Among these non-self-complementary sequences, four pairs of sequences had identical NN sets (SI Appendix, Table S1). The ultraviolet (UV) melting measurements showed that all of the designed sequences exhibited two-state melting behavior under the crowding conditions imposed by PEG 200. Before the thermodynamic analysis, we assessed the structures of the DNA sequences using circular dichroic spectra and confirmed that all of the sequences were B-type DNA duplexes that did not significantly differ in the absence and presence of 40 wt% PEG 200 (SI Appendix, Fig. S1). Small changes in the peak positions and ellipticities of the DNA sequences in the presence of PEG 200 were attributed to slight alterations in the spatial orientation of each base chromophore without affecting the global conformation of the DNAs.

We determined the thermodynamic data (∆H°, ∆S°, and ∆G°₃₇) for DNA duplexes from UV melting studies (Fig. 1 and SI Appendix, Figs. S2 and S3), as we previously described (17). We assumed that the heat capacity change (ΔC_p) of the two states (single strand and duplex) was zero, following the standard practice. Table 1 shows the thermodynamic data for all of the sequences in 40 wt% PEG 200 with 100 mM NaCl and their values in a solution without a cosolute. Although the experimental solution contained some Na⁺ derived from buffer components (10 mM Na₂HPO₄ and 1 mM Na₂EDTA) in addition to NaCl, the concentration was too low to significantly affect the stability of the DNA duplexes. Consistent with previous findings (23, 30, 31), the thermal stability of all of the duplexes decreased in the crowded environment as the water activity decreased. Duplex destabilization did not specifically correlate with the number of base pairs in the sequences, suggesting that length of the DNA duplexes did not play a significant role in the duplex stability among the studied sequences (SI Appendix, Fig. S4). Like the self-complementary sequences, the thermodynamic parameters and T_m for non-self-complementary DNA sequences with identical NN sets were also similar (Table 1), validating the NN model for non-self-complementary sequences in 40 wt% PEG 200 with 100 mM NaCl.

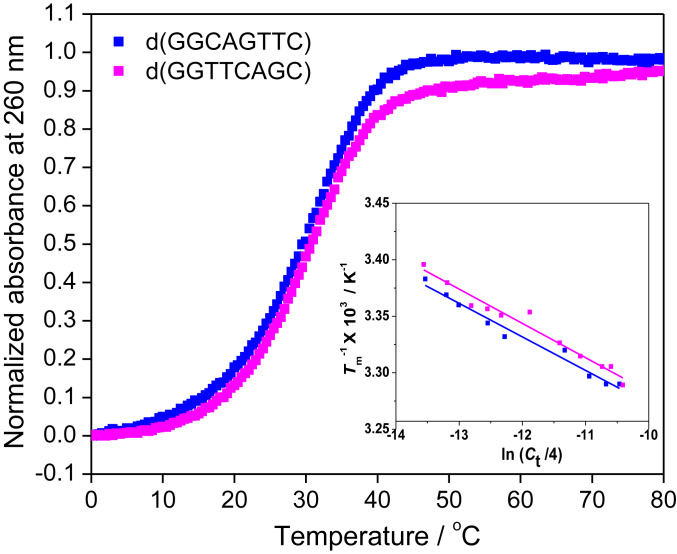
Fig. 1.

Representative UV melting curves of 100 µM d(GGCAGTTC) and d(GGTTCAGC) (sequence nos. NS1 and NS2, respectively, in Table 1) in 40 wt% PEG 200 with 100 mM NaCl. Inset shows T_m⁻¹ vs. ln (C_t/4) plots for these sequences.

Table 1.

Thermodynamic parameters for DNA sequences measured under crowding conditions of 40 wt% PEG 200 at 100 mM NaCl and predicted without PEG 200 in 100 mM NaCl solution

No.	Sequence*	Measured in the presence of 40 wt% PEG 200†				Predicted in absence of cosolute‡		Difference between with and without cosolute
		ΔH° (kcal mol−1)	TΔS° (kcal mol−1)	ΔG°37 (kcal mol−1)	Tm§ (°C)	ΔG°37 (kcal mol−1)	Tm§ (°C)	ΔΔG°37 (kcal mol−1)	ΔTm (°C)
NS1	d(GGCAGTTC)¶	−67.4 ± 3.4	−62.3 ± 3.2	−5.1 ± 0.4	30.8	−7.1	42.0	2.0	−11.2
NS2	d(GGTTCAGC)¶	−61.0 ± 3.5	−55.9 ± 3.2	−5.1 ± 0.5	29.4	−7.1	42.0	2.0	−12.6
NS3	d(CGCTGTAG)¶	−64.3 ± 2.7	−58.9 ± 2.6	−5.4 ± 0.4	31.7	−6.9	39.3	1.5	−7.6
NS4	d(CGTGCTAG)¶	−68.1 ± 2.8	−62.9 ± 2.6	−5.2 ± 0.4	31.9	−6.9	39.3	1.7	−7.4
NS5	d(AGTAACGCCAT)¶	−83.3 ± 4.4	−76.4 ± 4.1	−6.9 ± 0.6	38.3	−8.7	50.2	1.8	−11.9
NS6	d(AATGCCGTAGT)¶	−77.8 ± 1.8	−71.1 ± 1.6	−6.7 ± 0.2	37.8	−8.7	50.2	2.0	−12.4
NS7	d(CCATCGCTACC)¶	−93.5 ± 2.5	−85.1 ± 2.3	−8.4 ± 0.4	43.4	−9.8	55.2	1.4	−11.8
NS8	d(CGATGGCCTAC)¶	−95.8 ± 3.2	−87.1 ± 2.9	−8.7 ± 0.4	44.1	−9.8	55.2	1.1	−11.1
NS9	d(CGCTTGTTAC)¶	−76.4 ± 1.9	−70.2 ± 1.8	−6.2 ± 0.3	35.2	−8.2	46.3	2.0	−11.1
NS10	d(CCGTAACGTTGG)¶	−95.0 ± 2.6	−87.3 ± 2.4	−8.7 ± 0.4	44.2	−10.6	59.1	1.9	−14.9
NS11	d(ACTGACTGACTG)¶	−88.4 ± 2.1	−80.4 ± 1.9	−8.0 ± 0.3	42.2	−9.5	51.5	1.5	−9.3
NS12	d(ACTGACTGACTGACTG)¶	−124.9 ± 3.2	−113.0 ± 2.9	−11.9 ± 0.5	51.0	−13.1	61.6	1.2	−10.6
S1	d(GGACGTCC)#	−63.0 ± 2.8	−57.7 ± 2.6	−5.3 ± 0.4	35.4	−7.5	48.0	2.2	−12.6
S2	d(GACCGGTC)#	−64.1 ± 6.0	−58.7 ± 5.5	−5.4 ± 0.8	35.6	−7.5	48.0	2.1	−12.4
S3	d(CGTCGACG)#	−63.9 ± 2.2	−57.8 ± 2.0	−6.1 ± 0.3	39.0	−7.9	53.0	1.8	−14.0
S4	d(CGACGTCG)#	−63.2 ± 3.7	−57.0 ± 3.4	−6.2 ± 0.5	39.3	−7.9	53.0	1.7	−13.7
S5	d(CAAGCTTG)#	−79.7 ± 2.4	−76.1 ± 2.3	−3.6 ± 0.3	28.9	−6.2	37.0	2.6	−8.1
S6	d(CTTGCAAG)#	−72.5 ± 3.4	−68.6 ± 3.2	−3.9 ± 0.4	29.6	−6.2	37.0	2.3	−7.4
S7	d(CGGTACCG)#	−69.5 ± 2.7	−64.9 ± 2.6	−4.6 ± 0.3	32.3	−7.6	45.5	3.0	−13.2
S8	d(CCGTACGG)#	−60.5 ± 5.4	−55.1 ± 5.0	−5.4 ± 0.7	34.7	−7.6	45.5	2.2	−10.8
S9	d(GATCCGGATC)#	−82.5 ± 5.1	−76.8 ± 4.8	−5.7 ± 0.7	37.3	−8.4	52.6	2.7	−15.3
S10	d(GGATCGATCC)#	−77.9 ± 2.2	−71.9 ± 2.0	−6.0 ± 0.3	38.2	−8.4	52.6	2.4	−14.4
S11	d(ATGAGCTCAT)#	−71.8 ± 0.9	−66.8 ± 0.8	−5.0 ± 0.1	34.3	−7.6	43.9	2.6	−9.6
S12	d(ATCAGCTGAT)#	−77.1 ± 2.0	−72.2 ± 1.9	−4.9 ± 0.3	34.0	−7.6	43.9	2.7	−9.9
S13	d(CATAGGCCTATG)#	−86.0 ± 4.3	−79.5 ± 4.0	−6.5 ± 0.6	39.8	−8.8	51.3	2.3	−11.5
S14	d(CTATGGCCATAG)#	−91.9 ± 3.6	−85.1 ± 3.4	−6.8 ± 0.5	40.5	−8.8	51.3	2.0	−10.8
S15	d(GCGAATTCGC)#	−66.9 ± 1.9	−59.9 ± 1.7	−7.0 ± 0.3	43.1	−9.4	55.7	2.4	−12.6
S16	d(AGTCATGACT)#	−69.8 ± 4.3	−65.3 ± 4.0	−4.5 ± 0.5	32.3	−6.9	39.3	2.4	−7.0
S17	d(GACGACGTCGTC)#	−95.0 ± 4.4	−85.9 ± 4.0	−9.1 ± 0.6	48.2	−11.5	64.9	2.4	−16.7
S18	d(ATCGCTAGCGAT)#	−59.8 ± 9.0	−53.1 ± 8.0	−6.7 ± 1.3	43.1	−9.8	53.3	3.1	−10.2
S19	d(GCAAGCCGGCTTGC)#	−96.2 ± 8.2	−84.0 ± 7.9	−12.2 ± 0.4	58.5	−14.1	74.0	1.9	−15.5
S20	d(CGATCGGCCGATCG)#	−90.9 ± 8.5	−79.4 ± 8.3	−11.5 ± 0.3	56.9	−13.8	63.2	2.3	−6.3
S21	d(CATATGGCCATATG)#	−129.4 ± 5.8	−122.2 ± 5.5	−7.2 ± 0.7	40.7	−10.0	55.4	2.8	−14.7
S22	d(CAAGATCGATCTTG)#	−116.4 ± 9.9	−108.2 ± 9.3	−8.2 ± 1.3	44.6	−10.7	55.2	2.5	−10.6
S23	d(CGCGTACGCGTACGCG)#	−126.9 ± 6.7	−113.3 ± 6.0	−13.6 ± 1.0	57.9	−16.9	77.2	3.3	−19.3
S24	d(CGCAAGCCGGCTTGCG)#	−109.4 ± 6.8	−94.6 ± 6.4	−14.8 ± 0.4	64.2	−16.7	79.8	1.9	−15.6

^*DNA duplex consists of denoted DNA strand and complementary DNA strand.

^†All experiments proceeded in buffer containing 100 mM NaCl, 10 mM Na₂HPO₄ (pH 7.0), and 1 mM Na₂EDTA.

^‡∆G°₃₇ values in 100 mM NaCl were calculated from those in 1 M NaCl using our previously proposed relationship (32), and T_m values were calculated from those in 1 M NaCl using the equation proposed by Owczarzy et al. (13). Values in 1 M NaCl were predicted using parameters described by SantaLucia et al. (11).

^§Melting temperatures were calculated for total strand concentration of 100 µM.

^¶Non-self-complementary sequences.

^#Self-complementary sequences. Data were taken from our earlier study (17).

NN Parameters in the Presence of 40 wt% PEG 200 with 100 mM NaCl.

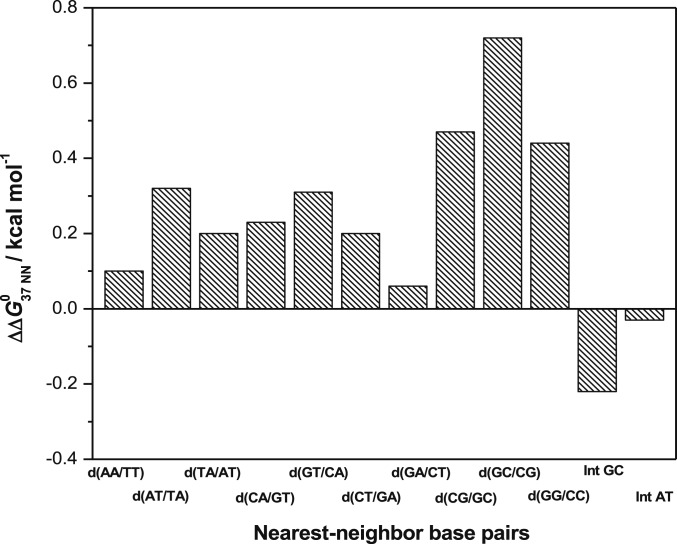
We used our original software written in Python to determine the NN parameters. Details of the algorithm of the program are described in SI Appendix, Materials and Methods. Briefly, we applied linear least square fitting to the measured values of the thermodynamic parameters of the DNA duplexes in 40 wt% PEG 200 with 100 mM NaCl using the software to obtain the 10 NN pairs and two initiation factors. We confirmed the accuracy and reliability of our software before assessing the NN parameters under crowded conditions, by reproducing the NN parameters for DNA duplexes in solutions without cosolute at 1 M NaCl, that we previously reported (SI Appendix, Table S2). The NN parameters for dilute condition calculated herein using our software and the previously reported values differed by averages of only 0.4, 0.5, and 0.7% for ∆G°₃₇, ∆H°, and ∆S°, respectively (SI Appendix, Table S2), suggesting that the software could accurately determine NN parameters. Table 2 shows the NN parameters determined under crowded condition. The ∆G°₃₇ values of all NN base pairs were destabilized compared with the absence of a cosolute at 100 mM NaCl (SI Appendix, Table S3). The order of decreasing stability was d(CG/GC) ∼ d(GC/CG) ∼ d(GG/CC) > d(CA/GT) ∼ d(GT/CA) ∼ d(GA/CT) ∼ d(CT/GA) > d(AA/TT) > d(AT/TA) > d(TA/AT), which was the same as that in 100 mM NaCl without a cosolute (SI Appendix, Table S3) (33). The ∆G°₃₇ for the d(TA/AT) pair was notably close to zero (Table 2), suggesting that this NN pair easily dissociates under crowded conditions. Therefore, more d(TA/AT) base pairs render a gene more flexible, resulting in a bend in the duplex structure in that region, which affects gene regulation (34, 35). Moreover, a high content of d(TA/AT) pairs at the sites of replication origin in DNA can be justified by the very minute stabilization effect of d(TA/AT) pairs under such crowded conditions that facilitate duplex DNA dissociation to initiate replication (36). To understand the quantitative impact of molecular crowding on each of the NN parameters, we plotted changes in the ∆G°₃₇ of the parameters, namely ∆∆G°_{37 NN} (∆G°_{37 NN, 40 wt% PEG 200} – ∆G°_{37 NN, no cosolute}). Fig. 2 shows that molecular crowding differently affected each NN parameter, and the relative destabilization of NN with only GC pairs [d(CG/GC), d(GC/CG), and d(GG/CC)] was considerably higher than that of other NN pairs. This might be because in environment with low water activity caused by PEG 200, NN pairs comprising only GC are destabilized more as GC pairs require more water molecules for stabilization than AT pairs (37).

Table 2.

NN parameters for DNA duplexes in 40 wt% PEG 200 and 100 mM NaCl at 37 °C

Sequence	ΔH°NN (kcal mol−1)	ΔS°NN (cal mol−1 K−1)	ΔG°37 NN (kcal mol−1)
d(AA/TT)	−6.5 ± 0.3	−19.2 ± 0.8	−0.55 ± 0.07
d(AT/TA)	−9.4 ± 0.3	−29.4 ± 0.8	−0.28 ± 0.05
d(TA/AT)	−4.3 ± 0.5	−13.3 ± 1.3	−0.16 ± 0.14
d(CA/GT)	−13.1 ± 0.1	−38.8 ± 0.1	−1.00 ± 0.05
d(GT/CA)	−9.2 ± 0.1	−26.8 ± 0.1	−0.89 ± 0.01
d(CT/GA)	−3.4 ± 0.6	−7.9 ± 1.6	−0.91 ± 0.11
d(GA/CT)	−4.9 ± 0.7	−13.0 ± 2.1	−0.87 ± 0.06
d(CG/GC)	−6.4 ± 0.7	−16.1 ± 2.0	−1.38 ± 0.12
d(GC/CG)	−4.2 ± 0.7	−9.3 ± 2.0	−1.31 ± 0.06
d(GG/CC)	−4.0 ± 0.6	−8.9 ± 2.0	−1.25 ± 0.03
Initiation per GC	−10.1 ± 0.2	−35.1 ± 0.5	0.76 ± 0.06
Initiation per AT	−2.9 ± 0.3	−12.7 ± 0.9	1.00 ± 0.07
Self-complementary	0	−1.4	0.40
Non-self-complementary	0	0	0

Experiments proceeded in 10 mM Na₂HPO₄, 1 mM Na₂EDTA, 100 mM NaCl, and 40 wt% PEG 200 at pH 7.0.

Fig. 2.

Differences between ∆G°₃₇ of NN pairs with or without 40 wt% PEG 200 (∆∆G°_{37 NN}) at 100 mM NaCl concentration. Int GC and Int AT refer to initiation free energy change for GC and AT terminals, respectively, of duplex.

Differences between the NN parameters under crowded condition and a solution without cosolute were the most remarkable among the initiation factors. The ∆H° for both helix initiation factors was favorable in the crowded environment (Table 2), which is in contrast to the solution without cosolute (SI Appendix, Table S3). On the other hand, the ∆S° was unfavorable for helix initiation parameters. This might be due to preferential hydration around duplex terminals under crowded conditions. Osmometric, ultrasonic velocimetric, and solvatochromic measurements have suggested that Watson–Crick duplex formation is associated with changes in hydration around duplex structures (23, 30, 32, 37–41). Molecular dynamic simulations have also shown that the ordered water network around a DNA duplex is disrupted in a cosolute solution (42). Nucleotides in terminal pairs can interact more with these disordered water molecules via hydrogen bonding as they remain more exposed to the surrounding environment compared with the nucleotides of other propagating base pairs, resulting in a favorable ∆H° for helix initiation. As more hydrogen bonding sites are located in GC than AT pair (43), the magnitude of ∆H° is higher for initiation at GC pair. However, the accumulation of water molecules around terminal pairs resulted in an unfavorable ∆S° for helix initiation under crowded condition. A larger contribution of unfavorable ∆S° than of favorable ∆H° rendered the ∆G°₃₇ for helix initiations unfavorable, as in the solution without a cosolute, even though the magnitude was reduced. The direct interaction of crowder molecules with terminal pairs could be another reason for the exceptional values of initiation factors under crowded conditions. Free energy change due to the entropic penalty for maintaining the C₂ symmetry for self-complementary sequences was not altered since it is independent of the environment (Table 2). Therefore, the thermodynamic contribution of molecular crowding depends on the specific composition of the DNA duplexes. The NN parameters described herein would be important to understand biological reactions involving duplex dissociations such as DNA replication and transcription. For example, in replication, we previously reported that the hairpin structure on the template, which has a structure similar to that of a duplex, can stall DNA polymerase depending on the stability of the hairpin (44). In the case of transcription, elongation and termination of the transcription reaction within the long genomic DNA depend on the energetics of the transcription bubble, which is generally 15- to 18-bp long depending on the operative polymerase (45). The energy of the transcription bubble can be estimated by adding the free energies of the constituting NN pairs and the initiation factors at both the terminals of the bubble. Notably, the interaction between the nucleic acids and proteins, including polymerase, must be considered to more precisely understand the reaction. The parameters can also be beneficial in antisense oligonucleotide (ASO) technology for selecting effective DNA oligonucleotides in crowded environments because a recent report showed that NN parameters are also suitable predictor for chemically modified ASO/RNA duplexes (46).

Among the 36 DNA tested duplexes (SI Appendix, Table S4), the average differences in ∆H°, ∆S°, and ∆G°₃₇ between the predicted and measured values were 5.7, 6.3, and 4.3%, respectively, which were within the limits of reported NN parameters (9–11, 18). The average difference for T_m was also very small (1.0 °C) compared with those for DNA (2.0 °C) (11) and RNA (1.9 °C) (9) duplexes, using the NN model in the absence of cosolute. We assessed the predictive nature of our derived parameters using leave-one-out analyses in which one selected test sequence was removed from the dataset and the NN parameters were calculated based on the remaining sequences. We then predicted the thermodynamics of the test sequence based on the resulting parameters and repeated the same procedure for every sequence in the dataset. We obtained average differences between the predicted and the measured values of 7.5, 8.4, and 5.6% for ∆H°, ∆S°, and ∆G°₃₇, respectively, suggesting that the prediction is good. Therefore, our parameters can adequately predict the stability and thermodynamics of DNA duplex formation under molecular crowding conditions under a physiological salt concentration.

Improvement of NN Parameters for Diverse Crowding Conditions.

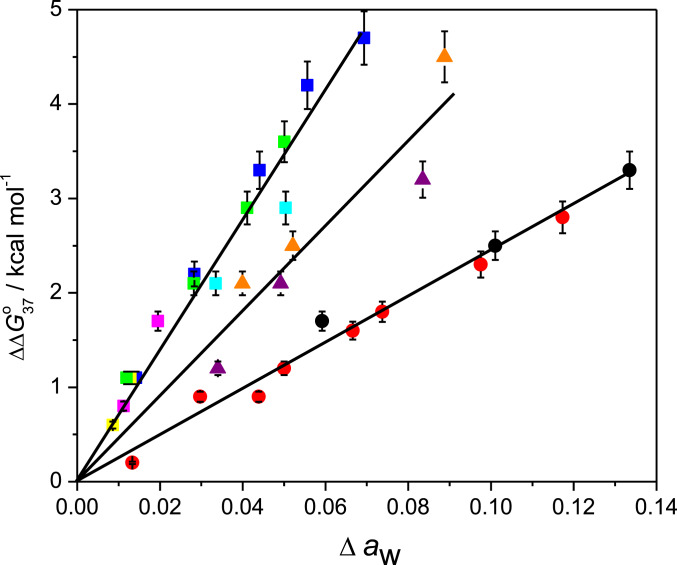
Based on the NN parameters in 40 wt% PEG 200, we expanded them for applicability to any crowded condition. The chemical contributions of molecular crowding to each NN base pair need to be determined to improve NN parameters. Among the physicochemical factors affected by molecular crowding, water activity mainly affects the stability of short DNA duplexes (23, 30, 38). Although other factors such as the dielectric constant might influence the stability of DNA duplexes under crowded conditions, their contribution can be considered minimal because of the following. The dielectric constant of the medium regulates cation binding efficiency that screens the electronegative potential of nucleotide phosphates (47). Therefore, reduction of the dielectric constant in a cosolute solution should stabilize DNA duplexes since it enhances electrostatic attraction between phosphate groups and cations overcoming electrostatic repulsion between the backbone phosphate groups. However, DNA duplexes become destabilized in cosolute solutions, which might be due to the dominant effect of reduced water activity over the stabilization due to the dielectric constant effect for the short DNAs in crowding conditions. Spink and Chaires (48) also showed that compared with the effect of the dielectric constant, water activity plays the major role in DNA stability in solutions containing cosolutes. The steric effect of large cosolutes also stabilizes DNA duplexes, mainly long or polymeric duplexes (23, 48–50). Therefore, to improve NN parameters, we rated water activity as the most important factor affecting the stability of short DNA duplexes in cosolute solutions. The relationship between duplex destabilization under crowded conditions and water activity is shown as a simple linear correlation. Fig. 3 shows a plot of ∆∆G°₃₇, which is the difference in ∆G°₃₇ values (∆G°_{37, cosolute} – ∆G°_{37, no cosolute}) for a short DNA sequence [d(ATGCGCAT)] against changes in water activity, ∆a_w (∆a_w = a_{w no cosolute} – a_{w cosolute}) in different cosolute solutions of varying concentrations (SI Appendix, Table S5). We selected d(ATGCGCAT) as the reference sequence because it had equal GC and AT contents and the average destabilization of the constituting NN base pairs (0.4 kcal mol⁻¹) was similar to that of the 10 NN base pairs in 40 wt% PEG 200 solution (0.3 kcal mol⁻¹). The plot of ∆∆G°₃₇ vs. ∆a_w shows that DNA duplex destabilization increased linearly as ∆a_w increased. We obtained three linear correlations that depended on the nature of cosolutes. PEGs of different molecular weights and 1,2-dimethoxyethane (1,2 DME) belonged to one group. Ethylene glycol (EG) and glycerol similarly correlated, whereas 1,3-propanediol (1,3 PDO) and 2-methoxyethanol (2-ME) belonged to a different group. Interestingly, the correlations for PEG 200 in both 1 M and 100 mM NaCl (blue and green squares, respectively, in Fig. 3) were notably the same, suggesting that destabilization with a change in water activity is independent of the ionic concentration of the solution. This is supported by the report showing that the number of sodium ions associated with the duplex formation remains invariant to the change in the water activity of the solution by the addition of EG (48).

Fig. 3.

Difference in ∆G°₃₇ between crowded conditions and those without cosolute (∆∆G°₃₇) vs. ∆a_w for d(ATGCGCAT) with EG (red circles); glycerol (black circles); 1,3 PDO (purple triangles); 2-ME (orange triangles); 1, 2-dimethoxy ethane (cyan squares); PEG 200 (blue squares); PEG 2000 (magenta squares); and PEG 8000 (yellow squares) at 1 M NaCl and with PEG 200 at 100 mM NaCl (green squares). PEGs of different molecular weights and 1,2 DME belong to the same group. EG and glycerol are also in one group, whereas 1,3 PDO and 2-ME are in another. Data are shown in SI Appendix, Table S5. Bars represent 6% error.

The stability parameters for each NN base pair under crowded conditions can be expressed as follows:

$$\mathrm{\Delta }G{°}_{37\hspace{0.17em}\text{NN}}=\mathrm{\Delta }G{°}_{37\hspace{0.17em}\text{NN},\left[\text{cation}\right]}+\mathrm{\Delta }G{°}_{37\hspace{0.17em}\text{NN},\left[\text{crowder}\right]}$$ [1]

where ∆G°_{37 NN,[cation]} and ∆G°_{37 NN,[crowder]} represent the portion of NN parameters determined by cation and crowder concentrations, respectively. The ∆G°_{37 NN,[cation]} parameters in 100 mM NaCl can be calculated from those in 1 M NaCl using the dependence of [Na⁺] for each NN base pair (14). Because DNA duplex destabilization in the presence of crowder (∆∆G°₃₇) linearly correlated with changes in water activity under crowded conditions (∆a_w) (Fig. 3) and duplex destabilization can be represented as the sum of destabilizations of individual NN pairs and initiation factors, it is reasonable to assume that ∆G°_{37,NN[crowder]} and initiation factors are linear functions of ∆a_w as follows:

$$\mathrm{\Delta }G{°}_{37\hspace{0.17em}\text{NN},\left[\text{crowder}\right]}=m_{\text{cs}}•\mathrm{\Delta }{a}_{\text{w}}$$ [2]

where m_cs is a prefactor for cosolutes, which is equivalent to the energy parameter for NN base pairs in the presence of a cosolute, and it depends on the NN base pair as well as the nature of cosolute. We found three distinct straight lines for the cosolutes (Fig. 3), depending on their chemical structures. Poly(ethylene) glycols and 1,2 DME maximally destabilized, whereas EG and glycerol minimally destabilized, and 1,3 PDO and 2-ME destabilized to an extent between these two. Previous studies suggested that the extent of destabilization, in the presence of cosolutes, depends on the number and position of the hydroxyl groups present in the cosolutes (23, 38). Destabilization by a cosolute might be due to disrupting the network of water molecules around the duplex. Ethylene glycol and glycerol have three and two vicinal hydroxyl groups, respectively, that are suitable for hydrogen bond formation with water molecules. This might contribute to maintaining the ordered water structure around the duplex even in the crowding condition resulted in least destabilization of the duplex. Hydroxyl groups on PEG are separated by an EG chain, and the vicinal position of 1,2 DME does not contain a hydroxyl group. Therefore, these cosolutes could not stabilize duplexes in a crowded environment by maintaining the solvent network around the duplex, whereas 1,3 PDO and 2-ME, each having one hydroxyl group in the vicinal position, caused a degree of destabilization between these two classes of cosolutes.

We calculated the contribution of these classes of cosolutes to each NN parameter. Subtracting ∆G°_{37 NN,[cation]} from the parameters shown in Table 2 provided ∆G°_{37 NN,[crowder]} for 40 wt% PEG 200 (Table 3). The m_cs values for PEG, including 1,2 DME (m_{PEG/1,2 DME}), were calculated from the ∆G°_{37 NN,[crowder]} values using Eq. 2 (Table 3). The m_cs values for the other two types of cosolutes were calculated as follows:

$$m_{\text{cs}}=m_{\text{PEG}}•\left(S_{\text{CS}}/S_{\text{PEG}}\right)$$ [3]

where S_CS and S_PEG are the slopes for the cosolute of interest and PEG, respectively, in the ∆∆G°₃₇ vs. ∆a_w plot (Fig. 3). The ∆G°_{37 NN,[cation]} for any concentration of Na⁺ or divalent cations such as Mg²⁺ can be obtained from the dependence of NN parameters on the salt concentration (14, 51). The ∆G°_{37 NN,[crowder]} for different cosolutes at their different concentrations can be calculated by multiplying m_cs (Table 3) and ∆a_w. Water activities under different crowded conditions can be found in the literature or determined by osmometric measurements (SI Appendix, Table S6). Therefore, the DNA duplex stability in the presence of various cosolutes of different concentrations can be predicted using the parameters listed in Table 3.

Table 3.

NN parameters for ∆G°_{37 NN,[cation]} and ∆G°_{37 NN,[40 wt% PEG 200]} in 100 mM NaCl with prefactors (m_cs) for different cosolutes

Sequence	∆G°37 NN,[cation] (kcal mol−1)	∆G°37 NN,[40 wt% PEG 200] (kcal mol−1)	mPEG/1,2 DME (kcal mol−1)	mEG/GOL (kcal mol−1)	m1,3PDO/2-ME (kcal mol−1)
d(AA/TT)	−0.65	0.10	2.0	0.7	1.3
d(AT/TA)	−0.60	0.32	6.4	2.2	4.2
d(TA/AT)	−0.36	0.20	4.0	1.4	2.6
d(CA/GT)	−1.23	0.23	4.6	1.6	3.0
d(GT/CA)	−1.20	0.31	6.2	2.2	4.1
d(CT/GA)	−1.11	0.20	4.0	1.4	2.6
d(GA/CT)	−0.93	0.06	1.2	0.4	0.8
d(CG/GC)	−1.85	0.47	9.4	3.3	6.2
d(GC/CG)	−2.05	0.72	14.4	5.0	9.5
d(GG/CC)	−1.69	0.44	8.8	3.0	5.8
Initiation per GC	0.98	−0.22	−4.4	−1.5	−2.9
Initiation per AT	1.03	−0.03	−0.6	−0.2	−0.4

Correction factor for self-complementary sequences is 0.4 kcal mol⁻¹ for all cosolutes as it is independent of crowding environment.

These generalized treatments for crowding condition can expand to the application using relatively longer chains, which have large effect of the excluded volume on the duplex formation. For example, 30-mer duplex (5′-A₂₇GCG-3′/5′-CGC​T₂₇-3′) is slightly stabilized by 10% PEG 8000 (0.8 °C increase of T_m) (23), although the prediction by Eq. 1 above indicates that the 30-mer duplex is destabilized (∆G°₃₇ in the absence of PEG is −29.7 kcal mol^–1, while ∆G°₃₇ in the presence of 10% PEG 8000 is −29.1 kcal mol^-1). According to the Hermans theory, the effect of excluded volume on the duplex formation can be separately quantified from water activity (52). When the energetic contribution of the excluded volume (−1.3 kcal mol^–1) is included, the revised ∆G°₃₇ is calculated as −30.4 kcal mol^–1, which suggests slight stabilization by 10% PEG 8000 as the experimental result. Furthermore, the NN parameters here can be useful to predict the duplex stability of uncharged oligonucleotides such as morpholinos and peptide nucleic acid (PNA). The degrees of hydration on these modified oligonucleotides can suggest the modification of ∆G°_{37 NN,[crowder]}. In the case of DNA-PNA hybrid duplexes, destabilization with the change in the water activity of the solution were nearly half of the corresponding DNA duplex destabilization, which suggests that ∆G°_{37 NN,[crowder]} for DNA–PNA hybrid duplexes should be roughly half of that of the DNA duplexes (38). Thus, according to Eq. 2, m_cs values for DNA–PNA hybrid duplexes can be considered as half of their respective values for DNA duplexes.

We obtained improved NN parameters for ∆H° and ∆S° that would be applicable to different crowding conditions, in a similar manner to those described above for ∆G°₃₇ (SI Appendix, Figs. S5 and S6 and Tables S7 and S8). Among parameters for 10 NN sets, the values for all ∆H°_{NN,[40 wt% PEG 200]} and ∆S°_{NN,[40 wt% PEG 200]} were positive except for those of d(AT/TA), d(CA/GT), and d(GT/CA), which were negative. Since the ∆G°_{37 NN,[40 wt% PEG 200]} values for all 10 NN sets were positive (Table 2), these exceptions among the NN sets are entropy dominant. As in case of initiation factors, hydration on these three NN sets might be enhanced under crowded conditions. Compared with the minor groove of B-type duplex DNA where the hydration spine is located, the major groove in each base pair has a variable geometry of donors and accepters for hydrogen bonding (53). Therefore, hydration in the major groove of d(AT/TA), d(CA/GT), and d(GT/CA) might be specifically altered by the crowding condition. Moreover, both the ∆H° and ∆S° plots of EG and glycerol at higher concentrations deviated from linearity (SI Appendix, Figs. S5 and S6), perhaps because other factors such as the viscosity and dielectric constant affected the ∆H° and ∆S° values at higher crowder concentrations.

Validation of Improved NN Parameters In Vitro and in Simulated Intracellular Conditions.

We used our improved parameters to predict the thermodynamics of several DNA duplex sequences with different NN compositions to verify the predictive nature and versatility of the parameters in various solution conditions. We examined the parameters in different concentration of NaCl with different concentration of PEG 200 (1 M NaCl and 10, 20, or 30 wt% PEG 200), different cosolutes categorized in the same class (1 M NaCl and 20 wt% PEG 1000 or PEG 6000), and different cosolutes categorized in the different classes (100 mM NaCl and 20 wt% EG or 1,3 PDO). Fig. 4 illustrates the calculation of ∆G°₃₇ for the sequence d(CCGTACGG) in 20 wt% 1,3 PDO and 100 mM NaCl using the improved parameters listed in Table 3. ∆H° and ∆S° parameters were analogously predicted using the improved parameters, and the predicted values are listed in Table 4. As shown in Table 4, the average difference between the predicted and measured ∆G°₃₇ values for the sequences in studied solutions was only 4.4%, indicating that the improved NN parameters can predict DNA stabilities (∆G°₃₇) in different cosolutes and salt conditions with significant accuracy. The parameters also allowed good predictions of ∆H° and ∆S° with average differences of 10.8 and 11.2%, respectively.

Fig. 4.

Application of improved NN parameters (Table 3) to predict ∆G°₃₇ of sequence d(CCGTACGG) in solution containing 20 wt% 1,3 PDO and 100 mM NaCl. Each arrow represents one NN set. ∆a_w value of the solution was calculated from the data shown in SI Appendix, Table S6. This duplex is self-complementary, with symmetry factor of 0.4 kcal mol⁻¹.

Table 4.

Experimental and predicted thermodynamic parameters of DNA sequences in different cosolute and salt conditions

Solution	Measured			Predicted
	ΔH° (kcal mol−1)	ΔS° (cal mol−1 K−1)	ΔG°37 (kcal mol−1)	ΔH° (kcal mol−1)	ΔS° (cal mol−1 K−1)	ΔG°37 (kcal mol−1)
d(GAGGTCGT) in 1 M NaCl*
10 wt% PEG 200	−48.7 ± 3.1	−129.8 ± 9.7	−8.4 ± 0.1	−56.6	−154.1	−8.3
20 wt% PEG 200	−46.6 ± 1.9	−125.5 ± 5.4	−7.7 ± 0.1	−56.0	−153.6	−7.9
30 wt% PEG 200	−44.8 ± 1.3	−121.8 ± 2.3	−7.0 ± 0.3	−55.3	−153.1	−7.0
d(ATGCGCAT) in 1 M NaCl*
20 wt% PEG 1000	−54.1 ± 2.1	−148.0 ± 6.9	−8.2 ± 0.3	−60.2	−162.9	−8.1
20 wt% PEG 6000	−52.5 ± 3.7	−142.0 ± 12.0	−8.6 ± 0.6	−59.8	−162.6	−8.4
d(CCGTACGG) in 100 mM NaCl
20 wt% EG	−65.2 ± 5.2	−186.9 ± 14.9	−7.2 ± 0.8	−62.6	−182.8	−6.7
20 wt% 1,3 PDO	−57.2 ± 1.7	−163.0 ± 4.8	−6.6 ± 0.3	−62.3	−174.9	−6.2
d(CCGTAACGTTGG) in 100 mM NaCl
20 wt% EG	−94.5 ± 5.1	−269.5 ± 14.6	−10.9 ± 0.8	−96.9	−281.5	−10.5
20 wt% 1,3 PDO	−86.3 ± 5.3	−243.5 ± 15.9	−10.8 ± 0.9	−96.4	−275.9	−9.9

Experiments proceeded in buffer containing 10 mM Na₂HPO₄ (pH 7.0), 1 mM Na₂EDTA, and NaCl.

^*Measured values collected from our previous studies (23, 31).

We then investigated whether the expanded NN parameters could be used to estimate DNA duplex stability in cells. First, we tested the nuclear lysate from human HeLa cells. As shown in SI Appendix, Fig. S7, the melting temperature of the duplex d(AGTAACGCCAT) decreased with increasing concentration of the lysate (from 48.6 °C in the 5 mg/mL lysate to 45.7 °C in the 25 mg/mL concentrated lysate), suggesting that the intracellular components actually destabilized DNA duplexes, as well as the artificial cosolutes used in this study. ∆G°₃₇ for the sequence increased from −11.4 kcal mol⁻¹ in buffer to −10.5 kcal mol⁻¹ in the concentrated lysate. The degree of the destabilization caused by the concentrated lysate (2.5 wt%) corresponded to that obtained in about 10 wt% PEG 200 solution. The results suggest that the natural cell extracts have decreased the DNA duplex more than PEG 200. Interaction between single-stranded DNA and positively charged proteins might have additional effect on the destabilization. Thus, this result suggests that the lysate is too heterogeneous to predict the duplex stability by improved NN parameters determined by a single cosolute. We next targeted the condition in a localized intracellular region, where the condition was more homogenous. Nott et al. (54) analyzed the stability of DNA d(ACTG)₃ and d(ACTG)₄ duplex in the disordered Ddx4 protein that mimics the nucleolus (membraneless compartment of the nucleus). The reported ∆∆G°₂₅ values (difference between ∆G°₂₅ of DNA duplexes inside and outside the nucleolus) were 3.0 kcal mol⁻¹ for d(ACTG)₃ and 2.3 kcal mol⁻¹ for d(ACTG)₄. These values corresponded to the destabilization due to the crowded condition inside the nucleolus (54). We initially confirmed the stability of each of these sequences in the absence of crowders based on the adjusted parameters at 25 °C (SI Appendix, Table S9). The predicted stability was −12.4 kcal mol⁻¹ for d(ACTG)₃ and −18.0 kcal mol⁻¹ for d(ACTG)₄, which agreed well with the experimental ∆G°₂₅ of −13.8 and −19.5 kcal mol⁻¹ for d(ACTG)₃ and d(ACTG)₄, respectively, outside the cell measured using Förster resonance energy transfer (FRET) (54). To determine the exact crowding conditions inside the nucleolus, we calculated ∆G°_{25 NN,[crowder]} for d(ACTG)₃ and d(ACTG)₄ at different crowder concentrations and found that 50% PEG 200 in 100 mM NaCl condition for nucleolus and 0% PEG 200 in 100 mM NaCl condition for nucleus were the optimal conditions to predict ∆G°₂₅ for the stabilities of both the DNA duplexes (SI Appendix, Table S10). We recently showed that the crowded conditions in the nucleolus could be simulated using PEG 200, whereas that in the nucleus more resembled a Ficoll 70-like condition (27). However, Ficoll 70 cannot destabilize short DNA duplexes due to a reduced effect on decreasing water activity (17). Thus, the crowded condition in the nucleus can also be predicted as a dilute condition because the contribution of crowding on NN parameters depends on water activity (Eqs. 1 and 2). Our results agreed with those of a recent study, in which the folding stability for an RNA hairpin structure in the nucleus of a HeLa cell did not remarkably differ from that in a diluted buffer solution (55). Therefore, the NN parameters of DNA in the presence of 50% PEG 200 could be used to determine the thermodynamic parameters for DNA duplex formation inside the nucleolus. Our results indicated that thermodynamic parameters in any target region of a cell could be determined using our improved NN parameters in the presence of a cosolute that can simulate the target region.

Conclusion

We determined the NN parameters for DNA duplexes under crowded condition containing 40 wt% PEG 200. We then expanded the NN parameters and successfully established a method to utilize these parameters in any crowding conditions. Predicting the stability of DNA duplexes under any crowded condition is helpful to determine the behavior of DNA in live cells because local intracellular conditions are likely to differ among cells and organelles. A local crowded environment in a living cell can be annotated with the specific crowded condition of a cosolute created in vitro. Therefore, our improved NN parameters will be useful not only for developing technologies but also, for investigating biological reactions controlled by specific intracellular crowded conditions.

Materials and Methods

The structure and melting temperatures of DNAs were characterized using circular dichroism and UV spectrometry, respectively. The materials and methods used herein are detailed in SI Appendix, Materials and Methods.

Data Availability.

All data are available in the text or SI Appendix.