Large enhancement of thermoelectric performance in MoS₂/h-BN heterostructure due to vacancy-induced band hybridization

Significance

The study of correlated phenomena in 2D semiconductors opens up new pathways toward understanding and engineering material functionalities (such as thermoelectrics) in easily accessible van der Waals solids. Local structural defects such as vacancies inevitably exist in natural as well as synthetic TMD crystals and have been predicted to serve as magnetic impurities capable of enhancing the strongly correlated effect. Herein we discover unusual thermoelectric behavior in sulfur vacancy-enriched MoS₂ by rationally selecting h-BN as the substrate. We demonstrate that the thermoelectric transport properties can be strongly manipulated by vacancy-induced Kondo hybridization. A significant enhancement of thermoelectric power factor by two orders of magnitude is achieved in the MoS₂/h-BN device.

Abstract

Local impurity states arising from atomic vacancies in two-dimensional (2D) nanosheets are predicted to have a profound effect on charge transport due to resonant scattering and can be used to manipulate thermoelectric properties. However, the effects of these impurities are often masked by external fluctuations and turbostratic interfaces; therefore, it is challenging to probe the correlation between vacancy impurities and thermoelectric parameters experimentally. In this work, we demonstrate that n-type molybdenum disulfide (MoS₂) supported on hexagonal boron nitride (h-BN) substrate reveals a large anomalous positive Seebeck coefficient with strong band hybridization. The presence of vacancies on MoS₂ with a large conduction subband splitting of 50.0 ± 5.0 meV may contribute to Kondo insulator-like properties. Furthermore, by tuning the chemical potential, the thermoelectric power factor can be enhanced by up to two orders of magnitude to 50 mW m⁻¹ K⁻². Our work shows that defect engineering in 2D materials provides an effective strategy for controlling band structure and tuning thermoelectric transport.

Thermoelectrics are solid state energy converters that can be used to harvest electrical energy from waste heat; thus, they are attractive as a sustainable energy resource. The performance of thermoelectric materials is characterized by the thermoelectric figure of merit (ZT, defined as S²σT/κ, where T is the absolute temperature): the key bottleneck is the interdependency between the Seebeck coefficient (S), electrical (σ), and thermal (κ) conductivities. An ideal thermoelectric material should exhibit simultaneously large S and σ (1). It has been proposed that van der Waals materials, in their two-dimensional (2D) form with discretized density of states (DOS) (quantum confinement), may show better performance in thermoelectrics compared to bulk materials (2). For instance, bulk layered SnSe has been found to have a figure of merit (ZT) of 2.8 ± 0.5. The remarkably high ZT is not due to quantum confinement but instead due to the anharmonicity of its chemical bonds, giving it an ultralow thermal conductivity at high temperature (700 to 900 K) (3, 4). However, the power factor (PF = S²σ) is still relatively modest (1 mW m⁻¹ K⁻²) (3). New transport mechanisms are needed to push the PF of thermoelectric materials beyond the well-known S-σ anticorrelation limit (1). For example, the violation of the Mott relation results in enhanced PF in the hydrodynamic charge transport regime in graphene due to strong inelastic scattering among electrons (5). It is well known that impurity states, especially magnetic impurities, not only strongly couple with itinerant charge carriers but can also significantly affect the band structure and even reverse charge transport behavior (6–8). Few-atoms-thick layered materials are highly sensitive to such extrinsic effects, and therefore, they serve as a good platform for exploiting thermoelectric properties by introducing such impurities. Among these materials, MoS₂ has attracted special attention because of its well-defined spin-splitting under light illumination and/or applied magnetic fields (9–11). Extrinsic magnetic impurities in MoS₂ can be introduced by vacancies, dislocations, edges, strain, or doping by magnetic ions (12–16). However, due to its extreme sensitivity to external fluctuations and turbostratic interfaces, there has not yet been a clear correlation between the thermoelectric properties of layered 2D materials and impurities.

In this work, we report that when few-layer MoS₂ flakes are interfaced to hexagonal boron nitride (h-BN) substrate, a correlation between charge carriers and vacancy impurities in MoS₂ is clearly observed. This is in part due to reduced scattering by charged surface states and surface roughness on the atomically smooth and chemically inert h-BN substrate. Using low-temperature scanning tunneling microscopy (LT-STM), single-atom sulfur vacancies (up to ∼1.81 ± 0.4 × 10¹² cm⁻²) were observed on MoS₂. The conduction subband near the vicinity of such a sulfur vacancy shows a colossal band splitting of 50 ± 5 meV. Density functional theory (DFT) simulations reveal that this band hybridization may originate from sulfur vacancy-induced magnetic states. When fabricated into a MoS₂/h-BN field effect transistor (FET) device, we observed an anomalous sign change of the Seebeck coefficient and an extremely large positive Seebeck value (∼2 mV/K) even in the metallic regime at 60 K. Furthermore, an electrostatically tunable PF of MoS₂/h-BN device larger by two orders of magnitude is achieved due to strong interactions between conducting charges and the observed vacancy states, attaining a value as high as 50 mW m⁻¹ K⁻² in the temperature range from 30 to 50 K. Our results demonstrate that engineering vacancies in 2D layered crystals provide a material platform for next generation thermoelectric and energy applications.

Results

Vacancy-Induced Band Hybridization in MoS₂/h-BN Heterostructure.

Inversion symmetry breaking at vacancy or edge sites of MoS₂ has been theoretically predicted to enable local magnetic moments and induces band splitting of both valence and conduction bands (17). To probe band splitting induced by vacancies in MoS₂, an atomically flat h-BN substrate is employed to avoid spurious effects from impurities at the interfaces. The MoS₂/h-BN heterostructure device was fabricated by a well-established transfer technique and then loaded into the LT-STM chamber and annealed in ultrahigh vacuum $\left(<1\times {10}^{-10}\hspace{0.17em}\mathrm{torr}\right)$ to ensure better electrical and thermal contact and a cleaner surface (more details in SI Appendix, Notes S1 and S2).

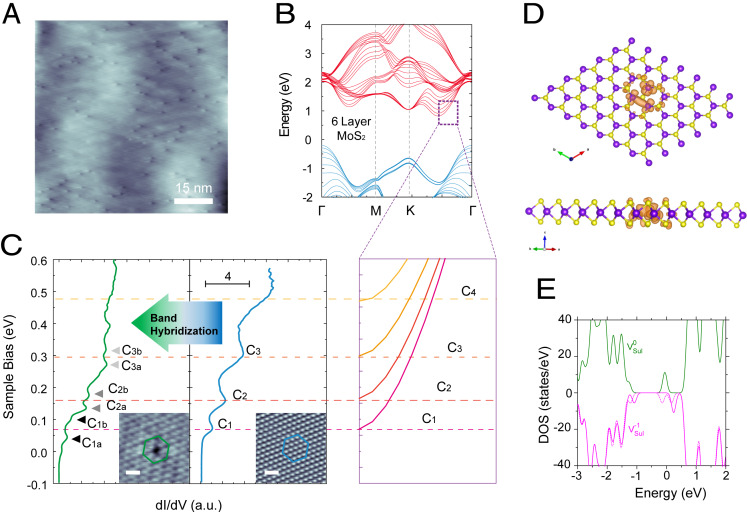
Fig. 1A shows a typical STM topographic image of MoS₂ flake on h-BN for a scan area of 75 nm × 75 nm at liquid helium temperatures. The thickness of MoS₂ flake was confirmed to be six layers using atomic force microscopy and verified subsequently by scanning tunneling spectroscopy (STS) (Fig. 1C). The dark topographic contrast in the STM image (Fig. 1A) and lattice discontinuity are hallmarks of single sulfur vacancies (18), with a concentration of ∼1.81 ± 0.4 × 10¹² cm⁻². In the high-resolution image inserted in Fig. 1C, Center, a hexagonal lattice with a periodicity of 3.15 ± 0.5 Å is seen (SI Appendix, Fig. S3), corresponding to the atomic lattice of the top sulfur layer in the MoS₂ crystal (19). The defects are experimentally observed at the center of sulfur lattice sites, excluding other defect types such as interstitials, Mo vacancy, or antisite defects (a Mo atom substituting a S₂ column or vice versa) (20). STS, which probes the local density states, was applied to study the effect of such sulfur vacancy defects on the electronic properties. To better resolve the effect of sulfur vacancies, a lower set point (V_S = −0.7 V, I = 1.3 nA) was used to collect the dI/dV spectrum from the vicinity of sulfur vacancy as well as far away from it (Fig. 1C). At regions where the MoS₂ is pristine (Fig. 1C, Center), a series of oscillation peak/dip features were observed at the conduction band region spaced ∼98.0, ∼134.3, and ∼169.0 meV apart, in good agreement with the subband (C₁, C₂, and C₃; Fig. 1C, Right) structure of six-layer MoS₂ predicted by DFT calculations. Intrinsically, such subbands are associated with quantum confinement of electronic states. When the STM tip is located on top of a vacancy, however, a splitting (energy of 50.0 ± 5.0 meV) of these subbands (into C_1a and C_1b, C_2a and C_2b, and C_3a and C_3b) was clearly captured, which is similar to observations of band hybridization in Kondo insulators (21). A survey scan using X-ray photoelectron spectroscopy over the whole MoS₂ flake shows no evidence of magnetic elemental impurities (SI Appendix, Fig. S4).

Fig. 1.

Electronic properties and band structure of six-layer MoS₂ with sulfur vacancy. (A) Large-area STM image of the bare MoS₂ on h-BN substrate (V_S = 1.0 V, I = 0.7 nA). The dark topographic contrast, which shows the single sulfur vacancy features, can be found over the whole scanned area. (B) DFT calculation of six-layer MoS₂. The zoomed-in image shows the conduction subbands (C_n) near the CBM at point of six-layer MoS₂. (C) dI/dV spectrum (V_S = −0.7 V, I = 1.3 nA) at the vicinity of a sulfur vacancy (Left side) (scale bar, 0.6 nm) and pristine region (Right) (scale bar, 0.8 nm) of MoS₂ near CBM. Conduction subbands C₁, C₂, and C₃ can be revealed from the resonance peaks in STS curve of pristine MoS₂. However, each of those subbands split into two bands (C_na and C_nb) due to band hybridization in the vicinity of a sulfur vacancy. (D) Top and side views of spin density associated with single sulfur vacancy in monolayer MoS₂. (Purple larger spheres represent molybdenum atoms, and smaller yellow spheres represent sulfur atoms.) The spin density associated with V_Sul⁻¹, with a significant component localized at the three exposed Mo atoms. (E) Electronic DOS of the sulfur vacancy in neutral (V_Sul⁰) and −1 charged state (V_Sul⁻¹) (for intuitive understanding, the VBMs for the two cases were aligned).The charging of the vacancy leads to the lifting of the degeneracy of defective level indicated by the splitting of curves of spin-up (dashed line) and spin-down (solid line) states for V_Sul⁻¹.

In order to investigate the local effect of vacancies on electronic structure in MoS₂, first-principle calculations were conducted on monolayer MoS₂ (more calculation details in SI Appendix, Note S4). The removal of one sulfur atom in the MoS₂ sheet creates a single sulfur vacancy (V_Sul), accompanied by dangling states and exposure of Mo atoms in the vacancy core. Single neutral V_Sul has two states: a fully occupied singlet A state and an empty doubly degenerate E state (22). When carriers are injected into the MoS₂, the V_Sul state becomes negatively charged, and the V_Sul⁻¹ is spin-polarized, accompanied by a spin moment of μ = 1/2. The spin density associated with V_Sul⁻¹, with a significant component localized at the three exposed Mo atoms, is shown in Fig. 1 D and E. Charging via gating alters the local magnetic moment and state-splitting of the V_Sul, which in turn, tunes the scattering of charge carriers, especially at low temperatures (23).

Electrical Performance Due to Band Hybridization.

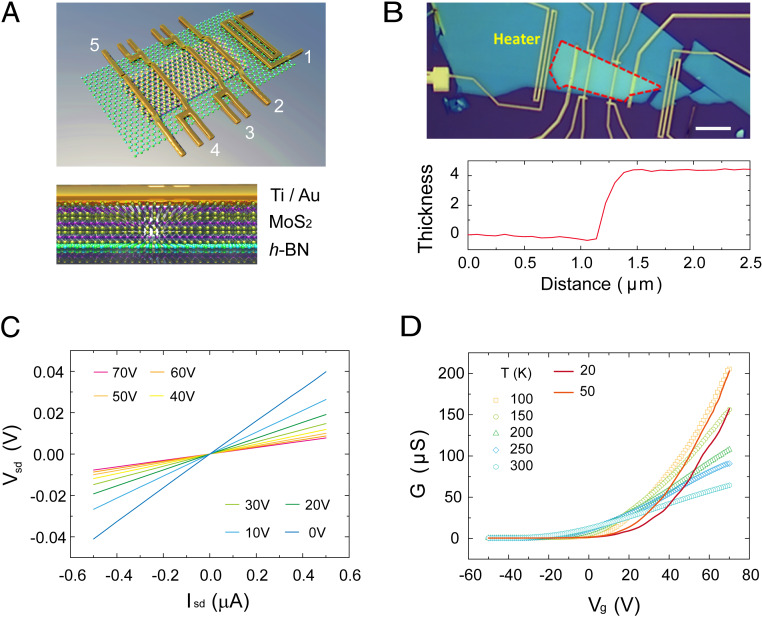
To investigate the influence of vacancy-induced band hybridization, temperature-dependent transport measurements were carried out. Fig. 2A shows the top and section view of the MoS₂/h-BN heterostructure, and a representative optical image is shown in Fig. 2B. To be consistent, a MoS₂ flake with thickness 4.2 ± 0.3 nm was selected (six layers; Fig. 1C) (more transport results of various thicknesses are provided in SI Appendix, Note S15). Four-probe measurements were performed to exclude the effects of electrical contact resistance, and the nanofabricated heater allows thermoelectric measurements. The linear I_sd–V_sd curves collected at room temperature (Fig. 2C) indicate ohmic contacts between metal electrode and MoS₂ flake (SI Appendix, Fig. S6). The carrier concentration $\left(n\right)$ in MoS₂ is modulated by applying a back-gate voltage $\left(V_g\right)$. Fig. 2D shows an increasing conductance (G) with $V_g$ for the MoS₂/h-BN sample within the measured temperature (T) range, indicating typical n-type FET behavior. From 300 to 100 K, a clear crossing point (at $V_g\sim 20\text{V}$) appeared, indicating that MoS₂ undergoes a routine metal-to-insulator transition (MIT), where the conductance changes from decreasing with temperature to increasing with temperature (24–26). At T < 100 K, the conductance drops anomalously as T decreases, in contrast with the trend exhibited by MoS₂ on Si/SiO₂ devices. This can be explained by the strong hybridization between localized impurities states and conduction electrons, which will be further discussed later.

Fig. 2.

Structural and electronic properties of MoS₂/h-BN heterostructure. (A) Schematic diagram of the device. Electrode 1 acts as an electrical heater. Electrodes 2 and 5 act as a current source for four-probe electrical measurements, while electrodes 3 and 4 act as thermometers. (Bottom) The section view of the heterostructure. (B) Optical image of a complete device. The dotted red dashed box outlines the MoS₂ flake. (Scale bar, 10 μm.) (Bottom) AFM scan gives the thickness of MoS₂ flakes as 4.2 ± 0.3 nm. (C) Four-probe I_sd-V_sd curves at different V_g values at 300 K. (D) Four-probe FET characterization at different temperatures. Clear crossover can be found at $V_g\sim 20\text{V}$ for T > 100 K, which is defined as the MIT. For $V_g>V_{\mathrm{MIT}}$, MoS₂ shows metallic behavior, and conductance decreases with increasing T. For $V_g<V_{\mathrm{MIT}}$, conductance increases with increasing T, which is a typical insulating behavior. When T < 100 K, the conductance (in the metallic region) drops anomalously as T decreases.

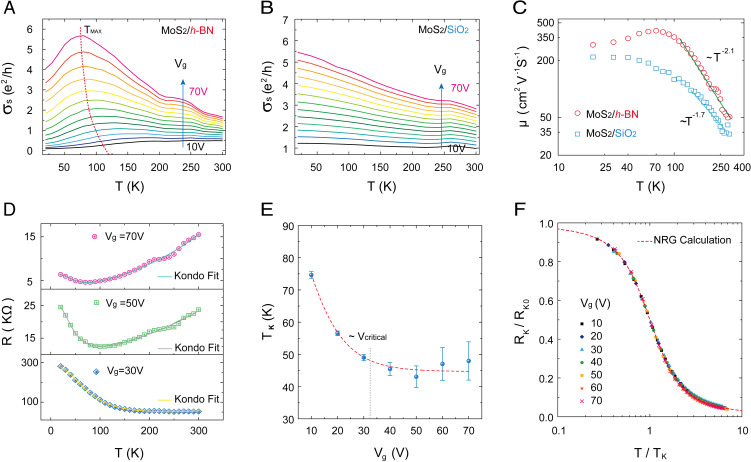
In order to better understand the electronic transport in MoS₂/h-BN, temperature-dependent four-probe sheet conductivity (σ_s = G·L/W, where L and W are the length and width of sample channel, respectively) was plotted as a function of V_g for both MoS₂/h-BN (Fig. 3A) and MoS₂/SiO₂ (Fig. 3B) devices for comparison. In the high temperature range (T > 100 K), and close to σ_s ∼ e²/h, the metal-insulator transition driven by electron correlations can be observed clearly in both devices. For MoS₂/SiO₂ device, such behavior exists over the temperature range from 300 to 20 K. However, for the MoS₂/h-BN device, instead of saturating at a residual value as T→0, a conductance peak (temperature at this critical point is defined as T_max; red dashed line in Fig. 3A) in the metallic region is observed. This observed anomalous resistance minimum at low temperature is another signature of a Kondo insulator behavior.

Fig. 3.

Carrier density and temperature-dependent properties of defective MoS₂ on h-BN substrate. (A) Four-probe sheet conductivity of MoS₂/h-BN devices as a function of T and V_g. MIT can be observed when σ_s ∼ e²/h. The anomalous peaks T_max at low temperatures are marked out by the red dashed line. (B) Four-probe sheet conductivity of MoS₂/SiO₂ devices as a function of T and V_g. (C) Temperature-dependent field effect mobility. The solid line shows the phonon-limited power law ${\mu }_{ph}\sim T^{-\text{γ}}$. $\text{γ}=1.7$ and $\mu \sim 200\hspace{0.17em}{\text{cm}}^2{\text{V}}^{-1}{\text{s}}^{-1}$ for MOS₂/SiO₂ sample. For MoS₂ on h-BN, $\text{γ}=2.1$ and $\mu$ reaches $405\hspace{0.17em}{\text{cm}}^2{\text{V}}^{-1}{\text{s}}^{-1}$. For T < 100 K, $d{\mu }_{FE}/dT>0$ is observed for MoS₂/h-BN sample indicating an anomalous scattering mechanism. (D) Temperature dependence of four-probe resistance at V_g = 70, 50, and 30 V for MoS₂/h-BN device, with the resistance minima at 70, 89, and 135 K, respectively. (E) Gate tuning of the Kondo temperature T_k. (F) Normalized Kondo resistance versus normalized temperature for the data from V_g = 10 V to V_g = 70 V. The red dashed line describes the universal Kondo behavior from numerical renormalization group calculations (35).

This effect is suppressed in the MoS₂/SiO₂ device due to the imperfect interface between MoS₂ and SiO₂ but clearly detectable for the six-layer MoS₂/h-BN devices (more data on six-layer MoS₂/SiO₂ and MoS₂/h-BN as well as monolayer and bilayer MoS₂/h-BN are in SI Appendix, Note S15). At low temperatures, the hybridization of the conduction band with the localized impurity state manifests in a large band splitting. Kondo resonant scattering can dominate charge transport in this temperature range and give rise to the anomalous component of the resistance. Such a picture is also complemented by the change in four-probe mobility $\left(\mu \right)$ with temperature (Fig. 3C). For MoS₂ on SiO₂, $\mu$ is mainly limited by optical phonon scattering when T > 100 K, and its temperature dependence follows a power law of $\mu \sim T^{-\text{γ}}$ (27). Once T < 100 K, most optical phonons are deactivated, and saturation is observed, resulting in $d\mu /dT\sim 0$ as T→ 0 (27). On the contrary, MoS₂/h-BN device deviates from this trend where its mobility decreases as T < 100 K and shows $d\mu /dT>0.$

Fig. 3D shows the four-probe resistance plots of MoS₂/h-BN device at three different back gates. For each curve, a clear resistance minimum can be observed at 70, 89, and 135 K. For a better understanding of this data, apart from 2D Block–Gruneisen resistance $\left(\propto T^4\right)$ (28, 29) and electron–phonon high temperature resistance $\left(\propto T\right)$, we employ a Kondo resistance model [$R_K\left(T_K,T\right)$, full expression in SI Appendix, Note S11]:

$$R=A{T}^4+BT+R_K\left(T_K,T\right)+R_0,$$ [1]

where $R_0$ is the temperature-independent term arising from a residual zero temperature resistance (Fig. 3D). In the Kondo picture, close to a characteristic temperature (Kondo temperature, T_K), magnetic impurities quantum-mechanically exchange spin with conduction electrons of many wave vectors (momenta) (30), thereby creating a resonant scattering state at the Fermi level with a width $\sim k_B{T}_K$ [$k_B{T}_K\sim \mathrm{\Delta }\hspace{0.17em}\text{exp}\left(\frac{-1}{D\left(E_F\right)J_0}\right)$, where D(E_F) is the electron DOS at the Fermi level, $\mathrm{\Delta }$ is the bandwidth, and J₀ is a constant representing a Kondo scattering exchange energy] (31, 32). As a result, a dip in the resistance vs. temperature curve appears. Fig. 3E summarizes the T_K variation as a function of V_g for MoS₂/h-BN sample. At V_g > V_MIT, T_K remains nearly unchanged because of the constant 2D DOS. When V_g < V_MIT, the Fermi level shifts toward the gap region; therefore, T_K starts to increase with lower doping, similar to the behavior observed in heavily doped fermion bulk systems such as CePd₃ (33). We also scale the R(T) curves at each V_g and observe a universal Kondo behavior (6, 34), in which the normalized Kondo resistance R_k/R_k0 vs. T/T_k at all gate voltages collapses onto a single universal Kondo behavior curve (Fig. 3F). This is in accordance with numerical renormalization group theory (35), which attests to the Kondo-driven transport in MoS₂/h-BN devices.

Thermoelectric Performance Driven by Band Hybridization.

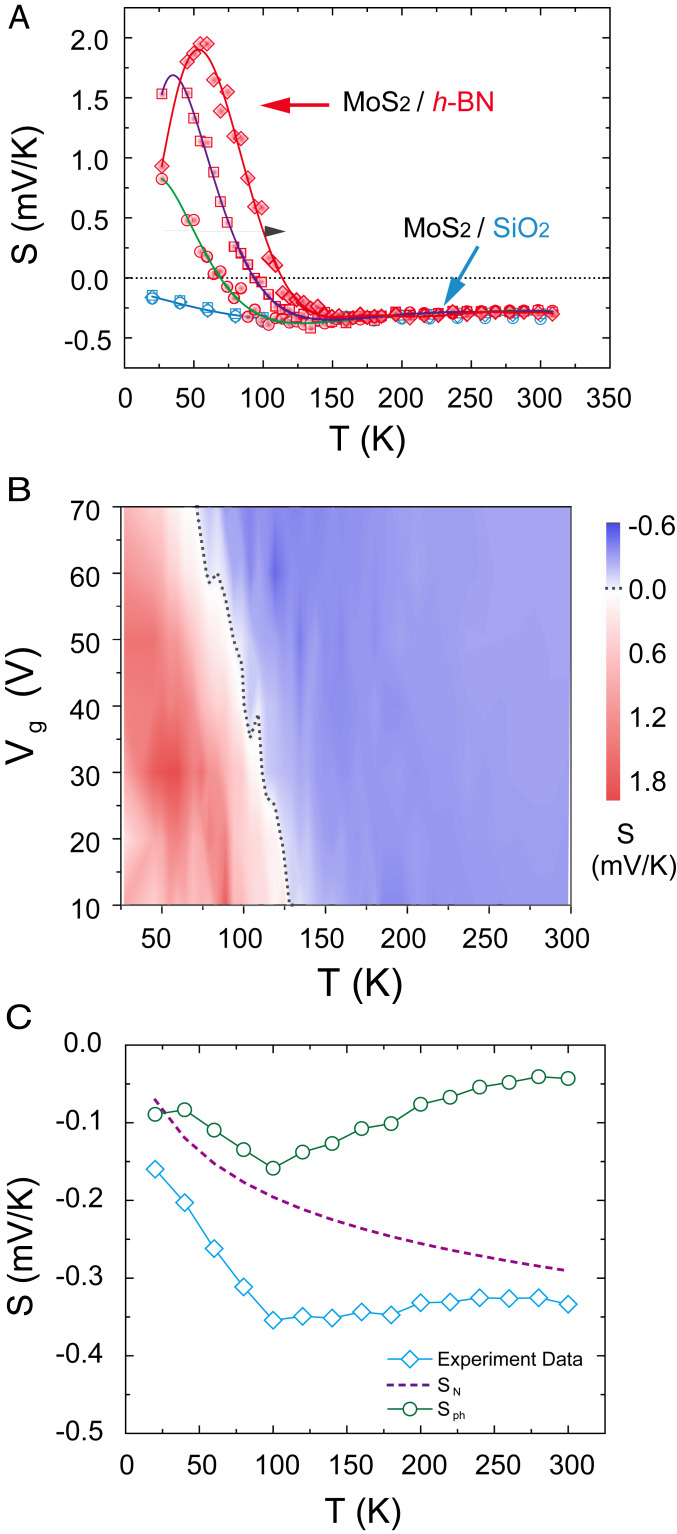
To investigate further if the thermoelectric values show a similar effect, a DC current is introduced via a nanofabricated heater to create a temperature gradient along the devices (Fig. 2A). Fig. 4A shows the Seebeck coefficient (S) as a function of temperature at V_g = 70, 50, and 30 V for both MoS₂/h-BN and SiO₂ devices. The absolute |S| decreases with increasing carrier concentration in the MoS₂ channel (details in SI Appendix, Note S13 and Fig. S19), comparable to the reported trends in earlier work (36, 37). From the temperature-dependent behavior of S for both samples, a clear dip located around 100 to 150 K can be observed which is very close to the thermal conductivity peak of MoS₂ (38, 39), indicating the contribution of acoustic phonons in MoS₂ to the Seebeck coefficient via the phonon drag effect, S_ph (40). Both MoS₂/SiO₂ and MoS₂/h-BN samples show similar values of negative S and behavior for T > 120 K. However, when T < 120 K, an anomalous sign change (from negative to positive) in S is observed in MoS₂/h-BN sample even though electrons remain as the dominant charge carriers. The positive S reaches a magnitude as high as 2 mV/K for V_g = 30 V at 60 K, which is almost one order of magnitude enhancement compared to MoS₂/SiO₂ sample (−270 μV/K) under the same experimental conditions. This is a remarkably large value for a material in the metallic state. To better illustrate the sign change of S, a 2D map of S as a function of both T and V_g is plotted in Fig. 4B. Clearly, S changes from negative to positive values at all gate voltages. It is also found that the critical temperature (defined as the temperature at which S = 0) and the maximum positive S (highest intensity; red in Fig. 4B) increases as V_g decreases, suggesting that the Seebeck coefficient can be tuned by electrostatic gating. Importantly, this critical temperature across all temperatures for S = 0 is identical to the conduction maximum line T_max in Fig. 3A, further evidencing that this anomalous thermoelectric transport has the same origins as the electronic transport.

Fig. 4.

Thermoelectric transport and Seebeck coefficient measurement of defective MoS₂ on h-BN substrate. (A) Comparison of S vs. T of MoS₂/SiO₂ and MoS₂/h-BN device at V_g = 70 V (circle), 50 V(square), and 30 V (diamond) (from left to right; black arrow). The solid lines guide the eye. MoS₂/SiO₂ sample shows negative values due to the diffusive type n-type charge carriers. For MoS₂/h-BN sample, at low temperatures, an anomalous sign change in S occurs where the majority carriers are electrons. (B) Color contour plot of S values versus V_g and T for MoS₂/h-BN device. The black dotted line indicates the point with S ∼ 0 mV/K. (C) Total S values of MoS₂/SiO₂ sample at n = 2 × 10¹² cm⁻² and its respective contributions from the energy-dependent diffusion $S_{\mathrm{N}}$ and phonon-drag S_ph.

Since the transfer curve shows unambiguous n-type behavior and the quasiparticle bandgap of six-layer MoS₂ is relatively large (41), the valence band states of MoS₂ are inaccessible and hence cannot result in a positive S, especially at low temperatures. When electrons are the majority carriers, the single-particle Boltzmann transport equation (BTE) can be employed to describe thermoelectric transport and is defined as S_BTE. In the degenerate state (highly conducting on-state), the BTE reduces to the Mott formula described below (42):

$$S_{BTE}=-\frac{{\pi }^2}{3}\frac{k_B^{2}T}{\left|e\right|}{\left[\frac{\partial \text{ln}\hspace{0.17em}\tau }{\partial E}+\left(\frac{\partial \ln \hspace{0.17em}g}{\partial E}+\frac{\partial \ln \hspace{0.17em}{v}^2}{\partial E}\right)\right]|}_{E=E_F}=S_{\text{τ}}+S_{\text{N}},$$ [2]

with $S_{\text{τ}}=-\frac{{\pi }^2}{3}\frac{k_B^{2}T}{\left|e\right|}{\frac{\partial ln\tau }{\partial E}|}_{E=E_F}$ and $S_{\text{N}}=-\frac{{\pi }^2}{3}\frac{k_B^{2}T}{\left|e\right|}{\left(\frac{\partial \ln \hspace{0.17em}g}{\partial E}+\frac{\partial \ln \hspace{0.17em}{v}^2}{\partial E}\right)|}_{E=E_F}$.

Here k_B, τ, $g$, and $v$ indicate the Boltzmann constant, relaxation time, DOS, and group velocity, respectively. $S_{\text{τ}}$ and $S_{\text{N}}$ are the contributions arising from the energy-dependent scattering and diffusion. The sign of $S_{\text{N}}$ only depends on the charge carrier type; thus, an n-type MoS₂ will only exhibit a negative $S_{\text{N}}$. As such, the Seebeck coefficient (S) comprises the sum of S_BTE and S_ph. For the MoS₂/SiO₂ sample, the low-temperature thermoelectric transport is dominated by acoustic phonon scattering where the acoustic phonon scattering relaxation time (τ) is energy independent (43) in the 2D limit. Hence, the S_BTE of our MoS₂/SiO₂ is dominated by negative $S_{\text{N}}$ and phonon drag S_ph. Here $S_{\text{N}}$ can be calculated by solving the linearized BTE under a relaxation time approximation (detailed calculations are provided in SI Appendix, Note S12) (36, 44). Consequently, the overall phonon drag Seebeck coefficient $\left(S_{ph}=S_{total}-S_{\text{N}}\right)$ can be estimated. Fig. 4C shows the measured Seebeck coefficient $\left(S\right)$ as a function of temperature of MoS₂/SiO₂ device at a carrier concentration of n = 2 × 10¹² cm⁻². The phonon drag contribution $S_{ph}$ shows clear peaks around 100 K as expected where the largest concentration of heat-carrying phonons (acoustic phonons) can interact with carriers (45). Hence, the peak position is not changing across different back gate voltages (SI Appendix, Fig. S18). At temperatures below 100 K, $S_{ph}$ diverges from unity. A first-order quantitative estimation of phonon drag S is given by $S_{ph}=\beta v_s{l}_s/\mu T$ (46–48), where $v_s$ is the velocity of sound and $l_s$ is the phonon mean free path. $\beta \subset \left(0,\hspace{0.17em}1\right)$ indicates the relative contribution of electron–phonon interaction to electron mobility. The phonon mean free path can be evaluated using the Debye equation $\text{κ}=\frac{1}{3}c{v}_s{l}_s$, yielding $l_s\sim 5\text{.}5\hspace{0.17em}\text{to}\hspace{0.17em}14\text{nm}$ which is consistent with the calculated values from literature (49). We remark that this estimated $l_s$ is an effective lower bound involving all phonons. The resulting estimate of $S_{ph}\sim {10}^2\mu V/K$ is also comparable to our results (details in SI Appendix, Note S12).

However, an anomalous sign change in S is observed for the MoS₂/h-BN sample accompanied by large positive values in the low-temperature region. Typically, a sign change in S occurs when the type of charge carrier changes, like in ambipolar materials [graphene (50) and black phosphorus (51)] or in complicated Fermi surface nesting systems such as charge density wave phase transition materials [NbSe₃ (52) and TaSe₃ (53)]. In addition, it has been observed that longer phonon mean free paths such as those in h-BN may contribute to an anomalously large thermoelectric behavior through the phonon drag effect (45). In such cases, the phonon drag S_ph peak should occur at higher temperatures due to the higher Debye temperature of h-BN. On the contrary, the observed peak in $S_{total}$ is located at lower temperatures in our experiments (Fig. 4A). Moreover, our experiment further shows that the sign change in $S_{total}$ is strongly dependent on the modulation of electron carrier concentration (gate effect) and vacancy concentration in MoS₂ (controlled via annealing). Hence, the anomalous thermoelectric transport can be mainly attributed to the strong correlation transport induced by the hybridized band structure, as shown in our STS results, in addition to phonon drag in MoS₂.

In fact, the vacancy-induced band hybridization and Kondo effect have been studied in 2D materials like graphene (6, 54, 55). In such a case, the scattering is highly energy-dependent, and the mobility is known to be proportional to $1/\tau$ (56), which is opposite to the conventional one-band system where $\mu \propto \tau$. Approximating $1/\partial \text{E}$ as $1/\left({\text{k}}_{\text{B}}\partial T\right)$ (57) in $S_{\tau }$, $\frac{\partial \text{lnτ}}{\partial T}\propto -\frac{d\mu }{dT}$ could be derived to describe the relationship between Seebeck coefficient and mobility. From Fig. 5A, we can see that the measured S is positive in the region where $\frac{d\mu }{dT}<0$, in good agreement with the Kondo physics model. In this model, the interaction between electrons at Fermi energy and hybridized band strongly influence the nonequilibrium energy spectrum, thereby generating a Kondo resonance that reverses the sign of Seebeck coefficient. This is further corroborated by the peak position of the S values occurring near the Kondo temperature.

Fig. 5.

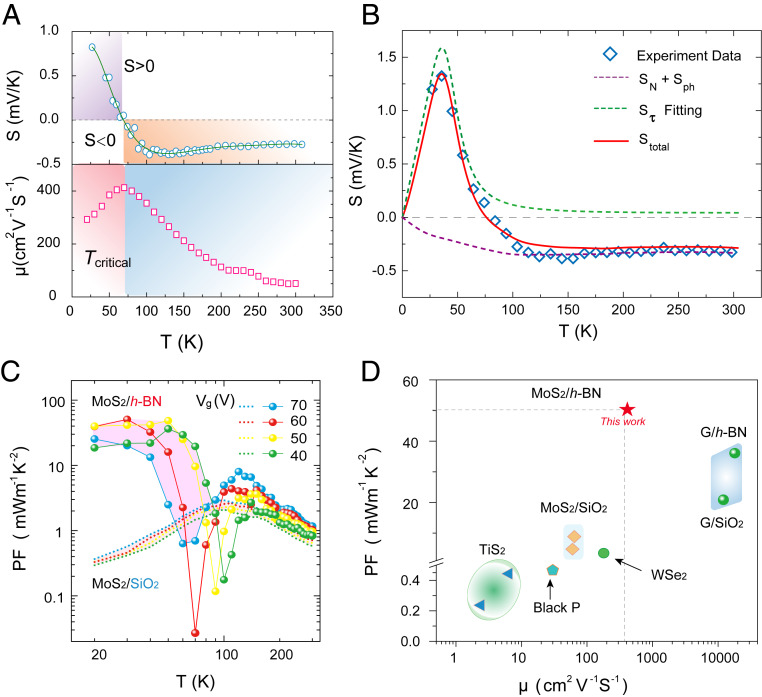
Thermolectric performance of MoS₂/h-BN heterostructure. (A) Seebeck coefficient and mobility as function of temperature at V_g = 70 V for MoS₂/h-BN device. (B) Total S values of MoS₂/h-BN sample at n = 2 × 10¹² cm⁻² are contributions from the energy-dependent diffusive part $S_{\mathrm{N}}$, phonon-drag part S_ph, and the Kondo scattering part $S_{\tau }$. At a fixed n, the total S first exhibits a diffusive negative value at high temperatures from conducting electrons described by $S_{\text{N}}+S_{ph}$. As the temperature decreases, the conventional diffusive contribution is weakened, and the Kondo scattering term $S_{\text{τ}}$ starts to dominate and shows large positive values. As temperature is decreased further, all of the physical interactions start to freeze, and the total S goes back to zero as expected (64). (C) Comparison of PF of MoS₂/h-BN and MoS₂/SiO₂ sample as a function of temperature at different gate voltages. Additional band hybridization-induced peaks as high as 50 mW m⁻¹ K⁻² can be observed at 30 K ∼ 50 K for MoS₂/h-BN sample. (D) The PF value of our MoS₂/h-BN heterostructure shows superior thermoelectric performance compared to even the highest reported values in other 2D materials at room temperature. [G/SiO₂ and h-BN (50), MoS₂ (36, 37), WSe₂ (60), TiS₂ (61, 62), and BP (51).]

To understand how the S is related to resonant scattering $\left(S_{\tau }\right)$, the two-band approach originating from the Hirst model is adopted (58):

$$S_{\tau }=\text{A}\frac{T{\text{ε}}_0}{{\epsilon }_0^2+{\left[T_{\text{Γ}}exp\left(-T_{\text{Γ}}/T\right)\right]}^2}.$$ [3]

Here the conduction electrons are scattered by an extraband induced by the hybridization. This band is described using a Lorentzian form with a width ${\text{Γ}}_0$ located at ε₀ with respect to the Fermi level. ${\text{Γ}}_0$ varies with temperature as ${\text{Γ}}_0=T_{\text{Γ}}\text{exp}\left(-T_{\text{Γ}}/T\right)$. $T_{\text{Γ}}$ is a temperature-dependent parameter and represents the quasi-elastic linewidth of the Kondo resonance. ε₀ can be positive or negative depending on whether the position of the extraband is above or below the Fermi level, respectively. Consequently, the overall Seebeck coefficient $\left(S_{total}=S_{\text{N}}+S_{\tau }+S_{ph}\right)$ can be estimated. Fig. 5B shows that the measured Seebeck coefficient as a function of temperature of MoS₂/h-BN device for n = 2 × 10¹² cm⁻² is well captured by this scattering model (more details in SI Appendix, Fig. S18). At higher gate voltages, the Fermi level of the MoS₂/h-BN sample is raised toward the conduction band, causing resonant scattering to be present only at lower temperatures (Fig. 4B). Due to the strong interaction of electrons with the hybridized band through such resonant scattering, the larger S values in the on state of MoS₂ lead to an unusually strong enhancement in the thermoelectric PF (S²σ, where σ is calculated from the four-probe sheet conductivity σ_s by considering the thickness of MoS₂) at an equivalent high bulk carrier concentration of ∼4.7 × 10¹⁸ cm⁻³. This is distinct from the S enhanced only due to the phonon drag effect, which occurs at a much lower doping concentration (∼10¹⁵ cm⁻³) without a sign change (59), thereby translating to a much lower PF. Fig. 5C shows the PF comparison between MoS₂/h-BN and MoS₂/SiO₂ samples as a function of temperature. When T > 120 K, the PF of the MoS₂/h-BN sample is comparable with that of the MoS₂/SiO₂ sample. However, with decreasing temperature, the PF of the MoS₂/h-BN sample drops significantly due to the positive $S_{\tau }$ contribution which cancels the contribution from traditional negative $S_{\text{N}}$. When temperature further decreases, Kondo scattering starts to dominate the thermoelectric transport. A large enhancement in PF up to two orders of magnitude is observed. Such a high PF value of 50 mW m⁻¹ K⁻² (T = 30 to 50 K), originating from band hybridization-enhanced S, is two to four orders of magnitude larger than the PF of other 2D materials (36, 37, 50, 51, 60–62) in the same temperature regime and exhibits the highest PF in 2D materials at all reported temperatures (Fig. 5D).

Conclusion

In summary, we discover that band hybridization due to sulfur vacancies exerts a strong influence on the thermoelectric properties of few-layer MoS₂ supported on h-BN substrate, whereas these effects are suppressed on SiO₂ substrate. The electric and thermoelectric transport in few-layer MoS₂ on h-BN match well with a strongly correlated Kondo-like behavior, leading to a large anomalous positive Seebeck coefficient of 2 mV/K in n-type MoS₂ in the on state. Importantly, our work demonstrates that such an effect can be electrostatically tuned to manipulate the Seebeck coefficient, leading to two orders of magnitude enhancement in thermoelectric PF. The ability to exhibit both negative Seebeck (diffusive) and positive Seebeck (band hybridized) coefficients in n-type MoS₂ suggests that a singly doped material could be used to fabricate thermoelectric devices, thus bypassing the need for multiple materials in thermoelectric devices. This work also points to the possibility of dopant engineering to make Kondo lattices (63) for nanothermoelectric devices.

Methods

MoS₂ and h-BN flakes were separately mechanically exfoliated onto SiO₂/Si substrates. The flakes are then examined by observing the contrast an optical microscope (in both bright-field and dark-field mode) and atomic force microscopy (AFM) to ensure that the surface, geometry, and thickness are suitable for subsequent measurements. MoS₂ flake was transferred onto h-BN flakes using standard wet transfer techniques by poly(methyl methacrylate) (PMMA). After that, electrodes were defined by standard electron beam lithography (EBL), followed by deposition of titanium/gold (Ti/Au) with thickness of 3 nm for Ti and 70 nm for Au. Ti was chosen owing to its low work function, comparable to the electron affinity of MoS₂ to form ohmic contacts. The STM measurements were performed using Omicron ultrahigh-vacuum LT-STM (<10⁻¹⁰ torr). Before the measurement, the tungsten tip was calibrated by Au (111) crystal. During STM measurements, the sample is grounded through the deposited Ti/Au electrode on top of the MoS₂ flake. The gate electrode is lead out by an aluminum wire. After wire bonding, the MoS₂/h-BN sample was annealed at 220 °C in the preparation chamber (<10⁻¹⁰ torr) to remove absorbents and form a better contact. STM and STS data were collected at liquid helium temperatures. Constant-current mode was employed to capture STM images, and external lock-in technique was employed to record STS data. Four-probe measurements were employed to eliminate contact resistance and extract a precise electrical conductivity of MoS₂ flakes for different gate voltages. The temperature-dependent mobility is extracted from transfer characteristics, via ${\mu }_{FE}=\frac{1}{C_{ox}}\frac{d\sigma }{d{V}_g}$, where $C_{ox}=12\times {10}^{-9}\hspace{0.17em}\text{F}/{\text{cm}}^2$ is the capacitance for 285-nm-thick SiO₂. The sheet conductivity $\left({\sigma }_s=\frac{L}{W}G\right)$ is converted from G by considering the length (L) and width (W) of the MoS₂ flake, and electrical conductivity is calculated from $\sigma =\frac{{\sigma }_s}{d}$ by considering its thickness (d). To measure the Seebeck coefficient S = V_TEP/ΔT, a temperature gradient is realized by applying a DC current bias (I) through a metal heater using a source meter (Keithley 6221); therefore, Joule heat and a temperature gradient along the sample are generated. The temperature gradient generates the thermoelectric voltage V_TEP, which is measured by a voltmeter (Keithley 6430). As a series of DC current bias with increasing values are applied to the heater, the corresponding V_TEP were recorded. The temperature gradient is measured through the four-probe resistance of thermometers.

Data and Materials Availability.

All data supporting the findings of this study are available within the article or SI Appendix.