Significance
The hexagonal flow pattern on Saturn is a striking example of turbulent self-organization. However, the mechanism of its formation and its depth remain unclear. There are two hypotheses: in one, the hexagon is shallow, extending to depths ranging from tens to hundreds of kilometers; in the other, it extends to thousands of kilometers. Here, we argue that the hexagon is likely very deep. Our model simultaneously and self-consistently produces alternating zonal jets, the polar cyclone, and hexagon-like polygonal structures similar to those observed on Saturn. These results show that compressible convection in rotating spherical shells is sufficient to produce Saturn-like polygonal zonal jets.
Keywords: planetary atmospheres, rotating convection, turbulence
Abstract
Numerous land- and space-based observations have established that Saturn has a persistent hexagonal flow pattern near its north pole. While observations abound, the physics behind its formation is still uncertain. Although several phenomenological models have been able to reproduce this feature, a self-consistent model for how such a large-scale polygonal jet forms in the highly turbulent atmosphere of Saturn is lacking. Here, we present a three-dimensional (3D) fully nonlinear anelastic simulation of deep thermal convection in the outer layers of gas giant planets that spontaneously generates giant polar cyclones, fierce alternating zonal flows, and a high-latitude eastward jet with a polygonal pattern. The analysis of the simulation suggests that self-organized turbulence in the form of giant vortices pinches the eastward jet, forming polygonal shapes. We argue that a similar mechanism is responsible for exciting Saturn’s hexagonal flow pattern.
In 1988, Godfrey (1) analyzed the 1981 flyby data from Voyager 2 and reported one of the most visually spectacular features in planetary atmospheres: the presence of a hexagonal pattern in the prograde zonal jet at around 15° away from Saturn’s north pole. Since its discovery, Saturn’s hexagon (hereafter “hexagon”) has been repeatedly observed, and we know that at least in the last 40 y or so, the hexagon has been present and relatively unchanged (2, 3). The hexagon exhibits some dynamical behavior, including drifting slowly in the westward/eastward direction with speeds ranging from −0.06 to 0.01° per day (in Saturn’s System III reference frame) (2, 4), although given the uncertainty associated with Saturn’s rotation period (5–7), it is rather difficult to infer the actual drift rate of the hexagon. The hexagon also encloses a circumpolar cyclonic (spinning in the planetary rotation direction) vortex that is also known to be a stable feature (3, 8). We refer the reader to a recent comprehensive review by Sayanagi et al. (9) for more detail on the observational and modeling history of Saturn’s atmosphere.
The existence of such a prominent and stable feature on Saturn gives us an opportunity to test different possibilities for how atmospheric dynamics in Saturn generates such features. Over the years, several models have been proposed. Shortly after the discovery of the hexagon, Allison et al. (10) argued that the hexagon is essentially a stationary Rossby wave produced by the interaction of the eastward jet with a large anticyclonic vortex to the south of the jet visible in the Voyager 2 data. When Cassini later visited Saturn, this large anticyclonic vortex was no longer present (8), questioning the idea of a forced Rossby wave. On the other hand, Sánchez-Lavega et al. (11) argue that the hexagon is a stationary unforced Rossby wave that exists on a deep (maybe deeper than 10-bars) quasigeostrophic zonal jet. In the most recent development on the modeling front, Morales-Juberías et al. (12) study how perturbations affect an eastward jet stream. In their model, perturbations evolve into hexagonal-shaped meanders when the jet decays below the 2-bar level. The speed, decay rate, and the curvature of the jet determine the dominant wave number of the meander in this model.
Laboratory experiments have also shed light on the possible mechanisms for hexagon formation. Sommeria et al. (13) performed experiments on a rotating annulus where barotropic zonal jets were generated using mechanical forcing in the form of mass sources and sinks. Depending on the mass flow rate and the rotation rate of the container, they reported the existence of wavy jets with different azimuthal wave numbers (from three to eight). They interpret these features as Rossby waves excited in the region where the potential vorticity has sharp gradients. Each edge of the wavy perturbation on the jet was accompanied by an adjacent vortex. More recently, Aguiar et al. (14) also reported wavy shapes in a barotropic zonal jet excited in rotating tanks using external forcing. Depending on the rotation rate of the tank and the flow speed of the forced jet, they report wavy features with wave numbers ranging from two to eight. They suggest that these polygonal patterns are the manifestation of a fully developed barotropic instability in a zonal jet. They also observe vortical features adjacent to the polygon edges on the zonal jet.
Considering the various theoretical models, simulations, and laboratory experiments discussed above, the essential idea emerges that jets can become unstable and give rise to polygonal features. However, we note that all of these studies either assume a zonal jet or it is generated via external forcing. Furthermore, the deep planetary convection, which might be the fundamental driving force behind the zonal jets, has not been modeled in the earlier studies of hexagon formation. A model of how highly nonlinear fluid turbulence self-organizes and gives rise to zonal jets with geometrical shapes is lacking.
The situation is rather different if we take a broader perspective of Saturn’s atmospheric dynamics. The planetary-scale alternating zonal jets on Saturn have been studied in great detail and have been generated in a completely spontaneous and self-consistent manner in models incorporating fluid turbulence. Here, two schools of thoughts have developed: on one hand, the alternating jets on gas giant planets are “shallow,” existing above 10 bars or so (15–17); on the other hand, zonal jets are “deep,” extending to tens of thousands of bars (18–22). In this regard, exciting developments were made recently shortly before Cassini took its final plunge into Saturn (the “Cassini Grand Finale”): the interpretation of the gravity harmonics from the final Cassini orbit hints at Saturnian zonal jets retaining their strength down to at least 100,000 bars (23), strongly suggestive of the deep jets scenario.
The recent Cassini results and the fact that the hexagon has remained stable for the last 40 y or so (unperturbed by the solar radiation forcing through Saturn’s year) suggest that it might be a deep-rooted feature as previously noted by Sánchez-Lavega et al. (11). Following this line of reasoning, here we report a global simulation where our primary aim is to simulate one of the most basic phenomena happening in the outer layers of Saturn, namely deep turbulent compressible convection in a rotating spherical shell. Several simulation studies have been conducted in the past to investigate the deep convection-driven atmospheric dynamics of gas and ice giant planets. They have reproduced the equatorial superrotation (19–22), similar to Saturn and Jupiter, as well as subrotation (24, 25), similar to the ice giants. Several (26, 27) have also investigated the properties (number of jets and their strength) of mid- to high-latitude alternating zonal jets on Saturn and Jupiter. However, none of these studies report Saturn-like polygonal jets.
Method
We assume that Saturn’s interior consists of a deep dynamo region, where strong magnetic fields are generated that inhibit strong zonal flows, and an outer “atmospheric” layer where the electrical conductivity of the fluid is low, allowing strong zonal flows. Here, we simulate hydrodynamic convection only in the outer layer. We assume a spherical shell with inner radius fixed at 0.9 (where is Saturn’s radius) and the outer radius at . The aspect ratio of the shell is then defined as , which is 0.9 in this case. The shell rotates with angular velocity . We employ the widely used anelastic approximation (28, 29) that allows density stratification in the fluid but filters out sound waves. In this approximation, thermodynamic quantities are decomposed as a static background and a small fluctuation . Here, we assume a density-stratified hydrostatic and adiabatic reference state defined by
| [1] |
where is reference-state temperature, is gravity, and is specific heat at constant pressure; is assumed constant. We assume an ideal gas fluid, giving a polytropic equation of state where the background density and temperature are related by , where (assumed to be two) is the polytropic index. Gravity is inversely proportional to ( being the radius), which assumes that most of the planetary mass is below 0.9 (30, 31). We refer the reader to Jones and Kuzanyan (30) for a more detailed discussion about the anelastic equations used in the planetary deep convection community.
Anelastic Equations.
The nondimensional evolution equation for velocity is
| [2] |
where is pressure; is velocity; is entropy; and are rotation and radial unit vectors, respectively; and
| [3] |
is the traceless rate-of-strain tensor with being the identity matrix and
| [4] |
The entropy is governed by
| [5] |
where
| [6] |
with . The viscous heating contribution is given by
| [7] |
The anelastic approximation also demands that
| [8] |
The above equations have been nondimensionalized using the shell thickness as the length scale; the inverse rotation rate as the timescale; the entropy contrast between top and bottom as the entropy scale; and density and temperature at top boundary as the density and temperature scales, respectively.
Several fundamental control parameters determine the behavior of the above set of equations: the Ekman number , the Prandtl number , and the Rayleigh number , where is viscosity, is the thermal diffusivity, and is gravity at . We assume viscosity and thermal diffusivity to be constant throughout the shell.
Simulation Code.
The hydrodynamic anelastic system of equations is solved using the open-source “MagIC” code (https://magic-sph.github.io/), which has been extensively benchmarked against other community codes (32). It uses a toroidal–poloidal decomposition to maintain strict divergenceless condition where needed: for example, mass flux is given by
where and are scalar potentials. The code is pseudospectral in nature and uses spherical harmonic functions horizontally and Chebyshev polynomials radially. The code utilizes the open-source library SHTns (33) to perform spherical harmonic transforms. The system of equations is time advanced using an explicit second-order Adams–Bashforth scheme for Coriolis and nonlinear terms and an implicit Crank–Nicolson scheme for the rest of the terms (34).
Control Parameters.
In this paper, we analyze and report results from one simulation case that acts as a proof of concept. The constant nondimensional control parameters for this case are , , and . We span five density-scale heights in the simulation, giving a density contrast of about 150 across the shell. The simulation was performed on a grid with 160, 960, and 1,920 points in , , and directions, respectively; the latitude–longitude grid has a maximum spherical harmonic degree of 640. Due to the highly demanding nature of the simulation, we could simulate it for about 0.1 viscous diffusion time (about 1,600 rotations), which is similar to earlier high-resolution studies (21, 35). Such a time span is likely not enough to resolve all of the available timescales in the system. For instance, the strength and number of zonal jets will evolve on a much longer viscous diffusion time (36). However, the jet meanders and the corresponding vortices (re-)form and evolve on the much faster convective turnover time. Furthermore, except for a slow change in the overall zonal flow energy, the kinetic energy also quickly settles to a statistically stationary state. These indicators suggest that the simulation results we discuss below are robust and nontransient phenomena.
Similar to Heimpel et al. (35), we employ hyperdiffusivity in which the viscosity becomes a function of spherical harmonic degree after a certain cutoff. MagIC code implements it by multiplying the following function to the primary viscous diffusion operator:
| [9] |
where defines the amplitude of the function, is the maximum spherical harmonic degree utilized in the simulation, is the degree after which the hyperdiffusion starts, and defines the rise of the function for degrees higher than . For our simulation, we use , , and .
The boundaries at and are impenetrable and stress free to the flow. Furthermore, the entropy is assumed constant on each boundary.
Results and Discussion
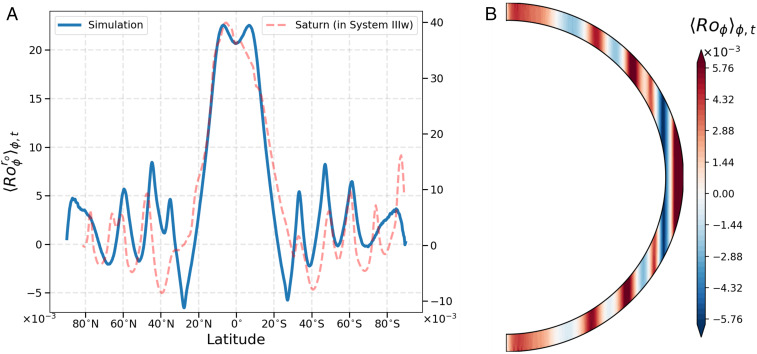
As the simulation progresses, rotating turbulent convection gradually builds up strong zonal flows. The generated zonal flow profile is shown in Fig. 1. With the control parameters that we use, the simulation generates a strong prograde jet, up to about 20° from the equator, which is followed by a strong retrograde jet in the vicinity of the tangent cylinder (an imaginary cylindrical surface tangent to the inner boundary and aligned with the rotation axis). Several more alternating jets form at mid- and high latitudes. These jets are by far the most energetic component of the flow, carrying more than 10 times the energy contained in the meridional and radial flow components, which is a generic property of simulations with a low-enough Ekman number and free slip boundaries (24, 37). The zonal jets in the simulation are qualitatively as well as quantitatively (within a factor of two) similar to the zonal jets observed on Saturn. Heimpel and Aurnou (26) show that the zonal flow velocity and the topographic effect (i.e., changing axially vertical fluid column height with latitude) due to the spherical geometry have a large impact on the width and number of zonal jets in such simulations. The fact that the shell thickness and the Rossby number of the zonal flows are similar to the values on Saturn is likely responsible for the good match of the simulation zonal flow profile with the observations.
Fig. 1.
A shows the azimuthally averaged zonal flow on the outer boundary of the simulation (left axis) and for Saturn (right axis). B shows the azimuthally averaged zonal flow on a meridional plane. The simulation data are time averaged over a few rotations of the shell. The zonal velocity magnitude is given in terms of the Rossby number defined here as , where is velocity, is shell rotation rate, and is outer radius of the shell. The Rossby number for Saturn is calculated using the observed cloud-level zonal flow velocities, Saturn’s mean radius m, and the rotation period rad/s in System IIIw (6).
The zonal jets are largely invariant along the rotation axis (despite a density drop of about 150 across the shell), demonstrating the strong influence of the rotation on the flow at these Rossby numbers. The westward jets north and south of the equator in the simulation are at a somewhat lower latitude than the corresponding jets on Saturn. Noting that these jets usually form in the vicinity of the tangent cylinder in such simulations (21, 31, 35), we speculate that Saturn’s atmosphere might extend somewhat deeper than 0.9, thereby giving a tangent cylinder at a slightly higher latitude.
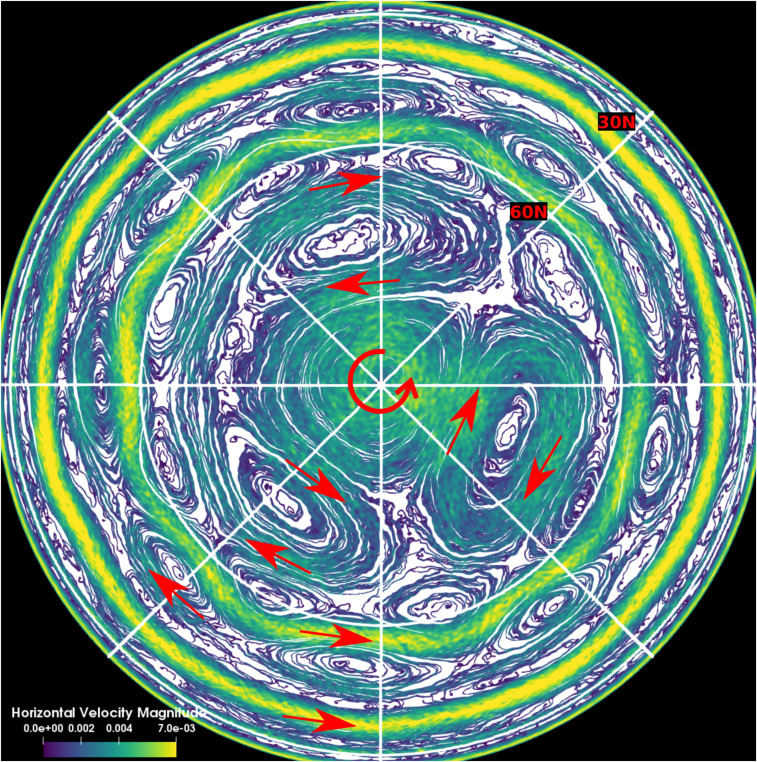
To reveal the various dynamical structures present in the simulation, in Fig. 2 we visualize a snapshot of the simulation using flow streamlines on a spherical surface at radius 0.95. The figure shows that the system dynamics is much richer than just zonal jets. Along with the jets, there are well-defined large-scale vortices at mid- and high latitudes. One large cyclonic vortex sits on the pole, accompanied by three anticyclonic neighbors. Another set of smaller cyclonic vortices follows to the south of these three anticyclones, followed by a strong eastward jet at about 60°N of the equator. In the polar region, (anti-)cyclones are arranged such that they roughly define an eastward jet with a triangular pattern. The pattern formed in the 60°N jet is one with nine edges. The other eastward jet visible close to 30°N also contains a polygonal pattern but with a higher wave number and less well-defined edges than the jet close to 60°N. The generation of such large-scale structures by convection plumes—whose size is similar to the wiggles in individual streamlines—shows the presence of an efficient inverse cascade of energy from small to large scales. As mentioned above, the number and the widths of the zonal jets are likely determined by the zonal flow strength and the topographic effect (26). However, which system parameters control the size and properties of the giant vortices remain unclear and demand a broad control parameter study.
Fig. 2.
Orthographic view of flow streamlines on a spherical surface at radius 0.95, as viewed from a north pole vantage point. The streamlines were generated by randomly placing 4,000 massless seed particles in the northern hemisphere and then tracing their trajectories governed by the local horizontal flow. The streamlines help us to visualize the instantaneous velocity structures. Since there is only a finite number of tracer particles, some of the regions on the spherical surface remain untraced. We fill this empty region with white color for clarity. The color of each streamline represents the magnitude of the local horizontal flow velocity in Rossby number. The 30°N and 60°N latitudes are highlighted in the plot using white circles. The red arrows indicated the general flow direction of the streamlines.
A view of the simulation from a midlatitude vantage point (SI Appendix, Fig. S1) reveals that broadly speaking, circular jets dominate at low latitudes, while large vortices form and appear to induce polygonal shapes in jets at mid- and high latitudes. This is likely driven by the topographical effect, due to the spherical shell geometry, which is stronger near the equator, promoting strong axisymmetric jets, while at higher latitudes, the effect decreases and the system approaches a rotating plane layer where the formation of giant vortices is favored (e.g., refs. 15–17, 26, 38, and 39).
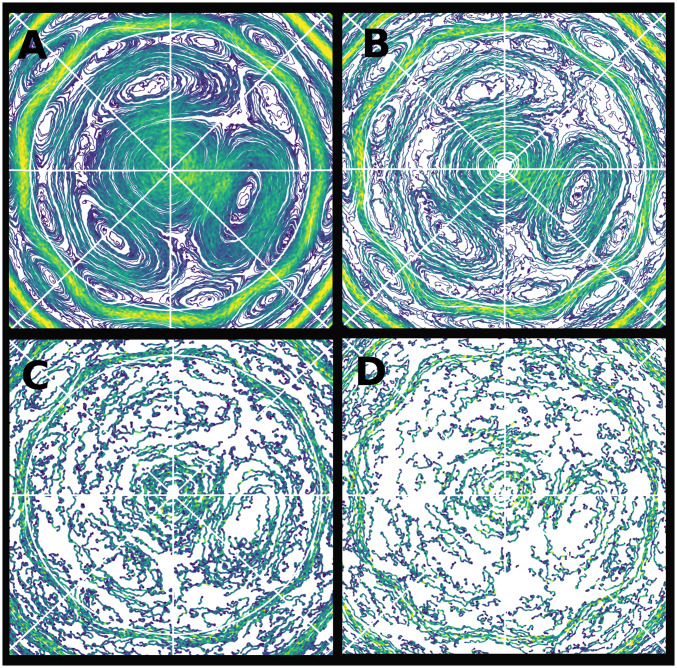
A remarkable property of the simulation is revealed when we inspect the flow structure as a function of radius in Fig. 3 where streamlines are plotted on spherical surfaces with different depths. As we look at shallower depths, the flow morphology in high-latitude regions changes from smoother streamlines, polar storm, polygonal jet, and coherent large vortices to one with more irregular-looking streamlines, a fainter polygonal jet, and a central cyclonic storm. We interpret this transition as follows. In density-stratified convection, shallower and lighter fluid must overturn faster to respond to the momentum of fluid parcels coming from deeper, thicker layers. This leads to a gradual increase in the mean velocity with increasing radius (e.g., refs. 31 and 40). In the current simulation, the mean velocity increases by a factor of three or more in shallower layers (SI Appendix, Fig. S2). Therefore, within one simulation, the Rossby number, which depends on the convective timescale (changing with radius) and the rotational timescale (staying constant), changes with depth. This leads to a situation where deeper layers with smaller Rossby number promote more coherent vortices and jets, while shallower layers with larger Rossby number favor more incoherent convection (31). This point is elucidated further by SI Appendix, Fig. S3, which shows regular streamlines in the deep and chaotic ones at shallower depths in a large vortex. Coexistence of both these regimes allows a scenario where the deeper energetic zonal jets manage to extend to the outermost layers, but the large vortices with weaker flow and smaller energy get overpowered by the shallower chaotic convection and therefore, lose their identity. The central cyclone, which can be thought of as a tiny zonal jet at the pole, survives since it carries significantly stronger flows than other nonpolar vortices. A similar scenario can be imagined for Saturn where the hexagonal shape of the jet is sustained by adjacent six large vortices, which are hidden by the more chaotic convection in the shallower layers.
Fig. 3.
Zoomed in streamline plots of the north polar regions of spherical surfaces at different depths: 0.95 in A, 0.97 in B, 0.99 in C, and 0.993 in D. All panels show the simulation case presented in Figs. 1 and 2. The figure highlights the gradual emergence of large coherent vortices as well as more coherent jets with depth. Note that the full white circle, representing a constant latitude, is located at 60°N of the equator in the local coordinates of each spherical surface. The 60°N latitude is omitted in D for clarity. Due to less coherent flow structures at progressively shallower depths (from A to D), flow streamlines become shorter and less surface filling, exposing more of the hypothetical white surface that is shown for highlighting the colored streamlines.
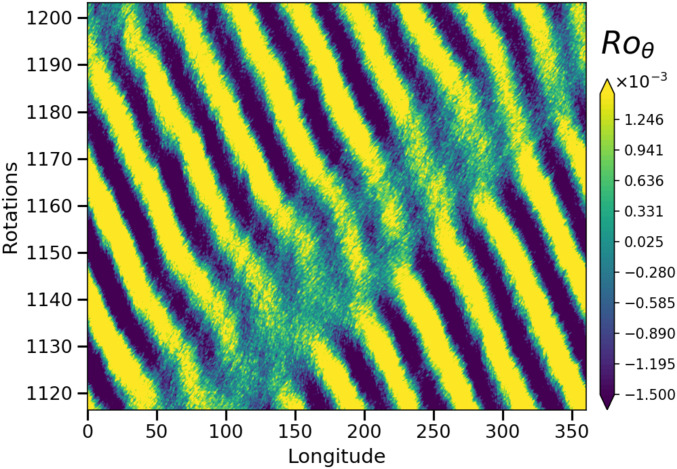
The southern hemisphere of the simulation also exhibits similar flow structures (SI Appendix, Fig. S4). However, the precise arrangement is different from the northern region. The polar cyclone is shifted away from the pole and is pinched by two large surrounding anticyclones. Here, too, a polygonal jet exists at around 60°S, albeit with polygonal edges only in a limited range of longitudes. Here, we note the observation of a similar ephemeral limited-longitude polygonal shape observed by Cassini on Saturn’s eastward jet at about 60°S (41). The polygonal edges are washed out in the eastward jet close to 30°S. This demonstrates the rich dynamics created by the turbulent fluid interactions. The strength and longitudinal extent of polygonal shapes in the jet are dynamic and evolve (Movie S1 shows evolution spanning about 90 rotations) due to nonlinear interactions. The wavy pattern, as well as the adjacent vortices, drifts in the westward direction on the 60°N/S eastward jets. Fig. 4 shows a time evolution of the meridional flow at 55°N demonstrating a coherent drift of about −2° per rotation. Saturn’s hexagon, on the other hand, is much more stable with −0.06° to 0.01° per day (2, 4). The eastward jet close to 30°N/S portrays similar behavior; however, this jet has less pronounced and short-lived modulations. Since the vortices become less favored at low latitudes, the low-latitude jets can indeed be expected to be less influenced by them.
Fig. 4.
The latitudinal velocity at 55°N of the equator as a function of time.
The polygonal modulations in the zonal jets are sensitive to the azimuthal length scale available. When we restrict our simulation domain to only one-quarter of the 0° to 360° longitudes, with periodic boundary conditions on the edges, the polygonal patterns disappear, and only circular jets remain. Here, the azimuthal length scale of the mid- to high-latitude zonal jets becomes similar to the length scale of the polygonal modulation. Such conditions do not support the formation of wavy jets in our setup. When we increased the size of the simulated wedge to cover 0° to 180° longitudes, the polygonal jets appeared again. Furthermore, the polygonal jets are also sensitive to the Rayeligh number of the simulation, which sets the mean Rossby number attained in the simulation. When we decreased the Rayleigh number from (used above) to , the polygonal shapes disappeared, and only circular jets remained. When we increased the Rayleigh number to (simulated for about 140 rotations due to computational constraints), the number of polygonal edges decreased from nine in the case discussed above to seven (SI Appendix, Fig. S5). This trend is similar to those found in earlier laboratory experiment where the wave number of the modulation on a zonal jet decreased as the Rossby number of the jet increased (13, 14).
Although the model does not capture every aspect of the observations of Saturn, it does, however, produce polygonal zonal jets self-consistently in a deep convection setup. The polygonal shapes form due to mid- to high-latitude vortices pinching adjacent zonal jets [see Marcus and Lee (42) for a similar interpretation]. The vortices, however, have much weaker flow (as compared with jets) that gets masked by the more incoherent convection at shallower layers, leaving only polygonal jets as the prevalent flow profile. We find that simulating the entire azimuthal extent of the shell is crucial for modeling meandering jets, which explains why earlier models with wedge simulation geometries did not produce such features. The westward drift of the polygonal shapes was faster (about −2° per rotation) than observations in our reported case. However, this drift was significantly lower (about −1.3° per rotation) in a simulation at a higher Rayleigh/Rossby number (SI Appendix, Fig. S5). Therefore, it is conceivable that a simulation with higher Rossby numbers than what we could achieve will show polygonal jets with much weaker drifts. A more detailed parameter study of the control parameter space should be possible in the future with increased computational resources, which will help us narrow down the finer ingredients needed to produce more observations simultaneously in a single model.
Data Availability.
The simulation input file that can be used to reproduce the results is available at https://doi.org/10.6084/m9.figshare.12110982.v1. The simulation code used is open access and is available at https://github.com/magic-sph/magic/.
Supplementary Material
Acknowledgments
R.K.Y. thanks Hao Cao for interesting discussions. The initial stages of this work were supported by the NASA Juno project. The computing resources were provided by the Research Computing, Faculty of Arts & Sciences, Harvard University, and NASA High-End Computing Program through the NASA Advanced Supercomputing Division at Ames Research Center.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
Data deposition: The simulation input file that can be used to reproduce the results is available at figshare: https://doi.org/10.6084/m9.figshare.12110982.v1. The simulation code used is open access and is available at https://github.com/magic-sph/magic/.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2000317117/-/DCSupplemental.
References
- 1.Godfrey D., A hexagonal feature around Saturn’s north pole. Icarus 76, 335–356 (1988). [Google Scholar]
- 2.Caldwell J., Turgeon B., Hua X. M., Barnet C. D., Westphal J. A., The drift of Saturn’s north polar spot observed by the Hubble Space Telescope. Science 260, 326–329 (1993). [DOI] [PubMed] [Google Scholar]
- 3.Sánchez-Lavega A., Lecacheux J., Colas F., Laques P., Ground-based observations of Saturn’s north polar spot and hexagon. Science 260, 329–332 (1993). [DOI] [PubMed] [Google Scholar]
- 4.Hueso R., et al. , Saturn atmospheric dynamics one year after Cassini: Long-lived features and time variations in the drift of the hexagon. Icarus 336, 113429 (2019). [Google Scholar]
- 5.Anderson J. D., Schubert G., Saturn’s gravitational field, internal rotation, and interior structure. Science 317, 1384–1387 (2007). [DOI] [PubMed] [Google Scholar]
- 6.Read P., Dowling T., Schubert G., Saturn’s rotation period from its atmospheric planetary-wave configuration. Nature 460, 608–610 (2009). [Google Scholar]
- 7.Mankovich C., Marley M. S., Fortney J. J., Movshovitz N., Cassini ring seismology as a probe of Saturn’s interior. I. Rigid rotation. Astrophys. J. 871, 1 (2019). [Google Scholar]
- 8.Fletcher L., et al. , Temperature and composition of Saturn’s polar hot spots and hexagon. Science 319, 79–81 (2008). [DOI] [PubMed] [Google Scholar]
- 9.Sayanagi K. M., et al. , “Saturn’s polar atmosphere” in Cambridge Planetary Science, Baines K. H., Flasar F. M., Krupp N., Stallard T., Eds. (Cambridge University Press, 2018), pp. 337–376. [Google Scholar]
- 10.Allison M., Godfrey D., Beebe R., A wave dynamical interpretation of Saturn’s polar hexagon. Science 247, 1061–1063 (1990). [DOI] [PubMed] [Google Scholar]
- 11.Sánchez-Lavega A., et al. , The long-term steady motion of Saturn’s hexagon and the stability of its enclosed jet stream under seasonal changes. Geophys. Res. Lett. 41, 1425–1431 (2014). [Google Scholar]
- 12.Morales-Juberías R., Sayanagi K. M., Simon A., Fletcher L. N., Cosentino R., Meandering shallow atmospheric jet as a model of Saturn’s north-polar hexagon. Astrophys. J. Lett. 806, L18 (2015). [Google Scholar]
- 13.Sommeria J., Meyers S. D., Swinney H. L., Laboratory model of a planetary eastward jet. Nature 337, 58–61 (1989). [Google Scholar]
- 14.Aguiar A. C. B., Read P. L., Wordsworth R. D., Salter T., Yamazaki Y. H., A laboratory model of Saturn’s north polar hexagon. Icarus 206, 755–763 (2010). [Google Scholar]
- 15.Williams G., Jovian dynamics. Part III. Multiple, migrating, and equatorial jets. J. Atmos. Sci. 60, 1270–1296 (2003). [Google Scholar]
- 16.Cho J. Y., Polvani L. M., The morphogenesis of bands and zonal winds in the atmospheres on the giant outer planets. Science 273, 335–337 (1996). [DOI] [PubMed] [Google Scholar]
- 17.Liu J., Schneider T., Mechanisms of jet formation on the giant planets. J. Atmos. Sci. 67, 3652–3672 (2010). [Google Scholar]
- 18.Busse F., A simple model of convection in the Jovian atmosphere. Icarus 29, 255–260 (1976). [Google Scholar]
- 19.Christensen U. R., Zonal flow driven by deep convection in the major planets. Geophys. Res. Lett. 28, 2553–2556 (2001). [Google Scholar]
- 20.Aurnou J. M., Olson P. L., Strong zonal winds from thermal convection in a rotating spherical shell. Geophys. Res. Lett. 28, 2557–2559 (2001). [Google Scholar]
- 21.Heimpel M., Aurnou J., Wicht J., Simulation of equatorial and high-latitude jets on jupiter in a deep convection model. Nature 438, 193–196 (2005). [DOI] [PubMed] [Google Scholar]
- 22.Kaspi Y., Flierl G. R., Showman A. P., The deep wind structure of the giant planets: Results from an anelastic general circulation model. Icarus 202, 525–542 (2009). [Google Scholar]
- 23.Galanti E., et al. , Saturn’s deep atmospheric flows revealed by the Cassini grand finale gravity measurements. Geophys. Res. Lett. 46, 616–624 (2019). [Google Scholar]
- 24.Aurnou J., Heimpel M., Wicht J., The effects of vigorous mixing in a convective model of zonal flow on the ice giants. Icarus 190, 110–126 (2007). [Google Scholar]
- 25.Gastine T., Wicht J., Aurnou J., Zonal flow regimes in rotating anelastic spherical shells: An application to giant planets. Icarus 225, 156–172 (2013). [Google Scholar]
- 26.Heimpel M., Aurnou J., Turbulent convection in rapidly rotating spherical shells: A model for equatorial and high latitude jets on Jupiter and Saturn. Icarus 187, 540–557 (2007). [Google Scholar]
- 27.Gastine T., Heimpel M., Wicht J., Zonal flow scaling in rapidly-rotating compressible convection. Phys. Earth Planet. In. 232, 36–50 (2014). [Google Scholar]
- 28.Braginsky S. I., Roberts P. H., Equations governing convection in earth’s core and the geodynamo. Geophys. Astrophys. Fluid Dyn. 79, 1–97 (1995). [Google Scholar]
- 29.Lantz S., Fan Y., Anelastic magnetohydrodynamic equations for modeling solar and stellar convection zones. ApJS 121, 247–264 (1999). [Google Scholar]
- 30.Jones C. A., Kuzanyan K. M., Compressible convection in the deep atmospheres of giant planets. Icarus 204, 227–238 (2009). [Google Scholar]
- 31.Gastine T., Wicht J., Effects of compressibility on driving zonal flow in gas giants. Icarus 219, 428–442 (2012). [Google Scholar]
- 32.Jones C., et al. , Anelastic convection-driven dynamo benchmarks. Icarus 216, 120–135 (2011). [Google Scholar]
- 33.Schaeffer N., Efficient spherical harmonic transforms aimed at pseudospectral numerical simulations. Geochem., Geophys., Geosyst. 14, 751–758 (2013). [Google Scholar]
- 34.Glatzmaier G. A., Numerical simulations of stellar convective dynamos. I. The model and method. J. Comp. Phys. 55, 461–484 (1984). [Google Scholar]
- 35.Heimpel M., Gastine T., Wicht J., Simulation of deep-seated zonal jets and shallow vortices in gas giant atmospheres. Nat. Geosci. 9, 19–23 (2016). [Google Scholar]
- 36.Manfroi A., Young W., Slow evolution of zonal jets on the beta plane. J. Atmos. Sci. 56, 784–800 (1999). [Google Scholar]
- 37.Yadav R. K., Gastine T., Christensen U. R., Duarte L., Reiners A., Effect of shear and magnetic field on the heat-transfer efficiency of convection in rotating spherical shells. Geophys. J. Int. 204, 1120–1133 (2016). [Google Scholar]
- 38.Rhines P. B., Waves and turbulence on a beta-plane. J. Fluid Mech. 69, 417–443 (1975). [Google Scholar]
- 39.Guervilly C., Hughes D. W., Jones C. A., Large-scale vortices in rapidly rotating Rayleigh–Bénard convection. J. Fluid Mech. 758, 407–435 (2014). [Google Scholar]
- 40.Hotta H., Rempel M., Yokoyama T., High-resolution calculation of the solar global convection with the reduced speed of sound technique. II. Near surface shear layer with the rotation. Astrophys. J. 798, 51 (2014). [Google Scholar]
- 41.Vasavada A. R., et al. , Cassini imaging of Saturn: Southern hemisphere winds and vortices. J. Geophys. Res. Planets 111, E05004 (2006). [Google Scholar]
- 42.Marcus P., Lee C., A model for eastward and westward jets in laboratory experiments and planetary atmospheres. Phys. Fluids 10, 1474–1489 (1998). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The simulation input file that can be used to reproduce the results is available at https://doi.org/10.6084/m9.figshare.12110982.v1. The simulation code used is open access and is available at https://github.com/magic-sph/magic/.