Consistent scaling of inbreeding depression in space and time in a house sparrow metapopulation

Significance

Inbreeding often causes negative effects that, according to theory, may vary in severity with population size or harshness of the environment. Studying this in wild vertebrates has been prevented by the difficulty of collecting long-term data on multiple populations. We used genomic estimates of inbreeding to investigate its effects on fitness components and morphological traits in bird populations. Inbred individuals had lower survival and produced fewer offspring compared with noninbred individuals. Inbreeding depression was constant across populations with differing environments and population sizes. Consequently, populations with more resident inbreeding suffered higher total loss of fitness due to inbreeding. Our results highlight the importance of considering inbreeding in conservation and management of populations with a wide range of characteristics.

Abstract

Inbreeding may increase the extinction risk of small populations. Yet, studies using modern genomic tools to investigate inbreeding depression in nature have been limited to single populations, and little is known about the dynamics of inbreeding depression in subdivided populations over time. Natural populations often experience different environmental conditions and differ in demographic history and genetic composition, characteristics that can affect the severity of inbreeding depression. We utilized extensive long-term data on more than 3,100 individuals from eight islands in an insular house sparrow metapopulation to examine the generality of inbreeding effects. Using genomic estimates of realized inbreeding, we discovered that inbred individuals had lower survival probabilities and produced fewer recruiting offspring than noninbred individuals. Inbreeding depression, measured as the decline in fitness-related traits per unit inbreeding, did not vary appreciably among populations or with time. As a consequence, populations with more resident inbreeding (due to their demographic history) paid a higher total fitness cost, evidenced by a larger variance in fitness explained by inbreeding within these populations. Our results are in contrast to the idea that effects of inbreeding generally depend on ecological factors and genetic differences among populations, and expand the understanding of inbreeding depression in natural subdivided populations.

Inbreeding depression manifests in life-history and morphological traits and has widespread consequences at both individual and population levels (1). The most severe effects are commonly found in fitness-related traits (1–4). Reductions in survival and reproductive success due to inbreeding can be substantial and eventually lead to extinction of a population (5–7).

At the population level, inbreeding can be defined, in a narrow sense, as mating between relatives that occurs more often than expected under random mating. More broadly, inbreeding also includes any mating between relatives (whether random or nonrandom at the population level) and the loss of heterozygosity caused by genetic drift (1). As parental relatedness varies, individual inbreeding also varies within a population, a heterogeneity that can be captured by individual estimates of inbreeding. Such estimates can be extracted from individual pedigrees (1, 8). Until recently, the effects of inbreeding have been challenging to study in natural populations due to the lack of deep and accurate pedigrees. However, as individual inbreeding always results in higher genomic homozygosity, it can be directly quantified based on genomic data (9). Here we use realized estimates of inbreeding that are based on genome-wide homozygosity caused by both mating between relatives and genetic drift. Genomic inbreeding estimates have enabled quantification of realized inbreeding levels without bias caused by shallow or incomplete pedigree information; however, empirical studies in natural populations are still rare (9–13).

Population demography has profound consequences for inbreeding levels and potentially for the strength of inbreeding depression (see SI Appendix, Table S1 for theoretical expectations). In large populations, selection against deleterious alleles is more efficient, due to weaker genetic drift. Also, a slow rate of inbreeding due to low probability of mating with relatives contributes to maintaining heterozygosity at overdominant loci (14, 15). In contrast, small populations experience higher inbreeding levels that result in a higher proportion of homozygous loci. This exposes recessive deleterious alleles to selection and eventually to purging in small populations (14, 16). In addition, genetic drift drives alleles either to fixation or loss at a higher rate in small than in large populations, and recessive alleles with deleterious effects may, consequently, drift to fixation. Therefore, when a population is at mutation–selection–drift equilibrium, the mean fitness of a large population is expected to be higher than the mean fitness of a small population, but inbreeding depression is expected to be stronger in a large population (14). The quantitative importance of the effect of population size on inbreeding depression is highly dependent on the architecture of the genetic load; especially important are the level of dominance at relevant loci and the number of deleterious alleles within the effect size range [i.e., selection coefficient close to 1/(4N_e) (17), where N_e is effective population size] that could cause differences in inbreeding depression between populations of differing sizes (18, 19). However, natural populations are rarely at equilibrium (19) and the actual importance of purging in nature is controversial (1, 5, 14). For instance, purging may be counteracted by dispersal in subdivided populations, because dispersal increases effective population size and introduces both beneficial and harmful alleles through gene flow (20, 21). Dispersal may also generate heterosis (i.e., hybrid vigor), that is, increased fitness of offspring produced by parents from different populations, caused by masking of negative inbreeding effects (22).

Environmental heterogeneity is also expected to cause variation in inbreeding effects between and within populations (23–26). Harsher environments have been documented to lead to stronger selection and inbreeding depression, especially in laboratory conditions (27). However, due to the difficulty of collecting appropriate data, testing whether inbreeding by environment interactions are important in the wild is challenging (28, 29).

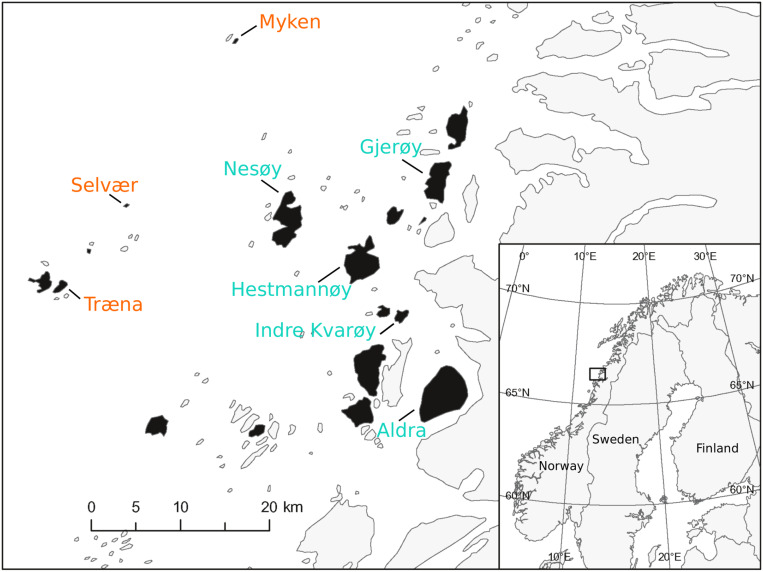
Studies on spatiotemporal variation in inbreeding depression of natural vertebrate populations are lacking. In addition, we know little about how the total impact of inbreeding changes due to variation in inbreeding depression and variation in the amount of inbreeding, effects which can go in opposite directions (e.g., small populations can experience more inbreeding but less inbreeding depression than large ones)—resulting in an uncertain outcome at the population level. To fill this knowledge gap, it is crucial to quantify the heterogeneity in inbreeding depression and inbreeding levels within and among wild subdivided populations with different environmental and demographic characteristics. Here we used data on more than 3,100 adult individuals to study inbreeding depression in multiple island populations of house sparrows (Passer domesticus) in northern Norway that have been monitored since 1993 (30–33) (Fig. 1). To estimate pedigree inbreeding coefficients and recruit production, we constructed a metapopulation pedigree using single-nucleotide polymorphism (SNP) data (34). First, we compared pedigree (F_PED) and genomic inbreeding coefficients (F_GRM, for genomic relatedness matrix (35); F_ROH, for runs of homozygosity (36) based on 183k SNPs, and examined whether the level of inbreeding varied between populations and years. Second, we quantified the effect of realized genomic inbreeding on annual and lifetime reproductive success, survival, and morphology. Third, we examined whether inbreeding effects on individual fitness and morphology varied across years and populations. In our system, this spatiotemporal variation reflects differences in, for example, habitat type (37, 38) (SI Appendix, Table S2), population size (32) (SI Appendix, Fig. S1), and environmental conditions such as climate and weather (30, 37).

Fig. 1.

Map of the ∼1,600-km² house sparrow study system at the Helgeland coast in Norway. The 18 islands in the study metapopulation are shown in black, and other islands (without sparrows) and the mainland are in gray. The eight islands included in the current study are indicated with their names. The study system consists of two distinct habitat types: 1) farm islands (turquoise names), and 2) nonfarm islands (orange names), where the sparrows live on dairy farms and in gardens, respectively.

Results

Spatiotemporal Variation in Genomic Inbreeding.

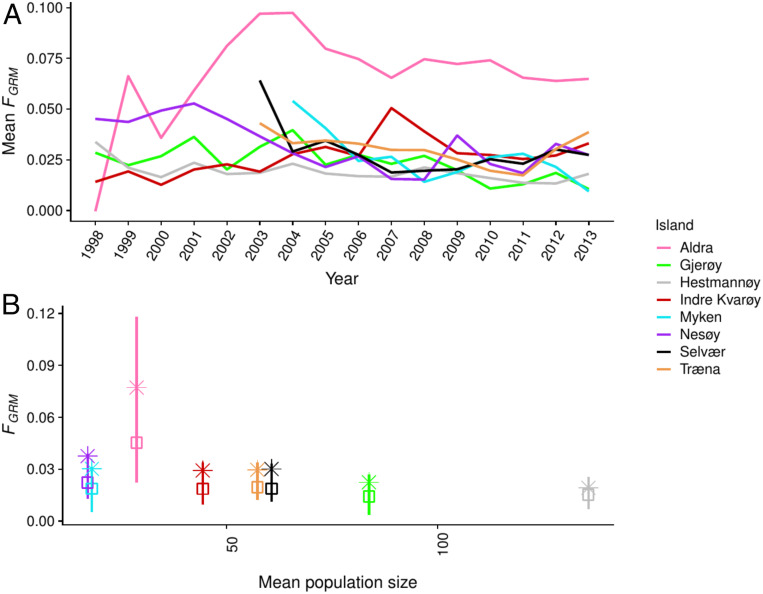
Levels of inbreeding differed between islands (Fig. 2A and SI Appendix, Table S3) and years (Fig. 2A), with strong correlations between F_GRM, F_ROH, and F_PED at the individual level (r > 0.8; SI Appendix, Fig. S2). Variation among islands accounted for 8.5% of the total variation in individual inbreeding estimates (F_GRM; i.e., islands differed in their mean values of inbreeding, calculated from posterior modes; Table 1). In contrast, annual variation within islands (“island-year”) explained only 2.5% of the variance in inbreeding. Randomization tests showed that both island and island-year variances in F_GRM were larger than expected under the null hypothesis that inbreeding varied randomly across islands and years (1,000 replicates for mode of island, P < 0.001, and island-year, P = 0.006). Inbreeding levels were highest on the island of Aldra, where the median F_GRM was 0.045 (interquartile range [IQR] = 0.022 to 0.118; median F_ROH = 0.028, IQR = 0.008 to 0.085; Fig. 2 and SI Appendix, Table S3). The high inbreeding level in the Aldra population was likely caused by a rather recent colonization event, small population size, and lower immigration rates compared with other populations (39). In contrast, the median F_GRM in the largest population (Hestmannøy) was 0.015 (IQR = 0.007 to 0.026; median F_ROH = 0.005, IQR = 0.000 to 0.011). The other islands showed more similar intermediate levels of inbreeding, and mean inbreeding level decreased when population size increased (Spearman’s correlation coefficient ρ = −0.833, P = 0.015; Fig. 2). Among-island variation in mean inbreeding was not associated with broad-scale habitat differences, since sparrows had similar inbreeding levels on farm islands (median F_GRM = 0.017, IQR = 0.007 to 0.030) and nonfarm islands (median F_GRM = 0.019, IQR = 0.011 to 0.033; 95% Bayesian credible interval [BCI] for difference in means of standardized F_GRM from −0.735 to 0.471; SI Appendix, Fig. S3A and Table S4).

Fig. 2.

Inbreeding levels of adult individuals on each study island. (A) Mean inbreeding coefficient (F_GRM) on each study island over the study period. (B) The median (□), interquartile range (|), and mean (*) of F_GRM on each island plotted against the mean population size over the study period.

Table 1.

Partitioning of variance in standardized F_GRM into spatial (island) and temporal (island-year) components

Random variances	Mean	Mode [95% BCI]
Island	0.147	0.086 [0.044, 0.405]
Island-year	0.032	0.025 [0.012, 0.065]
Residual variance	0.902	0.901 [0.855, 0.952]

A linear mixed-effects model was fitted with sex as a fixed factor and random intercepts for island and island-year. Means and modes of parameter estimates are presented, along with 95% BCIs.

To examine whether our data provided a sufficient range of inbreeding levels to be able to detect inbreeding depression within each population, we estimated identity disequilibrium [ID, quantified as g₂ (40)] that measures the variance in inbreeding among individuals. ID was positive for all study populations (SI Appendix, Fig. S4), showing there was potential to detect inbreeding effects within all of them. Concordant to F_GRM levels, ID was highest on Aldra (g₂ = 0.0049, 95% confidence interval [CI] from 0.0036 to 0.0061) and lowest on Hestmannøy (g₂ = 0.0014, 95% CI from 0.0010 to 0.0018).

Strong and Consistent Inbreeding Depression in Fitness Components across Time and Space.

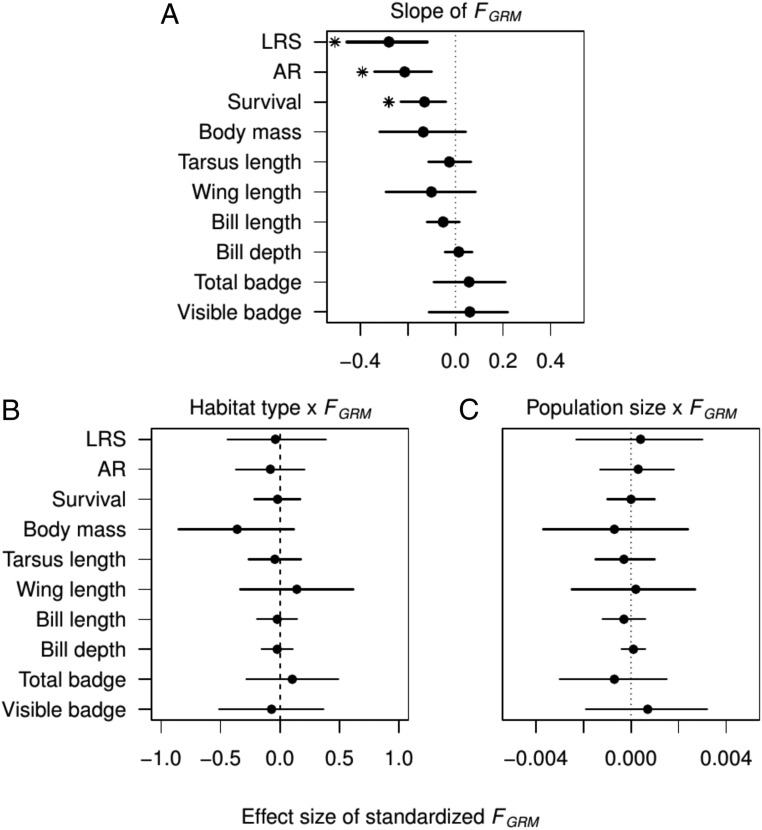
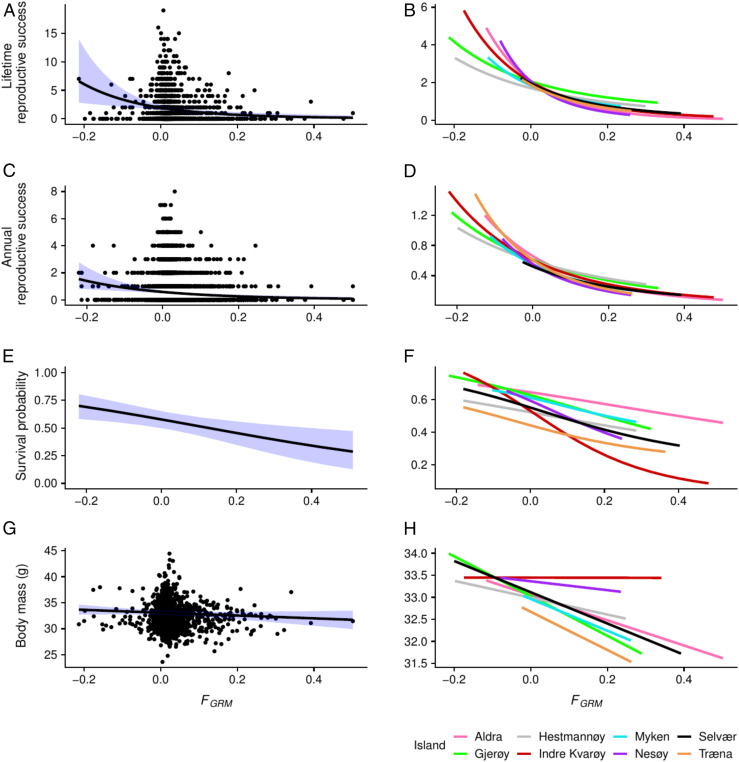
To study the effect of inbreeding on reproductive success using animal models (41), we constructed a SNP pedigree at the metapopulation level (for details, see SI Appendix, Results). Our results showed a strong negative effect of inbreeding on individual fitness across all island populations: Lifetime reproductive success (LRS) decreased when inbreeding increased (Figs. 3 and 4 and SI Appendix, Fig. S5). For example, individuals with F_GRM = 0.125 produced on average 47% (95% BCI from 40 to 57%) fewer offspring during their lifetime than individuals with F_GRM = 0. For comparison, using F_ROH as the measure of inbreeding, the LRS of individuals with F_ROH = 0.125 was on average 61% (95% BCI from 50 to 72%) lower than individuals with F_ROH = 0 (SI Appendix, Fig. S5). This strong and negative effect of inbreeding on lifetime reproductive success was a consequence of both decreased adult survival and lower annual reproductive success (AR; Figs. 3 and 4 and SI Appendix, Fig. S5; for more details, see SI Appendix, Table S5). There was no evidence that males and females differed with respect to effects of inbreeding on reproductive success or adult survival (SI Appendix, Table S6).

Fig. 3.

Estimates of the main effect of inbreeding and its interaction with environmental variables on life-history and morphological traits. (A) Effect of inbreeding estimated with standardized F_GRM on lifetime reproductive success, annual reproductive success, survival probability, and seven morphological traits. (B) Interaction effect between F_GRM and habitat type (farm island as the baseline) on the same fitness components and morphological traits as in A. (C) Interaction effect between F_GRM and annual population size on the studied traits. Results are from animal models fitted in INLA for LRS, AR, and morphological traits, and from capture–mark–recapture models fitted in JAGS for survival probability. The interaction terms between F_GRM and habitat type, annual population size, and sex were included in the models fitted for B and C but not in the model fitted for A. Posterior mean effect size is indicated with a dot, and the corresponding 95% BCI is indicated with a horizontal line. A strong effect, when the 95% BCI does not overlap 0, is indicated with an asterisk.

Fig. 4.

Effect of inbreeding on reproductive success, survival, and body mass. (A, C, E, and G) Lines are predicted mean effects of inbreeding (F_GRM) over the metapopulation system, shaded blue areas show 95% BCIs, and individual observations are plotted as points (omitted from E for clarity). (B, D, F, and H) Island-specific predicted mean effects of inbreeding. (A–D) Lifetime reproductive success (A and B) and annual reproductive success (C and D) were estimated as the number of offspring recruiting the adult population that an individual produced during its lifetime or per year, respectively. (E and F) The relationship between survival probability and inbreeding. (G and H) Body mass is based on all adult measurements and adjusted to trait value as 1-y-old. The predicted lines were produced using animal models fitted in INLA (A, D, G, and H), or capture–mark–recapture models in JAGS (E and F). The results of these models are presented in SI Appendix, Table S5.

We found no evidence for the effect of inbreeding on fitness components to vary with either habitat type (farm vs. nonfarm island) or population size, as indicated by the 95% BCIs of the interactions between inbreeding and habitat type or annual population size for all fitness components (Fig. 3 B and C and SI Appendix, Table S6). To examine if inbreeding depression varied spatiotemporally, we included two random slope terms in the mixed-effects models: an inbreeding by island interaction (i.e., F_GRM x island) that captured spatial variation, and an inbreeding by island-year interaction (i.e., F_GRM x island-year) that captured temporal variation. These models indicated that inbreeding depression of both annual and lifetime reproductive success was similar among the islands (SI Appendix, Fig. S6A and Table S5), as well as between years within islands (SI Appendix, Fig. S7 and Table S5). Accordingly, variation in inbreeding effects on reproductive success among islands or among years within islands explained only small amounts of the variation in inbreeding depression (e.g., F_GRM x island for LRS: mean σ² = 0.030, 95% BCI from 0.004 to 0.100; SI Appendix, Fig. S7 and Table S5). To examine whether these variances were larger than expected by chance, we conducted permutations randomizing the island and island-year variables in our data. These randomization tests suggest that the variances in inbreeding depression between islands and years were not larger than would be expected by chance given the data structure (P > 0.05 in all tests for LRS and AR; SI Appendix, Table S7). Hence, we conclude that the strong inbreeding depression in both annual and lifetime reproductive success was remarkably consistent across time and space. Nevertheless, the proportion of variance in fitness components explained by inbreeding was larger in smaller populations, as indicated by highly negative relationships between the proportion of variance explained by F_GRM and population size (ρ between −0.881 and −0.710; P values between 0.007 and 0.058; SI Appendix, Fig. S8), that is, the relative effect of inbreeding on fitness decrease was stronger when population size was smaller. This result is likely caused by higher variance in inbreeding in smaller populations, which in turn is suggested by a negative correlation between g₂ and population size (ρ = −0.738, P = 0.046).

The overall negative effect of inbreeding on survival probability was strong at the metapopulation level (β = −0.155, 95% BCI from −0.179 to −0.051; Figs. 3 and 4E and SI Appendix, Table S5). Furthermore, we found evidence for spatially homogeneous inbreeding depression in survival across the islands (the 95% BCIs of all island x F interaction terms overlapped 0; Fig. 4F and SI Appendix, Table S8). This result was also supported by a lower deviance information criterion (DIC) value of the model including island only as a fixed factor (DIC = 9,555) compared with the model also including an interaction term between inbreeding and island (DIC = 9,678). Similarly, inbreeding effects on survival were consistent through years, as indicated by the lower DIC value of the model including year only as a fixed factor (DIC = 9,780) than the model including also an interaction term between inbreeding and year (DIC = 9,801; SI Appendix, Table S9).

To further compare the inbreeding load among populations, we estimated the number of lethal equivalents, that is, the group of deleterious alleles that have a cumulative lethal effect when homozygous (1, 42), for each fitness component on each island. The estimated number of lethal equivalents ranged from 6.16 to 23.80 for LRS, 8.84 to 15.97 for AR, and 1.03 to 14.19 for survival (SI Appendix, Table S10). The general pattern was that the numbers of lethal equivalents were higher for LRS and AR than for survival, and relatively similar across islands for each fitness component (all 95% BCIs overlapped among the islands).

Weak Evidence for Inbreeding Depression in Morphological Traits.

We found weak evidence that inbreeding affected house sparrow morphology: Inbred individuals tended to be lighter (β = −0.14 gram per unit change in standardized F_GRM, 95% BCI from −0.32 to 0.04) and have shorter bills (β = −0.05 millimeter per unit change in standardized F_GRM, 95% BCI from −0.12 to 0.017) than noninbred individuals (Figs. 3A and 4 and SI Appendix, Table S5). However, wing length, bill depth, tarsus length, and total and visible badge sizes did not show any effect of inbreeding (Fig. 3A and SI Appendix, Table S5). Likewise, we found little spatial and temporal variation in the effects of inbreeding on morphological traits; in general, there was no evidence that the effect differed between islands or years within islands (SI Appendix, Fig. S6 and Tables S5 and S7). Only the effect of inbreeding on wing length varied more across islands than expected by chance (mean σ² = 0.048; randomization test: P = 0.009; SI Appendix, Tables S5 and S7). Furthermore, the variance among years within islands in the effect of inbreeding was larger than expected by chance only for wing length (mean σ² = 0.032; randomization test: P = 0.003) and bill depth (mean σ² = 0.003; randomization test: P = 0.03). However, island-specific inbreeding effects on morphology were generally weak (SI Appendix, Fig. S6).

Discussion

Contrary to theoretical predictions (14, 16, 23, 25, 26), the negative inbreeding effects on fitness components of wild house sparrow populations were consistent both in space and time—despite the large variation in inbreeding levels, population sizes, and environmental conditions. Thus, after accounting for differences in mean fitness of our study populations, a given proportion of autozygous loci caused a strikingly similar reduction in fitness of inbred individuals relative to noninbred individuals across environments. Our results differ from more common studies conducted on single populations of mammals (28) and birds (29, 43), which have found inbreeding effects to vary over time. Although only few other studies have been able to compare inbreeding depression in natural environments across populations within the same species, our results add to the current empirical evidence suggesting that inbreeding depression in fitness-related traits may not be strongly dependent on ecological conditions (5, 44). Here, we conducted temporal and spatial analyses that capture the combined environmental differences among habitat types, islands, and years within islands, and thus broad inbreeding by environment interactions (I x E). Further studies are needed to study the effects of, for example, more specific weather phenomena or small-scale ecological differences on inbreeding depression.

Population size explained only a small proportion of the variance in inbreeding depression across the metapopulation (Fig. 3C). This implies that our range of local population sizes (N_e), which is approximately between 10 and 100 (32, 45), did not result in measurable differences in the strength of selection against inbred individuals via the processes of purging or fixation of deleterious alleles. There may be several reasons why the expected decrease in inbreeding depression in small populations was not observed. First, in isolated populations at mutation–selection–drift equilibrium, the impact of effective population size depends on the genetic architecture of the load; only deleterious alleles with a proportional effect on fitness near the range of 1/(4N_e) (17) (here ca. 1/40 to 1/400) have a fate that varies with N_e; they tend to either go to fixation or be lost due to drift in small populations, while they remain at low frequencies and contribute to inbreeding depression in large ones (18, 19). This category of large-effect alleles may be rare in our study populations. If inbreeding depression is polygenic and mostly caused by deleterious alleles at many loci where each allele has a small effect on fitness (2), the combined effect of all slightly deleterious alleles could vary little among populations, even if there was spatial variation (due to, e.g., differences in N_e) in the relative frequencies of some of these small-effect alleles. Second, the populations are not isolated; the F_ST estimates between them are rather small (SI Appendix, Table S11), and results from previous studies in the same metapopulation suggest that dispersal rates may be relatively high [0.05 to 0.30 (37)], while variation in local effective size is approximately one order of magnitude (table S4 in ref. 32). Thus, dispersal may be enough to homogenize the distribution of deleterious alleles and ensure constant inbreeding depression at the metapopulation scale. Finally, local populations may not be at equilibrium (19). For example, the most inbred population on Aldra has a relatively small population size, but due to a recent founder effect, it is not at equilibrium and there has possibly not yet been enough time to fix or efficiently purge deleterious alleles. Consequently, inbreeding depression is as strong on Aldra as in other populations within the metapopulation. However, Aldra still keeps the memory of the recent bottleneck in terms of a high degree of resident inbreeding and high variance in inbreeding. Thus, this population pays a larger total cost of inbreeding than expected from its size, since a larger proportion of variance in fitness traits is due to losses caused by inbreeding (SI Appendix, Fig. S8). This illustrates that although metapopulation dynamics may maintain a similar inbreeding depression among local populations, some of them may still experience stronger total impact of inbreeding, due to their demographic history.

Inbreeding depression may vary with environmental conditions, which could result in not only spatial variation but also variation among years within local populations. The actual developmental and physiological effects of inbreeding in the studied house sparrow metapopulation are not known but, due to the temporally constant inbreeding depression (SI Appendix, Fig. S7 and Table S7), our results suggest that these changes are not strongly affected by extrinsic factors. For example, if inbreeding depression was caused by genes affecting energy metabolism (46), environmental factors, such as extreme weather phenomena, could be expected to mediate even stronger inbreeding depression (26). On the other hand, the strength of inbreeding depression caused by genes affecting intrinsic factors, such as sperm (47) or egg quality (48, 49), would likely be less affected by the environment. Nevertheless, laboratory studies have shown that inbreeding depression can be more severe under stress caused by extrinsic factors, such as heat and intraspecific competition, than under benign environmental conditions (27). Interactions between environmental conditions and inbreeding may appear less important for the severity of inbreeding depression in natural populations than in experimental studies, for example, because experiments have manipulated the environmental variation outside the natural range of the study organism (28). It is also possible that environmental factors could counteract each other, so that a closer examination of ecological and genetic mechanisms would be required to understand why inbreeding depression appears consistent. For example, in our study system, nestling and adult survival and population densities increase with temperature (30, 37). In addition, inbred individuals may suffer higher fitness costs of competition (14, 50) at higher population densities. Thus, the net effect of temperature-dependent survival and differential costs of competition could be that we observe similar inbreeding depression at different densities.

We found strong inbreeding depression in fitness components but weak inbreeding effects in morphological traits. Traits with large directional dominance variance, such as reproductive success, have also previously been shown to exhibit more severe inbreeding depression than traits with less directional dominance (1, 4, 51). The presence of small effects of inbreeding on morphology in adult individuals can be difficult to detect. However, because some morphological traits have been found to affect individual fitness in our study system (52), small effects in multiple traits may add up to stronger inbreeding depression observed in fitness components. We examined inbreeding effects only in adults, and it is possible that inbreeding has stronger effects on morphology during development and growth (53). Such inbreeding depression may also translate into lower survival of inbred juveniles, which has been documented in our study system (39, 54).

We show that inbreeding has consistent negative fitness consequences in a natural subdivided vertebrate population, in which subpopulations experience different environmental conditions. Importantly, our study populations have sizes typical for natural populations of conservation concern, and our results support previous evidence that purging cannot be relied upon as a mechanism to aid conservation of small populations (5, 14, 44, 55). We found that inbreeding has a larger relative negative effect on fitness in small than in large populations, which is caused by a higher mean level of inbreeding and consequently larger variance in inbreeding in small populations; this suggests higher total loss of fitness due to inbreeding in small populations. Our results imply that conservation and management decisions should prioritize minimizing inbreeding in populations from diverse ecological and genetic backgrounds. Future studies should aim to utilize the full power of genome-wide datasets and disentangle the extrinsic and intrinsic ecological and genomic mechanisms causing such consistent inbreeding depression within and among populations. Finding the genomic regions that account for inbreeding depression will help in managing endangered populations by detecting the most homozygous regions with strongest deleterious effects and targeting genetic rescue programs based on this information (56), and in answering broader evolutionary questions about the maintenance of genetic variation in fitness-related traits (2, 57).

Materials and Methods

Study System.

The study system (Fig. 1) consists of two habitat types: 1) farm islands, where the sparrows live in colonies on dairy farms and nest primarily inside barns and cowsheds, with access to cattle feed and shelter all year round, and 2) nonfarm islands, where the sparrows live exclusively outdoor in gardens and nest mostly in nest boxes. Thus, on nonfarm islands, sparrows are more exposed to variation in food availability and weather conditions (37, 38, 58). The discrete island populations together with high resighting rates (mean 74%) allow estimating population sizes, interisland dispersal, individual survival, and reproductive success with high accuracy (37, 59, 60). Adult population sizes [N between 4 and 240 (32); SI Appendix, Fig. S1] and dispersal rates (37) differ between the islands and years, which is known to cause low to moderate genetic population differentiation [SI Appendix, Table S11 (31)]. The differences in demography, along with spatiotemporal variation in the environment, suggest that inbreeding levels and the strength of inbreeding depression may differ (39, 54).

Samples and Genotyping.

Blood samples from 3,253 adult house sparrows were genotyped for 200,000 SNPs using a custom house sparrow Affymetrix Axiom array (34) at Centre for Integrative Genetics (CIGENE). Virtually all adult house sparrows (∼90% of adults annually) present on eight of the islands during the years 1998 to 2013 were included in this study (SI Appendix, Table S2). The samples comprised five farm islands: Aldra, Gjerøy, Hestmannøy, Indre Kvarøy, and Nesøy. Due to sharp declines in population sizes on nonfarm islands in 2000 (32), only samples from adults present between 2003 and 2013 were included from the islands Selvær and Træna, and between 2004 and 2013 from Myken. After quality control (SI Appendix, Methods), the final dataset consisted of 3,116 house sparrow individuals (1,580 females and 1,536 males) that had genotypes for 1,626 Z-chromosomal loci and 181,529 autosomal loci distributed across 28 autosomes (34, 61).

Pedigree Construction.

A metapopulation-level pedigree was constructed for 3,116 adult house sparrows from the Helgeland archipelago using the R (62) package sequoia (63). A heavily pruned dataset of 605 highly informative and independent SNPs was used for pedigree construction. Parenthoods in the SNP-based pedigree (“SNP pedigree”) were compared with those in a previous microsatellite (MS) pedigree that was constructed using between 8 and 13 microsatellite loci separately for each study island including nestlings, fledged juveniles, and adult individuals as described in previous studies (39, 64–66) (SI Appendix, Results, Fig. S9, and Table S12). To validate the SNP pedigree, correlations were estimated between pairwise relatedness estimates based on SNP pedigree, MS pedigree, and genomic relatedness (SI Appendix, Results, Methods, and Fig. S10).

Inbreeding Analyses.

Individual inbreeding coefficients were estimated using pedigree- and SNP-based methods. Pedigree-based inbreeding coefficients (F_PED) were estimated from the SNP pedigree using the R package pedigree (67). Only individuals with at least two full ancestral generations were included in further analyses with F_PED, which reduced the sample size to 1,241 individuals. Genome-wide heterozygosity was estimated using all 181,529 autosomal SNPs. Two genomic inbreeding coefficients, based on weighted average homozygosity over all loci (F_GRM) (35) and runs of homozygosity (F_ROH), (36) were estimated using 118,810 autosomal loci not in strong linkage disequilibrium. F_GRM was estimated using GCTA (35) software for the whole metapopulation simultaneously. PLINK (version 1.9) (68) was used to extract homozygous sequence blocks and F_ROH was calculated as the proportion of SNP-covered genome within these homozygous sequence blocks (SI Appendix, Methods). Pairwise correlation between the inbreeding estimates was estimated using Pearson’s correlation coefficient (r). Since all estimates correlated strongly (SI Appendix, Fig. S2), only results for analyses including F_GRM are presented in the main text, whereas key results for F_ROH are presented in SI Appendix, Results.

To estimate the contribution of island and year nested within island (island-year) to variance in inbreeding, variance partitioning was done for standardized (to variance equal to 1 and centered to the metapopulation mean) F_GRM estimates using Bayesian mixed-effects models that were fitted with the R package R-INLA (69). Identity disequilibrium between SNP loci was estimated using g₂ as implemented in the R package inbreedR (70) for each island population separately. In addition, F statistics (pairwise F_ST and population-specific F_IS) were estimated for each population using the R package hierfstat (71).

Phenotypic and Life-History Data Used in the Inbreeding Depression Analyses.

The effect of realized inbreeding on individual reproductive success, survival probability, and morphology was estimated using slightly different datasets depending on the question. Individual reproductive success was measured in two ways: 1) the number of offspring produced that recruited to the adult metapopulation per year (annual reproductive success), and 2) the number of offspring produced that recruited to the adult metapopulation during an individual’s lifetime (lifetime reproductive success). Recruits that hatched in the years 1998 to 2012 were included in these analyses. However, since the sampling time periods differed between the islands, LRS was estimated for adult individuals that hatched at earliest 1 y before the sampling of the adults on an island started (SI Appendix, Table S2): 1997 on the farm islands (Aldra, Gjerøy, Hestmannøy, Indre Kvarøy, and Nesøy), 2002 on the nonfarm islands Selvær and Træna, and 2003 on the nonfarm island Myken. In total, 2,062 unique individuals were included in the LRS dataset and 2,739 in the AR dataset (5,267 records; SI Appendix, Methods). The dataset used for survival analyses included 2,728 house sparrows that were observed as adults on one of the eight study islands between May and December in a specific year. Individuals that hatched before 1997 were excluded from the analyses.

The inbreeding effect on adult morphology was estimated for seven traits: body mass (g), tarsus length (mm), wing length (mm), bill length (mm), bill depth (mm), visible badge size (square root of mm², only males), and total badge size (square root of mm², only males). For a more detailed description of the field procedures, see previous publications from the study system (52, 65, 72). Each individual had been measured a varying number of times during their lifetime and at different times of the year. To make the measurements comparable, a general linear mixed-effects model using the R package lme4 (73) was fitted separately for each sex and trait (72) (SI Appendix, Methods and Table S13). Parameter estimates from the fitted models were used to adjust each measurement to May in the second calendar year, before the mean phenotypic values were calculated for each individual (72). The dataset used in the morphology analyses included 1,786 birds (941 females and 845 males) that hatched between 1997 and 2012 on the farm islands, 2002 and 2012 on Træna and Selvær, and 2003 and 2012 on Myken. Measurements taken from these birds until 2016 were used.

Inbreeding Depression Analyses.

The effect of realized inbreeding on individual survival, reproductive success, and morphology was investigated using standardized (to variance equal to 1 and centered to the metapopulation mean) genomic inbreeding estimates F_GRM and F_ROH. Because recapture rates varied between the islands (74), the effect of inbreeding on survival probability was estimated using capture–mark–recapture models (75, 76). The model-fitting options provided by the programming language BUGS were used (77). The models were fitted in JAGS (78) (version 3.2.0) using the R package jagsUI (79). To study the effect of inbreeding on reproductive success and morphology, Bayesian animal models (80) were fitted within the INLA (81) framework, using the R-INLA package in R. LRS models were fitted with a zero-inflated Poisson distribution, AR models with a Poisson distribution, and morphological trait models with a Gaussian distribution. Results from all models are given in SI Appendix, Results and Tables S5 and S6. The proportion of total variance that was explained by inbreeding (F_GRM) in each fitness component was estimated for each island using variance estimates from the inbreeding depression models fitted as explained above.

To produce estimates of inbreeding load that are directly comparable with other study systems, we also estimated the number of lethal equivalents (42) for all fitness components (LRS, AR, and survival) within each island, using the inbreeding depression models described above. The numbers of lethal equivalents were estimated as twice the negation of the regression slope (−2β) of F_ROH on each fitness component [because the species is diploid (82)].

Since all individuals were measured for all traits (badge sizes only in males), the measurements are not independent between traits. Furthermore, we know from previous studies that the morphological traits are phenotypically and genetically correlated to various degrees (64, 65). To account for such nonindependence, multivariate animal models were also fitted for the morphological data. Results were concordant between multivariate analyses conducted using the R package MCMCglmm (83) and univariate INLA analyses (SI Appendix, Results and Table S14). For simplicity, only univariate results are presented in the main results. Details of all inbreeding depression models are given in SI Appendix, Methods.

Statistical Inference from Random-Effects Estimates Using Permutation Tests.

The statistical support for a non-0 value of the variance explained by spatiotemporal random effects in our models testing for inbreeding depression in LRS, AR, and morphological traits was assessed separately. This was done because variance components are bound to be positive, and because prior choice may influence the BCIs derived from the posterior distribution (84). We therefore determined the probability that the estimated variance explained by island (spatial variation) and island-year (temporal variation) was different from a null expectation based on permutation tests [(85) see details of permutation tests in SI Appendix, Methods].

Data Availability.

Data and the main R scripts used in this study are deposited in Dryad with a 2-year embargo for the data (https://doi.org/10.5061/dryad.m0cfxpp10). During the embargo time, the data are available from the authors on request.