Three dimensions of scientific impact

Significance

What are the mechanisms behind one’s research success as measured by one’s papers’ citability? By acknowledging the perceived esteem might be a consequence not only of how valuable one’s works are but also of pure luck, we arrived at a model that can accurately recreate a citation record based on just three parameters: the number of publications, the total number of citations, and the degree of randomness in the citation patterns. As a by-product, we show that a single index will never be able to embrace the complex reality of the scientific impact. However, three of them can already provide us with a reliable summary.

Abstract

The growing popularity of bibliometric indexes (whose most famous example is the h index by J. E. Hirsch [J. E. Hirsch, Proc. Natl. Acad. Sci. U.S.A. 102, 16569–16572 (2005)]) is opposed by those claiming that one’s scientific impact cannot be reduced to a single number. Some even believe that our complex reality fails to submit to any quantitative description. We argue that neither of the two controversial extremes is true. By assuming that some citations are distributed according to the rich get richer rule (success breeds success, preferential attachment) while some others are assigned totally at random (all in all, a paper needs a bibliography), we have crafted a model that accurately summarizes citation records with merely three easily interpretable parameters: productivity, total impact, and how lucky an author has been so far.

Ever since Garfield’s (1) impact factor for journals and Hirsch’s (2) $h$ index for individual researchers, the popularity of bibliometric impact measures has been growing rapidly. The fact that they summarize one’s scientific performance with just a single number is appealing to many. However, some argue (3) that the nature of scientific activities is too multidimensional for such a simple description to be possible and a few quantitative metrics will never be sufficient to capture this complex reality in its entirety.

In this paper we address this issue from the perspective of the increasingly popular science of science (Sci-Sci) (4, 5) approach, which can be dated back to the classical book by de Solla Price, Little Science, Big Science (6). The modern Sci-Sci utilizes complex systems methodology and can be considered a fusion of agent-based modeling and big data analysis.

We have developed a model of an author’s research activity that is based on two simple assumptions: 1) In each time step one new paper is added into the simulation. 2) Each newly added paper cites the existing publications according to a combination of a) the preferential attachment rule—highly cited papers are more likely to attract even more citations [compare the rich get richer mechanism (7), the success breeds success phenomenon (8), and the effect of a scientist’s reputation (9)]—and b) sheer chance—papers might be discovered by the citing authors by accident or be included in the bibliography completely at random.

While the importance of the rich get richer rule (7) in bibliometrics is unquestionable [first part of Merton’s (10) Matthew effect, referred to as the cumulative advantage process by de Solla Price (8) or success-breeds-success phenomenon (6, 11), confirmed experimentally (12)], we argue here that a purely preferential model is incapable of explaining our reality well enough and the accidental component is necessary (13, 14).

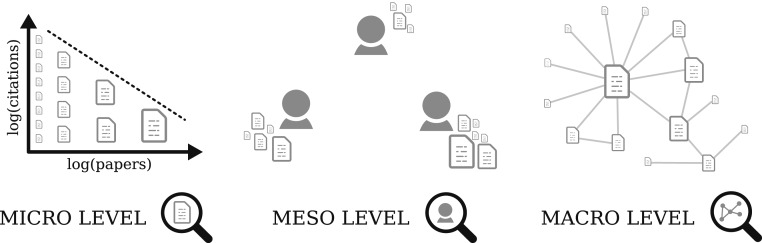
Furthermore, in our case we adopt different levels of analysis [as known from social sciences (15)] (Fig. 1) for generated bibliometric data. Agent-based models are formulated at the microlevel—from the perspective of an individual paper. The Sci-Sci perspective usually investigates the structure of the citation network in its entirety, for instance to describe general citation patterns across the whole scientific discipline (macrolevel). Here we are mainly focusing on the rarely considered mesolevel (Table 1), which is the perspective of a single scientist, i.e., a small-sample one. As such, the above publication–citation process can be thought of as an extension of the iterative procedure known as the Ionescu–Chopard model (16, 17) (Materials and Methods, Model Description).

Fig. 1.

Different levels of analysis of bibliometric datasets. On the microlevel we describe the distribution of the number of citations of individual papers, irrespective of who authored them as well as which articles actually referenced them. The rarely studied mesolevel, which is the perspective of this contribution, accounts for the author-specific differences. The structure of the citation network in its entirety is studied at the macrolevel.

Table 1.

Overview of the related literature on the modeling of the distribution of citations

	Microlevel	Mesolevel	Macrolevel
Purely preferential	Distribution of the number of citations (21–30)	Lotkaian informetrics (19), Ionescu–Chopard model (16, 17)	Barábasi–Albert model and its modifications (31)
Preferential and/or accidental	Microscopic model (14) implies Tsalis–Pareto distribution (32)	This paper	Empirical data (33, 34), models studied in refs. 35–46

By assuming that citations might be assigned completely at random as well as follow the rich get richer rule, we revealed the underlying dimensionality of the mesolevel, leading to an accurate description of the output of an individual author.

Model Derivation

Assume $X_1,X_2,\dots ,X_N$ is a descending sequence of citation counts for each of the $N$ papers of an author. In other words, $X_1$ denotes the number of bibliographic references to the author’s most cited paper, $X_2$ is the second most cited, …, and $X_N$ is the least cited one. Famous approaches (18) to the problem of approximating observed citation records $X_1,\dots ,X_N$ with simple mathematical models ${\widehat{X}}_1\left(\cdots \right),\dots ,{\widehat{X}}_N\left(\cdots \right)$ that depend on a small number of parameters were mostly based on the power law (19) or other functions (20). Unfortunately, they do not provide a good fit at the mesolevel—they are usually applied for describing papers sampled from the whole citation network (21, 22).

Our model, on the other hand, not only has a clear interpretation (recall the two simple assumptions above), but also provides high-accuracy approximations of citation records of individuals. Due to this, we are able to describe this complex reality with merely three self-explanatory parameters: the number of papers $N$; the total number of citations $C=X_1+X_2+\cdots +X_N$; and the ratio of citations distributed according to the preferential attachment rule $\rho$, where $\rho \simeq 0$ means that all papers receive citations completely at random and $\rho \simeq 1$ that all of them follow the rich get richer rule.

For the derivation of the model please refer to Materials and Methods, Model Description. The citation process proposed above, after all of the $N$ papers have been published and all of the citations have been distributed, yields the following analytic formula for the estimated number of citations of the $k$th most cited paper (Materials and Methods, Exact Solution of the Model):

$$\begin{array}{ll}\hfill {\widehat{X}}_k\left(N,C,\rho \right)& =\frac{1-\rho }{\rho }\frac{C}{N}\left(\prod _{i=k}^N\frac{i}{i-\rho }-1\right)\hfill \\ \hfill & =\frac{1-\rho }{\rho }\frac{C}{N}\left(\frac{k}{k-\rho }\cdot \frac{k+1}{k+1-\rho }\cdots \frac{N}{N-\rho }-1\right).\hfill \end{array}$$ [1]

Dataset Description

To demonstrate the usefulness of the model, we study the DBLP Computer Science Bibliography (47) dataset of computer science papers; see Materials and Methods, Data Availability for description. We consider citation records of all 123,621 scholars whose $h$ index is at least 5. To determine the three model parameters characterizing each author, we omit the papers with no citations (as overfitting to a tail composed of zeros cannot lead to a good overall description). Then we compute the author’s $N$ (number of papers that were cited at least once) and $C$ (the total number of citations) and then estimate $\rho$ using the least-squares fit with respect to the Cauchy loss ${\sum }_{k=1}^N\log \left(1+{\left({\widehat{X}}_k\left(N,C,\rho \right)-X_k\right)}^2\right)$ to weaken the influence of any potential outliers.

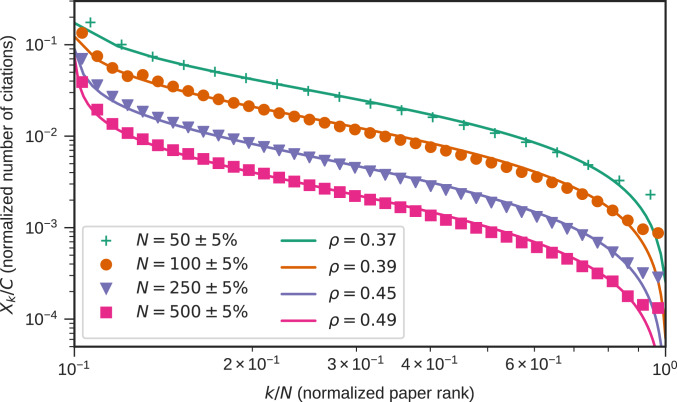
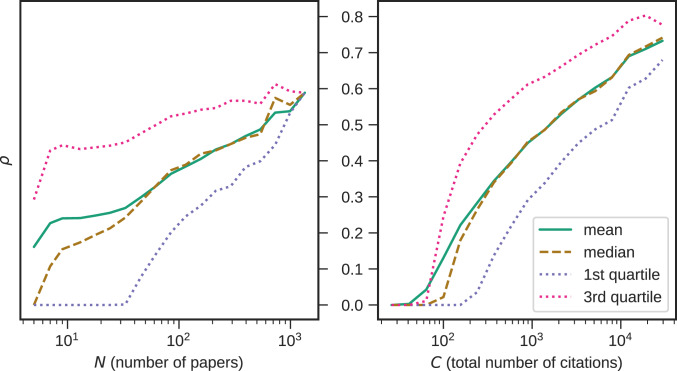
Once we obtain an author’s $N$, $C$, and $\rho$, we can reproduce the author’s citation record quite accurately (Fig. 2). The high variance of $\rho$ for each fixed $N$ and $C$ (Fig. 3) indicates that this parameter is necessary for a precise description of data. This suggests that indeed the modeled reality might be three-dimensional (3D), which roughly agrees with the estimates in ref. 48.

Fig. 2.

Normalized average number of citations $X_k/C$ as a function of the normalized paper rank $k/N$ on a double-logarithmic scale. Each plotting character corresponds to citation sequences of different lengths: “$+$,” all of the 2,624 authors with 48 to 52 papers in total; “$•$,” 1,113 authors with 95 to 105 papers; “$▾$,” 131 authors with 238 to 262 papers; and “$■$,” 18 authors with 475 to 525 papers. The curves represent the corresponding predictions ${\widehat{X}}_k/C$ as generated by our model with $\rho$ equal to the averages over the individual authors’ fitted rich get richer ratios. A particularly good fit is observed in the case of highly and moderately influential papers.

Fig. 3.

The more productive and/or influential an author is, the more likely the author’s papers are cited according to the rich get richer rule.

Results and Discussion

It turns out that ca. $30\%$ of the authors have their corresponding $\rho \approx 0$, which means that, under our model, their citations appear to be distributed in an almost purely accidental manner. These authors publish on average half as many papers as those with $\rho >0$, which might indicate that they are at the beginning of their careers or their best papers are still yet to come. We observe a positive correlation between $\rho$ and $N$ as well as $C$ (Fig. 3). In other words, more productive and/or influential authors tend to have more papers distributed according to the rich get richer rule. This observation is consistent with the well-known fact (5) that one’s highest-impact paper can occur at any time during the course of one’s career; thus, authors with more papers are more likely to have published their best work already. However, as there is a considerable variability in $\rho$ at all levels, even some outstanding careers might still be a result of more luck than reason (13, 49).

By indicating that the citation record space is 3D, we have proved that any single citation measure, including the $h$ index and the author’s ranking it generates, necessarily yields an oversimplified projection of a more complex space (3). In other words, whenever one chooses a single citation index, some information must inherently be lost; we will never be able to see the whole picture through the lenses of any single measure.

The proposed model emphasizes the use of multiple indexes in the evaluation of scientific work. We have indicated that merely three parameters are sufficient to provide an accurate description of our reality. In the near future, we plan to perform a broad study of bibliometric indexes to come up with an intuitive and insightful classification for which of the three dimensions each index focuses on the most. This will allow policy makers to make better-informed decisions when choosing particular evaluation tools. The questions of how to best combine $N$, $C$, and $\rho$ to cause the least information loss and how well popular citation indexes perform with regard to the quality of data approximation will also be explored.

Materials and Methods

Model Description.

Let us introduce the proposed model in a formal manner. For the description of the citation dynamics we use the following parameters: the total number of papers $N$, the total number citations $C$ that will be distributed among all papers, and ratio of the number of preferential citations to the total number of citations $\rho \in \left(\mathrm{0,1}\right)$.

Due to the assumed boundary conditions in Eq. 3, we disallow both $\rho =0$ and $\rho =1$.

The stages of the model’s simulation are strictly connected to the scientific activity of the considered author. Each of the $N$ steps corresponds to the publication of one of the author’s papers. At the $t$th step, the $t$ articles already in existence are to receive $n_a+n_p=\frac{C}{N}$ citations in total, where $n_p=\rho \frac{C}{N}$ citations are distributed according to the preferential attachment rule, and $n_a=\left(1-\rho \right)\frac{C}{N}$ citations are uniformly distributed between the $t$ papers

Note that both $n_p$ and $n_a$ do not need to be integers—we consider them as averages.

The rate equation for the number of citations of the $k$th mostly cited paper at the $t$th stage of the simulation, $X_k^{\left(t\right)}$, takes the form

$$X_k^{\left(t\right)}=\underset{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{v}\mathrm{i}\mathrm{o}\mathrm{u}\mathrm{s}\hspace{0.17em}\mathrm{v}\mathrm{a}\mathrm{l}\mathrm{u}\mathrm{e}}{\underbrace{X_k^{\left(t-1\right)}}}+\underset{\mathrm{a}\mathrm{c}\mathrm{c}\mathrm{i}\mathrm{d}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{a}\mathrm{l}\hspace{0.17em}\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{e}}{\underbrace{\frac{n_a}{t}}}+\underset{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{f}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{a}\mathrm{l}\hspace{0.17em}\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{e}}{\underbrace{n_p\frac{X_k^{\left(t-1\right)}+\frac{n_a}{t}}{n_a+\sum _{l=1}^{t-1}{X}_l^{\left(t-1\right)}}}},$$ [2]

for $k=1,\dots ,\hspace{0.17em}t$. As each paper has initially no citations, we introduce the following boundary conditions:

$$X_k^{\left(k-1\right)}=0,\hspace{0.17em}\mathrm{f}\mathrm{o}\mathrm{r}\hspace{0.17em}k=1,\hspace{0.17em}2,\hspace{0.17em}\dots$$ [3]

Note that in the rightmost term in Eq. 2, i.e., the preferential part, we assume that accidental citations are distributed first to avoid singularities with the very natural boundary conditions of the form given by Eq. 3. This explains the occurrence of $n_a$ there. The structure of the preferential part is the expected value of the Bernoulli distribution with the number of trials $n_p$ and the probability resulting from the assumed rich get richer mechanism—the number of citations thus obtained is proportional to the actual number of citations (i.e., $X_k^{\left(t-1\right)}+n_a/t$).

Exact Solution of the Model.

Below we derive the exact formula for $X_k^{\left(t\right)}$. Note that Eq. 2 can be simplified as

$$X_k^{\left(t\right)}=\left[X_k^{\left(t-1\right)}+\frac{n_a}{t}\right]\left[1+\frac{n_p}{n_a+\sum _{l=1}^{t-1}{X}_l^{\left(t-1\right)}}\right].$$

Moreover, the second term can be further simplified due the fact that in each of the $\left(t-1\right)$ steps, the papers receive $n_a+n_p$ citations; i.e.,

$$\sum _{l=1}^{t-1}{X}_l^{\left(t-1\right)}=\left(n_a+n_p\right)\left(t-1\right).$$

Therefore,

$$\begin{array}{ll}\hfill & 1+\frac{n_p}{n_a+\sum _{l=1}^{t-1}{X}_l^{\left(t-1\right)}}=1+\frac{n_p}{n_a+\left(n_a+n_p\right)\left(t-1\right)}\hfill \\ \hfill =& \frac{\left(n_a+n_p\right)t}{\left(n_a+n_p\right)t-n_p}=\frac{t}{t-\frac{n_p}{n_a+n_p}}.\hfill \end{array}$$

Furthermore, since $\rho =n_p/\left(n_a+n_p\right)$, the following holds:

$$X_k^{\left(t\right)}=X_k^{\left(t-1\right)}\frac{t}{t-\rho }+\frac{n_a}{t-\rho }.$$ [4]

Moreover,

$$\begin{array}{ll}\hfill X_k^{\left(t\right)}=& \left[X_k^{\left(t-2\right)}\frac{t-1}{t-1-\rho }+\frac{n_a}{t-1-\rho }\right]\frac{t}{t-\rho }+\frac{n_a}{t-\rho }\hfill \\ \hfill =& \left[X_k^{\left(t-3\right)}\frac{t-2}{t-2-\rho }+\frac{n_a}{t-2-\rho }\right]\frac{t\left(t-1\right)}{\left(t-\rho \right)\left(t-1-\rho \right)}\hfill \\ \hfill & +\frac{n_{a}t}{\left(t-\rho \right)\left(t-1-\rho \right)}+\frac{n_a}{t-\rho }\hfill \\ \hfill =& X_k^{\left(t-3\right)}\frac{t\left(t-1\right)\left(t-2\right)}{\left(t-\rho \right)\left(t-1-\rho \right)\left(t-2-\rho \right)}\hfill \\ \hfill & +\frac{n_{a}t\left(t-1\right)}{\left(t-\rho \right)\left(t-1-\rho \right)\left(t-2-\rho \right)}\hfill \\ \hfill & +\frac{n_{a}t}{\left(t-\rho \right)\left(t-1-\rho \right)}+\frac{n_a}{t-\rho }.\hfill \end{array}$$ [5]

Keeping in mind that the Euler gamma function $\mathrm{\Gamma }$ (e.g., ref. 50, chap. 5), defined as

$$\mathrm{\Gamma }\left(z\right)={\int }_0^{\infty }{x}^{z-1}{e}^{-x}\hspace{0.17em}dx,$$

satisfies the factorial-like relation (equation 5.5.1 in ref. 50)

$$\mathrm{\Gamma }\left(z+1\right)=z\mathrm{\Gamma }\left(z\right),$$ [6]

for every number $z$, we can transform Eq. 5 as

$$\begin{array}{ll}\hfill X_k^{\left(t\right)}=X_k^{\left(t-3\right)}& \frac{\mathrm{\Gamma }\left(t-2-\rho \right)\mathrm{\Gamma }\left(t+1\right)}{\mathrm{\Gamma }\left(t+1-\rho \right)\mathrm{\Gamma }\left(t-2\right)}+n_a\frac{\mathrm{\Gamma }\left(t-2-\rho \right)\mathrm{\Gamma }\left(t+1\right)}{\mathrm{\Gamma }\left(t+1-\rho \right)\mathrm{\Gamma }\left(t-1\right)}\hfill \\ \hfill +\hspace{0.17em}{n}_a& \frac{\mathrm{\Gamma }\left(t-1-\rho \right)\mathrm{\Gamma }\left(t+1\right)}{\mathrm{\Gamma }\left(t+1-\rho \right)\mathrm{\Gamma }\left(t\right)}+n_a\frac{\mathrm{\Gamma }\left(t-\rho \right)\mathrm{\Gamma }\left(t+1\right)}{\mathrm{\Gamma }\left(t+1-\rho \right)\mathrm{\Gamma }\left(t+1\right)}.\hfill \end{array}$$ [7]

By continuing evaluation of Eq. 4 of the form given by Eq. 7, we obtain

$$\begin{array}{ll}\hfill X_k^{\left(t\right)}=& \underset{=\hspace{0.17em}0}{\underbrace{X_k^{\left(k-1\right)}}}\frac{\mathrm{\Gamma }\left(t+1\right)}{\mathrm{\Gamma }\left(t+1-\rho \right)}\frac{\mathrm{\Gamma }\left(k-\rho \right)}{\mathrm{\Gamma }\left(k\right)}\hfill \\ \hfill & +n_a\frac{\mathrm{\Gamma }\left(t+1\right)}{\mathrm{\Gamma }\left(t+1-\rho \right)}\sum _{r=0}^{t-k}\frac{\mathrm{\Gamma }\left(t-r-\rho \right)}{\mathrm{\Gamma }\left(t-r+1\right)}.\hfill \end{array}$$ [8]

In Eq. 8 we can stop the nesting procedure by using the boundary conditions given by Eq. 3. The final formula for $X_k^{\left(t\right)}$ with the change of the summation variable $\ell =t-r$ takes the form

$$X_k^{\left(t\right)}=n_a\frac{\mathrm{\Gamma }\left(t+1\right)}{\mathrm{\Gamma }\left(t+1-\rho \right)}\sum _{\ell =k}^t\frac{\mathrm{\Gamma }\left(\ell -\rho \right)}{\mathrm{\Gamma }\left(\ell +1\right)}.$$

This can be simplified further, because the sum of the ratios of gamma functions satisfies the identity

$$\sum _{\ell =k}^t\frac{\mathrm{\Gamma }\left(\ell -\rho \right)}{\mathrm{\Gamma }\left(\ell +1\right)}=\frac{1}{\rho }\left[\frac{\mathrm{\Gamma }\left(k-\rho \right)}{\mathrm{\Gamma }\left(k\right)}-\frac{\mathrm{\Gamma }\left(t+1-\rho \right)}{\mathrm{\Gamma }\left(t+1\right)}\right],$$ [9]

which leads to

$$X_k^{\left(t\right)}=\frac{n_a}{\rho }\left[\frac{\mathrm{\Gamma }\left(k-\rho \right)}{\mathrm{\Gamma }\left(k\right)}\frac{\mathrm{\Gamma }\left(t+1\right)}{\mathrm{\Gamma }\left(t+1-\rho \right)}-1\right].$$ [10]

Finally, we put $t=N$, which leads to the situation where each paper has been published and every citation has been distributed. This yields ${\widehat{X}}_k\hspace{0.17em}≔\hspace{0.17em}{X}_k^{\left(N\right)}$ such that

$${\widehat{X}}_k\left(N,C,\rho \right)=\frac{1-\rho }{\rho }\frac{C}{N}\left[\frac{\mathrm{\Gamma }\left(k-\rho \right)}{\mathrm{\Gamma }\left(k\right)}\frac{\mathrm{\Gamma }\left(N+1\right)}{\mathrm{\Gamma }\left(N+1-\rho \right)}-1\right].$$ [11]

Gamma functions, although very elegant, are not computationally well behaving. This is the reason why we should be interested in deriving the following equivalent of Eq. 11. Due to Eq. 6, we can substitute the gamma functions with the following product:

$${\widehat{X}}_k\left(N,C,\rho \right)=\frac{1-\rho }{\rho }\frac{C}{N}\left(\prod _{\ell =k}^N\frac{\ell }{\ell -\rho }-1\right).$$ [12]

The Pochhammer symbol (section 5.2 in ref. 50) is defined as

$${\left(k\right)}_m=\frac{\mathrm{\Gamma }\left(k+m\right)}{\mathrm{\Gamma }\left(k\right)}=k\left(k+1\right)\dots \left(k+m-1\right).$$ [13]

Employing it in Eq. 11 yields

$${\widehat{X}}_k\left(N,C,\rho \right)=\frac{1-\rho }{\rho }\frac{C}{N}\frac{{\left(k\right)}_{N-k+1}-{\left(k-\rho \right)}_{N-k+1}}{{\left(k-\rho \right)}_{N-k+1}}.$$ [14]

Note that the Pochhammer symbol is implemented in many numerical software packages, thus enabling fast and accurate computations.

Data Availability.

Empirical data analysis conveyed in this paper is based on the DBLP V10 bibliography database (47) (https://aminer.org/citation), consisting of 3,079,007 papers and 25,16,994 citation relationships. DBLP includes most of the journals related to computer science. It also tracks numerous conference proceedings papers from the field.

We have extracted citation records of 1,762,044 authors. Most of them have published a small number of papers or have received very few citations. Therefore, we restricted the analysis to the subset of researchers characterized by the $h$ index not less than 5. This gave 123,621 citation records. Moreover, papers with 0 citations have been omitted from the analysis, as they are problematic when performing computations on the log scale. Note that most impact indexes, including the $h$ index, ignore zeros anyway.

The raw citation sequences, estimated parameters, and source code used to perform the data analysis can be accessed at the GitHub repository: https://github.com/gagolews/three_dimensions_of_scientific_impact (51).