Mathematical modeling of PDGF-driven glioma reveals the dynamics of immune cells infiltrating into tumors

Abstract

Background: Tumor-infiltrated immune cells compose a significant component of many cancers. They have been observed to have contradictory impacts on tumors. Although the primary reasons for these observations remain elusive, it is important to understand how immune cells infiltrating into tumors is regulated. Recently our group conducted a series of experimental studies, which showed that muIDH1 gliomas have a significant global reduction of immune cells and suggested that the longer survival time of mice with CIMP gliomas may be due to the IDH mutation and its effect on reducing of the tumor-infiltrated immune cells. However, to comprehend how IDH1 mutants regulate infiltration of immune cells into gliomas and how they affect the aggressiveness of gliomas, it is necessary to integrate our experimental data into a dynamical system to acquire a much deeper understanding of subtle regulation of immune cell infiltration. Methods: The method is integration of mathematical modeling and experiments. According to mass conservation laws and assumption that immune cells migrate into the tumor site along a chemotactic gradient field, a mathematical model is formulated. Parameters are estimated from our experiments. Numerical methods are developed to solve the problem. Numerical predictions are compared with experimental results. Results: Our analysis shows that the net rate of increase of immune cells infiltrated into the tumor is approximately proportional to the 4/5 power of the chemoattractant production rate, and it is an increasing function of time while the percentage of immune cells infiltrated into the tumor is a decreasing function of time. Our model predicts that wtIDH1 mice will survive longer if the immune cells are blocked by reducing chemotactic coefficient. For more aggressive gliomas, our model shows that there is little difference in their survivals between wtIDH1 and muIDH1 tumors, and the percentage of immune cells infiltrated into the tumor is much lower. These predictions are verified by our experimental results. In addition, wtIDH1 and muIDH1 can be quantitatively distinguished by their chemoattractant production rates, and the chemotactic coefficient determines possibilities of immune cells migration along chemoattractant gradient fields. Conclusions: The chemoattractant gradient field produced by tumor cells may facilitate immune cells migration to the tumor cite. The chemoattractant production rate may be utilized to classify wtIDH1 and muIDH1 tumors. The dynamics of immune cells infiltrating into tumors is largely determined by tumor cell chemoattractant production rate and chemotactic coefficient.

Introduction

Tumor-infiltrated immune cells compose a significant component of many cancers [1], [2]. A plethora of studies have been conducted to explore the impacts of tumor-infiltrated immune cells on associated tumors [3], [4]. Numerous studies have shown that direct contact between infiltrated immune cells and tumor cells correlates with destruction of cancer cells, reduction of tumor sizes, and improved clinical prognosis [5], [6]. On the other hand, a large number of studies has shown that increased infiltration of immune cells may promote tumor progression and invasion [7], [8], [9], and many clinical data have also indicated that tumor infiltration of certain immune cells associates with poor prognosis of patients with cancers [10], [11], [12]. Although the primary reasons for these contradictory observations remain elusive, an understanding of how immune cells infiltrating into tumors is regulated is essentially important [13], [14].

Recently our group conducted a series of experimental studies on regulation of the tumor-associated immune system in gliomas [15]. According to CpG island methylator phenotype (CIMP), gliomas can be divided into two types, CIMP and non-CIMP, with a significantly longer survival of patients with CIMP [16]. CIMP gliomas have mutants in isocitrate dehydrogenase 1/2 (IDH1/2). Non-CIMP wild-type IDH1/2 (wtIDH1/2) gliomas are more aggressive compared with their CIMP counterparts, CIMP mutant IDH1/2 (muIDH1/2). To understand the primary reasons of aggressive differences in gliomas, we compared the infiltrated immune cell contents of wtIDH1 and muIDH1 gliomas. Using human glioma tissues, we observed that human CIMP gliomas have significantly lower numbers of several immune cell types relative to non-CIMP tumors. To understand the specific effects of IDH1 mutants on immune cell infiltrating into gliomas in vivo, we used the RCAS/tva system to create isogenic glioma pairs from PDGF-driven glioma mouse models whose initial events differed only in the presence or absence of muIDH1. The results showed that the muIDH1 gliomas have a significant global reduction of immune cell contents [15]. Our experimental data suggested that the longer survival time of CIMP gliomas of patients or mice may be due in part to the IDH mutation and its effect on reducing of the tumor-infiltrated immune cells that enhances aggressiveness [15]. These experimental results also showed a regulatory role of muIDH1 on infiltration of immune cells into gliomas. However, to comprehend how IDH1 mutants regulate infiltration of immune cells into gliomas and how they affect the aggressiveness of gliomas or survival of patients or mice with gliomas, it is necessary to integrate our experimental data into a dynamical system to acquire a much deeper understanding of subtle regulation of immune cell infiltration.

In this study, we formulate and analyze a mathematical model of 3-dimensional gliomas driven by PDGF. Our mathematical model includes glioma cells, necrotic tumor cells, chemoattractants secreted by glioma cells, and infiltrated immune cells. It is a free boundary problem where the tumor boundary is evolving in space and time. In the literature, there are several mathematical models that describe glioma growth. An early mathematical model built by Murray and colleagues [17] studied glioma growth rates and diffusion coefficients. Swanson and colleagues proposed mathematical models for glioma growth based on diffusion processes [18]. In the same line, Sander and colleagues also proposed some diffusion-type models for glioma growth [32]. All other mathematical models for gliomas are based on either reaction diffusion equations or ordinary differential equations [19]. Based on principles in incompressible fluid dynamics, Wu et al proposed a mathematical model to study viral therapy for gliomas [20]. To study innate immune response in viral therapy, we proposed a similar mathematical model by using fluid dynamics principles [21]. There are several mathematical models that study tumor–immune interactions [22], [23]. A complete survey about tumor–immune interaction modeling can be found in books [24], [25]. However, immune cells in all these mathematical models were considered to be generated at tumor sites instead of infiltrating into tumors. In this study, we formulate a mathematical model according to conservation laws, where immune cells migrate into the tumor along a chemoattractant gradient field. This is a new mathematical model that describes the infiltration dynamics of immune cells into tumors.

Our mathematical model distinguishes wtIDH1 tumors and muIDH1 tumors by different parameter values of the maximum rate of chemoattractant production by glioma cells. This parameter is built into our mathematical model according to Michaelis–Menten kinetics. Our mathematical model reveals the details of the dynamics how wtIDH1 tumors reach death volume earlier than muIDH1 tumors do. Our computational analysis shows that the net rate of increase of immune cells infiltrated into the tumor is approximately proportional to the 4/5 power of the chemoattractant production rate, and it is an increasing function of time while the percentage of immune cells infiltrated into the tumor is a decreasing function of time. Our mathematical model predicts that the mice with wtIDH1 tumors will survive longer if the immune cells are blocked by reducing chemotactic coefficient. However, for more aggressive gliomas, our mathematical model shows that there is little difference in their survivals between wtIDH1 tumors and muIDH1 tumors. Our numerical results also show that, for such more aggressive gliomas, the percentages of immune cells infiltrated into the tumor are much lower. This may indicate that the immune system has little effects on such aggressive gliomas. Our analysis characterizes the roles of two important parameters of the model, the chemoattractant production rate and chemotactic coefficient. The chemoattractant production rate determines the strength of the gradient field of chemotaxis in the mouse body, and the chemotactic coefficient determines the possibility of immune cell migration. If the two parameters decrease, although the net rate of increase of immune cells infiltrated into the tumor still increases, the percentage of immune cells infiltrated into the tumor will decrease when mice die. Therefore, the mice will gain longer survivals.

Materials and methods

In our experiments [15] RCAS retroviral vectors are used to transfer genes to specific cell types in vivo that express the receptor tv-a to develop a pair of isogenic mouse tumor models which differed only in IDH status. Both mutant and wild types of gliomas were driven by PDGF in combination with p53 loss mimicking the frequent p53 mutation in IDH mutant astrocytomas. Mice were injected with RCAS-PDGF producing DF1 cells together with either DF1 cells producing RCAS-wtIDH1-shp53 (wtIDH1) or RCAS-muIDH1-shp53 (muIDH1). Tumors were generated from these injections that had identical genomic backgrounds differing only in IDH1 mutation status. We euthanized mice when they showed signs of CNS pathology and harvested tumors. Our mathematical model describes this tumor growth process.

As mentioned in Introduction, spatial modeling of glioma growth has two types, diffusion type and fluid dynamics type. Friedman and colleagues had some glioma models of fluid dynamics type [33] and we also built models for glioma treatments based on fluid dynamics [21], [34]. To explicitly describe tumor growing boundary, we construct our model based on free-surface fluids. For simplicity, the tumor is approximated by a sphere with a growing boundary R(t), where t represents time. Tumor cells (G) proliferate, and some of tumor cells become necrotic cells (H). Tumor cells stimulate or produce chemoattractants (A). The chemoattractants diffuse and form a gradient field in the mouse body. Some types of immune cells (N) migrate along the chemotactic gradient field into the tumor. Based on mass conservation laws in fluid dynamics, interactions among these types of cells, and chemotaxis, we propose a new system of partial differential equations for tumor cells, necrotic tumor cells, infiltrated immune cells, and chemoattractants, which is in Appendix and Supplement. The quantity G represents the number density of glioma cells (i.e., the number of glioma cells in a cubic millimeter), and it is a function of space and time. The same meaning is associated with the quantities H and N. The quantity A represents the concentration of the chemoattractants (with unit of picogram per cubic milliliter), and it also is a function of space and time. From our experimental results, the chemoattractants found in gliomas are CCL-2, CXCL-2, and C5. The quantity A stands for the mixture of these chemoattractants. We do not distinguish these chemoattractants in our mathematical model. However, we can use our mathematical model to make some predictions for different chemoattractants. For infiltrated immune cells, our experiments found that there are microglia, monocytes, polymorphonuclear leukocytes, CD4+ T helper cells, and CD8+ T cells in the tumor. For simplicity, our mathematical model does not distinguish these immune cell types, and considers them as the quantity N.

The glioma cells proliferate at a rate λ, where the value of λ is taken from our previous study [21]. Necrotic cells are removed at the average time of 2–3 days [26]; we take the removal rate δ to be 0.45 per day. To estimate glioma cell lysis rate μ, we use the early stage growth law of gliomas $G\left(t\right)=G\left(0\right)e^{\left(\lambda -\mu \right)t}$ and the data in [27] and obtain that μ is between 0.33 and 0.38 per day. The cell number density of the tumor tissue is a constant θ [21]. The chemoattractants diffuse within the mouse body with the diffusion coefficient D, where the value of D is from [28]. The chemoattractants degrade with a rate γ, where γ can be computed from the data in [28], [27] and we then actually obtain a range for the chemoattractant degradation rate. We use Michaelis–Menten Kinetics to model glioma cells producing chemoattractants. That is, the stimulating rate of the chemoattractants is proportional to $\frac{\mathit{mG}}{\beta +G}$, where β is Michaelis constant which also can be interpreted as the half-saturation rate, and the parameter m is the maximum of the chemoattractant production rate. To estimate these parameters, we use data about CCL-2 in [30]. We assume CCL-2 is secreted constantly and is degraded proportionally. By solving an ordinary differential equation, we then obtain a range for the values of the parameter m. The chemotactic coefficient α is estimated by combining data in [29] and dynamic data in [31]. Immune cells enter the tumor through the tumor boundary R(t). The flux of immune cells into the tumor is proportional to the gradient of the chemoattractant at the boundary. These parameters and their estimated values are listed in Table 1. The details of the parameter estimation can be found in Supplementary materials.

Table 1.

Model parameters and their numerical values.

Parameters	Description	Numerical Values	Dimensions
$\lambda$	Proliferation rate of glioma cells	0.48	day−1
$\mu$	Glioma cell lysis rate	0.33–0.38	day−1
$\delta$	Removal rate of necrotic cells	0.45	day−1
D	Diffusion coefficient of chemoattractant	6.048	mm2/day
m	Maximum of chemoattractant production rate	0.7–17	105pg/ml.day
$\beta$	Michaelis constant	105	cells/mm3
$\gamma$	Chemoattractant degradation rate	0.17–4.2	102/day
a	Chemotactic coefficient	0.6	mm2.ml/day.pg
$\rho$	Clearance rate of immune cells	0.9	day−1
$\theta$	Cell density of tumor issue	106	cells/mm3

Our mathematical model is a free boundary problem. Analysis or numerically solving free boundary problems is always difficult. Because of the distinct feature of our free boundary problem that immune cells migrate into the tumor along the chemoattractant gradient filed and there also is the velocity field within the tumor, and there is no numerical solver available, we have to construct numerical methods based on conservation laws, then develop algorithm and computer codes, and implement the codes in supercomputers to obtain numerical solutions. A brief description of our methods can be found in Supplementary materials.

Results

Fitting of data

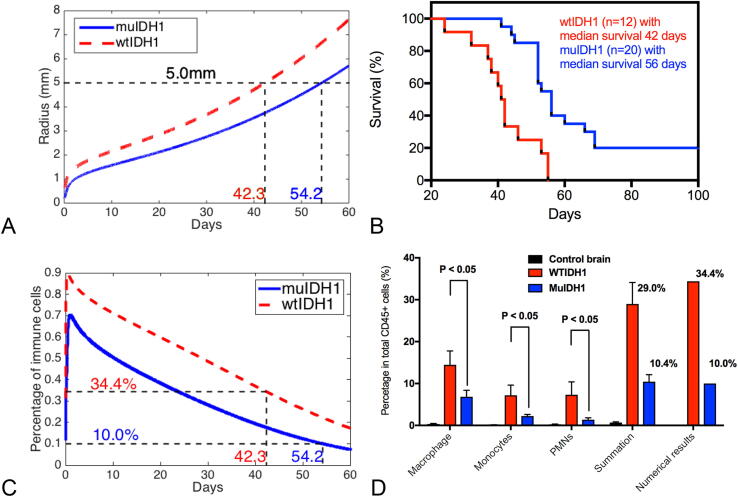
From our experimental data for Ink4a/Arf^+/− mouse models, the median survival of wtIDH1 mice is 42 days while the median survival of muIDH1 mice is 56 days (Fig. 1B, or data in [15]). And, the percentage of immune cells infiltrated in wtIDH1 mice is about 30% while the percentage of immune cells infiltrated in muIDH1 mice is about 10% when mice die (Fig. 1D and data in [15]). From our experimental measurements, we know that the tumor radius is about 5 mm when glioma-bearing mice die. Now, we need to fit that, when a mouse with wtIDH1 tumor dies after its glioma grows about 42 days, the radius of its glioma is about 5 millimeters, and its glioma has about 30% infiltrated immune cells; when a mouse with muIDH1 tumor dies after its glioma grows about 56 days, the radius of its glioma is about 5 mm, and its glioma has about 10% infiltrated immune cells. We fix all parameter values as obtained from the literature except the maximum rate of the chemoattractant production m. This parameter reflects the strength of the chemotactic gradient generated by glioma cells. To fit the data that a mouse with wtIDH1 tumor dies at 42 days old of its glioma when the radius of its glioma is about 5 mm and a mouse with muIDH1 tumor dies at 56 days old of its glioma when the radius of its glioma is about 5 millimeters, we choose $m_1=5.5$ and $m_2=1.5$ respectively. Fig. 1A shows our numerical fitting. Although it is not exact fitting, we consider this is a good fit in the following sense. Once we choose $m_1$ and $m_2$ for wtIDH1 and muIDH1 respectively, our mathematical model predicts that a mouse with wtIDH1 tumor has about 34% infiltrated immune cells when it dies and a mouse with muIDH1 tumor has about 10% infiltrated immune cells when it dies. Fig. 1C and Fig. 1D show our numerical simulations. Therefore, our mathematical model can distinguish wtIDH1 and muIDH1 by different maximum values of the chemoattractant production rate m.

Fig. 1.

(A) Numerical fitting: if $m_1=5.5$ and $m_2=1.5$ are assigned to wtIDH1 and muIDH1 tumors respectively, our mathematical model shows wtIDH1 and muIDH1 tumor mice die at 42.3 days and 54.2 days respectively, when their tumor grow to the volume of radius 5 millimeters. (B) Experimental data: we have 12 wtIDH1 tumor mice and their median survival is 42 days, 20 muIDH1 tumor mice and their median survival is 56 days. (C) For chosen m values, percentage profiles of infiltrated immune cells produced by our mathematical model. (D) Comparison of immune cell percentages when glioma-bearing mice die between experimental data and numerical results produced by our mathematical model, noticing we lumped macrophages, monocytes, PNMs, etc. together.

Growth dynamics

Our mathematical model can describe the details of the tumor growth dynamics. When the tumor starts, the glioma cell population increases exponentially. The chemoattractants secreted by tumor cells nonlinearly increase. They diffuse within the mouse body and form a dynamic chemotactic gradient field quickly. Then immune cells migrate into the tumor along the chemotactic gradient field. The immune cell population within the tumor, however, approximately follows a linear growth pattern. Fig. 2A demonstrates each cell population within the tumor in the first 10 days.

Fig. 2.

Infiltrating dynamics of immune cells into the tumor. (A) Profiles of each cell population in the first 10 days of both types of tumors. (B) Profiles of each cell population within both types of tumors after initial growth. (C) Numerical results about the net rate of increase of immune cell infiltrating into gliomas. (D) Numerical results about the net rate of increase of glioma cells.

As the tumor volume increases, our mathematical model shows distinct growth patterns for wtIDH1 and muIDH1 tumors. For both tumors, the growth of glioma cell population remains the same. That is, the total number (mass) of glioma cells is the same for wtIDH1 and muIDH1 tumors at any moment after 10 days. For necrotic cells in both wtIDH1 and muIDH1 tumors, their total numbers are also the same at each moment after 10 days. However, the total number of infiltrated immune cells into wtIDH1 tumor is much greater (almost twice more) than that into muIDH1 tumor at each moment after 10 days. Fig. 2B shows the growth curves for each population in both types of tumors. This reveals how wtIDH1 tumor reaches the death volume, the tumor sphere with radius 5 mm, earlier than muIDH1 tumor does.

It is better to compare the net rate of change (increasing) of immune cells infiltrated in wtIDH1 and in muIDH1 tumors. At each time point, immune cells enter into the tumor via chemotaxis, and some of infiltrated immune cells are cleared by natural degradation process. The difference is the net increasing immune cells. The rate of this net increasing immune cells is an important indicator of immune cell infiltration. Fig. 2C shows our numerical analysis of the net rate of increase in wtIDH1 tumor and muIDH1 tumor. Although an explicit relation between the net rate of increase of immune cells infiltrated in wtIDH1 tumors and that of muIDHI1 tumors is beyond reach analytically, we find clues by numerical experiments. On the one hand, the net rate of increase of infiltrated immune cells into tumors is approximately proportional to the 4/5 power of the chemoattractant production rate m after tumor initial growth, and it is an increasing function of time. On the other hand, we also notice that the percentage of infiltrated immune cells in tumor is a decreasing function of time, showed in Fig. 1C. Putting these numerical results together, as tumor volume increases in both types of gliomas in time, the net rate of increase of infiltrated immune cells increases while the percentage of immune cells infiltrated into the tumor is decreasing.

If we compare the net rate of increase of glioma cells in wtIDH1 and in muIDH1 tumors, we numerically found that they are the same as showed in Fig. 2D.

Predictions

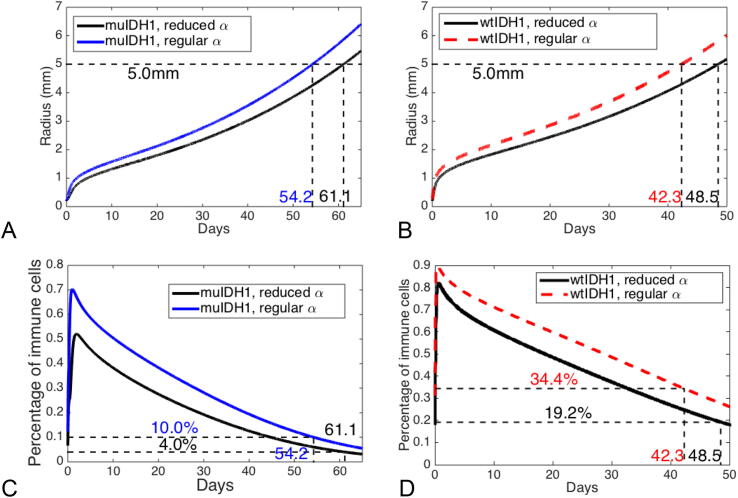
One of our hypotheses is that the high immune cells, particularly, neutrophil, infiltration in wtIDH1 gliomas may stimulate tumor aggressiveness, and that blocking neutrophil migration to wtIDH1 tumor may lengthen survival. Our experimental data shows that the wtIDH1 mice treated with Ly6G-1A8 survived longer than isotype-2A3-treated wtIDH1 tumor-bearing mice (See data in Fig. 3B or in [15]). To study this hypothesis using our mathematical model, we block immune migration by reducing chemotactic strength which is represented by the chemotactic coefficient α. If we reduce α to one fourth of its estimated value, our model predicts that wtIDH1 tumor-bearing mice will survive two weeks longer than wtIDH1 tumor-bearing mice without blocking immune cell migration, which matches our experimental data in Fig. 3B. Our mathematical model also shows that the percentage of infiltrated immune cells into the tumor decreases by 25% when Ly6G-1A8 mice die, and the net rate of increase of infiltrated immune cells also decrease significantly. Fig. 3 shows those results.

Fig. 3.

Immune cell blockage hypothesis in wtIDH1 glioma: immune cells are blocked by reducing the chemotactic coefficient to one fourth of its estimated value in wtIDH1 tumors. (A) Numerical results about wtIDH1 tumor mice with and without immune blocked, ones with immune blocked have two-week longer survival. (B) Experimental data: 15 wtIDH1 tumor mice with Ly6G blocking antibody have a median survival of 55 days, while18 wtIDH1 tumor mice have a median survival of 42 days. (C) Numerical results about the net rate of increase of immune cell infiltrating into gliomas. D: Percentage profiles of immune cells: the infiltrated immune cells decreases 25% when tumor mice die.

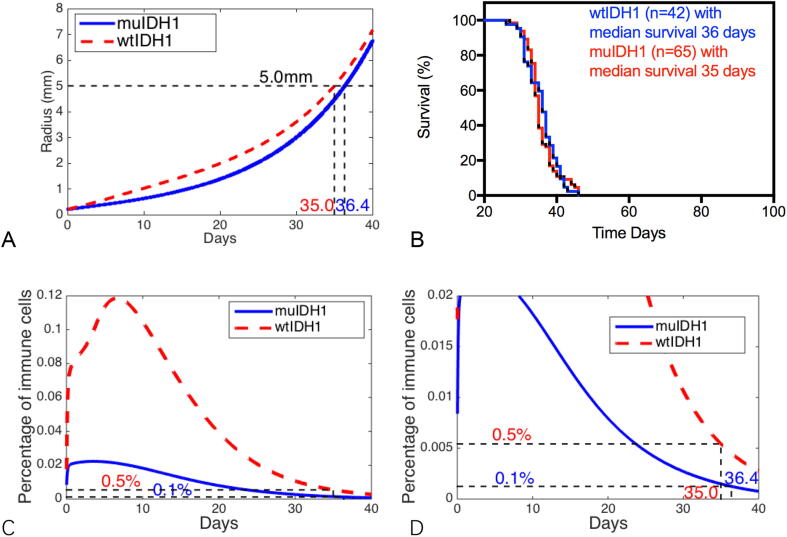
As our mathematical model setup, the aggressiveness of tumors can be characterized by the proliferation rate of glioma cells λ, the glioma cell lysis rate μ, and chemotactic coefficient α. Our experimental results show that the tumors that formed in the Ink4a/Arf^−/− background did not show any difference in median survival between the wtIDH1 and muIDH1 group (see data in Fig. 4B or in [15]). It is presumably due to the aggressiveness of the tumors in this background. If we double the proliferation rate λ of glioma cells, increase tumor cell lysis rate by one third, and take the chemotactic coefficient to be one thirtieth of its estimated value, our mathematical model predicts that there is only one day difference in survival between wtIDH1 tumors and muIDH1 tumors, 35 days and 36 days as in our experimental results. However, when both wtIDH1 and muIDH1 mice die, the percentages of infiltrated immune cells in the tumor are very low, about 0.5% and 0.1% respectively. Fig. 4 shows our computational predictions of tumor mice survivals.

Fig. 4.

Aggressive tumor growth: tumors with doubling the proliferation rate λ, increasing tumor cell lysis rate by one third, and reducing the chemotactic coefficient to be one thirtieth of its estimated value are considered to be aggressive gliomas. (A) Numerical results show that there is only one day difference in survivals for wtIDH1 and muIDH1 aggressive tumors. (B) Experimental data for tumor mice in Ink4a/Arf^−/− background: 42 wtIDH1 tumor mice have a median survival of 36 days while 65 muIDH1 tumor mice have a median survival of 35 days. (C) Mathematical model prediction for profiles of infiltrated immune cells. (D) Truncations of infiltrated immune cell percentages, 0.5% and 0.1% for wtIDH1 tumor and muIDH1 tumor, respectively, when mice die.

In our experiments, there are three different chemoattractants, CCL-2, CXC-2, and C5 (see data in Fig. 6 in [15]). These chemoattractants may have different effects on different types of immune cells. Although our mathematical model does not distinguish these chemoattractants and immune cells, we still can simulate our mathematical model by choosing different chemotactic coefficient α which may be interpreted as different chemoattractants. For a mouse with wtIDH1 glioma, if we reduce the chemotactic coefficient to half of its estimated value, we obtain one more week longer survival. For a mouse with muIDH1 glioma, if we reduce the chemotactic coefficient to half of its estimated value, we also obtain one more week longer survival. However, the reductions of infiltrated immune cells are quite different. For muIDH1 mice, the percentage of infiltrated immune cells is decreased by 6% when mice die, while for wtIDH1 mice, the percentage of infiltrated immune cells is decreased by 25%. Fig. 5 shows these results.

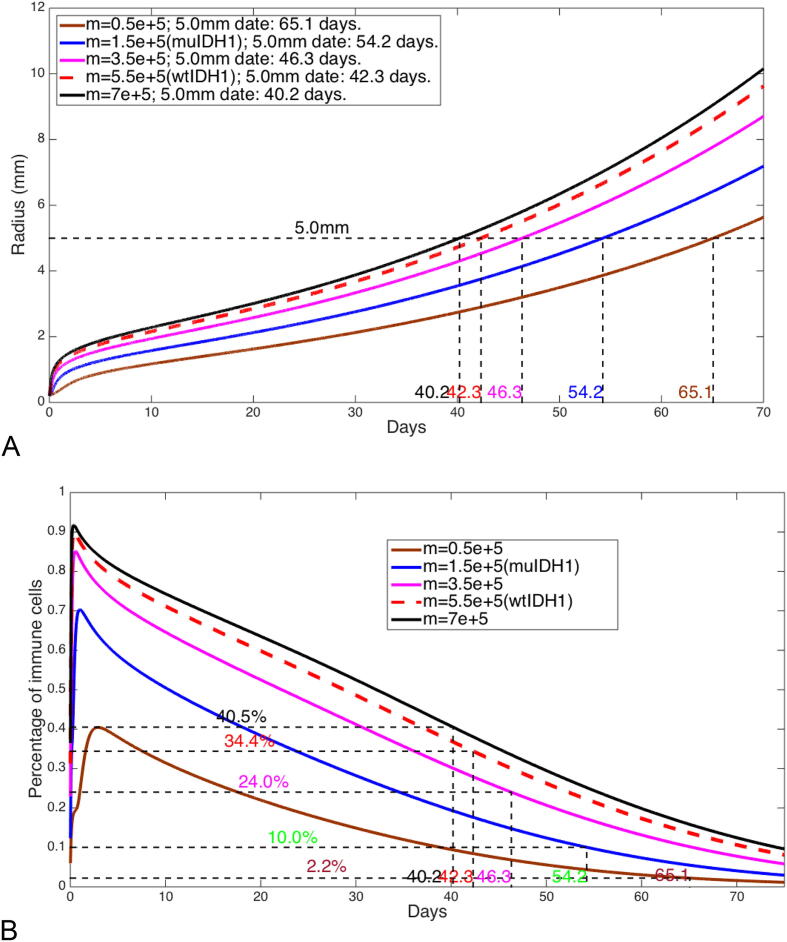
Fig. 6.

(A) Tumor radius growth for different chemoattractant production rates. (B) Profiles of immune cell percentages for different chemoattractant production rates.

Fig. 5.

Tumor growth with two different chemotactic coefficients, one is estimated value, and the other is half of the estimated value. (A) Comparison of growth curves for muIDH1 tumors correspond to two chemotactic coefficients. (B) Comparison of growth curves for wtIDH1 tumors correspond two chemotactic coefficients. (C) Profiles of infiltrated immune cells for muIDH1 tumors correspond two chemotactic coefficients. (D) Profiles of infiltrated immune cells for wtIDH1 tumors correspond two chemotactic coefficients.

Discussion

From the numerical analysis of our mathematical model, the chemoattractant production rate and chemotactic coefficient play important roles in the infiltrating dynamics of immune cells into the tumor. The chemoattractant production rate determines the strength of the chemotaxis gradient field, and the chemotactic coefficient determines the possibility of immune cell migration. From Fig. 5, we see how the chemotaxis coefficient affects both wtIDH1 tumor and muIDH1 tumor. That is, if the chemotaxis coefficient is decreasing, the possibility of immune cell migration into the tumor is decreasing, therefore, both types of tumor mice gain a longer survival.

In our experiments with wtIDH1 gliomas and muIDH1 gliomas, we observed that a significant decrease in infiltrated immune cells into muIDH1 gliomas is due to some reduction of chemoattractants and chemotaxis (see data in Fig. 6 in [15]), and concluded that mutant IDH1 has a regulatory role in infiltration of immune cells into tumors. It is known that from wtIDH1 to muIDH1 is a gain-of-function mutation, as in our mathematical model, there are two different values of the chemoattractant production rate that correspond to wtIDH1 tumors and muIDH1 tumors respectively. However, in our mathematical analysis, we can vary the chemoattractant production rate continuously to obtain a complete picture about how infiltrated immune cells are regulated by the chemoattractant production rate of tumor cells. Fig. 6 shows several cases where the chemoattractant production rate assumes different values. From these computational results, we can conclude that if the chemoattractant production rate increases, the percentage of infiltrated immune cells into the tumor increases, and the mice survival decreases.

In order to fit the data about the tumors that formed in the Ink4a/Arf^−/− background, the aggressiveness of gliomas in our mathematical model is defined by doubling the proliferation rate λ of glioma cells, increasing tumor cell lysis rate by one third, and reducing the chemotactic coefficient to be one thirtieth of its estimated value. Our mathematical model predicts that such a tumor grows very fast no matter which type of glioma, wtIDH1 or muIDH1, and reaches death volume at 35 or 36 days. However, our mathematical model also predicts that the percentage of infiltrated immune cells in tumor are very low. This may imply that in such an aggressiveness background, glioma growth majorly depends on the process of tumor cell proliferation, and the infiltration process of immune cells has little effects on glioma growth.

One feature of our computational results is that the percentage of immune cells infiltrated in the tumor is decreasing in time although the total number of immune cells infiltrated in tumor is increasing in time for both wtIDH1 and muIDH1 gliomas. We may explain this phenomenon as follows. In the early stage of the tumor, glioma cells secrete chemoattractants that form a dynamic gradient field to facilitate migration of immune cells into the tumor, and a relatively greater portion of immune cells is accumulated comparing with the portion of glioma cells in the tumor. The infiltrated immune cells help tumor growth not only in increasing tumor volume but also in increasing production of chemoattractants since glioma percentage (and density) is low. This is the reason why we see the percentage of infiltrated immune cells increases first, and reaches a peak as the chemoattractant production rate approaches its maximum. When the chemoattractant production rate approaches its maximum, the chemotactic gradient field may reach a steady state, and consequently immune cell migration undergoes a slowdown phase comparing with proliferation process of glioma cells. Therefore, the percentage of infiltrated immune cells decreases, although the total number or net rate of increase of infiltrated immune cells keeps increasing.

As all mathematical models, some simplifications must be made. In the study, our mathematical model considers gliomas to be spherical and includes three types of cells. However, these simplifications have little effects on immune cell infiltrating dynamics. The spherical geometry is convenient for determining the tumor boundary in space and time. Our interest is immune cell infiltration dynamics, it is suitable to include several cell populations as in our experiments we measured several relevant cell populations, and so we can compare our computational results and experimental data. As all mathematical models in terms of differential equations, the sensitivity of the solutions to parameters should be considered when the models make any predictions. Our numerical experiments with different parameter values around their estimates show that the numerical results are not sensitive in the sense of dramatic changes of solution behaviors.

The insights from our mathematical modeling could potentially be of utility in clinical research and practice. Classifying gliomas needs a set of criteria. Our mathematical model uses the chemoattractant production rate of glioma cells to distinguish wtIDH1 and muIDH1 gliomas. This offers a possibility to classify these two types of gliomas by comparing their chemoattractant production rates in clinical. From our modeling study, there are several ways to increase the survival time of glioma-bearing mice. For instance, if the percentage of immune cells or the number of immune cells infiltrated in gliomas are reduced, the survival time of glioma-bearing mice will increase. For this purpose, our modeling tells that we need to reduce the chemoattractant production rate, or the chemotactic coefficient, or both of these two parameter values. This observation could inspire new genetic methods that are designed to reduce these two parameter values, in order to prolong the survival time in clinical. In addition, chemotherapy may be designed to weaken the chemoattractant gradient field in order to reduce migration ability of immune cells into the tumor. An inspired experiment was done in [30]. It also can be expected that our mathematical model is able to incorporate tumor therapies, radiation, chemotherapy, and virotherapy, to study treatment optimal outcomes for these two types of gliomas. We will pursue it in the future study.

Conclusions

In this study, we develop and analyze a mathematical model for the infiltrating dynamics of immune cells into tumors. We find the infiltrating dynamics of immune cells into tumors is largely determined by tumor cell chemoattractant production rate and chemotactic coefficient. Using different values of the chemoattractant production rate, we can characterize wtIDH1 gliomas and muIDH1 gliomas. Our mathematical model shows that muIDH1 mice have more survival time because they recruit for less immune cells while they have the same amount of tumor cells as wtIDH1 mice do when they die. For more aggressive gliomas, our mathematical model predicts there is little difference in their survival between wtIDH1 mice and muIDH1 mice and both have very low infiltrated immune cells. Our numerical computations show that if we reduce the chemoattractant production rate and the chemotactic coefficient, tumor mice will have a longer survival. All our model predictions are verified by our experimental data. It may be concluded that the chemoattractant gradient field produced by tumor cells facilitate immune cells migration to the tumor cite. The chemoattractant production rate may be utilized to distinguish wtIDH1 and muIDH1 tumors.

Consent for publication

All authors have read the manuscript and approved for publication.

Competing Interests statement

All authors declares that they have no competing financial, or non-financial interests that might have influenced the performance or presentation of the work described in this manuscript.

Funding

National Institutes of Health grants U54CA132381, U01-CA60882, R01 CA195718, and U54CA193461 (to ECH), U54CA132383 and National Science Foundation of US (DMS-1446139) (to JPT).

Authorship contribution statement

BN estimated parameter values and performed computation, XZ developed numerical algorithm and performed computation, TAP analyzed mathematical model. FS managed experimental data, SH provided suggestion for parameter estimation, JPT constructed mathematical model and wrote manuscript, ECH leaded experiments and completed the manuscript.

Appendix A.

Consider a radially symmetrical tumor and denote by r the distance from a point to the center of the tumor. We denote the boundary of the tumor by $r=R\left(t\right)$. Set

• G(r,t) = the number density of glioma cells

• H(r,t) = the number density of necrotic cells

• N(r,t) = the number density of infiltrated immune cells

• A(r,t) = the concentration of chemoattractants

The proliferation and removal of cells cause a movement of cells within the tumor, with a convection term, for tumor cell G, in the form $\frac{1}{r^2}\frac{\partial }{\partial r}\left(r^{2}G\left(r,t\right)V\left(r,t\right)\right)$, where $V\left(r,t\right)$ is the radial velocity, $V\left(0,t\right)=0$. The necrotic cells undergo the same convection. Tumor cells produce chemoattractants. The chemoattractants diffuse within the mouse body and form the gradient field $\frac{\partial A\left(r,t\right)}{\partial r}$. The immune cells move along the chemoattractant gradient field into the tumor, and then undergo the same convection besides chemotaxis within the tumor. By mass conservation laws, based on previous models in [21], [33], [34], we deduce the following equations for r > R(t):

$$\frac{\partial G\left(r,t\right)}{\partial t}+\frac{1}{r^2}\frac{\partial }{\partial r}\left[r^{2}G\left(r,t\right)V\left(r,t\right)\right]=\lambda G\left(r,t\right)-\mu G\left(r,t\right),r\in \left[0,R\left(t\right)\right)$$

$$\frac{\partial H\left(r,t\right)}{\partial t}+\frac{1}{r^2}\frac{\partial }{\partial r}\left[r^{2}H\left(r,t\right)V\left(r,t\right)\right]=\mu G\left(r,t\right)-\delta H\left(r,t\right),r\in \left[0,R\left(t\right)\right)$$

$$\frac{\partial A\left(r,t\right)}{\partial t}=D\frac{1}{r^2}\frac{\partial }{\partial r}\left[r^2\frac{\partial A\left(r,t\right)}{\partial r}\right]+\frac{\chi mG\left(r,t\right)}{\beta +G\left(r,t\right)}-\gamma A\left(r,t\right),r\in \left[0,\infty \right)$$

$$\frac{\partial N\left(r,t\right)}{\partial t}+\frac{1}{r^2}\frac{\partial }{\partial r}\left[r^{2}N\left(r,t\right)V\left(r,t\right)\right]=-\alpha \frac{1}{r^2}\frac{\partial }{\partial r}\left[r^{2}N\left(r,t\right)\frac{\partial A\left(r,t\right)}{\partial r}\right]-\rho N\left(r,t\right),r\in \left[0,R\left(t\right)\right),$$

where χ is an indicator that takes value 1 when 0 ≤ r < R(t), and 0 otherwise.

We assume that all cells have the same size. Since the number density of the tumor tissue is constant, we have G(r,t) + H(r,t) + N(r,t) = θ within the tumor. Then, combining above equations, we have the equation for the velocity,

$$\frac{\theta }{r^2}\frac{\partial }{\partial r}\left[r^{2}V\left(r,t\right)\right]=\lambda G\left(r,t\right)-\delta H\left(r,t\right)-\alpha \frac{1}{r^2}\frac{\partial }{\partial r}\left[r^{2}N\left(r,t\right)\frac{\partial A\left(r,t\right)}{\partial r}\right]-\rho N\left(r,t\right).$$

The free boundary condition is given by $\frac{dR\left(t\right)}{\mathit{dt}}=V\left(R\left(t\right),t\right)$.

The initial conditions are specified as R(0) = ε, where ε is a very small number; G(r,0), H(r,0), N(r,0), for 0 < r < ε; and A(r,0), for 0 < r < ∞. The boundary conditions for the chemoattractant concentration A(r, t) are specified as $\frac{\partial A}{\partial r}\left(0,t\right)=0$ and A(r,t) vanishes at the infinite, and V(0,t) = 0 for t ≥ 0.

Appendix B. Supplementary data

The following are the Supplementary data to this article: